Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Towards a quantitative description of excitonic couplings in photosynthetic pigment–protein complexes: quantum chemistry driven multiscale approaches†
Christian
Friedl
a,
Dmitri G.
Fedorov
 *b and
Thomas
Renger
*b and
Thomas
Renger
 *a
*a
aInstitut für Theoretische Physik, Johannes Kepler Universität Linz, Altenberger Str. 69, 4040 Linz, Austria. E-mail: thomas.renger@jku.at
bResearch Center for Computational Design of Advanced Functional Materials (CD-FMat), National Institute of Advanced Industrial Science and Technology (AIST), Central 2, Umezono 1-1-1, Tsukuba, 305-8568, Japan. E-mail: d.g.fedorov@aist.go.jp
First published on 3rd January 2022
Abstract
A structure-based quantitative calculation of excitonic couplings between photosynthetic pigments has to describe the dynamical polarization of the protein/solvent environment of the pigments, giving rise to reaction field and screening effects. Here, this challenging problem is approached by combining the fragment molecular orbital (FMO) method with the polarizable continuum model (PCM). The method is applied to compute excitonic couplings between chlorophyll a (Chl a) pigments of the water-soluble chlorophyll-binding protein (WSCP). By calibrating the vacuum dipole strength of the 0–0 transition of the Chl a chromophores according to experimental data, an excellent agreement between calculated and experimental linear absorption and circular dichroism spectra of WSCP is obtained. The effect of the mutual polarization of the pigment ground states is calculated to be very small. The simple Poisson-Transition-charge-from-Electrostatic-potential (Poisson-TrEsp) method is found to accurately describe the screening part of the excitonic coupling, obtained with FMO/PCM. Taking into account that the reaction field effects of the latter method can be described by a scalar constant leads to an improvement of Poisson-TrEsp that is expected to provide the basis for simple and realistic calculations of optical spectra and energy transfer in photosynthetic light-harvesting complexes. In addition, we present an expression for the estimation of Huang–Rhys factors of high-frequency pigment vibrations from experimental fluorescence line-narrowing spectra that takes into account the redistribution of oscillator strength by the interpigment excitonic coupling. Application to WSCP results in corrected Huang–Rhys factors that are less than one third of the original values obtained by the standard electronic two-state analysis that neglects the above redistribution. These factors are important for the estimation of the dipole strength of the 0–0 transition of the chromophores and for the development of calculation schemes for the spectral density of the exciton-vibrational coupling.
1. Introduction
Charge and energy transfer in materials is a broad field of research, including the transfer of excitation energy in systems with multiple chromophores.1 Förster resonance energy transfer (FRET)2 and related transfer mechanisms3,4 are very important phenomena in spectroscopy for measuring distances in fluorescent-labeled biomolecules,5,6 as well as for light harvesting in nano particles7 including organic solar cells8 and in photosynthesis with chlorophylls, carotenoids and related molecules serving as chromophores.3,9For a molecular system composed of multiple chromophores, one can calculate excited states, e.g., using multireference configuration interaction (MRCI)10 or time-dependent density functional theory (TDDFT).11 However, the cost of such calculations scales steeply with the system size. An alternative to this brute force approach is to compute individual chromophores at a high level and the interactions between them using a simplified model.12,13 Chromophores can be treated as fragments in fragment-based approaches,14–22 for some of which the excitonic coupling23,24 and delocalized excitations25 can be calculated. The excitonic couplings are responsible for energy transfer, and the delocalization of excited states results in a shift of optical transition energies and a redistribution of oscillator strength measured in optical spectroscopy on molecular aggregates.
The fragment molecular orbital method (FMO)26–29 at the TDDFT level30,31 has been interfaced with FRET in vacuum.32 Alternatively, there is an FMO method based on CI with single excitations, for computing excitonic couplings33–35 in vacuum, and a Green's function approach.36 In this work, FMO-based TDDFT and Hartree–Fock and configuration interaction with singles (HF/CIS) are combined with FRET and the polarizable continuum model (PCM)37 so that effects of the protein/solvent environment on the excitonic couplings38,39 can be studied. PCM has been applied to the calculation of excitonic couplings.38–40 In PCM calculations the polarization of the electronic ground state of the chromophores by the environment is taken into account by using a continuum description of the latter. In the present application, in addition, the mutual polarization of electronic ground states of all chromophores is studied, and we investigate how the regular PCM approach can be calibrated and used to improve other methods.
The excitonic couplings obtained with the quantum-mechanical (QM) FMO/PCM method in protein/solvent environment, developed in this work, are compared to two simpler models: the point-dipole approximation (PDA) and the Poisson-Transition-charges-from-Electrostatic-potential (Poisson-TrEsp) method.41–43 It is shown how screening and reaction field effects caused by the dynamical polarization of the protein/solvent environment influence the effective transition dipole moment of the chromophores and their excitonic couplings. While the Poisson-TrEsp method only takes into account the screening of the Coulomb coupling between non-polarizable transition densities of the chromophores, the present FMO/PCM method includes the polarization of the pigments by the reaction field of the protein/solvent environment in a self-consistent way. One aim of the present work is to find out whether this polarization effect leads to qualitative changes of the transition density of the chromophores. Our working hypothesis is that there are no strong qualitative changes and that the polarization effect, together with a correction for limitations of the quantum chemical methods, can be included in a simple calibration factor in an improved Poisson-TrEsp method.
The different methods for the calculation of the excitonic coupling are applied in the calculation of linear absorption and circular dichroism spectra of the water-soluble chlorophyll-binding protein (WSCP). The tetrameric WSCP binds 4 chlorophyll a (Chl a) molecules, which are arranged in two dimers with weak inter-dimer and strong intra-dimer excitonic couplings. The phytyl chains of the pigments form a hydrophobic knot in the center of the complex, which keeps the tetramer together (Fig. 1). Due to weak inter-dimer couplings, the optical spectra of WSCP are determined by the excitonic dimers. The transition dipole moments of the two Chl a pigments in each dimer are arranged in an ‘open sandwich’ geometry. This geometry leads to a large oscillator strength of the upper exciton state and a small oscillator strength of the lower exciton state of the dimer.44,45
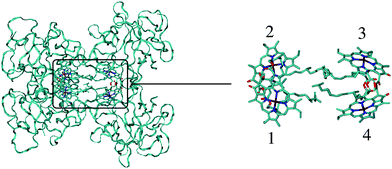 | ||
| Fig. 1 Structure of the WSCP complex from Lepidium virginicum.87 The left part shows the whole pigment–protein complex with the protein in ribbon style and the right part contains an enlarged view on the four central Chl a pigments. The whole complex has an approximate 222 symmetry that is disrupted only by the outer loop of the protein tetramer and the phytyl tails of the Chls forming a hydrophobic knot in the center of the complex.87 | ||
WSCP is not involved in photosynthetic light-harvesting. It is built up in plants when they experience drought, heat or salt stress.46 The exact functional role of WSCP has not been discovered yet.47 Due to its relatively simple structure, WSCP has been an important model system for the study of fundamental pigment–pigment and pigment–protein interactions.48–59 Because of the approximate D2 symmetry (Fig. 1), all four Chl a pigments have an equal average local excitation energy (site energy), and the excitonic coupling determines the splitting between exciton states that is seen in the spectra. Based on experimentally determined satellite holes in hole-burning spectra of Chl a – WSCP, an excitonic coupling of 100 cm−1 has been estimated in the dimers,50 that has been refined to 83 cm−1 from a fit of linear absorption and circular dichroism spectra.59 With this coupling, quantitative agreement with hole-burning data50 was obtained.59
WSCP is a rare example of a pigment–protein complex, where a direct experimental estimate of the excitonic coupling between 0–0 transitions of two strongly coupled Chl a chromophores is possible. There are four reasons that make WSCP a unique system for such an estimate and the development of new methods. (1) Due to its approximate D2 symmetric structure, the site energies of the Chl a chromophores are identical, as noted above. Hence, the splitting between optical lines is only determined by the excitonic coupling. (2) The chromophores are far enough apart such that electron exchange interaction can be neglected, greatly simplifying the theoretical analysis. (3) The high-energy exciton transition carries the major part of the oscillator strength of the 0–0 transitions of the chromophores in the dimers. This exciton transition can have a certain overlap with the vibrational sideband of the low-energy exciton transition. Therefore, a strong high-energy exciton transition is easier to identify in the spectrum. (4) The Franck–Condon factors involving excitations of the high-frequency intramolecular vibrational modes of Chl a are sufficiently small, so that this part of the vibronic coupling can be simply included by rescaling the excitonic coupling between the 0–0 transitions of the chromophores. Property (3) is consistent with the fact that WSCP is not a light-harvesting protein. A strong low-energy exciton transition would have advantages for energy transfer.
From hybrid quantum mechanics/molecular calculations that include a heterogeneous polarizability of the protein environment (QM/MMPol) with an induced dipole model, an excitonic coupling of 186 cm−1 was reported.52 At first glance, this coupling seems to overestimate the experimental value by more than a factor of two. Several reasons for this discrepancy, like an overestimation of the transition dipole moments by the quantum chemical method, were discussed.52 In order to relate this dipole strength to the experiment, the authors considered an analysis of the experimental dipole strength in different solvents by Knox,60 using a Lorentz local field factor and came to the conclusion that the excitonic coupling calibrated on these grounds would be too small (38 cm−1). Hence, up to now, there is no ab initio based explanation of the excitonic coupling value in the Chl a dimers of WSCP inferred from the fit of optical experiments. In the present work, we explain this value.
2. Methodology
2.1 Excitonic couplings from transition density
The basic approach to computing the important long-range part of excitonic couplings between chromophores is to calculate an excited state of interest in each chromophore and a transition density for an electronic excitation from the ground state to the excited state.32 The excitonic couplings are obtained from the Coulomb interaction between the transition densities of the chromophores. Other properties derived from the transition density are the transition dipole moment and the atomic transition charges. In contrast to the electron density of an electronic state, that has a very complex shape describing the electron distribution between atoms driven by their electronegativity, the transition density often has a simpler dipolar form. FMO provides a convenient framework for dealing with chromophores as fragments (one can also include non-chromophore fragments). By virtue of the availability of a covalent fragment boundary treatment the present formulation can be applied to bio61 and nano62 materials. To simplify the description, the following discussion assumes that chromophores are not split into multiple fragments.The methodology for calculations in vacuum was developed earlier.32 In this work, the focus is on incorporating a PCM description of the protein/solvent environment of the pigments. We calculate chromophores with TDDFT, and the interaction of the chromophores with the protein/solvent environment is described in the framework of PCM. PCM is used to model the protein environment in the same way as the solvent. For excitonic couplings, the major contribution comes from the optical dielectric constant of the environment, which is very similar for proteins and aqueous solvents. Hence, the environment can be described by a homogeneous dielectric continuum surrounding the optically active pigments.
In FMO/PCM,63 a cavity is constructed around the whole molecular system containing all chromophores, and each fragment calculation is performed in this total cavity. On the cavity surface, divided into NTS small pieces, called tesserae, point charges are placed, which represent the effect of the polarization of the environment by the chromophore. These charges are determined self-consistently with respect to the electronic ground state of the chromophore (that is, taking into account the mutual polarization of the environment and the chromophore). For this treatment, the response of the protein/solvent environment should be in equilibrium. This response is determined by the static dielectric constant εs, which is much smaller for the protein than for the aqueous solvent. Because chromophores are surrounded by the protein, we use only the protein dielectric constants to describe the environment of the chromophores, indicated by the term “protein/solvent environment”. Note that the excitonic couplings for the present system essentially do not depend on εs, as shown below.
Typically, the fragments in FMO are calculated in an embedding potential generated by the other fragments, except that the lowest order of FMO, denoted as FMO0, uses no embedding. In this work, FMO0, previously introduced in vacuum,64 is extended to include a homogeneous dielectric. This dielectric is described by a static dielectric constant εs and an optical dielectric constant ε = n2 (n is the refractive index). Whereas εs is used in the calculation of the electronic ground state density, ε is used for the electronic transition density, reflecting the fact that the slow part of the dielectric environment has no time to react during an electronic transition. In the calculations we only distinguish two regions, the cavity of the chromophores (with ε = εs = 1) and the environment (with ε = 2 and εs = 4) that includes both the protein and the solvent.
The inclusion or neglect of the polarization of one chromophore by all others is indicated by n in FMOn (FMO1: included, FMO0 neglected). In FMO-based PCM, the whole molecular cavity is constructed and used in each fragment calculation. In PCM[0], the solvent charges are induced by each fragment separately. In PCM[1], the solvent charges are induced by all fragments together. FMO0 can be combined with both PCM schemes, but FMO1 can only be used with PCM[1]. There exist also higher order embedding schemes, e.g., FMO2,65 which can include explicit higher many-body TDDFT corrections for a single chromophore. However, FMO2-TDDFT is difficult to apply to multiple chromophores,66 so FMO2 is not used in the present work.
The coupling matrix element between two excited states of the complex that are localized on chromophores (fragments) M and N is given as a sum of three contributions67
| VMN = VESMN + VXCMN + VCTMN, | (1) |
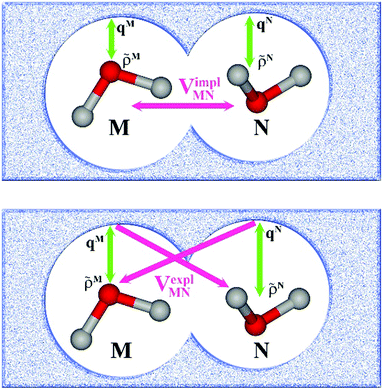
In an environment described by the PCM,38–40 the electrostatic coupling VESMN between the transition densities of the pigments contains implicit and explicit environmental contributions, VESMN = VimplMN + VexplMN (Fig. 2). The implicit (impl) contribution VimplMN describes the effect of the dynamic polarization of the transition density of the chromophores by the reaction field of the environment. The explicit (expl) environmental contribution VexplMN contains the screening effects. It is the electrostatic interaction between the transition density of one pigment with the dynamic polarization of the protein/solvent environment (represented by surface charges) induced by the transition density of another pigment, very much like the typical solute–solvent screening.68,69
The transition densities of the two chromophores that enter VimplMN and VexplMN are determined by quantum chemical calculations on the chromophore monomers embedded in a dielectric continuum representing the protein/solvent environment. Due to mutual dynamic polarization of the chromophore and the environment, the transition dipole moment of the chromophore is enhanced. A calculation scheme for the electrostatic coupling in vacuum VESMN(ε = 1) between transition densities of the chromophores in the framework of the FMO methodology was developed before.32 It can be used to obtain the implicit contribution VimplMN by replacing the vacuum transition densities of the solutes by the transition densities obtained in the protein/solvent environment, described by PCM.
The explicit protein/solvent contribution VexplMN, arising from the coupling of the dynamic protein/solvent polarization, induced by the transition density of one chromophore with the transition density of the other chromophore, is obtained by perturbation theory in the sense that the dynamic protein/solvent polarization on one chromophore is not affected by the coupling to the transition density of the other chromophore. The explicit term can be computed as
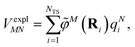 | (2) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) M(r) of chromophore M, an interaction that is described by the ESP
M(r) of chromophore M, an interaction that is described by the ESP ![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) M(r = Ri) of chromophore M acting at the position Ri, where
M(r = Ri) of chromophore M acting at the position Ri, where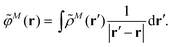 | (3) |
The electrostatic interaction VexplMN in eqn (2) should be symmetric with respect to the chromophore indices M and N, VexplMN = VexplNM. In order to avoid a violation of this symmetry by the numerical artifacts in PCM, we enforce the symmetry by using the following expression
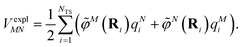 | (4) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) M is used in eqn (3), and there is no nuclear contribution to
M is used in eqn (3), and there is no nuclear contribution to ![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) M(r).
M(r).
The components a of the transition dipole moment of a chromophore M for a = x, y or z can be evaluated as
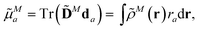 | (5) |
![[D with combining tilde]](https://www.rsc.org/images/entities/b_char_0044_0303.gif) N is the transition density matrix for chromophore M. Both matrices are in the atomic orbital basis.
N is the transition density matrix for chromophore M. Both matrices are in the atomic orbital basis.
An alternative description of the explicit protein contribution VexplMN in eqn (2) is given by
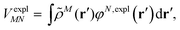 | (6) |
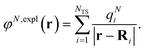 | (7) |
The surface charges qNi that represent the dynamic polarization of the protein/solvent environment, induced by the transition density of chromophore N, can be used to define an explicit dipole moment of the dynamic environmental polarization
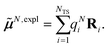 | (8) |
This dipole moment is used below to quantify the screening of the interaction between the transition dipole moments of the chromophores, within the point-dipole approximation (PDA) of the excitonic coupling. While absolute values of couplings strongly depend on the distance between pigments (for interpigment distances, see Table S1, ESI†), the ratios introduced below are much more uniform. The reaction field (rf) factor
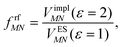 | (9) |
Here, ε = 1 corresponds to vacuum and ε = 2 is the optical dielectric constant of the protein/solvent embedding (more details on the choice of ε are given in Section 3). The screening factor is defined as the ratio between the total electrostatic coupling and the implicit contribution38–40
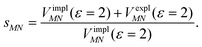 | (10) |
2.2. Excitonic couplings in the point-dipole approximation (PDA)
The implicit contribution to the Coulomb coupling between the transition densities of chromophores (fragments) M and N in the PDA is obtained as32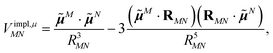 | (11) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) M and
M and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) N of chromophores M and N, respectively, and the vector RMN = RM − RN that connects the centers of the two chromophores. Note that, the dipole moments include the implicit environmental effects via mutual dynamic chromophore-environment polarization.
N of chromophores M and N, respectively, and the vector RMN = RM − RN that connects the centers of the two chromophores. Note that, the dipole moments include the implicit environmental effects via mutual dynamic chromophore-environment polarization.
The explicit protein contribution (screening) in PDA is evaluated as
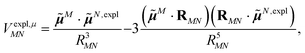 | (12) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) N,expl (eqn (8)) is the dipole moment of the dynamic environmental polarization induced by the transition density of chromophore N.
N,expl (eqn (8)) is the dipole moment of the dynamic environmental polarization induced by the transition density of chromophore N.
Adding eqn (11) and (12), one obtains the total excitonic coupling in PDA as
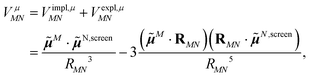 | (13) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) N,screen =
N,screen = ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) N +
N + ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) N,expl contains implicit and explicit contributions of the environment.
N,expl contains implicit and explicit contributions of the environment.
2.3. Excitonic coupling with the Poisson-TrEsp method
In the Poisson-TrEsp method,41–43 atomic transition charges are introduced to approximate the electrostatic potential of the transition density. These transition charges are placed in a molecule-shaped cavity. An important difference to PCM, as discussed above, is the neglect of the polarization of the chromophores by the protein/solvent environment. The transition charges of the chromophores in the original Poisson-TrEsp method are rescaled based on the vacuum transition dipole moment that was extracted by Knox from an analysis of the dipole strength of Chl a in different solvents,60 using an empty spherical cavity model, discussed in more detail in Section 2.4.In Poisson-TrEsp, perturbation theory is used to describe the screening effects. This perturbation theory can be translated into classical electrostatics.43 The Poisson equation is solved for the electrostatic potential ![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) M(r) of pigment M using its atomic transition charges
M(r) of pigment M using its atomic transition charges ![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) Mα obtained from the fit of the ESP of the transition density
Mα obtained from the fit of the ESP of the transition density
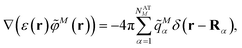 | (14) |
![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) Mα is used to distinguish them from the surface transition charges qNi representing the dynamic polarization of the protein/solvent environment, introduced above (eqn (2)). The excitonic coupling between pigments M and N is obtained as
Mα is used to distinguish them from the surface transition charges qNi representing the dynamic polarization of the protein/solvent environment, introduced above (eqn (2)). The excitonic coupling between pigments M and N is obtained as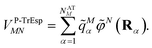 | (15) |
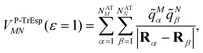 | (16) |
For the Poisson-TrEsp method, we define the screening factor as
 | (17) |
In this work, we want to investigate how this factor relates to the screening factor of PCM (eqn (10)) and how the reaction field effects, neglected in previous publications, can be incorporated in the Poisson-TrEsp method. In a first step, we study the dependence of the dipole strength of the chromophores on the optical dielectric constant ε of the protein/solvent environment, how it is described in the empty spherical cavity model and which role reaction field effects play.
2.4. Dependence of dipole strength of chromophores on the optical dielectric constant ε
In the empty spherical cavity model, the transition density of the chromophore is described by a non-polarizable point-dipole that is located in the center of a spherical cavity, which is surrounded by a homogeneous medium with dielectric constant ε. Inside the cavity we have ε = 1 (vacuum). In such a cavity an external field is enhanced by a factor 3ε/(2ε + 1),72 caused by the polarization effects of the dielectric by the external field. Only the optical dielectric constant is relevant, because the slow part of the polarization cannot follow the oscillations of the light field. Since the intensity for the absorption of light is proportional to the square of the scalar product between the field and the transition dipole moment, the enhanced field inside the cavity can be implicitly treated by an increased dipole strength of the chromophore| D(n) = f(n)D0. | (18) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) 0|2 with the vacuum transition dipole moment
0|2 with the vacuum transition dipole moment ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) 0. Hence, the enhancement cavity field factor f, for such a spherical cavity is (note that ε = n2)
0. Hence, the enhancement cavity field factor f, for such a spherical cavity is (note that ε = n2)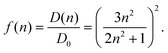 | (19) |
A fit of the experimental dipole strengths with this model (the blue line in Fig. 3) results in a vacuum dipole strength of 21.0 D2.60 However, the real molecular cavity is not spherical, and the transition density of the chromophore can be polarized by the solvent.
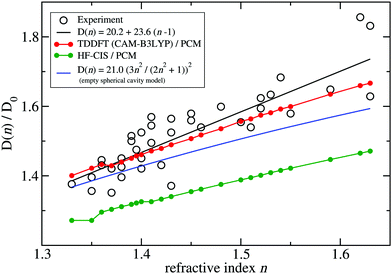 | ||
| Fig. 3 Ratio of the dipole strength D(n) of chlorophyll a for a given refractive index n of the solvent and the vacuum value D0 = D(n = 1). The experimental data60 (open circles) are compared with prediction of the empty spherical cavity model (blue line),60 an empirical linear fit of the data60 (black line) and the ratio of the square of the respective transition dipole moments, obtained with PCM calculations, using either TDDFT with the CAM-B3LYP functional (red line) or HF-CIS (green line) quantum chemical calculations on the 4 Chl a chromophores of WSCP (for contributions of individual Chls see ESI,† Fig. S5–S8 and S9–S12). The D0 value of the experimental data (20.2 D2) has been obtained by a fit of the experimental dipole strength D(n) by the empirical relation, given in the figure legend. | ||
To investigate the latter effect using a realistic shape of the molecular cavity, we study the dependence of the transition dipole moment of Chl a in solution on the optical dielectric constant ε with TDDFT/PCM and HF/CIS/PCM calculations by varying ε. Note that in these calculations also the static dielectric constant εs enters, because the electronic ground state of the chromophore is polarized by the protein/solvent environment, before the optical excitation occurs. However, by doing preliminary calculations, it was found that the dependence on the static dielectric constant is weak (Tables S6–S11, ESI†) and, hence, the same static dielectric constant εs = 4 is used for every data point in Fig. 3. The transition dipole moment of the chromophore is enhanced by the reaction field effects that occur because of the mutual dynamic polarization of the chromophore and the protein/solvent environment. In this case, the enhancement factor of the dipole strength is obtained as
f(n) = |![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) (ε)|2/| (ε)|2/|![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) (ε = 1)|2, (ε = 1)|2, | (20) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) (ε) is the transition dipole moment, calculated for a given optical dielectric constant ε. The different enhancement factors f(n) are compared in Fig. 3 with the experimental data, where for the latter D0 = 20.2 D2 was obtained from the empirical relation60
(ε) is the transition dipole moment, calculated for a given optical dielectric constant ε. The different enhancement factors f(n) are compared in Fig. 3 with the experimental data, where for the latter D0 = 20.2 D2 was obtained from the empirical relation60| D(n) = 20.2 + 23.6(n − 1). | (21) |
TDDFT(CAM-B3LYP)/PCM (red curve, Fig. 3) or HF/CIS/PCM (green curve), properly treat the reaction field effects for a realistic molecular cavity and show qualitative agreement with experiment, in particular for the former, even though the cavity field effect is neglected. The reaction field factors of the two methods (TDDFT and HF/CIS) for 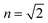 , relevant for the protein environment, differ by about 10%.
, relevant for the protein environment, differ by about 10%.
Do the neglected cavity field effects have an effect on the excitonic coupling and/or the optical spectra? Since the matrix element for the excitonic coupling does not depend on the external field, for the couplings, there is no effect. On the other hand, the optical spectra are measured with an external field and, hence, include cavity field effects. However, for a molecular aggregate made of identical chromophores, these effects have no influence on the shape of the spectrum. The equal shape of the subcavities of the chromophores leads to an equal enhancement of the electromagnetic field. Therefore, the peak heights in the spectrum, related to the square of the scalar product between transition dipole moments and the field, are affected by the cavity field effect identically for each peak. Hence, adding the cavity field effect would simply scale the total spectrum. In principle, the PCM calculations could be extended to include the cavity field effect.73 Such an extension could be useful in order to provide a more quantitative description of the experimental dipole strengths, and on this basis evaluate the reaction field effects obtained with different quantum chemical methods.
Although at present there is still an uncertainty concerning the exact magnitude of the reaction field factor, reflected by the 10% variation obtained between TDDFT/CAM-B3LYP and HF/CIS calculations, we can already conclude that the agreement of the empty spherical cavity model (the blue line in Fig. 3) with the experimental data is fortuitous, attributed to error compensation effects between using a spherical cavity and neglecting reaction field effects.
2.5 Delocalized excited states and optical spectra
To obtain the excitation energies of the low-energy delocalized states, one diagonalizes the exciton Hamiltonian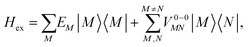 | (22) |
In eqn (22), we adopt the 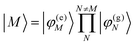 Hartree ansatz for a localized excited state of the complex, in which chromophore M is excited and the remaining chromophores N ≠ M are in their electronic ground state, where |φ(e)M〉 and |φ(g)N〉 are the electronic excited and ground state wave functions. Note that the local excited states of the complex are orthogonal, 〈M|N〉 = δMN, because the ground- and excited state wave functions of a chromophore M are orthogonal, that is, 〈φ(e)M|φ(g)M〉 = 0. A non-negligible overlap between local chromophore states would render the Hartree product ansatz invalid. For WSCP this neglect is justified by the large interchromophore distances. A proper antisymmetrization of |M〉 would yield the third (“exchange”) and fourth (“overlap”) term in eqn (1).
Hartree ansatz for a localized excited state of the complex, in which chromophore M is excited and the remaining chromophores N ≠ M are in their electronic ground state, where |φ(e)M〉 and |φ(g)N〉 are the electronic excited and ground state wave functions. Note that the local excited states of the complex are orthogonal, 〈M|N〉 = δMN, because the ground- and excited state wave functions of a chromophore M are orthogonal, that is, 〈φ(e)M|φ(g)M〉 = 0. A non-negligible overlap between local chromophore states would render the Hartree product ansatz invalid. For WSCP this neglect is justified by the large interchromophore distances. A proper antisymmetrization of |M〉 would yield the third (“exchange”) and fourth (“overlap”) term in eqn (1).
After the diagonalization of the matrix of the Hex operator in the basis of local excited states |M〉, one can rewrite eqn (22) as
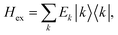 | (23) |
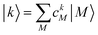 . The coefficient ckM represents the Mth component of the kth eigenvector of the exciton matrix (eqn (22)). The matrix size of Hex is equal to the number of states coupled; if one state per chromophore is used, the matrix size is equal to the number of chromophores.
. The coefficient ckM represents the Mth component of the kth eigenvector of the exciton matrix (eqn (22)). The matrix size of Hex is equal to the number of states coupled; if one state per chromophore is used, the matrix size is equal to the number of chromophores.
The Hamiltonian in eqn (22) is often applied to quasidegenerate chromophores, i.e., when fragments are chemically the same, and their excitation energies are only slightly different due to their different local environments. The matrix in eqn (22) is usually constructed for a single excited state per chromophore, whereby one has to specify which excited state to pick, because the order of the excited states may depend on the chromophore, so that for example, the second excited state in chromophore M = 2 can correspond to the third excited state in chromophore M = 5. In complicated cases it may be necessary to analyze the nature of the excited states in detail and manually pick those that should be coupled. If an excited state is far separated in terms of EM from all other states, then it will stay localized after the matrix diagonalization and, hence, does not need to be included in the exciton matrix. If needed, a perturbative inclusion of these off-resonant states is possible, as used, e.g., in the description of non-conservative circular dichroism spectra of pigment–protein complexes.74,75 If two excited states in one monomer are close in energy and nearly resonant to an excited state in another monomer, all three states may be included in the exciton matrix. In the present application to a Chl a dimer of WSCP an inclusion of the first excited state in each chromophore is enough to analyze the low-energy region of the optical spectra. Note, that the current implementation of FMO-FRET supports just one excited state per fragment.
The linear absorption spectrum of the complex is obtained as
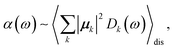 | (24) |
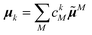 | (25) |
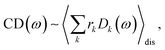 | (26) |
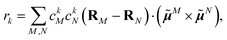 | (27) |
The conformational dynamics of the protein leads to fluctuations of the exciton Hamiltonian (eqn (22)), that is, the site energies and the excitonic couplings become time-dependent. The fluctuations that are fast compared to the excited state lifetimes of the pigments are taken into account in the homogeneous lineshape function Dk(ω) and the slow fluctuations are described by the disorder average 〈O(ω)〉dis of the intensity O(ω) of a homogeneous spectrum.
The fast fluctuations give rise to exciton relaxation-induced lifetime broadening and vibrational sidebands in the line-shape function Dk(ω). A time-local density matrix theory expression is used for the lineshape function, as described earlier.59,76 This lineshape function includes the low-frequency continuous intermolecular part of the spectral density of the exciton–vibrational coupling. Note that in the present lineshape function uncorrelated diagonal disorder is considered, that is, we neglect a fluctuation of the excitonic couplings and the correlation between fluctuations of local excitation energies (site energies) of different pigments. A microscopic justification for this assumption was obtained in a normal mode analysis of the spectral density.77,78 The discrete high-frequency intramolecular part is not explicitly taken into account, since it contributes only at the high-frequency wing of the spectrum. The respective transitions are localized by static disorder, because small Franck–Condon factors lead to small effective excitonic couplings. Here, we concentrate on the main part of the spectrum that is dominated by delocalized 0–0 transitions. The high-frequency intramolecular vibrations are implicitly taken into account by a renormalization of the excitonic coupling as discussed in detail below (Section 2.6).
The disorder average of a spectral intensity O(E1, E2,…, ENchr, ω) (in this case the homogeneous absorption or circular dichroism), that depends on the local excitation energies EM, M = 1,…,Nchr of the Nchr chromophores, is defined as
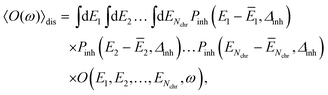 | (28) |
Note that, the choice of a Gaussian distribution function can be motivated by the central limit theorem of statististics and was recently justified by structure-based simulations for a pigment–protein complex,79 where it was also shown that the variation in excitonic couplings is much smaller than that of the site energies and that correlations in static disorder are very small. The quantum chemical calculations only need to be performed once for the geometry-optimized structure, revealing the local transition dipole moments of the chromophores and the excitonic couplings, which are assumed to be constant across the inhomogeneous ensemble of complexes. In the present application to Chl a dimers in WSCP, the maximum of the distribution function ĒM of the site energies of the two pigments in the dimers are identical for symmetry reasons. This Ē = Ē1 = Ē2 is treated as a fit parameter, together with the width Δinh of the distribution function. A change in Ē essentially leads to a displacement of the whole spectrum along the energy axis. Hence, this parameter can be inferred easily from experimental data. Note that, the excitonic couplings between Chls in different dimers in WSCP are so small that they have practically no influence on the shape of the linear absorption and circular dichroism spectrum of the complex.
2.6. Coupling of electronic excitations with high-frequency intrachromophore vibrations
In order to understand the physical nature of the scaling factor that relates the total excitonic coupling VMN to the coupling of the intramolecular 0–0 transitions of the chromophores V0–0MN, we sketch the framework for the vibronic coupling. A key quantity is the overall Huang–Rhys factor S of intramolecular modes of the chromophores. In Section 2.7 an expression is derived to estimate S from fluorescence spectra of the dimer.In order to describe the coupling of the electronic and vibrational degrees of freedom, we extend the monomer basis in eqn (22) to be a product of the electronic and vibrational wave functions. Each chromophore is described by an electronic ground (g) state 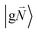 and an excited (e) state
and an excited (e) state 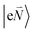 , where the vector
, where the vector 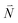 contains the vibrational quantum numbers Nν of the different intramolecular modes ν.
contains the vibrational quantum numbers Nν of the different intramolecular modes ν.
Linear absorption starts from the ground state 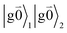 with no vibrational excitation in both monomers (indicated by
with no vibrational excitation in both monomers (indicated by 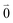 ). Because of the excitonic coupling V12 between the chromophores their excited states get mixed. If the excitonic coupling between the
). Because of the excitonic coupling V12 between the chromophores their excited states get mixed. If the excitonic coupling between the 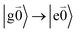 transition (in short the 0–0 transition) of one chromophore and the
transition (in short the 0–0 transition) of one chromophore and the 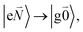 transition (with
transition (with 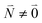 ) of the other chromophore is small compared to the energy difference between the two transitions, the 0–0 transition of one chromophore mixes mainly with the 0–0 transition of the other chromophore and the two lowest excited states (k = 1, 2) of the dimer are in good approximation obtained as
) of the other chromophore is small compared to the energy difference between the two transitions, the 0–0 transition of one chromophore mixes mainly with the 0–0 transition of the other chromophore and the two lowest excited states (k = 1, 2) of the dimer are in good approximation obtained as
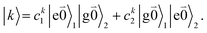 | (29) |
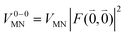 between the 0–0 transitions that contains the respective Franck–Condon factors for the ground vibrational state
between the 0–0 transitions that contains the respective Franck–Condon factors for the ground vibrational state 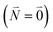 ,
,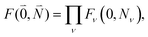 | (30) |
| Fν(0, Nν) = 〈χ(g)0(Qν)|χ(e)Nν(Qν)〉 | (31) |
Including the intrachromophore exciton–vibrational coupling by the above renormalization of the overall excitonic coupling VMN with the square of the Franck–Condon factor of the 0–0 transition is valid, as long as the Franck–Condon factors involving excited vibrational states (e.g. Fν(0,Nν)) are sufficiently small, such that the excitonic coupling 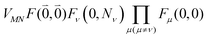 is small compared to the intramolecular vibrational energy ħων. If this inequality does not hold, the mixing between the 0–0 transition of one chromophore with the 0–Nν transition of the other chromophore would affect the whole spectrum and not just the high-frequency wing.80
is small compared to the intramolecular vibrational energy ħων. If this inequality does not hold, the mixing between the 0–0 transition of one chromophore with the 0–Nν transition of the other chromophore would affect the whole spectrum and not just the high-frequency wing.80
The quantum chemically determined excitonic coupling VMN is calibrated below by taking into account the experimental vacuum dipole strength 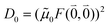 of the 0–0 transition of Chl a, where
of the 0–0 transition of Chl a, where ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 0 = |
0 = |![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) 0|. Noting that the quantum chemical vacuum transition dipole moment
0|. Noting that the quantum chemical vacuum transition dipole moment ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) M0 of pigment M is the first moment of the vacuum transition density
M0 of pigment M is the first moment of the vacuum transition density ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e4.gif) M(r), the calibrated excitonic coupling of the 0–0 transition is given as
M(r), the calibrated excitonic coupling of the 0–0 transition is given as
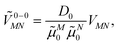 | (32) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) M0 = |
M0 = |![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) M0|. Note that, the experimental Franck–Condon factor of the 0–0 transition is contained in the experimental vacuum dipole strength
M0|. Note that, the experimental Franck–Condon factor of the 0–0 transition is contained in the experimental vacuum dipole strength 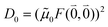 of this transition. Besides the Franck–Condon factor, the calibration factor contains the ratio
of this transition. Besides the Franck–Condon factor, the calibration factor contains the ratio 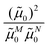 of experimental and quantum chemical vacuum transition dipole moment magnitudes. This factor corrects for limitations in the quantum chemical calculations. Note that this calibration neglects any change of the transition dipole moments caused by the distortion of the chromophores by their protein environment in WSCP, since D0 is extrapolated from dipole strengths of isolated Chl a measured in different solvents.
of experimental and quantum chemical vacuum transition dipole moment magnitudes. This factor corrects for limitations in the quantum chemical calculations. Note that this calibration neglects any change of the transition dipole moments caused by the distortion of the chromophores by their protein environment in WSCP, since D0 is extrapolated from dipole strengths of isolated Chl a measured in different solvents.
As long as the differences between the experimental and calculated vacuum transition dipole moments are small, their effect on the reaction field and thereby on the excitonic coupling can be approximated by the linear scaling factor in eqn (32). Larger changes in the vacuum transition dipole moment most likely affect the reaction field in a non-linear way, and, therefore, cannot be taken into account by such a simple factor. Hence, the calibration of the Poisson-TrEsp and the FMO/PCM couplings should only be valid if the vacuum dipole strength calculated for the chromophores is close to the experimental value. The latter value 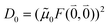 was determined for the 0–0 transition. In order to compare this value with the quantum chemical vacuum dipole strength we need to know the factor
was determined for the 0–0 transition. In order to compare this value with the quantum chemical vacuum dipole strength we need to know the factor 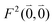 that can be expressed as1 exp(−S), where S is the overall Huang–Rhys factor
that can be expressed as1 exp(−S), where S is the overall Huang–Rhys factor
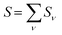 | (33) |
2.7. Determination of the Huang–Rhys factor of high-frequency intramolecular modes of Chl a in WSCP
For the discussion of our results, we extract the Huang–Rhys factor of the high-frequency intramolecular modes of the optical transition of the Chl a pigments in WSCP from experimental difference fluorescence line-narrowing spectra (Δ-FLN) of WSCP.49Using the standard electronic two-state theory, Pieper et al.49 arrived at an overall Huang–Rhys factor S of 0.8 for the high-frequency modes of the Chl a pigments. A subtlety in the analysis is that this Huang–Rhys factor, which determines the relative intensity of the high-frequency vibrational sideband with respect to the 0–0 transition, may depend on the excitonic coupling between the chromophores. Recently, Reppert81 approached this problem by numerical diagonalization of a large exciton Hamiltonian that explicitly included 49 high-frequency intramolecular modes per chromophore. These modes were taken from the analysis of Δ-FLN experiments,49 that can unmask the inhomogeneous broadening. For simplicity, Reppert81 assumed an orthogonal orientation of molecular transition dipole moments. His extensive numerical analysis revealed that while there is a reduction of the Huang–Rhys factor of the low-frequency modes by the excitonic coupling, the high-frequency modes essentially exhibit the same Huang–Rhys factor as a local optical excitation of an isolated Chl a chromophore, in the parameter range of excitonic couplings that is typical for pigment–protein complexes. We want to investigate how this result changes, if non-orthogonal transition dipole moments (as present in WSCP) are taken into account. It is shown below that the orientation of transition dipoles is indeed critical for the estimation of the Huang–Rhys factor.
The fluorescence at cryogenic temperatures starts from the lowest excited state |k = 1〉 of the dimer. As discussed above and also shown by the numerical studies of Reppert,81 this state is dominated by the 0–0 transitions of the two chromophores, (eqn (29)), with the exciton coefficients c11 and c12 of the lowest exciton state, that are obtained by diagonalization of the exciton Hamiltonian (eqn (22)) for different realizations of static disorder in local excitation energies EM.
From this initial state, a radiative transition is possible to the electronic and vibrational ground state of the complex 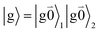 (the 0–0 transition) with transition dipole moment
(the 0–0 transition) with transition dipole moment
μ00 = 〈k|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) |g〉 = c11 |g〉 = c11![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) 1 + c22 1 + c22![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) 2. 2. | (34) |
Here 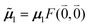 and
and 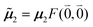 are the 0–0 transition dipole moments of pigments one and two, respectively, with the total electronic transition dipole moments μi = 〈e|
are the 0–0 transition dipole moments of pigments one and two, respectively, with the total electronic transition dipole moments μi = 〈e|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) |g〉i (i = 1 or 2) and the Franck–Condon factors of the 0–0 transition (eqn (30) and (31)), arising from integration of the vibrational degrees of freedom in |k〉 and |g〉.
|g〉i (i = 1 or 2) and the Franck–Condon factors of the 0–0 transition (eqn (30) and (31)), arising from integration of the vibrational degrees of freedom in |k〉 and |g〉.
In addition to the 0–0 transition described above, intramolecular vibrations may be excited during the radiative transition from the low energy exciton state |k〉 to an electronic ground state 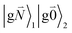 or
or 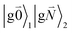 with vibrational excitation in chromophore one or two, respectively. These transitions are visible as discrete peaks in fluorescence line narrowing spectra,49 occurring at large vibrational energies (ħω > 200 cm−1), as compared to the continuous vibrational sideband of the 0–0 transition that has a maximum at low vibrational frequencies (ħω ≈ 20 cm−1). The vector
with vibrational excitation in chromophore one or two, respectively. These transitions are visible as discrete peaks in fluorescence line narrowing spectra,49 occurring at large vibrational energies (ħω > 200 cm−1), as compared to the continuous vibrational sideband of the 0–0 transition that has a maximum at low vibrational frequencies (ħω ≈ 20 cm−1). The vector 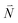 contains the vibrational quantum numbers Nν of the different intramolecular modes ν excluding the case where all quantum numbers Nν are simultaneously zero. The respective transition dipole moments are obtained, using eqn (29), as
contains the vibrational quantum numbers Nν of the different intramolecular modes ν excluding the case where all quantum numbers Nν are simultaneously zero. The respective transition dipole moments are obtained, using eqn (29), as
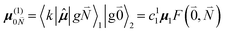 | (35) |
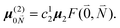 | (36) |
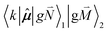 , using eqn (29) for the exciton state |k = 1〉, is obtained as
, using eqn (29) for the exciton state |k = 1〉, is obtained as 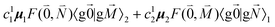 and is found to vanish for
and is found to vanish for 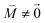 and, simultaneously,
and, simultaneously, 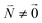 because of the orthogonality of vibrational wavefunctions of the same electronic state (here the electronic ground state).
because of the orthogonality of vibrational wavefunctions of the same electronic state (here the electronic ground state).
The relative intensity of the high-frequency vibrational sideband and 0–0 transition in the fluorescence spectrum can then be estimated using eqn (34)–(36) as
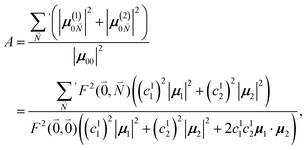 | (37) |
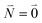 . Taking into account that the pigments have the same magnitude of the transition dipole moment, |μ1| = |μ2|, and the normalization of the excitonic wave function, (c11)2 + (c12)2 = 1, results in a relative intensity
. Taking into account that the pigments have the same magnitude of the transition dipole moment, |μ1| = |μ2|, and the normalization of the excitonic wave function, (c11)2 + (c12)2 = 1, results in a relative intensity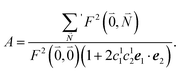 | (38) |
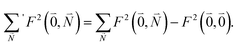 | (39) |
Due to the basis set completion when summed over all possible 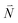 , we have1
, we have1
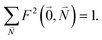 | (40) |
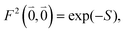 | (41) |
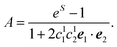 | (42) |
For orthogonal transition dipole moments e1·e2 = 0 and the Reppert rule,81
| A = eS − 1 | (43) |
| S = ln{(eS′ − 1)(1 + 2〈c(1)1c(1)2〉dise1·e2) + 1} | (44) |
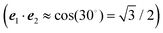 .
.
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) N = |
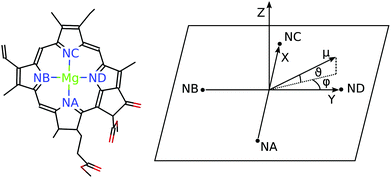
N = |![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) N| and orientations (defined by angles ϑN and φN, see Fig. 4) of the transition dipole moments of individual Chl a chromophores N computed with FMO0-TDDFT in vacuum (none), or in the protein environment with FMO0/PCM[0] revealing the implicit (impl) and explicit (expl) contributions to the transition dipole moment (eqn (5) and (8) and main text below eqn (13))
N| and orientations (defined by angles ϑN and φN, see Fig. 4) of the transition dipole moments of individual Chl a chromophores N computed with FMO0-TDDFT in vacuum (none), or in the protein environment with FMO0/PCM[0] revealing the implicit (impl) and explicit (expl) contributions to the transition dipole moment (eqn (5) and (8) and main text below eqn (13))
| N | Embeddingab | ω N (eV) | Dipole moments (D) | ϑ N (°) | φ N (°) |
|---|---|---|---|---|---|
| a ω N has no explicit embedding contribution. b The respective symbols for the dipole moments are given in parentheses. | |||||
| 1 | None (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 10) 10) |
2.140 | 5.31 | 0.0 | −6.9 |
Impl (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 1) 1) |
2.102 | 6.39 | −0.1 | −6.4 | |
Impl + expl(![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 1,screen) 1,screen) |
2.102 | 3.69 | −0.8 | −4.8 | |
| 2 | None (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 20) 20) |
2.131 | 5.32 | −1.8 | −6.6 |
Impl (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 2) 2) |
2.092 | 6.41 | −1.8 | −6.1 | |
Impl + expl(![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 2,screen) 2,screen) |
2.092 | 3.66 | −2.4 | −4.8 | |
| 3 | None (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 30) 30) |
2.136 | 5.36 | 0.1 | −6.4 |
Impl (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 3) 3) |
2.098 | 6.43 | 0.0 | −6.1 | |
Impl + expl(![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 3,screen) 3,screen) |
2.098 | 3.72 | −1.1 | −4.9 | |
| 4 | None ((![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 40) 40) |
2.134 | 5.32 | −1.4 | −6.2 |
Impl (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 4) 4) |
2.095 | 6.40 | −1.7 | −5.8 | |
Impl + expl(![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 4,screen) 4,screen) |
2.095 | 3.67 | −3.6 | −4.4 | |
This value is less than one third of the original estimate49 that is based on an electronic-two-state theory. This result demonstrates that care should be taken in the estimates of Huang–Rhys factors of high-frequency modes of excitonically coupled pigments, where the local transition dipole moments of the chromophores are non-orthogonal. In this case the Reppert rule,81 which would allow for an analysis with the standard two-level system theory, does not apply. The WSCP is an extreme example, since there is a strong redistribution of oscillator strength by the excitonic coupling between the 0–0 transitions. The redistribution is so strong that the low-energy exciton state, from where the fluorescence starts, appears only as a shoulder in the linear absorption spectrum. Since the absolute intensity of the high-frequency vibrational sideband is not influenced by the excitonic coupling,81 the relative intensity of this sideband with respect to the 0–0 transition is much larger than for a localized excited state, explaining the large value of S estimated before.49 Consequently, the present estimate of the Huang–Rhys factor is in the same range as estimates from experimental fluorescence and absorption data of isolated Chl a in different solvents82 (S = 0.28 in ether and in pyridine, S = 0.41 in 1-propanol and S = 0.38 in 2-propanol).
3. Computational details
The solvent screening model for excitonic interactions was implemented for FMO29,83 in GAMESS84,85 and parallelized with the generalized distributed data interface.86 GAMESS was used for all quantum chemical calculations. The initial coordinates of all atoms except hydrogens belonging to Chl a chromophores were extracted from the X-ray structure (PDB: 2DRE).87 From each chromophore, the phytyl chain was removed, while the C1 carbon was retained. Hydrogen atoms were added using the Jmol software.88 In FMO, each chromophore was treated as a separate fragment (4 fragments in total).Using the CAM-B3LYP functional89 with the 6-31-G* basis set, a geometry optimization was performed for each isolated chromophore in vacuum separately in a two-step process. In the first step, an optimization was done with nitrogen coordinates held fixed. A second optimization was performed without any constraints. This two-step procedure was chosen to preserve the relative orientation of the chromophores as much as possible. The inter-pigment distances in WSCP are large enough, so that no steric clashes were observed after merging the coordinates of the geometry-optimized pigments. The obtained coordinates are listed in Table S2 (ESI†). These coordinates were used in all subsequent calculations on the WSCP complex unless otherwise noted. As a check, the complete optimization was also applied to Chl a dimers revealing very small differences in atomic coordinates (Table S3, ESI†) and electronic structure (Table S4 and S5, ESI†), as compared to the monomer optimization described above.
FMO/PCM calculations on the WSCP complex were done using TDDFT with the range-separated CAM-B3LYP exchange correlation (XC) functional and the 6-31+G* basis set for the transition from the ground singlet state S0 to the first excited singlet state S1 of each chromophore, unless otherwise noted. In TDDFT/PCM, the ground state is computed for DFT/PCM using the static dielectric constant εs. Then, the TDDFT equations are solved in the presence of the solvent field. For the latter step, two scenarios are possible:90 (a) the non-equilibrium case suitable for vertical excitations, where ε is set to be the optical dielectric constant (ε = n2) and (b) the equilibrium case suitable for studying energy minima for excited states, in which case the static dielectric constant εs is used in TDDFT. In FRET, the former approach is taken, because during the excitation energy transfer there is no time for nuclear relaxation.
For the calculations involving a continuum solvent, IEF-PCM was used in the non-equilibrium formulation of TDDFT (IEF-PCM is the appropriate model for small dielectric constants91,92). The static dielectric constant εs was set to 4 (a typical value for proteins93), while the optical dielectric constant ε = 2, as determined earlier from an analysis of the oscillator strength of protein-extracted chlorophylls.45 The molecular cavity was constructed in PCM using the Bondi radii,94 multiplied by a scaling factor of 1.2, such that the cavity surface is at the solvent accessible surface rather than the van der Waals surface.
The transition density between two states has an arbitrary phase. As a consequence, its first moment, that is, the transition dipole moment also has an arbitrary phase. Physically observable properties do not depend on the phase, but if one is to compare transition dipoles in various calculations, it is necessary to devise a scheme for fixing the phase (as the phase is real, the issue is whether to multiply by −1 or not). For simplicity, all couplings in which the pigment with a reversed transition dipole moment is involved are also multiplied by a factor of −1. The convention for the transition dipole direction used in the present work is defined in the following. Note, however, that this multiplication of couplings and transition dipole moments has no influence on the observables, e.g., the linear absorption spectrum.
For discussing the dipole moments and excitonic couplings, it is necessary to define the orientation of the former, as noted above. In each individual Chl a chromophore the four nitrogen atoms NA, NB, NC, ND can be used to define a local coordinate system. X is the direction NA–NC, while the direction NB–ND is Y. The direction perpendicular to the XY plane is Z. Together, Y, X and Z form a right handed coordinate system (Fig. 4). The phase of the transition dipole moment is chosen such that its projection on the Y-axis is positive. The angle between a particular transition dipole moment and the respective molecular XY plane is denoted ϑ. A positive angle ϑ means that the component of the transition dipole moment in the direction of Z is positive. φ is the angle between a particular transition dipole moment and the molecular Y direction measured in the XY plane. A positive angle φ means that the component of the transition dipole moment in X direction is positive.
When the dipole model in eqn (11)–(13) is applied, one has to define a distance between two chromophores RMN. We found that the PDA performs best if the point dipoles are placed at the geometric centers of the four nitrogen atoms (see Fig. 4 and Table S1, ESI†),
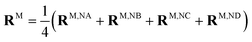 | (45) |
Using these centers, the distance is calculated as RMN = |RM − RN|. For a comparison with the Poisson-TrEsp method, atomic transition charges were obtained from a fit of the ESP of the transition densities of the chromophores71,95 using the CHELPG grid96 implemented in the potential derived charges (PDC) method.95 In the fit, the dipole moment of the fitted charges was constrained to the value obtained from the transition density (eqn (5)). The Poisson-TrEsp calculations were performed with the program MEAD97,98 (see ESI† for more information).
Besides the excitonic couplings, the following parameters are used in the calculation of the optical spectra, as determined before.59 A mean transition energy Ē1 = Ē2 of the two Chl a chromophores corresponding to a wavelength of 675 nm, a full width at half maximum Δinh of 170 cm−1 for the Gaussian distribution function of the local transition energies of the chromophores, a Huang–Rhys factor S = 0.8 for the low-frequency part of the spectral density, that is assumed to have a functional form, extracted earlier from fluorescence line-narrowing spectra of the B777 pigment–protein complex.76 In addition, a pure dephasing time of 2750 fs was assumed as determined earlier59 from a simulation of hole-burning spectra of the WSCP complex and comparison with experimental data.50 The pure dephasing time describes the finite width of the 0–0 line, but its effect is masked by the inhomogeneous broadening in the present ensemble spectra, which practically do not depend on the value used for this dephasing time.
4 Results
4.1 Transition dipoles and excitonic couplings calculated with FMO0 (no mutual polarization of the chromophores)
The computed excitation energies and dipole moments of the 4 Chl a chromophores in WSCP are shown in Table 1. For the isolated chromophores (in vacuum) the angle ϑ varies between 0.1° and −1.8° and φ varies between −6.2° and −6.9°, which means that the S0–S1 transition dipole lies in the XY plane and is practically oriented in the Y-direction (NB–ND axis) with a slight clockwise rotation (Fig. 4) in agreement with similar TDDFT calculations on Chl a.74 Including the implicit polarization by the protein/solvent environment (“impl” in Table 1) enhances the transition dipole moment of the pigment by about 20% while the change in direction is very small (<0.4° for ϑ and <0.6° for φ). Adding the screening contribution due to the protein/solvent environment (“impl + expl” in Table 1) reduces the magnitude of the effective dipole moment by about 40% and causes a slight rotation (<2.0° for ϑ and <1.7° for φ).The couplings computed from the transition density are presented in Table 2. Three coupling values for each pair of chromophores are given: the vacuum coupling VESMN(ε = 1), the protein-embedded coupling VimplMN(ε = 2), obtained by taking into account the mutual dynamic polarization of the chromophores and the protein/solvent environment (reaction field effects), and the total coupling VimplMN(ε = 2) + VexplMN(ε = 2) including, in addition, the explicit environmental contributions, representing screening effects.
| M | N | V ES MN (ε = 1) | V impl MN (ε = 2)a | V impl MN (ε = 2) + VexplMN(ε = 2)a | f rf MN | s MN |
|---|---|---|---|---|---|---|
| a Using TDDFT calculations with the CAM-B3LYP XC-functional. The last two columns contain the reaction field and screening factors, defined in eqn (9) and (10), respectively. | ||||||
| 3 | 4 | 147 | 209 | 130 | 1.423 | 0.621 |
| 1 | 2 | 142 | 204 | 126 | 1.429 | 0.621 |
| 2 | 3 | 35 | 48 | 29 | 1.383 | 0.600 |
| 1 | 4 | 32 | 44 | 27 | 1.396 | 0.603 |
| 2 | 4 | 10 | 15 | 10 | 1.504 | 0.682 |
| 1 | 3 | 9 | 13 | 9 | 1.494 | 0.713 |
In Table 2 one can see three groups of couplings with two couplings in each group: (I) 3–4 and 1–2 (II) 2–3 and 1–4, (III) 2–4 and 1–3, with large, intermediate and small excitonic couplings, respectively. The reason for this grouping can be inferred from Fig. 1: the WSCP complex has an approximate D2 symmetry. This means that every relative orientation between pigment pairs appears twice. The vacuum couplings are enhanced due to the implicit dynamic polarization effect of the protein/solvent environment by the reaction field factor frfMN that varies between 1.38 and 1.50. The coupling is reduced by the explicit dynamic polarization of the environment by a screening factor sMN varying between 0.60 and 0.71.
These factors are somewhat larger for group (III) than for group (I) and group (II). This variation is rationalized further below in terms of a rotation of the transition dipole moments. Interestingly, there is a certain compensation between the implicit and the explicit protein-embedding effects, such that the overall scaling factor between the vacuum and protein couplings frfMNsMN is not so far from unity.
4.2 Couplings calculated with FMO1: the role of the mutual polarization of chromophores
In order to investigate the role of the mutual polarization of the electronic ground state of the chromophores, the results of Tables 1 and 2 (obtained with FMO0: no pigment–pigment polarization) can be compared with those of Tables 3 and 4, respectively, obtained with FMO1 (with such polarization). The polarization in FMO1 is taken into account by including in the Hamiltonian a self-consistently determined embedding potential describing the electrostatic field of the ground state of fragments.29| N | Embedding | ω N (eV) | μ N (D) | ϑ N (°) | φ N (°) |
|---|---|---|---|---|---|
| 1 | None | 2.150 | 5.28 | 0.0 | −6.2 |
| Impl | 2.115 | 6.32 | −0.1 | −5.7 | |
| Impl + expl | 2.115 | 3.65 | −0.7 | −4.3 | |
| 2 | None | 2.140 | 5.27 | −1.8 | −6.4 |
| Impl | 2.101 | 6.33 | −1.8 | −5.7 | |
| Impl + expl | 2.101 | 3.61 | −2.4 | −4.4 | |
| 3 | None | 2.147 | 5.31 | 0.1 | −5.7 |
| Impl | 2.112 | 6.35 | 0.1 | −5.6 | |
| Impl + expl | 2.112 | 3.67 | −1.1 | −4.4 | |
| 4 | None | 2.144 | 5.28 | −1.3 | −5.6 |
| Impl | 2.106 | 6.32 | −1.6 | −5.3 | |
| Impl + expl | 2.106 | 3.62 | −3.6 | −3.9 |
| M | N | V ES MN (ε = 1) | V impl MN (ε = 2) | V impl MN (ε = 2) + VexplMN(ε = 2) | f rf MN | s MN |
|---|---|---|---|---|---|---|
| 3 | 4 | 144 | 203 | 126 | 1.413 | 0.621 |
| 1 | 2 | 140 | 199 | 123 | 1.421 | 0.621 |
| 2 | 3 | 34 | 47 | 28 | 1.369 | 0.600 |
| 1 | 4 | 31 | 43 | 26 | 1.381 | 0.602 |
| 2 | 4 | 10 | 15 | 10 | 1.494 | 0.680 |
| 1 | 3 | 9 | 13 | 9 | 1.466 | 0.710 |
Due to the polarization, the excitation energies are increased by ∼10 meV, while the transition dipole moments generally are 1–2% smaller. It can be noted that the embedding shifts both the ground and excited state energies (although not equally) and thus the effect on the transition energy is relatively weak. As can be seen from Fig. 4, chlorophylls are neutral non-polar molecules, although they do include a cation Mg2+, but its charge is compensated by the donating lone pairs on the nitrogens. In addition, the centers of chlorophylls are quite far separated from each other (Table S1, ESI†). Thus, the polarization of chlorophylls by each other is not very strong. The chromophore polarization lowers the couplings by a few percent at most (Table 4vs.Table 2), which can be rationalized by the slightly smaller transition dipoles (Table 3vs.Table 1). The polarization has a negligible effect on the screening factor sMN and a very small effect on the reaction field factor frfMN.
The small effect of the mutual polarization between the chromophores on the excitonic couplings obtained with FMO1, using an atomistic description of the chromophores, is consistent with the weak dependence of the excitonic coupling on the static dielectric constant εs used in FMO0 and FMO1 to describe the polarization of the electronic ground state of the chromophores by the homogeneous dielectric representing the protein and solvent environment. The excitonic couplings vary by at most 0.2% when εs is varied between εs = 2 and εs = 20 (Table S19, ESI†). Note that the polarization of the excited states of the pigments can be expected to be similarly small, since the change in permanent dipole moment between excited and ground state of Chl a is small.99
4.3 Excitonic couplings in the point-dipole approximation
In order to judge the plausibility of the PDA and to investigate reaction field and screening effects, the ESP![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) 1(r) (eqn (3)) of the molecular transition density of pigment 1 including also the ESP of the dynamic solvent polarization induced by the latter φ1,expl(r) (eqn (7)) is plotted in Fig. 5 in the molecular plane defined by the nitrogen atoms NA, NB, NC, and ND. The potential is clearly dominated by the dipole contribution. A visual comparison of panels (a), (b) and (d) in Fig. 5 shows that the change of the potential from vacuum to protein-embedding (both with and without the explicit contribution from the solvent polarization φ1,expl(r) can mainly be attributed to a global amplification or attenuation. The attenuation is due to the sign inversion of φ1,expl(r) with respect to the ESP in vacuum in Fig. 5(c) and (a), respectively. This observation is confirmed in Fig. 5(e) and (f) where the differences of the ESPs in the protein/solvent environment with respect to the ESP in vacuum scaled with the ratio of the respective transition dipole moment magnitudes
1(r) (eqn (3)) of the molecular transition density of pigment 1 including also the ESP of the dynamic solvent polarization induced by the latter φ1,expl(r) (eqn (7)) is plotted in Fig. 5 in the molecular plane defined by the nitrogen atoms NA, NB, NC, and ND. The potential is clearly dominated by the dipole contribution. A visual comparison of panels (a), (b) and (d) in Fig. 5 shows that the change of the potential from vacuum to protein-embedding (both with and without the explicit contribution from the solvent polarization φ1,expl(r) can mainly be attributed to a global amplification or attenuation. The attenuation is due to the sign inversion of φ1,expl(r) with respect to the ESP in vacuum in Fig. 5(c) and (a), respectively. This observation is confirmed in Fig. 5(e) and (f) where the differences of the ESPs in the protein/solvent environment with respect to the ESP in vacuum scaled with the ratio of the respective transition dipole moment magnitudes ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 1/
1/![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 10 and (
10 and (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 1 +
1 + ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 1,expl)/
1,expl)/![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 10, respectively, are shown, where
10, respectively, are shown, where ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 10 is the magnitude of the vacuum transition dipole moment of chromophore 1. The potential differences are somewhat larger if both implicit and explicit environmental contributions are taken into account (Fig. 5f) as compared to the case where only implicit effects contribute (Fig. 5e).
10 is the magnitude of the vacuum transition dipole moment of chromophore 1. The potential differences are somewhat larger if both implicit and explicit environmental contributions are taken into account (Fig. 5f) as compared to the case where only implicit effects contribute (Fig. 5e).
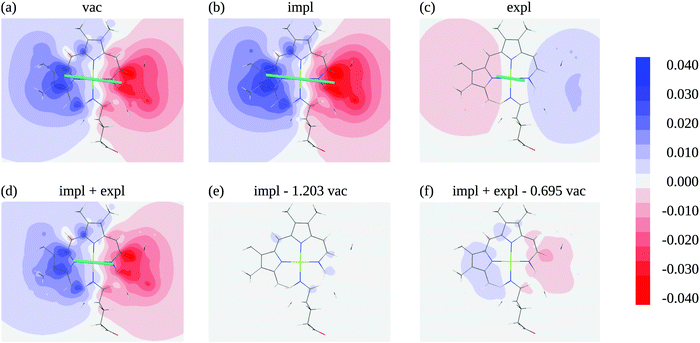 | ||
Fig. 5 Electrostatic potential (ESP) of chromophore 1 evaluated in the molecular plane in vacuum (a) and in protein/solvent environment (b–d). In the ESP in panel (b) the implicit solvent contribution is included (![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) 1(r), eqn (3)), the ESP in panel (c) contains the explicit solvent contribution (φ1,expl(r), eqn (7)), panel (d) shows the overall ESP in the protein/solvent environment, panel (e) contains the difference between the implicit ESP in panel (b) and a scaled vacuum ESP of panel (a); the scaling factor 1(r), eqn (3)), the ESP in panel (c) contains the explicit solvent contribution (φ1,expl(r), eqn (7)), panel (d) shows the overall ESP in the protein/solvent environment, panel (e) contains the difference between the implicit ESP in panel (b) and a scaled vacuum ESP of panel (a); the scaling factor ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 1/ 1/![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 10 is the ratio of the magnitudes of the pigment transition dipole moment 10 is the ratio of the magnitudes of the pigment transition dipole moment ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 1 = 6.39 D and the moment in vacuum 1 = 6.39 D and the moment in vacuum ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 10 = 5.31 D, panel (f) shows the difference between the overall ESP in (c) and a scaled vacuum ESP of (a); the scaling factor 10 = 5.31 D, panel (f) shows the difference between the overall ESP in (c) and a scaled vacuum ESP of (a); the scaling factor ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 1,screen/ 1,screen/![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 10 is the ratio of the magnitudes of the screened transition dipole moment 10 is the ratio of the magnitudes of the screened transition dipole moment ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 1,screen = | 1,screen = |![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) 1 + 1 + ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) 1,expl| = 3.69 D, where 1,expl| = 3.69 D, where ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) 1,expl (eqn (8)) is the dipole moment of the solvent polarization induced by the transition density of chromophore 1, and the moment in vacuum. The teal lines in (a)–(d) show the direction and magnitude of the transition dipole moment. All quantum chemical calculations for this figure were performed with TDDFT using the CAM-B3LYP functional. 1,expl (eqn (8)) is the dipole moment of the solvent polarization induced by the transition density of chromophore 1, and the moment in vacuum. The teal lines in (a)–(d) show the direction and magnitude of the transition dipole moment. All quantum chemical calculations for this figure were performed with TDDFT using the CAM-B3LYP functional. | ||
The excitonic couplings in PDA computed with FMO0 are shown in Table 5. From a comparison to the results obtained with the transition density (Table 2), it can be seen that the dipole approximation is quite accurate, especially in the case where both implicit and explicit environmental effects are considered (Table 5, column 5). The PDA couplings are a few percent larger than the transition density couplings. Interestingly, the increase of the couplings in PDA with respect to the transition density couplings is somewhat stronger in vacuum than in the medium, indicating a partial error compensation effect. Apparently, in PDA the larger vacuum couplings are partially compensated by the stronger screening (smaller s values). While the order of the reaction field and screening factors frfMN and sMN in Tables 5 and 2 is not the same, the factors in group (III) (couplings 2–4 and 1–3) are the largest in both tables.
| M | N | V ES,μ MN (ε = 1) | V impl,μ MN (ε = 2) | V impl,μ MN (ε = 2) + Vexpl,μMN (ε = 2) | f rf,μ MN | s μ MN |
|---|---|---|---|---|---|---|
| 3 | 4 | 167 | 241 | 136 | 1.441 | 0.566 |
| 1 | 2 | 161 | 233 | 133 | 1.449 | 0.569 |
| 2 | 3 | 36 | 51 | 30 | 1.444 | 0.581 |
| 1 | 4 | 34 | 50 | 29 | 1.447 | 0.578 |
| 2 | 4 | 8 | 12 | 8 | 1.527 | 0.635 |
| 1 | 3 | 7 | 11 | 7 | 1.503 | 0.626 |
From analyzing the trends of the three kinds of couplings (vacuum, impl, impl + expl), it can be hypothesized that the results obtained with the transition density can be accurately modeled by a change in the transition dipole vector. This change can be separated into two aspects: a change in the vector length and a change in the direction (a rotation). To separate these two aspects, the vacuum PDA couplings in Table 5 were scaled by factors containing different transition dipole magnitudes
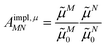 | (46) |
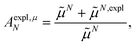 | (47) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) M0 and
M0 and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) N0 are the magnitudes of the vacuum transition dipole moments of chromophores M and N, respectively. The dipole moment magnitudes
N0 are the magnitudes of the vacuum transition dipole moments of chromophores M and N, respectively. The dipole moment magnitudes ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) M and
M and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) N are computed for pigments in the protein/solvent environment, and
N are computed for pigments in the protein/solvent environment, and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) N,expl is the magnitude of the explicit transition dipole moment of the environment induced by the transition density of chromophore N (eqn (8)).
N,expl is the magnitude of the explicit transition dipole moment of the environment induced by the transition density of chromophore N (eqn (8)).
The scaled couplings shown in Table 6 agree very well with the respective values in Table 5. Hence, the magnitude of the transition dipole moments is the decisive factor. Also, the polarization and screening factors factors frf,μMN and sμMN in Tables 5 and 6 are very similar. A closer inspection shows that for group (III) the screening factors (sμ24, sμ13) are more similar to the values for group (I) and (II) in Table 6 than in Table 5. Hence, this difference can be attributed to an effective rotation of transition dipole moments of the pigments by the polarization of the environment.
| M | N | A impl,μ MN V μ MN (ε = 1) | A expl,μ MN A impl,μ MN V μ MN (ε = 1) | f rf,μ MN | s μ MN |
|---|---|---|---|---|---|
| 3 | 4 | 241 | 138 | 1.444 | 0.573 |
| 1 | 2 | 233 | 133 | 1.448 | 0.570 |
| 2 | 3 | 52 | 30 | 1.446 | 0.578 |
| 1 | 4 | 50 | 28 | 1.446 | 0.573 |
| 2 | 4 | 12 | 7 | 1.449 | 0.573 |
| 1 | 3 | 10 | 6 | 1.443 | 0.578 |
4.4 Comparison of the FMO0/PCM[0] and the Poisson-TrEsp couplings and their calibration
For comparison, Poisson-TrEsp calculations were performed with the atomic charges obtained from the transition density in protein (FMO0/PCM[0]) and in vacuum (FMO0). The results are shown in Table 7 and can be compared with the original excitonic couplings obtained with the FMO0/PCM[0] method (Table 2). An excellent agreement is obtained between the vacuum Poisson-TrEsp couplings VP-TrEspMN(ε = 1) of the unpolarized chromophores in vacuum (![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) Mα(ε = 1)) as well as well as the chromophores polarized by the protein/solvent environment (
Mα(ε = 1)) as well as well as the chromophores polarized by the protein/solvent environment (![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) Mα(ε = 2)) shown in Table 7 and the corresponding results in Table 2. Including the dielectric continuum in the Poisson-TrEsp calculations leads to a reduction (screening) of the excitonic coupling, as described by the respective screening factors sP-TrEspMN in Table 7. Identical screening factors are obtained for the two sets of charges, indicating that, except for their magnitude, the polarized and unpolarized transition densities of the chromophores are very similar, as noted already above. Moreover, the screened excitonic couplings VP-TrEspMN(ε = 2) of the polarized transition densities obtained with Poisson-TrEsp agree quite well with the total excitonic couplings obtained in FMO0/PCM[0] in Table 2. Hence, Poisson-TrEsp provides an accurate description of the screening part of the FMO[0]/PCM[0] calculations. As discussed below in more detail, this result reflects similarities in the quantum mechanical perturbation theory and the interpretation of the quantum-mechanical results in terms of classical electrostatics.43,67,100
Mα(ε = 2)) shown in Table 7 and the corresponding results in Table 2. Including the dielectric continuum in the Poisson-TrEsp calculations leads to a reduction (screening) of the excitonic coupling, as described by the respective screening factors sP-TrEspMN in Table 7. Identical screening factors are obtained for the two sets of charges, indicating that, except for their magnitude, the polarized and unpolarized transition densities of the chromophores are very similar, as noted already above. Moreover, the screened excitonic couplings VP-TrEspMN(ε = 2) of the polarized transition densities obtained with Poisson-TrEsp agree quite well with the total excitonic couplings obtained in FMO0/PCM[0] in Table 2. Hence, Poisson-TrEsp provides an accurate description of the screening part of the FMO[0]/PCM[0] calculations. As discussed below in more detail, this result reflects similarities in the quantum mechanical perturbation theory and the interpretation of the quantum-mechanical results in terms of classical electrostatics.43,67,100
![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) Mα obtained from FMO0 in vacuum (ε = 1) or FMO0/PCM[0] in a protein/solvent embedding (ε = 2); sP-TrEspMN is the screening factor (eqn (17))
Mα obtained from FMO0 in vacuum (ε = 1) or FMO0/PCM[0] in a protein/solvent embedding (ε = 2); sP-TrEspMN is the screening factor (eqn (17))
| M | N |
![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) M
α
(ε = 1) from FMO0
M
α
(ε = 1) from FMO0 |
![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) M
α
(ε = 2) from FMO0/PCM[0]
M
α
(ε = 2) from FMO0/PCM[0] |
||||
|---|---|---|---|---|---|---|---|
| V P-TrEsp MN (ε = 1) | V P-TrEsp MN (ε = 2) | s P-TrEsp MN | V P-TrEsp MN (ε = 1) | V P-TrEsp MN (ε = 2) | s P-TrEsp MN | ||
| 3 | 4 | 147 | 90 | 0.62 | 211 | 130 | 0.62 |
| 1 | 2 | 141 | 87 | 0.62 | 202 | 125 | 0.62 |
| 2 | 3 | 35 | 21 | 0.60 | 48 | 29 | 0.60 |
| 1 | 4 | 32 | 19 | 0.60 | 44 | 27 | 0.60 |
| 2 | 4 | 10 | 7 | 0.74 | 14 | 11 | 0.74 |
| 1 | 3 | 8 | 6 | 0.78 | 13 | 10 | 0.77 |
Because the polarization of the transition density in the PCM calculations effectively corresponds to a multiplication of the vacuum transition dipole moment by a constant polarization factor  , we can take into account this polarization by just multiplying the vacuum transition charges in Poisson-TrEsp by this factor. To correct for limitations in the quantum chemical calculations on the isolated chromophores, the experimental vacuum transition dipole moment of the 0–0 transition of Chl a is taken into account, obtained from the empirical relation of Knox,60 discussed above. The transition charges
, we can take into account this polarization by just multiplying the vacuum transition charges in Poisson-TrEsp by this factor. To correct for limitations in the quantum chemical calculations on the isolated chromophores, the experimental vacuum transition dipole moment of the 0–0 transition of Chl a is taken into account, obtained from the empirical relation of Knox,60 discussed above. The transition charges ![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) Mα used in the Poisson-TrEsp calculations should be scaled such that the first moment, i.e., the transition dipole moment, satisfies the relation
Mα used in the Poisson-TrEsp calculations should be scaled such that the first moment, i.e., the transition dipole moment, satisfies the relation
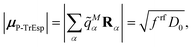 | (48) |
For the present Chl a chromophores,60D0 = 20.2 D2 and from the reaction field factors frfMN in Table 2, an average polarization (reaction field) factor frf = 1.44 is obtained. These two factors give rise to a transition dipole moment of μP-TrEsp = 5.39 D for Chl a. Hence, considering the present Poisson-TrEsp (P-TrEsp) calculations, the calibration factor is
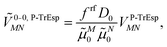 | (49) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) M0 and
M0 and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) N0, respectively.
N0, respectively.
Note, that the experimental vacuum dipole strength D0 of the 0–0 transition also serves as a calibration factor of the FMO/PCM couplings. In this case the polarization effect is explicitly included in the calculations and, therefore, the calibrated FMO/PCM coupling is given by eqn (32). The rationale behind this scaling is that without environment the transition densities should be consistent with the experimental vacuum transition dipole moments.
The calibrated couplings of the FMO0/PCM[0] approach and the Poisson-TrEsp values are compared in Table 8, revealing excellent agreement. In the calculations presented in Table 7, “direct” transition charges resulting from the PCM calculations are used in the Poisson-TrEsp calculations. In contrast, in the Poisson-TrEsp calculations in the 4th column of Table 8 only the average reaction field factor is introduced. Nevertheless, these Poisson-TrEsp calculations still give identical results to the FMO0/PCM[0] method.
| M | N | FMO0/PCM[0]a | Poisson-TrEsp (![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) Mα (ε = 1) from FMO0)bc Mα (ε = 1) from FMO0)bc |
Poisson-TrEsp (original)d | Poisson-TrEsp (improved)be | QM/MMPolaf |
|---|---|---|---|---|---|---|
a Calibrated as described in the text and in eqn (32).
b Calibrated as described in the text and in eqn (49).
c The vacuum transition charges ![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) Mα(ε = 1) of the FMO0 method (with TDDFT/CAM-B3LYP) are used.
d Calibrated as described in the text and in eqn (49), but setting frf = 1 and using the vacuum dipole strength 0 = 21.0 D2 of the 0–0 transition of Chl a,60 obtained from an analysis of the dipole strength using an empty spherical cavity local field factor (the blue line in Fig. 3).
e Transition dipole moments Mα(ε = 1) of the FMO0 method (with TDDFT/CAM-B3LYP) are used.
d Calibrated as described in the text and in eqn (49), but setting frf = 1 and using the vacuum dipole strength 0 = 21.0 D2 of the 0–0 transition of Chl a,60 obtained from an analysis of the dipole strength using an empty spherical cavity local field factor (the blue line in Fig. 3).
e Transition dipole moments ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) M0 and M0 and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) N0 and the uncalibrated Poisson-TrEsp couplings VP-TrEspMN are obtained as in the original Poisson-TrEsp method.41–43
f Uncalibrated values in parentheses are taken from Table 1 of ref. 52. N0 and the uncalibrated Poisson-TrEsp couplings VP-TrEspMN are obtained as in the original Poisson-TrEsp method.41–43
f Uncalibrated values in parentheses are taken from Table 1 of ref. 52.
|
||||||
| 3 | 4 | 92 | 92 | 62 | 86 | 76 (188) |
| 1 | 2 | 90 | 90 | 60 | 83 | 75 (183) |
| 2 | 3 | 21 | 21 | 17 | 24 | 12 (31) |
| 1 | 4 | 19 | 20 | 17 | 24 | 12 (31) |
| 2 | 4 | 7 | 7 | 6 | 8 | 4 (9) |
| 1 | 3 | 6 | 6 | 5 | 7 | 6 (15) |
Next, we investigate how the standard Poisson-TrEsp calculations that are based on atomic transition charges of the non-hydrogen atoms, obtained from a fit of the ESP of the transition density of isolated geometry optimized Chl a,71 can be improved by taking into account the average reaction field factor frf = 1.44 obtained from the present FMO0/PCM[0]/TDDFT/CAM-B3LYP calculations. The standard Poisson-TrEsp couplings are obtained by placing the TDDFT/B3LYP transition charges (taken from Table 1 in the supporting information of ref. 71) on the respective non-hydrogen atom positions of the chromophores in the crystal structure (PDB: 2DRE), resulting in uncalibrated Poisson-TrEsp couplings VP-TrEspMN and transition dipole moment magnitudes ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) M0 and
M0 and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) N0. The calibrated couplings of the 0–0 transition Ṽ0–0,P-TrEspMN are obtained from VP-TrEspMN using eqn (49), but setting the reaction field factor frf = 1 and applying D0 = 21.0 D2 of the empty spherical cavity model. The couplings obtained with this original Poisson-TrEsp approach (Table 8, 5th column) are significantly smaller than the FMO0/PCM[0] values. The largest couplings differ by about 30%. In the improved Poisson-TrEsp approach we use the same uncalibrated couplings VP-TrEspMN and transition dipole moment magnitudes
N0. The calibrated couplings of the 0–0 transition Ṽ0–0,P-TrEspMN are obtained from VP-TrEspMN using eqn (49), but setting the reaction field factor frf = 1 and applying D0 = 21.0 D2 of the empty spherical cavity model. The couplings obtained with this original Poisson-TrEsp approach (Table 8, 5th column) are significantly smaller than the FMO0/PCM[0] values. The largest couplings differ by about 30%. In the improved Poisson-TrEsp approach we use the same uncalibrated couplings VP-TrEspMN and transition dipole moment magnitudes ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) M0 and
M0 and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) N0 as in the original approach, but include the average reaction field factor frf = 1.44 from the present FMO0/PCM[0]/TDDFT/CAM-B3LYP calculations. In addition, we replace the D0 value of the empty spherical cavity model by the D0 = 20.2 D2 obtained from the empirical fit of the experimental dipole strength of the 0–0 transition of Chl a (the black line in Fig. 3). The resulting excitonic couplings Ṽ0–0,P-TrEspMN are within 10% of the FMO0/PCM[0] values and the values for the strongly coupled pigments are close to the value of 83 cm−1 that has been inferred59 from a fit of the optical spectra. The latter are analyzed next.
N0 as in the original approach, but include the average reaction field factor frf = 1.44 from the present FMO0/PCM[0]/TDDFT/CAM-B3LYP calculations. In addition, we replace the D0 value of the empty spherical cavity model by the D0 = 20.2 D2 obtained from the empirical fit of the experimental dipole strength of the 0–0 transition of Chl a (the black line in Fig. 3). The resulting excitonic couplings Ṽ0–0,P-TrEspMN are within 10% of the FMO0/PCM[0] values and the values for the strongly coupled pigments are close to the value of 83 cm−1 that has been inferred59 from a fit of the optical spectra. The latter are analyzed next.
4.5 Optical spectra of WSCP
The optical spectra obtained for the calibrated FMO0/PCM[0] excitonic couplings and couplings obtained with the original and the improved Poisson-TrEsp approach are compared with the experimental data48 in Fig. 6. The parameters of our exciton model (namely, local excitation energy, width of the inhomogeneous distribution function for the local excitation energies, Huang–Rhys-factor of the low-frequency part of the spectral density, pure-dephasing time) have been inferred before from comparison of calculated and measured absorption and hole-burning spectra.59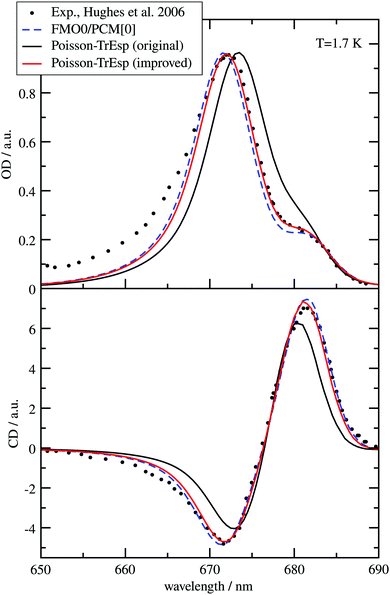 | ||
| Fig. 6 Comparison of low-temperature optical spectra of WSCP dimers calculated with calibrated excitonic couplings (the average of 1–2 and 3–4 couplings in the 3rd, 5th and 6th column of Table 8), obtained in the present work (lines), with experimental absorption (upper part) and circular dichroism (lower part) spectra48 (circles). The black solid line is obtained for the standard Poisson-TrEsp coupling that neglects reaction field effects, the blue dashed line is calculated with the FMO0/PCM[0] coupling and the solid red line with the improved Poisson-TrEsp coupling. | ||
Due to the open-sandwich geometry of the transition dipole moments of the two chromophores in the dimer, the upper exciton state has the major part of the oscillator strength and the low-energy exciton transition appears only as a shoulder in the linear absorption spectrum. The obtained excitonic CD spectrum clearly shows the two transitions, that have a sign-inverted rotational strength of the same magnitude. Whereas the original Poisson-TrEsp method underestimates the splitting between the two exciton transitions, the FMO[0]/PCM[0] and improved Poisson-TrEsp couplings result in optical spectra that fit the experimental optical spectra very well. Because the high-frequency intramolecular modes were not explicitly included in the calculations of the spectra, deviations appear between the calculated and measured absorption spectra (Fig. 6) at high energies (λ < 665 nm). Whereas the low-frequency vibrations, which appear close to the 0–0 transitions determining the main part of the spectra (λ > 665 nm), are included in our lineshape theory, the high-frequency intramolecular vibrations would have to be treated separately, because an unphysical scaling of the Huang–Rhys factors with the inverse participation ratio of exciton states would result.81 Note however that, the effect of the intramolecular vibronic coupling on the dipole strength of the 0–0 transition is included in the calculations.
5. Discussion
The Förster resonance energy transfer method based on the fragment molecular orbital and time-dependent density functional theory has been extended to describe excitonic couplings in solvent/protein environment that is approximated by a homogeneous continuum characterized by an optical dielectric constant.By varying the calculation level, it is possible to extract valuable physical insight into the physicochemical factors affecting the excitonic coupling. Namely, from the difference between FMO0 and FMO1 results, one can evaluate the importance of the polarization of a chromophore by the other chromophores. From the difference between the results obtained from the transition density in vacuum and in protein/solvent environment, one can evaluate the importance of the polarization of the chromophores by the chromophore-induced dynamic environmental polarization (the reaction field effect). From the explicit contribution of the dynamic environmental polarization, one can evaluate the screening of the electrostatic coupling between the transition densities of the chromophores.
Key features of the different methods to calculate excitonic coupling here, are summarized in Table 9. The original Poisson-TrEsp method misses the reaction field enhancement of the dipole strength of the chromophores. The improved Poisson-TrEsp method includes this effect, using an average reaction field factor derived from FMO0/PCM[0] calculations. The latter method allows for a site-specific calculation of the reaction field enhancement. Finally, the FMO1/PCM[1] method includes the mutual polarization of ground state charge densities of the chromophores, that is neglected by the other three methods.
| Method | Screeninga | Reaction fieldb | Mutual polarizationc |
|---|---|---|---|
| a Explicit screening by the chromophore-protein/solvent electrostatic interaction. b Implicit polarization of the chromophores by the protein/solvent environment. c Mutual polarization of the chromophores. | |||
| Poisson-TrEsp (original) | Yes | No | No |
| Poisson-TrEsp (improved) | Yes | Yes | No |
| FMO0/PCM[0] | Yes | Yes | No |
| FMO1/PCM[1] | Yes | Yes | Yes |
The developed methods have been applied to the WSCP complex containing four chromophore units, in which electronic excitations are coupled. It has been shown that both the reaction field enhancement of the dipole strength of the chromophores as well as the explicit screening of the excitonic coupling are very important, whereas the site-dependence of the reaction field effect and the mutual polarization of electronic ground states are small effects. An improvement of the standard Poisson-TrEsp model has been suggested based on these findings, namely, to use a single scaling factor describing the polarization of the chromophore due to the reaction field, that was neglected before.
Note that the error compensation effect present in the description of the dipole strength with the empty spherical cavity model in Fig. 3, resulting from the assumption of a spherical cavity and the neglect of reaction field effects, is practically absent in the standard Poisson-TrEsp calculations, because a realistic molecular cavity is used in the latter. The only remaining relict of this error compensation is given by the calibration of the vacuum dipole strength of the chromophores with respect to the value D0 = 21.0 D2 obtained from the empty spherical cavity analysis of the experimental dipole strength that is slightly larger than the empirical value D0 = 20.2 D2. However, the ratio of these two values (1.04) is much smaller than the average reaction field factor frf = 1.44 resulting from the present FMO0/PCM[0] calculations. For complete error compensation these two factors should be equal.
One might wonder, if instead of going one step ahead in the theory and include reaction field effects in Poisson-TrEsp, it would also be possible to go one step back, rely again on error compensation effects, and use a spherical cavity in the calculation of the screening. In order to obtain an analytical estimate, we approximate the transition density of each chromophore M by a non-polarizable point dipole ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) M0 in the center of a spherical cavity with ε = 1 inside and ε = n2 outside the cavity. Neglecting the presence of the cavity of all other chromophores in the solution of the Poisson equation for the ESP φM(r) of the Mth chromophore, results in72
M0 in the center of a spherical cavity with ε = 1 inside and ε = n2 outside the cavity. Neglecting the presence of the cavity of all other chromophores in the solution of the Poisson equation for the ESP φM(r) of the Mth chromophore, results in72
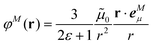 | (50) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) M0 is expressed as
M0 is expressed as ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 0eMμ using a unit vector eMμ. In the spirit of eqn (3) and (7), this ESP may be dissected,
0eMμ using a unit vector eMμ. In the spirit of eqn (3) and (7), this ESP may be dissected,| φM(r) = φM,0(r) + φM,expl(r), | (51) |
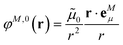 | (52) |
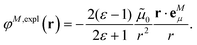 | (53) |
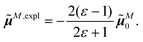 | (54) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) M0 and
M0 and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) N0 and Vexpl,μMN is the coupling between the explicit transition dipole
N0 and Vexpl,μMN is the coupling between the explicit transition dipole ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) M,expl of the solvent (induced by chromophore M) and the vacuum transition dipole
M,expl of the solvent (induced by chromophore M) and the vacuum transition dipole ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0e0.gif) N0 of chromophore N. With eqn (54), Vexpl,μMN can be expressed as
N0 of chromophore N. With eqn (54), Vexpl,μMN can be expressed as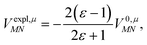 | (55) |
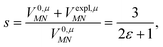 | (56) |
Because the screening factors obtained in the analytical model and in the numerical calculations (Tables 2 and 5) are close, the assumption of a spherical cavity in the screening calculations cannot compensate for the neglect of the reaction field effects in the calculation of excitonic couplings. This kind of error compensation seems to be unique for the calculation of the dipole strength in different solvents (the blue line in Fig. 3).
Improving the Poisson-TrEsp method by including the reaction field effects, results in an average excitonic coupling of 85 cm−1 between the strongly coupled Chl a chromophores in WSCP providing an excellent agreement between calculated and experimental linear absorption and circular dichroism spectra (Fig. 6). Can this reaction field factor be applied to other antenna complexes containing Chl a chromophores? What are the limitations and uncertainties of the present estimate of frf and calibration of the excitonic couplings? These and related questions are discussed in the following.
Our average reaction field factor frf = 1.44 neglects any qualitative change of the transition density of the chromophore by the reaction field of the protein/solvent environment, not described by a single scaling factor. The present analysis of the transition dipole moments of the chromophores and of the electrostatic potential of the reaction field contribution to the transition density (Fig. 5b) indeed show that the major effect of the environment is on the magnitude and not on the direction of the transition dipole. Further support is obtained from the perfect correlation between the ESP of the transition density of the chromophores calculated in vacuum and in the dielectric environment (Fig. S3, ESI†). Consequently, the calibrated Poisson-TrEsp couplings (neglecting the change in shape of the transition density) and the calibrated FMO/PCM couplings (taking into account a change in shape of the transition density) agree very well. From the present FMO0/PCM[0] calculations of the excitonic couplings between the 4 Chl a chromophores the reaction field factors are all within a few percent, suggesting that it is the immediate pigment environment that has the strongest influence. Indeed, a very similar reaction field factor frf = 1.46 is obtained, if instead of all pigment subcavities just the one of the pigments, for which the transition density is calculated, is included. This result is in agreement with independent PCM calculations on a different system (the reaction center of photosystem II).39 As seen in Fig. S1 (ESI†), the ratio between the dipole strength obtained by including just the subcavity of one pigment and that by including also that of the other, varies by at most 8 percent between short and long inter-pigment distances.
As noted before, by calibrating the Poisson-TrEsp as well as the FMO[0]/PCM[0] couplings, according to the experimental vacuum dipole strength of the chromophore we implicitly assume that the quantum chemical vacuum transition dipole moment is not too far from the experimental value. Since the reaction field factor is determined in a self-consistent way in PCM calculations, the reaction field can, in principle, depend in a non-linear way on the transition density of the chromophore, which limits a linear correction to small differences in the transition densities. In order to compare the calculated and measured transition dipole moments, we also have to take into account that the experimental value refers to the 0–0 transition of Chl a, that is, the transition that does not involve the excitation of high-frequency intramolecular vibrational modes. In the Condon approximation,1 the transition dipole moment of the 0–0 transition is related to the full dipole moment by a factor exp(−S/2) with the total Huang–Rhys factor S (eqn (33)).
The relevant quantum-mechanical dipole strength D(0–0)0 of the 0–0 transitions is related to the calculated vacuum dipole moment magnitude by
| D(0–0)0 = e−Sμ02. | (57) |
With the average vacuum dipole moment magnitude of 5.34 D (Table 1) and the total Huang–Rhys factor S = 0.23 of the high-frequency intramolecular modes of Chl a in WSCP, determined above, a quantum chemical vacuum dipole strength of the 0–0 transition D(0–0)0 = 22.7 D2 results, which is reasonably close to the experimental value (D(0–0)exp = 20.2 D2) to justify a linear correction. A certain robustness of this calibration procedure is seen in the improved Poisson-TrEsp method, where the transition charges of non-hydrogen atoms, obtained earlier71 from a fit of the ESP of the transition density of isolated Chl a, calculated with TDDFT/B3LYP are placed on the respective atom positions of the chromophores in the crystal structure of WSCP. The average dipole strength obtained in this way for the 4 chromophores is 25.9 D2, which deviates somewhat stronger from the experimental value than the FMO0/PCM[0]/CAM-B3LYP value. Nevertheless, the calibrated excitonic couplings, obtained with the two methods, are very close.
In order to investigate the robustness of this calibration procedure further, we performed additional FMO[0]/PCM[0] calculations, where the excited state calculations were performed with CIS (configuration interaction with single excitations) using molecular orbitals from Hartree–Fock (HF/CIS) and with TDDFT/B3LYP calculations, in order to compare these results with those obtained above using TDDFT/CAM-B3LYP. In case of HF/CIS, an average vacuum transition dipole moment of 6.23 D is obtained (for individual values see Table S12, ESI†) that gives rise to a 0–0 transition dipole strength of 30.8 D2. This value is considerably larger than the experimental value (20.2 D2). Nevertheless, the majority of the calibrated excitonic couplings is within 10% of the corresponding TDDFT/CAM-B3LYP values (Table 10, 3rd and 6th columns). The largest deviations of 20% are obtained for the intermediate couplings. The smaller values of the HF/CIS couplings reflect the smaller reaction field effect obtained with this method (Fig. 3). An estimation of the cavity field effect with PCM calculations could help to improve the description of the experimental dipole strengths in Fig. 3 and on this basis decide which of the two descriptions (TDDFT or HF/CIS) is more realistic. In case of TDDFT/B3LYP the deviations with respect to the TDDFT/CAM-B3LYP values are less than 10% for all couplings (Table 10, 3rd and 5th columns).
| M | N | CAM-B3LYPa | CAM-B3LYPb | B3LYPc | HF/CISd | HF/CISe |
|---|---|---|---|---|---|---|
| a Same as in 3rd column of Table 8. b Using a different optimized geometry based on dimer calculations (coordinates are given in the ESI, Table S3), as described in the methods section, original data are given in the ESI, Tables S4 and S5. c Full data are given in Tables S14 and S15 (ESI). d Full data are given in Tables S12 and S13 (ESI). e Using a different geometry optimization (coordinates are given in Table S16, ESI), based on HF, original data are given in Tables S17 and S18 (ESI). | ||||||
| 3 | 4 | 92 | 84 | 93 | 85 | 91 |
| 1 | 2 | 90 | 85 | 91 | 83 | 92 |
| 2 | 3 | 21 | 21 | 23 | 17 | 15 |
| 1 | 4 | 20 | 20 | 21 | 16 | 14 |
| 2 | 4 | 7 | 7 | 6 | 6 | 7 |
| 1 | 3 | 6 | 7 | 6 | 5 | 5 |
If the geometry optimization, performed above with DFT/CAM-B3LYP, is instead done with HF, the HF/CIS calculations result in calibrated excitonic couplings that in the majority of cases are even closer to the TDDFT/CAM-B3LYP results (Table 10, 3rd and 7th columns). If rather than a monomer, a dimer optimization with DFT/CAM-B3LYP is used, as described in the methods section, the resulting calibrated TDDFT/CAM-B3LYP couplings are all within 10% of the original TDDFT/CAM-B3LYP couplings (Table 10, 3rd and 4th columns). These results on one hand justify our linear scaling procedure and on the other hand they demonstrate a great robustness of our methods with respect to the details of the quantum chemical method used. Note that, besides the redistribution of oscillator strength discussed in Section 2.7, there are additional subtleties as a Dushinsky rotation of normal modes,101 Jahn–Teller corrections102 to the Condon approximation that have an influence on the exact value of the (effective) Huang–Rhys factor. However, these additional effects are small compared to the 3.5 fold correction found above (eqn (44)).
Our estimates rely on the validity of the PCM model, that describes the solvent and protein environment by a simple homogeneous dielectric continuum. One way to check this approximation is to include the heterogeneous polarizability of the protein in the calculations. QM/MMPol calculations that take into account the chromophores on a quantum mechanical level and the protein/solvent environment by a classical polarizable force field, revealed a somewhat larger variation of the screening factor but a similar average value as PCM calculations for the excitonic couplings in a light-harvesting antenna of cryptophytes.103 As for the present system, screening factors smaller than one were obtained for cryptohytes. A detailed investigation of the contribution of environmental molecules to the screening factor of excitonic couplings in the LH2 light-harvesting complex of purple bacteria with QM/MMPol104 revealed that there can be parts of the environment that enhance the excitonic coupling and other parts that decrease it. The latter seem to prevail so that overall the excitonic coupling gets smaller, in agreement with the present and our earlier43 calculations which use a continuum description of the environment. Note, however, that in very few cases an enhancement was obtained.43
As discussed in the introduction, the QM/MMPol method was also applied to WSCP. This complex has the advantage that the largest coupling can be directly estimated from the splitting between the optical transitions in the spectra, as discussed above. Rosnik and Curutchet52 report that the average transition dipole moment magnitude of 8.75 D for the Chl a pigments in WSCP in their calculations includes a 25% increase by the protein/solvent environment. Hence, we obtain that the magnitude of the average vacuum transition dipole moment in their calculation is equal to 7.00 D. Using this value for ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) M0 and
M0 and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) N0 in eqn (32) together with the experimental vacuum dipole strength D0 = 20.2 D2 and the original average intradimer coupling52 (V12 + V34)/2 = 186 cm−1 results in a calibrated average coupling (Ṽ12 + Ṽ34)/2 = 76 cm−1, which is now within a 10 percent margin of the coupling obtained with the improved Poisson-TrEsp method that describes the optical spectra very well (Fig. 6).
N0 in eqn (32) together with the experimental vacuum dipole strength D0 = 20.2 D2 and the original average intradimer coupling52 (V12 + V34)/2 = 186 cm−1 results in a calibrated average coupling (Ṽ12 + Ṽ34)/2 = 76 cm−1, which is now within a 10 percent margin of the coupling obtained with the improved Poisson-TrEsp method that describes the optical spectra very well (Fig. 6).
The individual QM/MMPol couplings are given in the last column of Table 8. Let us have a look at the physical origin of the calibration factor, used above, that brought the ab initio coupling value of the QM/MMPol method so close to the experimental estimate. One part of the calibration is due to the renormalization of the excitonic coupling by the vibronic coupling. Using the total Huang–Rhys factor of the high-frequency intramolecular modes S = 0.23, discussed in Section 2.7, the overall excitonic coupling (V12 + V34)/2 = 186 cm−1 is reduced by a factor e−S = 0.79 to yield a coupling of 148 cm−1 between 0–0 transitions of the chromophores. The remaining deviation is due to the limitations of the semi-empirical Zerner's intermediate neglect of differential overlap (ZINDO) method used in the quantum-chemical calculations, which results in a vacuum transition dipole strength of the 0–0 transition of 49 D2 × e−S = 39 D2 (eqn (57)), which is almost twice as large as the experimental value D0 = 20.2 D2. Therefore, the linear calibration of the excitonic coupling (eqn (32)) becomes questionable and the good agreement of the calibrated coupling with the experimental estimate appears somewhat fortuitous.
Interestingly, the calibrated QM/MMPol couplings between chromophores 2 and 3 and between 1 and 4 are 30% smaller than the respective Poisson-TrEsp and FMO0/PCM[0] values, an effect that could be caused by the heterogeneous polarizability of the environment (an advantage of QM/MMPol). The 50% variation between the two smallest QM/MMPol couplings (1–3 and 2–4) implies that the D2 symmetry of the complex was broken in the MD simulations. The QM/MMPol calculations took into account protein-induced distortions of the pigments that should affect their excitonic couplings. In addition to the excitonic couplings, the spectral density of the exciton-vibrational coupling has been calculated in the QM/MMPol study52 and good agreement with the spectral density extracted by Pieper et al. from their experimental Δ-FLN spectra,49 using the standard electronic two state approach, was reported. The present 3.5 fold correction of the intramolecular Huang–Rhys factor of the chromophores (see Section 2.7) suggests that the above agreement is not as good as it was thought.52
The present analysis shows that the mutual polarization of the ground states of the chromophore, included in FMO1/PCM[1] and neglected in FMO0/PCM[0] has only a very minor effect on the excitonic couplings in WSCP. This result is consistent with the fact that the excitonic couplings obtained for different static dielectric constants are practically identical (Table S19, ESI†).
It might be surprising at first glance that the FMO-TDDFT/PCM calculations and the Poisson-TrEsp calculations practically obtain identical screening factors of the excitonic interaction. As noted above, both calculations rely on a perturbative treatment of the screening and on classical electrostatics,43,67,100 solving the Poisson equation for the ESP of the transition density of the chromophores that are surrounded by a dielectric continuum with optical dielectric constant ε. In PCM a boundary element method is used for the solution of the Poisson equation, which allows one to represent the influence of the solvent by apparent surface charges on the chromophore subcavities. These surface charges are self-consistently determined with the transition density that polarizes the dielectric. Using perturbation theory,67,100 the overall Coulomb coupling is dissected into a direct interaction term that contains the influence of the solvent on the transition density and an indirect (screening) part that contains the Coulomb interaction of the solvent polarization induced by the transition density of one chromophore with the transition density of the other chromophore.
In Poisson-TrEsp,42,43 the Poisson equation is solved by a finite difference method revealing the overall ESP of the transition density of the chromophores that is used to calculate the overall excitonic coupling. By comparing this coupling with the vacuum coupling, the screening factor is obtained. In PCM this factor results from comparing the excitonic coupling with and without the explicit contribution of the solvent, but taking into account the implicit contribution of the solvent to the transition density of the chromophores. Since, however, the Poisson equation is linear in the transition density, the implicit contribution of the solvent, present in PCM and absent in Poisson-TrEsp, cancels out in the ratio of electrostatic couplings that defines the screening factor, as long as the transition densities with and without implicit environmental contribution differ only by a scalar constant. Therefore, both methods give the same value for the screening factor. Hence, Poisson-TrEsp is fully capable to resolve the slight rotation of the screened transition dipole moment seen in Fig. 5d.
There is a long-standing controversy concerning the distance dependence of the screening factor obtained with HF/CIS/PCM38,39 and Poisson-TrEsp calculations.43 Now that we know that Poisson-TrEsp and PCM-based methods should give almost identical screening factors, this controversy can be discussed in a more stringent manner. Whereas the PCM-based calculations on D1D2cytb559 complexes of photosystem II (containing 6 chlorophyll a and 2 pheophytin a pigments)38,39 reported an exponential distance dependence of the screening factor, the Poisson-TrEsp calculations on photosystem I trimers (containing 288 chlorophyll a pigments) suggested no systematic distance dependence.43 Instead, the screening factor was found to depend on the mutual orientation of the pigments. The present results are in agreement with this finding (see the screening factors in Table 2 and the distances in Table S1, ESI†). Chromophore pairs 1–2 and 3–4 with the smallest interchromophore distance (10 Å) have a larger screening factor than 2–3 and 1–4 and a smaller one than 2–4 and 1–3, although all the latter 4 pairs have a much larger pigment–pigment distance (20–21 Å). It seems that, either the number of pigment pairs in the PCM study38,39 was simply too small to draw any general conclusions, or the different assignment of the dielectric environment in the two methods is responsible for the different distance dependencies found. Whereas in the HF/CIS/PCM38,39 study the subcavities were just assigned to the two pigments for which the interaction was calculated, in the Poisson-TrEsp study43 all pigment subcavities were considered simultaneously, as done in the present study. Which of the two assigments is more realistic still has to be evaluated. If two pigments interact, the remaining pigments can be seen as polarizable environment. However, part of this polarization (the resonant transition) is explicitly included in the exciton Hamiltonian (eqn (22)). Hence, the polarization of the pigments via the remaining high-energy transitions has to be evaluated.
6. Conclusions
The polarizable continuum model (PCM) for the calculation of excitonic couplings in solvent/protein environments was implemented in the fragment molecular orbital (FMO) method and used for an in-depth analysis of the excitonic couplings in the water soluble chlorophyll binding protein WSCP.The previous QM/MMPol study52 of WSCP could not provide an explanation for the excitonic coupling in the Chl dimers of WSCP. In this work, the FMO/PCM method has been used to investigate this question. An important aspect of the analysis is to recognize that the splitting between the two low-energy exciton peaks in the experiment is determined by the excitonic coupling between the 0–0 transitions of the Chls. The dipole strength of the latter was inferred60 from experimental oscillator strengths in different solvents. Adjusting the quantum chemical transition density of the chromophores such that without surrounding medium, the experimental vacuum transition dipole moment of the 0–0 transition results, gives an excitonic coupling in the Chl a dimers of WSCP that is within 10% of the experimental estimate, not only for our FMO/PCM calculations and the improved Poisson-TrEsp method but also for the QM/MMPol value,52 providing excellent agreement between calculated and experimental optical spectra.
Our scaling in the calibrated excitonic couplings is robust against variations of the details of the quantum chemical method, as demonstrated by using different functionals in the TDDFT calculations and the HF/CIS method, different geometry optimizations (Table 10), as well as heavy atom transition charges71 and crystal-structure chromophore geometries used in the original and the present improved Poisson-TrEsp methods. Whereas previously59 the excitonic coupling in WSCP had to be treated as a free parameter, in this work, a structure-based calculation of this coupling has become possible. The coupling obtained with the original Poisson-TrEsp method is too small to reveal the full signature of the low-energy exciton state, which is hidden under the main absorption peak dominated by the high-energy exciton state (Fig. 6).
A detailed analysis of the FMO/PCM calculations reveals that the enhancement of the dipole strength of the chromophores by the polarization of the solvent/protein environment of one chromophore is rather insensitive to the presence of the other chromophores and that the main effect of the reaction field is indeed just a scalar amplification of the transition dipole moment. The screening part of the FMO/PCM calculations can be described quantitatively by the electrostatic Poisson-TrEsp method. The present results suggest a new calibration scheme for the atomic transition charges used in Poisson-TrEsp calculations. This new scheme takes into account reaction field effects by an average reaction field factor determined with FMO0/PCM[0] calculations. Together with the experimental vacuum dipole strength60D0 = 20.2 D2, this factor results in an effective transition dipole moment magnitude μP-TrEsp = 5.39 D to which the Poisson-TrEsp transition charges are to be scaled in the calculation of screening part of the coupling. Because the screening part of the coupling involves the solution of the Poisson equation that is linear in the transition charges, the previous Poisson-TrEsp couplings,105–108 that were obtained with transition charges scaled to a dipole moment squared equal to 21.0 D2 (obtained from an empty spherical cavity analysis of experimental dipole strengths), need to be multiplied by a factor (5.39 D)2/21.0 D2 = 1.38. Please note that this calibration factor contains the average reaction field factor, obtained by the present FMO0/PCM[0]/CAM-B3LYP calculations and a correction for the different vacuum dipole strengths used in the original and the improved Poisson-TrEsp method. In case of WSCP, the improved Poisson-TrEsp method leads to a significantly better agreement between calculated and experimental optical spectra than the original method (Fig. 6). We expect a similar improvement for the optical spectra and energy transfer calculations of other pigment–protein complexes containing Chl a chromophores.
The scaling factor of the improved Poisson-TrEsp method uses only the outcome from theoretical calculations (FMO-TDDFT/PCM) and a single experimental value of the vacuum dipole strength of the 0–0 transition of the pigments, that can be extrapolated from experimental values of the oscillator strength of a given pigment measured in solvents with different refractive index. Note that, such experimental data and extrapolations are available also for some other photosynthetic pigments (Chl b, bacteriochlorophyll a (BChl a), BChl c),60 but with somewhat larger uncertainty than for Chl a. Hence, additional experiments for these and other pigments would be helpful. Besides the molecular structure and the vacuum dipole strength of the pigments, no other experimental input is needed to accurately predict the excitonic couplings with the present methods.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Support by the Austrian Science Fund (FWF) through grant P 33155-NBL (T. R.) is gratefully acknowledged.References
- V. May and O. Kühn, Charge and energy transfer dynamics in molecular systems. Wiley, Weinheim, 2011 Search PubMed.
- in FRET – Förster resonance energy transfer, ed. I. Medintz and N. Hildebrandt, Wiley, Weinheim, 2013 Search PubMed.
- in Light-harvesting in photosynthesis, ed. R. Croce, R. van Grondelle, H. van Amerongen and I. van Stokkum, CRC Press, Boca Rata, 2018 Search PubMed.
- T. Renger and F. Müh, Understanding photosynthetic light-harvesting: A bottom up theoretical approach, Phys. Chem. Chem. Phys., 2013, 15, 3348–3371 RSC.
- L. Stryer and R. P. Haugland, Energy transfer – a spectroscopic ruler, Proc. Natl. Acad. Sci. U. S. A., 1967, 58, 719–726 CrossRef CAS PubMed.
- B. Schuler, Single-molecule fluorescence spectroscopy of protein folding, ChemPhysChem, 2005, 6, 1206–1220 CrossRef CAS PubMed.
- F. Villafiorita-Monteleone, A. Cappelli, M. Paolino, M. Colombo, E. Cariati, A. Mura, G. Bongiovanni and C. Botta, Aggregation-induced Förster resonance energy transfer in polybenzofulvene/dye nanoparticles, J. Phys. Chem. C, 2015, 119, 18986–18991 CrossRef CAS.
- K. Feron, W. J. Belcher, C. J. Fell and P. C. Dastoor, Organic solar cells: Understanding the role of Förster resonance energy transfer, Int. J. Mol. Sci., 2012, 13, 17019–17047 CrossRef CAS PubMed.
- R. E. Blankenship, Molecular Mechanisms of Photosynthesis, Blackwell Science, 2002 Search PubMed.
- P. G. Szalay, T. Müller, G. Gidofalvi, H. Lischka and R. Shepard, Multiconfiguration self-consistent field and multireference configuration interaction methods and applications, Chem. Rev., 2012, 112, 108–181 CrossRef CAS PubMed.
- M. E. Casida and M. Huix-Rotllant, Progress in time-dependent density-functional theory, Annu. Rev. Phys. Chem., 2012, 63, 287–323 CrossRef CAS PubMed.
- Z.-Q. You and C.-P. Hsu, Theory and calculation for the electronic coupling in excitation energy transfer, Int. J. Quantum Chem., 2014, 114, 102–115 CrossRef CAS.
- L. Cupellini, M. Corbella, B. Mennucci and C. Curutchet, Electronic energy transfer in biomacromolecules, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 9, e1392 Search PubMed.
- M. S. Gordon, S. R. Pruitt, D. G. Fedorov and L. V. Slipchenko, Fragmentation methods: A route to accurate calculations on large systems, Chem. Rev., 2012, 112, 632–672 CrossRef CAS PubMed.
- T. Fang, Y. Li and S. Li, Generalized energy-based fragmentation approach for modeling condensed phase systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1297 Search PubMed.
- J. Liu, J. Z. H. Zhang and X. He, Fragment quantum chemical approach to geometry optimization and vibrational spectrum calculation of proteins, Phys. Chem. Chem. Phys., 2016, 18, 1864–1875 RSC.
- S. S. Khire, L. J. Bartolotti and S. R. Gadre, Harmonizing accuracy and efficiency: A pragmatic approach to fragmentation of large molecules, J. Chem. Phys., 2018, 149, 064112 CrossRef PubMed.
- B. Thapa and K. Raghavachari, Decomposition analysis of protein–ligand interactions using molecules-in-molecules fragmentation-based method, J. Chem. Inf. Model., 2019, 59, 3474–3484 CrossRef CAS PubMed.
- K.-Y. Liu and J. M. Herbert, Energy-screened many-body expansion: A practical yet accurate fragmentation method for quantum chemistry, J. Chem. Theory Comput., 2020, 16, 475–487 CrossRef PubMed.
- A. Sisto, D. R. Glowacki and T. J. Martinez, Ab initio nonadiabatic dynamics of multichromophore complexes: A scalable graphical-processing-unit-accelerated exciton framework, Acc. Chem. Res., 2014, 47, 2857–2866 CrossRef CAS PubMed.
- J. M. Herbert, X. Zhang, A. F. Morrison and J. Liu, Beyond time-dependent density functional theory using only single excitations: Methods for computational studies of excited states in complex systems, Acc. Chem. Res., 2016, 49, 931–941 CrossRef CAS PubMed.
- X. Li, R. M. Parrish, F. Liu, S. I. L. K. Schumacher and T. J. Martinez, An ab initio exciton model including charge-transfer excited states, J. Chem. Theory Comput., 2017, 13, 3493–3504 CrossRef CAS PubMed.
- R. A. Mata, H. Stoll and B. J. C. Cabral, A simple one-body approach to the calculation of the first electronic absorption band of water, J. Chem. Theory Comput., 2009, 5, 1829–1837 CrossRef CAS PubMed.
- Y. Kim, D. Morozov, V. Stadnytskyi, S. Savikhin and L. V. Slipchenko, Predictive first-principles modeling of a photosynthetic antenna protein: The Fenna–Matthews–Olson complex, J. Phys. Chem. Lett., 2020, 11, 1636–1643 CrossRef CAS PubMed.
- M. Kobayashi and H. Nakai, How does it become possible to treat delocalized and/or open-shell systems in fragmentation-based linear-scaling electronic structure calculations? The case of the divide-and-conquer method, Phys. Chem. Chem. Phys., 2012, 14, 7629–7639 RSC.
- K. Kitaura, E. Ikeo, T. Asada, T. Nakano and M. Uebayasi, Fragment molecular orbital method: An approximate computational method for large molecules, Chem. Phys. Lett., 1999, 313, 701–706 CrossRef CAS.
- D. G. Fedorov and K. Kitaura, Extending the power of quantum chemistry to large systems with the fragment molecular orbital method, J. Phys. Chem. A, 2007, 111, 6904–6914 CrossRef CAS PubMed.
- S. Tanaka, Y. Mochizuki, Y. Komeiji, Y. Okiyama and K. Fukuzawa, Electron-correlated fragment-molecular-orbital calculations for biomolecular and nano systems, Phys. Chem. Chem. Phys., 2014, 16, 10310–10344 RSC.
- D. G. Fedorov, The fragment molecular orbital method: Theoretical development, implementation in GAMESS, and applications, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1322 Search PubMed.
- M. Chiba, D. G. Fedorov and K. Kitaura, Time-dependent density functional theory with the multilayer fragment molecular orbital method, Chem. Phys. Lett., 2007, 444, 346–350 CrossRef CAS.
- M. Chiba, D. G. Fedorov and K. Kitaura, Polarizable continuum model with the fragment molecular orbital-based time-dependent density functional theory, J. Comput. Chem., 2008, 29, 2667–2676 CrossRef CAS PubMed.
- D. S. Kaliakin, H. Nakata, Y. Kim, Q. Chen, D. G. Fedorov and L. V. Slipchenko, FMOxFMO: Elucidating excitonic interactions in the Fenna–Matthews–Olson complex with the fragment molecular orbital method, J. Chem. Theory Comput., 2020, 16, 1175–1187 CrossRef CAS PubMed.
- Y. Mochizuki, S. Koikegami, S. Amari, K. Segawa, K. Kitaura and T. Nakano, Configuration interaction singles method with multilayer fragment molecular orbital scheme, Chem. Phys. Lett., 2005, 406, 283–288 CrossRef CAS.
- T. Fujita and Y. Mochizuki, Development of the fragment molecular orbital method for calculating nonlocal excitations in large molecular systems, J. Phys. Chem. A, 2018, 122, 3886–3898 CrossRef CAS PubMed.
- T. Ikegami, T. Ishida, D. G. Fedorov, K. Kitaura, Y. Inadomi, H. Umeda, M. Yokokawa and S. Sekiguchi, Fragment molecular orbital study of the electronic excitations in the photosynthetic reaction center of Blastochloris viridis, J. Comput. Chem., 2010, 31, 447–454 CAS.
- T. Fujita and Y. Noguchi, Fragment-based excited-state calculations using the GW approximation and the Bethe–Salpeter equation, J. Phys. Chem. A, 2021, 125, 10580–10592 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Quantum mechanical continuum solvation models, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- G. D. Scholes, C. Curutchet, B. Mennucci, R. Cammi and J. Tomasi, How solvent controls electronic energy transfer and light harvesting, J. Phys. Chem. B, 2007, 111, 6978–6982 CrossRef CAS PubMed.
- C. Curutchet, G. D. Scholes, B. Mennucci and R. Cammi, How solvent controls electronic energy transfer and light harvesting: Toward a quantum-mechanical description of reaction field and screening effects, J. Phys. Chem. B, 2007, 111, 13253–13265 CrossRef CAS PubMed.
- B. Mennucci and C. Curutchet, The role of the environment in electronic energy transfer: A molecular modeling perspective, Phys. Chem. Chem. Phys., 2011, 13, 11538–11550 RSC.
- J. Adolphs and T. Renger, How proteins trigger excitation energy transfer in the FMO complex of green sulfur bacteria, Biophys. J., 2006, 91, 2778–2797 CrossRef CAS PubMed.
- J. Adolphs, F. Müh, M. E. Madjet and T. Renger, Calculation of pigment transition energies in the FMO protein: From simplicity to complexity and back, Photosynth. Res., 2008, 95, 197–209 CrossRef CAS PubMed.
- T. Renger and F. Müh, Theory of excitonic couplings in dielectric media: Foundation of Poisson-TrEsp method and application to photosystem I trimers, Photosynth. Res., 2012, 111, 47–52 CrossRef CAS PubMed.
- T. Renger, I. Trostmann, C. Theiss, M. E. Madjet, M. Richter, H. Paulsen, H.-J. Eichler, A. Knorr and G. Renger, Refinement of a structural model of a pigment–protein complex by accurate optical line shape theory and experiments, J. Phys. Chem. B, 2007, 111, 10487–10501 CrossRef CAS PubMed.
- T. Renger, M. E. Madjet, F. Müh, I. Trostmann, F.-J. Schmitt, C. Theiss, H. Paulsen, H.-J. Eichler, A. Knorr and G. Renger, Thermally activated superradiance and intersystem crossing in the water-soluble chlorophyll binding protein, J. Phys. Chem. B, 2009, 113, 9948–9957 CrossRef CAS PubMed.
- H. Satoh, A. Uchida, K. Nakayama and M. Okada, Water-soluble chlorophyll protein in brassicaceae plants is a stress-induced chlorophyll-binding protein, Plant Cell Physiol., 2001, 42, 906–911 CrossRef CAS PubMed.
- P. Girr and H. Paulsen, How water-soluble chlorophyll protein extracts chlorophyll from membranes, Biochim. Biophys. Acta, 2021, 1863, 183479 CrossRef CAS PubMed.
- J. L. Hughes, R. Razeghifard, M. Logue, A. Oakley, T. Wydrzynski and E. Krausz, Magneto-optic spectroscopy of a protein tetramer binding two exciton-coupled chlorophylls, J. Am. Chem. Soc., 2006, 128, 3649–3658 CrossRef CAS PubMed.
- J. Pieper, M. Rätsep, I. Trostmann, H. Paulsen, G. Renger and A. Freiberg, Excitonic energy level structure and pigment–protein interactions in the recombinant water-soluble chlorophyll protein. I. Difference fluorescence line-narrowing, J. Phys. Chem. B, 2011, 115, 4042–4052 CrossRef CAS PubMed.
- J. Pieper, M. Rätsep, I. Trostmann, F.-J. Schmitt, C. Theiss, H. Paulsen, H. J. Eichler, A. Freiberg and G. Renger, Excitonic energy level structure and pigment–protein interactions in the recombinant water-soluble chlorophyll protein. II. Spectral hole-burning experiments, J. Phys. Chem. B, 2011, 115, 4053–4065 CrossRef CAS PubMed.
- J. Alster, H. Lokstein, J. Dostál, A. Uchida and D. Zigmantas, 2D spectroscopy study of water-soluble chlorophyll-binding protein from Lepidium virginicum, J. Phys. Chem. B, 2014, 118, 3524–3531 CrossRef CAS PubMed.
- A. M. Rosnik and C. Curutchet, Theoretical characterization of the spectral density of the water-soluble chlorophyll-binding protein from combined quantum mechanics/molecular mechanics molecular dynamics simulations, J. Chem. Theory Comput., 2015, 11, 5826–5837 CrossRef CAS PubMed.
- D. Bednarczyk, O. Dym, V. Prabahar, Y. Peleg, D. H. Pike and D. Noy, Fine tuning of chlorophyll spectra by protein-induced ring deformation, Angew. Chem., Int. Ed., 2016, 55, 6901–6905 CrossRef CAS PubMed.
- A. Agostini, D. M. Palm, H. Paulsen and D. Carbonera, Optically detected magnetic resonance of chlorophyll triplet statesin water-soluble chlorophyll proteins from Lepidium virginicum: Evidence for excitonic interaction among the four pigments, J. Phys. Chem. B, 2018, 122, 6156–6163 CrossRef CAS PubMed.
- D. M. Palm, A. Agostini, V. Averesch, P. Girr, M. Werwie, S. Takahashi, H. Satoh, E. Jaenicke and H. Paulsen, Chlorophyll a/b binding-specificity in water-soluble chlorophyll protein, Nat. Plants, 2018, 4, 920–929 CrossRef CAS PubMed.
- V. Prabahar, L. Afruiat-Jurnou, I. Paluy, Y. Peleg and D. Noy, New homologues of Brassicaceae water-soluble chlorophyll proteins shed light on chlorophyll binding, spectral tuning, and molecular evolution, FEBS J., 2020, 287, 991–1004 CrossRef CAS PubMed.
- E. Fresch, E. Meneghin, A. Agostini, H. Paulsen, D. Carbonera and E. Collini, How the protein environment can tune the energy, the coupling, and the ultrafast dynamics of interacting chlorophylls: The example of the water-soluble chlorophyll protein, J. Phys. Chem. Lett., 2020, 11, 1059–1067 CrossRef CAS PubMed.
- Y. Lahav, D. Noy and I. Schapiro, Spectral tuning of chlorophylls in proteins – electrostatics vs. ring deformation, Phys. Chem. Chem. Phys., 2021, 23, 6544–6551 RSC.
- J. Adolphs, M. Berrer and T. Renger, Hole-burning spectroscopy on excitonically coupled pigments in proteins: Theory meets experiment, J. Am. Chem. Soc., 2016, 138, 2993–3001 CrossRef CAS PubMed.
- R. S. Knox, Dipole and oscillator strengths of chromophores in solution, Photochem. Photobiol., 2003, 77, 492–496 CrossRef CAS PubMed.
- T. Nakano, T. Kaminuma, T. Sato, Y. Akiyama, M. Uebayasi and K. Kitaura, Fragment molecular orbital method: Application to polypeptides, Chem. Phys. Lett., 2000, 318, 614–618 CrossRef CAS.
- D. G. Fedorov, J. H. Jensen, R. C. Deka and K. Kitaura, Covalent bond fragmentation suitable to describe solids in the fragment molecular orbital method, J. Phys. Chem. A, 2008, 112, 11808–11816 CrossRef CAS PubMed.
- H. Li, D. G. Fedorov, T. Nagata, K. Kitaura, J. H. Jensen and M. S. Gordon, Energy gradients in combined fragment molecular orbital and polarizable continuum model (FMO/PCM) calculation, J. Comput. Chem., 2010, 31, 778–790 CrossRef CAS PubMed.
- D. G. Fedorov and K. Kitaura, Pair interaction energy decomposition analysis, J. Comput. Chem., 2007, 28, 222–237 CrossRef CAS PubMed.
- M. Chiba, D. G. Fedorov and K. Kitaura, Time-dependent density functional theory based upon the fragment molecular orbital method, J. Chem. Phys., 2007, 127, 104108 CrossRef PubMed.
- H. Fukunaga, D. G. Fedorov, M. Chiba, K. Nii and K. Kitaura, Theoretical analysis of the intermolecular interaction effects on the excitation energy of organic pigments: Solid state quinacridone, J. Phys. Chem. A, 2008, 112, 10887–10894 CrossRef CAS PubMed.
- M. F. Iozzi, B. Menucci, J. Tomasi and R. Cammi, Excitation energy transfer (EET) between molecules in condensed matter: A novel application of the polarizable continuum model (PCM), J. Chem. Phys., 2004, 120, 7029–7040 CrossRef CAS PubMed.
- D. G. Fedorov, Solvent screening in zwitterions analyzed with the fragment molecular orbital method, J. Chem. Theory Comput., 2019, 15, 5404–5416 CrossRef CAS PubMed.
- D. G. Fedorov, Partition analysis for density-functional tight-binding, J. Phys. Chem. A, 2020, 124, 10346–10358 CrossRef CAS PubMed.
- D. G. Fedorov, A. Brekhov, V. Mironov and Y. Alexeev, Molecular electrostatic potential and electron density of large systems in solution computed with the fragment molecular orbital method, J. Phys. Chem. A, 2019, 123, 6281–6290 CrossRef CAS PubMed.
- M. E. Madjet, A. Abdurahman and T. Renger, Intermolecular Coulomb couplings from ab initio electrostatic potentials: Application to optical transitions of strongly coupled pigments in photosynthetic antennae and reaction centers, J. Phys. Chem. B, 2006, 110, 17268–17281 CrossRef CAS PubMed.
- C. J. F. Böttcher, Theory of Electric Polarization, Elsevier, 1973 Search PubMed.
- R. Cammi, B. Mennucci and J. Tomasi, On the calculation of local field factors for microscopic static hyperpolarizabilities of molecules in solution with the aid of quantum-mechanical methods, J. Phys. Chem. A, 1998, 102, 870–875 CrossRef CAS.
- D. Lindorfer, F. Müh and T. Renger, Origin of non-conservative circular dichroism of the CP29 antenna complex of photosystem II, Phys. Chem. Chem. Phys., 2017, 19, 7524–7536 RSC.
- D. Lindorfer, F. Müh, R. Purchase, E. Krausz and T. Renger, Non-conservative circular dichroism of photosystem II reaction centers: Is there an enhancement by a coupling with charge transfer states?, J. Photochem. Photobiol., A, 2021, 404, 112883 CrossRef CAS.
- T. Renger and R. A. Marcus, On the relation of protein dynamics and exciton relaxation in pigment–protein complexes: An estimation of the spectral density and a theory for the calculation of optical spectra, J. Chem. Phys., 2002, 116, 9997–10019 CrossRef CAS.
- T. Renger, A. Klinger, F. Steinecker, M. Schmidt am Busch, J. Numata and F. Müh, Normal mode analysis of the spectral density of the Fenna–Matthews–Olson light-harvesting protein: How the protein dissipates the excess energy of excitons, J. Phys. Chem. B, 2012, 116, 14565–14580 CrossRef CAS PubMed.
- A. Klinger, D. Lindorfer, F. Müh and T. Renger, Normal mode analysis of spectral density of FMO trimers: Intra- and intermonomer energy transfer, J. Chem. Phys., 2020, 153, 215103 CrossRef CAS PubMed.
- M. L. Chaillet, F. Lengauer, J. Adolphs, F. Müh, A. S. Fokas, D. J. Cole, A. W. Chin and T. Renger, Static disorder in excitation energies of the Fenna–Matthews–Olson protein: Structure-based theory meets experiment, J. Phys. Chem. Lett., 2020, 11, 10306–10314 CrossRef CAS PubMed.
- F. Caycedo-Soler, A. Mattioni, J. Lim, T. Renger, S. F. Huelga and M. B. Plenio, Exact simulation of pigment—protein complexes: Vibronic renormalisation of electronic parameters in ultrafast spectroscopy, https://arxiv.org/abs/2106.14286.
- M. Reppert, Delocalization effects in chlorophyll fluorescence: Nonperturbative line shape analysis of a vibronically coupled dimer, J. Phys. Chem. B, 2020, 124, 10024–10033 CrossRef CAS PubMed.
- J. R. Reimers, Z. L. Cai, R. Kobayashi, M. Rätsep, A. Freiberg and E. Krausz, Assignment of the Q-bands of the chlorophylls: Coherence loss via Qx–Qy mixing, Sci. Rep., 2013, 3, 2761 CrossRef PubMed.
- D. G. Fedorov and K. Kitaura, The importance of three-body terms in the fragment molecular orbital method, J. Chem. Phys., 2004, 120, 6832–6840 CrossRef CAS PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen and S. Su, et al., General atomic and molecular electronic structure system, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. D. Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina and E. Guidez, et al., Recent developments in the general atomic and molecular electronic structure system, J. Chem. Phys., 2020, 152, 154102 CrossRef CAS PubMed.
- D. G. Fedorov, R. M. Olson, K. Kitaura, M. S. Gordon and S. Koseki, A new hierarchical parallelization scheme: Generalized distributed data interface (GDDI), and an application to the fragment molecular orbital method (FMO), J. Comput. Chem., 2004, 25, 872–880 CrossRef CAS PubMed.
- D. Horigome, H. Satoh, N. Itoh, K. Mitsunaga, I. Oonishi, A. Nakagawa and A. Uchida, structural mechanism and photoprotective function of water-soluble chlorophyll-binding protein, J. Biol. Chem., 2007, 282, 6525–6531 CrossRef CAS PubMed.
- Jmol: An open-source Java viewer for chemical structures in 3D, http://www.jmol.org/.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- M. Cossi and V. Barone, Time-dependent density functional theory for molecules in liquid solutions, J. Chem. Phys., 2001, 115, 4708–4717 CrossRef CAS.
- A. W. Lange and J. M. Herbert, Symmetric versus asymmetric discretization of the integral equations in polarizable continuum solvation models, Chem. Phys. Lett., 2011, 509, 77–87 CrossRef CAS.
- A. Klamt, C. Moya and J. Palomar, A comprehensive comparison of the IEFPCM and SS(V)PE continuum solvation methods with the COSMO approach, J. Chem. Theory Comput., 2015, 11, 4220–4225 CrossRef CAS PubMed.
- G. M. Ullmann and E.-W. Knapp, Electrostatic models for computing protonation and redox equilibria in proteins, Eur. Biophys. J., 1999, 28, 533–551 CrossRef CAS PubMed.
- A. Bondi, van der Waals volumes and radii, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- M. A. Spackman, Potential derived charges using a geodesic point selection scheme, J. Comput. Chem., 1996, 17, 1–18 CrossRef CAS.
- C. M. Breneman and K. B. Wiberg, Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- D. Bashford and K. Gerwert, Electrostatic calculations of the pKa values of ionizable groups in bacteriorhodopsin, J. Mol. Biol., 1992, 224, 473–486 CrossRef CAS PubMed.
- D. Bashford, An object-oriented programming suite for electrostatic effects in biological molecules, in Scientific computing in object-oriented parallel environments, ed. I. Yutaka, R. O. Rodney, V. W. R. John and T. Marydell, 1997, pp. 233–240 Search PubMed.
- S. Krawczyk, Electrochromism of chlorophyll-a monomer and special-pair dimer, Biochim. Biophys. Acta, 1991, 1056, 64–70 CrossRef CAS.
- C.-P. Hsu, G. R. Fleming, M. Head-Gordon and T. Head-Gordon, Excitation energy transfer in condensed media, J. Chem. Phys., 2001, 114, 3065–3072 CrossRef CAS.
- J. R. Reimers, M. Rätsep and A. Freiberg, Asymmetry in the Qy fluorescence and absorption spectra of chlorophyll a pertaining to exciton dynamics, Front. Chem., 2020, 8, 588289 CrossRef CAS PubMed.
- M. Rätsep, J. Linnanto and A. Freiberg, Mirror symmetry and vibrational structure in optical spectra of chlorophyll a, J. Chem. Phys., 2009, 130, 194501 CrossRef PubMed.
- C. Curutchet, J. Kongsted, A. Munoz-Losa, H. Hossein-Nejad, G. D. Scholes and B. Mennucci, Photosynthetic light-harvesting is tuned by the heterogeneous polarizable environment of the protein, J. Am. Chem. Soc., 2011, 133, 3078–3084 CrossRef CAS PubMed.
- M. Nottoli, S. Jurinovich, L. Cupellini, A. T. Gardiner, R. Cogdell and B. Mennucci, The role of charge-transfer states in the spectral tuning of antenna complexes of purple bacteria, Photosynth. Res., 2018, 137, 215–226 CrossRef CAS PubMed.
- J. Adolphs, F. Müh, M. E.-A. Madjet, M. Schmidt am Busch and T. Renger, Structure-based calculations of optical spectra of photosystem I suggest an asymmetric light-harvesting process, J. Am. Chem. Soc., 2010, 132, 3331–3343 CrossRef CAS PubMed.
- F. Müh, M. E.-A. Madjet and T. Renger, Structure-based identification of energy sinks in plant light-harvesting complex II, J. Phys. Chem. B, 2010, 114, 13517–13535 CrossRef PubMed.
- F. Müh, M. E.-A. Madjet and T. Renger, Structure-based simulation of linear optical spectra of the CP43 core antenna of photosystem II, Photosynth. Res., 2012, 111, 87–101 CrossRef PubMed.
- F. Müh, D. Lindorfer, M. Schmidt am Busch and T. Renger, Towards a structure-based exciton Hamiltonian for the CP29 antenna of photosystem II, Phys. Chem. Chem. Phys., 2014, 16, 11848–11863 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03566e |
| This journal is © the Owner Societies 2022 |