Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Real-time monitoring of aerosol particle formation from sulfuric acid vapor at elevated concentrations and temperatures†
Daniel
Becker
 a,
Jonas
Heitland
a,
Jonas
Heitland
 a,
Philip T. M.
Carlsson
a,
Philip T. M.
Carlsson
 b,
Jonas
Elm
b,
Jonas
Elm
 c,
Tinja
Olenius
c,
Tinja
Olenius
 d,
Sophia
Tödter
a,
Amir
Kharrazizadeh
a and
Thomas
Zeuch
d,
Sophia
Tödter
a,
Amir
Kharrazizadeh
a and
Thomas
Zeuch
 *a
*a
aGeorg-August-Universität Göttingen, Tammannstraße 6, 37077 Göttingen, Germany. E-mail: tzeuch1@gwdg.de
bForschungszentrum Jülich GmbH, Wilhelm-Johnen-Straße, 52425 Jülich, Germany
cAarhus Univerity, Langelandsgade 140, 8000 Aarhus C, Denmark
dSwedish Meteorological and Hydrological Institute, Air Quality Research Unit, Folkborgsvägen 17, SE-601 76 Norrköping, Sweden
First published on 31st January 2022
Abstract
In the present study, time-resolved aerosol particle formation from sulfuric acid vapor is examined with special attention to the stabilization of molecular clusters in the early phase of unary nucleation. An important factor governing this process is the amount of condensable acid vapor. Here it is produced from fast gas-phase reactions in a batch-type reaction cell for which we introduce modifications enabling real-time monitoring. The key component for size- and time-resolved detection of ultrafine particles is a new 1 nm-SMPS. With this new tool at hand, the effect of varying the precursor concentration over two orders of magnitude is investigated. We demonstrate the ability to tune between different growth scenarios as indicated by the size-resolved particle traces which exhibit a transition from sigmoidal over quasi-stationary to peak-like shape. The second key parameter relevant for nucleation studies is the temperature-dependent cluster evaporation. Due to a temperature rise during the mixing stage of the experiment, evaporation is strongly promoted in the early phase. Therefore, the present study extends the T-range used in, e.g., smog chambers. We investigate this temperature effect in a kinetic simulation and can successfully combine simulated and measured data for validating theoretical evaporation rates obtained from DLPNO-CCSD(T0)-calculations.
1 Introduction
Atmospheric properties are coupled to various dynamic processes, such as new particle formation from gas-phase precursors. Field observations have demonstrated the importance of secondary aerosol formation for the appearance of cloud condensation nuclei. They identified sulfuric acid as one crucial ingredient to initiate the nucleation process.1,2 The combination of laboratory, field and theoretical studies is a promising approach for a better understanding of nucleation mechanisms and the interaction of involved molecules. An illustrative example for this interplay of disciplines is the EUCAARI project, able to observe sub-2 nm particle formation at atmospheric concentrations of sulfuric acid.3 In that study, the strong correlation of total particle number and vapor concentration highlights the special role of H2SO4 as also demonstrated by flow tube4–6 and chamber experiments.7,8 It is known that nucleation parameters obtained from experiments depend on the gas injection method. For instance, the commonly used oxidation of SO2 by OH-radicals leads to a more homogeneous concentration profile of H2SO4 than the liquid injection. Therefore, it allows for longer growth times and lower critical saturation ratios.3,9,10 Another in situ source of sulfuric acid is the fast oxidation of SO2via stabilized Criegee Intermediates (sCIs).11,12 Approximately ten years ago, our group started applying this method in a batch-type reaction cell to produce high supersaturations within a few seconds.13,14 In addition to the independence from any inlet geometry (as opposed to liquid injection), working with high concentrations of acid is beneficial regarding the potential influence of impurities. For instance, ammonia is omnipresent in nucleation studies and has been identified as a contaminant in the CLOUD chamber.15 However, the high concentration of sulfuric acid used in our experiments minimizes the influence of trace amounts of ammonia on nucleation.16Building on that high supersaturation approach, a kinetic model incorporating molecular gas-phase reactions and particle dynamics was derived. Results from simulations based on this model are compared to particle size distributions (PSDs) measured at the end of each batch indicating a strong dependency on molecular cluster stabilities.17 This finding was supported in a recent study, in which kinetic modeling and comparison to final PSDs at elevated relative humidity were used to validate quantum chemically derived cluster evaporation rates and their humidity dependency.16
Due to limitations of the previous experimental setup, the particle measurements could not be started directly after gas expansion. However, such transient data is an essential target for further validation of the H2SO4 nucleation model. In this work, a new experimental setup is characterized and applied within a wide concentration range. By variation of the initial SO2 concentration, the kinetic traces of the smallest measured particles (down to around 2 nm) can be tuned from a sigmoidal to a peaked shape, also including transition-like profiles. In addition to time-dependent measurements, we also report the influence of precursor concentration on the final PSDs measured at the end of the experiment. To complete the picture, we performed kinetic simulations of PSDs and time profiles, now also including an explicit treatment of the temperature profile after expansion.
2 Experimental
2.1 Reaction cell and new gas filling procedure
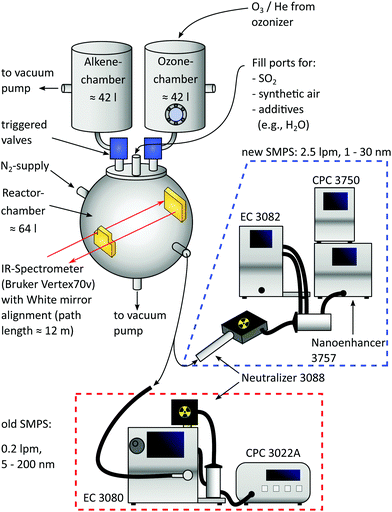
As shown in Fig. 1, the central part of the apparatus is a spheric reaction cell with a volume of 64 l, pumped down to <0.04 mbar between individual batches and operated at 1000 mbar during measurements, as originally introduced by Wolf et al.13 Teflon coating on the inner wall minimizes adsorption of reaction products. Coolant (ethylene glycol/water) is pumped between this inner and an outer wall by a cryostat (LAUDA WK 500) to maintain a temperature of 22.5 ± 0.5 °C for most of the time, being monitored by thermocouples at four different positions.Two additional, opposite flanges equipped with KBr windows and a White mirror alignment18,19 (gold coating, 12 m path length) allow coupling of an IR spectrometer (Bruker Vertex 70v) used for calibrating the concentration of the precursor species SO2 (Messer, ≥99.98%) diluted with N2 (Air Liquide, ≥99.9990%). Small amounts of SO2 (ppb range) are filled in the pre-evacuated system from this calibrated mixture by monitoring the pressure rise (MKS Baratron, 10−4 mbar precision).
Other precursors to produce sulfuric acid via Criegee Intermediates are O3 and trans-2-butene, both filled in separated premixing chambers having volumes of 42 l and made of stainless steel. While the alkene (abcr, ≥99.0%) is filled into its chamber directly, O3 is freshly produced from O2 (Linde, ≥99.9990%) with a silent discharge lab ozonizer (Sander 301.7) and stored on silica beads at 220–230 K. It is subsequently transported into the ozone chamber with helium (Linde, ≥99.996%) as the carrier gas and the exact amount of O3 is determined by means of UV absorption (lamp: NNI 60/35 XL, absorption path = 37.6 cm, pressure independent absorption coefficient20 (253.7 nm, 293–298 K) = 298.3 m2 mol−1, changing less than 1% in this temperature window21). Furthermore, the O3 concentration was cross-calibrated with the IR system of the reaction cell.
Afterwards, both premixing chambers are filled with synthetic air (Air Liquide, ≥99.9990%) to 2.1 bar and expansion into the reaction cell is done within 1.15 s by triggered valves (VAT, model: 21628-KE61-000). Due to the elevated premixing pressure, the expansion ends at 1 bar in the reactor cell and thus allows for immediate sampling with the new Scanning Mobility Particle Sizer (SMPS), being a crucial improvement compared to the former design. The reactor concentrations of O3 and butene after expansion are 0.8 ± 0.1 ppm and 18 ± 1 ppm, corresponding to 26 ± 1% of the initial filling (see ESI†). Blind batches only containing these two species were performed to check the reactor's purity, expecting no significant particle formation.22 Especially at working with high amounts of acid, this background is negligible.
2.2 Implementation of the SMPS
The installation of a second SMPS enables the operation in tandem mode: the initial phase of the experiment is sampled with a 1 nm-SMPS (TSI 3938E57) consisting of an electrostatic classifier (TSI 3082), aerosol neutralizer (TSI 3088), 1 nm-DMA (TSI 3086), condensation particle counter (TSI 3750) and a Nanoenhancer (TSI 3757). Two key improvements of implementing this system are a high sample flow rate (2.5 l min−1), reducing the transport time from the reactor to the CPC (see ESI†), and the lower detection cutoff size. To further reduce transport time and particle losses, the 1 nm-SMPS was operated in a compact design23 allowing sampling from 1.4 to 30 nm. With this tool at hand, tracking of transient species is realized by two approaches: in the first case, the 1 nm-SMPS is operated at a fixed voltage, hence providing continuous concentration–time profiles of particles with a defined electrical mobility diameter. This is very similar to the DMA train approach of Stolzenburg et al.,24 but instead of operating six instruments at the same time in one experiment, we change the voltage with each batch and combine the data afterwards. This is a better choice for our setup, because the reactor volume is much smaller than a large chamber and the observation time would be limited by the summed up flow rate of six instruments. In the second mode, the rod voltage is rapidly scanned yielding an averaged particle size distribution much like a “snapshot”. With a preset purging time, it provides new PSDs in intervals of 30 s (see Section 4.3). Any time frames can be captured by introducing a delay between the expansion pulse and the beginning of the first scan.The second SMPS, as used in previous studies, consists of the electrostatic classifier (TSI 3080), aerosol neutralizer (TSI 3088), NDMA (TSI 3085) and condensation particle counter (TSI 3022A). Because of its lower flow rate (0.2 l min−1), it is only operated at the end of the experiment providing PSDs from 5 to 200 nm of the relaxed and “quasi-static” system. Such a final PSD evolves only very slowly, merely by coagulation17 and wall deposition (0.5–0.8% min−1).13
While sampling with both SMPS systems, the withdrawn volume is replaced by N2 (Air Liquide, ≥99.9990%) to maintain a constant pressure in the cell.
In contrast, absolute numbers are not essential for focusing on the relative evolution of a particular size class by examining the time profiles. A more practical reason in this context is that plotting absolute numbers could cover a number-concentration range of several orders of magnitude. Therefore, the visibility of less abundant species would be impaired. We circumvent this issue by normalizing the traces to their respective maximum. As a result, figure clarity is improved while important parameters such as appearance times27 of different size classes are still depicted. In very few cases, artifacts were detected, probably resulting from switching the SMPS's bypass to the cell outlet. Minor and temporary pressure changes, which are corrected manually, can then cause false counts on the CPC, resulting in a strong and unphysical signal peak. Fortunately, such artifacts are easy to distinguish from the actual signal and are not considered in the plots (see ESI†).
3 Theory and modeling
3.1 Quantum chemical calculations
Theoretical T-dependent evaporation rate constants of non-hydrated sulfuric acid clusters (SA)2–5 were calculated using electronic structure methods. The initial cluster configurations were taken from the workflow presented by Kubečka et al.28 (for full details, see the ESI†). The cluster sampling procedure was performed at 298.15 K. The formation free energies at different temperatures T were calculated using the standard relation| ΔGbind = ΔHbind − TΔSbind, | (1) |
The evaporation rate constants, that is, the frequencies at which a cluster of i + j molecules decomposes to constituents of i and j molecules, were calculated from the thermochemistry by the standard relation34–36
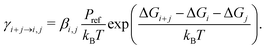 | (2) |
Here βi,j is the rate constant of the corresponding collision between parties i and j, kB is the Boltzmann constant, and Pref is the reference pressure at which the quantum chemical calculations are performed. Following the common approach, βi,j is calculated as the hard-sphere collision rate, which results in the following temperature dependence for the evaporation rate:
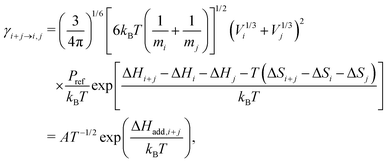 | (3) |
3.2 Kinetic model and particle dynamics
The kinetic model used to validate the upper evaporation rates has recently been presented16,17,37 and combines solving of the gas phase and cluster kinetics (Logesoft software package, version 1.02.01338) and particle dynamics. For the latter, we use a sectional method,39 whose bins are chosen in agreement with those of the SMPS and are given by eqn (4):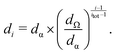 | (4) |
Here, di is the diameter of the i-th section and dα/dΩ correspond to the smallest/largest bin. The smallest species, treated as a particle, is the sulfuric acid hexamer, for which a diameter of 1.032 nm can be derived from its mass and density of 1.7 g cm−3, assuming a spherical cluster shape. Said value was reported by Murphy et al.40 and is based on the correlation of scattered light (∝ optical equivalent diameter) and aerodynamic equivalent diameter (∝ density).
As one main interest of this work is the investigation of temperature effects on molecular cluster evaporation (for a detailed discussion, see Section 4.5), we have modified the model in the following way: measured temperature profiles from our reactor cell were used as an additional input. With this, the simulation temperature and all T-dependent rates are updated every second. The temperature-dependent evaporation rates of initial acid clusters up to the pentamer were fitted according to eqn (3) in the interval from 296 to 325 K. The resulting parameters, given in Table 1, were used as input for the gas phase solver. In accordance with earlier work,16 the obtained rates were multiplied by a scaling factor (SF) to reproduce the experimental data. Hence, this paper provides a simple parametrization for SA evaporation being evaluated under kinetic control.
| Reaction | A (s−1) | ΔHadd (kJ mol−1) |
|---|---|---|
| SA2 → 2SA | 5.39 × 1019 | −74.3 |
| SA3 → SA2 + SA | 3.85 × 1019 | −67.7 |
| SA4 → SA3 + SA | 2.21 × 1022 | −89.9 |
| SA4 → 2SA2 | 3.28 × 1021 | −83.3 |
| SA5 → SA4 + SA | 2.84 × 1021 | −90.2 |
| SA5 → SA3 + SA2 | 4.25 × 1023 | −105.8 |
In addition to the T-dependency of cluster evaporation, we have included a temperature-dependent reaction rate for the decomposition of stabilized Criegee Intermediates as k(T) = A exp(−Ea/kBT). For this, an Arrhenius parameter of A = 1.4 × 1013 s−1 and an activation energy of Ea = 64.6 kJ mol−1 were fitted from theoretical data provided by Kuwata et al.41 It is consistent with the formerly used rate constant of 76 s−1 (room temperature) reported by Fenske et al.42
4 Results and discussion
In the following subsections, we will retrace and discuss the consecutive steps of the experiment, starting with the mixing of the gaseous reactants in the new setup. After that, monitoring of transient particle species under different conditions is demonstrated and completed by inspecting the final PSDs. Finally, results from kinetic modeling17 are compared to the experimental findings.4.1 Characterization of the gas expansion
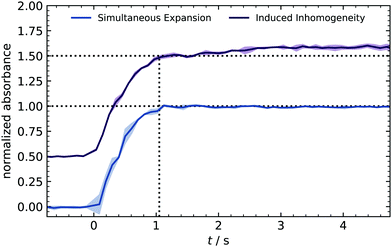
At the very beginning, a series of time-resolved IR measurements is used to crosscheck the homogeneous distribution of reactants expanded into the reactor. Ozone was used as a tracer substance because its strong IR absorption results in a clear signal for concentrations above 10 ppm. Furthermore, the bands (970–1073 cm−1) are isolated from other compounds (e.g., water absorption), making the integration easier and more reliable. With the rapid scan mode, IR spectra were recorded every 0.1 s, and the integrated absorption is plotted in Fig. 2.During the valve opening (1 s), the signal shows a sharp rise and stays constant afterward. The absence of fluctuations indicates a homogeneous distribution of species because a control expansion with intentional inhomogeneity caused a slight drift.
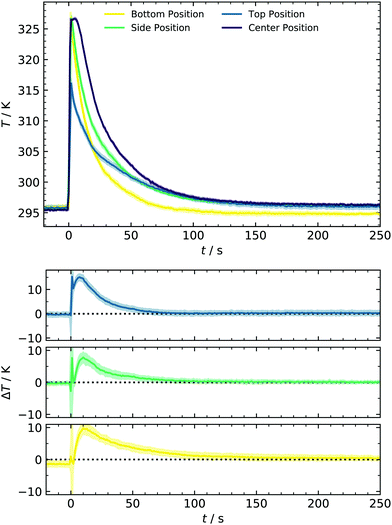
Another aspect of concentration linked to the filling method is the sCI yield. Previous alkene ozonolysis studies reported suppression of aerosol formation at low pressures, caused by a decreased stabilization of CIs due to the lower collision rate.14,22 Since the reduction of sCI stabilization starts below 200 mbar, we assume that yields at 1000 mbar (new expansion) are comparable to those calibrated at 450 mbar in earlier work. Control experiments at 1 ppm SO2 where [sCI] represents the bottleneck confirm this assumption.37 The second point inspected in this section is temperature evolution. Collisions of monomers, clusters and particles that determine the forward reaction rate of particle formation are relatively weak functions of temperature. Contrastingly, temperature significantly affects the backward reaction rate in terms of evaporation in an atmospherically relevant temperature range. This importance of temperature on particle formation has been reported in various studies, for example, for binary systems of sulfuric acid and water10,43 or in the presence of ammonia.44,45 To better understand the monitored particle formation, we characterized the temperature profile during the experiment and compared this data for the bottom, side, and top of the reactor, as shown in Fig. 3. Here, three regimes can be identified: for times prior to the expansion (t <0 s) and at later times (t >80 s), the temperature is ≈296 K as maintained by the cryostat. At the bottom position, this temperature recovers slightly earlier, most likely due to proximity to the cooling system. However, the deviation is small enough to be neglected.
In contrast, a significant and interesting change in the expansion time regime (0–80 s) is observed. All thermocouples show a rapid temperature rise of 31.5 K at the bottom/side and 20.3 K at the top position. As can be seen here, our setup provides a unique setting for testing cluster evaporation at a relatively high T and complements, e.g., chamber studies. The latter are usually performed between approx. 200–300 K because only low and steady-state acid concentrations can be produced.8,10 Temperatures recover to values of <300 K after 35 s for the bottom of the cell and 70 s for the other positions. As opposed to other techniques,46 in which expansion of small amounts of carrier gas results in adiabatic cooling, this experimental setup behaves like a shock tube, accounting for the temperature rise. However, it should be noted that the maximum temperature changes are limited due to the deviant geometry and the relatively moderate pressure difference of 2 bar. This deviation from optimal shock tube geometry can also weaken the reflected wave and thus account for a smaller T-change at the top. Additionally, a slight temperature drop of the remaining gas in the premixing chamber is measured (not shown) as it would be expected on a shock tube's driver side. In other shock tubes, temperature drops of 50 K were measured in that zone and introduced for nucleation studies by Peters.47
A complete temperature profile was obtained by additional measurements in the cell center using a second thermocouple with identical response characteristics. From Fig. 3, a similar temperature rise of approx. 30.7 K is observed, decaying in a comparable way as at the other positions. As illustrated in the lower panel of Fig. 3, the spatial gradient is close to zero for t >70 s. Contrarily, an initial gradient is present, representing the cooling process from the walls to the reactor center. With the temperature profiles from different positions at hand, we can describe the whole system's temperature evolution and consequently incorporate this behavior in the improved kinetic model discussed in Section 4.5. We have chosen to use the T-profile of the center position since it represents the majority of the total reactor volume. Due to the mentioned gradient, it furthermore represents an upper limit of accessible gas phase temperatures and temperature effects on nucleation in the current setup.
4.2 Time profiles of individual particle size classes
After expanding the gases into the reaction chamber, the experiment continues with monitoring the particle formation for 5 min, which was chosen to agree with previous studies of our group. This observation period is much shorter compared to chamber experiments7 due to working with high sulfuric acid concentrations. An example of controlling the nucleation behavior by changing [SO2] is depicted in Fig. 4. It shows the normalized kinetic traces of representative particle sizes. In panel (a), all size classes have a sigmoidal trace. Although even the lowest concentration of approx. 2–3 ppb SO2 is high compared to other experimental work,4 the participation of some oxidation products from the ozonolysis is likely. Simulations performed in this [SO2]-range required additional cluster stabilization to reproduce the experimental findings and therefore support this assumption.16 Key characteristics like the appearance times can be seen in the subplots. They are linked to the apparent growth rate since the difference in appearance times is the period required to grow from one to the next size bin.9,27 In our case, the growth of smaller particles with DP = 2–3 nm is seemingly slower than that of the larger ones because the traces of small species are separated, and that of larger start to converge. This observation stands in contrast to measurements from CLOUD.7 However, the different concentration-time profiles of condensable vapors in both experiments must be considered. While chamber experiments work at low but quasi-constant concentrations of H2SO4, the production of high amounts of acid in our batch apparatus has a pulse-like profile, occurring parallel to the formation of the first particles. In another study, such ramping of vapor concentrations (in that case HOM) was shown to lead to enhanced and non-linear growth rates at larger particles,48 generally showing the importance of time-dependent vapor concentrations. Another major reason for discrepancies is the difference in relative humidity (RH). We present dry experiments at RH ⪅ 0.1%, whereas said CLOUD chamber experiments were performed at RH of 60%. As reported by Chen et al. and Hamil, such a high humidity supports particles growing to detectable sizes.49,50 The special role of sub-3 nm particles is also reflected in the next scenario with doubled precursor material [4.5 ppb, panel (b)], leading to a very significant particle formation. A clear shift towards earlier appearance times is observed for all particle diameters. In addition to that, the traces of small species start to change from a sigmoidal to a peak-like shape. As an important finding, the concentration of particles with DP = 2.5 nm is quasi-stationary at t ≈110 s. This system reflects a sensitive transition state and is thus a promising test scenario for future work. For example, it would be interesting how the temporal behavior of the system and hence the traces change when stabilizing compounds are added. Therefore, our novel method of detecting transient behavior provides a potential indicator for the impact of atmospheric substances on sulfuric acid nucleation.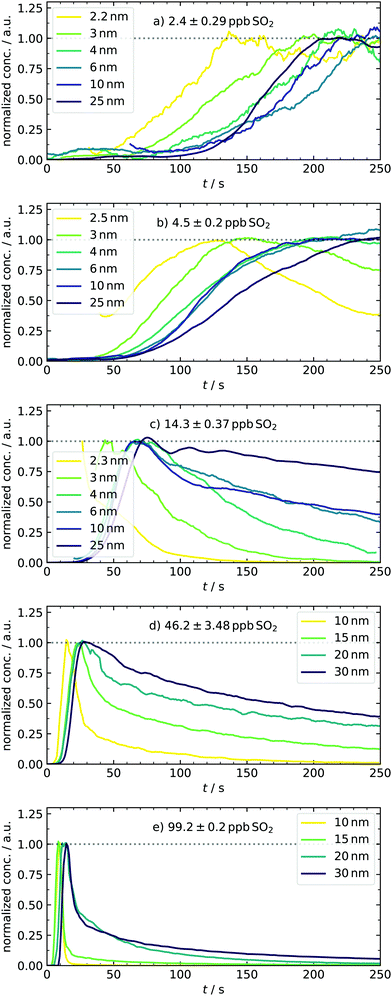 | ||
| Fig. 4 Normalized traces of representative particle diameters (for DMA bin resolution and H2SO4-concentration profiles see ESI†) under various amounts of initial SO2, demonstrating the strong variations of the system's growth behavior. For the sake of clarity, data were smoothed using the Savitzky–Golay filter. The mentioned pressure-related artifacts were not plotted, accounting for the gaps. | ||
At 14.3 ppb of initial SO2 [panel (c)], a level is reached at which the kinetic model starts to predict the particle formation correctly as an unary nucleation process.16 This is underlined by the slight jump of the best scaling factor (BSF = best scaling factor, applied to match simulated to experimental PSDs) between the 4.5 and 14.2 ppb simulation (Table 2). This additional increase of SO2 leads to further reduction of characteristic times. Here, not only the appearance and maximum-concentration time can be extracted, but we can also observe the complete vanishing of smaller particles as they grow into larger size bins. In accordance with the definition of appearance time,27 we could identify size-dependent vanishing times. Another thing to note about the first set of conditions is that the particles appear only after full recovery of the temperature peak or during its advanced decline. The variable appearance times for these first scenarios raise an interesting question regarding the nucleation process: is the late appearance mainly controlled by a reduced collision rate of vapor molecules as expected when less precursor material is used? Or are clusters already present, but their growth is suppressed during the period of enhanced temperature and evaporation? At this point, it remains elusive which of the two effects dominates and explains the observed profiles. This is a nice example where the interplay of our new transient data and theory can clarify the underlying nucleation mechanics, as shown in Section 4.5. In contrast to the observed delay, the experiments conducted at the highest sulfuric acid amounts [46.2 and 99.2 ppb, panels (d and e)] show particle formation already during times of elevated temperatures. Because nucleation occurs simultaneous to the enhanced T here, we expect cluster evaporation to play a role. Unfortunately, it was not possible to measure sub-10 nm particles in these cases because the separation of actual signal and possible artifacts is less reliable due to the rapid growth. The representative size bins are thus different for these conditions, with diameters of up to 30 nm. For 46.2 ppb SO2, the trend of more peak-like traces is continued, being most pronounced for the smallest particle diameter, whereas larger ones decay significantly slower. At the highest concentration (99.2 ppb), the individual traces are all peak-like and start to converge, corresponding to rapid growth. Because of this observation, a further increase of the SO2 concentration is not useful for investigating this size range. Overall, the system showcases very different growth behaviors accessible by tuning the initial amount of SO2 in a range of two orders of magnitude.
| [SO2]/ppb | BSF1 (with T) | BSF2 (without T) | BSF2/BSF1 (%) |
|---|---|---|---|
| 2.0 | 0.0026 | 0.0066 | 254 |
| 4.0 | 0.004 | 0.0115 | 288 |
| 14.2 | 0.008 | 0.034 | 425 |
| 46.8 | 0.011 | 0.075 | 682 |
| 99.2 | 0.015 | 0.115 | 767 |
4.3 Transient particle size distributions
The above-discussed approach of monitoring narrow electrical mobility diameter bins over a certain period of time is only one possibility to investigate the system's evolution in phase space. An alternative approach is switching from continuous time and discrete sizes to a full size distribution measured at individual time frames. Using a second method is important to crosscheck the results mentioned above. Such measurements can easily be applied in atmospheric studies51 since the scan time of an SMPS is short (seconds) compared to the particle dynamics (hours to days). In the reaction cell with a fast-growing system, this condition is hard to fulfill and scan times were therefore set as short as possible. However, the settings are limited by some factors: on the one hand, fixed down scan and purge times have to be considered.25 On the other hand, the upscan time as a free parameter can cause smearing effects if it is below 10 s.52 Thus, a scan time of 12 s was chosen, resulting in a total of 30 s for a complete cycle. Exemplary results are displayed for two concentrations of SO2 in Fig. 5. The initial offset of 20 s between expansion and start of the first scan was introduced as a delay in the experiment control software. By changing this delay, other sample times can be accessed. In the left column (≈4 ppb) of Fig. 5, we can observe an intense mode at Dp ≈ 2 nm, decaying to a tenth within the next time frame. At 80 s, the formation of larger species can be seen, which agrees with the observation from the monitoring of single size bins. The subsequent particle growth, indicated by the mode diameter shift from 15 to 25 nm (see t = 110 and 140 s), also agrees with the measured traces. The corresponding time frames at 14 ppb SO2 are shown in the right column. Here, the number of initial particles is approx. one order of magnitude higher than before. Again, their number decreases as they are consumed by condensational growth, and a larger particle size mode appears at t ≈50 s, agreeing well with the values obtained from time profiles. The general finding of an enhanced formation and growth is also reflected in the next frames, in which the distribution's mode diameter grows out of the upper detection bound.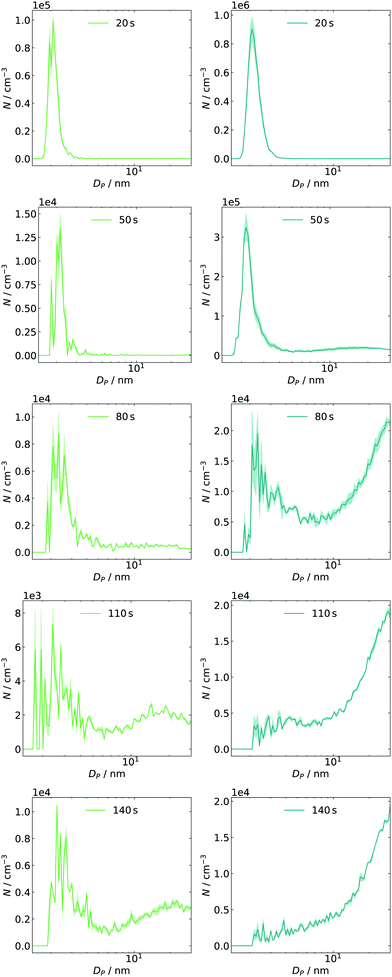 | ||
| Fig. 5 Time-dependent size distributions for 4 ppb (left, green) and 14 ppb (right, blue) of initial SO2 including post-processed diffusion loss correction for SMPS and tubing. | ||
In both cases, particles are less abundant in the intermediate diameter range (approx. 4–10 nm). This finding could be interpreted as a barrier in the growth process resulting in a pre-equilibrium of the sub-3 nm particles. Once such a barrier is passed and growth gets more efficient again, they are removed quickly (also by efficient coagulation).
4.4 Final particle size distributions
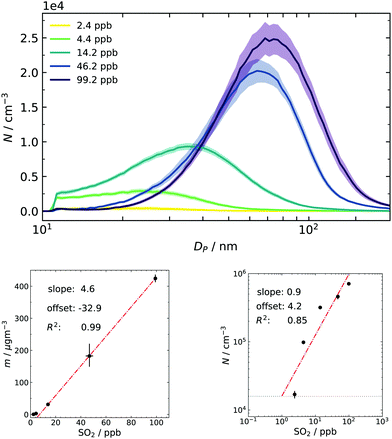
Finally, particle size distributions are scanned from approx. 5 nm to 200 nm at t = 460 s (and thenceforth every two minutes), replicating the experimental procedure from our earlier work.17 Especially the total particle mass concentration obtained from the PSDs is an important quantity for comparison since it is only a function of produced sulfuric acid.22 One purpose of collecting final distributions is to use them as a consistency check between individual batches: every repetition done with the same nominal amount of SO2 resulted in the same total mass (within the measurement uncertainty of approx. a factor of 2). Thus, the combination of the dynamic data sets from different batches, as shown in Fig. 4, is permitted. The other application is to have them as a final reference for the simulation.The resulting averaged PSDs (Fig. 6) also take diffusion loss correction and multiple charge correction25 (for large particles) into account. The data were fitted with a lognormal distribution because noise at large sizes disproportionally impacts the mass calculation in the SMPS software (cubic relationship of size and mass). The resulting fit parameters and a particle density of 1.7 g cm−340 (also see Section 3.2) were then used to recalculate the total mass concentration. The same fit was done to obtain the total number concentration and results are given as subplots of Fig. 6. From the linear correlation of mass and gas-phase concentration it can be deduced that SO2 is the limiting ingredient in the system for the whole range of examined conditions. This is important for two reasons: firstly, the substantial excess of ozone and consequently the formed sCI makes the method robust towards small deviations of the ozone filling. Secondly, high excess of O3/butene/sCI over SO2 results in pseudo-first-order kinetics for its oxidation process and results in rapid and high supersaturations of H2SO4.
A closer look at the lower concentration regime of sulfur dioxide in the mass plot shows a slight deviation from the linear behavior and a small negative offset. This can be interpreted as a hint for activation or co-nucleation of sulfuric acid and probably small traces of products from the ozonolysis. Further support for this hypothesis was also seen in earlier simulation results, in which the model underestimated particle formation at very low concentrations of pure sulfuric acid because it did not include these possibilities.16 Another tentative support is given by the double logarithmic plot of number and precursor concentration: usually, a slope close to unity is associated with activation of preexisting clusters/particles.6,53 An offset was needed to obtain a reasonable fit. This offset can be physically interpreted as the concentration of background species, which is seemingly in the same order of magnitude as the lowest concentration of SO2 in our experimental series.
4.5 Kinetic modeling
At first, we discuss the influence of including the measured temperature profile in the model by comparing experimental and simulated final PSDs. In the example case of around 50 ppb SO2, a reasonable match was found when a scaling factor of 0.011 was applied (Fig. 7). However, the simulation result does not reproduce the experimental data when the simulation temperature is set to a constant value of 296 K. As a result the simulation does not account for the enhanced temperature and cluster evaporation in the mixing stage. As clusters in the early phase are stabilized, the final particle number is increased, but the mean diameter is reduced. The latter finding is explained by the fact that the total amount of condensable vapor is limited and redistributed between a high number of initial small particles, leading to less condensable monomer per seed species.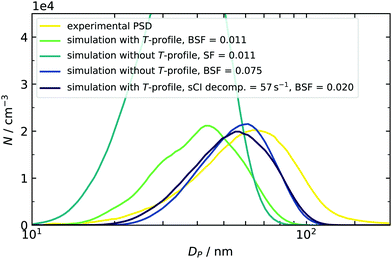 | ||
| Fig. 7 Temperature effect on the simulated PSD at an initial SO2 concentration of 46.8 ppb. The simulated size distributions were smoothed to compensate their jagged shape, resulting from the sectional simulation scheme.17,37 Smoothing of the distribution was done with a moving average filter of five adjacent data points. | ||
A second control simulation was used to get a quantitative estimate of the importance of temperature. Here, T was held constant at 296 K and a higher SF was applied. This leads to two similar distributions. In one case, the dynamics were governed by temperature, and in the other, by artificially increased destabilization. We can therefore compare both and conclude that the role of the temperature profile is similar to more than a doubling of the evaporation rates. This is true for all concentration scenarios covered in this work, and the scaling factors with and without using temperature profiles are listed in Table 2. Within the five quotients of the BSFs (right column of Table 2), a trend from 254% (2 ppb) to 767% (99.2 ppb) can be found, indicating that using the correct temperature profile becomes more important at enhanced amounts of SO2. A plausible explanation can be given by a correlation of times, when small clusters are present in the simulation and the corresponding temperature at this time: in the high concentration case, the model predicts initial clusters, e.g., sulfuric acid dimers to be present in the first seconds. Because the temperature is enhanced here, the sensitivity towards T is very pronounced. On the other hand, using low initial amounts of SO2 results in a later appearance of clusters when the temperature already begins to recover, and the effect of T is therefore reduced (for simulated time profiles of SA dimers, see ESI†). Even if the T-effect is reduced, it is still significant and can partly be responsible for the late appearance of species. This indicates that our nucleation mechanism is not limited by a low collision number. In other words, the assumption of working in a high-level concentration regime is justified in all cases. Values for BSF2 (without T-profile) given above can reproduce the findings of a preceding study.16 However, the new data sets require slightly more stabilization for the same or comparable conditions (10 and 100 ppb vs. 14.2 and 99.2 ppb, both RH < 0.1%) because the evaporation rates described in Sections 3.1 and 3.2 have increased as well. This is caused by using different starting geometries28,54 and using the quasi-harmonic approximation for calculating vibrational frequencies, which can increase the free energies of clusters.55 Looking at the individual set of scaling factors with and without explicit treatment of T-profiles reveals two additional results: firstly, the BSF never exceeds a value of 1. This means that the rates derived from quantum chemical calculations tend to overpredict the cluster evaporation. This finding is consistent with our previous observations16 and other literature, in which the DLPNO method is said to have a general “underbinding” tendency.56 It should be noted here that other methods, such as RICC2/aug-cc-pV(T+d)Z, are known to have an opposed bias,33 resulting in scaling factors larger than 1.16 The mentioned underbinding of DLPNO rates becomes more pronounced at very low concentrations of SO2, as smaller scaling factors are required for sufficient stabilization. As mentioned above and in our previous study, such further reduction of the BSF could also hint at the presence of additional low volatile components in our experiment, leading to an additional stabilization.16 Oxidation products from the 2-butene ozonolysis are not only a possible candidate for stabilization in the low SO2 concentration regime, but they can also be scavenged by existing particles. This additional condensation of organic vapors was indicated by comparing the simulated and experimentally derived particle mass. At high concentrations of 50–100 ppb, the model underestimated the total particle mass. In Fig. 7, this is indicated by the shift of both simulated PSDs towards smaller particle diameters. The distribution with an included temperature profile (green line in Fig. 7) has even smaller diameters and hence less particle mass compared to that at constant 296 K (dark blue line in Fig. 7). This is explained by the faster decomposition of the sCIs in the first case, which are then not available for oxidation of SO2 and formation of sulfuric acid. An additional simulation (purple PSD) was done to separate the effect of sCI decomposition and, hence, to check the influence of deviations of produced particle mass. For this purpose, a fixed sCI decomposition rate (chosen in accordance to Kuwata at 296 K) was employed, while cluster decomposition remained temperature-dependent. As the BSF only required a small adjustment, we can conclude that slight mass deviations are of minor importance, but that the correct description of cluster evaporation is crucial.
As an additional and independent criterion for validating our model, we now focus on the simulated time profiles for particles of a certain size bin, as displayed in Fig. 8. As the first finding, we can see a shift of the apparent appearance times when the amount of SO2 is increased. As a second result, we observe a change of the shape for the time profiles from sigmoidal to progressively more peak-like cases. Also, the smallest clusters are now completely depopulated at later times. Both observations agree qualitatively very well with the experimental data of Fig. 4. Nonetheless, some differences between simulated and measured traces exist. The modeled traces and final PSDs are very sensitive to small variations of the scaling factors. Slight deviations of the simulated PSD can cause significant changes in the profiles. One example of a deviation between measured and simulated profiles is that the model predicts a too-fast growth of particles, which is seen as vanishing traces at the low concentration of 4 ppb of initial SO2 (Fig. 8, panel b). At this concentration and also at 2 ppb, the simulated particle mass is higher than the experimental result. In particular for the 2 ppb case the mass fitted from the experiment is uncertain since the size distribution is at the level of the background counts, which could partly explain the different masses. We can also identify reasons in the underlying model: in the current version, it assumes only unary nucleation. Therefore, clusters are only stabilized by downscaling their evaporation rate. Once they reach a certain size, they start to grow and scavenge the gaseous species. As a possible modification, stabilizing species for binary nucleation could be implemented in the kinetic mechanism. First test simulations indicated that introducing clusters of type (H2SO4)(n−1)X led to a similar stabilization as for (H2SO4)n clusters with downscaled evaporation rates. The main difference is that in the first case, the number of clusters becoming a seed species can additionally be controlled by the amount of species X. This is ongoing work and beyond the scope of this paper in which the experimental procedure and the underlying temperature offsets were addressed. The comparison of both T-cases shows the importance of including the temperature in our simulations and demonstrates that dynamic experiments can support and complement steady-state experiments (such as chamber studies) and simulations.45
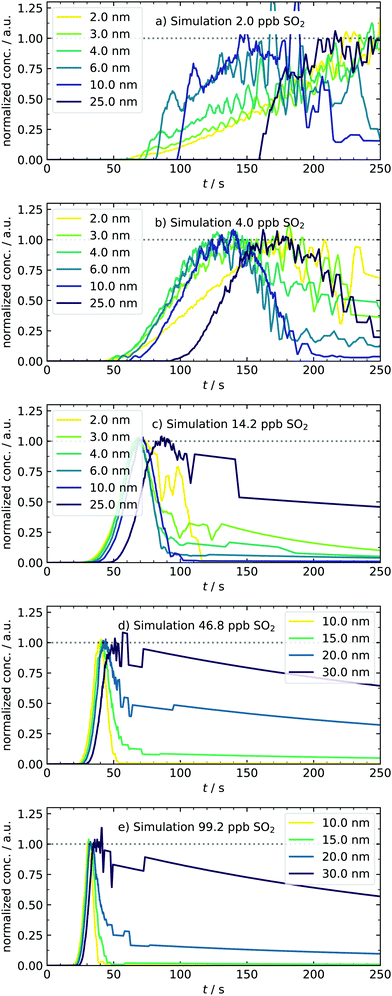 | ||
| Fig. 8 Normalized traces of representative particle diameters under various amounts of initial SO2, obtained from the temperature-dependent kinetic model. Simulated concentration–time profiles for H2SO4 monomers and dimers are provided in the ESI.† | ||
5 Conclusion and outlook
Crucial improvements of our batch reactor experiment opened new possibilities for investigating sulfuric acid nucleation in the early phase under high vapor concentrations and at elevated temperatures (296–325 K). We characterized the temperature evolution resulting from a shock tube-like gas expansion. In addition, the homogeneous distribution of gaseous reactants in the cell was shown utilizing time-resolved IR measurements.With the new 1 nm-SMPS, transient data of nanometer-sized particles (approx. 2–30 nm) can be recorded for different amounts of precursor species, either by monitoring the concentration profile of certain particle size classes or by fast scanned size distributions.
One main finding from the variation of SO2 was the ability to manipulate the temporal evolution of the nucleating vapor–particle system and prepare quasi-stable nanoparticle concentration–time profiles. Especially for future work, such latter conditions are a promising indicator for testing binary systems since a strong sensitivity towards the addition of stabilizing compounds (e.g., water) is expected, based on previous measurements of final PSDs under elevated RH.16 The measured time traces also serve as additional references for a modified kinetic simulation which now incorporates the experimental temperature evolution. Strong promotion of cluster evaporation was expected based on the elevated temperature within the first seconds of the experiment. The simulation reproduced this enhanced evaporation, taking temperature-dependent evaporation rates into account. Rates were derived from DLPNO-CCSD(T0) calculations and provided in Arrhenius form. For more experimental control of evaporation dynamics, the temperatures should be kept high for a long time after the expansion pulse, too. Therefore, implementing a heating unit is planned as a convenient modification. Further work is planned with special interest on temperature-dependent evaporation under elevated RH, for which the cluster evaporation rates are usually non-trivial. With the improved simulation tools and the new experimental data, the system's complexity can be extended stepwise. The ultimate aim is to cover many different trace gases found in the atmosphere and to investigate their nucleation behavior by our novel approach of observing and modeling particle kinetics in the early stage.
Conflicts of interest
There are no conflicts of interest.Acknowledgements
D. B. acknowledges support by the Fonds der Chemischen Industrie, grant no. 104371. T. Z. thanks the Deutsche Forschungsgemeinschaft for support (grants ZE890 3-1 and 3-2, numbers: 250936489 and 417233848). J. E. thanks the Independent Research Fund Denmark grant number 9064-00001B for financial support. The numerical results presented in this work were obtained at the Centre for Scientific Computing, Aarhus https://phys.au.dk/forskning/faciliteter/cscaa/. T. O. gratefully acknowledges the Swedish Research Council Vetenskapsrådet (grant no. 2019-04853) for financial support. For support in installing new parts and solving many technical questions, we thank Mike Zippert, Reinhard Hildebrandt, Andreas Knorr and their team from the mechanical/electronics workshop of our faculty. We thank Steven Celik for helping test the functions of the new parts of the apparatus and Alea Miako Tokita for performing test simulations with the modified kinetic mechanism. Furthermore, we thank Prof. Dr. Martin A. Suhm for his ongoing support. Finally, we thank Dr. Sebastian H. Schmitt, Dr. Torsten Tritscher and Dr. Carsten Kylkal for helpful advice on implementing the SMPS devices.References
- R. J. Weber, P. H. McMurry, R. L. Mauldin, D. J. Tanner, F. L. Eisele, A. D. Clarke and V. N. Kapustin, Geophys. Res. Lett., 1999, 26, 307–310 CrossRef CAS
.
- J. Merikanto, D. V. Spracklen, G. W. Mann, S. J. Pickering and K. S. Carslaw, Atmos. Chem. Phys., 2009, 9, 8601–8616 CrossRef CAS
.
- V.-M. Kerminen, T. Petäjä, H. E. Manninen, P. Paasonen, T. Nieminen, M. Sipilä, H. Junninen, M. Ehn, S. Gagné, L. Laakso, I. Riipinen, H. Vehkamäki, T. Kurten, I. K. Ortega, M. D. Maso, D. Brus, A. Hyvärinen, H. Lihavainen, J. Leppä, K. E. J. Lehtinen, A. Mirme, S. Mirme, U. Hõrrak, T. Berndt, F. Stratmann, W. Birmili, A. Wiedensohler, A. Metzger, J. Dommen, U. Baltensperger, A. Kiendler-Scharr, T. F. Mentel, J. Wildt, P. E. W. P. M. Winkler, A. Petzold, A. Minikin, C. Plass-Dülmer, U. Pöschl, A. Laaksonen and M. Kulmala, Atmos. Chem. Phys. Discuss., 2010, 10, 16497–16549 Search PubMed
.
- T. Berndt, O. Böge, F. Stratmann, J. Heintzenberg and M. Kulmala, Science, 2005, 307, 698–700 CrossRef CAS PubMed
.
- T. Berndt, F. Stratmann, S. Bräsel, J. Heintzenberg, A. Laaksonen and M. Kulmala, Atmos. Chem. Phys., 2008, 8, 6365–6374 CrossRef CAS
.
- M. Sipilä, T. Berndt, T. Petäjä, D. Brusa, J. Vanhanen, F. Stratmann, J. Patokoski, R. L. Mauldin III, A.-P. Hyvärinen, H. Lihavainen and M. Kulmala, Science, 2010, 327, 1243–1246 CrossRef PubMed
.
- D. Stolzenburg, M. Simon, A. Ranjithkumar, A. Kürten, K. Lehtipalo, H. Gordon, S. Ehrhart, H. Finkenzeller, L. Pichelstorfer, T. Nieminen, X.-C. He, S. Brilke, M. Xiao, A. Amorim, R. Baalbaki, A. Baccarini, L. Beck, S. Bräkling, L. C. Murillo, D. Chen, B. Chu, L. Dada, A. Dias, J. Dommen, J. Duplissy, I. E. Haddad, L. Fischer, L. G. Carracedo, M. Heinritzi, C. Kim, T. K. Koenig, W. Kong, H. Lamkaddam, C. P. Lee, M. Leiminger, Z. Li, V. Makhmutov, H. E. Manninen, G. Marie, R. Marten, T. Müller, W. Nie, E. Partoll, T. Petäjä, J. Pfeifer, M. Philippov, M. P. Rissanen, B. Rörup, S. Schobesberger, S. Schuchmann, J. Shen, M. Sipilä, G. Steiner, Y. Stozhkov, C. Tauber, Y. J. Tham, A. Tomé, M. Vazquez-Pufleau, A. C. Wagner, M. Wang, Y. Wang, S. K. Weber, D. Wimmer, P. J. Wlasits, Y. Wu, Q. Ye, M. Zauner-Wieczorek, U. Baltensperger, K. S. Carslaw, J. Curtius, N. M. Donahue, R. C. Flagan, A. Hansel, M. Kulmala, J. Lelieveld, R. Volkamer, J. Kirkby and P. M. Winkler, Atmos. Chem. Phys., 2020, 20, 7359–7372 CrossRef CAS
.
- A. Kürten, T. Jokinen, M. Simon, M. Sipilä, N. Sarnela, H. Junninen, A. Adamov, J. Almeida, A. Amorim, F. Bianchi, M. Breitenlechner, J. Dommen, N. M. Donahue, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, J. Hakala, A. Hansel, M. Heinritzi, M. Hutterli, J. Kangasluoma, J. Kirkby, A. Laaksonen, K. Lehtipalo, M. Leiminger, V. Makhmutov, S. Mathot, A. Onnela, T. Petäjä, A. P. Praplan, F. Riccobono, M. P. Rissanen, L. Rondo, S. Schobesberger, J. H. Seinfeld, G. Steiner, A. Tomé, J. Tröstl, P. M. Winkler, C. Williamson, D. Wimmer, P. Ye, U. Baltensperger, K. S. Carslaw, M. Kulmala, D. R. Worsnop and J. Curtius, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15019–15024 CrossRef PubMed
.
- L. Dada, K. Lehtipalo, J. Kontkanen, T. Nieminen, R. Baalbaki, L. Ahonen, J. Duplissy, C. Yan, B. Chu, T. Petäjä, K. Lehtinen, V.-M. Kerminen, M. Kulmala and J. Kangasluoma, Nat. Protoc., 2020, 15, 1013–1040 CrossRef CAS PubMed
.
- J. Duplissy, J. Merikanto, A. Franchin, G. Tsagkogeorgas, J. Kangasluoma, D. Wimmer, H. Vuollekoski, S. Schobesberger, K. Lehtipalo, R. C. Flagan, D. Brus, N. M. Donahue, H. Vehkamäki, J. Almeida, A. Amorim, P. Barmet, F. Bianchi, M. Breitenlechner, E. M. Dunne, R. Guida, H. Henschel, H. Junninen, J. Kirkby, A. Kürten, A. Kupc, A. Määttänen, V. Makhmutov, S. Mathot, T. Nieminen, A. Onnela, A. P. Praplan, F. Riccobono, L. Rondo, G. Steiner, A. Tome, H. Walther, U. Baltensperger, K. S. Carslaw, J. Dommen, A. Hansel, T. Petäjä, M. Sipilä, F. Stratmann, A. Vrtala, P. E. Wagner, D. R. Worsnop, J. Curtius and M. Kulmala, J. Geophys. Res.: Atmos., 2016, 121, 1752–1775 CrossRef CAS
.
- O. Welz, J. D. Savee, D. L. Osborn, S. S. Vasu, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Science, 2012, 335, 204–207 CrossRef CAS PubMed
.
- C. A. Taatjes, O. Welz, A. J. Eskola, J. D. Savee, A. M. Scheer, D. E. Shallcross, B. Rotavera, E. P. F. Lee, J. M. Dyke, D. K. W. Mok, D. L. Osborn and C. J. Percival, Science, 2013, 340, 177–180 CrossRef CAS PubMed
.
- J. L. Wolf, S. Richters, J. Pecher and T. Zeuch, Phys. Chem. Chem. Phys., 2011, 13, 10952 RSC
.
- P. T. M. Carlsson, C. Keunecke, B. C. Krüger, M.-C. Maaß and T. Zeuch, Phys. Chem. Chem. Phys., 2012, 14, 15637 RSC
.
- J. Kirkby, J. Curtius, J. Almeida, E. Dunne, J. Duplissy, S. Ehrhart, A. Franchin, S. Gagné, L. Ickes, A. Kürten, A. Kupc, A. Metzger, F. Riccobono, L. Rondo, S. Schobesberger, G. Tsagkogeorgas, D. Wimmer, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, A. Downard, M. Ehn, R. C. Flagan, S. Haider, A. Hansel, D. Hauser, W. Jud, H. Junninen, F. Kreissl, A. Kvashin, A. Laaksonen, K. Lehtipalo, J. Lima, E. R. Lovejoy, V. Makhmutov, S. Mathot, J. Mikkilä, P. Minginette, S. Mogo, T. Nieminen, A. Onnela, P. Pereira, T. Petäjä, R. Schnitzhofer, J. H. Seinfeld, M. Sipilä, Y. Stozhkov, F. Stratmann, A. Tomé, J. Vanhanen, Y. Viisanen, A. Vrtala, P. E. Wagner, H. Walther, E. Weingartner, H. Wex, P. M. Winkler, K. S. Carslaw, D. R. Worsnop, U. Baltensperger and M. Kulmala, Nature, 2011, 476, 429–433 CrossRef CAS PubMed
.
- P. T. M. Carlsson, S. Celik, D. Becker, T. Olenius, J. Elm and T. Zeuch, J. Phys. Chem. Lett., 2020, 11, 4239–4244 CrossRef CAS PubMed
.
- P. T. M. Carlsson and T. Zeuch, J. Chem. Phys., 2018, 148, 104303 CrossRef PubMed
.
- J. U. White, J. Opt. Soc. Am., 1942, 32, 285 CrossRef
.
- B. L. Anderson, S. A. Collins, E. A. Beecher, C. A. Klein and S. B. Brown, Appl. Opt., 1997, 36, 8493 CrossRef CAS PubMed
.
-
S. P. Sander, D. M. Golden, M. J. Kurylo, G. K. Moortgat, P. H. Wine, A. R. Ravishankara, C. E. Kolb, M. J. Molina, B. J. Finlayson-Pitts, R. E. Huie and V. L. Orkin, Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Jet Propulsion Laboratory, National Aeronautics and Space Administration, 2006 Search PubMed
.
- A. Serdyuchenko, V. Gorshelev, M. Weber, W. Chehade and J. P. Burrows, Atmos. Meas. Tech., 2014, 7, 625–636 CrossRef CAS
.
- P. T. M. Carlsson, J. E. Dege, C. Keunecke, B. C. Krüger, J. L. Wolf and T. Zeuch, Phys. Chem. Chem. Phys., 2012, 14, 11695 RSC
.
- Diffusion Correction Using TSI's 1 nm SMPS System Model 3938, 2019, Application Note.
- D. Stolzenburg, G. Steiner and P. M. Winkler, Atmos. Meas. Tech., 2017, 10, 1639–1651 CrossRef
.
- TSI, Aerosol Instrument Manager Software For Scanning Mobility Particle Size (SMPS) Spectrometers, Revision N edn., 2018.
- S. C. Soderholm, J. Aerosol Sci., 1979, 10, 163–175 CrossRef
.
- K. Lehtipalo, J. Leppä, J. Kontkanen, J. Kangasluoma, A. Franchin, D. Wimmer, S. Schobesberger, H. Junninen, T. Petäjä, M. Sipilä, J. Mikkilä, J. Vanhanen, D. R. Worsnop and M. Kulmala, Boreal Environ. Res., 2014, 19(suppl. B), 215–236 Search PubMed
.
- J. Kubečka, V. Besel, T. Kurtén, N. Myllys and H. Vehkamäki, J. Phys. Chem. A, 2019, 123, 6022–6033 CrossRef PubMed
.
- S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed
.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed
.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed
.
- J. Elm and K. Kristensen, Phys. Chem. Chem. Phys., 2017, 19, 1122–1133 RSC
.
- G. Schmitz and J. Elm, ACS Omega, 2020, 5, 7601–7612 CrossRef CAS PubMed
.
- J. Elm, J. Kubečka, V. Besel, M. J. Jääskeläinen, R. Halonen, T. Kurtén and H. Vehkamäki, J. Aerosol Sci., 2020, 149, 105621 CrossRef CAS
.
- J. N. Smith, D. C. Draper, S. Chee, M. Dam, H. Glicker, D. Myers, A. E. Thomas, M. J. Lawler and N. Myllys, J. Aerosol Sci., 2021, 153, 105733 CrossRef CAS
.
- I. K. Ortega, O. Kupiainen, T. Kurtén, T. Olenius, O. Wilkman, M. J. McGrath, V. Loukonen and H. Vehkamäki, Atmos. Chem. Phys., 2012, 12, 225–235 CrossRef CAS
.
-
P. T. M. Carlsson, PhD thesis, Georg-August-Universität Göttingen, 2018
.
- LOGEresearch, LOGEresearch Manual, Book 1, 2017.
- F. Gelbard and J. H. Seinfeld, J. Colloid Interface Sci., 1980, 78, 485–501 CrossRef CAS
.
- D. M. Murphy, D. J. Cziczo, P. K. Hudson, M. E. Schein and D. S. Thomson, J. Aerosol Sci., 2004, 35, 135–139 CrossRef CAS
.
- K. T. Kuwata, M. R. Hermes, M. J. Carlson and C. K. Zogg, J. Phys. Chem. A, 2010, 114, 9192–9204 CrossRef CAS PubMed
.
- J. D. Fenske, A. S. Hasson, A. W. Ho and S. E. Paulson, J. Phys. Chem. A, 2000, 104, 9921–9932 CrossRef CAS
.
- B. E. Wyslouzil, J. H. Seinfeld, R. C. Flagan and K. Okuyama, J. Chem. Phys., 1991, 94, 6842–6850 CrossRef CAS
.
- A. Kürten, Atmos. Chem. Phys., 2019, 19, 5033–5050 CrossRef
.
- A. Shcherbacheva, T. Balehowsky, J. Kubečka, T. Olenius, T. Helin, H. Haario, M. Laine, T. Kurtén and H. Vehkamäki, Atmos. Chem. Phys., 2020, 20, 15867–15906 CrossRef CAS
.
- B. E. Wyslouzil and J. Wölk, J. Chem. Phys., 2016, 145, 211702 CrossRef PubMed
.
- F. Peters, Exp. Fluids, 1983, 1, 143–148 CrossRef CAS
.
- J. Tröstl, W. K. Chuang, H. Gordon, M. Heinritzi, C. Yan, U. Molteni, L. Ahlm, C. Frege, F. Bianchi, R. Wagner, M. Simon, K. Lehtipalo, C. Williamson, J. S. Craven, J. Duplissy, A. Adamov, J. Almeida, A.-K. Bernhammer, M. Breitenlechner, S. Brilke, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, M. Gysel, A. Hansel, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, H. Keskinen, J. Kim, M. Krapf, A. Kürten, A. Laaksonen, M. Lawler, M. Leiminger, S. Mathot, O. Möhler, T. Nieminen, A. Onnela, T. Petäjä, F. M. Piel, P. Miettinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, K. Sengupta, M. Sipilä, J. N. Smith, G. Steiner, A. Tomè, A. Virtanen, A. C. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, K. S. Carslaw, J. Curtius, J. Dommen, J. Kirkby, M. Kulmala, I. Riipinen, D. R. Worsnop, N. M. Donahue and U. Baltensperger, Nature, 2016, 533, 527–531 CrossRef PubMed
.
- H. Chen, M. J. Ezell, K. D. Arquero, M. E. Varner, M. L. Dawson, R. B. Gerber and B. J. Finlayson-Pitts, Phys. Chem. Chem. Phys., 2015, 17, 13699–13709 RSC
.
- P. Hamill, J. Aerosol Sci., 1975, 6, 475–482 CrossRef
.
- F. Bianchi, J. Tröstl, H. Junninen, C. Frege, S. Henne, C. R. Hoyle, U. Molteni, E. Herrmann, A. Adamov, N. Bukowiecki, X. Chen, J. Duplissy, M. Gysel, M. Hutterli, J. Kangasluoma, J. Kontkanen, A. Kürten, H. E. Manninen, S. Münch, O. Peräkylä, T. Petäjä, L. Rondo, C. Williamson, E. Weingartner, J. Curtius, D. R. Worsnop, M. Kulmala, J. Dommen and U. Baltensperger, Science, 2016, 352, 1109–1112 CrossRef CAS PubMed
.
- J. Tröstl, T. Tritscher, O. F. Bischof, H.-G. Horn, T. Krinke, U. Baltensperger and M. Gysel, J. Aerosol Sci., 2015, 87, 75–87 CrossRef
.
- M. Kulmala, K. E. J. Lehtinen and A. Laaksonen, Atmos. Chem. Phys., 2006, 6, 787–793 CrossRef CAS
.
- H. Henschel, T. Kurtén and H. Vehkamäki, J. Phys. Chem. A, 2016, 120, 1886–1896 CrossRef CAS PubMed
.
- N. Myllys, J. Elm and T. Kurtén, Int. J. Comput. Theor. Chem., 2016, 1098, 1–12 CrossRef CAS
.
- N. Myllys, J. Elm, R. Halonen, T. Kurtén and H. Vehkamäki, J. Phys. Chem. A, 2016, 120, 621–630 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04580f |
| This journal is © the Owner Societies 2022 |