Facet-dependent CO₂ reduction reactions on kesterite Cu₂ZnSnS₄ photo-electro-integrated electrodes

Abstract

Photoelectrochemical CO₂ reduction by Cu₂ZnSnS₄ (CZTS) photocathodes is a potentially low-cost and high-efficiency CO₂ conversion approach. However, the current CZTS-based photocathodes for the CO₂ reduction reaction (CO₂RR) are challenged by the active side reaction of the hydrogen evolution reaction (HER) and the incompatibility with efficient electrocatalysts. In this work, by means of density functional theory (DFT), we predict that a (220)-facet-suppressed kesterite CZTS could be an efficient photo-electro-integrated photocathode for formic acid production in the CO₂RR. The results show that the competitive HER is mostly favored on the (220) facet. And the CO₂RR for formic acid production on the (112) and (312) facets exhibits a thermodynamic energy barrier lower than 0.26 eV. Different from the d-band theory in metal electrocatalysts, it is found that the density of low energy unoccupied states in the S 3p orbital plays a key role in determining the CO₂RR reaction path of the kesterite CZTS. Furthermore, two different trends of adsorption energy depending on the chemical characteristic of adsorbates are analyzed. Our study unveils the potential for selectively reducing CO₂ into formic acid with kesterite CZTS and provides a possible route for manipulating the electrocatalytic properties of metal sulfide catalysts.

---

1. Introduction

The increase of human activities accompanied by combustion of fossil fuels is threatening the balance of the natural carbon cycle.¹ Converting CO₂ into valuable chemicals, such as formic acid (HCOOH), carbon monoxide (CO), and methanol (CH₃OH), can harness the rising levels of CO₂ concentration in the atmosphere and reduce the industrial fossil fuel demand at the same time.^2,3 Among these products, formic acid is a valuable liquid chemical with a high production and versatile utilization in many industrial processes.⁴

One approach to utilizing CO₂ is via the electrochemical CO₂ reduction reaction (CO₂RR). While a range of metal electrocatalysts have been developed for the CO₂RR, large bias potentials (<−0.6 V_RHE) are usually required to achieve a desirable product selectivity and efficiency.^5–12 Photoelectrochemically reducing CO₂ by photoelectrodes in an aqueous electrolyte is an alternative route with a lower bias potential. In a single-junction photoelectrode device, wide bandgap materials, such as TiO₂ and SrTiO₃, are needed to reduce CO₂ and oxidize water at the same time.^13,14 Assembling a dual-junction system with narrower bandgap materials can largely improve the theoretical solar conversion efficiency.¹⁵ Compared with the CO₂RR candidate materials of CdS, CuInS₂, and Cu(In,Ga)Se₂, Cu₂ZnSnS₄ (CZTS) has the advantages of a low cost, non-toxicity, earth-abundance and an ideal bandgap.^16–20

In the current studies of a bare CZTS photocathode for the CO₂RR, the reported photoelectrochemical CO₂ reducing performances are negligible, in which the amount of hydrogen produced from water is about 20 times higher than that of the CO₂RR products.^21,22 Moreover, the conclusions about the CO₂RR activity and product selectivity of a bare CZTS photocathode are controversial.^21–24 Yoshida et al. verified that a stoichiometric CZTS photocathode was able to reduce CO₂ into CO in aqueous solution by an isotope trace experiment.²¹ Kamimura et al. reported the CO₂RR activity of a Zn-rich CZTS photocathode for CO and HCOOH production in aqueous solution²² while Arai et al. and Ikeda et al. found that the Sn-rich CZTS showed no activity for the CO₂RR.^23,24 To further improve the conversion efficiency and product selectivity, surface modifications are generally adopted.^22–29 The idea of directly loading the state-of-art CO₂RR metal catalysts on the CZTS photocathodes has been proven to be negative, probably due to the increased carrier recombination between the heterointerfaces.²⁴ Although building a p–n junction or a Z-scheme system on CZTS can partly improve the performance, the achieved overall conversion efficiencies are still far below the criterion for practical application.^{22,24,26–29} Therefore, an investigation and understanding of the basic CO₂RR mechanism of CZTS is urgently needed.

In our work, the influence of the kesterite CZTS facets on the reaction paths, thermodynamic energy barrier and product selectivity of the CO₂RR is investigated using DFT. A facet-dependent product selectivity for formic acid and carbon monoxide is identified in the CO₂RR. To improve the CO₂RR product selectivity, the suppression of the competitive HER on (220) facets is suggested. Different from the d-band theory for metal electrocatalysts, the density of low energy unoccupied states is found to determine the CO₂RR thermodynamic reaction path on kesterite CZTS. Two different trends of adsorption energy depending on the type of adsorbates are firstly observed and analyzed through the density of unoccupied states. The relationship between the adsorption energy and the density of unoccupied states provides a new perspective on understanding the catalytic mechanism of metal sulfides electrocatalysts.

2. Computational details

The first-principles calculations were carried out using the projector augmented wave (PAW) method in the Vienna Ab initio Simulation Package (VASP) code.³⁰ To describe the exchange and correlation potential, the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA) was employed with a plane wave energy cutoff of 450 eV.^31,32 The break conditions for the electronic self-consistent loop and the ionic relaxation loop were 10⁻⁵ eV and 0.01 eV Å⁻¹, respectively.

Before building a slab model, the lattice constants of the kesterite CZTS structure were firstly optimized as 5.48 Å, 5.48 Å, and 10.94 Å, respectively. The (112), (220)-CuZn, (220)-CuSn, and (312) surfaces of the kesterite CZTS structure were then modeled by a four-layer slab, using a p(2 × 2) supercell with the top layer relaxed and the rest fixed to the bulk distances. To avoid the interaction between layers, a 15.0 Å vacuum region along the c-axis of a slab model was introduced. The Brillouin zone for geometry optimization of (112), (220)-CuZn, (220)-CuSn, and (312) was sampled with a Gamma-centered k-mesh of 4 × 4 × 1, 4 × 4 × 1, 4 × 4 × 1, and 4 × 2 × 1, respectively. For calculating the density of states, the Gamma-centered k-mesh was increased to 8 × 8 × 1. To prevent the underestimation of bandgaps by the PBE method, a hybrid functional method of HSE06 was utilized to calculate the band structure. The Bader charge analysis for different facets (Table S2, ESI†) was performed with the code of Henkelman and co-workers.³³ The transition states were estimated via the CI-NEB method.³⁴

In order to investigate the thermodynamic reaction path, the free energy profiles of the HER, CO₂RR, and CORR were computed using the computational hydrogen electrode (CHE) model proposed by Nørskov and co-workers.³⁵ One water molecule was added in the slab model to simulate the environment of aqueous solution. The reaction free energy change of an electrochemical reaction was calculated by ΔG = ΔE + ΔZPE − TΔS, where ΔE, ΔZPE, ΔS and T are the difference of total energy, zero potential energy, entropy and the temperature (300 K), respectively. The entropy and zero potential energy were taken from the database of NIST. The zero potential energies of all adsorbed intermediates were calculated by adding the energy of each vibration mode in the VASP.

3. Results and discussion

3.1 Chemical properties of different facets

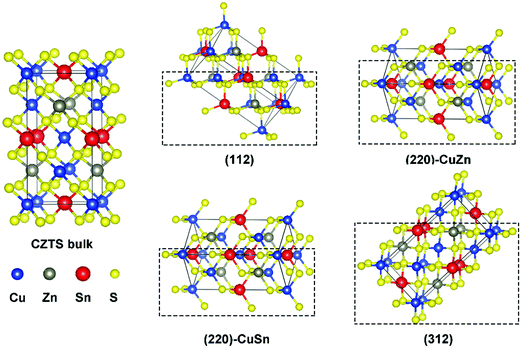
Fig. 1 presents the kesterite structure, which is generally considered as the most stable structure of CZTS.³⁶ In the X-ray diffraction patterns of experimentally fabricated CZTS films, the diffraction peaks of (112), (220), and (312) planes are commonly identified.^19,37 In this work, the (112) facet, the (220) facet with Cu and Zn atoms exposed ((220)-CuZn), the (220) facet with Cu and Sn atoms exposed ((220)-CuSn), and the (312) facet are compared in detail. For crystal orientations of [112] and [312], there is only one type of plane (A), which includes all metal elements (Fig. S1, ESI†) while for [220], there are two types of planes (B and C), which include the metal elements of Cu, Sn (B) and Cu, Zn (C), respectively. Hence, both types of (220) facet are discussed due to their probably different thermodynamic behavior. The surface energies of the above four facets are listed in Table S1 (ESI†). The (112) facet shows the lowest surface energy, suggesting the highest exposure ratio, consistent with the experimental results.^19,37 The (220)-CuZn and (220)-CuSn are a pair of facets obtained by cleaving the kesterite structure along the [220] direction. After surface relaxation, (220)-CuZn shows a lower surface energy than that of (220)-CuSn. The above results indicate the relative exposure ratio of the facets in crystalline CZTS, enabling us to discuss the reaction products in the later paragraphs.

Fig. 1 Illustration of the kesterite CZTS structure and different facets.

In order to analyze the chemical properties of the facets, the isosurface of the electron localization function (ELF) is introduced. ELF (defined by ELF = 1/[1 + (D(r)/D_h(r))²], D(r) denotes the electron density, D_h(r) represents the uniform-density of electron gas) is a dimensionless localization index restricted in the range of (0,1).³⁸ An isosurface level of 0.5 stands for the electron density equal to the uniform-density of electron gas. ELF in the isosurface corresponds to a value higher than 0.5, which suggests a more localized electron. In our previous work, the bonding nature of the kesterite CZTS structure was studied in detail.²⁰ Since the electronegativity of the Sn element (1.96) is larger than that of Cu (1.90) and Zn (1.65), the Sn–S bond in CZTS exhibits a covalent bonding nature, in contrast to the ionic bonding nature of Cu–S and Zn–S bonds. Thus, the electrons mainly distribute around the Sn–S bond in the bulk of CZTS as shown in Fig. 2(a)–(d). On the surface of CZTS, the electron distribution varies with the facet. Fig. 2(a) illustrates that the Sn atoms on (112) have more electrons than the Sn atoms in the bulk. This phenomenon is less pronounced on (220)-CuSn (Fig. 2(c)) and (312) (Fig. 2(d)). On the surface of (220)-CuZn (Fig. 2(b)), there is no Sn atom, and thus electrons mainly locate around S atoms. These results are further confirmed by Bader charge analysis. The atom's net charge is calculated by subtracting the element valence charge from the total Bader charge. Table S2 (ESI†) lists the net charge of each atom in the top, second layer of the facets and the bulk counterpart. Among the facets, the Sn atom in the top layer of (112) shows the largest total Bader charge (3.12 |e|), consistent with Fig. 2. The sums of the top layer atom's net charge (denoted as the surface net charge) of (112), (220)-CuZn, (220)-CuSn, and (312) are −0.76 |e|, −0.18 |e|, −0.01 |e|, and 0.55 |e|, respectively. The difference of electron distribution on the facets indicates a diverse thermodynamic reaction path.

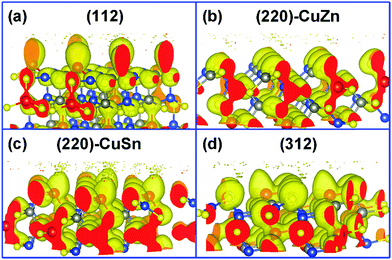Fig. 2 The isosurface of electron localization function on the (a) (112), (b) (220)-CuZn, (c) (220)-CuSn, and (d) (312) facets (isosurface level = 0.5).

3.2 HER, CO₂RR and CORR profiles of different facets

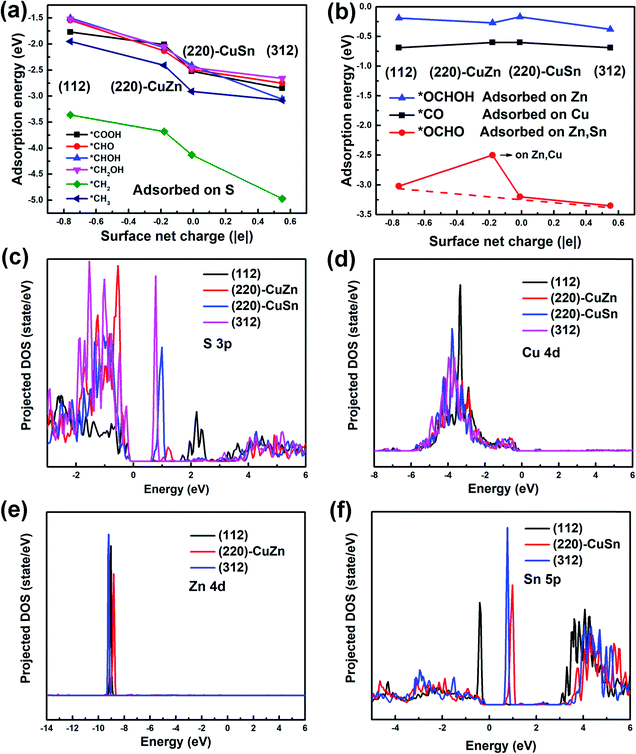
In aqueous solution, the HER competes with every proton coupled electron transfer (PCET) step in the CO₂RR path, lowering the CO₂RR faradaic efficiency. Therefore, the HER profiles on different facets are firstly studied by the CHE model.³⁵ The HER free energy profiles and the most stable intermediate structures of adsorbed H (*H) on different facets are demonstrated in Fig. 3(a) and Fig. S2 (ESI†), respectively. It is observed that the adsorption sites of *H on all facets are on the top of the S atom (Fig. S2, ESI†). However, the free energy of *H on (112), (220)-CuZn, (220)-CuSn and (312) gradually decreases from 0.74 eV, 0.27 eV, −0.17 eV, to −0.61 eV, respectively (Fig. 3(a)). As mentioned in Table S2 (ESI†), the surface net charge of (112), (220)-CuZn, (220)-CuSn, and (312) gradually increases from −0.76 |e|, −0.18 |e|, −0.01 |e|, to 0.55 |e|, respectively. By depicting the adsorption energy vs. surface net charge plot in Fig. 3(b), a near-linear relationship is found. This effect demonstrates that the adsorption energy of *H on S atom is affected by the surface net charge, which determines the thermodynamic energy barrier of the HER. Complicated engineering methods are generally employed to suppress the HER on the CO₂RR electrocatalysts. For instance, the amine functional group and chloride anions were adsorbed on the surface of Ag and Au to suppress the HER activity.^39,40 Delicate porous structures and graphene shells were designed for inhibiting the active proton transferring sites on metal oxides and Ni single atom catalysts, respectively.^41–43 In the present system, the HER on the (112) and (312) facet of the kesterite CZTS can be suppressed by the facet-dependent effect, providing a new guidance for designing other sulfide electrocatalysts.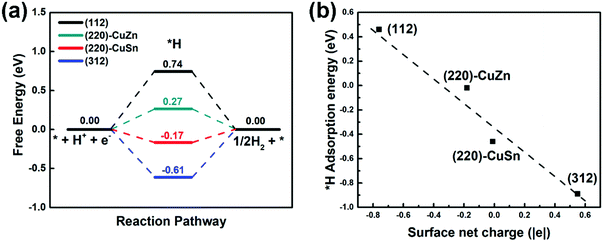

Fig. 3 (a) The HER profiles on different facets. (b) The *H adsorption energy vs. surface net charge plot.

The CO₂RR can proceed through various pathways to form different products depending on the number of electrons involved in the reaction. CO and formic acid (or formate) are the typical products in CO₂RR involving only two electrons. Generally, *CO₂ (the surface-adsorbed CO₂, * denotes the atom binding to surface) is considered as the starting point of CO₂RR.^5,6 The next intermediate product of reducing *CO₂ with one electron determines the following reaction pathway.⁴⁴ If *COOH was formed, the reaction pathway would lead to the formation of *CO and eventually the release of CO from the surface or further reducing to CH₃OH/CH₄ with more electrons. If *OCHO was produced, the reaction pathway would probably end with the formation of formic acid.

Since chalcogenide materials are known to degrade under exposure to open air, the CZTS catalyst should be applied for CO₂RR in aqueous electrolyte rather than in open air. The aqueous electrolyte not only facilitates the hydrogenation step in the CO₂RR process but also protects the catalyst from being oxidized. To simulate the aqueous environment, one water molecule is added on the surface of the slab model. Considering the above possible reaction pathways, the free energy profiles of the CO₂RR on the facets are demonstrated in Fig. 4(a–d). On (112) (Fig. 4(a)), (220)-CuSn (Fig. 4(c)) and (312) (Fig. 4(d)), the *OCHO path for formic acid production dominates over the *COOH path for CO or CH₃OH production. While the production of CO through *COOH path is preferred over the production of formic acid through the *OCHO path on (220)-CuZn (Fig. 4(b)). This facet-dependent selectivity is caused by the higher adsorption energy of *OCHO on (220)-CuZn, which is analyzed in detail in Section 3.3. Among these facets, (220)-CuSn shows the lowest thermodynamic barrier (0.09 eV) for formic acid production, lower than the HER energy barriers of (220)-CuZn (0.27 eV) and (220)-CuSn (0.17 eV). However, considering the CO₂RR kinetic energy barrier and the slow reaction kinetics of multi-electron process compared to HER, the suppression of the exposure of (220)-CuZn and (220)-CuSn facets for higher CO₂RR product selectivity is suggested. The transition states and kinetic energy barrier for formic acid production on the (112) facet are further estimated using the CI-NEB method.³⁴ In Fig. S3 (ESI†), the maximum energy barrier of 0.56 eV for formic acid production on the (112) facet is lower than that of HER (0.74 eV), supporting the conclusion that formic acid is preferentially produced on the (112) facet. The above results conclude that hydrogen, formic acid and carbon monoxide are possible products of the CO₂RR on CZTS in an aqueous electrolyte, well matching with the reported experimental results.^21–24 In these studies, hydrogen was reported as the main product of the CO₂RR, probably due to the low energy barrier for hydrogen production on (220)-CuSn and (220)-CuZn.^21–24 Yoshida et al. demonstrated the reduction of CO₂ into CO on a stoichiometric nanocrystalline CZTS photocathode in an aqueous solution, which can be explained by the preference for CO production on the (220)-CuZn facet.²¹

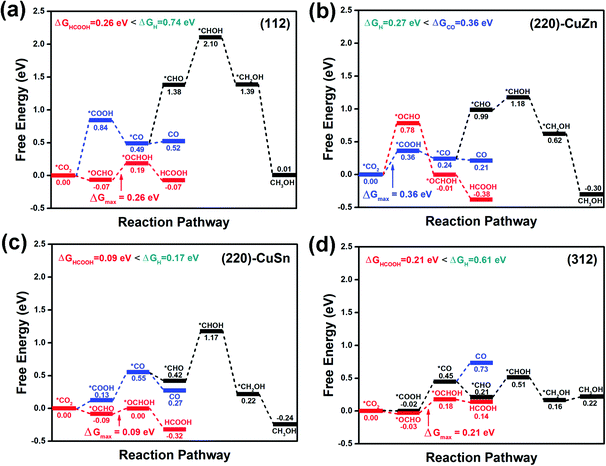Fig. 4 The CO₂RR profiles on (a) (112), (b) (220)-CuZn, (c) (220)-CuSn, and (d) (312) facets with one water molecule in the model.

Since CO is an important intermediate product in the reaction path of the CO₂RR, the facet effect of the kesterite CZTS on the CO Reduction Reaction (CORR) is investigated. Two paths of the CORR for CH₄ and CH₃OH production are considered with one water molecule in the slab model.⁴⁵ From Fig. S4(a–c) (ESI†), it is seen that CH₃OH is the preferred product of the CORR rather than CH₄ on the (112), (220)-CuZn and (220)-CuSn facets, due to the weak adsorption of *CH₂. On the (312) facet (Fig. S4(d), ESI†), the *CH₂ path for CH₄ production is more thermodynamically stable, due to the stronger adsorption of *CH₂. By comparing the free energy of *CH₂ on different facets, a decreasing trend from (112), (220)-CuZn, (220)-CuSn to (312) is observed, consistent with the effect of *H adsorption in Fig. 3(b). Besides *CH₂, the adsorbates of *CHO, *CHOH, *CH₂OH and *CH₃ also exhibit a similar decreasing trend of free energy, leading to the variation of the rate-determining step. The CORR thermodynamic barrier of 0.30 eV on CZTS (312) in this work is lower than that of the stepped Cu(211) surface (0.74 eV) and the B-doped black phosphorene under compressive strain (0.38 eV).^45,46 In accordance with the results of CO₂RR, suppressing the exposure of (220)-CuZn and (220)-CuSn is suggested to improve the CORR faradaic efficiency by inhibiting the HER.

3.3 The mechanism of facet-dependent CO₂RR and CORR selectivity

To understand the facet dependence of the CO₂RR and CORR free energy profiles, the influence of water solvent is excluded from the model, since the addition of water solvent generally lowers the adsorption energy of the intermediates. In Fig. 5, the adsorption energies of all reaction intermediates on the dry (112), (220)-CuZn, (220)-CuSn and (312) facets are investigated. The adsorption energy vs. surface net charge plots are depicted in Fig. 5(a) and (b). It is observed that the relationship between the intermediate adsorption energy and the surface net charge can be categorized into two types, depending on the intermediate adsorption site. In the first type (Fig. 5(a)), the adsorption energies of the intermediates majorly adsorbed on S atom decrease with the increasing of surface net charge (the adsorption sites of *COOH, *CHO, *CHOH, *CH₂OH, *CH₂ and *CH₃ in Fig. S5–S10, ESI†). In the second type (Fig. 5(b)), the adsorption energies of the intermediates primarily adsorbed on Cu, Zn and Sn atoms are less influenced by the surface net charge (the adsorption sites of *CO, *OCHO and *OCHOH in Fig. S11–S13, ESI†). This observation is consistent with Fig. 3(b), in which the adsorption energy of *H on the S atom varies near-linearly with the surface net charge.

Fig. 5 (a) and (b) The adsorption energy vs. surface net charge plots of (a) *COOH, *CHO, *CHOH, *CH₂OH, *CH₂, and *CH₃ (type I) and (b) *OCHOH, *CO, and *OCHO (type II) adsorbed on the (112), (220)-CuZn, (220)-CuSn and (312) facets without water molecules in the model. (c)–(f) The projected density of states (PDOS) of S 3p (c), Cu 4d (d), Zn 4d (e) and Sn 5p (f) orbitals of the adsorption-site atoms on (112), (220)-CuZn, (220)-CuSn and (312), which are calculated using the HSE hybrid functional and the Fermi level is set to 0 eV.

In order to find the possible origin of these phenomena, the projected density of states (PDOS) for the adsorption-site atoms on the surface of (112), (220)-CuZn, (220)-CuSn and (312) facets are demonstrated in Fig. 5(c)–(f). In Fig. 5(c), the S atoms on the (312) and (220)-CuSn facets show significantly higher density of unoccupied states near the CBM than that of (220)-CuZn and (112) facets. Due to the unpaired electrons on the C atom in type I adsorbates before adsorption (Fig. 6(a)), type I adsorbates are preferentially adsorbed on S atoms with a lower energy of unoccupied states rather than Cu, Zn and Sn atoms. Furthermore, the adsorption strength on the facet increases with the increasing density of low energy unoccupied states in the S 3p orbital (Fig. 5(c)). Thus, an obvious decreasing trend in the adsorption energies of type I adsorbates is observed in Fig. 3(b) and 5(a). In contrast to type I adsorbates, the adsorption energies of type II adsorbates are less influenced by the facet. In Fig. 5(d) and (e), the Cu 4d and Zn 4d orbitals show no unoccupied states in the conduction band. As a consequence, the adsorption energies of *CO on Cu and *OCHOH on Zn almost remain constant among the facets. For *OCHO on (112), (220)-CuSn and (312), which is preferentially adsorbed between Zn and Sn, a slowly decreasing trend of adsorption energy is demonstrated (red dashed line in Fig. 5(b)). This effect can be explained by the PDOS of Zn and the increasing density of low energy unoccupied states in the Sn 5p orbital from (112) to (312) (Fig. 5(f)). Different from the other facets, no Sn atom is exposed on (220)-CuZn, resulting in the adsorption of *OCHO between Cu,Zn atoms and a much higher adsorption energy.

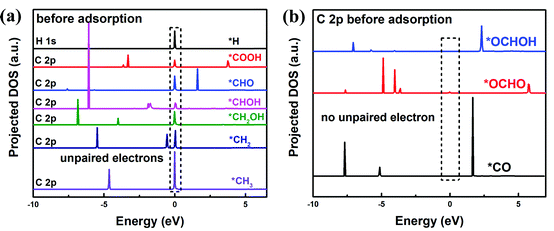Fig. 6 Projected density of states (PDOS) of C 2p orbital in type I (a) and type II (b) adsorbates, which are calculated using the PBE method.

To answer why the adsorbates of *H, *COOH, *CHO, *CHOH, *CH₂OH, *CH₂, and *CH₃ (type I) are preferentially adsorbed on the S atom and the adsorbates of *OCHOH, *CO, and *OCHO (type II) are majorly adsorbed on metal atoms, we propose a mechanism as follows. As mentioned above, in the type I adsorbates, unpaired electrons distribute around the C atom (or the H atom for *H), like the property of a free radical (Fig. 6(a)), which leads to a high total energy of the slab model. To lower the total energy, type I adsorbates are preferentially adsorbed on S atoms with the highest density of unoccupied states near the CBM. Fig. S14 (ESI†) demonstrates that the unpaired electrons on C in *CHO disappear after adsorbing on the (112) facet; meanwhile, the unoccupied states in the S 3p orbital are occupied. In the type II adsorbates, no unpaired electron distributes around the C atom, similar to the situation in a molecule (Fig. 6(b)). In this case, the adsorption of intermediates through the C–S bond no longer stabilizes the system. Thus, type II adsorbates are preferentially adsorbed on metal atoms, due to the effects such as p–d hybridization. The above analysis concludes that the density of unoccupied states in the S 3p orbital of the adsorption-site atom plays a key role in determining the reaction path. Different from transition metal catalysts identified by the d-band center of metal atoms, the kesterite CZTS shows a unique electrocatalytic property.¹¹ Further investigation of manipulating the density of unoccupied states is expected to explore the potential of the kesterite CZTS and other metal sulfide catalysts.

4. Conclusions

In summary, we demonstrate that the kesterite CZTS shows product selectivity for formic acid and carbon monoxide in the CO₂RR based on DFT calculations. To suppress the competitive HER, a lower exposure ratio of the (220) facet is suggested. Two different trends of adsorption energy depending on the type of adsorbate are observed. The adsorbates with unpaired electrons on the C atom (*COOH, *CHO, *CHOH, *CH₂OH, *CH₂ and *CH₃) are found to preferentially adsorb on the S atom, in which the adsorption energy decreases with a higher density of low energy unoccupied states in the S 3p orbital while the adsorbates with no unpaired electron on the C atom (*CO, *OCHO and *OCHOH) are favorably adsorbed on metal atoms, showing comparable adsorption energies among the facets. This effect of unoccupied states in the S 3p orbital leads to the facet-dependent HER and CO₂RR electrocatalytic properties. Our work unveils the encouraging prospect of kesterite CZTS for the selective reduction of CO₂ into formic acid and provides a new perspective on the understanding and manipulation of the catalytic property of metal sulfide electrocatalysts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is financially supported by the National Natural Science Foundation of China (51802051, 51761006, 52061010, 52101245, 51971068, 551671062, and 5187011196), the National Key Research and Development Program (2018YFB1502103 and 2018YFB1502105), the Joint Funds of the National Natural Science Foundation of China (U20A20237), Chinesisch-Deutsche Kooperationsgruppe: Integrated Computational Materials Engineering of Electrochemical Storage Systems (GZ1528), the Guangxi Bagui Scholars Foundation, Guangxi Collaborative Innovation Centre of Structure and Property for New Energy and Materials (2012GXNSFGA06002), the Guangxi Science and Technology Project (2021GXNSFBA075057, AD17195073 and 2017AD23029) and the Science and Technology Base and Talent Special Project of Guangxi Province (AD19110032 and 2018AD19098). We also thank the Guangxi Advanced Functional Materials Foundation and Application Talents Small Highlands, jointly sponsored by the Guangxi Key Laboratory of Information Materials (Guilin University of Electronic Technology), P. R. China (Project No. 191010-K).

References

1. D. W. Keith, Science, 2009, 325, 1654–1655.
2. F. P. García de Arquer, C.-T. Dinh, A. Ozden, J. Wicks, C. McCallum, A. R. Kirmani, D.-H. Nam, C. Gabardo, A. Seifitokaldani, X. Wang, Y. C. Li, F. Li, J. Edwards, L. J. Richter, S. J. Thorpe, D. Sinton and E. H. Sargent, Science, 2020, 367, 661–666.
3. S. Zhang, Q. Fan, R. Xia and T. J. Meyer, Acc. Chem. Res., 2020, 53, 255–264.
4. G. Centi, E. A. Quadrelli and S. Perathoner, Energy Environ. Sci., 2013, 6, 1711–1731.
5. M. G. Kibria, J. P. Edwards, C. M. Gabardo, C.-T. Dinh, A. Seifitokaldani, D. Sinton and E. H. Sargent, Adv. Mater., 2019, 31, 1807166.
6. N. Han, P. Ding, L. He, Y. Li and Y. Li, Adv. Energy Mater., 2020, 10, 1902338.
7. X. Zheng, P. De Luna, F. P. G. de Arquer, B. Zhang, N. Becknell, M. B. Ross, Y. Li, M. N. Banis, Y. Li, M. Liu, O. Voznyy, C. T. Dinh, T. Zhuang, P. Stadler, Y. Cui, X. Du, P. Yang and E. H. Sargent, Joule, 2017, 1, 1–12.
8. M. Liu, Y. Pang, B. Zhang, P. De Luna, O. Voznyy, J. Xu, X. Zheng, C. T. Dinh, F. Fan, C. Cao, F. P. G. de Arquer, T. S. Safaei, A. Mepham, A. Klinkova, E. Kumacheva, T. Filleter, D. Sinton, S. O. Kelley and E. H. Sargent, Nature, 2016, 537, 382–386.
9. M. Ma, B. J. Trześniewski, J. Xie and W. A. Smith, Angew. Chem., 2016, 128, 9900–9904.
10. C.-T. Dinh, T. Burdyny, M. G. Kibria, A. Seifitokaldani, C. M. Gabardo, F. P. García de Arquer, A. Kiani, J. P. Edwards, P. De Luna, O. S. Bushuyev, C. Zou, R. Quintero-Bermudez, Y. Pang, D. Sinton and E. H. Sargent, Science, 2018, 360, 783–787.
11. D. Gao, R. M. Arán-Ais, H. S. Jeon and B. Roldan Cuenya, Nat. Catal., 2019, 2, 198–210.
12. W. Ma, S. Xie, T. Liu, Q. Fan, J. Ye, F. Sun, Z. Jiang, Q. Zhang, J. Cheng and Y. Wang, Nat. Catal., 2020, 3, 478–487.
13. L. Wei, C. Yu, Q. Zhang, H. Liu and Y. Wang, J. Mater. Chem. A, 2018, 6, 22411–22436.
14. Q. Wang, J. Warnan, S. Rodríguez-Jiménez, J. J. Leung, S. Kalathil, V. Andrei, K. Domen and E. Reisner, Nat. Energy, 2020, 5, 703–710.
15. M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473.
16. J.-H. Guo, X.-Y. Dao and W.-Y. Sun, Chem. Commun., 2021, 57, 2033–2036.
17. A. Aljabour, D. H. Apaydin, H. Coskun, F. Ozel, M. Ersoz, P. Stadler, N. S. Sariciftci and M. Kus, ACS Appl. Mater. Interfaces, 2016, 8, 31695–31701.
18. J. Kim, Y. W. Lee, E.-G. Choi, P. Boonmongkolras, B. W. Jeon, H. Lee, S. T. Kim, S. K. Kuk, Y. H. Kim, B. Shin and C. B. Park, J. Mater. Chem. A, 2020, 8, 8496–8502.
19. X. Wen, W. Luo, Z. Guan, W. Huang and Z. Zou, Nano Energy, 2017, 41, 18–26.
20. R. Zhang, X. Wen, F. Xu, Q. Zhang and L. Sun, J. Phys. Chem. C, 2020, 124, 11922–11929.
21. T. Yoshida, A. Yamaguchi, N. Umezawa and M. Miyauchi, J. Phys. Chem. C, 2018, 122, 21695–21702.
22. S. Kamimura, Y. Sasaki, M. Kanaya, T. Tsubota and T. Ohno, RSC Adv., 2016, 6, 112594.
23. T. Arai, S. Tajima, S. Sato, K. Uemura, T. Morikawa and T. Kajino, Chem. Commun., 2011, 47, 12664–12666.
24. S. Ikeda, S. Fujikawa, T. Harada, T. H. Nguyen, S. Nakanishi, T. Takayama, A. Iwase and A. Kudo, ACS Appl. Energy Mater., 2019, 2, 6911–6918.
25. A. Iwase, S. Yoshino, T. Takayama, Y. H. Ng, R. Amal and A. Kudo, J. Am. Chem. Soc., 2016, 138, 10260–10264.
26. K. Kim, A. Razzaq, S. Sorcar, Y. Park, C. A. Grimes and S. Il In, RSC Adv., 2016, 6, 38964–38971.
27. M. Zubair, A. Razzaq, C. A. Grimes and S. Il In, J. CO₂ Util., 2017, 20, 301–311.
28. A. Raza, H. Shen, A. A. Haidry, L. Sun, R. Liu and S. Cui, J. CO₂ Util., 2020, 37, 260–271.
29. A. Raza, H. Shen and A. A. Haidry, Appl. Catal., B, 2020, 277, 119239.
30. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
31. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
33. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
34. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
35. B. Hinnemann, P. G. Moses, J. Bonde, K. P. Jørgensen, J. H. Nielsen, S. Horch, I. Chorkendorff and J. K. Nørskov, J. Am. Chem. Soc., 2005, 127, 5308–5309.
36. A. Walsh, S. Chen, S. H. Wei and X. G. Gong, Adv. Energy Mater., 2012, 2, 400–409.
37. Z. Guan, W. Luo, Y. Xu, Q. Tao, X. Wen and Z. Zou, ACS Appl. Mater. Interfaces, 2016, 8, 5432–5438.
38. B. Silvi and A. Savin, Nature, 1994, 371, 683–686.
39. C. Kim, T. Eom, M. S. Jee, H. Jung, H. Kim, B. K. Min and Y. J. Hwang, ACS Catal., 2017, 7, 779–785.
40. M. Cho, J. T. Song, S. Back, Y. Jung and J. Oh, ACS Catal., 2018, 8, 1178–1185.
41. Y. He, W.-J. Jiang, Y. Zhang, L.-B. Huang and J.-S. Hu, J. Mater. Chem. A, 2019, 7, 18428–18433.
42. H. Jung, S. Y. Lee, C. W. Lee, M. K. Cho, D. H. Won, C. Kim, H. S. Oh, B. K. Min and Y. J. Hwang, J. Am. Chem. Soc., 2019, 141, 4624–4633.
43. K. Jiang, S. Siahrostami, A. J. Akey, Y. Li, Z. Lu, J. Lattimer, Y. Hu, C. Stokes, M. Gangishetty, G. Chen, Y. Zhou, W. Hill, W. Bin Cai, D. Bell, K. Chan, J. K. Nørskov, Y. Cui and H. Wang, Chem, 2017, 3, 950–960.
44. J. T. Feaster, C. Shi, E. R. Cave, T. Hatsukade, D. N. Abram, K. P. Kuhl, C. Hahn, J. K. Nørskov and T. F. Jaramillo, ACS Catal., 2017, 7, 4822–4827.
45. Z. Chen, X. Liu, J. X. Zhao, Y. Jiao and L. Yin, J. Mater. Chem. A, 2020, 8, 11986–11995.
46. A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Nørskov, Energy Environ. Sci., 2010, 3, 1311–1315.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03595a

---