The lowest-energy structure of the gold cluster Au₁₀: planar vs. nonplanar?

Abstract

The onset of the transition from 2D to 3D structures in pure gold clusters remains a matter of continuing debate. In this theoretical study we revisit several planar and non-planar structural motifs of the size Au₁₀ with the aim to clarify this issue. Computations using a long-range corrected exchange–correlation functional LC-BLYP, coupled-cluster theories CCSD(T) and PNO-LCCSD(T)-F12 reveal that, at variance with previous reports on the preference of a planar elongated hexagon, both planar and nonplanar isomers of the neutral Au₁₀ are energetically degenerated up to 300 K. Its 3D equilibrium geometry is a core–shell structure which can be built up from a trigonal prism by capping four extra Au atoms outside. A comparison to the available experimental vibrational spectra allows us to argue that both lowest-lying 2D and 3D isomers of Au₁₀ likely coexist in the molecular beam during measurement of its FIR spectra. This result also suggests that the 2D–3D transition of neutral gold clusters occurs at the size Au₁₀.

---

Gold and gold-based clusters continue to receive special attention from many researchers in the fields of chemistry, physics and nanomaterials, in part due to their interesting intrinsic properties and technological uses in a variety of applications including, among others, chemical/biological sensors,¹ biomedical sciences,² catalysis for chemical reactions,^3–5etc. As a fundamental step to clarify their molecular properties and the interplay of the latter with feasible applications, it is critical to determine their ground state structures with the possible lowest-lying isomeric forms. It can be argued that the pure gold clusters are amongst the most characterized atomic aggregates to date by both experimental techniques^6–10 and quantum mechanical calculations.^11–16 These earlier studies demonstrated that a gold cluster, at each small size, tends to possess several quasi-degenerate isomers in such a way that many isomers could simultaneously be present when they are experimentally produced.⁶

Previous studies revealed that not only structural features and chemical bonding, but also characteristic properties of gold clusters are dominated by strong relativistic effects.^17–19 As a result, they exhibit many unexpected physiognomies. In fact, while small pure Au_n clusters inherently prefer a planar shape, a structural transition from 2D to 3D shape could take place at a relatively large size, namely from n = 8 to 13 depending on their charge state.^20–22 For the neutral series, a consensus has emerged that such a conversion is likely to start at the size Au₁₁ where both 2D and 3D conformations were frequently predicted to be energetically quasi-degenerate.^19,20 This implies that the smaller size Au₁₀ still has a planar or quasi-planar form.

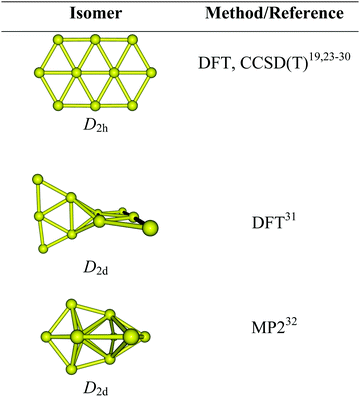
As a matter of fact, most previous studies reported that the lowest-energy structure of Au₁₀ is a planar elongated hexagon with a D_2h symmetry.^23–25 Such a form was consistently determined as the most preferred shape in several theoretical studies^19,24,26 using either density functional theory (DFT) or wave function methods. This isomer was again proposed to be the global energy minimum by recent DFT and perturbatively corrected tight-binding methods.^27–29 The energetic preference of the planar Au₁₀ structure was further reinforced by extensive calculations using not only a variety of density functionals but also wave function-based methods including the high accuracy coupled-cluster theory.³⁰ A recent analysis of the experimental far IR spectrum of Au₁₀ on the basis of DFT simulated vibrational spectra provided strong support for a planar ground state.²⁴ Nevertheless, this favorable planarity for Au₁₀ turns out to be dubious as some other investigations proposed different 3D motifs as its lowest-energy isomer.^31–34Scheme 1 displays some structural motifs formerly assigned as the most stable form of Au₁₀, which appears to be method-dependent, and the onset of the planar-globular–transition in the pure gold clusters still has not been convincingly elucidated yet, and both issues remain open for debate.

Scheme 1 Some structural motifs previously assigned as the most stable form of Au₁₀.

In view of such an inconsistency and the special position of Au₁₀ within the 2D–3D transition and growth pattern of gold clusters, we set out to revisit the relative energies of some of its lower-lying isomers with the aim to clarify these points. We present here our computed results using different density functionals including the PBE,³⁵ TPSS³⁶ and LC-BLYP³⁷ in conjunction with the cc-pVTZ-PP basis set,³⁸ in which PP stands for effective potentials for core electrons including relativistic corrections. For a further calibration, the coupled-cluster theory CCSD(T)^39,40 and explicitly correlated local coupled cluster PNO-LCCSD(T)-F12^41,42 approaches are also performed for lower-lying isomers using their PBE/cc-pVTZ-PP optimized geometries. The one-electron basis sets employed for these single point calculations are the cc-pVDZ-PP, cc-pVTZ-PP and aug-cc-pVTZ-PP that are hereafter denoted as VDZ-PP, VTZ-PP and aVTZ-PP, respectively. Let us note that the PNO-LCCSD(T)-F12^41,42 is a recent approximation to the conventional CCSD(T) theory constructed including two components. The first component is the use local pair and domain approximations exploiting the short-range nature of dynamical correlation. Such a local correlation is based on pair natural orbitals, and then combined with the explicit correlation F12 technique whose terms are also correct for part of the domain errors. The performance of this method was well benchmaked.^41,42 The PNO-LCCSD(T)-F12 method will be denoted hereafter as LCCSD(T). All electronic structure calculations in this study are carried out using the Gaussian 16⁴³ and Molpro 2020⁴⁴ packages. The most remarkable result is that we find a non-planar 3D structure which was previously identified as a high energy isomer,²⁴ but now emerges as the lowest-lying isomer of Au₁₀.

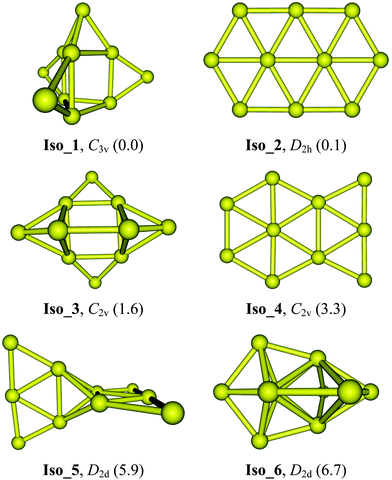
Optimized geometries along with their symmetry point groups and relative energies (kcal mol⁻¹) of six lower-lying Au₁₀ isomers are presented in Fig. 1. The latter includes two planar Iso_2 and Iso_4, the 3D Iso_1 which was previously considered in ref. 24, and two 3D Iso_5 and Iso_6 isomers that were assigned as the global energy minimum in ref. 31 and 32, respectively. Geometrical shapes along with optimized Cartesian coordinates for these lower-lying isomers are given in Table S1 of the ESI.†

Fig. 1 Optimized geometries and symmetry point groups of the lower-lying Au₁₀ isomers. Values given in parentheses are relative energies (kcal mol⁻¹) obtained from PNO-LCCSD(T)-F12/aug-cc-pVTZ-PP+ZPE based on PBE/cc-pVTZ-PP optimized geometries.

In previous studies using various DFT functionals and coupled-cluster theory CCSD(T),^23,30 the D_2h elongated hexagon Iso_2 (Fig. 1) was reported as the global energy minimum of Au₁₀. More recent calculations using the PBE and HSE06 functionals also confirmed the energetic preference of this planar form.²⁴ However, such assignment is not consistent with single reference second-order perturbation theory (MP2) results obtained by David and co-workers.³² Accordingly, the MP2 lowest-energy structure of Au₁₀ has a 3D D_2d conformation, i.e.Iso_6 in Fig. 1. This 3D structure, on the other hand, differs much from the D_2d joint-flat Iso_5 suggested earlier by Wells et al.³¹ using the B3LYP functional. It can be argued that the MP2 results are less reliable than those derived from the high accuracy CCSD(T) counterparts, and perhaps the popular hybrid B3LYP functional is not quite reliable for gold clusters. Until now, the most convincing analysis was reported by Goldsmith et al.²⁴ in which the computed vibrational spectra of three planar isomers and one 3D isomer of Au₁₀ were carefully compared to the experimental spectrum recorded from the far-IR multiple photodissociation (FIR-MPD) spectrometric experiment. As stated above, these authors concluded that the planar hexagonal ribbon Iso_2 represents the isomer having a vibrational spectrum closest to experiments.²⁴

Previous theoretical studies^30,45,46 pointed out that energetic parameters of small gold clusters are strongly method-dependent. Relative energies of Au₁₀ isomers obtained with different methods summarized in Table 1 clearly lend further support for this judgment. The CCSD(T) results are indeed dependent on the basis sets employed (Table 1). With a double-zeta basis set, Iso_1 is ∼2.8 kcal mol⁻¹ lower in energy than Iso_2, whereas a triple-zeta basis set predicts a reversed ordering, with Iso_1 lying 2.0 kcal mol⁻¹ above. For its part, the LCCSD(T) more consistently predicts that the 3D Iso_1 is marginally more favored over the 2D Iso_2 counterpart. Results obtained from the three functionals also fluctuate; the long-range corrected functional LC-BLYP reproduces an energy ordering similar to that by LCCSD(T) but the LC-BLYP energy gap turns out to be larger, being increased to ∼4 kcal mol⁻¹ in favor of Iso_1. In particular, the isomer Iso_6 becomes much less stable with a relative energy of 22 kcal mol⁻¹ above. The remaining structures including two nonplanar Iso_3 and Iso_5 and the planar Iso_4 conformations are now 3–4 kcal mol⁻¹ higher in energy. As reported in previous papers, calculations using the PBE and TPSS functionals yield a much different energy landscape in which Iso_2 has the lowest energy whereas Iso_1 is ∼6 kcal mol⁻¹ above (Table 1). Thus, the LC-BLYP results in which the dispersion component is taken into account, appear to be more consistent with the LCCSD(T) in prediction for the most stable equilibrium geometry of Au₁₀. In contrast, the PBE and TPSS functionals tend to favor the thermodynamic stability of planar structures at the expense of their 3D counterparts.

Table 1 Relative energies (kcal mol⁻¹) of six lower-lying structures of Au₁₀ computed at different levels

Isomer	LC-BLYP	PBE	TPSS	CCSD(T)		PNO-LCCSD(T)-F12
	VTZ-PP			VDZ-PP	VTZ-PP	VTZ-PP	aVTZ-PP
Iso_1	0.0	5.6	5.8	0.0	2.0	0.0	0.0
Iso_2	4.2	0.0	0.0	2.8	0.0	0.6	0.1
Iso_3	4.5	7.4	6.7	0.4	3.8	1.6	1.8
Iso_4	3.7	2.7	3.4	3.2	3.2	4.3	3.3
Iso_5	3.4	8.7	9.4	6.7	6.7	6.3	5.9
Iso_6	22	19	12	1.5	10.0	7.0	6.7

---

At variance with most of the previous reports using either DFT or wave function-based methods, our LCCSD(T) calculations using both VTZ-PP and aVTZ-PP basis sets (Table 1) show that the 3D Iso_1, which can be built up from a trigonal prism by capping four extra Au atoms outside, strongly competes with the planar Iso_2 that was previously assigned as the global minimum, to be the lowest-energy isomer. At the LCCSD(T) level with either a VTZ-PP or an aVTZ-PP basis set, Iso_1 is computed to be meaninglessly lower in energy than Iso_2, being from 0.1 to 0.6 kcal mol⁻¹ (Table 1). It can be argued that both isomers are best considered as energetically quasi-degenerate. For their parts, the 3D Iso_3 and 2D Iso_4 conformations are found at 2–4 kcal mol⁻¹ less stable than Iso_1. Both 3D isomers Iso_5 and Iso_6 that were formerly reported as global minima in ref. 31 and 32, respectively, are now located at 6 to 7 kcal mol⁻¹ higher in energy. Calculated Gibbs energies confirm the nearly degenerate stability of both isomers Iso_1 and Iso_2 at temperatures T = 100, 200 and 300 K (cf. free energy ΔG values in Table S2 of the ESI†).

We now examine the vibrational signatures of the two lowest-lying Au₁₀ isomers in comparison to the available experimental results recently reported by Goldsmith and co-workers.²⁴ First of all, in order to calibrate the performance of computational methods on reproduction of vibrational frequencies, we carry out some benchmark calculations for some small Au_n clusters (n = 2, 7, 19, 20) using several functionals, namely the PW91,⁴⁷ PBE,³⁵ B3LYP,⁴⁸ TPSS,³⁶ and LC-BLYP,³⁷ in conjunction with the effective core potential (ECP) cc-pVTZ-PP⁴⁹ basis set. The IR spectra are generated at their corresponding optimized equilibrium structures that have unambiguously been assigned as regular and truncated pyramids for Au₂₀ and Au₁₉, respectively, and a planar shape with a C_s symmetry for Au₇ (Fig. S1 of the ESI†).⁴⁶ The simulated spectra are then compared and assigned with respect to the measured data reported in ref. 50 and 51.

In the experimental FIR spectra recorded with the presence of Kr messenger atoms, the Au₂₀ system is characterized by a dominant band at 148 cm⁻¹, corresponding to a triply degenerate T₂ mode.⁵¹ This degenerate resonance is observed to split into two intense peaks at 149 and 166 cm⁻¹ for the radical Au₁₉ due to a symmetry reduction from a regular tetrahedron (T_d) to the truncated pyramid (C_3v). The observed IR signatures of the radical Au₇ turn out to be more complicated with three distinctive signals centered at 165, 186 and 201 cm⁻¹. As presented in Table 2, the B3LYP, PW91, TPSS and PBE functionals generally do not reproduce well the experimental absorption positions for these clusters and greatly underestimate the observed frequencies with an RMSD value in the range of 7 cm⁻¹ (TPSS) to 24 cm⁻¹ (B3LYP). The LC-BLYP appears to be more reliable in predicting vibrational signatures as it gets the smallest deviations with respect to the experiment with an RMSD value of 3.5 cm⁻¹. In principle, the normal modes of vibration are determined by the force constants between the atoms and thereby strongly depend on internal positions within a chemical system. Both TPSS and PBE functionals overestimate the Au–Au bond length with deviations from experiments varying from 0.05 to 0.06 Å for Au₂, respectively. Therefore, these approaches inherently underestimate the vibrational energies of gold clusters. In contrast, the LC-BLYP value of 2.50 Å for Au–Au bond length in the dimer is comparable to the experimental value of 2.47 Å.⁴¹ The LC-BLYP exhibits the smallest deviations from experimental bond lengths with an error margin of ±0.03 Å. As a result, this functional turns out to be more reliable in prediction of vibrational frequencies, and can be used without any scaling as the most appropriate choice for generation of vibrational spectra of small gold clusters.

Table 2 Vibrational frequencies (cm⁻¹) of the most intense peaks in some small Au_n clusters at their equilibrium structures, computed with different functionals in conjunction with the cc-pVTZ-PP basis set along with experimental data

Method	Au2	Au7			Au19		Au20	RMSD^b
a Taken from ref. 51. Values for Au2 are taken from ref. 50. b Root-mean-square deviations from experimental values.
PW91	173	155	175	188	135	152	137	13.2
PBE	172	154	174	186	135	153	136	13.9
B3LYP	166	145	163	177	122	144	125	23.5
TPSS	178	159	180	193	144	160	144	7.4
LC-BLYP	190	162	183	198	143	164	144	3.5
Experiment^a	191	165	186	201	149	166	148	—

---

In order to examine the effect of Kr on the energetic order and spectra of Au₁₀ isomers, we further carried out some investigations on the IR spectra of Iso_1·Kr and Iso_2·Kr complexes, and the results are listed in Fig. S1 of the ESI.† The LC-BLYP results show that the Kr complex of Iso_1 remains more stable than that of Iso_2, being ∼6 kcal mol⁻¹ below. Moreover, the introduction of a Kr atom is found to cause minor changes in the intensities in the low-energy region, whereas the peak positions remain almost unchanged (Fig. S2 of the ESI†).

A comparison of the FIR-MPD spectra and the theoretically simulated counterparts of Au₁₀ (Fig. 2) clearly indicates that either the 3D Iso_1 or the 2D Iso_2 can in part be assigned as the carrier of the experimental peaks, and they are thus likely present in the experimental beam. Accordingly, the intense peak found experimentally at ∼180 cm⁻¹ can be assigned to the highest signal at 178 cm⁻¹ in the predicted spectrum of Iso_1. However, the experimental peaks at 90 and 160 cm⁻¹ are missing in that of Iso_1, but they can be assigned to the strong signals centered at 91 and 160 cm⁻¹ in the theoretical spectrum of Iso_2. The 3D Iso_3 also contains a broad band near 180 cm⁻¹ and some lower ones in the higher-energy region. In view of the energetic near-degeneracy of these isomers, it can be deduced that the observed spectrum likely arises from a superposition of absorption of several isomers, rather than from a sole carrier. In contrast, the simulated IR spectra of Iso_4, Iso_5 and Iso_6 do not match the experiment well (Fig. 2).

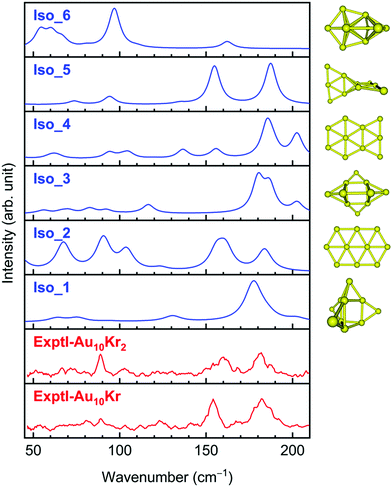Fig. 2 Experimental and theoretical IR spectra of Au₁₀ isomers. The experimental FIR spectra are taken from ref. 24. Simulations are made using harmonic vibrational frequencies (without scaling) and intensities obtained by LC-BLYP/cc-pVTZ-PP computations.

In summary, we performed a thorough investigation on the energetically quasi-degenerate structures of the gold cluster Au₁₀ by using DFT, CCSD(T) and PNO-LCCSD(T)-F12 methods. Of the three density functionals considered, LC-BLYP emerges to reach closer to the PNO-LCCSD(T)-F12 results for relative energies than both TPSS and PBE. In particular, the 3D form emerges as energetically degenerate with respect to the planar hexagon counterpart, and both 2D and 3D isomers are likely to contribute to the population of Au₁₀ at low temperatures from 100 to 300 K, rather than the sole elongated hexagonal 2D isomer as reported in most previous studies.

Relative energies between the lower-lying isomers of atomic clusters are extremely method-dependent and we cannot unambiguously assign the global minimum by relying merely on computed energetic results. Experimental information, such as infrared spectra, appears crucial for providing us with more convincing evidence on the identity of an equilibrium structure. However, a comparison of theoretical spectra with the experimental FIR-MPD spectrum of Au₁₀ also does not clearly support a preference of one isomer over another. It appears that they likely co-exist in the molecular beam with different populations depending on experimental conditions, foremost the temperature. We would also suggest that the 2D–3D structural transition of pure neutral gold clusters begins to occur at the size Au₁₀, and such a transition is likely to continue in a few following sizes.

Funding information

This work was funded by VinGroup (Vietnam) and supported by VinGroup Innovation Foundation (VinIF) under project code VinIF.2020.DA21.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

We greatly appreciate a valuable discussion with Dr André Fielicke at the Fritz-Haber Institute Berlin, Germany, on the assignment of their experimental infrared spectra of gold clusters reported in ref. 24.

References

1. K. Saha, S. S. Agasti, C. Kim, X. Li and V. M. Rotello, Gold nanoparticles in chemical and biological sensing, Chem. Rev., 2012, 112, 2739–2779.
2. L. A. Austin, M. A. Mackey, E. C. Dreaden and M. A. El-Sayed, The optical, photothermal, and facile surface chemical properties of gold and silver nanoparticles in biodiagnostics, therapy, and drug delivery, Arch. Toxicol., 2014, 88, 1391–1417.
3. J. H. Teles, S. Brode and M. Chabanas, Cationic gold (I) complexes: highly efficient catalysts for the addition of alcohols to alkynes, Angew. Chem., Int. Ed., 1998, 37, 1415–1418.
4. R. M. Veenboer, S. Dupuy and S. P. Nolan, Stereoselective gold(I)-catalyzed intermolecular hydroalkoxlation of alkynes, ACS Catal., 2015, 5, 1330–1334.
5. M. Rudolph and A. S. K. Hashmi, Heterocycles from gold catalysis, Chem. Commun., 2011, 47, 6536–6544.
6. P. V. Nhat, N. T. Si, V. G. Kiselev and M. T. Nguyen, Another look at energetically quasi-degenerate structures of the gold cluster Au₂₇^q with q = 1, 0, −1, J. Comput. Chem., 2021, 42, 2145–2153.
7. B. A. Collings, K. Athanassenas, D. M. Rayner and P. A. Hackett, Optical spectroscopy of Ag₇, Ag₉⁺, and Ag₉. A test of the photodepletion method, Chem. Phys. Lett., 1994, 227, 490–495.
8. S. Krückeberg, G. Dietrich, K. Lützenkirchen, L. Schweikhard, C. Walther and J. Ziegler, The dissociation channels of silver clusters Ag_n⁺, 3 ≤ n ≤ 20, Int. J. Mass Spectrom., 1996, 155, 141–148.
9. M. Harb, F. Rabilloud, D. Simon, A. Rydlo, S. Lecoultre, F. Conus, V. Rodrigues and C. Félix, Optical absorption of small silver clusters: Ag_n, (n = 4–22), J. Chem. Phys., 2008, 129, 194108.
10. A. Shayeghi, D. A. Götz, R. L. Johnston and R. Schäfer, Optical absorption spectra and structures of Ag₆⁺ and Ag₈⁺, Eur. Phys. J. D, 2015, 69, 1–5.
11. X. Yang, W. Cai and X. Shao, Structural variation of silver clusters from Ag₁₃ to Ag₁₆₀, J. Phys. Chem. A, 2007, 111, 5048.
12. R. Fournier, Theoretical study of the structure of silver clusters, J. Chem. Phys., 2001, 115, 2165–2177.
13. V. Bonačić-Koutecky, V. Veyret and R. Mitrić, Ab initio study of the absorption spectra of (n = 5–8) clusters, J. Chem. Phys., 2001, 115, 10450–10460.
14. M. Chen, J. E. Dyer, K. Li and D. A. Dixon, Prediction of structures and atomization energies of small silver clusters, (Ag)_n, n < 100, J. Phys. Chem. A, 2013, 117, 8298–8313.
15. Y. Jin, Y. Tian, X. Kuang, C. Zhang and C. Lu, Ab initio search for global minimum structures of pure and boron doped silver clusters, J. Phys. Chem. A, 2015, 119, 6738–6745.
16. K. Duanmu and D. G. Truhlar, Validation of methods for computational catalyst design: Geometries, structures, and energies of neutral and charged silver clusters, J. Phys. Chem. C, 2015, 119, 9617–9626.
17. P. Pyykko, Relativistic Effects in Structural Chemistry, Chem. Rev., 1988, 88, 563–594.
18. P. Schwerdtfeger, M. Dolg, W. H. E. Schwarz, G. A. Bowmaker and P. D. W. Boyd, Relativistic Effects In Gold Chemistry. I. Diatomic Gold Compounds, J. Chem. Phys., 1989, 91, 1762–1774.
19. B. Assadollahzadeh and P. Schwerdtfeger, A systematic search for minimum structures of small gold clusters Au_n (n = 2–20) and their electronic properties, J. Chem. Phys., 2009, 131, 064306.
20. M. P. Johansson, I. Warnke, A. Le and F. Furche, At What Size Do Neutral Gold Clusters Turn Three-Dimensional?, J. Phys. Chem. C, 2014, 118, 29370–29377.
21. P. Pyykkö, Theoretical chemistry of gold. III, Chem. Soc. Rev., 2008, 37, 1967–1997.
22. M. Gruber, G. Heimel, L. Romaner, J.-L. Brédas and E. Zojer, First-principles study of the geometric and electronic structure of Au₁₃ clusters: importance of the prism motif, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 165411.
23. T.-W. Yen, T.-L. Lim, T.-L. Yoon and S. Lai, Studying the varied shapes of gold clusters by an elegant optimization algorithm that hybridizes the density functional tight-binding theory and the density functional theory, Comput. Phys. Commun., 2017, 220, 143–149.
24. B. R. Goldsmith, J. Florian, J.-X. Liu, P. Gruene, J. T. Lyon, D. M. Rayner, A. Fielicke, M. Scheffler and L. M. Ghiringhelli, Two-to-three dimensional transition in neutral gold clusters: the crucial role of van der Waals interactions and temperature, Phys. Rev. Mater., 2019, 3, 016002.
25. M. Khatun, R. S. Majumdar and A. Anoop, A Global Optimizer for Nanoclusters, Front. Chem., 2019, 7, 644.
26. Y. C. Choi, W. Y. Kim, H. M. Lee and K. S. Kim, Neutral and anionic gold decamers: planar structure with unusual spatial charge-spin separation, J. Chem. Theory Comput., 2009, 5, 1216–1223.
27. X.-J. Kuang, X.-Q. Wang and G.-B. Liu, All-Electron Scalar Relativistic Calculation on the Adsorption of Carbon Monoxide onto Small Gold Clusters, Catal. Lett., 2010, 137, 247–254.
28. X. Kuang, X. Wang and G. Liu, All-electron scalar relativistic calculation on the interaction between nitric monoxide and small gold cluster, Eur. Phys. J. D, 2011, 61, 71–80.
29. L. Rincon, A. Hasmy, M. Marquez and C. Gonzalez, A perturbatively corrected tight-binding method with hybridization: application to gold nanoparticles, Chem. Phys. Lett., 2011, 503, 171–175.
30. D. A. Götz, R. Schäfer and P. Schwerdtfeger, The performance of density functional and wavefunction-based methods for 2D and 3D structures of Au₁₀, J. Comput. Chem., 2013, 34, 1975–1981.
31. D. H. Wells Jr, W. N. Delgass and K. T. Thomson, Density functional theory investigation of gold cluster geometry and gas-phase reactivity with O₂, J. Chem. Phys., 2002, 117, 10597–10603.
32. J. David, D. Guerra and A. Restrepo, Structure, stability and bonding in the ¹Au₁₀ clusters, Chem. Phys. Lett., 2012, 539, 64–69.
33. H. Häkkinen and U. Landman, Gold clusters (Au_N, 2 ≤ N ≤ 10) and their anions, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R2287.
34. J. Wang, G. Wang and J. Zhao, Density-functional study of Au_n (n = 2–20) clusters: lowest-energy structures and electronic properties, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 035418.
35. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865.
36. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the density functional ladder: Nonempirical meta-generalized gradient approximation designed for molecules and solids, Phys. Rev. Lett., 2003, 91, 146401.
37. H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, A long-range correction scheme for generalized-gradient-approximation exchange functionals, J. Chem. Phys., 2001, 115, 3540–3544.
38. J. P. Perdew, K. Burke and Y. Wang, Generalized gradient approximation for the exchange–correlation hole of a many-electron system, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533.
39. M. Rittby and R. J. Bartlett, An open-shell spin-restricted coupled cluster method: application to ionization potentials in nitrogen, J. Phys. Chem., 1988, 92, 3033–3036.
40. P. J. Knowles, C. Hampel and H. J. Werner, Coupled cluster theory for high spin, open shell reference wave functions, J. Chem. Phys., 1993, 99, 5219–5227.
41. M. Schwilk, Q. Ma, C. Köppl and H.-J. Werner, Scalable electron correlation methods. 3. Efficient and accurate parallel local coupled cluster with pair natural orbitals (PNO-LCCSD), J. Chem. Theory Comput., 2017, 13, 3650–3675.
42. Q. Ma and H. J. Werner, Explicitly correlated local coupled-cluster methods using pair natural orbitals, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1371.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. B.01, Gaussian, Inc., Wallingford CT, 2016.
44. P. Knowles and H. Werner, in MOLPRO is a package of ab initio programs, written byH. J. Werner, R. Lindh, F. R. Manby, M. Schütz, P. Celani, T. Korona, G. Rauhut, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, C. Hampel, G. Hetzer, A. W. Lloyd, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nickla, P. Palmieri, R. Pitzer, U. Schumann, H. Stoll, A. J. Stone, R. Tarroni and T. Thorsteinsson, MOLPRO, version, 2020.
45. P. V. Nhat, N. T. Si and M. T. Nguyen, Structural evolution and stability trend of small-sized gold clusters Au_n (n = 20–30), J. Phys. Chem. A, 2020, 124, 1289–1299.
46. P. V. Nhat, N. T. Si, J. Leszczynski and M. T. Nguyen, Another look at structure of gold clusters Au_n from perspective of phenomenological shell model, Chem. Phys., 2017, 493, 140–148.
47. J. P. Perdew, P. Ziesche and H. Eschrig, Electronic structure of solids’ 91, 1991.
48. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
49. K. A. Peterson, Systematically convergent basis sets with relativistic pseudopotentials. I. Correlation consistent basis sets for the post-d group 13–15 elements, J. Chem. Phys., 2003, 119, 11099–11112.
50. M. D. Morse, Clusters of transition-metal atoms, Chem. Rev., 1986, 86, 1049–1109.
51. P. Gruene, D. M. Rayner, B. Redlich, A. F. van der Meer, J. T. Lyon, G. Meijer and A. Fielicke, Structures of neutral Au₇, Au₁₉, and Au₂₀ clusters in the gas phase, Science, 2008, 321, 674–676.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04440k

---