Metallic C5N monolayer as an efficient catalyst for accelerating redox kinetics of sulfur in lithium–sulfur batteries†
Zhihao
Wang‡
a,
Zhihao
Zeng‡
 a,
Wei
Nong
a,
Wei
Nong
 a,
Zhen
Yang
b,
Chenze
Qi
b,
Zhengping
Qiao
a,
Zhen
Yang
b,
Chenze
Qi
b,
Zhengping
Qiao
 *a,
Yan
Li
*a,
Yan
Li
 *a and
Chengxin
Wang
*a and
Chengxin
Wang
 a
a
aState Key Laboratory of Optoelectronic Materials and Technologies, School of Materials Science and Engineering, Sun Yat-Sen (Zhongshan) University, Guangzhou 510275, People's Republic of China. E-mail: cesqzp@mail.sysu.edu.cn; liyan266@mail.sysu.edu.cn
bZhejiang Key Laboratory of Alternative Technologies for Fine Chemicals Process, College of Chemistry and Chemical Engineering, Shaoxing University, Shaoxing, 312000, P. R. China
First published on 22nd November 2021
Abstract
Lithium–sulfur battery is one of the most promising applicants for the next generation of energy storage devices whose commercial applications are impeded by the key issue of the shuttle effect. To overcome this obstacle, various two-dimensional (2D) carbon-based metal-free compounds have been proposed to serve as anchoring materials for immobilizing soluble lithium polysulfides (LiPs), which however suffer from low electronic conductivity implying unsatisfactory performance for catalyzing sulfur redox. Therefore, we have predicted metallic C5N monolayers, possessing hexagonal (H) and orthorhombic (O) phases, exhibiting excellent performance for suppressing the shuttle effect. First-principles simulations demonstrate that O-C5N could serve as a bifunctional anchoring material due to its strong adsorption capability to LiPs and excellent catalytic performance for sulfur redox with active sites from both basal plane and zigzag edges. Furthermore, the rate of Li2S oxidation over O-C5N is fast due to the low energy barrier of 0.93 eV for Li2S decomposition. While for H-C5N, only N atoms located at the armchair edges can efficiently trap LiPs and boost the formation and dissociation of Li2S during discharge and charge processes, respectively. The current work opens an avenue of designing 2D metallic carbon-based anchoring materials for lithium–sulfur batteries, which deserves further experimental research efforts.
1. Introduction
The ever-increasing demand for an energy storage device with a long cycle life, high specific capacity, environmental friendliness and low cost has driven the development of new battery systems. Due to the high theoretical gravimetric energy density of 2600 W h kg−1, which is three to six times higher than that of currently used lithium-ion batteries (LIB), lithium–sulfur (Li–S) batteries have attracted tremendous research attention.1–4 But there still exists a couple of severe problems remaining unresolved hindering their large-scale commercial applications. For example, the intermediate products of lithium polysulfides (LiPs) generated during the charge–discharge process would dissolve into the electrolyte, which traverses the diaphragm and eventually accumulate on the anode of the battery. Moreover, poor ionic/electronic conductivity of sulfur and the discharge intermediate products (such as Li2S2/Li2S) restrict the rate performance of batteries.5–8 It has been proposed that the introduction of anchoring materials into the cathode of Li–S batteries could address those obstacles simultaneously due to their enhanced performances in trapping LiPs and accelerating the redox kinetics.5 Therefore, searching for ideal anchoring materials is an efficient strategy to overcome such issues, which can help achieve the practical application of Li–S batteries.9–12 To this end, a large number of two-dimensional (2D) materials have been extensively investigated to alleviate LiPs shuttle due to their high surface volume ratio, which includes metal sulfides,5,13 graphene,14 phosphorene,15 silicone,16 borophene17 and MXene.18Owing to its advantage of high electrical conductivity, lightweight and mature preparation methods,19 graphene has been regarded as one of the most promising candidates for anchoring material. However, pristine graphene exhibits poor performance in suppressing the shuttle effect due to weak binding affinity to LiPs.5 Therefore, graphene prepared by multiple doping has been investigated for electrodes in Li–S batteries because of more polar adsorption sites and enhanced trapping capability toward LiPs.20,21 As neighboring elements of carbon, N and B are the two most used elements for doping in order to tailor the intrinsic properties of graphene. The N atoms with higher electronegativity compared to the C atom are considered Lewis-bases in sp2 lattice, which strongly interacts with Li atoms in lithium polysulfides.22 However, doping strategy is confronted with the problem of a low density of active sites and inhomogeneous distribution of dopants. Therefore, tremendous research efforts have recently been boosted to explore the anchoring performances of the crystalline phase of carbon-based monolayers, which are either synthesized experimentally or theoretically designed. The trapping capabilities of BN, C2N, and C3N4 toward LiPs are theoretically evaluated based on adsorption energies.23 A new monolayer of BC2N has been investigated for anchoring LiPs with and without defects demonstrating its suitability for anchoring material.24 Recently, a novel 2D material, C4N4, has been theoretically designed and explored as a sulfur host, which exhibits not only superior performance of adsorbing long-chain LiPs but also fast kinetics of LiPs diffusion.25 Qie reported a C3B monolayer as an anchoring material for lithium–sulfur batteries, which showed competitive anchoring performance for LiPs.26 Nevertheless, the redox of sulfur has not been extensively investigated on those aforementioned carbon-based metal-free monolayers, which is of paramount importance as well as the entrapment of LiPs. Furthermore, those 2D monolayers suffer from low conductivity due to the existence of an electronic bandgap, which indicates their poor performance for catalyzing the sulfur redox and requires LiPs to diffuse from anchoring materials to the surface of conducting agents for their conversions to Li2S.27 This means that the transformation from LiPs to Li2S during the discharge process has to undergo adsorption-diffusion-conversion. Accordingly, it is promising to search for metallic 2D carbon-based anchoring materials, which not only possess strong trapping capability for LiPs but also catalyze effectively the sulfur redox.
Based on their generic family molecular formula of CxNy, the 2D carbon nitride family including CN (C3N3,28 C4N4,25 C6N628), C2N,29 C3N,30 C3N2,31 C3N4,32 C4N,33 C4N3,34 C5N,35 C6N8,36 C9N4,37 C9N7,37 C10N3,38 C10N939 and C14N12,40–42 have been theoretically or experimentally designed, which have attracted a lot of research efforts for applications in energy conversion and energy storage.38 Among them, g-C3N4,43 C2N,44 C3N30 and C4N45 monolayers have been experimentally synthesized. Up to date, however, a monolayer with the chemical stoichiometry of C5N has rarely been reported. Only the prediction of the bulk phase of C5N was reported whose ground state crystallizes in hexagonal lattice.46 Wang et al. designed a C5N monolayer by simply introducing vacancies in a perfect C3N monolayer.35 However, other possible structural configurations of 2D C5N possessing lower energies have not been extensively investigated. Accordingly, to confirm the existence of more energetically stable 2D C5N appealed to us to perform further investigations.
In this study, we theoretically designed metallic C5N monolayers with hexagonal and orthorhombic lattices, respectively, via a swarm structural search.47 We then extensively investigated the adsorption of LiPs on both the basal plane and edge of C5N and found that edge sites have stronger binding strength to reaction intermediates of Li–S chemistry. Finally, the redox kinetics of sulfur were extensively investigated by calculating free energy changes of the discharge process and energy barrier of Li2S decomposition on both phases. Our calculations demonstrate that on the orthorhombic phase of C5N redox kinetics of Li2S could be significantly elevated by active sites from the basal plane and edge N atoms, which showed excellent catalytic performance even better than that of single-atom catalysts. While the performance of the hexagonal phase of C5N for trapping LiPs and catalyzing the redox of Li2S could only be assigned to the edge atoms.
2. Theoretical approach
We searched the structure by means of a particle swarm optimization (PSO) algorithm, which is implemented in the CALYPSO code.47 We discovered a ground state as well as one metastable structure of 2D C5N by PSO simulation, which requires only chemical composition benefiting from its efficient and multiple algorithms. Each generation consisted of 20 structures, in which 60% of the structures were constructed on the basis of the PSO evolution algorithms, whereas the remaining 40% were randomly generated to avoid premature convergence of structural prediction. The calculation of atomic structure relaxation, electronic structure, and total energy was performed based on the density functional theory (DFT) method, which is integrated with the code of the Vienna Ab initio Simulation Package (VASP).48 The projector augmented wave (PAW) has been used to describe the interaction between the ion and electron. Within the generalized gradient approximation, the Perdew–Burke–Ernzerhof form (GGA-PBE) is utilized for describing the exchange–correlation functional.49K-Point grids in reciprocal space for all systems corresponding to the simulations of structural relaxation, self-consistent field and the density of states (DOS) are summarized in Tables S1 and S2 in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 A vacuum distance of 20 Å was used to avoid interaction between the adjacent layers. The threshold for forces of structural relaxation is 0.03 eV Å−1. A DFT-D3 scheme was employed in order to take the van der Waals (vdW) interactions into account.51 In order to explore the adsorption performance of C5N monolayers, we used 3 × 3 × 1 supercell for hexagonal phase and 2 × 4 × 1 supercell for orthorhombic phase, respectively. The equations for calculating the adsorption energy (Eads) and cohesive energy (Ecoh) are labeled as eqn (S1) and (S2), as listed in ESI.†
50 A vacuum distance of 20 Å was used to avoid interaction between the adjacent layers. The threshold for forces of structural relaxation is 0.03 eV Å−1. A DFT-D3 scheme was employed in order to take the van der Waals (vdW) interactions into account.51 In order to explore the adsorption performance of C5N monolayers, we used 3 × 3 × 1 supercell for hexagonal phase and 2 × 4 × 1 supercell for orthorhombic phase, respectively. The equations for calculating the adsorption energy (Eads) and cohesive energy (Ecoh) are labeled as eqn (S1) and (S2), as listed in ESI.†
To investigate the kinetic stability of C5N monolayers, the phonon dispersion curves were calculated using the PHONOPY program interfaced with the finite displacement method.52 To evaluate its thermodynamic stability, the ab initio molecular dynamics (AIMD) simulations with a time step of 3.0 fs lasting for 6 ps under the NVT ensemble were performed using a 3 × 3 × 1 and 2 × 4 × 1 supercell for hexagonal and orthorhombic phases, respectively. The temperature (T = 300 K) was controlled using the Nosé–Hoover thermostat.53 The Gibbs free-energy change (ΔG) for surface-mediated lithiation during the discharge process was computed based on eqn (S3)–(S8) in ESI.†
3. Results and discussion
3.1 Capturing capabilities of the C5N monolayer for LiPs and S8 clusters
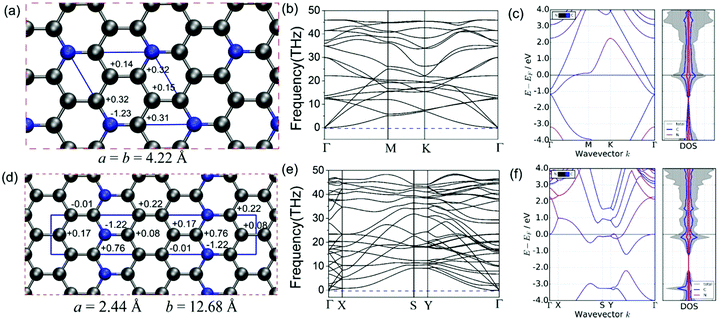
We utilized the CALYPSO code to identify the ground state of the C5N monolayer with the hexagonal lattice (H-C5N, P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) 2m, Z = 1) as well as a metastable state in an orthorhombic structure (O-C5N, Pmn21, Z = 2), which have a tiny total energy difference of 0.134 eV per formula. The complete structural optimization gives rise to the lattice constants of a = b = 4.22 Å for H-C5N and a = 12.68 Å and b = 2.44 Å for O-C5N, respectively. As shown in Fig. 1(a) and (d), there exists only one type of honeycomb ring in H-C5N consisting of five C atoms and one N atom while O-C5N consists of three types of rings, which combine carbon atoms with 0, 1 and 2 nitrogen atoms, respectively, to form a 6-membered hexagonal ring. That different structural feature is also reflected by atomic charge values of C and N atoms (see Fig. 1(a) and (d)) as well as the C–N/C–C bond length of 1.39 Å/1.40 Å and 1.41 Å/1.44 Å in H-C5N and O-C5N, respectively. Note that C atoms bonded to two N atoms in O-C5N have the largest atomic charge value of 0.76 e.
2m, Z = 1) as well as a metastable state in an orthorhombic structure (O-C5N, Pmn21, Z = 2), which have a tiny total energy difference of 0.134 eV per formula. The complete structural optimization gives rise to the lattice constants of a = b = 4.22 Å for H-C5N and a = 12.68 Å and b = 2.44 Å for O-C5N, respectively. As shown in Fig. 1(a) and (d), there exists only one type of honeycomb ring in H-C5N consisting of five C atoms and one N atom while O-C5N consists of three types of rings, which combine carbon atoms with 0, 1 and 2 nitrogen atoms, respectively, to form a 6-membered hexagonal ring. That different structural feature is also reflected by atomic charge values of C and N atoms (see Fig. 1(a) and (d)) as well as the C–N/C–C bond length of 1.39 Å/1.40 Å and 1.41 Å/1.44 Å in H-C5N and O-C5N, respectively. Note that C atoms bonded to two N atoms in O-C5N have the largest atomic charge value of 0.76 e.
The dynamical stability is confirmed from phonon dispersion curves, which, as shown in Fig. 1(b) and (e), exhibit no imaginary phonon frequencies for both H-C5N and O-C5N. We also explored the thermodynamic stability of H-C5N and O-C5N monolayers by performing AIMD simulations, which show that both phases can maintain structural integrity at 300 K (see Fig. S1 and S2, ESI†).
Cyclability and rate performance of the lithium–sulfur battery are strongly correlated with the electron conductivity of cathodes.38 We then explored the electronic properties of C5N by calculating the electronic band structure and DOS. Fig. 1(c) and (f) clearly show that for both phases valence bands cross the Fermi level implying that they possess metallic states, which facilitate the discharge–charge process of LiPs when used as anchoring materials.
Cohesive energy (Ecoh) is widely utilized to evaluate the experimental feasibility of fabrication and the calculated values of Ecoh for both H-C5N and O-C5N are −7.36 and −7.34 eV, respectively, which possess a very tiny difference of 0.02 eV rendering the possibility that both hexagonal and orthorhombic phases could be simultaneously synthesized. They are slightly higher than that of graphene (−7.95 eV)54 but significantly lower than those previously reported for 2D materials of C4N4, C3N, g-CN, g-C4N3 and C2N whose cohesive energies are −7.27,25 −7.07,55 −5.71,56 −6.757 and −5.59 eV,58 respectively. Note that C3N, g-CN, g-C4N3 and C2N have been experimentally synthesized indicating that our newly predicted H-C5N and O-C5N are highly possible to be prepared experimentally. More interestingly, both of our predicted C5N monolayers are more energetically stable than another 2D C5N proposed in the previous literature, which was designed by simply introducing double vacancies within 2D C3N with Ecoh = −7.20 eV (see Fig. S3, ESI†).35
We also computed elastic constants of H-C5N and O-C5N monolayers, which are summarized in Table 1, together with the results of graphene for comparison.57 For H-C5N, the independent elastic constants are C11 = 371.59 and C12 = 62.66 N m−1, while those for O-C5N are C11 = 368.83, C12 = 61.25, C22 = 374.53, and C66 = 38.55 N m−1. These results conform to the Born criteria, where C11 > 0, C66 > 0 and C11 > |C12| for H-C5N and C66 > 0 and C11C22 > C122 for O-C5N, demonstrating that both phases of C5N are mechanically stable.59,60
| H-C5N | O-C5N | Graphene57 | |
|---|---|---|---|
| C 11 | 371.59 | 368.83 | 351.71 |
| C 22 | 374.53 | ||
| C 12 | 62.66 | 61.25 | 58.63 |
| C 66 | 154.47 | 38.55 | 146.52 |
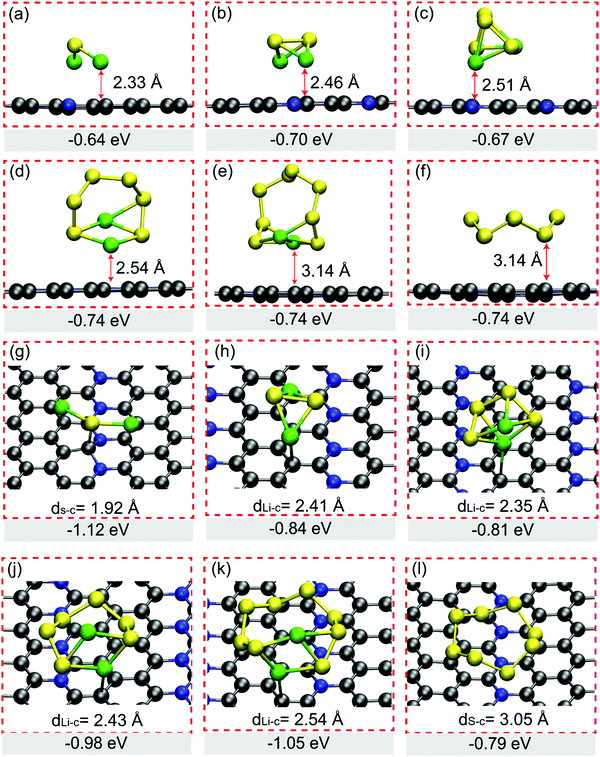
The promising anchoring material in Li–S batteries should have strong interaction intensity with LiPs in particular long-chain clusters of Li2S4, Li2S6 and Li2S8, which is usually evaluated from Eads based on eqn (S1) shown in ESI.† We tried various adsorption configurations of LiPs on H-C5N and O-C5N, of which only those patterns with the lowest Eads are presented in Fig. 2. In adsorbed systems, the vertical distance between LiPs and substrates, as summarized in Fig. 2, ranges from 2.33 to 3.14 Å on H-C5N and from 2.01 to 2.41 Å on O-C5N. When it turns to the case of adsorbed S8, the distance increases to 3.14 Å on H-C5N and 3.05 Å on O-C5N, indicating vdW interaction is a decisive factor for the binding between S8 cluster and substrates.
The Eads values of LiPs on H-C5N are in the range of −0.60 to −0.74 eV as listed in Fig. 2, indicating worse trapping capability for LiPs compared to the electrolyte solvent molecule of 1,2-dimethoxyethane (DME). Taking Li2S4 as an exaple, its Eads value on H-C5N is higher than that on DME by the difference of 0.13 eV,26 leading to the poor performance of the H-C5N monolayer for inhibiting the shuttle effect. In contrast, the binding strength of all LiPs and O-C5N is clearly stronger than that of H-C5N as reflected by their lower Eads ranging from −0.81 eV to −1.12 eV. Moreover, we believe that O-C5N could suppress the shuttle effect by immobilizing soluble Li2S4 because its Eads on O-C5N was calculated to be −0.81 eV, lower than that of −0.80 eV on DME.26 Bader charge analysis shows charge transfers from adsorbed LiPs to O-C5N, while for the adsorbed S8, the charge transfer is directed in the reverse direction as summarized in Table S3 (ESI†). In addition, no linear correlation was found between charge transfers and adsorption energy, which might be ascribed to the localized polarization of the O-C5N monolayer that induces extra electrostatic interactions.26
3.2 Adsorption performance of C5N edges toward LiPs and S8 clusters
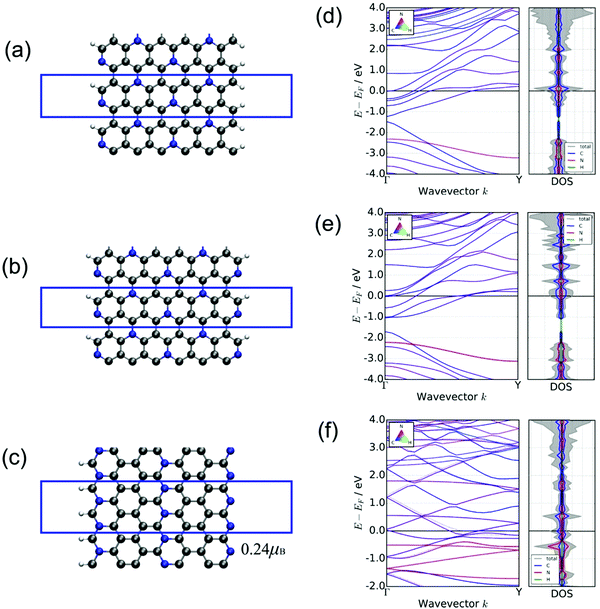
To extend the anchoring capability toward LiPs, we also investigated the performances of the edges of both phases of C5N because the enhanced binding affinity has been found in the presence of edge defects in heteroatoms doped graphene.20,61,62 Therefore, the edge defects are fabricated by cutting both phases of C5N to nanoribbons along the direction of the zigzag edge or armchair edge. The specific atomic arrangements of N and C in H-C5N and O-C5N render a wide variety of nanoribbons with different termination stoichiometries, which in total include 13 kinds of nanoribbons (see Fig. 3 and Fig. S4, S5, ESI†). Among them, three nanoribbons depicted in Fig. 3 are filtered by giving rise to lower Eads for the long-chain Li2S6 clusters than other nanoribbons as illustrated in Table S4 and Fig. S6–S8 (ESI†), which is in the window of −1.72 < Eads < −1.03 eV. While the rest ten nanoribbons possess a much weaker binding affinity toward Li2S6 as reflected by their higher Eads values (see Table S4, ESI†) as shown in Fig. S4 and S5 (ESI†). Those three nanoribbons depicted in Fig. 3(a)–(c) are named as H-A-C1N1-C2N0 and H-A-C1N1-C1N1 (achieved from H-C5N with armchair edges) and O-Z-C2N0-C0N2 (achieved from O-C5N with a zigzag edge). Regarding the names of nanoribbons, hereafter in this study, those cleaved from the hexagonal phase (H-) with armchair/zigzag edges are labeled as H-A/H-Z and otherwise as O-A/O-Z, which are constructed on the basis of the orthorhombic phase. In addition, those names as well contain information on the arrangements of edge atoms. Taking H-A-C1N1-C2N0 as an example, it denotes the nanoribbon with armchair edges derived from H-C5N with successive edge atoms of one C and one N atom at the left side and two C atoms and zero N atom at the right side of the ribbon, with more details shown in Fig. S4(a) (ESI†). Furthermore, this nomenclature enables us to easily distinguish the adsorption position on nanoribbons. We marked the adsorption site in bold, for instance, H-A-C1N1-C2N0 (shown in Fig. 3(a)) refers to the situation that an adsorbate adsorbs on the left side of the nanoribbon terminated with one C and one N. Note that the C atom exposed at the edge of nanoribbons would be saturated with hydrogen atom while N atoms are not.We next briefly explored the structural and electronic properties of those three nanoribbons. They all maintain the conductive nature as confirmed by their band structures and DOS, which have no gaps as illustrated in Fig. 3(d)–(f). Note that O-Z-C2N0-C0N2 has a spin-polarized ground state with the total magnetism of 0.24 μB per cell, while it is absent in the other two ribbons.
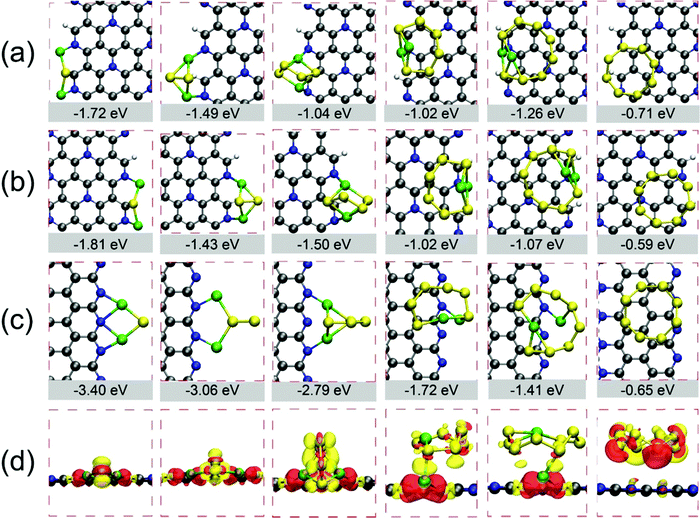
Next, we explored the performances of edge atoms of C5N for trapping LiPs and S8 clusters by calculating Eads of those clusters on three types of nanoribbons, as shown in Fig. 4 and in Fig. S9–S11 (ESI†). Our DFT calculations demonstrate that edges of H-A-C1N1-C2N0, H-A-C1N1-C1N1 and O-Z-C2N0-C0N2 possess strong chemisorption toward LiPs as shown in Fig. 4, which leads to the chemical bond formed between Li atoms and N atoms. The corresponding Eads values are lower than −1.02 eV, indicating that the edges of those three nanoribbons qualify to suppress the shuttle effect. In particular, the binding strength between LiPs and O-Z-C2N0-C0N2 (see Fig. 4(c)) was found the strongest, which was due to the most abundant edge N atoms in this structure configuration. The adsorption energies of LiPs on O-Z-C2N0-C0N2 are −3.40, −3.06, −2.79, −1.72, −1.41 and −0.65 eV for Li2S, Li2S2, Li2S4, Li2S6, Li2S8 and S8, respectively, which are much lower than those on H-A-C1N1-C1N1 and H-A-C1N1-C2N0. These data also demonstrate that O-Z-C2N0-C0N2 does better than graphene nanoribbons on entrapping LiPs (GNR) with corresponding values of Eads of −0.49, −0.38, −0.36, −0.36 and −0.38 eV.20 Moreover, the anchoring performance of GNR for LiPs could be enhanced by introducing heteroatoms X at the edges of GNR (X-GNR, X = O, N and F), which leads to the Eads for Li2S4 decreasing from −0.36 eV for GNR to −2.56, −2.00 and −1.89 eV for O-GNR, N-GNR and F-GNR, respectively.20 Nevertheless, our calculations clearly demonstrate that O-Z-C2N0-C0N2 could bind LiPs stronger than X-GNR.
Such strong interaction between LiPs and C5N nanoribbons could be also evidenced from the structural deformation in adsorbed phases of LiPs as summarized in Tables S5–S7 (ESI†). One can clearly see that variations in bond length and bond angle as LiPs are adsorbed on O-Z-C2N0-C0N2 are more pronounced than those on H-A-C1N1-C1N1 and H-A-C1N1-C2N0. The charge density difference was also calculated for the adsorbed systems on O-Z-C2N0-C0N2 to shed light on the interaction intensity between LiPs and S8 clusters and nanoribbons. As shown in Fig. 4(d), there is a clear charge transfer between adsorbed clusters and nanoribbon. The charge exchange mainly occurs between Li atoms and edge N atoms, indicating a strong chemical bond of Li–N, while the charge around S atoms is found to be reduced due to the adsorption effect. Moreover, the Bader charge analysis was performed to obtain quantitative values of charge transfer between adsorbates and substrate.63,64 Our calculations demonstrate that the charge transfer from Li2S, Li2S2, Li2S4, Li2S6, Li2S8, and S8 clusters to O-Z-C2N0-C0N2 nanoribbon by 0.81, 0.99, 0.83, 0.25, 0.23 and 0.01 e, respectively.
3.3 Redox kinetics of sulfur on basal plane and edges of C5N
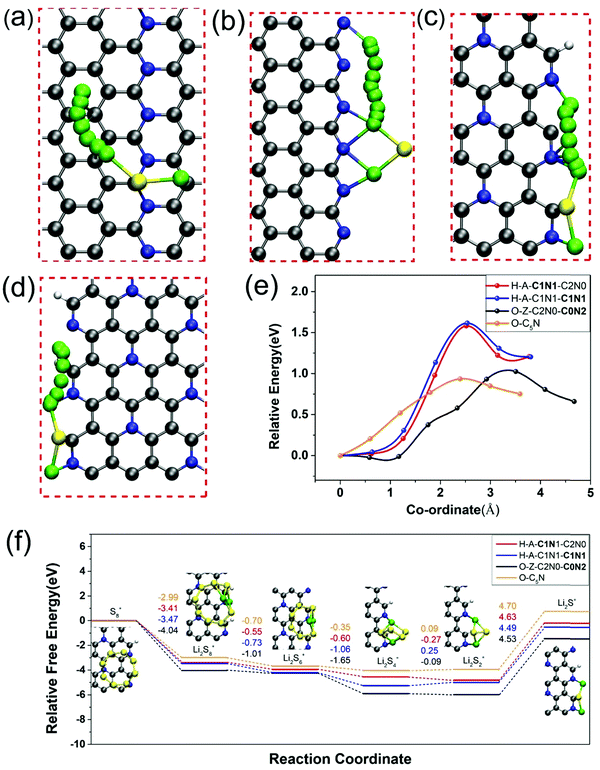
In addition to the strong chemisorption of LiPs, the fast reaction kinetics of reverse conversion between S8 and Li2S is highly demanded as well as suppressing the shuttle effect and improving the utilization of sulfur. Therefore, we next probed the catalytic performance of O-C5N and nanoribbons of H-A-C1N1-C1N1, H-A-C1N1-C2N0 and O-Z-C2N0-C0N2 for the redox reaction of Li2S. The oxidation process of Li2S was firstly investigated for which the rate of reaction kinetics was evaluated by the energy barrier (Eb) for the breaking of the Li–S bond, which was calculated by the climbing-image nudged elastic band (CI-NEB) method.65 The energetically optimal reaction pathways of Li2S decomposition on those four systems are plotted in Fig. 5(a)–(d), which demonstrate barriers of 0.93, 1.02, 1.61, and 1.58 eV for Li2S dissociation catalyzed by basal sites of O-C5N and edges of O-Z-C2N0-C0N2, H-A-C1N1-C1N1 and H-A-C1N1-C2N0, respectively, as shown in Fig. 5(e). Our DFT calculations demonstrate that the rate of Li2S decomposition is much higher on O-C5N than those on the edges of O-Z-C2N0-C0N2, H-A-C1N1-C1N1 and H-A-C1N1-C2N0. Interestingly, the catalytic capability of O-C5N for Li2S dissociation is even more enhanced than those over single-atom catalysts of VN4@G and CoN4@G with Eb values of 1.1066 and 1.37 eV,67 respectively. Overall, O-C5N exhibits better catalytic capability for Li2S decomposition than H-C5N given the active sites from the basal plane to the edges of nanoribbons.Next, the reduction process of sulfur through the opening of the ring structure was extensively investigated, for which we calculated the Gibbs free energy changes corresponding to the discharge process from S8 to Li2S accompanied by the generation of gas-phase of Li2S2 clusters based on the eqn (S3)–(S8) listed in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 68 The overall free energy change over O-C5N and the edges of O-Z-C2N0-C0N2, H-A-C1N1-C1N1 and H-A-C1N1-C2N0 are −0.76, −1.46, −0.52 and −0.19 eV, respectively, indicating that the reduction process of sulfur is exothermic. Consistent with previous works, the rate-determining step (RDS) for the conversions from S8 to Li2S on those four systems all refer to the reaction from Li2S2 to Li2S, as shown in Fig. 5(f).69 The free energy change of RDS (ΔGRDS) could be considered as a simple descriptor for assessing the performance of catalysts toward sulfur reduction. One can see that the values of ΔGRDS on those three nanoribbons are 4.53, 4.49 and 4.63 eV, respectively, as shown in Fig. 5(f). Among them, H-A-C1N1-C1N1 exhibits the best catalytic performance for sulfur reduction due to the lowest ΔGRDS = 4.49 eV. Nevertheless, other systems of O-C5N, O-Z-C2N0-C0N2 and H-A-C1N1-C2N0 show comparable performance for catalyzing the sulfur reduction due to their similar values of ΔGRDS as that of H-A-C1N1-C1N1.
68 The overall free energy change over O-C5N and the edges of O-Z-C2N0-C0N2, H-A-C1N1-C1N1 and H-A-C1N1-C2N0 are −0.76, −1.46, −0.52 and −0.19 eV, respectively, indicating that the reduction process of sulfur is exothermic. Consistent with previous works, the rate-determining step (RDS) for the conversions from S8 to Li2S on those four systems all refer to the reaction from Li2S2 to Li2S, as shown in Fig. 5(f).69 The free energy change of RDS (ΔGRDS) could be considered as a simple descriptor for assessing the performance of catalysts toward sulfur reduction. One can see that the values of ΔGRDS on those three nanoribbons are 4.53, 4.49 and 4.63 eV, respectively, as shown in Fig. 5(f). Among them, H-A-C1N1-C1N1 exhibits the best catalytic performance for sulfur reduction due to the lowest ΔGRDS = 4.49 eV. Nevertheless, other systems of O-C5N, O-Z-C2N0-C0N2 and H-A-C1N1-C2N0 show comparable performance for catalyzing the sulfur reduction due to their similar values of ΔGRDS as that of H-A-C1N1-C1N1.
Considering the balance between both oxidation and reduction processes, we believe that O-C5N possesses superior catalytic performance for sulfur chemistry in Li–S batteries. Our calculations have affirmed that active sites from both basal plane and edge (modeled by O-Z-C2N0-C0N2) of O-C5N exhibit superior catalytic performance for Li2S oxidation and sulfur reduction, respectively. This is reflected by the low values of energy barrier of Li2S decomposition and free energy change of RDS, indicating fast kinetics of sulfur redox. While for the case of H-C5N, the rate of conversion between S8 and Li2S could be elevated only by the edge atoms. Overall, nanoflakes of O-C5N having the zigzag edges would probably serve as good anchoring materials at suppressing the shuttle effect.
4. Conclusions
In summary, we have theoretically predicted two metallic 2D monolayers of C5N crystallizing in hexagonal (H-C5N) and orthorhombic phases (O-C5N), respectively, which are more energetically stable than that proposed in the previous literature. Our calculations demonstrate that O-C5N could serve as a superior anchoring material for inhibiting the shuttle effect due to its competitive performance for trapping LiPs and accelerating the rate of redox kinetics of sulfur with active sites coming from both basal plane and edges. The LiPs could be strongly chemisorbed onto the basal plane and edges of O-C5N with the adsorption energies (Eads) of −0.81 to −3.40 eV, lower than −0.80 eV, indicating stronger binding strength than that on the electrolyte molecule of DME. O-C5N facilitates both charge and discharge processes as reflected by the energy barrier (Eb) of 0.93 eV for Li2S decomposition catalyzed by the sites from the basal plane and free energy change of RDS (ΔGRDS) of 4.53 eV over the zigzag edges, respectively. While, for H-C5N, only the edge atoms are found to be able to trap LiPs and catalyze the redox of Li2S with Eads of −1.02 to −1.81 eV, Eb of 1.57–1.61 eV and ΔGRDS of 4.49–4.63 eV. These results call for a further experimental synthesis of C5N for its application as promising anchoring material for Li–S batteries and in particular for other applications of electrochemistry.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grants No. U1801255, 51972350). The calculations were carried out using supercomputers ‘Tianhe-2’ at NSCC Guangzhou.References
- H.-J. Peng, J.-Q. Huang, X.-B. Cheng and Q. Zhang, Review on High-Loading and High-Energy Lithium-Sulfur Batteries, Adv. Energy Mater., 2017, 7, 1700260 CrossRef.
- R. P. Fang, S. Y. Zhao, Z. H. Sun, W. Wang, H. M. Cheng and F. Li, More Reliable Lithium-Sulfur Batteries: Status, Solutions and Prospects, Adv. Mater., 2017, 29, 1606823 CrossRef.
- Y. X. Yin, S. Xin, Y. G. Guo and L. J. Wan, Lithium-sulfur batteries: electrochemistry, materials, and prospects, Angew. Chem., Int. Ed., 2013, 52, 13186–13386 CrossRef CAS.
- A. Manthiram, Y. Fu, S. H. Chung, C. Zu and Y. S. Su, Rechargeable lithium-sulfur batteries, Chem. Rev., 2014, 114, 11751–11787 CrossRef CAS.
- Q. Zhang, Y. Wang, Z. W. Seh, Z. Fu, R. Zhang and Y. Cui, Understanding the Anchoring Effect of Two-Dimensional Layered Materials for Lithium-Sulfur Batteries, Nano Lett., 2015, 15, 3780–3786 CrossRef CAS PubMed.
- A. Heyden, A. T. Bell and F. J. Keil, Efficient methods for finding transition states in chemical reactions: comparison of improved dimer method and partitioned rational function optimization method, J. Chem. Phys., 2005, 123, 224101 CrossRef.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS.
- J. Klimeš, D. R. Bowler and A. Michaelides, van der Waals density functionals applied to solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 246401 CrossRef.
- C. Barchasz, J.-C. Leprêtre, F. Alloin and S. Patoux, New insights into the limiting parameters of the Li/S rechargeable cell, J. Power Sources, 2012, 199, 322–330 CrossRef CAS.
- Y. V. Mikhaylik and J. R. Akridge, Polysulfide Shuttle Study in the Li/S Battery System, J. Electrochem. Soc., 2004, 151, A1969–A1976 CrossRef CAS.
- K. Xu, X. Liu, J. Liang, J. Cai, K. Zhang, Y. Lu, X. Wu, M. Zhu, Y. Liu, Y. Zhu, G. Wang and Y. Qian, Manipulating the Redox Kinetics of Li–S Chemistry by Tellurium Doping for Improved Li–S Batteries, ACS Energy Lett., 2018, 3, 420–427 CrossRef CAS.
- Z. Shi, M. Li, J. Sun and Z. Chen, Defect Engineering for Expediting Li–S Chemistry: Strategies, Mechanisms, and Perspectives, Adv. Energy Mater., 2021, 2100332 CrossRef CAS.
- G. Zhou, H. Tian, Y. Jin, X. Tao, B. Liu, R. Zhang, Z. W. Seh, D. Zhuo, Y. Liu, J. Sun, J. Zhao, C. Zu, D. S. Wu, Q. Zhang and Y. Cui, Catalytic oxidation of Li2S on the surface of metal sulfides for Li-S batteries, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 840–845 CrossRef CAS PubMed.
- S. P. Jand, Y. Chen and P. Kaghazchi, Comparative theoretical study of adsorption of lithium polysulfides (Li2Sx) on pristine and defective graphene, J. Power Sources, 2016, 308, 166–171 CrossRef CAS.
- J. Zhao, Y. Yang, R. S. Katiyar and Z. Chen, Phosphorene as a promising anchoring material for lithium–sulfur batteries: a computational study, J. Mater. Chem. A, 2016, 4, 6124–6130 RSC.
- Z. Liu, P. B. Balbuena and P. P. Mukherjee, Evaluating silicene as a potential cathode host to immobilize polysulfides in lithium–sulfur batteries, J. Coord. Chem., 2016, 69, 2090–2105 CrossRef CAS.
- L. Zhang, P. Liang, H.-B. Shu, X.-L. Man, F. Li, J. Huang, Q.-M. Dong and D.-L. Chao, Borophene as Efficient Sulfur Hosts for Lithium–Sulfur Batteries: Suppressing Shuttle Effect and Improving Conductivity, J. Phys. Chem. C, 2017, 121, 15549–15555 CrossRef CAS.
- E. S. Sim, G. S. Yi, M. Je, Y. Lee and Y.-C. Chung, Understanding the anchoring behavior of titanium carbide-based MXenes depending on the functional group in Li-S batteries: A density functional theory study, J. Power Sources, 2017, 342, 64–69 CrossRef CAS.
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, The electronic properties of graphene, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef CAS.
- T. Z. Hou, X. Chen, H. J. Peng, J. Q. Huang, B. Q. Li, Q. Zhang and B. Li, Design Principles for Heteroatom-Doped Nanocarbon to Achieve Strong Anchoring of Polysulfides for Lithium-Sulfur Batteries, Small, 2016, 12, 3283–3291 CrossRef CAS PubMed.
- F. Li, Y. Su and J. Zhao, Shuttle inhibition by chemical adsorption of lithium polysulfides in B and N co-doped graphene for Li-S batteries, Phys. Chem. Chem. Phys., 2016, 18, 25241–25248 RSC.
- T.-Z. Hou, H.-J. Peng, J.-Q. Huang, Q. Zhang and B. Li, The formation of strong-couple interactions between nitrogen-doped graphene and sulfur/lithium (poly)sulfides in lithium-sulfur batteries, 2D Mater., 2015, 2, 14011–14020 CrossRef.
- Y. Zheng, H. Li, H. Yuan, H. Fan, W. Li and J. Zhang, Understanding the anchoring effect of Graphene, BN, C2N and C3N4 monolayers for lithium−polysulfides in Li–S batteries, Appl. Surf. Sci., 2018, 434, 596–603 CrossRef CAS.
- Y. Shao, Q. Wang, L. Hu, H. Pan and X. Shi, BC2N monolayers as promising anchoring materials for lithium-sulfur batteries: First-principles insights, Carbon, 2019, 149, 530–537 CrossRef CAS.
- T. Li, C. He and W. Zhang, A novel porous C4N4 monolayer as a potential anchoring material for lithium–sulfur battery design, J. Mater. Chem. A, 2019, 7, 4134–4144 RSC.
- Y. Qie, J. Liu, S. Wang, S. Gong and Q. Sun, C3B monolayer as an anchoring material for lithium-sulfur batteries, Carbon, 2018, 129, 38–44 CrossRef CAS.
- Y. Song, W. Cai, L. Kong, J. Cai, Q. Zhang and J. Sun, Rationalizing Electrocatalysis of Li–S Chemistry by Mediator Design: Progress and Prospects, Adv. Energy Mater., 2020, 10, 1901075 CrossRef CAS.
- H. Qiu, Z. Wang and X. Sheng, First-principles prediction of an intrinsic half-metallic graphitic hydrogenated carbon nitride, Phys. Lett. A, 2013, 377, 347–350 CrossRef CAS.
- A. Bafekry, C. Stampfl, M. Ghergherehchi and S. Farjami Shayesteh, A first-principles study of the effects of atom impurities, defects, strain, electric field and layer thickness on the electronic and magnetic properties of the C2N nanosheet, Carbon, 2020, 157, 371–384 CrossRef CAS.
- J. Mahmood, E. K. Lee, M. Jung, D. Shin, H.-J. Choi, J.-M. Seo, S.-M. Jung, D. Kim, F. Li, M. S. Lah, N. Park, H.-J. Shin, J. H. Oh and J.-B. Baek, Two-dimensional polyaniline (C3N) from carbonized organic single crystals in solid state, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7414–7419 CrossRef CAS.
- D. Mpoutas and L. Tsetseris, Magnetic two-dimensional C3N2 carbonitrides: semiconductors, metals and half-metals, Phys. Chem. Chem. Phys., 2017, 19, 26743–26748 RSC.
- J. Li, W. Cui, Y. Sun, Y. Chu, W. Cen and F. Dong, Directional electron delivery via a vertical channel between g-C3N4 layers promotes photocatalytic efficiency, J. Mater. Chem. A, 2017, 5, 9358–9364 RSC.
- L. Li, X. Kong, O. Leenaerts, X. Chen, B. Sanyal and F. M. Peeters, Carbon-rich carbon nitride monolayers with Dirac cones: Dumbbell C4N, Carbon, 2017, 118, 285–290 CrossRef CAS.
- X. Li, S. Zhang and Q. Wang, Stability and physical properties of a tri-ring based porous g-C4N3 sheet, Phys. Chem. Chem. Phys., 2013, 15, 7142–7146 RSC.
- D. Wang, H. Li, L. Zhang, Z. Sun, D. Han, L. Niu and J. Zhao, 2D Nitrogen-Containing Carbon Material C5N as Potential Host Material for Lithium Polysulfides: A First-Principles Study, Adv. Theory Simul., 2018, 2, 1800165 CrossRef.
- X. Zhang, M. Zhao, A. Wang, X. Wang and A. Du, Spin-polarization and ferromagnetism of graphitic carbon nitride materials, J. Mater. Chem. C, 2013, 1, 6265–6270 RSC.
- H. Li, H. Hu, C. Bao, J. Hua, H. Zhou, X. Liu, X. Liu and M. Zhao, Tensile strain induced half-metallicity in graphene-like carbon nitride, Phys. Chem. Chem. Phys., 2015, 17, 6028–6035 RSC.
- D. Adekoya, S. Qian, X. Gu, W. Wen, D. Li, J. Ma and S. Zhang, DFT-Guided Design and Fabrication of Carbon-Nitride-Based Materials for Energy Storage Devices: A Review, Nano-Micro Lett., 2020, 13, 13–56 CrossRef PubMed.
- X. Zhang and M. Zhao, Prediction of quantum anomalous Hall effect on graphene nanomesh, RSC Adv., 2015, 5, 9875–9880 RSC.
- A. Bafekry, S. F. Shayesteh and F. M. Peeters, Two-dimensional carbon nitride (2DCN) nanosheets: Tuning of novel electronic and magnetic properties by hydrogenation, atom substitution and defect engineering, J. Appl. Phys., 2019, 126, 215104 CrossRef.
- K. S. Lakhi, D. H. Park, K. Al-Bahily, W. Cha, B. Viswanathan, J. H. Choy and A. Vinu, Mesoporous carbon nitrides: synthesis, functionalization, and applications, Chem. Soc. Rev., 2017, 46, 72–101 RSC.
- X. Zhang, A. Wang and M. Zhao, Spin-gapless semiconducting graphitic carbon nitrides: A theoretical design from first principles, Carbon, 2015, 84, 1–8 CrossRef CAS.
- K. R. Reddy, C. H. V. Reddy, M. N. Nadagouda, N. P. Shetti, S. Jaesool and T. M. Aminabhavi, Polymeric graphitic carbon nitride (g-C3N4)-based semiconducting nanostructured materials: Synthesis methods, properties and photocatalytic applications, J. Environ. Manage., 2019, 238, 25–40 CrossRef CAS.
- Z. Liang, D. Yang, P. Tang, C. Zhang, J. Jacas Biendicho, Y. Zhang, J. Llorca, X. Wang, J. Li, M. Heggen, J. David, R. E. Dunin-Borkowski, Y. Zhou, J. R. Morante, A. Cabot and J. Arbiol, Atomically dispersed Fe in a C2N Based Catalyst as a Sulfur Host for Efficient Lithium–Sulfur Batteries, Adv. Energy Mater., 2020, 11, 2003507 CrossRef.
- Z. Fang, Y. Li, J. Li, C. Shu, L. Zhong, S. Lu, C. Mo, M. Yang and D. Yu, Capturing Visible Light in Low-bandgap C4N Derived Responsive Bifunctional Air Electrodes for Solar Energy Conversion/Storage, Angew. Chem., Int. Ed, 2021, 60, 17615–17621 CrossRef CAS.
- Q. Wu, Q. Hu, Y. Hou, H. Wang, A. Zhou and L. Wang, Ground-state structures, physical properties and phase diagram of carbon-rich nitride C5N, J. Phys.: Condens. Matter, 2018, 30, 385402 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, CALYPSO: A method for crystal structure prediction, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- A. M. Ali and A. H. Al-Mowali, Ceramic Expansion by Water Layers on Magnesium Oxide: AB InitioStudy, Am. J. Mater. Sci. Eng., 2013, 1, 50–53 Search PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- G. J. Martyna, M. L. Klein and M. Tuckerman, Nosé–Hoover chains: The canonical ensemble via continuous dynamics, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- Y. Li, Y. Liao and Z. Chen, Be(2)C monolayer with quasi-planar hexacoordinate carbons: a global minimum structure, Angew. Chem., Int. Ed., 2014, 53, 7248–7252 CrossRef CAS.
- W. Nong, Y. Li and C. Wang, C3N monolayer with substitutional doping and strain modulation serving as anode material of lithium-ion batteries, Appl. Surf. Sci., 2020, 510, 145324 CrossRef CAS.
- J. Li, C. Cao and H. Zhu, Synthesis and characterization of graphite-like carbon nitride nanobelts and nanotubes, Nanotechnology, 2007, 18, 115605 CrossRef.
- A. Du, S. Sanvito and S. C. Smith, First-principles prediction of metal-free magnetism and intrinsic half-metallicity in graphitic carbon nitride, Phys. Rev. Lett., 2012, 108, 197207 CrossRef PubMed.
- J. Mahmood, E. K. Lee, M. Jung, D. Shin, I.-Y. Jeon, S.-M. Jung, H.-J. Choi, J.-M. Seo, S.-Y. Bae, S.-D. Sohn, N. Park, J. H. Oh, H.-J. Shin and J.-B. Baek, Nitrogenated holey two-dimensional structures, Nat. Commun., 2015, 6, 6486 CrossRef CAS.
- M. Maździarz, Comment on ‘The Computational 2D Materials Database: high-throughput modeling and discovery of atomically thin crystals’, 2D Mater., 2019, 6, 48001 CrossRef.
- C. Zhu, C. Wang, M. Zhang, H. Chen, Y. Geng and Z. Su, Effective CO Migration among Multiabsorbed Sites Achieves the Low-Barrier and High-Selective Conversion to C2 Products on the Ni2B5 Monolayer, ACS Appl. Mater. Interfaces, 2021, 13, 3845–3855 CrossRef CAS.
- J. Wang, H. Yang, Z. Chen, L. Zhang, J. Liu, P. Liang, H. Yang, X. Shen and Z. X. Shen, Double-Shelled Phosphorus and Nitrogen Codoped Carbon Nanospheres as Efficient Polysulfide Mediator for High-Performance Lithium–Sulfur Batteries, Adv. Sci., 2018, 5, 1800621 CrossRef.
- G. Zhou, E. Paek, G. S. Hwang and A. Manthiram, Long-life Li/polysulphide batteries with high sulphur loading enabled by lightweight three-dimensional nitrogen/sulphur-codoped graphene sponge, Nat. Commun., 2015, 6, 7760 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Zhou, S. Zhao, T. Wang, S. Z. Yang, B. Johannessen, H. Chen, C. Liu, Y. Ye, Y. Wu, Y. Peng, C. Liu, S. P. Jiang, Q. Zhang and Y. Cui, Theoretical Calculation Guided Design of Single-Atom Catalysts toward Fast Kinetic and Long-Life Li-S Batteries, Nano Lett., 2020, 20, 1252–1261 CrossRef CAS.
- Z. Du, X. Chen, W. Hu, C. Chuang, S. Xie, A. Hu, W. Yan, X. Kong, X. Wu, H. Ji and L. J. Wan, Cobalt in Nitrogen-Doped Graphene as Single-Atom Catalyst for High-Sulfur Content Lithium-Sulfur Batteries, J. Am. Chem. Soc., 2019, 141, 3977–3985 CrossRef CAS PubMed.
- Q. He, B. Yu, H. Wang, M. Rana, X. Liao and Y. Zhao, Oxygen defects boost polysulfides immobilization and catalytic conversion: First-principles computational characterization and experimental design, Nano Res., 2020, 13, 2299–2307 CrossRef CAS.
- C. Lu, Y. Chen, Y. Yang and X. Chen, Single-atom Catalytic Materials for Lean-electrolyte Ultrastable Lithium-Sulfur Batteries, Nano Lett., 2020, 20, 5522–5530 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04192d |
| ‡ These authors contributed equally. |
| This journal is © the Owner Societies 2022 |