Uptake and hydration of sulfur dioxide on dry and wet hydroxylated silica surfaces: a computational study†
Ivan
Gladich
 *a,
Chen
Lin
b,
Alessandro
Sinopoli
*a,
Chen
Lin
b,
Alessandro
Sinopoli
 a and
Joseph S.
Francisco
a and
Joseph S.
Francisco
 *c
*c
aQatar Environment and Energy Research Institute, Hamad Bin Khalifa University, P.O. Box 34410, Doha, Qatar. E-mail: igladich@hbku.edu.qa
bDepartment of Chemistry and Biochemistry, University of California Los Angeles, CA, USA
cDepartment of Earth and Environmental Science and Department of Chemistry, University of Pennsylvania, Philadelphia, Pennsylvania 19104, USA. E-mail: frjoseph@sas.upenn.edu
First published on 17th November 2021
Abstract
We present a first-principles molecular dynamics study on the uptake and hydration of sulfur dioxide on the dry and wet fully hydroxylated surfaces of (0001) α-quartz, which are a proxy for suspended silica dust in the atmosphere. The average adsorption energy for SO2 is about −10 kcal mol−1 on both dry and wet surfaces. The adsorption is driven by hydrogen bond formation between SO2 and the interfacial hydroxyl groups (on dry silica), or with water molecules (in the wet case). In the dry system, we report an additional electrostatic interaction between the interfacial hydroxyl oxygen and the sulfur atom, which further stabilizes the adsorbate. On dry silica, the interfacial hydroxyl group coordinates to SO2 yielding a surface bound bisulfite (Si–SO3H) complex. On the wet surface, SO2 reacts with water forming bisulfite (HSO3−), and the latter remains solvated inside the adsorbed water layer. The hydration barrier for sulfur dioxide is 1 kcal mol−1 and 3 kcal mol−1 on dry and wet silica, respectively, while for the backward reaction (i.e., bisulfite to SO2) the barrier is 6 kcal mol−1 on both surfaces. The modest backward barrier rationalizes earlier experimental findings showing no SO2 uptake on silica. These results underline the importance of the surface hydroxylation and/or adsorbed water layers for the SO2 uptake and its hydration on silica. Moreover, the hydration to bisulfite may prevent direct SO2 photochemistry and be an additional source of sulfate; this is especially relevant in atmospheres subject to a high level of suspended mineral dust, intense solar radiation and atmospheric oxidizers.
Introduction
Sulfur dioxide (SO2) conversion to sulfate is considered one of the most important chemical processes in the atmosphere: sulfate is a cloud condensation nucleus and a major component of acid rains, and it significantly modifies the light scattering properties of aerosols.1–4 SO2 concentration ranges between 20 ppt to 1 ppb in unpolluted continental areas and between 20 ppt to 50 ppt in the unpolluted marine boundary layer, but values reach up to hundreds of ppb in polluted urban areas.1 The highest concentration of SO2 is observed during volcanic eruptions and, interestingly, this has been also connected to important prebiotic chemistry at the origin of life occurring in the early Earth atmosphere.5 Additionally, sulfur dioxide is a poisoning gas of catalytic surfaces used in industrial processes.6–9In the gas phase, the reaction of SO2 with OH radicals10 or ozone,11,12 and water vapor leads to the oxidation of sulfur dioxide into sulfate.1 This chemical pathway can considerably change upon SO2 uptake on a condensed phase. Due to its atmospheric relevance, SO2 uptake on liquid water has been extensively studied.13–16 SO2 is adsorbed at the air/liquid water interface,13,14,16 where several pathways for oxidation by atmospheric oxides (e.g., O3, H2O2etc.) or near UV excitation and radical formation (i.e., OH or HOSO) have been reported in the literature.16–19 Sulfur dioxide adsorption and oxidation have been also explored on solid substrates, thanks also to their relevance for some industrial applications.20 SO2 uptake and conversion on anatase (TiO2) has been extensively investigated in the dark21–23 and under UV conditions.20 By photoinduced adsorption on anatase, SO2 is converted to a sulfite ion and, finally, to superficially bound SO42− on the catalyst.20 Sulfur dioxide oxidation on iron oxides has been reported,24,25 showing the catalytic role of iron. The same catalytic effect has been also confirmed in other experimental studies considering SO2 uptake on aerosols containing transition metals.26 Finally, sulfur dioxide is also an aggressive atmospheric pollutant affecting building materials, and its uptake on dolomitic limestone has been experimentally observed to lead to the formation of epsomite.27,28
Studies on sulfur dioxide uptake have especially focused on materials that resemble suspended dust particles in the atmosphere.29–31 The group of Vicki Grassian has reported SO2 uptake and chemistry on different substrates: on TiO223,32 and ZnO33 nanoparticles, on hematite and goethite,34 on calcite,35 and on aluminum and magnesium particles,36 but to date no SO2 uptake has been detected on silica (SiO2).11 This might be the reason why, to the best of our knowledge, further studies on SO2 uptake on silica are absent. Earlier experimental studies reported sulfate formation under SO2 exposure on silica,37 but this was attributed to the presence of contaminants, such as aluminum, calcium, iron, magnesium and titanium present in natural dust, which could account for the SO2 uptake.11,37
There are few aspects of SO2 uptake and its reactivity on silica that have not been elucidated yet in the literature. Firstly, the impact of adsorbed water layers on the SO2 uptake on silica substrates cannot be straightforwardly extrapolated from the experimental results performed under vacuum or ultra-vacuum conditions.11 Secondly, when the surface of silica is exposed to air or liquid water it tends to be decorated by interfacial silanols (Si–OH), making the interfacial environment reactive.38–41 Recently, infrared spectroscopy and mass spectrometry experiments reported significant sulfate formation by exposing a silica substrate to the simultaneous presence of gas phase SO2 and O2, observing that “formation of sulfates on silica occurs with a concomitant removal/rearrangement of silanols”,8 which leaves open the question of whether sulfate formation from adsorbed SO2 on silica was primarily driven merely by the reaction with O2 or by a surface reaction with the contribution of silanols. Indeed, interfacial hydroxyl groups and adsorbed water molecules on TiO2 nanoparticles,32 or other solid substrates,42 have been shown to improve SO2 uptake. If and how the hydroxylation of the surface or adsorbed water layers on silica enhances sulfur dioxide oxidation to sulfate remains a valid question for many important applications. As an example, large scale weather and air quality models need to constrain SO2 reactivity into their chemical subroutines, especially when applied to industrialized areas in desert regions,43 where silica substrates are important components of dust particles suspended in the atmosphere.37,44
In this work, we present a molecular picture for SO2 adsorption on silica, which aims to clarify the impact of surface wetting and hydroxylation on SO2 uptake and hydration on silica-based suspended dust particles in the atmosphere. We employed first-principles molecular dynamics simulations coupled with enhanced sampling techniques for the SO2 uptake and hydration at the dry and wet air/hydroxylated silica (α-quartz) interface, which can be considered as a proxy for air/silica-based dust interfaces. Our results report SO2 adsorption energies of the order of about −10 kcal mol−1 on both dry and wet silica. The adsorption mechanism is driven by the formation of hydrogen bonds with water on the wet surface, or with interfacial silanols on the dry surface. For the latter, we also observe an electrostatic interaction between the sulfur atom and an adjacent interfacial hydroxyl oxygen, which further stabilizes the adsorbate. The hydration reaction of SO2 to bisulfite has an energy barrier of 1 kcal mol−1 and 3 kcal mol−1 on the dry and wet silica, respectively, while the dehydration reaction barrier (from sulfite to SO2) is 6 kcal mol−1 on both surfaces. The modest backward reaction barrier is not sufficient to prevent SO2 reformation from adsorbed bisulfite and subsequent gas desorption, which likely supports the no detection of SO2 on silica that has been reported experimentally elsewhere.11 Nevertheless, these results point toward two important implications in atmospheric sciences. First, the small reaction barrier for hydration implies that, contrary to the air/water case,16 direct photoexcitation of SO2 to its triplet state, which leads toward OH and HOSO radical production,16,18,19 may be prevented by hydration to bisulfite. Second, we report the feasibility of SO2 chemisorption on silica substrates: in areas subject to intense UV radiation, dust and atmospheric oxidizers, or in catalytic processes with high SO2 loading, bisulfite oxidation to sulfate may therefore prevail over dehydration and SO2 desorption back into the gas phase.
Methods
The silica surface was modelled using a fully hydroxylated (0001) α-quartz interface.40 The system was composed of 9 [–O–Si–O–] layers and 16 surface Si–OH silanols of the Q2 type (geminals). The initial dimensions of the system were ∼19.64 × 17 × 20 Å3 in the x, y, and z dimensions, respectively. The initial configuration was equilibrated at a constant pressure (1 bar) and temperature (300 K), also allowing the adjustment of the cell dimensions (i.e., NPT_F run) during a 5 ps molecular dynamics (MD) run using a time step of 0.2 fs. Afterward, the simulations box was enlarged along the z-direction to 40 Å, resulting in the formation of two vacuum/hydroxylated silica interfaces.From the equilibrated vacuum/hydroxylated silica, two simulation systems were prepared: (a) a dry silica system with one SO2 molecule placed on the top of one of the two interfaces, (b) a wet silica scenario by depositing a water layer of 26 water molecules on one silica interface and one SO2 molecule on top of that. The water layer represents more than one full monolayer, with at least one water molecule available for interaction with each silanol.38 After the deposition of SO2 and/or water, both dry and wet structures were relaxed by geometry optimization, followed by 15 ps constant volume and temperature (NVT) molecular dynamics runs with a time step of 0.5 fs.
All the MD simulations were run at the first-principles level (FPMD), i.e., the forces governing the dynamics of the system were calculated on-the-fly by employing PBE45,46 density functional theory and Grimme's dispersion correction (D3).47 The DZVP basis set was adopted and truncated at 400 Ry. The valence electrons were treated explicitly, while Goedecker–Teter–Hutter pseudopotentials48 were used to model core electrons. The temperature was kept at 300 K using a Nose–Hoover thermostat with a 50 fs time constant.49 The CP2K molecular dynamic package was adopted to run the FPMD.50
The SO2 adsorption energy has been evaluated by calculating the sulfur dioxide interaction energy with the dry and wet silica. From the last part of the 15 ps FPMD trajectories, we extracted 100 frames (spaced every 100 fs) from the trajectory with SO2 on the dry silica and 100 frames from the trajectory of SO2 on wet silica. Afterward, by energy minimization, we optimized the 200 snapshots and, starting from the optimized structures, we calculated the SO2 adsorption energy (Eads). The adsorption energy was defined as the difference between the energy of the silica/SO2 complex, ECompl, and the sum of the energy of each component, i.e., the silica substrate, ESub, and the SO2 in the gas phase. Thus, Eads = ECompl – (ESub + ESO2). Energies were corrected for basis set superposition error.51
In the time scale of FPMD simulations, the hydration of SO2 on dry and wet silica is a rare event. For this reason, we combined our FPMD with metadynamics (MTD)52 and umbrella sampling,53 to determine the free energy landscape for the reaction. As the reaction coordinate (also called collective variable, CV), we selected the coordination number, CN, to count bonds between the sulfur atom and all the oxygen atoms in the system. CN employs a smooth step function and a cutoff distance of 0.18 nm: CN assumes a value of ∼0.8–0.9 for each S–O bond and, thus, sulfur dioxide is associated with a CN value of ∼ 1.8. In the dry silica case, a 35 ps MTD run was performed starting from an optimized structure with SO2 adsorbed on the dry hydroxylated silica. The CN coordinate was biased by applying a history-bias potential constructed by depositing every 100 steps (i.e., every 50 fs) a Gaussian potential of σ-width 0.1 and height of ∼2.9 kcal mol−1 (i.e., 12 kJ mol−1). The MTD trajectory showed the formation of a Si–OSO2H complex on the silica surface after ∼14 ps. An identical set-up was adopted to perform 30 ps MTD simulations on the wet silica and formation of a bisulfite ion was observed at ∼11 ps. The MTD run was performed coupling our FPMD with the PLUMED plug-in.54 More details on the CN implementation are reported in the PLUMED manual.54
The MTD trajectories were used as starting points to calculate the 1D free energy profile by umbrella sampling.53 In both dry and wet cases, we employed at least ten independent FPMD runs constraining CN to different values using a harmonic potential. For the reaction on the dry surface, we adopted a harmonic potential of spring constant 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 (∼3900 kcal mol−1), while on the wet surface a milder spring was used, i.e., 8000 kJ mol−1 (∼1900 kcal mol−1). Our choice of the spring constants resulted in the overlapping of the probability distributions of the CN reaction coordinate among the umbrella windows, as shown in Fig. S1 and S2 (ESI†). The umbrella windows spanned from CN = 1.8 to CN = 2.6 and were not equally spaced. Table S1 in the ESI† reports the CN umbrella window values and associated spring constants. The starting configurations of each umbrella window were taken from the dry (or wet) MTD runs. Each umbrella window ran for 10 ps. The 1D free energy profiles were reconstructed using the weighted histogram analysis method (WHAM),55 discarding the initial 2 ps of each umbrella trajectory as equilibration. The errors on the 1D free energy profiles were determined by dividing the umbrella trajectories into two blocks: the first 4 ps (i.e., 2–6 ps) and the last 4 ps (6–10 ps). For each block, the 1D profile was determined and the final error assigned as the maximum difference between the two profiles. For both profiles the error was ±0.9 kcal mol−1. A similar approach has been used in the literature56,57 to construct the free energy reaction profiles by umbrella sampling from snapshots taken from the MTD trajectory.
000 kJ mol−1 (∼3900 kcal mol−1), while on the wet surface a milder spring was used, i.e., 8000 kJ mol−1 (∼1900 kcal mol−1). Our choice of the spring constants resulted in the overlapping of the probability distributions of the CN reaction coordinate among the umbrella windows, as shown in Fig. S1 and S2 (ESI†). The umbrella windows spanned from CN = 1.8 to CN = 2.6 and were not equally spaced. Table S1 in the ESI† reports the CN umbrella window values and associated spring constants. The starting configurations of each umbrella window were taken from the dry (or wet) MTD runs. Each umbrella window ran for 10 ps. The 1D free energy profiles were reconstructed using the weighted histogram analysis method (WHAM),55 discarding the initial 2 ps of each umbrella trajectory as equilibration. The errors on the 1D free energy profiles were determined by dividing the umbrella trajectories into two blocks: the first 4 ps (i.e., 2–6 ps) and the last 4 ps (6–10 ps). For each block, the 1D profile was determined and the final error assigned as the maximum difference between the two profiles. For both profiles the error was ±0.9 kcal mol−1. A similar approach has been used in the literature56,57 to construct the free energy reaction profiles by umbrella sampling from snapshots taken from the MTD trajectory.
Results and discussion
Sulfur dioxide adsorption on wet and dry silica
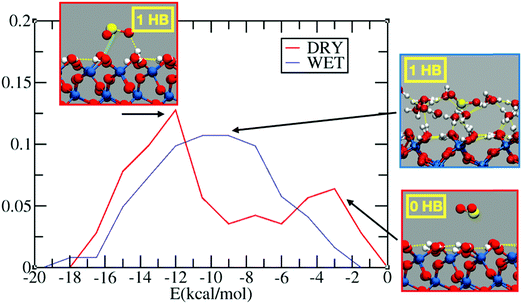
Fig. 1 reports the probability distribution for the adsorption energies of sulfur dioxide on the dry and wet silica. In the dry system, we observe a bimodal distribution (Fig. 1, in red) with two peaks, one around −12 kcal mol−1 and one at −2 kcal mol−1. The inspection of the FPMD shows, indeed, SO2 initially approaching on the top of the dry surface: this configuration is associated with the low adsorption peak in Fig. 1. After 10 ps, sulfur dioxide finds a stable adsorption configuration via hydrogen bond (HB) formation between the oxygen of SO2 and the interfacial hydroxyl group. The structure with 1 HB, which is the one associated with the peak at −12 kcal mol−1, is further stabilized by an electrostatic interaction between the sulfur atom and the oxygen of an interfacial hydroxyl (Oh). This electrostatic interaction, marked with a green line in the inset of Fig. 1, leads to a S–Oh distance of ∼2.7 Å stable over the last 5 ps of the FPMD trajectory. Sulfur dioxide has two resonant structures, with the sulfur atom positively and the oxygens negatively charged,58 which contributes to the overall structure of the molecule: this promotes an electrostatic interaction between the S atom and the interfacial Oh. Therefore, the energy of the most stable configuration (i.e., −12 kcal mol−1) is the sum of two interactions: one HB and an S–Oh electrostatic interaction.It is interesting to compare the SO2 adsorption energy with those of other compounds on the surface of dry silica. For example, on a dry fully hydroxylated (0001) α-quartz interface, classical MD reports an adsorption energy of about −13 kcal mol−1 for limonene,59 while FPMD-based calculation reports an adsorption energy of around −15 kcal mol−1 for pyruvic acid,38 and −9.0 kcal mol−1 for glyoxal.41 In all these cases, the adsorption was driven by formation of HBs between the adsorbate and the interfacial silanols. Experimental results on the adsorption of halide substituted benzene derivatives on silica show adsorption energies ranging from −8 to −11 kcal mol−1, driven by the HB formation between the interfacial silanols and the halide atoms and/or the aromatic ring (i.e., OH–π HB).60 In the case of diethyl sulfide, the adsorption energy was ∼ −9 kcal mol−151 again with HB formation between the interfacial hydroxyl group and the adsorbate. Even if SO2 is smaller in size than the aforementioned molecules, its adsorption energy is in the range of those discussed above. This can be attributed to the electronegativity of the SO2 oxygens, which drives the sulfur atom to be positively charged, enabling an electrostatic S–Oh interaction that further stabilizes the adsorbate.
In the wet silica scenario, there is a broad peak at ∼ −10 kcal mol−1 for the adsorption energy (Fig. 1, blue line), associated with configurations where SO2 forms one HB with water. The broadening of the peak is rationalized by the richer set of possible configurations for the adsorption on the wetted surface. A closer look at the 15 ps FPMD trajectory shows that SO2 tends to move more around the outer region of the adsorbed water layer, closer to the gas phase, rather than penetrating into the water layer. This behavior resembles the one observed at the air/liquid water interface where SO2 is (partially) solvated in the outer region of the liquid water interface.13,14,16 The solvation preference of SO2 therefore limits the number of HBs with water, while also the S–Oh interaction with the interfacial silanols is prevented, since the silanols are shielded by the adsorbed water layer. In conclusion, at least in the limited hydration regime considered here (∼1 full monolayer of adsorbed water), the adsorption energies on dry and wet silica seem to be comparable.
Hydration on wet and dry silica
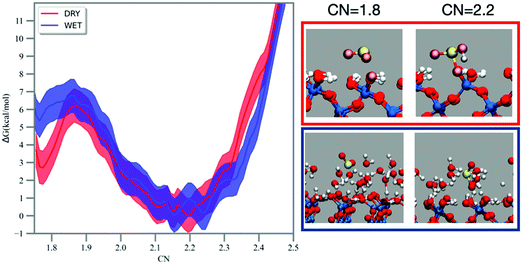
The hydration of sulfur dioxide has been studied by FPMD simulation coupled with free energy methods, such as metadynamics and umbrella sampling.52,53 The MTD trajectory shows SO2 moving on the dry silica surface and the formation of a bisulfite complex bound to the surface at ∼14 ps (see Fig. 2), which dehydrates back to SO2 after 34 ps. On the wet silica, formation of bisulfite is recorded at ∼11 ps and SO2 reformation at ∼28 ps. No multiple recrossings were observed in the MTD trajectories. The MTD runs were performed to explore the bias landscape and to provide viable configurations for the calculation of the 1D free energy profile by umbrella sampling/WHAM.55The free energy reaction profiles along the CN coordinate are reported in Fig. 2. In the dry case (red curve, Fig. 2), adsorbed sulfur dioxide (CN ∼1.7–1.8) experiences a forward reaction barrier of ∼3 kcal mol−1 towards the formation of bisulfite located at CN = 1.9, whereas this barrier is smaller (∼1 kcal mol−1) in the wet case (blue line, Fig. 2). As mentioned in the methodology, CN assumes a value of ∼0.8–0.9 for each S–O bond formed, which should result in a CN value of ∼2.4–2.7 for bisulfite. In our simulations and on both dry and wet surfaces, we recorded instead bisulfite formation at smaller values (e.g., CN = ∼2.2). Analysis of the MTD and umbrella trajectories reveals that prior to hydration, the S–O bond in sulfur dioxide is ∼1.5 Å. When bisulfite is formed, the S–O bond is still ∼1.5 Å but the S–OH bond is more elongated, about 1.7 Å. The CN coordinate discriminates the S–O bonds using a smooth step function at a cutoff distance, which is the same for both S–O and S–OH bonds. The longer S–OH bond in bisulfite has therefore a smaller contribution on CN and this explains why bisulfite is associated with a smaller CN = 2.2 in the free energy profile. For both reaction profiles on the dry and wet silica surface the backward reaction (i.e., dehydration of bisulfite to sulfur dioxide) is equal to 6 kcal mol−1.
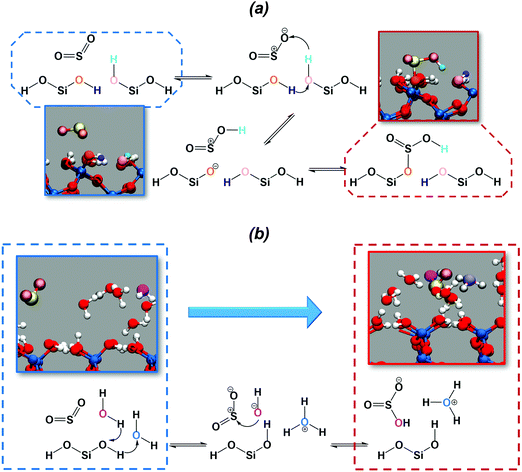
The chemical mechanism for the hydration of sulfur dioxide on the dry surface is reported in Fig. 3a. On the dry silica, adsorbed sulfur dioxide converts to bisulfite by a concerted proton transfer involving two interfacial silanols and SO2. Specifically, sulfur dioxide attracts one of the interfacial hydroxyl hydrogens (cyan atom in Fig. 3a), which induces a proton transfer (purple atom) from a neighbouring hydroxyl group. The deprotonated interfacial oxygen (orange atom) is then prone to attract the sulfur atom, leading to the formation of a Si–OSO2H complex (Fig. 3a). It is interesting to compare our reaction mechanism with the one reported on the dry hydroxylated surface of anatase (TiO2).32 By exposing anatase to SO2, a surface bound bisulfite was also formed in a mechanism that closely resembles the one in Fig. 3a. On anatase, the adsorbed bisulfite further reacts with an adjacent hydroxyl group, forming surface-bound sulfite and releasing a water molecule. This last step, converting bisulfite to sulfite, is not observed in our simulation on dry silica, which may be ascribed to the different distances between hydroxyl groups on silica and anatase surfaces.
In the presence of adsorbed water, the deprotonation of the interfacial silanols, which is expected on the wet hydroxylated silica surface,39 drives the hydration of SO2. The chemical mechanism is depicted in Fig. 3b: the deprotonation of the silanols drives a proton transfer from and toward the water phase, leading to the formation of hydronium (light blue atom in Fig. 3b) and hydroxyl ions (magenta atom) in the adsorbed water layer. The hydroxyl ion then attacks the sulfur atom, resulting in the formation of bisulfite. In the wet case the forward reaction barrier is smaller (∼1 kcal mol−1) compared to the dry case (∼3 kcal mol−1), which is rationalized by the fact that the adsorbed water layer facilitates the deprotonation of the interfacial silanols and the proton transfer, catalyzing the reaction. Moreover, the free energy difference between SO2 (CN = 1.8) and HSO3− (CN = 2.2) is ∼5 kcal mol−1, very close to those reported for SO2 hydration to bisulfite in small water clusters using a higher level of theory (i.e., MP2 or B3LYP).61 Finally, it is worthy to report that on wet silica the umbrella trajectory at CN = 2.2 occasionally shows formation of sulfurous acid as a result of a proton transfer from one interfacial silanol to one of the bisulfite oxygens. Sulfurous acid appears to be extremely unstable: during the 10 ps umbrella windows, we recorded only three events with the sulfurous acid lasting only for a few fs before reconverting into a bisulfite ion. This is consistent with common knowledge in aqueous solution where spectroscopic studies were not able to detect sulfurous acid.62
Environmental implication of SO2 uptake and hydration on silica
The results here reported help to rationalize previous experimental findings, highlighting the role of adsorbed water layers and surface hydroxylation for the SO2 reactivity on suspended mineral dust in the atmosphere. Previous experimental observation reported no SO2 uptake on dry silica.11 The small reaction barriers that we observe in Fig. 3 suggest that both forward (SO2 to bisulfite) and backward (bisulfite reconversion to SO2) reaction are kinetically feasible. Based on transition state theory a forward barrier of 3 kcal mol−1 for the SO2 to bisulfite reaction corresponds to a characteristic time τ = 1/κ of ∼23 ps. The backward barrier is 6 kcal mol−1 and, thus it corresponds to τ = 4 ns. These lifetimes suggest a fast dynamic: adsorbed SO2 is rapidly hydrated to bisulfite but, when formed, bisulfite can easily dehydrate to sulfur dioxide and, possibly, desorb as a gas. At the time scale of experimental FT-IR,11 formation of bisulfite cannot be detected because it can quickly reconvert to SO2 and escape to the gas phase. Ultrafast spectroscopy techniques may be needed to address the fast dynamics of SO2 uptake and hydration and to detect such a short-time living adsorbate.63Our results also point to the feasibility of SO2 chemisorption on wet and dry silica. In geographical areas subject to harsh conditions, such as a high level of ozone, pollution, solar UV radiation and suspended dust,64–66 even short living bisulfite adsorbates can affect the (photo)chemical pathways for sulfur dioxide oxidation. In desert areas, silica is an important component of suspended mineral dust aerosol44 and the relative humidity can easily drop below RH = 20%, especially at midday.67 At such low RH, a dry surface or, at maximum, one adsorbed water layer is expected on almost all mineral substrates, including silica.68 On such interfaces, our results indicate that sulfur oxide is rapidly, and reversibly, converted to bisulfite. Recent results have shown that the photochemistry of SO2 at the air/liquid water surface may be an important source of OH and HOSO radicals in the atmosphere:16,18,19 our results point out that, at least on the silica surface, the rapid hydration and de-hydration of SO2 are likely to hamper the direct photochemical activation of SO2. Moreover, harsh conditions (e.g., high level of ozone, pollution, solar UV radiation and suspended dust)64–66 may lead to an additional sulfate source coming from the oxidation1,20,69,70 of short-living bisulfite on the hydroxylated surface of silica. Further studies are needed to elucidate whether this chemistry may be an additional source of radicals and sulfate in the atmosphere of desert and polluted industrialized areas.
Conclusions
Highly industrialized areas and desert regions are subject to intense solar radiation, high levels of pollution, and suspended dust particles with silica representing a significant component of mineral dust aerosols. SO2 is an important trace (and pollutant) gas because its oxidation leads to the release of sulfate and radicals into the atmosphere. While previous experimental observations based on IR spectroscopy have shown no SO2 uptake on silica, here computational results based on atomistic first-principles simulations report sulfur dioxide adsorption and hydration to bisulfite on both dry and wet hydroxylated (α-quartz) silica surface. We report similar adsorption energies for SO2 on the wet and dry silica. The adsorption process is driven by hydrogen bond formation and electrostatic interactions between SO2 and adsorbed water and/or with the interfacial hydroxyl groups. The hydration barrier (from SO2 to bisulfite) is ∼1 kcal mol−1 and 3 kcal mol−1 on the dry and wet silica, respectively, while the dehydration reaction barrier (from bisulfite to SO2) is 6 kcal mol−1 on both surfaces. These small reaction barriers suggest a fast dynamic: adsorbed SO2 is rapidly hydrated to bisulfite, but bisulfite can rapidly dehydrate to sulfur dioxide and, possibly, desorb back into the gas phase. The time scale of this process (of the order of ns or less) likely explains why IR measurement cannot detect the adsorbed bisulfite. The fast hydration dynamics may limit direct SO2 photooxidation, which has been suggested as an important source of OH radicals at the air/liquid water surface. Moreover, SO2 chemisorption as bisulfite is likely to enhance sulfate production in catalytic processes with high SO2 loading or in atmospheres subject to intense UV radiation, dust and atmospheric oxidizers, where the oxidation process may prevail over bisulfite dehydration and SO2 desorption into the gas phase.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
For HPC resources and services, we acknowledge the Research Computing group in Texas A&M University at Qatar, founded by the Qatar Foundation for Education, Science and Community Development, and the use of Qatar Environment and Energy Research Institute (QEERI) HPC under Project ID HPC-P21003. IG acknowledges Prof. M. Ammann and Dr Pablo Corral Arroyo for fruitful discussions.References
- J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, Wiley, 2016 Search PubMed.
- C. C. Chuang, J. E. Penner, K. E. Taylor, A. S. Grossman and J. J. Walton, J. Geophys. Res.: Atmos., 1997, 102, 3761–3778 CrossRef CAS.
- F. J. Dentener, G. R. Carmichael, Y. Zhang, J. Lelieveld and P. J. Crutzen, J. Geophys. Res.: Atmos., 1996, 101, 22869–22889 CrossRef CAS.
- D. A. Hegg, R. Majeed, P. F. Yuen, M. B. Baker and T. V. Larson, Geophys. Res. Lett., 1996, 23, 2613–2616 CrossRef CAS.
- J. L. Bada, Chem. Soc. Rev., 2013, 42, 2186–2196 RSC.
- X. Fang, Y. Liu, Y. Cheng and W. Cen, ACS Catal., 2021, 11, 4125–4135 CrossRef CAS.
- Z.-Y. Chen, C. Chen, Y. Zhang, Z.-M. Xia, K.-F. Yan and X.-S. Li, Energy Procedia, 2017, 142, 3454–3459 CrossRef CAS.
- D. Bounechada, D. P. Anderson, M. Skoglundh and P.-A. Carlsson, J. Chem. Phys., 2017, 146, 084701 CrossRef PubMed.
- W. Benzinger, A. Wenka and R. Dittmeyer, Appl. Catal., A, 2011, 397, 209–217 CrossRef CAS.
- W. R. Stockwell and J. G. Calvert, Atmos. Environ. 1967, 1983, 17, 2231–2235 CAS.
- C. R. Usher, H. Al-Hosney, S. Carlos-Cuellar and V. H. Grassian, J. Geophys. Res.: Atmos., 2002, 107, 16–19 CrossRef.
- H. G. Maahs, J. Geophys. Res., C: Oceans Atmos., 1983, 88, 10721–10732 CrossRef CAS.
- E. S. Shamay, K. E. Johnson and G. L. Richmond, J. Phys. Chem. C, 2011, 115, 25304–25314 CrossRef CAS.
- E. S. Shamay, N. A. Valley, F. G. Moore and G. L. Richmond, Phys. Chem. Chem. Phys., 2013, 15, 6893–6902 RSC.
- E. M. Coddens, L. Huang, C. Wong and V. H. Grassian, ACS Earth Space Chem., 2019, 3, 142–149 CrossRef CAS.
- M. T. C. Martins-Costa, J. M. Anglada, J. S. Francisco and M. F. Ruiz-López, J. Am. Chem. Soc., 2018, 140, 12341–12344 CrossRef CAS.
- S. N. Pandis and J. H. Seinfeld, J. Geophys. Res.: Atmos., 1989, 94, 1105–1126 CrossRef CAS.
- J. A. Kroll, B. N. Frandsen, H. G. Kjaergaard and V. Vaida, J. Phys. Chem. A, 2018, 122, 4465–4469 CrossRef CAS.
- D. J. Donaldson, J. A. Kroll and V. Vaida, Sci. Rep., 2016, 6, 30000 CrossRef CAS.
- D. Langhammer, J. Kullgren and L. Österlund, J. Am. Chem. Soc., 2020, 142, 21767–21774 CrossRef CAS PubMed.
- H. Chen, C. E. Nanayakkara and V. H. Grassian, Chem. Rev., 2012, 112, 5919–5948 CrossRef CAS.
- H. Wang, H. Liu, Z. Chen, A. Veksha, G. Lisak and C. You, Chemosphere, 2020, 249, 126136 CrossRef CAS PubMed.
- J. Baltrusaitis, P. M. Jayaweera and V. H. Grassian, J. Phys. Chem. C, 2011, 115, 492–500 CrossRef CAS.
- D. J. Jacob and M. R. Hoffmann, J. Geophys. Res., C: Oceans Atmos., 1983, 88, 6611–6621 CrossRef CAS.
- B. C. Faust, M. R. Hoffmann and D. W. Bahnemann, J. Phys. Chem., 1989, 93, 6371–6381 CrossRef CAS.
- C. Brandt and R. van Eldik, Chem. Rev., 1995, 95, 119–190 CrossRef CAS.
- M. Olaru, M. Aflori, B. Simionescu, F. Doroftei and L. Stratulat, Materials, 2010, 3, 216–231 CrossRef CAS.
- X. He and Y.-H. Zhang, Spectrochim. Acta, Part A, 2019, 219, 121–128 CrossRef CAS PubMed.
- A. Zhanzakova, S. Tong, K. Yang, L. Chen, K. Li, H. Fu, L. Wang and L. Kong, Atmos. Environ., 2019, 213, 548–557 CrossRef CAS.
- W. Liu, X. He, S. Pang and Y. Zhang, Atmos. Environ., 2017, 167, 245–253 CrossRef CAS.
- G. Rubasinghege, S. Elzey, J. Baltrusaitis, P. M. Jayaweera and V. H. Grassian, J. Phys. Chem. Lett., 2010, 1, 1729–1737 CrossRef CAS.
- C. E. Nanayakkara, J. Pettibone and V. H. Grassian, Phys. Chem. Chem. Phys., 2012, 14, 6957–6966 RSC.
- C.-M. Wu, J. Baltrusaitis, E. G. Gillan and V. H. Grassian, J. Phys. Chem. C, 2011, 115, 10164–10172 CrossRef CAS.
- J. Baltrusaitis, D. M. Cwiertny and V. H. Grassian, Phys. Chem. Chem. Phys., 2007, 9, 5542–5554 RSC.
- A. P. Prince, P. Kleiber, V. H. Grassian and M. A. Young, Phys. Chem. Chem. Phys., 2007, 9, 3432–3439 RSC.
- A. L. Goodman, P. Li, C. R. Usher and V. H. Grassian, J. Phys. Chem. A, 2001, 105, 6109–6120 CrossRef CAS.
- C. R. Usher, A. E. Michel and V. H. Grassian, Chem. Rev., 2003, 103, 4883–4940 CrossRef CAS.
- Y. Fang, D. Lesnicki, K. J. Wall, M.-P. Gaigeot, M. Sulpizi, V. Vaida and V. H. Grassian, J. Phys. Chem. A, 2019, 123, 983–991 CrossRef CAS PubMed.
- M. Pfeiffer-Laplaud, M.-P. Gaigeot and M. Sulpizi, J. Phys. Chem. Lett., 2016, 7, 3229–3234 CrossRef CAS PubMed.
- M. Sulpizi, M.-P. Gaigeot and M. Sprik, J. Chem. Theory Comput., 2012, 8, 1037–1047 CrossRef CAS PubMed.
- I. Gladich, M. A. Carignano and J. S. Francisco, J. Chem. Phys., 2020, 152, 164702 CrossRef CAS.
- V. H. Grassian, Surf. Sci., 2008, 602, 2955–2962 CrossRef CAS.
- C. Fountoukis, L. Ackermann, M. A. Ayoub, I. Gladich, R. D. Hoehn and A. Skillern, Model. Earth Sys. Environ., 2016, 2, 115 CrossRef.
- B. Aïssa, R. J. Isaifan, V. E. Madhavan and A. A. Abdallah, Sci. Rep., 2016, 6, 31467 CrossRef PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 4, 15–25 Search PubMed.
- J. Abelard, A. R. Wilmsmeyer, A. C. Edwards, W. O. Gordon, E. M. Durke, C. J. Karwacki, D. Troya and J. R. Morris, J. Phys. Chem. C, 2015, 119, 365–372 CrossRef CAS.
- G. Bussi and A. Laio, Nat. Rev. Phys., 2020, 2, 200–212 CrossRef.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1995, 16, 1339–1350 CrossRef CAS.
- M. Bonomi, G. Bussi, C. Camilloni, G. A. Tribello, P. Banáš, A. Barducci, M. Bernetti, P. G. Bolhuis, S. Bottaro, D. Branduardi, R. Capelli, P. Carloni, M. Ceriotti, A. Cesari, H. Chen, W. Chen, F. Colizzi, S. De, M. De La Pierre, D. Donadio, V. Drobot, B. Ensing, A. L. Ferguson, M. Filizola, J. S. Fraser, H. Fu, P. Gasparotto, F. L. Gervasio, F. Giberti, A. Gil-Ley, T. Giorgino, G. T. Heller, G. M. Hocky, M. Iannuzzi, M. Invernizzi, K. E. Jelfs, A. Jussupow, E. Kirilin, A. Laio, V. Limongelli, K. Lindorff-Larsen, T. Löhr, F. Marinelli, L. Martin-Samos, M. Masetti, R. Meyer, A. Michaelides, C. Molteni, T. Morishita, M. Nava, C. Paissoni, E. Papaleo, M. Parrinello, J. Pfaendtner, P. Piaggi, G. Piccini, A. Pietropaolo, F. Pietrucci, S. Pipolo, D. Provasi, D. Quigley, P. Raiteri, S. Raniolo, J. Rydzewski, M. Salvalaglio, G. C. Sosso, V. Spiwok, J. Šponer, D. W. H. Swenson, P. Tiwary, O. Valsson, M. Vendruscolo, G. A. Voth, A. White and P. C. The, Nat. Methods, 2019, 16, 670–673 CrossRef.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- A. Sinopoli, A. Abotaleb, F. Pietrucci and I. Gladich, J. Phys. Chem. B, 2021, 125, 4890–4897 CrossRef CAS.
- S. Laporte, F. Pietrucci, F. Guyot and A. M. Saitta, J. Phys. Chem. C, 2020, 124, 5125–5131 CrossRef CAS.
- T. Y. Takeshita, B. A. Lindquist and T. H. Dunning, J. Phys. Chem. A, 2015, 119, 7683–7694 CrossRef CAS PubMed.
- Y. Fang, P. S. J. Lakey, S. Riahi, A. T. McDonald, M. Shrestha, D. J. Tobias, M. Shiraiwa and V. H. Grassian, Chem. Sci., 2019, 10, 2906–2914 RSC.
- J. Abelard, A. R. Wilmsmeyer, A. C. Edwards, W. O. Gordon, E. M. Durke, C. J. Karwacki, D. Troya and J. R. Morris, J. Phys. Chem. C, 2016, 120, 13024–13031 CrossRef CAS.
- R. Steudel and Y. Steudel, Eur. J. Inorg. Chem., 2009, 1393–1405 CrossRef CAS.
- M. Weller, J. Rourke, T. Overton and F. Armstrong, Inorganic Chemistry, Oxford University Press, 2014 Search PubMed.
- M. Maiuri, M. Garavelli and G. Cerullo, J. Am. Chem. Soc., 2020, 142, 3–15 CrossRef CAS.
- C. Fountoukis, M. A. Ayoub, L. Ackermann, D. Perez-Astudillo, D. Bachour, I. Gladich and R. D. Hoehn, Aerosol Air Qual. Res., 2018, 18, 1183–1197 CrossRef.
- R. R. Cordero, A. Damiani, G. Seckmeyer, J. Jorquera, M. Caballero, P. Rowe, J. Ferrer, R. Mubarak, J. Carrasco, R. Rondanelli, M. Matus and D. Laroze, Sci. Rep., 2016, 6, 22457 CrossRef CAS.
- C. Fountoukis, L. Martín-Pomares, D. Perez-Astudillo, D. Bachour and I. Gladich, Sol. Energy, 2018, 163, 347–355 CrossRef.
- L. Cáceres, B. Gómez-Silva, X. Garró, V. Rodríguez, V. Monardes and C. P. McKay, J. Geophys. Res.: Biogeosci., 2007, 112, G04S14 Search PubMed.
- M. Tang, D. J. Cziczo and V. H. Grassian, Chem. Rev., 2016, 116, 4205–4259 CrossRef CAS PubMed.
- F. Sheng, L. Jingjing, C. Yu, T. Fu-Ming, D. Xuemei and L. Jing-yao, RSC Adv., 2018, 8, 7988–7996 RSC.
- D. Littlejohn, K. Hu and S. G. Chang, Ind. Eng. Chem. Res., 1988, 27, 1344–1348 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The data that support the findings of this study are available within the article and its Supporting Information. See DOI: 10.1039/d1cp04747g |
| This journal is © the Owner Societies 2022 |