Nature of hydride and halide encapsulation in Ag8 cages: insights from the structure and interaction energy of [Ag8(X){S2P(OiPr)2}6]+ (X = H−, F−, Cl−, Br−, I−) from relativistic DFT calculations†
Raul
Guajardo Maturana
 a,
Alexandre O.
Ortolan
b,
Peter L.
Rodríguez-Kessler
c,
Giovanni F.
Caramori
a,
Alexandre O.
Ortolan
b,
Peter L.
Rodríguez-Kessler
c,
Giovanni F.
Caramori
 b,
Renato L. T.
Parreira
b,
Renato L. T.
Parreira
 d and
Alvaro
Muñoz-Castro
d and
Alvaro
Muñoz-Castro
 *c
*c
aUniversidad SEK, Facultad de Ciencias de la Salud, Instituto de Investigación Interdisciplinaren Ciencias Biomédicas SEK (I3CBSEK) Chile, Fernando Manterola 0789, Providencia, Santiago, Chile
bDepartamento de Química, Universidade Federal de Santa Catarina, Campus Universitário Trindade, CP 476, Florianópolis, SC 88040-900, Brazil. E-mail: giovanni.caramori@ufsc.br
cLaboratorio de Química Inorgánica y Materiales Moleculares, Facultad de Ingenieria, Universidad Autonoma de Chile, Llano Subercaceaux 2801, San Miguel, Santiago, Chile. E-mail: alvaro.munoz@uautonoma.cl
dNúcleo de Pesquisa em Ciências Exatas e Tecnológicas, Universidade de Franca, Franca, SP 14404-600, Brazil. E-mail: renato.parreira@unifran.edu.br
First published on 23rd November 2021
Abstract
Unraveling the different contributing terms to an efficient anion encapsulation is a relevant issue for further understanding of the underlying factors governing the formation of endohedral species. Herein, we explore the favorable encapsulation of hydride and halide anions in the [Ag8(X){S2P(OPr)2}6]+ (X− = H, 1, F, 2, Cl, 3, Br, 4, and, I, 5) series on the basis of relativistic DFT-D level of theory. The resulting Ag8–X interaction is sizable, which decreases along the series: −232.2 (1) > −192.1 (2) > −165.5 (3) > −158.0 (4) > −144.2 kcal mol−1 (5), denoting a more favorable inclusion of hydride and fluoride anions within the silver cage. Such interaction is mainly stabilized by the high contribution from electrostatic type interactions (80.9 av%), with a lesser contribution from charge-transfer (17.4 av%) and London type interactions (1.7 av%). Moreover, the ionic character of the electrostatic contributions decreases from 90.7% for hydride to 68.6% for the iodide counterpart, in line with the decrease in hardness according to the Pearson's acid–base concept (HSAB) owing to the major role of higher electrostatic interaction terms related to the softer (Lewis) bases. Lastly, the [Ag8{S2P(OPr)2}6]2+ cluster is able to adapt its geometry in order to maximize the interaction towards respective monoatomic anion, exhibiting structural flexibility. Such insights shed light on the physical reasoning necessary for a better understanding of the different stabilizing and destabilizing contributions related to metal-based cavities towards favorable incorporation of different monoatomic anions.
Introduction
Chemical bonding in confined spaces1 is of great interest towards the understanding of fundamental characteristics underlying anion recognition, receiving, and sensing, which are crucial to the rational design of supramolecular systems.2,3 Such understanding is of further interest owing to the relevant role of anions in fields ranging from biology, environmental science, drug delivery, catalysis, among others subjects4–10 to pursuing improved host cavities.3,11–14To achieve an effective incorporation of halides and hydrides into confined cavities, different stabilizing features are involved ranging from metal bonding,15 hydrogen bonding16 among other weak interactions,17 resulting in favorable aggregates.18 In this sense, prototypical templates provide reliable scenarios to further rationalize the stabilizing terms accounting for the nature of anion encapsulation when going from harder to a softer guest, with variable sizes.19–21 Stabilization of anion encapsulation involves different contributions to the electrostatic stabilization of the interaction such as ion–ion, ion–dipole, and dipole–dipole, among others terms,22–26 where analysis of their variation and characteristics of the suitable host species is crucial for the understanding and design of further anion receptors.
The reported [Ag8(X){S2P(OiPr)2}6]+ (X = H−, F−, Cl−, Br−, I−) series, hydride, and halogens are introduced in a confined cage provided by eight Ag atoms leading to an almost symmetrical cubic environment for anion encapsulation, denoting sizable structural distortions for H− case.27–30 Such features denote the flexibility of the Ag8 cage towards maximization of the host–guest interaction.31 Such species are prototypical examples to evaluate the characteristics of metal based cavities32–36 or metallocages as extension of the well-developed molecular recognition of anions traditionally performed on organic cavities.37–41
According to the HSAB concept,21,42 Ag+ ions involved in such clusters are considered as a soft acid, which interacts with soft and hard bases, providing recognition of relevant anion-binding characteristics for suitable confined cavities. In addition, theoretical studies on the bonding nature of coinage metals and different ligands denote silver as the least covalent counterpart, which decrease as follows: Au > Cu > Ag,43–45 offering the [Ag8{S2P(OiPr)2}6]2+ cage as a prototypical example of a weakly covalent environment to further explore non-covalent halide encapsulation.
In this report, we account for the main features related to the incorporation of hydride and halide anions into the confined Ag8 cavity provided by [Ag8{S2P(OiPr)2}6]2+ clusters, in the [Ag8(X){S2P(OiPr)2}6]+ cluster (X− = H, 1, F, 2, Cl, 3, Br, 4, and, I, 5). From density functional theory calculations, the anion-cavity interaction is rationalized under different energetic terms underlying the stabilization of the aggregate. The obtained interaction energy is further decomposed into the relative contribution towards the stabilization of the overall complex via a quantitative energy decomposition analysis (EDA).46–50 This approach provides quantities accounting for Pauli repulsion, electrostatics, charge transfer, and dispersion, which are informative for the understanding of the anion–cavity interaction nature, informative towards a rational design of efficient host cavities.
Computational details
Calculations were performed via relativistic density functional theory with Slater-type orbitals (STOs) of triple-zeta quality basis set plus two polarization functions (TZ2P),51 by using the ADF2019 suite.52 Relativistic effects were accounted through the scalar ZORA Hamiltonian.53,54 Becke exchange and the Perdew correlation functional (BP86),55,56 in conjunction with the Grimme's empirical dispersion correction with the Becke–Johnson damping functions, D3(BJ), were employed for all the calculations.57,58 Calculated geometries were optimized without any symmetry constraints. All the obtained structures correspond to a minimum on the potential energy surface by the absence of imaginary eigen values in the hessian matrix.Results and discussions
The representative structures for [Ag8(X){S2P(OPr)2}6]+ (X− = H, 1, F, 2, Cl, 3, Br, 4, and, I, 5) series are given in Fig. 1, denoting that the Ag8 cluster is able to offer tetrahedral Ag4 and hexahedral Ag8 cages in order to incorporate different monoatomic anions. For 1, the central tetrahedron is further capped by four Ag atoms, with the hydride located at the center. For the halide series (2–5), a hexahedral (cube) cage is depicted where the calculated shorter and longer Ag–Ag edge distances (Table 1), namely Ag–AgShort and Ag–AgLong, respectively, vary towards increased separations according to: Ag–AgShort: 3.088 (2) < 3.256 (3) < 3.308 (4) < 3.369 Å (5), and, Ag–AgLong: 3.291 (2) < 3.500 (3) < 3.443 (4) < 3.614 Å (5). In turn, the Ag–X average increases as 2.602 (2) < 2.882 (3) < 2.961 (4) < 3.068 Å (5). For 1, the Ag–H is 1.890 Å with an Ag4 cage of 3.024 Å edges. These values agree well with the available experimental data for 1–4, where differences from the experimental data may be originated from packing effects in the crystal.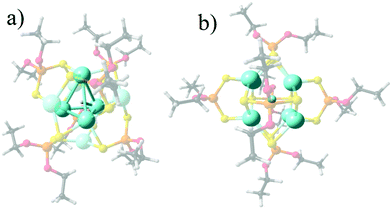 | ||
| Fig. 1 Calculated structures for 1 (a) and 2 (b), denoting the Ag4 encapsulating cage for 1, and the Ag8 cube for 2 as representative for 2–5. | ||
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| H− | F− | Cl− | Br− | I− | |
| Experimental values for 1–3 from ref. 27, and for 4 from ref. 28. Data not available for 5. | |||||
| Ag–X | 1.890 | 2.602 | 2.882 | 2.961 | 3.068 |
| Exp.a | 1.921 | 2.735 | 2.892 | 2.927 | |
| Ag–AgShort | 3.024 | 3.088 | 3.256 | 3.308 | 3.369 |
| Exp.a | 3.028 | 3.043 | 3.196 | 3.269 | |
| Ag–AgLong | 3.450 | 3.291 | 3.500 | 3.443 | 3.614 |
| Exp.a | 3.312 | 3.260 | 3.469 | 3.328 | |
| CShM-Cube | 6.60 | 0.35 | 0.17 | 0.17 | 0.15 |
The different structural deviations from ideal tetrahedral and hexahedral cages of the Ag8 core are depicted by employing the continuous-shape-measure (CShM) approach developed by Alvarez and coworkers,59–61 which correlate each structure in relation to the respective ideal polyhedron (Table 1). For a fully coincident structure, the root mean square deviation values of CShM analysis tend to zero and increases according to the distortion degree of the structure. For 1, the structure largely deviates from a perfect hexagonal structure (CShM = 6.60), where the central tetrahedron is distorted in relation to a tetrahedron (CShM = 1.49) owing to the main elongation of one vertex, where the outer capping of 4 Ag atoms lead to a more symmetrical tetrahedron (CShM = 0.059). In the 2–5 series, the hexahedral or cubic cage shows several distortion degrees, which decrease as the anion radius increases (CShM = 0.35 (2) > 0.17 (3) ≃ 0.17 (4) > 0.15 (5)).
Such different distortion degrees suggest amenable structural flexibility of the [Ag8{S2P(OPr)2}6]2+ cluster or cage, which is able to undergo geometrical distortions in order to maximize the interaction towards the endohedral anion involving small energy changes. In this sense, the preparation energy (ΔEprep) is related to the required energy to promote a geometry from an isolated state to its final geometry in each [Ag8(X){S2P(OPr)2}6]+ species and allows for the quantification of the related energy cost. For 2, ΔEprep amounts to 4.2 kcal mol−1, varying as 3.7 (3) < 4.9 (4) < 8.8 kcal mol−1 (5) along with the different halides, denoting that for the Cl− encapsulated counterpart (3) the geometry of the supporting cluster varies in a lesser amount, and for I− (5), in a larger degree. In contrast, for [Ag8(H){S2P(OPr)2}6]+ (1), the required geometrical arrangements favoring the observed encapsulation of the hydride are to a larger extent leading to a ΔEprep of 15.8 kcal mol−1. Hence, for the smaller hydride atom and the larger iodine (1 and 5), the cage–X interaction required a larger distortion in comparison to Cl− (3). Similar to previous calculations, the charge distribution in the overall cluster retains most of the negative charge at the endohedral atom.28
The favorable Ag8–X interaction is further evaluated by the interaction energy (ΔEint, Table 2). As a result, the interaction is decreasing considerably along the series amounting to: −232.2 (1) > −192.1 (2) > −165.5 (3) > −158.0 (4) > −144.2 kcal mol−1 (5), denoting a more favorable inclusion of hydride and fluoride atoms within the silver cage. Further analysis accounting for the nature of interaction is achieved by using the energy decomposition analysis (EDA) within the Morokuma–Ziegler scheme,46,62,63 which dissects the ΔEint quantity in different chemically meaningful terms, according to eqn (1):49,63–66
| ΔEint = ΔEPauli + ΔEelstat + ΔEorb + ΔEdisp | (1) |
| 1 | 1 cent | 2 | 3 | 4 | 5 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H | Hcent | F | Cl | Br | I | |||||||
| a Percentual values denote the contribution from each stabilizing term to the overall favorable interaction. | ||||||||||||
| ΔEprep | 15.8 | 4.2 | 4.2 | 3.7 | 4.9 | 8.8 | ||||||
| ΔEPauli | 427.2 | 149.6 | 75.2 | 157.2 | 213.9 | 276.0 | ||||||
| ΔEelstat | −556.7 | 84.4%a | −282.6 | 82.0%a | −190.6 | 71.3%a | −257.5 | 79.8%a | −308.9 | 83.1%a | −357.5 | 85.1%a |
| ΔEorb | −100.7 | 15.3%a | −58.8 | 17.1%a | −73.2 | 27.4%a | −57.3 | 17.8%a | −53.4 | 14.4%a | −51.5 | 12.3%a |
| ΔEdisp | −2.0 | 0.3%a | −3.1 | 0.9%a | −3.5 | 1.3%a | −7.8 | 2.4%a | −9.6 | 2.6%a | −11.3 | 2.7%a |
| ΔEint | −232.2 | −195.0 | −192.1 | −165.5 | −158.0 | −144.2 | ||||||
| i–d% | 90.7% | 97.1% | 84.2% | 76.6% | 72.2% | 68.6% | ||||||
From the relative contributions given by the stabilizing terms, ΔEorb, ΔEelstat, and ΔEdisp, the nature of the interaction (ΔEint) can be evaluated. For the [Ag8{S2P(OPr)2}6]2+–X− interaction, the contribution from ΔEelstat is to a large extent leading to an electrostatic character of the encapsulation of 71.3% to 85.1% along with the halide series (2–5), and of 84.4% for the hydride case (1). In addition, the ΔEorb related to charge transfer contributes 27.4 to 12.3% from 2 to 5, and 15.3% for 1, where London dispersion interactions (ΔEdisp) contribute to a lesser extent.
Moreover, ΔEelstat tends to be more favorable from 2 to 5, with values of −190.6 to −357.5 kcal mol−1, which is higher for 1 (−556.7 kcal mol−1). This shows the relevance of the electrostatic character in the halide and hydride encapsulation and how it increases towards the softer halides in terms of the Pearson's HSAB concept.21 Lastly, the repulsive term (ΔEPauli) increases from 2 to 5, according to the halide size within the Ag8 cage (75.2 to 276.0 kcal mol−1). ΔEPauli is higher for 1 owing to the rearrangement of the core into an Ag4H cage (427.2 kcal mol−1), which in turn is overcome by the sizable stabilizing terms of the interaction, mainly given by ΔEelstat increase, denoting the ability of the cage to modify its structure according to the incoming encapsulated species in order to favor stabilization. The ΔEorb remains similar from Cl− to I− (3–5), denoting the small variation in charge transfer between the endohedral atom and the silver cage, which is larger for 2 and 1. Moreover, the role of relativistic effects is evaluated by non-relativistic calculations (Table S1, ESI†), which denote small deviations from the obtained values at the relativistic level (Table 2) suggesting a decrease in the values of ΔEint for the clusters 2–5, given mainly by a small decrease of the ΔEorb term upon inclusion of the relativistic effects, which decreases the radial distribution of 5s-Ag orbitals, and hence affect the anion → Ag8 bonding. For the hydride case (1), the relativistic effect increases the ΔEorb term favoring the ΔEint value owing to a shorter Ag–X distance (Table 1).
For comparison, a hypothetical case with the hydride atom encapsulated in a hexagonal Ag8 cage, related to halide species is calculated in order to discuss the two different cage environments given by Ag4 in 1 and Ag8 in 2–5 clusters (Fig. 1), leading to the enhanced interaction energy in the former. For Ag8H (1cent), the ΔEint decreases to −195.0 kcal mol−1, in the range of halide cases particularly similar to 2 (Ag8F), owing to a large decrease of both stabilizing ΔEelstat and ΔEorb contributions. In addition, the steric hindrance accounted by ΔEPauli is also decreased when going from an Ag4 to an Ag8 encapsulating cage for the hydride case. Thus, the Ag4 cage offers a relevant increase in the stabilizing terms of interaction, leading in turn to a sizable increase in the steric hindrance for the encapsulation, which is only avoided for the hydride case. This comparison between 1 and 1cent supports the preference of Ag4H encapsulation.
Further evaluation of the nature of the electrostatic term involving ion–ion, ion–dipole, and other higher-order interactions, such as dipole–dipole, quadrupole–dipole, and quadrupole–quadrupole, is achieved by analysis of hypothetically related noble-gas (Ng) counter parts. Noble gases are isoelectronic to the corresponding hydride and halides, in a neutral case, effectively allowing to remove the contribution from the ionic character ascribed to the endohedral atom, unraveling the stabilizing contribution from higher-order interactions.69–72 As the electrostatic interactions accounted by ΔEelstat can be expressed as a multipole–multipole power series, the contribution from ion–ion and ion–dipole contribution (i–d) to ΔEelstat was estimated according to eqn (2), in which ΔEelstat,N is the electrostatic energy term for the isoelectronic neutral analogs of each anion (H−/He, F−/Ne, Cl−/Ar, Br−/Kr, and I−/Xe), as given in Table 2.
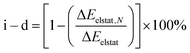 | (2) |
Moreover, the computed thermodynamic parameters denote an enthalpy change (ΔH) for [Ag8{S2P(OPr)2}6]2+ + X− → [Ag8(X){S2P(OPr)2}6]+, given by −397.6 kJ mol (1) > −295.9 (2) > −128.5 (3) > −103.0 (4) > −29.2 (5). These values denote a decrease in the favorable enthalpy change along the series, which is lowest for 5.
Lastly, the ligand–core interaction is calculated in order to evaluate the role of the endohedral atom (Table 3) and its related interaction energy in the bonding characteristics of the protecting ligands. The energy decomposition analysis (EDA) applied to the [Ag8(X){S2P(OPr)2}5]2+–{S2P(OPr)2}− interaction, showing ΔEint values in the range between −207.8 and −203.0 kcal mol−1, suggests similar features along the series with slight variation according to the respective endohedral atoms. The ligand–core interaction is mainly electrostatic (73.2 av%), with contributions from the orbital interaction character of 23.2 (av%) and lesser from London dispersion interactions (3.6 av%).
| 1 | 2 | 2 | 3 | 4 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| H | F | Cl | Br | I | ||||||
| a Percentual values denote the contribution from each stabilizing term to the overall favorable interaction. b Percentual values denote the contribution from each density deformation channel to the ΔEorb term (Fig. 2). | ||||||||||
| ΔEPauli | 215.4 | 215.8 | 210.1 | 208.0 | 201.0 | |||||
| ΔEelstat | −304.8 | 72.5%a | −308.5 | 72.8%a | −305.6 | 73.5%a | −304.0 | 73.6%a | −297.4 | 73.6%a |
| ΔEorb | −98.5 | 23.4%a | −101.2 | 23.9%a | −96.2 | 23.1%a | −94.7 | 22.9%a | −92.2 | 22.8%a |
| ΔEdisp | −17.0 | 4.0%a | −13.9 | 3.3%a | −14.3 | 3.4%a | −14.3 | 3.5%a | −14.4 | 3.6%a |
| ΔEint | −204.9 | −207.8 | −206.0 | −205.0 | −203.0 | |||||
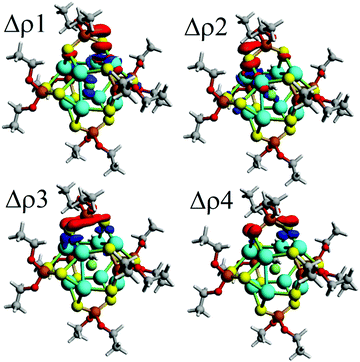
| Δρ1 | −24.1 | 24.5%b | −27.2 | 26.8%b | −22.5 | 23.3%b | −21.6 | 22.8%b | −19.9 | 21.6%b |
| Δρ2 | −17.8 | 18.0%b | −17.9 | 17.6%b | −16.2 | 16.8%b | −15.6 | 16.5%b | −14.8 | 16.1%b |
| Δρ3 | −11.4 | 11.6%b | −10.7 | 10.6%b | −11.7 | 12.1%b | −12.0 | 12.7%b | −12.6 | 13.7%b |
| Δρ4 | −8.2 | 8.3%b | −8.8 | 8.7%b | −9.9 | 10.3%b | −10.2 | 10.8%b | −10.9 | 11.9%b |
Moreover, the orbital contribution (ΔEorb) to the ligand–core interaction can be decomposed through the Natural Orbitals for Chemical Valence48,73,74 extension of EDA (EDA-NOCV),48 leading to the identification of individual deformation density channels accounting for contributions from each set of interacting orbitals (Fig. 2).75,76 From the inspection of resulting deformation densities (ΔρN), four relevant ligand→core charge-transfer channels are found associated with each ligand (Table 3). Particularly, Δρ1 and Δρ2 besides the ligand→core charge transfer involve a subsequent core→X charge transfer, which is not observed for the remaining Δρ3 and Δρ4. Hence, the ligands contribute towards retaining the ionic character of the endohedral atom, suggesting the plausible possibility to tune the ionic character by further modification of the ligand shell, which can be interesting for a series of ligands with variable donor/acceptor characteristics.77
Conclusion
The stabilizing factors ascribed to the hydride and halide encapsulation in a confined hard (Lewis) acid Ag8 cavity is evaluated by the relativistic DFT-D level of theory for the [Ag8(X){S2P(OPr)2}6]+ (X− = H, 1, F, 2, Cl, 3, Br, 4, and, I, 5) series. Our results indicated that the confined Ag8–X aggregate is mainly stabilized by high contribution from the electrostatic type interactions (80.9 av%), with additional stabilization in lesser extent from charge-transfer (17.4 av%) and London type interactions (1.7 av%). The resulting interaction considerably decreases along the series amounting to: −232.2 (1) > −192.1 (2) > −165.5 (3) > −158.0 (4) > −144.2 kcal mol−1 (5), denoting a more favorable inclusion of hydride and fluoride atoms within the silver cage.Further analysis of the electrostatic contribution in terms of the negatively charged nature of the encapsulated atoms reveals that ionic-based electrostatic contributions decrease from 90.7% for the hydride to 68.6% for the iodide counterpart, following the decrease in hardness according to the Pearson's HSAB concept. This observation is explained by the increasing major role of higher electrostatic interaction terms related to softer (Lewis) bases. Moreover, the ligand-core interaction remains almost independent along the series, denoting a ligand→core charge transfer.
The preparation energy (ΔEprep), accounting for the required energy to accommodate the cluster geometry to incorporate the respective monoatomic anion, ranges from 4.2 (2) to 15.8 (1) kcal mol−1, denoting the flexibility of [Ag8{S2P(OPr)2}6]2+ in order to maximize the Ag8–X interaction.
Such insights may contribute to the understanding of different stabilizing and destabilizing terms related to the formation of confined aggregates, where the use of metal-based cavities offers flexibility and versatility towards favorable incorporation of different monoatomic anions.
Author contributions
The manuscript was written through the contributions of all authors.Conflicts of interest
The authors have no conflicts to disclose.Acknowledgements
RLTP thanks Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) (313648/2018-2) for a research fellowship. GFC thanks CNPq (311132/2020) for a research fellowship. P. L. R.-K. thanks the financial support from FONDECYT under the postdoctoral grant number 3190329. A. M.-C. thanks Fondecyt 1180683.References
-
G. F. Caramori and A. Muñoz-Castro, Chemical Reactivity in Confined Systems, Wiley, 2021, pp. 395–416 Search PubMed
.
- X. Wu, A. M. Gilchrist and P. A. Gale, Prospects and challenges in anion recognition and transport, Chem, 2020, 6, 1296–1309 CAS
.
- L. Chen, S. N. Berry, X. Wu, E. N. W. Howe and P. A. Gale, Advances in anion receptor chemistry, Chem, 2020, 6, 61–141 CAS
.
-
P. Gale, W. S. Cho and J. L. Sessler, Anion Receptor Chemistry, Royal Society of Chemistry, Cambridge, 2007 Search PubMed
.
- C. Caltagirone and P. A. Gale, Anion receptor chemistry: Highlights from 2007, Chem. Soc. Rev., 2009, 38, 520–563 RSC
.
- P. A. Gale, Anion receptor chemistry: Highlights from 2008 and 2009, Chem. Soc. Rev., 2010, 39, 3746 RSC
.
- D. Yang, J. Zhao, Y. Zhao, Y. Lei, L. Cao, X.-J. Yang, M. Davi, N. de Sousa Amadeu, C. Janiak, Z. Zhang, Y.-Y. Wang and B. Wu, Encapsulation of halocarbons in a tetrahedral anion cage, Angew. Chem., Int. Ed., 2015, 54, 8658–8661 CrossRef CAS PubMed
.
- S. J. Allison, J. Bryk, C. J. Clemett, R. A. Faulkner, M. Ginger, H. B. S. Griffiths, J. Harmer, P. Jane Owen-Lynch, E. Pinder, H. Wurdak, R. M. Phillips and C. R. Rice, Self-assembly of an anion receptor with metal-dependent kinase inhibition and potent in vitro anti-cancer properties, Nat. Commun., 2021, 12, 3898 CrossRef CAS PubMed
.
- P. A. Gale, J. T. Davis and R. Quesada, Anion transport and supramolecular medicinal chemistry, Chem. Soc. Rev., 2017, 46, 2497–2519 RSC
.
- H. Sepehrpour, W. Fu, Y. Sun and P. J. Stang, Biomedically relevant self-assembled metallacycles and metallacages, J. Am. Chem. Soc., 2019, 141, 14005–14020 CrossRef CAS PubMed
.
- L. A. Joyce, S. H. Shabbir and E. V. Anslyn, The uses of supramolecular chemistry in synthetic methodology development: Examples of anion and neutral molecular recognition, Chem. Soc. Rev., 2010, 39, 3621 RSC
.
- T. R. Cook, V. Vajpayee, M. H. Lee, P. J. Stang and K.-W. Chi, Biomedical and biochemical applications of self-assembled metallacycles and metallacages, Acc. Chem. Res., 2013, 46, 2464–2474 CrossRef CAS PubMed
.
- H. Amouri, C. Desmarets and J. Moussa, Confined nanospaces in metallocages: Guest molecules, weakly encapsulated anions, and catalyst sequestration, Chem. Rev., 2012, 112, 2015–2041 CrossRef CAS PubMed
.
- A. E. Martín Díaz and J. E. M. Lewis, Structural flexibility in metal–organic cages, Front. Chem., 2021, 19, 706462 CrossRef PubMed
.
- E. J. O’Neil and B. D. Smith, Anion recognition using dimetallic coordination complexes, Coord. Chem. Rev., 2006, 250, 3068–3080 CrossRef
.
- V. Amendola, L. Fabbrizzi and L. Mosca, Anion recognition by hydrogen bonding: urea-based receptors, Chem. Soc. Rev., 2010, 39, 3889 RSC
.
- C. R. Rice, C. Slater, R. A. Faulkner and R. L. Allan, Self-assembly of an anion-binding cryptand for the selective encapsulation, sequestration, and precipitation of phosphate from aqueous systems, Angew. Chem., Int. Ed., 2018, 57, 13071–13075 CrossRef CAS PubMed
.
- F. J. Rizzuto, L. K. S. von Krbek and J. R. Nitschke, Strategies for binding multiple guests in metal–organic cages, Nat. Rev. Chem., 2019, 3, 204–222 CrossRef
.
- J. L. Reed, Hard and soft acids and bases: Small molecules, Inorg. Chem., 2009, 48, 7151–7158 CrossRef CAS PubMed
.
- H. Böhrer, N. Trapp, D. Himmel, M. Schleep and I. Krossing, From unsuccessful H2-activation with FLPs containing B(Ohfip)3 to a systematic
evaluation of the Lewis acidity of 33 Lewis acids based on fluoride, chloride, hydride and methyl ion affinities, Dalton Trans., 2015, 44, 7489–7499 RSC
.
- R. G. Pearson, Hard and soft acids and bases, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS
.
- M. Mammen, S.-K. Choi and G. M. Whitesides, Polyvalent interactions in biological systems: Implications for design and use of multivalent ligands and inhibitors, Angew. Chem., Int. Ed., 1998, 37, 2754–2794 CrossRef PubMed
.
- H. J. Schneider, T. Schiestel and P. Zimmermann, Host-guest supramolecular chemistry. 34. The incremental approach to noncovalent interactions: coulomb and van der Waals effects in organic ion pairs, J. Am. Chem. Soc., 1992, 114, 7698–7703 CrossRef CAS
.
- C. Stoffelen and J. Huskens, Soft supramolecular nanoparticles by noncovalent and host–guest interactions, Small, 2016, 12, 96–119 CrossRef CAS PubMed
.
- F. Biedermann and H.-J. Schneider, Experimental binding energies in supramolecular complexes, Chem. Rev., 2016, 116, 5216–5300 CrossRef CAS PubMed
.
- P. Ballester, Experimental quantification of anion–π interactions in solution using neutral host–guest model systems, Acc. Chem. Res., 2013, 46, 874–884 CrossRef CAS PubMed
.
- C. W. Liu, H.-W. W. Chang, C.-S. S. Fang, B. Sarkar and J.-C. C. Wang, Anion-templated syntheses of octanuclear silver clusters from a silver dithiophosphate chain, Chem. Commun., 2010, 46, 4571 RSC
.
- C. W. Liu, H.-C. Haia, C.-M. Hung, B. K. Santra, B.-J. Liaw, Z. Lin and J.-C. Wang, New halide-centered discrete AgI8 cubic clusters containing diselenophosphate ligands, {Ag8(X)[Se2P(OR)2]6}(PF6) (X = Cl, Br; R = Et, Pr, iPr): Syntheses, structures, and DFT calculations, Inorg. Chem., 2004, 43, 4464–4470 CrossRef CAS PubMed
.
- J.-H. Liao, C. Latouche, B. Li, S. Kahlal, J.-Y. Saillard and C. W. Liu, A twelve-coordinated iodide in a cuboctahedral silver(I) skeleton, Inorg. Chem., 2014, 53, 2260–2267 CrossRef CAS PubMed
.
- C. W. Liu, H.-W. Chang, B. Sarkar, J.-Y. Saillard, S. Kahlal and Y.-Y. Wu, Stable silver(I) hydride complexes supported by diselenophosphate ligands, Inorg. Chem., 2010, 49, 468–475 CrossRef CAS PubMed
.
- J.-H. Liao, H.-W. Chang, Y.-J. Li, C.-S. Fang, B. Sarkar, W. E. van Zyl and C. W. Liu, Anion templating from a silver(I) dithiophosphate 1D polymer forming discrete cationic and neutral octa- and decanuclear silver(I) clusters, Dalton Trans., 2014, 43, 12380 RSC
.
- A. Escuer, J. Esteban and M. Font-Bardia, Anion coordination by metallamacrocycles: A cryptand-like cavity, Chem. Commun., 2012, 48, 9777 RSC
.
- P. J. Altmann and A. Pöthig, Capsoplexes: Encapsulating complexes via guest recognition, Chem. Commun., 2016, 52, 9089–9092 RSC
.
- J. Pitarch-Jarque, H. R. Jiménez, E. Kalenius, S. Blasco, A. Lopera, M. P. Clares, K. Rissanen and E. García-España, Selective encapsulation of a chloride anion in a 1H-pyrazole Cu 2+ metallocage, Dalton Trans., 2021, 50, 9010–9015 RSC
.
- T. Nakamura, Development of artificial receptors based on assembly of metal complex units and desymmetrization of molecular components, Chem. Lett., 2021, 50, 1822–1830 CrossRef CAS
.
- J.-Y. Wu, M.-S. Zhong and M.-H. Chiang, Anion-directed metallocages: A study on the tendency of anion templation, Chem. – Eur. J., 2017, 23, 15957–15965 CrossRef CAS PubMed
.
- S. O. Kang, J. M. Llinares, V. W. Day and K. Bowman-James, Cryptand-like anion receptors, Chem. Soc. Rev., 2010, 39, 3980 RSC
.
- P. Ballester, Anion binding in covalent and self-assembled molecular capsules, Chem. Soc. Rev., 2010, 39, 3810 RSC
.
- S. Ruiz-Botella, P. Vidossich, G. Ujaque and E. Peris, Rim, side arms, and cavity: Three sites for the recognition of anions by tetraazolium resorcinarene cavitands, Chem. – Eur. J., 2016, 22, 15800–15806 CrossRef CAS PubMed
.
- S. Toyota and E. Tsurumaki, Exploration of nano-saturns: A spectacular sphere-ring supramolecular system, Chem. – Eur. J., 2019, 25, 6878–6890 CrossRef CAS PubMed
.
- H. Chen and J. Fraser Stoddart, From molecular to supramolecular electronics, Nat. Rev. Mater., 2021, 6, 804–828 CrossRef CAS
.
- R. G. Pearson, Recent advances in the concept of hard and soft acids and bases, J. Chem. Educ., 1987, 64, 561 CrossRef CAS
.
- H. V. R. Dias and J. Wu, Structurally characterized coinage-metal–ethylene complexes, Eur. J. Inorg. Chem., 2008, 509–522 CrossRef CAS
.
- I. Krossing and A. Reisinger, A stable salt of the tris(ethene)silver cation: Structure and characterization of [Ag(η2-C2H4)3] + [Al{OC(CF3)3}4]−, Angew. Chem., Int. Ed., 2003, 42, 5725–5728 CrossRef CAS PubMed
.
- R. H. Hertwig, W. Koch, D. Schröder, H. Schwarz, J. Hrušák and P. Schwerdtfeger, A comparative computational study of cationic coinage metal–ethylene complexes (C2H4)M + (M = Cu, Ag, and Au), J. Phys. Chem., 1996, 100, 12253–12260 CrossRef CAS
.
- T. Ziegler and A. Rauk, On the calculation of bonding energies by the Hartree Fock Slater method, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS
.
- K. Morokuma, Molecular orbital studies of hydrogen bonds. III. C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–O hydrogen bond in H2CO⋯H2O and H2CO⋯2H2O, J. Chem. Phys., 1971, 55, 1236–1244 CrossRef CAS
O⋯H–O hydrogen bond in H2CO⋯H2O and H2CO⋯2H2O, J. Chem. Phys., 1971, 55, 1236–1244 CrossRef CAS .
-
The Chemical Bond: Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2014 Search PubMed
.
-
G. Frenking, M. Bickelhaupt and F. Matthias Bickelhaupt, The Chemical Bond, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2014, pp. 121–157 Search PubMed
.
- G. F. Caramori, I. Østrøm, A. O. Ortolan, G. R. Nagurniak, V. M. Besen, A. Muñoz-Castro, R. P. Orenha, R. L. T. Parreira and S. E. Galembeck, The usefulness of energy decomposition schemes to rationalize host–guest interactions, Dalton Trans., 2020, 49, 17457–17471 RSC
.
- E. Van Lenthe and E. J. Baerends, Optimized Slater type basis sets for the elements 1 118, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed
.
- Amsterdam Density Functional (ADF 2019) Code, Vrije Universiteit: Amsterdam, The Netherlands, Available at: http://www.scm.com (accessed December 9th, 2021).
- E. van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic total energy using regular approximations, J. Chem. Phys., 1994, 101, 9783 CrossRef CAS
.
- E. van Lenthe, A. Ehlers and E.-J. Baerends, Geometry optimizations in the zero order regular approximation for relativistic effects, J. Chem. Phys., 1999, 110, 8943 CrossRef CAS
.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed
.
- J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- J. Cirera, E. Ruiz and S. Alvarez, Continuous shape measures as a stereochemical tool in organometallic chemistry, Organometallics, 2005, 24, 1556–1562 CrossRef CAS
.
- A. Ruiz-Martínez, D. Casanova and S. Alvarez, Polyhedral structures with an odd number of vertices: Nine-coordinate metal compounds, Chem. – Eur. J., 2008, 14, 1291–1303 CrossRef PubMed
.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Shape maps and polyhedral interconversion paths in transition metal
chemistry, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS
.
- K. Morokuma, Molecular orbital studies of hydrogen bonds. III. C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–O hydrogen bond in H2CO⋯H2O and H2CO⋯2H2O, J. Chem. Phys., 1971, 55, 1236–1244 CrossRef CAS
O⋯H–O hydrogen bond in H2CO⋯H2O and H2CO⋯2H2O, J. Chem. Phys., 1971, 55, 1236–1244 CrossRef CAS .
- G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders, T. Ziegler, G. T. E. Velde, C. F. Guerra and S. J. A. Gisbergen, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS
.
- M. von Hopffgarten and G. Frenking, Energy decomposition analysis, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43–62 CAS
.
- M. Solà, M. Duran and J. Poater, The energy components of the extended transition state energy decomposition analysis are path functions: The case of water tetramer, Theor. Chem. Acc., 2021, 140, 33 Search PubMed
.
- D. M. Andrada and C. Foroutan-Nejad, Energy components in energy decomposition analysis (EDA) are path functions; why does it matter?, Phys. Chem. Chem. Phys., 2020, 22, 22459–22464 RSC
.
- B. Pinter, T. Fievez, F. M. Bickelhaupt, P. Geerlings and F. De Proft, On the origin of the steric effect, Phys. Chem. Chem. Phys., 2012, 14, 9846 RSC
.
- S. Grimme, Density functional theory with London dispersion corrections, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CAS
.
- M. Ponce-Vargas and A. Muñoz-Castro, Metal containing cryptands as hosts for anions: evaluation of Cu(I)–X and π–X interactions in halide–tricopper(I) complexes through relativistic DFT calculations, Phys. Chem. Chem. Phys., 2015, 17, 18677–18683 RSC
.
- M. Ponce-Vargas and A. Muñoz-Castro, Heavy element metallacycles: Insights into the nature of host–guest interactions involving dihalide mercuramacrocycle complexes, J. Phys. Chem. C, 2014, 118, 28244–28251 CrossRef CAS
.
- M. Ponce-Vargas, Metallacycles capabilities in host–guest chemistry, ChemistryOpen, 2015, 4, 656–660 CrossRef CAS PubMed
.
- A. O. Ortolan, G. F. Caramori, F. Matthias Bickelhaupt, R. L. T. Parreira, A. Muñoz-Castro and T. Kar, How the electron-deficient cavity of heterocalixarenes recognizes anions: Insights from computation, Phys. Chem. Chem. Phys., 2017, 19, 24696–24705 RSC
.
- R. F. Nalewajski, J. Mrozek and A. Michalak, Two-electron valence indices from the Kohn–Sham orbitals, Int. J. Quantum Chem., 1997, 61, 589–601 CrossRef CAS
.
- A. Michalak, R. L. DeKock and T. Ziegler, Bond multiplicity in transition-metal complexes: Applications of two-electron valence indices, J. Phys. Chem. A, 2008, 112, 7256–7263 CrossRef CAS PubMed
.
- A. Michalak, M. Mitoraj and T. Ziegler, Bond orbitals from chemical valence theory, J. Phys. Chem. A, 2008, 112, 1933–1939 CrossRef CAS PubMed
.
- M. P. Mitoraj, A. Michalak and T. Ziegler, A combined charge and energy decomposition scheme for bond analysis, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef CAS PubMed
.
- A. Muñoz-Castro, D. MacLeod Carey and R. Arratia-Perez, Relativistic effects on dative carbon-coinage metal bond. Evaluation of NHC-MCl (M = Cu, Ag, Au) from relativistic DFT, Polyhedron, 2021, 197, 115020 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04249a |
| This journal is © the Owner Societies 2022 |