Unveiling the role of 2D monolayer Mn-doped MoS2 material: toward an efficient electrocatalyst for H2 evolution reaction
Joy
Ekka
 a,
Shrish Nath
Upadhyay
a,
Shrish Nath
Upadhyay
 b,
Frerich J.
Keil
b,
Frerich J.
Keil
 c and
Srimanta
Pakhira
c and
Srimanta
Pakhira
 *abd
*abd
aDepartment of Physics, Indian Institute of Technology Indore (IIT Indore), Simrol, Khandwa Road, Indore 453552, MP, India. E-mail: spakhira@iiti.ac.in; spakhirafsu@gmail.com
bDepartment of Metallurgy Engineering and Materials Science (MEMS), Indian Institute of Technology Indore (IIT Indore), Khandwa Road, Simrol, Indore 453552, MP, India
cDepartment of Chemical Reaction Engineering, Hamburg University of Technology, 21073 Hamburg, Germany
dCentre for Advanced Electronics (CAE), Indian Institute of Technology Indore (IIT Indore), Khandwa Road, Simrol, Indore 453552, MP, India
First published on 5th November 2021
Abstract
Two-dimensional (2D) monolayer pristine MoS2 transition metal dichalcogenide (TMD) is the most studied material because of its potential applications as nonprecious electrocatalyst for the hydrogen evolution reaction (HER). Previous studies have shown that the basal planes of 2D MoS2 are catalytically inert, and hence it cannot be used directly in desired applications such as electrochemical HER in industry. Here, we thoroughly studied a defect-engineered Mn-doped 2D monolayer MoS2 (Mn–MoS2) material, where Mn was doped in pristine MoS2 to activate its inert basal planes. Using the density functional theory (DFT) method, we performed rigorous inspection of the electronic structures and properties of the 2D monolayer Mn–MoS2 as a promising alternative to noble metal-free catalyst for effective HER. A periodic 2D slab of monolayer Mn–MoS2 was created to study the electronic properties (such as band gap, band structures and total density of states (DOS)) and the reaction pathways occurring on the surface of this material. The detailed HER mechanism was explored by creating an Mn1Mo9S21 non-periodic finite molecular cluster model system using the M06-L DFT method including solvation effects to determine the reaction barriers and kinetics. Our study revealed that the 2D Mn–MoS2 follows the most favorable Volmer–Heyrovsky reaction mechanism with a very low energy barrier during H2 evolution. It was found that the change in the free energy barrier (ΔG) during the H˙-migration (i.e., Volmer) and Heyrovsky reactions is about 10.34–10.79 kcal mol−1 (computed in the solvent phase), indicating that this material is an exceptional electrocatalyst for the HER. The Tafel slope (y) was lower in the case of the 2D monolayer Mn–MoS2 material due to the overlap of the s-orbital of hydrogen and d-orbitals of the Mn atoms in the HOMO and LUMO transition states (TS1 and TS2) of both the Volmer and Heyrovsky reaction steps, respectively. The better stabilization of the atomic orbitals in the HER rate-limiting step Heyrovsky TS2 is the key for reducing the reaction barrier, and thus the overall catalysis, indicating a better electrocatalytic performance for H2 evolution. This study focused on designing low-cost and efficient electrocatalysts for the HER using earth abundant transition metal dichalcogenides (TMDs) and decreasing the activation energy barriers by scrutinizing the kinetics of the reaction to achieve high reactivity.
1 Introduction
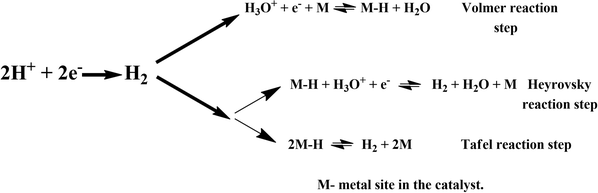
The global energy supply is heavily dependent on fossil fuels; however, energy production emanating from this source releases substances that are harmful to the environment. The rapid depletion of this energy source is also another concern, which drives the necessity to find eco-friendly and zero-emission energy sources. Thus, to resolve these issues, we need to increase the use of renewable energy sources to meet future energy demands. Hydrogen is a new and unconventional renewable source of energy due to its high energy density and zero-emission greenhouse gases among other available alternative energy sources and fuels.1 For the production of clean and efficient hydrogen, electrolysis of water has been demonstrated to be a viable method since its discovery in 1789.2 Electrochemical water splitting is a sustainable strategy to produce hydrogen (and oxygen) and replace conventional fossil fuels. Hydrogen is a non-polluting energy source given that water is the product of H2 combustion. However, the conventional water splitting process cannot simply separate water into hydrogen and oxygen, and similar to other chemical processes, this reaction requires energy input to overcome the energy barrier in the electrochemical process. Thus, electrochemical water splitting requires highly active catalysts to reduce the overpotential needed to produce hydrogen (+1.23 V; 25 °C; 1 atm). The hydrogen evolution reaction (HER), i.e., simply 2H+ + 2e− → H2, is a multiphase reaction for the sustainable production of hydrogen (H2), which can occur via two processes, either through the Volmer–Heyrovsky process or Volmer–Tafel process.3–5However, the above-mentioned reactions are competitive processes and are dependent on the electronic structure of the electrode surface. Thus, boosting the efficiency of the sluggish HER process is challenging. To date, platinum (Pt) is the best-known electrocatalyst for the HER due to its zero overpotential in acidic electrolytes.6 Because of their optimum Gibbs free energy (G) for the adsorption of atomic hydrogen, binding energy, and desorption of hydrogen from their surface with low activation energies, Pt-based catalysts have been long known as effective HER electrocatalysts.7,8 However, the limited availability and high cost of platinum limit its use as an efficient catalyst in large-scale commercial and industrial applications. To produce hydrogen on a global scale, we need to reduce the cost of its production. Thus, reducing the dependency on noble metal-based catalysts or even replacing them completely with non-noble metal alternatives would be a driving step towards a hydrogen economy. Accordingly, the search for Pt-free catalysts for the HER is of paramount importance in modern materials science and technology.
In the past few decades, countless exhaustive studies have focused on the development of earth abundant and ecofriendly materials showing excellent electrocatalytic effects for the efficient production of H2 through the HER. Consequently, many of them such as Pt, Au, and Pd noble metal-based electrocatalysts, nano-porous materials, two-dimensional transition metal dichalcogenides (2D TMDs), 2D–3D material alloys and 2D TMDs doped with other atom species have a significant impact as efficient HER catalysts.9–18 A plethora of breakthroughs has been achieved in this regard for the rational design of HER electrocatalysts. Recently, earth abundant layered TMDs, for example MoS2, have attracted tremendous interest due to their inherent properties, which produce hydrogen at a very low overpotential with a high current density.15,19,20 It is widely recognized that 2D monolayer MoS2 material can exist in several possible structures such as 1T (octahedral), 1T′ (distorted octahedral) and 2H (hexagonal) structures.21 The 2H phase structure (i.e., 2D monolayer 2H-MoS2) is the most stable21 and is commonly used for electrocatalysis of the HER.22–24 The high activity of 2D monolayer MoS2 is attributed to its appropriate Gibbs free energy of adsorption for atomic hydrogen.25 Other MoS2-based materials such as MoS2 di-anionic surface with controlled molecular substitution of their S sites with –OH functional group have also proven to be efficient electrocatalysts.26 However, although these materials show promising aspects, they are still not sufficient in their present form for large-scale industrial and commercial applications due to their inert basal plane. Theoretical calculations indicated that P-doped MoS2 shows good catalytic activity for the HER by reducing the change in free energy (ΔG). This is due to the P-doping in the pristine MoS2, which activates its inert basal plane;27 however, this non-metal doping is quite difficult because of the instantaneous formation of MoP.10 Furthermore, to avoid the formation of MoP, very expensive apparatus such as plasma ion implantation is required, and in some cases, special precautions have to be taken during P-doping in the MoS2.28 Thus, other methods and materials are required for developing low-cost and efficient HER catalysts to produce the desirable H2 for industrial and commercial applications. Several techniques have been developed to generate high-performance TMD-based materials, such as defect engineering, metal-atom doping, nanostructure engineering, interface and strain engineering, and phase engineering.15,29 However, another problem frequently encountered in the 2D TMDs is the stacking of their 2D layers, which decreases the number of exposed sites, and the conductivity along two stacked layers is extremely low,30 thereby impeding charge transfer and decreasing the HER performance of 2D TMDs. A prominent factor controlling the rate of the HER is conductivity; however, pristine 2D monolayer MoS2 shows semiconducting properties, indicating its low electrical conductivity, and thus is inadequate for large-scale commercial applications. One of the promising ways to enhance the HER activity of pristine 2D monolayer 2H-MoS2 is to expose its active sites.31 It was found that the most of the active sites of pristine 2D monolayer 2H-MoS2 for the HER are located at its Mo and S edge sites.32 Furthermore, to modulate its electron transport for achieving proper conducting pathways and enhance its hydrogen evolution activity, the doping of external elements in the pristine 2D monolayer 2H-MoS2 nanostructure is a promising way via modern technology.14 Therefore, mechanistic insights are important for designing efficient electrocatalysts for H2 evolution.
The development of operative, stable, and economic HER catalysts to overcome the challenges associated with H2 production via the electrolysis of water is significant in reducing production costs and extending the hydrogen economy. For example, engineering the HER activity of MoS2via co-confining selenium and cobalt on its surface and inner plane, respectively, has shown promising results.33 We propose that Mn-doping in the pristine 2D monolayer MoS2 TMD material can activate its inert basal plane and the Mn-doped 2D MoS2 (in short Mn–MoS2) can be a promising material for efficient H2 evolution.34,35 For transition metal-based catalysts, their performance is correlated with their surface electronic structures and the electronic configuration of the d-orbital of the transition metal.11 In this regard, we computationally developed a two-dimensional (2D) single-layer Mn-doped MoS2 material (i.e., Mn–MoS2) and investigated its electrocatalytic performance for efficient HER. Firstly, we performed first principles-based quantum mechanical (QM) hybrid periodic density functional theory (DFT)36–41 calculations to determine its electronic properties such as electronic band structures, band gap and total density of states (DOS). Recently, QM DFT approaches and molecular simulations have been employed for modeling heterogeneous catalytic reactions, adsorption, and chemical reactions on the surface of 2D metals.42–45 We found that the 2D monolayer Mn–MoS2 shows a zero band gap due to Mn-doping in the pristine 2D MoS2. The density of states calculation indicated that there is a large number of electronic states available around the Fermi energy (EF) level with a high availability of electrons due to the doping of Mn atoms in the pristine 2D monolayer MoS2 material.
One of the key features in determining the smooth flow of a reaction is the change in free energy (ΔG) of the possible reaction intermediates. Thus, to screen an appropriate candidate among the options available, it is important to compute the value of ΔG during hydrogen adsorption, which is an important parameter for evaluating the catalytic activity during the HER process. Lately, the quantum computational method has provided feasible procedures for calculating the free energy changes based on density functional theory (DFT).46–49 By modeling the possible reaction intermediates during the hydrogen evolution process on the surface of the electrocatalyst, its thermodynamic properties can be obtained using DFT methods. Therefore, we prepared a finite molecular cluster model system of the Mn–MoS2 material and carefully studied each reaction intermediate appearing during the HER process by employing the DFT method in both gas and solvent phase calculations. Our study showed that the 2D monolayer Mn–MoS2 TMD shows excellent catalytic activity for H2 evolution.
2 Methodology and computational details
2.1 Periodic structure calculations
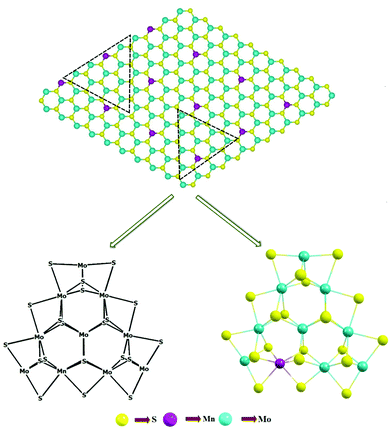
We systematically investigated the electronic properties, i.e., band structures and total density of states (DOS), of both 2D monolayer pristine MoS2 and Mn-doped MoS2, i.e., Mn–MoS2. For the periodic 2D layer structure (i.e., 2D slab) computations, a single 2D TMD (here both MoS2 and Mn-doped MoS2) layer terminated on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) (Mo-/Mn-edge) and (
0) (Mo-/Mn-edge) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 010) (S-edge) boundaries with three Mo per unit cell was considered, as shown in Fig. 2. It should be mentioned here that the exposed surfaces are generally the (001) basal plane of the S–Mo–S (Mn-doped in the case of Mn–MoS2) tri-layer, Mo-/Mn-edge (10
010) (S-edge) boundaries with three Mo per unit cell was considered, as shown in Fig. 2. It should be mentioned here that the exposed surfaces are generally the (001) basal plane of the S–Mo–S (Mn-doped in the case of Mn–MoS2) tri-layer, Mo-/Mn-edge (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) plane and S-edge (
0) plane and S-edge (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 010) plane. The rigid periodic structure computations and the equilibrium structures were obtained by performing hybrid dispersion corrected periodic density functional theory (in short DFT-D), i.e., B3LYP-D3 method,50–59 implemented in the ab initio-based CRYSTAL17 suite code.60 The electronic property calculations were performed by using the same B3LYP-D3 method.61–64 We performed spin polarized calculations to obtain the equilibrium structures and study the electronic properties during the periodic hybrid DFT-D calculations. A spin-polarized solution was computed after the definition of the (α, up spin and β, down spin) electron occupancy. Specifically, it should be noted here that spin-unrestricted wave functions were used in the present calculations to incorporate spin polarization. This was performed by using the keywords “ATOMSPIN” and “SPINLOCK” implemented in the ab initio CRYSTAL17 program.60 In the present calculations, we accounted for the weak long-range van der Waals (vdW) dispersion effects65 resulting from the interaction between atoms by including semi-empirical corrections (Grimme's “-D3” corrections).57 The weak vdW interaction between the layers of both materials (MoS2 and Mn–MoS2) was included in the present DFT calculations by adding Grimmes's semi-empirical dispersion parameters.51–55 Triple-ζ valence with polarization function quality (TZVP) Gaussian basis sets were used for the sulphur (S)66,67 and manganese (Mn)66 atoms, and the HAYWSC-311 (d31) G-type basis sets with Hay and Wadt small effective core pseudopotentials (ECPs) for molybdenum (Mo).68 The DFT-D method provides a good quality geometry of 2D layered structure materials after reducing the spin contamination effects so that they will not show any effect on the electronic structure and electronic property calculations (i.e., band structure and total density of states (DOS)).38,54,69–72 The threshold used for evaluating the convergence of the energy, forces and electron density was set to 10−7 a.u. for each parameter. The height of the unit cell was formally set to 500 Å (which considers there is no periodicity in the z-direction in the 2D slab model in the CRYSTAL17 code), i.e., the vacuum region of approximately 500 Å was considered in the present calculations to accommodate the vacuum environment.39,73 The unit cell of the 2D monolayer MoS2 was extended to 3 × 3 × 1 to form a supercell and Mn atom was doped by replacing the Mo atoms. It was found that the Mn-doping concentration was 12.5% in the 2D Mn–MoS2 material (given that the optimized supercell consisted of 9 Mo atoms, among which 1 Mo atom at the exposed edge was replaced with an Mn atom, which led to the ratio of Mn
010) plane. The rigid periodic structure computations and the equilibrium structures were obtained by performing hybrid dispersion corrected periodic density functional theory (in short DFT-D), i.e., B3LYP-D3 method,50–59 implemented in the ab initio-based CRYSTAL17 suite code.60 The electronic property calculations were performed by using the same B3LYP-D3 method.61–64 We performed spin polarized calculations to obtain the equilibrium structures and study the electronic properties during the periodic hybrid DFT-D calculations. A spin-polarized solution was computed after the definition of the (α, up spin and β, down spin) electron occupancy. Specifically, it should be noted here that spin-unrestricted wave functions were used in the present calculations to incorporate spin polarization. This was performed by using the keywords “ATOMSPIN” and “SPINLOCK” implemented in the ab initio CRYSTAL17 program.60 In the present calculations, we accounted for the weak long-range van der Waals (vdW) dispersion effects65 resulting from the interaction between atoms by including semi-empirical corrections (Grimme's “-D3” corrections).57 The weak vdW interaction between the layers of both materials (MoS2 and Mn–MoS2) was included in the present DFT calculations by adding Grimmes's semi-empirical dispersion parameters.51–55 Triple-ζ valence with polarization function quality (TZVP) Gaussian basis sets were used for the sulphur (S)66,67 and manganese (Mn)66 atoms, and the HAYWSC-311 (d31) G-type basis sets with Hay and Wadt small effective core pseudopotentials (ECPs) for molybdenum (Mo).68 The DFT-D method provides a good quality geometry of 2D layered structure materials after reducing the spin contamination effects so that they will not show any effect on the electronic structure and electronic property calculations (i.e., band structure and total density of states (DOS)).38,54,69–72 The threshold used for evaluating the convergence of the energy, forces and electron density was set to 10−7 a.u. for each parameter. The height of the unit cell was formally set to 500 Å (which considers there is no periodicity in the z-direction in the 2D slab model in the CRYSTAL17 code), i.e., the vacuum region of approximately 500 Å was considered in the present calculations to accommodate the vacuum environment.39,73 The unit cell of the 2D monolayer MoS2 was extended to 3 × 3 × 1 to form a supercell and Mn atom was doped by replacing the Mo atoms. It was found that the Mn-doping concentration was 12.5% in the 2D Mn–MoS2 material (given that the optimized supercell consisted of 9 Mo atoms, among which 1 Mo atom at the exposed edge was replaced with an Mn atom, which led to the ratio of Mn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mo atoms of 1
Mo atoms of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8, thus making the doping concentration 12.5% near the desired active edges, as shown in Fig. 1). In the atomic structure relaxation simulation, a vacuum slab of 500 Å was inserted between the layers to prevent the interlayer interaction.
8, thus making the doping concentration 12.5% near the desired active edges, as shown in Fig. 1). In the atomic structure relaxation simulation, a vacuum slab of 500 Å was inserted between the layers to prevent the interlayer interaction.
 | ||
| Fig. 1 Non-periodic finite molecular cluster model (Mn1Mo9S21) as derived from the 2D Mn–MoS2 monolayer material (represented by the dotted triangle). | ||
The electronic band structures and total DOS calculations were performed on the equilibrium structures of the TMDs by employing the same DFT-D method. All the integrations of the first Brillouin zone were sampled on 20 × 20 × 1 Monkhorst–Pack74k-mesh grids for the pristine 2D MoS2 and 4 × 4 × 1 for 2D Mn–MoS2. The k-vector path taken for plotting the band structure was selected as Γ–M–K–Γ for both materials (i.e., pristine MoS2 and Mn–MoS2). The atomic orbitals of Mo, S, and Mn were used to compute and plot the total DOS for the α electrons, which is enough to describe the electronic properties of the 2D Mn–MoS2 material. The single-point calculation was performed at the equilibrium geometry to form the normalized wave function at zero Kelvin temperature with respect to vacuum. To create the graphics and analysis of the 2D layer structures studied here, the visualization software VESTA75 was used. We are aware that the lateral interactions of the adsorbed species may change the free energies for different surface coverages. The same applies for different temperatures.42,44,45
2.2 Finite cluster modeling
Further, we developed a finite non-periodic molecular cluster model system for both the 2D monolayer pristine MoS2 and Mn–MoS2 materials to investigate the HER mechanism using the GAUSSIAN 1647 suite code. A non-periodic finite molecular cluster model, Mo10S21 system, for the pristine 2D monolayer MoS2 and Mn1Mo9S21 for the 2D monolayer Mn–MoS2 TMD (as shown in Fig. 1) was considered to investigate the HER in both the gas phase and solvent phase calculations, and the M06-L57,76 DFT method with a spin-unrestricted wavefunction was applied to investigate the reaction pathways, kinetics, barriers, and mechanism. Fig. 1 shows how we extracted a triangular cluster from the periodic array to expose only the Mo edges. A schematic representation of the finite molecular cluster Mn1Mo9S21 is shown in Fig. 1. This M06-L DFT method is a technique used for energetics, equilibrium structures, thermochemistry, and frequency calculations of the molecular cluster structures, and it has been found that the M06-L method provides reliable energy barriers for reaction mechanisms of organometallic catalysts.9,10,40,76–78 We focused on the energy barriers and changes in free energy during the reaction to explore the reaction pathways by employing Minnesota density functional based on the meta-GGA approximation, which is intended to be good and fast for transition metals.76,77,79 We used the 6-31G** Gaussian basis sets for H,80,81 S,82 O83 and Mn84 atoms, while the LANL2DZ Gaussian basis set with effective core potentials for the Mo85,86 atom. The transition state theory (TST) was applied to locate the Volmer, Tafel and Heyrovsky transition states (TSs), and the OPT = QST2 and OPT = QST3 algorithms were used to find all the TSs, which were implemented in the GAUSSIAN 1647 suite code. The transition structures or saddle points (Volmer, Tafel and Heyrovsky reaction steps) were computed to find the reaction barriers by confirming one imaginary frequency, modes of vibration, and intrinsic reaction coordinate (IRC) calculations.9,10 Different transition states (TSs) were computed at the optimized geometry and to visualize them, ChemCraft87 was used. Moreover, the Heyrovsky reaction mechanism was studied by deliberately adding three water molecules and a hydronium ion in the vicinity of the intended reaction region. The water cluster model (4H2O + H+) was prepared as follows: 4 water molecules were placed adjacent to each other connected via a hydrogen bond and a proton was attached to one of the water molecules. This model was prepared to simulate the reaction of H2 formation during the Heyrovsky process.The two horizontal dashed lines indicate terminations along the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) Mn-/Mo-edge and (
0) Mn-/Mo-edge and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 010) S-edge. The two triangles represent the terminations for the Mn-/Mo-edge and S-edge clusters and the dangling bonds in the finite cluster were set by considering a triangle, as shown in Fig. 2. Each Mo atom in the (001) basal plane of the finite molecular cluster model has an oxidation state of 4+ (and the oxidation state of the Mn atom is 4+) and they are bonded with 6 S atoms (3 S at the upper plane and 3 S at the lower plane of Mo), which gives a contribution of 4/6 = 2/3 electrons towards each Mo–S bonding, resulting in a stabilized structure. The same can be understood with the oxidation state of S in the basal plane. The sulfur (S) atom has an oxidation state of −2 and bonds with 3 Mo atoms, which results in a contribution of 2/3 electrons towards each Mo–S bond. Similarly, the edges of the (00
010) S-edge. The two triangles represent the terminations for the Mn-/Mo-edge and S-edge clusters and the dangling bonds in the finite cluster were set by considering a triangle, as shown in Fig. 2. Each Mo atom in the (001) basal plane of the finite molecular cluster model has an oxidation state of 4+ (and the oxidation state of the Mn atom is 4+) and they are bonded with 6 S atoms (3 S at the upper plane and 3 S at the lower plane of Mo), which gives a contribution of 4/6 = 2/3 electrons towards each Mo–S bonding, resulting in a stabilized structure. The same can be understood with the oxidation state of S in the basal plane. The sulfur (S) atom has an oxidation state of −2 and bonds with 3 Mo atoms, which results in a contribution of 2/3 electrons towards each Mo–S bond. Similarly, the edges of the (00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) periodic molecular cluster is stabilized with 2 local electron Mo–S bonds (as well as Mn–S bonds) having a single electron contribution towards each bond. Thus, at the edges each Mo atom contributes 2 × 1 electrons towards the local Mo–S bonds plus 4 × (2/3) electron contribution towards 4 Mo–S bonding in the basal plane, as shown in the Fig. 1. This 14/3 {i.e., (2 × 1) + [4 × (2/3)]} contribution of electrons towards the Mo–S bonding of the edge Mo atom is satisfied with the d2 configuration of one Mo atom and d1 configuration of two Mo atoms at the edges. This configuration leads to a molecular system with the periodicity of 3, which results in the achievement of a stabilized molecular cluster model having three edges without any unsatisfied valency.88
0) periodic molecular cluster is stabilized with 2 local electron Mo–S bonds (as well as Mn–S bonds) having a single electron contribution towards each bond. Thus, at the edges each Mo atom contributes 2 × 1 electrons towards the local Mo–S bonds plus 4 × (2/3) electron contribution towards 4 Mo–S bonding in the basal plane, as shown in the Fig. 1. This 14/3 {i.e., (2 × 1) + [4 × (2/3)]} contribution of electrons towards the Mo–S bonding of the edge Mo atom is satisfied with the d2 configuration of one Mo atom and d1 configuration of two Mo atoms at the edges. This configuration leads to a molecular system with the periodicity of 3, which results in the achievement of a stabilized molecular cluster model having three edges without any unsatisfied valency.88
To model the solvation effects, we used the polarizable continuum model89 (PCM) with water as the solvent. The PCM method using GAUSSIAN1647 uses an external iteration method, where the energy in the solution is computed by making the solvent reaction field self-consistent with the solute electrostatic potential, given that the real reaction occurs in the solvent phase. For specifying the molecular cavity used in PCM, we used the UAHF set, i.e., the United Atom Topological Model.90 We modeled our reaction mechanism in water having a static dielectric constant of 78.36 (zero-frequency, 298.15 K, 1 atm).90,91 The geometric optimization and molecular energy in the solvent phase were calculated using the above-mentioned method.
2.3 Theoretical calculations and equations
It is important here that we examine the equilibrium structures to find the free energy difference (here Gibbs free energy difference: ΔG, i.e., relative Gibbs free energy) between the intermediate states, and ultimately the lowest-barrier pathway. All the HER steps were explored with respect to the standard hydrogen electrode (SHE). For each species, the free energy (G) can be expressed using the following equation: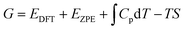 | (1) |
| ΔG = ∑GProducts − ∑GReactants | (2) |
| ΔH = ∑HProducts − ∑HReactants | (3) |
| ΔE = ∑EProducts − ∑EReactants | (4) |
3 Results and discussion
3.1 Periodic vacuum slab inference
The equilibrium lattice parameters and average bond distances are listed in Table 1. The lattice constants (a and b) and the average Mo–S bond distance of the pristine 2D monolayer MoS2 obtained by the DFT-D method are consistent with the previous reported results.69 The value of the lattice constants (a = b) is 3.18 Å and the Mo–S bond distance is about 2.41 Å, which are consistent with the previously reported values, and it has a hexagonal 2D layer P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 symmetry.92 This is a good estimation compared to the work where the 2D monolayer MoS2 structure was doped with 4% impurity and the bond distance was 2.39 Å between the Mn and the nearest S atom.92 The doping of a transition metal in the 3 × 3 × 1 supercell of the 2D monolayer MoS2 changed its symmetry from P
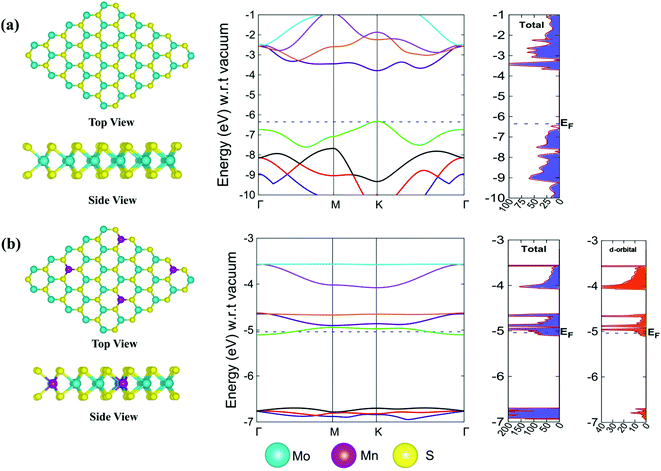
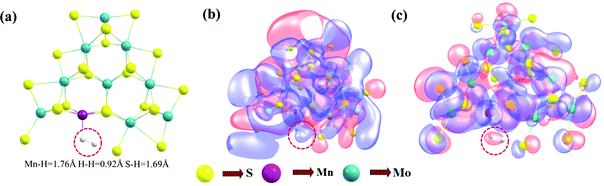
m2 symmetry.92 This is a good estimation compared to the work where the 2D monolayer MoS2 structure was doped with 4% impurity and the bond distance was 2.39 Å between the Mn and the nearest S atom.92 The doping of a transition metal in the 3 × 3 × 1 supercell of the 2D monolayer MoS2 changed its symmetry from P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 to P1 when 2D Mn–MoS2 was formed. The average bond distance between Mn and the nearest S atom was computed to be 2.30 Å, which agrees well the previous result within 0.09 Å.69 According to the electronic properties calculations obtained by the same DFT-D method, we observed a direct band gap of 2.6 eV at the K point in the Brillouin zone of the pristine 2D single-layer MoS2 material, as shown in Fig. 2a, which is in good agreement with the previous theoretical and experimental results. The computed electronic band gap is slightly lower than the band gap obtained by the GW approximation of the 2D monolayer MoS2 TMD, which was 2.8 eV.93 The Fermi level (EF) was found at −6.36 eV, as depicted in the non-normalized band structure and DOS calculations and shown in Fig. 2a highlighted by the dotted blue color. After Mn-doping in the pristine 2D monolayer MoS2 material, the band structures changed, i.e., the Fermi level (EF) shifted to −5.04 eV (with respect to the EF of the 2D pristine MoS2) and it was computationally found that the bands overlapped around the EF, as shown in Fig. 2b. The present DFT-D study showed that the Fermi level was found at −5.04 eV in the case of the 2D monolayer Mn–MoS2 with a zero band gap, indicating the conducting character of the material. Specifically, this zero-band gap suggests that the Mn-doping in the pristine TMD makes the 2D semi-conducting MoS2 material a conducting material in nature. This can also be justified by computing the electron density contribution from the 3d-subshells of the Mn atoms doped in the 2D monolayer MoS2 material (as can be seen from the d-orbital DOS at the right-hand side in Fig. 2b). Specifically, due to the addition of Mn atoms in the pristine MoS2 to form the 2D monolayer Mn–MoS2 material, the electronic band gap of Mn–MoS2 decreased to zero, as depicted in the band structures and DOS calculations in Fig. 2b. The addition of Mn to the pristine 2D TMD MoS2 changes the electron accumulation in the bands, as shown in the DOS calculations, suggesting high electron mobility and possibly good catalytic activity for the HER.
m2 to P1 when 2D Mn–MoS2 was formed. The average bond distance between Mn and the nearest S atom was computed to be 2.30 Å, which agrees well the previous result within 0.09 Å.69 According to the electronic properties calculations obtained by the same DFT-D method, we observed a direct band gap of 2.6 eV at the K point in the Brillouin zone of the pristine 2D single-layer MoS2 material, as shown in Fig. 2a, which is in good agreement with the previous theoretical and experimental results. The computed electronic band gap is slightly lower than the band gap obtained by the GW approximation of the 2D monolayer MoS2 TMD, which was 2.8 eV.93 The Fermi level (EF) was found at −6.36 eV, as depicted in the non-normalized band structure and DOS calculations and shown in Fig. 2a highlighted by the dotted blue color. After Mn-doping in the pristine 2D monolayer MoS2 material, the band structures changed, i.e., the Fermi level (EF) shifted to −5.04 eV (with respect to the EF of the 2D pristine MoS2) and it was computationally found that the bands overlapped around the EF, as shown in Fig. 2b. The present DFT-D study showed that the Fermi level was found at −5.04 eV in the case of the 2D monolayer Mn–MoS2 with a zero band gap, indicating the conducting character of the material. Specifically, this zero-band gap suggests that the Mn-doping in the pristine TMD makes the 2D semi-conducting MoS2 material a conducting material in nature. This can also be justified by computing the electron density contribution from the 3d-subshells of the Mn atoms doped in the 2D monolayer MoS2 material (as can be seen from the d-orbital DOS at the right-hand side in Fig. 2b). Specifically, due to the addition of Mn atoms in the pristine MoS2 to form the 2D monolayer Mn–MoS2 material, the electronic band gap of Mn–MoS2 decreased to zero, as depicted in the band structures and DOS calculations in Fig. 2b. The addition of Mn to the pristine 2D TMD MoS2 changes the electron accumulation in the bands, as shown in the DOS calculations, suggesting high electron mobility and possibly good catalytic activity for the HER.
| System | Lattice constants (a = b) | Interfacial angles (α, β and γ) | Space group symmetry | Average bond distance | |
|---|---|---|---|---|---|
| Mo–S | Mn–S | ||||
| MoS2 | 3.180 Å | α = β = 90.0° and γ = 120.0° |
P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 m2 |
2.411 Å | — |
| Mn–MoS2 (3 × 3 × 1 supercell) | 9.451 Å | α = β = 90.0° and γ = 119.9 ° | P1 | 2.409 Å | 2.303 Å |
Here, it is confirmed from the electronic structure and properties calculations that the 2D monolayer Mn–MoS2 TMD material shows conducting properties (i.e., conducing in nature), and thus we proceeded with our study in the direction of theoretical and computational development of the optimum electrocatalyst. Hydrogen production from the electrolysis of water is conceived as suitable for the growing need for alternative green energy sources. In this regard, we carefully audit the fundamentals of the HER and control parameters of the kinetics of the reaction. We outline molecular simulation approaches that will help us to tackle the challenges in the design of cheap and practical catalysts.
3.2 HER recapitulation
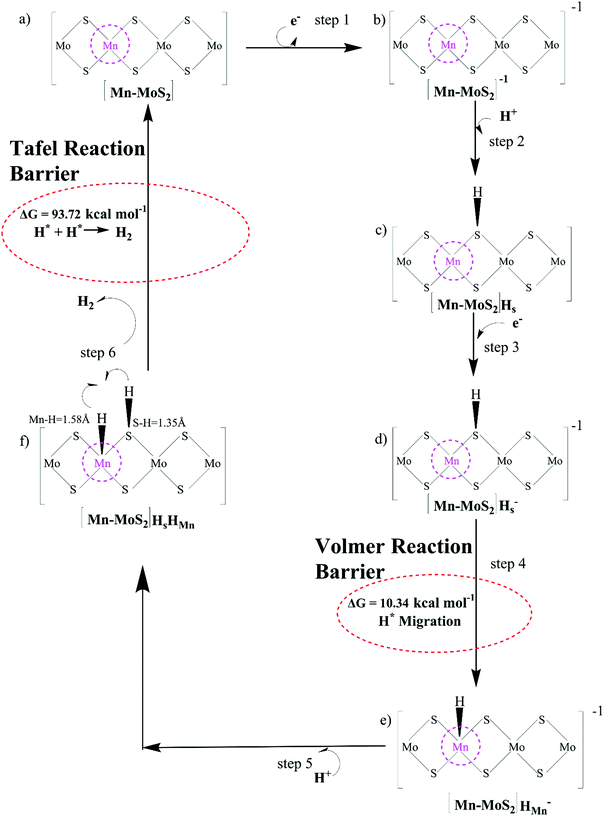
Here, we turned our attention to investigate the detailed HER mechanism by predicting energetics for the various reaction steps relevant to the HER in the case of the 2D monolayer Mn–MoS2 material. Using the molecular cluster model system of the 2D monolayer Mn–MoS2 material, we could add or subtract electrons (e−) and protons (H+) independently in the discrete H2 evolution reaction steps. Firstly, we calculated the free energies of the most likely intermediates to serve as a basis for describing the thermodynamics of the HER. Then, we examined the barriers of the various reaction steps to locate the rate-limiting step during the reactions. In general, the HER is a two-way reaction mechanism, and the most generally accepted reaction mechanism is given as follows: the HER can occur via the Volmer–Heyrovsky process or the Volmer–Tafel process, as depicted in Fig. 3. The process begins with the adsorption and dissociation of water, where initially, H2O reacts with an electron (e−) to produce H+ and OH−, which occurs at the active site of the electrocatalyst (more specifically the active surface of the electrocatalyst). The further mechanism can occur either through the Heyrovsky reaction step or the Tafel step. In the Heyrovsky reaction, the adsorbed hydride ion reacts with an adjacent water molecule or more specifically with the solvated proton of an adjacent water molecule to produce H2. In the Tafel reaction step, where two adsorbed hydrogens are adjacent to each other, they recombine to form H2 during the reaction.Generally, it has been found that the Volmer–Heyrovsky reaction mechanism is more likely to be predominant when transition metal-based catalysts are used because of their good adsorption free energy.94 Thus, the proposed catalyst was analyzed for its involvement in the mechanics and kinetics of the reaction (as mentioned in Fig. 3). To study the HER mechanism, we computationally developed a cluster model system for the 2D monolayer Mn–MoS2 and performed non-periodic M06-L DFT theory. The two processes were carefully studied and discussed further.
3.3 Volmer–Heyrovsky mechanism
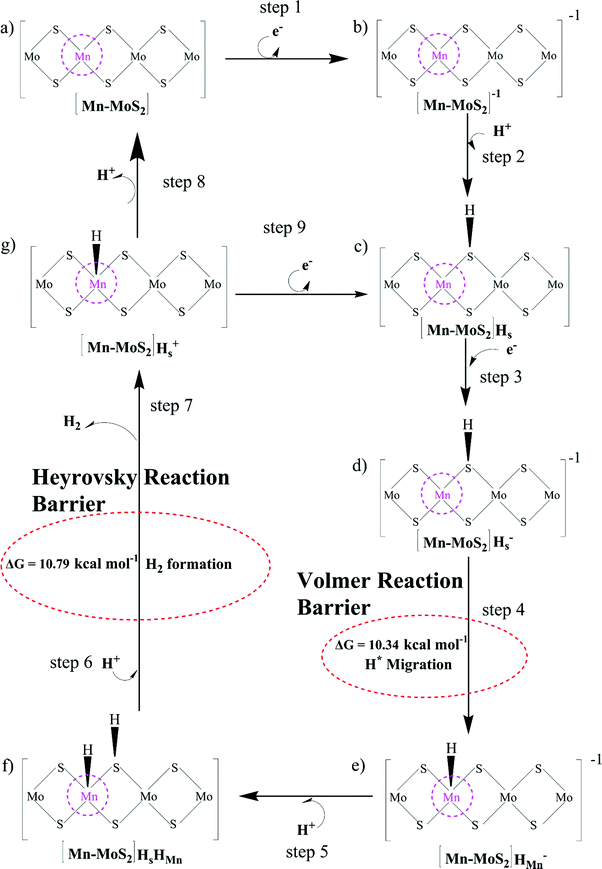
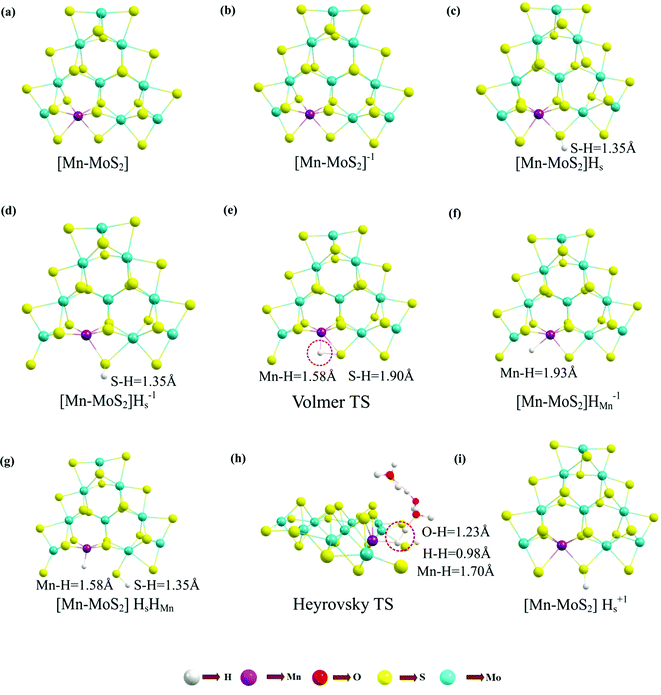
The Volmer–Heyrovsky reaction pathway in the vicinity of the active site of the 2D monolayer Mn–MoS2 TMD is schematically presented in Fig. 4. This process is a multistep electrode reaction, which is described and the reaction steps above, intermediates and transition states (TSs) occurring during the HER process are reported here.For the evolution of an H2 molecule, protons and electrons must be added to the 2D Mn–MoS2 molecular cluster Mn1Mo9S21. Here, it is useful to initially examine the most stable structures with each number of extra electrons and each number of extra protons to understand the free energy differences between the intermediate states, and ultimately find the lowest-barrier pathway. A detailed description of the HER process involved in the subject reaction is required to explain the electrochemistry. The first process is the dissociation of water in the Heyrovsky reaction step. To initiate the HER, one electron is absorbed on the surface of the 2D monolayer Mn–MoS2 TMD, as depicted in Fig. 4. This step takes place under the SHE conditions, which is the basis of the thermodynamic potentials for oxidation and reduction processes. The first reduction is achieved with a reduction potential, ΔG, about −129.66 mV, resulting in the formation of [Mn–MoS2]− from [Mn–MoS2] with the changes in enthalpy (ΔH) and electronic energy (ΔE) of about −2.93 and −2.97 kcal mol−1, respectively, as shown in Table 2. Thereafter, H+ from the solvent medium is adsorbed on the sulfur site, which is the most energetically conducive site at that time, forming an [Mn–MoS2]Hs solvated cluster (as the first adsorption of H at the Mn site has an energy cost of ΔG = 3.57 kcal mol−1, the lower barrier path is to follow [Mn–MoS2]− → [Mn–MoS2]Hs rather than the [Mn–MoS2]− → [Mn–MoS2]HMn path). In the following step, the [Mn–MoS2]Hs−1 complex is formed due to the addition of another electron from the solvent with a second reduction potential of −199.91 mV. Hence, we report this HER as a two-electron transfer reaction. In the next step, the hydride (H−) ion from the sulfur site migrates to the neighboring responsive Mn site. The migration of H˙ from the S to Mn site is the H˙-migration Volmer reaction step. This transition structure, i.e., the Volmer transition state (TS) or H˙-migration reaction TS (TS1), is corroborated by the detection of an imaginary vibrational frequency at the site of the transition of hydride ion from S to Mn. The formation of the TS was accompanied by a positive free energy change of 7.23 kcal mol−1 in the gas phase calculations. H+ from the medium again attacks, and from here either the Tafel or the Heyrovsky process can take place. The Heyrovsky part is further shown in Fig. 4. Computationally, we explicitly added a 4H2O–H+ cluster (i.e., specifically 3 water molecules and one hydronium ion (H3O+)) in the vicinity of the active site of the catalyst and observed according to the simulation that the H− from the metal site (here Mn) and the H+ from the water cluster (i.e., adjacent hydronium ion) create a bond, and then evolve as H2. This process is called the Heyrovsky process, which is often mentioned as the Heyrovsky transition state (TS2) in the reaction mechanism during HER. The Mn–S bond distance during TS2 was recorded to be 2.311 Å, which is higher than the strain free bond distance of 2.303 Å, as mentioned in Table 1. Finally, H+(H3O+) splits off to form a neutral Mn–MoS2 surface. Alternatively, an electron is absorbed to obtain the neutral [Mn–MoS2]Hs. All the optimized reaction intermediates, reactants and products with the TSs of our proposed reaction scheme are illustrated in Fig. 5.
| Reaction intermediates | ΔE (kcal mol−1) | ΔH (kcal mol−1) | ΔG (kcal mol−1) | |
|---|---|---|---|---|
| Step 1 | [Mn–MoS2] → [Mn–MoS2]−1 | −2.93 | −2.97 | −2.99 |
| Step 2 | [Mn–MoS2]−1 → [Mn–MoS2]Hs | −26.98 | −27.21 | −27.25 |
| Step 3 | [Mn–MoS2]Hs → [Mn–MoS2]Hs−1 | −2.48 | −2.91 | −4.61 |
| TS1 | [Mn–MoS2]Hs−1 → Volmer TS | 8.17 | 8.03 | 7.23 |
| Step 4 | Volmer TS → [Mn–MoS2]HMn−1 | −36.36 | −36.41 | −36.49 |
| Step 5 | [Mn–MoS2]HMn−1 → [Mn–MoS2]HsHMn | −34.67 | −35.00 | −35.19 |
| Step 6 | [Mn–MoS2]HsHMn → [Mn–MoS2]HsHMn + 4H2O_H+ | 0.04 | 0.02 | 0.01 |
| TS2 | [Mn–MoS2]HsHMn4H2O_H+ → Heyrovsky TS | 10.69 | 10.63 | 10.59 |
| Step 7 | Heyrovsky TS → [Mn–MoS2]Hs+1 | −28.20 | −28.83 | −29.38 |
We keenly followed the different reaction pathway schemes, as shown in Fig. 4, but kept our focus on the two important saddle points, i.e., the Volmer reaction where an H˙ atom migrates from S to the transition metal site (here Mn site), i.e., H˙-migration reaction TS1, and the other the Heyrovsky reaction step, where H+ from an adjacent water cluster and the H− from the Mn site recombine to form H2. It was observed that the Heyrovsky reaction step is the rate-determining step of the HER for our system of interest (i.e., 2D monolayer Mn–MoS2). The changes in free energy (ΔG), enthalpy (ΔH) and electronic energy (ΔE) at each reaction step during the HER process in the gas phase calculations are listed in Table 2. In summary, we observed that the Volmer activation barrier is about 7.23 kcal mol−1 and the H2 formation reaction barrier, i.e., Heyrovsky reaction barrier, is about 10.59 kcal mol−1 computed in the gas phase (as illustrated in Fig. 6). The values of the activation barriers for the respective steps in the gas and solvent phases, i.e., the values of ΔG during the formation of the TSs are summarized and listed in Table 3. The changes in enthalpy (ΔH) and electronic energy (ΔE) during the formation of TS1, i.e., H˙-migration TS, are 8.03 kcal mol−1 and 8.17 kcal mol−1, and similarly, the values of ΔH and ΔE during H2 formation, i.e., TS2, are 10.63 kcal mol−1 and 10.69 kcal mol−1, respectively, as reported in Table 2.
 | ||
| Fig. 6 Free energy diagram, i.e., potential energy surfaces (PES) of the Volmer–Heyrovsky reaction pathway on the surface of the 2D monolayer Mn–MoS2 material computed in the gas phase. | ||
| Activation barrier | ΔG (kcal mol−1) in the gas phase | ΔE (kcal mol−1) in the solvent phase | ΔH (kcal mol−1) in the solvent phase | ΔG (kcal mol−1) in the solvent phase |
|---|---|---|---|---|
| Volmer reaction barrier | 7.23 | 11.84 | 9.60 | 10.34 |
| Heyrovsky reaction barrier | 10.59 | 12.56 | 10.36 | 10.79 |
PCM calculations have been developed to incorporate the solvation effects during the HER. According to our present DFT calculations considering the PCM system, we predicted that the Volmer step energy barrier, i.e., the reaction barrier (ΔG) of TS1, is about 10.34 kcal mol−1 in the solvent phase with a change in electronic energy (ΔE) of about 11.84 kcal mol−1, as reported in Table 3. Recently, Yu et al.9 reported that the TS1 H˙-migration reaction energy barriers during the Volmer step in the case of 2D monolayer pristine MoS2, WS2 and the hybrid W0.4Mo0.6S2 TMD alloy are about 17.7 kcal mol−1, 18.1 kcal mol−1 and 11.9 kcal mol−1, respectively, computed in the solvent phase by considering PCM. Moreover, the Heyrovsky TS barriers for the pristine MoS2, WS2 and W0.4Mo0.6S2 TMD alloy were calculated to be 23.8 kcal mol−1, 21.3 kcal mol−1 and 13.3 kcal mol−1, respectively. In the case of the 2D monolayer Mn–MoS2 material, the calculated value of ΔG during the Heyrovsky reaction step, TS2, was 10.79 kcal mol−1 with a change of electronic energy of 12.56 kcal mol−1 in the solvent phase calculation. The changes in enthalpy (ΔH) during the formation of the TSs TS1 and TS2 computed in the solvent phase are about 9.60 and 10.36 kcal mol−1, respectively, obtained by using the M06-L DFT method. The energy barriers for the different materials are mentioned in Table 4. We reported from our DFT calculations that the proposed catalyst shows much lower activation energies during the HER, and thus the 2D monolayer Mn–MoS2 can be characterized as a highly efficient HER catalyst. Specifically, the present DFT calculations revealed that both the H˙-migration (TS1) and Heyrovsky reaction (TS2) barriers during the HER process on the active surfaces of the 2D monolayer Mn–MoS2 TMD material are the lowest compared to the other TMDs and their hybrid alloys, indicating an excellent electrocatalyst for effective H2 evolution. The potential energy surfaces (PES) of the Volmer–Heyrovsky reaction pathway for HER on the active surface of the 2D monolayer Mn–MoS2 material computed in the gas phase is shown in Fig. 6 with the values of ΔG during the reactions.
A comparison of different electrocatalysts based on their activation barriers in the reaction computed in the solvent phase can be visualized by the graphical illustration shown in Fig. 7. The figures depict that the 2D monolayer Mn–MoS2 TMD material shows the lowest activation barriers (i.e., both the Volmer and Heyrovsky reaction barriers) among the operational electrocatalysts mentioned in Table 4.
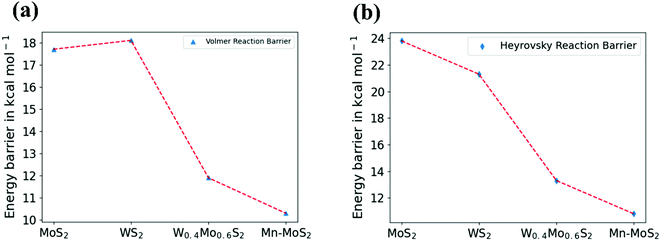 | ||
| Fig. 7 Graphical illustration of (a) Volmer and (b) Heyrovsky reaction barrier in the solvent phase for different materials. | ||
According to the transition state theory95 (TST) or the activated complex theory by including DFT calculations, we determined the turnover frequency (TOF) for H2 evolution per edge of Mn atom in the 2D monolayer Mn–MoS2 catalyst. According to the theoretical determination, we used the formula: rate = (kBT/h) × exp(−ΔG/RT);88 where kB is the Boltzmann constant, T (here 298.15 K) is temperature, h is Planck's constant, R is the universal gas constant and ΔG corresponds to the free energy barrier. The TOF obtained for the 2D monolayer Mn–MoS2 from the H2 formation reaction energy barrier in the Heyrovsky mechanism (in solvent phase) is about 7.74 × 104 s−1. A high TOF value is suitable for efficient H2 evolution during the reaction. For example, the excellent and well-functioning electrocatalyst developed by Yu et al. (hybrid W0.4M0.6S2 alloy material) showed a TOF value as high as 1.1 × 103 s−1. The TOF values of other practical catalysts such has 2D monolayer MoS2 and WS2 are mentioned in Table 5 for comparison. The 2D Mn–MoS2 material showed a very high TOF value, supporting the fact that this material will show excellent and efficient performances during the HER.
We can observe that the 2D monolayer Mn–MoS2 shows comparable results to the 2D monolayer hybrid W0.4Mo0.6S2 alloy material. Therefore, it can be concluded that the 2D Mn–MoS2 is a better and practical alternative for superb catalytic performance in the HER. Another electrochemical parameter, i.e., the Tafel slope (y) (which gives information about the kinetics, rate-determining steps of the electrochemical reaction and the energy required to achieve activity), is also one of the important factors to assess the performance of electrocatalysts. The experimentally observed Tafel slope (y) for the 1T phase of MoS2 and WS2 is about 40 mV dec−1 and 55 mV dec−1, respectively (synthesized via lithium intercalation at room temperature).96,97 The Tafel slope of another efficient and functional catalyst, MoS2 nanoparticles grown on graphene, is 41 mV dec−1, where electrochemical desorption was the rate-limiting step during hydrogen catalysis.22 The Tafel slope for the hybrid W0.4Mo0.6S2 alloy material synthesized via the wet chemical route was reported to be 38.7 mV dec−1.9 The Tafel slope can also be calculated theoretically by considering the number of electrons transferred during the HER. As stated earlier, the proposed reaction is a two-electron transfer mechanism, and thus our DFT-D computed Tafel slope was 29.58 mV dec−1 for the 2D Mn–MoS2, which is 9.12 mV dec−1 lower than that of the hybrid W0.4Mo0.6S2 alloy material, indicating that the 2D Mn–MoS2 is an excellent electrocatalyst for the HER.
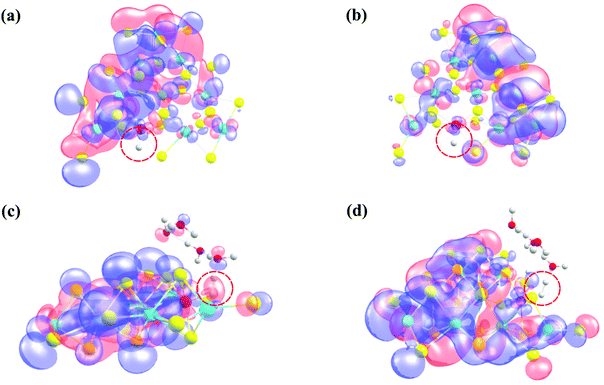
Our present computations are in strong favor of low energy barriers for both the Volmer and Heyrovsky steps in the HER using the 2D monolayer Mn–MoS2, which is a favorable candidate as an HER electrocatalyst. To further support our development, we implemented natural bond orbital (NBO), highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) calculations in the DFT analysis. These calculations were performed to show an appropriate perspective of H2 formation at the active site from an electronic charge and molecular orbital overlapping point of view. Precise Lewis structures, i.e., structures that have maximum electronic charge in their Lewis orbitals, can be found by calculating the NBO. This study conveyed the interaction density or the overlap density from the wavefunctions. The solution to a multielectron atomic system requires an approximation called the linear combination of atomic orbitals (LCAO approximation). The qualitative picture of the molecular orbital is analyzed by expanding the molecular orbital into a complete basis set of all the atomic orbitals of the nuclei. Thus, the multi-electron wavefunction in a molecule at a specific configuration of the nuclei can be given by expanding the orbital approximation to molecules. The wavefunction obtained from the NBO calculations is a linear combination of the atomic orbitals of the Mn, S, Mo and H atoms for the Volmer TS and the Mn, S, Mo, H and O atoms for the Heyrovsky TS. The HOMO–LUMO was obtained from the optimized transition structures (both Volmer and Heyrovsky transition states TS1 and TS2), as shown in Fig. 8. The red color represents the in-phase bonding of the orbitals and the blue color shows the out-of-phase bonding. The boundary value outlining the isosurface shown in Fig. 8 was set at 0.009. The interval of the values at which the isosurface is colored (from blue to red) was set from −0.1 to 0.1.
Insight can be gained into the role of the electronic structure in the HER mechanism from the HOMO calculations of the transition states and H2 formation in a steady state due to the better overlap of the d-orbital of the Mn atom and the s-orbital of H2 compared to the pristine 2D monolayer MoS2 or WS2. Therefore, one conclusion can be drawn here is that in the rate-limiting step of the HER, i.e., the Heyrovsky step, the stabilization of the atomic orbitals is also one of the key features for reducing this reaction barrier. The electron cloud around the H atoms in the Heyrovsky TS is highlighted by a red dotted circle (Fig. 8(c)). This step is supported by the overlap of the atomic orbitals of the H and Mn atoms together with H3O+ ion when H2 is evolved. This is also one of the reasons why the 2D monolayer Mn–MoS2 shows excellent activity for the HER. The energy difference between the HOMO and LUMO, also known as the HOMO–LUMO gap, is used to predict the stability of transition metal-based complexes98,99 given that it is the lowest energy electronic excitation that is possible in a molecule.
3.4 Volmer–Tafel mechanism
The proposed Volmer–Tafel reaction scheme is illustrated in Fig. 9. The Volmer–Tafel reaction steps are similar up to the formation of the [Mn–MoS2]HsHMn complex. From here the process takes place as follows: two adsorbed hydrogens on the surface of the catalyst combine and H2 is evolved. The equilibrium structure of the Volmer–Tafel transition state (TS3) can be seen in Fig. 10a.In this reaction, the adsorbed hydrogen at the sulfur site and the adsorbed hydrogen at the transition metal site combine to form H2 (2H* → H2, where H* represents hydrogen adsorbed on the active site of the catalyst). The Tafel reaction barrier (ΔG) in the gas phase was recorded to be 90.13 kcal mol−1 and 93.72 kcal mol−1 in the solvent phase, which are extremely higher than the Volmer–Heyrovsky reaction barrier. The changes in enthalpy (ΔH) and electronic energy (ΔE) during the formation of H2 in the Tafel reaction step are 92.27 kcal mol−1 and 93.66 kcal mol−1, respectively, computed by the DFT method, as reported in Table 6. The Tafel reaction barrier (ΔG) of TS3 is higher than the Heyrovsky reaction barrier TS2, indicating that the Volmer–Tafel reaction step is thermodynamically less favorable. HOMO–LUMO calculations were also performed to better visualize the Tafel reaction mechanism (Fig. 10(b) and (c), respectively). The electron cloud represents both positive and negative parts of the wavefunction in red and blue color, respectively. The electron cloud around hydrogen is highlighted by a red dotted circle. Fig. 10b presents the HOMO of the Tafel TS and the orbitals around H2 formed during the formation of the Tafel TS are highlighted by blue. This means that the orbital mixing is out of phase. The red cloud around H2 in the LUMO of the Tafel TS suggests the in-phase interaction of the electronic wavefunctions. The phase or orbital is a direct consequence of the wave-like property of electrons, where generally the in-phase mixing suggests a lower energy state and the out-of-phase mixing indicates anti-bonding orbitals or higher energy state. The corresponding TOF in both the gas and solvent phases was calculated to be 6.19 × 10−45 s−1 and 1.25 × 10−58 s−1, respectively. This TOF value is very low, and hence the process is less likely to occur.
| Activation barrier | ΔG (kcal mol−1) in the gas phase | ΔE (kcal mol−1) in the solvent phase | ΔH (kcal mol−1) in the solvent phase | ΔG (kcal mol−1) in the solvent phase |
|---|---|---|---|---|
| Volmer reaction barrier | 7.23 | 11.84 | 9.60 | 10.34 |
| Heyrovsky reaction barrier | 10.59 | 12.56 | 10.36 | 10.79 |
| Tafel reaction barrier | 90.13 | 93.66 | 92.27 | 93.72 |
It is clear from the data (Table 6) that the Tafel barrier is much higher than the calculated Heyrovsky barrier, and hence the Volmer–Heyrovsky reaction will be more dominant than the Volmer–Tafel reaction when using 2D monolayer Mn–MoS2 material-based catalysts. Therefore, heteroatom doping in the pristine 2D monolayer MoS2 will lead to a significant change in the electronic properties of the material. As shown in our present computed results, the 2D monolayer Mn–MoS2 TMD material shows an excellent electrocatalytic performance. The results of the descriptor-based method aided by DFT computations were thoroughly discussed above. This indicates that 2D Mn–MoS2 driven catalysis is a viable and efficient hydrogen production method.
4 Conclusion
In summary, we developed a 2D monolayer of Mn-doped MoS2 catalyst for the HER with the aid of DFT simulations. By applying the first-principles-based B3LYP-D3 method, we studied the electronic properties, i.e., band structure and total density of states (DOS), of this material. The DFT-D method applied to the periodic 2D slab of Mn–MoS2 showed that it has a zero band gap, and the DOS calculations showed that it became electron rich due to the addition of Mn in MoS2. In this comprehensive study, we summarized the relationship between the structure and morphology of the material that characterizes its catalytic activity. The examination of the performance of the 2D monolayer Mn–MoS2 TMD material for catalytic activity was done using the Mn1Mo9S21 molecular cluster model. The detailed reaction mechanism together with the transition states was calculated using the M06-L DFT method considering the finite non-periodic molecular cluster model system Mn1Mo9S21. The H2 evolution reaction followed two-electron transfer kinetics with the highly favorable Volmer–Heyrovsky mechanism. The Volmer and Heyrovsky barriers were computed to be 10.34 kcal mol−1 and 10.79 kcal mol−1, respectively, in the solvent phase. Lowering of the activation barrier is one of the key features of a catalyst, and the electronic overlap between the s-orbitals of H and the d-orbitals of the transition metal in TMDs favors H2 formation during the HER process. The low activation barrier energies, high TOF (7.74 × 104 s−1) and the theoretically determined Tafel slope (29.58 mV dec−1) are attributed to the electrochemical stability during HER, and the 2D monolayer Mn-doped MoS2 TMD has been demonstrated to be a promising and efficient electrocatalyst for the HER. The strategy used in this work can also be extended to model and design other low-cost and high-efficiency catalysts.Author contributions
Dr Pakhira developed the complete idea of this current research work, and he computationally studied the electronic structures and properties of the 2D Mn–MoS2 TMD. Dr Pakhira and Mr Joy Ekka explored the whole reaction pathways; transitions states and reactions barriers and Dr Pakhira explained the HER mechanism by the DFT calculations. Quantum calculations and theoretical models were designed and performed by Dr Pakhira and Mr Joy Ekka. Dr Pakhira and Mr Joy Ekka wrote the whole manuscript and prepared all the tables and figures in the manuscript. Prof. Keil edited the manuscript. Mr Shrish Nath Upadhyay helped Dr Pakhira to organize the manuscript.Conflicts of interest
The authors declare no competing financial interest. There is no conflict of interests.Acknowledgements
This work was financially supported by the Science and Engineering Research Board-Department of Science and Technology (SERB-DST), Government of India under the Grant No. ECR/2018/000255. Dr Srimanta Pakhira thanks the Science and Engineering Research Board, Department of Science and Technology (SERB-DST), Govt. of India for providing his highly prestigious Ramanujan Faculty Fellowship under the scheme no. SB/S2/RJN-067/2017, and for his Early Career Research Award (ECRA) under the grant no. ECR/2018/000255. Mr Upadhyay thanks Indian Institute of Technology Indore, MHRD, Government of India for providing the doctoral fellowship. The authors would like to acknowledge the SERB-DST for providing the computing cluster and programs. We acknowledge National Supercomputing Mission (NSM) for providing computing resources of ‘PARAM Brahma’ at IISER Pune, which is implemented by C-DAC and supported by the Ministry of Electronics and Information Technology (MeitY) and Department of Science and Technology (DST), Government of India.References
- S. E. Hosseini and M. A. Wahid, Renewable Sustainable Energy Rev., 2016, 57, 850–866 CrossRef CAS.
- R. De Levie, J. Electroanal. Chem., 1999, 476, 92–93 CrossRef CAS.
- J. Heyrovský, Recl. Trav. Chim. Pays-Bas, 1927, 46, 582–585 CrossRef.
- T. Erdey-Grúz and M. Volmer, Z. Phys. Chem., 1930, 150A, 203–213 CrossRef.
- G. T. Burstein, Corros. Sci., 2005, 47, 2858–2870 CrossRef CAS.
- N. Cheng, S. Stambula, D. Wang, M. N. Banis, J. Liu, A. Riese, B. Xiao, R. Li, T. K. Sham, L. M. Liu, G. A. Botton and X. Sun, Nat. Commun., 2016, 7, 1–9 Search PubMed.
- J. Rossmeisl, E. Skúlason, M. E. Björketun, V. Tripkovic and J. K. Nørskov, Chem. Phys. Lett., 2008, 466, 68–71 CrossRef CAS.
- G. S. Karlberg, J. Rossmeisl, T. Bligaard, J. Greeley and H. Jo, Phys. Chem. Chem. Phys., 2007, 9, 3241–3250 RSC.
- Y. Lei, S. Pakhira, K. Fujisawa, X. Wang, O. O. Iyiola, N. Perea López, A. Laura Elías, L. Pulickal Rajukumar, C. Zhou, B. Kabius, N. Alem, M. Endo, R. Lv, J. L. Mendoza-Cortes and M. Terrones, ACS Nano, 2017, 11, 5103–5112 CrossRef CAS PubMed.
- K. Liang, S. Pakhira, Z. Yang, A. Nijamudheen, L. Ju, M. Wang, G. E. Sterbinsky, Y. Du, Z. Feng, J. L. Mendoza-cortes and Y. Yang, ACS Catal., 2018, 1, 651–659 Search PubMed.
- S. Z. Qiao, Y. Zheng, Y. Jiao, M. Jaroniec and S. Z. Qiao, Angew. Chem., Int. Ed., 2014, 54, 52–65 Search PubMed.
- X. Zheng, J. Xu, K. Yan, H. Wang, Z. Wang and S. Yang, Chem. Mater., 2014, 26, 2344–2353 CrossRef CAS.
- P. Liu and J. A. Rodriguez, J. Am. Chem. Soc., 2005, 127, 14871–14878 CrossRef CAS PubMed.
- A. K. Singh, J. Prasad, U. P. Azad, A. K. Singh, R. Prakash, K. Singh, A. Srivastava, A. A. Alaferdov and S. A. Moshkalev, RSC Adv., 2019, 9, 22232–22239 RSC.
- H. Jin, C. Guo, X. Liu, J. Liu, A. Vasileff, Y. Jiao, Y. Zheng and S. Z. Qiao, Chem. Rev., 2018, 118, 6337–6408 CrossRef CAS PubMed.
- Y. Shi, Y. Zhou, D. R. Yang, W. X. Xu, C. Wang, F. Bin Wang, J. J. Xu, X. H. Xia and H. Y. Chen, J. Am. Chem. Soc., 2017, 139, 15479–15485 CrossRef CAS PubMed.
- C. Meng, X. Chen, Y. Gao, Q. Zhao, D. Kong, M. Lin, X. Chen, Y. Li and Y. Zhou, Molecules, 2020, 25, 1–18 Search PubMed.
- Y. Cheng, H. Song, H. Wu, P. Zhang, Z. Tang and S. Lu, Chem. – Asian J., 2020, 15, 3123–3134 CrossRef CAS PubMed.
- A. E. Russell, Faraday Discuss., 2008, 140, 9–10 RSC.
- L. Wu, X. Xu, Y. Zhao and K. Zhang, Appl. Surf. Sci., 2017, 425, 470–477 CrossRef CAS.
- Y. P. Venkata Subbaiah, K. J. Saji and A. Tiwari, Adv. Funct. Mater., 2016, 26, 2046–2069 CrossRef CAS.
- Y. Li, H. Wang, L. Xie, Y. Liang, G. Hong and H. Dai, J. Am. Chem. Soc., 2011, 133, 7296–7299 CrossRef CAS PubMed.
- D. Kong, H. Wang, J. J. Cha, M. Pasta, K. J. Koski, J. Yao and Y. Cui, Nano Lett., 2013, 13, 1341–1347 CrossRef CAS PubMed.
- J. Yang and H. S. Shin, J. Mater. Chem. A, 2014, 2, 5979–5985 RSC.
- Y. Yan, B. Xia, Z. Xu and X. Wang, ACS Catal., 2014, 4, 1693–1705 CrossRef CAS.
- Z. Luo, H. Zhang, Y. Yang, X. Wang, Y. Li, Z. Jin, Z. Jiang, C. Liu, W. Xing and J. Ge, Nat. Commun., 2020, 11, 1–9 Search PubMed.
- R. Ye, P. Del Angel-Vicente, Y. Liu, M. J. Arellano-Jimenez, Z. Peng, T. Wang, Y. Li, B. I. Yakobson, S. H. Wei, M. J. Yacaman and J. M. Tour, Adv. Mater., 2016, 28, 1427–1432 CrossRef CAS PubMed.
- A. Nipane, D. Karmakar, N. Kaushik, S. Karande and S. Lodha, ACS Nano, 2016, 10, 2128–2137 CrossRef CAS PubMed.
- X. Gao, G. Zhou, H. Wang, J. Yin, L. Zhang, F. Xiao, K. Siddharth, S. Zhu and M. Shao, Catalysis, 2020, 10, 1–31 Search PubMed.
- X. Shang, W. H. Hu, X. Li, B. Dong, Y. R. Liu, G. Q. Han, Y. M. Chai and C. G. Liu, Electrochim. Acta, 2017, 224, 25–31 CrossRef CAS.
- Y. Yin, J. Han, Y. Zhang, X. Zhang, P. Xu, Q. Yuan, L. Samad, X. Wang, Y. Wang, Z. Zhang, P. Zhang, X. Cao, B. Song and S. Jin, J. Am. Chem. Soc., 2016, 138, 7965–7972 CrossRef CAS PubMed.
- T. F. Jaramillo, K. P. Jørgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Science, 2007, 317, 100–102 CrossRef CAS PubMed.
- Z. Zheng, L. Yu, M. Gao, X. Chen, W. Zhou, C. Ma, L. Wu, J. Zhu, X. Meng, J. Hu, Y. Tu, S. Wu, J. Mao, Z. Tian and D. Deng, Nat. Commun., 2020, 11, 1–10 Search PubMed.
- M. Chen, X. Jian, H. Wu, J. Huang, W. Liu and Y. Liu, Nanotechnology, 2020, 31, 205403 CrossRef CAS PubMed.
- L. Zhang, M. Li, A. Zou, S. H. Yu, T. Xiong, L. Wang, J. He, Q. Fu, K. Sun, D. H. C. Chua and J. Xue, ACS Appl. Energy Mater., 2019, 2, 493–502 CrossRef CAS.
- A. D. Becke and A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Pakhira, T. Debnath, K. Sen and A. K. Das, J. Chem. Sci., 2016, 128, 621–631 CrossRef CAS.
- S. Pakhira and J. L. Mendoza-Cortes, Phys. Chem. Chem. Phys., 2019, 21, 8785–8796 RSC.
- S. Pakhira and J. L. Mendoza-Cortes, J. Phys. Chem. C, 2018, 122, 4768–4782 CrossRef CAS.
- W. Niu, S. Pakhira, K. Marcus, Z. Li and J. L. Mendoza-cortes, Adv. Energy Mater., 2018, 8, 1800480 CrossRef.
- S. Pakhira, RSC Adv., 2019, 9, 38137–38147 RSC.
- F. J. Keil, Annu. Rev. Chem. Biomol. Eng., 2018, 9, 201–227 CrossRef PubMed.
- N. Hansen, T. Kerber, J. Sauer and A. T. Bell, J. Am. Chem. Soc., 2010, 132, 11525–11538 CrossRef CAS PubMed.
- F. J. Keil, Comput. Math. Appl., 2013, 65, 1674–1697 CrossRef.
- C. Lazo and F. J. Keil, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 1–18 CrossRef.
- A. J. Freeman, J. Comput. Appl. Math., 2002, 149, 27–56 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci and J. B. Hratch, Gaussian 16 (Revision C.01), Gaussian, Inc., Wallin, 2016 Search PubMed.
- H. Li, C. Tsai, A. L. Koh, L. Cai, A. W. Contryman, A. H. Fragapane, J. Zhao, H. S. Han, H. C. Manoharan, F. Abild-Pedersen, J. K. Nørskov and X. Zheng, Nat. Mater., 2016, 15, 48–53 CrossRef CAS PubMed.
- D. C. Tranca and F. J. Keil, J. Chem. Phys., 2011, 134, 104708 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 2005, 98, 5648–5652 CrossRef.
- E. Caldeweyher, C. Bannwarth, S. Grimme, E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- S. Grimme, J. Antony, S. Ehrlich, H. Krieg, S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Pakhira, M. Takayanagi and M. Nagaoka, J. Phys. Chem. C, 2015, 119, 28789–28799 CrossRef CAS.
- S. Pakhira, K. P. Lucht and J. L. Mendoza-Cortes, J. Phys. Chem. C, 2017, 121, 21160–21170 CrossRef CAS.
- S. Pakhira, K. Sen, C. Sahu and A. K. Das, J. Chem. Phys., 2013, 138, 164319 CrossRef PubMed.
- N. Sinha and S. Pakhira, ACS Appl. Electron. Mater., 2021, 3, 720–732 CrossRef CAS.
- R. Puttaswamy, R. Nagaraj, P. Kulkarni, H. K. Beere, S. N. Upadhyay, R. G. Balakrishna, N. Sanna Kotrappanavar, S. Pakhira and D. Ghosh, ACS Sustainable Chem. Eng., 2021, 9, 3985–3995 CrossRef CAS.
- J. Hui, S. Pakhira, R. Bhargava, Z. J. Barton, X. Zhou, A. J. Chinderle, J. L. Mendoza-Cortes and J. Rodríguez-López, ACS Nano, 2018, 12, 2980–2990 CrossRef CAS PubMed.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 1–36 CAS.
- K. Sen, S. Pakhira, C. Sahu and A. K. Das, Mol. Phys., 2014, 112, 182–188 CrossRef CAS.
- S. N. Upadhyay and S. Pakhira, J. Mater. Chem. C, 2021, 9, 11331–11342 RSC.
- S. Pakhira, C. Sahu, K. Sen and A. K. Das, Struct. Chem., 2013, 24, 549–558 CrossRef CAS.
- S. Pakhira and A. K. Das, Eur. Phys. J. D, 2012, 66, 144–154 CrossRef.
- S. Pakhira, B. Mondal and A. K. Das, Chem. Phys. Lett., 2011, 505, 81–86 CrossRef CAS.
- D. Vilela Oliveira, J. Laun, M. F. Peintinger and T. Bredow, J. Comput. Chem., 2019, 40, 2364–2376 CrossRef CAS PubMed.
- M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2013, 34, 451–459 CrossRef CAS PubMed.
- F. Cora, A. Patel, N. Harrison, C. Roetti and C. Catlow, J. Mater. Chem., 1997, 7, 959–967 RSC.
- A. Montoya, T. N. Truong and A. F. Sarofim, J. Phys. Chem. A, 2000, 104, 6108–6110 CrossRef CAS.
- S. Pakhira and J. L. Mendoza-Cortes, J. Phys. Chem. C, 2020, 124, 6454–6460 CrossRef CAS.
- S. Pakhira, B. S. Lengeling, O. Olatunji-Ojo, M. Caffarel, M. Frenklach and W. A. Lester, J. Phys. Chem. A, 2015, 119, 4214–4223 CrossRef CAS PubMed.
- J. Baker, A. Scheiner and J. Andzelm, Chem. Phys. Lett., 1993, 216, 380–388 CrossRef CAS.
- S. Pakhira, K. P. Lucht and J. L. Mendoza-cortes, J. Chem. Phys., 2018, 148, 064707 CrossRef PubMed.
- J. D. Monkhorst and H. J. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- A. J. Garza, S. Pakhira, A. T. Bell, J. L. Mendoza-Cortes and M. Head-Gordon, Phys. Chem. Chem. Phys., 2018, 20, 24058–24064 RSC.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 720–723 CrossRef.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- Chemcraft – graphical software for visualization of quantum chemistry computations, https://www.chemcraftprog.com.
- Y. Huang, R. J. Nielsen, W. A. Goddard and M. P. Soriaga, J. Am. Chem. Soc., 2015, 137, 6692–6698 CrossRef CAS PubMed.
- F. Lipparini and B. Mennucci, J. Chem. Phys., 2016, 144, 160901 CrossRef PubMed.
- C. J. Fennell, L. Li and K. A. Dill, J. Phys. Chem. B, 2012, 116, 6936–6944 CrossRef CAS PubMed.
- D. R. Lide, CRC Handbook of Chemistry and Physics, 84th edn, 2004 Search PubMed.
- X. L. Fan, Y. R. An and W. J. Guo, Nanoscale Res. Lett., 2016, 11, 154–163 CrossRef PubMed.
- J. Ryou, Y. S. Kim, K. C. Santosh and K. Cho, Sci. Rep., 2016, 6, 1–8 CrossRef PubMed.
- C. Li, H. Gao, W. W. Wan and T. Mueller, Phys. Chem. Chem. Phys., 2019, 21, 24489–24498 RSC.
- P. C. Jordan and P. C. Jordan, Chem. Kinet. Transp., 1979, 269–323 Search PubMed.
- D. Voiry, M. Salehi, R. Silva, T. Fujita, M. Chen, T. Asefa, V. B. Shenoy, G. Eda and M. Chhowalla, Nano Lett., 2013, 13, 6222–6227 CrossRef CAS PubMed.
- D. Voiry, H. Yamaguchi, J. Li, R. Silva, D. C. B. Alves, T. Fujita, M. Chen, T. Asefa, V. B. Shenoy, G. Eda and M. Chhowalla, Nat. Mater., 2013, 12, 850–855 CrossRef CAS PubMed.
- R. Srinivasaraghavan, S. Thamaraikannan, S. Seshadri and T. Gnanasambandan, Spectrochim. Acta, Part A, 2015, 137, 1194–1205 CrossRef CAS PubMed.
- S. N. Upadhyay, J. A. K. Shatrughna and S. Pakhira, Emergent Mater., 2021, 4, 951–970 CrossRef CAS.
| This journal is © the Owner Societies 2022 |