A chemical dynamics study of the reaction of the methylidyne radical (CH, X2Π) with dimethylacetylene (CH3CCCH3, X1A1g)†
Chao
He‡
 a,
Kazuumi
Fujioka‡
a,
Anatoliy A.
Nikolayev‡
a,
Kazuumi
Fujioka‡
a,
Anatoliy A.
Nikolayev‡
 bc,
Long
Zhao
a,
Srinivas
Doddipatla
a,
Valeriy N.
Azyazov
bc,
Alexander M.
Mebel
bc,
Long
Zhao
a,
Srinivas
Doddipatla
a,
Valeriy N.
Azyazov
bc,
Alexander M.
Mebel
 *d,
Rui
Sun
*d,
Rui
Sun
 *a and
Ralf I.
Kaiser
*a and
Ralf I.
Kaiser
 *a
*a
aDepartment of Chemistry, University of Hawai’i at Manoa, Honolulu, Hawaii 96822, USA. E-mail: ralfk@hawaii.edu; ruisun@hawaii.edu
bLebedev Physical Institute, Samara 443011, Russia
cSamara National Research University, Samara 443086, Russia
dDepartment of Chemistry and Biochemistry, Florida International University, Miami, Florida 33199, USA. E-mail: mebela@fiu.edu
First published on 6th December 2021
Abstract
The gas-phase reaction of the methylidyne (CH; X2Π) radical with dimethylacetylene (CH3CCCH3; X1A1g) was studied at a collision energy of 20.6 kJ mol−1 under single collision conditions with experimental results merged with ab initio calculations of the potential energy surface (PES) and ab initio molecule dynamics (AIMD) simulations. The crossed molecular beam experiment reveals that the reaction proceeds barrierless via indirect scattering dynamics through long-lived C5H7 reaction intermediate(s) ultimately dissociating to C5H6 isomers along with atomic hydrogen with atomic hydrogen predominantly released from the methyl groups as verified by replacing the methylidyne with the D1-methylidyne reactant. AIMD simulations reveal that the reaction dynamics are statistical leading predominantly to p28 (1-methyl-3-methylenecyclopropene, 13%) and p8 (1-penten-3-yne, 81%) plus atomic hydrogen with a significant amount of available energy being channeled into the internal excitation of the polyatomic reaction products. The dynamics are controlled by addition to the carbon–carbon triple bond with the reaction intermediates eventually eliminating a hydrogen atom from the methyl groups of the dimethylacetylene reactant forming 1-methyl-3-methylenecyclopropene (p28). The dominating pathways reveal an unexpected insertion of methylidyne into one of the six carbon–hydrogen single bonds of the methyl groups of dimethylacetylene leading to the acyclic intermediate, which then decomposes to 1-penten-3-yne (p8). Therefore, the methyl groups of dimethylacetylene effectively ‘screen’ the carbon–carbon triple bond from being attacked by addition thus directing the dynamics to an insertion process as seen exclusively in the reaction of methylidyne with ethane (C2H6) forming propylene (CH3C2H3). Therefore, driven by the screening of the triple bond, one propynyl moiety (CH3CC) acts in four out of five trajectories as a spectator thus driving an unexpected, but dominating chemistry in analogy to the methylidyne – ethane system.
1. Introduction
The methylidyne radical (CH, X2Π) represents the simplest organic radical and has received considerable attention from the combustion science,1–14 astrochemistry,15–21 and planetary science communities13,22–27 as a highly reactive, fundamental C1 molecular growth species. Since the very first detection of the methylidyne radical in the interstellar medium (ISM) in 1937, methylidyne has been dubbed ‘ubiquitous’ in deep space and has been observed toward diffuse clouds namely ζ Per,15 molecular clouds like TMC-1,28,29 and star forming regions such as SgrB2.30–33 In hydrocarbon-rich atmospheres of planets and their moons such as Saturn's moon Titan, the methylidyne radical can be formed through Lyman-α (121.567 nm) photolysis of atmospheric methane34 and has been suggested as a critical C1-building block to extend the carbon skeleton in saturated and unsaturated hydrocarbons by one carbon atom at a time.35–42 Methylidyne can be further photo dissociated to ground state atomic carbon.43 The importance of methylidyne radicals as a critical molecular building block is also reflected in a wealth of kinetics examinations at elevated temperatures up to 700 K44–50via room temperature studies51–53 down to temperatures as low as 23 K54,55 exploiting the CRESU (Kinetics of Reactions in Uniform Supersonic Flows) technique; these studies exposed barrierless reactions with hydrocarbons with rate constants of a few 10−10 cm3 s−1. These kinetics investigations, which predominantly are short of the identification of the ‘heavy’ hydrocarbon product, called for a systematic exploration of the actual reaction products under single collision conditions exploiting crossed molecular beams.56–69 Crossed molecular beam studies of methylidyne (CH, X2Π) and D1-methylidyne (CD, X2Π) reactions with unsaturated C2–C8 hydrocarbons revealed a rich organic chemistry on the molecular level leading via atomic and also molecular hydrogen loss channels to the build-up of hydrocarbons by one carbon atom (Scheme 1).70–79 The barrierless reactions are initiated through addition of the methylidyne radical to the π-electron density of the hydrocarbon reactant followed by isomerization through ring closure, ring opening, and hydrogen migration prior to unimolecular decomposition of the doublet radical intermediates highlighted by the formation of, e.g., the cyclic hydrocarbons cyclopropenylidene (c-C3H2, X1A1),77,78 vinylcyclopropenes (C5H6, X1A′),70,71 methylcyclopropene (C4H8, X1A′),72 triafulvene (C4H4, X1A1),76 fulvenallene (C7H6, X1A1),73 and indene (C9H8, X1A′)75 along with the exotic carbenes triplet pentadiynylidene (C5H2, X3Σg−) and singlet ethynylcyclopropenylidene (c-C5H2, X1A′)74 in overall exoergic reactions.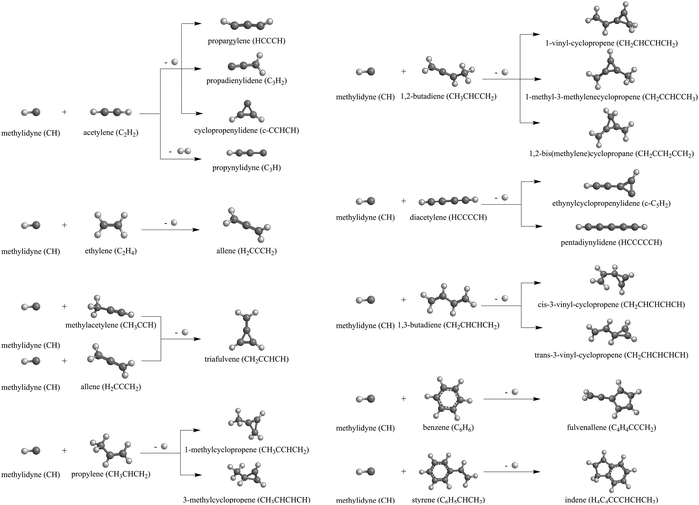 | ||
| Scheme 1 Dominant products formed in the crossed molecular beam reactions of methylidyne (CH, X2Π) radicals with unsaturated C2–C8 hydrocarbons. | ||
Here, we expand our crossed molecular beam studies of elementary reactions of methylidyne radicals and explore the chemical dynamic of the methylidyne (CH, X2Π) – dimethylacetylene (CH3CCCH3; X1A1g) system. These experiments are combined with electronic structure calculations and ab initio molecule dynamics (AIMD) simulations to expose the unexpected reaction dynamics leading predominantly to 1-penten-3-yne (p8) (81%) and 1-methyl-3-methylenecyclopropene (p28) (13%) products under single collision conditions initiated by insertion of methylidyne into a carbon–hydrogen single bond and addition of the methylidyne radical to the carbon–carbon triple bond, respectively. This behavior was quite distinguishing with the related reactions of methylidyne (CH; X2Π) radical with methylacetylene (CH3CCH, X1A1)/allene (H2CCCH2, X1A1), propylene (CH3CHCH2; X1A′), 1,3-butadiene (CH2CHCHCH2; X1Ag), and 1,2-butadiene (CH2CCHCH3; X1A′);70–72,76 the latter reactions carry similar reaction mechanism, which reveal non-RRKM behavior and are initiated dominantly through the barrierless addition of the methylidyne radical to the carbon–carbon double bonds and/or carbon–carbon triple bonds of the unsaturated carbon hydrogen reactants and eventually yield atomic hydrogen elimination products. By contrast, the interesting and surprising point of the current research on the reaction of methylidyne (CH, X2Π) radical with dimethylacetylene (CH3CCCH3, X1A1g) suggests the most active reaction pathway is the insertion of the CH radical to one of the six C–H bonds other than the addition to the triple bond of dimethylacetylene. The main product p8 (1-penten-3-yne) is statistically formed and is internally excited under our experimental conditions.
2. Method
2.1. Experimental
The reaction of the (D1-)methylidyne (CH/CD; X2Π) radical with dimethylacetylene (CH3CCCH3; X1A1g) was studied under single collision conditions in a crossed molecular beam machine at the University of Hawaii.22 The pulsed methylidyne molecular beam was carried out via photodissociation (COMPex 110, Coherent, Inc.; 248 nm; 30 Hz) of (D1)-bromoform (CHBr3/CDBr3, Aldrich Chemistry, ≥99%) seeded at a level of 0.1% in helium (99.9999%; AirGas) with a backing pressure of 2.2 atm.73,76 The methylidyne radical beam passed a skimmer and was velocity selected by a four-slot chopper wheel holding a peak velocity vp of 1826 ± 20 m s−1 and speed ratio S of 13.0 ± 1.4. The rotational temperature of the methylidyne beams were confirmed to be 14 ± 1 K through the technology of laser induced fluorescence (LIF).72 The methylidyne beam collides perpendicularly with a supersonic beam of dimethylacetylene at a collision energy EC of 20.6 ± 0.3 kJ mol−1 and a center of mass (CM) angle ΘCM of 60.5 ± 0.7° (Table 1). The pulsed dimethylacetylene reactant was formed in the secondary source chamber with vp of 776 ± 15 m s−1 and S of 9.6 ± 0.5. Each supersonic reactant beam was generated via a piezoelectric pulse valve, which was operated at a repetition rate of 60 Hz, a pulse width of 80 μs, and a peak voltage of −400 V. Considering the natural isotope abundance of carbon (12C, 98.9%; 13C 1.1%) and the potential presence of the molecular (H2) and atomic (H) hydrogen emission channels, reactive scattering signal for the bimolecular reaction of the methylidyne radical (CH; X2Π) with dimethylacetylene (CH3CCCH3; X1A1g) was probed at mass-to-charge ratios (m/z) of 67, 66, and 65. For the CD–CH3CCCH3 system, the reaction was conducted at a collision energy of EC = 21.7 ± 0.4 kJ mol−1 and a center of mass (CM) angle of ΘCM of 58.8 ± 0.5° (Table 1).| Beam | v p (m s−1) | S | E C (kJ mol−1) | Θ CM (degree) |
|---|---|---|---|---|
| CH (X2Π) | 1826 ± 20 | 13.0 ± 1.4 | 20.6 ± 0.3 | 60.5 ± 0.7 |
| CD (X2Π) | 1817 ± 14 | 13.0 ± 0.8 | 21.7 ± 0.4 | 58.8 ± 0.5 |
| CH3CCCH3 (X1A1g) | 776 ± 15 | 9.6 ± 0.5 |
The detector comprises a Brink-type ionizer,80 a quadrupole mass spectrometer (QMS), and a Daly-type ion counter81 housed within a triply differentially pumped chamber rotatable in the plane defined by both supersonic reactant beams. The neutral reaction products entering the detector are ionized via electron impact ionization (80 eV, 2 mA),80 then filtered according to their mass-to-charge ratios (m/z) through a QMS (Extrel; QC 150) operated with a 2.1 MHz oscillator, and ultimately detected by a Daly-type ion counter.81 Time-of-flight (TOF) spectra were recorded at laboratory (LAB) angles in the range of 0° ≤ Θ ≤ 69° with respect to the methylidyne radical beam (Θ = 0°). A forward-convolution routine was used to fit the laboratory data; this procedure represents an iterative method exploiting a user-defined center-of-mass (CM) translational energy P(ET) and angular T(θ) flux distributions. These functions are varied iteratively until best fits of the TOF data and angular distribution are achieved.82,83 These functions define the reactive differential cross section I(u, θ) ∼ P(u) × T(θ) with the center-of-mass velocity u.84–88 The error ranges of the P(ET) and T(θ) functions are determined within 1σ limits of the errors in the corresponding laboratory angular distribution, velocity spreads, and beam velocities, while maintaining a good fit of the laboratory TOF spectra.
2.2. Electronic structure calculations
The long-range corrected hybrid density functional ωB97X-D89 with the 6-311G(d,p) basis set was used for geometry optimization of different species on the C5H7 potential energy surface (PES) accessed by the methylidyne plus dimethylacetylene reaction, including the reactants, products, intermediates, and transition states. The same ωB97X-D/6-311G(d,p) level of theory was then employed to compute vibrational frequencies for each stationary structure. The frequencies were utilized in the evaluation of zero-point vibrational energy corrections (ZPE) and in the calculations of rate constants. In order to obtain chemically accurate relative energies of various species on the C5H7 PES, the explicitly correlated coupled clusters method with single and double excitations and with perturbative treatment of triple excitations CCSD(T)-F1290,91 in conjunction with Dunning's correlation-consistent cc-pVTZ-f12 basis set92 was used to refine single-point energies of all optimized structures. The final CCSD(T)-F12/cc-pVTZ-f12//ωB97X-D/6-311G(d,p) + ZPE(ωB97X-D/6-311G(d,p)) relative energies are anticipated to be accurate within 4 kJ mol−1 or even better.93 The GAUSSIAN 0994 and MOLPRO 201095 quantum chemistry software codes were used for the ab initio calculations.The Rice–Ramsperger–Kassel–Marcus (RRKM) approach96–98 utilizing the energetic and molecular parameters from the electronic structure calculations was employed to evaluate energy-dependent rate constants for all unimolecular reaction steps taking place on the C5H7 PES following the initial bimolecular association stage. In the calculations of the energy-dependent rate constants, the internal energy for each C5H7 intermediate or transition state was assumed to be equal to the sum of the collision and chemical activation energies, where the chemical activation energy is a negative of the relative energy of the species relative to the separated methylidyne plus dimethylacetylene reactants. The rate constants calculations were performed using our in-house Unimol code at the zero-pressure limit,99 with the aim to reproduce the crossed molecular beams conditions, which in turn emulate those in the outer space. The RRKM-computed rate constants were used to assess the reaction product branching ratios within the framework of steady-state approximation.99,100
2.3. Molecular dynamics simulations
Since ab initio molecule dynamics (AIMD) simulations demand millions of energy gradients, an accurate yet computationally efficient quantum chemistry method is essential to its success. Therefore, the potential energy profile of CCSD(T)-F12/cc-pVTZ-f12//ωB97X-D/6-311G(d,p) is employed as the benchmark to evaluate the performance of a series of affordable methods such as MP2101 and DFTs102–107 combined with a commonly used triple-zeta basis set, 6-311(d,p).108 Table S1 in the ESI† lists the potential energy profile of this reaction calculated from various candidate methods. The root mean square deviation (RMSD) between the benchmark and the potential energies (Table S2, ESI†) from a candidate methods is computed with eqn (1)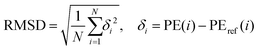 | (1) |
The AIMD simulations are set to model the conditions of the crossed molecular beams experiment. The reactant molecules, dimethylacetylene (C4H6) and the methylidyne radical (CH), are initially separated by 10 Å, sufficiently far enough that the interaction between them is negligible. The relative orientation between these two molecules is randomly sampled. The reactants are set to collide with a fixed relative translational energy of 20.6 kJ mol−1. The initial vibrational and rotational energies for dimethylacetylene (C4H6) are selected from a canonical ensemble at 10 K, respectively, while the methylidyne radical (CH) is set to be at its ground state. This setting has been shown to accurately model bimolecular collisions of similar conditions. The positions of atoms are propagated by VENUS112,113 (a chemical dynamics software) using the velocity Verlet algorithm with energy gradients calculated with B3LYP/6-311G(d,p) in NWChem114,115 (a quantum chemistry software). Most of the AIMD trajectories use a 0.2 fs time step and the conservation of the physical properties such as total energy of the system is rigorously verified. The time step is decreased to as low as 0.05 fs for some unstable trajectories, which are defined as either having energy jumps between adjacent steps greater than 4 kJ mol−1 or energy drift over the entire trajectory greater than 8 kJ mol−1 with a normal (0.2 fs) time step. The trajectories are halted once either reactants (non-reactive collision) or products (reactive collision) are formed. The trajectories are also halted once they have exceeded 8 ps. In order to accurately capture the dynamics of the experiment, the AIMD simulations need to sample a large enough number of trajectories to represent the physical ensemble of the crossed molecular beam experiment. For each collision energy, the largest impact parameter, bmax, is calculated by systematically increasing the impact parameter b. Starting from b = 0.0 Å with an increment of Δb = 1.0 Å, 40 trajectories are sampled at each impact parameter. bmax is identified as the largest b where at least one of the 40 trajectories is reactive. Further sampling of b > bmax is deemed as unnecessary for extreme low reaction probability. Since the trajectories are sampled at discrete b values, the number of trajectories at each impact parameter, N(b), needs to be proportional to its area defined by the ring, 2πbΔb. 40 trajectories are sampled at the smallest impact parameter of bmin = 1.0 Å and N(b) is computed as in eqn (2).
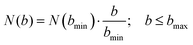 | (2) |
3. Results and discussion
3.1. Laboratory system
After scaling, the TOFs are superimposable suggesting that signal at m/z = 67, 66, and 65 originates from the same reaction channel, namely the formation of C5H6 isomers along with atomic hydrogen (reaction (R1)). Signal at m/z = 65 (C5H5+) is the result of dissociative electron impact ionization of the m/z = 66 (C5H6+) parent product(s), whereas ion counts at m/z = 67 (13CC4H6+) arose from the natural abundance of carbon atom isotopes yielding 13CC4H6 with signal collected at a level of 3 ± 1%. Since the ion counts of the parent ion m/z = 66 (C5H6+) were accumulated only at a level of 38 ± 4% compared to the fragment ion at m/z = 65 (C5H5+), the TOF spectra and the laboratory angular distributions were extracted at the best signal-to-noise ratio at m/z = 65 (C5H5+). The laboratory angular distribution is nearly symmetric around the center-of-mass angle ΘCM of 60.5° and spans the angular range from 40.25° to 67.75° in the laboratory frame (Fig. 1). These findings suggest that the CH–CH3CCCH3 reaction proceeds via indirect scattering dynamics through C5H7 reaction intermediate(s) ultimately dissociating to C5H6via hydrogen atom loss.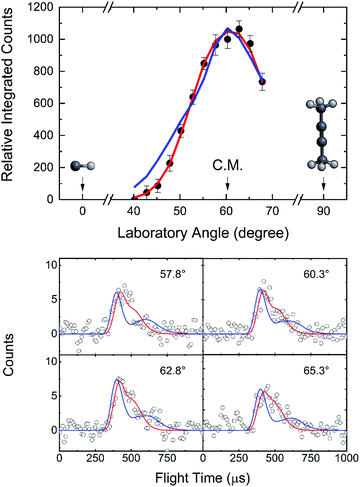 | ||
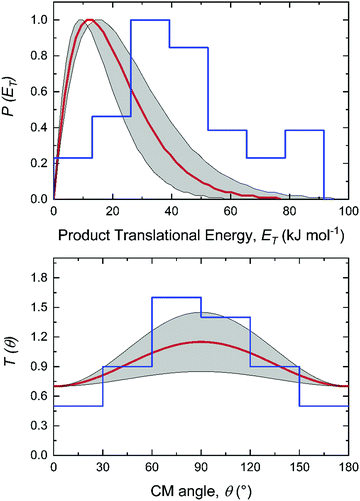
| Fig. 1 Laboratory angular distribution (top) and time-of-flight (TOF) spectra (bottom) recorded at mass-to-charge (m/z) 65 (C5H5+) from the reaction of the methylidyne radical (CH; C∞v; X2Π) with dimethylacetylene (CH3CCCH3; D3d; X1A1g). The directions of the methylidyne radical and dimethylacetylene beams are defined as 0° and 90°, respectively. The red and blue solid lines represent the best-fits exploiting center-of-mass functions depicted in Fig. 2 from the experimentally derived (red) and from the dynamics simulations (blue) with black circles defining the experimental data. | ||
Considering hydrogen atom can be emitted from the methylidyne and/or from the six chemically equivalent hydrogen atoms of the dimethylacetylene reactant, we also explored for the reaction of D1-methylidyne (CD) with dimethylacetylene to extract detailed information on the hydrogen atom loss position(s). For the CD-dimethylacetylene system, TOFs were recorded at m/z = 67 (C5DH5+) (reaction (R2)) and 66 (C5DH4+/C5H6+) (reaction (R3)) at a center-of-mass angle of 58.8° (Fig. S1, ESI†). Ion counts at m/z = 66 may also arise from dissociative electron impact ionization of C5DH5 if formed. Signal was observed both at m/z = 67 and 66 (Fig. S1, ESI†). Accounting for the 13C isotopic contribution of 5.5% for five carbon atoms, the ratio of the ion counts at m/z = 67 versus 66 is determined to be 35 ± 3%. This ratio matches the ratio of m/z = 66 to m/z = 65 in the CH–dimethylacetylene system. These findings reveal that for the CD–dimethylacetylene reaction, ion counts at m/z = 66 can be attributed to a dissociative electron impact ionization of m/z = 67 (C5DH5+) product(s) in the electron impact ionizer, whereas the C5DH5 product(s) was (were) formed via hydrogen atom loss from the dimethylacetylene reactant. Therefore, we may conclude that, in the reaction of the methylidyne radical (CH; 13 amu) with dimethylacetylene (CH3CCCH3, 54 amu), the H loss originates at least from the dimethylacetylene reactant.
| CH (13 amu) + CH3CCCH3 (54 amu) → C5H6 (66 amu) + H (1 amu) | (R1) |
| CD (14 amu) + CH3CCCH3 (54 amu) → C5DH5 (67 amu) + H (1 amu) | (R2) |
| CD (14 amu) + CH3CCCH3 (54 amu) → C5H6 (66 amu) + D (2 amu) | (R3) |
3.2. Center-of-mass system
For the methylidyne radical (CH; X2Π) – dimethylacetylene (CH3CCCH3; X1A1g) reaction, the TOF spectra and LAD (Fig. 1) can be fit with a single reaction channel CH (13 amu) + C4H6 (54 amu) → C5H6 (66 amu) + H (1 amu). The best-fit CM functions are shown in Fig. 2 with the hatched areas of the P(ET) and T(θ) representing 1σ error limits. Considering the principle of conservation of energy, the maximum energy Emax of the CM translational energy distribution P(ET) (Fig. 2), the collision energy (EC), and the reaction energy (ΔrG) are linked via Emax = EC − ΔrG for those molecules born without internal excitation. The maximum P(ET) was derived to be 77 ± 19 kJ mol−1 suggests a reaction energy of −56 ± 19 kJ mol−1 to form C5H6 isomers plus atomic hydrogen. The distribution maximum of P(ET) at 12 ± 3 kJ mol−1 hints to a rather loose exit transition state resulting to C5H6 molecules formation.116 An average translational energy of the products calculated to be 21 ± 5 kJ mol−1 reveals that only 27 ± 6% of the total available energy is channeled into the product translation degrees of freedom. These findings suggest indirect reactive scattering dynamics leading to C5H6 isomer(s) via C5H7 intermediate(s).88,117 Additional information on the reaction dynamics can be obtained by examining the CM angular distribution T(θ). The T(θ) displays non-zero intensity over the complete angular range from 0° to 180° as well as forward–backward symmetric with a maximum at 90° (sideways scattering). This forward–backward symmetry implies that the lifetime of the C5H7 intermediate is longer than its rotational period(s).118 The sideways scattering suggests significant geometrical constraints in the exit transition state with the hydrogen atom eliminated nearly perpendicular to the rotational plane of the decomposing intermediate and hence almost parallel to the total angular momentum vector.84,1193.3. Potential energy surfaces
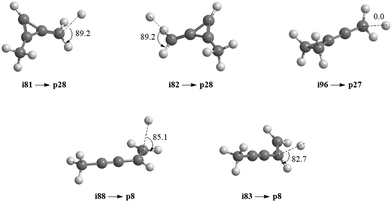
It is always beneficial to merge the experimental data with electronic structure and statistical calculations to propose the underlying reaction mechanism(s) leading to C5H6 formation (Fig. 3–8, Table 2 and Fig. S2–S5, Tables S3 and S4, ESI†). The C5H7 PES has been adapted from the methylidyne – 1,3-butadiene71 and methylidyne – 1,2-butadiene reactions systems70 and expanded to be linked to the reaction intermediates and distinct products of the reaction of methylidyne with dimethylacetylene. Overall, the methylidyne radical (CH) can add to the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond and/or insert into one of C–H bonds of dimethylacetylene involving 35 distinct C5H7 intermediates (i3–i6, i8, i15, i31, i32, i36, i45, i49, i60, i66, i68, i70, i71, i80–i97) and 91 transition states yielding hydrogen atom loss product (C5H6; p1–p3, p8, p10, p12, p27, p28, p40, p41, p41′), methyl (CH3) emission products (C4H4; p23, p39), vinyl (C2H3) group loss product (C3H4; p38), and propargyl (C3H3) emission products (C2H4; p24, p42) (Fig. 3–7). Note that, because of the background counts of CH3+, C2H3+, C2H4+, C3H3+, C3H4+, C4H4+ species originated from dissociative electron impact ionization of the dimethylacetylene reactant, C4H4/C3H4/C2H4 products formed via CH3/C2H3/C3H3 losses cannot be probed under our experimental conditions. Therefore, pathways related to the atomic hydrogen loss products are discussed here.
C bond and/or insert into one of C–H bonds of dimethylacetylene involving 35 distinct C5H7 intermediates (i3–i6, i8, i15, i31, i32, i36, i45, i49, i60, i66, i68, i70, i71, i80–i97) and 91 transition states yielding hydrogen atom loss product (C5H6; p1–p3, p8, p10, p12, p27, p28, p40, p41, p41′), methyl (CH3) emission products (C4H4; p23, p39), vinyl (C2H3) group loss product (C3H4; p38), and propargyl (C3H3) emission products (C2H4; p24, p42) (Fig. 3–7). Note that, because of the background counts of CH3+, C2H3+, C2H4+, C3H3+, C3H4+, C4H4+ species originated from dissociative electron impact ionization of the dimethylacetylene reactant, C4H4/C3H4/C2H4 products formed via CH3/C2H3/C3H3 losses cannot be probed under our experimental conditions. Therefore, pathways related to the atomic hydrogen loss products are discussed here.
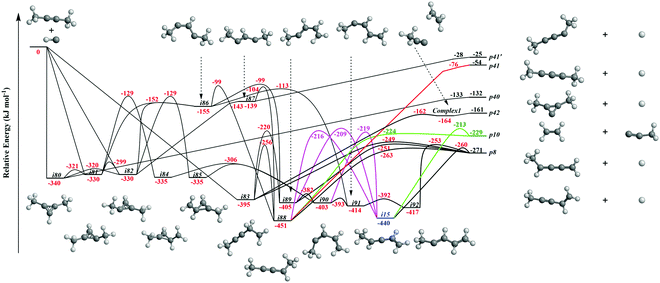 | ||
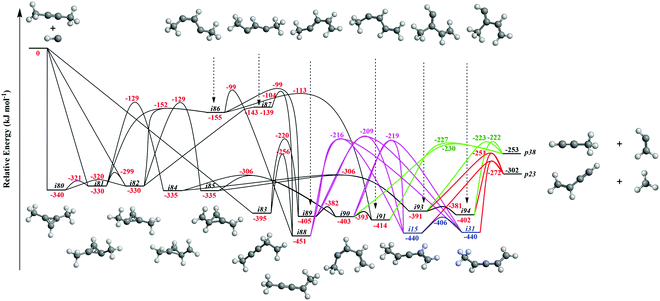
| Fig. 3 Sections of the C5H7 potential energy surface (PES) leading to p8, p10, p40, p41, p41′, and p42. | ||
| Products | Initial complexes | |||||||
|---|---|---|---|---|---|---|---|---|
| i80 | i81 | i82 | i83 | |||||
| E C = 0 | E C = 20.6 | E C = 0 | E C = 20.6 | E C = 0 | E C = 20.6 | E C = 0 | E C = 20.6 | |
| p2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.20 | 0.20 |
| p3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.15 | 0.20 |
| p8 | 0.02 | 0.00 | 0.02 | 0.00 | 0.02 | 0.00 | 91.94 | 90.10 |
| p10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 2.62 | 3.00 |
| p23 | 0.01 | 0.00 | 0.01 | 0.00 | 0.01 | 0.00 | 1.96 | 2.10 |
| p27 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.10 | 0.06 |
| p28 | 97.37 | 96.50 | 97.39 | 96.60 | 97.39 | 96.60 | 0.00 | 0.00 |
| p38 | 0.01 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.72 | 0.90 |
| p39 | 1.54 | 2.00 | 1.54 | 2.00 | 1.54 | 2.00 | 0.00 | 0.00 |
| p40 | 1.04 | 1.50 | 1.02 | 1.40 | 1.01 | 1.40 | 0.00 | 0.00 |
| p42 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 2.25 | 3.40 |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e002.gif) C bond and insertion into the C–H bond of dimethylacetylene (Fig. 3).
The calculations reveal that the CH radical can add barrierlessly to the C
C bond and insertion into the C–H bond of dimethylacetylene (Fig. 3).
The calculations reveal that the CH radical can add barrierlessly to the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond of dimethylacetylene and may insert into one of the C–H bonds of dimethylacetylene forming the three-member ring adducts i80, i81, and/or i82, and to acyclic intermediate i83, respectively. The collision complexes i80, i81, and i82 are linked through low barriers of only 19 to 41 kJ mol−1 above i80. The decomposition of intermediate i80 yields p40via atomic hydrogen emission from the cyclic C3H moiety in i80. A hydrogen atom migration from the CH3 group to the adjacent carbon atom in i81 and/or i82 forms intermediate i84 and/or i85, respectively; the opening of the three-membered ring in intermediates i81 and i82 leads to acyclic intermediates i86 and i87, respectively. The product p41′ in singlet electronic state can be formed via atomic hydrogen emission from the CH moiety in i87. The ring opening of intermediate i84 and/or i85 results in the formation of intermediate i90. Hydrogen migrations from the CH2 group in i83 to the terminal CH2 moiety and bare carbon atom lead to intermediates i88 and i89, respectively. Intermediate i88 can be formed via hydrogen migration from the CH group to the adjacent carbon atom in i86 and i87. The decomposition of the intermediate i88 leads to p41 in the triplet state via atomic hydrogen emission from the CH moiety of i88. A hydrogen migration from the terminal CH3 moiety to the adjacent carbon atom in i86 results in intermediates i89 and i91. The intermediates i89, i90, i91, and i92 are connected via low barriers of 23, 12, and 13 kJ mol−1 above i89, respectively. The hydrogen migration from the CH moiety to the adjacent carbon atom in i89 and/or i90 leads to i15; the latter can also be formed via the hydrogen migration from the terminal CH3 group to the bare carbon atom of the CH3C moiety in i88. The decomposition of intermediates i83, i88, i89, i15, and i92 would lead to the product p8via atomic hydrogen loss from the nonterminal CH2 group of i83, hydrogen atom emission from the CH3 group in CHCH3 moiety of i88, atomic hydrogen loss from the central CH group of i89, the hydrogen atom emission from CH moiety in i15, and the atomic hydrogen loss from central CH moiety in i92. Product p10 can be formed via the hydrogen atom loss from CH moiety in i15 and atomic hydrogen emission from the terminal CH3C group of i88. It should be noted that in some cases, in particular, for i80–p40, i82–i87, i87–p41′, i88–p41, transition states could be located at the DFT ωB97X-D/6-311G(d,p) level of geometry optimization, but the further energy refinement at CCSD(T)-F12/cc-pVTZ-f12 brings their energies below those of the corresponding products. For H loss reaction steps, this result means that those occur without an exit barrier, i.e., without a barrier in the reverse direction, whereas for i82–i87, the lower energy of the transition state compared to that of i87 points at instability/metastability of this intermediate.
C bond of dimethylacetylene and may insert into one of the C–H bonds of dimethylacetylene forming the three-member ring adducts i80, i81, and/or i82, and to acyclic intermediate i83, respectively. The collision complexes i80, i81, and i82 are linked through low barriers of only 19 to 41 kJ mol−1 above i80. The decomposition of intermediate i80 yields p40via atomic hydrogen emission from the cyclic C3H moiety in i80. A hydrogen atom migration from the CH3 group to the adjacent carbon atom in i81 and/or i82 forms intermediate i84 and/or i85, respectively; the opening of the three-membered ring in intermediates i81 and i82 leads to acyclic intermediates i86 and i87, respectively. The product p41′ in singlet electronic state can be formed via atomic hydrogen emission from the CH moiety in i87. The ring opening of intermediate i84 and/or i85 results in the formation of intermediate i90. Hydrogen migrations from the CH2 group in i83 to the terminal CH2 moiety and bare carbon atom lead to intermediates i88 and i89, respectively. Intermediate i88 can be formed via hydrogen migration from the CH group to the adjacent carbon atom in i86 and i87. The decomposition of the intermediate i88 leads to p41 in the triplet state via atomic hydrogen emission from the CH moiety of i88. A hydrogen migration from the terminal CH3 moiety to the adjacent carbon atom in i86 results in intermediates i89 and i91. The intermediates i89, i90, i91, and i92 are connected via low barriers of 23, 12, and 13 kJ mol−1 above i89, respectively. The hydrogen migration from the CH moiety to the adjacent carbon atom in i89 and/or i90 leads to i15; the latter can also be formed via the hydrogen migration from the terminal CH3 group to the bare carbon atom of the CH3C moiety in i88. The decomposition of intermediates i83, i88, i89, i15, and i92 would lead to the product p8via atomic hydrogen loss from the nonterminal CH2 group of i83, hydrogen atom emission from the CH3 group in CHCH3 moiety of i88, atomic hydrogen loss from the central CH group of i89, the hydrogen atom emission from CH moiety in i15, and the atomic hydrogen loss from central CH moiety in i92. Product p10 can be formed via the hydrogen atom loss from CH moiety in i15 and atomic hydrogen emission from the terminal CH3C group of i88. It should be noted that in some cases, in particular, for i80–p40, i82–i87, i87–p41′, i88–p41, transition states could be located at the DFT ωB97X-D/6-311G(d,p) level of geometry optimization, but the further energy refinement at CCSD(T)-F12/cc-pVTZ-f12 brings their energies below those of the corresponding products. For H loss reaction steps, this result means that those occur without an exit barrier, i.e., without a barrier in the reverse direction, whereas for i82–i87, the lower energy of the transition state compared to that of i87 points at instability/metastability of this intermediate.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e002.gif) C bond and insertion into the C–H bond of dimethylacetylene (Fig. 5 and 6).
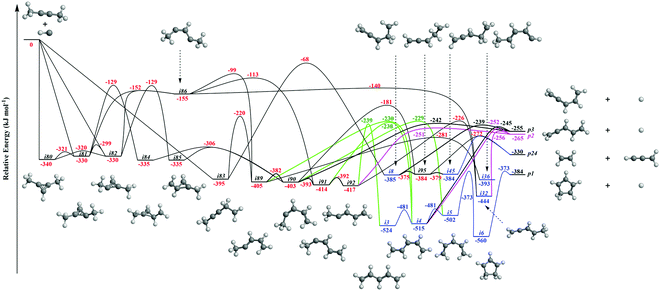
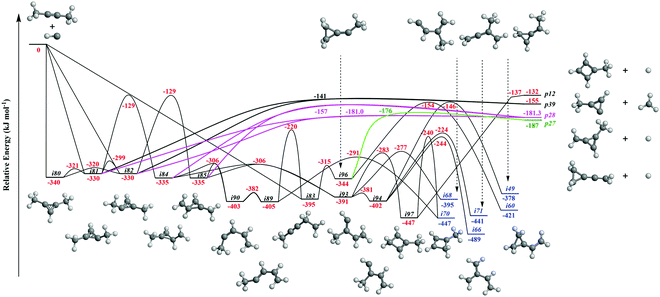
Fig. 4 illustrates reaction pathways leading to products p23 and p38 of the loss of methyl and vinyl radicals, respectively. Since only the atomic hydrogen loss products could be observed in experiment, we do not discuss these pathways here. As seen in Fig. 5, the hydrogen migration from the CH3 group to the nonadjacent bare carbon atom in i86 and/or i83 leads to i32 and i8, respectively. Product p2 can be formed via atomic hydrogen emission from the CH3 group in i32via a rather loose transition state lying 9 kJ mol−1 above the energy of the separated products. The decomposition of intermediate i8 yields p3via hydrogen atom loss from the nonterminal CH2 moiety in i8. The hydrogen shift from the CH3 group to the carbon atom in i89 leads to i4; a hydrogen shift from the CH2 group to the carbon atom in i89 yields i36. The hydrogen atom migration from the CH3 group to the carbon atom in i90, i91, and i92 can form i5, i4, and i3, respectively. The conformers i3, i4, i5 are linked via barriers of 43 kJ mol−1 above i3. The cyclic intermediate i6 can be formed via ring closure of i5. The hydrogen shift from the CH moiety to the nonadjacent bare carbon atom and/or from terminal CH3 group to the CH2 group in i92 leads to i32. Product p1 can be formed via atomic hydrogen emission from the CH2 group of i6via a loose transition state lying 11 kJ mol−1 above the separated products. The decomposition of intermediates i4, i32, and i92 yield product p2. Product p3 can be formed via hydrogen loss from the CH group of i4, from the nonterminal CH2 group of i8, and from the CH3 group of i90via loose transition states lying 10–16 kJ mol−1 above the separated products. The decomposition of intermediates i81, i82, i84, and i85 yields p28. The ring closure of i83 results in the intermediate i96. The product p27 can be formed via hydrogen atom emission from the CH3 group of i97via a loose transition state lying 11 kJ mol−1 above the separated products. The intermediate i97 can be formed via ring closure of i93; the decomposition of i97 yields the product p12via atomic hydrogen emission from the CH2 group of i97.
C bond and insertion into the C–H bond of dimethylacetylene (Fig. 5 and 6).
Fig. 4 illustrates reaction pathways leading to products p23 and p38 of the loss of methyl and vinyl radicals, respectively. Since only the atomic hydrogen loss products could be observed in experiment, we do not discuss these pathways here. As seen in Fig. 5, the hydrogen migration from the CH3 group to the nonadjacent bare carbon atom in i86 and/or i83 leads to i32 and i8, respectively. Product p2 can be formed via atomic hydrogen emission from the CH3 group in i32via a rather loose transition state lying 9 kJ mol−1 above the energy of the separated products. The decomposition of intermediate i8 yields p3via hydrogen atom loss from the nonterminal CH2 moiety in i8. The hydrogen shift from the CH3 group to the carbon atom in i89 leads to i4; a hydrogen shift from the CH2 group to the carbon atom in i89 yields i36. The hydrogen atom migration from the CH3 group to the carbon atom in i90, i91, and i92 can form i5, i4, and i3, respectively. The conformers i3, i4, i5 are linked via barriers of 43 kJ mol−1 above i3. The cyclic intermediate i6 can be formed via ring closure of i5. The hydrogen shift from the CH moiety to the nonadjacent bare carbon atom and/or from terminal CH3 group to the CH2 group in i92 leads to i32. Product p1 can be formed via atomic hydrogen emission from the CH2 group of i6via a loose transition state lying 11 kJ mol−1 above the separated products. The decomposition of intermediates i4, i32, and i92 yield product p2. Product p3 can be formed via hydrogen loss from the CH group of i4, from the nonterminal CH2 group of i8, and from the CH3 group of i90via loose transition states lying 10–16 kJ mol−1 above the separated products. The decomposition of intermediates i81, i82, i84, and i85 yields p28. The ring closure of i83 results in the intermediate i96. The product p27 can be formed via hydrogen atom emission from the CH3 group of i97via a loose transition state lying 11 kJ mol−1 above the separated products. The intermediate i97 can be formed via ring closure of i93; the decomposition of i97 yields the product p12via atomic hydrogen emission from the CH2 group of i97.
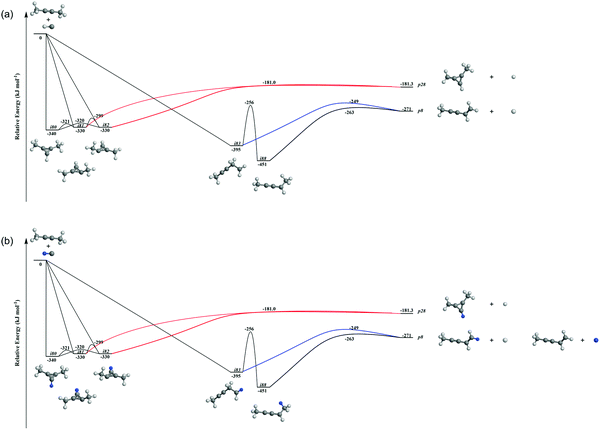
Accounting for the results of our isotopic substitution experiments showing that the hydrogen atom emission originates from the dimethylacetylene reactant, we can exclude the formation of p40, p41′, and i86 → i91 → i92 → p8; these pathways would require a hydrogen elimination from the methylidyne reactant or from both the methylidene and dimethylacetylene reactants (Fig. S2–S5, ESI†). For the initial adducts i80, i81, i82, and i83, considering significant barriers of over 180 kJ mol−1, the hydrogen shifts between i81 → i84, i82 → i85, i83 → i8 are less competitive than the decomposition of intermediates i81, i82, i83. Further, compared to lower barriers of i83 → i88, i83 → p8, i88 → p8, and isomerization of the key intermediates (i89, i90, i91, i92), the pathways i83 → i89, i88 → p41, i88 → p10, i89 → i4, i90 → i5, i90 → p3, i91 → i4, i92 → i3, i92 → i32, and i83 → i89 would carry minor contribution. Therefore, the formation of products p1, p2, p3, p12 can be ruled out. These findings suggest that p8, p27, and p28 are likely products. Recall that the best fit center-of-mass angular distribution peaked at 90° (sideways scattering); this reveals that the dominating decomposition pathway of the C5H7 intermediate(s) involve(s) a hydrogen atom ejected perpendicularly to the rotational plane of the decomposing complex nearly parallel to the total angular momentum vector. The computed geometries of the exit transition states for i81 → p28, i82 → p28, i88 → p8, and i83 → p8 can account for the sideways scattering (Fig. 7), but likely not i96 → p27. Hence, p8, and p28 are the most likely products as compiled in the reduced PES (Fig. 8). Furthermore, rather loose exit transition states for the decomposition pathways i81 → p28, i82 → p28, i88 → p8, and i83 → p8 match our experimental data well. RRKM calculations predict in case of the CH radical addition to the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond of dimethylacetylene, p28 along with atomic hydrogen to be the most likely product (97%), whereas p39 (2%), and p40 (1%) are minor products (Table 2). p8 (90%) is the main product via CH radical insertion into the C–H bond of dimethylacetylene along with p10 (3%), p23 (2%), p38 (1%), p42 (3%) being minor products. It is interesting to note that the computed reaction energies for the formation of the dominating products formed via addition (p28, 97%) and insertion (p8, 90%) are −181 and −271 kJ mol−1, respectively. These exoergicities do not correlate with our experimentally determined reaction energy of −56 ± 19 kJ mol−1. This could mean that the reaction dynamics are non-statistical and a thermodynamically less stable product is formed or that the reaction are statistically leading to p28 and/or p8, but a significant amount of available energy is channeled into internal excitation of the polyatomic reaction products. This would in turn lead to a shift of the maximum energy release to values significantly lower than in the limit of zero internal excitation. To discriminate between these two possibilities, quasiclassical trajectory (QCT) studies of the CH–CH3CCCH3 system are conducted.
C bond of dimethylacetylene, p28 along with atomic hydrogen to be the most likely product (97%), whereas p39 (2%), and p40 (1%) are minor products (Table 2). p8 (90%) is the main product via CH radical insertion into the C–H bond of dimethylacetylene along with p10 (3%), p23 (2%), p38 (1%), p42 (3%) being minor products. It is interesting to note that the computed reaction energies for the formation of the dominating products formed via addition (p28, 97%) and insertion (p8, 90%) are −181 and −271 kJ mol−1, respectively. These exoergicities do not correlate with our experimentally determined reaction energy of −56 ± 19 kJ mol−1. This could mean that the reaction dynamics are non-statistical and a thermodynamically less stable product is formed or that the reaction are statistically leading to p28 and/or p8, but a significant amount of available energy is channeled into internal excitation of the polyatomic reaction products. This would in turn lead to a shift of the maximum energy release to values significantly lower than in the limit of zero internal excitation. To discriminate between these two possibilities, quasiclassical trajectory (QCT) studies of the CH–CH3CCCH3 system are conducted.
3.4. Molecular dynamics simulations
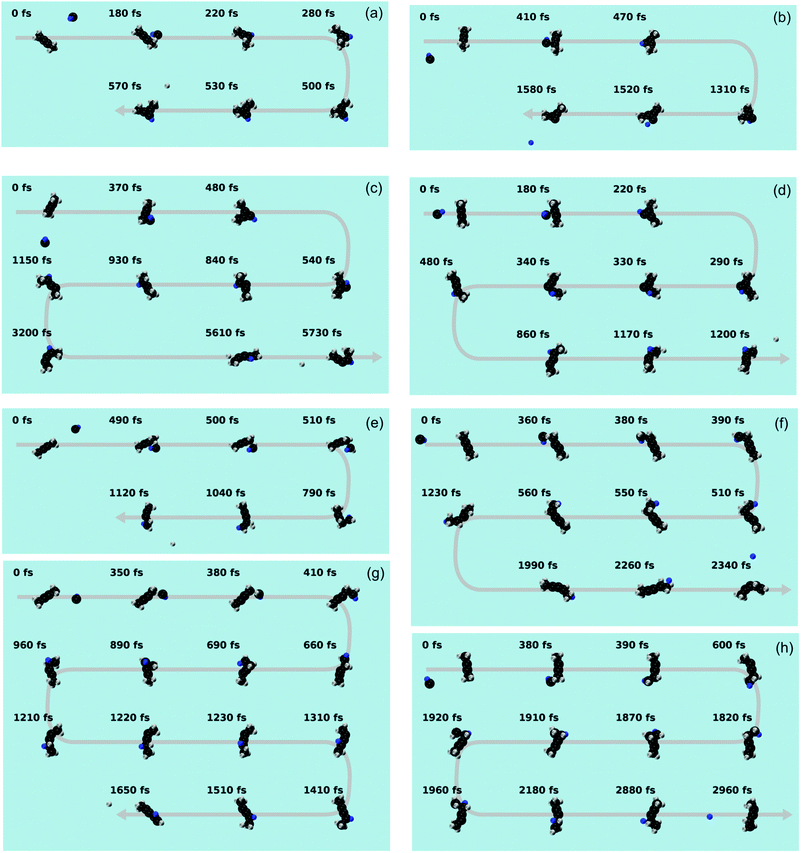
Considering the aforementioned open questions, ab initio molecule dynamics (AIMD) simulations are employed to probe the dynamics of the reaction of the methylidyne radical with dimethylacetylene.111 As discussed in Section 2.3, B3YLP/6-311G(d,p) theory is utilized for the AIMD simulations after carefully calibrating this level of theory with the benchmark potential energy profile. It is important to note that due to the excess energy, geometries observed in the trajectories are nearly all non-optimized structures deviating from those reported in the potential energy surface; however, for the conciseness of the manuscript, a trajectory is regarded as to have “visited” an intermediate over some period of time, if its geometries oscillate around the optimized structures of the intermediate. In this way, by labeling the sequence of the intermediates that a trajectory has visited over the whole course of the trajectory, the lifetime of the intermediates and reaction mechanism can be analyzed.The products of the AIMD simulations of the bimolecular collision between dimethylacetylene and methylidyne radicals are summarized in Fig. 9(a). Since the number of trajectories at each impact parameter has been properly controlled as detailed in Section 2.3, the fraction reported in Fig. 9(a) can be interpreted as the product branching ratio. As observed in the experiments, the simulations reveal that the hydrogen loss products, including p8, p28, p10, and p40 represent the majority of the products of this reaction. The analysis of the minor products is beyond the scope of this manuscript. The snapshots of representative AIMD trajectories can be found in Fig. 10. The AIMD simulations show that none of the hydrogen atom loss trajectories are direct; in other words, all of them involve indirect scattering dynamics viai80–i82 through addition or i83 through insertion-triggered hydrogen transfer before forming the products p8, p28, p10, and p40. Among these trajectories, the overall observed ratio between the i80–i82vs.i83 entrance-channel complexes is about 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, i.e., the dominance of insertion versus addition; its dependence on the impact parameter can be seen in Fig. 9(b). It is interesting to note that the amount of i80–i82 in the entrance-channel is nearly independent on the impact parameter except for the largest value (5 Å), where the methylidyne is too far away from the center of the dimethylacetylene to trigger addition of methylidyne to the carbon–carbon triple bond. In contrast, the amount of i83 in the entrance channel demonstrates a sharp peak at an impact parameter of 3 Å, which is nearly half of the length of dimethylacetylene, which facilitates the insertion of methylidyne into the methyl group.
4, i.e., the dominance of insertion versus addition; its dependence on the impact parameter can be seen in Fig. 9(b). It is interesting to note that the amount of i80–i82 in the entrance-channel is nearly independent on the impact parameter except for the largest value (5 Å), where the methylidyne is too far away from the center of the dimethylacetylene to trigger addition of methylidyne to the carbon–carbon triple bond. In contrast, the amount of i83 in the entrance channel demonstrates a sharp peak at an impact parameter of 3 Å, which is nearly half of the length of dimethylacetylene, which facilitates the insertion of methylidyne into the methyl group.
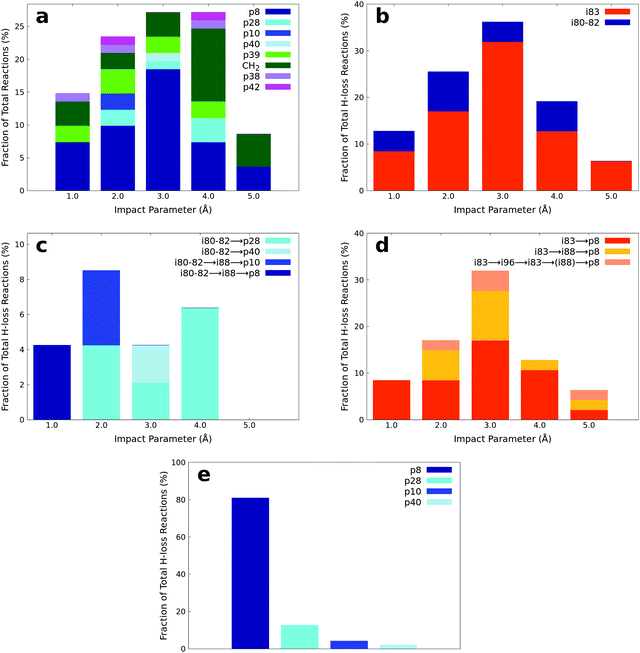 | ||
| Fig. 9 (a) Fractions of products predicted to be formed from AIMD simulations at various impact parameters. Note that ‘CH2’ (Fig. 9a) corresponds to the channel forming H2CCCCH3 plus CH2. (b) The fraction of two entrance channels leading to i80–i82vs.i83 trough addition versus insertion and eventually to p28, p40, p10, and p8 at various impact parameters. (c) The fraction of different reaction pathways traversing through the i80–i82 entrance channel at various impact parameters. (d) The fraction of different reaction pathways traversing through the i83 entrance channel at various impact parameters. (e) The fraction of various hydrogen atom loss products integrated over all impact parameters. | ||
The statistics of the trajectories traversing through i80–82 are illustrated in Fig. 9(c). About 60% of the trajectories form p28 (i80–82 → p28; SA1.mp4 (ESI†) for the animation of a representative trajectory) and 10% p40 (i80–82 → p40, SA2.mp4, ESI†). The remaining 30% of the trajectories isomerize to i88 before dissociating to products p10 (i80–82 → i88 → p10, SA3.mp4, ESI†) and p8 (i80–82 → i88 → p8, SA4.mp4, ESI†) with a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. These pathways reveal a strong impact parameter dependence. For example, the pathways involving i88 are only observed at low impact parameters of 1 and 2 Å, while p40 is only formed at large impact parameters of 3 Å.
1. These pathways reveal a strong impact parameter dependence. For example, the pathways involving i88 are only observed at low impact parameters of 1 and 2 Å, while p40 is only formed at large impact parameters of 3 Å.
In contrast, among those trajectories passing through i83, only one product (p8) is observed. As Fig. 9(d) shows, about 61% of those trajectories lose a hydrogen atom and form p8 (i83 → p8, SA5.mp4, ESI†), about 28% isomerize to i88 before forming p8 (i83 → i88 → p8, SA6.mp4, ESI†), and the remaining fraction of 11% isomerizes back and forth viai96 before forming p8 with (i83 (↔i96) → i88 → p8, SA7.mp4, ESI†) or without (i83 (↔i96) → p8, SA8.mp4, ESI†) eventually isomerizing to i88. The i83 → p8 pathway is the predominant pathway in almost all impact parameters except for the largest one. Comparing the i83 entrance channel (Fig. 9(d)) to the i80–82 entrance channel (Fig. 9(c)), it is interesting to note that p8 can be formed in all impact parameter trajectories, in contrast to only the smallest (1 Å) in the latter.
It is essential to verify the validity of the results from dynamics simulations with experiments and RRKM calculations. The branching ratio of the hydrogen loss products is depicted in Fig. 9(e). As shown, AIMD simulations report that the final hydrogen loss product distribution is predominantly p8 (81.0%) followed by p28 (12.7%) and trace amounts of p10 (4.3%) and p40 (2.0%). The product p8 (100%) is the sole products through the i83 entrance channel along with the dominant pathways i83 → p8 (∼61%) and i83 → i88 → p8 (∼28%), whereas p28 (∼60%), p40 (∼10%), p10 and p8 (∼30%) are the products via the i80–i82 entrance channel through pathways i80–i82 → p28 (∼60%). These findings match the experimental results derived from the comparison of the geometries of the exit transition states with the experimentally observed sideways scattering (p8, p10, and p28; Fig. 8) and RRKM calculations (Table 2), which predicts p28 (99%) and p40 (1%) in case of the methylidyne radical addition to the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond of dimethylacetylene; p8 (97%) and p10 (3%) via methylidyne radical insertion into the C–H bond of dimethylacetylene. The distribution of the relative translational energy of all four observed hydrogen atom loss products is summarized in Fig. 2. Although demonstrating a similar trend and matching the experimentally derived maximum translational energy, the AIMD simulations overestimate the most probable (AIMD: 40 ± 8 kJ mol−1, exp: 12 ± 3 kJ mol−1) relative translational energy of the products. Considering that our experimentally determined reaction energy of −56 ± 19 kJ mol−1 does not correlate with the computed reaction energies of the dominating products formed via addition (p28, −181 ± 4 kJ mol−1) and insertion (p8, −271 ± 4 kJ mol−1), the AIMD simulations verified that the reaction dynamics are statistical leading to p28 and/or p8, but a significant amount of available energy is channeled into internal excitation of the polyatomic reaction products. Another factor is an artifact of AIMD; as stated in Section 2.3, AIMD simulation are halted when the products/reactants are formed, or the length of the trajectories has exceeded 8 ps due to the computation cost. As such, small portion of trajectories are stopped when still trapped in an intermediate. Due to the excess energy in the system, these trajectories will eventually dissociate given unlimited computing power, which would have be considered as long-lived, indirect trajectories that render products of low relative translational energy. Both factors result in a shift of the maximum energy release to values significantly lower than in the limit of zero internal excitation. In regard to the CM angular distribution, the AIMD simulations show “sideways scattering” (Fig. 2), which is in remarkable agreement with the experiments. These CM functions (Fig. 2) derived from the dynamics simulations fail to fit the TOF data and the laboratory angular distribution well (Fig. 1); this is predominantly due to the distribution maximum in the center-of-mass translational energy distribution, which is shifted to higher energies compared to the experimental data. This in turn leads to simulated TOFs which are too fast and also to a simulated LAB distribution which is too broad compared to the experimental findings. Further, the individual CM functions of each dominant product channels to p8 and p28 are also compared with the experimental results (Fig. S6–S10, ESI†). Considering the center-of-mass translational energy distributions, a similar maximum translational energy of p8 is revealed in AIMD simulations (98 kJ mol−1) and in the experimental results (77 ± 19 kJ mol−1) (Fig. S7, ESI†). However, the AIMD simulations predict the most probable relative translational energy of p8 to be 41 ± 8 kJ mol−1 compared with experimental results of 12 ± 3 kJ mol−1. Both AIMD simulations and experimental results featured with “sideway scattering” of CM angular distribution T(θ) of p8 (Fig. S7, ESI†). The CM functions of p8 (Fig. S7, ESI†) from the AIMD simulations fit the TOF data and the laboratory angular distribution well (Fig. S6, ESI†). For the formation of p28, the AIMD simulations reveal the relative translational energy distribution P(ET) of p28 terminated at about 65 kJ mol−1 which is in good agreement with 77 ± 19 kJ mol−1 from the experiments (Fig. S9, ESI†). The distribution maximum of P(ET) of p28 in AIMD simulations is 33 ± 16 kJ mol−1, once again higher than the experimental value of 12 ± 3 kJ mol−1 (Fig. S9, ESI†). The CM angular distribution T(θ) of p28 (Fig. S9, ESI†) derived in the AIMD simulations and experimental results are both characterized as “sideway scattering”, but AIMD simulations also carries a slightly backward scattering. The difference of the CM functions between AIMD simulations and the experimental results leads to the deviation to fit the TOF data and the laboratory angular distribution (Fig. S8, ESI†).
C bond of dimethylacetylene; p8 (97%) and p10 (3%) via methylidyne radical insertion into the C–H bond of dimethylacetylene. The distribution of the relative translational energy of all four observed hydrogen atom loss products is summarized in Fig. 2. Although demonstrating a similar trend and matching the experimentally derived maximum translational energy, the AIMD simulations overestimate the most probable (AIMD: 40 ± 8 kJ mol−1, exp: 12 ± 3 kJ mol−1) relative translational energy of the products. Considering that our experimentally determined reaction energy of −56 ± 19 kJ mol−1 does not correlate with the computed reaction energies of the dominating products formed via addition (p28, −181 ± 4 kJ mol−1) and insertion (p8, −271 ± 4 kJ mol−1), the AIMD simulations verified that the reaction dynamics are statistical leading to p28 and/or p8, but a significant amount of available energy is channeled into internal excitation of the polyatomic reaction products. Another factor is an artifact of AIMD; as stated in Section 2.3, AIMD simulation are halted when the products/reactants are formed, or the length of the trajectories has exceeded 8 ps due to the computation cost. As such, small portion of trajectories are stopped when still trapped in an intermediate. Due to the excess energy in the system, these trajectories will eventually dissociate given unlimited computing power, which would have be considered as long-lived, indirect trajectories that render products of low relative translational energy. Both factors result in a shift of the maximum energy release to values significantly lower than in the limit of zero internal excitation. In regard to the CM angular distribution, the AIMD simulations show “sideways scattering” (Fig. 2), which is in remarkable agreement with the experiments. These CM functions (Fig. 2) derived from the dynamics simulations fail to fit the TOF data and the laboratory angular distribution well (Fig. 1); this is predominantly due to the distribution maximum in the center-of-mass translational energy distribution, which is shifted to higher energies compared to the experimental data. This in turn leads to simulated TOFs which are too fast and also to a simulated LAB distribution which is too broad compared to the experimental findings. Further, the individual CM functions of each dominant product channels to p8 and p28 are also compared with the experimental results (Fig. S6–S10, ESI†). Considering the center-of-mass translational energy distributions, a similar maximum translational energy of p8 is revealed in AIMD simulations (98 kJ mol−1) and in the experimental results (77 ± 19 kJ mol−1) (Fig. S7, ESI†). However, the AIMD simulations predict the most probable relative translational energy of p8 to be 41 ± 8 kJ mol−1 compared with experimental results of 12 ± 3 kJ mol−1. Both AIMD simulations and experimental results featured with “sideway scattering” of CM angular distribution T(θ) of p8 (Fig. S7, ESI†). The CM functions of p8 (Fig. S7, ESI†) from the AIMD simulations fit the TOF data and the laboratory angular distribution well (Fig. S6, ESI†). For the formation of p28, the AIMD simulations reveal the relative translational energy distribution P(ET) of p28 terminated at about 65 kJ mol−1 which is in good agreement with 77 ± 19 kJ mol−1 from the experiments (Fig. S9, ESI†). The distribution maximum of P(ET) of p28 in AIMD simulations is 33 ± 16 kJ mol−1, once again higher than the experimental value of 12 ± 3 kJ mol−1 (Fig. S9, ESI†). The CM angular distribution T(θ) of p28 (Fig. S9, ESI†) derived in the AIMD simulations and experimental results are both characterized as “sideway scattering”, but AIMD simulations also carries a slightly backward scattering. The difference of the CM functions between AIMD simulations and the experimental results leads to the deviation to fit the TOF data and the laboratory angular distribution (Fig. S8, ESI†).
Finally, the origin of the hydrogen atom – either from dimethylacetylene or methylidyne reactant – in the atomic hydrogen loss pathways is also analyzed; the results are summarized in Table 3. As shown, AIMD trajectories show that over 90% of the hydrogen atom in the hydrogen atom loss pathways originates from the methyl groups of the dimethylacetylene reactant, which is in agreement with the experiment exploiting D1-methylidyne radical reactants.
| Products | Impact parameter (A) | Overall (%) | ||||
|---|---|---|---|---|---|---|
| 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | ||
| H-loss | 0 | 8.3 | 17.6 | 0 | 33.3 | 10.6 |
| p8 | 0 | 12.5 | 13.3 | 0 | 33.3 | 10.5 |
| p28 | — | 0 | 0 | 0 | — | 0 |
| p10 | — | 0 | — | — | — | 0 |
| p40 | — | — | 100 | — | — | 100 |
4. Conclusion
Our crossed molecular beam experiment of the methylidyne (CH; X2Π) radical with dimethylacetylene (CH3CCCH3; X1A1g) reveals that the reaction proceeds barrierlessly via indirect scattering dynamics through long-lived C5H7 reaction intermediate(s) ultimately dissociating to C5H6 isomers along with atomic hydrogen. Experiments were also conducted by replacing the CH with CD; these studies revealed that in the methylidyne–dimethylacetylene reaction, the hydrogen atom is lost predominantly from the methyl groups of the dimethylacetylene reactant. The center of mass functions suggest an overall reaction energy of −56 ± 19 kJ mol−1 with the CM angular distribution T(θ) depicting a “sideway scattering” and hence a hydrogen atom loss predominantly parallel to the total angular momentum vector. Ab initio electronic structure and statistical Rice–Ramsperger–Kassel–Marcus (RRKM) calculations suggest that 1-penten-3-yne (p8) and 1-methyl-3-methylenecyclopropene (p28) are the most likely atomic hydrogen loss products. The reaction has no entrance barrier; all barriers involved in the formation of 1-penten-3-yne (p8) and 1-methyl-3-methylenecyclopropene (p28) are well below the energy of the separated reactants, and the overall reactions to prepare both isomers are exoergic by −181 ± 4 kJ mol−1 (p28) and −271 ± 4 kJ mol−1 (p8), respectively. These energetics do not match the experimentally derived reaction energy of −56 ± 19 kJ mol−1, suggesting that the reaction is either non-statistical or that a significant amount of the energy is channeled into the internal rovibrational modes of the heavy products. To untangle the actual reaction pathways, AIMD simulations were carried out. The latter verified that the reaction dynamics are statistical leading predominantly to p28 (13%) and p8 (81%), but a significant amount of available energy is channeled into the internal excitation of the polyatomic reaction products. The dynamics are controlled by addition to the carbon–carbon triple bond with the reaction intermediates i80, i81, and i82 eventually eliminating a hydrogen atom from the methyl groups of the dimethylacetylene reactant forming 1-methyl-3-methylenecyclopropene p28 (13%). The dominating pathways reveal an unexpected insertion of methylidyne into one of the six carbon-hydrogen single bonds of the methyl groups of dimethylacetylene leading to the acyclic intermediate i83; intermediate i88 is formed via hydrogen atom shift in i83; the decomposition of i83 and i88 lead to 1-penten-3-yne (p8, −271 ± 4 kJ mol−1) – also called 1-vinylmethylacetylene – with relative fractions of p8 formation of 66% from i83 and 34% from i88. Since the involvement of i88 is expected in the release of atomic hydrogen and atomic deuterium (Fig. 8), the low percentage of i88 in the formation of p8 is also supported by the experimental findings of the D1-methylidyne–dimethylacetylene reaction. Therefore, the methyl groups of dimethylacetylene effectively ‘screen’ the carbon–carbon triple bond from being attacked by addition (i80, i81, i82) thus directing the dynamics to an insertion process forming i83. The AIMD simulations suggest that the overall ratio in the entrance channel of insertion (i80–i82) vs. addition (i83) is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, while the ratio between the final hydrogen loss products p8vs.p28 is about 6
4, while the ratio between the final hydrogen loss products p8vs.p28 is about 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. These findings propose that the combination of the crossed molecular beam experiments with electronic structure calculations and quasiclassical trajectory (QCT) studies provide persuasive evidence on the formation of 1-penten-3-yne (p8) and 1-methyl-3-methylenecyclopropene (p28) under single collision conditions via the bimolecular reaction of the methylidyne radical with dimethylacetylene in the gas phase involving indirect scattering dynamics.
1. These findings propose that the combination of the crossed molecular beam experiments with electronic structure calculations and quasiclassical trajectory (QCT) studies provide persuasive evidence on the formation of 1-penten-3-yne (p8) and 1-methyl-3-methylenecyclopropene (p28) under single collision conditions via the bimolecular reaction of the methylidyne radical with dimethylacetylene in the gas phase involving indirect scattering dynamics.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U.S. Department of Energy, Basic Energy Sciences DE-FG02-03ER15411 and DE-FG02-04ER15570 to the University of Hawaii and to Florida International University, respectively. Ab initio calculations at Lebedev Physics Institute were supported by the Ministry of Science and Higher Education of the Russian Federation under Grant No. 075-15-2021-597.References
- C. E. Otis, J. L. Knee and P. M. Johnson, J. Chem. Phys., 1983, 78, 2091–2092 CrossRef CAS
.
- N. Nakashima and K. Yoshihara, J. Chem. Phys., 1982, 77, 6040–6050 CrossRef CAS
.
- H. R. Ward and J. S. Wishnok, J. Am. Chem. Soc., 1968, 90, 5353–5357 CrossRef CAS
.
- J. P. Reilly and K. L. Kompa, J. Chem. Phys., 1980, 73, 5468–5476 CrossRef CAS
.
- W. Radloff, T. Freudenberg, H.-H. Ritze, V. Stert, F. Noack and I. V. Hertel, Chem. Phys. Lett., 1996, 261, 301–306 CrossRef CAS
.
- J. Park, R. Bersohn and I. Oref, J. Chem. Phys., 1990, 93, 5700–5708 CrossRef CAS
.
- J. K. Foote, M. H. Mallon and J. N. Pitts Jr, J. Am. Chem. Soc., 1966, 88, 3698–3702 CrossRef CAS PubMed
.
- H. R. Ward and P. D. Sherman, J. Am. Chem. Soc., 1967, 89, 1962–1963 CrossRef CAS
.
- L. Kaplan and K. E. Wilzbach, J. Am. Chem. Soc., 1967, 89, 1030–1031 CrossRef CAS
.
- L. Kaplan, S. P. Walch and K. E. Wilzbach, J. Am. Chem. Soc., 1968, 90, 5646–5647 CrossRef CAS
.
- F. Mellows and S. Lipsky, J. Phys. Chem., 1966, 70, 4076–4077 CrossRef CAS
.
- A. Yokoyama, X. Zhao, E. J. Hintsa, R. E. Continetti and Y. T. Lee, J. Chem. Phys., 1990, 92, 4222–4233 CrossRef CAS
.
- L. K. Madden, A. M. Mebel, M.-C. Lin and C. F. Melius, J. Phys. Org. Chem., 1996, 9, 801–810 CrossRef CAS
.
- A. M. Mebel, M.-C. Lin, T. Yu and K. Morokuma, J. Phys. Chem. A, 1997, 101, 3189–3196 CrossRef CAS
.
- H. Wiesemeyer, R. Güsten, K. M. Menten, C. A. Durán, T. Csengeri, A. M. Jacob, R. Simon, J. Stutzki and F. Wyrowski, Astron. Astrophys., 2018, 612, A37 CrossRef
.
- M. Gerin, M. De Luca, J. R. Goicoechea, E. Herbst, E. Falgarone, B. Godard, T. A. Bell, A. Coutens, M. Kazmierczak, P. Sonnentrucker, J. H. Black, D. A. Neufeld, T. G. Phillips, J. Pearson, P. B. Rimmer, G. Hassel, D. C. Lis, C. Vastel, F. Boulanger, J. Cernicharo, E. Dartois, P. Encrenaz, T. Giesen, P. F. Goldsmith, H. Gupta, C. Gry, P. Hennebelle, P. Hily-Blant, C. Joblin, R. Koos, J. Kreowski, J. Matrín-Pintado, R. Monje, B. Mookerjea, M. Perault, C. Persson, R. Plume, M. Salez, M. Schmidt, J. Stutzki, D. Teyssier, S. Yu, A. Contursi, K. Menten, T. R. Geballe, S. Schlemmer, P. Morris, W. A. Hatch, M. Imram, J. S. Ward, E. Caux, R. Güsten, T. Klein, P. Roelfsema, P. Dieleman, R. Schieder, N. Honingh and J. Zmuidzinas, Astron. Astrophys., 2010, 521, L16 CrossRef
.
- A. C. Danks, S. R. Federman and D. L. Lambert, Astron. Astrophys., 1984, 130, 62–66 CAS
.
- B. H. Andrew, L. W. Avery and N. W. Broten, Astron. Astrophys., 1978, 66, 437–439 CAS
.
- M. Sumitani, D. V. O'Connor, Y. Takagi, N. Nakashima, K. Kamogawa, Y. Udagawa and K. Yoshihara, Chem. Phys., 1985, 93, 359–371 CrossRef CAS
.
- K. Shindo and S. Lipsky, J. Chem. Phys., 1966, 45, 2292–2297 CrossRef CAS
.
- S.-T. Tsai, C.-K. Lin, Y. T. Lee and C.-K. Ni, J. Chem. Phys., 2000, 113, 67–70 CrossRef CAS
.
- R. I. Kaiser, P. Maksyutenko, C. Ennis, F. Zhang, X. Gu, S. P. Krishtal, A. M. Mebel, O. Kostko and M. Ahmed, Faraday Discuss., 2010, 147, 429–478 RSC
.
- R. I. Kaiser and N. Hansen, J. Phys. Chem. A, 2021, 125, 3826–3840 CrossRef CAS PubMed
.
- M. A. Duncan, T. G. Dietz, M. G. Liverman and R. E. Smalley, J. Phys. Chem., 1981, 85, 7–9 CrossRef CAS
.
- S.-T. Tsai, C.-L. Huang, Y. T. Lee and C.-K. Ni, J. Chem. Phys., 2001, 115, 2449–2455 CrossRef CAS
.
- T. C. Hsu, J. Shu, Y. Chen, J. J. Lin, Y. T. Lee and X. Yang, J. Chem. Phys., 2001, 115, 9623–9626 CrossRef CAS
.
- T. C. Hsu, J. Shu, Y. Chen, J. J. Lin, Y. T. Lee and X. Yang, J. Chin. Chem. Soc., 2002, 49, 1–6 CrossRef CAS
.
- D. Xu and D. Li, Astrophys. J., 2016, 833, 90 CrossRef
.
- K. Sellgren, R. G. Smith and T. Y. Brooke, Astrophys. J., 1994, 433, 179–186 CrossRef CAS
.
- B. Larsson and R. Liseau, Astron. Astrophys., 2017, 608, A133 CrossRef
.
- Y. C. Minh, H. B. Liu and R. Galvań-Madrid, Astrophys. J., 2016, 824, 99 CrossRef
.
- O. Kochina and D. Wiebe, Origins Life Evol. Biosphere, 2014, 44, 169–174 CrossRef CAS PubMed
.
- J. L. Neill, E. A. Bergin, D. C. Lis, P. Schilke, N. R. Crockett, C. Favre, M. Emprechtinger, C. Comito, S.-L. Qin, D. E. Anderson, A. M. Burkhardt, C. Jo-Hsin, B. J. Harris, S. D. Lord, B. A. McGuire, T. D. McNeill, R. R. Monje, T. G. Phillips, A. L. Steber, T. Vasyunina and S. Yu, Astrophys. J., 2014, 789, 8 CrossRef
.
- B. Gans, S. Boyé-Péronne, M. Broquier, M. Delsaut, S. Douin, C. E. Fellows, P. Halvick, J.-C. Loison, R. R. Lucchese and D. Gauyacq, Phys. Chem. Chem. Phys., 2011, 13, 8140–8152 RSC
.
- Z. Peng, M. Dobrijevic, E. Hébrard, N. Carrasco and P. Pernot, Faraday Discuss., 2010, 147, 137–153 RSC
.
- M. Dobrijevic, J. C. Loison, K. M. Hickson and G. Gronoff, Icarus, 2016, 268, 313–339 CrossRef CAS
.
- J. M. Ribeiro and A. M. Mebel, Mol. Phys., 2015, 113, 1865–1872 CrossRef CAS
.
- M. Dobrijevic, E. Hébrard, J. C. Loison and K. M. Hickson, Icarus, 2014, 228, 324–346 CrossRef CAS
.
- P. Lavvas, M. Galand, R. V. Yelle, A. N. Heays, B. R. Lewis, G. R. Lewis and A. J. Coates, Icarus, 2011, 213, 233–251 CrossRef CAS
.
- A. Faure, V. Vuitton, R. Thissen and L. Wiesenfeld, J. Phys. Chem. A, 2009, 113, 13694–13699 CrossRef CAS PubMed
.
- E. Hébrard, M. Dobrijevic, P. Pernot, N. Carrasco, A. Bergeat, K. M. Hickson, A. Canosa, S. D. Le Picard and I. R. Sims, J. Phys. Chem. A, 2009, 113, 11227–11237 CrossRef PubMed
.
- A. Canosa, I. R. Sims, D. Travers, I. W. M. Smith and B. R. Rowe, Astron. Astrophys., 1997, 323, 644–651 CAS
.
- X. Zhang, J. M. Ajello and Y. L. Yung, Astrophys. J. Lett., 2009, 708, L18–L21 CrossRef
.
- M. R. Berman and M.-C. Lin, Chem. Phys., 1983, 82, 435–442 CrossRef CAS
.
- M. R. Berman, J. W. Fleming, A. B. Harvey and M.-C. Lin, Chem. Phys., 1982, 73, 27–33 CrossRef CAS
.
- A. Merkel, I. Borger, H. J. Spangenberg and L. Zuelicke, Z. Phys. Chem., 1982, 263, 449–460 CrossRef CAS
.
- J. E. Butler, J. W. Fleming, L. P. Goss and M.-C. Lin, Chem. Phys., 1981, 56, 355–365 CrossRef CAS
.
- W. Boullart, K. Devriendt, R. Borms and J. Peeters, J. Phys. Chem., 1996, 100, 998–1007 CrossRef CAS
.
-
A. M. Mebel, in Reviews of Modern Quantum Chemistry, ed. G. Maroulis and K. D. Sen, World Scientific, Singapore, 2002, p. 340 Search PubMed
.
- H. F. Bettinger, P. R. Schreiner, H. F. Schaefer and P. V. R. Schleyer, J. Am. Chem. Soc., 1998, 120, 5741–5750 CrossRef CAS
.
- J.-C. Loison and A. Bergeat, Phys. Chem. Chem. Phys., 2009, 11, 655–664 RSC
.
- A. M. Mebel, M.-C. Lin, D. Chakraborty, J. Park, S. H. Lin and Y. T. Lee, J. Chem. Phys., 2001, 114, 8421–8435 CrossRef CAS
.
- J. A. Miller and C. F. Melius, Combust. Flame, 1992, 91, 21–39 CrossRef CAS
.
- N. Daugey, P. Caubet, B. Retail, M. Costes, A. Bergeat and G. Dorthe, Phys. Chem. Chem. Phys., 2005, 7, 2921–2927 RSC
.
- C. F. Melius, J. A. Miller and E. M. Evleth, Symp. (Int.) Combust., 1992, 24, 621–628 CrossRef
.
- R. I. Kaiser, D. S. N. Parker and A. M. Mebel, Annu. Rev. Phys. Chem., 2015, 66, 43–67 CrossRef CAS PubMed
.
- D. S. N. Parker, A. M. Mebel and R. I. Kaiser, Chem. Soc. Rev., 2014, 43, 2701–2713 RSC
.
- R. I. Kaiser and A. M. Mebel, Chem. Soc. Rev., 2012, 41, 5490–5501 RSC
.
- N. Balucani, F. Zhang and R. I. Kaiser, Chem. Rev., 2010, 110, 5107–5127 CrossRef CAS PubMed
.
- X. Gu and R. I. Kaiser, Acc. Chem. Res., 2009, 42, 290–302 CrossRef CAS PubMed
.
- X. Gu, R. I. Kaiser and A. M. Mebel, ChemPhysChem, 2008, 9, 350–369 CrossRef CAS PubMed
.
- R. I. Kaiser and A. M. Mebel, Int. Rev. Phys. Chem., 2002, 21, 307–356 Search PubMed
.
- R. I. Kaiser, Chem. Rev., 2002, 102, 1309–1358 CrossRef CAS PubMed
.
- D. S. N. Parker and R. I. Kaiser, Chem. Soc. Rev., 2017, 46, 452–463 RSC
.
- N. Balucani, Chem. Soc. Rev., 2012, 41, 5473–5483 RSC
.
- N. Balucani, Int. J. Mol. Sci., 2009, 10, 2304–2335 CrossRef CAS PubMed
.
- N. Balucani, G. Capozza, F. Leonori, E. Segoloni and P. Casavecchia, Int. Rev. Phys. Chem., 2006, 25, 109–163 Search PubMed
.
- P. Casavecchia, N. Balucani and G. G. Volpi, Annu. Rev. Phys. Chem., 1999, 50, 347–376 CrossRef CAS PubMed
.
- P. Casavecchia, N. Balucani, M. Alagia, L. Cartechini and G. G. Volpi, Acc. Chem. Res., 1999, 32, 503–511 CrossRef CAS
.
- C. He, A. A. Nikolayev, L. Zhao, A. M. Thomas, S. Doddipatla, G. R. Galimova, V. N. Azyazov, A. M. Mebel and R. I. Kaiser, J. Phys. Chem. A, 2021, 125, 126–138 CrossRef CAS PubMed
.
- C. He, L. Zhao, S. Doddipatla, A. M. Thomas, A. A. Nikolayev, G. R. Galimova, V. N. Azyazov, A. M. Mebel and R. I. Kaiser, ChemPhysChem, 2020, 21, 1295–1309 CrossRef CAS PubMed
.
- C. He, A. M. Thomas, G. R. Galimova, A. M. Mebel and R. I. Kaiser, J. Phys. Chem. A, 2019, 123, 10543–10555 CrossRef CAS PubMed
.
- C. He, A. M. Thomas, G. R. Galimova, A. N. Morozov, A. M. Mebel and R. I. Kaiser, J. Am. Chem. Soc., 2020, 142, 3205–3213 CrossRef CAS PubMed
.
- C. He, G. R. Galimova, Y. Luo, L. Zhao, A. K. Eckhardt, R. Sun, A. M. Mebel and R. I. Kaiser, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 30142–30150 CrossRef CAS PubMed
.
- S. Doddipatla, G. R. Galimova, H. Wei, A. M. Thomas, C. He, Z. Yang, A. N. Morozov, C. N. Shingledecker, A. M. Mebel and R. I. Kaiser, Sci. Adv., 2021, 7, eabd4044 CrossRef CAS PubMed
.
- A. M. Thomas, L. Zhao, C. He, G. R. Galimova, A. M. Mebel and R. I. Kaiser, Angew. Chem., Int. Ed., 2019, 58, 15488–15495 CrossRef CAS PubMed
.
- R. I. Kaiser, X. Gu, F. Zhang and P. Maksyutenko, Phys. Chem. Chem. Phys., 2012, 14, 575–588 RSC
.
- P. Maksyutenko, F. Zhang, X. Gu and R. I. Kaiser, Phys. Chem. Chem. Phys., 2011, 13, 240–252 RSC
.
- F. Zhang, P. Maksyutenko and R. I. Kaiser, Phys. Chem. Chem. Phys., 2012, 14, 529–537 RSC
.
- G. O. Brink, Rev. Sci. Instrum., 1966, 37, 857–860 CrossRef CAS
.
- N. R. Daly, Rev. Sci. Instrum., 1960, 31, 264–267 CrossRef CAS
.
-
P. S. Weiss, Reaction Dynamics of Electronically Excited Alkali Atoms with Simple Molecules, PhD thesis, University of California at Berkeley, Berkeley, CA, 1986 Search PubMed
.
-
M. F. Vernon, Molecular Beam Scattering, PhD thesis, University of California at Berkeley, Berkeley, CA, 1983 Search PubMed
.
- R. I. Kaiser, Y. T. Lee and A. G. Suits, J. Chem.
Phys., 1996, 105, 8705–8720 CrossRef CAS
.
- R. I. Kaiser, D. Stranges, Y. T. Lee and A. G. Suits, J. Chem. Phys., 1996, 105, 8721–8733 CrossRef CAS
.
- R. I. Kaiser, C. Ochsenfeld, D. Stranges, M. Head-Gordon and Y. T. Lee, Faraday Discuss., 1998, 109, 183–204 RSC
.
- X. Gu, Y. Guo, F. Zhang, A. M. Mebel and R. I. Kaiser, Faraday Discuss., 2006, 133, 245–275 RSC
.
- A. M. Mebel and R. I. Kaiser, Int. Rev. Phys. Chem., 2015, 34, 461–514 Search PubMed
.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC
.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed
.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed
.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef
.
- J. Zhang and E. F. Valeev, J. Chem. Theory Comput., 2012, 8, 3175–3186 CrossRef CAS PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A. 1, Gaussian, Gaussian Inc., Wallingford, CT, 2009, vol. 200, p. 28 Search PubMed
.
-
H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, P. Celani, T. Korona, G. Rauhut, R. D. Amos and A. Bernhardsson, MOLPRO, Version 2010.1, A Package of Ab Initio Programs, University of Cardiff, Cardiff, UK, 2010 Search PubMed
.
-
P. J. Robinson and K. A. Holbrook, Unimolecular Reactions, Wiley, New York, 1972 Search PubMed
.
-
H. Eyring, S. H. Lin and S. M. Lin, Basic Chemical Kinetics, John Wiley and Sons, Inc., New York, 1980 Search PubMed
.
-
J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical Kinetics and Dynamics, Prentice Hall Englewood Cliffs (New Jersey), 1982 Search PubMed
.
- C. He, L. Zhao, A. M. Thomas, A. N. Morozov, A. M. Mebel and R. I. Kaiser, J. Phys. Chem. A, 2019, 123, 5446–5462 CrossRef CAS PubMed
.
- V. V. Kislov, T. L. Nguyen, A. M. Mebel, S. H. Lin and S. C. Smith, J. Chem. Phys., 2004, 120, 7008–7017 CrossRef CAS PubMed
.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS
.
- A. D. Becke, J. Chem. Phys., 1997, 107, 8554–8560 CrossRef CAS
.
- H. L. Schmider and A. D. Becke, J. Chem. Phys., 1998, 108, 9624–9631 CrossRef CAS
.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 6908–6918 CrossRef CAS
.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13126–13130 CrossRef CAS PubMed
.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS
.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS
.
- S. Doddipatla, C. He, R. I. Kaiser, Y. Luo, R. Sun, G. R. Galimova, A. M. Mebel and T. J. Millar, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 22712–22719 CrossRef CAS PubMed
.
- Y. Luo, K. Fujioka, A. Shoji, W. L. Hase, K.-M. Weitzel and R. Sun, J. Phys. Chem. A, 2020, 124, 9119–9127 CrossRef CAS PubMed
.
- S. Pratihar, X. Ma, Z. Homayoon, G. L. Barnes and W. L. Hase, J. Am. Chem. Soc., 2017, 139, 3570–3590 CrossRef CAS PubMed
.
- W. L. Hase, R. J. Duchovic, X. Hu, A. Komornicki, K. F. Lim, D.-H. Lu, G. H. Peslherbe, K. N. Swamy, S. R. V. Linde, A. Varandas, H. Wang and R. J. Wolf, QCPE, 1996, 16, 671 Search PubMed
.
- X. Hu, W. L. Hase and T. Pirraglia, J. Comput. Chem., 1991, 12, 1014–1024 CrossRef CAS
.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS
.
- U. Lourderaj, R. Sun, S. C. Kohale, G. L. Barnes, W. A. de Jong, T. L. Windus and W. L. Hase, Comput. Phys. Commun., 2014, 185, 1074–1080 CrossRef CAS
.
- R. D. Levine, R. B. Bernstein and Y. T. Lee, Phys. Today, 1988, 41, 90–92 CrossRef
.
-
R. D. Levine, Molecular Reaction Dynamics, Cambridge University Press, Cambridge, 2005 Search PubMed
.
- D. R. Herschbach, Discuss. Faraday Soc., 1962, 33, 149–161 RSC
.
- W. B. Miller, S. A. Safron and D. R. Herschbach, Discuss. Faraday Soc., 1967, 44, 108–122 RSC
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04443e |
| ‡ Contributed equally to this work. |
| This journal is © the Owner Societies 2022 |