How many methanol molecules effectively solvate an excess proton in the gas phase? Infrared spectroscopy of H+(methanol)n–benzene clusters†
Takeru
Kato
and
Asuka
Fujii
 *
*
Department of Chemistry, Graduate School of Science, Tohoku University, Sendai 980-8578, Japan. E-mail: asuka.fujii.c5@tohoku.ac.jp
First published on 26th November 2021
Abstract
An excess proton in a hydrogen-bonded system enhances the strength of hydrogen bonds of the surrounding molecules. The extent of this influence can be a measure of the number of molecules effectively solvating the excess proton. Such extent in methanol has been discussed by the observation of the π-hydrogen-bonded OH stretch bands of the terminal sites of protonated methanol clusters, H+(methanol)n, in benzene solutions, and it has been concluded that ∼8 molecules effectively solvate the excess proton (Stoyanov et al., Chem. Eur. J. 2008, 14, 3596–3604). In the present study, we performed infrared spectroscopy of H+(methanol)n–benzene clusters in the gas phase. The cluster size and hydrogen-bonded network structure are identified by the tandem mass spectrometric technique and the comparison of the observed infrared spectra with density functional theory calculations. Though changes of the preferred hydrogen bond network type occur with the increase of cluster size in the gas phase clusters, the observed size dependence of the π-hydrogen bonded OH frequency agrees well with that in the benzene solutions. This means that the observations in both the gas and condensed phases catch the same physical essence of the excess proton solvation by methanol.
Introduction
When multiple hydrogen bonds (H-bonds) are formed in a molecular system, the strength of each H-bond can be largely enhanced by other H-bonds. This is called the cooperative effect of H-bonds, and this effect plays a crucial role in H-bonded networks in the condensed phase.1–4 In a protonated system, the excess proton further enhances the strength of surrounding H-bonds by strong induction due to its positive charge.5–8 The extent of this enhancement to surrounding H-bonds can be regarded as the number of molecules effectively solvating the excess proton. In other words, this is the range of surrounding molecules influenced by the excess proton.To explore the extent of the influence of an excess proton to surrounding H-bonds, a one-dimensional H-bond chain would be the simplest system. Such a system can be realized by protonated methanol clusters, H+(MeOH)n.8–24 The protonated site of methanol has the Eigen (CH3OH2+) or Zundel [CH3O(H)–H+–O(H)CH3] type form, and a one-dimensional H-bond chain (OH⋯OH⋯OH⋯) can be extended from both the sides of the protonated site. Each end of this one-dimensional chain is terminated by a single acceptor site, which has a free OH of methanol. The acidity of this terminal site should reflect the influence of the excess proton (protonated site) located at the center of the H-bond chain, and it can be estimated by the magnitude of the redshift of the OH stretch band of the terminal site when the terminal site forms an H-bond with a proton acceptor molecule. Based on this idea, Stoyanov et al. studied the infrared (IR) spectra of H+(MeOH)n in benzene solutions.8 The protonation of methanol was carried out with strong carborane acids, of which conjugate base anions would have a minimum effect on the structure of the cations. The spectra of the H+(MeOH)n clusters were obtained by using the spectral subtraction techniques, and the size of the cluster was controlled by changing the methanol concentration in the benzene solution while the proton concentration was kept constant. The one-dimensional chain structures with the Eigen (for odd n) or Zundel (for even n) protonated site were supposed, and both the ends of the chain were bound to benzene with π-hydrogen bonds. The π-hydrogen bond is weaker than the typical σ-hydrogen bonds between methanol molecules, and the π-hydrogen bonded OH stretch band can be isolated from other hydrogen-bonded OH stretch bands. Stoyanov et al. observed that the OH stretch frequency of the π-hydrogen-bonded site shows remarkable blueshifts with an increasing n in the size range of n = 2–4, which indicates the reduction of cooperative enhancement by the excess proton. The OH frequency shift with the increasing n becomes much moderate in n ≥ 5 and the OH frequency almost converges to a constant value in n ≥ 8. Therefore, Stoyanov et al. concluded that the influence of the excess proton extends in the chain up to four methanol molecules on either sides of the excess proton. In their measurements, an isosbestic point was observed in the size (methanol concentration) change from n = 2 to 4 and the cluster size identification seems rigorous in this region. In the larger size, however, the spectral changes with the size are complicated, and the size identification basically relied on the methanol concentration in the solution.
On the other hand, the H-bonded structures of H+(MeOH)n and related clusters have been extensively studied in the gas phase.9–28 Before the study by Stoyanov et al. was reported, we have qualitatively discussed the development process of the possible H-bond network structures of H+(MeOH)n, from the simplest linear chain structure to the most complicated double ring (“bicyclic”) structure, based on IR spectroscopy and density functional theory (DFT) computations of the size-selected clusters.14,15 After the study by Stoyanov et al. was reported,8 we have revisited H+(MeOH)n in the gas phase with the adavanced IR experimental techniques and much more extensive density functional theory (DFT) computations.16–19 The H-bond network structure development of the most stable cluster with the increasing n was clarified. In addition, upon the increase of the cluster temperature, remarkable network structure changes, i.e., H-bond ring opening to form more flexible linear chain structures, were also found.16–19,24 The size and temperature dependence of the H-bond structures of H+(MeOH)n in the gas phase is now fully established, and this enables us to shed light on the extent of excess proton solvation in methanol. In the present study, we revisit the enhancement of H-bond strength by an excess proton with IR spectroscopy of H+(methanol)n–benzene clusters, H+(MeOH)n–Bz, in the gas phase. In gas phase cluster studies, we can achieve rigorous cluster size selection by using mass spectrometric techniques, and the cluster structures can also be identified using IR spectroscopy combined with theoretical computations. Direct comparisons of protonated clusters in the condensed and gas phases have been very scarce. Such a comparison should be very helpful to discuss the identity and difference of the clusters in the two phases. We demonstrate that the gas phase cluster results show good agreement with those in the benzene solutions reported by Stoyanov et al.8
Experimental
The IR spectra of size-selected H+(MeOH)n–Bz clusters in the OH stretch region were recorded by predissociation spectroscopy. The gaseous mixture of methanol and benzene seeded in the He carrier gas (stagnation pressure of 4 atm) was supersonically expanded into a vacuum through a pulsed valve (General Valve Series #9). A nozzle with a channel of 1 mm diameter and 1 cm length was attached to the valve, and the gas pulse was expanded through this channel. In the channel, discharge by an electric pulse of −600 V synchronized with the gas pulse was applied, and protonated clusters were efficiently produced by collisions in the channel. The produced clusters were introduced into a tandem-type quadrupole mass spectrometer through a skimmer. The cluster of interest was mass (size)-selected by the first stage of the mass spectrometer, and it was introduced into an octopole ion guide. The mass-selected cluster was irradiated by IR light, and fragment ions produced by vibrational predissociation were mass selected by the second stage of the mass spectrometer. By monitoring the intensity of the Bz-loss fragment (H+(MeOH)n fragment) while scanning the IR frequency, an IR spectrum of H+(MeOH)n–Bz was measured. All the observed spectra were normalized by the IR power. The IR frequency was calibrated by the ambient water absorption lines.Stable isomer structures and their vibrational spectra were calculated using the Gaussian 16 program suite at the ωB97X-D/6-31+G(d) level.29
Results and discussion
A. Possible H-bond networks of H+(MeOH)n
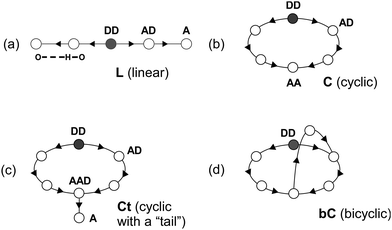
Our previous IR spectroscopic and theoretical studies on H+(MeOH)n in the gas phase have revealed that their H-bond network structures depend both on the size and temperature.16–19 Prior to the presentation of the present results, here we briefly summarize the established knowledge on the H-bond networks of H+(MeOH)n, which is necessary for the interpretation of spectra of H+(MeOH)n–Bz. The possible network structures of H+(MeOH)n can be categorized into only four types, linear (L), cyclic (C), cyclic with a “tail” (Ct), and bicyclic (bC), as schematically shown in Fig. 1.14–19,24 In all the types, the protonated site is always a double donor (DD) site. The L type has a one-dimensional chain-like structure, and is generally the most flexible structure type. Each of the ends of the chain is a single acceptor (A) site and has a free OH. Sites between the protonated site and terminal site of the chain are single acceptor–single donor (AD) sites. When the two ends of an L structure are bound to each other by an H-bond, a C structure is formed. One of the terminal A sites becomes an AD site, and the other becomes a double acceptor (AA) site, which has a free OH. Ct is a structure in which a side chain (“tail”) is extended from the free OH of a C structure. This side chain is terminated by an A site. When the A site of a Ct structure is bound to the ring moiety, a bC structure is formed. It should be noted that free OH no longer exists in bC. The bC type is the most complicated H-bonded network structure of protonated alcohols. For n = 2 and 3, possible structures are practically limited to the L type, but in n ≥ 4, multiple different H-bond network types can compete with each other. The L, C, Ct, and bC type isomers are the lowest energy ones for n = 4–7, respectively.12,13,17 Clusters in low temperature have their lowest energy form, but more flexible (vibrationally denser) isomers are preferentially populated with increase of temperature because of the entropy factor of the free energy. The L type isomer is the most flexible one and is preferred at high temperatures in all the sizes. The jet expansion cooling through the channel nozzle we employed is not enough to fully remove the large excess energy of protonation. Therefore, the produced “bare” clusters (H+(MeOH)n) are warm (typically ≥200 K), and only the L type isomer, which is the most flexible type, is produced for all the sizes. However, in the case of H+(MeOH)n–Bz, the attachment of benzene with a weak π-hydrogen bond causes the “tagging” effect.16–18,30,31 When a weak intermolecular bond is involved in a cluster, the total internal energy of the cluster is effectively restricted to be lower than the bond energy of the weak intermolecular interaction because higher energy clusters dissociate prior to observation. Therefore, H+(MeOH)n–Bz can be colder than simultaneously produced bare H+(MeOH)n, and can be isomers other than the L type, as has been demonstrated by Ar-tagging, which makes the cluster the lowest energy type isomer.16–18 In the study by Stoyanov et al., only the L type structures are supposed,8 and that is a quite reasonable assumption for the condensed phase experiments under the room temperature condition. On the other hand, in the gas phase, the L type structure may not necessarily be the preferred one for H+(MeOH)n–Bz, and we need to examine the structure of each size of the cluster.B. Observed spectra of H+(MeOH)n–Bz
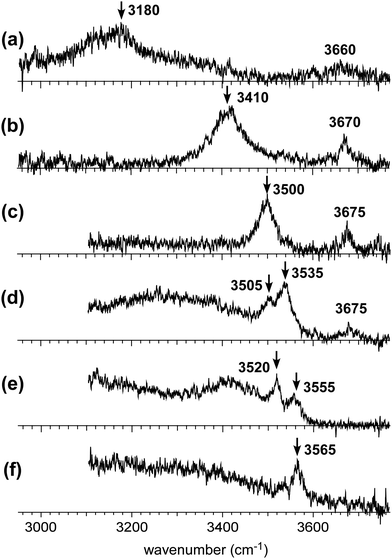
Fig. 2 shows the observed IR spectra of H+(MeOH)n–Bz (n = 2–7) in the OH stretch region. All the spectra were measured by monitoring the H+(MeOH)n fragment intensity. Contribution of plausible protonated benzene–(MeOH)n (C6H7+–(MeOH)n) isomers can be excluded by this choice of the observed fragment because MeOH-loss should occur in the fragmentation of C6H7+–(MeOH)n.32–34 Spectra of n = 5 and 7 have been reported in our previous papers on the temperature dependence of isomer structures,18,19 but the present spectra were carefully remeasured with the other spectra in this time. This is because the π-hydrogen bonded OH stretch bands are buried in the background absorption and are not clearly seen in these previous spectra.In the observed spectra, two types of bands appear. Bands above 3600 cm−1 are assigned to free OH stretches of the terminal sites in the H-bonded network of the H+(MeOH)n moiety. Bands below 3600 cm−1 are attributed to H-bonded OH stretches. A π-hydrogen bond between methanol and benzene is expected to be weaker than a typical σ-hydrogen bond (O–H⋯O hydrogen bond) between methanol molecules. Therefore, benzene is excluded from the H-bond network of H+(MeOH)n, and is π-hydrogen bonded to the terminal site of the H-bond network. Because the magnitude of the redshift of the OH stretch band upon the H-bond formation correlates with the strength of the H-bond,5,35,36 the highest frequency band in the H-bonded OH stretch region (<3600 cm−1) can be assigned to the π-hydrogen bonded OH between H+(MeOH)n and benzene. The π-hydrogen bonded OH bands are marked with arrows in the observed spectra. Their frequencies show a clear blueshift trend with an increase in cluster size, as has been observed in the condensed phase experiment by Stoyanov et al.8 This trend demonstrates the weakening of the influence of the excess proton on the terminal site.
The free OH bands in the observed spectra also show a weak blueshift trend with the increasing size. This trend is also attributed to the separation of the terminal site from the charged (protonated) site. It has been confirmed for H+(MeOH)n that the free OH frequencies of the L type isomer (A site) and C type isomer (AA site) are different; the former is ∼3670 cm−1 while the latter is ∼3640 cm−1.17 All the observed free OH bands are clearly attributed to those of the L type isomers. Here we should note that the free OH bands can be seen only in n ≤ 5, and they disappear in n ≥ 6. In the case of the L type isomer, there are two terminal sites (free OHs). Even though one of the terminal sites is π-hydrogen bonded to benzene, the other terminal site should show a free OH band. Therefore, the disappearance of the free OH band in n ≥ 6 means that the H-bond network structure changes from the L type of n ≤ 5 to other types.
C. Identification of the cluster structure types
In this subsection, we identify the H-bonded structures of H+(MeOH)n–Bz on the basis of their observed spectral features as well as comparison with simulated spectra. It has been shown that hundreds of stable isomer structures exist even for the observed size range of the bare clusters (H+(MeOH)n),17 and a greater number of isomers are expected for H+(MeOH)n–Bz. Therefore, a complete survey of possible isomer structures and the evaluation of their thermal distribution are practically difficult in the present study. Moreover, in the present study, our aim is not to precisely determine the structures of the clusters, but is to identify the H-bond network type of the carrier of the observed π-hydrogen bonded OH band. Therefore, in the following discussion, we pick up only one isomer structure for each H-bond network type, and its calculated spectrum is compared with the observed spectrum. This is because IR spectra of the OH stretch region of protonated alkylalcohol clusters essentially depend only on their H-bond network type and do not largely change their spectral features with detailed conformations/configurations.17,19 We should note that the calculated isomer structures in the following are shown to represent the expected spectral pattern and roughly evaluate relative energy, but they do not necessarily correspond to the exact structures of the spectral carriers. The structures of the calculated stable isomers are summarized in Fig. S1 (n = 2–4) in the ESI† and Fig. 3 (n = 5–7), and their detailed coordinate information is also shown in the ESI.†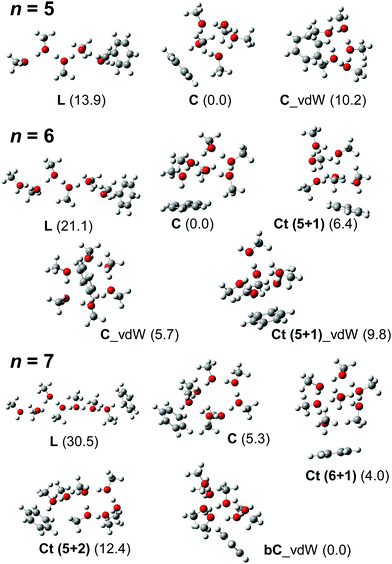 | ||
| Fig. 3 Schematic structures of energy-optimized isomers of H+(MeOH)n–Bz (n = 5–7). These isomer structures were used to simulate the spectra shown in Fig. 4–6. All the computations were performed at ωB97X-D/6-31+G(d). Numbers in parentheses are relative energies (kJ mol−1) in each size with zero-point energy corrections. | ||
For n = 2 and 3, the H-bonded network structures are uniquely assigned to the L type. This is also supported by the observed free OH band at 3660 and 3670 cm−1, respectively.17 The π-hydrogen-bonded OH stretch bands, which should be the highest frequency H-bonded OH bands, are observed at 3180 and 3410 cm−1, respectively. The σ-hydrogen-bonded OH stretch band (H-bonded of stretch of the protonated site) are expected in the much lower frequency region than the observed frequency range.21 A π-hydrogen-bonded OH stretch band is ordinarily observed in the 3500 to ∼3600 cm−1 region.37 The π-hydrogen-bonded OH band frequencies of the n = 2 and 3 clusters are very low, indicating the remarkable enhancement of the π-hydrogen bond strength by the excess proton. In the calculation of n = 2 at the ωB97X-D/6-31+G(d) level, the Zundel motif of the “bare” cluster changes to the Eigen motif with the π-hydrogen bond formation and the protonated (DD) site contacts with benzene (see Fig. S1 in the ESI†). On the other hand, the direct contact of the protonated site with benzene is not stable in isomers of n = 3. All such initial structures of n = 3 finally converged to energy-optimized structures in which the excess proton is located at the central methanol site.
Competition between the L and C type isomers can occur in n = 4 and 5.12,13,17,19 In the case of the bare H+(MeOH)n clusters, the lowest energy isomers are the L and C types for n = 4 and 5, respectively. The observed free OH bands at 3675 cm−1 of n = 4 and 5 demonstrate that the L type isomers contribute to these spectra. In the case of the C type isomer, its free OH frequency is ∼3640 cm−1.12,17 However, once the terminal site (free OH) of the C type isomer is π-hydrogen bonded with Bz, the free OH band disappears. Therefore, missing of the free OH band of the C type isomer does not necessarily exclude its contribution to the observed spectrum. An alternative marker band of the C type isomer is a band at around ∼3400 cm−1, which is attributed to the stretching vibrations of the two OHs bound to the AA site.12,17,19 In the observed spectrum of n = 4, bands are missing at around ∼3400 cm−1, and therefore, the observed spectrum is attributed uniquely to the L type. The band at 3500 cm−1 is assigned to the OH stretch π-hydrogen-bonded to benzene. The σ-hydrogen bonded OH bands are expected to be in the lower frequency region than the observed range.17,19 Also in the calculated structure of n = 4 (Fig. S1 in ESI†), the Zundel motif of the bare cluster is changed to the Eigen motif with the π-hydrogen bond formation with benzene. But the excess proton does not directly contact with benzene. The protonated (DD) site is located next to the π-hydrogen bonded site.
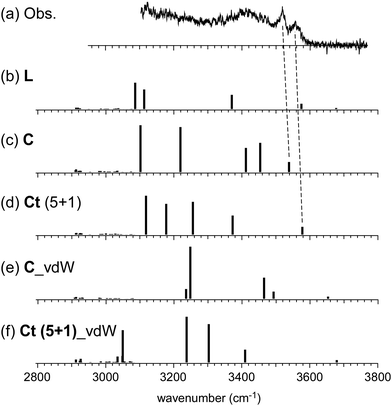
On the other hand, the observed spectrum of n = 5 shows two bands (3505 and 3535 cm−1) in the typical π-hydrogen-bonded OH stretch region, suggesting the coexistence of the C type isomer, in addition to the L type isomer indicated by the free OH band. The broadened absorption attributed to the σ-hydrogen bonded OH stretches appears below 3500 cm−1, and this does not conflict with the marker band (∼3400 cm−1) of the C type isomer. For further confirmation, comparison among (a) observed and (b)–(d) calculated spectra of n = 5 is shown in Fig. 4. The stable isomer structures for the spectral simulations are summarized in Fig. 3. The calculated spectra are based on three typical structures, (b) L type π-bound to Bz, (c) C type π-bound to Bz, and (d) C type bound to Bz with the van der Waals force. The computations were performed at the ωB97X-D/6-31+G(d) level, and the harmonic frequencies of the energy-optimized structures were scaled by the factor of 0.951, which was determined to reproduce the free OH stretch band of the MeOH monomer (3681 cm−1).38 The calculated π-hydrogen bonded OH frequencies are slightly overestimated, but they reproduce well the observed bands. The comparison shows that the observed two bands are well explained by the coexistence of the π-bound L and C type isomers. The 3535 and 3505 cm−1 bands are assigned to the π-hydrogen bonded OHs of the L and C type isomers, respectively. The L type isomer has much higher energy relative to the C type isomer, but the L type is more flexible, and its population can be driven by the entropy factor under warm conditions (as summarized in the ESI,† the L type is the lowest Gibbs free energy isomer at a high temperature (298 K)). The coexistence of the van der Waals bound C type isomer can be excluded because of the missing of the corresponding free OH band, which is lower than that of the L type isomer by ∼30 cm−1.13,17 The van der Waals bound isomer is higher in energy than the π-bound isomer. No advantage of the entropy factor is expected for the van der Waals bound isomer (this is also indicated by its higher Gibbs free energy, summarized in the ESI†). Therefore, its absence is reasonable.
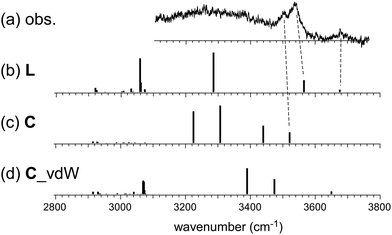 | ||
| Fig. 4 Comparison among (a) observed and (b)–(d) simulated spectra of H+(MeOH)5–Bz. Observed spectrum (a) is reproduced from Fig. 2. Simulated spectra (b)–(d) are based on the optimized structures of n = 5 shown in Fig. 3. All the computations were performed at ωB97X-D/6-31+G(d). The calculated vibrational frequencies were scaled by the factor of 0.951. Dashed lines indicate the correspondence among the observed and calculated bands. | ||
In the observed spectra of n = 6 and 7, no free OH band is seen, and therefore, the contribution of the L-type isomer is excluded. Structural change from the L type would be because the possible π-hydrogen bond with Bz becomes weak enough to make the clusters colder (lower energy but less entropy structures are preferentially formed) by the “tagging” effect. It has been confirmed that the lowest energy isomers of bare H+(MeOH)6,7 are the Ct and bC types, respectively.17 Comparison among (a) observed and (b)–(f) calculated spectra of n = 6 is shown in Fig. 5. The stable isomer structures for the spectral simulations are summarized in Fig. 3. In the calculations, the H-bond network structures are (b) L, (c) C, (d) Ct (5 molecule ring + 1 molecule sidechain), (e) C (the same as (c)), and (f) Ct (the same as (d)) types, respectively. In (b)–(d), Bz is π-hydrogen-bonded to the terminal site (free OH of the corresponding bare cluster), while Bz is bound with the van der Waals force in (e) and (f). Contribution of the L and van der Waals type isomers to observed spectrum (a) is practically excluded because of the absence of the free OH band. Their spectra are shown in Fig. 5 for reference. Though the lowest energy isomer of the bare cluster is the Ct type,17 the C type isomer becomes the lowest energy one by the interaction with Bz. This may be due to the stronger acidity of the terminal site (AA site) of the C type isomer than that (A site) of Ct. In addition, the closer contact of the aromatic ring and the H-bonded ring moiety is also expected in the C type. In observed spectrum (a), the two bands at 3555 and 3520 cm−1 are attributed to π-hydrogen bonded OH stretches. The appearance of these two bands and the absence of the free OH band are interpreted well with the coexistence of the π-hydrogen bonded Ct and C type isomers. In the observed spectrum of n = 7, a single band (3565 cm−1) is seen in the π-hydrogen bonded OH stretch region. In Fig. 6, observed spectrum (a) is compared with the calculated spectra based on (b) L, (c) C, (d) Ct (6 molecule ring + 1 molecule sidechain), (e) Ct (5 molecule ring + 2 molecule sidechain), and (f) bC type isomers. In both the bare cluster and cluster with Bz of n = 7, the bC type isomer is the lowest energy one.16,17 However, the bC isomer has no terminal site (free OH) and cannot be bound to Bz with a π-hydrogen bond (only the van der Waals type is plausible). Therefore, bC cannot contribute to the observed π-hydrogen bonded OH stretch band, even if it populates. The Ct (6 + 1) type isomer is the lowest energy one among the π-hydrogen-bonded isomers. No clear free OH stretch band is seen in observed spectrum (a), and therefore, the major contribution of the L type isomer is excluded. On the other hand, calculated spectra (c) of the C isomer and (d) and (e) of the Ct isomers reproduce well the observed π-hydrogen bonded OH band. Therefore, we assign the π-hydrogen bonded OH band at 3565 cm−1 to the Ct and C type isomers. The ring size of the observed isomer cannot be determined because these isomers show a very similar π-hydrogen bonded OH band frequency and the energy differences among them are small.
 | ||
| Fig. 5 Comparison among (a) observed and (b)–(f) simulated spectra of H+(MeOH)6–Bz. Observed spectrum (a) is reproduced from Fig. 2. Simulated spectra (b)–(f) are based on the optimized structures of n = 6 shown in Fig. 3. All the computations were performed at ωB97X-D/6-31+G(d). The calculated vibrational frequencies were scaled by the factor of 0.951. Dashed lines indicate the correspondence among the observed and calculated bands. | ||
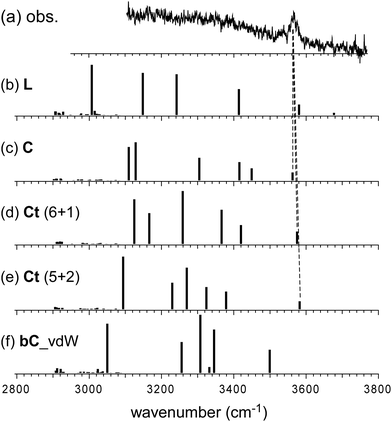 | ||
| Fig. 6 Comparison among (a) observed and (b)–(f) simulated spectra of H+(MeOH)7–Bz. Observed spectrum (a) is reproduced from Fig. 2. Simulated spectra (b)–(f) are based on the optimized structures of n = 7 shown in Fig. 3. All the computations were performed at ωB97X-D/6-31+G(d). The calculated vibrational frequencies were scaled by the factor of 0.951. Dashed lines indicate the correspondence among the observed and calculated bands. | ||
All the observed and calculated OH frequencies with the isomer type assignments are summarized in Table S1 in the ESI.† The calculated free and π-hydrogen bonded O–H bond length and the shortest OH⋯C distance of each isomer are also shown in the table. Reflecting the blue-shift trend of the π-hydrogen-bonded OH frequency with the increase of cluster size, the π-hydrogen bonded O–H bond length becomes shorter and the OH⋯C distance becomes longer. This is a clear indication of the weakening of the π-hydrogen bond though the bond length (distance) is not directly observed in the present experiment.
D. Comparison with the condensed phase
The cluster size dependence of the π-hydrogen bonded OH stretch band of H+(MeOH)n in the condensed phase has been reported by Stoynaov et al.8 They observed π-hydrogen bonded OH bands in the benzene solutions with two different counter carborane anions (CHB11H5Br6− and CHB11Cl11−). Their data of the latter counter anion are plotted in Fig. 7 (filled green square). This choice of data is because the binding of the terminal sites of H+(MeOH)n with the CHB11H5Br6− counter anion is plausible, while with less basic CHB11Cl11−, Bz must successfully compete for the π-hydrogen bond with the terminal sites. The L type structure of H+(MeOH)n, in which each of the two terminal sites is π-hydrogen-bonded to Bz, was supposed to interpret the observed spectra. This is a reasonable assumption for the room temperature experiment; the population of the entropy-driven L type isomer is expected to be dominant in ≥200 K (in the gas phase).17,19 Short chain structures have also been suggested for liquid methanol,39–42 while cyclic structures have been confirmed for cold neutral methanol clusters in the gas phase.43–48 In the plot, it is seen that the π-hydrogen bonded OH frequency of the terminal site shows a clear blueshift trend with the increasing cluster size, reflecting the weakening of the influence of the excess proton located at the center of the H-bond network. The slope of the frequency shift is steep in n = 2–4, but it becomes almost saturated during n = 4–8. Therefore, Stoyanov et al. concluded that the influence of the excess proton in the linear chain extends up to four molecules in each side of the excess proton (surrounding total ∼8 molecules).8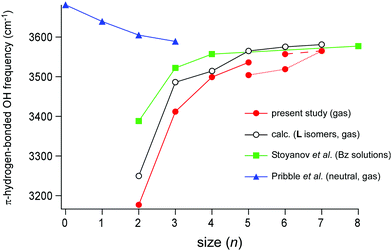 | ||
| Fig. 7 Plots of the cluster size (n) dependence of the π-hydrogen-bonded OH stretch frequencies. Filled red circle: H+(MeOH)n–Bz in the gas phase observed in the present study. Open black circle: the L type isomer of H+(MeOH)n–Bz calculated in the present study (ωB97X-D/6-31+G(d), scaled by the factor of 0.951). Filled green square: H+(MeOH)n–Bz2 in the benzene solution observed by Stoyanov et al. (taken from ref. 8). Filled blue triangle: neutral (MeOH)n–Bz in the gas phase observed by Pribble et al. (taken from ref. 37). The point at n = 0 of neutral (MeOH)n–Bz shows the free OH stretch frequency of the neutral methanol monomer in the gas phase (taken from ref. 38). | ||
The π-hydrogen bonded OH stretch frequencies of H+(MeOH)n–Bz observed in the present gas phase study (filled red circle) are also plotted in Fig. 7 with the calculated frequencies of the L type isomers (the open black circle). In the present observation of the gas phase clusters, the H-bonded network type changes with the cluster size: the L type in n = 2–5, the C type in n = 5–7, and the Ct type in n = 6–7. Though small zigzags by the network structure changes are seen, the blueshift trend of the frequency with the increasing n is clear. The plot of the calculated frequencies based only on the L type isomers reproduces well the slope of the plot though the frequencies are somewhat overestimated. The shape of the slope of the observed frequency is quite similar to that of the Bz solution: the steep slope in n = 2–4, and moderate saturation during n = 4–7. This indicates that both the measurements catch the same physical essence of the solvation of the excess proton with methanol. Because the cluster size is definitely determined in the gas phase study, we certainly confirm the conclusion given by the condensed phase experiment that the influence of the excess proton is limited to the surrounding ∼8 molecules in H-bond networks of MeOH.
The π-hydrogen-bonded OH frequency only weakly depends on the H-bond network type in the gas phase clusters (and therefore, the plot of simulations of the L isomers is a good approximation of the observed size dependence). This can be rationalized by considering the preferred location of the excess proton. The protonated site tends to locate at the center of the H-bond network in all the isomer types and the network structure becomes (nearly) symmetric for the two sides of the central protonated DD site.17 Therefore, the terminal site (π-hydrogen bonded site) is the furthest site from the protonated site. The number of methanol molecules between the protonated site and the terminal site along with the H-bonded chain is essentially determined only by the cluster size and does not (largely) depend on the type of the network.
Here we also note on some obvious differences between the condensed phase and gas phase clusters, which would be responsible for the frequency difference, especially remarkable in the smaller sizes: (i) the cluster in the solution is, of course, further solvated by the surrounding solvent Bz, while the gas phase cluster is isolated in the vacuum. There would be small charge (electron) transfer from Bz directly contacting the protonated site, which can reduce the net charge of the H+(MeOH)n moiety and weaken the hydrogen bond enhancement by the charge; (ii) in the condensed phase, both the terminal sites of the L type are bound to Bz, but only one terminal site is solvated in the present gas phase clusters; (iii) influence of the counter anion in the condensed phase.
Finally, we compare the results on the protonated clusters with that of neutral (MeOH)n–Bz. A linear-chain structure of neutral (MeOH)n consists of AD sites terminated by a single-donor (D) and single-acceptor (A) sites. The terminal A site has a free OH and can be π-hydrogen-bonded to Bz. In the neutral linear chain, the acidity of the free OH at the terminal A site would increase with the increasing n because of the cooperative effect of H-bonds. The π-hydrogen-bonded OH stretch frequencies of neutral (MeOH)n–Bz of the linear-chain structure were reported by Zwier and coworkers in the size range of n = 1–3,37 and their data (blue triangle) are also plotted in Fig. 7. The MeOH moiety in (MeOH)n–Bz changes to the closed cyclic structures in n ≥ 4, which have no terminal site (free OH) and are bound to Bz with the van der Waals force.37 Therefore, only the experimental data of n ≤ 3 are available (the point of n = 0 is the free OH frequency of the MeOH monomer, 3681 cm−1).38 As we expected with the cooperativity of the H-bonds, the π-hydrogen-bonded OH frequency of the neutral cluster shows the redshift trend with the increasing n, indicating the enhancement of the π-hydrogen bond strength. Also, in the protonated cluster, H+(MeOH)n–Bz, this cooperative enhancement with the increase of cluster size is expected. However, the reduction of the influence of the excess proton is superior to the cooperative enhancement, and the resultant blueshift trend occurs in the protonated cluster. It is expected that the π-hydrogen-bonded OH frequencies of the neutral and protonated clusters would converge to the same value in a large size. The magnitude of the shift of the neutral clusters seems to show the beginning of the saturation at n = 3 and the frequency of neutral n = 3 (3589 cm−1) is close to that of n = 8 of the protonated cluster in the condensed phase (3577 cm−1).8,37 Here, we should note that in the protonated cluster of the L type, the effective length of the H-bond chain for cooperative enhancement becomes n/2 because the H-bond directions are opposite in the two sides of the central protonated site (see Fig. 1). Therefore, it can be concluded that the extent of cooperative enhancement of H-bonds in the linear chain of MeOH is within ∼4 molecules, and the π-hydrogen bonded OH frequency converges to ∼3580 cm−1.
Concluding remarks
In the present study, the size-selective infrared spectra of H+(methanol)n–benzene (n = 2–7) clusters in the gas phase were observed in the OH stretch region, and the size-dependence of the π-hydrogen bonded OH stretch band frequencies was discussed. The H-bond network structures of the clusters changed from the linear type (n = 2–5) to the cyclic type (n = 5–7) and the cyclic with a “tail” type (n = 6 and 7). Irrespective of such hydrogen bond network structure changes, the π-hydrogen-bonded OH stretch frequencies show an almost smooth blueshift trend with the increasing cluster size, reflecting the weakening of the influence of the excess proton, at the terminal site of the network. The frequency shift trend in the gas phase agrees well with that observed in the benzene solutions by Stoyanov et al.,8 and this confirms the conclusion of the condensed phase study that the extent of the influence of the excess proton is up to the surrounding ∼8 molecules. The good agreement between the gas and condensed phase studies also means that both the observations catch the same physical essence of the proton solvation by methanol, and it demonstrates the limited influence of the second solvation shell and the counter anion to the H+(methanol)n clusters. The present gas phase study clarified that the extent of the influence of the excess proton hardly depends on the hydrogen bond network types of the methanol moiety. This is because the hydrogen bond network of methanol is essentially one-dimensional even though some exceptional sites are included in the types more complicated than the linear type, and the number of molecules between the protonated and terminal (π-bound) sites is almost the same in all the observed isomer types at the same cluster size. In the case of three-dimensional hydrogen bond networks such as water,6,7 the property of the network would more strongly depend on its structure,49 and further care would be needed to compare the results of the gas and condensed phases.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by the Grant-in-Aid for Scientific Research (Project No. 21H04671) from JSPS. A part of the computation was performed at the Research Center for Computational Science, Okazaki, Japan.References
- H. S. Frank and W.-Y. Wen, Discuss. Faraday Soc., 1957, 24, 133–140 RSC
.
- H. Kleeberg, D. Klein and W. A. P. Luck, J. Phys. Chem., 1987, 91, 3200–3203 CrossRef CAS
.
-
S. Sheiner, Hydrogen Bonding, Oxford University Press, Oxford, 1997 Search PubMed
.
- J. Nochebuena, C. Cuautli and J. Ireta, Phys. Chem. Chem. Phys., 2017, 19, 15256–15263 RSC
.
-
G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, Oxford, 1997 Search PubMed
.
- J. M. Headrick, E. G. Dicken, R. S. Walters, N. I. Hammer, R. A. Christie, J. Cui, E. M. Myshakin, M. A. Duncan, M. A. Johnson and K. D. Jordan, Science, 2005, 308, 1765–1769 CrossRef CAS
.
- E. S. Stoyanov, I. V. Stoyanova and C. A. Reed, Chem. Sci., 2011, 2, 462–472 RSC
.
- E. S. Stoyanov, I. V. Stoyanova and C. A. Reed, Chem. – Eur. J., 2008, 14, 3596–3604 CrossRef CAS PubMed
.
- X. Zhang, X. Yang and A. W. Castleman Jr., Chem. Phys. Lett., 1991, 185, 298–302 CrossRef CAS
.
- M. Meot-Ner, J. Am. Chem. Soc., 1992, 114, 3312–3322 CrossRef CAS
.
- M. Meot-Ner, Chem. Rev., 2012, 112, PR22–PR103 CrossRef PubMed
.
- H.-C. Chang, J.-C. Jiang, S. H. Lin, Y. T. Lee and H.-C. Chang, J. Phys. Chem. A, 1999, 103, 2941–2944 CrossRef CAS
.
- H.-C. Chang, J.-C. Jiang, H.-C. Chang, L. R. Wang and Y. T. Lee, Isr. J. Chem., 1999, 39, 231–243 CrossRef CAS
.
- A. Fujii, S. Enomoto, M. Miyazaki and N. Mikami, J. Phys. Chem. A, 2005, 109, 138–141 CrossRef CAS
.
- J.-L. Kuo, A. Fujii and N. Mikami, J. Phys. Chem. A, 2007, 111, 9438–9445 CrossRef CAS
.
- T. Hamashima, Y. C. Li, M. C. H. Wu, K. Mizuse, T. Kobayashi, A. Fujii and J.-L. Kuo, J. Phys. Chem. A, 2013, 117, 101–107 CrossRef CAS
.
- Y.-C. Li, T. Hamashima, R. Yamazaki, T. Kobayashi, Y. Suzuki, K. Mizuse, A. Fujii and J.-L. Kuo, Phys. Chem. Chem. Phys., 2015, 17, 22042–22053 RSC
.
- T. Shimamori, J.-L. Kuo and A. Fujii, J. Phys. Chem. A, 2016, 120, 9203–9208 CrossRef CAS
.
- A. Fujii, N. Sugawara, P.-J. Hsu, T. Shimamori, Y.-C. Li, T. Hamashima and J.-L. Kuo, Phys. Chem. Chem. Phys., 2018, 20, 14971–14991 RSC
.
- Y. J. Hu, F. B. Fu and E. R. Bernstein, J. Chem. Phys., 2006, 125, 154306 CrossRef CAS PubMed
.
- T. D. Fridgen, L. Macaleese, T. B. McMahon, J. Lemaire and P. Maitre, Phys. Chem. Chem. Phys., 2006, 8, 955–966 RSC
.
- K. Tono, J.-L. Kuo, M. Tada, K. Fukazawa, N. Fukushima, C. Kasai and K. Tsukiyama, J. Chem. Phys., 2008, 129, 084304 CrossRef PubMed
.
- J. J. Fifen, M. Nsangou, Z. Dhaouadi, O. Motapon and N.-E. Jaidane, J. Chem. Theory Comput., 2013, 9, 1173–1181 CrossRef CAS
.
- J. J. Fifen, M. Nsangou, Z. Dhaouadi, O. Motapon and N.-E. Jaidane, J. Chem. Phys., 2013, 138, 184301 CrossRef PubMed
.
- N. Solcà and O. Dopfer, J. Am. Chem. Soc., 2004, 126, 9520–9521 CrossRef
.
- N. Solcà and O. Dopfer, J. Phys. Chem. A, 2005, 109, 6174–6186 CrossRef PubMed
.
- N. Sugawara, P.-J. Hsu, A. Fujii and J.-L. Kuo, Phys. Chem. Chem. Phys., 2018, 20, 25482–25494 RSC
.
- P.-J. Hsu, T. Shinkai, P.-H. Tai, A. Fujii and J.-L. Kuo, Phys. Chem. Chem. Phys., 2020, 22, 13223–13239 RSC
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, F. Ding Williams, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallin, 2016 Search PubMed
.
- M. Okumura, L. I. Yeh, J. D. Myers and Y. T. Lee, J. Chem. Phys., 1986, 85, 2328–2329 CrossRef CAS
.
- C. T. Wolke, F. S. Menges, N. Tötsch, O. Gorlova, J. A. Fournier, G. H. Weddle, M. A. Johnson, N. Heine, T. K. Esser, H. Knorke, K. R. Asmis, A. B. McCoy, D. J. Arismendi-Arrieta, R. Prosmiti and F. Pasani, J. Phys. Chem. A, 2015, 119, 1859–1866 CrossRef CAS PubMed
.
- N. Solcá and O. Dopfer, Angew. Chem., Int. Ed., 2002, 41, 3628–3631 CrossRef
.
- G. E. Douberly, A. M. Ricks, P. v. R. Schleyer and M. A. Dumcan, J. Phys. Chem. A, 2008, 112, 4869–4874 CrossRef CAS PubMed
.
- M. Bahou, Y.-J. Wu and Y.-P. Lee, J. Chem. Phys., 2012, 136, 154304 CrossRef
.
- R. M. Badger and S. H. Bauer, J. Chem. Phys., 1937, 5, 839–851 CrossRef CAS
.
- P. Banerjee, D. P. Mukhopadhyay and T. Chakraborty, J. Chem. Phys., 2015, 143, 204306 CrossRef PubMed
.
- R. N. Pribble, F. C. Hagemeister and T. S. Zwier, J. Chem. Phys., 1997, 106, 2145–2157 CrossRef CAS
.
-
T. Shimanouchi, Tables of Molecular Vibrational Frequencies, Consolidated, National Standard Reference Data Series, National Bureau of Standards, Washington DC, 1972, vol. 1 Search PubMed
.
- A. H. Narten and A. Habenschuss, J. Chem. Phys., 1984, 80, 3387–3391 CrossRef CAS
.
- M. Matsumoto and K. E. Gubbins, J. Chem. Phys., 1990, 93, 1981–1994 CrossRef CAS
.
- T. Ishiyama, V. V. Sokolov and A. Morita, J. Chem. Phys., 2011, 134, 024509 CrossRef
.
- P. Gomez-Alvarez, L. Romani and D. Gonzalez-Salgado, J. Chem. Phys., 2013, 138, 044509 CrossRef PubMed
.
- U. Buck, J.-G. Siebers and R. J. Wheatley, J. Chem. Phys., 1998, 108, 20–32 CrossRef CAS
.
- U. Buck and F. Huisken, Chem. Rev., 2000, 100, 3863–3890 CrossRef CAS
.
- A. K. Sum and S. I. Sandler, J. Phys. Chem. A, 2000, 104, 1121–1129 CrossRef CAS
.
- H. B. Fu, Y. J. Hu and E. R. Bernstein, J. Chem. Phys., 2006, 124, 024302 CrossRef CAS
.
- H.-L. Han, C. Camacho, H. A. Witek and Y.-P. Lee, J. Chem. Phys., 2011, 134, 144309 CrossRef PubMed
.
- P. J. Hsu, K.-L. Ho, S.-H. Lin and J.-L. Kuo, Phys. Chem. Chem. Phys., 2017, 19, 544–556 RSC
.
- J. M. Guevara-Vela, E. Rometo-Montalvo, V. A. M. Gómez, R. Chávez-Calvillo, M. García-Revilla, E. Francisco, Á. M. Pendás and T. Rocha-Rinza, Phys. Chem. Chem. Phys., 2016, 18, 19557–19566 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04689f |
| This journal is © the Owner Societies 2022 |