Estimation of electrochemical cell potentials and reaction energies using Fermi energies†
Mohammad Mahdi
Kalantarian
 *a and
Amir
Haghipour
*a and
Amir
Haghipour
 b
b
aCeramic Department, Materials and Energy Research Center, P.O. Box, Tehran, 31787-316, Iran. E-mail: m.kalantarian@merc.ac.ir; kalantarian@gmail.com
bMaterials Research Institute Aalen, Aalen University, Beethovenstr. 1, Aalen D-73430, Germany
First published on 22nd November 2021
Abstract
This paper suggests that cell voltage and reaction energy can be estimated using the difference between the Fermi energies of the products and reactants. DFT calculations for important Li-ion cathode case studies show that the Fermi approach is adequate. The GGA method makes better approximations than the GGA+U and internal energy approaches.
Energy is one of humanity's most important modern challenges. Therefore, energy storage devices play essential roles in the future of technology. The development of rechargeable energy storage devices is highly required nowadays due to their role in the storage of green energy and their usage in (hybrid-)electric vehicles. Intercalation-based Li-ion batteries (LIBs) are currently the most efficient candidate for these purposes.1 Therefore, LIBs and beyond-LIB intercalation batteries are the most promising option for developing the storage of green energy. Understanding the characteristics of LIBs and their behaviour is mandatory to improve and develop these batteries.2–4
Electrochemical cell potential/voltage is a vital characteristic of batteries that must be understood. It directly influences the energy/power density of the cells. Ab initio studies, namely density functional theory (DFT), provide a powerful method to investigate and understand electrochemical systems.5,6 DFT studies are widely used to predict and understand the relevant properties of intercalation batteries.7 The electrochemical cell potential/voltage is a characteristic that DFT can estimate.8,9
Usually, in DFT studies, the cell voltage is estimated via the difference between the calculated internal energies of products and reactants.8,10 This approach is applicable for intercalation batteries, namely LIBs and beyond-LIB batteries, since the products and reactants of their chemical reactions are solids. Thus, the internal energies can be calculated by DFT or other relevant calculation methods (in contrast with some conversion batteries whose reactants/products are liquids). The other key characteristics that DFT can calculate are electrical properties such as the density of states (DOS), Fermi level, band-gap, and rate capability.6,8,11–13
The Fermi level is an essential parameter for evaluating solids and their behaviour.14,15 Fermi energy can be interpreted as the (electro)chemical potential of electrons in solids14–19 and solutions.20,21 Accordingly, it has been suggested that the voltage of photovoltaic (PV) cells (solar cells) could be related to the difference between the Fermi level of the electrodes, i.e., qV = EFA − EFB.22 Besides, for a thermal cell, it has been experimentally shown that the voltage in thermal excitation depends on the entire semiconductor electrode's Fermi level.23 Although the importance of the Fermi level and its influence in the cell voltage seems to be understood,14,24 hitherto (to our knowledge), for the evaluation of intercalation batteries, the Fermi energy has not been directly employed to approximate cell voltage.19
On the other hand, it has been established that the reacted-unreacted (i.e., lithiated–delithiated, sodiated–desodiated, etc.) joint in intercalation batteries can be considered as a semiconductor (P–N or P–P) junction.11–13,25–27 In these approaches, the Fermi level of the reacted–unreacted materials should be aligned to consider the semiconductor junction for assessed materials. Besides, in solid semiconductor materials, the electric field associated with the depletion region of the semiconductor junctions generates a potential.28 Consideration of the reacted–unreacted joint as a semiconductor junction provides a similarity between PV cells and intercalation batteries.
The two above paragraphs suggest that intercalation battery electrochemical cell potentials/voltages can be estimated using calculated Fermi energies. To confirm this suggestion, this paper considers several important cathode materials as case studies for the most important intercalation batteries: LIBs. The considered case studies were LiMO2 (M = Co, Mn, Fe, and Ni), LiNi1/3Co1/3Mn1/3O2 (called NCM), LiMn2O4, LiFePO4, LiFeSO4F, Li2MSiO4, and LiMBO3 (M = Fe, Mn, and Co). The cell voltages, estimated using Fermi energies, are compared with the results obtained using internal energies and experimental data. The Fermi and internal energies were calculated by DFT (GGA and GGA+U methods).
All the calculations in this work were performed using the full-potential linear augmented plane wave (FP-LAPW) method as implemented in WIEN2k code29 within the framework of DFT.30 Convergence of the self-consistent iterations was performed within 0.0001 Ry. The references that the initial structures were obtained from and the space groups of the structures are given in Table 1. Full relaxation was performed for atomic positions and cell parameters using Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA),31 called the GGA method. The calculations were carried out using GGA31 and GGA plus an on-site Coulomb self-interaction correction potential (GGA+U).32 The U value was considered to be equal to 6 eV for Mn and Co and 5 eV for Fe atom.10,33,34 Spin polarization was considered for transition metals, and major spin was set up. Integrals were calculated over the Brillouin zone with k-points based on the values given in Table 1. More details regarding the calculation methodology are given in the (ESI†)
The general electrochemical charge (for instance) reaction equations for a LIB can be written as eqn (1) and (2) for the cathodic and anodic reactions, respectively. Summing eqn (1) and (2), the general chemical charge reaction equation of a LIB electrode is eqn (3). To calculate the reaction energy (Er), eqn (4) should be used. The item E in eqn (4) should be the Gibbs free energy. In this case, the cell potential (Vocell; it is usually denoted as Eocell, but we changed the denotation to prevent it being mistaken for Er) should be calculated using Eqn 5.19
Assuming perfect structures in the ground-state and fixed crystallographic positions, it can be interpreted that the DFT calculations take place in T = 0 K and P = 0 GPa.39–43 On this basis, the calculated internal energies equal the Gibbs free energies and are used to estimate the reaction energies, i.e., assuming TΔS ≈ 0.41–45 Accordingly, the calculated internal energies are considered for the estimation of cell voltage and reaction energies in the DFT studies (ΔG ≈ ΔU).43,45–47
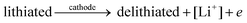 | (1) |
 | (2) |
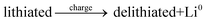 | (3) |
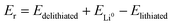 | (4) |
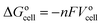 | (5) |
Notably, taking the internal energy values in eV and counting Er for one formula unit, the cell potential (in volts) can be directly calculated by eqn (4) without using eqn (5). It should be noted that computational codes usually report the calculated energy values for one unit cell. In this case, the internal energy value of each component should be divided by the number of formulas per unit cell. Notably, this method should not be employed for the Fermi energy approach.
Let us move toward the estimation of cell voltage by the usage of Fermi energies. There is an opinion that Fermi energy is associated with the (electro)chemical potential.14–21,48,49 On the other hand, cell voltage/potential (and thus the related chemical reaction energy) is indeed the difference between the (electro)chemical potentials of the reactants and products, as indicated by eqn (4). In turn, the potential difference causes the movement of electrons in the electrical circuit. Therefore, it might be deduced that the (electro)chemical reaction energy of the batteries can be calculated/estimated using Fermi energies.
Let us justify this concept in another way. In an electrochemical cell, the component that plays a prominent role in the reaction is the electron (see eqn (1) and (2)). The electron should move between the lithiated and delithiated structures and the Li metal to complete the reaction/circuit. By definition, the Fermi level is the thermodynamic work required to add the electron to the considered body (i.e. the lithiated structure, delithiated structure, and Li metal). Therefore, it is rational that the required energy (potential) to perform the reaction can be estimated by the difference between the Fermi energies. In other words, transferring the electron to a lower energy level causes the electrochemical reaction. Accordingly, the difference between the energy levels should be the electrochemical reaction energy (potential). Hence, due to eqn (1)–(3), the energy level of the electron in the lithiated, delithiated, and Li metal components should be considered. By definition, this energy corresponds to the Fermi energy of the components.
Usage of Fermi energy for the estimation of cell voltage has been considered previously for PV cells.15,16,22 As a matter of fact, it has been rational, since PV cells have been manufactured by joints of different types of semiconductors, and the Fermi level plays an important role in semiconductor assessment. On the other hand, it has been proposed that the lithiated–delithiated junction can be considered a semiconductor junction.11–13,25 Accordingly, the proposed approach herein is a rational deduction from the previous studies on PV and intercalation cells. However, to our knowledge, this paper is the first study that proposes using Fermi energy for the straightforward estimation of the cell voltage of batteries.
According to the above discussion, the basic equation for estimating the cell voltage by the Fermi energy approach should be eqn (4), considering term E as Fermi energy. Here, to calculate the reaction/cell potential in volts, the unit of Fermi energy should be eV. Consequently, using the relevant Fermi energies in eV in eqn (4), the cell voltage can be directly calculated/estimated in volts.
The calculated Fermi energies (eV) for the lithiated and delithiated structures of the considered cathode materials are given in Table 2. The calculated Fermi energy by GGA for Li metal was equal to 0.239 eV. Accordingly, utilizing eqn (4), the cell potentials calculated by the Fermi energy approach for our case studies are given in Table 2.
| Material | Method | Fermi energy (eV) | V cell (V) | |
|---|---|---|---|---|
| Lithiated | Delithiated | By Fermi | ||
| LiCoO2 | GGA | 6.36 | 3.43 | 2.69 |
| GGA+U | 6.14 | 3.72 | 2.18 | |
| LiMnO2 | GGA | 8.26 | 4.97 | 3.05 |
| GGA+U | 7.88 | 4.33 | 3.31 | |
| LiFeO2 | GGA | 7.45 | 4.40 | 2.81 |
| GGA+U | 6.91 | 4.02 | 2.65 | |
| LiNiO2 | GGA | 6.73 | 2.78 | 3.70 |
| GGA+U | 5.80 | 2.91 | 2.65 | |
| NCM | GGA | 6.70 | 3.27 | 3.19 |
| GGA+U | 6.18 | 3.05 | 2.89 | |
| LiMn2O4 | GGA | 6.82 | 3.96 | 2.62 |
| GGA+U | 6.76 | 3.53 | 2.99 | |
| LiFePO4 | GGA | 7.30 | 3.85 | 3.22 |
| GGA+U | 6.04 | 3.12 | 2.67 | |
| LiFeSO4F | GGA | 5.82 | 2.19 | 3.39 |
| GGA+U | 4.49 | 2.16 | 2.09 | |
| Li2FeSiO4 | GGA | 6.33 | 3.34 | 2.75 |
| GGA+U | 4.58 | 2.67 | 1.68 | |
| Li2MnSiO4 | GGA | 6.44 | 3.37 | 2.82 |
| GGA+U | 5.65 | 3.18 | 2.23 | |
| Li2CoSiO4 | GGA | 6.16 | 2.59 | 3.34 |
| GGA+U | 5.29 | 2.59 | 2.47 | |
| LiFeBO3 | GGA | 7.03 | 4.00 | 2.79 |
| GGA+U | 5.83 | 3.02 | 2.57 | |
| LiMnBO3 | GGA | 6.46 | 2.32 | 3.90 |
| GGA+U | 6.19 | 2.47 | 3.48 | |
| LiCoBO3 | GGA | 6.93 | 3.70 | 2.98 |
| GGA+U | 6.14 | 3.05 | 2.85 | |
To validate the proposed Fermi approach, the calculated cell potentials of the considered cathode materials, employing Fermi energies and internal energies, are given in Table 3. For each case, the reported values of the Fermi and internal energies have resulted from the same calculation. An experimental cell voltage value is also given for the sake of comparison. As ref. 3, 4 and 50–53 have proposed, the experimental cell voltage values in Table 3 were taken from the charge potential for low rates. The difference between the Fermi/internal energy cell voltage and the experimental value is also given for more clarity. The lower difference is highlighted by italic and bold type in Table 3.
| Method | Material | Cell voltage (V) | V exp − Vth | |||
|---|---|---|---|---|---|---|
| By Fermi | By I.E. | Experimental | By Fermi | By I.E. | ||
| GGA | LiCoO2 | 2.69 | 3.37 | 3.654 | 0.91 | 0.23 |
| LiMnO2 | 3.05 | 2.34 | 3 and 455 | −0.05 | 0.66 | |
| LiFeO2 | 2.81 | 2.89 | 2.856 | −0.01 | −0.09 | |
| LiNiO2 | 3.70 | 3.00 | 3.957 | 0.20 | 0.90 | |
| NCM | 3.19 | 2.75 | 3.654 | 0.41 | 0.85 | |
| LiMn2O4 | 2.62 | 3.36 | 2.858 | 0.18 | −0.56 | |
| LiFePO4 | 3.22 | 2.93 | 3.4759 | 0.25 | 0.54 | |
| LiFeSO4F | 3.39 | 3.61 | 3.660 | 0.21 | −0.01 | |
| Li2FeSiO4 | 2.75 | 2.69 | 2.8 or 3.110,61 | 0.35 | 0.41 | |
| Li2MnSiO4 | 2.82 | 3.55 | 3 and 4.562 | 0.18 | −0.55 | |
| Li2CoSiO4 | 3.34 | 2.82 | 4.163 | 0.76 | 1.28 | |
| LiFeBO3 | 2.79 | 2.53 | 2.864 | 0.01 | 0.27 | |
| LiMnBO3 | 2.98 | 1.85 | 3.565 | 0.52 | 1.65 | |
| LiCoBO3 | 3.90 | 2.91 | 466 | 0.10 | 1.09 | |
| GGA+U | LiCoO2 | 2.18 | 3.78 | 3.654 | 1.42 | −0.18 |
| LiMnO2 | 3.31 | 2.69 | 3 and 455 | −0.31 | 0.31 | |
| LiFeO2 | 2.65 | 4.00 | 2.856 | 0.15 | −1.20 | |
| LiNiO2 | 2.61 | 3.86 | 3.957 | 1.29 | 0.04 | |
| NCM | 2.89 | 3.73 | 3.654 | 0.71 | −0.13 | |
| LiMn2O4 | 2.99 | 3.35 | 2.858 | −0.19 | −0.55 | |
| LiFePO4 | 2.67 | 2.96 | 3.4759 | 0.80 | 0.51 | |
| LiFeSO4F | 2.09 | 3.87 | 3.660 | 1.51 | −0.27 | |
| Li2FeSiO4 | 1.68 | 3.12 | 2.8 or 3.110,61 | 1.42 | −0.02 | |
| Li2MnSiO4 | 2.23 | 4.37 | 3 and 4.562 | 0.77 | −1.37 or 0.13 | |
| Li2CoSiO4 | 2.47 | 4.02 | 4.163 | 1.63 | 0.08 | |
| LiFeBO3 | 2.57 | 2.58 | 2.864 | 0.23 | 0.22 | |
| LiMnBO3 | 2.85 | 2.75 | 3.565 | 0.65 | 0.75 | |
| LiCoBO3 | 3.48 | 4.10 | 466 | 0.52 | −0.10 | |
In the case of Li2FeSiO4, the difference between the cell voltage for the first (3.1 V) and second (2.8 V) cycles was remarkable. Here, we considered the first cycle voltage since it is nearer to the theoretical voltage.50
According to Tables 2 and 3, for the GGA+U calculations, the Fermi approach's estimated cell voltage values are mostly lower than that of the internal energy approach. Except LiMnO2, and LiMn2O4, in the Fermi approach, the estimated cell voltage value by GGA+U is lower than that obtained by the GGA method. The inverse order was obtained for the internal energy approach, i.e. cell voltage estimated by GGA+U is usually higher than that of GGA (except LiMn2O4).
By taking into account the reported experimental values in Table 3, generally speaking, the Fermi approach with the GGA and GGA+U methods underestimated the cell voltage. Evidently, in the Fermi approach framework, GGA calculations estimated the cell voltage more accurately than the GGA+U ones. According to the results, we found the Fermi approach by the GGA method to be the most accurate approximation of the cell voltage.
Regarding the internal energy approach, the GGA+U method commonly overestimated the cell voltages. On the other hand, the GGA method usually underestimated the values. Generally, in the internal energy approach, unlike the Fermi approach, GGA+U calculations seem to make better approximations than GGA.
As far as the GGA method is considered, the Fermi approach made a better cell voltage approximation than the internal energy approach. On the other hand, in the framework of the GGA+U method, it seems that the internal energy approach maybe performs a better approximation than the Fermi approach.
Notably, the calculated cell voltage values may be tuned by changing the relevant parameters of the computational calculation, such as the relaxation process. As another example, in our case (Wien2K code), changing the RMT parameter may limitedly adjust the values. Here, we used regular calculation parameters with rational parameters and took the Fermi and internal energy values from the same calculation.
Conclusions
According to the above discussion, the Fermi approach is an adequate approach to estimate the cell voltage of intercalation batteries. For our case studies, calculating cell voltage by the Fermi approach and GGA method made better approximations than the common internal energy approach. However, generally, in the Fermi approach framework, GGA+U underestimated the cell voltages (in contrast with the internal energy approach where GGA+U overestimated the values). Despite this conclusion, it is worth noting that for the approaches that consider the lithiated–delithiated joint as a semiconductor junction and align the Fermi level for the DOS diagrams,7,11–13,67 using the Fermi approach for cell voltage approximation is unavoidable even for the GGA+U method. In other words, aligning the Fermi level in the DOS diagrams is mandatory for evaluations in such approaches. Indeed, by this alignment, the Fermi approach's cell voltage was assumed inevitably.This paper may open new landscapes for future investigations. The Fermi approach may justify some voltage behaviours which cannot be explained by previous approaches. Furthermore, cell voltage can be estimated and reported by the Fermi approach in ab initio studies. It can be used to evaluate the influence of the effective parameters, e.g., electrode composition, additives, compositing, current-collector nature, etc., on battery cell voltages. The stated parameters may affect the cell voltage by affecting the Fermi level. Additionally, this approach may help understand the underlying mechanisms of the corresponding electrochemical systems. On this basis, this concept may help design new generations of batteries.
Author contributions
Mohammad Mahdi Kalantarian: Term, conceptualization, methodology, validation, formal analysis, investigation, writing – original draft, writing – review & editing, supervision, project administration, funding acquisition. Amir Haghipour: writing – review & editing, formal analysis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from Materials and Energy Research Center (MERC, Iran) through an internal grant (Project No. 391398001) is gratefully acknowledged. The authors acknowledge access to WIEN2k code.Notes and references
- H. Ji, J. Wu, Z. Cai, J. Liu, D.-H. Kwon, H. Kim, A. Urban, J. K. Papp, E. Foley and Y. Tian, Nat. Energy, 2020, 5, 213–221 CrossRef CAS.
- G. Assat and J.-M. Tarascon, Nat. Energy, 2018, 3, 373–386 CrossRef CAS.
- M. M. Kalantarian, A. Haghipour and M. TaherTalari, in press, 2021.
- M. M. Kalantarian, H. Yousefi-Mashhour, M. Tahertalari and P. Mustarelli, J. Energy Storage, 2021, 42, 103055 CrossRef.
- V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243–3262 RSC.
- M. M. Kalantarian, S. Asgari and P. Mustarelli, J. Mater. Chem. A, 2013, 1, 2847–2855 RSC.
- M. M. Kalantarian, M. Oghbaei, S. Asgari, S. Ferrari, D. Capsoni and P. Mustarelli, J. Mater. Chem. A, 2014, 2, 19451–19460 RSC.
- A. Jain, Y. Shin and K. A. Persson, Nat. Rev. Mater., 2016, 1, 15004 CrossRef CAS.
- Y. S. Meng and M. E. Arroyo-de Dompablo, Energy Environ. Sci., 2009, 2, 589–609 RSC.
- M. M. Kalantarian, S. Asgari, D. Capsoni and P. Mustarelli, Phys. Chem. Chem. Phys., 2013, 15, 8035–8041 RSC.
- M. Momeni, H. Y. Mashhour and M. M. Kalantarian, J. Alloys Compd., 2019, 787, 738–743 CrossRef CAS.
- H. Yousefi Mashhour and M. M. Kalantarian, Phys. Chem. Chem. Phys., 2021, 23, 16013–16022 RSC.
- M. M. Kalantarian, H. Y. Mashhour and M. H. Barjini, Ceram. Int., 2020, 46, 15222–15227 CrossRef CAS.
- M. Braga, N. Grundish, A. Murchison and J. Goodenough, Materials Theory, 2019, vol. 3, pp. 1–15 Search PubMed.
- J. A. Nelson, The physics of solar cells, World Scientific Publishing Company, 2003 Search PubMed.
- A. H. Smets, K. Jäger, O. Isabella, R. A. Swaaij and M. Zeman, Solar Energy: The physics and engineering of photovoltaic conversion, technologies and systems, UIT Cambridge, 2015 Search PubMed.
- S. Al-Hilli and M. Willander, Sensors, 2009, 9, 7445–7480 CrossRef CAS.
- P. Peljo, J. A. Manzanares and H. H. Girault, Chem. Sci., 2017, 8, 4795–4803 RSC.
- G. Cherkashinin, R. Hausbrand and W. Jaegermann, J. Electrochem. Soc., 2019, 166, A5308 CrossRef CAS.
- S. Khan, R. Kainthla and J. Bockris, J. Phys. Chem., 1987, 91, 5974–5977 CrossRef CAS.
- P. Peljo and H. H. Girault, Energy Environ. Sci., 2018, 11, 2306–2309 RSC.
- J. Bisquert, The Physics of Solar Energy Conversion, CRC Press, 2020 Search PubMed.
- S. Matsushita, S. Sugawara, T. Ikeda, T. Araki, H. Sekiya, H. Kohata, T. Isobe and A. Nakajima, Chem. Lett., 2020, 49, 1013–1016 CrossRef CAS.
- J. B. Goodenough and Y. Kim, J. Power Sources, 2011, 196, 6688–6694 CrossRef CAS.
- M. M. Kalantarian, S. Asgari and P. Mustarelli, J. Mater. Chem. A, 2014, 2, 107–115 RSC.
- L. Zhang, S. Zheng, L. Wang, H. Tang, H. Xue, G. Wang and H. Pang, Small, 2017, 13, 1700917 CrossRef.
- Z. Zhang, W. Li, T.-W. Ng, W. Kang, C.-S. Lee and W. Zhang, J. Mater. Chem. A, 2015, 3, 20527–20534 RSC.
- M. Muhibbullah and A. M. A. Haleem, Trans. Mater. Res. Soc. Jpn., 2015, 40, 247–252 CrossRef CAS.
- P. Blaha, K. Schwarz, G. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, An augmented plane wave plus local orbitals program for calculating crystal properties, Vienna University of Technology, Austria, 2001 Search PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- V. Anisimov, I. Solovyev, M. Korotin, M. Czyżyk and G. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 16929 CrossRef CAS PubMed.
- C. Eames, A. Armstrong, P. Bruce and M. Islam, Chem. Mater., 2012, 24, 2155–2161 CrossRef CAS.
- Y. S. Meng and M. E. Arroyo-de Dompablo, Acc. Chem. Res., 2013, 46, 1171–1180 CrossRef CAS.
- J. Akimoto, Y. Gotoh and Y. Oosawa, J. Solid State Chem., 1998, 141, 298–302 CrossRef CAS.
- H. Björk, T. Gustafsson, J. O. Thomas, S. Lidin and V. Petříček, J. Mater. Chem., 2003, 13, 585–589 RSC.
- Y. Piffard, K. K. Rangan, Y. An, D. Guyomard and M. Tournoux, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1998, 54, 1561–1563 CrossRef.
- R. Tripathi, G. Popov, X. Sun, D. H. Ryan and L. F. Nazar, J. Mater. Chem. A, 2013, 1, 2990–2994 RSC.
- J. S. G. Myrdal, D. Blanchard, D. Sveinbjornsson and T. Vegge, J. Phys. Chem. C, 2013, 117, 9084–9091 CrossRef CAS.
- S. Kirklin, B. Meredig and C. Wolverton, Adv. Energy Mater., 2013, 3, 252–262 CrossRef CAS.
- E. M. Siriwardane, I. Demiroglu, C. Sevik, F. M. Peeters and D. Çakır, J. Phys. Chem. C, 2020, 124, 21293–21304 CrossRef CAS.
- H. Benzidi, M. Lakhal, M. Garara, M. Abdellaoui, A. Benyoussef and O. Mounkachi, Phys. Chem. Chem. Phys., 2019, 21, 19951–19962 RSC.
- A. Urban, D.-H. Seo and G. Ceder, npj Comput. Mater., 2016, 2, 1–13 CrossRef.
- R. Longo, F. Kong, K. Santosh, M. Park, J. Yoon, D.-H. Yeon, J.-H. Park, S.-G. Doo and K. Cho, Phys. Chem. Chem. Phys., 2014, 16, 11233–11242 RSC.
- M. H. Alfaruqi, S. Kim, S. Park, S. Lee, J. Lee, J.-Y. Hwang, Y.-K. Sun and J. Kim, ACS Appl. Mater. Interfaces, 2020, 12, 16376–16386 CrossRef CAS PubMed.
- S. Gao, G. Shi and H. Fang, Nanoscale, 2016, 8, 1451–1455 RSC.
- G. Ramos-Sanchez, A. Callejas-Tovar, L. Scanlon and P. Balbuena, Phys. Chem. Chem. Phys., 2014, 16, 743–752 RSC.
- J. Gao, S.-Q. Shi and H. Li, Chin. Phys. B, 2015, 25, 018210 CrossRef.
- J. O. M. Bockris and S. U. Khan, Appl. Phys. Lett., 1983, 42, 124–125 CrossRef CAS.
- M. M. Kalantarian and H. Yousefi Mashhour, Electrochim. Acta, 2020, 343, 136127 CrossRef CAS.
- M. M. Kalantarian, M. Momeni, A. Haghipour and H. Yousefi Mashhour, in press.
- W. Dreyer, J. Jamnik, C. Guhlke, R. Huth, J. Moškon and M. Gaberšček, Nat. Mater., 2010, 9, 448–453 CrossRef CAS PubMed.
- M. M. Kalantarian, H. Yousefi Mashhour, H. Shahroudi, N. Osanloo and P. Mustarelli, Phys. Chem. Chem. Phys., 2020, 22, 6351–6360 RSC.
- N. Nitta, F. Wu, J. T. Lee and G. Yushin, Mater. Today, 2015, 18, 252–264 CrossRef CAS.
- G. Vitins and K. West, J. Electrochem. Soc., 1997, 144, 2587 CrossRef CAS.
- T. Matsumura, R. Kanno, Y. Inaba, Y. Kawamoto and M. Takano, J. Electrochem. Soc., 2002, 149, A1509 CrossRef CAS.
- H. Liu, Z. Zhang, Z. Gong and Y. Yang, Electrochem. Solid-State Lett., 2004, 7, A190 CrossRef CAS.
- F. Luo, C. Wei, C. Zhang, H. Gao, J. Niu, W. Ma, Z. Peng, Y. Bai and Z. Zhang, J. Energy Chem., 2020, 44, 138–146 CrossRef.
- T. Sasaki, Y. Ukyo and P. Novák, Nat. Mater., 2013, 12, 569–575 CrossRef CAS PubMed.
- N. Recham, J.-N. Chotard, L. Dupont, C. Delacourt, W. Walker, M. Armand and J.-M. Tarascon, Nat. Mater., 2009, 9, 68–74 CrossRef PubMed.
- A. Nytén, A. Abouimrane, M. Armand, T. Gustafsson and J. O. Thomas, Electrochem. Commun., 2005, 7, 156–160 CrossRef.
- P. Ghosh, S. Mahanty and R. N. Basu, J. Electrochem. Soc., 2009, 156, A677 CrossRef CAS.
- Z. Gong, Y. Li and Y. Yang, J. Power Sources, 2007, 174, 524–527 CrossRef CAS.
- A. Yamada, N. Iwane, Y. Harada, S. I. Nishimura, Y. Koyama and I. Tanaka, Adv. Mater., 2010, 22, 3583–3587 CrossRef CAS PubMed.
- Y.-S. Lee and H. Lee, Mater. Lett., 2014, 132, 401–404 CrossRef CAS.
- S. Afyon, C. Mensing, F. Krumeich and R. Nesper, Solid State Ionics, 2014, 256, 103–108 CrossRef CAS.
- M. M. Kalantarian, M. Hafizi Barjini and M. Momeni, ACS Omega, 2020, 5, 8952–8961 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04800g |
| This journal is © the Owner Societies 2022 |

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif)