Open Access Article
Open Access ArticleThe photodissociation of solvated cyclopropanone and its hydrate explored via non-adiabatic molecular dynamics using ΔSCF
Eva
Vandaele
 ,
Momir
Mališ
and
Sandra
Luber
,
Momir
Mališ
and
Sandra
Luber
 *
*
Department of Chemistry, University of Zürich, Winterthurerstrasse 190, 8057 Zürich, Switzerland. E-mail: sandra.luber@chem.uzh.ch
First published on 18th February 2022
Abstract
The decay of cyclopropanone is a typical example of a photodecomposition process. Ethylene and carbon monoxide are formed following the excitation to the first singlet excited state through a symmetrical or asymmetrical pathway. The results obtained with non-adiabatic molecular dynamics (NAMD) using the delta self-consistent field (ΔSCF) method correspond well to previous experimental and multireference theoretical studies carried out in the gas phase. Moreover, this efficient methodology allows NAMD simulations of cyclopropanone in aqueous solution to be performed, which reveal analogue deactivation mechanisms, but a shorter lifetime and reduced photodissociation as compared to the gas-phase. The excited state dynamics of cyclopropanone hydrate, an enzyme inhibitor, in an aqueous environment are reported as well. Cyclopropanone hydrate strongly interacts with the surrounding solvent via the formation of hydrogen bonds. Excitation to the first singlet excited state shows an asymmetric pathway with cyclopropanone hydrate and propionic acid as the main photoproducts.
1 Introduction
Cyclopropanone is the smallest cyclic ketone and is known for its high reactivity.1 In fact, it was first studied as a reaction intermediate,2–4e.g. in the Favorskii reaction,5 before a synthetic method was developed.6,7 Cyclopropanone can be examined at low temperatures or after the addition of polymerisation inhibitors. It is also formed from ethylene and carbon monoxide in interstellar ice, where astrophysicists identified it as a tracer for rapid low temperature non-equilibrium synthesis.8 An experimental study of the gas-phase photochemistry yielded ethylene, carbon monoxide and polymers as photoproducts.9 However, polycyclopropanone was formed in negligible amounts and was ascribed to the thermal reaction. Fluorescence was observed only at wavelengths above 365 nm.10,11 Based on the rapid photolysis with a reaction time of ≤200 ps, a predissociation process to a biradical was proposed, in contrast to the intersystem crossing mechanism of other cyclic ketones.9,12 The excitation to the 1(n→π*) state weakens the lateral C–C bond (i.e. the C–C bond adjacent to the carbonyl group) strength of the already strained cyclopropanone resulting in the asymmetric dissociation.After the first few experimental studies, several types of computational investigations on the photodissociation of a cyclopropanone molecule were performed as well.9–11,13–15 A minimum-energy conical intersection (MECI) near the first singlet excited state (S1) minimum promoting ultrafast internal conversion was identified with complete active space self-consistent field (CASSCF) calculations.10 Upon excitation to the S1 state, a fast non-radiative relaxation process, internal conversion and dissociation in the ground state were observed using non-adiabatic molecular dynamics (NAMD). The S1 minimum and CI geometries exhibit an out-of-plane oxygen position. A successive state-averaged CASSCF study identified a second MECI and corresponding decarbonylation mechanism.11 The second pathway is comprised of a symmetrical structure where the lateral C–C bonds are broken simultaneously. Whereas the multistate multireference complete active space second-order perturbation (MS-MR-CASPT2) method provided a lower energy for the asymmetrical CI, ensemble density functional theory (DFT) returned an insignificant energy difference.13 Nevertheless, both methods found that the majority of the trajectories decay through the former mechanism in the surface hopping calculations. Hopping events were found to fit a bi-Gaussian curve, while the S1 population follows a biexponential decay function with lifetimes of 33 fs and 95 fs.13
Once the existence and molecular structure of cyclopropanone were confirmed in the mid-1960s, the reactivity with a range of electrophiles and nucleophiles in various media was studied.16–18 The first experiments in aqueous environment generated an adduct without ring opening at the low yield of approximately 30%.19 Later studies found that the 1,1-dihydroxycyclopropane is stable in water for several days, after which propionic acid is slowly formed.2,20 Biochemists use cyclopropanone hydrate to design enzyme inhibitors.21–24 The hydrate yield depends on the water–cyclopropanone ratio. Purification of the hydrate at room temperature, heating or basic conditions result in isomerisation to propionic acid.2,21,25 Polymerisation of the hydrate into dihydroxy ether was observed using traces of water in the presence of methylene chloride.25 To the best of our knowledge, no quantitative data on the equilibrium constant between cyclopropanone and cyclopropanone hydrate in an aqueous environment is available. Therefore, the photodynamics of both the hydrate and cyclopropanone in water were simulated in this work.
To date, only cyclopropanone in a vacuum has been explored by means of NAMD. Quantum mechanics/molecular mechanics (QM/MM) is the most popular method to perform NAMD calculations of molecules in solution.26–28 Nevertheless, as the photodynamics is unknown, the prior partitioning of the system and the deficient description of polarisation effects could result in inadequate conclusions regarding the photodissociation process of cyclopropanone and its hydrate in an aqueous environment.29 The delta self-consistent field (ΔSCF) method has been successfully applied to examine surface hopping dynamics in solvated systems with full atomistic DFT simulations, using a mixed Gaussian and plane wave approach.30,31 The method can be a more accurate alternative to QM/MM, while still computationally efficient, for the description of liquids or other systems obeying periodic boundary conditions.
2 Methods
2.1 Theory
NAMD is a popular method to investigate the time evolution of electronic populations after photoexcitation.32,33 It is a non-Born–Oppenheimer, mixed quantum-classical approach, in which the nuclei are propagated classically based on the quantum mechanically calculated electronic structure. More specifically, the nuclear coordinates are updated using the gradients of the occupied electronic state. Non-adiabatic transitions between electronic states are stochastic and instantaneous.34 A multitude of independent trajectories are propagated to derive statistically relevant conclusions. Of the various NAMD algorithms and formulations, Tully's fewest-switches surface-hopping (TFSSH)35 was used in this work.The time evolution of the electronic wavefunction |Ψ(r;t;R)〉 is obtained by expansion in a linear combination of adiabatic electronic eigenfunctions |ψi(Rt)〉 corresponding to electronic state i with energy Ei
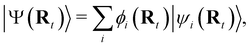 | (1) |
| Ĥe(Rt)|ψi(Rt)〉 = Ei(Rt)|ψi(Rt)〉, | (2) |
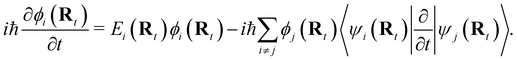 | (3) |
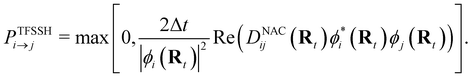 | (4) |
2.2 ΔSCF
In NAMD, the trajectories are propagated on-the-fly. To be more precise, the state coefficients and nuclear coordinates are evolved simultaneously based on the state energies, gradients and NACs calculated at each integration step. Hence, the accuracy of the dynamics is determined by the underlying electronic structure theory. The DFT-based ΔSCF method is a variational method that independently optimizes excited state electronic densities (ρi(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) corresponding to electronic state i).38–45 Excited electronic states of systems with discrete eigenstates are obtained by a Kohn–Sham (KS) DFT optimisation with non-Aufbau fixed KS molecular orbital (MO) occupations (nij corresponding to KS MO φij(
) corresponding to electronic state i).38–45 Excited electronic states of systems with discrete eigenstates are obtained by a Kohn–Sham (KS) DFT optimisation with non-Aufbau fixed KS molecular orbital (MO) occupations (nij corresponding to KS MO φij(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )) using the ground-state algorithms, so that the total final electron density resembles that of a certain excited electronic state i.
)) using the ground-state algorithms, so that the total final electron density resembles that of a certain excited electronic state i.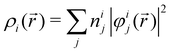 | (5) |
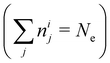 and each KS MO φij(
and each KS MO φij(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is an eigenfunction of the KS equation corresponding to eigenenergy εij
) is an eigenfunction of the KS equation corresponding to eigenenergy εij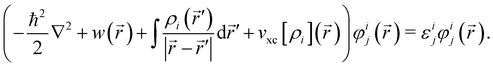 | (6) |
The kinetic energy operator for non-interacting electrons, the external electrostatic interaction, electron–electron repulsion and exchange–correlation potentials are summed in the left-hand side respectively.
To reproduce the desired electronic state multiplicity, the individual electron spin densities must also match the spin properties of the targeted excited electronic state. In the case of singlet excited electronic states the alpha and beta spin densities must be equal. This can be assured by using the restricted KS formulation,43,46,47 while by using rounded MO occupation numbers, a single Slater determinant is adequate to approximate the wave function of a single reference excited electronic state.30 MO occupation numbers for the excited state, either fractional or rounded, have to be provided, for example using time-dependent DFT (TDDFT).30 ΔSCF has provided good results for a variety of systems,48–50 thereby showing an improved performance as compared to TDDFT e.g. for the description of low-lying charge transfer states,51,52 and for NAMD studies in the liquid phase.30,31,44
2.3 Transition dipole moment
As the electronic states optimised by ΔSCF are not mutually orthogonal, a procedure to expand the excited state's approximated Slater determinant into a linear combination of singly-excited Slater determinants constructed from ground state KS MOs has been recently developed in our group.53 This alleviates the non-orthogonality between the ground and excited electronic ΔSCF states. The transition dipole moment (TDM) operator![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e0b3.gif) between the ground and singlet excited state i is given by
between the ground and singlet excited state i is given by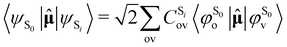 | (7) |
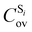 being the expansion coefficients from the projection of the singlet ΔSCF excited electronic state Slater determinant ψSi onto the singly-excited Slater determinants constructed by promoting one electron from the ground state KS occupied (o) MO
being the expansion coefficients from the projection of the singlet ΔSCF excited electronic state Slater determinant ψSi onto the singly-excited Slater determinants constructed by promoting one electron from the ground state KS occupied (o) MO 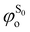 to a virtual (v) MO
to a virtual (v) MO 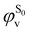 ,
,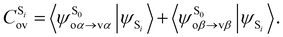 | (8) |
Depending on the exact dipole moment operator ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e0b3.gif) , the oscillator strength of the excitation in the length representation
, the oscillator strength of the excitation in the length representation 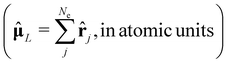 then is
then is
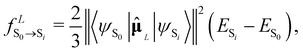 | (9) |
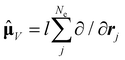 , in atomic units)
, in atomic units) 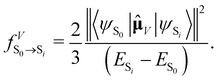 | (10) |
The procedure can be applied to calculate various observables, including the spin–orbit coupling between singlet and triplet states.53
2.4 Computational settings
The NAMD calculations were performed by the Zagreb surface hopping code54 interfaced with a modified version of the CP2K program package.55 A new interface script was written in Python to couple the codes in a simpler and versatile manner. The interface script provides the input geometry and setup to the CP2K code, and reads the energies, nuclear gradients and KS MO coefficients. It calculates the NAC terms using the Tully–Hammes-Schiffer approximation56 and provides all the required components to the NAMD code. The same Python script was used for the calculation of absorption spectra with expressions (9) and (10). Phases between KS MOs of consecutive steps are adjusted to maintain the NAC continuity. All DFT and ΔSCF electronic structure calculations were performed with CP2K.Initial gas-phase configurations were sampled from the thermalised Wigner distribution at 300 K, based on the projected Hessian obtained at a ground electronic state optimised geometry at the BLYP/TZV2P-GTH level of theory.57,58 Since the mixed Gaussian and plane wave method for DFT as implemented in the CP2K programme was used, the cyclopropanone molecule was confined at the center of a non-periodic cubic box with a side length of 15 Å.
Initial configurations for the condensed phase were sampled from DFT-MD simulations. The solutes were centered in a pre-equilibrated box containing 32 water molecules at ambient conditions, thereby replacing 7 water molecules. The cubic box was relaxed using the isotropic isothermal–isobaric (NPT) ensemble at 300 K and 1 bar, using corresponding Nose–Hoover algorithms with time constants of 20 fs and 200 fs for the thermostat and barostat respectively and a 0.5 fs timestep at the BLYP/TZV2P-GTH level of theory. The 250 final initial phase space points were evenly spaced sampled from a 45 ps long trajectory using the canonical ensemble (NVT) at 300 K with a fixed cell box length of 9.26 Å and 9.12 Å for the solvated cyclopropanone and cyclopropanone hydrate respectively.
The UV absorption spectrum was constructed from the initial conformations, as sampled from the Wigner distribution or DFT-MD NVT trajectories, by calculating the wavelengths and corresponding oscillator strengths of the first singlet excitation at the BLYP/TZV2P-GTH level of theory. The spectra were broadened using a Lorentzian function with a half-width at half-maximum height of 10 nm.
The TFSSH algorithm, with a 0.5 fs timestep, was used for all trajectories which were propagated for 500 steps. For each system, 250 NAMD trajectories were propagated. ΔSCF single point calculations were performed at the B3LYP/TZV2P-GTH level of theory using the Goedecker–Teter–Hutter pseudopotentials and Grimme D3 dispersion correction without damping.59,60 These settings lead to good agreement with experimental data in previous hybrid Gaussian plane wave simulations of liquid water.61,62 The Coulomb potential was truncated at 10 Å and a 500 Ry cutoff for the plane wave basis was set.
In analogy to previous studies, only the ground and first singlet excited state populations were evolved in the NAMD.10,11,13–15 The optimised ground state MOs served as an initial guess for the optimisation of the excited state. The first singlet excited state was obtained by promoting an electron from the highest occupied MO (HOMO) to the lowest unoccupied MO (LUMO). By default, the SCF was performed using the standard diagonalisation method in CP2K,63 where density mixing was employed for each SCF iteration and the mixing fraction of the new density was reduced from 0.4 to 0.1 after 25 steps. The interface script calling CP2K on the fly contained an SCF convergence procedure, which was automatically applied in case the default SCF energy minimisation could not converge.30 In the case of energy oscillations, the fraction of new density included in the density mixing procedure was further reduced. In the case of convergence problems, a level shift of 0.1 Hartree during the SCF convergence, the orbital transformation method and the self-consistent subspace refinement by diagonalisation of the Hamiltonian were consecutively tried. The trajectory was discarded if no method converged. Trajectories with cumbersome excited state convergence after deexcitation to the ground electronic state were further propagated using DFT-MD.
The MECI structures were obtained at the ΔSCF level with the aid of the CIOpt programme.64 TDDFT calculations were performed in Turbomole,65 while the state-averaged CASSCF results were obtained using Gaussian66 and the extended multistate complete active space second-order perturbation theory (XMS-CASPT2) results were calculated using the BAGEL programme.67 For the latter two methods, an active space consisting of eight electrons in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O π and π* orbitals, the σ and σ* orbitals of both lateral C–C bonds, and one non-bonding n orbital on the oxygen atom has been used, in analogy to previous cyclopropanone studies.14,15 The def2-TZVPP basis set68 was used with Turbomole and Gaussian, while TZVPP69 was used with BAGEL. The XMS-CASPT2 based NAMD studies were performed by coupling the BAGEL electronic structure programme67,70–72 to the Zagreb surface hopping code.54
O π and π* orbitals, the σ and σ* orbitals of both lateral C–C bonds, and one non-bonding n orbital on the oxygen atom has been used, in analogy to previous cyclopropanone studies.14,15 The def2-TZVPP basis set68 was used with Turbomole and Gaussian, while TZVPP69 was used with BAGEL. The XMS-CASPT2 based NAMD studies were performed by coupling the BAGEL electronic structure programme67,70–72 to the Zagreb surface hopping code.54
3 Results and discussion
3.1 Cyclopropanone in a vacuum
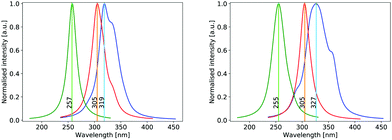
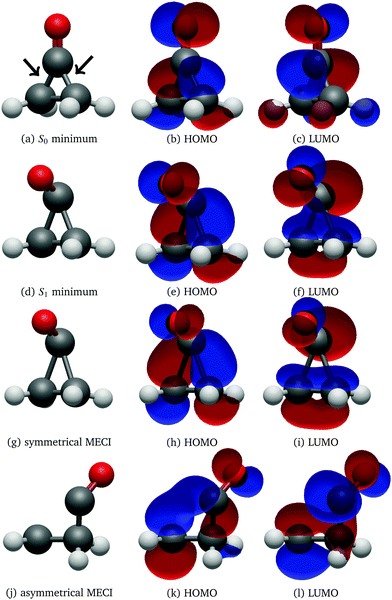
The UV absorption spectrum of isolated cyclopropanone was calculated from the 250 sampled NAMD initial configurations using the procedure for calculating the TDM detailed above. Its absorption spectra in both the length and the velocity representation are very similar to the experimental and theoretical spectra in ref. 13. The maxima are red-shifted by 7 nm and 15 nm for the length and velocity representations respectively as compared to the experimental value of 312 nm, as indicated in Fig. 1. Hence, the initial conditions sampled for the NAMD form a good representation for the distribution of the cyclopropanone excitation energies.The optimised geometries and corresponding frontier orbitals at the minima and MECIs as obtained with the B3LYP/TZV2P-GTH ΔSCF method are depicted in Fig. 2. The geometrical parameters at the S0 minimum correspond well to experimental values obtained from microwave spectral data,73 as listed in Table 1. The optimised S1 minimum geometry is characterised by slightly elongated lateral C–C bonds as compared to previous theoretical results (1.7 Å with ΔSCF versus 1.6 Å at the CASSCF(10,8)10 and the SSR-ωPBEh13 levels of theory). Consequently, the lateral C–C bond lengths at the symmetrical MECI are equally elongated by ∼0.1 Å as compared to multireference results (1.9 Å with ΔSCF versus 1.8 Å and 1.7 Å optimised with SA-CASSCF(8,7)11 and SSR-ωPBEh13 methods respectively). At the asymmetrical MECI the lateral C–C bond lengths are in line with the SA-CASSCF(8,7)11 results (1.4 Å versus 1.5 Å and 2.3 Å versus 2.2 Å obtained with ΔSCF and SA-CASSCF(8,7) respectively), whereas a smaller difference between both bonds was measured using the ensemble DFT method.13 The asymmetric MECI is about 0.3 eV more stable than the symmetric MECI at the ΔSCF B3LYP/TZV2P-GTH level, comparable to 0.7 eV at the MS-MR-CASPT2/cc-pVDZ level11 and 0.09 eV at the SSR-ωPBEh/6-31G* level.13 There is no significant difference in electronic structure at these stationary points, analogous to previous results.13
After 500 propagation steps (250 fs of simulation time) 29 trajectories out of 250 still remained in the S1 state. In fact, 14 trajectories never hopped to the ground state despite passing through several CIs, while the other 15 have reactivated back to S1 through the second CI shortly after hopping to the ground electronic state via the first CI, as the time between the two CI encounters was insufficient to effectively redistribute the excess electronic energy into vibrational degrees of freedom. With the exception of two trajectories, all trajectories displayed carbon monoxide ejection, which is cleaved off in the first excited state. All NAMD trajectories started with the pyramidalisation of the carbonyl C atom and prolongation of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond length, a ubiquitous pattern of the n→π* C
O bond length, a ubiquitous pattern of the n→π* C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group excited state, as visualised in Fig. 2.74
O group excited state, as visualised in Fig. 2.74
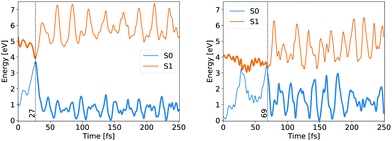
Whether the lateral C–C bond lengths stay equal or start to deviate, the trajectory takes the symmetric or the asymmetric pathway. Distinction between the two mechanisms was made on the complete evolution of lateral C–C bond lengths. If their difference did not exceed 0.1 Å while both were still shorter than 2 Å then the mechanism was classified as symmetric, otherwise as asymmetric. 54 trajectories evolved initially within the first criteria, while the remaining 193 fell under the latter, giving the same ratio between symmetric and asymmetric pathways as counted by Filatov and coauthors which distinguished between the two pathways based on the difference of lateral C–C bond lengths at the CI points while omitting other details.13 We avoided such a simplified criterion, but rather used the full evolution of each system to distinguish between pathways, because the symmetric and asymmetric MECIs belong to the same CI seam, differing just slightly in energy, as discussed above. The energy evolution of exemplary NAMD trajectories undergoing symmetric and asymmetric pathways is shown in Fig. 3.
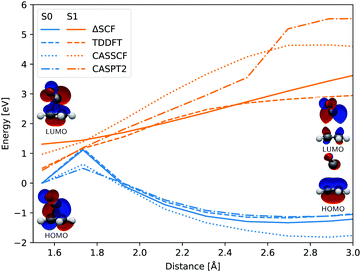
In both cases the electronic ground state energy increases while the first excited state decreases, closing the gap between the two states as the system moves towards the S1 excited state local minimum, shown in Fig. 2. The S1 minimum is Cs symmetric, with an out of cyclopropane plane positioned CO group lying in the reflection plane that intersects the distal C–C bond (i.e. the C–C bond not adjacent to the carbonyl group). The C atom of the CO group is displaced from ethylene by an additional 0.3 Å compared to the ground state minimum structure. Any further extension brings the system to the CI between the S1 and S0 states, which at the ΔSCF level is just 0.1 eV above the S1 minimum. Given that the sampled population excitation energy in its starting Franck–Condon region is on average 1.48 eV (individual trajectories range from 0.80 to 3.24 eV) above the S1 minimum energy, the CI seam with the ground electronic state is easily accessible. Trajectories exhibiting an immediate SH to the ground state continue distancing the CO group further from ethylene. In fact, the cleavage is accelerated by the repulsive nature of the ground state gradient in this configuration region. The CO group dissociation is mostly symmetrical with the lateral C–C bonds extending simultaneously, and as the CO group has gained initial angular momentum in rotation out of the carbon atoms plane during the motion towards the S1 minimum, it continues to rotate in the initial Cs plane after splitting from ethylene. Because the system contained no initial angular momentum, the ethylene rotates in the counter direction around its newly formed double carbon bond canceling the system's total angular momentum. The ethylene double bond shows an increase in vibrational amplitude, while it diminishes in the cleaved CO. Those trajectories that overshoot the first CI and remained in the S1 state also continue with the CO dissociation although the pattern is more asymmetric. This is because the symmetrical stretch of the CO from ethylene within the reflection plane in the S1 state is not dissociative. In fact, the S1 energy rises at the ΔSCF level as observed from a detailed analysis of the CO dissociation by symmetrically increasing the distance between the carbon CO atom and the midpoint of the distal C–C bond in the S1 minimum structure (see Fig. 4). The same trend is reproduced with state-averaged CASSCF, XMS-CASPT2 and TDDFT applying the hybrid B3LYP functional. All three methods agree on the state character change from the localised CO n→π* to a charge transfer from an ethylene localised π MO to a CO localised π* MO, which occurs adiabaticaly around the CI. At the CASSCF and CASPT2 levels, the flattened S1 line starting from a distance of 2.7 Å and 2.9 Å respectively corresponds to a π→π* excitation localised on CO. At short distances, the inclusion of dynamic correlation by the CASPT2 method reduces the excitation energy as compared to the CASSCF results. A steep increase in the S1 energy calculated with the CASPT2 method between 2.5 Å and 2.9 Å is remarked. Whereas several orbitals in the active space at a distance of 2.5 Å involve contributions from both molecules, they are located on either the carbon monoxide or the ethylene molecule at a distance of 2.9 Å.
Steered by the repulsive symmetrical S1 CO dissociation part, the CO dissociation continues asymmetrically in the excited state and one of the lateral C–C bonds breaks before the other. In this process, an excitation transfer from the CO to the ethylene is observed, adiabatically changing from the CO n→π* excitation character to π→π* of the ethylene S1 excited state. With the electronic excitation transferred on ethylene, it starts to move towards its local S1 minimum with a profound torsion between the two CH2 groups. Because a CI with the ground electronic state resides near this minimum, a non-adiabatic transition to S0 can easily occur when the torsional angle between the two CH2 groups approaches 90°. If the SH happens, the ethylene reforms its double carbon bond and repositions its CH2 groups into their mutual plane, with extensive torsional vibrations as the system tries to reach its ground state minimum. The CO dissociation continues as there is no strong interaction between the two systems in the ground state. If, however, no NA transition takes place at the ethylene type CI, the two CH2 groups continue twisting around the C–C bond in the excited state, as being barrierless, until another ethylene type CI is reached as the ground state energy rises periodically with torsion of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond.
C bond.
A randomly selected subset of trajectories have also been propagated using the XMS-CASPT2(8,7) method.70–72 The resulting deexcitation pathways were analogous to the observations detailed above.
3.2 Solvated cyclopropanone
In aqueous solution, the oxygen atom of cyclopropanone can form hydrogen bonds (H-bonds) with the surrounding water molecules. During a 45 ps long ground state DFT-MD trajectory the Ocyc.⋯Hwat. distance with the closest water molecule was about half the time below 2 Å, not becoming shorter than 1.5 Å at any point (see Fig. 5). At around a quarter of the time, two hydrogen atoms of distinct water molecules are within 2 Å. The position of the first peak in the radial distribution function (RDF) of the Ocyc.⋯Hwat. distances coincides with the value of 1.95 Å determined in cyclobutanone–water and cyclohexanone–water complexes studied in the gas phase.75,76 The top left-hand-side of the first Ocyc.⋯Owat. radial distribution peak at 2.85 Å, belonging to the oxygen atoms of water involved in H-bonds with cyclopropanone, is similar to the corresponding distance of 2.91 Å measured in cyclobutanone–water.75 The absence of any structure in the Hcyc.⋯Owat. RDF curve indicates no significant water interaction with the alkane part of the ring. A more detailed spatial distribution of the location of the closest water hydrogen atoms around the carbonyl oxygen atom indicates that the majority of water molecules lay in the same plane as the cyclopropanone ring. This is in line with the position of the non-bonding electron pairs on the oxygen atom, and that the perpendicular π orbital engages less in interaction with water molecules. The overall effect of the solvent and H-bonds on the structure of cyclopropanone is negligible. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and the distal C–C bond are extended by on average 0.015 and 0.007 Å respectively, while the two lateral C–C bonds are compressed by 0.011 Å, when compared to the corresponding minimum ground state vacuum structure. The C–H bonds are on average longer by merely 0.002 Å.
O and the distal C–C bond are extended by on average 0.015 and 0.007 Å respectively, while the two lateral C–C bonds are compressed by 0.011 Å, when compared to the corresponding minimum ground state vacuum structure. The C–H bonds are on average longer by merely 0.002 Å.
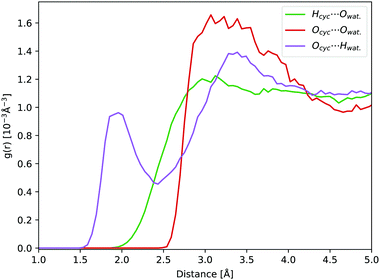 | ||
| Fig. 5 RDFs obtained from a 45 ps ground state DFT-MD trajectory of cyclopropanone in aqueous solution: Ocyc.⋯Owat. (red line), Ocyc.⋯Hwat. (purple line), and Hcyc⋯Owat. (green line). | ||
The theoretical absorption spectrum of solvated cyclopropanone in the periodic water box was calculated from the 250 initial configurations sampled from the same 45 ps long MD simulation. The spectrum maxima in the length and velocity representation are blue-shifted by 14 and 22 nm respectively compared to the corresponding vacuum values of cyclopropanone (Fig. 1). The effect was traced to the H-bonds and electrostatic interaction of the n→π* excitation character with the water molecules that stabilises the ground state, whereas the first singlet excited state is destabilised by the decreased electron density in the oxygen n orbital. The aforementioned geometrical effects exerted on the cyclopropanone induce in fact a slight red-shift when the vertical excitation is computed in vacuum on an average solvated cyclopropanone geometry. In the velocity representation, the prominent shoulder at around 355 nm observed in the gas-phase spectrum is not present in the liquid phase. In the length representation, a small shoulder can still be discerned at 335 nm.
The encountered mechanisms resemble those in a vacuum, namely 13% and 87% of the jumps exhibit a symmetric or asymmetric character respectively, categorised based on the same criteria as the vacuum trajectories. 5% did not deactivate to the ground state at the end of the simulation time. In contrast to the gas-phase, 14% of the trajectories restore cyclopropanone after deexcitation, following either symmetrical or asymmetrical pathways. The first trajectory displaying reconnection of a broken bond hopped after 57.5 fs. In fact, none of the former trajectories deactivated at the first CI encounter. The excess energy after the hop is manifested in the vibrational motion of the cyclopropanone ring.
The H-bonds between the cyclopropanone and water molecules are disrupted in the first stage of the NAMD. As the time evolution of the Ocyc.⋯Hwat. RDF shown in Fig. 6 reveals, the dissociative motion of the CO group stretches the H-bonds present between the oxygen atom of cyclopropanone and the hydrogen atoms of water as the CO moves from the ethylene. This process takes about 50 fs to complete, as illustrated by the disappearance of the first peak of the Ocyc.⋯Hwat. radial distribution density in Fig. 6. The very first step of this process is the carbonyl group out-of-plane movement, which disrupts some of the H-bonds but the geometric change is still localised within its first solvation shell so the peak remains. Only when the CO starts to significantly move from the ethylene part (either by complete or partial cleavage) is a decay of the first peak observed. Since the departing CO moves away with significant kinetic energy, no H-bonds were observed reforming with the water molecules.
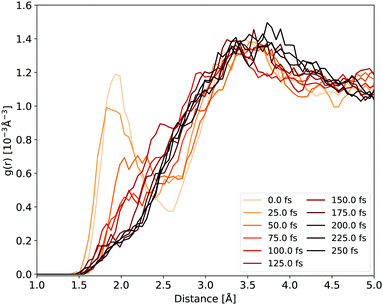 | ||
| Fig. 6 Ocyc.⋯Hwat. RDF evolution during the NAMD evolution, averaged over all solvated cyclopropanone trajectories. | ||
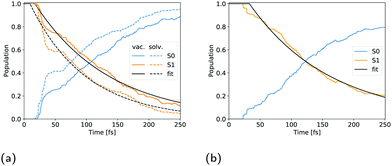
3.3 Cyclopropanone S1 lifetimes
Filatov et al.13 fitted the S1 population decay of cyclopropanone in a vacuum with a biexponential function giving lifetimes of 33 fs and 95 fs using 100 trajectories propagated at the SSR-ωPBEh/6-31G* level of theory, whereby 15 non-deactivated trajectories were excluded from the analysis. Cui et al. obtained S1 lifetimes ranging from 71 fs to 126 fs at the SA-CASSCF(8,7)/cc-pVDZ level of theory, depending on the initial sampling conditions.11 More specifically, four sets of initial conditions were sampled in their work, each corresponding to a vibrational mode of the CO group in cyclopropanone as these modes are mostly correlated with the S1 to S0 transition. In our work, a monoexponential function proved accurate to fit the S1 population decay of an isolated cyclopropanone molecule. The fitted parameters are given in Table 2 and the corresponding S1 state decay curves are shown in Fig. 7. The cyclopropanone lifetime is longer as compared to the results of Filatov et al.13 and Cui et al.,11 presumably since a larger number of trajectories were propagated, and all trajectories that reached 250 fs were included in the calculation of the lifetime and all vibrational modes were sampled. The first hop happens at 21 fs and 17.5 fs for cyclopropanone in a vacuum and in solution respectively. In the condensed phase, a shorter lifetime of 98 fs is found compared to 137 fs in a vacuum. More trajectories hop between 30 fs and 40 fs after the start of the dynamics for cyclopropanone in the condensed phase as compared to the gas phase, all of which result in the formation of ethylene and carbon monoxide through either a symmetrical or asymmetrical pathway.| Cyclopropanone | t 0 [fs] | τ [fs] | R 2 |
|---|---|---|---|
| Gas | 17.4 ± 0.5 | 119.6 ± 0.8 | 98.8% |
| Solution | 8.9 ± 0.5 | 89.3 ± 0.7 | 98.5% |
3.4 Cyclopropanone hydrate
In water, carbonyl functional groups are in equilibrium with a geminal diol.77 The equilibrium of the nucleophilic addition reaction of a water molecule is shifted towards the hydrate form for cyclopropanone, as the angle strain in the three-membered ring is reduced by the formation of an sp3 hybridisation of the carbonyl carbon atom.2,20 However, determination of the equilibrium constant is experimentally complicated.78 Hence, not only the photodynamics of cyclopropanone, but also of its hydrate were modelled in this work.Compared to solvated cyclopropanone, the H-bond network between water and cyclopropanone hydrate is more versatile. In the starting conformation of the ground state DFT-MD NVT simulation, both hydrate O–H bonds were facing the same parallel orientation giving Cs symmetry, as shown in Fig. 8. 45 ps of NVT dynamics reveal that both OH groups are strongly interacting with neighbouring water molecules. The H atoms of cyclopropanone hydrate constantly connect to oxygen atoms of water, interrupted only when changed between water molecules. Oxygen atoms of the hydrate are also interacting with neighbouring water H atoms with a frequent observation of both oxygen lone pairs simultaneously bonding two neighboring water molecules. Since the OH groups are geminal, another observed feature is a single water molecule located close to both groups which switches the H-bond between the two hydrate oxygen atoms. As a result, the conformation of the hydroxyl groups changes minimally. Hence, the initial Cs symmetry is maintained. Prominent peaks of the corresponding radial distribution function curves (see Fig. 8) confirm the strong H-bondings, particularly the HO,cyc.⋯Owat. and Ocyc.⋯Owat., where the maximum of the latter is separated by the average OH water bond length from the maximum of the former curve. The height of the Ocyc.⋯Hwat. is almost half the size of HO,cyc.⋯Owat. due to more frequent H-bond changes between water hydrogen and hydrate oxygen atoms. Again, no significant H-bond interaction was observed with the hydrate alkane part.
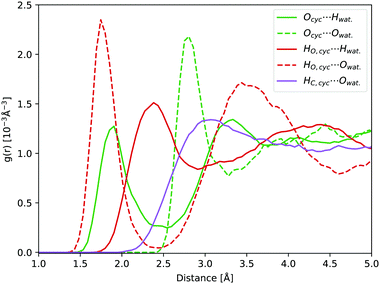 | ||
| Fig. 8 Hydrate NVT RDFs: Ocyc.⋯Owat. (green dashed line), Ocyc.⋯Hwat. (green line), HO,cyc.⋯Owat. (red dashed line), HO,cyc.⋯Hwat. (red line), and HC,cyc.⋯Owat. (purple line). | ||
The hydrate's first excited singlet state is a transition originating from the σ orbitals of the lateral C–C bonds to the σ* KS MO located on both hydroxyl groups, as shown in Fig. 9. In the Frank–Condon region, two higher excited states are close in energy, the former being the n→σ* located on the OH groups, while the latter has a similar character to S1, but involves a different σ bonding orbital. However, in solution, preliminary analyses showed that the energy gap between these states and the S1 state quickly increased in energy during the dynamics, making the S1 sufficient for the NAMD simulation. In addition, calculations of the S2 and S3 states contained contributions from the orbitals of non-surrounding solvent molecules. The cyclopropanone hydrate absorption spectrum was calculated on the 250 sampled NAMD initial points from the NVT trajectory (see Fig. 1). The maxima are blue-shifted by 48 and 50 nm for the length and velocity representations respectively as compared to the corresponding maxima of solvated cyclopropanone.
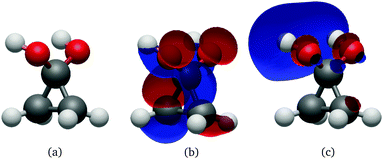 | ||
| Fig. 9 Geometry (a), HOMO (b) and LUMO (c) at the Cs S0 minimum of cyclopropanone hydrate optimised using the ΔSCF method. | ||
Overall, 20% of the trajectories were still in the S1 state after 250 fs of NAMD. At the end of the simulation time, one lateral C–C bond was broken in all trajectories which remained in the first singlet excited state and three quarters of the geminal diols lost a proton to the solvent through the Grotthuss mechanism.79 In contrast to the decay of cyclopropanone in an aqueous environment, where 3% and 87% of the trajectories decayed following the symmetrical and asymmetrical pathways respectively, all solvated cyclopropanone hydrate trajectories decayed to the ground state through an asymmetrical pathway. In the majority of the cases one of the lateral C–C bonds was already broken (based on the 2 Å criterium) at the point of the non-adiabatic hop, where only in a very small fraction both lateral C–C bonds were still under 2 Å. The minimum difference between the lateral C–C bond lengths at the jump was ∼0.4 Å, whereas the threshold distinguishing symmetrical from asymmetrical trajectories was defined in section 3.1 as 0.1 Å. In addition, several trajectories showed a proton transfer to the solvent, which initiated a proton exchange between water molecules via the Grotthuss mechanism79 while still in the first excited state.
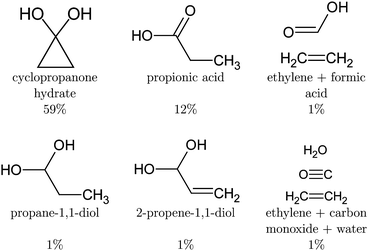
After deexcitation, in 59% of the trajectories the broken lateral C–C bond was restored by the end of the simulation time. Therefore, vibrationally hot cyclopropanone hydrate is the main product of the non-radiative deactivation mechanism, as shown in Fig. 10. In 15% of the NAMD trajectories, the second lateral C–C bond was also broken, resulting in the formation of ethylene and a carbene fragment. The latter is stabilised by the hydrogen atoms of the surrounding water molecules. An intramolecular proton transfer from a hydroxyl group to the carbene carbon atom resulted in the formation of formic acid in one trajectory. Several other trajectories displayed a clear carbene–water interaction, however, the simulation time was too short to observe any intermolecular formation of formic acid. It is noteworthy that in one trajectory, an additional fragmentation of the carbene fragment yielded carbon monoxide, hydroxide and a solvated proton as photoproducts. Although decarboxylation is the main decomposition pathway of formic acid in aqueous solution, the dehydration is known to be catalysed by water as well.80,81 Finally, in the remaining 26% of the trajectories the lateral C–C bonds were not restored nor broken forming a three carbon atom straight chain whereby the central methylene group relaxes to the unstrained tetrahedral structure. The second methylene group exhibits profound vibrational motion, displaying in particular scissoring and wagging modes, before pyramidalising when interaction with a solvent molecule is established. If a hydroxyl proton is expelled, the carboxyl group planarises. Remarkably, in two trajectories, an intramolecular proton transfer from the central methylene group to the carbon atom of the diol occurred, creating 2-propene-1,1-diol. A hydroxyl proton was expelled at the end of the simulation time for half of the diols, mostly after the deactivation to the ground state. In most of these trajectories, the non-central methylene group extracted a proton from a nearby water molecule thereby forming propionic acid. In one case, propane-1,1-diol was created as the non-central methylene group extracted a proton from the solvent without deprotonation of a hydroxyl group. All photoproducts of the cyclopropanone hydrate NAMD calculations are summarised in Fig. 10.
The population decay of the S1 excited state was fitted with a monoexponential function as shown in Fig. 7b. The obtained lifetime of 163 fs with a 33 fs offset and R2 of 99.1 is slightly longer than for solvated cyclopropanone.
4 Conclusions
The photodissociation of cyclopropanone in a vacuum and in solution has been studied using NAMD with ΔSCF. The gas-phase results are consistent with previous multireference studies,11,13 proving that ΔSCF is a viable method to simulate photodecomposition processes, particularly for systems exhibiting single reference excited states. A lifetime of 137 fs was obtained by a monoexponential fit of the S1 population decay and cyclopropanone dissociated in 99% of the NAMD trajectories. The deactivation was found to proceed through a symmetrical pathway for 22% of the molecules.Moreover, the ΔSCF method can be easily applied to the condensed phase, which has been shown with DFT using a mixed Gaussian and plane wave approach and periodic boundary conditions, also using subsystem DFT.30,31 Solvated in water, cyclopropanone is in equilibrium with cyclopropanone hydrate. Whereas the hydrate readily engages in hydrogen bonding with the surrounding solvent molecules, the oxygen atom of cyclopropanone forms hydrogen bonds only in half of the ground state DFT-MD simulation time. No significant geometrical changes of the cyclopropanone molecule are observed after solvation. The excitation of solvated cyclopropanone to the first singlet excited state results in less photolysis as compared to the gas-phase deactivation. More specifically, the decay pathway manifested a reformation of the lateral C–C bond following a hop at either a symmetrical or asymmetrical CI in 14% of the trajectories. The deactivation mechanisms are analogous to the pathways in a vacuum. Due to the increased kinetic energy, manifested as energetic vibrational motion or dissociation, the hydrogen bonds with the solvent are disrupted during the NAMD.
The NAMD simulations of cyclopropanone hydrate revealed the cyclopropanone hydrate, propionic acid, 2-propene-1,1-diol, propane-1,1-diol and formic acid as photoproducts, in addition to conformers where one or both lateral C–C bonds were broken, but no proton was transferred yet after 250 fs of NAMD. All trajectories deexcited following an asymmetrical mechanism. A lifetime of 98 fs and 163 fs was obtained for cyclopropanone and cyclopropanone hydrate in an aqueous environment respectively. Finally, UV absorption spectra at a ΔSCF level were calculated using a new procedure involving an expansion of the mutually non-orthogonal states into a linear combination of singly-excited Slater determinants constructed from the ground state molecular orbitals. Compared to the experimental maximum of 312 nm, the maxima in the length and velocity representations are red-shifted by merely 7 nm and 15 nm respectively. The spectra of cyclopropanone and its hydrate in the condensed phase are blue-shifted with respect to the gas-phase due to the favourable hydrogen bonding interaction in the ground state and reduced electrostatic interaction with the surrounding water molecules after excitation. In conclusion, the photodynamics of cyclopropanone and its hydrate in an aqueous environment were explored using full atomistic NAMD with ΔSCF, which allowed the hydrogen bonding and proton transfer after deactivation to be studied, offering the first insights into their condensed phase photochemistry.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work has been supported by the University of Zurich and the Swiss National Science Foundation (grant no. PP00P2 170667). We thank the Swiss National Supercomputing Center for the computing resources (project IDs: s875, s1001, and s1036).Notes and references
- N. De Kimpe, in Cyclopropanone, American Cancer Society, 2001 Search PubMed.
- V. P. Lipp, J. Buchkremer and H. Seeles, Justus Liebigs Ann. Chem., 1932, 499, 1–25 CrossRef.
- A. D. Semenow, E. F. Cox and J. D. Roberts, J. Am. Chem. Soc., 1956, 78, 3221–3223 CrossRef.
- W. B. DeMore, H. O. Pritchard and N. Davidson, J. Am. Chem. Soc., 1959, 81, 5874–5879 CrossRef CAS.
- B. J. G. Burr and M. J. S. Dewar, J. Chem. Soc., 1954, 1201–1203 RSC.
- N. J. Turro, W. B. Hammond, P. A. Leermakers and N. J. Turro, Recl. Trav. Chim. Pays-Bas, 1966, 387, 70 Search PubMed.
- S. E. Schaafsma, H. Steinberg and T. J. D. Boer, Recl. Trav. Chim. Pays-Bas, 1966, 85, 1170–1172 CrossRef CAS.
- M. J. Abplanalp, A. Borsuk, B. M. Jones and R. I. Kaiser, Astrophys. J., 2015, 814, 45 CrossRef.
- H. J. Rodriguez, J.-C. Chang and T. F. Thomas, J. Am. Chem. Soc., 1976, 98, 2027–2034 CrossRef CAS.
- G. Cui, Y. Ai and W. Fang, J. Phys. Chem. A, 2010, 114, 730–734 CrossRef CAS PubMed.
- G. Cui and W. Fang, J. Phys. Chem. A, 2011, 115, 1547–1555 CrossRef CAS PubMed.
- T. F. Thomas and H. J. Rodriguez, J. Am. Chem. Soc., 1971, 93, 5918–5920 CrossRef CAS.
- M. Filatov, S. K. Min and C. H. Choi, Phys. Chem. Chem. Phys., 2019, 21, 2489–2498 RSC.
- J. Suchan, J. Janoš and P. Slavíček, J. Chem. Theory Comput., 2020, 16, 5809–5820 CrossRef CAS PubMed.
- L. M. Ibele, Y. Lassmann, T. J. Martínez and B. F. Curchod, J. Chem. Phys., 2021, 154, 104110 CrossRef CAS PubMed.
- N. J. Turro and W. B. Hammond, Tetrahedron, 1968, 24, 6017–6028 CrossRef CAS.
- N. J. Turro and W. B. Hammond, Tetrahedron, 1968, 24, 6029–6035 CrossRef CAS.
- N. J. Turro, Acc. Chem. Res., 1969, 2, 25–32 CrossRef CAS.
- B. S. E. Schaafsma, H. Steinberg and T. J. D. Boer, Recl. Trav. Chim. Pays-Bas, 1967, 86, 1170 Search PubMed.
- K. B. Wiberg, K. M. Morgan and H. Maltz, J. Am. Chem. Soc., 1994, 116, 11067–11077 CrossRef CAS.
- T. H. Cromartie, Biochem. Biophys. Res. Commun., 1982, 105, 785–790 CrossRef CAS PubMed.
- J. S. Wiseman and R. H. Abeles, Biochemistry, 1979, 18, 427–435 CrossRef CAS PubMed.
- J. S. Wiseman, J. S. Nichols and M. X. Kolpak, J. Biol. Chem., 1982, 257, 6328–6332 CrossRef CAS.
- K. W. Schmid, A. Hittmair, H. Schmidhammer and B. Jasani, J. Histochem. Cytochem., 1989, 37, 473–477 CrossRef CAS PubMed.
- H. H. Wasserman, G. M. Clark and P. C. Turley, Stereochemistry I, Springer, Berlin, Heidelberg, 1974, pp. 73–156 Search PubMed.
- I. Tavernelli, Acc. Chem. Res., 2015, 48, 792–800 CrossRef CAS PubMed.
- M. De Vetta, M. F. Menger, J. J. Nogueira and L. González, J. Phys. Chem. B, 2018, 122, 2975–2984 CrossRef CAS PubMed.
- F. Santoro, J. A. Green, L. Martinez-Fernandez, J. Cerezo and R. Improta, Phys. Chem. Chem. Phys., 2021, 23, 8181–8199 RSC.
- K. Sneskov, T. Schwabe, O. Christiansen and J. Kongsted, Phys. Chem. Chem. Phys., 2011, 13, 18551–18560 RSC.
- M. Mališ and S. Luber, J. Chem. Theory Comput., 2020, 16, 4071–4086 CrossRef PubMed.
- M. Mališ and S. Luber, J. Chem. Theory Comput., 2021, 17, 1653–1661 CrossRef PubMed.
- R. Crespo-Otero and M. Barbatti, Chem. Rev., 2018, 118, 7026–7068 CrossRef CAS PubMed.
- T. R. Nelson, A. J. White, J. A. Bjorgaard, A. E. Sifain, Y. Zhang, B. Nebgen, S. Fernandez-Alberti, D. Mozyrsky, A. E. Roitberg and S. Tretiak, Chem. Rev., 2020, 120, 2215–2287 CrossRef CAS PubMed.
- E. Tapavicza, G. D. Bellchambers, J. C. Vincent and F. Furche, Phys. Chem. Chem. Phys., 2013, 15, 18336–18348 RSC.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- G. Granucci and M. Persico, J. Chem. Phys., 2007, 126, 134114 CrossRef PubMed.
- B. F. Curchod, U. Rothlisberger and I. Tavernelli, ChemPhysChem, 2013, 14, 1314–1340 CrossRef CAS PubMed.
- T. Ziegler, A. Rauk and E. J. Baerends, Theor. Chim. Acta, 1977, 43, 261–271 CrossRef CAS.
- R. O. Jones and O. Gunnarsson, Rev. Mod. Phys., 1989, 61, 689–746 CrossRef CAS.
- A. Hellman, B. Razaznejad and B. Lundqvist, J. Chem. Phys., 2004, 120, 4593–4602 CrossRef CAS PubMed.
- J. Gavnholt, T. Olsen, M. Engelund and J. Schiøtz, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075441 CrossRef.
- T. Ziegler, M. Seth, M. Krykunov, J. Autschbach and F. Wang, J. Chem. Phys., 2009, 130, 154102 CrossRef PubMed.
- R. J. Maurer and K. Reuter, J. Chem. Phys., 2013, 139, 014708 CrossRef PubMed.
- E. Pradhan, K. Sato and A. V. Akimov, J. Condens. Matter Phys., 2018, 30, 484002 CrossRef PubMed.
- G. Levi, A. V. Ivanov and H. Jónsson, J. Chem. Theory Comput., 2020, 6968–6982 CrossRef CAS PubMed.
- J. Behler, K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115421 CrossRef.
- G. Levi, M. Pápai, N. E. Henriksen, A. O. Dohn and K. B. Møller, J. Phys. Chem. C, 2018, 122, 7100–7119 CrossRef CAS.
- T. Kowalczyk, S. R. Yost and T. V. Voorhis, J. Chem. Phys., 2011, 134, 1–8 CrossRef PubMed.
- K. Yang, R. Peverati, D. G. Truhlar and R. Valero, J. Chem. Phys., 2011, 135, 044118 CrossRef PubMed.
- S. B. Worster, O. Feighan and F. R. Manby, J. Chem. Phys., 2021, 154, 124106 CrossRef PubMed.
- T. Baruah, M. Olguin and R. R. Zope, J. Chem. Phys., 2012, 137, 084316 CrossRef PubMed.
- D. Hait and M. Head-Gordon, J. Phys. Chem. Lett., 2021, 12, 4517–4529 CrossRef CAS PubMed.
- M. Mališ, E. Vandaele and S. Luber, Manuscriptsubmitted for publication.
- M. Sapunar, T. Piteša, D. Davidović and N. Došlić, J. Chem. Theory Comput., 2019, 15, 3461–3469 CrossRef CAS PubMed.
- CP2K Program Package, CP2K Developers Group, Version 6.1, https://www.cp2k.org/.
- S. Hammes-Schiffer and J. C. Tully, J. Chem. Phys., 1994, 101, 4657–4667 CrossRef CAS.
- M. Hillery, R. F. O'Connell, M. O. Scully and E. P. Wigner, Distribution functions in physics: Fundamentals, 1984 Search PubMed.
- J. P. Zobel, J. J. Nogueira and L. González, Phys. Chem. Chem. Phys., 2019, 21, 13906–13915 RSC.
- M. Krack, Theor. Chem. Acc., 2005, 114, 145–152 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. Schmidt, J. Vandevondele, I. F. W. Kuo, D. Sebastiani, J. I. Siepmann, J. Hutter and C. J. Mundy, J. Phys. Chem. B, 2009, 113, 11959–11964 CrossRef CAS PubMed.
- J. VandeVondele, F. Mohamed, M. Krack, J. Hutter, M. Sprik and M. Parrinello, J. Chem. Phys., 2005, 122, 014515 CrossRef PubMed.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- B. G. Levine, J. D. Coe and T. J. Martínez, J. Phys. Chem. B, 2008, 112, 405–413 CrossRef CAS PubMed.
- TURBOMOLE V6.6 2014, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian˜16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- BAGEL, Brilliantly Advanced General Electronic-structure Library., http://www.nubakery.org under the GNU General Public License.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- B. Vlaisavljevich and T. Shiozaki, J. Chem. Theory Comput., 2016, 12, 3781–3787 CrossRef CAS PubMed.
- J. W. Park and T. Shiozaki, J. Chem. Theory Comput., 2017, 13, 2561–2570 CrossRef CAS PubMed.
- T. Shiozaki, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 1–7 Search PubMed.
- J. M. Pochan, J. E. Baldwin and W. H. Flygare, J. Am. Chem. Soc., 1968, 90, 1072–1073 CrossRef CAS.
- D. W. Liao, A. M. Mebel, M. Hayashi, Y. J. Shiu, Y. T. Chen and S. H. Lin, J. Chem. Phys., 1999, 111, 205–215 CrossRef CAS.
- S. Melandri, A. Maris, B. M. Giuliano and W. Caminati, J. Chem. Phys., 2005, 123, 164304 CrossRef PubMed.
- J. Gao, N. A. Seifert and W. Jäger, Phys. Chem. Chem. Phys., 2019, 21, 12872–12880 RSC.
- H.-J. Buschmann, H.-H. Füldner and W. Knoche, Bunsen-Ges. Phys. Chem., Ber., 1980, 84, 41–44 CrossRef CAS.
- R. Gómez-Bombarelli, M. González-Pérez, M. T. Pérez-Prior, E. Calle and J. Casado, J. Phys. Chem. A, 2009, 113, 11423–11428 CrossRef PubMed.
- N. Agmon, Chem. Phys. Lett., 1995, 244, 456–462 CrossRef CAS.
- J. Yu and P. E. Savage, Ind. Eng. Chem. Res., 1998, 37, 2–10 CrossRef CAS.
- N. Akiya and P. E. Savage, AIChE J., 1998, 44, 405–415 CrossRef CAS.
| This journal is © the Owner Societies 2022 |