A computational study of competing conformational selection and induced fit in an abiotic system

Abstract

Host–guest complexations can be described by two competing mechanisms, conformational selection (CS) and induced fit (IF). In this work, we used a combination of nudged elastic band (NEB), adaptive steered molecular dynamics (ASMD), and density functional theory (DFT, with a correction for dispersion) to study the dynamics of the pathways (IF/CS) by which two conformers of basket B(+) and B(−) interconvert and trap CX₄ guests (X = Cl and Br). While the results from NEB/DFT studies disclosed host–guest noncovalent contacts reducing the basket's conformational dynamics, ASMD methodology suggested an associative mechanism for the guest complexation. With theory in excellent agreement with experiments, NEB and ASMD emerge as the methods of choice for studying dynamics of supramolecular systems.

---

Introduction

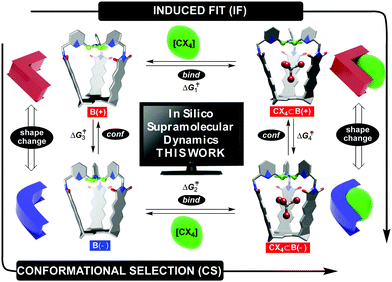
Fundamental studies of molecular recognition¹ are essential for deciphering complex biological processes and their regulatory features in addition to designing supramolecular assemblies capable of performing increasingly demanding tasks.² For instance, it is well recognized that the binding of ligands to natural receptors (bind step in Fig. 1) is coupled with conformational adjustment(s) (conf step in Fig. 1).³ The two processes constitute a critical part of allostery⁴ to enable the emergence of complex natural systems with intriguing mechanisms of action.⁵ Importantly, the chronological order of bind and conf steps gives rise to two mechanistic alternatives by which the recognition takes place (Fig. 1).⁶ For conformational selection (CS), a receptor exists as an ensemble of interconvertible conformers from which the optimal one gets selected for binding to a ligand (conf→bind, Fig. 1). Induced fit (IF) encompasses a non-optimal conformer of the receptor associating with the ligand first, followed by a reshaping of the receptor to complement the guest (bind→conf, Fig. 1). Indeed, deciphering the order of bind and conf steps requires a structural characterization of all of the conformational states involved, including determination of rate coefficients corresponding to their interconversion.⁷ In addition to elaborate biological molecules, the interplay of CS and IF has, in recent years, also been probed with supramolecular systems.⁸ We recently found⁹ that two conformers of basket B(+) and B(−) (each with the top twisted to the right or left, Fig. 1) would trap a molecule of tetrahalomethane (CCl₄ or CBr₄) to give CX₄⊂B(+) and CX₄⊂B(−).¹⁰ After the kinetics of the four-state equilibrium was elucidated, we used a flux-based analysis⁷ to reveal relative proportions of CS and IF pathways. Both mechanistic alternatives can occur simultaneously over a range of experimental conditions – lower concentrations of guests favoring CS, while higher concentrations favor IF. We wondered: would a computational study of our system's dynamics¹¹ provide further mechanistic insight about the four processes? Why is the conformational interconversion of baskets (conf steps in Fig. 1) slowed down⁹ in the presence of halogenated guests? How does the exchange of guests (bind steps in Fig. 1) to and from baskets B(+)/B(−) take place?¹² Are solvent molecules playing a particular role during entrance/departure of guests?¹³ While the majority of computational host–guest studies focus on elucidating the binding thermodynamics,¹⁴ we herein and for the first time used a combination of nudged elastic band (NEB),^9,15 adaptive steered molecular dynamics (ASMD),¹⁶ and density functional theory (DFT) to reveal mechanisms¹⁷ by which the four coupled equilibria, comprising IF and CS in Fig. 1,⁹ take place.

Fig. 1 Basket conformers B(+) (red) and B(−) (blue) trap tetrahalomethane CX₄ (X = Cl or Br) to give CX₄⊂B(+) and CX₄⊂B(−) complexes, with all four states being in a thermal equilibrium; (+) and (−) signs correspond to clockwise and counterclockwise arrangement of equatorial TPA hydrogens (green) around the capsule's C₃ axis. A change in basket's shape and host–guest complementarity are depicted schematically on the left and right.

Results and discussion

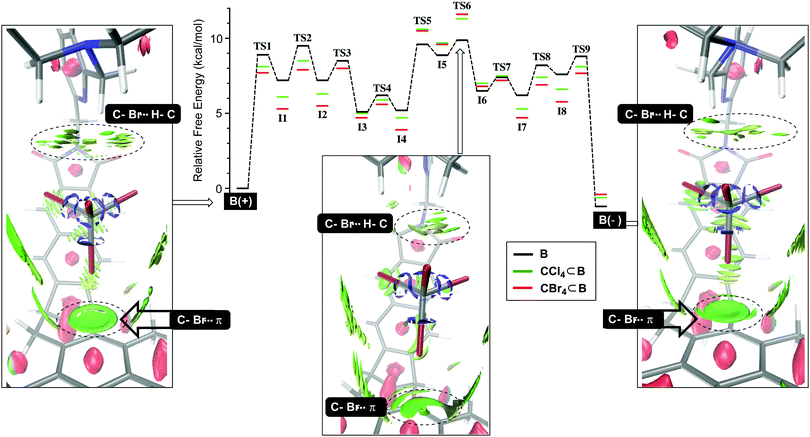
We began by studying the conversion of B(+) into B(−) using NEB simulations (Fig. 2) to identify transition states (TS) between minima. Then, the normal mode for the imaginary vibrational frequency in each TS was followed by manual displacement to find the nearest minima on the potential energy surface (PES).⁹ After using new localized minima to find additional TSs and then continuing the procedure, the PES in Fig. 2 emerged, consisting of eight intermediates I1-8 and nine transition states TS1-9 for which TS6 acts as the rate-limiting state; all states were computed using DFT at the B3LYP/6-31+G(d) level of theory; for a dispersion correction, see Tables S9 and S10 (ESI†). Computationally derived barriers for the empty basket B(+)↔B(−) isomerization (ΔG_3/−3^‡, Table 1; conf step in Fig. 1) are close to the experimental ones although the computational studies ignore dichloromethane which is present as the bulk solvent. Next, we sought to understand how tetrahalomethanes disturb the conformational isomerization of CCl₄⊂B and CBr₄⊂B. Using previously derived intermediates and transition states for B (see ESI† for details), we found that the activation energies corresponding to CCl₄⊂B(+)↔CCl₄⊂B(−) and CBr₄⊂B(+)↔CBr₄⊂B(−) conversions (ΔG_4/−4, Table 1; conf step in Fig. 1) were higher than the experimental ones. Nevertheless, they accurately describe the measured relative binding energies ΔG₄° corresponding to difference in the forward and backward rates of encapsulation (ΔG₄° = ΔG₄^‡ − ΔG−₄^‡, Table 1). The result is important, providing support to our hypothesis about the role of solvent governing the conformational dynamics of B. With similar TS structures and intermediates along the PES in Fig. 2, the conformational twisting at the top of the basket^9,10 follows the same pathway regardless of being empty or holding a CX₄. On the other hand, the normalized PES shows that most of the TS structures and intermediates from the CX₄⊂B routes (Fig. 2) are more stable than their congeners corresponding to uncomplexed B interconverting. The exceptions are TS5-6 and I5-6 states that appear higher (<1.5 kcal mol⁻¹) in energy. Importantly, the normalized PES plot discounts the notion that CX₄⊂B(+)/CX₄⊂B(−) hosts are thermodynamically more stable (1.1–2.5 kcal mol⁻¹, Table 2)⁹ than B(+) and B(−). By lowering PESs corresponding to CCl₄⊂B and CBr₄⊂B for ca. 1–2 kcal mol⁻¹, the ground states of the basket become more stabilized than transition state TS6 pertaining CX₄⊂B(+)↔CX₄⊂B(−) interconversion. To further examine such stabilization of CX₄⊂B(+) and CX₄⊂B(−) states, we used DFT (B3LYP/6-31+G(d)) to conduct noncovalent interaction analysis (NCIplot)¹⁸ in which the reduced density gradient s (where s is a function of electron density ρ and its first derivative)¹⁹ is computed to show areas where noncovalent interactions are taking place. The NCIplots for CBr₄⊂B(+), CBr₄⊂B(−) and TS6 (green surfaces in Fig. 2) depict: (1) C–Br⋯π halogen bonding¹⁰ at the bottom of the capsule with CBr₄ as a guest and (2) C–H⋯X–C hydrogen-bonding¹⁰ interactions with the capsule's lid.

Fig. 2 Computed and normalized PES surfaces (NEB and DFT:B3LYP/6-31+G(d)) for the conformational interconversion of B(+)↔B(–) (black), CCl₄⊂B(+)↔CCl₄⊂B(–) (green) and CBr₄⊂B(+)↔CBr₄⊂B(–) (red). Non-covalent interaction plots (green surfaces, DFT:B3LYP/6-31+G(d)) for B(+), B(−) and CBr₄⊂TS6 depict the weakening of C–Br⋯π and C–Br⋯H–C interactions in the rate-limiting TS6 with respect to the ground states; for NCI plots, we used BGR color scale with density cutoff −0.035 to 0.02 and isovalue of 0.3.

Table 1 Experimental (178 K) and computed (NEB and DFT:B3LYP/6-31+G(d)) free energies of activation for the conformational isomerization of B, CCl₄⊂B, and CBr₄⊂B

ΔGn^‡ [kcal mol^−1]	B Exp./Comp.	CCl4⊂B Exp./Comp.	CBr4⊂B Exp./Comp.
ΔG3^‡ or ΔG4^‡	9.6/9.9	9.7/11.3	9.7/11.6
ΔG−3^‡ or ΔG−4^‡	9.5/11.1	10.1/11.9	10.0/12.0
ΔG3° or ΔG4°	0.1/−1.2	−0.4/−0.6	−0.3/−0.4

---

Table 2 Experimental and computed (ASMD) activation barriers and standard free energies (178 K) for guest dissociating from CX₄⊂B(+) (ΔG₋₁) and CX₄⊂B(−) (ΔG₋₁); experimental rates for the complexation of CBr₄ were not determined

ΔGn^‡ [kcal mol^−1]	CCl4⊂B Exp./Comp.	CBr4⊂B Exp./Comp.
ΔG−1^‡	8.1/4.4 ± 0.0	N.A./7.1 ± 0.3
ΔG−1°	1.1/0.4 ± 0.3	1.9/1.4 ± 0.6
ΔG−2^‡	8.4/5.3 ± 0.0	N.A./7.7 ± 0.2
ΔG−2°	1.5/0.9 ± 0.2	2.4/1.9 ± 0.6
ΔΔG−1^‡	−0.4/−0.9	N.A./−0.6

---

As the two major noncovalent contacts are stronger for CBr₄⊂B(+) and CBr₄⊂B(−) than CBr₄⊂TS6, they are contributing to a greater stabilization of the former two. In essence, the basket-haloalkane attractive contacts are acting as glue, holding the two molecules together and reducing the dynamic character of the host. To simulate the binding of tetrahalomethanes (bind steps in Fig. 1), we ran molecular dynamics (MD; 200 ns, 300 K; Fig. S3, ESI†) using the available CHCl₃ force field; the experimental results were obtained with CH₂Cl₂ as the bulk solvent. The MD results for either B(+) or B(–) in CHCl₃ revealed that B(+)↔B(–) interconversion (conf step in Fig. 1) would take place at ca. 50 ns. The same conformational change was observed for CCl₄⊂B(+) (150 ns, Fig. S6, ESI†) but not CCl₄⊂B(−) (Fig. S5, ESI†). On the other hand, CCl₄ would exit CCl₄⊂B(−) at 75 ns (bind steps, Fig. S5 ESI†) but not CCl₄⊂B(+) (Fig. S6, ESI†). In MD simulations with CBr₄⊂B(+) and CBr₄⊂B(−), there was conformational switching observed for the former stereoisomer at 50 ns (Fig. S6, ESI†) while no other structural changes took place. With these results, a concerted bind-conf step is highly unlikely and is in agreement with previously reported experimental observations.⁹ Also, the lower odds of bind steps taking place during 200 ns of the conventional MD simulations prompted us to use adaptive steered molecular dynamics (ASMD).^16a This computational method allowed us to examine dynamics of CX₄⊂B complexes, as the guest was pulled over a series of stages from inside the basket to bulk solvent, to generate an average potential of mean force (PMF) along the chosen reaction coordinate for pulling out the guest (via the Jarzynski average).^16a We ran four ASMD simulations (each in triplicate) in chloroform starting with CCl₄⊂B(–) (Fig. S7–S10, ESI†), CCl₄⊂B(+) (Fig. S15–S18, ESI†), CBr₄⊂B(–) (Fig. S11–S14, ESI†), and CBr₄⊂B(+) (Fig. S19–S22, ESI†).

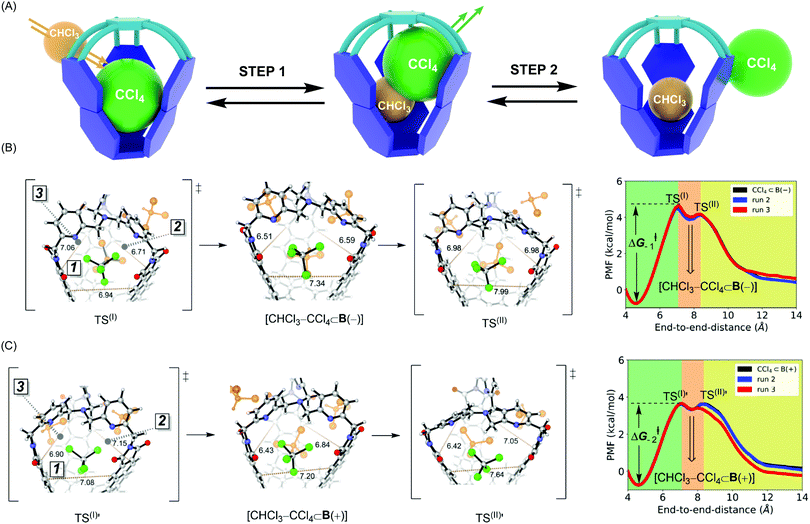
In the ASMD simulations, the departure of each guest turned out to be a two-step process occurring via an associative mechanism (Fig. 3A).²⁰ In the first step, a molecule of CHCl₃ solvent would combine with CX₄⊂B to form intermediate [CHCl₃–CX₄⊂B], followed by guest departure in step 2 (Fig. 3A). We will only discuss the departure of CCl₄, while the remaining results are shown in Table 2 and ESI.† In reaching TS^(I) of the CCl₄⊂B(–) turning into B(–) (Fig. 3B), all three apertures expanded, thereby enabling CHCl₃ to enter the cage via apertures 2 or 3 while simultaneously pushing CCl₄ into aperture 1. Such structural changes resulted in loosening C–Cl⋯π halogen bonds while maintaining weak C–H⋯Cl–C contacts within TS^(I) (Fig. 3B and Fig. S7b, c, ESI†).¹⁰ As for TS^(I) → I portion of the PES, apertures 2 and 3 began to contract around the newly encapsulated CHCl₃ solvent, thereby increasing the stabilizing host–guest contacts within the [CHCl₃–CX₄⊂B(−)] intermediate. While traversing from this intermediate to TS^(II), aperture 1 continued its expansion to enable the complete expulsion of CCl₄ (Fig. 3B and Fig. S7c, d, ESI†). At TS^(II), C–Cl⋯π and C–H⋯Cl–C host–guest contacts were lost. During the TS^(II) → CHCl₃⊂B(−) transition, aperture 1 contracted to a value corresponding to the solvated host (Fig. S7d, ESI†). The pulling simulation of CCl₄⊂B(+) followed a similar associative, two-step pathway (Fig. 3B) as in the case of CCl₄⊂B(−). However, the activation barrier for CCl₄ exiting CCl₄⊂B(+) was computed to be ΔG₋₁^‡ = 4.4 kcal mol⁻¹ and thus more favorable than the one corresponding to CCl₄⊂B(−) (ΔG₋₂^‡ = 5.3 kcal mol⁻¹, Table 2). The result agrees with experiment⁹ in which the departure of CCl₄ from B(+) basket was also a more facile process (Table 2). Finally, the trend in computed thermodynamic affinities of B(+) (ΔG₁°, Table 2) and B(−) (ΔG₂°, Table 2) toward CCl₄ also agreed with the experiment, thereby demonstrating the potential of ASMD methodology in describing supramolecular systems.

Fig. 3 (A) A schematic representation of two-step association mechanism corresponding to departure of CCl₄ from its complex with basket B, as assisted with solvent molecule CHCl₃. (B) (Right) Reaction profile for CCl₄ departing from CCl₄⊂B(–), obtained by ASMD simulations, in explicit CHCl₃ solvent. (Left) Stick and ball structures from to TS^(I), CHCl₃–CCl₄⊂B(–) and TS^(II). (C) (Right) Reaction profile for CCl₄ departing from CCl₄⊂B(+), obtained by ASMD simulations, in explicit CHCl₃ solvent. (Left) Stick and ball structures from to TS^(I)′, CHCl₃–CCl₄⊂B(+) and TS^(II)′.

Why is the departure of CCl₄ from B(+) host a more favorable process? As the binding mechanism is associative and therefore necessitating an expansion of the basket for transiently accommodating two of the exchanging molecules (Fig. 3A), we decided to evaluate the change in the basket's volume¹³ along each ASMD trajectory (Table S8, ESI†). The average volume of basket B(+) for CCl₄⊂B(+), TS^(I), [CHCl₃–CCl₄⊂B(+)] and TS^(II) increased in the order 209, 236, 237 and 229 ų (Fig. 3B). In the case of B(−), the volume for CCl₄⊂B(−), TS^(I), [CHCl₃–CCl₄⊂B(−)] and TS^(II) changed from 201, 230, 230 to 229 ų (Fig. 3C). Evidently, the complexed and less spacious B(−) had to increase its size more (from 201 ų to 230–237 ų) than B(+) (from 209 ų to 230–237 ų) for accommodating two molecules in its inner space. We reason that a greater steric strain imposed on B(−) than B(+) plays a role in the slower release of CCl₄ by B(−) (Table 2). In support of this hypothesis, the departure of larger CBr₄ is followed by a more dramatic change in volumes of B(+)/B(−) hosts (Table S8, ESI†), resulting in higher activation barriers characterizing the exchange.

Conclusions

In summary, the conformational dynamics of the basket (conf steps in Fig. 1) was computed (NEB and DFT) to slow down after the encapsulation of CX₄. The attractive C–X⋯π and C–H⋯X–C contacts, between this capsule and its CX₄ guest, are strong enough in the ground, but weaker in the rate-limiting transition state, to limit structural changes of the host required to twist its top. Fascinatingly, an associative and two-step mechanism describes the CX₄ guest entering the basket (bind steps in Fig. 1). From ASMD simulations, in which a guest is being pulled from its host, we found that a solvent molecule enters the capsule to form an intermediate and then CX₄ is ejected in the second step. As both kinetics and thermodynamics of the computed mechanism agree well with the experimental data,^9,10 ASMD in combination with NEB/DFT emerge as suitable methods for in silico examination of CS and IF operating in supramolecular systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported with funds from the NSF under CHE-2002781. Generous computational allocations from the Ohio Supercomputer Center are gratefully acknowledged.

Notes and references

1. (a) E. Persch, O. Dumele and F. Diederich, Angew. Chem., Int. Ed., 2015, 54, 3290–3327; (b) H.-J. Schneider, Angew. Chem., Int. Ed., 2009, 48, 3924–3977; (c) M. F. J. Mabesoone, A. R. A. Palmans and E. W. Meijer, J. Am. Chem. Soc., 2020, 142, 19781–19798; (d) K. D. Shimizu, Nat. Chem., 2013, 5, 989–990.
2. (a) S. Amano, S. D. P. Fielden and D. A. Leigh, Nature, 2021, 594, 529–534; (b) Y. Feng, M. Ovalle, J. S. W. Seale, C. K. Lee, D. J. Kim, R. D. Astumian and J. F. Stoddart, J. Am. Chem. Soc., 2021, 143, 5569–5591; (c) I. Aprahamian, ACS Cent. Sci., 2020, 6, 347–358; (d) M. Baroncini, S. Silvi and A. Credi, Chem. Rev., 2020, 120, 200–268.
3. J.-P. Changeux and S. Edelstein, F1000Prime Biol Rep., 2011, 3, 19.
4. (a) H. N. Motlagh, J. O. Wrabl, J. Li and V. J. Hilser, Nature, 2014, 508, 331–339; (b) J.-P. Changeux and S. J. Edelstein, Science, 2005, 308, 1424–1428.
5. N. E. Martin, S. Malik, N. Calimet, J.-P. Changeux and M. Cecchini, PLoS Comput. Biol., 2017, 13, 1005781.
6. P. Csermely, R. Palotai and R. Nussinov, Trends Biochem. Sci., 2010, 35, 539–546.
7. G. G. Hammes, Y.-C. Chang and T. G. Oas, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 13737–13741.
8. (a) C. M. Hong, D. M. Kaphan, R. G. Bergman, K. N. Raymond and F. D. Toste, J. Am. Chem. Soc., 2017, 139, 8013–8021; (b) L.-P. Yang, L. Zhang, M. Quan, Y.-L. Ma, H. Zhou, W. Jiang, S. Ward Jas and K. Rissanen, Nat. Commun., 2020, 11, 2740.
9. R. Z. Pavlovic, R. F. Lalisse, A. L. Hansen, C. A. Waudby, Z. Lei, M. Gueney, X. Wang, C. M. Hadad and J. D. Badjic, Angew. Chem., Int. Ed., 2021, 60, 19942–19948.
10. R. Z. Pavlovic, Z. Lei, M. Gueney, R. F. Lalisse, R. G. Hopf, J. Gallucci, C. Moore, H. Xie, C. M. Hadad and J. D. Badjic, Chem. – Eur. J., 2019, 25, 13124–13130.
11. (a) L. Pesce, C. Perego, A. B. Grommet, R. Klajn and G. M. Pavan, J. Am. Chem. Soc., 2020, 142, 9792–9802; (b) F. Liu, R. C. Helgeson and K. N. Houk, Acc. Chem. Res., 2014, 47, 2168–2176.
12. S. Rieth, K. Hermann, B.-Y. Wang and J. D. Badjic, Chem. Soc. Rev., 2011, 40, 1609–1622.
13. Y. Ruan, B.-Y. Wang, J. M. Erb, S. Chen, C. M. Hadad and J. D. Badjic, Org. Biomol. Chem., 2013, 11, 7667–7675.
14. (a) J. Hostas, D. Sigwalt, M. Sekutor, H. Ajani, M. Dubecky, J. Rezac, P. Y. Zavalij, L. Cao, C. Wohlschlager, K. Mlinaric-Majerski, L. Isaacs, R. Glaser and P. Hobza, Chem. – Eur. J., 2016, 22, 17226–17238; (b) E. Boz and M. Stein, Int. J. Mol. Sci., 2021, 22, 3078; (c) A. Manandhar, M. Kang, K. Chakraborty, P. K. Tang and S. M. Loverde, Org. Biomol. Chem., 2017, 15, 7993–8005.
15. M. K. Nguyen, L. Jaillet and S. Redon, J. Comput.-Aided Mol. Des., 2018, 32, 853–867.
16. (a) J. Zhu, Y. Li, J. Wang, Z. Yu, Y. Liu, Y. Tong and W. Han, Front. Chem., 2018, 6, 437; (b) S. Park and K. Schulten, J. Chem. Phys., 2004, 120, 5946–5961.
17. (a) G. Qiu, D. E. Khatmi, A. Martinez and P. Nava, RSC Adv., 2021, 11, 13763–13768; (b) X. Wang and K. N. Houk, Org. Lett., 1999, 1, 591–594.
18. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
19. J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
20. L. C. Palmer and J. Rebek, Jr., Org. Biomol. Chem., 2004, 2, 3051–3059.

---

Footnote

† Electronic supplementary information (ESI) available: A detailed description of computational methods and results. See DOI: 10.1039/d1cp05253e

---