The L–G phase transition in binary Cu–Zr metallic liquids

Abstract

The authors recently reported that undercooled liquid Ag and Ag–Cu alloys both exhibit a first order phase transition from the homogeneous liquid (L-phase) to a heterogeneous solid-like G-phase under isothermal evolution. Here, we report a similar L–G transition and heterogenous G-phase in simulations of liquid Cu–Zr bulk glass. The thermodynamic description and kinetic features (viscosity) of the L-G-phase transition in Cu–Zr simulations suggest it corresponds to experimentally reported liquid–liquid phase transitions in Vitreloy 1 (Vit1) and other Cu–Zr-bearing bulk glass forming alloys. The Cu–Zr G-phase has icosahedrally ordered cores versus fcc/hcp core structures in Ag and Ag–Cu with a notably smaller heterogeneity length scale Λ. We propose the L–G transition is a phenomenon in metallic liquids associated with the emergence of elastic rigidity. The heterogeneous core–shell nano-composite structure likely results from accommodating strain mismatch of stiff core regions by more compliant intervening liquid-like medium.

---

1. Introduction

The glass transition occurs in many diverse substances such as ceramics, polymers, metals, etc. as the high temperature liquid is supercooled below its melting temperature without the intervention of crystallization.^1–5 The glass transition can be viewed as either a dynamic transition with a dramatic slow-down of kinetics, or as a thermodynamic transition characterized by the freezing out of configurational entropy.⁶ From a thermodynamic point of view, glassy states frozen from deeply undercooled liquids are selected from the inherent states of the potential energy landscape (PEL) in configuration space that depend on cooling rate as well as the quenching trajectory.⁷ For example, two types of Au-based metallic glass were classified experimentally with different critical cooling and heating rates.⁸ Recently reported liquid–liquid phase transitions (LLPT's) in strongly interacting liquids such as Si,⁹ P,¹⁰ and Ge–Sb,¹¹ molecular liquids,¹² ionic liquids,¹³ and metallic liquids^14,15 suggest that undercooled liquids exist in distinct metastable phases. In molecular liquids, LLPT's have been explained by either a defect ordered phase^16,17 or by arrested crystallization.^18,19 For metallic alloys, it was recently reported that the glass transition itself evolves into a first order melting transition for metallic glasses in the ultra-fragile Pt–Cu–P ternary alloy system.²⁰ This work demonstrates the existence of two glass phases, a high temperature disordered liquid-like glass and a configurationally ordered low temperature solid-like glass, separated by a first order thermodynamic melting transition. Similarly, a metallic glacial glass (MGG) with a higher hardness was recently reported in a rare-earth-element-based BMG and observed to display an apparent first order melting transition upon heating.²¹

To investigate the origin of an underlying thermodynamic glass transition and its connection with the LLPT's in metallic liquids, we previously performed molecular dynamics (MD) simulations on elementary Ag and binary Cu–Ag liquids under both ultrafast quenching and under isothermal evolution conditions below the melting temperature.^22–24 We demonstrated that both elementary undercooled Ag and Ag–Cu binary liquids undergo a first-order configurational freezing transition from a homogeneous disordered liquid phase (L-phase) to a heterogeneous, configurationally ordered G-phase under isothermal evolution.^22,23 This ordered G-phase exhibits strong first order melting behavior upon rapid re-heating, very different from the traditional view of the glass transition. A significantly increased shear modulus (∼20 GPa) accompanies the L–G transition suggesting that G-phase formation is accompanied by the emergence of persistent long-range elasticity and driven by the reduction of local distortion energy arising from deviatoric strain energy in the liquid L-phase.²⁴ We conjectured that G-phase formation may explain experimentally observed LLPT's in metallic glass systems.^14,15

Here, we employ MD simulations to investigate the L–G transition in binary Cu–Zr alloys known to form bulk metallic glass (BMG) in the laboratory. Specifically, the compositions Cu₆₆Zr₃₄ and Cu₄₆Zr₅₄ are well studied BMG's.^25,26 Here, we examined the Cu₂Zr and Cu₇₀Zr₃₀ compositions, close to the composition Cu₆₆Zr₃₄. In the simulations, the binary Cu–Zr liquids are ultrafast quenched to room temperature with a cooling rate of 3.4 × 10¹² K s⁻¹ and freeze to a homogeneous L-phase glass with homogeneous liquid-like character. In contrast, when the undercooled liquids are isothermally evolved at 900 K (336 K below the alloy melting temperature), a first order L–G transition occurs over several hundred nanoseconds. The time scale for the Cu–Zr alloys is orders of magnitude longer than for the elemental Ag L–G transition. The product G-phase is clearly glassy, lacking long range atomic order beyond ∼ 1 nm, but displays inherently heterogeneous character with icosahedral local ordering in the G-phase cores. The ordered core regions are separated by disordered regions (the matrix); with the overall structure displaying a characteristic heterogeneity length scale Λ of 1.5–1.7 nm, significantly less than that seen in Ag and Ag–Cu alloys (∼4 nm and ∼2 nm, respectively). The thermodynamics state functions are derived for all phases observed under the assumption of metastability in MD simulations. Elastic shear rigidity and persistent stress fields in the G-phase are characterized to demonstrate that the L–G transition corresponds to the emergence of elastic rigidity. Combined with our earlier work on Ag and Ag–Cu, the present study suggests that the L–G transition from a homogeneous fluid-like to heterogeneous solid-like phase may be a universal feature of undercooled metallic liquids. While the specific local atomic ordering of the core regions varies (i.e. fcc/hcp local order in Ag and Ag–Cu versus icosahedral order in Cu–Zr), the emergence of a heterogeneous core-liquid shell structure at a nanometer length scale Λ, the onset of shear rigidity, and the absence of long range order are universal features of the product G-phase.

2. Simulation procedures

2.1 Model construction and MD simulations

We performed the MD simulations using LAMMPS software²⁷ to investigate the L–G transition in binary Cu–Zr systems. The embedded atom model (EAM) potential is applied in MD simulations to describe the interatomic interactions. Most simulations were performed using the Sheng's Cu–Zr EAM potential.²⁸ Another Cu–Zr EAM potential²⁹ was used to confirm the L–G transition and metastability of the G-phase on the MD time scale. The velocity Verlet algorithm is used for integrating the equations of motion with a timestep of 1.0 fs in all MD simulations. Periodic boundary conditions (PBC) were applied along three directions to minimize the possible surface effects. We focused on the compositions Cu₂Zr and Cu₇Zr₃ for the detailed analyses of the first order L–G transition, structural characterization, thermodynamic state functions, kinetics, and elastic rigidity.

The L-phase glass was obtained from ultrafast quenching simulations as discussed in the literature.^22,23,30 The well equilibrated liquid was first achieved at 2000 K using 5 ns NPT dynamics. The liquid is then quenched to ambient conditions using a high cooling rate of 3.4 × 10¹² K s⁻¹. The G-phase is not obtained directly from the ultrafast MD quenching simulations. Instead, it is produced by isothermally aging the supercooled liquids at 900 K. It requires 500–1000 nanoseconds (∼1 μs) to complete the L–G transition at 900 K for both compositions of Cu₂Zr and Cu₇Zr₃. Following isothermal aging, we quench the G-phase to the room temperature using the same cooling rate to produce the L-phase (3.4 × 10¹² K s⁻¹). The NPT ensemble is applied in all simulations to account for the possible volume changes during L–G transition. For the composition Cu₇Zr₃, the cell parameters were adjusted isotopically to the pressure change in NPT ensemble. But the L–G transition does not occur (for times up to 1 μs) for Cu₂Zr if the cell parameters were isotopically changed. Therefore, we allowed the cell parameters to change independently of each other. This means the cell length and angles all vary in NPT simulations. This method permits relaxation of arbitrary average stresses within the MD cell. The Nose–Hoover thermostat and barostat were applied to control the temperature and pressure (stresses) in NPT ensemble with the damping constants of 200 fs and 2000 fs, respectively. We have tested the dumping constants for thermostat and barostat using the G-phase melting process, as shown in Fig. S1 of the ESI.† These results indicated the selected dumping constants are robust in the present study. We used the system size of 32 000 atoms for the composition Cu₇Zr₃ case, which is large enough to examine the heterogeneity of G-phase. For Cu₂Zr the system size was increased to 41 472 atoms to make comparisons with single crystal Laves phase which has the similar local ordered structure as the core region of G-phase. The unit cell of Laves phase (MgCu₂-type) consists of 24 atoms and the initial L-phase for Cu₂Zr is obtained by melting the 12 × 12 × 12 supercell of the Laves phase, leading to a total of 41 472 atoms. The equilibrium MD simulations were performed to obtain the thermodynamics state functions of L-phase, G-phase, and Laves phase, including enthalpy, entropy, free energy, and molar volume.

2.2 Structure analysis: radial distribution function, Honeycut–Anderson analysis, bond-orientational order parameter, and PE-density map

The structures of all phases were characterized by various techniques including radial distribution function (RDF), Honeycut–Anderson (HA) topological analysis,³¹ bond-orientational order parameters (BOOP),^32,33 and PE-density maps.^22,23 The RDF represents the average number density variation of neighboring atoms as a function of distance, and is widely used to distinguish the liquid phase, crystal phase, and glass phase. The local order within several atomic distances cannot be determined directly from RDF analysis. Instead, we use the HA analysis and BOOP to characterize the local atomic ordering. The HA index is determined by the topological relationship of neighboring pairs, where fcc, hcp, and icosahedral orders are identified by various HA indices 1421, 1422, and 1551, respectively.³¹ Besides HA index, the local ordered structures can be further illustrated using the BOOP, q_l (l = 2,4,6,8,…).^32,33 In BOOP, the local symmetry is determined by the quadratic and third-order invariants of bond spherical harmonics. Among all BOOP, the q₈ and q₁₀ order parameters are very sensitive to icosahedral, fcc and hcp orders, and disordered structures, and are adopted to characterize the L-phase and G-phase in the present study. The cutoff distance for neighboring pairs in both HA analysis and BOOP calculations is determined by the first minimum position in the RDF.

The potential energy (PE) density map illustrates the configurational enthalpy of each atom by averaging the PE, ϕ, over a period of two picoseconds, much longer than the timescale of atomic vibrational motions. Thus, vibrational noise is removed and only the configurational contribution to the enthalpy is left. The PE-density map has been used successfully to characterize the G-phase in Ag²³ and Ag–Cu.^23,24 With respect to different atomic PE values for Cu and Zr, we first calculated the average PE per atom for Cu and Zr in the whole MD cell, respectively. Then the deviation from the average PE for each atom is computed and normalized by the mean variance of the PE per atom. The relative PE then is comparable for the different types of atoms. To determine the correlation length, Λ, of the local ordered regions, we computed the PE pair distribution function (PE-PDF) using the same approach as computing RDF.^23,24 We do the average of PE for 100 picoseconds to obtain the smooth curve of PE-PDF.

2.3 Thermodynamic functions calculations

The PE curves of both L- and G-phases reach steady state and are therefore well equilibrated (for at least several nanoseconds) for temperatures below its melting temperature. This indicates their robust metastability and the plausible application of equilibrium thermodynamics. The configurational entropy of the liquid may be defined as s_C(ϕ) = k_B ln W_C(ϕ) from potential energy landscape (PEL) theory,^25,34 where W_C(ϕ) is the density of inherent configurations per atom and k_B is the Boltzmann constant. Therefore, the thermodynamic state functions of a liquid, enthalpy h, entropy s, and free energy g, are approximately composed of well separated configurational and vibrational contributions that are weakly coupled via anharmonic effects.²⁰ In our MD simulations at zero pressure, the potential energy of the liquid at fixed temperature T is thus given by ϕ_L(T) = ϕ^v_L(T) + ϕ^C_L(T), where ϕ^v_L(T) is the vibrational term that has the form ϕ^v_χ(T) = 3/2RT + aT² which includes the classical Dulong–Petit contribution (3/2 RT) and an anharmonic term (2nd order term); and ϕ^C_L(T) is the specific configurational enthalpy of a liquid. Our simulations were performed at zero pressure, making the enthalpy the same as the potential energy. The ϕ^C_L(T) term follows a “1/T” temperature dependence if one assumes a Gaussian distribution of inherent state energies in the liquid.³⁵ The G-phase and Laves phase are solid-like phases for which the configuration changes only insignificantly over the MD timescale. Therefore, the potential energy of these two phases was treated as the summation of the vibrational terms along with a temperature independent constant configurational term. The L-phase reaches equilibrium within the first 100 ps at temperatures above 900 K and only the data above this temperature were used in fitting the ϕ_L(T).

Under the assumption of a metastable equilibrium state for the G-phase, for the L-phase on supercooling, and for the Laves phase upon superheating, other thermodynamic state functions such as entropy, free energy, specific heat, etc. can be readily computed directly from MD simulations.^22,23 The entropy of each phase is computed through the integration of dh/T. The integration constant for each phase must be determined independently. Here, we use the single crystal phase (Laves phase) as the thermodynamic reference state. At its melting temperature (determined from the two-phase coexistence simulations) the entropy of fusion determines the liquid entropy. Here we assume that the entropy of the single crystal is zero [s_X(T = 300 K, P = 0) = 0] at room temperature and zero pressure. Room temperature is selected to avoid quantum effects on vibrational modes since our simulations employ classical molecular dynamics. Thus, the entropy of fusion determines the integration constant for the liquid (relative to the crystal), giving the entropy curves for the L- and X-phases. Using the same approach, we determined the entropy curve of the G-phase using L-phase as the reference phase.

2.4 Two-phase coexistence simulations to predict melting temperature

The two-phase coexistence simulation is a powerful tool to determine the melting temperature from MD simulations.³⁶ In this technique, the liquid phase and crystal phase are joined together at various temperatures with about one atomic distance between two phases. Then the system is equilibrated, and one observes the evolution of the combined system to determine whether the temperature is above or below the melting temperature. If the temperature is above melting temperature, T_X,M, the interfaces between two phases move towards the crystal phase and the system melts to liquid phase eventually. The PE of the whole system increases, indicating the melting process. If T < T_X,M, the interfaces move towards the liquid phase and PE decreases. If T ≈ T_X,M, the interfaces are stable and PE barely changes in the MD timescale. The two-phase coexistence simulation can also be applied to determine the melting temperature of G-phase, T_G,M. Similar to the crystal case, the liquid phase and G-phase are first combined and then the mixed system evolves at various temperatures.

The slope of the PE curves of two-phase coexistence simulation is correlated to the speed of the interface's movement and it is close to zero at T ≈ T_X,M (or T_G,M). The kinetics of solidification in binary alloys is very slow compared to the MD timescale, as indicated by the sluggish L–G transition in the Cu–Zr system. To determine the T_X,M (or T_G,M) using the two-phase coexistence simulation, the slope of PE is applied near the equilibrium temperature.

For the two-phase coexistence of Cu₇Zr₃ composition, the crystal phase is necessary to obtain T_X,M. Assuming that the crystal phase remains the Laves phase in this composition, we constructed it by randomly substituting the Zr atoms with Cu atoms in Cu₂Zr Laves phase to match the proper atomic ratio. Then the Monte Carlo (MC) simulations were performed for over 1.0 × 10⁶ steps to find the lowest energy structures by swapping atoms in the lattice.

2.5 Von-Mises stress and viscosity calculations

The reduction of distortion strain energy, U_distortion, is correlated with the Von-Mises stress, σ_v,²⁴ and therefore we computed the σ_v from the atomic stress that consists of kinetic and Virial contributions,³⁷ and atomic volume using Voronoi tessellation.³⁸ To remove the thermal noise at high temperature, the σ_v is averaged over two picoseconds, much longer than the atomic vibrations.

The viscosity of L-phase was computed from the Green–Kubo formalism³⁹ relating the ensemble average of the autocorrelation of shear stress σ^αβ. Since a liquid is isotropic, the shear viscosity is computed by averaging over the three independent shear components: σ^xy, σ^xz, and σ^yz. For the G-phase, the viscosity is estimated from a simple Maxwell model η = μ × τ where μ is the shear modules and τ is the relaxation time. The shear modulus was computed from the elastic constants C_ij and stiffness constants S_ij using the Voigt–Reuss–Hill average.⁴⁰ The elastic constant, C_ij, is calculated by evaluating the stress tensor as the lattice is deformed elastically along possible directions.⁴¹ Then the S_ij is derived from the inversion matrix of C_ij. The relaxation time, τ, is obtained by allowing a pre-deformed supercell with 2% shear strain evolve and examining the shear stress relaxation.

3. Results and discussion

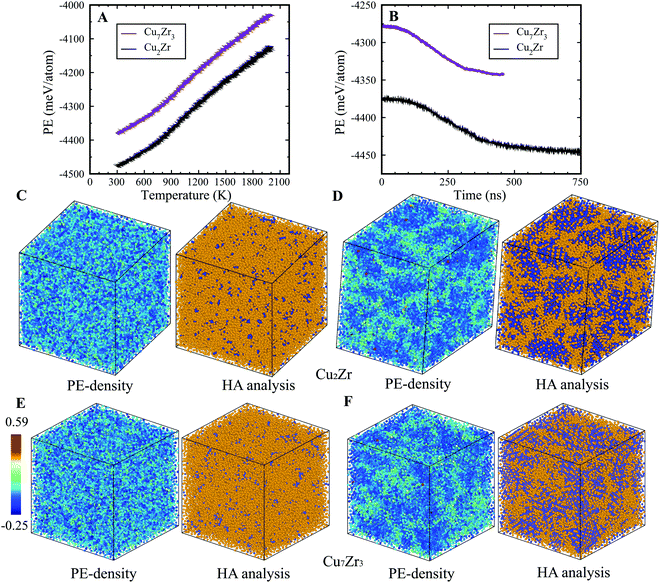
3.1 Glass formation in binary Cu–Zr system

In the present study, we examined two compositions: Cu₂Zr and Cu₇Zr₃ which are close to the experimentally reported bulk metallic glass composition Cu_64.5Zr_35.5.²⁵ On rapid quenching at constant cooling rate from the high temperature melt to ambient T, both compositions show an inflection in Potential Energy (PE) vs. T curves at ∼900 K, indicating configurational freezing to an L-Glass as shown in Fig. 1(A) – a result similar to many other MD studies.^26,28–30 If rapid quenching is interrupted at 900 K, and the system configuration is allowed to evolve in time under isothermal MD dynamics, we observe a strikingly different behavior. In contrast to L-phase formation, the metastable liquids for both compositions initially equilibrate, then subsequently undergo a systematic drop in the PE that leads to a final state that is well-defined but with significantly lower PE as seen in Fig. 1(B). This PE drop under isothermal conditions is very similar to that previously reported for the L–G transition in Ag–Cu,²³ but the time required for L–G transition is substantially longer in the Cu–Zr alloys (several hundred ns) compared to Ag–Cu alloys (several ns). To test whether this result might depend in the specific EAM potential²⁹ we carried out simulations using a very different EAM on the L-phase and G-phase but obtained qualitatively equivalent results, as shown in see Fig. S2 of the ESI.† The product G-phase at 900 K is found to be metastable, albeit with somewhat lower PE difference with L-phase.

Fig. 1 L-Glass and G-glass formation in the binary Cu₂Zr and Cu₇Zr₃ systems, including their structure characterization: (A) PE vs. Temperature during quenching from 2000 to 300 K, indicating the formation of L-phase glass. (B) PE vs. Time during the isothermal MD runs at 900 K, leading to the formation of the G-phase. (C) Atomic structure of the L-phase for Cu₂Zr composition at 300 K. (D) Atomic structures of the G-phase for Cu₂Zr at 300 K. (E) Atomic structure of the L-phase for Cu₇Zr₃ composition at 300 K. (F) Atomic structures of the G-phase for Cu₇Zr₃ at 300 K. The icosahedral and liquid atoms determined from the Honeycutt-Anderson analysis are represented by purple and yellow balls, respectively.

We characterized both the G-phase and L-phase using PE-density and Honeycutt–Anderson³¹ analysis, as shown in Fig. 1(C–F). The PE-density map of the G-phase displays a heterogenous structure with low PE ordered core regions that are randomly orientated and separated by high PE matrix regions (Fig. 1(D and F)). The Honeycutt–Anderson analysis indicates that the low PE core regions have ordered structures characterized by significant icosahedral short-range order while the high PE regions have a more disordered structure characteristic of a liquid phase. No other local atomic ordering, such as fcc, bcc, or hcp, was identified. To illustrate the correlation between PE density and HA analysis, we plotted the PE density distribution for icosahedral and non-icosahedral atoms for both Cu₂Zr and Cu₇Zr₃ at room temperature, as shown in Fig. S3 of ESI.† The results clearly show that the icosahedral atoms have a lower PE density compared to non-icosahedral atoms, confirming the good correlation between PE-density and HA analysis. In contrast to the G-phase, the L-phase displays significantly more homogenous character, as shown in Fig. 1(C and E). Far fewer icosahedral atoms were identified in the L-phase; only ∼6% compared to ∼38% in the G-phase. While icosahedral atoms are homogenously distributed in the L-phase, the G-phase exhibits a heterogeneous distribution with high icosahedral concentrations in its core regions.

Fig. S4 (ESI†) displays the icosahedral atoms in the G-phase. Three sectional slabs, each with a width of 8 Å, are shown to better illustrate the microstructure. These results indicate that each icosahedral region (ordered core region) has a different orientation and that they are generally separated by liquid phase. Interestingly, most icosahedral regions are linked by a line of atoms (indicated by the brown ellipses), suggesting that after formation of the G-phase, the ordered cores may percolate. Also interesting is a twin like structure in Fig. S4 of ESI† where the apparent twin boundary is shown by a red line.

The G-phase does not exhibit long-range order in contrast to crystalline phases. This is clearly confirmed by the Radial Distribution Function (RDF) plots of the L-phase and G-phase as shown in Fig. 2(A). Both the L-phase and G-phase display no long-range order beyond ∼1 nm. To further characterize the ordered core structure in the G-phase, we compared the RDF of the G-phase to that of the intermetallic Cu₂Zr Laves phase. The comparison of partial RDFs in Fig. 2(B–D) indicates that the ordered core structure in the G-phase closely resembles the intermetallic Laves phase. A similar RDF analysis was also performed on the composition Cu₇Zr₃; with similar results as shown in Fig. S5 of ESI.†

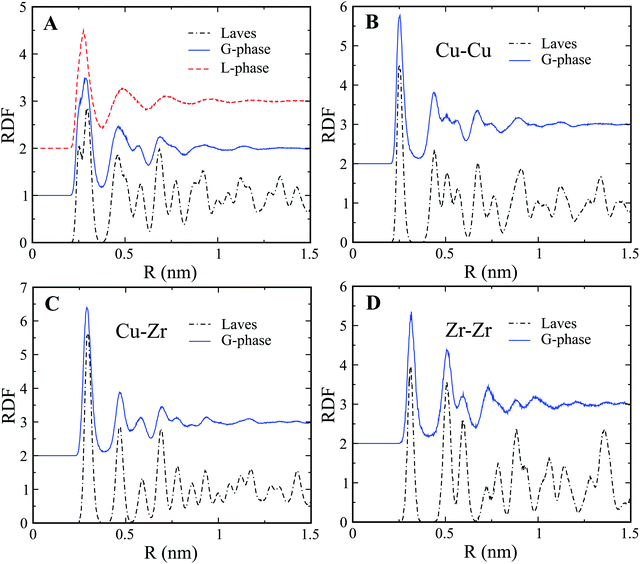Fig. 2 RDF analysis of L-phase and G-phase for Cu₂Zr composition. (A) Total RDF of L-phase, G-phase, and Laves phase. (B–D) Comparison of partial RDFs of Cu–Cu (B), Cu–Zr (C), and Zr–Zr (D).

3.2 Thermodynamic functions of the G-phase and latent heat of the L–G transition

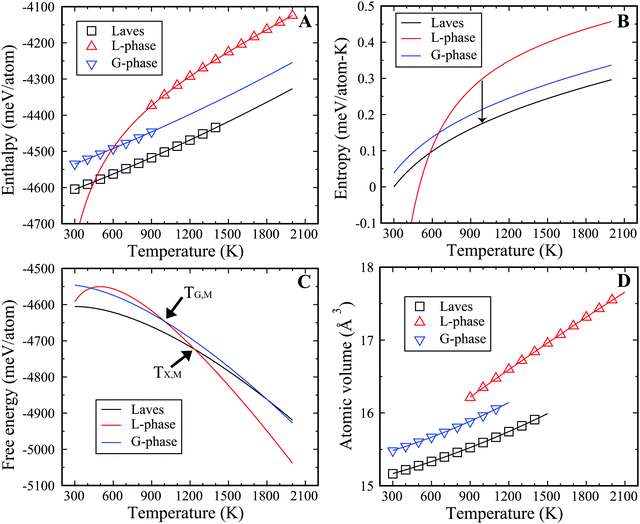
To illustrate the thermodynamic driving force for the L–G transition in the binary Cu–Zr system, we computed the thermodynamic state functions of both phases, such as enthalpy, entropy, and free energy. The thermodynamic state functions for the Laves phase were also computed as the lowest energy structure at low temperature. The enthalpies of all phases for Cu₂Zr were calculated for various temperatures ranging from 300 to 2000 K and are displayed in Fig. 3(A). Fitting these data at varying temperature yields the enthalpy curves and the ϕ_χ(T), (χ = L, G, Laves) listed in the eqn (1)–(3). We find the latent heat for the L–G transition to be 67.7 meV per atom at 900 K, which provides the thermodynamic driving force for the L–G transition. The enthalpy of the L-phase is reduced by forming the locally ordered regions in the G-phase. But these ordered regions comprise only a fraction of the volume of the MD cell. For comparison, the latent heat of solidification for the liquid to Laves phase transition is much larger, computed to be 143.8 meV per atom at 900 K. Therefore, the latent heat of L–G transition is only ∼47% of that for the liquid-to-crystalline Laves phase transition.

ϕ_L(T) = −4348.5 mV per atom + 0.1293T + 0.8 × 10⁻⁵T² − 133468.0/T (1)

ϕ_G(T) = −4675.2 mV per atom + 0.1293T + 1.6 × 10⁻⁵T² (2)

ϕLaves(T) = −4645.4 mV per atom + 0.1293T + 1.5 × 10⁻⁵T² (3)

Fig. 3 Thermodynamic functions. (A) Enthalpy map of various phases extracted from MD simulations. (B and C) entropy (B) and free energy (C) of the L-phase, G-phase, and Laves phase. (D) Molar volume vs. T.

The G-phase formed at 900 K was subsequently heated to higher temperatures. Fig. S6 of ESI† indicates the G-phase reversibly melts at ∼1300 K under constant heating back to the L-phase. This remelting essentially establishes that the L–G transition is reversible, albeit with thermal hysteresis; evidenced by undercooling of the liquid and overheating of the G-phase above its melting temperature on continuous heating.

To obtain the entropy, we need to obtain the equilibrium melting temperature for crystal phase and G-phase, which can be derived from two-phase coexistence simulations. Fig. S7 (ESI†) shows the PE curves of Cu₂Zr composition near the equilibrium temperature in the two-phase coexistence simulations. The slope of PE vs. time is linear in the region close to T_X,M (or T_G,M). The T_X,M is 1236 K for the Laves phase and the T_G,M is 1002 K for the G-phase. Fig. 3(B) displays the entropy curves for all three phases. In the MD simulations, the Laves phase displays a heat of fusion of 178.4 meV per atom at its melting point of 1236 K. The Laves phase entropy of fusion is thus 13.9 J mol⁻¹ K⁻¹, of which roughly 3/4 (10.7 J mol⁻¹ K⁻¹) is vibrational, with the balance configurational. Combining the enthalpy and entropy curves, we obtained the specific Gibbs free energy of all three phases at zero pressure, with the results displayed in Fig. 3(C). Thermodynamically, the G-phase is metastable at all temperatures, but it is an intermediate state since the L-phase transforms to the Laves phase in the deep undercooling region. It is worth noting the entropy of the L-phase is lower than the G-phase at ∼600 K, in analogy with the traditional Kauzmann paradox. As such, the extrapolated entropy and free energy of L-phase below 600 K should be viewed as non-physical.

Previous experimental studies suggest that the specific volume in the cooling–heating cycle drops by ∼0.7% during the liquid–liquid transition observed experimentally in Vitreloy 1 (Vit1) at 890 K.¹⁵ The molar volume of Cu₂Zr (Fig. 3(D)) decreases by ∼2.0% during the L–G transition at 900 K, which is roughly similar to experimental observation on Vit 1. This suggests that the L–G transition in the present study may be fundamentally related to the experimentally observed liquid–liquid transition in Vit1. The thermodynamic state functions for the Cu₇Zr₃ composition are displayed in Fig. S8 of ESI.†

3.3 Structure of the G-phase from PE density maps and the correlation length

The structure of the heterogenous G-phase is significantly different from the L-phase. The spatial PE-density map of the G-phase (Fig. 4(A)) reveal an obvious heterogeneous structure. In contrast, the same map for the L-phase reveals a homogenous structure (Fig. 5(A)). To correlate the PE-density map with local deviatoric strain energy of the G-phase, we analyzed the atomic level von-Mises shear stress (Fig. 4(B)). The low PE density regions correspond to a low von-Mises shear stress and thus a lower distortion energy.²⁴ The positive correlation suggests that the driving force of the L–G transition is indeed the local deviatoric strain energy in Cu–Zr. For comparison, the von-Mises stress map for the L-phase displays a more homogenous character (Fig. 5(B)).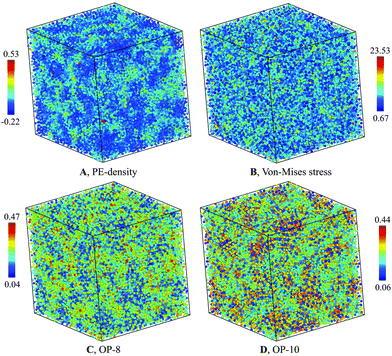

Fig. 4 Characterization of G-phase at 900 K for composition Cu₂Zr: (A) PE-density map, (B) Von-mises stress, (C) OP-8, and (D) OP-10.

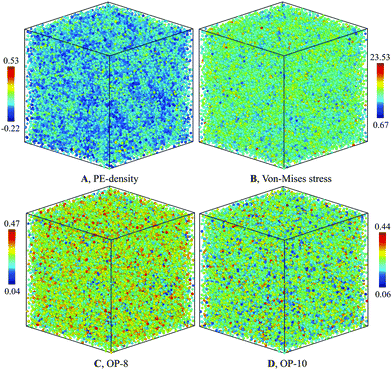Fig. 5 Characterization of L-phase at 900 K for composition Cu₂Zr: (A) PE-density map, (B) Von-mises stress, (C) OP-8, and (D) OP-10.

The PE density map also correlates closely with local atomic structures. The bond-orientational order parameters analysis^32,33 indicates a good correlation with the PE-density maps (Fig. 4(C and D)). Several features of the G-phase are notable. The heterogeneous G-phase consists of low configurational enthalpy regions, ϕ^C_G(T), with icosahedral-ordered core structures (low OP-8 and high OP-10), embedded in a higher ϕ^C_G(T) matrix with more disordered structures (high OP-8 and low OP-10). The ordered core regions possess substantial icosahedral short-range order without significant fcc, bcc, or hcp character. These ordered regions are on the ∼1 nm scale but topologically isolated and surrounded by the disordered matrix of “liquid-like” regions. The G-phase structure is a spatially correlated well-defined mixture of ordered core regions embedded in a surrounding liquid-like disordered medium.

To understand the correlation between PE-density with other order parameters in Fig. 4, we performed the correlation analysis of PE-density with these parameters for Cu and Zr atoms separately. As shown in Fig. S9 of ESI,† the PE-density is correlated with HA analysis, Von-mises stress, the OP-8 and OP-10 order parameters for Cu atoms. However, the large atomic fluctuations on these parameters lead to small correlation coefficients. The PE density correlates best with OP-8 order parameter with a correlation coefficient of 0.28. The next best correlation is with the OP-10 order parameter with a correlation coefficient of 0.09. The Von-mises stress is less correlated with PE-density with a correlation coefficient of 0.06. For Zr atoms we performed the analysis on Von-mises stress, the OP-8 and OP-10 since very few Zr atoms are identified as icosahedral atoms. As shown in Fig. S10 of ESI,† the PE density correlates best with OP-8 order parameter with a correlation coefficient of 0.25. But the next correlated parameter is Von-mises stress with a correlation coefficient of 0.10. The OP-10 is the least correlated with PE-density and a correlation coefficient is just 0.02.

Fig. 5(C and D) shows the bond-orientational order parameters of the L-phase at 900 K which display a far more homogenous structural character. A similar structure analysis was performed for the G-phase of composition Cu₇Zr₃; with character similar to Cu₂Zr as shown in Fig. S11 of ESI.†

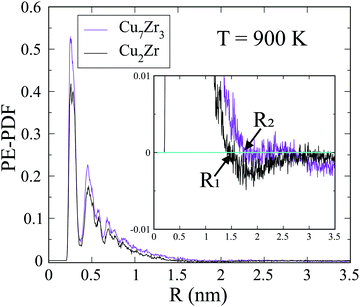
The spatial scale of the core regions can be characterized by the length scale of heterogeneity, Λ, which is computed from the PE pair distribution function (PE-PDF). Fig. 6 displays the PE-PDF of the G-phase at 900 K for the composition Cu₂Zr and Cu₇Zr₃, respectively. We obtain Λ ∼1.5 nm for Cu₂Zr and it increases slightly to ∼1.8 nm for Cu₇Zr₃, suggesting that the scale of the low PE core regions depends slightly on alloy composition. Comparison to the G-phase for single component systems,²² show that both Λ and the latent heat of the L–G transition are significantly reduced. This may explain why the L–G transition is kinetically far more sluggish in the binary Cu–Zr system compared with a single component liquid (e.g. Ag or Cu).^22,23 The Λ is not well defined in liquid phase and the same analysis on L-phase at 300 K leads to Λ = ∼0.27 nm which is similar to near neighbor atomic distance.

Fig. 6 PE-PDF at 900 K. PE-PDF at 900 K showing the correlation length of G-phase is ∼1.5 nm for Cu₂Zr (R1) and ∼1.8 nm for Cu₇Zr₃ (R2). The insert figure is zoom in y axis to show the correlation length.

3.4 Elastic rigidity and persistent stress fields in G-phase

The underlying physical origin of the G-phase likely relates to long-range elasticity and minimization of deviatoric strain energy. In terms of elasticity, it is important to recognize that both the L- and G-phases are macroscopically isotropic. But the shear rigidity exhibits very different time scales for the G-phase compared to the supercooled liquid L-phase. It is generally assumed that liquids do not support shear on any practical time scale, which we find here also. In contrast, the G-phase support shear over a far longer but finite time scale. Thus, we obtained a stress relaxation time of τ_α ∼ 6.0 ns for the G-phase (Fig. 7(A)) at 900 K. We determined the shear stress relaxation time for the G-phase by imposing a 2% shear strain, ε_xz, and then holding the MD cell fixed and allowing relaxation of the shear stress σ_xz. In contrast, the relaxation of L-phase is of order τ₂ ∼ 20 ps, 300 times shorter, as shown in Fig. 7(B). A stress relaxation time scale that exceeds the configurational hopping time, implies a persistent contribution of frozen elastic stress fields to the configurational potential energy of the inherent states in the G-phase. This alters the distribution of inherent state energies, or equivalently alters the configurational density of states in the G-phase versus the L-phase (since the high hopping rate time averages this contribution to the PE of the inherent state for the L phase). Effectively, the inherent state energies are renormalized by the long-range power law of elastic interactions. This renormalization alters the density of inherent states and consequently the thermodynamic functions of the G-phase.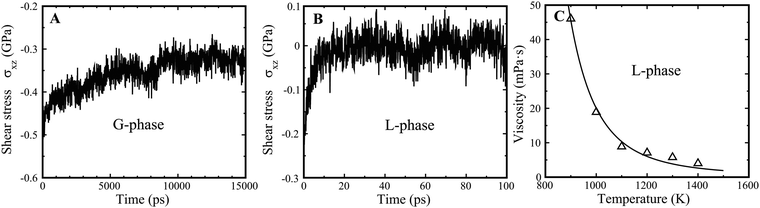

Fig. 7 Relaxation of G-phase and G-phase, as well as viscosity of L-phase. (A) The relaxation process of G-phase at 900 K. (B) The relaxation process of L-phase at 900 K. (C) The MD derived viscosity of L-phase at high temperature from 900 K to 1400 K. The viscosity is fitted by the equation η = η₀ × exp(C/T × exp(−(2 + λ) × αT)).⁴² The fitted parameters are η₀ = 0.153 × 10⁻³ Pa s, C = 8075, λ = 4.21, and α = 8.13 × 10⁻⁵ K⁻¹.

The shear modulus (μ) for the G-phase is 24.1 GPa, much larger than that of L-phase, 1.5 GPa. Using a simple Maxwell model, we estimate the viscosity of the G-phase to be η_G (900 K) = μ × τ ∼ 144.8 Pa s. This is ∼1500 times higher than the viscosity of L-phase at 900 K, calculated to be 4.6 × 10⁻² Pa s (Fig. 7(C)). Therefore, the L–G transition is accompanied by a dramatic discontinuous jump in the liquid viscosity. This is consistent with an experimentally observed viscosity jump of roughly two orders of magnitude accompanying an apparent discontinuous liquid–liquid transition in Vit 1 at temperatures ∼900–1100 K.¹⁴ The viscosity in the experimentally reported LLPT jumps from ∼0.2 to ∼20.0 Pa s at 1100 K.¹⁴ The G-phase at high temperature is a relatively viscous liquid with a shear modulus that persists over the time scale of its stability. This implies that configurational rearrangements in the G-phase are subject to long range elastic constraints that arise from elastic compatibility requirements. Such constraints reduce the configurational entropy of the G-phase relative to that of the L-phase, consistent with the entropy drop we observe to accompany the L–G transition.

The L-phase is characterized by both the lack of long-range order and the lack of rigidity. In contrast the G-phase lacks long-range order (as indicated from the RDF analysis, Fig. 2) and is non-crystalline, but manifests a large shear modulus and exhibits more substantial and persistent shear rigidity, i.e. is solid-like. The experimental liquid–liquid transition in Vit1 and other Zr-based bulk metallic glasses^14,15 bears a remarkable resemblance to the behavior of the L–G transition reported here. We propose that the two transitions may be one and the same.

4. Conclusion

In summary, we examined the L–G transition in binary Cu–Zr liquids, in which the isotropic undercooled L-phase liquid transforms to another, elastically rigid, solid-like G-phase. The L-phase is homogeneous on the atomic scale while the G-phase displays a distinctly heterogeneous topological structure with a characteristic length scale Λ of 1.5 and 1.8 nm for Cu₂Zr and Cu₇Zr₃, respectively. The G-phase contains locally ordered core regions with icosahedral short-range order and low configurational enthalpy. These core regions are embedded in a continuous matrix composed of a disordered liquid-like structure with high configurational enthalpy. In addition to its heterogeneous structure, the G-phase is further distinguished from the L-phase by the emergence of elastic rigidity with a finite persistent shear modulus. Based on our present and prior work, we propose that the first order L–G transition may be a universal liquid-like to solid-like phase transition in metallic liquids, that is driven by reduction of strain energy. The disordered high potential energy regions are expected to be more elastically compliant (smaller shear modulus) than the stiffer and lower PE ordered cores regions. In the composite structure of the G-phase, stored elastic strain energy arising from elastic incompatibility of neighboring core regions will then be substantially reduced by accommodation in the intervening disordered regions, leading to overall elastic compatibility with a minimum energy cost.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

W. L. J. and S. L. C. are supported by NSF grant with the award number DMR 1710744. K. S. is supported by the DFG, grant Sa337/10.

Notes and references

1. Q. An, L.-Q. Zheng and S.-N. Luo, J. Non-Cryst. Solids, 2006, 352, 3320–3325.
2. J. D. Ferry, Viscoelastic Properties of Polymers, John Wiley & Sons Inc., New York, USA, 1961.
3. W. Kauzmann, Chem. Rev., 1948, 43, 219–256.
4. W. Klement, Jr., R. H. Willens and P. Duwez, Nature, 1960, 187, 869–870.
5. P. Duwez, R. H. Willens and R. C. Crewdson, J. Appl. Phys., 1965, 36, 2267–2269.
6. D. Tabor, Gases, Liquids, and Solids (and other States of Matter), Cambridge University Press, Cambridge, UK, 1991.
7. M. Goldstein, J. Chem. Phys., 1969, 51, 3728–3739.
8. J. E. K. Schawe and J. F. Löffler, Nat. Commun., 2019, 10, 1337.
9. P. F. McMillan, M. Wilson, D. Daisenberger and D. Machon, Nat. Mater., 2005, 4, 680–684.
10. G. Monaco, S. Falconi, W. A. Crichton and M. Mezouar, Phys. Rev. Lett., 2004, 90, 255701.
11. P. Zalden, F. Quirin, M. Schumacher, J. Siegel, S. Wei, A. Koc, M. Nicoul, M. Trigo, P. Andreasson, H. Enquist, M. J. Shu, T. Pardini, M. Chollet, D. Zhu, H. Lemke, I. Ronneberger, J. Larsson, A. M. Lindenberg, H. E. Fischer, S. Hau-Riege, D. A. Reis, R. Mazzarello, M. Wuttig and K. Sokolowski-Tinten, Science, 2019, 364, 1062–1067.
12. M. Zhu, J.-Q. Wang, J. H. Perepezko and L. Yu, J. Chem. Phys., 2015, 142, 244504.
13. M. A. Harrisa, T. Kinsey, D. V. Wagle, G. A. Baker and J. Sangoro, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2020878118.
14. C. Way, P. Wadhwa and R. Busch, Acta Mater., 2007, 55, 2977–2983.
15. J. J. Z. Li, W. K. Rhim, C. P. Kim, K. Samwer and W. L. Johnson, Acta Mater., 2011, 59, 2166–2171.
16. I. Cohen, A. Ha, X. Zhao, M. Lee, T. Fischer, M. J. Strouse and D. Kivelson, J. Phys. Chem., 1996, 100, 8518–8526.
17. G. Tarjus, C. Alba-Simionesco, M. Grousson, P. Viot and D. Kivelson, J. Phys.: Condens. Matter, 2003, 15, S1077–S1084.
18. A. Hedoux, Y. Guinet, P. Derollez, O. Hernandez, R. Lefort and M. Descamps, Phys. Chem. Chem. Phys., 2004, 6, 3192–3199.
19. M. Tarnacka, O. Madejczyk, M. Dulski, P. Maksym, K. Kaminski and M. Paluch, J. Phys. Chem. C, 2017, 121, 19442–19450.
20. J. Na, S. L. Corona, A. Hoff and W. L. Johnson, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 2779–2787.
21. J. Shen, Z. Lu, J.-Q. Wang, S. Lan, F. Zhang, A. Hirata, M. W. Chen, X. L. Wang, P. Wen, Y. H. Sun, H. Y. Bai and W. H. Wan, J. Phys. Chem. Lett., 2020, 11, 6718–6723.
22. Q. An, W. L. Johnson, K. Samwer, S. L. Corona and W. A. Goddard III, J. Phys. Chem. Lett., 2020, 11, 632–645.
23. Q. An, W. L. Johnson, K. Samwer, S. L. Corona and W. A. Goddard III, Acta Mater., 2020, 195, 274–281.
24. Q. An, W. L. Johnson, K. Samwer, S. L. Corona and W. A. Goddard III, Scr. Mater., 2021, 194, 113695.
25. D. Wang, Y. Li, B. Sun, M. Sui, K. Lu and E. Ma, Appl. Phys. Lett., 2004, 84, 4029–4031.
26. G. Duan, D.-H. Xu, Q. Zhang, G.-Y. Zhang, T. Cagin, W. L. Johnson and W. A. Goddard, III, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 224208.
27. S. Plimpton, J. Comp. Physiol., 1995, 117, 1–19.
28. Y.-Q. Cheng, E. Ma and H.-W. Sheng, Phys. Rev. Lett., 2009, 102, 245501.
29. M. I. Mendelev, Y. Sun, F. Zhang, C. Z. Wang and K. M. Ho, J. Chem. Phys., 2019, 151, 214502.
30. Q. An, K. Samwer, M. D. Demetriou, M. C. Floyd, D. O. Duggins, W. L. Johnson and W. A. Goddard III, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7053–7058.
31. J. D. Honeycutt and H. C. Andersen, J. Phys. Chem., 1987, 91, 4950–4963.
32. P. Steinhardt, D. Nelson and M. Ronchetti, Phys. Rev. B: Solid State, 1983, 28, 784–805.
33. W. Mickel, S. C. Kapfer, G. E. Schroeder-Turkand and K. Mecke, J. Chem. Phys., 2013, 138, 044501.
34. D. J. Wales, Energy landscapes: applications to clusters, biomolecules, and glasses, Cambridge University Press, Cambridge, UK, 2004.
35. G. Williams and D. C. Watts, Trans. Faraday Soc., 1970, 66, 80–85.
36. Q. An, L.-Q. Zheng, R.-S. Fu, S.-D. Ni and S.-N. Luo, J. Chem. Phys., 2006, 125, 154510.
37. J. F. Lutsko, J. Appl. Phys., 1989, 65, 2991–2997.
38. P. A. Burrough, R. McDonnell and C. D. Lloyd, Principles of Geographical Information Systems, Oxford University Press, 2015.
39. R. Stadler, D. R. Bowler, D. Alfe and M. J. Gillan, J. Phys.: Condens. Matter, 2000, 12, 5109.
40. R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–354.
41. Y. Le Page and P. Saxe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104104.
42. J. Krausser, K. Samwer and A. Zaccone, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 13762–13767.

---

Footnote

† Electronic supplementary information (ESI) available: (1) The G-phase melting using different damping constants for barostat and thermostat; (2) the L-G transition of Cu₂Zr composition using the 2nd EAM potential; (3) the PE density distribution for Cu₂Zr and Cu₇Zr₃ G-phase structures at room temperature; (4) the icosahedral atoms in Cu₂Zr at 300 K; (5) RDF analysis of Cu₇Zr₃; (6) remelt of G-phase from 900 K to 1500 K; (7) the two-phase coexistence simulation for Cu₂Zr; (8) thermodynamic state functions for Cu₇Zr₃; (9) the correlation analysis for Cu atoms in Cu2Zr; (10) the correlation analysis for Zr atoms in Cu₂Zr; and (11) characterization of G-phase at 900 K for composition Cu₇Zr₃. See DOI: 10.1039/d1cp04157f

---