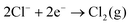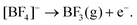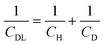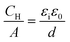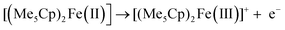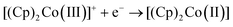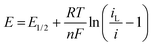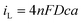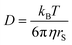Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Selection and characterisation of weakly coordinating solvents for semiconductor electrodeposition†
Alexander W.
Black
 and
Philip N.
Bartlett
and
Philip N.
Bartlett
 *
*
School of Chemistry, University of Southampton, Southampton, SO17 1BJ, UK. E-mail: p.n.bartlett@soton.ac.uk
First published on 17th March 2022
Abstract
Weakly coordinating solvents, such as dichloromethane, have been shown to be attractive for the electrodeposition of functional p-block compound and alloy semiconductors for electronic device applications. In this work the use of solvent descriptors to define weakly coordinating solvents and to identify new candidates for electrochemical applications is discussed. A set of solvent selection criteria are identified based on Kamlet and Taft's π*, α and β parameters: suitable solvents should be polar (π* ≥ 0.55), aprotic and weakly coordinating (α and β ≤ 0.2.). Five candidate solvents were identified and compared to dichloromethane: trifluorotoluene, o-dichlorobenzene, p-fluorotoluene, chlorobenzene and 1,2-dichloroethane. The solvents were compared using a suite of measurements including electrolyte voltammetric window, conductivity, and differential capacitance, and the electrochemistry of two model redox couples (decamethylferrocene and cobaltocenium hexafluorophosphate). Ion pairing is identified as a determining feature in weakly coordinating solvents and the criteria for selecting a solvent for electrochemistry is considered. o-dichlorobenzene and 1,2-dichloroethane are shown to be the most promising of the five for application to electrodeposition because of their polarity.
Introduction
Compound semiconductors and alloys based upon main group elements are of considerable interest for use in advanced electronic devices and memory. The possible combination of elements is significant and comprises binary compounds as well as ternary or quaternary alloys of elements from groups II to VI of the periodic table. These materials have a wide range of properties and band-gaps that permits a diversity of applications. For example: infra-red detection (indium antimonide), phase change memory (germanium antimony telluride), photovoltaics (cadmium telluride) and thermoelectrics (bismuth telluride) are all types of devices where compound p-block semiconductors have been used.1The particular features of electrodeposition offer distinct advantages over other common methods such as chemical vapour deposition, sputtering, ALD, etc. In electrodeposition, deposition only occurs in areas with electrical contact, allowing precise control over the size and shape of the deposit, and deposition occurs under the control of the potential or current providing a tuneable composition, and it occurs outwards from the electrode surface, in other words ‘bottom up’, permitting growth of large aspect ratio nanostructures. In contrast, with ‘top down’ approaches such as vapour deposition, it is not possible to reliably penetrate the entire depth of high aspect ratio structures such as deep pores due to blocking at the pore mouth.
Complexes of the p-block elements are particularly labile and undergo facile ligand exchange. For example, for all p-block elements that form aqua complexes, the mean lifetime for a primary shell water molecule is less than 1 s,2 and they lie on the labile side of Taube's inert/labile boundary.3 In solution the solvent molecules can compete with the ligands present in the initial complex for coordination to the metal cation. As such, a complex with labile ligands in a Lewis basic solvent is vulnerable to displacement by the solvent molecule. Different metal cations differ in their interaction with the solvent, and therefore in a donor solvent differences in speciation across different metal precursors and oxidation states will occur. For electrodeposition of alloys and compounds this is a problem because more than one metal complex must be present and because speciation affects all aspects of an electron transfer reaction. Unpredictable changes in metal speciation greatly complicates the process of metal codeposition. Hence, a plating bath composed of metal precursors sharing common ligands in a weakly coordinating solvent is an attractive proposition.
The interactions between an ion and its solvent can broadly be divided into two classes: non-specific and specific interactions.4 Non-specific interactions are electrostatic in nature and collectively known as van der Waals interactions. Specific interactions are of a chemical type and include hydrogen bonding and Lewis acid/base interactions. Quantifying the myriad and dynamic nature of interactions between solvents and solutes is difficult. However, insight can be achieved with the use of solvent descriptors: quantitative measures of some property of a solvent, for example using dielectric constant as an estimate of solvent polarity.
Dichloromethane (DCM) has been used recently as a weakly coordinating solvent in the electrodeposition of p-block metals and semiconductors. A generalised plating bath composed of [NnBu4]Cl as the supporting electrolyte and halometallate, [NnBu4]y−x[Mx+Cly], based metal precursors was developed and used with success.5–8 However, the use of this category of solvent for electrochemistry in general, and electrodeposition in particular, is relatively poorly explored. Furthermore, DCM has a low boiling point (40 °C) and performing electrodeposition in a less volatile solvent and at elevated temperatures would be of interest because of the expected improvement in deposit properties.
In the present work, a method using solvent descriptors is presented and used to make informed choices about solvent selection. This method was used to select several potential weakly coordinating solvents for application to p-block electrodeposition. Subsequently, the candidate solvents were characterised in a variety of ways to understand the nature of electrochemistry in these solvents. The potential window, conductivity and double layer properties were all examined. Additionally, the electrochemistry of the model redox couples decamethylferrocene and cobaltocenium hexafluorophosphate was investigated. From this, the understanding of electrochemistry in weakly coordinating solvents can be improved and weakly coordinating solvents suitable for electrodeposition at elevated temperatures can be identified.
Experimental
Chemicals
Dichloromethane, CH2Cl2 (95%, Sigma-Aldrich), α,α,α-trifluorotoluene, C7H5F3 (>99%, Sigma-Aldrich), o-dichlorobenzene, C6H4Cl2 (>99%, Sigma-Aldrich), p-fluorotoluene, C7H7F (97%, Sigma-Aldrich) were dried and degassed by refluxing with CaH2 followed by distilling, and were stored in an inert atmosphere of N2. The water content in the solvents was measured with Karl–Fischer titration (KF 899 Coloumeter, Metrohm, UK). There was less than 35 ppm of water in all solvents. Tetrabutylammonium chloride, [NnBu4]Cl (Sigma-Aldrich, >99%) and tetrabutylammonium tetrafluoroborate, [NnBu4][BF4] (Sigma-Aldrich, >99%) were dried by heating at 100 °C under vacuum for several hours. Decamethylferrocene, (C5(CH3)5)2Fe (Sigma-Aldrich, 97%) and cobaltocenium hexafluorophosphate, [(C5H5)2Co][PF6] (Sigma-Aldrich, 98%) were purified by sublimation. All solvents and reagents were stored in a glovebox.Electrodes
Working electrodes used were inlaid Pt macrodiscs of radius 0.5 mm, and microdiscs of radii 5, 12.5 and 25 μm, sealed in glass. The working electrodes were polished sequentially with 5, 1 and 0.3 μm alumina pastes on a microcloth polishing pad (Buehler, USA). Microelectrodes were calibrated using SEM (Philips XL30 ESEM). A Pt grid was used as a counter electrode, the reference electrode was Ag/AgCl immersed in a storage solution of 100 mM [NnBu4]Cl for dichloromethane, o-dichlorobenzene and 1,2-dichloroethane, separated from the electrolyte by a porous glass frit, and a Pt wire pseudo reference for α,α,α-trifluorotoluene, p-fluorotoluene and chlorobenzene.Electrochemical measurements
All glassware was cleaned by soaking in Decon 90 (Decon Laboratories Ltd, UK) for at least 24 h, followed by rinsing with ultrapure water, 0.055 μS cm−1 and then dried in an oven for a further 24 h.All experiments were performed with a standard pear shaped cell in a glovebox (Belle Technology, UK) under an inert atmosphere of N2 in the presence of <5 ppm O2 and H2O. Measurements were performed with a PGSTAT μIII or PGSTAT 302N (Metrohm Autolab, UK) potentiostat. Data was recorded with NOVA 1.11 (Metrohm Autolab, UK). The ambient temperature in the glovebox was monitored using a digital thermometer to an accuracy of ±0.05 °C (Hama, UK).
Conductivity measurements were performed in a two electrode cell with electrodes of 0.25, 0.375 and 1 mm radius Pt and a Pt grid. The electrolyte contained supporting electrolyte only. The measurements were performed using a PGSTAT 302N with a FRA32M module. Electrochemical impedance spectroscopy was used potentiostatically at open circuit with 50 frequencies logarithmically spaced between 40 kHz and 10 Hz at an amplitude of 5 mV RMS. Data was fitted using ZView 3.5 (Scribner) to an equivalent circuit of a resistor in series with a constant phase element (CPE). The CPE exponent, α, was greater than 0.9 for all measurements. The uncompensated resistance, Ru, was converted to the specific conductivity, κ, with Newman's equation: Ru = 1/4aκ, where a is the electrode radius using a plot of Ruvs. 1/a.9 The molar conductivity, Λm, was calculated using Λm = κ/c, where c is the electrolyte concentration. For double layer capacitance measurements, electrochemical impedance spectroscopy was performed as described above with 20 frequencies. However, a three electrode cell was used, with sat. Ag/AgCl used as the reference for TFT, pFT and CB. Additionally, a 100 nF capacitor and 0.25 mm radius Pt wire was used in parallel with the reference electrode.10 Measurements were performed as a function of potential within the potential window of the electrolyte, at intervals of 200 mV with a wait time of 30 s between each potential.
Results and discussion
Weakly coordinating solvents
Kamlet and Taft's (KT) set of empirical solvent descriptors have been extensively used to understand the effect of the solvent on a variety of chemical processes. They are composed of three descriptors: π*, α and β which describe the polarity, Lewis acidity and Lewis basicity respectively.11 By definition, therefore, a weakly coordinating solvent might be expected to have a negligible or zero β. There are however, other requirements if a solvent is to be suitable for electrochemistry. The solvent must be to some extent polar; to permit the dissolution and separation of charged species so that a conducting electrolyte solution is formed. It must also be aprotic to give a large potential window for the reduction of more stable elements. As such, within the framework of the KT parameters a useful weakly coordinating solvent for electrodeposition would have a large π* parameter, and a zero, or low, value for the α and β parameters.Fig. 1 shows in red a plot of solvents with KT parameter values of π* ≥ 0.55, α ≤ 0.2 and β ≤ 0.2. These represent solvents with properties expected to be useful based upon the above criteria. As can be seen, the solvents occupy a specific volume of the 3D solvent descriptor space. The solvents in this region are primarily halogenated aromatics or short chain aliphatics. Also shown in the same plot are a selection of solvents commonly used in electrochemistry (in blue) and some typical ionic liquids (in yellow). Details of the solvents and their KT parameters are given in Table S1 (ESI†). Clearly the weakly coordinating solvents form a separate group distinct from the ionic liquids and solvents commonly used in electrochemistry. Interpretation of the absolute values of the KT descriptors must be done with caution. The methods of acquiring the descriptors have been criticised,4 nevertheless they have been shown to correlate well with other solvent descriptors, suggesting that they all measure broadly the same property.12 Furthermore with the advent of high powered computing, more advanced models, such as CODESSA or COSMO-RS,13,14 have emerged. These allow the accurate prediction of solute and solvent properties and deepen understanding of the underlying factors affecting solute–solvent interactions. Empirical solvent descriptors may have been superseded, but they remain an accessible tool for quick understanding of the properties of a solvent to the chemist.
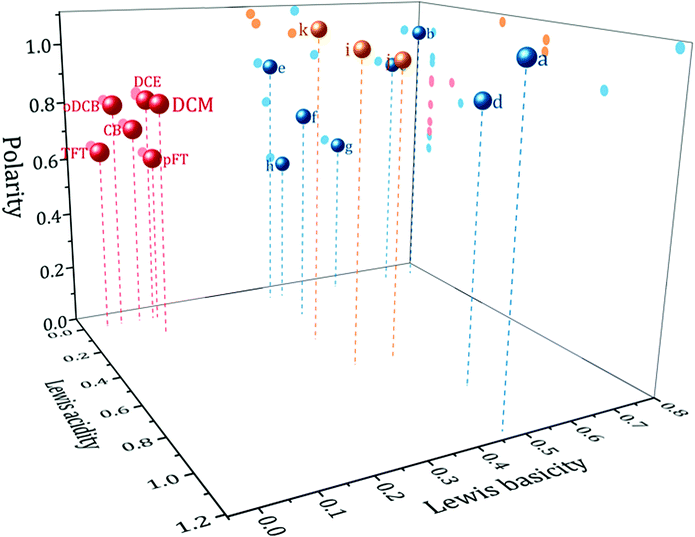 | ||
| Fig. 1 Weakly coordinating solvent selection map. Showing Kamlet and Taft's descriptors solvent polarity, π*, Lewis acidity, α and Lewis basicity, β, for red: weakly coordinating solvents, blue: common electrochemical solvents, yellow: typical ionic liquids. Solvent identities can be found in Table S1 (ESI†). | ||
Of the solvents in the correct region of solvent space, six were selected as candidate solvents for study: dichloromethane (DCM), α,α,α-trifluorotoluene (TFT), o-dichlorobenzene (oDCB), p-fluorotoluene (pFT), chlorobenzene (CB) and 1,2-dichloroethane (DCE). DCM is included for comparison since it has previously been examined in the literature. A compilation of relevant physical properties of these solvents is given in Table 1. The candidate solvents all possess boiling points higher than DCM. Additionally, all have similar α and β values but vary in their π*. Therefore it would be expected that the solvents behave similarly, except for properties determined by their polarity. All solvents are readily available at a low cost from standard chemical suppliers. There are varying degrees of safety considerations associated with the solvents (see Table 1), oDCB is fairly benign whereas DCE is restricted by the European Union's REACH regulations for example. But the risks are no greater than for other solvents regularly used in chemistry.
| Solvent | T b/°C | p v/kPa | η/mPa s | ρ/g cm−3 | ε r | n | μ/D | Hazardsa |
|---|---|---|---|---|---|---|---|---|
| a From safety data sheet available at http://www.sigmaaldrich.com, accessed 03/2022. b Ref. 50. c Ref. 51. d Ref. 52. e Ref. 53. f Ref. 54. g Ref. 55. | ||||||||
| DCMb | 40 | 58.3 | 0.41 | 1.39 | 8.9 | 1.42 | 1.1 | Suspected carcinogen |
| TFT | 102c | 5.3c | 0.47d | 1.18c | 9.2e | 1.48e | 2.9c | Highly flammable |
| Harmful to the environment | ||||||||
| oDCBb | 181 | 0.2 | 1.32 | 1.30 | 9.9 | 1.55 | 2.5 | Harmful to the environment |
| pFT | 117e | 3.0f | 0.62g | 1.00e | 5.9e | 1.47e | 2.0e | Highly flammable |
| CBb | 132 | 1.6 | 0.76 | 1.10 | 5.6 | 1.52 | 1.7 | Flammable |
| Harmful to the environment | ||||||||
| DCEb | 83 | 10.6 | 0.78 | 1.25 | 10.4 | 1.44 | 1.8 | Highly flammable |
| Suspected carcinogen | ||||||||
| Toxic | ||||||||
Potential window
The definition of the electrolyte potential window is somewhat arbitrary since the current generally increases approximately exponentially at the anodic and cathodic limit. In this work the potential window of each solvent was determined with the use of decamethylferrocene (DMFc) as an internal current reference. The electrolyte was considered to have reached its solvent limit, anodic or cathodic, when the current was equal to the anodic or cathodic peak current for 1 mM DMFc. All measurements were made using a 0.25 mm radius Pt disc at a scan rate of 50 mV s−1. The results are shown in Table 2. In those cases where 100 mM [NnBu4]Cl was insoluble in the solvent (TFT, pFT and CB) 100 mM [NnBu4][BF4] was used instead. The voltammograms used to measure the solvent potential window, along with windows at Au and glassy carbon (GC) electrodes are shown in Fig. S1 (ESI†).| Solvent | E a vs. DMFc0/+/V | E c vs. DMFc0/+/V | E window/V |
|---|---|---|---|
| DCM | 0.89 | −2.18 | 3.07 |
| TFT | 1.45 | −2.30 | 3.76 |
| oDCB | 0.78 | −2.31 | 3.09 |
| pFT | 1.40 | −2.56 | 3.97 |
| CB | 1.45 | −2.51 | 3.95 |
| DCE | 0.75 | −1.77 | 2.52 |
For the majority of solvents, the available potential window, Ewindow, is similar for the solvents with the same electrolyte. Additionally, all solvents have a similar cathodic limit, Ec, and those that share a common anion have a similar anodic limit, Ea. Ea is greater when [BF4]− is used, indicating that Cl− is more easily oxidised. It has been shown that the addition of strongly withdrawing groups in the anion can increase its resistance to oxidation.15 The electrochemistry of the chloride/chlorine system at a Pt surface was studied by Sereno et al. in the aprotic solvent acetonitrile.16 The overall redox reaction appeared to be
The similarity of the windows suggest that the available window of the system is limited by decomposition of the supporting electrolyte rather than the solvent itself. The exception to this rule is DCE which has a much lower cathodic limit, suggesting the solvent itself is decomposing. The electrochemical reduction of DCE has been studied at GC and Ag electrodes in acetonitrile and dimethylformamide.18,19 The proposed mechanism is one of stepwise dechlorination forming a carbon radical followed by a carbanion, with the reaction terminated by the formation of ethylene.19 Protonation of the anion by trace water to give chloroethane or ethane is also possible. However considering the minimal water content in the solvents (see above), this is likely to only be a very minor product.
Slight variations of the limits can still be observed between solvents, this could be the effect of trace water impurities, which have been observed to narrow the potential window of ionic liquids.20 Nevertheless, the key consideration for electrodeposition is the cathodic limit, which is comparable to DCM for all solvents and indicates that the candidate solvents have a useful window for cathodic semiconductor deposition.
Conductivity
Table 3 shows conductivities of the selected solvents with 100 mM [NnBu4]Cl and [NnBu4][BF4], except from TFT, pFT and CB where 100 mM [NnBu4]Cl was insoluble, as noted above. Its insolubility is presumably caused by the lower polarity of the solvents (π* ≤ 0.71). Also shown is the conductivity viscosity product, Λmη, in an attempt to account for the effect of gross difference in solvent viscosity on conductivity; Λmη should be approximately proportional to the degree of ion pairing in the solvent. The values obtained are comparable with those previously reported in the literature under the same or similar conditions for DCM,21–24 TFT,21,25oDCB24 and DCE.22,24| Electrolyte | Solvent | R u a/kΩ cm | Λ m/S cm2 mol−1 | Λ m η/S cm2 mPa s mol−1 |
|---|---|---|---|---|
| [NnBu4]Cl | DCM | 0.28(1) | 9.04(2) | 3.71(8) |
| TFT | — | — | — | |
| oDCB | 2.33(3) | 1.07(2) | 1.42(2) | |
| pFT | — | — | — | |
| CB | — | — | — | |
| DCE | 0.34(1) | 7.42(11) | 5.78(8) | |
| [NnBu4][BF4] | DCM | 0.22(1) | 11.61(38) | 4.76(16) |
| TFT | 0.43(2) | 2.30(5) | 1.17(2) | |
| oDCB | 1.44(1) | 1.74(2) | 2.29(3) | |
| pFT | 3.50(15) | 0.71(3) | 0.44(2) | |
| CB | 3.22(7) | 0.78(2) | 0.59(1) | |
| DCE | 0.23(1) | 10.69(12) | 8.33(10) |
In the solvents where both salts are soluble, [NnBu4][BF4] imparts greater conductivity than does [NnBu4]Cl. This can be rationalized in less polar solvents since the larger [BF4]− anion has a lower charge density than Cl− and, consequently is expected to be less strongly ion paired.26 The increased size of the anion does reduce mobility but this is compensated by the increase in free ions. The ratio of conductivity, Λmη ([NnBu4][BF4])/Λmη ([NnBu4]Cl) is similar for DCM, oDCB and DCE with values of 1.3, 1.6 and 1.4 respectively; indicating that the relative strength of the electrolyte remains the same. Such effects have been previously observed in DCM and TFT by Geiger et al.21 When measuring the conductivity of various tetrabutylammonium salts, they found that the conductivity was increased and KA, the association constant, lowered for larger anions.
It is also interesting to note that although many of the solvents have similar dielectric constants, the measured conductivities are not similar. The experimental order of Λmη is pFT < CB < TFT < oDCB < DCM < DCE, however that predicted by εr is CB < pFT < DCM ≈ TFT < oDCB < DCE (Fig S2, ESI†). The conductivities for TFT and oDCB solutions appear to be significantly lower than those for DCM and DCE with similar dielectric constants. This suggests that the isodielectric rule, which states that for a given electrolyte salt the ion pair association constant should be the same in solvents of the same electrolyte,27 breaks down here due to short range specific interactions in these aromatic solvents.28 The formation of ion pairs is ultimately a competition between solvent and counter ion for interaction with the ion. Such an effect has been observed in water where ion pairing increases with size since larger ions disrupt the H bonding network of water and so are forced into ion pairs to preserve it.26 One measure of the structure of a solvent is the Kirkwood correlation parameter, gK, which gives information on the orientation of the solvent molecule's dipole.29 For a solvent with no alignment: 0.7 ≤ gK ≤ 1.3 and it is considered unstructured. When gK > 1.3, the dipoles are oriented parallel to each other. gK < 0.7 corresponds to neighbouring dipoles oriented in an antiparallel fashion. Values for the present solvents can be taken from the literature (ref. 29) or calculated, giving values for DCM, TFT, oDCB and DCE of 1.04, 0.56, 0.68 and 1.17 respectively. This would suggest DCM and DCE are unstructured, but in TFT and oDCB some of the solvent molecules are oriented in an antiparallel manner and this arrangement is preferred to ion solvation, causing a greater degree of ion pairing. There is no direct evidence of such structures in TFT or oDCB but dielectric measurements of bromobenzene and benzonitrile, two solvents with gK < 0.7, have shown them to form stable antiparallel dimers.30 Furthermore, crystal structures of TFT and oDCB showed TFT molecules arranged in a head to tail fashion, and favourable Cl-Cl interactions leading to a ‘zig-zag’ structure in oDCB,31,32 suggesting that associations of this type are energetically favourable in solution.
Double-layer structure
Fig. 2 shows differential capacitance curves for 100 mM [NnBu4][BF4] at a Pt electrode. A simple model of the electrical double layer (EDL) describes the total capacitance, CDL, as the sum of two capacitors in serieswhere CH is the capacitance of the Helmholtz layer and CD is the capacitance of the diffuse layer.33 At high electrolyte concentrations such as that in Fig. 2, CD becomes large enough so that it no longer contributes to CDL, which is then primarily determined by CH.34CH can be described as a parallel plate capacitor, such that
where A is the area of the electrode, εi is the dielectric constant of the inner layer, ε0 is the permittivity of free space and d is the distance between the two plates. This model predicts capacitance to be independent of potential, which is clearly not the case here. Instead, generally, a decrease in CDL with potential is observed, before plateauing at the most negative potentials. Curves measured by scanning in the opposite direction showed no changes (see Fig. S3, ESI†). This appears to be in agreement with the work of Fawcett at the Hg/propylene carbonate interface with 100 mM [NnBu4][ClO4]. As the potential decreases, solvent molecules are replaced by [NnBu4]+ on the electrode and εi decreases. Taking a value of 6.5 μF cm−2 for the capacitance of the plateau, and assuming a dielectric constant of the inner layer of 3.2,35 gives a thickness of 0.44 nm. This is comparable to 0.41 nm, the crystallographic radius of the [NnBu4]+ cation,36 indicating that the inner layer is populated by [NnBu4]+ at negative potentials. Although, since the size reported here is larger than the crystallographic radius, this might suggest that the dielectric constant of the inner layer is less than 3.2. Abbott reported a value of 2.6 in DCE for example.37
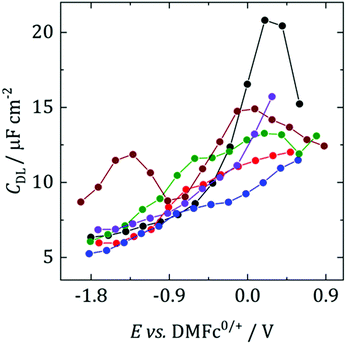 | ||
| Fig. 2 Differential capacitance curves for 100 mM [NnBu4][BF4] at a r = 0.25 mm Pt electrode, scanning in the anodic direction. Black: DCM, red: TFT, blue: oDCB, green: pFT, brown: CB, purple: DCE. | ||
The exception to this rule appears to be CB, where two humps are observed. This was also observed by Abbott for 300 mM [NnBu4][BF4] in DCE at a Pt surface.37 These humps were demonstrated to be caused by adsorption of ions or ion aggregates onto the electrode surface. Although it is not clear why it is only observed in CB.
Fawcett also investigated the structure of the double layer with a dropping mercury electrode (DME) in tetrahydrofuran (THF), a solvent of similar polarity to those studied here.38 In their work diffuse layer effects were observed in the form of a capacitance minimum, caused by a decrease in effective ionic strength due to ion pairing. Ion pairing is undoubtedly present in the studied solvents but it does not appear to be observable here. It could point to the advantage of using a DME for EDL studies, where the history of the electrode is not a factor.
Electrochemistry of decamethylferrocene and cobaltocenium hexafluorophosphate
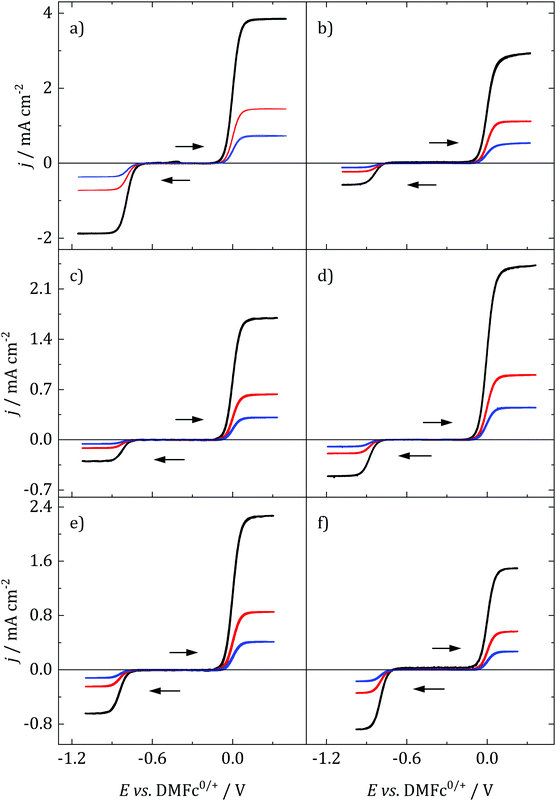
Decamethylferrocene (DMFc) and cobaltocenium hexafluorophosphate (CcPF6) were used as model redox probes to investigate the nature of electrochemistry in the candidate solvents. Metallocene electron transfer is an outer sphere, mechanistically simple electron transfer process with a low inner and outer sphere reorganisation energy. They are characterised by fast, stable electrochemistry and as such are regularly used for the characterisation of unknown solvents. For example, metallocenes have been used to understand behaviour in novel media such as ionic liquids.39 It was also imprtant to understand the behaviour of DMFc since it was to be used as a solvent independent internal reference; DMFc has been shown to be a superior internal reference to the commonly used ferrocene.40Fig. 3 shows voltammograms for DMFc and CcPF6 at three different sizes of microelectrode in the selected solvents. One major advantage of microelectrodes is that their smaller size results in smaller currents and therefore minimisation of distortions associated with iR drop. This feature becomes particularly important in low polarity solvents such as those studied here, and was exploited to achieve artefact free, quantitative analysis of voltammograms.
Starting from −0.3 V vs. DMFc0/+, one oxidation process can be observed, corresponding to the oxidation of decamethylferrocene to decamethylferricenium
As can be seen, a limiting current plateau forms for both DMFc and CcPF6 at all electrode sizes in all solvents, indicative of a diffusion limited process. This is also supported by the observation of linear Randles-Sevčik plots at larger electrodes (Fig. S4, ESI†). The behaviour was investigated at different electrode materials, with voltammograms recorded at Au and glassy carbon (GC) macroelectrodes, shown in Fig. S5 (ESI†). No changes are observed, as would be expected for an outer-sphere electron transfer.
where R is the gas constant, T absolute temperate, n the number of electrons transferred, F the Faraday and iL the limiting current. Therefore, plots of E vs. ln(iL/i − 1) should be linear with an intercept of E1/2. Such plots are shown in Fig. S5 (ESI†) and the obtained values vs. Ag/AgCl and DMFc0/+, averaged over three electrode sizes and three repeats are shown in Table 4. No relationship between E1/2 and electrode size was observed, demonstrating the absence of any iR drop effects. Some shifts in the redox potential of DMFc vs. Ag/AgCl are evident, we attribute these to solvent shifts in the Ag/AgCl reference electrode potential. It is then possible to reference E1/2(CcPF6) against DMFc, so now all changes in the CcPF6 redox potential can be attributed to the effect of the solvent.
| Solvent | DMFc | CcPF6 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| E 1/2 vs. Ag/AgCl/V | |E3/4–E1/4|/mV | b/mV | D/10−5 cm2 s−1 | E 1/2 vs. Ag/AgCl/V | E 1/2 vs. DMFc0/+/V | |E3/4–E1/4|/ mV | b/mV | D/10−5 cm2 s−1 | |
| DCM | 0.438(10) | 58(1) | 26.6(3) | 1.68(2) | −0.350(10) | −0.788(1) | 56(1) | 25.4(3) | 1.35(1) |
| TFT | 0.192(4) | 63(2) | 28.6(6) | 1.18(3) | −0.637(2) | −0.830(1) | 57(1) | 26.0(1) | 0.38(2) |
| oDCB | 0.499(20) | 59(1) | 26.8(1) | 0.52(1) | −0.323(20) | −0.822(1) | 55(2) | 24.8(8) | 0.24(1) |
| pFT | 0.198(7) | 62(1) | 28.9(8) | 1.10(11) | −0.678(7) | −0.875(2) | 57(1) | 26.2(1) | 0.31(3) |
| CB | 0.145(1) | 62(2) | 28.2(8) | 0.87(3) | −0.692(1) | −0.840(4) | 58(1) | 26.3(9) | 0.32(3) |
| DCE | 0.376(1) | 57(1) | 26.1(2) | 0.88(3) | −0.418(1) | −0.795(2) | 55(1) | 25.0(1) | 0.61(3) |
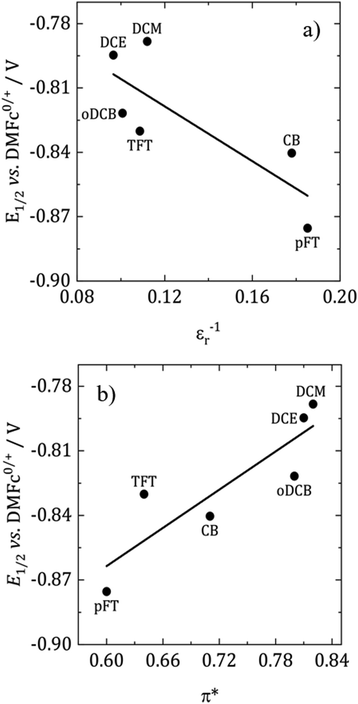
According to the Born equation for the electrostatic solvation energy of an ion, E1/2 should be proportional to 1/εr.41 With DMFc as an internal reference it is possible to examine this relationship for CcPF6. Based upon the solvent descriptors above, it should be expected that there are minimal specific interactions between solvent and solute, and the primary form is electrostatic in nature. Consequently, simplistically the Born equation might be expected to be a reasonable descriptor of solvent solute interactions. Fig. 4a shows such a plot for the selected solvents. A weak linear relationship is observed (R2 = 0.65), with redox potential decreasing with solvent polarity. Clearly in this case the Born equation is not a good descriptor; previous attempts at correlation in the literature have been similarly unsuccessful.41 Also shown in Fig. 4b is the relationship with π*, where the correlation is improved, R2 = 0.77. Suggesting that π* is the superior descriptor of solvent polarity. Correlations of redox potential with π* have previously proved successful.42
The direction of the correlation is, however, opposite to what is expected. For a cation that is reduced to a neutral species, more polar solvents would more strongly solvate the cation and decrease the redox potential. One effect that potentially could cause a reversal of this trend is ion pairing. If the Cc+ ion was paired with [BF4]− or Cl− then this could stabilise the cation, thus decreasing the redox potential. As the polarity of the solvent decreases, the degree of ion pairing is greater and so is the stabilisation. The presence of ion pairing effects on voltammetry has been reported in DCM for ferrocene and DMFc.43,44
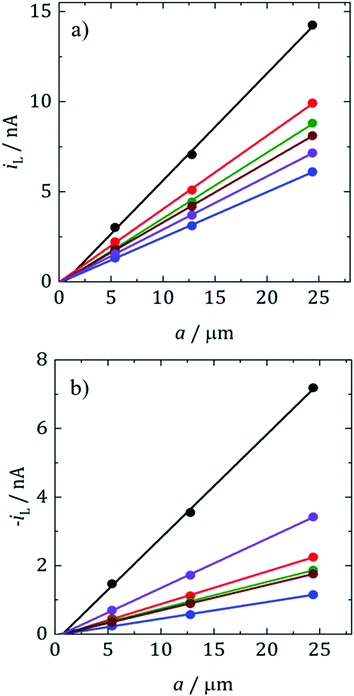
where D is the diffusion coefficient, c is the concentration of electroactive species in the bulk and a is the radius of the microelectrode. Consequently, plots of iLvs. a for different sizes of microelectrode should be linear and D can be obtained from the slope. Fig. 5 shows such plots for DMFc and CcPF6. Uncertainty in the concentration was alleviated by performing a potential step at a microelectrode. The resulting transient was fitted to the Shoup–Szabo equation, giving c.48 The average value for all three electrode sizes was taken and used as c in calculating D. The resulting D values are shown in Table 4. Diffusion coefficients obtained from potential steps at a microelectrode corroborate the results here and are shown in Table S2 (ESI†). Where available, the values here agree with those in the literature. In DCM Weaver obtained a value of 1.30 × 10−5 cm2 s−1 for DMFc using DC polarography at 23 °C.49 Matsumoto and Swaddle reported a mean value of 1.07 × 10−5 cm2 s−1 using peak currents of voltammograms at 25 °C.46 Branch obtained a value for DMFc of 1.48 × 10−5 cm2 s−1 from a microelectrode voltammogram and a mean value of 7.95 × 10−6 cm2 s−1 from macrodisc voltammograms at 25 °C.45 Tsierkezos reported a value of 1.35 × 10−5 cm2 s−1 for the neutral Cc species in DCM, similar to the value obtained here.47 There appears to be no literature data of measurements for DMFc nor CcPF6 in the remaining solvents.
Diffusion coefficients are often interpreted using the Stokes–Einstein (SE) equation
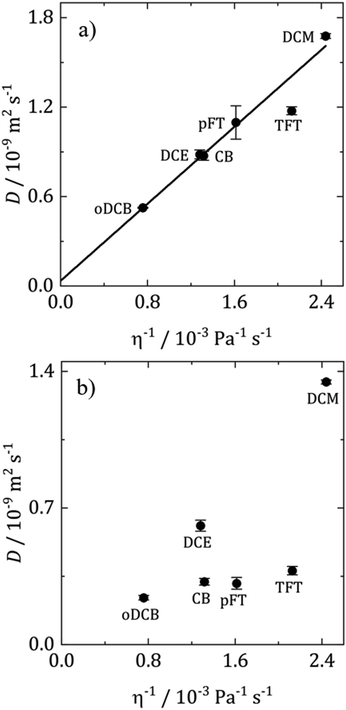 | ||
| Fig. 6 Stokes–Einstein plots of (a) DMFc and (b) CcPF6 at 25 °C. D obtained from microelectrode voltammograms. Values are the average of three repeats and the error bars the standard deviation. | ||
In Fig. 6a for DMFc it can be seen that the plot is linear (R2 = 0.98) with an intercept close to the origin, demonstrating that DMFc obeys the Stokes Einstein equation. For the charged Cc+ in Fig. 6b the situation is markedly different. Assuming that the choice of redox couples does not significantly affect the solution viscosity, the most likely explanation for this lack of correlation is the presence of ion pairing increasing the size of the diffusing particle, rS. This has been observed before for diffusion coefficients of DMFc+ in DCM by Goldfarb and Corti.44 The interpretation of diffusion coefficients in weakly coordinating solvents is complicated and will be discussed further in a subsequent publication.
Conclusions
The aim of this study was to improve the understanding of electrochemistry in weakly coordinating solvents and identify alternative solvents to DCM that might be useful for electrodeposition. To this end, Kamlet and Taft solvent descriptors were employed to identify solvents with similar properties to DCM. As a part of this method it was established that other solvents commonly used in electrochemistry were not suitable and would not be useful. The selected solvents were subjected to thorough characterisation, comprised of measurements of potential window, conductivity, double-layer capacitance and behaviour of model redox couples. Earlier, a prediction was made that all solvents would behave similarly except for those properties determined by polarity and this appears partially true. Whilst the advantage of solvent descriptors and Kamlet Taft parameters for choosing a solvent has been demonstrated, it was also shown that they do not tell the whole story which leaves an element of uncertainty. Increasing the number of descriptors considered would be a solution but this greatly increases the complexity of the selection process and it is not plausible to identify them all a priori. The most profitable approach would seem to be to choose 2–4 key descriptors and use those to identify several candidate solvents for investigation, then choosing the optimum solvent(s). This may be more resource intensive but allows for the possibility of unforeseen behaviours.In a general sense, all solvents investigated appear to be useful as weakly coordinating solvents for electrochemistry. However due to the low polarity of some, they are unlikely to be useful for electrodeposition. The ability to dissolve and dissociate salts in reasonable quantities is a key requirement for a useful plating bath. Therefore, oDCB and DCE as the most polar solvents appear the most promising for application to electrodeposition. This will be the subject of future research.
Finally, in solvents with a low polarity such as those studied here, ion pairing is clearly an important factor in determining the electrochemical response. The consequences of ion pairing were observed in measurements of conductivity, redox potential and diffusion coefficient and must be considered when interpreting electrochemical data in solvents of intermediate or low polarity. Furthermore, charged species are likely to exist in a combination of forms including free ions, ion pairs and potentially triple ions. Meaning the experimental response is an average of the species’ behaviour in all its arrangements.
Author contributions
AWB: conceptualization, methodology, validation, formal analysis, investigation, data curation, writing – original draft, visualization. PNB: conceptualization, methodology, validation, formal analysis, writing – review & editing, supervision, funding acquisition, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Dr Wenjian Zhang is thanked for the supply of solvents and reagents. This work was supported by EPSRC through the Advanced Devices by Electroplating program grant (ADEPT; EP/N035437/1).Notes and references
- Nanoelectronics and Information Technology: Advanced Electronic Materials and Novel Devices, ed. R. Waser, Wiley-VCH, Weinheim, 3rd edn, 2012 Search PubMed.
- D. T. Richens, Chem. Rev., 2005, 105, 1961–2002 CrossRef CAS PubMed.
- H. Taube, Chem. Rev., 1952, 50, 69–126 CrossRef CAS.
- C. Reichardt and T. Welton, Solvents and Solvent Effects in Organic Chemistry, Wiley-VCH Verlag GmbH, Weinheim, 4th edn, 2011 Search PubMed.
- P. N. Bartlett, D. Cook, C. H. de Groot (Kees), A. L. Hector, R. Huang, A. Jolleys, G. P. Kissling, W. Levason, S. J. Pearce and G. Reid, RSC Adv., 2013, 3, 15645–15654 RSC.
- G. P. Kissling, R. Huang, A. Jolleys, S. L. Benjamin, A. L. Hector, G. Reid, W. Levason, C. H. K. De Groot and P. N. Bartlett, J. Electrochem. Soc., 2018, 165, D557–D567 CrossRef CAS.
- L. Meng, K. Cicvarić, A. L. Hector, C. H. de Groot and P. N. Bartlett, J. Electroanal. Chem., 2019, 839, 134–140 CrossRef CAS.
- G. P. Kissling, M. Aziz, A. W. Lodge, W. Zhang, M. Alibouri, R. Huang, A. L. Hector, G. Reid, C. H. de Groot, R. Beanland, P. N. Bartlett and D. C. Smith, J. Electrochem. Soc., 2018, 165, D802–D807 CrossRef CAS.
- J. Newman, J. Electrochem. Soc., 1966, 113, 501–502 CrossRef CAS.
- C. C. Herrmann, G. G. Perrault and A. A. Pilla, Anal. Chem., 1968, 40, 1173–1174 CrossRef CAS.
- M. J. Kamlet, J. L. M. Abboud, M. H. Abraham and R. W. Taft, J. Org. Chem., 1983, 48, 2877–2887 CrossRef CAS.
- Y. Marcus, Chem. Soc. Rev., 1993, 22, 409–416 RSC.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. R. Katritzky, V. S. Lobanov and M. Karelson, Chem. Soc. Rev., 1995, 24, 279–287 RSC.
- J. Barthel and H. J. Gores, in Handbook of Battery Materials, ed. C. Daniel and J. O. Besenhard, Wiley-VCH Verlag GmbH, Weinheim, 2nd edn, 2011, pp. 457–497 Search PubMed.
- L. Sereno, V. A. Macagno and M. C. Giordano, Electrochim. Acta, 1972, 17, 561–575 CrossRef CAS.
- L. Xiao and K. E. Johnson, J. Electrochem. Soc., 2003, 150, E307–E311 CrossRef CAS.
- O. Scialdone, C. Guarisco, A. Galia and R. Herbois, J. Electroanal. Chem., 2010, 641, 14–22 CrossRef CAS.
- G. Fiori, S. Rondinini, G. Sello, A. Vertova, M. Cirja and L. Conti, J. Appl. Electrochem., 2005, 35, 363–368 CrossRef CAS.
- A. M. O’Mahony, D. S. Silvester, L. Aldous, C. Hardacre and R. G. Compton, J. Chem. Eng. Data, 2008, 53, 2884–2891 CrossRef.
- R. J. LeSuer, C. Buttolph and W. E. Geiger, Anal. Chem., 2004, 76, 6395–6401 CrossRef CAS PubMed.
- K. M. Kadish, J. Q. Ding and T. Malinski, Anal. Chem., 1984, 56, 1741–1744 CrossRef CAS PubMed.
- I. Svorstol and J. Songstad, Acta Chem. Scand., Ser. B, 1985, 39, 639–655 CrossRef.
- T. Sigvartsen, B. Gestblom, E. Noreland and J. Songstad, Acta Chem. Scand., Ser. B, 1989, 43, 103–115 CrossRef CAS.
- S. Boitsov, K. J. Borve, S. Rayyan, K. W. Tornroos and J. Songstad, J. Mol. Liq., 2003, 103–104, 221–233 CrossRef CAS.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS PubMed.
- R. M. Fuoss, Proc. Natl. Acad. Sci. U. S. A., 1978, 75, 16–20 CrossRef CAS PubMed.
- R. M. Fuoss, J. Solution Chem., 1986, 15, 231–235 CrossRef CAS.
- Y. Marcus, J. Solution Chem., 1992, 21, 1217–1230 CrossRef CAS.
- T. Shikata, N. Sugimoto, Y. Sakai and J. Watanabe, J. Phys. Chem. B, 2012, 116, 12605–12613 CrossRef CAS PubMed.
- K. Merz, M. V. Evers, F. Uhl, R. I. Zubatyuk and O. V. Shishkin, Cryst. Growth Des., 2014, 14, 3124–3130 CrossRef CAS.
- M. Bujak, K. Dziubek and A. Katrusiak, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63, 124–131 CrossRef CAS PubMed.
- B. B. Damaskin and O. A. Petrii, J. Solid State Electrochem., 2011, 15, 1317–1334 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley-VCH, Hoboken, NJ, 2nd edn, 2001 Search PubMed.
- W. R. Fawcett, M. Fedurco and M. Opallo, J. Phys. Chem., 1992, 96, 9959–9964 CrossRef CAS.
- Y. Marcus, Ions in Solution and Their Solvation, Wiley, Hoboken, NJ, 2015 Search PubMed.
- A. P. Abbott and J. C. Harper, J. Chem. Soc., Trans., 1997, 93, 3981–3984 RSC.
- M. A. Drogowska and W. R. Fawcett, J. Electroanal. Chem., 1987, 222, 293–303 CrossRef CAS.
- E. I. Rogers, D. S. Silvester, D. L. Poole, L. Aldous, C. Hardacre and R. G. Compton, J. Phys. Chem. C, 2008, 112, 2729–2735 CrossRef CAS.
- I. Noviandri, K. N. Brown, D. S. Fleming, P. T. Gulyas, P. A. Lay, A. F. Masters and L. Phillips, J. Phys. Chem. B, 1999, 103, 6713–6722 CrossRef CAS.
- G. Gritzner, Rev. Inorg. Chem., 1990, 11, 81–122 CAS.
- P. A. Lay, N. S. McAlpine, J. T. Hupp, M. J. Weaver and A. M. Sargeson, Inorg. Chem., 1990, 29, 4322–4328 CrossRef CAS.
- T. Kondo, M. Okamura and K. Uosaki, J. Organomet. Chem., 2001, 637–639, 841–844 CrossRef CAS.
- D. L. Goldfarb and H. R. Corti, J. Electroanal. Chem., 2001, 509, 155–162 CrossRef CAS.
- J. A. Branch, Electrochemical Studies of Diffusion in Supercritical Fluids, PhD Thesis, University of Southampton, 2015 Search PubMed.
- M. Matsumoto and T. W. Swaddle, Inorg. Chem., 2004, 43, 2724–2735 CrossRef CAS PubMed.
- N. G. Tsierkezos, J. Mol. Liq., 2008, 138, 1–8 CrossRef CAS.
- D. Shoup and A. Szabo, J. Electroanal. Chem., 1982, 140, 237–245 CrossRef CAS.
- T. Gennett, D. F. Milner and M. J. Weaver, J. Phys. Chem., 1985, 89, 2787–2794 CrossRef CAS.
- Y. Marcus, The Properties of Solvents, Wiley, Chichester, 1998 Search PubMed.
- J. J. Maul, P. J. Ostrowski, G. A. Ublacker, B. Linclau and D. P. Curran, in Modern Solvents In Organic Synthesis, ed. P. Knochel, Springer-Verlag, Berlin, 1999, pp. 79–105 Search PubMed.
- L. De Lorenzi, M. Fermeglia and G. Torriano, J. Chem. Eng. Data, 1996, 41, 1121–1125 CrossRef CAS.
- W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Handbook of Chemistry and Physics, CRC Press, New York, 96th edn, 2016 Search PubMed.
- D. R. Lide, Basic Laboratory and Industrial Chemicals: A CRC Quick Reference Handbook, CRC Press, Boca Raton, 1993 Search PubMed.
- O. Ivanciuc, T. Ivanciuc, P. A. Filip and D. Cabrol-Bass, J. Chem. Inf. Comput. Sci., 1999, 39, 515–524 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d2cp00696k |
| This journal is © the Owner Societies 2022 |