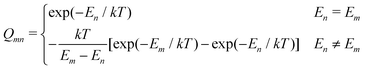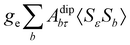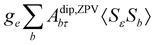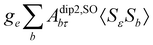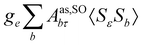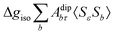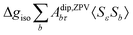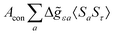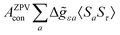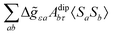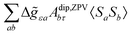Electron correlation and vibrational effects in predictions of paramagnetic NMR shifts†
Received
12th March 2022
, Accepted 26th May 2022
First published on 27th May 2022
Abstract
Electronic structure calculations are fundamentally important for the interpretation of nuclear magnetic resonance (NMR) spectra from paramagnetic systems that include organometallic and inorganic compounds, catalysts, or metal-binding sites in proteins. Prediction of induced paramagnetic NMR shifts requires knowledge of electron paramagnetic resonance (EPR) parameters: the electronic g tensor, zero-field splitting D tensor, and hyperfine A tensor. The isotropic part of A, called the hyperfine coupling constant (HFCC), is one of the most troublesome properties for quantum chemistry calculations. Yet, even relatively small errors in calculations of HFCC tend to propagate into large errors in the predicted NMR shifts. The poor quality of A tensors that are currently calculated using density functional theory (DFT) constitutes a bottleneck in improving the reliability of interpretation of the NMR spectra from paramagnetic systems. In this work, electron correlation effects in calculations of HFCCs with a hierarchy of ab initio methods were assessed, and the applicability of different levels of DFT approximations and the coupled cluster singles and doubles (CCSD) method was tested. These assessments were performed for the set of selected test systems comprising an organic radical, and complexes with transition metal and rare-earth ions, for which experimental data are available. Severe deficiencies of DFT were revealed but the CCSD method was able to deliver good agreement with experimental data for all systems considered, however, at substantial computational costs. We proposed a more computationally tractable alternative, where the A was computed with the coupled cluster theory exploiting locality of electron correlation. This alternative is based on the domain-based local pair natural orbital coupled cluster singles and doubles (DLPNO-CCSD) method. In this way the robustness and reliability of the coupled cluster theory were incorporated into the modern formalism for the prediction of induced paramagnetic NMR shifts, and became applicable to systems of chemical interest. This approach was verified for the bis(cyclopentadienyl)vanadium(II) complex (Cp2V; vanadocene), and the metal-binding site of the Zn2+ → Co2+ substituted superoxide dismutase (SOD) metalloprotein. Excellent agreement with experimental NMR shifts was achieved, which represented a substantial improvement over previous theoretical attempts. The effects of vibrational corrections to orbital shielding and hyperfine tensor were evaluated and discussed within the second-order vibrational perturbation theory (VPT2) framework.
1 Introduction
NMR spectroscopy has evolved over the last few decades into a major instrument for probing the structure and dynamics in liquid, crystalline, and amorphous solid chemical systems. It has wide applications in chemistry, biology, and materials science. The shieldings (and therefore NMR chemical shifts) of nuclei contain accurate information about the surroundings of the corresponding atoms, including the local structure and chemical bonding. The relationships are most often complex, and as a result, theoretical NMR parameter predictions are critical for accurate signal assignment and understanding of local atomic environments in complex systems. The foundation of our understanding of experimentally observed NMR chemical shifts and spin–spin coupling constants, and the theories that connect these to electronic wavefunction were established by Norman Ramsey in the series of articles published between 1950 and 1953.1–5 As put by Pyykkö,6 “These papers should be regarded as a whole. Together they are among the most influential ones in the quantum chemistry of the twentieth century.” Indeed, they still provide definitive answers and a comprehensive theory for closed-shell systems within the nonrelativistic limit. In addition to these, the prediction by Ramsey for the modest influence of the NMR shift on the magnetic field strength in 19707 has lately been proven.8 Implementation of the efficient gauge-independent atomic orbital (GIAO) approach9 has allowed density functional theory (DFT) and ab initio methods of quantum chemistry to be routinely and successfully applied to the prediction of NMR shifts and spin–spin coupling constants in electronic structure calculations.10–14
Acquisition and interpretation of NMR data from paramagnetic systems, on the other hand, is still far from routine, when chemical insight into ligand atoms in close proximity to a paramagnetic transition metal (TM) or rare-earth (RE) ion is required. The total shift is measured in experimental NMR on paramagnetic systems in terms of three separate mechanisms:
| | δ = δorbital![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + δcontact + δcontact![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + δpseudocontact + δpseudocontact | (1) |
where the
δorbital (Ramsey) chemical shift is the single shift contribution in diamagnetic systems and the other two terms relate to the unpaired electrons. The
δcontact term reflects the through-bond polarization and is connected with the electron–nucleus hyperfine coupling constant (HFCC) between unpaired electron(s) and the nucleus. This mechanism called contact shift is operative in close vicinity to paramagnetic ions and can induce shifts as large as 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000 ppm.
15 The pseudocontact shift (PCS, pseudocontact) is a long-range term (1/
r3) from the electron–nucleus dipolar coupling and magnetic anisotropy of the paramagnetic center. Paramagnetic ions can induce PCS effects for NMR active nuclei at distances of 25–40 Å.
16,17 However, at close distances to the paramagnetic center (≲8 Å) both mechanisms are effective, and can shift NMR signals in either (positive or negative) direction. As a result, the theoretical prediction of induced paramagnetic NMR shifts is critical for exploring the local structure and chemical surroundings of nuclei in paramagnetic systems.
Unlike the Ramsey theory for closed-shell systems, the counterpart for paramagnetic NMR shifts necessitates the evaluation of the ensemble of thermally populated electronic states, as well as the inclusion of spin–orbit (SO) and zero-field splitting (ZFS) effects. Over the last two decades, substantial efforts have been spent on the development of a theory for prediction of NMR shifts for systems in an arbitrary spin state, and resulted in excellent contributions by Vaara et al.,18–25 Soncini et al.,26–28 Autschbach et al.,29–34 Kaupp et al.,35,36 and Neese et al.37,38 The modern implementation of the Kurland–McGarvey theory39,40 by Vaara et al.22 constitutes the current state-of-the-art.41–43 Within this formalism the induced paramagnetic NMR shift is parametrized with electron paramagnetic resonance (EPR) parameters: hyperfine A tensor, electronic g tensor, and the ZFS D tensor.
These parameters are accessible from a practical standpoint using electronic structure computations at various levels of theory. The g and D are local properties of the paramagnetic metal ion and are affected by the chemical environment only in proximity. Hence, ab initio calculations using the complete active space self-consistent field (CASSCF)44 method followed by the second-order multi-reference perturbation theory (NEVPT2)45–48 can be performed routinely, although within the limitation that only orbitals of the considered metal ion are included in the active space. In comparison to more elaborated and expensive multi-reference configuration interaction (MRCI) approaches, the CASSCF/NEVPT2 method is a suitable compromise.44,49–51 It accounts for both static and dynamic electron correlation. On the other hand, prediction of the A tensor, and its isotropic component, HFCC, imposes substantial challenges: (i) it requires accurate quantum chemical treatment over the entire system, including all nuclei of NMR interest and their local environments, and (ii) flexible basis sets and high-quality wavefunctions to describe core-level spin polarization. Hence, accurate computations of HFCCs are very demanding. With exceptions to very small systems, multi-reference approaches are not viable because too many electrons and orbitals need to be included in the active space. With (ii) dynamic correlation effects should be included, and Hartree–Fock (HF) level of theory (within the unrestricted UHF formalism) provides often erratic results. The lowest correlation method, second-order Møller–Plesset perturbation theory (MP2) suffers from spin contamination of the UHF reference, which can be mitigated by orbital-optimization (OO-MP2).52–54 DFT has been the only method chosen for routine calculations of A because it scales well with the system size and it partly accounts for electron correlation. However, the predictive power of DFT is compromised especially for TM systems.34,55–57 These limitations can be related to the DFT exchange–correlation functionals and how those are affected by the Kohn–Sham self-interaction (also referred to as delocalization) error, which is critical in the prediction of HFCCs. Stepping up on the Jacob's ladder for DFT with more sophisticated descriptions of the exchange–correlation functional does not guarantee more accuracy for HFCCs, as those parameterizations are typically targeted to reproduce thermodynamic properties and not the spin polarization effects over different shells explicitly.58,59 Performance of different exchange–correlation approximations is known to be clearly system dependent.60,61 The “parameter-free” hybrid PBE0 functional62 is considered the safest choice across the periodic table in this case. The Görling–Levy perturbation theory justifies using a fraction of 25% of the admixture of exact Hartree–Fock exchange (HFX) in the PBE0,63,64 and modifying this fraction has a dramatic effect on core-level spin polarization and the predicted HFCCs. However, due to limitations of DFT approximations, the practice of making arbitrary HFX parameter adjustments to increase the agreement between calculated and experimentally observed NMR shifts in paramagnetic systems has recently evolved.65,66 Such calculations use the “standard” PBE0 functional and “modified” ones (with HFX fractions up to 50%) with the hope that the HFCCs obtained would describe the paramagnetic NMR shifts observed experimentally. Due to the nature of chemical bonding, the optimal HFX will vary even among different elements and atomic positions within the same molecule, greatly limiting the predictive power for signal assignments, etc. The DFT is essentially used as an empirical method, which is not in line with “the right answer for the right reason” spirit.
On the other hand, the most accurate results among the practical ab initio electronic structure theories are offered by the coupled cluster (CC) methods.67 The CC theory was initially developed for problems in nuclear physics and adopted for quantum chemistry because of its remarkable prediction power for correlation energies.68–72 Apart from improvements in multi-reference CC methods,73,74 single-reference CC methods are useful for predictions in relation to radicals or 3rd and 4th row TM systems if the multi-reference character is monitored.75–78 The HFCCs predicted by the coupled cluster singles and doubles (CCSD) method were consistently in very good agreement with experimental results for small radicals and TM-containing molecules.58,60,79–82 Especially for TM systems Kaupp83 and Neese84 showed that CC methods are needed for consistently accurate predictions of HFCCs. Inclusion of perturbative triples correction (CCSD(T)) in the calculations led to rather minor improvements, although descriptions of higher-order excitations as well as vibrational corrections were shown to be necessary to obtain spectroscopic accuracy.58,85 However, the applicability of the CC methods to systems of chemical interest has been limited until very recently as the computational cost scales with the size of the system for the CCSD and CCSD(T) models as N6 and N7. This steep scaling has been reduced with the new and efficient implementation of CC theory, the DLPNO-CC approach by Neese and coworkers, exploiting the local nature of electron correlation.86–89 The DLPNO-CCSD(T) method is capable of recovering 99.9% of the correlation energy of the canonical CCSD(T) counterpart at significantly lower computational cost, assuring careful setting of the pair natural orbital (PNO) truncation thresholds.90–93 Quantitative insights into challenging noncovalent interactions in endohedral fullerene complexes have for example been achieved with the DLPNO-CCSD(T) scheme in recent years.94 A complementary formulation for high-spin open-shell systems has also been developed.95,96 Moreover, within the DLPNO-CCSD scheme the use of Λ-equations for unrelaxed coupled cluster density provides spin densities and first-order properties.97 The extensive benchmark studies for HFCCs prediction on a large set of radicals performed by Saitow and Neese,97 and Witwicki et al.,61 revealed that DLPNO-CCSD spin densities converge towards their canonical counterparts. Excellent performance and reliability of the DLPNO-CCSD method for prediction of hyperfine and quadrupolar coupling constants was quickly recognized.98–102
The main objectives of this study were to (i) demonstrate the applicability of the DLPNO-CCSD method for hyperfine tensor calculations within the current formalism for prediction of induced paramagnetic NMR shifts, and to (ii) incorporate vibrational corrections to isotropic orbital NMR shielding and hyperfine tensor. The inclusion of additional physics through electron correlation (i) and vibrational effects (ii) aimed at improving the accuracy and reliability of the existing protocol. We compared the robustness for predictions of HFCCs using the DLPNO-CCSD method against the parent CCSD model, other ab initio methods, and different DFT approximations. This analysis was performed on a variety of difficult systems including an organic radical, and complexes involving paramagnetic TM and RE ions. We evaluated the performance of the new approach for prediction of induced paramagnetic NMR shifts and the significance of vibrational corrections for the bis(cyclopentadienyl)vanadium(II) complex (vanadocene). Finally, we showed that the method worked well for the model of the metal-binding site in the Zn2+ → Co2+ substituted superoxide dismutase (SOD) metalloprotein.
2 Methods
Within the modern implementation of the Kurland–McGarvey theory by Vaara, the total NMR shielding tensor for the system with spin quantum number S > 1/2 can be expressed as:21,22,39| | 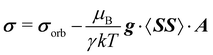 | (2) |
where μB, γ, k, and T are the Bohr magneton, gyromagnetic ratio of the nucleus, Boltzmann constant, and absolute temperature, respectively. The orbital shielding tensor σorb corresponds to the Ramsey shielding theory for closed-shell systems, whereas the electronic g tensor and hyperfine A tensor operate with dyadic:| | 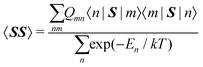 | (3) |
where
which represents the thermal average over the zero-field split ground state multiplet of |n〉 states (eigenfunctions) with En energies (eigenvalues) of the ZFS S·D·S Hamiltonian. The isotropic shielding σ and subsequently the isotropic chemical shift δ are obtained according to| | 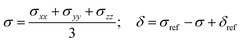 | (4) |
where σref and δref are the shielding and chemical shifts of the reference compound. The hyperfine tensor A is decomposed as:| | | A = Acon1 + AZPVcon1 + Adip + AZPVdip + ASOcon21 + ASOdip2 + ASOas | (5) |
where 1 is a 3 × 3 unit matrix, Acon denotes the contact isotropic HFCC, and Adip is the dipolar anisotropic coupling part of the hyperfine tensor, whereas AZPVcon and AZPVdip denote the respective zero-point vibrational corrections (ZPV). The second contact ASOcon2, the second dipolar ASOdip2, and the antisymmetric ASOas terms arise due to perturbational spin–orbit corrections. The electronic g tensor is decomposed into:| | g = ge1 + Δgiso1 + Δ![[g with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0067_0303.gif) | (6) |
where ge is the electron g-factor, and Δgiso and Δ![[g with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0067_0303.gif) are the isotropic and anisotropic parts of the g-shift tensor (deviation from ge). By evaluation of the respective components of A and g tensors the total NMR shift can be expressed as a sum of 17 physical contributions listed in Table 1. The antisymmetric σas term does not contribute to isotropic shielding, and only provides corrections to the shielding anisotropy. Note that to this end, vibrational effects were not considered in calculations of induced paramagnetic NMR shifts within the Kurland–McGarvey theory. Therefore, the seven shielding terms due to vibrational corrections (σZPVorb, σZPVcon, σZPVcon3, σZPVdip, σZPVdip3, σZPVca, σZPVpc) have not been evaluated before in other studies. The shielding terms in Table 1 can be grouped together and in this notation, they approximate the nomenclature used in experimental studies.
are the isotropic and anisotropic parts of the g-shift tensor (deviation from ge). By evaluation of the respective components of A and g tensors the total NMR shift can be expressed as a sum of 17 physical contributions listed in Table 1. The antisymmetric σas term does not contribute to isotropic shielding, and only provides corrections to the shielding anisotropy. Note that to this end, vibrational effects were not considered in calculations of induced paramagnetic NMR shifts within the Kurland–McGarvey theory. Therefore, the seven shielding terms due to vibrational corrections (σZPVorb, σZPVcon, σZPVcon3, σZPVdip, σZPVdip3, σZPVca, σZPVpc) have not been evaluated before in other studies. The shielding terms in Table 1 can be grouped together and in this notation, they approximate the nomenclature used in experimental studies.| | 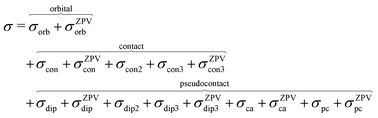 | (7) |
Table 1 NMR shielding terms and the respective tensorial ranks for a system with spin quantum number S > 1/2
| Contribution origin |
Shielding term |
Tensorial rank |
| Orbital shielding |
σ
orb
|
0, 2, 1 |
| ZPV correction to σorb |
σ
ZPVorb
|
0, 2, 1 |
|
g
e
A
con〈SεSτ〉 |
σ
con
|
0, 2 |
|
g
e
A
ZPVcon〈SεSτ〉 |
σ
ZPVcon
|
0, 2 |
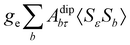
|
σ
dip
|
0, 2, 1 |
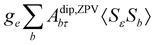
|
σ
ZPVdip
|
0, 2, 1 |
|
g
e
A
SOcon2〈SεSτ〉 |
σ
con2
|
0, 2 |
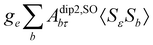
|
σ
dip2
|
0, 2, 1 |
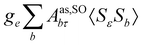
|
σ
as
|
2, 1 |
| Δgiso-Acon〈SεSτ〉 |
σ
con3
|
0, 2 |
| ΔgisoAZPVcon〈SεSτ〉 |
σ
ZPVcon3
|
0, 2 |
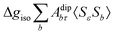
|
σ
dip3
|
0, 2, 1 |
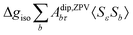
|
σ
ZPVdip3
|
0, 2, 1 |
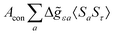
|
σ
ca
|
0, 2, 1 |
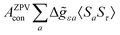
|
σ
ZPVca
|
0, 2, 1 |
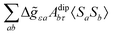
|
σ
pc
|
0, 2, 1 |
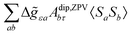
|
σ
ZPVpc
|
0, 2, 1 |
3 Computational details
All calculations were performed with the ORCA code103,104 in either version 4.2.1 (geometry optimizations, EPR parameters) or 5.0.1 (orbital shieldings, vibrational corrections) and employed a very tight self-consistent field (SCF) convergence tolerance of 1 × 10−9Eh. Evaluation of Coulomb and exchange integrals was accelerated with the RIJCOSX approximation105 employing very tight grids (GridX8 in version 4.2.1 and DefGrid3 in 5.0.1) and either def2/J106 or automatically generated (AutoAux)107 Coulomb-fitting basis sets (for augmented or relativistic orbital basis sets). DFT calculations involved very tight integration grids (Grid7 NoFinalGrid and DefGrid3 in version 4.2.1 and 5.0.1, respectively). Geometry optimizations were converged to very tight thresholds (VeryTightOpt) and no symmetry constraints were imposed. DFT optimizations employed density dependent atom-pairwise dispersion correction (D4).108 Optimizations of transition metal systems involved the cc-pVTZ basis set109–111 and the def2-TZVP basis set112,113 was used for the optimization of the ytterbium complex. The global energy minima at the potential energy surfaces were confirmed by analytical Hessian calculations. The geometry of the staggered conformer of vanadocene was obtained from transition state calculation. The all electron CCSD(T)/aug-cc-pCVTZ geometry optimization of the cyanomethyl radical was performed with numerical gradients. DLPNO-CCSD(T) calculations for the vanadocene conformers employed TightPNO setting, the correlation-consistent (aug-)cc-p(wC)VXZ orbital basis sets114,115 together with the corresponding auxiliary (aug-)cc-p(wC)VXZ/C basis sets.116,117 Cartesian coordinates of the models are provided in the ESI.† All calculations of properties involved all electrons (NoFrozenCore). The EPR/NMR properties of chemically equivalent atoms were averaged. The orbital shielding tensors σ were calculated with the GIAO approach9 at the PBE0 level using the pcSseg-2 basis set specifically developed to provide fast convergence towards the complete basis set limit for NMR shieldings.118 Methane was used as the NMR shift reference for 1H and 13C since chemical shifts measured in the gas phase are available for this molecule.119 The NMR parameters of the CH4 reference (in ppm) are 1H: σref = 31.25, σZPVref = −0.61, δref = 2.17; for 13C: σref = 191.82, σZPVref = −3.47, δref = −8.65. Calculations of hyperfine tensors were performed with the core-property basis sets specifically developed for predictions of HFCCs: the aug-cc-pVTZ-J basis set developed by Sauer and coworkers120,121 (with aug-cc-pwCVTZ/C auxiliary basis set) or the smaller EPR-II basis set developed by Barone and coworkers122–125 (together with cc-pwCVDZ/C). For the ytterbium complex, the relativistic second-order Douglas–Kroll–Hess (DKH2) Hamiltonian was used with the SARC-DKH-TZVP126 basis set for Yb, and the NMR-DKH127,128 basis set for the ligand atoms. The AutoAux procedure for the generation of auxiliary basis sets, picture-change effects to the respective operators and finite nucleus model were used.129–132 The sensitivity of the computed HFCCs to the completeness of the auxiliary basis sets with the DLPNO-CCSD method is shown in Table S1 in the ESI.† The CCSD and DLPNO-CCSD calculations of the hyperfine A tensors employed unrelaxed coupled cluster density, Λ-equations, and quasi-restricted orbitals (QROs; default for DLPNO-CCSD in ORCA). For all coupled cluster calculations the multi-reference T1 diagnostic was ≤0.015 for both open-shell CCSD and Λ/Z_vector iterations. For the cyanomethyl radical and the TM/RE complexes, the HFC1 and HFC2 PNO truncation settings were used. The model of the CoSOD protein was divided into fragment 1 that included metal ion, nitrogen donors and Asp83 unit (atoms rendered with spheres in Fig. 2a) and fragment 2, which comprised the remaining atoms in the model (rendered with sticks in Fig. 2a). The HFC1 or HFC2 settings were invoked for the calculation, however, to reduce computational costs, the inter- and intrafragment settings for fragment 2 were reduced to LoosePNO using fragment specific settings. Spin–orbit corrections to A were estimated with at the PBE0 level (with basis sets corresponding to those used in DLPNO-CCSD calculations) using a mean-field/effective potential approach including 1-electron terms, Coulomb terms, exchange via one-center exact integrals including the spin-other-orbit interaction, and local DFT correlation, as implemented in ORCA. Calculations of A with the double hybrid DFT involved relaxed MP2 density. For calculations of vibrational corrections to σ and A the second-order vibrational perturbation theory (VPT2) was employed, as implemented in ORCA. Hessian calculations for the anharmonic VPT2 force fields involved the PBE0-D4/cc-pVTZ level starting from the respective optimized geometries, and property calculations involved the PBE0/pcSseg-2 level for σ and PBE0/aug-cc-pVTZ-J for A. For the numerical calculations of Hessian and property derivatives a step size of 0.05 was used for both the anharmonic and property displacements. The g and D tensors were calculated with a state-averaged, complete active space self-consistent field (CASSCF) method distributing n d-shell electrons (n = 3 for V and n = 7 for Co) over five 3d orbitals of a metal ion; CAS(n,5), followed by invoking an N-electron valence state second-order perturbation theory (NEVPT2). CASSCF calculation for vanadocene included 10 quartet and 15 doublet roots, whereas for the CoSOD protein model 10 quartet and 40 doublet roots were evaluated. In the CASSCF/NEVPT2 calculations the aug-cc-pwCVTZ-DK133 basis set was used for V and Co, while the aug-cc-pVTZ-DK134 basis set was used for the ligand atoms in vanadocene, and the cc-pVDZ-DK for the ligand atoms in the CoSOD model. Auxiliary basis sets generated with AutoAux were employed. Both scalar-relativistic (via the DKH2 approach, picture-changed operators, finite nucleus model) and spin–orbit effects were included.44,50 Induced paramagnetic NMR shifts were evaluated assuming temperatures of 298 and 280 K for the vanadocene and protein model, respectively, in accordance to the experimental conditions. Computations were performed on a cluster node equipped with the two Intel® Xeon® Gold 6126 CPUs (2.6 GHz; 12-core) and 256 GB of RAM.
4 Results and discussion
4.1 Prediction of hyperfine coupling: the challenge
In this section the impact of electron correlation on the prediction of HFCCs was evaluated by comparing results at the HF, MP2 (different variants), DLPNO-CCSD, and canonical CCSD levels of theory with those obtained at four different levels of DFT approximations. There were three types of systems considered (with available experimental data). First, the HFCC for the 14N in cyanomethyl radical N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–˙CH2 was calculated. The nitrogen atom is in general challenging for calculations of EPR/NMR parameters. For example, the CCSD(T) level of theory was needed to provide quantitative agreement with experimental estimates for the HFCC of the nitrogen atom in its ground state80 or NMR shielding in the N
C–˙CH2 was calculated. The nitrogen atom is in general challenging for calculations of EPR/NMR parameters. For example, the CCSD(T) level of theory was needed to provide quantitative agreement with experimental estimates for the HFCC of the nitrogen atom in its ground state80 or NMR shielding in the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N molecule.13 Previous DFT studies on nitrogen containing organic radicals have revealed that the results depend on the particular choice of the exchange–correlation functional and the basis set, which often have led to fortuitous cancellation of errors.58,135–138 Second, we considered challenging calculations of both metal and ligand-related HFCCs in transition metal complexes: [V(H2O)6]2+, [Cr(H2O)6]3+, and [Mn(H2O)6]2+. Although the spin–orbit contributions to the hyperfine tensor cannot be currently assessed at the DLPNO-CCSD level, these are expected to be small for high-spin d3 and d5 configurations of the V2+, Cr3+, and Mn2+ ions.84,97 As the last, yet the most challenging system, a RE metal ion complex was considered: [Yb(H2O)8]3+.
N molecule.13 Previous DFT studies on nitrogen containing organic radicals have revealed that the results depend on the particular choice of the exchange–correlation functional and the basis set, which often have led to fortuitous cancellation of errors.58,135–138 Second, we considered challenging calculations of both metal and ligand-related HFCCs in transition metal complexes: [V(H2O)6]2+, [Cr(H2O)6]3+, and [Mn(H2O)6]2+. Although the spin–orbit contributions to the hyperfine tensor cannot be currently assessed at the DLPNO-CCSD level, these are expected to be small for high-spin d3 and d5 configurations of the V2+, Cr3+, and Mn2+ ions.84,97 As the last, yet the most challenging system, a RE metal ion complex was considered: [Yb(H2O)8]3+.
The results for the prediction of hyperfine and quadrupolar coupling constants for the 14N nucleus of the cyanomethyl radical are presented in Table 2. The 14N hyperfine coupling constant (Acon) in the cyanomethyl radical calculated with the simplest DFT method for open-shell systems, local spin density approximation (LSDA),141 was severely underestimated compared to experimental values, but the predicted 14N quadrupolar coupling constant (χ) was quite close to the experiment. As one could assume, predicting the spin density at the nucleus is substantially more challenging than predicting the electric field gradients. Incorporation of electron density gradient corrections to the LSDA in the generalized gradient approximation (GGA) PBE functional142 significantly improved on the predictions of both Acon and χ. Nonetheless, the calculated Acon was still significantly underestimated. DFT underestimate the core-level spin polarization, whereas the Hartree–Fock method overestimates it. Incorporating 25% of the exact Hartree–Fock exchange energy component in the hybrid-GGA PBE0 exchange–correlation functional62 improved prediction of Acon significantly. However, further increase of the HF exchange admixture to 50% (PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX)) severely deteriorated the predictions of both Acon and χ when compared to the original PBE0 formulation. The last step on the Jacob's ladder for DFT approximations consists of double hybrid, “perturbatively corrected” exchange–correlation functionals that incorporate an exact HF exchange component and a perturbative second-order correlation contribution.145 The double hybrid DSD-PBEP86 functional146 that incorporates HF exchange, PBE and P86 exchange and correlation potentials, as well as spin-component-scaled (SCS) MP2 mixing, constitutes one of the most accurate DFT methods for general chemistry applications.147 It is also known to provide excellent predictions of NMR shifts in closed-shell systems of main group elements.101,148–152 However, as shown in Table 2, for the case of cyanomethyl radicals the DSD-PBEP86 functional suffered from instabilities that resulted in erratic spin density on the nitrogen atom. Special care has to be taken when applying double hybrid functionals to open-shell systems.60 This also indicated that in general, no systematic improvements for prediction of the hyperfine coupling constants were feasible within the current DFT framework.61 The Hartree–Fock and MP2/SCS-MP2 methods provided essentially erratic results, and values obtained with MP2 and its SCS-MP2 variant were similar. Orbital optimization (OO-MP2/OO-SCS-MP2) remarkably improved the results by removing spin contamination of the reference wavefunction, however, the predicted HFCCs were still far from experimental ones. The robustness of the CCSD level of theory was clearly necessary to provide good agreement with experimental data for the N
HFX)) severely deteriorated the predictions of both Acon and χ when compared to the original PBE0 formulation. The last step on the Jacob's ladder for DFT approximations consists of double hybrid, “perturbatively corrected” exchange–correlation functionals that incorporate an exact HF exchange component and a perturbative second-order correlation contribution.145 The double hybrid DSD-PBEP86 functional146 that incorporates HF exchange, PBE and P86 exchange and correlation potentials, as well as spin-component-scaled (SCS) MP2 mixing, constitutes one of the most accurate DFT methods for general chemistry applications.147 It is also known to provide excellent predictions of NMR shifts in closed-shell systems of main group elements.101,148–152 However, as shown in Table 2, for the case of cyanomethyl radicals the DSD-PBEP86 functional suffered from instabilities that resulted in erratic spin density on the nitrogen atom. Special care has to be taken when applying double hybrid functionals to open-shell systems.60 This also indicated that in general, no systematic improvements for prediction of the hyperfine coupling constants were feasible within the current DFT framework.61 The Hartree–Fock and MP2/SCS-MP2 methods provided essentially erratic results, and values obtained with MP2 and its SCS-MP2 variant were similar. Orbital optimization (OO-MP2/OO-SCS-MP2) remarkably improved the results by removing spin contamination of the reference wavefunction, however, the predicted HFCCs were still far from experimental ones. The robustness of the CCSD level of theory was clearly necessary to provide good agreement with experimental data for the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–˙CH2. We noted however that the CCSD seemed to slightly overestimate the 14N hyperfine coupling in cyanomethyl radical. This was attributed to the lack of perturbative triple correction (CCSD(T)) that was shown to slightly lower the HFCCs predictions compared to CCSD.82 Before we discuss the predictions with the DLPNO-CCSD method, we add a remark. To facilitate the accuracy and performance control of the DLPNO-CCSD calculations, five levels of predefined PNO truncation settings have been developed: LoosePNO, NormalPNO, TightPNO, HFC1, and HFC2. These settings provide convergence towards the canonical limit at increasing computational cost,90,97 by invoking refined thresholds for the electron pair correlation energies evaluation. Essential pairs are selected for accurate coupled cluster treatment, and those pairs with a less critical contribution to the total correlation energy are subjected to a much more computationally efficient second-order perturbation theory. The LoosePNO, NormalPNO, and TightPNO thresholds were designed for general chemistry applications, i.e. evaluations of total energies or intermolecular interactions. The tighter HFC1 and HFC2 settings were specifically developed for calculations of hyperfine coupling constants. As shown in Table 2, for predictions of the 14N quadrupolar coupling constants both the HFC1 and HFC2 settings provided converged results of CCSD quality. They were clearly better than those from hybrid DFT. However, the convergence for the prediction of the 14N hyperfine coupling constants was more difficult to achieve. With the HFC1 setup full convergence was not achieved and the more conservative (and expensive) HFC2 setting was needed to provide results close to the CCSD reference. This in turn indicated that electron correlation effects in N
C–˙CH2. We noted however that the CCSD seemed to slightly overestimate the 14N hyperfine coupling in cyanomethyl radical. This was attributed to the lack of perturbative triple correction (CCSD(T)) that was shown to slightly lower the HFCCs predictions compared to CCSD.82 Before we discuss the predictions with the DLPNO-CCSD method, we add a remark. To facilitate the accuracy and performance control of the DLPNO-CCSD calculations, five levels of predefined PNO truncation settings have been developed: LoosePNO, NormalPNO, TightPNO, HFC1, and HFC2. These settings provide convergence towards the canonical limit at increasing computational cost,90,97 by invoking refined thresholds for the electron pair correlation energies evaluation. Essential pairs are selected for accurate coupled cluster treatment, and those pairs with a less critical contribution to the total correlation energy are subjected to a much more computationally efficient second-order perturbation theory. The LoosePNO, NormalPNO, and TightPNO thresholds were designed for general chemistry applications, i.e. evaluations of total energies or intermolecular interactions. The tighter HFC1 and HFC2 settings were specifically developed for calculations of hyperfine coupling constants. As shown in Table 2, for predictions of the 14N quadrupolar coupling constants both the HFC1 and HFC2 settings provided converged results of CCSD quality. They were clearly better than those from hybrid DFT. However, the convergence for the prediction of the 14N hyperfine coupling constants was more difficult to achieve. With the HFC1 setup full convergence was not achieved and the more conservative (and expensive) HFC2 setting was needed to provide results close to the CCSD reference. This in turn indicated that electron correlation effects in N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–˙CH2 are substantial.
C–˙CH2 are substantial.
Table 2
14N hyperfine (Acon) and quadrupolar (χ) coupling constants (MHz) in cyanomethyl radical N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–˙CH2 calculated with different methods using the aug-cc-pVTZ-J basis set
C–˙CH2 calculated with different methods using the aug-cc-pVTZ-J basis set
| Method |
A
con
|
χ
|
| DFT |
| LSDA |
2.35 |
−4.39 |
| PBE |
5.55 |
−4.26 |
| PBE0 |
8.84 |
−4.41 |
PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) HFX) |
15.39 |
−4.59 |
| DSD-PBEP86 |
−2.52 |
−4.37 |
|
Ab initio
|
| HF |
45.29 |
−4.86 |
| MP2 |
−41.28 |
−4.60 |
| SCS-MP2 |
−44.23 |
−4.67 |
| OO-MP2 |
6.47 |
−3.90 |
| OO-SCS-MP2 |
6.25 |
−3.97 |
| DLPNO-CCSD |
| HFC1 |
9.17 |
−4.28 |
| HFC2 |
9.81 |
−4.27 |
| CCSD |
9.86 |
−4.27 |
|
|
| Experiment |
| Saito et al.139 |
9.51 ± 0.06 |
−4.18 ± 0.10 |
| Ozeki et al.140 |
9.49 ± 0.01 |
−4.20 ± 0.01 |
The sum of first-order components of 51V, 53Cr, and 55Mn hyperfine tensors (Axx/yy/zzcon+dip) and the isotropic components of the 17O hyperfine tensors (Acon) in [V(H2O)6]2+, [Cr(H2O)6]3+, [Mn(H2O)6]2+, and [Yb(H2O)8]3+ complexes are shown in Table 3. For predictions related to 51V, 53Cr, and 55Mn similar patterns were observed as for the cyanomethyl radical. Calculations with the two lowest levels of DFT approximations, LSDA and GGA, severely underestimated the magnitudes of hyperfine couplings. Although the hybrid DFT method provided considerable improvements, the predicted values were still significantly underestimated. In contrast to the cyanomethyl radical case, where the increase of Hartree–Fock exchange admixture to 50% deteriorated the results severely, the predictions of the hyperfine couplings were improved for 51V, 53Cr, and 55Mn. However, the hyperfine couplings obtained with the PBE0 and PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) approximations were lower than the experimental values. The double hybrid DSD-PBEP86 approximation did offer improvements, and the predictions with this functional were generally closer to the experimental values than those with hybrid DFT. Considering the ab initio methods, HF was expected to overestimate hyperfine couplings, although this effect was much smaller for the TM complexes than for the cyanomethyl radical. The predictions with MP2 and orbital-optimized MP2 were quite close to the experimental values. The values were notably closer than those calculated with DFT, with the exception of 55Mn. Finally, both the CCSD and DLPNO-CCSD predictions were in good agreement with the experimental results for 51V and 53Cr, with somewhat larger deviations for 55Mn, which might be attributed to the lack of triples correction. Although the results for the radical and metal hyperfine couplings provide an assessment of the applicability of the respective computational methods, the accuracy for the prediction of EPR and NMR properties of the ligand atoms in the TM and RE complexes is the most important, from the point of view of practical calculations for the prediction of induced paramagnetic shifts. Let us focus first on the 17O isotropic hyperfine coupling constant (Acon) in [Mn(H2O)6]2+, for which experimental result is available. Both the CCSD and DLPNO-CCSD methods provided excellent predictions that were almost exact matches with experimental data. The MP2 and OO-MP2 results were also close, whereas the HF values deviated. When it comes to DFT, predictions with the LSDA and PBE approximations resulted in severe errors. Also, the calculations with the PBE0 and PBE0(50%
HFX) approximations were lower than the experimental values. The double hybrid DSD-PBEP86 approximation did offer improvements, and the predictions with this functional were generally closer to the experimental values than those with hybrid DFT. Considering the ab initio methods, HF was expected to overestimate hyperfine couplings, although this effect was much smaller for the TM complexes than for the cyanomethyl radical. The predictions with MP2 and orbital-optimized MP2 were quite close to the experimental values. The values were notably closer than those calculated with DFT, with the exception of 55Mn. Finally, both the CCSD and DLPNO-CCSD predictions were in good agreement with the experimental results for 51V and 53Cr, with somewhat larger deviations for 55Mn, which might be attributed to the lack of triples correction. Although the results for the radical and metal hyperfine couplings provide an assessment of the applicability of the respective computational methods, the accuracy for the prediction of EPR and NMR properties of the ligand atoms in the TM and RE complexes is the most important, from the point of view of practical calculations for the prediction of induced paramagnetic shifts. Let us focus first on the 17O isotropic hyperfine coupling constant (Acon) in [Mn(H2O)6]2+, for which experimental result is available. Both the CCSD and DLPNO-CCSD methods provided excellent predictions that were almost exact matches with experimental data. The MP2 and OO-MP2 results were also close, whereas the HF values deviated. When it comes to DFT, predictions with the LSDA and PBE approximations resulted in severe errors. Also, the calculations with the PBE0 and PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) functionals were not able to approach the experimental result. In fact, considering the results for ligand atoms for all systems in Table 3, the predictions with the PBE0 and PBE0(50%
HFX) functionals were not able to approach the experimental result. In fact, considering the results for ligand atoms for all systems in Table 3, the predictions with the PBE0 and PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) functionals never encompassed experimental results or the CCSD predictions. Furthermore, the effect of increasing the HF exchange admixture was not always beneficial. It deteriorated the predictions for [V(H2O)6]2+ and [Cr(H2O)6]3+ as compared to the genuine PBE0 formulation. The predictions as presented in Table 3 suggested that it is not possible to assess the intrinsic DFT errors in the prediction of HFCCs by performing computations with PBE0 and PBE0(50%
HFX) functionals never encompassed experimental results or the CCSD predictions. Furthermore, the effect of increasing the HF exchange admixture was not always beneficial. It deteriorated the predictions for [V(H2O)6]2+ and [Cr(H2O)6]3+ as compared to the genuine PBE0 formulation. The predictions as presented in Table 3 suggested that it is not possible to assess the intrinsic DFT errors in the prediction of HFCCs by performing computations with PBE0 and PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) approximations. Predictions of properties with hybrid DFT for the ligand atoms were inconclusive as shown in Table 3, and for the RE complex, it was not even possible to establish the sign of the coupling constant. In contrast, the predictions performed with the double hybrid DSD-PBEP86 functional consistently improved on the hybrid DFT, although the deviations from experimental values or reference CCSD calculations were still significant. The results for [Yb(H2O)8]3+ displayed an even more complicated pattern. The predictions performed by LSDA, PBE, and PBE0 provided erratic values. For this complex, the DFT-based calculations benefited from high HF exchange admixtures. PBE0(50%
HFX) approximations. Predictions of properties with hybrid DFT for the ligand atoms were inconclusive as shown in Table 3, and for the RE complex, it was not even possible to establish the sign of the coupling constant. In contrast, the predictions performed with the double hybrid DSD-PBEP86 functional consistently improved on the hybrid DFT, although the deviations from experimental values or reference CCSD calculations were still significant. The results for [Yb(H2O)8]3+ displayed an even more complicated pattern. The predictions performed by LSDA, PBE, and PBE0 provided erratic values. For this complex, the DFT-based calculations benefited from high HF exchange admixtures. PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) and DSD-PBEP86 (which incorporates 72% HFX) improved on the predictions. With HF the calculated HFCCs were overestimated, but with MP2 improvements were achieved. Predictions with DLPNO-CCSD using HFC1 and HFC2 thresholds revealed convergence towards the experimental value, which was encouraging in the perspective of future studies involving RE systems. The OO-MP2 calculation did not converge even with significantly increased number of iterations, whereas the computational cost of each canonical CCSD iteration was so high that it was not expected to converge within a reasonable time frame.
HFX) and DSD-PBEP86 (which incorporates 72% HFX) improved on the predictions. With HF the calculated HFCCs were overestimated, but with MP2 improvements were achieved. Predictions with DLPNO-CCSD using HFC1 and HFC2 thresholds revealed convergence towards the experimental value, which was encouraging in the perspective of future studies involving RE systems. The OO-MP2 calculation did not converge even with significantly increased number of iterations, whereas the computational cost of each canonical CCSD iteration was so high that it was not expected to converge within a reasonable time frame.
Table 3 First-order components of the hyperfine tensors in [V(H2O)6]2+, [Cr(H2O)6]3+, [Mn(H2O)6]2+, and [Yb(H2O)8]3+ complexes. Calculations for transition metal complexes involved the aug-cc-pVTZ-J (V,Cr,Mn) and EPR-II (H2O) basis sets, whereas calculations for the ytterbium complex were performed with the relativistic SARC-DKH-TZVP (Yb) and NMR-DKH (H2O) basis sets and DKH2 Hamiltonian
| Method |
[V(H2O)6]2+ |
[Cr(H2O)6]3+ |
[Mn(H2O)6]2+ |
[Yb(H2O)8]3+ |
|
51V |
17O |
53Cr |
17O |
55Mn |
17O |
17O |
|
A
xx/yy/zzcon+dip
|
A
con
|
A
xx/yy/zzcon+dip
|
A
con
|
A
xx/yy/zzcon+dip
|
A
con
|
A
con
|
|
From ref. 84, 143 and 144.
|
| DFT |
| LSDA |
−143.54/−143.78/−143.98 |
8.13 |
32.13/32.17/32.20 |
9.20 |
−112.22/−112.24/−112.31 |
−10.56 |
−3.74 |
| PBE |
−163.83/−164.03/−164.19 |
5.73 |
33.13/33.16/33.20 |
6.91 |
−163.59/−163.60/−163.69 |
−11.39 |
−3.21 |
| PBE0 |
−196.19/−196.37/−196.51 |
5.26 |
39.19/39.22/39.26 |
7.01 |
−200.86/−200.88/−200.99 |
−9.52 |
−0.10 |
PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) HFX) |
−226.34/−226.49/−226.60 |
3.93 |
43.41/43.44/43.48 |
5.87 |
−230.54/−230.55/−230.70 |
−8.78 |
0.40 |
| DSD-PBEP86 |
−226.27/−226.42/−226.55 |
5.83 |
44.75/44.78/44.82 |
7.49 |
−238.86/−238.87/−239.02 |
−8.11 |
0.60 |
|
Ab initio
|
| HF |
−299.62/−299.70/−299.77 |
6.00 |
56.00/56.02/56.06 |
7.48 |
−301.67/−301.68/−301.88 |
−6.35 |
1.20 |
| MP2 |
−241.66/−241.80/−241.93 |
6.89 |
47.79/47.83/47.87 |
8.92 |
−261.09/−261.10/−261.26 |
−7.22 |
1.09 |
| OO-MP2 |
−237.90/−238.05/−238.18 |
7.21 |
46.43/46.46/46.49 |
9.06 |
−254.37/−254.38/−254.53 |
−7.82 |
— |
| DLPNO-CCSD |
| HFC1 |
−245.09/−245.44/−245.50 |
6.07 |
47.13/46.19/47.26 |
7.72 |
−273.22/−273.23/−273.42 |
−7.37 |
1.08 |
| HFC2 |
−245.85/−246.03/−246.26 |
6.25 |
46.67/46.72/46.78 |
7.83 |
−272.93/−273.05/−273.20 |
−7.50 |
1.04 |
| CCSD |
−244.70/−244.84/−244.95 |
6.39 |
48.10/48.13/48.16 |
8.07 |
−267.66/−267.61/−267.77 |
−7.64 |
— |
|
|
| Experimenta |
−247/−247/−247 |
n/a |
55/55/55 |
n/a |
−245/−245/−245 |
−7.5 |
0.88 |
To summarize, results, as presented in Tables 2 and 3, confirmed outstanding reliability of the CCSD method for the prediction of HFCCs for all systems considered. Most importantly, DLPNO-CCSD spin densities were shown to converge towards the canonical CCSD counterparts. Given the substantially reduced computational cost of the DLPNO-CCSD method compared to CCSD, predictions of coupled cluster quality can be achieved for large systems of chemical interest. Notably, although the open-shell DLPNO-CCSD method in its current implementation exhibits very favorable scaling (linear to quadratic) when considering the iterative part, integral transformations on larger systems add substantial prefactors. In fact, the memory and disk space requirements of these integral transformations limit the feasibility of the method on large systems rather than long computation times. Yet, the open-shell formulation of the DLPNO-CCSD method is twice more demanding compared to its closed-shell counterpart. Therefore, although the HFC2 setup produced excellent results, very close to canonical CCSD, it is not a practical choice to employ such tight thresholds for large systems, which was indicated by Saitow and Neese. The HFC1 setup produces HFCCs “of desirable accuracy while maximizing the balance between acceptable computational cost and high accuracy.”97 Thus, in the rest of this current study, the HFC1 setup is assumed when discussing the DLPNO-CCSD results unless otherwise specified.
4.2 From news to everyday use: prediction of NMR shifts in vanadocene
The bis(cyclopentadienyl)vanadium(II) complex (Cp2V; vanadocene) was chosen as a test case for an improved method for predictions of NMR shifts. High-quality experimental and theoretical EPR/NMR data are available for comparison, and the spin–orbit contributions to hyperfine tensor (which cannot be examined at the coupled cluster level) are expected to be modest for the high-spin d3 configuration of the V2+ ion in the complex. Vanadocene can have two distinct conformations, eclipsed and staggered, see Fig. 1(a) and (b). The gas phase electron diffraction analysis by Gard et al.153 found an average distance between the vanadium and cyclopentadienyl rings r(V–C5H5) = 1.928 ± 0.006b Å and an eclipsed conformation, however, the staggered configuration could not be ruled out completely. The single crystal X-ray diffraction study by Rogers et al.154 indicated a distance r(V–C5H5) = 1.92 ± 0.02 Å and although the vanadium atom resided on a crystallographic center of inversion, the cyclopentadienyl rings were dynamically disordered at room temperature. This was further corroborated by a temperature-dependent X-ray study by Antipin et al.155 Optimization of the molecular geometry of vanadocene was performed at the PBE0-D4/cc-pVTZ level of theory without symmetry constrains and resulted in the eclipsed conformer with a distance r(V–C5H5) = 1.929 Å, which agreed excellently with the experimental estimates. The energy difference between the two conformers was found to be small, which we have also corroborated by high-level DLPNO-CCSD(T) calculations, see Table 4. Our most accurate calculation of the energy difference between eclipsed and staggered conformers (Eeclipsed − Estaggered) was −0.17 kcal mol−1. These calculations were performed using the all electron DLPNO-CCSD(T) method with the aug-cc-pwCVTZ basis set, incorporating diffuse functions and core-valence correlation. The small difference in turn indicated that the energy barrier for the rotational diffusion of the rings would be very small too.
 |
| | Fig. 1 Eclipsed (a) and staggered (b) conformers of vanadocene. Spin densities calculated at the DLPNO-CCSD/aug-cc-pVTZ-J level of theory shown with an isodensity of 0.002 (panel c), 0.0002 (d), and 0.00002 (e) e bohr−3; orange and cyan denote the positive and negative regions, respectively. | |
 |
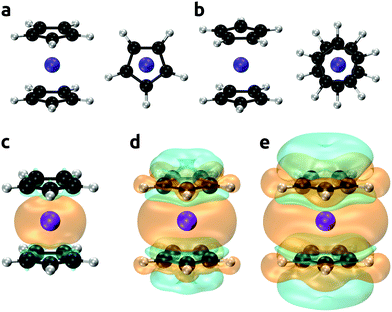
| | Fig. 2 Model of the binding site of Co2+ ion with His63, His71, His80, and Asp83 residues in CoSOD metalloprotein (panel a). Calculated NMR shifts for 13Cβ (Asp83) (panel b); DFT results for models A–J from ref. 65, predictions with DLPNO-CCSD for models E and F from this work. Spin densities calculated at the DLPNO-CCSD/aug-cc-pVTZ-J/EPR-II level of theory shown with an isodensity of 0.002 (panel c), 0.0002 (d), and 0.00002 (e) e bohr−3; orange and cyan denote the positive and negative regions, respectively. | |
Table 4 Energy difference between the eclipsed and staggered conformers (Eeclipsed − Estaggered; kcal mol−1) of vanadocene
| Method |
Basis set |
E
eclipsed − Estaggered |
|
Fully iterative triples correction.89,96
All electron, no frozen core.
|
| PBE0-D4 |
cc-pVTZ |
−0.10 |
| DLPNO-CCSD(T) |
cc-pVDZ |
−0.19 |
| DLPNO-CCSD(T1)a |
cc-pVDZ |
−0.20 |
| DLPNO-CCSD(T) |
cc-pVTZ |
−0.23 |
| DLPNO-CCSD(T) |
aug-cc-pVTZ |
−0.07 |
| DLPNO-CCSD(T)b |
aug-cc-pwCVTZ |
−0.17 |
Experimental and calculated parameters are shown in Table 5 for both the eclipsed and staggered conformers of vanadocene. These include the calculated hyperfine coupling constants and zero-field splitting parameters and actual ZFS data, as well as theoretical predictions with a multi-reference configuration interaction approach: spectroscopy oriented configuration interaction (SORCI) method.156–162 The calculated EPR properties of both conformers were nearly identical. The isotropic components of the hyperfine tensor (Acon) were positive for 1H and negative for 13C, which was also reflected by the corresponding positive and negative regions of the spin densities plotted in Fig. 1(c)–(e). Vibrational corrections to the hyperfine coupling constant (AZPVcon) were minor, but they were more than twice as large as the corresponding spin–orbit corrections (ASOcon2). Both the vibration and spin–orbit corrections were more important for 13C than for 1H. The calculated ZFS parameters D and E/D were in very good agreement with the experiment. Note that within the CASSCF/NEVPT2 approach, only the spin–orbit coupling (SOC) contribution to the ZFS tensor was calculated, whereas with the SORCI method both the SOC and spin–spin coupling (SSC) contributions can be obtained. However, for TM complexes the SSC contributions are typically small, so the CASSCF/NEVPT2 approach is a good approximation, as was the case here.
Table 5 Molecular geometries and EPR properties of vanadocene
| Property |
Cp2V |
Cp2V calculationa |
| Experiment |
Eclipsed |
Staggered |
|
Calculated at the respective level of theory: A DLPNO-CCSD/aug-cc-pVTZ-J; AZPV PBE0-D4/cc-pVTZ/VPT2/PBE0/aug-cc-pVTZ-J; ASO PBE0/aug-cc-pVTZ-J; g and D at DKH2-CASSCF/NEVPT2/aug-cc-pwCVTZ-DK(V)/aug-cc-pVTZ-DK(C,H).
From ref. 153.
From ref. 162.
|
| Distances (Å) |
|
r(V–C5H5) |
1.928 ± 0.006b |
1.929 |
1.930 |
|
r(V–C) |
2.280 ± 0.005b |
2.273 |
2.274 |
|
r(C–C) |
1.434 ± 0.003b |
1.415 |
1.415 |
|
r(C–H) |
1.133 ± 0.014b |
1.079 |
1.079 |
|
|
| HFCC (MHz) |
|
1H |
|
|
|
|
A
con
|
|
2.31 |
2.29 |
|
A
ZPVcon
|
|
0.04 |
— |
|
A
SOcon2
|
|
0.01 |
0.01 |
|
13C |
|
|
|
|
A
con
|
|
−1.23 |
−1.22 |
|
A
ZPVcon
|
|
0.05 |
— |
|
A
SOcon2
|
|
0.02 |
0.02 |
|
|
|
g
tensor |
|
|
|
|
g
iso
|
|
1.987 |
1.987 |
|
g-Eigenvalues |
|
1.979 |
1.979 |
|
|
|
1.979 |
1.979 |
|
|
|
2.002 |
2.002 |
|
g
‖
|
2.001 ± 0.002c |
|
|
|
g
⊥
|
1.991 ± 0.002c |
|
|
|
|
| ZFS (cm−1) |
|
D
|
2.836 ± 0.002c |
2.71 |
2.71 |
|
|
|
(SORCI: 2.90)c |
(SORCI: 2.87)c |
|
E/D |
0.00c |
0.05 |
0.05 |
|
|
|
(SORCI: 0.07)c |
(SORCI: 0.06)c |
When considering computational expenses, the DLPNO-CCSD/aug-cc-pVTZ-J calculation for A, and the DKH2-CASSCF/NEVPT2/aug-cc-pwCVTZ-DK/aug-cc-pVTZ-DK calculation of g and D, each took less than 2 days on our hardware. Even though the coupled-perturbed equations have to be solved for all ligand nuclei in the system, the PBE0/aug-cc-pVTZ-J calculation of the spin–orbit corrections to A required only a few hours. The computations of vibrational corrections to A, with the VPT2 PBE0-D4/cc-pVTZ//PBE0/aug-cc-pVTZ-J method took 10 days, since it required 114 Hessian and property calculations. On the other hand, the computed Hessian and displaced geometries data could be used again for the VPT2 calculation of vibrational corrections to the orbital shielding (this time with the PBE0/pcSseg-2 property evaluation), avoiding repetition of the most time consuming part of the calculation. We also note that the VPT2 approach is much more convenient than setting up molecular dynamics DFT (MD-DFT) simulations and performing calculations of σorb and A for tens or hundreds of system evolution trajectory frames. After collection and evaluation of the obtained A, g, D, and σorb data, the resulting 16 shielding terms contributing to the isotropic 1H and 13C NMR shifts in the eclipsed conformer of vanadocene are shown in Table 6. The largest contributions originated from orbital (σorb) and contact (σcon) terms together with the respective vibrational corrections (σZPVorb and σZPVcon). In the case of 13C, terms originating from the spin–orbit corrections (σcon2) and g-shift tensor (σcon3) made important contributions. The calculated total 1H and 13C NMR shifts were very close to the experimental values (within 2% of error). 1H and 13C NMR shifts for vanadocene have been computed by Kaupp,36 Vaara,20,24 and Autschbach.31 In those studies, the hyperfine tensors were obtained at the DFT level using different implementations (including four-component relativistic approach)24 and several exchange–correlation approximations. The range of previously reported NMR shifts is shown in the last row of Table 6. By including additional physics through the inclusion of electron correlation (DLPNO-CCSD) and vibrational effects (VPT2) we were able to significantly improve the predictions of 1H and 13C NMR shifts in vanadocene. To illustrate better the relative importance of NMR shielding mechanisms in vanadocene, the shielding terms were grouped according to the classification in eqn (7) in Table 7. The contact mechanism had by far the largest contribution to 1H and 13C NMR shifts. Due to the cancellation of σdip and σpc terms the contribution from the pseudocontact mechanism was minimal (see Table 6). To provide an assessment on the necessity to include vibrational and spin–orbit corrections to the predictions of the hyperfine tensor, the summed contributions to induced paramagnetic NMR shielding in vanadocene are shown in Table 8. These shielding contributions originated from the first-order, ZPV, and SO components of A. Components beyond the first-order were significantly more important for 13C than for 1H. Although the first-order components of A already accounted for 94% of the calculated induced paramagnetic 13C NMR shielding for vanadocene, the remaining 6% could easily be imagined to be crucial in situations when many resonances with small shift differences were to be assigned in the spectrum. These contributions relate to the ZPV and SO components of A.
Table 6 Contributions (in ppm) to isotropic 1H and 13C NMR shielding for the eclipsed conformer of vanadocene
| Shielding term |
1H |
13C |
|
From ref. 163.
From ref. 20, 24, 31 and 36.
|
|
σ
orb
|
26.21 |
84.10 |
|
σ
ZPVorb
|
−0.47 |
−4.12 |
|
σ
con
|
−305.88 |
661.61 |
|
σ
ZPVcon
|
−4.86 |
−26.09 |
|
σ
dip
|
0.75 |
3.27 |
|
σ
ZPVdip
|
0.01 |
−0.01 |
|
σ
con2
|
−0.72 |
−12.11 |
|
σ
dip2
|
0.00 |
−0.06 |
|
σ
con3
|
2.38 |
−5.14 |
|
σ
ZPVcon3
|
0.04 |
0.20 |
|
σ
dip3
|
−0.01 |
−0.03 |
|
σ
ZPVdip3
|
0.00 |
0.00 |
|
σ
ca
|
0.01 |
−0.03 |
|
σ
ZPVca
|
0.00 |
0.00 |
|
σ
pc
|
−0.55 |
−2.41 |
|
σ
ZPVpc
|
−0.01 |
0.01 |
|
|
| Total σ |
−283.10 |
699.20 |
|
δ
|
315.91 |
−519.50 |
| Experimenta |
318 |
−510 |
| Previous theoreticalb |
333.3⋯362.8 |
−433.3⋯−218.9 |
Table 7 Contributions (in ppm) to isotropic 1H and 13C NMR shielding for the eclipsed conformer of vanadocene grouped according to the classification in eqn (7)
| Shielding mechanism |
1H |
13C |
| Orbital |
25.74 |
79.98 |
| Contact |
−309.04 |
618.48 |
| Pseudocontact |
0.20 |
0.75 |
Table 8 Origin of contributions to induced isotropic paramagnetic 1H and 13C NMR shielding (in ppm) for the eclipsed conformer of vanadocene
| Contribution origin |
1H |
13C |
| First-order |
−303.29 |
657.28 |
| ZPV |
−4.82 |
−25.89 |
| SO |
−0.73 |
−12.17 |
We expect that the remaining shortcomings and errors in the proposed protocol are dominated by the lack of corrections for the triples excitations (T) and spin–orbit effects within the coupled cluster calculations of A (these are not implemented; the SO part has to be done with DFT), as well as by deficiencies in the DFT level prediction of the orbital part of the shielding. Although the excellent agreement with experimental data for vanadocene indicated that these effects are minor, however, it is not guaranteed to be the case for other systems. The current formalism is limited to the ground-state multiplet, which could cause issues with molecular systems having low-lying excited states. Considering the calculation of σorb, unfortunately no improvements beyond the hydrid DFT level are currently feasible. This is because MP2 and double hybrid DFT (e.g. DSD-PBEP86) are unreliable when applied to calculations of σorb in transition metal complexes, as illustrated in Table S2 (ESI†) for the closed-shell ferrocene molecule. In this molecule, the orbital mechanism is the sole contributor to the 1H and 13C NMR shielding.
4.3 Application to Co(II) biding site in SOD metalloprotein
Usign Co2+ as a spectroscopic surrogate for Zn2+ is established in metallobiochemistry.164 The high-spin d7 Co2+ ion usually adopts a coordination geometry similar to the native Zn2+. The Co2+ allows EPR, paramagnetic NMR, and ENDOR spectroscopies to be used for probing local environments in enzymes and proteins. This approach was employed in the study by Bertarello et al.65 where the geometry of metal-binding site in the thermostable mutant of human superoxide dismutase 1 (SOD) was investigated with magic-angle spinning (MAS) NMR. By probing induced paramagnetic NMR shifts of ligand nuclei, information on the coordination sphere of Co2+ ion in Co-substituted superoxide dismutase (CoSOD) could be obtained, see Fig. 2a. Progress in MAS NMR hardware and radiofrequency irradiation (pulse) schemes together with a very fast MAS rate (100 kHz) enabled improved excitation and detection conditions compared to earlier NMR studies of the same system.165 It was in this way possible to observe resonances from nuclei relatively close to the paramagnetic Co2+ ion. To assign the signals affected by the induced paramagnetic NMR shifts, Bertarello et al. used quantum chemistry methods in a set of 10 models (86 atoms each, labeled from A to J). These models resulted from ten potential binding sites of Zn2+ in ten protein chains derived from the X-ray crystal structure of SOD.166 After Zn2+ → Co2+ substitution, the geometries of the models were optimized with a few constraints to keep the overall fold of the metal ion coordination sphere. Orbital and induced paramagnetic NMR shifts were evaluated for each model: σorb and A at the DFT level, and g and D with the CASSCF/NEVPT2 approach. Calculations of A were performed with the genuine PBE0 functional, and that with the HF admixture increased to 50% (PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX)). Hence, a broad range of NMR shifts was obtained for each nucleus in the model. Only for models C, E, and F, did the calculated ranges of shifts provided agreement with the experimental ones. The authors discussed the dependence of the 13C NMR shift of β-carbon in the Asp83 residue on the bond lengths in the coordination sphere of the Co2+ ion. We took the two most promising models E and F and recalculated the 13Cβ (Asp83) NMR shifts with our protocol that involve coupled cluster calculations of A. To facilitate direct comparison of the (DFT) results from the study by Bertarello et al. and our calculations (DLPNO-CCSD), Fig. 2b and Table 9 were prepared. The ranges of shifts obtained by Bertarello et al. with the PBE0/PBE0(50%
HFX)). Hence, a broad range of NMR shifts was obtained for each nucleus in the model. Only for models C, E, and F, did the calculated ranges of shifts provided agreement with the experimental ones. The authors discussed the dependence of the 13C NMR shift of β-carbon in the Asp83 residue on the bond lengths in the coordination sphere of the Co2+ ion. We took the two most promising models E and F and recalculated the 13Cβ (Asp83) NMR shifts with our protocol that involve coupled cluster calculations of A. To facilitate direct comparison of the (DFT) results from the study by Bertarello et al. and our calculations (DLPNO-CCSD), Fig. 2b and Table 9 were prepared. The ranges of shifts obtained by Bertarello et al. with the PBE0/PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) approach for A were very wide, with a span of around 200 ppm for each model. In contrast, when the DLPNO-CCSD method was employed for the prediction of A, the accuracy and consistency of NMR shift prediction improved remarkably. Considering models E and F, the PBE0/PBE0(50%
HFX) approach for A were very wide, with a span of around 200 ppm for each model. In contrast, when the DLPNO-CCSD method was employed for the prediction of A, the accuracy and consistency of NMR shift prediction improved remarkably. Considering models E and F, the PBE0/PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) calculations provided rather inconclusive chemical shifts ranging from 299 to 531 ppm, whereas with the DLPNO-CCSD approach the values of 337 and 331 ppm were obtained for model E and F, respectively; both very close to the experimental result of 350 ppm. These results suggested that model E might be closer to the real coordination sphere of Co2+ ion in CoSOD. We note however that vibrational corrections to σorb and A could not be evaluated because models derived from the X-ray structure of protein and optimized with constraints did not allow for Hessian evaluations. We checked the DLPNO-CCSD convergence for Model E, and δ for 13Cβ changed only marginally from 337.29 to 337.23 ppm when going from HFC1 to HFC2 thresholds and keeping all other parameters same. This indicated that results for 13Cβ in the Asp83 residue in our calculations were close to the CCSD limit. Larger changes of HFCCs were observed for nuclei directly bonded to the Co2+ ion, however, signals from those nuclei were not observed in the experiments. This presence of a “NMR blind sphere” around the paramagnetic Co2+ ion in CoSOD is indicted in Fig. 2c–e where spin densities rendered with the isodensity of 0.002 e bohr−3 are observed for the donor nitrogen and oxygen atoms. Since the magnetic and EPR properties of CoSOD have been measured,167,168 comparisons of the calculated g and D with experimental results could provide further insights. The calculated isotropic g-values of 2.228 and 2.225 for the models E and F were similar, but that from model E was slightly closer to the experimental result of 2.24. However, the calculated D-values of 5.62 and 4.25 cm−1 for model E and F, respectively, were significantly lower than the experimental estimate of 10.8 cm−1. In general, the ZFS of tetrahedral, high-spin Co2+ complexes is strongly dominated by the SOC interaction,161,169 and errors in the DKH2-CASSCF/NEVPT2 approach are not expected to be significant. Moreover, reported experimental D-values in four-coordinated Co2+ complexes involving nitrogen donors were in the range from 2.4 to 7.5 (cm−1),170,171 which corresponded very well with our theoretical predictions for CoSOD. In the work by Bertarello et al. it was indicated that the experimental estimate of D obtained by fitting of temperature dependent magnetic susceptibility data with susceptibility equations derived by using isotropic g-factors and axial parameters D might not be accurate. Nonetheless, all three: the NMR shift of 13Cβ (Asp83), isotropic g-value, and D parameter indicated that the coordination geometry of model E was the most accurate.
HFX) calculations provided rather inconclusive chemical shifts ranging from 299 to 531 ppm, whereas with the DLPNO-CCSD approach the values of 337 and 331 ppm were obtained for model E and F, respectively; both very close to the experimental result of 350 ppm. These results suggested that model E might be closer to the real coordination sphere of Co2+ ion in CoSOD. We note however that vibrational corrections to σorb and A could not be evaluated because models derived from the X-ray structure of protein and optimized with constraints did not allow for Hessian evaluations. We checked the DLPNO-CCSD convergence for Model E, and δ for 13Cβ changed only marginally from 337.29 to 337.23 ppm when going from HFC1 to HFC2 thresholds and keeping all other parameters same. This indicated that results for 13Cβ in the Asp83 residue in our calculations were close to the CCSD limit. Larger changes of HFCCs were observed for nuclei directly bonded to the Co2+ ion, however, signals from those nuclei were not observed in the experiments. This presence of a “NMR blind sphere” around the paramagnetic Co2+ ion in CoSOD is indicted in Fig. 2c–e where spin densities rendered with the isodensity of 0.002 e bohr−3 are observed for the donor nitrogen and oxygen atoms. Since the magnetic and EPR properties of CoSOD have been measured,167,168 comparisons of the calculated g and D with experimental results could provide further insights. The calculated isotropic g-values of 2.228 and 2.225 for the models E and F were similar, but that from model E was slightly closer to the experimental result of 2.24. However, the calculated D-values of 5.62 and 4.25 cm−1 for model E and F, respectively, were significantly lower than the experimental estimate of 10.8 cm−1. In general, the ZFS of tetrahedral, high-spin Co2+ complexes is strongly dominated by the SOC interaction,161,169 and errors in the DKH2-CASSCF/NEVPT2 approach are not expected to be significant. Moreover, reported experimental D-values in four-coordinated Co2+ complexes involving nitrogen donors were in the range from 2.4 to 7.5 (cm−1),170,171 which corresponded very well with our theoretical predictions for CoSOD. In the work by Bertarello et al. it was indicated that the experimental estimate of D obtained by fitting of temperature dependent magnetic susceptibility data with susceptibility equations derived by using isotropic g-factors and axial parameters D might not be accurate. Nonetheless, all three: the NMR shift of 13Cβ (Asp83), isotropic g-value, and D parameter indicated that the coordination geometry of model E was the most accurate.
Table 9 Calculated 13C NMR shifts (ppm) of β-carbon in the Asp83 residue of CoSOD
| Method for A |
δ
13Cβ(Asp83) |
| Model E |
Model F |
|
From ref. 65.
This work: A DLPNO-CCSD aug-cc-pVTZ-J(Co)/EPR-II(H,C,N); ASO PBE0 aug-cc-pVTZ-J(Co)/EPR-II(H,C,N); g and D at DKH2-CASSCF/NEVPT2 aug-cc-pwCVTZ-DK(Co)/cc-pVDZ-DK(H,C,N).
|
PBE0⋯PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX)a HFX)a |
531⋯340 |
477⋯299 |
| DLPNO-CCSDb |
337.28 |
330.75 |
|
|
| Experimenta |
350 |
5 Conclusions
We improved on the implementation of the Kurland–McGarvey theory for prediction of NMR shifts in paramagnetic systems by using the DLPNO-CCSD method to predict the critical hyperfine coupling tensor A, and by including vibrational corrections to the orbital shielding and the A tensor. The description of the additional physics involved electron correlation and vibrational effects and improved the accuracy and reliability of the calculations over existing protocols. The calculated NMR shifts for vanadocene were within 2% of the experimental result, indicating the importance of vibrational corrections, especially for 13C. For the much larger and challenging model of the CoSOD metalloprotein, the predicted values were within 4% of the experiment. For these calculations, the vibrational corrections could not be calculated, and a smaller basis set had to be used. The advancement over earlier studies is a significant step towards reliable interpretation of NMR spectra from paramagnetic molecular systems. In terms of application of an alternative approach using hybrid DFT methods, the calculations for complexes with transition metal and rare-earth ions indicated that the hybrid DFT approach is not able to reliably predict the HFCCs for the ligand atoms. Manipulation of the Hartree–Fock exchange ratios did not lead to conclusive results, and we advise against this. On the other hand, double hybrid DFT demonstrated systematic improvements, but should be used with caution due to the risk of instabilities associated with deficiencies of the HF and MP2 components in open-shell systems. Finally, predictions of HFCCs with the DLPNO-CCSD method were shown to converge towards the canonical CCSD limit at much lower computational cost. This method exhibited outstanding reliability and consistency for all systems considered in this study. This confirmed that DLPNO-CCSD is the method of choice for calculations of A tensors within the current formalism for the prediction of NMR shifts in paramagnetic systems.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Prof. Juha Vaara (NMR Research Unit, University of Oulu, Finland) is gratefully acknowledged for the initial discussions and suggestions on calculations of EPR and NMR parameters. Computational resources of the Department of Materials and Environmental Chemistry, Stockholm University, are acknowledged. The financial support from the Swedish Research Council through the SwedNMR network is acknowledged.
Notes and references
- N. F. Ramsey, Phys. Rev., 1950, 77, 567 CrossRef CAS.
- N. F. Ramsey, Phys. Rev., 1950, 78, 699–703 CrossRef CAS.
- N. F. Ramsey, Phys. Rev., 1951, 83, 540–541 CrossRef CAS.
- N. F. Ramsey, Phys. Rev., 1952, 86, 243–246 CrossRef CAS.
- N. F. Ramsey, Phys. Rev., 1953, 91, 303–307 CrossRef CAS.
- P. Pyykkö, Theor. Chem. Acc., 2000, 103, 214–216 Search PubMed.
- N. F. Ramsey, Phys. Rev. A: At., Mol., Opt. Phys., 1970, 1, 1320 CrossRef.
- A. M. Kantola, P. Lantto, I. Heinmaa, J. Vaara and J. Jokisaari, Phys. Chem. Chem. Phys., 2020, 22, 8485–8490 RSC.
- K. Wolinski, J. F. Hilton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- T. Helgaker, M. Jaszuński and K. Ruud, Chem. Rev., 1999, 99, 293–352 CrossRef CAS PubMed.
- J. Vaara, Phys. Chem. Chem. Phys., 2007, 77, 5399–5418 RSC.
- T. Kupka, M. Stachów, M. Nieradka, J. Kaminsky and T. Pluta, J. Chem. Theory Comput., 2010, 6, 1580–1589 CrossRef CAS PubMed.
- T. Kupka, M. Stachów, M. Nieradka, J. Kaminsky, T. Pluta and S. P. A. Sauer, Magn. Reson. Chem., 2011, 49, 231–236 CrossRef CAS PubMed.
- T. Kupka, M. Nieradka, M. Stachów, T. Pluta, P. Nowak, H. Kjær, J. Kongsted and J. Kaminsky, J. Phys. Chem. A, 2012, 116, 3728–3738 CrossRef CAS PubMed.
- J. C. Ott, E. A. Suturina, I. Kuprov, J. Nehrkorn, A. Schnegg, M. Enders and L. H. Gade, Angew. Chem., Int. Ed., 2021, 60, 22856–22864 CrossRef CAS PubMed.
- M. Allegrozzi, I. Bertini, M. B. L. Janik, Y. M. Lee, G. Liu and C. Luchinat, J. Am. Chem. Soc., 2000, 122, 4154–4161 CrossRef CAS.
- I. Bertini, C. Luchinat and G. Parigi, Concepts Magn. Reson., 2002, 14, 259–286 CrossRef CAS.
- Z. Rinkevicius, J. Vaara, L. Telyantyk and O. Vahtras, J. Chem. Phys., 2003, 118, 2550 CrossRef CAS.
- T. O. Pennanen and J. Vaara, J. Chem. Phys., 2005, 123, 174102 CrossRef PubMed.
- T. O. Pennanen and J. Vaara, Phys. Rev. Lett., 2008, 100, 133002 CrossRef PubMed.
- S. A. Rouf, J. Mareš and J. Vaara, J. Chem. Theory Comput., 2015, 11, 1683–1691 CrossRef CAS PubMed.
- J. Vaara, S. A. Rouf and J. Mareš, J. Chem. Theory Comput., 2015, 11, 4840–4849 CrossRef CAS PubMed.
- L. Benda, J. Mareš, E. Ravera, G. Parigi, C. Luchinat, M. Kaupp and J. Vaara, Angew. Chem., 2016, 128, 14933–14937 CrossRef.
- S. A. Rouf, J. Mareš and J. Vaara, J. Chem. Theory Comput., 2017, 13, 3731–3745 CrossRef CAS PubMed.
- J. Mareš and J. Vaara, Phys. Chem. Chem. Phys., 2018, 20, 22547–22555 RSC.
- W. Van den Heuvel and A. Soncini, Phys. Rev. Lett., 2012, 109, 073001 CrossRef PubMed.
- A. Soncini and W. Van den Heuvel, J. Chem. Phys., 2013, 138, 021103 CrossRef PubMed.
- W. Van den Heuvel and A. Soncini, J. Chem. Phys., 2013, 138, 054113 CrossRef PubMed.
- J. Autschbach, S. Patchkovskii and B. Pritchard, J. Chem. Theory Comput., 2011, 7, 2175–2188 CrossRef CAS PubMed.
- B. Pritchard and J. Autschbach, Inorg. Chem., 2012, 51, 8340–8351 CrossRef CAS PubMed.
- F. Aquino, B. Pritchard and J. Autschbach, J. Chem. Theory Comput., 2012, 8, 598–609 CrossRef CAS PubMed.
- B. Martin and J. Autschbach, J. Chem. Phys., 2015, 142, 054108 CrossRef PubMed.
- F. Gendron, K. Sharkas and J. Autschbach, J. Phys. Chem. Lett., 2015, 6, 2183–2188 CrossRef CAS PubMed.
- B. Martin and J. Autschbach, Phys. Chem. Chem. Phys., 2016, 18, 21051–21068 RSC.
- A. V. Arbuznikov, J. Vaara and M. Kaupp, J. Chem. Phys., 2004, 120, 2127 CrossRef CAS PubMed.
- P. Hrobárik, R. Reviakine, A. V. Arbuznikov, O. L. Malkina, V. G. Malkin, F. H. Köhler and M. Kaupp, J. Chem. Phys., 2007, 126, 024107 CrossRef PubMed.
- L. Lang Ravera, G. Parigi, C. Luchinat and F. Neese, J. Phys. Chem. Lett., 2020, 15, 8735–8744 CrossRef PubMed.
- E. Ravera, L. Gigli, B. Czarniecki, R. Lang, L. Kümmerle, G. Parigi, F. Neese and C. Luchinat, Inorg. Chem., 2021, 60, 2068–2075 CrossRef PubMed.
- R. J. Kurland and B. R. McGarvey, J. Magn. Reson., 1970, 2, 286–301 CAS.
-
S. Moon and S. Patchkovskii, Calculation of NMR and EPR Parameters: Theory and Applications, Wiley-VCH, Weinheim, 2004 Search PubMed.
- S. A. Rouf, V. B. Jakobsen, J. Mareš, N. D. Jensen, C. J. McKenzie, J. Vaara and U. G. Nielsen, Solid State Nucl. Magn. Reson., 2017, 87, 29–37 CrossRef CAS PubMed.
- A. Pyykkönen, R. Feher, F. Köhler and J. Vaara, Inorg. Chem., 2020, 59, 9294–9307 CrossRef PubMed.
- A. B. Andersen, A. Pyykkönen, H. J. Jensen, V. McKee, J. Vaara and U. G. Nielsen, Phys. Chem. Chem. Phys., 2020, 22, 8048–8059 RSC.
- S. Jiang, D. Maganas, N. Levesanos, E. Ferentinos, S. Haas, K. Thirunavukkuarasu, J. Krzystek, M. Dressel, L. Bogani and F. Neese, J. Am. Chem. Soc., 2015, 137, 12923–12928 CrossRef CAS PubMed.
- C. Angeli and R. Cimiraglia, Theor. Chem. Acc., 2002, 107, 313–317 Search PubMed.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138 CrossRef CAS.
- S. Ye and F. Neese, J. Chem. Theory Comput., 2012, 8, 2344–2351 CrossRef CAS PubMed.
- D. Ganyushin and F. Neese, J. Chem. Phys., 2013, 138, 104113 CrossRef PubMed.
- S. K. Singh, M. Anatasov and F. Neese, J. Chem. Theory Comput., 2018, 14, 4662–4677 CrossRef CAS PubMed.
- F. Neese, T. Schwabe, S. Kossmann, B. Schirmer and S. Grimme, J. Chem. Theory Comput., 2009, 5, 3060–3073 CrossRef CAS PubMed.
- S. Kossmann and F. Neese, J. Phys. Chem. A, 2010, 114, 11768–11781 CrossRef CAS PubMed.
- B. Sandhoefer, S. Kossmann and F. Neese, J. Chem. Phys., 2013, 138, 104102 CrossRef PubMed.
- A. J. Cohen, P. Mori-Sanchez and W. Yang, Science, 2008, 321, 792–794 CrossRef CAS PubMed.
- T. Z. H. Gani and H. J. Kulik, J. Chem. Theory Comput., 2016, 12, 5931–5945 CrossRef CAS PubMed.
- C. J. Schattenberg, T. M. Maier and M. Kaupp, J. Chem. Theory Comput., 2018, 14, 5653–5672 CrossRef CAS PubMed.
- R. Improta and V. Barone, Chem. Rev., 2004, 104, 1231–1254 CrossRef CAS PubMed.
- V. Barone and P. Cimino, Chem. Phys. Lett., 2008, 454, 139–143 CrossRef CAS.
- S. Kossmann, B. Kirchner and F. Neese, Mol. Phys., 2007, 105, 2049–2071 CrossRef CAS.
- M. Witwicki, P. K. Walencik and J. Jezierska, J. Mol. Model., 2020, 138, 104113 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982 CrossRef CAS.
- C. Adamo and V. Barone, Chem. Phys. Lett., 1997, 274, 242–250 CrossRef CAS.
- A. Bertarello, L. Benda, K. J. Sanders, A. J. Pell, M. J. Knight, V. Pelmenschikov, L. Gonnelli, I. C. Felli, M. Kaupp, L. Emsley, R. Pierattelli and G. Pintacuda, J. Am. Chem. Soc., 2020, 142, 16757–16765 CrossRef CAS PubMed.
- J. Blahut, L. Benda, A. L. Lejeune, K. J. Sanders, E. Burcher, B. Jeanneau, D. Proriol, L. Catita, P. A. R. Breuil, A. J. Quoineaud, A. A. Pell and G. Pintacuda, RSC Adv., 2021, 11, 29870–29876 RSC.
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- F. Coester and H. Kümmel, Nucl. Phys., 1960, 17, 477–485 CrossRef CAS.
- J. Čížek, J. Chem. Phys., 1966, 45, 4256 CrossRef.
- J. Paldus, J. Čížek and I. Shavitt, Phys. Rev. A: At., Mol., Opt. Phys., 1972, 5, 50 CrossRef.
- R. J. Bartlett and G. D. Purvis, Int. J. Quantum Chem., 1978, 14, 561–581 CrossRef CAS.
- R. J. Bartlett and G. D. Purvis, Phys. Scr., 1980, 21, 255 CrossRef CAS.
- D. I. Lyakh, M. Musiał, V. F. Lotrich and R. J. Bartlett, Chem. Rev., 2012, 112, 182–243 CrossRef CAS PubMed.
- J. Wang, S. Manivasagam and A. K. Wilson, J. Chem. Phys., 2015, 155, 014105 Search PubMed.
- T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199–207 CrossRef.
- T. J. Lee, J. E. Rice, G. E. Scuseria and H. F. Schaefer, Theor. Chim. Acta, 1989, 75, 81–98 CrossRef CAS.
- W. Jiang, N. J. DeYonker and A. K. Wilson, J. Chem. Theory Comput., 2012, 8, 460–468 CrossRef CAS PubMed.
- J. Wang, S. Manivasagam and A. K. Wilson, J. Chem. Theory Comput., 2015, 11, 5865–5872 CrossRef CAS PubMed.
- S. A. Perera, J. D. Watts and R. J. Bartlett, J. Chem. Phys., 1994, 100, 1425 CrossRef CAS.
- M. Kaupp, A. V. Arbuznikov, A. Heßelmann and A. Görling, J. Chem. Phys., 2010, 132, 184107 CrossRef.
- P. Verma, A. Perera and J. A. Morales, J. Chem. Phys., 2013, 139, 174103 CrossRef PubMed.
- D. Datta and J. Gauss, J. Chem. Theory Comput., 2019, 15, 1572–1592 CrossRef CAS PubMed.
- M. Munzarová and M. Kaupp, J. Phys. Chem. A, 1999, 103, 9966–9983 CrossRef.
- F. Neese, J. Chem. Phys., 2003, 118, 3939 CrossRef CAS.
- C. Puzzarini and V. Barone, J. Chem. Phys., 2010, 133, 184301 CrossRef PubMed.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- C. Riplinger, P. Pinski, U. Becker, E. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov and F. Neese, J. Chem. Phys., 2018, 148, 011101 CrossRef PubMed.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. L. Martin and F. Neese, J. Chem. Theory Comput., 2015, 11, 1525–1539 CrossRef CAS PubMed.
- M. Sparta, M. Retegan, P. Pinski, C. Riplinger, U. Becker and F. Neese, J. Chem. Theory Comput., 2017, 13, 3198–3207 CrossRef CAS PubMed.
- F. Neese, M. Atanasov, G. Bistoni, D. Maganas and S. Ye, J. Am. Chem. Soc., 2019, 141, 2814–2824 CrossRef CAS PubMed.
- D. Liakos, Y. Guo and F. Neese, J. Phys. Chem. A, 2020, 124, 90–100 CrossRef CAS PubMed.
- A. Jaworski and N. Hedin, Phys. Chem. Chem. Phys., 2021, 23, 21554–21567 RSC.
- M. Saitow, U. Becker, C. Riplinger, E. F. Valeev and F. Neese, J. Chem. Phys., 2017, 146, 164105 CrossRef PubMed.
- Y. Guo, C. Riplinger, D. G. Liakos, U. Becker, M. Saitow and F. Neese, J. Chem. Phys., 2020, 152, 024116 CrossRef CAS PubMed.
- M. Saitow and F. Neese, J. Chem. Phys., 2018, 149, 034104 CrossRef PubMed.
- A. A. Auer, V. A. Tran, B. Sharma, G. L. Stoychev, D. Marx and F. Neese, Mol. Phys., 2020, 118, e1797916 CrossRef.
- O. I. Gromov, J. Mol. Model., 2021, 27, 194 CrossRef CAS PubMed.
- Z. Ma, C. Lu, J. Chen, A. Rokicińska, R. Kuśtrowski, P. Coridan, R. Dronskowski, A. Slabon and A. Jaworski, Z. Naturforsch., 2021, 76((5)b), 275–280 CrossRef CAS.
- A. Jaworski, J. Piatek, L. Mereacre, C. Braun and A. Slabon, Z. Naturforsch., 2021, 76((10–12)b), 745–750 CrossRef CAS.
- B. Sharma, V. A. Tran, T. Pongratz, L. Galazzo, I. Zhurko, E. Bordignon, S. M. Kast, F. Neese and D. Marx, J. Chem. Theory Comput., 2021, 17, 6366–6386 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 73–78 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2017, 13, 554–562 CrossRef CAS PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, J. Chem. Phys., 1999, 110, 7667 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- R. Gulde, P. Pollak and F. Weigend, J. Chem. Theory Comput., 2012, 8, 4062–4068 CrossRef CAS PubMed.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef CAS.
- K. A. Peterson and T. H. Dunning, J. Chem. Phys., 2002, 117, 10548 CrossRef CAS.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS.
- C. Hättig, Phys. Chem. Chem. Phys., 2005, 7, 59–66 RSC.
- F. Jensen, J. Chem. Theory Comput., 2015, 11, 132–138 CrossRef CAS PubMed.
- A. Antušek, K. Jackowski, M. Jaszuński, W. Makulski and M. Wilczek, Chem. Phys. Lett., 2005, 411, 111–116 CrossRef.
- P. F. Provasi, G. A. Aucar and S. P. A. Sauer, J. Chem. Phys., 2001, 115, 614–620 CrossRef.
- E. D. Hedegård, J. Kongsted and S. P. A. Sauer, J. Chem. Theory Comput., 2011, 7, 4077–4087 CrossRef PubMed.
-
V. Barone, Recent Advances in Density Functional Methods, Part I, World Scientific Publ. Co., Singapore, 1995 Search PubMed.
- N. Rega, M. Cossi and V. Barone, J. Chem. Phys., 1996, 105, 11060 CrossRef CAS.
- N. Rega, M. Cossi and V. Barone, J. Am. Chem. Soc., 1997, 119, 12960–12967 CrossRef.
- N. Rega, M. Cossi and V. Barone, J. Am. Chem. Soc., 1998, 120, 5723–5732 CrossRef CAS.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2009, 37, 2360–2373 Search PubMed.
- D. Paschoal, C. Guerra Fonseca, M. A. L. de Oliveira, T. C. Ramalho and H. F. Dos Santos, J. Comput. Chem., 2016, 5, 2229–2238 Search PubMed.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 756 CrossRef CAS PubMed.
- B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 333, 3742 CrossRef PubMed.
- G. Jansen and B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 6016 CrossRef PubMed.
- L. Visscher and K. G. Dyall, At. Data Nucl. Data Tables, 1997, 67, 207–224 CrossRef CAS.
- N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 64107 CrossRef PubMed.
- W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48 CrossRef CAS.
- A. R. Jaszewski, J. Jezierska and A. Jezierski, Chem. Phys. Lett., 2000, 319, 611–617 CrossRef CAS.
- L. Hermosilla, P. Calle, J. M. Garcia de la Vega and C. Sieiro, J. Phys. Chem. A, 2006, 110, 13600–13608 CrossRef CAS PubMed.
- A. Rogowska, S. Kuhl, R. Schneider, A. Walcariuse and B. Champagne, Phys. Chem. Chem. Phys., 2007, 9, 828–836 RSC.
- L. Hermosilla, J. M. García de la Vega, C. Sieiro and P. Calle, J. Chem. Theory Comput., 2011, 7, 169–179 CrossRef CAS PubMed.
- S. Saito and S. Yamamoto, J. Chem. Phys., 1997, 107, 1732 CrossRef CAS.
- H. Ozeki, S. Hirao, S. Saito and S. Yamamoto, Astrophys. J., 2004, 617, 680–684 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 15, 3865 CrossRef PubMed.
- D. Baute and D. Goldfarb, J. Phys. Chem. A, 2005, 109, 7865–7871 CrossRef CAS PubMed.
- C. Cossy, L. Helm and A. E. Merbach, Inorg. Chem., 1988, 27, 1973–1979 CrossRef CAS.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- S. Kozuch and J. M. L. Martin, Phys. Chem. Chem. Phys., 2011, 13, 20104–20107 RSC.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2018, 14, 4756–4771 CrossRef CAS PubMed.
- P. Rzepka, Z. Bacsik, A. J. Pell, N. Hedin and A. Jaworski, J. Phys. Chem. C, 2019, 123, 21497–21503 CrossRef CAS.
- A. Dittmer, G. L. Stoychev, D. Maganas, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2020, 16, 6950–6967 CrossRef CAS PubMed.
- I. Szewczyk, A. Rokicińska, M. Michalik, C. Jianhong, A. Jaworski, R. Aleksis, A. J. Pell, N. Hedin, A. Slabon and P. Kuśtrowski, Chem. Mater., 2020, 32, 7263–7273 CrossRef CAS.
- C. J. Schattenberg and M. Kaupp, J. Chem. Theory Comput., 2021, 17, 7602–7621 CrossRef CAS PubMed.
- E. Gard, A. Haaland, D. P. Novak and R. Seip, J. Organomet. Chem., 1975, 88, 181–189 CrossRef CAS.
- R. D. Rogers, J. L. Atwood, F. Foust and M. D. Rausch, J. Cryst. Mol. Struct., 1981, 11, 183–188 CrossRef CAS.
- M. Y. Antipin and R. Boese, Acta Crystallogr., Sect. B: Struct. Sci., 1996, 52, 314–322 CrossRef.
- F. Neese, J. Chem. Phys., 2003, 119, 9428 CrossRef CAS.
- F. Neese, Magn. Reson. Chem., 2004, 42, 187–198 CrossRef PubMed.
- F. Neese, J. Am. Chem. Soc., 2006, 128, 10213–10222 CrossRef CAS PubMed.
- D. M. Liakos, D. Ganyushin and F. Neese, Inorg. Chem., 2009, 48, 10572–10580 CrossRef CAS PubMed.
- S. Ye, F. Neese, A. Ozarowski, D. Smirnov, J. Krzystek, J. Telser, J.-H. Liao, C.-H. Hung, W.-C. Chu, Y.-F. Tsai, R.-C. Wang, K.-Y. Chen and H.-F. Hsu, Inorg. Chem., 2010, 49, 977–988 CrossRef CAS PubMed.
- D. Maganas, S. Sottini, P. Kyritsis, E. J. J. Groenen and F. Neese, Inorg. Chem., 2011, 50, 8741–8754 CrossRef CAS PubMed.
- T. A. Jackson, J. Krzystek, A. Ozarowski, G. B. Wijeratne, B. F. Wicker, D. J. Mindiola and J. Telser, Organometallics, 2012, 31, 8265–8274 CrossRef CAS.
- F. H. Köhler and X. Xie, Magn. Reson. Chem., 1997, 35, 487–492 CrossRef.
-
R. R. Baum, C. D. James and D. L. Tierney, Future Directions in Metalloprotein and Metalloenzyme Research, Springer International Publishing, 2017 Search PubMed.
- I. Bertini, C. Luchinat and M. Piccioli, Prog. Nucl. Magn. Reson. Spectrosc., 1994, 26, 91–139 CrossRef CAS.
- H. E. Parge, R. A. Hallewell and J. A. Tainer, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 6109–6113 CrossRef CAS PubMed.
- G. Rotilio, L. Calabrese, B. Mondovi and W. E. Blumberg, J. Biol. Chem., 1974, 249, 3157–3160 CrossRef CAS PubMed.
- I. Morgenstern-Badarau, D. Coceo, A. Desideri, G. Rotilio, J. Jordanov and N. Dupre, J. Am. Chem. Soc., 1986, 108, 300–302 CrossRef CAS.
- M. Sundararajan, D. Ganyushin, S. Ye and F. Neese, Dalton Trans., 2009, 6021–6036 RSC.
- J. A. Larrabee, C. M. Alessi, E. Asiedu, J. O. Cook, K. R. Hoerning, L. J. Klingler, G. S. Okin, S. G. Santee and T. L. Volkert, J. Am. Chem. Soc., 1997, 119, 4182–4196 CrossRef CAS.
- J. Krzystek, D. C. Swenson, S. A. Zvyagin, D. Smirnov, A. Ozarowski and J. Telser, J. Am. Chem. Soc., 2010, 132, 5241–5253 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
Niklas
Hedin
* and
Niklas
Hedin

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + δcontact
+ δcontact![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + δpseudocontact
+ δpseudocontact![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm.15 The pseudocontact shift (PCS, pseudocontact) is a long-range term (1/r3) from the electron–nucleus dipolar coupling and magnetic anisotropy of the paramagnetic center. Paramagnetic ions can induce PCS effects for NMR active nuclei at distances of 25–40 Å.16,17 However, at close distances to the paramagnetic center (≲8 Å) both mechanisms are effective, and can shift NMR signals in either (positive or negative) direction. As a result, the theoretical prediction of induced paramagnetic NMR shifts is critical for exploring the local structure and chemical surroundings of nuclei in paramagnetic systems.
000 ppm.15 The pseudocontact shift (PCS, pseudocontact) is a long-range term (1/r3) from the electron–nucleus dipolar coupling and magnetic anisotropy of the paramagnetic center. Paramagnetic ions can induce PCS effects for NMR active nuclei at distances of 25–40 Å.16,17 However, at close distances to the paramagnetic center (≲8 Å) both mechanisms are effective, and can shift NMR signals in either (positive or negative) direction. As a result, the theoretical prediction of induced paramagnetic NMR shifts is critical for exploring the local structure and chemical surroundings of nuclei in paramagnetic systems.
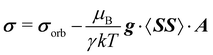
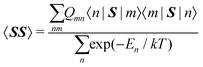
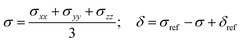
![[g with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0067_0303.gif)
![[g with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0067_0303.gif) are the isotropic and anisotropic parts of the g-shift tensor (deviation from ge). By evaluation of the respective components of A and g tensors the total NMR shift can be expressed as a sum of 17 physical contributions listed in Table 1. The antisymmetric σas term does not contribute to isotropic shielding, and only provides corrections to the shielding anisotropy. Note that to this end, vibrational effects were not considered in calculations of induced paramagnetic NMR shifts within the Kurland–McGarvey theory. Therefore, the seven shielding terms due to vibrational corrections (σZPVorb, σZPVcon, σZPVcon3, σZPVdip, σZPVdip3, σZPVca, σZPVpc) have not been evaluated before in other studies. The shielding terms in Table 1 can be grouped together and in this notation, they approximate the nomenclature used in experimental studies.
are the isotropic and anisotropic parts of the g-shift tensor (deviation from ge). By evaluation of the respective components of A and g tensors the total NMR shift can be expressed as a sum of 17 physical contributions listed in Table 1. The antisymmetric σas term does not contribute to isotropic shielding, and only provides corrections to the shielding anisotropy. Note that to this end, vibrational effects were not considered in calculations of induced paramagnetic NMR shifts within the Kurland–McGarvey theory. Therefore, the seven shielding terms due to vibrational corrections (σZPVorb, σZPVcon, σZPVcon3, σZPVdip, σZPVdip3, σZPVca, σZPVpc) have not been evaluated before in other studies. The shielding terms in Table 1 can be grouped together and in this notation, they approximate the nomenclature used in experimental studies.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–˙CH2 was calculated. The nitrogen atom is in general challenging for calculations of EPR/NMR parameters. For example, the CCSD(T) level of theory was needed to provide quantitative agreement with experimental estimates for the HFCC of the nitrogen atom in its ground state80 or NMR shielding in the N
C–˙CH2 was calculated. The nitrogen atom is in general challenging for calculations of EPR/NMR parameters. For example, the CCSD(T) level of theory was needed to provide quantitative agreement with experimental estimates for the HFCC of the nitrogen atom in its ground state80 or NMR shielding in the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N molecule.13 Previous DFT studies on nitrogen containing organic radicals have revealed that the results depend on the particular choice of the exchange–correlation functional and the basis set, which often have led to fortuitous cancellation of errors.58,135–138 Second, we considered challenging calculations of both metal and ligand-related HFCCs in transition metal complexes: [V(H2O)6]2+, [Cr(H2O)6]3+, and [Mn(H2O)6]2+. Although the spin–orbit contributions to the hyperfine tensor cannot be currently assessed at the DLPNO-CCSD level, these are expected to be small for high-spin d3 and d5 configurations of the V2+, Cr3+, and Mn2+ ions.84,97 As the last, yet the most challenging system, a RE metal ion complex was considered: [Yb(H2O)8]3+.
N molecule.13 Previous DFT studies on nitrogen containing organic radicals have revealed that the results depend on the particular choice of the exchange–correlation functional and the basis set, which often have led to fortuitous cancellation of errors.58,135–138 Second, we considered challenging calculations of both metal and ligand-related HFCCs in transition metal complexes: [V(H2O)6]2+, [Cr(H2O)6]3+, and [Mn(H2O)6]2+. Although the spin–orbit contributions to the hyperfine tensor cannot be currently assessed at the DLPNO-CCSD level, these are expected to be small for high-spin d3 and d5 configurations of the V2+, Cr3+, and Mn2+ ions.84,97 As the last, yet the most challenging system, a RE metal ion complex was considered: [Yb(H2O)8]3+.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX)) severely deteriorated the predictions of both Acon and χ when compared to the original PBE0 formulation. The last step on the Jacob's ladder for DFT approximations consists of double hybrid, “perturbatively corrected” exchange–correlation functionals that incorporate an exact HF exchange component and a perturbative second-order correlation contribution.145 The double hybrid DSD-PBEP86 functional146 that incorporates HF exchange, PBE and P86 exchange and correlation potentials, as well as spin-component-scaled (SCS) MP2 mixing, constitutes one of the most accurate DFT methods for general chemistry applications.147 It is also known to provide excellent predictions of NMR shifts in closed-shell systems of main group elements.101,148–152 However, as shown in Table 2, for the case of cyanomethyl radicals the DSD-PBEP86 functional suffered from instabilities that resulted in erratic spin density on the nitrogen atom. Special care has to be taken when applying double hybrid functionals to open-shell systems.60 This also indicated that in general, no systematic improvements for prediction of the hyperfine coupling constants were feasible within the current DFT framework.61 The Hartree–Fock and MP2/SCS-MP2 methods provided essentially erratic results, and values obtained with MP2 and its SCS-MP2 variant were similar. Orbital optimization (OO-MP2/OO-SCS-MP2) remarkably improved the results by removing spin contamination of the reference wavefunction, however, the predicted HFCCs were still far from experimental ones. The robustness of the CCSD level of theory was clearly necessary to provide good agreement with experimental data for the N
HFX)) severely deteriorated the predictions of both Acon and χ when compared to the original PBE0 formulation. The last step on the Jacob's ladder for DFT approximations consists of double hybrid, “perturbatively corrected” exchange–correlation functionals that incorporate an exact HF exchange component and a perturbative second-order correlation contribution.145 The double hybrid DSD-PBEP86 functional146 that incorporates HF exchange, PBE and P86 exchange and correlation potentials, as well as spin-component-scaled (SCS) MP2 mixing, constitutes one of the most accurate DFT methods for general chemistry applications.147 It is also known to provide excellent predictions of NMR shifts in closed-shell systems of main group elements.101,148–152 However, as shown in Table 2, for the case of cyanomethyl radicals the DSD-PBEP86 functional suffered from instabilities that resulted in erratic spin density on the nitrogen atom. Special care has to be taken when applying double hybrid functionals to open-shell systems.60 This also indicated that in general, no systematic improvements for prediction of the hyperfine coupling constants were feasible within the current DFT framework.61 The Hartree–Fock and MP2/SCS-MP2 methods provided essentially erratic results, and values obtained with MP2 and its SCS-MP2 variant were similar. Orbital optimization (OO-MP2/OO-SCS-MP2) remarkably improved the results by removing spin contamination of the reference wavefunction, however, the predicted HFCCs were still far from experimental ones. The robustness of the CCSD level of theory was clearly necessary to provide good agreement with experimental data for the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–˙CH2. We noted however that the CCSD seemed to slightly overestimate the 14N hyperfine coupling in cyanomethyl radical. This was attributed to the lack of perturbative triple correction (CCSD(T)) that was shown to slightly lower the HFCCs predictions compared to CCSD.82 Before we discuss the predictions with the DLPNO-CCSD method, we add a remark. To facilitate the accuracy and performance control of the DLPNO-CCSD calculations, five levels of predefined PNO truncation settings have been developed: LoosePNO, NormalPNO, TightPNO, HFC1, and HFC2. These settings provide convergence towards the canonical limit at increasing computational cost,90,97 by invoking refined thresholds for the electron pair correlation energies evaluation. Essential pairs are selected for accurate coupled cluster treatment, and those pairs with a less critical contribution to the total correlation energy are subjected to a much more computationally efficient second-order perturbation theory. The LoosePNO, NormalPNO, and TightPNO thresholds were designed for general chemistry applications, i.e. evaluations of total energies or intermolecular interactions. The tighter HFC1 and HFC2 settings were specifically developed for calculations of hyperfine coupling constants. As shown in Table 2, for predictions of the 14N quadrupolar coupling constants both the HFC1 and HFC2 settings provided converged results of CCSD quality. They were clearly better than those from hybrid DFT. However, the convergence for the prediction of the 14N hyperfine coupling constants was more difficult to achieve. With the HFC1 setup full convergence was not achieved and the more conservative (and expensive) HFC2 setting was needed to provide results close to the CCSD reference. This in turn indicated that electron correlation effects in N
C–˙CH2. We noted however that the CCSD seemed to slightly overestimate the 14N hyperfine coupling in cyanomethyl radical. This was attributed to the lack of perturbative triple correction (CCSD(T)) that was shown to slightly lower the HFCCs predictions compared to CCSD.82 Before we discuss the predictions with the DLPNO-CCSD method, we add a remark. To facilitate the accuracy and performance control of the DLPNO-CCSD calculations, five levels of predefined PNO truncation settings have been developed: LoosePNO, NormalPNO, TightPNO, HFC1, and HFC2. These settings provide convergence towards the canonical limit at increasing computational cost,90,97 by invoking refined thresholds for the electron pair correlation energies evaluation. Essential pairs are selected for accurate coupled cluster treatment, and those pairs with a less critical contribution to the total correlation energy are subjected to a much more computationally efficient second-order perturbation theory. The LoosePNO, NormalPNO, and TightPNO thresholds were designed for general chemistry applications, i.e. evaluations of total energies or intermolecular interactions. The tighter HFC1 and HFC2 settings were specifically developed for calculations of hyperfine coupling constants. As shown in Table 2, for predictions of the 14N quadrupolar coupling constants both the HFC1 and HFC2 settings provided converged results of CCSD quality. They were clearly better than those from hybrid DFT. However, the convergence for the prediction of the 14N hyperfine coupling constants was more difficult to achieve. With the HFC1 setup full convergence was not achieved and the more conservative (and expensive) HFC2 setting was needed to provide results close to the CCSD reference. This in turn indicated that electron correlation effects in N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–˙CH2 are substantial.
C–˙CH2 are substantial.![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–˙CH2 calculated with different methods using the aug-cc-pVTZ-J basis set
C–˙CH2 calculated with different methods using the aug-cc-pVTZ-J basis set
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX)
HFX)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) approximations were lower than the experimental values. The double hybrid DSD-PBEP86 approximation did offer improvements, and the predictions with this functional were generally closer to the experimental values than those with hybrid DFT. Considering the ab initio methods, HF was expected to overestimate hyperfine couplings, although this effect was much smaller for the TM complexes than for the cyanomethyl radical. The predictions with MP2 and orbital-optimized MP2 were quite close to the experimental values. The values were notably closer than those calculated with DFT, with the exception of 55Mn. Finally, both the CCSD and DLPNO-CCSD predictions were in good agreement with the experimental results for 51V and 53Cr, with somewhat larger deviations for 55Mn, which might be attributed to the lack of triples correction. Although the results for the radical and metal hyperfine couplings provide an assessment of the applicability of the respective computational methods, the accuracy for the prediction of EPR and NMR properties of the ligand atoms in the TM and RE complexes is the most important, from the point of view of practical calculations for the prediction of induced paramagnetic shifts. Let us focus first on the 17O isotropic hyperfine coupling constant (Acon) in [Mn(H2O)6]2+, for which experimental result is available. Both the CCSD and DLPNO-CCSD methods provided excellent predictions that were almost exact matches with experimental data. The MP2 and OO-MP2 results were also close, whereas the HF values deviated. When it comes to DFT, predictions with the LSDA and PBE approximations resulted in severe errors. Also, the calculations with the PBE0 and PBE0(50%
HFX) approximations were lower than the experimental values. The double hybrid DSD-PBEP86 approximation did offer improvements, and the predictions with this functional were generally closer to the experimental values than those with hybrid DFT. Considering the ab initio methods, HF was expected to overestimate hyperfine couplings, although this effect was much smaller for the TM complexes than for the cyanomethyl radical. The predictions with MP2 and orbital-optimized MP2 were quite close to the experimental values. The values were notably closer than those calculated with DFT, with the exception of 55Mn. Finally, both the CCSD and DLPNO-CCSD predictions were in good agreement with the experimental results for 51V and 53Cr, with somewhat larger deviations for 55Mn, which might be attributed to the lack of triples correction. Although the results for the radical and metal hyperfine couplings provide an assessment of the applicability of the respective computational methods, the accuracy for the prediction of EPR and NMR properties of the ligand atoms in the TM and RE complexes is the most important, from the point of view of practical calculations for the prediction of induced paramagnetic shifts. Let us focus first on the 17O isotropic hyperfine coupling constant (Acon) in [Mn(H2O)6]2+, for which experimental result is available. Both the CCSD and DLPNO-CCSD methods provided excellent predictions that were almost exact matches with experimental data. The MP2 and OO-MP2 results were also close, whereas the HF values deviated. When it comes to DFT, predictions with the LSDA and PBE approximations resulted in severe errors. Also, the calculations with the PBE0 and PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) functionals were not able to approach the experimental result. In fact, considering the results for ligand atoms for all systems in Table 3, the predictions with the PBE0 and PBE0(50%
HFX) functionals were not able to approach the experimental result. In fact, considering the results for ligand atoms for all systems in Table 3, the predictions with the PBE0 and PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) functionals never encompassed experimental results or the CCSD predictions. Furthermore, the effect of increasing the HF exchange admixture was not always beneficial. It deteriorated the predictions for [V(H2O)6]2+ and [Cr(H2O)6]3+ as compared to the genuine PBE0 formulation. The predictions as presented in Table 3 suggested that it is not possible to assess the intrinsic DFT errors in the prediction of HFCCs by performing computations with PBE0 and PBE0(50%
HFX) functionals never encompassed experimental results or the CCSD predictions. Furthermore, the effect of increasing the HF exchange admixture was not always beneficial. It deteriorated the predictions for [V(H2O)6]2+ and [Cr(H2O)6]3+ as compared to the genuine PBE0 formulation. The predictions as presented in Table 3 suggested that it is not possible to assess the intrinsic DFT errors in the prediction of HFCCs by performing computations with PBE0 and PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) approximations. Predictions of properties with hybrid DFT for the ligand atoms were inconclusive as shown in Table 3, and for the RE complex, it was not even possible to establish the sign of the coupling constant. In contrast, the predictions performed with the double hybrid DSD-PBEP86 functional consistently improved on the hybrid DFT, although the deviations from experimental values or reference CCSD calculations were still significant. The results for [Yb(H2O)8]3+ displayed an even more complicated pattern. The predictions performed by LSDA, PBE, and PBE0 provided erratic values. For this complex, the DFT-based calculations benefited from high HF exchange admixtures. PBE0(50%
HFX) approximations. Predictions of properties with hybrid DFT for the ligand atoms were inconclusive as shown in Table 3, and for the RE complex, it was not even possible to establish the sign of the coupling constant. In contrast, the predictions performed with the double hybrid DSD-PBEP86 functional consistently improved on the hybrid DFT, although the deviations from experimental values or reference CCSD calculations were still significant. The results for [Yb(H2O)8]3+ displayed an even more complicated pattern. The predictions performed by LSDA, PBE, and PBE0 provided erratic values. For this complex, the DFT-based calculations benefited from high HF exchange admixtures. PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) and DSD-PBEP86 (which incorporates 72% HFX) improved on the predictions. With HF the calculated HFCCs were overestimated, but with MP2 improvements were achieved. Predictions with DLPNO-CCSD using HFC1 and HFC2 thresholds revealed convergence towards the experimental value, which was encouraging in the perspective of future studies involving RE systems. The OO-MP2 calculation did not converge even with significantly increased number of iterations, whereas the computational cost of each canonical CCSD iteration was so high that it was not expected to converge within a reasonable time frame.
HFX) and DSD-PBEP86 (which incorporates 72% HFX) improved on the predictions. With HF the calculated HFCCs were overestimated, but with MP2 improvements were achieved. Predictions with DLPNO-CCSD using HFC1 and HFC2 thresholds revealed convergence towards the experimental value, which was encouraging in the perspective of future studies involving RE systems. The OO-MP2 calculation did not converge even with significantly increased number of iterations, whereas the computational cost of each canonical CCSD iteration was so high that it was not expected to converge within a reasonable time frame.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX)
HFX)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX)). Hence, a broad range of NMR shifts was obtained for each nucleus in the model. Only for models C, E, and F, did the calculated ranges of shifts provided agreement with the experimental ones. The authors discussed the dependence of the 13C NMR shift of β-carbon in the Asp83 residue on the bond lengths in the coordination sphere of the Co2+ ion. We took the two most promising models E and F and recalculated the 13Cβ (Asp83) NMR shifts with our protocol that involve coupled cluster calculations of A. To facilitate direct comparison of the (DFT) results from the study by Bertarello et al. and our calculations (DLPNO-CCSD), Fig. 2b and Table 9 were prepared. The ranges of shifts obtained by Bertarello et al. with the PBE0/PBE0(50%
HFX)). Hence, a broad range of NMR shifts was obtained for each nucleus in the model. Only for models C, E, and F, did the calculated ranges of shifts provided agreement with the experimental ones. The authors discussed the dependence of the 13C NMR shift of β-carbon in the Asp83 residue on the bond lengths in the coordination sphere of the Co2+ ion. We took the two most promising models E and F and recalculated the 13Cβ (Asp83) NMR shifts with our protocol that involve coupled cluster calculations of A. To facilitate direct comparison of the (DFT) results from the study by Bertarello et al. and our calculations (DLPNO-CCSD), Fig. 2b and Table 9 were prepared. The ranges of shifts obtained by Bertarello et al. with the PBE0/PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) approach for A were very wide, with a span of around 200 ppm for each model. In contrast, when the DLPNO-CCSD method was employed for the prediction of A, the accuracy and consistency of NMR shift prediction improved remarkably. Considering models E and F, the PBE0/PBE0(50%
HFX) approach for A were very wide, with a span of around 200 ppm for each model. In contrast, when the DLPNO-CCSD method was employed for the prediction of A, the accuracy and consistency of NMR shift prediction improved remarkably. Considering models E and F, the PBE0/PBE0(50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX) calculations provided rather inconclusive chemical shifts ranging from 299 to 531 ppm, whereas with the DLPNO-CCSD approach the values of 337 and 331 ppm were obtained for model E and F, respectively; both very close to the experimental result of 350 ppm. These results suggested that model E might be closer to the real coordination sphere of Co2+ ion in CoSOD. We note however that vibrational corrections to σorb and A could not be evaluated because models derived from the X-ray structure of protein and optimized with constraints did not allow for Hessian evaluations. We checked the DLPNO-CCSD convergence for Model E, and δ for 13Cβ changed only marginally from 337.29 to 337.23 ppm when going from HFC1 to HFC2 thresholds and keeping all other parameters same. This indicated that results for 13Cβ in the Asp83 residue in our calculations were close to the CCSD limit. Larger changes of HFCCs were observed for nuclei directly bonded to the Co2+ ion, however, signals from those nuclei were not observed in the experiments. This presence of a “NMR blind sphere” around the paramagnetic Co2+ ion in CoSOD is indicted in Fig. 2c–e where spin densities rendered with the isodensity of 0.002 e bohr−3 are observed for the donor nitrogen and oxygen atoms. Since the magnetic and EPR properties of CoSOD have been measured,167,168 comparisons of the calculated g and D with experimental results could provide further insights. The calculated isotropic g-values of 2.228 and 2.225 for the models E and F were similar, but that from model E was slightly closer to the experimental result of 2.24. However, the calculated D-values of 5.62 and 4.25 cm−1 for model E and F, respectively, were significantly lower than the experimental estimate of 10.8 cm−1. In general, the ZFS of tetrahedral, high-spin Co2+ complexes is strongly dominated by the SOC interaction,161,169 and errors in the DKH2-CASSCF/NEVPT2 approach are not expected to be significant. Moreover, reported experimental D-values in four-coordinated Co2+ complexes involving nitrogen donors were in the range from 2.4 to 7.5 (cm−1),170,171 which corresponded very well with our theoretical predictions for CoSOD. In the work by Bertarello et al. it was indicated that the experimental estimate of D obtained by fitting of temperature dependent magnetic susceptibility data with susceptibility equations derived by using isotropic g-factors and axial parameters D might not be accurate. Nonetheless, all three: the NMR shift of 13Cβ (Asp83), isotropic g-value, and D parameter indicated that the coordination geometry of model E was the most accurate.
HFX) calculations provided rather inconclusive chemical shifts ranging from 299 to 531 ppm, whereas with the DLPNO-CCSD approach the values of 337 and 331 ppm were obtained for model E and F, respectively; both very close to the experimental result of 350 ppm. These results suggested that model E might be closer to the real coordination sphere of Co2+ ion in CoSOD. We note however that vibrational corrections to σorb and A could not be evaluated because models derived from the X-ray structure of protein and optimized with constraints did not allow for Hessian evaluations. We checked the DLPNO-CCSD convergence for Model E, and δ for 13Cβ changed only marginally from 337.29 to 337.23 ppm when going from HFC1 to HFC2 thresholds and keeping all other parameters same. This indicated that results for 13Cβ in the Asp83 residue in our calculations were close to the CCSD limit. Larger changes of HFCCs were observed for nuclei directly bonded to the Co2+ ion, however, signals from those nuclei were not observed in the experiments. This presence of a “NMR blind sphere” around the paramagnetic Co2+ ion in CoSOD is indicted in Fig. 2c–e where spin densities rendered with the isodensity of 0.002 e bohr−3 are observed for the donor nitrogen and oxygen atoms. Since the magnetic and EPR properties of CoSOD have been measured,167,168 comparisons of the calculated g and D with experimental results could provide further insights. The calculated isotropic g-values of 2.228 and 2.225 for the models E and F were similar, but that from model E was slightly closer to the experimental result of 2.24. However, the calculated D-values of 5.62 and 4.25 cm−1 for model E and F, respectively, were significantly lower than the experimental estimate of 10.8 cm−1. In general, the ZFS of tetrahedral, high-spin Co2+ complexes is strongly dominated by the SOC interaction,161,169 and errors in the DKH2-CASSCF/NEVPT2 approach are not expected to be significant. Moreover, reported experimental D-values in four-coordinated Co2+ complexes involving nitrogen donors were in the range from 2.4 to 7.5 (cm−1),170,171 which corresponded very well with our theoretical predictions for CoSOD. In the work by Bertarello et al. it was indicated that the experimental estimate of D obtained by fitting of temperature dependent magnetic susceptibility data with susceptibility equations derived by using isotropic g-factors and axial parameters D might not be accurate. Nonetheless, all three: the NMR shift of 13Cβ (Asp83), isotropic g-value, and D parameter indicated that the coordination geometry of model E was the most accurate.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFX)a
HFX)a