Open Access Article
Open Access ArticlePolarizable molecular dynamics simulations on the conductivity of pure 1-methylimidazolium acetate systems†
Florian
Joerg
 ab and
Christian
Schröder
ab and
Christian
Schröder
 *a
*a
aUniversity of Vienna, Faculty of Chemistry, Department of Computational Biological Chemistry, Währingerstr. 17, A-1090 Vienna, Austria. E-mail: christian.schroeder@univie.ac.at
bUniversity of Vienna, Vienna Doctoral School in Chemistry (DoSChem), Währingerstr. 42, A-1090 Vienna, Austria
First published on 6th June 2022
Abstract
The protic ionic liquid 1-methylimidazolium acetate is in equilibrium with its neutral species 1-methylimidazole and acetic acid. Although several experimental data indicate that the equilibrium favors the neutral species, the system exhibits a significant conductivity. We developed a polarizable force field to describe the ionic liquid accurately and applied it to several mixtures of the neutral and charged species. In addition to comparing single values, such as density, diffusion coefficients, and conductivity, with experimental data, the complete frequency-dependent dielectric spectrum ranging from several MHz to THz can be used to determine the equilibrium composition of the reaction mentioned above.
1 Introduction
High demands are imposed on current battery and fuel cell generations, thus implying continuous research of more efficient and improved components. A promising approach is the application of ionic liquids (ILs), which are basically molten salts.1–3 They have gained broad scientific interest during the last decades, not only because of countless ways of designing different candidates but also due to their specific and adjustable properties such as non-flammability, high thermal and electrochemical windows, as well as low volatility.4Among the multitude of different ILs, a subclass called protic ionic liquids (PILs) is especially interesting in terms of electrochemistry applications.2 This family of substances is formed by a proton transfer from a Brønsted acid (AH) to a Brønsted base (B).
| HA + B ⇌ A− + BH+ | (1) |
The available proton and ability to form hydrogen-bonded networks,5,6 distinguishes PILs from aprotic ILs. Additionally, they usually have higher conductivities and lower viscosities.
Strictly speaking, only if the equilibrium in eqn (1) is shifted far to the right, the substance can be properly named an IL. The more the equilibrium shifts to the left, the more neutral species are in the mixture. Still, a remarkable difference to common ionic solutions remains, as the neutral species are in direct chemical relation to the ions.7,8 Since it is not very likely that the proton transfer is fully complete, all four different species of eqn (1) may be present, resulting in the possible formation of (non-)neutral aggregates.6
The Walden rule is often employed to access the ionicity of ILs, which states that the product of the molar conductivity and viscosity is constant.9 On a log–log plot of these two properties, also known as the Walden plot, 1 M KCl solution is used as an ideal reference.10 Many ILs lie below the reference line, indicating incomplete proton transfer and poor conductivity. Still, some ILs are remarkably close to the ideal line, although they are quite different from a dilute electrolyte solution in terms of ion correlation.11 Angell and co-workers concluded that ILs with a ΔpKa value above 10 are good ionic liquids, where ΔpKa = pKa(BH+) − pKa(AH). Regarding the main transport mechanisms, vehicle and Grotthus transport, the KCl-line in the Walden plot resembles vehicle transport by the fully dissociated species. On the other hand, Grotthus transport could exceed vehicle transport, as it is less hindered by diffusion, thus playing an important role, especially for ILs.12,13
The ΔpKa for the IL 1-methylimidazolium (Im1H+) acetate (OAc−) of 2.2 indicates that the equilibrium favors the neutral species acetic acid (HOAc) and 1-methylimidazole (Im1).14 This finding is supported by several spectroscopic data also reporting on the dominance of the neutral species.11,15 Nevertheless, a significant conductivity of about 3.3 mS cm−1 to 4.4 mS cm−1 was reported by several groups which argues for a significant amount of charged species.15–18 In the light of these remaining ambiguities, this study aims to provide further insight and a better understanding of the interplay between high conductivity in PILs on the one hand and the dominance of neutral species on the other hand, by investigating the PIL [Im1H]OAc using polarizable molecular dynamics (PMD) simulations. While some methods, such as constant pH simulations,19–21 exist to emulate proton transfer in MD simulations, these are not suitable for the studied PILs where several hundreds of cations and anions are subject to (de-)protonation. Therefore, we model the equilibrium of HOAc + Im1 ⇌ OAc− + Im1H+ by sampling various ratios of charged and neutral molecules and comparing them to experimental data. In addition to comparing single values like density and conductivity, a more profound test is the juxtaposition of the frequency-dependent dielectric spectrum ranging from several MHz to THz and covering all local and collective motions of the liquid.
2 Methods
Classical force fields have fixed charges located at the nuclei positions. These force fields are additive since the total electrostatic energy emerges from the sum of the pairwise interactions. While this description is often sufficient for reproducing structural properties, they fail at describing dynamical properties of ILs,22,23 as flexible electronic charge distributions are essential to properly capture the response of the charged system to fluctuations in the local environment.23–25 The induced dipoles implemented in polarizable molecular dynamics (MD) simulation, however, may model this essential electronic flexibility.23,262.1 Parametrization process
The starting point for the parametrization was the CHARMM General Force Field (CGenFF).27 First, the initial parameters of the molecules were obtained by using the PARAMCHEM website.28 Molecules, which are not already fully featured in the CGenFF, are built based on analogy. Subsequently, the recently published FFParam package29 was used to convert the atom types of the molecules to Drude force field compatible ones since polarizable MD was used throughout the whole study. The optimization procedure of FFParam covers the inspection of structural similarities and fitting of electrostatic as well as bonded parameters in the given order. After each step, checks were made to ensure the quality of the parameters by comparison to the reference data. The whole procedure was done in a self-consistent-field-like approach.The quantum mechanical (QM) reference data was generated using Gaussian0930 as well as Psi431 for dipoles and polarizabilities since the more efficient RI-MP2 algorithm is implemented. According to the Drude Generalized Force Field (DGenFF) standard CHARMM procedure, all intermolecular potentials were parametrized using water. These water interactions were calculated at a MP2/aug-cc-pVDZ, dipoles and polarizabilities at MP2/cc-pVQZ, and PES scans of important bonded parameters at a MP2/aug-cc-pVDZ level of theory.
On top of that, force matching was applied to optimize force constants and equilibrium distances further. The total force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) MM of a force field is the sum of intra- and intermolecular interactions. The superscript MM denotes that the forces are from a classical molecular mechanics force field, and Θ represents the physical parameters.
MM of a force field is the sum of intra- and intermolecular interactions. The superscript MM denotes that the forces are from a classical molecular mechanics force field, and Θ represents the physical parameters.
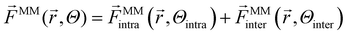 | (2) |
The goal of force matching, as portrayed in ref. 32, is to fit intramolecular parameters to high level forces ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) QM, e.g. derived from QM calculations. This is done via a Bayesian formalism which minimizes the negative log-likelihood and thus the force residuals:
QM, e.g. derived from QM calculations. This is done via a Bayesian formalism which minimizes the negative log-likelihood and thus the force residuals:
 | (3) |
The last term subtracts the intermolecular interactions from the QM-derived forces before fitting, as the difference between intramolecular forces of the empirical force field and the QM-derived forces should be minimized. zt(j) is an estimate of the mean square error of the force for atom type t(j).
The generation of force data was done by extracting conformations from a CHARMM33 trajectory at different time steps and calculating the forces using GAUSSIAN09. The calculations were done at PBE1PBE/cc-pVDZ level of theory and using the FORCE keyword to request the calculation of forces. Since the results were still not satisfying, additional charge fitting was done. Instead of the standard Mulliken method for calculating partial atomic charges, calculation of the charges from electrostatic potentials using a grid-based method (CHELPG) was utilized. They depend less on the underlying level of theory.34,35
Due to the introduction of Drude particles to a MD simulation, van der Waals interactions between induced dipoles are modeled explicitly. To account for this fact in the simulation, the depth of the Lennard-Jones potential, εLJβ is scaled. Otherwise, London forces would be counted twice, as they are also covered in the general Lennard-Jones term of the force field. This adjustment was made using the formula of Vlugt and co-workers,36
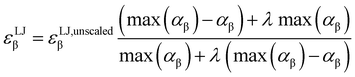 | (4) |
2.2 Computational setup
As our goal is to determine the composition of the equilibrium depicted in Fig. 1, the nine systems in Table 1 were studied.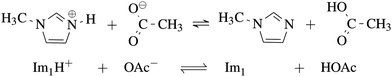 | ||
| Fig. 1 Equilibrium between the IL 1-methylimidazolium acetate [Im1H]OAc and its neutral analogues 1-methylimidazole Im1 and acetic acid HOAc. | ||
| ϕ IL | Im1H+/OAc− | Im1/HOAc | Sim. period | |
|---|---|---|---|---|
| [# molecules] | [# replica] | [ns] | ||
| 0.0 | 0 | 500 | 3 | 50 |
| 0.1 | 50 | 450 | 3 | 50 |
| 0.2 | 100 | 400 | 3 | 50 |
| 0.3 | 150 | 350 | 3 | 50 |
| 0.4 | 200 | 300 | 3 | 50 |
| 0.5 | 250 | 250 | 3 | 50 |
| 0.7 | 350 | 150 | 3 | 50 |
| 0.9 | 450 | 50 | 3 | 50 |
| 1.0 | 500 | 0 | 3 | 50 |
All systems studied contained a total of 1000 molecules and fulfilled charge neutrality, as always the same amount of cations and anions was used. The relative content ϕIL of ionic/neutral pairs varied between the pure systems containing 500 pairs of only neutral molecules Im1 and HOAc to 500 ion pairs of only Im1H+ and OAc−. Three replicas of each system were generated to increase the statistical accuracy of our results.
As Drude oscillators emulate the induced forces in our polarizable simulations, only non-hydrogens can be made polarizable. Nevertheless, the polarizabilities of the hydrogens are added to the next atom to which they are bonded. Drude particles were assigned a mass of 0.4 u and a force constant k = 1000 kcal mol−1 Å−2. To obtain stable simulation, the maximum distance for the mobile Drudes was set to 0.2 Å. Lennard-Jones interactions were reduced according to eqn (4) using λ values between 0.2 and 0.5. A previous study37 showed that a λ value of 0.4 yielded best results. However, in this work, best results are recorded for a λ of 0.25.
Trajectories were generated by first getting the initial configuration of the system using Packmol.38 After an initial minimization using CHARMM33 a timestep of 0.1 fs for 20 ps at 300 K was used to obtain stable simulations. Afterwards the timestep was changed to 0.5 fs. The temperature was increased to 500 K to ensure proper mixing. After 2 ns the temperature was decreased to 300 K again for another 3 ns. A Monte–Carlo barostat at 1.0 atm was used for these NPT runs. The average boxlength of the last nanosecond was then used for the subsequent 50 ns NVT production run. All simulations were done using periodic boundary conditions with an initial boxlength of 48 Å. The final boxlengths are given in Table S7 (ESI†).
The OpenMM package39 was used for generating trajectories with a time step of 0.5 fs. Integration was done using the velocity Verlet algorithm with the temperature-grouped Dual–Nosé–Hoover thermostat as described in ref. 40 and 41, which implements an additional temperature group for the center-of-mass translations. The non-Drude particles were kept at 300 K and the Drudes at 1 K. The collision frequency was set to 10 ps−1 for the atoms and to 200 ps−1 for the Drude particles. Keeping the vibrations of the Drude particle at a extremely low temperature results in an effective energy minimization on the fly, i.e. finding the optimal positions of the Drude particles.
Electrostatic interactions were treated using the Particle Mesh Ewald algorithm with a cut-off distance of 11 Å and a switch distance of 10 Å to truncate the interactions smoothly. Bonds containing hydrogens were fixed using the constraints = HBonds option. The error tolerance δ was set to 0.0001. From the given error tolerance and cut-off, the number of mesh nodes is specified internally, via #mesh = 2/3αdδ−1/5 with d being the box length in each dimension, and 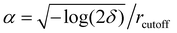 . Simulations were run on the CUDA platform using the default setting of mixed precision, which means that forces are calculated in single precision, and integration is done in double precision.
. Simulations were run on the CUDA platform using the default setting of mixed precision, which means that forces are calculated in single precision, and integration is done in double precision.
The input files for OpenMM were provided as CHARMM psf and crd files, as well as the Drude General Force Field (DGenFF)42 stream files. Coordinates were saved every 200 steps. For the analysis of the trajectories, the MDAnalysis package43,44 was applied.
3 Theory
3.1 Nernst–Einstein conductivity σNE
Charge transport depends on the number of charge carriers and their mobility. Quite generally, the mobility of a molecular species k is characterized by its diffusion coefficient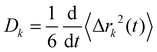 | (5) |
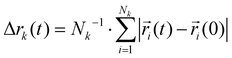 using an index i for each molecule belonging to species k. The number of charge carriers correlates with the number density ρk = Nk/V. As a result the conductivity of a system can be estimated via the Nernst–Einstein equation
using an index i for each molecule belonging to species k. The number of charge carriers correlates with the number density ρk = Nk/V. As a result the conductivity of a system can be estimated via the Nernst–Einstein equation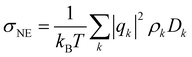 | (6) |
| σ(0) = σNE·(1 − Δ(ϕIL)) | (7) |
3.2 Frequency-dependent conductivity σ(ω)
Consequently, the static conductivity is usually computed via the collective translational dipole moment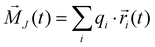 which describes an intermolecular dipole moment using the molecular charges qi and the center-of-mass positions
which describes an intermolecular dipole moment using the molecular charges qi and the center-of-mass positions ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t) of the molecules i. Applying an Einstein–Helfand approach,46 the static conductivity yields
i(t) of the molecules i. Applying an Einstein–Helfand approach,46 the static conductivity yields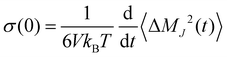 | (8) |
![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) J(t) =
J(t) = ![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) J(t) −
J(t) − ![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) J(0) between the time interval t.
J(0) between the time interval t.
The frequency-dependent conductivity σ(ω) can be derived from the auto-correlation function of the electric current 〈![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) (0)·
(0)·![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) (t)〉:
(t)〉:
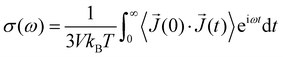 | (9) |
Actually, we showed47 that this correlation function correlates with the mean-squared displacement of the collective translational dipole moment:
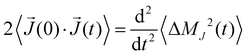 | (10) |
![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) (t) = d
(t) = d![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) J(t)/dt is the time derivative of the collective translational dipole moment. In principle, the static conductivity can also be obtained from eqn (9) but with less statistical accuracy.
J(t)/dt is the time derivative of the collective translational dipole moment. In principle, the static conductivity can also be obtained from eqn (9) but with less statistical accuracy.
3.3 Spectrum of the generalized dielectric constant Σ0(ω)
The charged species also contribute to the frequency-dependent spectrum of the generalized dielectric constant Σ0(ω), in particular to the frequency-dependent dielectric conductivity ϑ0(ω) which is defined as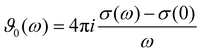 | (11) |
The second significant contribution to the generalized dielectric constant stems from the permittivity ε(ω)
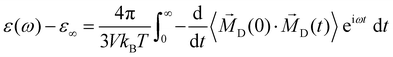 | (12) |
![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) D(t) is the sum of molecular dipole moments
D(t) is the sum of molecular dipole moments ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i(t). As
i(t). As ![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) D(t) can be computed for each species k separately, a decomposition of the permittivity into molecular contribution is feasible, i.e.
D(t) can be computed for each species k separately, a decomposition of the permittivity into molecular contribution is feasible, i.e.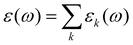 .
.
The comparison between the computational and experimental spectra are done on the level of the generalized dielectric constant Σ0(ω),47,48 which consists of the overlapping contributions from the permittivity ε(ω) and dielectric conductivity ϑ0(ω) and additionally the high-frequency limit of the dielectric constant ε∞.
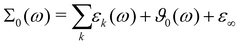 | (13) |
Please keep in mind that experimenter uses the frequency ν = ω/(2π) instead of the pulsatance ω.
3.4 Voronoi-shell resolved potential of mean force
The potential of mean force PMFkl is a measure for the aggregation of a species l in the proximity of a species k. Commonly, it is defined as a function of the distance from the central molecule. However, as our molecules are not spherical but have significant anisotropic shapes, we apply here a shell-resolved PMFkl(s) which can be defined for each non-spherical solvation shell s:49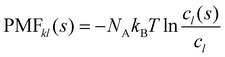 | (14) |
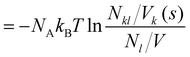 | (15) |
The ratio of the concentration cl(s) of species l in solvation shell s and the bulk concentration cl resembles the distance resolved radial distribution function g(r) which is also a ratio of local and global mass density.
Here, we restrict ourselves to the first solvation shell s = 1, which can be unambiguously determined by Voronoi tesselation.50,51 The coordination number Nkl = Nlk counts the number of molecules of species l in the first solvation shell of molecules of species k. The volume Vk (s = 1) is the averaged sum of molecular volumes of all molecules in the first solvation shell of a molecule of species k. Nl is the total number of molecules of species l in the simulation box, and V is the box's volume.
4 Results and discussion
The top panel of Fig. 2 depicts the overall mass density ρ as a function of ϕIL. The mass density ρ(ϕIL) increases linearly with increasing content of charged molecules. The Coulomb interaction between the oppositely charged ions is stronger, leading to closer distances between the ions. As a result, the overall density of molecules is increased. The density line ρ(ϕIL) crosses the experimental density52 of ρ = 1.07 g cm−3 at ϕIL = 45%. Lowering the Lennard-Jones scaling factor λ (see eqn (4)) has only marginal consequences for the density.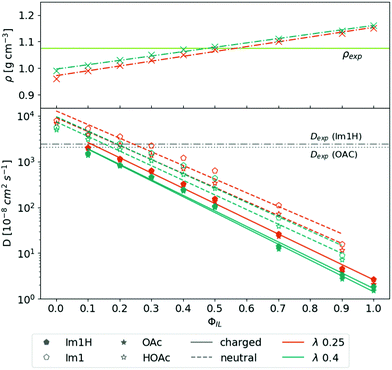 | ||
| Fig. 2 Density and diffusion coefficients as a function of the share of the charged species. Experimental density and diffusion coefficients are taken from ref. 18 and 52, respectively. For clarity only the best λ-value 0.25 and the reference λ-value of 0.4 are displayed. | ||
4.1 Diffusion
The diffusion coefficients of all four species are calculated using the Einstein relation in eqn (5) and depicted as a function of ϕIL in the bottom panel of Fig. 2.The simulation systems become more viscous with an increasing number of charged molecules because of the overall increased Coulombic interactions. Therefore, the diffusion coefficients of the charged species Im1H+ (filled pentagons) and OAc− (filled stars) as well as the neutral species Im1 (empty pentagons) and HOAc (empty stars) decrease exponentially with ϕIL. Im1 and HOAc have higher diffusion coefficients than their charged analogs which can also be explained by the additional Coulomb interactions between the molecular charge and the surrounding dipoles of the ions.
Since the proton transfer HOAc + Im1 ⇌ OAc− + Im1H+ is very fast compared to the NMR measurements, experimental diffusion coefficients always contain contributions from the charged and neutral species.53 However, simulation mixtures containing ϕIL = 10% to 30% charged molecules are close to the experimental data of ref. 18. Reducing the λ-value from 0.40 (green curves) to λ = 0.25 (orange curves) improves the agreement with the experiment. Applying smaller λ-values than 0.25 does not improve the results but may increase stability issues.
As already mentioned in the Theory section, the conductivity is determined by the number of charge carriers and their mobility. In Fig. 3, the Nernst–Einstein conductivity σNE based on eqn (7) is displayed as a function of ϕIL. The bell-shaped behavior can be described by an empirical fit:
| σ = a·ϕIL·exp(−bϕIL2) | (16) |
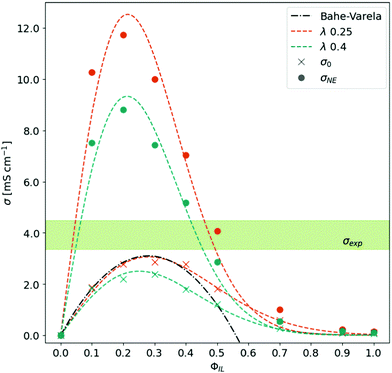 | ||
| Fig. 3 Conductivity as a function of the ratio between neutral and charged species. The experimental conductivity range is taken from ref. 15–18. | ||
The corresponding fit parameters for λ = 0.25 and λ = 0.40 are given in Table 2. This fit can also be used to determine the maximum conductivity max(σNE) and the respective composition 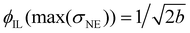 . Although the maximum conductivity for λ = 0.25 is higher than that for λ = 0.40, the respective ϕIL coincides.
. Although the maximum conductivity for λ = 0.25 is higher than that for λ = 0.40, the respective ϕIL coincides.
| σ NE | a | b | max(σ) [mS cm−1] | ϕ IL (max(σ)) |
|---|---|---|---|---|
| λ = 0.25 | 96.3 | 10.9 | 12.5 | 0.21 |
| λ = 0.40 | 72.3 | 11.0 | 9.3 | 0.21 |
| σ(0) | a | b | max(σ) [mS cm−1] | ϕ IL (max(σ)) |
|---|---|---|---|---|
| λ = 0.25 | 17.9 | 6.3 | 3.1 | 0.28 |
| λ = 0.40 | 16.4 | 7.9 | 2.5 | 0.25 |
Up to a fraction ϕIL of roughly 0.2, the increased number of charge carriers promotes the conductivity of the system. Beyond ϕIL = 0.2, the Nernst–Einstein conductivity σNE drops down significantly as the diffusion coefficients of species decrease exponentially with ϕIL. This is the first indication that only a small number of charged molecules (≈20%) are sufficient to realize a significant conductivity in the system. However, the Nernst–Einstein approach neglects all correlations between the motion of the molecular species. Consequently, we continue our analysis with the collective static conductivity σ(0).
4.2 Conductivity
The Einstein–Helfand approach of eqn (8) can be applied to the unfolded trajectories of MD simulations straightforwardly. As the mean-squared displacement of the collective translational dipole moment is usually noisy, we averaged the corresponding 〈ΔMJ2(t)〉 of the three replicas before determining the slope between 500 ps and 2 ns. The obtained σ(0) as a function of ϕIL is shown in Fig. 3 in comparison to the σNE(ϕIL). The bell-shaped curves are again fitted by eqn (16).As visible from the fit parameter in Table 2 the maximum values of σ(0) are roughly a quarter from the σNE-values arguing for a significant Δ-value in eqn (7). This indicates a strong correlation between the (charged) species. Additionally, this overestimation on the basis of σNE prohibits the discrimination which λ-value suits better the experimental data. Moreover, the position of the maximum has shifted to ϕIL(max(σ(0))) = 0.25–0.28. This shift casts additional doubts on the usefulness of σNE for the interpretation of conductivity phenomena in ionic liquids as not only the absolute values are overestimated by a factor (1 − Δ) but also this factor Δ(ϕIL) changes drastically with the composition ϕIL (see ESI† for further information).
The maximum conductivity σ(0) = 3.1 mS cm−1 can be obtained for the trajectories with λ = 0.25 at ϕIL = 0.28. This value is still lower than 3.3 mS cm−1 to 4.4 mS cm−1 (light green area in Fig. 3) found in experiment.15–18 On the one hand, small amounts of water increase mobility and, hence, conductivity in experiments. Various water and impurity contents may also explain the variance of the experimental σ(0)-values indicated by the green area in Fig. 3. These impurities are not present in the simulations. On the other hand, our simulations do not allow proton transfer. As a result, our polarizable MD simulations mainly monitor vehicle transport. The simulation's lack of explicit Grotthus transport may also explain the slightly lower conductivity than experimental data.
The conductivity near the maximum can also be described by the Bahe–Varela theory54–56
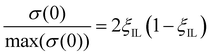 | (17) |
4.3 Dielectric spectroscopy
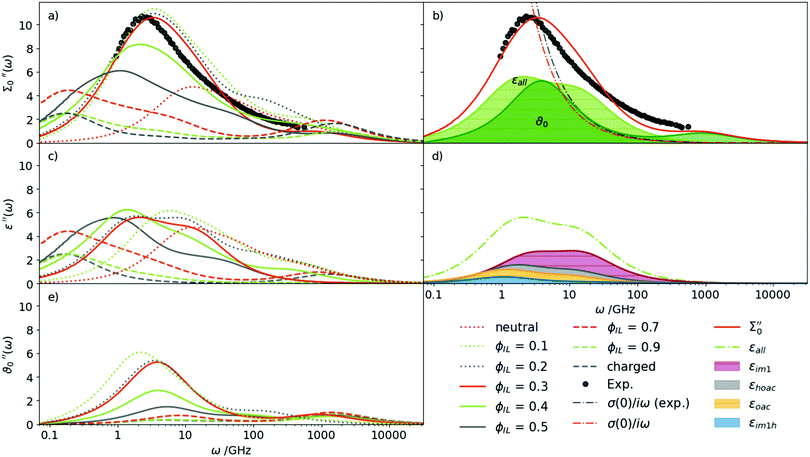
Based on our findings for the conductivity and density, a mixture of roughly 30% charged Im1H+ + OAc− and 70% neutral Im1 + HOAc seems most probable. This finding is also in agreement with AIMD simulations, which found concentrations of 70% to 80% neutral species in a [IM1H]OAc system.57 However, this optimal ratio is found by comparing single values of the diffusion coefficients, the conductivity, and the density in our study. A more profound check can be made on the basis of the dielectric spectrum Σ0′′(ω) as it covers the rotational and translational motion of the system over several orders of magnitude in frequency ω.Fig. 4(a) shows the imaginary part of the total dielectric spectra Σ0′′(ω) of all investigated mixtures in Table 1. A continuous shift to higher frequencies for increasing content of neutral species is observed. The amplitude increases as well, except for the neutral system. The mixtures with ϕIL = 10% to 30% match the experimental spectrum best. In particular, the ϕIL = 0.30 mixture agrees very well in terms of peak height as well as the position of the maximum. It can be clearly seen that neither the pure IL nor the neutral species reproduce the experimental spectrum satisfactorily. It is also impossible to reproduce the experimental spectrum with a linear combination of the pure neutral and the pure ionic system. This finding clearly demonstrates that neutral and charged species interact to a vast extent, changing the individual components' properties in the mixture.
Fig. 4(b) demonstrates the exhaustive overlap between the permittivity ε(ω) and dielectric conductivity ϑ0(ω) for ϕIL = 0.30. In addition, the conductivity parabola σ(0)/ω for the experimental data and the mixture at ϕIL is shown in Fig. 4(b) as dash-dotted line. As already deduced from Fig. 3, the computational static conductivity σ(0) at ϕIL = 0.30 matches the experimental one best. Shifting to lower ϕIL would increase the gap between the orange dash-dotted line (computational) and the gray dash-dotted line (experimental conductivity). The static dielectric constant Σ0(0) of 31.3 (see Table 3) in our simulations at ϕIL = 0.30 agrees well to the experimentally found value of 33.3. At ϕIL = 0.20, the static dielectric constant is slightly overestimated with 36.7.
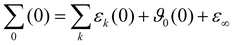
| ϕ IL | ε k (0) | ϑ 0(0) | ε ∞ | Σ 0(0) | |
|---|---|---|---|---|---|
| 0.0 | Im1 | 12.2 | — | 2.2 | 16.7 |
| HOAc | 2.3 | — | |||
| 0.2 | Im1H+ | 1.2 | 12.5 | 2.2 | 36.7 |
| OAc− | 3.0 | ||||
| Im1 | 11.5 | — | |||
| HOAc | 6.3 | — | |||
| 0.3 | Im1H+ | 1.3 | 12.1 | 2.2 | 31.3 |
| OAc− | 3.1 | ||||
| Im1 | 8.2 | — | |||
| HOAc | 4.4 | — | |||
| 1.0 | Im1H+ | 0.8 | 2.8 | 2.3 | 10.6 |
| OAc− | 4.7 | ||||
The permittivity ε(ω) in Fig. 4(c) emerges from the collective rotation of the molecular ions. The maximum amplitude does not change very much with varying mole fractions of the ions. Only the shift to lower frequencies with increasing ion content (as already noticed for Σ0(ω)) is found again. Taking a closer look at ε(ω) for ϕIL = 0.30 in Fig. 4(d) reveals that all molecular species contribute to the permittivity. The largest share comes from the neutral 1-methylimidazole (red area, εIm1(0) = 8.2, Table 3) which has also the broadest peak. Interestingly, the second most important contribution stems from the acetic acid molecules (gray area, εHOAc(0) = 4.4). This is counter-intuitive as acetic acid has a low molecular dipole moment μHOAc of 1.7 D (see ESI†). Furthermore, pure acetic acid is known to form dimers with hydrogen bonds between the hydroxy–hydrogen of one acetic acid molecule with the carbonyl oxygen of the other acetic acid molecule (see Fig. 5).
Thus, the dipoles of the two hydrogen-bonded acetic acid molecules should cancel out, which results in a dielectric constant of 6.2 in pure acetic acid. However, in our mixtures, the acetic acid prefers to interact with the 1-methylimidazole as shown by the first shell potential of mean force PMF(s=1) = −0.36 kJ mol−1. In contrast, the first shell potential of mean force PMF(s=1) between two acetic acid molecules is +0.43 kJ mol−1 at ϕIL = 0.30, meaning an overall depletion of acetic acid molecules in the first solvation shell around acetic acid. Additionally, the formation of hydrogen bonds and especially dimers of HOAc molecules is reduced. About 5.6% of the acetic acid molecules have at least one hydrogen bond to another acetic acid molecule, of which only 2.2% form HOAc dimers at ϕIL = 0.30. The maximum distance between the hydrogen donor and oxygen acceptor atom was set to 3 Å to define a hydrogen bond in our analysis.
Obviously, as shown by the overlap of ε(ω) and ϑ0(ω) in Fig. 4(b), the amplitude Sk of the peak cannot be used to evaluate an effective dipole moment μeff,k based on the Cavell equation58
| Sk ∝ ck · μeff,k2 | (18) |
The maximum amplitude at ω = 2.5 GHz for the ϕIL = 0.30 mixture comes from equal contributions of ε(ω) and ϑ0(ω). The latter only depends on the translation of the ions but not their dipoles. However, a decomposition into permittivity contributions εk(0) of the molecular species k is possible for the MD trajectory. The respective contributions are listed in Table 3. Thus, we are not only able to remove the translational contribution but analyze each species separately. Nevertheless, there is no correlation between εk(0) and Sk computed from the Cavell equation (see ESI†).
The dielectric conductivity ϑ0(ω) in Fig. 4(e) shows an opposite trend to higher frequencies with increasing ϕIL but this trend is less pronounced compared to that of the permittivities. Interestingly, the amplitude decreases with increasing ion content ϕIL which is surprising at first sight as only the ions Im1H+ and OAc− can contribute. However, the interactions between a central ion and its neighboring ions are stronger at lower ϕIL as characterized by the first shell potential of mean force PMF(s=1). This PMF(s=1) of a central 1-methylimidazolium (blue filled pentagons) and a central acetate (orange filled circles) in Fig. 6 is most negative at low ϕIL showing an aggregation of oppositely charged ions around a central ion. These strong interactions go along with librational motion between the ions leading to significant contributions to ϑ0(ω). With increasing ionic concentrations, these ion clusters transform into an ionic network in which the neutral molecules penetrate. As a result, the local concentration cl(s = 1) of the oppositely charged ions converges to the bulk density cl of these ions, and fewer particular ion clusters are found. The dashed lines in Fig. 6 correspond to a Gaussian fit f(ϕIL) = a·exp(−bϕIL2) + c of the PMF. The corresponding fit parameters are also given in Fig. 6. Interestingly, the exponential b-factor of 10.7 and 11.4 is very close to 10.9 found for the Nernst–Einstein conductivity as a function of ϕIL in Table 2.
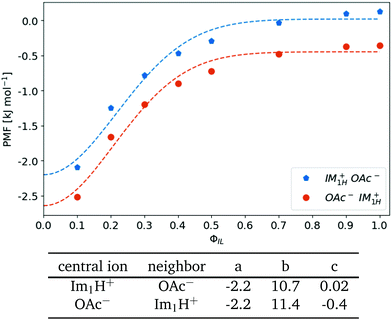 | ||
| Fig. 6 Shell-resolved PMFkl (s = 1) as a function of ionic content ϕIL. The dashed lines correspond to a Gaussian fit f(ϕIL) = a·exp(−bϕIL2) + c. | ||
5 Conclusions
The position of the equilibrium HOAc + Im1 ⇌ OAc− + Im1H+ is not so easy to determine as various experiments came to different conclusions. By comparing density, diffusion coefficients and conductivity of various mixtures modelled by polarizable molecular dynamics with the experimental data, a ratio of 20% to 30% ionic and 80% to 70% neutral molecules seems most probable.In addition to comparing these single values, we also computed the frequency-dependent dielectric spectrum of all these mixtures and compared the computational results with the experimental spectrum over several orders of magnitude in frequency. It turned out that the mixture with 30% ions fits the experimental data best. In addition, the dielectric spectrum cannot be reproduced by a linear combination of systems containing only ionic or only neutral molecules. Consequently, there have to be strong correlations between all species altering their individual dynamic properties. For example, the shell-resolved potential of mean force PMF(s=1) decays Gaussian-like with increasing ion content ϕIL for the interaction of a central ion and its oppositely charged neighboring ions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Johannes Hunger for providing the experimental data on 1-methylimidazolium acetate. Also very helpful discussions with Othmar Steinhauser are appreciated.This work was supported by Project No. I4383N of the FWF Austrian Science Fund.
Notes and references
- A. Guerfi, M. Dontigny, P. Charest, M. Petitclerc, M. Lagacé, A. Vijh and K. Zaghib, J. Power Sources, 2010, 195, 845–852 CrossRef CAS.
- S. Menne, J. Pires, M. Anouti and A. Balducci, Electrochem. Commun., 2013, 31, 39–41 CrossRef CAS.
- S. Menne, R.-S. Kühnel and A. Balducci, Electrochim. Acta, 2013, 90, 641–648 CrossRef CAS.
- T. Welton, Biophys. Rev., 2018, 10, 691–706 CrossRef CAS PubMed.
- K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., Int. Ed., 2009, 48, 3184–3186 CrossRef CAS PubMed.
- T. L. Greaves and C. J. Drummond, Chem. Rev., 2008, 108, 206–237 CrossRef CAS PubMed.
- J. N. C. Lopes and L. P. N. Rebelo, Phys. Chem. Chem. Phys., 2010, 12, 1948–1952 RSC.
- D. R. MacFarlane and K. R. Seddon, Aust. J. Chem., 2007, 60, 3–5 CrossRef CAS.
- D. R. MacFarlane, M. Forsyth, E. I. Izgorodina, A. P. Abbott, G. Annat and K. Fraser, Phys. Chem. Chem. Phys., 2009, 11, 4962–4967 RSC.
- M. Yoshizawa, W. Xu and C. A. Angell, J. Am. Chem. Soc., 2003, 125, 15411–15419 CrossRef CAS PubMed.
- H. Doi, X. Song, B. Minofar, R. Kanzaki, T. Takamuku and Y. Umebayashi, Chem. – Eur. J., 2013, 19, 11522–11526 CrossRef CAS PubMed.
- M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190–7239 CrossRef CAS PubMed.
- M. Anouti, J. Jacquemin and P. Porion, J. Phys. Chem. B, 2012, 116, 4228–4238 CrossRef CAS PubMed.
- W. M. Haynes, D. R. Lide and T. J. Bruno, CRC handbook of chemistry and physics, CRC press, 2015 Search PubMed.
- D. R. MacFarlane, J. M. Pringle, K. M. Johansson, S. A. Forsyth and M. Forsyth, Chem. Commun., 2006, 1905–1917 RSC.
- H.-Y. Hou, Y.-R. Huang, S.-Z. Wang and B.-F. Bai, Acta Phys.-Chim. Sin., 2011, 27, 2512–2520 CAS.
- J. Chen, L. Chen, Y. Lu and Y. Xu, J. Mol. Liq., 2014, 197, 374–380 CrossRef CAS.
- S. Thawarkar, N. D. Khupse, D. R. Shinde and A. Kumar, J. Mol. Liq., 2019, 276, 986–994 CrossRef CAS.
- Y. Chen and B. Roux, J. Chem. Theory Comput., 2015, 11, 3919–3931 CrossRef CAS PubMed.
- E. J. Denning, D. Thirumalai and A. D. MacKerell, Biophys. Chem., 2013, 184, 8–16 CrossRef CAS PubMed.
- P. Dobrev, S. Donnini, G. Groenhof and H. Grubmüller, J. Chem. Theory Comput., 2017, 13, 147–160 CrossRef CAS PubMed.
- M. Salanne, Phys. Chem. Chem. Phys., 2015, 17, 14270–14279 RSC.
- D. Bedrov, J.-P. Piquemal, O. Borodin, A. D. MacKerell, Jr., B. Roux and C. Schröder, Chem. Rev., 2019, 119, 7940–7995 CrossRef CAS PubMed.
- C. Schröder, Phys. Chem. Chem. Phys., 2012, 14, 3089–3102 RSC.
- J. A. Lemkul, J. Huang, B. Roux and A. D. MacKerell, Chem. Rev., 2016, 116, 4983–5013 CrossRef CAS PubMed.
- A. Szabadi and C. Schröder, J. Comput. Biophys. Chem., 2022, 21, 415–429 CrossRef CAS.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell Jr., J. Comput. Chem., 2010, 31, 671–690 CAS.
- https://cgenff.umaryland.edu/ .
- A. Kumar, O. Yoluk and A. D. MacKerell Jr., J. Comput. Chem., 2020, 41, 958–970 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS PubMed.
- P. S. Hudson, S. Boresch, D. M. Rogers and H. L. Woodcock, J. Chem. Theory Comput., 2018, 14, 6327–6335 CrossRef CAS PubMed.
- B. R. Brooks, C. L. Brooks III, A. D. Mackerell Jr., L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- T. M. Becker, D. Dubbeldam, L.-C. Lin and T. J. Vlugt, J. Comput. Sci., 2016, 15, 86–94 CrossRef.
- E. Heid, P. A. Hunt and C. Schröder, Phys. Chem. Chem. Phys., 2018, 20, 8554–8563 RSC.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L.-P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, PLoS Comput. Biol., 2017, 13, e1005659 CrossRef PubMed.
- C. Y. Son, J. G. McDaniel, Q. Cui and A. Yethiraj, J. Phys. Chem. Lett., 2019, 10, 7523–7530 CrossRef CAS PubMed.
- Z. Gong and A. A. H. Padua, J. Chem. Phys., 2021, 154, 084504 CrossRef CAS PubMed.
- P. Chatterjee, E. Heid, C. Schröder and A. MacKerell, Biophys. J., 2019, 116, 142a CrossRef.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- R. J. Gowers, M. Linke, J. Barnoud, T. J. E. Reddy, M. N. Melo, S. L. Seyler, J. Domański, D. L. Dotson, S. Buchoux, I. M. Kenney and O. Beckstein, Proceedings of the 15th Python in Science Conference, 2016, pp. 98–105.
- V. Zeindlhofer, L. Zehetner, W. Paschinger, A. Bismarck and C. Schröder, J. Mol. Liq., 2019, 288, 110993 CrossRef CAS.
- C. Schröder, M. Haberler and O. Steinhauser, J. Chem. Phys., 2008, 128, 134501 CrossRef PubMed.
- C. Schröder, J. Chem. Phys., 2011, 135, 024502 CrossRef PubMed.
- C. Schröder and O. Steinhauser, J. Chem. Phys., 2010, 132, 244109 CrossRef PubMed.
- V. Zeindlhofer, M. Berger, O. Steinhauser and C. Schröder, J. Chem. Phys., 2018, 148, 193819 CrossRef PubMed.
- F. Aurenhammer and R. Klein, in Ch. 5 in Handbook of Computational Geometry, ed. J.-R. Sack and J. Urrutia, Elsevier, 2000, pp. 201–290 Search PubMed.
- C. Schröder, G. Neumayr and O. Steinhauser, J. Chem. Phys., 2009, 130, 194503 CrossRef PubMed.
- J. Chen, L. Chen, Y. Lu and Y. Xu, J. Mol. Liq., 2014, 197, 374–380 CrossRef CAS.
- B. Koeppe, S. A. Pylaeva, C. Allolio, S. Sebastiani, E. T. J. Nibbering, G. S. Denisov, H.-H. Limbach and P. M. Tolstoy, Phys. Chem. Chem. Phys., 2017, 19, 1010–1028 RSC.
- L. M. Varela, J. Carrete, M. García, L. J. Gallego, M. Turmine, E. Rilo and O. Cabeza, Fluid Phase Equilib., 2010, 298, 280–286 CrossRef CAS.
- L. M. Varela, J. Carrete, M. García, J. R. Rodríguez, L. Gallego, M. Turmine and O. Cabeza, Ionic Liquids: Theory, Properties, New Approaches, IntechOpen, London, 2011 Search PubMed.
- E. Rilo, J. Vila, S. García-Garabal, L. M. Varela and O. Cabeza, J. Phys. Chem. B, 2013, 117, 1411–1418 CrossRef CAS PubMed.
- J. Ingenmey, S. Gehrke and B. Kirchner, ChemSusChem, 2018, 11, 1900–1910 CrossRef CAS PubMed.
- E. A. S. Cavell, P. C. Knight and M. A. Sheikh, Trans. Faraday Soc., 1971, 67, 2225–2233 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01501c |
| This journal is © the Owner Societies 2022 |