Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Oxygen deficiency in Sr2FeO4−x: electrochemical control and impact on magnetic properties†
Peter
Adler
 *a,
Liane
Schröder
a,
Klaus
Teske
a,
Manfred
Reehuis
b,
Andreas
Hoser
b,
Patrick
Merz
a,
Walter
Schnelle
a,
Claudia
Felser
a and
Martin
Jansen
*a,
Liane
Schröder
a,
Klaus
Teske
a,
Manfred
Reehuis
b,
Andreas
Hoser
b,
Patrick
Merz
a,
Walter
Schnelle
a,
Claudia
Felser
a and
Martin
Jansen
 *ac
*ac
aMax-Planck-Institut für Chemische Physik fester Stoffe, 01187 Dresden, Germany. E-mail: adler@cpfs.mpg.de
bHelmholtz-Zentrum für Materialien und Energie, 14109 Berlin, Germany
cMax-Planck-Institut für Festkörperforschung, 70569 Stuttgart, Germany. E-mail: m.jansen@fkf.mpg.de
First published on 29th June 2022
Abstract
The oxygen-deficient system Sr2FeO4−x was explored by heating the stoichiometric Fe4+ oxide Sr2FeO4 in well-defined oxygen partial pressures which were controlled electrochemically by solid-state electrolyte coulometry. Samples with x up to about 0.2 were obtained by this route. X-ray diffraction analysis reveals that the K2NiF4-type crystal structure (space group I4/mmm) of the parent compound is retained. The lattice parameter a slightly decreases while the c-parameter increases with increasing x, which is in contrast to the Ruddlesden–Popper system Sr3Fe2O7−x and suggests removal of oxygen atoms from FeO2 lattice planes. The magnetic properties were studied by magnetization, 57Fe Mössbauer, and powder neutron diffraction experiments. The results suggest that extraction of oxygen atoms from the lattice progressively changes the elliptical spiral spin ordering of the parent compound to an inhomogeneous magnetic state with coexistence of long-range ordered regions adopting a circular spin spiral and smaller magnetic clusters.
1. Introduction
Perovskite-related ferrates with iron in the high oxidation state +4 constitute an interesting class of transition metal (TM) oxides due to their peculiar electronic, magnetic, and structural properties. Formally, the electronic structure of Fe4+ oxides can be discussed starting from the t32ge1g (S = 2) ligand field configuration of 3d4 ions, where the high oxidation state of the TM ion gives rise to strong covalency of Fe–O bonding and in turn to strong hybridization between Fe 3d and O 2p orbitals. In the framework of configuration interaction models the iron(IV) oxides, along with Cu3+ and Ni3+ oxides,1–4 belong to the class of negative-charge-transfer energy (negative-Δ) compounds, where the electronic ground state is rather dominated by holes in the oxygen bands (L−n, n = 1, 2), i.e. by a d5L−1 electron configuration instead of an ionic d4 configuration.5 Remarkable properties which are related to the negative-Δ situation are the metallic behavior of SrFeO3,6 a charge-disproportionation (CD) process which may be written as 2d5L−1 → d5 + d5L−2 or 2t32ge1g → t32ge2g + t32g in CaFeO3,7,8 Sr3Fe2O7,7,9–12 CaCu3Fe4O12,13 and Ca2FeMnO6,14 pressure-induced insulator-to-metal and/or high-spin to low-spin transitions in CaFeO3,15 Sr3Fe2O7,16 and CaCu3Fe4O12,17 as well as antiferromagnetic ordering with different types of helical spin structures in SrFeO3,18 CaFeO3,8 cubic BaFeO3,19 and Sr3Fe2O7.20 In particular, SrFeO3 features a sensitive response of the helical spin structure to temperature and magnetic fields,21,22 which makes this system an interesting model case for topological spin textures in the absence of Dzyaloshinskii–Moriya interactions.23Convenient ways for tuning the electronic and magnetic properties of TM oxides are cationic substitutions or variation of the oxygen content. In case of perovskite-related ferrates the great flexibility of the perovskite structure has allowed to vary the oxygen content in a wide range and thus to realize Fe in oxidation states between +2 and +4. For the SrFeO3−x system several structurally and magnetically distinct phases have been described,24,25 namely metallic and helimagnetic SrFeO3, Sr8Fe8O23 (SrFeO2.875) which reveals a charge-ordering transition,26,27 partially frustrated Sr4Fe4O12 (SrFeO2.75) where only the Fe3+ fraction orders magnetically, the antiferromagnetic Brownmillerite Sr2Fe2O5, and finally the Fe2+ oxide SrFeO2 with infinite FeO2 layers in the crystal structure.28 Similarly, in the bilayer Ruddlesden-Popper system Sr3Fe2O7−x the iron oxidation state could be tuned between +4 and +2, but in contrast to the SrFeO3−x system no well-defined vacancy-ordered phases were found.29 The end members of the former homogeneity range are Sr3Fe2O7 (Fe4+)30,31 and Sr3Fe2O5 (Fe2+).32 As changes in the oxygen content lead to changes in the oxidation states and coordination of the iron ions, also the magnetic properties are substantially affected. Oxygen-deficient perovskite-related ferrates are not only of interest as potential magnetic materials but also as mixed anionic conductors for applications in solid oxide fuel cells33 and in oxygen-separating membranes34 or as oxygen sources for NO oxidation.35
A less studied Fe4+ oxide is the K2NiF4-type phase Sr2FeO4 which was first reported by Scholder et al.36 and has an insulating ground state, but in contrast to Sr3Fe2O7 does not feature a CD of Fe4+.9,37 An unexpected oxygen-related phonon band in Raman spectra of Sr2FeO4 may indicate that the insulating ground state is associated with a tiny structural distortion which, however, has remained elusive so far.38 Recently, we have shown that Sr2FeO4 adopts an elliptical spiral spin structure which shows a spin-flop-type reorientation in external magnetic field of about 5 T.39 Sr2FeO4 can be considered as a negative-Δ insulator, which is supported by its high-pressure properties showing the disappearance of the additional Raman band near 6 GPa38 and a concomitant change from a spiral to a ferromagnetic spin structure.39,40 An insulator-to-metal transition near 18 GPa was attributed to the closure of the p–p-type excitation gap.40 Only few substituted phases based on Sr2FeO4 were reported so far,41–43 and to the best of our knowledge oxygen deficiency in the Sr2FeO4−x system has not been studied in detail. However, similar as for the 113 and 327 systems also for 214 a layered compound with Fe2+ in square planar coordination, Sr2FeO3, was synthesized.44
In the present study we have explored the oxygen-deficient system Sr2FeO4−x by heating fully oxidized Sr2FeO4 at increasing temperatures and a well-defined oxygen partial pressure. The oxygen contents were controlled and analyzed electrochemically using solid-state electrolyte coulometry. Sr2FeO4−x samples with oxygen deficiencies 0 < x ≤ 0.2 could be prepared by this route. Attempts to increase the oxygen deficiency further required heating at temperatures above 700 °C where decomposition into Sr3Fe2O7−x and SrO occurs. The impact of oxygen deficiency on the magnetic properties in Sr2FeO4−x was studied by magnetization, 57Fe Mössbauer spectroscopy, and powder neutron diffraction experiments.
2. Experimental details
2.1. Synthesis of Sr2FeO4
Sr2FeO4 was prepared by solid state reaction of home-made SrO and Fe2O3 while applying elevated oxygen pressure. For the synthesis of SrO, 50 g SrCO3 (Sigma-Aldrich, >99.99% metal basis) was mixed with 100 ml of H2O, and HNO3 (65% strength) was added with stirring until no gas evolution was evident. The solution was evaporated and the resulting Sr(NO3)2 was decomposed to SrO at 550 °C in dynamic vacuum in a Schlenk line. The purity of the product was verified by powder X-ray diffraction. For storage, the SrO was sealed in glass ampoules. Fe2O3 was synthesized by decomposition of FeC2O4·2H2O (Alfa Aesar, Puratronic, 99.999% metal basis) in a tube furnace under a slow flow of oxygen at 350 °C and prior to use stored in an argon-filled glove box.A mixture of SrO and Fe2O3 with a slight excess of SrO (molar ratio of 4.02/1.00) was finely ground in an agate mortar in a glove box under argon atmosphere. The mixture was placed in a corundum finger crucible, covered with a thin layer of SrO and a gold lid on top. High oxygen pressure synthesis was performed in a specifically designed, scale-resistant steel autoclave described earlier.45 The charged crucible was placed in the autoclave, which was closed, loaded with 10 ml of liquid O2 and subsequently heated at a rate of 20 K h−1 to 773 K, which generates an O2 pressure of 2.5 kbar (free volume ∼15 ml). This temperature was kept for 72 hours, next the heating source was switched off and the autoclave was allowed to cool to room temperature with a rate of about 300 K h−1. The reaction product as obtained was reground, and annealed along the same procedure as described, once again. Samples with enrichment of the isotope 57Fe to 10 or 20% for high-pressure synchrotron Mössbauer studies39 were obtained by using isotopically enriched Fe2O3 as starting material.
2.2. Characterization methods
Powder X-ray diffraction (PXRD) was performed using a Huber G670 camera (Guinier technique, Co Kα1 radiation, λ = 1.788965 Å, diffraction range 10° ≤ 2θ ≤ 100° in steps of 0.005°). Rietveld refinement46 of the PXRD data of Sr2FeO4 was performed with the program WinCSD.47Thermogravimetric (TGA) analysis of Sr2FeO4 was carried out on a Netzsch STA 449 F3 thermoanalyzer. About 30 mg of the sample was placed in a corundum crucible, which was heated at a rate of 5 K min−1 in the range of 300–1073 K under dynamic argon flow. The sample was kept at 1073 K (800 °C) for 4 hours where no further weight loss was observed. Finally, the sample was cooled down again.
Magnetization measurements of Sr2FeO4−x were recorded on samples sealed in Suprasil quartz tubes under He using an MPMS3 (Quantum Design) magnetometer in the temperature range of 1.8 to 400 K, in zero-field cooling (zfc) and field-cooling (fc) modes in applied fields up to 7 T. Isothermic magnetization measurements were performed after zero-field cooling by field ramping between 0 and 7 T.
57Fe Mössbauer spectra were collected at various temperatures using a standard WissEl spectrometer operated in the constant acceleration mode (57Co/Rh source) and a Janis SHI 850-5 closed cycle refrigerator. Powder samples of Sr2FeO4−x containing about 10 mg Fe cm−2 were homogeneously distributed in an acrylic glass sample container with an inner diameter of 13 mm. In some cases the samples were diluted with BN to ensure homogeneous distribution. All isomer shifts are given relative to α-iron. The data were evaluated with the MossWinn program48 using the thin absorber approximation. To model the shape of the spectra in the magnetically ordered phases hyperfine field distributions were either derived by the Hesse–Rübartsch method implemented in MossWinn or Gaussian hyperfine field distributions were assumed.
Magnetic structures were analyzed by powder neutron diffraction (PND) on two Sr2FeO4−x samples with x = 0.133(3) and x = 0.158(6). About 3 grams of material were placed in a vanadium sample container. Data were collected using the diffractometer E2 at the BER II reactor of the Helmholtz-Zentrum Berlin. This instrument is equipped with a pyrolytic graphite (PG) monochromator selecting the neutron wavelength λ = 2.380 Å. PND patterns were recorded at 1.8 and 80 K, well below and above the magnetic ordering temperatures, respectively. Additional PND patterns were measured within this temperature range to determine the temperature dependence of the lattice parameters and of the magnetic order parameters. The powder patterns were collected in the range of diffraction angles from 3.7° to 79.4°. Rietveld refinements of the PND data were carried out with the program FullProf,49 using the nuclear scattering lengths b(O) = 5.805 fm, b(Fe) = 9.54 fm, and b(Sr) = 7.02 fm.50 The magnetic form factors of the Fe atoms were taken from ref. 51.
2.3. Solid-state electrolyte coulometry
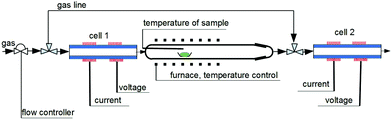
Solid-state electrolyte coulometry (SEC) was employed to analyze and adjust the oxygen content of Sr2FeO4−x, and to establish the corresponding pO2-T-x-diagram. The basic principle of the technique and an overview on its applications has been detailed in ref. 52–54. The setup used for the studies presented here is sketched in Fig. 1. The system operates in a carrier gas mode and consists of two identical solid-state electrolyte (SE) SGM5EL ZIROX cells (doped zirconium oxide, ZIROX-Sensoren und Elektronik GmbH, 17489 Greifswald). Each cell has two electrode systems for potentiometric measurement of the chemical potential of oxygen and coulometric dosing or pumping of oxygen, respectively. The cells are positioned upstream (cell 1) and downstream (cell 2) of a quartz-tube reactor containing the sample whose change in oxygen content in course of the solid-gas interaction is to be studied as a function of temperature. In this setup the space containing the specimen to be equilibrated is thermally decoupled from the SE cells, thus the latter may operate constantly at such a temperature which is optimal for the solid electrolyte (∼750 °C for doped zirconium oxide). This measure taken admits to conveniently optimize the parameters of the gas-solid interaction (temperature program, geometry and material of the reactor) appropriate to the sample under investigation.55 Current I, voltage U, O2 concentration, and temperature of each SE cell, as well as the temperature of the sample were recorded using a customized computer program based on LabVIEW.As carrier gases Ar, or gas mixtures Ar–H2 and Ar–H2–H2O, respectively, were used. The range of partial pressures of oxygen realizable in Ar/O2 is 10−6 to 10−3 bar and for Ar–H2–H2O mixtures 10−32 to 10−9 bar. For the latter, the oxygen partial pressures evolving as function of temperature for selected H2/H2O ratios are documented in Fig. S1 and Table S1 (ESI†). The actual oxygen chemical potential in the carrier gas was controlled in the upstream cell, whereas the uptake or loss of oxygen of the sample during the gas–solid equilibration was monitored in the downstream cell.
The mass of oxygen exchanged during solid-gas equilibration, ΔmO2, is obtained from Faraday's law,
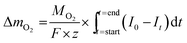 | (1) |
| Δx = ΔmO2 × Ms/(m − ΔmO2)MO2. | (2) |
The actual stoichiometry of the reduced specimen can be derived if the gas-solid reaction starts from a material with a well-defined oxygen content or if it leads to a well-defined final product. The samples of Sr2FeO4 used as starting materials were saturated with respect to oxygen content by annealing under elevated oxygen pressure.
The present experiments were carried out under the following conditions: depending on the size of the sample, the reaction chamber (quartz tube) had a diameter of approx. 18 mm outside and 16 mm inside, or alternatively 25/23 mm. A section of ∼17 cm of the total length of the reaction chamber (22 cm) was heated by a tube furnace. The sample was located in a quartz boat in the middle of the furnace. A thermocouple was attached close to the reaction site in a “quartz nose”, in order to enable a correct and continuous temperature registration at the reaction location.
In an exemplary run, an Ar gas flow of 5 l h−1 with about 3 × 10−6 bar O2 is used as carrier gas, the Sr2FeO4 samples are heated at a rate of 7 °C min−1 and held at the targeted temperatures for 8 h. The O2 activity is fine-tuned via the dosing current I0 (∼10 mA) of the upstream cell.
3. Results and discussion
3.1. Synthesis and characterization of Sr2FeO4
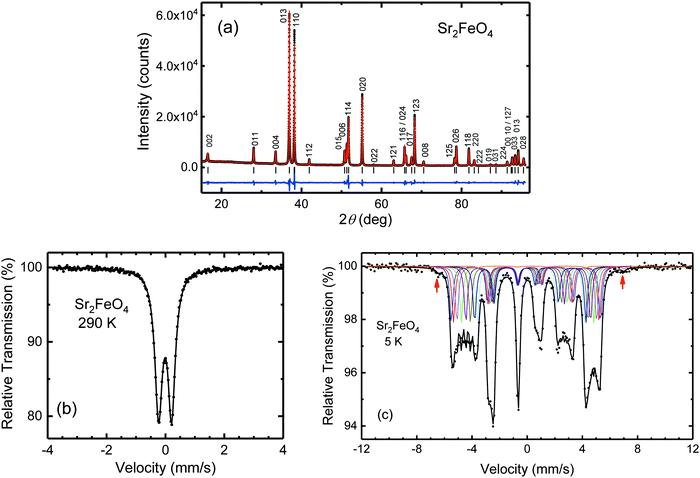
The synthesis of Sr2FeO4 is challenging because of the fact that the compound decomposes above 700 °C into the Ruddlesden-Popper phase Sr3Fe2O7−x and SrO. In previous work Sr2FeO4 was prepared either by heating of SrCO3 and Fe2O3 at 1300 °C and subsequent conversion of the two-phase primary product Sr3Fe2O7−x/SrO to Sr2FeO4 in a flow of high-pressure oxygen (200 bar) at 750 °C,56 or by direct reaction from SrO and Fe2O3 at 650 °C in flowing O2 atmosphere at ambient pressure.37 The latter samples always contained a certain amount of unreacted Fe2O3. Here, we have successfully prepared phase-pure Sr2FeO4 by reaction of SrO and Fe2O3 in an autoclave at an oxygen pressure of 2500 bar at a moderate temperature of 500 °C. A Rietveld profile analysis (Fig. 2(a)) underlines the absence of any impurity phase, and has resulted in crystal structure data (cf. Table S2, ESI†) fully complying with those from previous studies.56 Thermogravimetic analysis of a sample of Sr2FeO4 at 800 °C in an argon flow resulted in the composition Sr2FeO4.00(2) if decomposition of the sample to stoichiometric Sr3Fe2O6 and SrO is assumed.Any oxygen deficiency in Sr2FeO4 can also be estimated using 57Fe Mössbauer spectra. At room temperature (see Fig. 2(b)) the spectrum consists of a simple quadrupole doublet, assuring the absence of any Fe2O3 impurity and confirming that virtually all iron ions exist in the +4-oxidation state. Even more sensitive to small Fe3+ components is the Mössbauer spectrum in the magnetically ordered phase at 5 K which is shown Fig. 2(c). The spectrum is characterized by a complex hyperfine field (Bhf) distribution which reflects the elliptical spiral spin structure of Sr2FeO4 and was approximated by a superposition of eight hyperfine sextets having a typical Fe4+ isomer shift IS = 0.07 mm s−1.39 Detailed inspection of the spectrum reveals a tiny additional hyperfine component with an enlarged Bhf of ∼42 T and an intensity contribution of about 1% (marked by arrows in Fig. 2(c)) which is attributed to Fe3+. In different preparation runs the intensity fraction of this component slightly varied but was always ≤2%. Thus, using the Mössbauer spectra we estimate the oxygen deficiency in the high-pressure synthesized samples as ≤0.01. The good agreement with the results from the TGA reduction experiment at 800 °C in argon atmosphere indicates that under these conditions indeed reduction to the stoichiometric Fe3+ phase Sr3Fe2O6 was achieved.
3.2. Investigation of the oxygen homogeneity range in Sr2FeO4−x by SEC
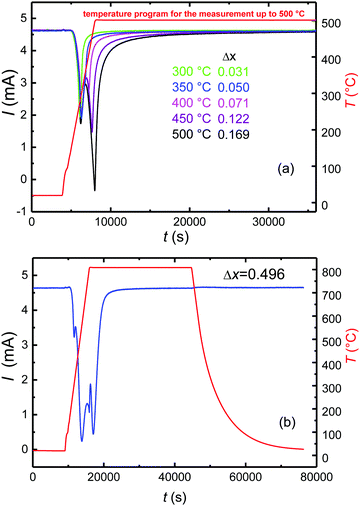
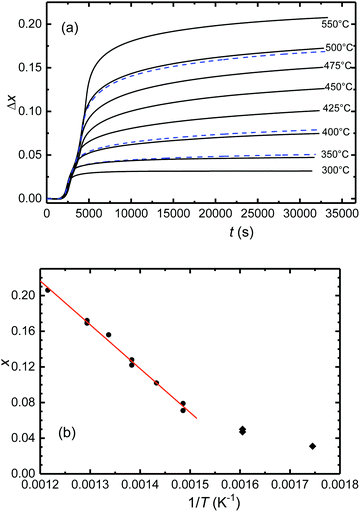
In exploring the homogeneity range of Sr2FeO4−x, pristine samples of Sr2FeO4 were equilibrated at constant temperatures and in argon carrier gas flows of defined oxygen partial pressure. The release of oxygen during solid/gas equilibration of the sample was compensated and monitored in the downstream cell, see section Experimental details.A representative plot of the reduction process as function of time for target temperatures up to 500 °C is displayed in Fig. 3(a). Here, and in all other respective experiments two steps of reduction are apparent. The desorption of oxygen starts at about 150 °C with the maximum occurring at 300 °C. A second peak is apparent for temperatures ≥400 °C and represents further oxygen desorption in the Sr2FeO4−x phase. Integration of the temperature programmed oxygen desorption (TPOD) reaction curves yields the change in oxygen content Δx according to eqn (1) and (2) (Fig. 4(a)). Since during temperature rise the sample and gas phase are not always in equilibrium, details of the shape of the TPOD curve depend on the experimental conditions applied, as sample mass, gas flow and temperature gradient. Using this method oxygen-deficiency in Sr2FeO4−x with x up to about ∼0.20 was realized, which corresponds to Fe3+ fractions up to about 40%. Between 400 and 550 °C (673 and 823 K) a linear relation between x and inverse temperature was observed (Fig. 4(b)).
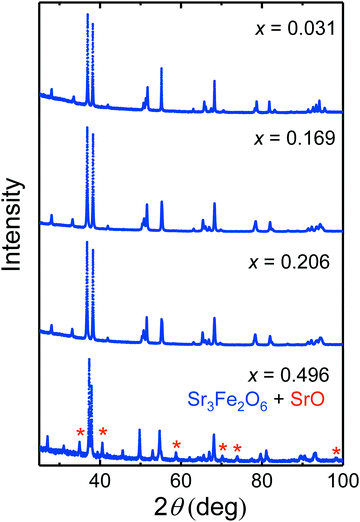
Running the experiments at even higher temperatures of up to 800 °C leads to further reduction steps (Fig. 3(b)) which according to PXRD characterization (see Fig. 5) is accompanied by decomposition of Sr2FeO4−x finally leading to the formation of Sr3Fe2O6 according to
| 2Sr2FeO4 → Sr3Fe2O6 + SrO + ½O2. |
At the same time this decomposition reaction demarcates the limit of oxygen deficiency in Sr2FeO4−x which can be achieved with this method. The change Δx = 0.496 in oxygen content obtained by reduction at 800 °C suggests a full reduction of Fe4+ in stoichiometric Sr2FeO4 to Fe3+ in Sr3Fe2O6 which compares well with the TGA result.
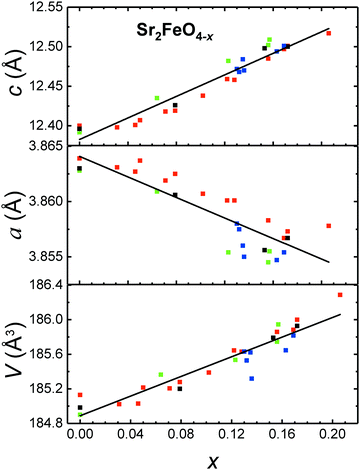
Samples of Sr2FeO4−x with different values of x were synthesized by choosing different target temperatures and subsequent cooling. The samples were characterized by PXRD, a representative set of patterns is displayed in Fig. 5. Up to x ∼ 0.2 (heating up to 550 °C) the patterns still exhibit only reflections which are typical for the tetragonal K2NiF4-type crystal structure (space group I4/mmm) adopted by stoichiometric Sr2FeO4. Line broadening which increases with x may reflect strain effects owing to the oxygen desorption process, stacking faults,39 and a certain inhomogeneity in x. For a sample with even higher x = 0.22 obtained by annealing at 600 °C a broad pattern was observed (not shown), which still shows the main reflections of the K2NiF4-type structure but also additional broad peaks. Further increase of temperature leads to degradation into Sr3Fe2O7−x (space group I4/mmm) and SrO. These results suggest that Sr2FeO4−x samples with x up to ∼0.2 can be prepared by the present route, but decomposition occurs for larger x requiring higher reaction temperatures. In Fig. 6 the lattice parameters a and c as well as the cell volume V are shown for all samples prepared within this study and where the parent structure was retained. It is evident that the c parameter and V increase with increasing x whereas a slightly decreases. The variation of a with x in the Sr2FeO4−x system is in sharp contrast to the behavior of a in the Sr3Fe2O7−x system,31 which contains double layers of FeOm polyhedra (m = 5, 6) and is the n = 2 member of the Srn+1FenO3n+1 Ruddlesden-Popper series. For Sr3Fe2O7−x the lattice parameter a increases linearly with increasing x, i.e. with increasing Fe3+ fraction, whereas the lattice parameter c shows a non-monotonic variation. This can be related to the fact that in Sr3Fe2O7−x the oxygen defects are created in the c direction, namely the oxygen atoms which connect the FeO6 octahedra of the double layers via corner-sharing in stoichiometric Sr3Fe2O7 are removed. Finally, this leads to square pyramidal coordination of Fe3+ in Sr3Fe2O6.31 The different behavior of a in Sr2FeO4−x suggests that mainly O atoms are removed from the FeO2 layers in the ab plane. Then two opposing trends occur: on the one hand, the smaller Fe4+ ions are replaced by larger Fe3+ ions which should lead to an increase in a but on the other hand, the removal of O atoms from the layers leads to a collapse in a such that the overall variation of a with x is quite small. The increase in c mainly reflects the larger size of Fe3+ ions compared to Fe4+ ions. These considerations are in agreement with the different hydride reduction mechanisms proposed for Sr3Fe2O7 and Sr2FeO4.32,44 While for the former the reduction to Sr3Fe2O5 proceeds via Sr3Fe2O6 as intermediate phase, the latter was suggested to be reduced directly to Sr2FeO3 without intermediate phases.44
3.3. Magnetic properties of Sr2FeO4−x
The peculiar electronic situation in strongly covalent Fe(IV) oxides, which is characterized by a negative charge-transfer energy,5 frequently gives rise to antiferromagnetic ordering with helical spin structures. Recently it was demonstrated that Sr2FeO4 adopts an elliptical spin spiral mainly oriented in the ab plane which undergoes a spin-flop transition in external magnetic fields of about 5 T.39 To study the impact of oxygen deficiency, the magnetic properties of Sr2FeO4−x samples with x = 0.13 and 0.16 were investigated by magnetization, powder neutron diffraction, and 57Fe Mössbauer measurements.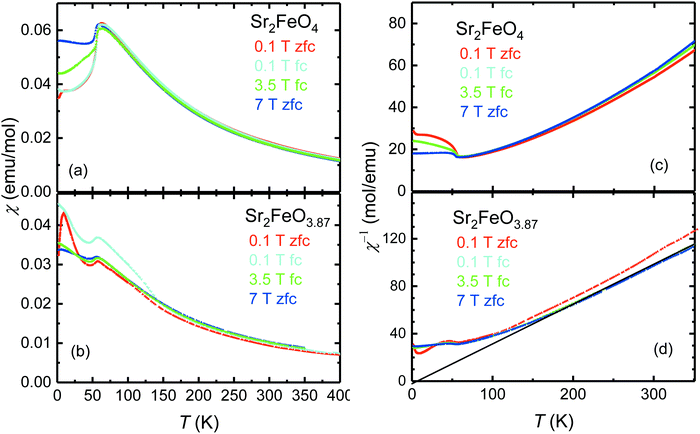 | ||
| Fig. 7 Comparison of the magnetic susceptibilities χ [(a), (b)] and inverse susceptibilities χ−1 [(c), (d)] as a function of temperature of Sr2FeO4 and Sr2FeO3.87. | ||
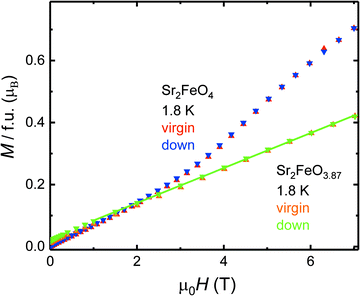 | ||
| Fig. 8 Comparison of the field dependence of the magnetic moments M(H) at T = 1.8 K of Sr2FeO4 and Sr2FeO3.87. | ||
For Sr2FeO3.87 a Curie–Weiss (CW) analysis in the paramagnetic regime using the linear region in the χ−1(T) data collected at 7 T (200–300 K) results in an effective magnetic moment μeff of 4.92 μB which is somewhat smaller than the spin-only value expected for a mixed-valence Fe4+/Fe3+ system with Fe4+ moments of 4.9 μB and Fe3+ moments of 5.9 μB. The corresponding θCW-parameter of +7 K in the CW law [χ(T) = C/(T − θCW), C is the Curie constant] suggests the presence of competing exchange interactions, where compared to Sr2FeO4 the relative strength of ferromagnetic interactions is reduced with respect to antiferromagnetic interactions. In the χ−1(T) data of Sr2FeO4 no well-defined linear region can be identified up to 350 K but the data indicate strong ferromagnetic correlations.
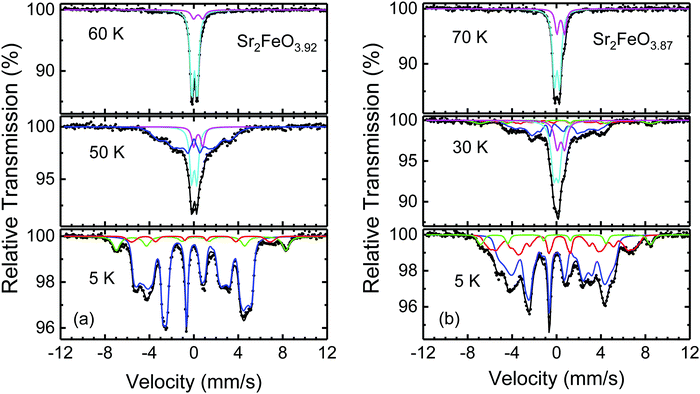
As expected, the Mössbauer spectra of a sample with composition Sr2FeO3.87 exhibit an enhanced fraction of Fe3+ sites (Fig. 9(b)). For fitting the complex shape of the spectrum at 5 K we extracted Bhf distributions for the Fe4+ component (IS = 0.07 mm s−1, 〈Bhf〉 = 25 T) and for the broad major Fe3+ contribution (〈Bhf〉 = 37 T) using the Hesse-Rübartsch method, while a smaller and less broad component with larger Bhf values (〈Bhf〉 = 47.5 T) was described by a Gaussian Bhf distribution. For the Fe4+ component still a linear correlation between Bhf and 2ε was assumed, for the Fe3+ components a single 2ε and equal IS = 0.39 mm s−1 were used. The shape of the Bhf distribution of Fe4+ (Fig. S3, ESI†) differs from that of the parent phase which suggests that the spin structure is modified. The strong disturbance of the spin structure by the oxygen deficiency is also apparent from the presence of about 50% paramagnetic phase even at 30 K which is well below the TN determined by neutron diffraction (see below). Similar spectra were obtained for a Sr2FeO3.84 sample but the fraction of magnetically ordered sites at 30 K is even smaller than in the Sr2FeO3.87 sample (see Fig. S4, ESI†).
The low-temperature spectra of all Sr2FeO4−x samples studied in this work revealed two different Fe3+ components, one with larger and one with smaller Bhf values. We have observed that samples from different reduction runs but with comparable oxygen deficiencies x resulted in different ratios of the two Fe3+ components. For instance, in the 5 K Mössbauer spectrum of a sample of Sr2FeO3.88 the area fraction of the Fe3+ component with larger Bhf (16%, Fig. S5, ESI†), is considerably enhanced compared to that (6%) in the spectrum of the Sr2FeO3.87 sample shown in Fig. 9(b). Remarkably, also the fraction of magnetically ordered sites at 30 K in the Sr2FeO3.88 sample is enhanced. The coexistence of magnetically ordered and collapsed phase below TN suggests that the statistical extraction of oxygen atoms from Sr2FeO4 leads to fragmentation of the magnetic exchange network which results in magnetically ordered regions differing in size and ordering or freezing temperatures. It may be anticipated that removal of apical oxygen atoms has a less drastic effect for the magnetic exchange than the removal of oxygen atoms from the FeO2 layers. A different ratio between apical and layer oxygen defects could be the reason for the differences in the low-temperature Mössbauer spectra of samples from different reduction runs. If we assign the Fe3+ component with larger Bhf to Fe3+ sites from regions where an apical O atom has been removed, it appears reasonable that at a given temperature a larger fraction of magnetically ordered regions persists in samples where the large Bhf-component dominates. Then the Fe3+ signal with smaller Bhf corresponds to regions where O atoms were removed from the layers, and thus for samples where this type of Fe3+ sites dominate, the fraction of magnetically ordered sites at a given temperature is smaller. It cannot be readily decided whether the oxygen vacancies occur around Fe3+ or Fe4+ sites. In the oxygen deficient SrFeO3−x system the formation of square-pyramidal Fe4+O5 units is known,24 whereas in the Sr3Fe2O7−x system Fe3+O5 units occur.31 Our observations suggest that in different sample reduction runs somewhat different microstructures leading to differences in the local Fe3+ environment were produced. Unfortunately, attempts to control the microstructure by varying the reduction conditions were not conclusive.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] which keeps μmax parallel to this axis. Thus, the component μmin may partially turn out of the ab plane in the direction to the c axis.
0] which keeps μmax parallel to this axis. Thus, the component μmin may partially turn out of the ab plane in the direction to the c axis.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]. Listed are the minor and major moments μmin and μmax, the averaged moment μav, the tilting angle β of the ellipse or circle to the c axis and the component τ of the propagation vector k = (τ, τ, 0). Also shown are the estimated correlation lengths ξ, the measured and calculated half widths at half maximum (HWHM) of the satellite (000)± labeled as Δθobs and Δθsam, respectively
0]. Listed are the minor and major moments μmin and μmax, the averaged moment μav, the tilting angle β of the ellipse or circle to the c axis and the component τ of the propagation vector k = (τ, τ, 0). Also shown are the estimated correlation lengths ξ, the measured and calculated half widths at half maximum (HWHM) of the satellite (000)± labeled as Δθobs and Δθsam, respectively
| Sample | Sr2FeO4 | Sr2FeO3.867 | Sr2FeO3.847 | |||
|---|---|---|---|---|---|---|
| T [K] | 1.8 | 80 | 1.8 | 80 | 1.8 | 80 |
| a From ref. 39, where the magnetic structure was analyzed based on the intensities of magnetic Bragg reflections, while here we performed Rietveld refinements using model II of ref. 39. | ||||||
| a [Å] | 3.8459(3) | 3.8457(4) | 3.8409(3) | 3.8414(4) | 3.8473(3) | 3.8480(4) |
| c [Å] | 12.374(2) | 12.370(2) | 12.431(2) | 12.432(3) | 12.475(2) | 12.474(2) |
| V [Å3] | 183.97(6) | 183.89(7) | 183.38(6) | 183.47(8) | 184.64(6) | 184.71(7) |
| z(Sr) | 0.3567(3) | 0.3554(3) | 0.3564(3) | 0.3566(4) | 0.3578(3) | 0.3576(4) |
| z(O1) | 0.1589(4) | 0.1596(4) | 0.1567(4) | 0.1569(5) | 0.1551(3) | 0.1553(4) |
| d ap(Fe–O1) [Å] | 1.967(5) | 1.975(6) | 1.947(5) | 1.948(6) | 1.934(5) | 1.937(6) |
| d eq(Fe–O2) [Å] | 1.9279(2) | 1.9278(2) | 1.9204(2) | 1.9208(2) | 1.9236(2) | 1.9240(2) |
| R F | 0.021 | 0.027 | 0.021 | 0.025 | 0.018 | 0.024 |
| μ min(Fe) [μB] | 2.1(2)/1.9(2)a | — | 1.27(17) | — | 1.23(5) | — |
| μ max(Fe) [μB] | 3.31(8)/3.46(5)a | — | 1.46(15) | — | 1.23 | — |
| μ av(Fe) [μB] | 2.65(6) | — | 1.33(3) | — | 1.23(5) | — |
| β (°) | −65(7)/−63(16)a | — | 0 | — | 0 | — |
| τ | 0.13696(14) | — | 0.1372(4) | — | 0.1371(10) | — |
| R M | 0.030 | — | 0.069 | — | 0.131 | — |
| Δθobs [°] | 0.446 | — | 0.475 | — | 0.731 | — |
| Δθsam [°] | 0 | — | 0.162 | — | 0.579 | — |
| ξ [Å] | — | — | 67 | — | 19 | — |
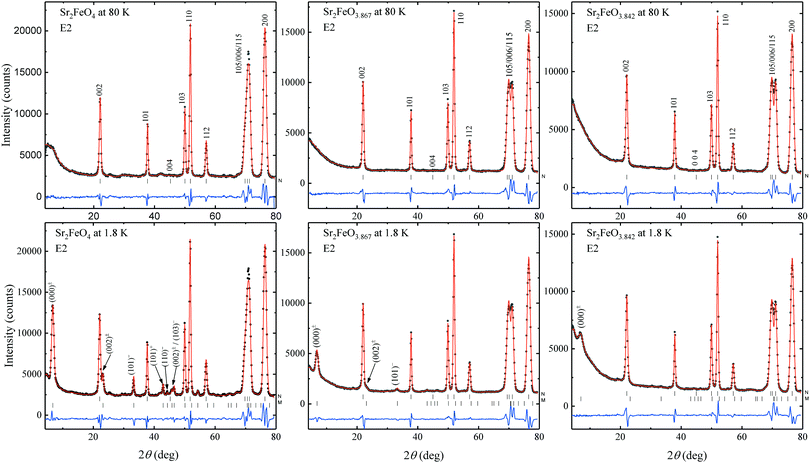
Rietveld refinement of the pattern of Sr2FeO3.87 at 1.8 K resulted in comparable moment components μmin = 1.27(17) μB and μmax = 1.46(15) μB which suggests that the anisotropy in the moments is much reduced compared to Sr2FeO4. The averaged magnetic moment μav = 1.33(3) μB is reduced by a factor of 2 compared to μav = 2.65(6) μB of the parent compound. The refinement of the tilting angle to the c axis leads to a value of 20(15)° which is not significantly different from zero, suggesting that one of the magnetic components is probably oriented parallel to the c axis. Thus, in the final refinement we assumed the presence of a circular helix, where the two components of the moment are aligned now parallel to the directions [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] and [001]. A somewhat increased oxygen deficiency in Sr2FeO3.84 leads to further reduction of the magnetic moment reaching the smaller value μav = 1.23(5) μB. The results of the refinements are summarized in Table 1.
0] and [001]. A somewhat increased oxygen deficiency in Sr2FeO3.84 leads to further reduction of the magnetic moment reaching the smaller value μav = 1.23(5) μB. The results of the refinements are summarized in Table 1.
In Fig. 11(a–c) the thermal variation of the averaged magnetic moments μav, the component τ of the propagation vector k = (τ, τ, 0), as well as the shapes of the magnetic (000)± peaks are shown. Most remarkably, only the magnetic moments and peak shapes are strongly changed in the oxygen-deficient samples, whereas the vector component τ and the Néel temperature TN remain nearly the same as for Sr2FeO4. The vector component τ slightly decreases with increasing temperature for each sample as well as with increasing O deficiency. Our results suggest that oxygen deficiency mainly changes the shape and orientation of the spiral spin configuration while the propagation vector and therefore the rotation angle between adjacent spins remains the same. The spin structures of stoichiometric Sr2FeO4 and Sr2FeO3.87 are illustrated in Fig. 12.
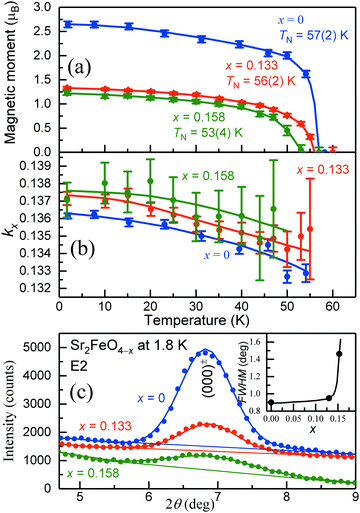 | ||
| Fig. 11 Results of the neutron diffraction study of samples of Sr2FeO4−x with x = 0, 0.133 and 0.158. (a and b) Temperature dependence of the total magnetic moments and vector components kx of Sr2FeO4−x. The averaged moments of Sr2FeO4 were determined from the components μmin and μmax of the ellipse taken from ref. 39. For the two oxygen-deficient samples the magnitudes of μmin and μmax were found to be similar indicating the presence of circular spiral. The solid lines are guides for the eye. (c) Change of the peak shape and intensity of the strongest magnetic satellite (000)± at 1.8 K with increasing oxygen deficiency. The insert shows the variation of the observed full widths at half maximum (FWHM). | ||
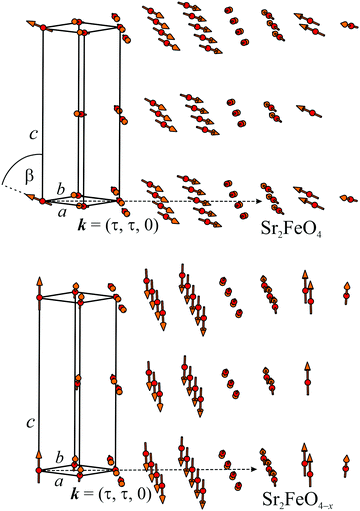 | ||
| Fig. 12 Incommensurate magnetic ordering in Sr2FeO4−x with the propagation vector k = (τ, τ, 0). The magnetic moments of the Fe atoms form ferromagnetic layers perpendicular to the propagation vector k pointing along the [110] direction. Stoichiometric Sr2FeO4 adopts a cycloidal elliptical spin spiral, where the magnetic moments are aligned within the tetragonal ab plane. Nevertheless, a small out-of-plane tilting of the ellipse cannot be excluded, where the moments are tilted away from the c axis by an angle β ∼ 70°.39 The magnetic ordering of the oxygen-deficient compound shows the same k vector, but the tilting angle is decreased to 0° which changes the spin structure to an almost circular spiral. | ||
To compare directly the magnetic intensity and peak shapes of the satellites (000)± the overall scale factors are normalized for all three samples in Fig. 11(c). To analyze the degree of peak broadening of the O-deficient samples more quantitatively we used the profile function parameters determined for the stoichiometric Sr2FeO4 sample. For Sr2FeO4 we assumed a perfect long-range magnetic order. Thus, its half width at half maximum HWHM (HWHM = FWHM/2, where FWHM is the full width at half maximum) represents the instrumental resolution (labeled as Δθinstr). While the difference between the moments of the two O-deficient samples is small, the peak width is strongly increased for Sr2FeO3.84 as shown in the insert of Fig. 11(c). For the estimation of the magnetic correlation lengths, defined as ξ = 1/q, the q-values (in units of Å−1) are determined using q = 4π/λ × sin(Δθsam). The intrinsic HWHMs of Sr2FeO4−x (labeled as Δθsam) are calculated according to Δθsam = √(Δθobs2 − Δθinstr2), where Δθobs is the observed HWHM of the satellite (000)±. The estimated correlation lengths of Sr2FeO3.87 and Sr2FeO3.84 are ξ = 67 Å and 19 Å, respectively. Further details are given in Table 1. The data suggest that increasing oxygen deficiency successively changes the spin arrangement from long-range order to a glassy state.
Such a scenario is supported by the Mössbauer spectra. The spectrum of Sr2FeO3.87 at 5 K indicates complete magnetic ordering or freezing of all iron moments (Fig. 9(b)). In particular, there is no drastic reduction in magnetic hyperfine fields which would be expected for a drastic reduction of the magnetic moments in the oxygen-deficient samples as suggested by the PND results. On the other hand, neutron diffraction yields average magnetic moments and only magnetically ordered regions with sufficiently large correlation length give rise to magnetic Bragg reflections. Thus, only larger-sized magnetically ordered regions are monitored in the PND experiment, whereas also the moments of smaller clusters not contributing to the neutron pattern are completely frozen at the lowest temperatures and seen by the local Mössbauer probe. This explains why the apparent magnetic moments of the iron ions appear to be reduced although Mössbauer spectra still reveal large hyperfine fields. A comparison of the magnetic moments of Sr2FeO3.87 and Sr2FeO4 suggests that only about 50% of the sample volume in the former shows long-range magnetic order detectable in PND experiments. This compares well with the area fraction of about 45% magnetically ordered phase in the 30 K Mössbauer spectrum of Sr2FeO3.87, whereas the other part is already paramagnetic. This fraction can be assigned to smaller magnetic clusters which do not contribute to magnetic Bragg reflections in the PND pattern. In Sr2FeO3.84 the coherence length is reduced and in fact the Mössbauer spectra of a sample at 30 K (Fig. S4, ESI†) show a decreased fraction of magnetically ordered sites which suggests a larger fraction of small magnetic clusters.
It is reasonable to attribute the long-range ordered magnetic regions detectable by powder neutron diffraction to regions where the exchange network is intact enough to maintain a spiral spin structure while the smaller clusters correspond to more disturbed regions. The varying magnetic properties may be related to some inhomogeneity in oxygen deficiency x but it is not clear whether there is a real phase separation which would imply vacancy clustering or ordering. It is known that the magnetic properties of perovskites featuring partial cation order at the transition metal site indeed depend much on the local composition and structure which is not readily apparent from diffraction studies but requires additional microstructural investigations.57 Our Mössbauer studies described above and the spectra depicted in Fig. S5 (ESI†) indicate possible variations in the microstructure in Sr2FeO4−x materials from different synthesis runs.
4. Conclusions
In this work we have explored the K2NiF4-type oxygen-deficient system Sr2FeO4−x by heating stoichiometric Sr2FeO4 in well-defined oxygen partial pressures which were controlled by solid state electrolyte coulometry. Heating to temperatures up to 550 °C allows to prepare samples with x up to about 0.2, while annealing at higher temperatures leads to decomposition into SrO and Sr3Fe2O7−x. The change of lattice parameters with increasing x suggests that oxygen atoms are mainly removed from the FeO2 planes, which has drastic consequences for the magnetic properties. Our magnetization, Mössbauer, and powder neutron diffraction studies on Sr2FeO4−x samples with x = 0.13 and x = 0.16 suggest fragmentation of the magnetic exchange network owing to the oxygen defects and the creation of Fe3+ sites. This leads to the coexistence of larger domains which are long-range ordered and possibly adopt a circular helical spin structure and smaller magnetic clusters with reduced ordering or freezing temperatures. Further studies on Sr2FeO4−x and related cation substituted phases including transport measurements may be of interest with respect to a potential relevance of the system for applications as mixed anionic conductors below 700 °C and in catalysis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to Ralf Koban for help with magnetization measurements and Marcus Schmidt and Susann Scharsach for performing the TGA measurement.Open Access funding provided by the Max Planck Society.
Notes and references
- T. Mizokawa, H. Namatame, A. Fujimori, K. Akeyama, H. Kondoh, H. Kuroda and N. Kosugi, Origin of the band gap in the negative charge-transfer-energy compound NaCuO2, Phys. Rev. Lett., 1991, 67, 1638 CrossRef CAS PubMed.
- T. Mizokawa, D. I. Khomskii and G. A. Sawatzky, Spin and charge ordering in self-doped Mott insulators, Phys. Rev. Lett., 2000, 61, 11263 CAS.
- S. Johnston, A. Mukherjee, I. Elfimov, M. Berciu and G. A. Sawatzky, Charge disproportionation without charge transfer in the rare-earth-element nickelates as a possible mechanism for the metal–insulator transition, Phys. Rev. Lett., 2014, 112, 106404 CrossRef PubMed.
- R. J. Green, M. W. Haverkort and G. A. Sawatzky, Bond disproportionation and dynamical charge fluctuations in the perovskite rare-earth nickelates, Phys. Rev. B, 2016, 94, 195127 CrossRef.
- A. E. Bocquet, A. Fujimori, T. Mizokawa, T. Saitoh, H. Namatame, S. Suga, N. Kimizuka, Y. Takeda and M. Takano, Electronic structure of SrFe4+O3 and related Fe perovskites, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 1561 CrossRef CAS PubMed.
- J. B. MacChesney, R. C. Sherwood and J. F. Potter, Electrical and magnetic properties of the strontium ferrates, J. Chem. Phys., 1965, 43, 1907 CrossRef CAS.
- M. Takano, N. Nakanishi, Y. Takeda, S. Naka and T. Takada, Charge disproportionation in CaFeO3 studied with the Mössbauer effect, Mater. Res. Bull., 1977, 12, 923 CrossRef CAS.
- P. M. Woodward, D. E. Cox, E. Moshopoulou, A. W. Sleight and S. Morimoto, Structural studies of charge disproportionation and magnetic order in CaFeO3, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 844 CrossRef CAS.
- S. E. Dann, M. T. Weller, D. B. Currie, M. F. Thomas and A. D. Al-Rawwas, Structure and magnetic properties of Sr2FeO4 and Sr3Fe2O7 studied by powder neutron diffraction and Mössbauer spectroscopy, J. Mater. Chem., 1993, 3, 1231 RSC.
- P. Adler, Electronic state, magnetism, and electrical transport behavior of Sr3AxFe2O7 (x ≤ 0.4, A = Ba, La), J. Solid State Chem., 1997, 130, 129 CrossRef CAS.
- K. Kuzushita, S. Morimoto, S. Nasu and S. Nakamura, Charge disproportionation and antiferromagnetic order of Sr3Fe2O7, J. Phys. Soc. Jpn., 2000, 69, 2767 CrossRef CAS.
- J.-H. Kim, D. C. Peets, M. Reehuis, P. Adler, A. Maljuk, T. Ritschel, M. C. Allison, J. Geck, J. R. L. Mardegan, P. J. Bereciartua Perez, S. Francoual, A. C. Walters, T. Keller, P. M. Abdala, P. Pattison, P. Dosanjh and B. Keimer, Hidden charge order in an iron oxide square-lattice compound, Phys. Rev. Lett., 2021, 127, 097203 CrossRef CAS PubMed.
- I. Yamada, K. Takata, N. Hayashi, S. Shimokura, M. Azuma, S. Mori, S. Muramaka, Y. Shimakawa and M. Takano, A perovskite containing quadrivalent iron as a charge-disproportionated ferrimagnet, Angew. Chem., Int. Ed., 2008, 47, 7032 CrossRef CAS PubMed.
- Y. Hosaka, N. Ichikawa, T. Saitoh, P. Manuel, D. Khalyavin, J. P. Attfield and Y. Shimakawa, Two-dimensional charge disproportionation of the unusual valence state Fe4+ in a layered double perovskite, J. Am. Chem. Soc., 2015, 137, 7468 CrossRef CAS PubMed.
- M. Takano, S. Nasu, T. Abe, K. Yamamoto, S. Endo, Y. Takeda and J. B. Goodenough, Pressure-induced high-spin to low-spin transition in CaFeO3, Phys. Rev. Lett., 1991, 67, 3267 CrossRef CAS PubMed.
- P. Adler, U. Schwarz, K. Syassen, G. K. Rozenberg, G. Yu. Machiavariani, A. P. Milner, M. P. Pasternak and M. Hanfland, Collapse of the charge disproportionation and covalency-driven insulator-metal transition in Sr3Fe2O7 under pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 4609 CrossRef CAS.
- T. Kawakami, Y. Sekiya, A. Mimura, K. Kobayashi, K. Tokumichi, I. Yamada, M. Mizukami, N. Kawamura, Y. Shimakawa, Y. Ohishi, N. Hirao, N. Ishimatsu, N. Hayashi and M. Takano, Two-step suppression of charge disproportionation in CaCu3Fe4O12 under pressure, J. Phys. Soc. Jpn., 2016, 85, 034716 CrossRef.
- T. Takeda, Y. Yamaguchi and H. Watanabe, Magnetic structure of SrFeO3, J. Phys. Soc. Jpn., 1972, 33, 967 CrossRef CAS.
- N. Hayashi, T. Yamamoto, H. Kageyama, M. Nishi, Y. Watanabe, T. Kawakami, Y. Matsushita, A. Fujimori and M. Takano, BaFeO3: a ferromagnetic iron oxide, Angew. Chem., Int. Ed., 2011, 50, 12547 CrossRef CAS PubMed.
- J.-H. Kim, A. Jain, M. Reehuis, D. C. Peets, C. Ulrich, J. T. Park, E. Faulhaber, A. Hoser, H. C. Walker, D. T. Adroja, A. C. Walters, D. S. Inosov, A. Maljuk and B. Keimer, Competing exchange interactions at the verge of a metal-insulator transition in the two-dimensional spiral magnet Sr3Fe2O7, Phys. Rev. Lett., 2014, 113, 147206 CrossRef PubMed.
- S. Ishiwata, M. Tokunaga, Y. Kaneko, D. Okuyama, S. Wakimoto, K. Kakurai, T. Arima, Y. Taguchi and Y. Tokura, Versatile helimagnetic phases under magnetic fields in cubic perovskite SrFeO3, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 05447 CrossRef.
- S. Chakraverty, T. Matsuda, H. Wadati, J. Okamoto, Y. Yamasaki, H. Nakao, Y. Murakami, S. Ishiwata, M. Kawasaki, Y. Taguchi, Y. Tokura and H. Y. Hwang, Multiple helimagnetic phases and topological Hall effect in epitaxial thin films of pristine and Co-doped SrFeO3, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 220405(R) CrossRef.
- S. Ishiwata, T. Nakajima, J. H. Kim, D. S. Inosov, N. Kanazawa, J. S. White, J. L. Gavilano, R. Geogii, K. Seemann, G. Brandl, P. Manuel, D. D. Khalyavin, S. Seki, Y. Tokunaga, M. Kinoshita, Y. W. Long, Y. Kaneko, Y. Taguchi, T. Arima, B. Keimer and Y. Tokura, Emergent topological spin structures in the centrosymmetric cubic perovskite SrFeO3, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 101, 134406 CrossRef CAS.
- J. P. Hodges, S. Short, J. D. Jorgensen, X. Xiong, B. Dabrowski, S. M. Mini and C. W. Kimball, Evolution of the oxygen-vacancy ordered crystal structures in the perovskite series SrnFenO3n+1 (n = 2, 4, 8, and ∞), and the relationship to electronic and magnetic properties, J. Solid State Chem., 2006, 151, 190 CrossRef.
- M. Reehuis, C. Ulrich, A. Maljuk, Ch Niedermeyer, B. Ouladdiaf, A. Hoser, T. Hofmann and B. Keimer, Neutron diffraction study of spin and charge ordering in SrFeO3−δ, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184109 CrossRef.
- A. Lebon, P. Adler, C. Bernhard, A. V. Boris, A. V. Pimenov, A. Maljuk, C. T. Lin, C. Ulrich and B. Keimer, Magnetism, charge order, and giant magnetoresistance in SrFeO3−δ single crystals, Phys. Rev. Lett., 2004, 92, 037202 CrossRef CAS PubMed.
- P. Adler, A. Lebon, V. Damljanović, C. Ulrich, C. Bernhard, A. V. Boris, A. Maljuk, C. T. Lin and B. Keimer, Magnetoresistance effects in SrFeO3−δ: dependence on phase composition and relation to magnetic and charge order, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094451 CrossRef.
- Y. Tsujimoto, C. Tassel, N. Hayashi, T. Watanabe, H. Kageyama, K. Yoshimura, M. Takano, M. Ceretti, C. Ritter and W. Paulus, Infinite-layer iron oxide with a square-planar coordination, Nature, 2007, 450, 1062 CrossRef CAS PubMed.
- D. C. Peets, J.-H. Kim, P. Dosanjh, M. Reehuis, A. Maljuk, N. Aliouone, C. Ulrich and B. Keimer, Magnetic phase diagram of Sr3Fe2O7−δ, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 214410 CrossRef.
- P. K. Gallagher, J. B. MacChesney and D. N. E. Buchanan, Mössbauer effect in the system Sr3Fe2O6–7, J. Chem. Phys., 1966, 45, 2466 CrossRef CAS.
- S. E. Dann, M. T. Weller and D. B. Currie, Structure and oxygen stoichiometry in Sr3Fe2O7−y, 0 ≤ y ≤ 1.0, J. Solid State Chem., 1992, 97, 179 CrossRef CAS.
- H. Kageyama, T. Watanabe, Y. Tsujimoto, A. Kitada, Y. Samida, K. Kanamori, K. Yoshimura, N. Hayashi, S. Muranaka, M. Takano, M. Ceretti, W. Paulus, C. Ritter and G. André, Spin-ladder iron oxide: Sr3Fe2O5, Angew. Chem., Int. Ed., 2008, 47, 5740 CrossRef CAS PubMed.
- B. Li, S. He, J. Li, X. Yue, J. T. S. Irvine, D. Xie, J. Ni and C. Ni, A Ce/Ru codoped SrFeO3−δ perovskite for a coke-resistant anode of a symmetrical solid oxide fuel cell, ACS Catal., 2020, 10, 14398 CrossRef CAS.
- K. Wiik, S. Aasland, H. L. Hansen, I. L. Tangen and R. Ødegård, Oxygen permeation in the system SrFeO3−x–SrCoO3−y, Solid State Ionics, 2002, 152–153, 675 CrossRef CAS.
- K. Tamai, S. Hosokawa, K. Kato, H. Asakura, K. Teramura and T. Tanaka, Low-temperaure NO oxidation using lattice oxygen in Fe-site substituted SrFeO3−δ, Phys. Chem. Chem. Phys., 2020, 22, 24181 RSC.
- R. Scholder, H. v Bunsen and W. Zeiss, Über Orthoferrate, Z. Anorg. Allg. Chem., 1956, 283, 330 CrossRef CAS.
- P. Adler, Properties of K2NiF4-type oxides Sr2FeO∼4, J. Solid State Chem., 1994, 108, 275 CrossRef CAS.
- P. Adler, A. F. Goncharov, K. Syassen and E. Schönherr, Optical reflectivity and Raman spectra of Sr2FeO4 under pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 11396 CrossRef CAS PubMed.
- P. Adler, M. Reehuis, N. Stüßer, S. A. Medvedev, M. Nicklas, D. C. Peets, J. Bertinshaw, C. K. Christensen, M. Etter, A. Hoser, L. Schröder, P. Merz, W. Schnelle, A. Schulz, Q. Mu, D. Bessas, A. Chumakov, M. Jansen and C. Felser, Spiral magnetism, spin flop, and pressure-induced ferromagnetism in the negative charge-transfer-gap insulator Sr2FeO4, Phys. Rev. B: Condens. Matter Mater. Phys., 2022, 105, 054417 CrossRef CAS.
- G. K. Rozenberg, A. P. Milner, M. P. Pasternak, G. R. Hearne and R. D. Taylor, Experimental confirmation of a p–p intraband gap in Sr2FeO4, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 10283 CrossRef CAS.
- Y. Takeda, K. Imayoshi, N. Imanishi, O. Yamamoto and M. Takano, Preparation and characterization of Sr2−xLaxFeO4 (0 ≤ x ≤ 1), J. Mater. Chem., 1994, 4, 19 RSC.
- T. Omata, K. Ueda, H. Hosono, M. Katada, N. Ueda and H. Kawazoe, Electrical and magnetic properties of hole-doped Sr1+xLa1−xFeO4, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 10194 CrossRef CAS PubMed.
- Q. Zhao, M. D. Smith and H.-C. zur Loye, Crystal growth and structure determination of the mixed-valent iron(III/IV) oxides Sr2−xLnxFeO4 (Ln = Nd, Sm, Eu), J. Chem. Crystallogr., 2011, 41, 674 CrossRef CAS.
- C. Tassel, L. Seinberg, N. Hayashi, S. Ganesanpotti, Y. Ajiro, Y. Kobayashi and H. Kageyama, Sr2FeO3 with stacked infinite chains of FeO4 square planes, Inorg. Chem., 2013, 52, 6096 CrossRef CAS PubMed.
- C. Linke and M. Jansen, Über Ag2SnO3, das erste Silberstannat, Z. Anorg. Allg. Chem., 1997, 623, 1441 CrossRef CAS.
- H. M. Rietveld, A profile refinement method for nuclear and magnetic structures, J. Appl. Crystallogr., 1969, 2, 65 CrossRef CAS.
- L. Akselrud and Y. Grin, WinCSD: software package for crystallographic calculations (Version 4), J. Appl. Crystallogr., 2014, 47, 803 CrossRef CAS.
- Z. Klencsár, E. Kuzmann and A. Vértes, User-friendly software for Mössbauer spectrum analysis, J. Radioanal. Nucl. Chem., 1996, 210, 105 CrossRef.
- J. Rodríguez-Carvajal, Recent advances in magnetic structure determination by neutron powder diffraction, Phys. B, 1993, 192, 55 CrossRef.
- V. F. Sears, in International Tables for Crystallography, ed. A. J. C. Wilson, Kluwer Academic Publishers, Dordrecht/Boston/London, 1995, vol. C, p. 383 Search PubMed.
- P. J. Brown, in International Tables for Crystallography, ed. A. J. C. Wilson, Kluwer Academic Publishers, Dordrecht/Boston/London, 1995, vol. C, p. 391 Search PubMed.
- K. Teske, H. Oppermann and G. Stöver, Zur Bestimmung der Phasenbreite von Zinkoxid, Z. Anorg. Allg. Chem., 1984, 511, 72 CrossRef CAS.
- M. Bode, K. Teske and H. Ullmann, Fest-Elektrolyt-Coulometrie (FEC). Eine vielseitige Methode zur Untersuchung von Gas-Festkörper-Wechselwirkungen, GIT-Fachz. Lab, 1994, 38, 495 CAS.
- K. Teske, H. Ullmann and N. Trofimenko, Thermal analysis of transition metal and rare earth oxide system-gas interactions by a solid electrolyte-based coulometric technique, J. Thermal Anal., 1997, 49, 1211 CrossRef CAS.
- V. Vashook, J. Zosel and U. Guth, Oxygen solid electrolyte coulometry (SEC), J. Solid State Electrochem., 2012, 16, 3401 CrossRef CAS.
- S. E. Dann, M. T. Weller and D. B. Currie, Synthesis and structure of Sr2FeO4, J. Solid State Chem., 1991, 92, 237 CrossRef CAS.
- M. Hendrickx, Y. Tang, E. C. Hunter, P. D. Battle and J. Hadermann, Structural and magnetic properties of the perovskites A2LaFe2SbO9 (A = Ca, Sr, Ba), J. Solid State Chem., 2021, 295, 121914 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02156k |
| This journal is © the Owner Societies 2022 |