Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploration and validation of force field design protocols through QM-to-MM mapping†
Chris
Ringrose
a,
Joshua T.
Horton
 a,
Lee-Ping
Wang
a,
Lee-Ping
Wang
 b and
Daniel J.
Cole
b and
Daniel J.
Cole
 *a
*a
aSchool of Natural and Environmental Sciences, Newcastle University, Newcastle upon Tyne NE1 7RU, UK. E-mail: daniel.cole@ncl.ac.uk
bDepartment of Chemistry, The University of California at Davis, Davis, California 95616, USA
First published on 29th June 2022
Abstract
The scale of the parameter optimisation problem in traditional molecular mechanics force field construction means that design of a new force field is a long process, and sub-optimal choices made in the early stages can persist for many generations. We hypothesise that careful use of quantum mechanics to inform molecular mechanics parameter derivation (QM-to-MM mapping) should be used to significantly reduce the number of parameters that require fitting to experiment and increase the pace of force field development. Here, we design and train a collection of 15 new protocols for small, organic molecule force field derivation, and test their accuracy against experimental liquid properties. Our best performing model has only seven fitting parameters, yet achieves mean unsigned errors of just 0.031 g cm−3 and 0.69 kcal mol−1 in liquid densities and heats of vaporisation, compared to experiment. The software required to derive the designed force fields is freely available at https://github.com/qubekit/QUBEKit.
1 Introduction
Classical molecular mechanics force fields are widely used approximations to recover the energy and forces of an atomistic system as a function of its nuclear coordinates.1,2 Force fields are an invaluable companion to quantum mechanical modelling in cases where the number of atoms or the time scale to be modelled would be otherwise restricted. Such techniques have seen applications in, for example, the modelling of battery materials,3,4 organic light-emitting diodes,5,6 crystal structure prediction,7 and particularly in computer-aided drug design where they form the basis of molecular dynamics, docking and free energy simulations for calculating protein–ligand binding affinity.8,9Typically, for modelling organic molecules in biology and chemistry, the force field is a sum of bonded (including harmonic bond-stretching and angle-bending terms, and anharmonic 4-body torsion potentials) and non-bonded (including Coulombic and Lennard-Jones interactions) terms. Small molecule force fields of this form include GAFF,10 CGenFF,11 OPLS,12 and the Open Force Field 1.0.0 (‘Parsley’) force field.13 In general, the bonded and charge parameters of the force field may be fit to quantum mechanical potential energy surfaces and electrostatic potentials, respectively. On the other hand, the Lennard-Jones parameters are nearly always fit to experimental pure liquid properties.12,14 To be broadly effective, small molecule force fields require accurate parameterisation of each of the above terms for all chemical space. While recent trends have seen parameters fit to larger datasets, complete coverage is challenging. Numerous studies, such as the SAMPL blind challenges15 have shown that there is plenty of room for improvement when it comes to predictive molecular modelling with force fields.
In contrast to the empirical molecular mechanics force fields common in biological modelling, interatomic potentials may instead be derived directly from quantum mechanics (QM). For example, intermolecular perturbation theory may be used to separate the full QM interaction energy into physically motivated components,16 or machine learning based potentials may be trained on QM energies and forces.17 These methods are attractive because they remove the empiricism of the force field approach, but they are computationally more expensive, and unless they fully incorporate, for example, many body and quantum nuclear effects they are unlikely to reproduce condensed phase observables with sufficient accuracy.
QM-to-MM mapping reduces size of parameter search space
Between the empiricism of typical classical force fields and the accurate, yet expensive, ab initio derived force fields, increasing attention is being drawn to mapping physically motivated parameters from QM into simple MM functional forms. By deriving bespoke force field parameters for the molecule under study directly from QM, the number of transferable, empirical parameters to be fit is significantly reduced. By retaining common MM functional forms, the potentials may readily be implemented in widely used MM software and used in, for example, free energy calculations. Bespoke intramolecular bond, angle and, particularly, torsion parameters may be readily derived from a small number of QM calculations either by fitting to Hessian matrices18–21 or potential energy surface scans.22,23 Atom-centred partial charges can be routinely derived from either semi-empirical calculations,24,25 or QM electrostatic potential fitting,26,27 or atoms-in-molecule electron density partitioning.28–31Less common, but perhaps most interestingly, is the possibility of using atoms-in-molecule electron density partitioning to derive other components of the non-bonded interaction from QM, in particular dispersion coefficients (C6,32–35C8,36,37…), atomic polarisabilities,37,38 and off-centre charges to model electronic anisotropy.33,34 For example, Visscher and Geerke have derived a polarisable force field model, with a higher order dispersion term derived from iterative Hirshfeld atoms-in-molecule analysis, and applied it to small-molecule amino acid analogues.39 Of the 138 nonbonded parameters in their model, 132 are determined from QM, leaving just six to be fit to experiment. Kantonen et al.40 employ a mapping of information from minimal basis iterative stockholder (MBIS) atomic electron densities (in particular the decay constants of the electron densities), to derive atom-specific Lennard-Jones parameters. The mapping parameters (two per element) are fit to experimental liquid properties using the ForceBalance software.41
Our own work has focused on the development of a QUantum mechanical BEspoke (QUBE) force field and associated toolkit (QUBEKit),34 built on QM-to-MM parameter mapping. QUBE bond and angle force field parameters are derived from the QM Hessian matrix of the molecule under study, using the modified Seminario method.42 Atomic partial charges are computed from the density derived electrostatic and chemical (DDEC) partitioned atomic electron densities.43,44 The Tkatchenko–Scheffler method32 is used to derive C6 parameters from the same atomic electron densities, and the repulsive part of the Lennard-Jones potential is derived from atoms-in-molecule atomic radii.33 Once all other parameters are in place, flexible torsion parameters can be fit to QM dihedral scans using interfaces between QUBEKit and external QM and MM software packages.34 A small number of mapping parameters (in this case free atom radii for use in the derivation of Lennard-Jones parameters) is used to ensure accuracy of condensed phase properties,34 and the resulting force fields have also been shown to perform well in the calculation of protein–ligand binding free energies.45–47
Force field design choices can be tested and optimised
The above mentioned force fields derived from QM-to-MM parameter mappings have a simple functional form, are straightforward to derive from a small number of simple QM calculations, and are bespoke to the system under study. However, despite the advantages, there are still multiple design choices that must be made when constructing a QM-derived force field. These range from the choice of functional form to use for the final force field, to the choice of underlying QM method to compute the electron density, how to partition it between atoms, and how to map the partitioned density to force field parameters. These choices may be regarded as hyperparameters of the model.48 Drawing on lessons from the machine learning field, separate models for each hyperparameter should be systematically trained and tested. However, these hyperparameters are often ‘baked in’ to the design of the force field, and correcting known problems can be challenging.49 Until recently, the manual training of force field parameters for a given set of hyperparameters (for example, Lennard-Jones parameters for a given charge model) would be extremely time-consuming. However, allied with improvements in data collection and retrieval,50 advances in automated parameter fitting to experimental liquid properties now make this possible.41,51,52 Most notably, the ForceBalance software enables reproducible and automated force field parameterisation against a set of target data that can include either QM or experimental input data. In the context of the current work, ForceBalance was used to tune the QM-to-MM mapping parameters against experimental liquid data in the aforementioned study by Kantonen et al.,40 and was also used to rapidly re-fit Lennard-Jones parameters for a range of proposed implicit solvent models (hyperparameters) in the development of the RESP2 method.27An automated toolkit for force field design, training and testing
Until now, the systematic testing of design choices in MM force fields has been rather limited, and it is almost impossible for individual users to undertake this task due to the scale of the parameter optimisation problem. In what follows, we describe our interface between the QUBEKit and ForceBalance software packages. This open source (including all dependencies) software workflow allows users to make a choice of force field hyperparameters, train the model against experimental liquid properties, and unambiguously test the resulting accuracy. We provide improved protocols for deriving the positions and magnitudes of off-site charges (virtual sites) to model anisotropic electron density from the output of atoms-in-molecule electron density partitioning calculations, as well as tools for including them in torsion parameter fitting. Using a train/test split of 15/51 small, organic molecules, we develop 15 force field protocols that aim to test the accuracy of different choices of (i) underlying QM method and basis set, (ii) atoms-in-molecule electron density partitioning method, (iii) implicit solvent model parameters (used to pre-polarise charges for use in the condensed phase), (iv) mapping of atomic electron densities to LJ parameters, (v) assignment of Lennard-Jones parameters to polar hydrogen atoms, and (vi) use of virtual sites to model anisotropic electron density. We show that a wide range of different choices can be made in the force field design process, some of which do not affect the overall accuracy, and some of which show marked improvements. For our best performing protocol, we provide all of the parameters (including those for halogens and sulphur) required for users to derive their own force fields using the QUBEKit software. With these developments comes the potential for future rapid design of next-generation force fields.2 Methods
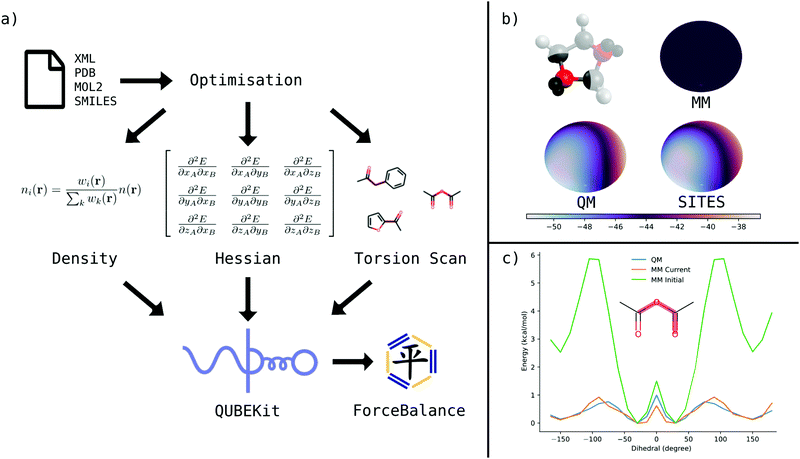
2.1 QUBEKit workflow
QUBEKit is a largely Python 3.6+ based force field derivation toolkit for mac and Linux operating systems. By combining multiple open-source bioinformatics and quantum chemistry packages into a single workflow, it is possible to generate bespoke force fields for molecular dynamics simulations (Fig. 1(a)). QUBEKit can be run using only Anaconda or PyPI installable open-source packages, with the option to use Gaussian53 for QM and torsion optimisations, and the fortran package Chargemol29,30 for atoms-in-molecule analysis.The general workflow of QUBEKit begins with generating a set of initial parameters for an OPLS-style force field:
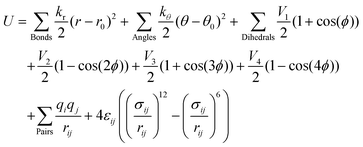 | (1) |
QUBE uses atoms-in-molecule (AIM) electron density partitioning to obtain all non-bonded parameters of the force field. AIM methods partition the total electron density n(r) into overlapping atomic densities ni(r) according to:
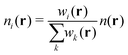 | (2) |
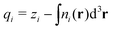 | (3) |
| Model | QM method | Solvent | V-Sites | AIM | LJ | MUE ρ | MUE ΔHvap |
|---|---|---|---|---|---|---|---|
| 0 | ωB97X-D/6-311++G(d,p) | IPCM, ε = 4 | No | DDEC6 | TS | 0.0274 | 0.766 |
| 1a | B3LYP-D3(BJ)/DZVP | IPCM, ε = 4 | No | DDEC6 | TS | 0.0271 | 0.726 |
| 1b | HF/6-31G(d) | None | No | DDEC6 | TS | 0.0248 | 0.731 |
| 2a | ωB97X-D/6-311++G(d,p) | IPCM, ε = 2 | No | DDEC6 | TS | 0.0296 | 0.772 |
| 2b | ωB97X-D/6-311++G(d,p) | IPCM, ε = 10 | No | DDEC6 | TS | 0.0237 | 0.783 |
| 2c | ωB97X-D/6-311++G(d,p) | IPCM, ε = 20 | No | DDEC6 | TS | 0.0285 | 0.678 |
| 3a | ωB97X-D/6-311++G(d,p) | IPCM, ε = 4 | No | DDEC3 | TS | 0.0213 | 0.475 |
| 3b | B3LYP-D3(BJ)/DZVP | Chloroform | No | MBIS | TS | 0.0159 | 0.578 |
| 4a | ωB97X-D/6-311++G(d,p) | IPCM, ε = 4 | No | DDEC6 | H0 | 0.0235 | 0.896 |
| 4b | ωB97X-D/6-311++G(d,p) | IPCM, ε = 4 | No | DDEC6 | α , β | 0.0206 | 0.587 |
| 5a | ωB97X-D/6-311++G(d,p) | IPCM, ε = 4 | Yes | DDEC6 | TS | 0.0190 | 0.441 |
| 5b | ωB97X-D/6-311++G(d,p) | IPCM, ε = 4 | Yes | DDEC6 | α , β | 0.0209 | 0.244 |
| 5c | ωB97X-D/6-311++G(d,p) | IPCM, ε = 4 | Yes | DDEC3 | TS | 0.0163 | 0.357 |
| 5d | B3LYP-D3(BJ)/DZVP | IPCM, ε = 4 | Yes | DDEC6 | TS | 0.0141 | 0.450 |
| 5e | B3LYP-D3(BJ)/DZVP | Chloroform | Yes | MBIS | α , β | 0.0175 | 0.480 |
In the original QUBE force field, the non-bonded part of the force field includes the Lennard-Jones interaction:
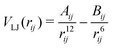 | (4) |
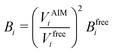 | (5) |
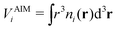 | (6) |
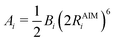 | (7) |
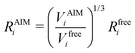 | (8) |
Transforming the Ai and Bi parameters to the σi and εi parameters of eqn (1), we obtain (a full derivation is given in ESI,† S1.1):
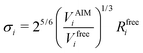 | (9) |
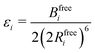 | (10) |
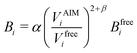 | (11) |
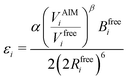 | (12) |
An additional choice in force field design is whether to include Lennard-Jones parameters on polar hydrogen atoms, or to effectively redistribute them onto the neighbouring heavy atom33 (see ESI,† S1.3). Different choices are made for example in the design of the TIP3P and CHARMM modified water model,65 while there is precedent for improved agreement with liquid data using Lennard-Jones parameters on polar hydrogen atoms.66 While separate mapping parameters have been previously proposed for polar and non-polar hydrogen atoms, the effect on accuracy has not been directly explored,40 and so we add this comparison to our list of model protocols to be tested (Table 1, model 4a).
A final consideration to be made when deriving the non-bonded parameter set is how to treat atoms with significant anisotropy in their electron density, such that an atom-centred point charge gives a poor approximation to the full QM electrostatic potential at the surface of the molecule. Such situations are commonly treated in MM force fields using an off-centre charge (or “virtual site”), as used in, for example, the TIP4P water model67 and various treatments of lone-pairs and σ-holes in common force fields.68–70 In keeping with our general force field philosophy, we previously proposed a method to derive the positions and magnitudes of off-site charges, where required, directly from the partitioned QM electron density. Full details are given elsewhere,34 but in brief the charges are positioned to minimise the quantity:
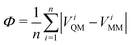 | (13) |
A similar protocol is followed in the current work. Key differences are discussed here and full implementation details are provided in the ESI,† Section S2. It is desirable to perform the optimisation of eqn (13) directly in QUBEKit, but storage and imports of the full atomic electron density is inefficient. Instead, ViQM is now reconstructed from the QM atomic multipole moments, up to quadrupole order, which are readily extracted from either Chargemol (using the DDEC AIM method)29,30 or the PSI4 software (using the MBIS AIM method).60 For atoms with isotropic electron density, the atomic multipoles are low, and the QM electrostatic potential is well-described by an atom-centred point charge (monopole). For atoms with anisotropic electron density (defined here as Φ > 1 kcal mol−1), eqn (13) is minimised with respect to the virtual site charge and position, using the Scipy python package.
Fig. 1(b) shows example surface plots of the electrostatic potential energy (ESP) at 1.4× the van der Waals surface of an oxygen atom in 1,3-dioxolane. The bottom-left plot shows the QM-calculated ESP, up to quadrupole order. The top-right plot shows the ESP using an atom-centred monopole, which simply gives a uniform, averaged ESP over the entire surface of the atom. The difference between these two plots at every point allows the calculation of the error function, eqn (13). The bottom-right plot shows an approximation of the QM ESP, constructed with the addition of just two virtual sites, which are able to recover the expected anisotropy in the ESP. Table 1 shows the experiments performed in what follows to test the effect of including virtual sites on our force field model accuracy (models 5a–5e).
In previous works, new non-bonded force field parameters tend to be investigated in conjunction with the bonded parameters of standard transferable force fields, which may lead to incompatibility given the close inter-dependency between parameter types. Here, the benefit of assembling the force fields using the QUBEKit package, is that torsion parameters for rotatable bonds may be re-fit in a simple, automated manner for compatibility with the rest of the bonded and non-bonded parameters. Using a new interface between QUBEKit, ForceBalance41 and TorsionDrive,71 dihedral parameters of any freely rotatable bonds were optimised via a least squares minimisation of the root mean square error (RMSE) between QM and MM torsional potential energy surfaces. We use the same procedure for parameter fitting as the recent Open Force Field Parsley force field,13 and full details are provided in ESI,† Section S3.1. A new feature in this work is that we have modified the ForceBalance code to allow parameter fitting in the presence of local coordinate virtual sites. These virtual sites then inherit their exceptions and exclusions from the parent atom meaning they interact with the same rules as the parent. The code may be obtained from conda-forge or github (https://github.com/leeping/forcebalance), and is available from version 1.9.0 onward. Fig. 1(c) demonstrates an example of bespoke dihedral parameter fitting for the molecule acetic anhydride, which has two virtual sites on the central oxygen atom. With the initial parameter set (which is incompatible with the new Lennard-Jones parameters and virtual sites), the RMS error is more than 3 kcal mol−1, but following fitting it falls to just 0.12 kcal mol−1. In fact, the average RMSE across all molecules in the 51 molecule test set (a total of 117 scans) after fitting was just 0.13 kcal mol−1.
2.2 ForceBalance workflow
As outlined in Fig. 1(a), for each choice of force field design protocol (Table 1), the ForceBalance software41 was employed to optimise the set of fitting parameters. These parameters were the Rfreei parameters of H, C, N and O (eqn (8)), and optionally the dispersion rescaling parameters α and β (eqn (11)). Where Lennard-Jones parameters were included on polar hydrogen atoms, it was found that a separate Rfreei parameter was required for these atoms. Optimisation was performed against the experimental liquid densities and enthalpies of vaporisation of a training set of 15 molecules. The training set comprised molecules containing H, C, N and O only, and a range of functional groups (ESI,† Section S4). It was identical to that used in the training of the RESP2 charge fitting procedure,27 except that one molecule (N1(C)CCOCC1) was replaced by CN(C)C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O to ensure that sampling complex potential energy surfaces did not influence the fit. For two of the best performing models, a further ten molecules containing halogens (F, Cl and Br) and sulphur atoms were added to the training set,51 and the fitting parameters were co-optimised for the combined set of 25 molecules.
O to ensure that sampling complex potential energy surfaces did not influence the fit. For two of the best performing models, a further ten molecules containing halogens (F, Cl and Br) and sulphur atoms were added to the training set,51 and the fitting parameters were co-optimised for the combined set of 25 molecules.
ForceBalance uses the reference data to produce an objective function, which is minimised with a non-linear optimisation algorithm through numerical differentiation of physical properties with respect to the fitting parameters. Further details are given in the ESI,† Section S3.2. To create the inputs required by ForceBalance, QUBEKit automatically combines the force fields of the individual molecules, along with algebraic expressions that transform the fitting parameters into the σi and εi parameters of the force field (see, for example, eqn (9) and (10)), into a single xml file. The full training sets, experimental data, example ForceBalance input files, and tutorial are provided in the ESI.†
Following the completion of ForceBalance training runs, the final fitting parameters are used to re-calculate the Lennard-Jones and re-fit the torsion parameters in QUBEKit. Training set accuracy was then confirmed by re-computing the liquid properties of the training set molecules using QUBEBench, which is an interface with OpenMM for the benchmarking of QUBE force fields (ESI,† Section S3.3). QUBEBench and ForceBalance estimates of force field accuracy (relative to experiment) deviated by just 0.002 g cm−3 and 0.11 kcal mol−1, on average, for density and heat of vaporisation calculations, respectively, indicating good convergence of the fit. Finally, four of the most encouraging force field protocols were taken forward to testing. Here, QUBEKit was used to fit force fields for a test set comprising a further 51 molecules taken from a previous study.27 An additional set was built to test parameters for molecules containing halogens and sulphur. The molecules in both test sets are listed in full in ESI,† Section S4. Physical properties were calculated using QUBEBench, and compared with experiment, to confirm transferability of the designed protocols.
3 Results
3.1 Training set accuracy
Using our new interface between the QUBEKit engine for QM-to-MM force field parameter mapping and the ForceBalance software for parameter tuning, we have trained a total of 15 different force field protocols to investigate the effects of choices made in force field design on model accuracy. Descriptions of the force field protocols are listed in full in Table 1, grouped roughly by the type of hyperparameter being investigated.The first groupings investigate the choice of underlying QM methods used to compute the total electron density for AIM partitioning and subsequent non-bonded parameter derivation (the same QM method is also used for Hessian matrix calculation and dihedral scans to obtain the bonded parameters). As mentioned, our first implementation of QUBEKit34 interfaced with the ONETEP DFT code,63 which uses the PBE exchange-correlation functional, for non-bonded parameter derivation. However, this new version of QUBEKit is interfaced, via QCEngine,61 with both Gaussian0953 and PSI4,60 which gives us access to a wide range of alternative quantum chemistry methods. If using PSI4, the electron density partitioning is performed using MBIS.28 If using Gaussian09, Chargemol is used to calculate the atom centred charges via either the DDEC3 or DDEC6 AIM schemes. In all cases, the AIM method returns atom-centred point charges, the third radial moment of the atomic electron density (for Lennard-Jones parameter derivation), and multipole moments of the atomic electron density (for virtual site derivation).
| Model | C | N | O | H | Polar H | α | β |
|---|---|---|---|---|---|---|---|
| 0 | 2.008 | 1.765 | 1.499 | 1.738 | 1.083 | — | — |
| 1a | 1.999 | 1.740 | 1.489 | 1.752 | 1.111 | — | — |
| 1b | 2.042 | 1.676 | 1.501 | 1.737 | 1.218 | — | — |
| 2a | 2.004 | 1.708 | 1.464 | 1.744 | 1.107 | — | — |
| 2b | 2.026 | 1.751 | 1.521 | 1.724 | 1.119 | — | — |
| 2c | 2.025 | 1.756 | 1.503 | 1.733 | 1.132 | — | — |
| 3a | 2.051 | 1.740 | 1.590 | 1.670 | 1.126 | — | — |
| 3b | 2.068 | 1.681 | 1.599 | 1.753 | 1.404 | — | — |
| 4a | 2.021 | 1.604 | 1.550 | 1.719 | — | — | — |
| 4b | 2.074 | 1.742 | 1.481 | 1.760 | 1.154 | 1.301 | 0.465 |
| 5a | 1.994 | 1.706 | 1.558 | 1.738 | 1.279 | — | — |
| 5b | 2.035 | 1.722 | 1.574 | 1.731 | 1.294 | 1.221 | 0.489 |
| 5c | 2.042 | 1.740 | 1.630 | 1.687 | 1.274 | — | — |
| 5d | 2.013 | 1.680 | 1.558 | 1.732 | 1.442 | — | — |
| 5e | 2.043 | 1.693 | 1.680 | 1.680 | 1.464 | 0.999 | 0.491 |
For comparison, in run 1b, we employed the HF/6-31G(d) method, which has been used historically for the fitting of force field ESP charges.26 The argument goes that this method produces a fortuitous over-polarisation of the electron density in the gas phase to yield charges that are suitable for condensed phase modelling, and so we perform these electron density calculations in vacuum (Table 1). The results are very similar to the two higher level QM methods in implicit solvent, but perhaps this is not too surprising, given the success of many force fields that are built from the HF/6-31G(d) method. However, as we will show, we can now do better with improved physics-based protocols.
In the previous sections, we employed the latest DDEC6 AIM approach for the first time in organic molecule force field design, through the interface between Gaussian09 and Chargemol. In model 3a, we investigate the effect of switching to the older DDEC3 approach. The accuracy is actually slightly better for DDEC3, with a decrease in both density and heat of vaporisation errors, compared to the baseline model 0. DDEC6 has several methodological improvements, which are summarised elsewhere29 and have been shown to result in more robust convergence, lower computation times, lower ESP errors, and higher transferability, when compared to DDEC3.29,30 However, most of these advantages will not be apparent in the small, relatively rigid, organic molecules, which lack buried atoms and are simulated here under standard conditions.
MBIS is similar in idea to the Hirshfeld family of AIM methods.28 In this method the total electron density is partitioned onto a minimal set of s-type Slater functions, whose parameters are fit to the input molecular electron density by minimising the Kullback–Leibler divergence. Like DDEC, it has been shown that the MBIS-derived charges reproduce the QM ESP to good accuracy and are robust to small conformational changes, while MBIS can also be used to derive Tkatchenko–Scheffler based dispersion coefficients.28 MBIS charges, along with all AIM properties (atomic multipoles up to quadrupole order and radial moments) that we require for force field derivation have recently been implemented in the PSI4 quantum chemistry package,60 which we can now access through our latest interface with QCengine.61 Model 3b thus investigates the use of MBIS as the AIM partitioning method in force field derivation. For technical reasons, it was necessary to use the B3LYP exchange-correlation functional, and the IEFPCM implicit solvent model (with a chloroform solvent to mimic a dielectric of approximately 4),76 for the underlying QM calculations. Again this combination of methods gave very good accuracy on our training set, with errors in the density and heat of vaporisation of 0.016 g cm−3 and 0.58 kcal mol−1, respectively.
Given the expected benefits of DDEC6 in larger, more flexible molecules, we retain this method as our standard approach, but do investigate both DDEC3 and MBIS further in what follows. It is gratifying that a range of AIM methods has been shown to be promising for flexible force field design, and is available through our QUBEKit interface with QCEngine.61
Fig. 2 plots the dispersion coefficients (summed over all atoms in the molecule) for all molecules in the larger test set, using the identical Lennard-Jones scheme (from model 5b, see later), against the corresponding quantities extracted from the Parsley force field. Unlike previous protocols (see our previous work,45 and Section S5.3, ESI†), there is a very good correlation between the two force fields, albeit with a consistent offset. While the Parsley parameters are extracted from a library, which in turn has been fit to condensed phase properties, and ours are derived from QM calculations specifically for the molecule under question, the convergence of the two approaches is encouraging.
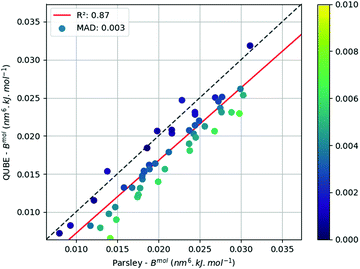 | ||
Fig. 2 Correlation between Parsley and QUBE (model 5b) summed molecular dispersion coefficients for each molecule in the test set  . . | ||
In addition, we investigate the question of whether to include Lennard-Jones parameters on polar hydrogen atoms, or to set them to zero and effectively absorb them onto the neighbouring heavy atom (Section S1.3, ESI†).33 In Table 1, we show that force field protocol 4a, which has no Lennard-Jones parameters on polar hydrogens (denoted ‘H0’), has a similar density error, but higher heat of vaporisation error (0.90 kcal mol−1) compared to the other protocols. Interestingly, this model has a much lower Rfreei for nitrogen than the other models, but the low density error indicates that this does not propagate through to too short hydrogen bonding distances in condensed phase simulations. Nevertheless, we conclude that explicitly including Lennard-Jones parameters on polar hydrogen atoms has accuracy benefits, and we continue to use this approach in the following force field models.
However, a more pertinent question is whether a force field model that more accurately captures the QM electrostatic potential also results in more accurate prediction of condensed phase properties. We have therefore trained a series of force field protocols that include virtual sites in the description of the electrostatics (models 5a–5e). Table 1 summarises the accuracy on the training set. As opposed to some of the other design choices, we now see significant accuracy gains for these models, with prediction errors in liquid densities in the range 0.014–0.021 g cm−3 and heats of vaporisation between 0.24–0.48 kcal mol−1. The lowest density error is observed when virtual sites are used in combination with the B3LYP-D3(BJ)/DZVP QM method (model 5d), and the lowest energy errors when used with rescaled Lennard-Jones interactions (model 5b). Although there is no significant trend in the fit Rfreei parameters on the heavy atoms for these force field protocols (Table 2), interestingly there is a consistent shift of the van der Waals radii of the polar hydrogen atoms to higher values (1.27–1.46 Å) when used in combination with virtual sites. This makes intuitive sense since these atoms are likely to be involved in hydrogen bonds with anisotropic polar atoms, like oxygen and nitrogen. The virtual sites will move the centre of electron density closer to the van der Waals surface of the heavy atom, meaning that the Lennard-Jones repulsion should increase to compensate the increase in electrostatic attraction. The improved condensed phase properties seem to indicate that this is a more physically-reasonable balance than the traditional atom-centred point charge approach.
3.2 Test set accuracy
To test the accuracy of the designed force fields on molecules outside the training set, we ran simulations of the condensed phase properties of a separate test set of 51 molecules containing H, C, N and O atoms only. The force fields brought through for study were models 0, 1a, 5b and 5d (Table 3). The first two were chosen as our simplest (but also amongst the least accurate) protocols, differing only by the choice of underlying QM method. In both cases, we see a drop in overall accuracy, compared to the training set, which is to be expected for the larger, more complex molecules found in the test set (Fig. S3, ESI†). Again, we do not observe a strong dependence of the results on the choice of QM method, and so the computationally less expensive model 1a, based on the B3LYP-D3(BJ)/DZVP method, should make a good compromise force field. For comparison, we have also run the test set using the Open Force Field Parsley force field13 using identical protocols. The accuracy in the simulated densities (0.038 g cm−3) is similar to our first two protocols, and the error in the heat of vaporisation (1.18 kcal mol−1) is slightly lower. The Parsley force field is based around the AM1-BCC charge scheme, with Lennard-Jones parameters largely retained from the SMIRNOFF99Frosst force field.77 Since our initial comparison, Open Force Field have released an updated force field (2.0.0, ‘Sage’) with further refinement of the Lennard-Jones parameters. This force field gives corresponding errors of 0.030 g cm−3 and 1.16 kcal mol−1 on our test set, albeit with many more adjustable parameters than we use in our QM-to-MM mapping potentials (the five Rfreei parameters in Table 2).| Force field | MUE ρ (g cm−3) | MUE ΔHvap (kcal mol−1) |
|---|---|---|
| Parsley | 0.0380.0480.028 | 1.181.530.87 |
| Model 0 | 0.0330.0430.024 | 1.531.871.17 |
| Model 1a | 0.0410.0520.030 | 1.331.581.11 |
| Model 5b | 0.0360.0460.027 | 0.69 0.860.51 |
| Model 5d | 0.031 0.0410.022 | 1.021.330.73 |
Two additional force field protocols were chosen for further investigation based on low training set errors. Model 5d uses the B3LYP-D3(BJ)/DZVP method, and virtual sites to model anisotropic electron density. In this case, we see moderate improvement in test set accuracy for both density and heat of vaporisation (Table 3). Model 5b uses our default quantum chemistry method, virtual sites and re-scaled Lennard-Jones interactions. With approximately the same density error, the error in the heat of vaporisation is significantly reduced to around 0.7 kcal mol−1 (Fig. 3). Only two compounds have heat of vaporisation errors exceeding 2 kcal mol−1, and these are two relatively long chain molecules containing hydroxyl groups (SMILES: OCCCCCO and CC(C)(O)CCC(C)(C)O). Further analysis of models 5b and 5d on an additional test set incorporating halogen and sulphur atoms is provided in ESI,† Section S5.5. Overall, the heat of vaporisation accuracy remains close to 1 kcal mol−1, and density errors increase relative to those shown in Table 3 (though still remain lower than Parsley).
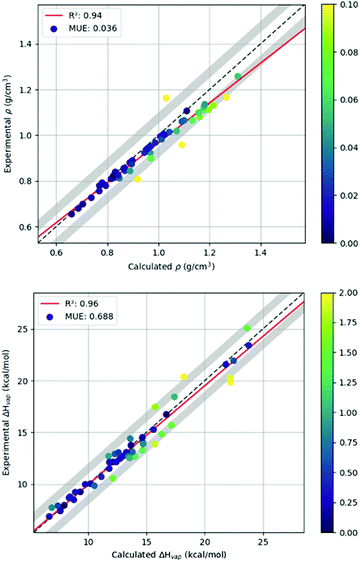 | ||
| Fig. 3 Correlation between experimental and calculated (model 5b) physical properties of liquids in the test set. | ||
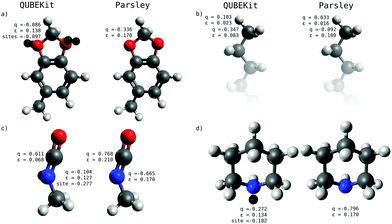
It is difficult to pinpoint reasons for improvement in accuracy, since the physical properties are derived from many competing effects. However, Fig. 4 shows some of the force field parameters for molecules that show differences in performance between our best model (5b), and Parsley. Fig. 4(a) shows 1,3-benzodioxolane, which has ΔHexpervap = 13.1, ΔHQUBEvap = 13.8 and ΔHparsleyvap = 15.3 kcal mol−1. The net charge and Lennard-Jones ε parameter are similar for both QUBE and Parsley, but the former has the charge roughly evenly spread over the atom centre and two virtual sites, showing the benefits of modelling anisotropy in the electron density. Fig. 4(b) shows heptane, and in this case both force fields are in excellent agreement with each other and experiment (ΔHexpervap = 8.8, ΔHQUBEvap = 8.4 and ΔHparsleyvap = 8.7 kcal mol−1). There are some small differences in charges on the terminal methyl hydrogen atoms, which add up to a large difference in charge on the carbon atoms, but this does not seem to significantly affect the liquid properties. Fig. 4(c) shows methyl isocyanate, for which QUBE model 5b is in much better agreement with experiment than Parsley (ΔHexpervap = 6.9, ΔHQUBEvap = 6.7 and ΔHparsleyvap = 11.0 kcal mol−1). This seems to be a general issue with the atom-centred fixed charge force fields, since using our model 0, we obtain ΔHQUBEvap = 10.1 kcal mol−1. Indeed, QUBE model 5b has a smaller net charge on the N atom of methyl isocyanate than Parsley, but some of the charge is spread onto a virtual site. Finally, Fig. 4(d) shows piperidine, for which slightly improved agreement with experiment is again obtained (ΔHexpervap = 9.2, ΔHQUBEvap = 8.9 and ΔHparsleyvap = 10.5 kcal mol−1) with a smaller net charge and a virtual site on the N atom.
We can compare the accuracy of the protocols developed here with other force fields tested on the same or similar test sets. Using the RESP2 charge assignment method, which is based on fitting to the QM electrostatic potential in implicit solvent, with optimised Lennard-Jones parameters, the density and heat of vaporisation errors on an identical test set are 0.024 g cm−3 and 1.67 kcal mol−1.27 Thus, substantial improvement in energetics is obtained in the current study, at the expense of a slight degradation in liquid density prediction. In that study, only a subset of ten Lennard-Jones parameters (the well depth and radius for each of C, O, N, H and polar H) were optimised for efficiency, though this is still more parameters than our most complex protocol (model 5b has seven adjustable parameters). Kantonen et al. have used a similar QM-to-MM parameter mapping approach. They derive Lennard-Jones parameters from the MBIS partitioned atomic electron densities, with two fitting parameters (used to map the electron density decay constants onto the Lennard-Jones σ and ε) for each of C, O, N, H, and polar H. These QM-derived Lennard-Jones parameters are used alongside the AM1-BCC charge model, and GAFF bonded parameters. On a test set of 23 small organic molecules, they report MUEs of 0.027 g cm−3 and 1.1 kcal mol−1 in density and heat of vaporisation, respectively, which is similar in performance to our model 5d protocol. Visscher and Geerke have used an AIM-based QM-to-MM mapping scheme, using both C6 and C8 dispersion coefficients, in combination with an ESP-based charge scheme and a charge-on-spring polarisable model.39 Our strategy of fitting a small number of Rfreei parameters was also employed there, but no off-site charges were used. Encouraging root-mean-square deviations from experiment of 0.024 g cm−3 and 0.39 kcal mol−1 in ρ and ΔHvap were reported on a combined train/test set of 49 small organic molecules.39 With our automated methods for force field derivation and training, it appears that further accuracy gains can be expected by moving in future to polarisable and beyond-Lennard-Jones models.
4 Conclusions
Force field design is a lengthy process, often requiring large teams of researchers working over a period of many years. Design decisions are typically made early in the process, and any inaccuracies stemming from these assumptions propagate through to the final force field. Even the minimal Parsley force field has a set of 35 Lennard-Jones parameters,13 and so large training sets are required to cover sufficient chemical space. Repeatedly performing the full training process to investigate alternative design decisions would substantially slow down the time to science. Furthermore, as we inevitably move to more complex and accurate functional forms, the size of the parameter space and danger of over-fitting will only increase.To solve this problem, we and others have advocated making use of QM-to-MM mapping procedures to significantly reduce the number of parameters that require fitting to experimental physical properties, while retaining a small amount of empiricism to ensure accurate condensed phase properties. Though there are isolated examples in the literature, QM-to-MM mapping potentials are not widely available for general use in deriving full MM force fields for organic molecules. In QUBEKit, and its interface with ForceBalance, we provide here a means to train, test and apply these force fields, deriving parameters for the majority of terms in the force field from QM. By using AIM-based charges, Lennard-Jones parameters and virtual sites, we have a consistent set of non-bonded parameters derived from a single set of atomic electron densities, available through widely-used quantum chemistry software packages. By coupling these parameter sets through QUBEKit, we can derive bonded parameters that are specific to the molecule under study, and fully consistent with the non-bonded parameter set. We estimate that for the 51 molecules in the test set, a total of around 20k parameters are derived from QM, while only seven parameters are fit to experiment (in model 5b). Despite this minimal fitting approach, the model achieves highly competitive accuracy on a challenging test set of liquid property data.
We have used this design and train cycle to answer a number of fundamental questions about force field design protocols. It was shown that the details of the underlying QM method and implicit solvent model have negligible effect on the accuracy of condensed phase modelling with the designed force fields. That is not to say that any set of charges gives identical results, but rather that as long as the charges and Lennard-Jones parameters are co-optimised, the overall accuracy of the force field is insensitive to the particular choice of model. In this case, future efforts should focus on the cheapest QM methods that continue to give reliable results. It is well known that there is no unique method to partition the total molecular electron density into atom-centred basins. We have therefore investigated two variants of the DDEC AIM method, and the MBIS approach. Surprisingly, the older DDEC3 method showed improvements over DDEC6, but given the improvements in the latter in robustness and transferability of the charges, we continue to use this approach. The MBIS method provides a useful alternative AIM approach, available through the open source PSI4 software package. Once atomic electron densities are assigned, the details of the Lennard-Jones parameterisation also makes a difference to force field accuracy. Based on our data, we advocate setting non-zero Lennard-Jones parameters on polar hydrogen atoms, and re-scaling the strength of the QM-derived dispersion parameter. The latter approach gives not only an improvement in accuracy, but brings QM-derived and Parsley empirical Lennard-Jones parameters into closer agreement. One aspect of the Lennard-Jones interaction that we were not able to investigate is the choice of combination rules for unlike atoms. The standard OpenMM nonbonded force, and its interface with ForceBalance, is currently limited to Lorentz–Berthelot combination rules, but it would be interesting to test alternatives in future. Finally, consistent improvement in both training and test set accuracy is achieved by introducing a small number of off-site charges to model anisotropy in the QM electron density. It is encouraging that improving the underlying physics of the force field model, with minimal costs to run time, results in such improvements.
In the current study, we have focused on liquid density and heat of vaporisation as measures of force field accuracy. However, it is important to also test force fields outside the training regime, on properties such as dielectric permittivity, binary density and enthalpy of mixing.78 In future, we will interface the outputs of QUBEKit with Open Force Field Evaluator,50 which will provide a more automated and efficient framework for force field testing and extend the confidence in the range of application of the force fields. More complex properties, such as free energies of hydration or even protein-ligand binding could be included (at least for testing), but would require infrastructure improvements to allow for virtual sites and the testing of a compatible water model. The current study gives confidence that this investment of time would be worthwhile. A notable feature of the current study is the number of force field models that can be rapidly designed. We have generated here 15 different models, with varying assumptions, which can be contrasted with the handful of general purpose small molecule force fields that are otherwise available. This opens up the possibility of new research into consensus property predictions using force field ensembles, which has been shown to be advantageous, for example, in recent protein-ligand binding free energy studies.79
More broadly, we envisage QM-to-MM mapping potentials, such as these, providing synergy with traditional force fields. For example, our conclusions concerning force field design protocols can be fed into large-scale fitting efforts, such as the Open Force Field Initiative, to focus efforts in areas where accuracy improvements are expected. This will be particularly important as the community moves towards more advanced functional forms, for which the number of parameters to be fit will only increase. With the advent of machine learning models for parameterising force fields,80 the force fields developed here could be used to provide regularisation of the parameter fits, to avoid unphysical predictions by the models. Or conversely, machine learning models could be trained to reproduce the outputs of our QM-to-MM mapping procedures to substantially reduce the computational cost of the parameterisation stage.81
All software required to derive and use the designed force fields is freely available at https://github.com/qubekit/QUBEKit.
Author contributions
Chris Ringrose: conceptualisation, data curation, formal analysis, investigation, methodology, software, validation, visualisation, writing – original draft. Joshua Horton: conceptualisation, data curation, investigation, methodology, software, validation, visualisation, writing – review & editing. Lee-Ping Wang: conceptualisation, software, writing – review & editing. Daniel Cole: conceptualisation, funding acquisition, methodology, project administration, resources, supervision, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. R. is grateful for International Partnership Seed Funding from Newcastle University. D. J. C. and J. H. acknowledge support from a UKRI Future Leaders Fellowship (grant MR/T019654/1). We thank the Open Force Field Initiative and PSI4 developers for scientific software support. This work made use of the facilities of the N8 Centre of Excellence in Computationally Intensive Research (N8 CIR) provided and funded by the N8 research partnership and EPSRC (grant EP/T022167/1).Notes and references
- P. Dauber-Osguthorpe and A. T. Hagler, J. Comput.-Aided Mol. Des., 2019, 33, 133–203 CrossRef CAS PubMed.
- A. T. Hagler, J. Comput.-Aided Mol. Des., 2019, 33, 205–264 CrossRef CAS PubMed.
- J. A. Dawson, P. Canepa, T. Famprikis, C. Masquelier and M. S. Islam, J. Am. Chem. Soc., 2017, 140, 362–368 CrossRef PubMed.
- A. A. Franco, A. Rucci, D. Brandell, C. Frayret, M. Gaberscek, P. Jankowski and P. Johansson, Chem. Rev., 2019, 119, 4569–4627 CrossRef CAS PubMed.
- L. Yang, J. T. Horton, M. C. Payne, T. J. Penfold and D. J. Cole, J. Chem. Theory Comput., 2021, 17, 5021–5033 CrossRef CAS PubMed.
- Y. Olivier, J.-C. Sancho-Garcia, L. Muccioli, G. D’Avino and D. Beljonne, J. Phys. Chem. Lett., 2018, 9, 6149–6163 CrossRef CAS PubMed.
- J. Nyman, O. S. Pundyke and G. M. Day, Phys. Chem. Chem. Phys., 2016, 18, 15828–15837 RSC.
- D. J. Huggins, P. C. Biggin, M. A. Dämgen, J. W. Essex, S. A. Harris, R. H. Henchman, S. Khalid, A. Kuzmanic, C. A. Laughton, J. Michel, A. J. Mulholland, E. Rosta, M. S. P. Sansom and M. W. van der Kamp, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 9, e1393 Search PubMed.
- A. S. Mey, B. K. Allen, H. E. B. Macdonald, J. D. Chodera, D. F. Hahn, M. Kuhn, J. Michel, D. L. Mobley, L. N. Naden, S. Prasad, A. Rizzi, J. Scheen, M. R. Shirts, G. Tresadern and H. Xu, Living J. Comput. Mol. Sci., 2020, 2, 18378 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. MacKerell Jr., J. Comput. Chem., 2010, 31, 671–690 CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- Y. Qiu, D. G. A. Smith, S. Boothroyd, H. Jang, D. F. Hahn, J. Wagner, C. C. Bannan, T. Gokey, V. T. Lim, C. D. Stern, A. Rizzi, B. Tjanaka, G. Tresadern, X. Lucas, M. R. Shirts, M. K. Gilson, J. D. Chodera, C. I. Bayly, D. L. Mobley and L.-P. Wang, J. Chem. Theory Comput., 2021, 17, 6262–6280 CrossRef CAS PubMed.
- E. Boulanger, L. Huang, C. Rupakheti, A. D. MacKerell and B. Roux, J. Chem. Theory Comput., 2018, 14, 3121–3131 CrossRef CAS PubMed.
- J. Yin, N. M. Henriksen, D. R. Slochower, M. R. Shirts, M. W. Chiu, D. L. Mobley and M. K. Gilson, J. Comput.-Aided Mol. Des., 2016, 31, 1–19 CrossRef PubMed.
- P. Xu, E. B. Guidez, C. Bertoni and M. S. Gordon, J. Chem. Phys., 2018, 148, 090901 CrossRef.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Chem. Rev., 2021, 121, 10142–10186 CrossRef CAS PubMed.
- V. Barone, I. Cacelli, N. D. Mitri, D. Licari, S. Monti and G. Prampolini, Phys. Chem. Chem. Phys., 2013, 15, 3736 RSC.
- J. R. Maple, M.-J. Hwang, T. P. Stockfisch, U. Dinur, M. Waldman, C. S. Ewig and A. T. Hagler, J. Comput. Chem., 1994, 15, 162–182 CrossRef CAS.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 490–519 CrossRef CAS.
- S. Sami, M. F. Menger, S. Faraji, R. Broer and R. W. A. Havenith, J. Chem. Theory Comput., 2021, 17, 4946–4960 CrossRef CAS PubMed.
- J. Morado, P. N. Mortenson, M. L. Verdonk, R. A. Ward, J. W. Essex and C.-K. Skylaris, J. Chem. Inf. Model., 2021, 61, 2026–2047 CrossRef CAS PubMed.
- B. Seo, Z.-Y. Lin, Q. Zhao, M. A. Webb and B. M. Savoie, J. Chem. Inf. Model., 2021, 61, 5013–5027 CrossRef CAS PubMed.
- A. Jakalian, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2002, 23, 1623–1641 CrossRef CAS PubMed.
- L. S. Dodda, J. Z. Vilseck, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2017, 121, 3864–3870 CrossRef CAS PubMed.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- M. Schauperl, P. S. Nerenberg, H. Jang, L.-P. Wang, C. I. Bayly, D. L. Mobley and M. K. Gilson, Commun. Chem., 2020, 3, 1–11 CrossRef.
- T. Verstraelen, S. Vandenbrande, F. Heidar-Zadeh, L. Vanduyfhuys, V. Van Speybroeck, M. Waroquier and P. W. Ayers, J. Chem. Theory Comput., 2016, 12, 3894–3912 CrossRef CAS PubMed.
- T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801 RSC.
- N. G. Limas and T. A. Manz, RSC Adv., 2016, 6, 45727–45747 RSC.
- M. Riquelme, A. Lara, D. L. Mobley, T. Verstraelen, A. R. Matamala and E. Vöhringer-Martinez, J. Chem. Inf. Model., 2018, 58, 1779–1797 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 6–9 CrossRef PubMed.
- D. J. Cole, J. Z. Vilseck, J. Tirado-Rives, M. C. Payne and W. L. Jorgensen, J. Chem. Theory Comput., 2016, 12, 2312–2323 CrossRef CAS PubMed.
- J. T. Horton, A. E. Allen, L. S. Dodda and D. J. Cole, J. Chem. Inf. Model., 2019, 59, 1366–1381 CrossRef CAS PubMed.
- M. Mohebifar, E. R. Johnson and C. N. Rowley, J. Chem. Theory Comput., 2017, 13, 6146–6157 CrossRef CAS PubMed.
- T. A. Manz and T. Chen, RSC Adv., 2019, 9, 33310–33336 RSC.
- T. Chen and T. A. Manz, RSC Adv., 2019, 9, 36492–36507 RSC.
- K. M. Visscher and D. P. Geerke, J. Chem. Theory Comput., 2019, 15, 1875–1883 CrossRef CAS PubMed.
- K. M. Visscher and D. P. Geerke, J. Phys. Chem. B, 2020, 124, 1628–1636 CAS.
- S. M. Kantonen, H. S. Muddana, M. Schauperl, N. M. Henriksen, L. P. Wang and M. K. Gilson, J. Chem. Theory Comput., 2020, 16, 1115–1127 CrossRef CAS PubMed.
- L.-P. Wang, J. Chen and T. Van Voorhis, J. Chem. Theory Comput., 2013, 9, 452–460 CrossRef CAS PubMed.
- A. E. Allen, M. C. Payne and D. J. Cole, J. Chem. Theory Comput., 2018, 14, 274–281 CrossRef CAS PubMed.
- T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2012, 8, 2844–2867 CrossRef CAS PubMed.
- L. P. Lee, N. G. Limas, D. J. Cole, M. C. Payne, C. K. Skylaris and T. A. Manz, J. Chem. Theory Comput., 2014, 10, 5377–5390 CrossRef CAS PubMed.
- D. J. Cole, I. Cabeza De Vaca and W. L. Jorgensen, MedChemComm, 2019, 10, 1116–1120 RSC.
- J. T. Horton, A. E. Allen and D. J. Cole, Chem. Commun., 2020, 56, 932–935 RSC.
- L. Nelson, S. Bariami, C. Ringrose, J. T. Horton, V. Kurdekar, A. S. J. S. Mey, J. Michel and D. J. Cole, J. Chem. Inf. Model., 2021, 61, 2124–2130 CrossRef CAS PubMed.
- T. Fröhlking, M. Bernetti, N. Calonaci and G. Bussi, J. Chem. Phys., 2020, 152, 230902 CrossRef PubMed.
- C. J. Fennell, K. L. Wymer and D. L. Mobley, J. Phys. Chem. B, 2014, 118, 6438–6446 CrossRef CAS PubMed.
- S. Boothroyd, L.-P. Wang, D. L. Mobley, J. D. Chodera and M. R. Shirts, J. Chem. Theory Comput., 2022, 18, 3566–3576 CrossRef CAS PubMed.
- M. P. Oliveira, M. Andrey, S. R. Rieder, L. Kern, D. F. Hahn, S. Riniker, B. A. C. Horta and P. H. Hünenberger, J. Chem. Theory Comput., 2020, 16, 7525–7555 CrossRef CAS PubMed.
- M. D. Pierro, M. L. Mugnai and R. Elber, J. Phys. Chem. B, 2014, 119, 836–849 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision A.2, 2009 Search PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- S. Riniker and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 2562–2574 CrossRef CAS PubMed.
- G. Landrum, RDKit: Open-source cheminformatics, http://www.rdkit.org/.
- X. Gao, F. Ramezanghorbani, O. Isayev, J. S. Smith and A. E. Roitberg, J. Chem. Inf. Model., 2020, 60, 3408–3415 CrossRef CAS PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 11, e1493 Search PubMed.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L.-P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, PLoS Comput. Biol., 2017, 13, e1005659 CrossRef PubMed.
- D. G. A. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio, A. Alenaizan, A. M. James, S. Lehtola, J. P. Misiewicz, M. Scheurer, R. A. Shaw, J. B. Schriber, Y. Xie, Z. L. Glick, D. A. Sirianni, J. S. O’Brien, J. M. Waldrop, A. Kumar, E. G. Hohenstein, B. P. Pritchard, B. R. Brooks, H. F. Schaefer, A. Y. Sokolov, K. Patkowski, A. E. DePrince, U. Bozkaya, R. A. King, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Phys., 2020, 152, 184108 CrossRef CAS PubMed.
- D. G. Smith, A. T. Lolinco, Z. L. Glick, J. Lee, A. Alenaizan, T. A. Barnes, C. H. Borca, R. Di Remigio, D. L. Dotson and S. Ehlert, et al. , J. Chem. Phys., 2021, 155, 204801 CrossRef CAS PubMed.
- D. L. Mobley, É. Dumont, J. D. Chodera and K. A. Dill, J. Phys. Chem. B, 2007, 111, 2242–2254 CrossRef CAS PubMed.
- J. C. A. Prentice, J. Aarons, J. C. Womack, A. E. A. Allen, L. Andrinopoulos, L. Anton, R. A. Bell, A. Bhandari, G. A. Bramley, R. J. Charlton, R. J. Clements, D. J. Cole, G. Constantinescu, F. Corsetti, S. M.-M. Dubois, K. K. B. Duff, J. M. Escartín, A. Greco, Q. Hill, L. P. Lee, E. Linscott, D. D. O’Regan, M. J. S. Phipps, L. E. Ratcliff, Á. R. Serrano, E. W. Tait, G. Teobaldi, V. Vitale, N. Yeung, T. J. Zuehlsdorff, J. Dziedzic, P. D. Haynes, N. D. M. Hine, A. A. Mostofi, M. C. Payne and C.-K. Skylaris, J. Chem. Phys., 2020, 152, 174111 CrossRef CAS PubMed.
- J. C. Womack, L. Anton, J. Dziedzic, P. J. Hasnip, M. I. J. Probert and C.-K. Skylaris, J. Chem. Theory Comput., 2018, 14, 1412–1432 CrossRef CAS PubMed.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed.
- A. Nikitin, J. Comput.-Aided Mol. Des., 2019, 34, 437–441 CrossRef PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- X. C. Yan, M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2017, 121, 6626–6636 CrossRef CAS PubMed.
- I. S. Gutiérrez, F.-Y. Lin, K. Vanommeslaeghe, J. A. Lemkul, K. A. Armacost, C. L. Brooks and A. D. MacKerell, Bioorg. Med. Chem., 2016, 24, 4812–4825 CrossRef PubMed.
- M. H. Kolář and P. Hobza, Chem. Rev., 2016, 116, 5155–5187 CrossRef PubMed.
- Y. Qiu, D. G. Smith, C. D. Stern, M. Feng, H. Jang and L. P. Wang, J. Chem. Phys., 2020, 152, 244116 CrossRef PubMed.
- A. E. Allen, M. J. Robertson, M. C. Payne and D. J. Cole, ACS Omega, 2019, 4, 14537–14550 CrossRef CAS PubMed.
- M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2015, 11, 3499–3509 CrossRef CAS PubMed.
- J. Řezáč, D. Bím, O. Gutten and L. Rulíšek, J. Chem. Theory Comput., 2018, 14, 1254–1266 CrossRef PubMed.
- J. B. Foresman, T. A. Keith, K. B. Wiberg, J. Snoonian and M. J. Frisch, J. Phys. Chem., 1996, 100, 16098–16104 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- D. L. Mobley, C. C. Bannan, A. Rizzi, C. I. Bayly, J. D. Chodera, V. T. Lim, N. M. Lim, K. A. Beauchamp, D. R. Slochower, M. R. Shirts, M. K. Gilson and P. K. Eastman, J. Chem. Theory Comput., 2018, 14, 6076–6092 CrossRef CAS PubMed.
- S. Boothroyd, O. Madin, D. Mobley, L.-P. Wang, J. Chodera and M. Shirts, J. Chem. Theory Comput., 2022, 18, 3577–3592 CrossRef CAS PubMed.
- V. Gapsys, L. Pérez-Benito, M. Aldeghi, D. Seeliger, H. van Vlijmen, G. Tresadern and B. L. de Groot, Chem. Sci., 2020, 11, 1140–1152 RSC.
- Y. Wang, J. Fass and J. D. Chodera, 2020, arXiv preprint arXiv:2010.01196.
- P. Bleiziffer, K. Schaller and S. Riniker, J. Chem. Inf. Model., 2018, 58, 579–590 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Lennard-Jones derivations, virtual site protocols, additional methods, images of training/test sets and supporting results (PDF). Training tutorial, example ForceBalance input files, raw data and all train/test force field files (ZIP). See DOI: https://doi.org/10.1039/d2cp02864f |
| This journal is © the Owner Societies 2022 |