Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effect of conformational disorder on exciton states of an azobenzene aggregate†
Evgenii
Titov

Theoretical Chemistry, Institute of Chemistry, University of Potsdam, Karl-Liebknecht-Straße 24-25, 14476 Potsdam, Germany. E-mail: titov@uni-potsdam.de
First published on 8th September 2022
Abstract
Azobenzene is a prototypical molecular photoswitch, widely used to trigger a variety of transformations at different length scales. In systems like self-assembled monolayers or micelles, azobenzene chromophores may interact with each other, which gives rise to the emergence of exciton states. Here, using first-principles calculations, we investigate how conformational disorder (induced, e.g., by thermal fluctuations) affects localization of these states, on an example of an H-type azobenzene tetramer. We find that conformational disorder leads to (partial) exciton localization on a single-geometry level, whereas ensemble-averaging results in a delocalized picture. The ππ* and nπ* excitons at high and low temperatures are discussed.
Aggregation of molecular chromophores gives rise to molecular excitons, featuring a collective nature of electronic excitation as opposed to excitation of individual molecules.1–3 The excitons play a crucial role in processes of light energy conversion.4,5 A particularly interesting class of light-triggered systems is photoswitchable materials.6 When photoswitch molecules are brought in close proximity to each other, exciton states are formed, as has been observed for azobenzene-containing self-assembled monolayers (SAMs)7 and micelles.8 The exciton formation has been proposed to hinder azobenzene isomerization,7 in addition to steric effects.9–11
Exciton states arise as delocalized states in classical theories of exciton formation in molecular crystals1 and in molecular dimers.2 Yet, conformational disorder, induced, e.g., by thermal fluctuations, has been shown to lead to (partial) localization of the exciton states in polymers and oligomers.12–17 To the best of our knowledge, this effect has not been explored for systems of aggregated photoswitchable molecules.
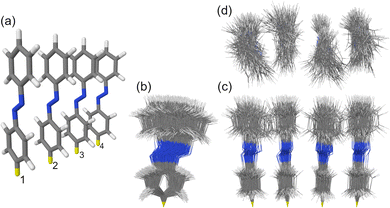
In this work, using first-principles calculations, we study how conformational disorder caused by nuclear motion affects the exciton states of a model azobenzene aggregate composed of four molecules (Fig. 1a). To this aim, we (i) perform ground-state Born–Oppenheimer molecular dynamics (BOMD) simulations employing dispersion-corrected density functional theory (DFT), (ii) calculate the electronic spectra for selected MD snapshots using linear response, long-range corrected time-dependent DFT (TD-DFT), and (iii) reveal the nature of the exciton states by means of a transition density matrix (TDM) analysis.
Specifically, in step (i) we perform B3LYP18,19+D3(BJ)20 constant-temperature, ground-state dynamics at ∼300 K,‡ for 10 ps. After that, 100 snapshots are selected from the BOMD trajectory (with a time interval of 100 fs) and subjected to TD-DFT calculations using the ωB97X-D functional22 (step ii). We use a long-range corrected functional in TD-DFT calculations to avoid a spurious charge transfer problem,23 which has been observed for azobenzene dimers when using standard hybrid functionals like B3LYP.24,25 All calculations are performed with the def2-SV(P) basis set26 using Gaussian 16.27 Further details about the model and the methods are provided in SI1 (ESI†).
In step (iii) we quantify localization and charge-transfer character of excited states using transition density matrix analysis.28,29 To this aim, the Löwdin-type30,31 “fraction of TDM” (FTDM) matrix F (defined for a certain excited state at a given geometry) is computed:24
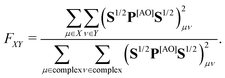 | (1) |
For an ensemble of Ns MD snapshots (labeled with α), we compute the averaged FTDM matrix 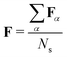 . Furthermore, for each snapshot α, we sort the diagonal of the Fα matrix to introduce the highest (H), lowest (L), and intermediate (H−1 and L+1) monomers: Fα,H > Fα,H−1 > Fα,L+1 > Fα,L.33 After that, we average these values over all snapshots, e.g., for the H fragment
. Furthermore, for each snapshot α, we sort the diagonal of the Fα matrix to introduce the highest (H), lowest (L), and intermediate (H−1 and L+1) monomers: Fα,H > Fα,H−1 > Fα,L+1 > Fα,L.33 After that, we average these values over all snapshots, e.g., for the H fragment 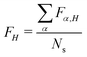 . This procedure allows one to judge about exciton localization on the single-geometry level.17,33
. This procedure allows one to judge about exciton localization on the single-geometry level.17,33
The studied H-type trans azobenzene tetramer is shown in Fig. 1a. The H-type arrangement is motivated by azobenzene packing in self-assembled monolayers.7 The used model with intermolecular distance of 3.5 Å is an extension of the densely-packed dimer model used in our previous works.10,34 The ensemble of 100 MD snapshots demonstrating the extent of conformational disorder at ∼300 K is presented in Fig. 1b–d.
We first examine the ππ* absorption band, corresponding to the bright, S0→S2 transition of the monomer. The spectra of the monomer and the tetramer calculated at the single geometries (with the monomer geometry optimized at the B3LYP/def2-SV(P) level) are shown in Fig. 2a. As can be expected for an H-aggregate, we observe a blue shift in comparison with the monomer spectrum, ∼0.24 eV in our case. The brightest transition in the tetramer is the S0→S13 transition. [We note that the tetramer stick spectrum turned out to be rather sensitive to the monomer geometry—see spectra of tetramers constructed from the B3LYP/def2-SV(P) and B3LYP/def2-TZVP26 optimized monomer geometries in Fig. S1 (ESI†) and FTDM matrices in Fig. S2, ESI†.] Using the simplest exciton model (which includes only local excitations and assumes large energy gaps between monomeric states), one would expect the brightest transition to be S0→S8. However, at the small intermolecular separation (3.5 Å) and with the ωB97X-D functional, we observe that transitions from S0→S8 to S0→S11 originate from the S0→S3/4 monomeric transition, and the S0→S12 transition is a charge-resonance29 transition corresponding to the monomeric S0→S2 transition. We also note that the S0→S6 transition in the tetramer at 3.47 eV has a small but nonzero oscillator strength of ∼0.01. This transition is red-shifted by ∼0.64 eV with respect to the peak of the monomeric ππ* band.
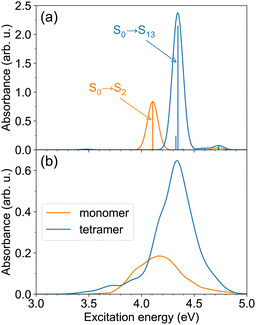 | ||
| Fig. 2 (a) The ππ* absorption bands of the monomer and the tetramer, calculated with TD-ωB97X-D/def2-SV(P), for single model geometries. The monomer geometry was optimized at the B3LYP/def2-SV(P) level; the tetramer geometry (see Fig. 1a) was constructed from the optimized monomer geometry. (b) The ππ* absorption bands of the monomer and the tetramer at T ≈ 300 K. The spectra are obtained using TD-ωB97X-D/def2-SV(P) calculations for 100 snapshots. | ||
The spectra at ∼300 K are shown in Fig. 2b. The spectra are broader in comparison to those for the model geometries in Fig. 2a due to nuclear motion. The tetramer absorption band with a peak at 4.34 eV is blue-shifted by ∼0.17 eV with respect to the monomer absorption maximum located at 4.17 eV. The maximum tetramer absorbance is ∼3.5 times larger than the maximum monomer absorbance. Apart from the intense blue-shifted band, the tetramer spectrum exhibits a tail extending in the red direction, up to ∼3.3 eV. This demonstrates that the spectrum of the H-aggregate is more complex than merely a blue-shifted absorption band, and that the aggregate may be excited not only at energies above the monomer absorption, but also below it.
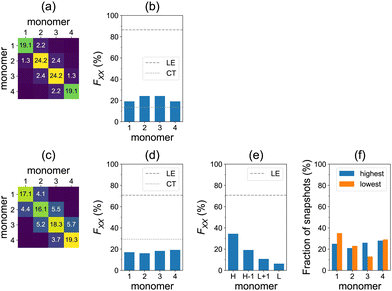
We turn now to the question of exciton delocalization. Fig. 3a shows the FTDM matrix for the S0→S13 transition of the tetramer, for the model geometry of Fig. 1a. The exciton is mostly composed of local excitations, whereas CT excitations represent a minor contribution. Specifically, the sum of diagonal elements of the FTDM matrix is 86%, whereas the sum of off-diagonal elements is 14%, as shown in Fig. 3b. Furthermore, we also show the diagonal FXX values in Fig. 3b. They demonstrate that the exciton is delocalized over the tetramer, with two molecules in the middle bearing ∼24% of excitation each, and two end molecules ∼19% each.
Furthermore, we calculated the FTDM matrix for the brightest transition of each of 100 MD snapshots (see distributions of the brightest state labels and corresponding oscillator strengths in Fig. S6 and S7 (ESI†), respectively). The averaged F matrix at ∼300 K is shown in Fig. 3c. We again see that the local excitations are dominant, but CT excitations are more pronounced than for the single model geometry (compare with Fig. 3a). Namely, we find 71% LE and 29% CT in total (Fig. 3d). The diagonal elements of the averaged F matrix range from ∼16 to ∼19%, showing exciton delocalization for the ensemble (Fig. 3d).
However, this delocalization represents an averaged picture only. Looking at Fig. 3c and d, it is not possible to conclude about the extent of delocalization for individual members of the ensemble. Therefore, we perform the additional analysis that identifies the highest to lowest monomers for each individual snapshot (as described above). The averaged highest to lowest FTDM values are shown in Fig. 3e. The H fragment acquires 34% of excitation, whereas the L fragment only 6%. The H−1 and L+1 carry 19% and 11%, respectively. Thus, the conformational disorder leads to a partial localization of the bright excitons in the studied azobenzene aggregate. Each of the four monomers may be the highest (or lowest) at that (Fig. 3f), depending on a given MD snapshot.
We have also calculated the spectra using the ωB97 functional35 (with no short-range exact exchange in contrast to ωB97X-D) to check the sensitivity of the results to a given functional. Qualitatively, the findings are the same as with ωB97X-D. Quantitatively, at the TD-ωB97 level, the spectra are blue-shifted (Fig. S4 and S5, ESI†), charge-transfer elements of FTDM are smaller (Fig. S8, ESI†), and the highest fragment acquires 53% of excitation (instead of the above-mentioned 34% on the TD-ωB97X-D level).
Next, we have also considered dynamics corresponding to much lower temperatures. To do so, we launched a constant-energy trajectory with zero initial velocities. The resultant temperatures are less than 26 K (Fig. S3, ESI†). Expectedly, spectral broadening is smaller than that at 300 K (Fig. S4, ESI†). Importantly, the brightest excitons are more delocalized at low temperatures, as revealed by the highest/lowest FTDM analysis (Fig. S9 and S10, ESI†).
The ππ* absorption band of the tetramer at ∼300 K possesses a tail in the low-energy range, at 3.3–4.0 eV (Fig. 2b), as mentioned above. We analyzed the exciton localization for the S0→S5 transition, which is the lowest energy ππ* transition and is located at the ππ* absorption onset (see SI2.2, ESI†). At the model tetramer geometry, this transition is predominantly delocalized over the central dimer (Fig. S12, ESI†). It also shows sizable CT excitations between the middle molecules. MD at ∼300 K again leads to considerable single-geometry localization, whereas the excitons are more delocalized at low temperatures (<26 K in our case), see SI2.2 (ESI†). In this respect, it is interesting to note that photoisomerization in the SAMs (if it occurs) is believed to be triggered by localized excitations.36
Furthermore, we turn to the lower energy nπ* band. The S0→S1 transition of the trans monomer is a dark transition (i.e., a transition with zero oscillator strength) located at ∼2.55 eV. The four lowest transitions in the tetramer (S0→S1 to S0→S4), which originate from the lowest monomeric transition, are also dark and reside at ∼2.43–2.52 eV. [The given excitation energies are obtained with TD-ωB97X-D/def2-SV(P) at the B3LYP/def2-SV(P) geometries.] The nπ* transitions become allowed (although they carry a weak oscillator strength) due to structural distortions,37 realized in the MD simulations. The nπ* absorption bands of the monomer and the tetramer at ∼300 K are shown in Fig. 4. Both exhibit a maximum at 2.53–2.54 eV. The tetramer absorbance at the maximum is ∼2.3 times larger than the monomer absorbance.
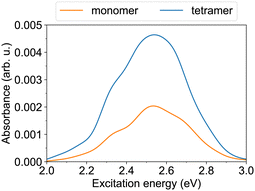 | ||
| Fig. 4 The nπ* absorption bands of the monomer and the tetramer at T ≈ 300 K. The spectra are obtained using TD-ωB97X-D/def2-SV(P) calculations for 100 snapshots. | ||
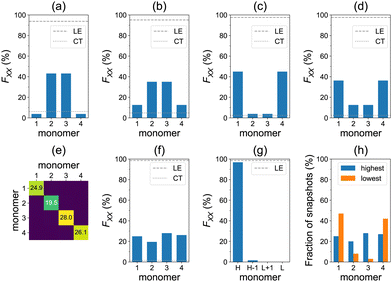
Furthermore, the lowest four transitions of the aggregate, at the model geometry of Fig. 1a, are dominated by local excitations as can be seen in Fig. 5a–d. The S0→S1 and S0→S2 transitions are predominantly delocalized over the dimer in the middle, whereas the S0→S3 and S0→S4 transitions are mostly delocalized over the terminal molecules.
The averaged F matrix for the brightest transition within the nπ* band is shown in Fig. 5e. Again, we see that the exciton is delocalized in the averaged picture (Fig. 5f). However, the analysis based on sorting diagonal values for individual snapshots reveals a pronounced exciton localization (FH = 97%) to a single azobenzene unit (Fig. 5g). This strong localization can be explained by a weak exciton coupling of the nπ* states.38 Each monomer may take a role of the highest monomer (Fig. 5h), which results in the delocalized averaged pictures of Fig. 5e and f. We also note that the CT contributions are negligible in this case (Fig. 5f). At low temperatures, the nπ* excitons are less localized (FH = 74%), see Fig. S18 (ESI†). The ωB97 results are very similar: FH = 97% at ∼300 K (Fig. S17, ESI†) and FH = 75% at <26 K (Fig. S19, ESI†).
In addition, we performed dynamics calculations employing ωB97X-D instead of B3LYP+D3 to check the effect of the functional used in step (i). The results are presented in SI3 (ESI†). While qualitatively we can draw the same conclusions, there are some quantitative differences, most noticeably for the spectra and the ensemble-averaged delocalization of the nπ* band.
Furthermore, to account for both LE and CT contributions in analysis of single-geometry (de)localization, we computed inverse participation ratio (IPR) (also known as participation number (PN) or delocalization length (DL)), which is defined (for a certain excited state at a given geometry) as:39
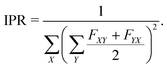 | (2) |
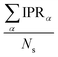 . IPR for the model geometry and mean IPR with standard deviation for ensembles of 100 snapshots for the studied excitons are shown in Table 1. The IPR values for individual snapshots are provided in Fig. S11, S16, S20, S29, S34 and S39 (ESI†). As can be seen from Table 1, IPRs corroborate the findings of the highest/lowest FTDM analysis discussed above.
. IPR for the model geometry and mean IPR with standard deviation for ensembles of 100 snapshots for the studied excitons are shown in Table 1. The IPR values for individual snapshots are provided in Fig. S11, S16, S20, S29, S34 and S39 (ESI†). As can be seen from Table 1, IPRs corroborate the findings of the highest/lowest FTDM analysis discussed above.
| Model geometryb | T (K) | B3LYP+D3 dynamics | ωB97X-D dynamics | |||
|---|---|---|---|---|---|---|
| TD-ωB97X-D | TD-ωB97 | TD-ωB97X-D | TD-ωB97 | TD-ωB97X-D | TD-ωB97 | |
| a Corresponding transitions for the model geometry are shown in square brackets. IPR standard deviations are shown in parentheses. b Tetramer geometry is constructed from the B3LYP/def2-SV(P) optimized monomer geometry. | ||||||
| Brightest ππ* transition | ||||||
| 3.91 [S0→S13] | 3.97 [S0→S10] | ∼300 | 3.1 (0.5) | 2.5 (0.6) | 2.9 (0.6) | 2.5 (0.6) |
| <26 | 3.8 (0.1) | 3.8 (0.2) | 3.8 (0.2) | 3.8 (0.2) | ||
| S0→S5 (ππ*) transition | ||||||
| 2.94 [S0→S5] | 2.88 [S0→S5] | ∼300 | 2.1 (0.5) | 1.9 (0.5) | 2.1 (0.4) | 1.9 (0.4) |
| <26 | 2.7 (0.2) | 2.6 (0.2) | 2.7 (0.2) | 2.7 (0.2) | ||
| Brightest nπ* transition | ||||||
| 2.40 [S0→S1] | 2.41 [S0→S1] | ∼300 | 1.1 (0.1) | 1.1 (0.2) | 1.1 (0.2) | 1.1 (0.2) |
| 3.29 [S0→S2] | 3.42 [S0→S2] | <26 | 1.8 (0.8) | 1.7 (0.8) | 1.9 (0.8) | 1.8 (0.8) |
| 2.39 [S0→S3] | 2.40 [S0→S3] | — | — | — | — | — |
| 3.28 [S0→S4] | 3.41 [S0→S4] | — | — | — | — | — |
Finally, to shed light on the strength of exciton–vibration coupling, we calculated time evolution of IPR and FH along with geometrical changes for the first 100 fs of the high temperature (∼300 K) MD trajectory (Fig. S40, ESI†). Fast uncorrelated intramolecular vibrations lead to rapid localization of excitonically weakly coupled nπ* states, whereas excitonically strongly coupled ππ* states undergo only moderate changes in (de)localization.
In summary, we studied the effect of conformational disorder on the exciton states of a model azobenzene tetramer by means of first-principles calculations. The ground-state MD was performed using dispersion-corrected DFT functionals, and the excited states were computed with long-range corrected functionals. Using transition density matrix analysis, we found that the conformational disorder at ∼300 K induces partial localization of the brightest, ππ* excitons, whereas the excitons at T < 26 K are more delocalized. The nπ* excitons undergo a strong localization (to a single monomer) at ∼300 K. At low temperatures (<26 K) the effect is weakened, but the nπ* localization is still pronounced.
Future research will be devoted to the investigation of the exciton dynamics in azobenzene aggregates by means of nonadiabatic mixed quantum-classical MD simulations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author thanks Peter Saalfrank for providing computational resources, for his comments on the manuscript and for his support. The author thanks Foudhil Bouakline for valuable discussions. The author also thanks the anonymous reviewer for useful comments on the manuscript. The author thanks the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for financial support—project number 454020933. (Gefördert durch die Deutsche Forschungsgemeinschaft (DFG)—Projektnummer 454020933.)Notes and references
- A. S. Davydov, Sov. Phys. Usp., 1964, 7, 145–178 CrossRef.
- M. Kasha, H. R. Rawls and M. A. El-Bayoumi, Pure Appl. Chem., 1965, 11, 371–392 CAS.
- N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163 CrossRef CAS PubMed.
- T. Mirkovic, E. E. Ostroumov, J. M. Anna, R. van Grondelle, Govindjee and G. D. Scholes, Chem. Rev., 2017, 117, 249–293 CrossRef CAS PubMed.
- G. J. Hedley, A. Ruseckas and I. D. W. Samuel, Chem. Rev., 2017, 117, 796–837 CrossRef CAS.
- A. Goulet-Hanssens, F. Eisenreich and S. Hecht, Adv. Mater., 2020, 32, 1905966 CrossRef CAS PubMed.
- C. Gahl, R. Schmidt, D. Brete, E. R. McNellis, W. Freyer, R. Carley, K. Reuter and M. Weinelt, J. Am. Chem. Soc., 2010, 132, 1831–1838 CrossRef CAS PubMed.
- E. Titov, A. Sharma, N. Lomadze, P. Saalfrank, S. Santer and M. Bekir, ChemPhotoChem, 2021, 5, 926–932 CrossRef CAS.
- D. T. Valley, M. Onstott, S. Malyk and A. V. Benderskii, Langmuir, 2013, 29, 11623–11631 CrossRef CAS PubMed.
- E. Titov, G. Granucci, J. P. Götze, M. Persico and P. Saalfrank, J. Phys. Chem. Lett., 2016, 7, 3591–3596 CrossRef CAS PubMed.
- V. Cantatore, G. Granucci, G. Rousseau, G. Padula and M. Persico, J. Phys. Chem. Lett., 2016, 7, 4027–4031 CrossRef CAS PubMed.
- T. E. Dykstra, E. Hennebicq, D. Beljonne, J. Gierschner, G. Claudio, E. R. Bittner, J. Knoester and G. D. Scholes, J. Phys. Chem. B, 2009, 113, 656–667 CrossRef CAS PubMed.
- W. Barford and D. Trembath, Phys. Rev. B, 2009, 80, 165418 CrossRef.
- T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Phys. Chem. Chem. Phys., 2013, 15, 9245–9256 RSC.
- L. Alfonso Hernandez, T. Nelson, M. F. Gelin, J. M. Lupton, S. Tretiak and S. Fernandez-Alberti, J. Phys. Chem. Lett., 2016, 7, 4936–4944 CrossRef CAS PubMed.
- D. Ondarse-Alvarez, T. Nelson, J. M. Lupton, S. Tretiak and S. Fernandez-Alberti, J. Phys. Chem. Lett., 2018, 9, 7123–7129 CrossRef CAS PubMed.
- E. Titov, A. Humeniuk and R. Mitrić, Phys. Chem. Chem. Phys., 2018, 20, 25995–26007 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- P. H. Hünenberger, in Thermostat Algorithms for Molecular Dynamics Simulations, ed. C. Holm and K. Kremer, Springer Berlin Heidelberg, Berlin, Heidelberg, 2005, pp. 105–149 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- A. Dreuw and M. Head-Gordon, J. Am. Chem. Soc., 2004, 126, 4007–4016 CrossRef CAS PubMed.
- E. Titov, Molecules, 2021, 26, 4245 CrossRef CAS PubMed.
- E. Titov and P. Saalfrank, J. Phys. Chem. A, 2016, 120, 3055–3070 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. J. Frisch et al. , Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- S. Tretiak and S. Mukamel, Chem. Rev., 2002, 102, 3171–3212 CrossRef CAS PubMed.
- F. Plasser and H. Lischka, J. Chem. Theory Comput., 2012, 8, 2777–2789 CrossRef CAS PubMed.
- A. A. Voityuk, J. Chem. Phys., 2014, 140, 244117 CrossRef PubMed.
- S. Mai, F. Plasser, J. Dorn, M. Fumanal, C. Daniel and L. González, Coord. Chem. Rev., 2018, 361, 74–97 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- D. Ondarse-Alvarez, S. Kömürlü, A. E. Roitberg, G. Pierdominici-Sottile, S. Tretiak, S. Fernandez-Alberti and V. D. Kleiman, Phys. Chem. Chem. Phys., 2016, 18, 25080–25089 RSC.
- C. Rietze, E. Titov, G. Granucci and P. Saalfrank, J. Phys. Chem. C, 2020, 124, 26287–26295 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- W. Bronsch, T. Moldt, L. Boie, C. Gahl and M. Weinelt, J. Phys.: Condens. Matter, 2017, 29, 484002 CrossRef PubMed.
- T. Cusati, G. Granucci, M. Persico and G. Spighi, J. Chem. Phys., 2008, 128, 194312 CrossRef PubMed.
- E. Titov, T. Kopp, J. Hoche, A. Humeniuk and R. Mitrić, Phys. Chem. Chem. Phys., 2022, 24, 12136–12148 RSC.
- J. J. Nogueira, F. Plasser and L. González, Chem. Sci., 2017, 8, 5682–5691 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Further details on models and methods, and further results. See DOI: https://doi.org/10.1039/d2cp02774g |
‡ In general, for a nonlinear polyatomic molecule with N atoms, temperature is related to the kinetic energy as 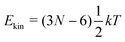 .21 However, in our models the four lowest hydrogen atoms are fixed and thus .21 However, in our models the four lowest hydrogen atoms are fixed and thus 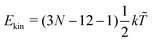 (here, 12 corresponds to frozen coordinates of four fixed atoms and 1 accounts for the rigid-body rotation around the axis going through the fixed atoms). Therefore, (here, 12 corresponds to frozen coordinates of four fixed atoms and 1 accounts for the rigid-body rotation around the axis going through the fixed atoms). Therefore, 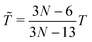 , which results in , which results in ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) ≈ 307.6 K for T = 300 K (N = 96). ≈ 307.6 K for T = 300 K (N = 96). |
| This journal is © the Owner Societies 2022 |