Open Access Article
Open Access ArticleInvestigating the abnormal conductivity behaviour of divalent cations in low dielectric constant tetraglyme-based electrolytes†
Long Hoang Bao
Nguyen‡
 ac,
Tanguy
Picard‡
ac,
Tanguy
Picard‡
 bc,
Cristina
Iojoiu
bc,
Cristina
Iojoiu
 *bc,
Fannie
Alloin
*bc,
Fannie
Alloin
 bc,
Nicolas
Sergent
bc,
Nicolas
Sergent
 b,
Marie-Liesse
Doublet
b,
Marie-Liesse
Doublet
 *ac and
Jean-Sébastien
Filhol
*ac and
Jean-Sébastien
Filhol
 *ac
*ac
aICGM, Univ Montpellier, CNRS, ENSCM, Montpellier, France. E-mail: Marie-Liesse.Doublet@umontpellier.fr; Jean-Sebastien.Filhol@umontpellier.fr
bUniv. Grenoble Alpes, Univ. Savoie Mont Blanc, CNRS, Grenoble INP, LEPMI, 38000, Grenoble, France. E-mail: Cristina.iojoiu@lepmi.grenoble-inp.fr
cRS2E French Network on Electrochemical Energy Storage, FR5439, Amiens, France
First published on 9th August 2022
Abstract
Solutions made of tetraglyme (G4) containing Ca(TFSI)2 have been studied as models to understand the solvation structure and the conductivity properties of multivalent ions in low dielectric constant ethereal electrolytes. These solutions have been characterised using electrochemical impedance spectroscopy, rheological measurement, and Raman spectroscopy. The ionic conductivity of these electrolytes shows an intriguing non-monotonic behaviour with temperature which deviates from the semi-empirical Vogel–Tammann–Fulcher equation at a critical temperature. This behaviour is observed for both Mg(TFSI)2 and Ca(TFSI)2, but not LiTFSI, indicating a difference in the solvation structure and the thermodynamic properties of divalent ions compared to Li+. The origin of this peculiar behaviour is demystified using temperature-controlled Raman spectroscopy and first-principles calculations combined with a thermodynamic analysis of the chemical equilibrium of Ca2+ ion-pairing versus solvation. As long-range electrostatic interactions are critical in solutions based on low dielectric ethereal solvents, a periodic approach is here proposed to capture their impact on the solvation structure of the electrolyte at different salt concentrations. The obtained results reveal that the thermodynamic and transport properties of Ca(TFSI)2/G4 solutions stem from a competition between enthalpic (ionic strength) and entropic factors that are directly controlled by the solution concentration and temperature, respectively. At high salt concentrations, the ionic strength of the solution favours the existence of free ions thanks to the strong solvation energy of the polydentate G4 solvent conjugated with the weak complexation ability of TFSI−. At elevated temperatures, the configurational entropy associated with the release of a coordinated G4 favours the formation of contact ion-pairs due to its flat potential energy surface (weak strain energy), offering a large configuration space. Such a balance between ion-pair association and dissociation not only rationalises the ionic conductivity behaviour observed for Ca(TFSI)2/G4 solutions, but also provides valuable information to extrapolate the ionic transport properties of other electrolytes with different M(TFSI)n salts dissolved in longer-chain glymes or even poly(ethylene oxide). These findings are essential for the understanding of solvation structures and ionic transport in low-dielectric media, which can further be used to design new electrolytes for Li-ion and post Li-ion batteries as well as electrocatalysts.
Introduction
The global battery market has been in constant expansion in recent years with tremendous development being foreseen in the next decades as induced as an immediate consequence of electrified transportation and the installation of electrical grid storage to accommodate intermittent energy production. In order to ensure a sustainable supply chain, battery productions need to be “green” regarding their environmental impact.1,2 So far, rechargeable lithium-ion batteries (LIBs) are the dominant energy storage technology for mobile devices, but lithium mining has caused significant ecological and social effects.3,4 Furthermore, the use of rare metals such as cobalt in these batteries has caused great impacts on the environment and the price of the full device.5 Academic and industrial research nowadays aim to minimise the use of rare metals in batteries, and improve the power and energy densities of the cells. In order to ensure an ecological and sustainable supply of batteries adapted to our modern life's demands, calcium-ion rechargeable batteries have been explored.6–9 Indeed, Ca is the fifth most abundant element on Earth, available in most countries at a reasonable extraction price, by-passing all the economic and political constraints in the technological transition to come. Furthermore, calcium is safer than lithium due to its lower reactivity when exposed to air and moisture.The growth of calcium-ion rechargeable batteries is conjugated to the development of new Ca2+-conducting electrolytes. In order to satisfy all the practical requirements, the newly developed electrolyte must possess a high Ca2+ conductivity (>10−4 S cm−1 at room temperature), a transference number of Ca2+ approaching 1, and high chemical and electrochemical stabilities.10,11 Moreover, materials used as electrolytes must be safe and non-flammable, with low toxicity and low manufacturing cost. Organic carbonates have long been used as solvents for electrolytes in LIBs thanks to their high dielectric constant, wide electrochemical windows, and the capability to dissolve a considerable amount of salts at ambient temperature.12 Nonetheless, recent research has shown that carbonate-based electrolytes are not ideal for multivalent batteries as the solvent molecules tend to be reduced before the metal deposition can occur.13–15 Promising Ca plating and stripping have recently been reported in electrolytes using glyme- or ether-based solvents, indicating the particular role of low dielectric media in the electrochemical activity of multivalent ions.16–19
To design proficient Ca2+ electrolytes, the solvation structure, the physical properties, and the conduction mechanism in Ca2+ electrolytes should be well comprehended. Among the glyme-based family, tetraethylene glycol dimethyl ether (tetraglyme or G4) exhibits intermediate properties between molecular and polymer glymes. A detailed investigation of the Ca2+–O interaction in tetraglyme solution is thus representative for the whole glyme family. Most glyme molecules possess a high donor number (DN), which is a measure of the Lewis basicity of the oxygen's electron lone pairs, helping them to dissolve a significant amount of Ca2+ salts. Nevertheless, glyme-based solvents possess a low dielectric constant (εr = 7.0–7.5), leading to great complexities when examining their physical properties. When dissolved in solution, a solvated ion can still interact with other cations and anions through the long-range electrostatic interaction, whose energy can be expressed by 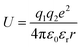 where r is the distance between the two ions of charge q1 and q2 that are present in a medium of εr dielectric constant. In conventional carbonate-based electrolytes, the dielectric constant is high (εr = 89.0 for ethylene carbonate or εr = 40–60 for mixtures of carbonated solvents) so that the ion–ion interactions are efficiently screened by the solvents, which significantly reduces their contribution to the system's total energy. Although the ionic interactions can be reasonably estimated using Debye–Hückel theory,20 it is only applicable to diluted solutions (∼0.01–0.1 M) in high-dielectric media and cannot be universally applied. In order to model and predict the thermodynamic properties of low-dielectric media in a qualitative way, it is necessary to develop a new modelling approach to account for the contribution of these long-range electrostatic interactions.
where r is the distance between the two ions of charge q1 and q2 that are present in a medium of εr dielectric constant. In conventional carbonate-based electrolytes, the dielectric constant is high (εr = 89.0 for ethylene carbonate or εr = 40–60 for mixtures of carbonated solvents) so that the ion–ion interactions are efficiently screened by the solvents, which significantly reduces their contribution to the system's total energy. Although the ionic interactions can be reasonably estimated using Debye–Hückel theory,20 it is only applicable to diluted solutions (∼0.01–0.1 M) in high-dielectric media and cannot be universally applied. In order to model and predict the thermodynamic properties of low-dielectric media in a qualitative way, it is necessary to develop a new modelling approach to account for the contribution of these long-range electrostatic interactions.
In this study, several Ca(TFSI)2/G4 solutions were prepared, and their ionic conductivity and viscosity were evaluated at different temperatures and concentrations, and then compared with those of the LiTFSI/G4 electrolyte. Abnormal behaviours were detected in Ca(TFSI)2/G4 solutions and the origin of these abnormalities was thoroughly investigated using a combined experimental and theoretical approach. In these solutions, contact ion-pairs occur preferentially at elevated temperatures, and differs from those usually observed in Li+ electrolytes. The ion-pair structure was elucidated using first-principles density functional theory (DFT) calculations combined with vibrational spectroscopy. Furthermore, the chemical equilibrium between ion-pair association and dissociation was estimated using periodic calculations to include the effect of the long-range electrostatic interactions on the energy of the charged ions at different salt concentrations. The obtained results reveal that the ion-pair formation is an endergonic process that turns to be exergonic at high temperatures or low salt concentrations due to a subtle balance between the ionic strength of low-dielectric media and entropy gain when G4 molecules are released during ion-pairing. Such a fundamental knowledge in ion-pair formation mechanism is vital to the understanding of solvation properties in low-dielectric media, which is not fully comprehended at the present time. Moreover, the results discovered in this work can be used as guidance to develop new electrolytes for rechargeable batteries, especially those using non-polar solvents.
Results
Conductivity and viscosity measurements
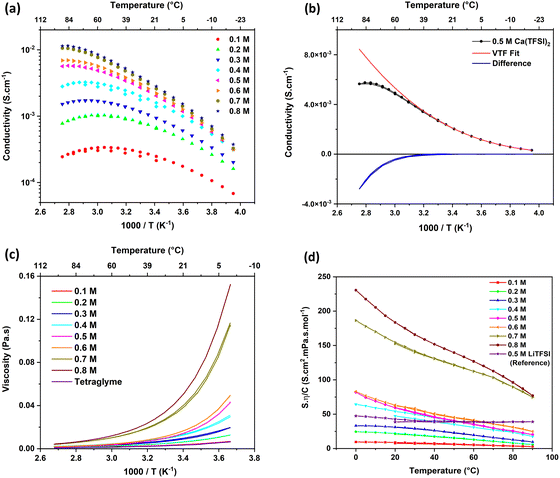
The conductivity (σ) of Ca(TFSI)2/G4 solutions was measured at different salt concentrations in a temperature range of −20 to 90 °C (Fig. 1a). By varying the salt concentration, the ionic conductivity of the Ca(TFSI)2/G4 solutions increases monotonically up to 0.8 M while in the case of Mg(TFSI)2/G4 the conductivity maxima was observed at 0.55 M.21 The reason for this difference is related to the solvation structure of Mg2+/Ca2+ in G4 and the energy of the M2+–O interaction. The measured conductivity was then fit using the semi-empirical Vogel–Tammann–Fulcher (VTF) model (eqn (1)), which generally describes the conductivity behaviour of amorphous polymer and liquid electrolytes vs. temperature.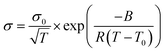 | (1) |
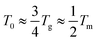 (where Tg is the glass transition temperature and Tm is the melting temperature) for polymer-based electrolytes.22–24
(where Tg is the glass transition temperature and Tm is the melting temperature) for polymer-based electrolytes.22–24
A severe deviation from the VTF model is observed at a relatively low temperature for all solutions, e.g. 37 °C for a 0.5 M Ca(TFSI)2/G4 solution (Fig. 1b). This behaviour is abnormal as in typical solutions, charge carriers’ mobility increases with temperature due to the viscosity decrease. Furthermore, the “critical temperature” (Tc) associated with the onset of the deviation from the VTF law, shifts to a lower temperature when lowering the salt concentration, from Tc = 333 K in 0.8 M Ca(TFSI)2/G4 to 293 K in a 0.1 M solution. Such a deviation is not observed in a 0.5 M LiTFSI/G4 solution (Fig. S2, ESI†) and has never been reported to the best of our knowledge. The presence of a “critical temperature” in Ca(TFSI)2/G4 electrolytes could be a consequence of the low dielectric constant value of G4 that strongly increases long-range cation/anion electrostatic interactions, in particular for solutions based on divalent cations. Forero-Saboya et al. investigated carbonate-based electrolytes and also observed a different behaviour for Mg2+ or Ca2+-based electrolytes compared to the Li+ one; nevertheless, the evolution in the conductivity of these carbonate-based electrolytes followed the VTF model, even at high temperatures.25
The temperature dependence of the viscosity of Ca(TFSI)2/G4 solutions at different salt concentrations is depicted in Fig. 1c. The addition of Ca(TFSI)2 into liquid tetraglyme led to an increase in the solution viscosity as a consequence of the interaction between Ca2+ and the G4 electron lone-pairs. By increasing temperature, the viscosity drops rapidly, and its evolution vs. temperature follows the VTF model perfectly, which is not the case for conductivity. At a given temperature, the conductivity increases continuously with the concentration while a discontinuity is noticed for the viscosity, i.e., a large increase in solution viscosity is observed when moving from 0.6 M to 0.7 M solution. This viscosity/conductivity non-correlated process could be related to the formation of a gel due to Ca2+–O interactions at a certain concentration. However, such a structure was not observed by rheology measurements showing that the Ca(TFSI)2/G4 electrolytes behave as a Newtonian liquid irrespectively of the salt concentration (Fig. S3, ESI†). DSC measurements were also performed (Fig. S4, ESI†) and contrarily to what has been observed for lithium electrolytes in G4,26,27 two melting points were observed up to 0.8 M, indicating the presence of crystalline solvate structures with a low melting point at around −32 °C. The eutectic point corresponds to the 0.8 M concentration, i.e., a molar ratio of four G4 per Ca(TFSI)2.
To further investigate the link between conductivity and viscosity, one can plot their product, normalised by the salt concentration, as a function of temperature (Fig. 1d), known as the Walden plot 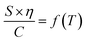 .28,29 In a liquid or amorphous polymer, the ionic conductivity is linked to the motion of both anions and cations, and the charge mobility is in turn linked to the ability of the host network to accommodate the charge transport, which is quantified by its viscosity and structural relaxation time. In general cases, the viscosity and conductivity are inversely proportional, making their normalised product a constant with respect to temperature, which is the case for 0.5 M LiTFSI/G4 (Fig. 1d). Nevertheless, the constant line in the Walden plot only holds in solutions, where the number of charge carriers is constant in the temperature range investigated. In 0.1–0.3 M Ca(TFSI)2/G4 solutions, the Walden plot shows a plateau at low temperature, followed by a slight deviation at higher temperatures. On the other hand, the Walden plot deviates brutally from the constant line in 0.4–0.8 M Ca(TFSI)2/G4 solutions, which might be related to a change in the number and/or the nature of charge carriers with temperature (Fig. 1d). This behaviour has been previously reported for Ca(NO3)2 hydrate melts, and this abnormality was assigned to structures formed in the liquid phase.30
.28,29 In a liquid or amorphous polymer, the ionic conductivity is linked to the motion of both anions and cations, and the charge mobility is in turn linked to the ability of the host network to accommodate the charge transport, which is quantified by its viscosity and structural relaxation time. In general cases, the viscosity and conductivity are inversely proportional, making their normalised product a constant with respect to temperature, which is the case for 0.5 M LiTFSI/G4 (Fig. 1d). Nevertheless, the constant line in the Walden plot only holds in solutions, where the number of charge carriers is constant in the temperature range investigated. In 0.1–0.3 M Ca(TFSI)2/G4 solutions, the Walden plot shows a plateau at low temperature, followed by a slight deviation at higher temperatures. On the other hand, the Walden plot deviates brutally from the constant line in 0.4–0.8 M Ca(TFSI)2/G4 solutions, which might be related to a change in the number and/or the nature of charge carriers with temperature (Fig. 1d). This behaviour has been previously reported for Ca(NO3)2 hydrate melts, and this abnormality was assigned to structures formed in the liquid phase.30
Origin of abnormal behaviours
The deviation in the conductivity and the Walden plots of Ca(TFSI)2/G4 solutions indicates a decrease in the number of charge carriers and the formation of new ionic species in the solution at elevated temperatures. One possibility for the change in the number of charge carriers is the ion-pair formation. Nevertheless, the actual structure of [Ca–TFSI]+ contact ion-pair in G4 solution has never been reported in the literature. Theoretical DFT calculations were thus employed to elucidate the structure and shed light on the mechanism of ion-pairing.In a recent study, we reported that Ca2+ ions in a 0.5 M Ca(TFSI)2/G4 solution are solvated mainly in the form of mer-[Ca(G4)2]2+, in which two G4 molecules participate in the solvation, each G4 donating four of its oxygens to the coordination to Ca2+, i.e. [4 + 4].31 The complexation to TFSI− requires the departure of one G4 molecule in mer-[Ca(G4)2]2+ and leads to a [5 + 2] solvation sphere in which one Ca–O bond is missing compared to the fully solvated [4 + 4] sphere (Fig. 2). In TFSI−, the negative charge is delocalised over the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S–N–S
S–N–S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group, in which both N and O atoms can act as electron donors. Experimental and theoretical data have shown that oxygen atoms in the sulfonyl groups have a higher affinity to cations than nitrogen in the imide.32–36 Furthermore, the nitrogen atom has a great steric hindrance in its surrounding; hence, only oxygen atoms participate in the ion-pair formation. Different conformations and structures of the TFSI− and [Ca(TFSI)(G4)]+ contact ion-pair were generated and are shown in Fig. S5 and S6 (ESI†). Results show that trans-[Ca(μ2-TFSI)(G4)]+ is the most stable form, contributing mainly to the thermodynamic properties of the solutions, which will be focused on in the following text.
O group, in which both N and O atoms can act as electron donors. Experimental and theoretical data have shown that oxygen atoms in the sulfonyl groups have a higher affinity to cations than nitrogen in the imide.32–36 Furthermore, the nitrogen atom has a great steric hindrance in its surrounding; hence, only oxygen atoms participate in the ion-pair formation. Different conformations and structures of the TFSI− and [Ca(TFSI)(G4)]+ contact ion-pair were generated and are shown in Fig. S5 and S6 (ESI†). Results show that trans-[Ca(μ2-TFSI)(G4)]+ is the most stable form, contributing mainly to the thermodynamic properties of the solutions, which will be focused on in the following text.
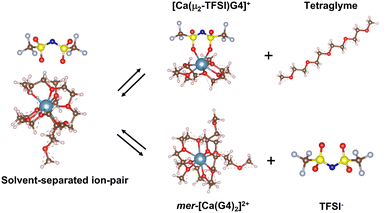 | ||
| Fig. 2 Molecular representation of the [mer-[Ca(G4)2]//TFSI]+ solvent-separated ion-pair and its evolution to the trans-[Ca(μ2-TFSI)(G4)]+ contacting ion-pair and free ions. | ||
Due to its high charge value, the mer-[Ca(G4)2]2+ complex can attract and interact with free TFSI− in the solution to form the solvent-separated ion-pair [[Ca(G4)2]//TFSI]+. In this structure, Ca2+ remains fully bonded to G4 molecules while TFSI− resides in its second solvation shell at a relatively close distance (Fig. S7, ESI†). Even though TFSI− is not directly bonded to the Ca2+ centre, the electrostatic interaction between them limits the free motion of the ions, thus having a direct impact on the solution's ionic conductivity. Due to the mechanical flexibility of long tetraglyme chains, [Ca(G4)2]2+ can adopt several solvation structures with different organisations of tetraglyme molecules. Instead of having a [4 + 4] coordination as in the mer-structure, [Ca(G4)2]2+ can adopt a [5 + 3] solvation sphere (Fig. S8, ESI†), where the energy difference between the two forms is only 37.7 kJ mol−1 (390 meV),31 which is accessible by a gain in the configurational entropy of the less coordinated G4 molecule or thermal excitation. By considering different conformers, the energy of the [[Ca(G4)2]//TFSI]+ solvent-separated ion-pair can then span over an energy range of 37.7 kJ mol−1 depending on the local configuration of the coordinated G4 molecules (Fig. 3); such an energy span is also expected for free ions. In reality, the energy of the [[Ca(G4)2]//TFSI]+ solvent-separated ion-pair spans over a wider range than that of free ions due to (i) different conformers of solvated Ca2+, (ii) the distance between solvated Ca2+ and TFSI−, and (iii) the direction where TFSI− approaches the solvated Ca2+. Nonetheless, all these factors cannot fully be captured due to the limitations of DFT calculations; we have thus limited our consideration in the conformer contribution.
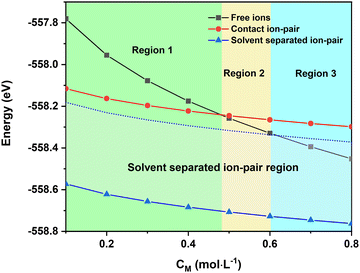
The total energy of different Ca2+ solvation and ion-pair structures as a function of the solution concentration is reported in Fig. 3. The results show that the [[Ca(G4)2]//TFSI]+ solvent-separated ion-pair is the most stable species, especially at low concentrations (Fig. 3). This result agrees with previous studies showing that multivalent ions were prone to ion-pairing even at modest concentrations.37–41 This emphasises that even though G4 is capable of dissolving the Ca(TFSI)2 salt thanks to the strong Ca2+–O interaction (see Table 1), the solvated [Ca(G4)2]2+ are not completely separated from TFSI−. The strong electrostatic interactions of Ca2+ with its surroundings thus make the motion and properties of solvated Ca2+ strongly correlated with those of its counter-ions at all concentrations.
| EM–O (kJ mol−1) | Average EM–O per bond (kJ mol−1) | Average EM–O (TFSI) per bond (kJ mol−1) | EStrain for G4 (kJ mol−1) | Percentage of EStrain (G4) compared to EM–O (%) | |
|---|---|---|---|---|---|
| mer-[Ca(G4)2]2+ [4 + 4] | −1463.0 | −182.9 | 97.5 | 6.7 | |
| [Ca(μ2-TFSI)(G4)]+ [5 + 2] | −1444.7 | −206.4 | −265.2 | 48.2 | 3.3 |
The energy of doubly-charged mer-[Ca(G4)2]2+ is more sensitive to the solution concentration than the singly-charged solvent separated [[Ca(G4)2]//TFSI]+ and contact ion-pair trans-[Ca(μ2-TFSI)(G4)]+. Consequently, the fully solvated species becomes more stable than the solvent-separated and contact ion-pair species at a critical concentration above which a higher molar fraction of mer-[Ca(G4)2]2+ should occur in the solution. This leads to the existence of three distinct regions in the phase diagram (Fig. 3), in which the thermodynamic stability of the solvated species is ranked as follows:
• Region 1 (low concentration): solvent-separated ion-pair > contact ion-pair > free ions.
• Region 2 (medium concentration): solvent-separated ion-pair > free ions > contact ion-pair.
• Region 3 (high concentration): free ions > solvent-separated ion-pair > contact ion-pair.
Interestingly, the conversion of the most stable species, i.e., solvent-separated ion-pairs or free ions, to contact ion-pairs is computed as an endergonic process (∼100–200 meV) at 0 K. As this process is accompanied by a release of a tetraglyme molecule which possesses high configurational entropy due to the long organic chain with several degrees of freedom associated with the rotations around the chemical C–O, C–C bonds, the chemical equilibrium should turn in favour of the ion pair formation at elevated temperatures due to significant entropy gain. Indeed, the energy difference between solvent-separated ion-pairs/free ions and contact ion-pairs is around 100 meV (Fig. 3), which can be easily compensated by vibrational and configurational entropy contributions of free tetraglyme molecules at elevated temperatures. Upon heating, it is therefore expected that the [Ca(μ2-TFSI)(G4)]+ contact ion-pair formation can occur, which can alter the ionic conductivity of the solution. The temperature at which [Ca(μ2-TFSI)(G4)]+ formation occurs can be considered as the “critical temperature”, which is associated with a decrease in solution ionic conductivity.
Ion-pair formation detection
In order to verify these theoretical predictions, Raman spectroscopy was employed to follow the evolution in the nature of TFSI− anions upon heating. This technique is capable of distinguishing TFSI− in the contact ion-pairs from those being in the outer-sphere of Ca2+ or free in the solution.
Fig. 4 shows the Raman spectra obtained for various Ca(TFSI)2/G4 solutions. The characteristic vibrational modes of TFSI− and Ca2+/G4 system are: (i) the symmetric and anti-symmetric SO2 wagging modes (ω) at 397 and 408 cm−1, (ii) the symmetric CF3 bending (δ) coupling with expansion–contraction of the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S–N–S
S–N–S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group at 740 cm−1, (iii) the deformation vibration of C–H, C–C, and C–O bonds of G4 molecules coordinated to Ca2+ at 868 and 879 cm−1, and (iv) the C–F stretching mode (ν) at 1242 cm−1.42 As shown in Fig. 4, the intensity of these characteristic vibrational modes increases gradually with the salt concentration.
O group at 740 cm−1, (iii) the deformation vibration of C–H, C–C, and C–O bonds of G4 molecules coordinated to Ca2+ at 868 and 879 cm−1, and (iv) the C–F stretching mode (ν) at 1242 cm−1.42 As shown in Fig. 4, the intensity of these characteristic vibrational modes increases gradually with the salt concentration.
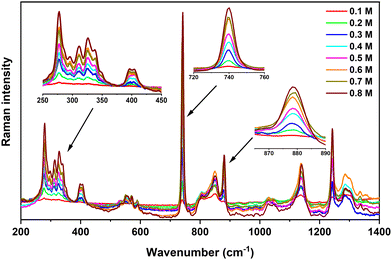 | ||
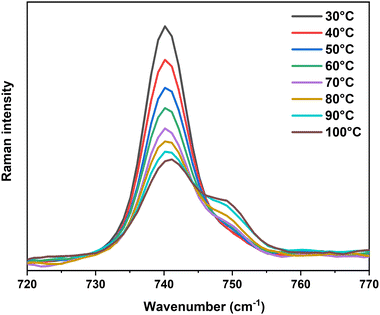
| Fig. 4 Raman spectra acquired on Ca(TFSI)2/G4 solutions at different salt concentrations. Insets focus on the zoom of some important vibrational modes. | ||
Among all characteristic vibrations, the essential one is the TFSI− contraction–expansion mode locating at 740 cm−1. It has a trivial intensity in IR spectroscopy but is the most intense band observed in Raman spectroscopy. It is originated from the symmetric CF3 bending (δ) and the expansion–contraction of the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S–N–S
S–N–S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group, the coupling of which could result from the wavenumber superposition or a Fermi resonance (Video S1, ESI†).42–45 The deconvolution of this signal required at least three components located at: (i) 731 cm−1 to take into account the background effect,43 (ii) 740 cm−1 corresponding to free TFSI−, including those residing in the second coordination sphere of Ca2+ in the G4 solution (3 cm−1 shifted compared to free TFSI−), and (iii) 748 cm−1 corresponding to the TFSI− coordinated to the Mn+ in the ion-pair (Video S2, ESI†), i.e. Ca2+ in this study (Fig. S9, ESI†). Even though the Ca2+–O stretching component in the vibrational eigenvector was relatively weak in this wavenumber range, it was sufficient to modify the force constant and the vibrational wavenumber of the TFSI− group. Assuming a similar sensitivity to Raman scattering of free and coordinated TFSI−, the Raman intensity ratio reflects the percentage of each kind of TFSI− that is present in the electrolyte. At a molar concentration greater than 0.3 M, the integrated area of the 748 cm−1 band always equals ca. 10% of the total area of the 740 cm−1-centered vibrations (Table S1, ESI†) indicating a nearly constant fraction of ion-pairs in the solution. At lower salt concentrations, i.e., 0.1 M and 0.2 M, the peak at 748 cm−1 has a higher contribution (Table S1, ESI†), indicating that [Ca(μ2-TFSI)(G4)]+ ion-pairs are formed and can be observed partially at ambient temperature. This result agrees with theoretical predictions and confirms the presence of free Ca2+ and TFSI− ions at high salt concentrations, consistent with the ionic conductivity of these concentrated solutions at moderated temperatures.
O group, the coupling of which could result from the wavenumber superposition or a Fermi resonance (Video S1, ESI†).42–45 The deconvolution of this signal required at least three components located at: (i) 731 cm−1 to take into account the background effect,43 (ii) 740 cm−1 corresponding to free TFSI−, including those residing in the second coordination sphere of Ca2+ in the G4 solution (3 cm−1 shifted compared to free TFSI−), and (iii) 748 cm−1 corresponding to the TFSI− coordinated to the Mn+ in the ion-pair (Video S2, ESI†), i.e. Ca2+ in this study (Fig. S9, ESI†). Even though the Ca2+–O stretching component in the vibrational eigenvector was relatively weak in this wavenumber range, it was sufficient to modify the force constant and the vibrational wavenumber of the TFSI− group. Assuming a similar sensitivity to Raman scattering of free and coordinated TFSI−, the Raman intensity ratio reflects the percentage of each kind of TFSI− that is present in the electrolyte. At a molar concentration greater than 0.3 M, the integrated area of the 748 cm−1 band always equals ca. 10% of the total area of the 740 cm−1-centered vibrations (Table S1, ESI†) indicating a nearly constant fraction of ion-pairs in the solution. At lower salt concentrations, i.e., 0.1 M and 0.2 M, the peak at 748 cm−1 has a higher contribution (Table S1, ESI†), indicating that [Ca(μ2-TFSI)(G4)]+ ion-pairs are formed and can be observed partially at ambient temperature. This result agrees with theoretical predictions and confirms the presence of free Ca2+ and TFSI− ions at high salt concentrations, consistent with the ionic conductivity of these concentrated solutions at moderated temperatures.
To demonstrate the important presence of contact ion-pairs upon heating, temperature-dependent in situ Raman spectroscopy was performed for the solution with the weakest ionic strength, 0.1 M Ca(TFSI)2/G4. The in situ experiment was focused especially on the vibrations around 740 cm−1 as they can provide quantitative information on the amount of bound and free TFSI− in the solution. Fig. 5 shows the evolution in intensity of this band as a function of temperature. Upon heating, the intensity of the signal corresponding to free TFSI− decreases while the one corresponding to bound TFSI− gradually grows (Fig. 5), indicating a temperature-driven formation of contact ion-pairs. The increasing amount of [Ca(μ2-TFSI)(G4)]+ ion-pair leads to a loss in the number of charge carriers and a change in the mean diffusion coefficient. These phenomena are entirely coherent with the loss in ionic conductivity of the 0.1 M Ca(TFSI)2/G4 solution, the deviation from the VTF-law, and the peculiar behaviour of Walden product at elevated temperatures. By taking into account the presence of free and bound TFSI−, the corrected Walden product shows a constant line in the whole temperature range, which ensured the sole role of ion-pairing in the abnormal behaviour of 0.1 M Ca(TFSI)2/G4 solution (Fig. S10, ESI†).
For comparison purposes, Raman measurement was also conducted for a 0.2 M LiTFSI/G4 solution (i.e. same TFSI− concentration as in 0.1 M Ca(TFSI)2/G4). Results show a gradual decrease in the band's intensity at 740 cm−1 when the temperature increased (Fig. S11, ESI†), which is due to a change in its Raman activity. Nevertheless, the signal of the [Li–TFSI] contact ion-pair is not detected in this temperature range. This comparison reveals different solvation and ion-pair structures for mono- and divalent cations, as discussed below.
Discussions
Organic carbonates have long been the focus of the battery community as a practical solvent for electrolytes in rechargeable LIBs.46 Nonetheless, carbonate molecules possess a high dipole moment that will be greatly polarised when they are coordinated to a highly charged cation, such as Mg2+, Ca2+, and Al3+. The carbonate molecules in the first coordination sphere of multivalent ions will consequently be reduced before the metal deposition can occur.13 On the other hand, non-polar solvents, such as glyme molecules, can exhibit great reduction in stability even if they are coordinated to a highly polarised cation. Nonetheless, it has long been considered that glyme-based solutions are not ideal electrolytes for batteries as they possess a low dielectric constant and would poorly dissociate the ions. Depending on the chain length, glyme molecules can actually act as multidentate ligands,47 and the solvated ions are highly stabilised through a chelating effect facilitated by the relatively low mechanical stress associated with the glyme strain. Long-chain glyme-based molecules, e.g., triglyme and tetraglyme, can thus dissolve a significant amount of salts, which can be used as electrolytes for rechargeable batteries.16The great influence of the ionic strength on the stability of charged ions is a peculiar property of solvents possessing a low dielectric constant value, in which long-range electrostatic interactions have a great contribution to the system's total energy. In most studies, the theoretical enthalpy or Gibbs free energy of a reaction in liquid phase is computed using a molecular approach (isolated molecules/ions surrounded by an implicit solvent model) that assumes an infinite dilution. Such a consideration is only appropriate when investigating highly dilute solutions in high dielectric constant media, where the ion–ion interaction is completely smeared out. In solutions containing a significant amount of solute, the ion–ion interaction must be included in the total energy by applying the Debye–Hückel solution model,20 only valid in high-dielectric media, as a data post-treatment process. As an alternative of the Debye–Hückel model for low dielectric constant media, the present study shows that affordable periodic calculations with varied simulation boxes including punctual counter-ions, e.g., Cl−, lead to reliable results that qualitatively compare with the experimental data.
Based on this methodology, the solvation properties of Ca(TFSI)2/G4 solutions at various concentrations were investigated to elucidate the abnormal behaviour experimentally observed for their ionic conductivity. Results show that solvated Ca2+ in G4 solutions has a great tendency to form solvent-separated ion-pairs due to the strong electrostatic interaction of Ca2+ with the counter TFSI− ion located in its outer-sphere. At high concentration, free ion mer-[Ca(G4)2]2+ is even more stabilised than the solvent-separated species (Fig. 3) making it the dominant species thanks to the strong ionic strength of the medium allowing long-range electrostatic stabilisation.
Upon heating, both the conductivity and temperature-dependent Raman measurements suggest that solvent-separated ion-pairs or free ions evolve toward [Ca(μ2-TFSI)(G4)]+ contact ion-pairs. Using the energy analysis approach as described in ref. 31, 48, the interaction energy of Ca2+–O bonds and strain energy required for the deformation of G4 molecules in free mer-[Ca(G4)2]2+ and [Ca(μ2-TFSI)(G4)]+ can be deconvoluted (Table 1). The Ca2+–O (TFSI−) interaction energy is 40% stronger than that of Ca2+–O (G4), i.e., −265 vs. −185 kJ mol−1, due to an enhanced electrostatic interaction between Ca2+ and TFSI−, inducing a competition between Ca2+–O (TFSI−) and Ca2+–O (G4). Nonetheless, the number of Ca2+–O bonds being one less in [Ca(μ2-TFSI)(G4)]+ [5 + 2] than in mer-[Ca(G4)2]2+ [4 + 4], the total Ca2+–O interaction energies in the two systems turn to be very similar (Table 1). The direction of the chemical equilibrium between these two species can be easily switched by a small energy variation due to concentration/temperature changes. Moreover, the replacement of a tetraglyme molecule in the doubly-charged mer-[Ca(G4)2]2+ complex by TFSI− leads to a decrease in the ionic strength of the media together with a significant increase in the system's entropy due to the multiple configurations of a free tetraglyme molecule. These two factors are the driving force for the contact ion-pair formation upon heating, which fully rationalises the decrease in the ionic conductivity with temperature.
Overall, the results presented in this study demonstrate a subtle chemical equilibrium existing in the Ca(TFSI)2/G4 solution between solvated Ca2+ and singly-charged ion-pairs (solvent-separated or contact). The weakly endergonic reaction enthalpy computed at 0 K for the [Ca(G4)2]2+ + TFSI− ⇌ [Ca(μ2-TFSI)(G4)]+ + G4 equilibrium is sufficient to explain why Ca(TFSI)2/G4 solutions are so sensitive to concentration and/or temperature effects. Whether this equilibrium turns in favour of ion-pair association or dissociation clearly lies in the enthalpy/entropy competition one may tune it through the modulation of concentration and temperature. Increasing salt concentration moves the equilibrium towards ion-pair dissociation thanks to the ionic strength (enthalpy gain) which stabilises solvated Ca2+ above a critical concentration (Region 2). While this is beneficial to ionic conductivity, the persistent occurrence of solvent-separated ion-pairs, irrespective of the concentration, contributes to reduce the optimal ionic conductivity one may envision in solutions with solely solvated Ca2+. One way to prevent the dominant contribution of solvent-separated ion-pairs at low salt concentrations would be to monitor the solution's ionic strength through the so-called “salt effect”. As an example, adding non-electroactive salts, such as [N(Bu)4]Cl, would increase the ionic strength of the solution and favour fully solvated mer-[Ca(G4)2]2+ species even at low Ca(TFSI)2 concentrations.
Increasing the temperature now moves the equilibrium towards ion-pair association thanks to the entropy gain associated with the conversion of Ca-chelating G4 having a few accessible conformations, into free G4 having around 316 accessible conformations. Remarkably, temperature does not act as a stabiliser of the contact ion-pair but triggers its formation indirectly from the large entropy gain associated with the increasing fraction of free tetraglymes in the solution. The detrimental impact of ion-pairing on the ionic conductivity of the solution could be easily prevented by using longer-chains glyme solvents up to polyethylene oxide (PEO) polymers. Indeed, while the enthalpy contribution to the solvation structures of Ca2+ is expected to be similar in Ca(TFSI)2/PEO polymer electrolytes and in liquid ethereal solutions, the important loss in configuration entropy in longer-chains free glymes and polymers should prevent or delay the formation of ion-pairs towards higher temperatures. Therefore, Ca(TFSI)2/PEO is expected not to be a strong entropy-driven system as tetraglyme and its properties should be mainly dictated by ionic strength making it a better ionic conductor than liquid Ca(TFSI)2/G4.
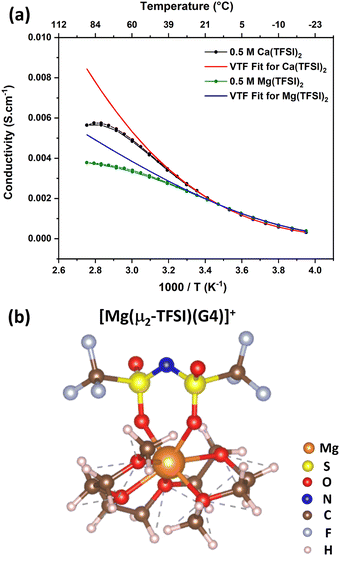
At this stage, one may wonder whether the peculiar behaviour observed in Ca(TFSI)2/G4 will also be encountered in other systems, such as Mg(TFSI)2/G4 solutions. In order to clarify this point, a 0.5 M Mg(TFSI)2/G4 solution was prepared, and its temperature-dependence conductivity was also measured (Fig. 6a). The 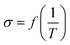 relation also shows a non-monotonic response; there exists a “critical” temperature, beyond which the solution conductivity starts to deviate from the VTF model, alike in Ca(TFSI)2/G4 solutions. This phenomenon is also assigned to the ion-pair formation at elevated temperatures. In a recent study, we have demonstrated that Mg2+ in G4 solution shows structural flexibility. Under G4-deficient conditions, Mg2+ exists in the form of [Mg(G4)]2+ while two G4 molecules participate in the solvation process to generate mer-[Mg(G4)2]2+ [3 + 3] when there is a G4 surplus.31 In 0.5 M Mg(TFSI)2/G4 solution, mer-[Mg(G4)2]2+ is the preferred solvation form and the [Mg(TFSI)(G4)]+ ion-pair formation reaction can be written as in Fig. S12 (ESI†). Nevertheless, there is a transformation in the coordination number of Mg2+ from [3 + 3] to [5 + 2] during the ion-pair association (Fig. S12, ESI†). Alike Ca2+, Mg2+ ion-pair can exist in the form [Mg(μ1-TFSI)(G4)]+ or [Mg(μ2-TFSI)(G4)]+ with the latter being more stable (Fig. 6b). The thermodynamic properties of ion-pair formation in 0.5 M Mg(TFSI)2/G4 solution are then expected to be similar to those in Ca(TFSI)2/G4 solutions, therefore favouring the [Mg(μ2-TFSI)(G4)]+ formation at elevated temperatures. These findings are consistent with previous studies showing that in low-permittivity solvents, such as monoglyme, diglyme, or triglyme, the fraction of free Mg2+ in Mg(TFSI)2-based electrolytes increases at higher salt concentrations.49–52 Table S2 (ESI†) summarises the Mg2+–O interaction energy with different glymes, from monoglyme up to tetraglyme; it is apparent that the strength of the Mg2+–O interaction is invariant with the chain length. Moreover, all glyme-based media exhibit a similar dielectric constant (εr = 7.2–7.5). The invariance in the magnitude of the short- and long-range interactions when varying the chain length is the origin of the abnormalities observed in glyme-based solutions containing divalent salts. The physical properties of low dielectric Mg(TFSI)2/G4 and Ca(TFSI)2/G4 solutions are thus very different from those known for conventional electrolytes. Therefore, a suitable ionic strength must be tuned through the “salt effect” when employing Mg(TFSI)2/G4 or Ca(TFSI)2/G4 as the electrolyte for rechargeable batteries in order to maximise the amount of free solvated ions.
relation also shows a non-monotonic response; there exists a “critical” temperature, beyond which the solution conductivity starts to deviate from the VTF model, alike in Ca(TFSI)2/G4 solutions. This phenomenon is also assigned to the ion-pair formation at elevated temperatures. In a recent study, we have demonstrated that Mg2+ in G4 solution shows structural flexibility. Under G4-deficient conditions, Mg2+ exists in the form of [Mg(G4)]2+ while two G4 molecules participate in the solvation process to generate mer-[Mg(G4)2]2+ [3 + 3] when there is a G4 surplus.31 In 0.5 M Mg(TFSI)2/G4 solution, mer-[Mg(G4)2]2+ is the preferred solvation form and the [Mg(TFSI)(G4)]+ ion-pair formation reaction can be written as in Fig. S12 (ESI†). Nevertheless, there is a transformation in the coordination number of Mg2+ from [3 + 3] to [5 + 2] during the ion-pair association (Fig. S12, ESI†). Alike Ca2+, Mg2+ ion-pair can exist in the form [Mg(μ1-TFSI)(G4)]+ or [Mg(μ2-TFSI)(G4)]+ with the latter being more stable (Fig. 6b). The thermodynamic properties of ion-pair formation in 0.5 M Mg(TFSI)2/G4 solution are then expected to be similar to those in Ca(TFSI)2/G4 solutions, therefore favouring the [Mg(μ2-TFSI)(G4)]+ formation at elevated temperatures. These findings are consistent with previous studies showing that in low-permittivity solvents, such as monoglyme, diglyme, or triglyme, the fraction of free Mg2+ in Mg(TFSI)2-based electrolytes increases at higher salt concentrations.49–52 Table S2 (ESI†) summarises the Mg2+–O interaction energy with different glymes, from monoglyme up to tetraglyme; it is apparent that the strength of the Mg2+–O interaction is invariant with the chain length. Moreover, all glyme-based media exhibit a similar dielectric constant (εr = 7.2–7.5). The invariance in the magnitude of the short- and long-range interactions when varying the chain length is the origin of the abnormalities observed in glyme-based solutions containing divalent salts. The physical properties of low dielectric Mg(TFSI)2/G4 and Ca(TFSI)2/G4 solutions are thus very different from those known for conventional electrolytes. Therefore, a suitable ionic strength must be tuned through the “salt effect” when employing Mg(TFSI)2/G4 or Ca(TFSI)2/G4 as the electrolyte for rechargeable batteries in order to maximise the amount of free solvated ions.
These findings now allow us to rationalise the different behaviour of the LiTFSI/G4 system, where no ion-paring is detected in 0.2 M solution even at elevated temperatures (Fig. S11, ESI†). According to our previous study, Li+ in G4 solution is solvated in the [Li(G4)]+ form with all five oxygen atoms of the G4 molecule participating in the coordination.31,53 The ion-pairing reaction, [Li(G4)]+ + TFSI− ⇌ [Li(TFSI)(G4)] is now associated with a loss in entropy due to the combination of ions, which cannot occur at high temperatures. Furthermore, [Li(G4)]+ bears one charge and is stabilised at all concentrations due to the ionic strength, which is not the case for the [Li(TFSI)(G4)] neutral species. In LiTFSI/G4 solutions, both enthalpic and entropic effects tend to favour the existence of solvated [Li(G4)]+, irrespective of the concentration and temperature.
In this study, the leading parameters governing the solvation properties of generic Mn+(TFSI)n/Gm solutions were identified and their associated ionic conductivity was fully rationalised. These factors should be listed as follows:
• Short-range chemical interactions: they are determined by the strength of the interaction between the solvated cation and the solvent molecules in the first solvation sphere and their magnitude is proportional to Z2, Z being the charge of the central ion.
• Long-range electrostatic interactions: they are dominant in low-dielectric media and their magnitude is proportional to the charge of the solvated species present in the solution.
• Solvent configuration entropy: this quantity is critical for solvents undergoing large entropy variation during the (de)solvation process.
• Solvent stress: this quantity is indirectly linked to the previous one and is related to the strain energy required for a solvent molecule to coordinate to the central ion. It is negligible in monodentate ligands/solvent molecules but might become important in some multidentate ligands when the electron–donor atoms need to drastically reorganise to coordinate the central cations. As a destabilizing factor competing with the solvation energy, it can prevent the separation of anions and cations.
The above-mentioned factors exist in all kinds of liquid electrolytes at different extents, influencing the stability and the reactivity of the solvated cations. In conventional carbonate-based electrolytes, the dielectric constant is usually quite large and the organic carbonate molecules are monodentate,54–58 so that their solvation properties are primarily dominated by the short-range chemical interactions. In the tetraglyme solvent, the G4 molecule is multidentate with five electron-donor oxygens and chelation occurs due to a moderate solvent stress. Therefore, these intermediate molecular weight glyme-based systems should be considered as “entropy-driven solvents”. Due to its low dielectric constant, the long-range electrostatic interaction is not negligible, which can directly affect the energy of the solvated ions. Nevertheless, the low-dielectric medium opens the possibility to modulate the solvent properties, such as the structure and the solvation energy, through a variation of the ionic strength at different solution concentrations, which might have a paramount impact on the interface stability and the reactivity of the solvated species.
Besides electrochemistry, several biochemical processes, such as enzyme activations or protein–inhibitor interaction, have been reported to occur in extremely low dielectric constant environments with the peculiar role of the ion-pairing process.59–61 Consequently, the results and methodology developed in this study can further be applied to these systems.
Conclusions
In this study, we have investigated the particular conductivity behaviour of Ca(TFSI)2/G4 and Mg(TFSI)2/G4 solutions vs. concentration and temperature. For weak ionic force solutions, a solvent-separated ion-pair is the most energetically favourable species and upon heating, a critical temperature exists, beyond which the ion-pair formation occurs, thus driving the ionic conductivity down and leading to a change of the Walden product with temperature. In high concentration solutions, the free solvated ions become favoured thanks to the high ionic strength of the solution. These behaviours are completely different from those observed in conventional carbonate-based electrolytes and in LiTFSI/G4 electrolytes, which is a consequence of the low-dielectric medium with divalent cations (in contrast to monovalent) and the high configuration entropy change coming from the release of multidentate flexible G4 molecules. These unexpected behaviours can be explained using periodic electrolyte models in which explicit solvated species are surrounded in an implicit solvent model and where the boundary conditions can be used to vary the salt concentration. This approach allows capturing the long-range electrostatic interactions and their influence on the energy of the different solvated species expected to occur in the solutions. The present analysis not only rationalises the abnormal ionic conductivity behaviour of [M2+(TFSI−)2]/G4 solutions but also sheds light on the three leading parameters that can be tuned to design better electrolytes: ionic strength, solvent conformational entropy, and solvation stress. These findings, hopefully, will lead to a paradigm shift in how solvated ions and molecular electrolytes are modelled, which might impact the development of new electrolytes, especially those for multivalent rechargeable batteries as well as electrolysis and electrocatalysis.Author contributions
L. H. B. N. conducted the DFT calculations, interpreted the data, and wrote the manuscript. T. P. carried out the sample preparation and experimental measurements. L. H. B. N. and T. P. contributed equally to this work. N. S. developed the in situ Raman apparatus and helped with the vibrational spectroscopy data treatment. C. I. and F. A. designed and helped with the experimental data treatment and supervised the experimental work. M.-L. D. and J.-S. F. developed the theoretical framework and supervised the theoretical work. All the authors discussed the results and edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research work has been funded by the European FET-Open project VIDICAT (Grant Agreement: 829145). This work was performed using HPC resources from GENCI-CINES (Grant 2021-A0100910369). The authors acknowledge Vincent Verdoot (Université Grenoble Alpes, Laboratoire de Rhéologie et Procédés, F-38000 Grenoble, France) for his help with the rheology measurements and the French National Research Agency (STORE-EX Labex project ANR-10LABX-76-01).References
- M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- D. Larcher and J.-M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed.
- R. B. Kaunda, J. Energy Nat. Resour. Law, 2020, 38, 237–244 CrossRef.
- D. B. Agusdinata, W. Liu, H. Eakin and H. Romero, Environ. Res. Lett., 2018, 13, 123001 CrossRef CAS.
- C. Banza Lubaba Nkulu, L. Casas, V. Haufroid, T. De Putter, N. D. Saenen, T. Kayembe-Kitenge, P. Musa Obadia, D. Kyanika Wa Mukoma, J. M. Lunda Ilunga, T. S. Nawrot, O. Luboya Numbi, E. Smolders and B. Nemery, Nat. Sustainable, 2018, 1, 495–504 CrossRef PubMed.
- A. Ponrouch, J. Bitenc, R. Dominko, N. Lindahl, P. Johansson and M. R. Palacin, Energy Storage Mater., 2019, 20, 253–262 CrossRef.
- Y. Tian, G. Zeng, A. Rutt, T. Shi, H. Kim, J. Wang, J. Koettgen, Y. Sun, B. Ouyang, T. Chen, Z. Lun, Z. Rong, K. Persson and G. Ceder, Chem. Rev., 2021, 121, 1623–1669 CrossRef CAS PubMed.
- A. Ponrouch and M. R. Palacin, Curr. Opin. Electrochem., 2018, 9, 1–7 CrossRef CAS.
- M. E. Arroyo-de Dompablo, A. Ponrouch, P. Johansson and M. R. Palacín, Chem. Rev., 2020, 120, 6331–6357 CrossRef CAS PubMed.
- J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- K. Xu, Chem. Rev., 2004, 104, 4303–4417 CrossRef CAS PubMed.
- A. Kopač Lautar, J. Bitenc, T. Rejec, R. Dominko, J. S. Filhol and M. L. Doublet, J. Am. Chem. Soc., 2020, 142, 5146–5153 CrossRef PubMed.
- A. Kopac Lautar, J. Bitenc, R. Dominko and J.-S. Filhol, ACS Appl. Mater. Interfaces, 2021, 13, 8263–8273 CrossRef CAS PubMed.
- C. Pechberty, A. Hagopia, J.-B. Ledeuil, D. Foix, J. Allouche, J.-N. Chotard, O. Lužanin, J. Bitenc, R. Dominko, R. Dedryvère, J.-S. Filhol, L. Stievano and R. Berthelot, Alloying electrode coatings towards better magnesium batteries, J. Mater. Chem. A, 2022, 10, 12104–12113 RSC.
- N. T. Hahn, S. A. McClary, A. T. Landers and K. R. Zavadil, J. Phys. Chem. C, 2022, 126, 10335–10345 CrossRef CAS.
- D. M. Driscoll, N. K. Dandu, N. T. Hahn, T. J. Seguin, K. A. Persson, K. R. Zavadil, L. A. Curtiss and M. Balasubramanian, J. Electrochem. Soc., 2020, 167, 160512 CrossRef CAS.
- N. T. Hahn, D. M. Driscoll, Z. Yu, G. E. Sterbinsky, L. Cheng, M. Balasubramanian and K. R. Zavadil, ACS Appl. Energy Mater., 2020, 3, 8437–8447 CrossRef CAS.
- A. M. Melemed, D. A. Skiba and B. M. Gallant, J. Phys. Chem. C, 2022, 126, 892–902 CrossRef CAS PubMed.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS PubMed.
- S. Terada, T. Mandai, S. Suzuki, S. Tsuzuki, K. Watanabe, Y. Kamei, K. Ueno, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2016, 120, 1353–1365 CrossRef CAS.
- J.-L. Souquet, M. L. F. Nascimento and A. C. M. Rodrigues, J. Chem. Phys., 2010, 132, 034704 CrossRef PubMed.
- J. L. Souquet, in Defects and Disorder in Crystalline and Amorphous Solids, Springer, Netherlands, Dordrecht, 1994, pp. 221–244 Search PubMed.
- S. B. Aziz, T. J. Woo, M. F. Z. Kadir and H. M. Ahmed, J. Sci.: Adv. Mater. Devices, 2018, 3, 1–17 Search PubMed.
- J. D. Forero-Saboya, E. Marchante, R. B. Araujo, D. Monti, P. Johansson and A. Ponrouch, J. Phys. Chem. C, 2019, 123, 29524–29532 CrossRef CAS PubMed.
- T. M. Pappenfus, W. A. Henderson, B. B. Owens, K. R. Mann and W. H. Smyrl, J. Electrochem. Soc., 2004, 151, A209 CrossRef CAS.
- D. Brouillette, D. E. Irish, N. J. Taylor, G. Perron, M. Odziemkowski and J. E. Desnoyers, Phys. Chem. Chem. Phys., 2002, 4, 6063–6071 RSC.
- M. Nakahara and K. Ibuki, J. Phys. Chem., 1986, 90, 3026–3030 CrossRef CAS.
- D. R. MacFarlane, M. Forsyth, E. I. Izgorodina, A. P. Abbott, G. Annat and K. Fraser, Phys. Chem. Chem. Phys., 2009, 11, 4962–4967 RSC.
- C. T. Moynihan, ECS Proc. Vol., 1981, 10, 256–274 CrossRef.
- L. H. B. Nguyen, T. Picard, N. Sergent, C. Raynaud, J.-S. Filhol and M.-L. Doublet, Phys. Chem. Chem. Phys., 2021, 23, 26120–26129 RSC.
- L. Xue, D. D. DesMarteau and W. T. Pennington, Solid State Sci., 2005, 7, 311–318 CrossRef CAS.
- L. Xue, C. W. Padgett, D. D. DesMarteau and W. T. Pennington, Solid State Sci., 2002, 4, 1535–1545 CrossRef CAS.
- S. Tsuzuki, T. Mandai, S. Suzuki, W. Shinoda, T. Nakamura, T. Morishita, K. Ueno, S. Seki, Y. Umebayashi, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2017, 19, 18262–18272 RSC.
- P. Johansson and P. Jacobsson, J. Phys. Chem. A, 2001, 105, 8504–8509 CrossRef CAS.
- K. Hashimoto, S. Suzuki, M. L. Thomas, T. Mandai, S. Tsuzuki, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2018, 20, 7998–8007 RSC.
- S. H. Lapidus, N. N. Rajput, X. Qu, K. W. Chapman, K. A. Persson and P. J. Chupas, Phys. Chem. Chem. Phys., 2014, 16, 21941–21945 RSC.
- N. N. Rajput, T. J. Seguin, B. M. Wood, X. Qu and K. A. Persson, Elucidating Solvation Structures for Rational Design of Multivalent Electrolytes—A Review, Springer International Publishing, 2018, vol. 376 Search PubMed.
- N. N. Rajput, X. Qu, N. Sa, A. K. Burrell and K. A. Persson, J. Am. Chem. Soc., 2015, 137, 3411–3420 CrossRef CAS PubMed.
- G. A. Giffin, A. Moretti, S. Jeong and S. Passerini, J. Phys. Chem. C, 2014, 118, 9966–9973 CrossRef CAS.
- N. T. Hahn, J. Self, D. M. Driscoll, N. Dandu, K. S. Han, V. Murugesan, K. T. Mueller, L. A. Curtiss, M. Balasubramanian, K. A. Persson and K. R. Zavadil, Phys. Chem. Chem. Phys., 2022, 24, 674–686 RSC.
- I. Rey, P. Johansson, J. Lindgren, J. C. Lassègues, J. Grondin and L. Servant, J. Phys. Chem. A, 1998, 102, 3249–3258 CrossRef CAS.
- L. Aguilera, S. Xiong, J. Scheers and A. Matic, J. Mol. Liq., 2015, 210, 238–242 CrossRef CAS.
- M. Herstedt, M. Smirnov, P. Johansson, M. Chami, J. Grondin, L. Servant and J. C. Lassègues, J. Raman Spectrosc., 2005, 36, 762–770 CrossRef CAS.
- L. Edman, J. Phys. Chem. B, 2000, 104, 7254–7258 CrossRef CAS.
- K. Xu, Chem. Rev., 2014, 114, 11503–11618 CrossRef CAS PubMed.
- R. Andersson, G. Hernández and J. Mindemark, Phys. Chem. Chem. Phys., 2022, 499–523 Search PubMed.
- P. Johansson, J. Tegenfeldt and J. Lindgren, Polymer, 1999, 40, 4399–4406 CrossRef CAS.
- N. Sa, N. N. Rajput, H. Wang, B. Key, M. Ferrandon, V. Srinivasan, K. A. Persson, A. K. Burrell and J. T. Vaughey, RSC Adv., 2016, 6, 113663–113670 RSC.
- M. Salama, I. Shterenberg, H. Gizbar, N. N. Eliaz, M. Kosa, K. Keinan-Adamsky, M. Afri, L. J. W. Shimon, H. E. Gottlieb, D. T. Major, Y. Gofer and D. Aurbach, J. Phys. Chem. C, 2016, 120, 19586–19594 CrossRef CAS.
- J. Self, N. T. Hahn, K. D. Fong, S. A. McClary, K. R. Zavadil and K. A. Persson, J. Phys. Chem. Lett., 2020, 11, 2046–2052 CrossRef CAS PubMed.
- T. Kimura, K. Fujii, Y. Sato, M. Morita and N. Yoshimoto, J. Phys. Chem. C, 2015, 119, 18911–18917 CrossRef CAS.
- S. Saito, H. Watanabe, Y. Hayashi, M. Matsugami, S. Tsuzuki, S. Seki, J. N. Canongia Lopes, R. Atkin, K. Ueno, K. Dokko, M. Watanabe, Y. Kameda and Y. Umebayashi, J. Phys. Chem. Lett., 2016, 7, 2832–2837 CrossRef CAS PubMed.
- J. C. Soetens, C. Millot and B. Maigret, J. Phys. Chem. A, 1998, 102, 1055–1061 CrossRef CAS.
- M. D. Bhatt, M. Cho and K. Cho, Appl. Surf. Sci., 2010, 257, 1463–1468 CrossRef CAS.
- V. Ponnuchamy, S. Mossa and I. Skarmoutsos, J. Phys. Chem. C, 2018, 122, 25930–25939 CrossRef CAS.
- K. Tasaki, A. Goldberg and M. Winter, Electrochim. Acta, 2011, 56, 10424–10435 CrossRef CAS.
- M. G. Giorgini, K. Futamatagawa, H. Torii, M. Musso and S. Cerini, J. Phys. Chem. Lett., 2015, 6, 3296–3302 CrossRef CAS.
- E. L. Mertz and L. I. Krishtalik, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 2081–2086 CrossRef CAS PubMed.
- L. I. Krishtalik, Photosynth. Res., 1999, 60, 241–246 CrossRef CAS.
- Y. Li, Y. Cong, G. Feng, S. Zhong, J. Z. H. Zhang, H. Sun and L. Duan, Struct. Dyn., 2018, 5, 064101 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03200g |
| ‡ Authors contributed equally. |
| This journal is © the Owner Societies 2022 |