BRD4: quantum mechanical protein–ligand binding free energies using the full-protein DFT-based QM-PBSA method

Abstract

Fully quantum mechanical approaches to calculating protein–ligand free energies of binding have the potential to reduce empiricism and explicitly account for all physical interactions responsible for protein–ligand binding. In this study, we show a realistic test of the linear-scaling DFT-based QM-PBSA method to estimate quantum mechanical protein–ligand binding free energies for a set of ligands binding to the pharmaceutical drug-target bromodomain containing protein 4 (BRD4). We show that quantum mechanical QM-PBSA is a significant improvement over traditional MM-PBSA in terms of accuracy against experiment and ligand rank ordering and that the quantum and classical binding energies are converged to a similar degree. We test the interaction entropy and normal mode entropy correction terms to QM- and MM-PBSA.

---

1 Introduction

The binding of a small molecule, or ligand, to a protein target is one of the main pharmaceutical mechanisms through which we can interact with the complex systems of the body in a targeted and effective manner. In-silico approaches to protein–ligand binding allow atomistic level insight into the mechanisms of binding and can estimate ligand binding affinity. Computational techniques like molecular dynamics (MD), docking, and binding energy estimations are playing an increasingly important role in modern drug discovery and design.

In the vast majority of all computational approaches used in the context of large biomolecular systems, like protein–ligand complexes, the system is described by the laws of classical mechanics. Consequently, key physical interactions that are governed by the laws of quantum mechanics are not (at least directly) accounted for. This includes polarization, charge transfer, halogen bonding and quantum mechanical many-body effects.^1,2

In classical mechanical methods, some quantum mechanical effects are included indirectly through severe approximations and/or highly empirical correction terms. These corrections, aimed at accounting for some of the quantum behavior of biomolecules, rely on empirical parameters fitted against experimental data or high-level quantum mechanical simulations and often benefit from fortuitous error compensation. An example are force fields that incorporate an approximate term for the polarization which in turn relies on fitted parameters.^3,4

In principle, if biomolecular simulations were performed at a quantum mechanical level of theory, all the known physical interactions in the system should be explicitly accounted for. This would reduce or eliminate the need for fitting parameters and correction terms, resulting in more accurate and transferable models.

However, the fundamental problem of simulating biomolecular systems of hundreds, thousands or even millions of atoms using quantum mechanical techniques is the intractable computational cost of solving the equations of quantum mechanics for such large systems. Traditional quantum chemistry models provide at best cubic scaling of computation cost with system size. However, in recent years, high accuracy quantum mechanical methods whose computational cost scales linearly with system size have been developed,^5,6 opening the path for the quantum mechanical study of large biomolecules.

In this paper, we present a quantum mechanical protein–ligand binding energy study using the QM-PBSA method^7–9 based on full-protein linear-scaling density functional theory (DFT) calculations with the ONETEP⁵ program. We calculate binding energies for 9 ligands binding to the clinically relevant bromodomain-containing protein 4 (BRD4) and compare quantum mechanical QM-PBSA with traditional classical mechanical MM-PBSA and MM-GBSA. We compute entropy correction terms using normal mode analysis (Nmode) and Interaction Entropy (IE).¹⁰ Finally, we compare the results in BRD4 with our previous QM-PBSA study of the much simpler T4-lysozyme⁷ protein binding with 7 ligands.

2 The BRD4(1) system

Bromodomains are small protein domains of about 110 amino acids which are responsible for recognizing acetyl-lysine residues on proteins. There are a wide variety of bromodomain-containing proteins. BRD4 is a member of the well studied BET family of bromodomain-containing proteins.¹¹ In this study we focus on the first bromodomain of the BRD4 protein commonly referred to as BRD4(1) which is pictured in Fig. 1. For convenience, the ‘(1)’ nomenclature is dropped in the remainder of the text. This bromodomain contains 121 amino acids and 2035 atoms. Its binding site has clear access to the solvent and is located between two hydrophobic loop structures called the ZA- and BC-loops which connect the four anti-parallel alpha helices that make up the body of the structure.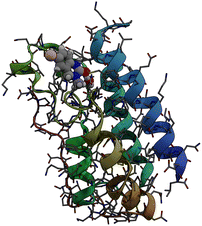

Fig. 1 Sticks and ribbons representation of the BRD4(1) protein structure. Ligand 4, represented as a space-filling model,is also shown in its binding site.

The BRD4 bromodomain and a set of 10 ligands, labeled 1–10 in order of ascending binding energy with a potency range of 5 kcal mol⁻¹, have been proposed by Mobley et al.¹² as a potential binding free energy benchmarking system and recently used in an absolute binding energy study by Huggins.¹³ High-quality co-crystal structures are available for most ligands along with experimental binding energies. The ligands are uncharged, chemically diverse and span a binding range of about 5 kcal mol⁻¹. The binding site is solvent accessible and many of the ligands form hydrogen bonds with the Asp96 residue inside the binding site.¹⁴ A full table including structures, SMILES, experimental energies and PDB codes is presented in¹² and an abridged version in the ESI† of this paper. The binding energies and PDB structures originate from the following papers.^15–21

The experimental binding energies of 4/10 ligands were obtained using Alphascreen technology with reported average estimated experimental errors of 0.20 kcal mol⁻¹ and a maximum estimated experimental error of 0.23 kcal mol⁻¹.^15,18,20 Among the Alphascreen ligands is a confirmed non-binder, ligand 1, which was found to be inactive at a concentration of 250 μM and a weak binder, ligand 2, with 32% inhibition at 250 μM. The experimental binding energies of the other 6 ligands, all binders, were measured using isothermal titration calorimetry with reported mean experimental error of 0.05 kcal mol⁻¹ and a maximum experimental error of 0.07 kcal mol⁻¹.^16,17,19,21

Due to the pharmaceutical relevance of bromodomain-containing proteins, BRD4 has been the subject of extensive computational research with a noticeable increase in interest in the past 4 years. A variety of binding energy studies on BRD4 have been performed using MD,²² QM/MM,^23,24 absolute binding free energy (ABFE) methods,^13,25,26 MM-PBSA^25,27,28 and MM-GBSA.^24,29–32

3 Methods

3.1 MM-PBSA and MM-GBSA

The MM-PBSA method, introduced by Kollman et al. in 2000,³³ is a popular end-point method for estimating relative free energies of binding. The method reduces computational cost by making two key simplifications: (1) sampling only at the endpoints of the binding process, and (2) treating the solvent implicitly. In the single-trajectory approach employed here, only the protein–ligand complex is simulated by MD and structures for the unbound ligand and host are extracted by deleting either the host or ligand from the complex trajectory respectively. A representative ensemble of snapshots is extracted to estimate binding free energies. The binding free energy of a ligand B to a receptor protein A is the difference between the average free energy of the complex and its constituents,

ΔG_bind = 〈G^AB〉 − 〈G^A〉 − 〈G^B〉 (1)

where each free energy term is composed of,

〈G〉 = 〈E〉 + 〈G_solvation〉 (2)

〈E〉 is the gas-phase energy calculated using a classical mechanical force field and 〈G_solvation〉 is the mean free energy of solvation calculated using an implicit solvent model. The solvation term is composed of a polar and non-polar term, 〈G_solvation〉 = 〈G_pol〉 + 〈G_non–pol〉, where the polar term is the electrostatic energy upon transfer of a molecule from the gas-phase to the solvent calculated with the PBSA³³ or GBSA³⁴ implicit solvent models. The non-polar term gives the free energy of cavity formation for the solute to be placed into the solvent. An optional entropy correction term, −T〈S〉, can be included in eqn (2) and represents the configurational entropy of the solute, usually estimated using normal mode analysis³⁵ or the Interaction Entropy term by Duan et al.¹⁰

3.2 QM-PBSA

Methodologically QM-PBSA^7–9 is a straightforward modification of MM-PBSA in which the gas phase energy 〈E〉 and solvation energy 〈G_solvation〉, calculated using the MM force field and PBSA implicit solvation scheme, are replaced by quantum mechanical gas phase and solvation energies from full-protein linear-scaling ab initio density functional theory calculations in ONETEP.⁵ The solvation energy is also estimated from an implicit solvent model which is implemented self-consistently with minimal parameters in the DFT single-point energy evaluation and contains dispersion–repulsion effects in addition to cavitation energy.³⁶ The implicit solvation term uses the QM electron density to define the solute cavity and the solvation in turn changes the electron density during the self-consistent iterative DFT calculation. By extension, QM-GBSA using the simpler Generalized Born model cannot be formulated in the same manner. The optional entropy correction term can be added to the QM- or MM-PBSA energy using either normal mode analysis or the Interaction Entropy method.¹⁰

3.3 Design of computational study

Three repeats of 300 ns of MD for each ligand binding to BRD4 are run based on the same equilibrated structure. From the combined 900 ns trajectory for each ligand 4500 snapshots are extracted and binding energies evaluated using MM-PBSA and MM-GBSA. A subset of 50 snapshots, equally-spaced in time, is taken from the 4500 and QM-PBSA binding energies are calculated for all ligands. Normal mode entropy estimates are calculated as well for the subset of 50 snapshots only. Interaction Entropy terms are calculated for MM-PBSA and MM-GBSA across all 4500 snapshots. For the QM-PBSA, MM-PBSA, and MM-GBSA results over 50 snapshots, the interaction entropy from only those 50 snapshots is considered.

3.4 Metrics, non-binders and errors

The QM-PBSA, MM-PBSA, and MM-GBSA methods are suitable only for the prediction of relative, rather than absolute, binding free energies. The root mean squared deviation after removal of the systematic error (mean signed error), called RMSDtr, is a convenient metric for assessing the accuracy of predicted against experimental relative binding energies. First, the mean signed error of the calculated absolute binding energies from the experimental energies is calculated for the entire ligand set. The mean signed error, or systematic error, is then subtracted from the absolute binding free energy of each ligand. Lastly, the root mean squared deviation of the binding free energy, after the removal of the systematic error, is calculated with respect to the experimental binding energies. The resulting RMSDtr indicates how far the calculated relative binding energies deviate from the experimental energies across the ligand set. While the RMSDtr metric assesses the closeness of predicted and experimental relative binding energies, Spearman's rank correlation factor r_s quantifies the predictive power of the relative binding energy rank ordering of the calculated binding energies. A value of 1 corresponds to a calculated rank order equivalent to that in the experimental binding energies. Because Spearman's r_s describes the rank ordering of binding energies, it can be applied directly to the calculated binding energies.

The chosen ligand set of 10 ligands contains one confirmed non-binder, ligand 1, and one ligand of very low binding affinity, ligand 2 (32% inhibition at 250 μM). As the actual binding energies of these ligands are not known, they are excluded from the RMSDtr calculations throughout. The non-binders are however naturally included in the rank orderings as quantified by the Spearman's r_s with ‘experimental’ binding energies of 0 kcal mol⁻¹.

Estimates of the statistical error due to finite sampling in the computed metrics are obtained using the block averaged standard error (BASE) method.³⁷ In this approach, the trajectory is split into M segments of length n and the metric of interest, for example Spearman's r_s, is calculated for each of the M segments. The standard deviation in r_s among the block averages, σ_n, is then used to estimate the overall standard error at block size n using 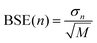. At n = 1 the BASE is equal to the analytic standard error (SE) of the metric across the whole trajectory. As n is increased to up to one fifth of the total trajectory length, the estimated BASE increases until it reaches a plateau. The value at which the BASE plateaus is a reliable estimator for the true standard error. In this paper, we use the maximum BASE value obtained as the upper bound on the uncertainty in the RMSDtr and r_s. In addition to the BASE, to provide a second estimate of statistical error, the standard error in the computed metrics is calculated using bootstrapping (with replacement) over 1000 iterations.

3.5 Computational details

3.5.1 System preparation. The initial structures for BRD4 in complex with the 10 ligands are taken from the published benchmarking data set of Mobley et al.¹² Co-crystal structures are available for 9/10 of the ligands. Hydrogen atoms were added to the ligands using Open Babel³⁸ and the AM1-BCC charge model as implemented in AMBERS's antechamber was used by Mobley et al. to assign ligand atom partial charges. Mol2 and sdf files are provided in the benchmarking dataset for each ligand. The ligand for which no experimental structure is available, named ligand 1 in the Mobley set, was docked, by Mobley et al., into BRD4 using AutoDock Vina.³⁹

Parameter files are generated by the authors of this paper for the protein using the AMBER's ff19SB force field.⁴⁰ For the ligands, the AMBER General Force Field 2 (GAFF2) is used. In the solvation step, 11 000 OPC3 waters⁴¹ and 32 Na⁺ and 35 Cl⁻ ions (0.15 M NaCl) are added to neutralize the net charge of the protein. Joung and Cheatham's TIP3P ion parameters are used.⁴² Our extensive equilibration protocol is applied and described in detail in the ESI.†

3.5.2 Molecular dynamics. All production calculations are performed in AMBER20⁴³ with the same settings in an NPT ensemble. The SHAKE algorithm is used to constrain bonds involving hydrogen and the time step is 2 fs. Temperature regulation is achieved using Langevin dynamics with a collision frequency of 2.0 ps⁻¹ at 300 K. The Berendsen barostat with isotropic position scaling at atmospheric pressure and pressure relaxation time of 2 ps regulates the pressure. A cutoff of 8.0 Å ngstrom is used for non-bonded interactions.

3.5.3 MM-PBSA and MM-GBSA. MM-PBSA and MM-GBSA are performed using AMBER20's MMPBSA.py utility.⁴³ For MM-GBSA, default settings in AMBER20 with a modified GB model (igb = 5) developed by A. Onufriev, D. Bashford and D.A. Case are used and parameters α, β, γ set to 1.0, 0.8, and 4.85, respectively. For MM-PBSA, the two-term non-polar solvation term is used in which the cavity and dispersion term are treated separately. The recommended values are used for the cavity offset (−0.5692) and cavity surface tension (0.0378). An ionic strength of 0, fill ratio of 4.0 and AMBER's pre-calculated atomic radii are used.

3.5.4 QM-PBSA, DFT. QM energy evaluations are carried out by the linear-scaling DFT code ONETEP.⁵ The general purpose exchange correlation functional PBE⁴⁴ and D3 dispersion correction⁴⁵ were found to be the most promising in our previous study on the T4-lysozyme.⁷ A kinetic energy cutoff of 800 eV is used. 4 non-orthogonal generalized Wannier functions (NGWFs) are used for carbon, nitrogen and oxygen and 1 NGWF is used for hydrogen. For sulfur and fluorine 9 NGWFs are used. An NGWF radius of 8.0a₀ is used throughout. ONETEP default parameters for water at room temperature are used. QM-PBSA input and output files are included in the ESI.†

3.5.5 Normal mode analysis. Normal mode analysis is performed in AMBER20 using MMPBSA.py and default settings.

3.5.6 Interaction entropy. The interaction entropy method by Duan et al.¹⁰ is a post-processing method that estimates the entropic term in MM-PBSA, −TΔS, directly from the MD simulation. The protein–ligand interaction energy, E^int_pl, is defined as the difference in the gas-phase energy of the protein–ligand complex and its constituents, i.e, the separate host and ligand. This energy is defined analogously in the context of MM- and QM-PBSA. The fluctuation of the interaction energy of each snapshot around the ensemble averaged interaction energy, 〈E^int_pl〉, is calculated, ΔE^int_pl = E^int_pl − 〈E^int_pl〉. The interaction entropy is an exponential average of the fluctuation in interaction energy around the ensemble average,where,where N is the number of snapshots and is ΔE^int_pl(t_i) calculated for each snapshot i.

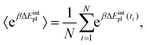4 Results

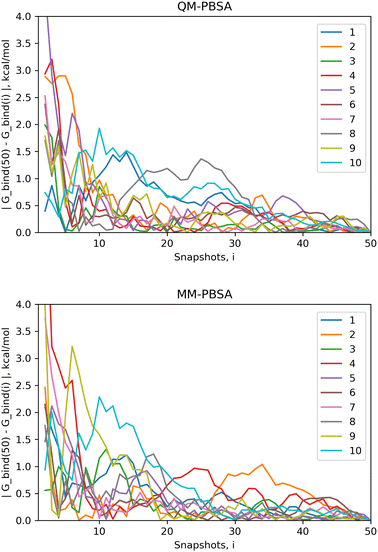
4.1 Convergence of energy terms

The standard error of the mean (SEM) is a measure of how far the mean of a sample is likely to deviate from the true population mean. Both the MM-PBSA and QM-PBSA methods average each energy term across the ensemble of snapshots, i.e., the population sample. Table 1 shows the SEM, averaged over the ligand set, for the absolute binding energies, net gas phase energies and net solvation energies for QM-PBSA and MM-PBSA. Net energies are the difference between the complex and its constituents. The SEM of the absolute binding energies and net gas phase energies over 50 snapshots of QM-PBSA and MM-PBSA are almost identical. For the net solvation energy, QM-PBSA actually has a slightly larger SEM by 0.2 kcal mol⁻¹. Fig. 2 shows the absolute deviation of the computed absolute binding energies at increasing numbers of snapshots from the ‘converged’ value at 50 snapshots with QM-PBSA and MM-PBSA. The convergence behaviour is comparable between MM and QM and beyond 30 snapshots the absolute deviations are below 0.5 kcal mol⁻¹ for most ligands. The mean absolute difference in absolute binding energies across the ligand set between MM-PBSA at 50 and 4500 snapshots is 0.36 kcal mol⁻¹. This means that on average, if all 4500 snapshots are included, the calculated binding energies differ by 0.36 kcal mol⁻¹ from those calculated over only 50 snapshots.

Table 1 Standard error of the mean (SEM) in kcal mol⁻¹ for the absolute binding energy (G_bind), net gas phase energy (Gas-phase) and net solvation energy (G_solv) averaged across the ligand set for QM-PBSA and MM-PBSA over 50 snapshots

Method/SEM (kcal mol^−1)	QM-PBSA	MM-PBSA
G_bind	0.44	0.47
Gas-phase	0.64	0.65
G_solv	0.40	0.63

---

Fig. 2 Absolute deviation of computed absolute binding energies at different numbers of snapshots from the computed energies at 50 snapshots for QM-PBSA (top) and MM-PBSA (bottom) in kcal mol⁻¹ for all ligands.

4.2 Predictive power

Ligand 4 (structure in ESI†) is a clear outlier and is excluded from the RMSDtr and Spearman's r_s analysis. The absolute binding energy of ligand 4 without entropy is 16 kcal mol⁻¹ more positive (weaker) than the average across the rest of the ligand set and 8 kcal mol⁻¹ weaker than the known non-binder, ligand 1. A full discussion of ligand 4 is presented in Section 5.2 of the discussion.

The RMSDtr and Spearman's r_s are used to quantify the closeness of calculated to experimental relative binding energies and rank ordering of ligands by binding energy. Table 2 shows the RMSDtr and Spearman's r_s values for QM-PBSA, MM-PBSA, and MM-GBSA. Results are shown over the ensemble subset of 50 snapshots evaluated using QM-PBSA and MM results are additionally shown across the entire ensemble of 4500 snapshots. Metrics are calculated without entropy, with normal mode entropy and with the Interaction Entropy term. As normal mode calculations for only 50 snapshots were performed, no results for MM-PBSA/GBSA over 4500 snapshots with normal mode correction are shown. BASE and bootstrapped SE for each metric are shown in Table S2 and S3 of the ESI.†

Table 2 Root mean squared deviation of calculated binding energies shifted by the mean signed error (RMSDtr) against the experimental binding energies of 7 binders in BRD4 in kcal mol⁻¹. Spearman's rank order coefficient, r_s, of calculated binding energies against the experimental binding energies of 9 ligands (binders and non-binders) in BRD4. Metrics shown for QM-PBSA, MM-PBSA, and MM-GBSA without entropy and with normal mode and Interaction Entropy term. Metrics for MM are shown over 50 and over the complete set of 4500 snapshots. Block average standard errors and bootstrapped standard errors provided in ESI\dag. Normal mode entropies only calculated for 50 snapshots

Snapshots	Method	Entropy	RMSDtr (kcal mol^−1)	Spearman's rs
50	QM-PBSA	No Entropy	1.77	0.83
		Normal mode	1.60	0.85
		Interaction entropy	2.30	0.76
	MM-PBSA	No entropy	2.99	0.01
		Normal mode	3.05	−0.30
		Interaction entropy	3.84	−0.13
	MM-GBSA	No entropy	2.66	0.79
		Normal mode	2.17	0.53
		Interaction entropy	3.22	0.48
4500	MM-PBSA	No entropy	2.89	−0.03
		Normal mode	NA	NA
		Interaction entropy	6.18	0.03
	MM-GBSA	No entropy	2.07	0.78
		Normal mode	NA	NA
		Interaction entropy	5.54	0.53

---

Consider first the results without entropy correction. QM-PBSA has an RMSDtr of 1.77 kcal mol⁻¹ and r_s of 0.83. This is 1.22 kcal mol⁻¹ lower than MM-PBSA and 0.89 kcal mol⁻¹ lower than MM-GBSA, over the same 50 snapshots, and thus a statistically significant improvement with respect to the estimated statistical error of less than 0.2 kcal mol⁻¹. MM-PBSA has no predictive power in terms of rank ordering the ligands (r_s = 0.01). The ligand rank order produced by MM-GBSA is comparable with that of QM-PBSA. Considering the full 4500 snapshots, MM-PBSA does not change significantly in terms of RMSDtr or r_s. MM-GBSA on the other hand shows an improved RMSDtr of 2.07 kcal mol⁻¹ which is 0.3 kcal mol⁻¹ larger than that of QM-PBSA over 50 snapshots.

Overall, the inclusion of the normal mode entropy correction term improves the performance of QM-PBSA, reducing the RMSDtr by 0.17 kcal mol⁻¹ and increasing r_s by 0.02. However, both these changes are within the estimated uncertainties of the two metrics. This is in part due to the fact that the inclusion of normal mode entropy increases the BASE and bootsrapped SE for both RMSDtr and r_s. MM-PBSA is further deteriorated by the inclusion of normal mode entropy. MM-GBSA shows a significant drop in r_s of 0.26 while improving RMSDtr by 0.49 kcal mol⁻¹ which is however of comparable magnitude as the BASE of 0.47 kcal mol⁻¹.

The inclusion of the Interaction Entropy correction consistently increases RMSDtr significantly and reduces r_s across the board. The increase in error against experiment caused by the interaction entropy term is much larger in the set of 4500 snapshots than in the set of only 50 snapshots ESI.† The BASE in RMSDtr also increase significantly from 50 to 4500 snapshots when the IE term is included ESI.†

5 Discussion

5.1 QM-PBSA

In the context of this set of ligands in BRD4, QM-PBSA produces relative binding free energies that are closer to experiment and have better rank ordering than MM-PBSA binding energies. MM-GBSA performs better than MM-PBSA but is still inferior to QM-PBSA in terms of RMSDtr and rank ordering. Normal mode entropies improve QM-PBSA results slightly but deteriorate MM-PBSA results significantly. In our hands, interaction entropy corrections reduce quality of estimated binding energies across the board and are difficult to converge, mirroring observations by other authors,^46–48 as discussed in the ESI.†

The ligand rank orderings produced by QM-PBSA are very good with r_s = 0.85 when normal mode entropy is included and BASE and bootsrapped SE of 0.08 and 0.06, respectively. Fig. 3 shows plots of the experimental against computed binding energies where the computed energies have been shifted by the mean signed error as in the calculation of the RMSDtr. Plots are shown with and without normal mode entropy and for the whole ligand set (excluding ligand 4). Visual comparison of QM-PBSA with MM-PBSA also clearly shows an improvement in predictive power.

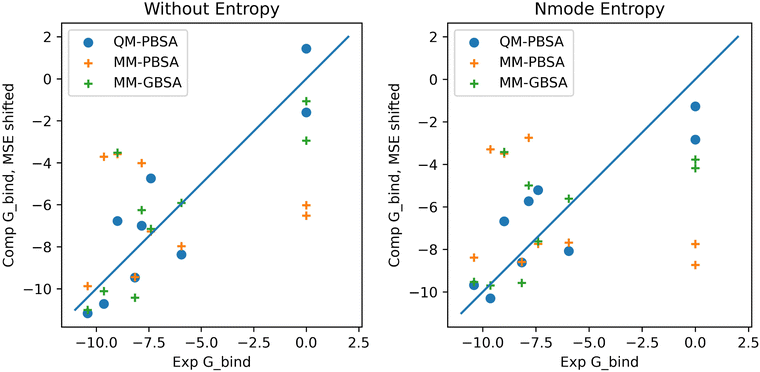Fig. 3 Plots of computed binding energies (shifted by mean signed error) against experimental binding energies for 9 ligands in BRD4 for QM-PBSA, MM-PBSA and MM-GBSA.

Comparing the results of this BRD4 study to our previous QM-PBSA study in T4-lysozyme we see similar results. In T4-lysozyme RMSDtr values of 1.84 kcal mol⁻¹ were obtained using the PBE exchange-correlation functional and D3 dispersion and normal mode entropy as compared to an RMSDtr of 1.60 kcal mol⁻¹ in BRD4. Interestingly, the standard error values for the absolute binding energies and net solvation energies are slightly lower, by about 0.3 kcal mol⁻¹, in BRD4 than in T4-lysozyme at 50 snapshots of sampling. This is because BRD4 has a solvent exposed binding site and does not require a cavity-correction term to account for the buried cavity binding site in the T4-lysozyme.^7,8 The cavity-correction term was the largest source of SE in the T4-lysozyme system. Both in BRD4 and T4-lysozyme, the QM energies converge at the same rate as the MM energies indicating that, for these systems, evaluating structures generated using classical mechanical force fields with a quantum mechanical energy Hamiltonian is viable. If this observation is shown to hold for more protein–ligand systems, the QM-PBSA or similar approaches can provide a realistic and accessible method of exploring protein–ligand binding at a quantum mechanical level of theory. While 50 snapshots of sampling appear sufficient in T4-lysozyme and BRD4, protein–ligand systems with higher flexibility may require more sampling. As in Fig. 2, convergent plots can be used to assess if additional snapshots should be included when new protein–ligand systems are investigated.

The application of classical mechanical normal mode entropies to the quantum mechanical enthalpies from QM-PBSA represents a methodological shortcoming. However, the calculation of QM harmonic entropy terms using DFT is not tractable as the computation of the QM Hessian matrix is extremely expensive. Furthermore, a geometry optimization is performed before the normal mode calculation, which is also extremely expensive at QM level. Additionally, the authors stipulate that the main source of error in the normal mode entropies arises from the harmonic approximation and not from the mismatch of MM and QM. Normal mode entropies derived from the SEQM method GFN2-XTB⁴⁹ could be used instead of force field based normal mode entropies. However, in our study of T4-lysozyme, this SEQM method performed quite poorly. Because only relative binding free energies are calculated in MM- and QM-PBSA, some entropic effects may also cancel.

In 2017, Aldeghi et al.²⁵ studied 11 ligands in BRD4(1) using both MM-PBSA and an absolute alchemical binding free energy method. The single-trajectory MM-PBSA approach achieved Spearman's r_s = 0.72 without entropy and 0.61 with an entropy correction term. Absolute alchemical energies improved upon this with r_s = 0.85. Also in 2017, Heinzelmann et al.²² applied the attach-pull-release method to 7 ligands binding to BRD4(1) achieving Kendall τ between 0.33 and 0.50 and RMSE of 1.14–3.21 kcal mol⁻¹ depending on the details of the method. In 2022 Guest et al.²⁶ applied FEP and multi-site lambda dynamics (MSλD) in BRD4 and reported Spearman's r_s of 0.7 and 0.8, respectively, for 14 compounds. Average accuracy against experiment for FEP was reported as 1.0 ± 1.3 kcal mol⁻¹ and 0.7 ± 0.5 kcal mol⁻¹ after exclusion of one outlier. Also in 2022, Huggins et al.¹³ applied an alchemical binding free energy method to the 8 binders from the Mobley BRD4 benchmark set also used in this study. Using the ff14SB protein force field, the previous iteration of the ff19SB force field used in this study, they reported RMSE of 1.44–3.36 kcal mol⁻¹ and Kendall τ of 0.31–0.56 depending on the choice of water model (TIP3P, TIP4P-Ewald, SPCE/E) and ligand charge model (AM1-BCC and RESP). Notably, ligand 4, which was excluded from our ligand set as an outlier for the QM-PBSA method, was not an outlier for the alchemical method employed by Huggins et al.¹³

In comparison, in this study the QM-PBSA method achieves RMSDtr of 1.6 kcal mol⁻¹ across 7 binders and an r_s of 0.85 across the 9 ligands (binders and non-binders) in BRD4. These results are in line with those of more thermodynamically rigorous classical mechanical methods however, as summarized in Section 5.3, the computational cost of QM-PBSA is orders of magnitude larger.

5.2 The outlier

The computed QM-PBSA binding energies of ligand 4, the outlier, are 16 kcal mol⁻¹ more positive than the average binding energy across the ligand set while the experimental binding energy for ligand 4 is essentially in the middle of the binding set. We discuss here the attempts made to explain and correct this outlier.

Ligand 4, pictured in ESI,† is the smallest ligand in the ligand set and undergoes the most motion during the MD simulation as measured by the ligand RMSD. During the 900 ns of MD, a number of similar binding poses are sampled by ligand 4. We re-ran the 900 ns MD for ligand 4 with a 2 kcal mol⁻¹ Å⁻² harmonic restraint imposed on the ligand, in an attempt to sample only the binding mode closest to the initial configuration. 10 restrained snapshots were evaluated by QM-PBSA but the resulting absolute binding energies for ligand 4 differed only by 0.5 kcal mol⁻¹ from those of the un-restrained trajectory. Thus we concluded that the sampling of multiple related binding modes in itself is not the cause of ligand 4's significantly underestimated QM binding energies.

Since ligand 4 has the only bromine atom in the test set, we examined if the DFT calculations might be treating the bromine incorrectly. We replaced the bromine in ligand 4 with a hydrogen and re-equilibrated and re-ran 900 ns of MD. This altered ligand, ligand 4H, is a real binder with similar binding energy as the bromine variant.²⁰ After evaluating three snapshots of ligand 4H with QM-PBSA we found that the net difference in absolute binding energies by changing the bromine to a hydrogen was only −0.52 kcal mol⁻¹ and thus we abandoned this hypothesis.

It is well established that the BRD4 binding site features a number of structural waters which are observed both in crystal structures and simulation.⁵⁰ Using AMBER20's cpptraj we analysed the bridging waters between the ligands and BRD4 protein. We observed that for ligand 4 the bridging water between the ligand and the protein residue Tyr97 is highly conserved and present in more than 70% of snapshots with the same water molecule being conserved over many nanoseconds of MD. While bridging waters are present in the trajectories for the other ligands, the average occupation is less than 30% with no single ligand,except ligand 4, having an occupation of more than 50% for the Tyr97 water bridge. We hypothesized that the small and loosely bound ligand 4 requires the bridging water interactions with the protein to bind and that the explicit inclusion of these bridging waters in the QM-PBSA calculation may ’fix’ the underestimated QM binding energies. We performed QM-PBSA over 50 snapshots for ligand 4 in which any bridging waters between the ligand and protein were explicitly included as part of the protein in the DFT calculations. This approach is analogous to explicit water MM-PBSA, which has successfully been applied in a number of studies.^{14,25,51–55} While the net gas-phase energy did become 10 kcal mol⁻¹ more favourable to binding, the solvation and normal mode entropy became less favourable for binding. As a result, the entropy corrected calculated binding energy of ligand 4 with explicit bridging waters was only about 1 kcal mol⁻¹ stronger than the original estimate. Thus the inclusion of the highly conserved bridging water in ligand 4 did not bring its outlier energy into line with the rest of the ligand set. There are two reported X-ray structures of ligand 4 in BRD4 (PDB:4HBV) and the highly conserved CREBBP bromodomain (PDB:4NYV) which shows subtle differences in the binding modes of the ligand and changes in the structure and number of waters in the binding site. A potential issue is, that our dynamics simulation does not sufficiently sample the different arrangements of structural waters in the binding site.

5.3 Computational cost

To calculate quantum mechanical protein–ligand binding energies using the QM-PBSA method on a total of 10 ligands binding to BRD4 using 50 snapshots per ligand required about 7.3 million core-hours on AMD EPYC 7742 62-core processors on the ARCHER2 supercomputer. A single solvated DFT single-point energy evaluation on the BRD4 protein (2035 atoms) has a wall-time of about 5 hours on 8 nodes with 128 cores each (dual socket AMD EPYC). Given access to the whole ARCHER2 supercomputer, the entire QM-PBSA BRD4 study could have been completed in less than 10 hours due to the trivially parallel nature of QM-PBSA. Including additional calculations and initial testing, we estimate a total usage of 10 million core-hours on ARCHER2 and IRIDIS5 (University of Southampton supercomputer). BRD4 is a small protein, but due to the linear-scaling of DFT calculations in ONETEP, larger proteins can, in principle, be investigated. Calculations of a 50 000 atom lipid bilayer and 14 000 atom amyloid fibril segment have already been performed in ONETEP.⁵

5.4 Recent quantum mechanical studies

The volume of research in the field of quantum mechanical protein–ligand free energy of binding prediction is still very limited. In the year 2022, excluding the author's own work, we could find only four publications on quantum mechanical protein–ligand binding energies. Vennelakanti et al.⁵⁶ published an opinion piece about the future of large-scale QM and QM/MMM for predictive modeling in enzymes and proteins. Maier et al.⁵⁷ benchmarked a QM molecule-in-molecules (MIM) approach, which partitions the protein system into small, overlapping fragments on which independent QM calculations are performed. The energies of the fragments are then recombined to recover the total energy. They reported improvements over traditional MM-PBSA/GBSA and Pearson correlation coefficients between 0.81 and 0.97. However, no errors against experiment were given, and the method is only applicable to sets of structurally similar ligands. Additionally, no sampling is performed in the MIM approach. Instead, single energy-minimized crystal structures are used to compute binding energy estimates. This eliminates the possibility of capturing multiple binding modes, binding site flexibility, and ligand flexibility. Chen et al.⁵⁸ applied the GFN-FF force field and the family of GFN-xTB SEQM methods to 90 protein–ligand complexes. They truncated the protein for the SEQM calculations and tested different truncation radii. GFN2-xTB was the best performing SEQM method tested with mean absolute errors after the removal of the systematic error of 7 kcal mol⁻¹ for charged systems and 5 kcal mol⁻¹ for neutral systems. The correlations of the SEQM approach and traditional MM-PBSA were comparable. Lastly, Kirsopp et al.⁵⁹ computed quantum mechanical protein–ligand interactions natively on a quantum computer. They studied 12 inhibitors to the BACE1 protein on different quantum computers and a simulated quantum computer. They obtained coefficients of determinants, R², of 0.55, 0.77, and 0.56, depending on the QM hardware. In comparison, a DFT-based approach achieved R² = 0.65.

6 Conclusion

This study is, to our knowledge, the first application of full-protein DFT binding energy calculations on a real-world, pharmaceutically relevant protein and ligand set. Building on our QM-PBSA validation study in T4-lysozyme,⁷ we demonstrate the application of QM-PBSA in BRD4. We find a significant improvement in accuracy against experiment and ligand rank ordering over classical mechanical MM-PBSA and the best results are obtained by including a normal mode entropy correction term. As in the T4-lysozyme study, the QM binding energies appear equally converged as the MM binding energies with SEM < 0.5 kcal mol⁻¹ at 50 snapshots of sampling. Exploring whole protein–ligand complexes at a quantum mechanical level of theory is both computationally and methodologically viable and opens a variety of opportunities for further investigation like the potential applications of extracting further information from the full-QM electronic densities for protein–ligand systems. It is our firm belief, that if a fraction of the scientific effort that has been invested into developing highly advanced and complicated classical mechanical methods for estimating protein–ligand binding over the past 60 years were to be invested in quantum-based approaches, significant improvements in accuracy, transferability, and domain of applicability could be achieved given the availability of modern high-performance computing resources.

Data and software availability

Protein and Ligand structures: the structures of the BRD4 protein and ligands were taken from Mobely's GitHub repository and are freely available (https://github.com/MobleyLab/benchmarksets).

Molecular dynamics simulations were prepared using the tleap program in Amber20 and MD simulations performed using the GPU (CUDA) implementation of Amber20, which can be purchased at https://ambermd.org/ (Academic License available). MD trajectories were processed before MM-PBSA/GBSA using the cpptraj program included in Amber20.

MM-PBSA, MM-GBSA and normal mode calculations were preformed in Amber20 using the MMPBSA.py program. This program is freely available with the free AmberTools21 suite (https://ambermd.org/). Inputs and generated output files for QM-PBSA are made available as described in the ESI.†

Structures and trajectories were visualized using VMD1.9 which is freely available at https://www.ks.uiuc.edu/Research/vmd/. Figures were generated in Python using Matplotlib and Seaborn freely available via Pip or Anaconda.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the use of the IRIDIS 5 High Performance Computing Facility, and associated support services at the University of Southampton, in the completion of this work. We are grateful for computational support from the UK Materials and Molecular Modelling Hub, which is partially funded by EPSRC (grant reference number EP/T022213/1). We are also grateful for access to the ARCHER2 national supercomputer which was obtained via the UKCP consortium, funded by EPSRC (grant reference number EP/P022030/1). L. G. would also like to thank the CDT for Theory and Modelling the Chemical Sciences (EPSRC grant reference number EP/L015722/1) and Boehringer Ingelheim for financial support in the form of a PhD studentship.

References

1. C. N. Cavasotto, N. S. Adler and M. G. Aucar, Front. Chem., 2018, 6, 188.
2. U. Ryde and P. Söderhjelm, Chem. Rev., 2016, 116, 5520–5566.
3. A. Warshel, M. Kato and A. V. Pisliakov, J. Chem. Theory Comput., 2007, 3, 2034–2045.
4. C. Zhang, C. Lu, Z. Jing, C. Wu, J. P. Piquemal, J. W. Ponder and P. Ren, J. Chem. Theory Comput., 2018, 14, 2084–2108.
5. J. C. Prentice, J. Aarons, J. C. Womack, A. E. Allen, L. Andrinopoulos, L. Anton, R. A. Bell, A. Bhandari, G. A. Bramley, R. J. Charlton, R. J. Clements, D. J. Cole, G. Constantinescu, F. Corsetti, S. M. Dubois, K. K. Duff, J. M. Escartín, A. Greco, Q. Hill, L. P. Lee, E. Linscott, D. D. O'Regan, M. J. Phipps, L. E. Ratcliff, Á. R. Serrano, E. W. Tait, G. Teobaldi, V. Vitale, N. Yeung, T. J. Zuehlsdorff, J. Dziedzic, P. D. Haynes, N. D. Hine, A. A. Mostofi, M. C. Payne and C. K. Skylaris, J. Chem. Phys., 2020, 152, 174111.
6. D. R. Bowler and T. Miyazaki, Rep. Prog. Phys., 2012, 75, 036503.
7. L. Gundelach, T. Fox, C. Tautermann and C.-K. Skylaris, Phys. Chem. Chem. Phys., 2021, 23, 9381.
8. S. J. Fox, J. Dziedzic, T. Fox, C. S. Tautermann and C. K. Skylaris, Proteins: Struct., Funct., Bioinf., 2014, 82, 3335–3346.
9. D. J. Cole, C. K. Skylaris, E. Rajendra, A. R. Venkitaraman and M. C. Payne, EPL, 2010, 91, 37004.
10. L. Duan, X. Liu and J. Z. Zhang, J. Am. Chem. Soc., 2016, 138, 5722–5728.
11. Y. Taniguchi, Int. J. Mol. Sci., 2016, 17, 1849.
12. D. L. Mobley and M. K. Gilson, Annu. Rev. Biophys., 2017, 46, 531–558.
13. D. J. Huggins, J. Chem. Theory Comput., 2022, 18, 2616–2630.
14. E. E. Guest, S. D. Pickett and J. D. Hirst, Org. Biomol. Chem., 2021, 19, 5632–5641.
15. L. R. Vidler, P. Filippakopoulos, O. Fedorov, S. Picaud, S. Martin, M. Tomsett, H. Woodward, N. Brown, S. Knapp and S. Hoelder, J. Med. Chem., 2013, 56, 8073–8088.
16. S. Picaud, C. Wells, I. Felletar, D. Brotherton, S. Martin, P. Savitsky, B. Diez-Dacal, M. Philpott, C. Bountra, H. Lingard, O. Fedorov, S. Müller, P. E. Brennan, S. Knapp and P. Filippakopoulos, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 19754–19759.
17. X. Lucas, D. Wohlwend, M. Hügle, K. Schmidtkunz, S. Gerhardt, R. Schüle, M. Jung, O. Einsle and S. Günther, Angew. Chem., Int. Ed., 2013, 52, 14055–14059.
18. V. S. Gehling, M. C. Hewitt, R. G. Vaswani, Y. Leblanc, A. Coîté, C. G. Nasveschuk, A. M. Taylor, J. C. Harmange, J. E. Audia, E. Pardo, S. Joshi, P. Sandy, J. A. Mertz, R. J. Sims, L. Bergeron, B. M. Bryant, S. Bellon, F. Poy, H. Jayaram, R. Sankaranarayanan, S. Yellapantula, N. Bangalore Srinivasamurthy, S. Birudukota and B. K. Albrecht, ACS Med. Chem. Lett., 2013, 4, 835–840.
19. P. Filippakopoulos, S. Picaud, O. Fedorov, M. Keller, M. Wrobel, O. Morgenstern, F. Bracher and S. Knapp, Bioorg. Med. Chem., 2012, 20, 1878–1886.
20. P. V. Fish, P. Filippakopoulos, G. Bish, P. E. Brennan, M. E. Bunnage, A. S. Cook, O. Federov, B. S. Gerstenberger, H. Jones, S. Knapp, B. Marsden, K. Nocka, D. R. Owen, M. Philpott, S. Picaud, M. J. Primiano, M. J. Ralph, N. Sciammetta and J. D. Trzupek, J. Med. Chem., 2012, 55, 9831–9837.
21. P. Filippakopoulos, J. Qi, S. Picaud, Y. Shen, W. B. Smith, O. Fedorov, E. M. Morse, T. Keates, T. T. Hickman, I. Felletar, M. Philpott, S. Munro, M. R. McKeown, Y. Wang, A. L. Christie, N. West, M. J. Cameron, B. Schwartz, T. D. Heightman, N. La Thangue, C. A. French, O. Wiest, A. L. Kung, S. Knapp and J. E. Bradner, Nature, 2010, 468, 1067–1073.
22. G. Heinzelmann, N. M. Henriksen and M. K. Gilson, J. Chem. Theory Comput., 2017, 13, 3260–3275.
23. M. Kuang, J. Zhou, L. Wang, Z. Liu, J. Guo and R. Wu, J. Chem. Inf. Model., 2015, 55, 1926–1935.
24. C. Cheng, H. Diao, F. Zhang, Y. Wang, K. Wang and R. Wu, Phys. Chem. Chem. Phys., 2017, 19, 23934–23941.
25. M. Aldeghi, M. J. Bodkin, S. Knapp and P. C. Biggin, J. Chem. Inf. Model., 2017, 57, 2203–2221.
26. E. E. Guest, L. F. Cervantes, S. D. Pickett, C. L. Brooks and J. D. Hirst, J. Chem. Inf. Model., 2022, 62, 1458–1470.
27. J. Su, X. Liu, S. Zhang, F. Yan, Q. Zhang and J. Chen, Chem. Biol. Drug Des., 2018, 91, 828–840.
28. J. Su, X. Liu, S. Zhang, F. Yan, Q. Zhang and J. Chen, J. Biomol. Struct. Dyn., 2018, 36, 1212–1224.
29. E. Wang, G. Weng, H. Sun, H. Du, F. Zhu, F. Chen, Z. Wang and T. Hou, Phys. Chem. Chem. Phys., 2019, 21, 18958–18969.
30. L. F. Wang, Y. Wang, Z. Y. Yang, J. Zhao, H. B. Sun and S. L. Wu, SAR QSAR Environ. Res., 2020, 31, 373–398.
31. Y. Wang, S. Wu, L. Wang, Z. Yang, J. Zhao and L. Zhang, RSC Adv., 2021, 11, 745–759.
32. Y. Rodríguez, G. Gerona-Navarro, R. Osman and M. M. Zhou, Proteins: Struct., Funct., Bioinf., 2020, 88, 414–430.
33. P. A. Kollman, I. Massova, C. Reyes, B. Kuhn, S. Huo, L. Chong, M. Lee, T. Lee, Y. Duan, W. Wang, O. Donini, P. Cieplak, J. Srinivasan, D. A. Case and T. E. Cheatham, Acc. Chem. Res., 2000, 33, 889–897.
34. W. Clark Still, A. Tempczyk, R. C. Hawley and T. Hendrickson, J. Am. Chem. Soc., 1990, 112, 6127–6129.
35. J. Srinivasan, T. E. Cheatham, P. Cieplak, P. A. Kollman and D. A. Case, J. Am. Chem. Soc., 1998, 120, 9401–9409.
36. J. Dziedzic, H. H. Helal, C. K. Skylaris, A. A. Mostofi and M. C. Payne, EPL, 2011, 95, 43001.
37. A. Grossfield and D. M. Zuckerman, Chapter 2 Quantifying Uncertainty and Sampling Quality in Biomolecular Simulations, NIH Public Access, 2009, vol. 5, pp. 23–48.
38. N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 1–14.
39. O. Trott and A. J. Olson, J. Comput. Chem., 2009, 31, 455–461.
40. C. Tian, K. Kasavajhala, K. A. Belfon, L. Raguette, H. Huang, A. N. Migues, J. Bickel, Y. Wang, J. Pincay, Q. Wu and C. Simmerling, J. Chem. Theory Comput., 2020, 16, 528–552.
41. S. Izadi and A. V. Onufriev, J. Chem. Phys., 2016, 145, 074501.
42. I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2008, 112, 9020–9041.
43. D. Case, H. Aktulga, K. Belfon, I. Ben-Shalom, J. Berryman, S. Brozell, D. Cerutti, T. Cheatham, G. Cisneros, V. Cruzeiro, T. Darden, R. Duke, G. Giambasu, M. Gilson, H. Gohlke, A. Goetz, R. Harris, S. Izadi, S. Izmailov, K. Kasavajhala, M. Kaymak, E. King, A. Kovalenko, T. Kurtzman, T. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, M. Machado, V. Man, M. Manathunga, K. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, K. O'Hearn, A. Onufriev, F. Pan, S. Pantano, R. Qi, A. Rahnamoun, D. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, A. Shajan, J. Shen, C. Simmerling, N. Skrynnikov, J. Smith, J. Swails, R. Walker, J. Wang, J. Wang, H. Wei, R. Wolf, X. Wu, Y. Xiong, Y. Xue, D. York, S. Zhao and P. Kollman, Amber20, University of California, San Francisco, 2022.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
45. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
46. G. Kohut, A. Liwo, S. Bösze, T. Beke-Somfai and S. A. Samsonov, J. Phys. Chem. B, 2018, 122, 7821–7827.
47. W. M. Menzer, C. Li, W. Sun, B. Xie and D. D. Minh, J. Chem. Theory Comput., 2018, 14, 6035–6049.
48. V. Ekberg and U. Ryde, J. Chem. Theory Comput., 2021, 17, 5379–5391.
49. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
50. E. E. Guest, S. D. Pickett and J. D. Hirst, Org. Biomol. Chem., 2021, 19, 5632–5641.
51. S. Wong, R. E. Amaro and J. Andrew McCammon, J. Chem. Theory Comput., 2009, 5, 422–429.
52. I. Maffucci and A. Contini, J. Chem. Theory Comput., 2013, 9, 2706–2717.
53. I. Maffucci and A. Contini, J. Chem. Inf. Model., 2016, 56, 1692–1704.
54. P. Mikulskis, S. Genheden and U. Ryde, J. Mol. Model., 2014, 20, 1–11.
55. Y. L. Zhu, P. Beroza and D. R. Artis, J. Chem. Inf. Model., 2014, 54, 462–469.
56. V. Vennelakanti, A. Nazemi, R. Mehmood, A. H. Steeves and H. J. Kulik, Curr. Opin. Struct. Biol., 2022, 72, 9–17.
57. S. Maier, B. Thapa, J. Erickson and K. Raghavachari, Phys. Chem. Chem. Phys., 2022, 24, 14525–14537.
58. Y. Q. Chen, Y. J. Sheng, Y. Q. Ma and H. M. Ding, Phys. Chem. Chem. Phys., 2022, 24, 14339–14347.
59. J. J. Kirsopp, C. Di Paola, D. Z. Manrique, M. Krompiec, G. Greene-Diniz, W. Guba, A. Meyder, D. Wolf, M. Strahm and D. Muñoz Ramo, Int. J. Quantum Chem., 2022, e26975,  DOI:10.1002/qua.26975.

---

Footnote

† Electronic supplementary information (ESI) available: Input and output files for QM-PBSA provided as well as additional details about the ligand set, equilibration protocol, standard errors and interaction entropy. See DOI: https://doi.org/10.1039/d2cp03705j

---