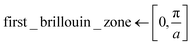Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
From vibrational spectroscopy and quantum tunnelling to periodic band structures – a self-supervised, all-purpose neural network approach to general quantum problems†
Jakob
Gamper‡
 a,
Florian
Kluibenschedl‡
a,
Alexander K. H.
Weiss
b and
Thomas S.
Hofer
a,
Florian
Kluibenschedl‡
a,
Alexander K. H.
Weiss
b and
Thomas S.
Hofer
 *a
*a
aTheoretical Chemistry, Division, Institute of General, Inorganic and Theoretical Chemistry, Center for Chemistry and Biomedicine, University of Innsbruck, Innrain 80-82, A-6020 Innsbruck, Austria
bResearch Institute for Biomedical Aging Research, University of Innsbruck, Rennweg 10, A-6020 Innsbruck, Austria
First published on 4th October 2022
Abstract
In this work, a feed-forward artificial neural network (FF-ANN) design capable of locating eigensolutions to Schrödinger's equation via self-supervised learning is outlined. Based on the input potential determining the nature of the quantum problem, the presented FF-ANN strategy identifies valid solutions solely by minimizing Schrödinger's equation encoded in a suitably designed global loss function. In addition to benchmark calculations of prototype systems with known analytical solutions, the outlined methodology was also applied to experimentally accessible quantum systems, such as the vibrational states of molecular hydrogen H2 and its isotopologues HD and D2 as well as the torsional tunnel splitting in the phenol molecule. It is shown that in conjunction with the use of SIREN activation functions a high accuracy in the energy eigenvalues and wavefunctions is achieved without the requirement to adjust the implementation to the vastly different range of input potentials, thereby even considering problems under periodic boundary conditions.
1 Introduction
Ever since the emergence of quantum mechanics in the early 1900s, a large number of approaches providing analytical or at the very least numerical solutions to Schrödinger's equation1 have been proposed. The Schrödinger picture enables inter alia a holistic representation of electrons in the non-relativistic limit. For this reason, solutions to the Schrödinger equation are of critical importance in many fields of physical and chemical sciences. Knowledge of the associated eigenfunctions provides a unique and unified approach to calculate the properties of virtually any molecular system as well as periodic solid-state structures. However, as a consequence of the inherent complexity associated to the subatomic interactions, no analytical solutions beyond those reported for one-electron systems are known to date. Recently, it has even been argued that no such solutions may be formulated for comparably simple systems such as the He atom.2 While routine applications in quantum chemistry rely on numerical frameworks such as Hartree–Fock (HF)3–6 and post-HF6,7 approaches as well as various implementations of density functional theory (DFT),8–10 the pursuit of alternative routes to provide more efficient as well as more accurate solutions to electronic structure problems is still a highly active field of research.11–16 Typically, simplified one-dimensional prototype systems such as harmonic and anharmonic oscillators, various instances of the particle-in-a-box system and multi-well potentials act as starting points to formulate alternative strategies to solve Schrödinger's equation. Following these initial model applications, the methodology can then be extended to more general frameworks involving an increased number of quantum particles, higher dimensionality and even antisymmetric constraints enabling the treatment of fermionic systems. However, despite the dimensional simplification, there is still a plethora of systems in quantum chemistry which are essentially 1D in nature. Typical examples are the stretch vibrations of diatomic molecules like H2, HD and D2,17 which due to their low effective mass represent highly sensitive quantum systems. Similarly, isolated stretch vibrations of carbon–halogen and oxygen–hydrogen bonds in organic compounds can be considered as 1D oscillators.18,19 Furthermore, a broad range of systems can be described by 1D double- and multi-well potentials. Prominent examples are the rotation of the hydroxy group in phenol20,21 and aliphatic alcohols like ethanol,22,23 described by periodic double- and triple-well potentials, as well as the transposition of atoms around the ideal bond axis in amorphous solids such as glasses.24,25 Recently, instances of heavy atom (i.e. carbon, nitrogen, oxygen) tunneling have been reported, greatly extending the importance of quantum mechanical tunnel effects for the understanding of chemical reactions.26,27 When turning to 1D periodic systems a frequent example encountered is the rectangular Kronig–Penney potential,28,29 which is a simplified model system corresponding to the periodic generalization of a prototype quantum particle bound to a finite square-well potential.30 Despite its simplicity this system already gives rise to an analytic dispersion relation, similar to band structures known from solid-state physics. Additionally, many 1D systems are analytically solvable, which makes them ideal candidates to assess the performance and applicability of newly formulated numerical techniques to solve the Schrödinger equation. Established numerical methods to solve the 1D Schrödinger equation for a given potential energy surface (PES) of general form, are the grid-based Numerov method,17,20,31,32 discrete variable representation (DVR) techniques,33,34 the Chebychev collocation approach35,36 as well as other finite-difference methods.37 However, recent developments in the theory and implementation of neural networks (NNs) paved the way for a new research area, focused on solving partial differential equations (PDEs) with NNs.38,39 Among others, neural networks have been successfully constructed to solve PDEs describing cosmological phase transitions40 and processes in fluid dynamics,41,42 both of which are known to be highly challenging problems in physical sciences. The innovation in these approaches is to regard the NN as a universal function approximator43–45 acting as test function for the solution of a given PDE. Network parameters are obtained in a self-supervised learning process aimed at solving the PDE within the constraints of preset boundary conditions.In this work, a feed-forward artificial neural network (FF-ANN)46 with 1 input, 1 output and a single hidden layer with 2n units was successfully implemented to solve the 1D Schrödinger equation given as
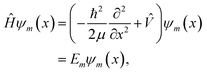 | (1) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) and the operator of the kinetic energy, with h being the reduced Planck constant and μ the (effective) mass of the quantum system. The output of the proposed FF-ANN implementation ψm(x) is a continuous function over the input domain, enabling inter- and extrapolation from any set of grid points employed in the learning process. This feature represents a distinct advantage of the introduced FF-ANN approach and distinguishes the method from the above mentioned grid-based frameworks, providing only output information at the employed grid points. Notable work in this direction already exists in ref. 47 and 48, however so far the discussion is restricted to relatively simple analytic systems, without any application to complex quantum mechanical systems characterized via experimental measurements. Furthermore, the presented approach differs in a significantly improved version of the network structure, which is considered to be more flexible and even permits the modelling of complex wave functions, a feature not discussed in existing NN-based approaches to solve Schrödinger's equation. In addition, the approach is applied to non-analytic PES, the solutions of which can be directly related to experimental data.
and the operator of the kinetic energy, with h being the reduced Planck constant and μ the (effective) mass of the quantum system. The output of the proposed FF-ANN implementation ψm(x) is a continuous function over the input domain, enabling inter- and extrapolation from any set of grid points employed in the learning process. This feature represents a distinct advantage of the introduced FF-ANN approach and distinguishes the method from the above mentioned grid-based frameworks, providing only output information at the employed grid points. Notable work in this direction already exists in ref. 47 and 48, however so far the discussion is restricted to relatively simple analytic systems, without any application to complex quantum mechanical systems characterized via experimental measurements. Furthermore, the presented approach differs in a significantly improved version of the network structure, which is considered to be more flexible and even permits the modelling of complex wave functions, a feature not discussed in existing NN-based approaches to solve Schrödinger's equation. In addition, the approach is applied to non-analytic PES, the solutions of which can be directly related to experimental data.
2 Methods
Network architecture and loss function
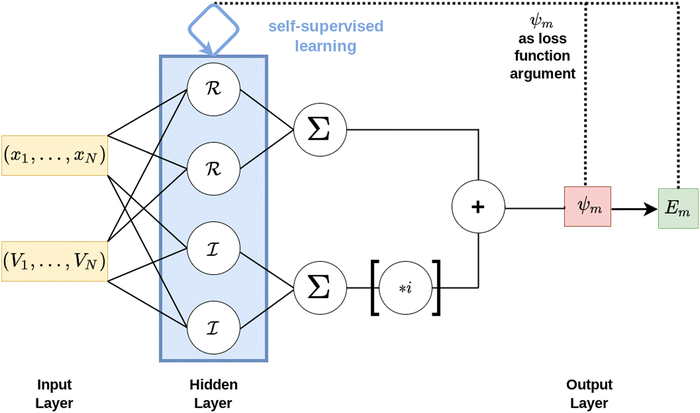
The target of the present approach is to locate the lowest k eigenenergies Em and their associated eigenstates ψm(x) of the spatial one-dimensional stationary Schrödinger equation as given in eqn (1). A feed-forward artificial neural network (FF-ANN) with 1 input, 1 output and a single hidden layer with 2n units (i.e. neurons) and special internal structure, as schematically depicted in Fig. 1, is considered as test function for every eigenstate ψm(x). In order to also enable the modeling of complex-numbered eigenfunctions, required for instance in the treatment of periodic systems based on Bloch's theorem,30,49 the hidden layer is grouped into sub-layers![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) and
and ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) , comprised of real and imaginary neurons, which enables the FF-ANN to access the complex plane.
, comprised of real and imaginary neurons, which enables the FF-ANN to access the complex plane.
The input of the FF-ANN is a set of N tuples (xi,Vi), where xi is the discretized input coordinate ranging from xmin to xmax and Vi = V(xi) is the respective value for the potential. Notably, this structure enables the use of various sources to generate the input potential, either via analytical potential energy functions such as harmonic or Morse oscillators or alternatively, input data obtained for instance via a point-wise potential energy scan from quantum chemical calculations.17,20 In contrast to the majority of grid-based formalisms such as the Numerov approach and DVR this potential input does not have to be provided on an equispaced grid. The output of the FF-ANN is denoted by ψm(x), given as
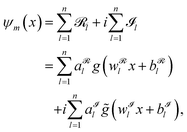 | (2) |
![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) :
: ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) →
→ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) denoting the respective activation functions. For the sake of generality, the latter can also be chosen differently for individual neurons. Unless otherwise specified, the activation function of choice in this work is the periodic function g(x) =
denoting the respective activation functions. For the sake of generality, the latter can also be chosen differently for individual neurons. Unless otherwise specified, the activation function of choice in this work is the periodic function g(x) = ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) (x) = sin(x), also referred to as SIREN (sinusoidal representation networks) activation function presented by Sitzmann et al. in 2020.50 Another approach realized for the presented FF-ANN is the use of Gaussian activation functions.51,52 A detailed comparison between these functions is provided in a separate section.
(x) = sin(x), also referred to as SIREN (sinusoidal representation networks) activation function presented by Sitzmann et al. in 2020.50 Another approach realized for the presented FF-ANN is the use of Gaussian activation functions.51,52 A detailed comparison between these functions is provided in a separate section.
To obtain approximate solutions of the Schrödinger equation for Em and ψm, the output of the FF-ANN is set equal to the wave function. From this the corresponding value for Em is then calculated according to
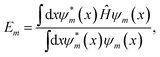 | (3) |
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ,
,![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) . This can be achieved by minimizing the respective loss function
. This can be achieved by minimizing the respective loss function ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) m given as
m given as![[script L]](https://www.rsc.org/images/entities/char_e144.gif) m = γ1Em + γ2ϕdiffm + γ3ϕbm + f(ϕom), m = γ1Em + γ2ϕdiffm + γ3ϕbm + f(ϕom), | (4) |
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) m. The explicit form for f is included below.
m. The explicit form for f is included below.
The general notion of the presented loss function was motivated from earlier works focusing on the application of NNs to find solutions to differential eigenvalue problems42,53 as for instance cosmological phase transitions presented by Piscopo et al. in 2019.40 In this work, these approaches are extended to account for the outlined non-linear contribution and associated choice of weighting factors, which is discussed in more detail below. In the following, the individual contributions that appear in eqn (4) are highlighted. The first term, γ1Em, corresponds to a linear eigenenergy penalty implying that the loss function is minimized for the lowest sensible eigenvalue. The second term
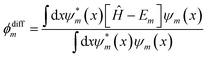 | (5) |
The behavior of the wave function at the boundaries of the spatial region is encoded in ϕbm. All systems considered in this study can be categorized into (a) finite PES with localized solutions (ε → 0) corresponding to Dirichlet boundary conditions on the input domain ranging from xmin to xmax, given as
| ϕbm = |ψm(xmin) − ε| + |ψm(xmax) − ε|, | (6) |
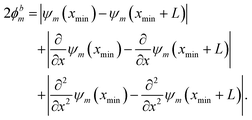 | (7) |
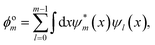 | (8) |
Following these definitions, the contribution of the eigenenergy is the only term that effectively contributes to the loss function ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) m once a converged solution has been identified, i.e. the contributions ϕdiffm, ϕbm and f(ϕom) are expected to be zero. In other words, any deviation from the correct eigenstate results in positive penalties to
m once a converged solution has been identified, i.e. the contributions ϕdiffm, ϕbm and f(ϕom) are expected to be zero. In other words, any deviation from the correct eigenstate results in positive penalties to ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) m. Since the goal is to minimize
m. Since the goal is to minimize ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) m, the first obtained solution is the one with the smallest eigenenergy corresponding to the quantum mechanical ground state. For all subsequent states the orthogonality condition applies, ensuring that the next minimum of the loss function corresponds to an excited eigenstate. Thus, the spectrum of the Hamiltonian can be found iteratively by minimizing
m, the first obtained solution is the one with the smallest eigenenergy corresponding to the quantum mechanical ground state. For all subsequent states the orthogonality condition applies, ensuring that the next minimum of the loss function corresponds to an excited eigenstate. Thus, the spectrum of the Hamiltonian can be found iteratively by minimizing ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) m, always taking into account all previously identified states for the given Hamiltonian. Schematically, this procedure for the training of the FF-ANN is illustrated in Algorithm 1.
m, always taking into account all previously identified states for the given Hamiltonian. Schematically, this procedure for the training of the FF-ANN is illustrated in Algorithm 1.
| Algorithm 1 Training of the FF-ANN | |
|---|---|
| LOSS(m,ψm,ψl,l<m): | |
| Em ← ENERGY (ψm,Ĥ) | \\ eqn (3) |
| ϕdiffm ← DIFF_EQ(ψm,Ĥ,Em) | \\ eqn (5) |
| if periodic_boundaries = false: | |
| ϕbm ← DIRICHLET_BOUND (ψm) | \\ eqn (6) |
| else periodic_boundaries = true: | |
| ϕbm ← PERIODIC_BOUND (ψm) | \\ eqn (7) |
| end if | |
| ϕom ← ORTHOGONAL (m,ψm,ψl,l<m) | \\ eqn (8) |
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) m ← γ1Em + γ2ϕdiffm + γ3ϕbm + f(ϕom) m ← γ1Em + γ2ϕdiffm + γ3ϕbm + f(ϕom) |
|
return ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) m m |
|
| end LOSS | |
| CALC_SPECTRUM (Ĥ,number_of_states): | |
spectrum ← {![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) } } |
|
| form ← 0 to NUMBER_OF_STATES − 1 do: | |
ψm ← INIT_NETWORK_PARAMS (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) ) |
|
ψm ← NORMALIZE_NEURONS (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) ) |
|
| ψm ← OPT_LOSS (LOSS) | |
| Em ← ENERGY (ψm,Ĥ) | \\ eqn (3) |
| spectrum ← spectrum∪{(ψm,Em)} | |
| end for | |
| return spectrum | |
| end CALC_SPECTRUM | |
Activation functions
In the following the different aspects in the design of the FF-ANN approach are outlined in detail. The SIREN activation function50 and its second derivative are given as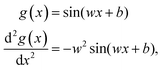 | (9) |
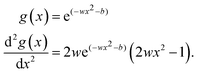 | (10) |
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) 01 and
01 and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) 02, in cm−1 for three different isotopologues of the hydrogen molecule: H2, HD and D2 at Full-CI/cc-pVQZ level obtained via the FF-ANN approach using 40 neurons compared to the associated Numerov results and experimental reference data
02, in cm−1 for three different isotopologues of the hydrogen molecule: H2, HD and D2 at Full-CI/cc-pVQZ level obtained via the FF-ANN approach using 40 neurons compared to the associated Numerov results and experimental reference data
For the construction of the loss function only analytic derivatives for both activation functions are considered, while all integrations were performed using the Simpsons method.55 Here, the SIREN activation function shows one further advantage over its Gaussian counterpart: The integral to calculate the scalar product between two eigenstates can be performed analytically for the SIREN type via eqn (S1) and (S2) given in the ESI.† However, this is in general not possible for the Gaussian ansatz, which is explicitly shown in eqn (S3) of the ESI.†
Orthogonality contribution
In the following the choice for the orthogonality contribution f(ϕom), with ϕom as given in eqn (8) is discussed. Empirically, it was found that an expression according to| f(ϕom) = 100·ϕom(|ϕom − 0.5| + 0.5) | (11) |
Choice of weighting factors γi
The loss function as defined in eqn (4) contains the real weighting factors γ1, γ2 and γ3. Ideally, these are set in such a way that no term in eqn (4) outweighs the other contribution by orders of magnitude. Otherwise the optimizer is steered to adjust the parameters in such a way that the FF-ANN output mainly minimizes the contribution associated to the highest weighted contribution, while poorly satisfying all other terms. While it can be argued that given a sufficient number of training periods the optimization algorithm might escape local minima, this is certainly not considered to be good practice. Choosing the weighting factors according to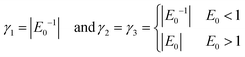 | (12) |
Initialization and training of the network
The parameters of the FF-ANN employing SIREN activation functions are initialized based on (a) a random uniform distribution or (b) a Fourier-transformation of an approximate harmonic oscillator state. For (a) the initial parameter values a![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ,
,![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) i, b
i, b![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ,
,![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) i and w
i and w![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ,
,![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) i are randomly chosen from the intervals [0,2], [0,2π] and
i are randomly chosen from the intervals [0,2], [0,2π] and 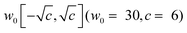 , respectively. Sitzmann et al. have shown that this random initialization provides an effective strategy for a large class of problems.50 For (b) a harmonic approximation of the potential in each minimum is generated. The eigenstates of the corresponding quantum harmonic oscillator Hamiltonian are well-known and serve as an initial guess for the desired network output. To obtain the parameter values for a
, respectively. Sitzmann et al. have shown that this random initialization provides an effective strategy for a large class of problems.50 For (b) a harmonic approximation of the potential in each minimum is generated. The eigenstates of the corresponding quantum harmonic oscillator Hamiltonian are well-known and serve as an initial guess for the desired network output. To obtain the parameter values for a![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ,
,![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) i, b
i, b![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ,
,![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) i and w
i and w![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ,
,![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) i a fast Fourier-transformation of the harmonic oscillator states is performed. This approach was motivated from the resemblance of the network output with a truncated Fourier-series in the case of SIREN activation functions. The basin-hopping algorithm56–59 was employed for the training of the FF-ANN due to its capability to locate global minima in high-dimensional parameter spaces. The algorithm works by randomly perturbing the network parameters followed by local minimization. Parameters are accepted based on a Metropolis criterion similar to Monte-Carlo algorithms,60,61 providing also the possibility of simulated annealing as the optimization is progressing. This procedure is repeated several times and outputs parameter values that minimize the loss function
i a fast Fourier-transformation of the harmonic oscillator states is performed. This approach was motivated from the resemblance of the network output with a truncated Fourier-series in the case of SIREN activation functions. The basin-hopping algorithm56–59 was employed for the training of the FF-ANN due to its capability to locate global minima in high-dimensional parameter spaces. The algorithm works by randomly perturbing the network parameters followed by local minimization. Parameters are accepted based on a Metropolis criterion similar to Monte-Carlo algorithms,60,61 providing also the possibility of simulated annealing as the optimization is progressing. This procedure is repeated several times and outputs parameter values that minimize the loss function ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) m. In this work local minimization is performed with the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm.62–65 For the implementation of the basin-hopping algorithm in conjunction with local BFGS minimization the scipy library66 was utilized. Convergence criteria of the local minimizer were set such that the change of the loss function is less than 10−12 for 5000 consecutive minimization steps.
m. In this work local minimization is performed with the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm.62–65 For the implementation of the basin-hopping algorithm in conjunction with local BFGS minimization the scipy library66 was utilized. Convergence criteria of the local minimizer were set such that the change of the loss function is less than 10−12 for 5000 consecutive minimization steps.
3 Results
Analytically solvable systems
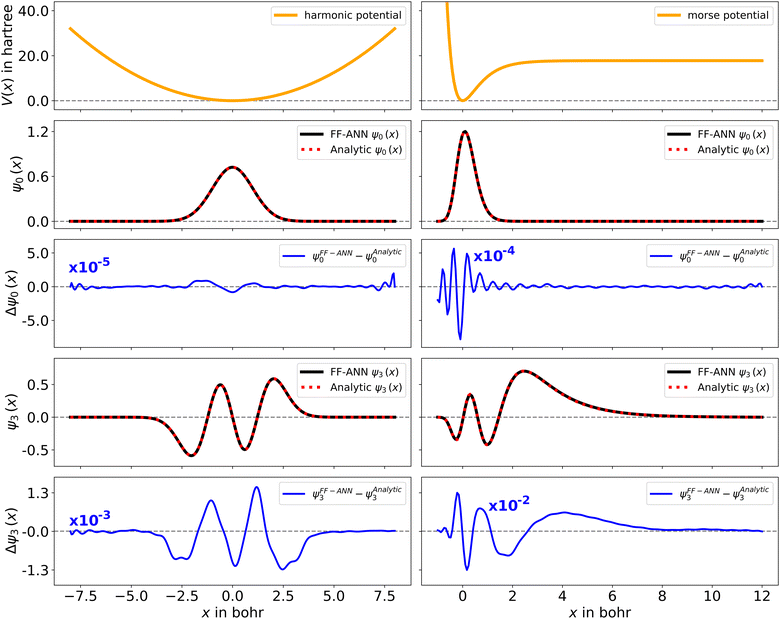
To demonstrate the efficiency of the method and benchmark the achievable accuracy, a number of analytically solvable systems has been analyzed. All FF-ANN calculations in this section have been performed excluding the![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) layer containing the imaginary functions in eqn (2), since the wave functions are exclusively real in these cases. Network parameters were initialized based on a Fourier-transform of a test eigenstate solving the harmonic approximation of the potential in each minimum. For convenience all calculations in this section were carried out employing atomic units, setting ħ = 1 and μ = 1. This implies that all energies and distances are given in units of hartree and bohr, respectively. First, the analytically solvable single-well potentials of the harmonic and Morse oscillators are considered, which are both widely employed to represent bonded vibrational states in simple molecules.67 The Hamiltonian for the harmonic oscillator is defined according to
layer containing the imaginary functions in eqn (2), since the wave functions are exclusively real in these cases. Network parameters were initialized based on a Fourier-transform of a test eigenstate solving the harmonic approximation of the potential in each minimum. For convenience all calculations in this section were carried out employing atomic units, setting ħ = 1 and μ = 1. This implies that all energies and distances are given in units of hartree and bohr, respectively. First, the analytically solvable single-well potentials of the harmonic and Morse oscillators are considered, which are both widely employed to represent bonded vibrational states in simple molecules.67 The Hamiltonian for the harmonic oscillator is defined according to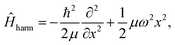 | (13) |
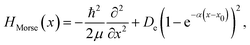 | (14) |
In general, the vibrational states of diatomic chemical species show relatively large spacings between the different excitations compared to those associated to molecular rotation. The rotational Hamiltonian Hrot in absence of any vibrational coupling about a single axis has a much simpler form compared to the vibrational Hamiltonians by not including any external potential, i.e.:
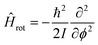 | (15) |
Even more challenging, yet highly relevant benchmark systems for the neural network are applications to double-well potentials. This way the adaptability of the FF-ANN to model wave functions of increasing complexity in terms of curvature in conjunction with small differences in values for the eigenenergy between ground and first excited state, an effect known as tunnel splitting, can be assessed.69,70 The first double-well potential under consideration is the Razavy potential,71,72 which is parameterized according to
V(x) = [ξ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cosh(2x) − M]2, cosh(2x) − M]2, | (16) |
V(x) = a2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh2(x) − k sinh2(x) − k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) tanh2(x), tanh2(x), | (17) |
Analytically solvable periodic system
In the following, the FF-ANN was used to solve a challenging periodic quantum system, namely the rectangular Kronig–Penney potential introduced already in 1931.28 It represents the periodic extension of the particle in a finite square-well potential, and despite its simplicity already leads to an analytically solvable dispersion relation associated to band structures known from solid-state physics.29 According to Bloch's theorem the wave function of a system subject to a periodic potential can be described by ψmk(x) = eikxumk(x), with crystal momentum k, band index m and the lattice periodic function umk.49 In order to obtain umk the following equation has to be solved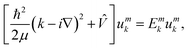 | (18) |
Since ψmk is unique up to a reciprocal lattice vector it is sufficient to only consider crystal momenta in the first Brillouin zone, i.e. k ∈ [0,π/a] with a being the size of the 1D unit cell.30,49 To enable a correct treatment of the Hamiltonian shown in eqn (18), the neurons permitting the inclusion of imaginary activation functions of sub-layer ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) have to be activated. In the following, a Kronig–Penney potential as depicted in Fig. 3a is considered. Energy values of the first and second band for selected values of the crystal momentum obtained using the FF-ANN with 70 neurons are compared with the corresponding analytical dispersion relation E(k)28,29 in Fig. 3b.
have to be activated. In the following, a Kronig–Penney potential as depicted in Fig. 3a is considered. Energy values of the first and second band for selected values of the crystal momentum obtained using the FF-ANN with 70 neurons are compared with the corresponding analytical dispersion relation E(k)28,29 in Fig. 3b.
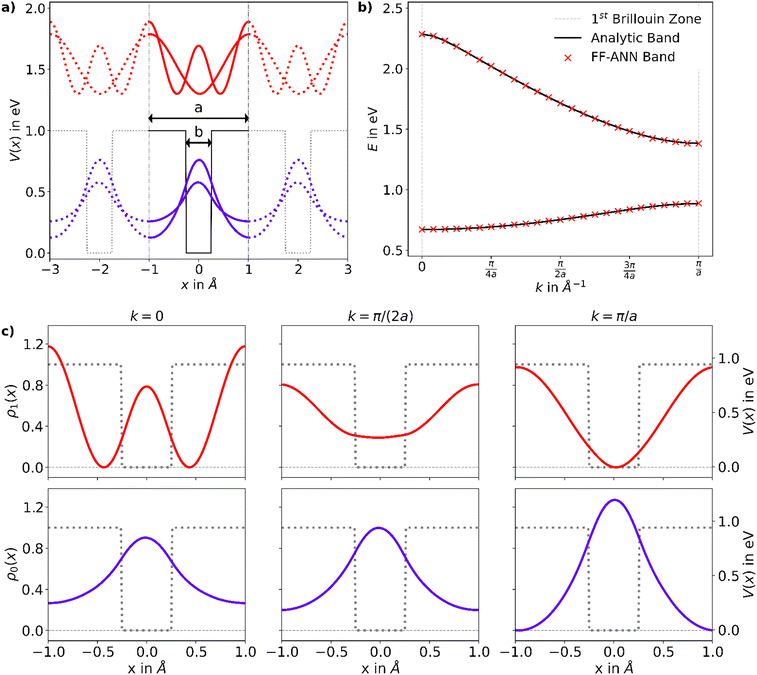 | ||
Fig. 3 (a) Rectangular Kronig–Penney potential with a = 2 Å, b = 0.5 Å and V = 1 eV, along with the probability densities 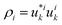 of the first (i = 0, blue) and second (i = 1, red) band, depicted for two different values of the crystal momentum k = 0 and π/a, corresponding to k-points in the center and at the border of the 1st Brillouin zone. (b) Comparison of the associated dispersion relation E(k) obtained from the FF-ANN against the analytical solution.29 (c) Probability densities for the first (blue) and second (red) band for k-values of of the first (i = 0, blue) and second (i = 1, red) band, depicted for two different values of the crystal momentum k = 0 and π/a, corresponding to k-points in the center and at the border of the 1st Brillouin zone. (b) Comparison of the associated dispersion relation E(k) obtained from the FF-ANN against the analytical solution.29 (c) Probability densities for the first (blue) and second (red) band for k-values of 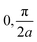 and and 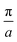 . The probability densities and band energies were obtained using 70 neurons. . The probability densities and band energies were obtained using 70 neurons. | ||
Probability densities for selected values of the crystal momentum are shown in Fig. 3c. The successful reproduction of the band structure demonstrates the capability to properly describe periodic PDEs with complex eigensolutions, a feature rarely encountered in the literature.50 A special characteristic of the presented FF-ANN is the possibility to determine the periodic function umk(x) at any given k-point, an analysis of which can be related to the finding that the tunnelling probability decreases with an increase in crystal momentum. To the best of knowledge the real-space wave functions umk(x) for general values of k have not yet been reported in the literature, since typically the solutions only provide the dispersion relation Emk.
Bond vibrations of H2, HD and D2
In addition to the analytical benchmark calculations, experimentally measured quantum mechanical systems were investigated to provide examples for the applicability of the presented approach beyond analytically solvable potentials. In the first example, the binding potential of molecular H2 was determined via accurate quantum chemical calculations and the associated vibrational eigenstates were evaluated using the FF-ANN approach. The bond length between the two hydrogen atoms was varied equidistantly with a step size of 0.025 Å starting from 0.4 Å up to 7.0 Å. For each generated configuration a single point configuration interaction (CI)6 calculation at the cc-pVQZ75 level using single and double excitations was performed (CISD) via gaussian16.76 Since the hydrogen molecule possesses only two electrons, the CISD approach can be considered as equivalent to Full-CI.6 According to the Born-Oppenheimer approximation,6 the Schrödinger equation can be applied on the same PES for H2, HD and D2 respectively, thereby only varying the effective mass μ within the vibrational Hamilton operator to obtain the associated eigenvalues and eigenstates. Therefore, three calculations were performed using the presented FF-ANN network on the described grid-based potential using 40 neurons. The effective masses were set to μH2 = 0.5039125 g mol−1, μHD = 0.6717112 g mol−1 and μD2 = 1.007051 g mol−1.For the FF-ANN routine two different activation functions were employed. In addition to the SIREN activation functions,50 their Gaussian-type analogues as described in Section 2 were used to perform the calculation for the respective isotopologues.
The resulting fundamental and first overtones are summarized in Table 1, while Fig. S8 of the ESI,† depicts the respective potential along with the calculated ground state and the seven lowest excited state wavefunctions for the three isotopologues H2, HD and D2. In addition, a comparison between the three lowest eigenstates of all three considered systems is shown in Fig. S8 (ESI†).
The data obtained via the FF-ANN approach for H2 are in excellent agreement with the experimental reference values, with the errors for the fundamental and first overtone being 1.1 cm−1 and 2.5 cm−1 respectively, corresponding to relative deviations of 0.026% and 0.031%. These deviations are greatly reduced in case of HD and D2, showing a difference of only 0.1 cm−1 and 0.4 cm−1 (i.e. 0.01% and 0.003%) for the fundamental excitation. This systematic improvement can be explained by the decreasing impact of rotational–vibrational coupling upon increasing mass of the oscillator. Since the 1D vibrational Schrödinger equation does not take these contributions into account, the largest deviations are observed in the H2 case, which is the lightest isotopologue considered. Furthermore, the neural network calculations including the SIREN activation functions match exactly the results obtained via the Numerov approach,17 which was applied to the same input potential.
The comparison of the data obtained by treating the test sets with the same FF-ANN settings, differing only in the choice of activation function, shows some minor advantages in favor of the SIREN approach, when referring to the Numerov and experimental data. Hence, the latter where chosen as default, which is further supported by the inherent periodicity of the sine function. This leads to further major advantages applying the FF-ANN on periodic potentials as already seen in case of the Kronig–Penney potential discussed above.
Torsional tunnel splitting in phenol
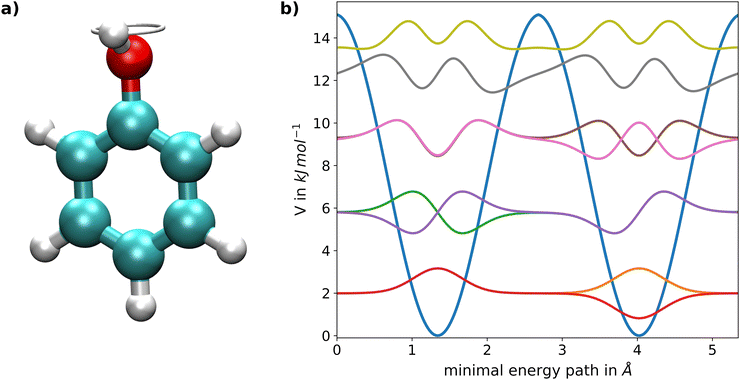
As a second application a complex target system featuring torsional tunnel splittings was investigated, namely the intramolecular rotation of the OH-group in the phenol molecule depicted in Fig. 4a. This degree of freedom represents a prime example of a quantum mechanical tunnelling phenomenon and has been investigated in detail from both the experimental21 and theoretical perspective.20,21 The associated potential energy along the reaction coordinate is shown in Fig. 4b and was taken from a previous study.20 The minimum energy path was determined via constrained energy minimizations at B3LYP level,79 thereby fixing the dihedral angle of the OH-group followed by re-calculation of the respective configurations using 2nd order Møller–Plesset perturbation theory (MP2).80 For the determination of the eigenvalues and eigenstates, the presented neural network approach was applied on the latter PES with a total of 20 neurons. The effective mass of 0.98868 g mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 is determined as the reduced mass of the four C–H groups in ortho- and meta-position, since two carbon atoms and one hydrogen atom of the phenyl molecule are located along the torsional axis and should therefore not be considered.
20 is determined as the reduced mass of the four C–H groups in ortho- and meta-position, since two carbon atoms and one hydrogen atom of the phenyl molecule are located along the torsional axis and should therefore not be considered.
The results for the first four torsional tunnel splittings obtained via the FF-ANN approach are listed in Table 2, along with a comparison to data determined via a periodic Numerov approach,20 quasiharmonic reaction path Hamiltonian (RPH) calculations21 as well as experimental measurements.21 Furthermore, the deviations of the three theoretical descriptions from the experimental reference are included.
The calculation results of the FF-ANN show a remarkably good agreement with the experimental data, especially when considering the low absolute wave numbers associated to the first and second tunnel splitting as well as the increase from the lowest (0.0019 cm−1) to the highest experimentally measured wave number (1.77 cm−1), spanning three orders of magnitude. Considering the relative deviation it can be observed that both the Numerov and RPH method tend to underestimate the torsional tunnel splitting. Thus, for the 30 → 31 splitting energy, for which no experimental data is provided, the result of 17.84 cm−1 can be regarded as a very reliable estimation.
4 Conclusion
In this work the capabilities of a feed-forward artificial neural network designed to identify solutions to Schrödinger's equation based on self-supervised learning were demonstrated. It has been shown that the presented strategy shows a large flexibility despite the variety in the considered one-dimensional quantum problems. Different classes of one-dimensional potentials were investigated, ranging from localized to periodic solutions with the extension to determine band structures for the associated potential energy surface. For the latter, half of the hidden layer neurons are set to act as imaginary units, which highlights a unique feature of the presented FF-ANN approach.Furthermore, it was demonstrated that the applicability of the FF-ANN is not limited to analytic benchmark scenarios. The presented implementation is capable of determining the vibrational excitation energies of the hydrogen molecule H2 and its isotopologues HD and D2 in very good agreement with experimental reference values. Additionally, the prominent torsional tunnel splitting of the intramolecular torsion of the OH-group in phenol could be resolved with exceptional accuracy without relying on any experimental input.
A remarkable feature regarding the flexibility of the FF-ANN is strongly related to the presented architecture. The neural network is able to perform calculations on any number of given input tuples (xi,Vi), without constraining the resulting eigenstates of the solution to a pre-specified output grid. Furthermore, the approach presented within this work is not limited to an equidistant potential input, which is a key advantage over the majority of grid-based approaches such as the Numerov framework and related methods. Thus, for the input of the PES only selected supporting points have to be provided, preferably in regions where the curvature in the eigenstate can be expected to be low. For example, a possible strategy is to provide more points near the respective minimum, while fewer are given at larger displacements.
In general, grid-point approaches only provide output data at the location of the associated input points. Hence, the eigenstate information in between these grid points can only be accessed via approximate interpolation schemes. In contrast, the output of the presented FF-ANN is represented as a function of the neurons in the hidden layer. Therefore, no interpolations have to be performed to access the output over the entire domain providing also the possibility of extrapolation outside the provided input without any further computational cost. The presented one-dimensional implementation displays a larger computational demand compared to grid-based methods such as DVR or Numerov approach. However, when aiming at a generalization of the framework to problems in higher dimensions, the computational demand as well as memory requirements of the grid-based problems increase by orders of magnitude even when employing a sparse matrix representation,17,81 since in this case the problem needs to be represented in terms of block matrices. This gives the FF-ANN the potential to provide a more efficient scalability compared to these established methodologies, in particular when combined with the advantages of providing a non-equispaced input potential along with a wavefunction output over the entire domain as discussed above.
Due to the FF-ANN's high flexibility and wide applicability, the extension to n-dimensional problems and the subsequent application to fermionic states by including an antisymmetric contribution in the loss function is considered as a promising outlook for further development of the presented FF-ANN. Comparing the methodology of the neural network to standard quantum mechanical calculation schemes such as Hartree Fock,3–6 which are based on pre-defined basis sets, a major distinction can be identified. While the commonly employed Gaussian-type basis functions are typically pre-parametrized for each type of element and contribute only linearly within these schemes by applying a linear combination approach, both the SIREN and Gaussian activation functions of the presented FF-ANN show no inherent parameterization and are optimized regarding all contributing parameters. This property holds great promise to consider the outlined FF-ANN implementation as a primer for the formulation of novel ab initio calculation schemes aimed at the treatment of many-electron systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial supports for this work via a PhD scholarship for J. Gamper issued by the Leopold-Franzens-University of Innsbruck (Vicerector Prof. Dr Ulrike Tanzer) are gratefully acknowledged. The computational results presented have been achieved (in part) using the HPC infrastructure of the University of Innsbruck.Notes and references
- E. Schrödinger, Ann. Phys., 1926, 386, 109–139 CrossRef.
- I. Toli and S. Zou, Chem. Phys. Lett., 2019, 737, 100021 CrossRef.
- P. Lykos and G. W. Pratt, Rev. Mod. Phys., 1963, 35, 496–501 CrossRef.
- J. R. Stone, J. Phys. G, 2005, 31, R211–R230 CrossRef CAS.
- P. Echenique and J. L. Alonso, Mol. Phys., 2007, 105, 3057–3098 CrossRef CAS.
- T. Helgaker, P. Jorgensen and J. Olsen, Molecular electronic-structure theory, John Wiley & Sons, Nashville, TN, 2013 Search PubMed.
- J. Townsend, J. K. Kirkland and K. D. Vogiatzis, Mathematical Physics in Theoretical Chemistry, Elsevier, 2019, pp. 63–117 Search PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- M. Orio, D. A. Pantazis and F. Neese, Photosynth. Res., 2009, 102, 443–453 CrossRef CAS PubMed.
- P. Popelier, Solving the Schrödinger equation, Imperial College Press, London, England, 2011 Search PubMed.
- J. Hermann, Z. Schätzle and F. Noé, Nat. Chem., 2020, 12, 891–897 CrossRef CAS PubMed.
- D. Pfau, J. S. Spencer, A. G. D. G. Matthews and W. M. C. Foulkes, Phys. Rev. Res., 2020, 2, 033429 CrossRef CAS.
- K. T. Schütt, M. Gastegger, A. Tkatchenko, K.-R. Müller and R. J. Maurer, Nat. Commun., 2019, 10, 5024 CrossRef PubMed.
- K. Mills, M. Spanner and I. Tamblyn, Phys. Rev. A, 2017, 96, 042113 CrossRef.
- X. Wang, A. Kumar, C. R. Shelton and B. M. Wong, Phys. Chem. Chem. Phys., 2020, 22, 22889–22899 RSC.
- U. Kuenzer, J.-A. Sorarù and T. S. Hofer, Phys. Chem. Chem. Phys., 2016, 18, 31521–31533 RSC.
- J. G. Dojahn, E. C. M. Chen and W. E. Wentworth, J. Phys. Chem., 1996, 100, 9649–9657 CrossRef CAS.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
- U. Kuenzer and T. S. Hofer, Chem. Phys. Lett., 2019, 728, 195–200 CrossRef CAS.
- S. Albert, P. Lerch, R. Prentner and M. Quack, Angew. Chem., Int. Ed., 2012, 52, 346–349 CrossRef PubMed.
- J. Castillo-Chará and E. L. Sibert, J. Chem. Phys., 2003, 119, 11671–11681 CrossRef.
- J. R. Durig, W. E. Bucy, C. J. Wurrey and L. A. Carreira, J. Phys. Chem., 1975, 79, 988–993 CrossRef CAS.
- P. W. Anderson, B. I. Halperin and C. M. Varma, Philos. Mag., 1972, 25, 1–9 CrossRef CAS.
- A. Alexander and S. Ben, Condensed Matter Field Theory, Cambridge University Press, 2nd edn, 2010, vol. 1 Search PubMed.
- C. Castro and W. L. Karney, Angew. Chem., Int. Ed., 2020, 59, 8355–8366 CrossRef CAS PubMed.
- S. Karmakar and A. Datta, J. Chem. Sci., 2020, 132, 127 CrossRef CAS.
- R. D. L. Kronig and W. G. Penney, Proc. R. Soc. A, 1931, 130, 499–513 Search PubMed.
- R. L. Pavelich and F. Marsiglio, Am. J. Phys., 2015, 83, 773–781 CrossRef.
- C. Cohen-Tannoudji, B. Diu and F. Laloe, Quantum Mechanics, Wiley-VCH, 1997, vol. 1 Search PubMed.
- B. V. Numerov, Trudy Glavnoi rossiiskoi astrofizicheskoi observatorii; t. 2, 1923, vol. 2, pp. 188–288.
- B. V. Numerov, Mitteilungen der Nikolai-Hauptsternwarte zu Pulkowo, 1924, vol. 10, pp. 58–155 Search PubMed.
- D. T. Colbert and W. H. Miller, J. Chem. Phys., 1992, 96, 1982–1991 CrossRef CAS.
- A. Bulgac and M. M. Forbes, Phys. Rev. C, 2013, 87, 051301 CrossRef.
- B. Fornberg, A practical guide to pseudospectral methods, Cambridge University Press, 1998 Search PubMed.
- J. C. Mason and D. C. Handscomb, Chebyshev polynomials, Chapman and Hall/CRC, 2002 Search PubMed.
- J. C. Strikwerda, Finite difference schemes and partial differential equations, SIAM, 2004 Search PubMed.
- I. Lagaris, A. Likas and D. Fotiadis, IEEE trans. neural netw., 1998, 9, 987–1000 CrossRef CAS PubMed.
- J. Blechschmidt and O. G. Ernst, GAMM Mitteilungen, 2021, 44, e202100006 Search PubMed.
- M. L. Piscopo, M. Spannowsky and P. Waite, Phys. Rev. D, 2019, 100, 016002 CrossRef CAS.
- M. Raissi, P. Perdikaris and G. Karniadakis, J. Comput. Phys., 2019, 378, 686–707 CrossRef.
- T. Dockhorn, CoRR, 2019, abs/1904.07200.
- K. Hornik, M. Stinchcombe and H. White, Neural Netw., 1989, 2, 359–366 CrossRef.
- K. Hornik, Neural Netw., 1991, 4, 251–257 CrossRef.
- B. C. Csáji, et al., Faculty of Sciences, MSc thesis, Etvs Lornd University, Hungary, 2001, vol. 24, p. 7 Search PubMed.
- M. Christopher, Pattern Recognition and Machine Learning, Springer, New York, NY, 1st edn, 2006 Search PubMed.
- M. Sugawara, Comput. Phys. Commun., 2001, 140, 366–380 CrossRef CAS.
- Y. Shirvany, M. Hayati and R. Moradian, Commun. Nonlinear Sci. Numer. Simul., 2008, 13, 2132–2145 CrossRef.
- F. Bloch, Z. Phys., 1929, 52, 555–600 CrossRef.
- V. Sitzmann, J. Martel, A. Bergman, D. Lindell and G. Wetzstein, Advances in Neural Information Processing Systems, 2020, pp. 7462–7473 Search PubMed.
- E. J. Hartman, J. D. Keeler and J. M. Kowalski, Neural Comput., 1990, 2, 210–215 CrossRef.
- B. Yuen, M. T. Hoang, X. Dong and T. Lu, Sci. Rep., 2021, 11, 18757 CrossRef CAS PubMed.
- I. Ben-Shaul, L. Bar and N. Sochen, Deep Learning Solution of the Eigenvalue Problem for Differential Operators, 2021, https://openreview.net/forum?id=m4baHw5LZ7M.
- P. M. Gill, Advances in Quantum Chemistry, Elsevier, 1994, pp. 141–205 Search PubMed.
- K. Atkinson, An introduction to numerical analysis, John Wiley and Sons (WIE), Brisbane, QLD, Australia, 1989 Search PubMed.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- D. J. Wales and H. A. Scheraga, Science, 1999, 5432, 1368–1372 CrossRef PubMed.
- D. J. Wales, Energy landscapes, Cambridge University Press, Cambridge, UK, 2003 Search PubMed.
- B. Olson, I. Hashmi, K. Molloy and A. Shehu, Adv. Artif. Intell., 2012, 2012, 1–19 CrossRef.
- Monte Carlo methods in statistical physics, Institut Fur Physik Kurt Binder, ed. K. Binder and D. M. Ceperley, Springer, New York, NY, 2nd edn, 1986 Search PubMed.
- D. P. Landau and K. Binder, A guide to Monte Carlo simulations in statistical physics, Cambridge University Press, Cambridge, England, 4th edn, 2014 Search PubMed.
- C. G. Broyden, IMA J. Appl. Math., 1970, 6, 76–90 CrossRef.
- R. Fletcher, Comput. J., 1970, 13, 317–322 CrossRef.
- D. F. Shanno, Math. Comput., 1970, 647–656 CrossRef.
- D. Goldfarb, Math. Comput., 1970, 23–26 CrossRef.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- Z. Rong, H. G. Kjaergaard and M. L. Sage, Mol. Phys., 2003, 101, 2285–2294 CrossRef CAS.
- J. P. Dahl and M. Springborg, J. Chem. Phys., 1988, 88, 4535–4547 CrossRef CAS.
- A. Garg, Am. J. Phys., 2000, 68, 430–437 CrossRef.
- A. Sitnitsky, Comput. Theor. Chem., 2018, 1138, 15–22 CrossRef CAS.
- M. Baradaran and H. Panahi, Adv. High Energy Phys., 2017, 2017, 1–13 Search PubMed.
- F. Finkel, A. González-López and M. A. Rodríguez, J. Phys. A: Math. Theor., 1999, 32, 6821–6835 CrossRef.
- M. Razavy, Am. J. Phys., 1980, 48, 285–288 CrossRef CAS.
- Q. Dong, G.-H. Sun, J. Jing and S.-H. Dong, Phys. Lett. A, 2019, 383, 270–275 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- G. D. Dickenson, M. L. Niu, E. J. Salumbides, J. Komasa, K. S. E. Eikema, K. Pachucki and W. Ubachs, Phys. Rev. Lett., 2013, 110, 193601 CrossRef CAS PubMed.
- H.-O. Hamaguchi, I. Suzuki and A. Buckingham, Mol. Phys., 1981, 43, 963–973 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- U. Kuenzer and T. S. Hofer, Chem. Phys., 2019, 520, 88–99 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03921d |
| ‡ J. Gamper and F. Kluibenschedl contributed equally to this work. |
| This journal is © the Owner Societies 2022 |