Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
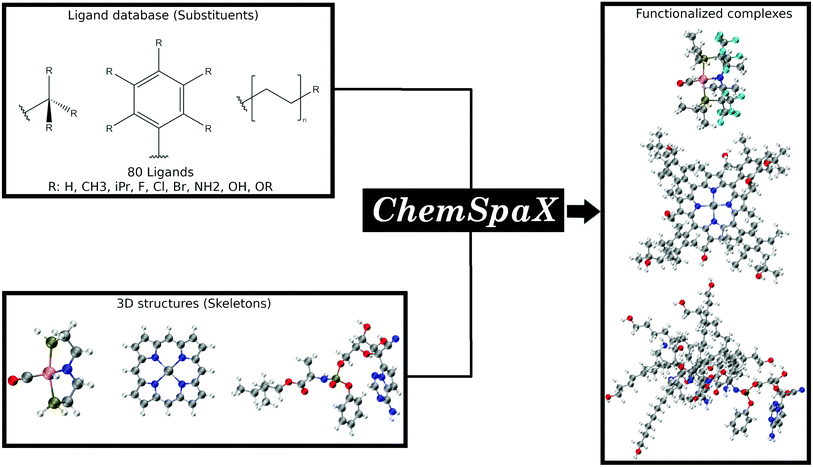
ChemSpaX: exploration of chemical space by automated functionalization of molecular scaffold†
Adarsh V.
Kalikadien
 ,
Evgeny A.
Pidko
,
Evgeny A.
Pidko
 * and
Vivek
Sinha
* and
Vivek
Sinha
 *
*
Inorganic Systems Engineering, Department of Chemical Engineering, Faculty of Applied Sciences, Delft University of Technology, Van der Maasweg 9, 2629 HZ, Delft, The Netherlands. E-mail: E.A.Pidko@tudelft.nl; V.Sinha@tudelft.nl
First published on 6th January 2022
Abstract
Exploration of the local chemical space of molecular scaffolds by post-functionalization (PF) is a promising route to discover novel molecules with desired structure and function. PF with rationally chosen substituents based on known electronic and steric properties is a commonly used experimental and computational strategy in screening, design and optimization of catalytic scaffolds. Automated generation of reasonably accurate geometric representations of post-functionalized molecular scaffolds is highly desirable for data-driven applications. However, automated PF of transition metal (TM) complexes remains challenging. In this work a Python-based workflow, ChemSpaX, that is aimed at automating the PF of a given molecular scaffold with special emphasis on TM complexes, is introduced. In three representative applications of ChemSpaX by comparing with DFT and DFT-B calculations, we show that the generated structures have a reasonable quality for use in computational screening applications. Furthermore, we show that ChemSpaX generated geometries can be used in machine learning applications to accurately predict DFT computed HOMO–LUMO gaps for transition metal complexes. ChemSpaX is open-source and aims to bolster and democratize the efforts of the scientific community towards data-driven chemical discovery.
1 Introduction
Chemical research has been driven by the ability and the need to create molecular scaffolds with desired (bio)chemical functions. Experimental chemistry, largely guided by intuition, chemical knowledge, and serendipity has been reasonably successful in discovering functional molecular scaffolds which can be improved further. For example, reactive catalytic scaffolds are decorated with diverse functional groups via post-functionalization (PF) to explore their activity and stability, and devise possible strategies for improvement.1–3 Although in vitro functionalization can reveal chemical design principles that underlie high activity, selectivity and stability, it is time and resource intensive. Computational molecular design has emerged as particularly promising in this regard, thanks to recent advances in quantum chemical methods and high performance computing.4–11 3D geometric information such as xyz coordinates and crystal structures of several catalytic scaffolds are known in the literature and databases. Using these known scaffolds, high-throughput computational methods can guide towards screening of highly effective PF strategies by systematically exploring geometries in the local chemical space of a given scaffold.12The chemical space is vast and a global exploration is difficult.13,14 Therefore, machine learning (ML) and other cost-effective computational methods are attractive solutions to navigate the chemical space in the search of novel molecules and materials.15 A data-driven statistical approach, rooted in quantum and statistical mechanics (QM and SM) is needed to explore and understand the chemical space.16 Such an approach is strongly dependent on the availability of trustworthy structure property databases (SPDBs). For (small) organic molecules, reliable data sets such as the GDB datasets (11, 13 and 17) exist which are being used for diverse data-driven chemical discovery applications.17–24 In contrast to small organic molecules, development of data-driven approaches have proven more challenging for transition metal complexes (TMCs). TMCs are often used as bio-inspired homogeneous catalysts which account for over 15% of all industrial catalytic processes and enable key catalytic transformations such as for pharmaceuticals, fine chemicals, and energy applications.25–32 Recent studies have revealed the promise of data-driven quantum chemical methods to understand structure–function relations in TMCs.33–38 Availability of structure–property data from QM calculations and/or experiments is central to the success of data-driven chemical approaches. SPDBs of homogeneous catalysts are currently not available.31 SPDBs with a dense representation of the chemical space of catalytic scaffolds can help discover design principles leading to the development of sustainable catalytic systems for various applications.31,39–44 Representations of the molecular structure is of high importance in SPDBs. Several approaches have been developed in this regard recently. For organic molecules string based SMILES representation is a popular and effective approach to encode the molecular structure.45,46 Generally SMILES encoding does not work well for TMCs and generation of 3D geometries using SMILES is an active research area.47,48
Low dimensional encoding of molecular representations of TMCs, while certainly desirable for ML applications, co-exists with the need to know the 3D geometry due to high structural sensitivity in catalysis. Therefore, automated approaches to rapidly generate accurate 3D molecular representations are also needed. Some automated tools have recently been developed to generate molecular geometries of TMCs, such as MolSimplify, Aarontools, stk and Molassembler.35,49–55 Although they are all open-source and pythonic, each have their own advantages and disadvantages. In Aarontools, substitute.py offers a similar functionality to ChemSpaX. However, the added substituents are only optimized by minimizing the Lennard-Jones (LJ) energy. In ChemSpaX we use a force-field based approach, which is more extensive compared to minimizing the LJ energy. The stk package is topology based and each structure needs to be built from the ground up. To our best knowledge, the post-functionalization of an already existing scaffold has not been implemented. Additionally, in their MetalComplex topology graphs, stk currently only handles mono- and bidentate coordination geometries, which limits its general applicability. In Molsimplify, it should be possible to implement automated functionalization using the ‘ligand decoration’ or ‘custom core’ functionality when building a structure as presented in their tutorials.56 However, high-throughput functionalization of an already existing scaffold in Python would require a new workflow using the functions contained in decoration_manager.py. While these tools represent a significant progress in automated rapid generation and modification of 3D molecular geometries, we sought to develop an easy-to-use tool which can quickly create reasonably accurate molecular geometries in the local chemical space of a given molecular scaffold.
In this manuscript we present ChemSpaX, a Python-based workflow that can be used for automated exploration of the chemical space of molecules. The exploration is done by automated placement of substituents on a given molecular scaffold while maintaining the quality of the initial scaffold. If a particular complex is known to be catalytically active, the 3D coordinates of this complex can be used as a starting point via ChemSpaX for exploration in the neighbourhood of its chemical space. The user has full control of the placement of substituent groups and can guide the exploration of the local chemical space. A general overview of the approach used in ChemSpaX is given in Fig. 1.
The computational methods employed in this manuscript are presented in the next section. A description of the code implementation to develop ChemSpaX follows. Subsequently, representative applications of ChemSpaX are presented. First, we applied ChemSpaX to generate a database of ∼1100 functionalized Cobalt Porphyrin (referred to as ‘Co porphyrin’ in the rest of this manuscript) complexes. Co porphyrins exist as stable metalloradicals and are used to catalyze carbene and nitrene transfer reactions.57–60 It has been shown that the quality of geometries obtained at the GFN2-xTB level of optimization are reasonably accurate compared to DFT.61–66 We therefore use the generated database to investigate if the quality of geometries generated by ChemSpaX is reasonably close to GFN2-xTB optimized geometries and to investigate the propagation of errors‡ upon creation of larger geometries. Additionally, a comparison of HOMO–LUMO gaps calculated by GFN2-xTB and DFT is made.
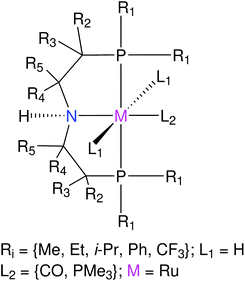
Next representative applications involve Ru and Mn catalysts based on pincer ligands. Pincer ligands have emerged as versatile ligand platforms enabling a plethora of catalytic reactions.67–70 The functionalization of a RuPNP pincer complex derived from the commercially available Ru-MACHO is described.28 TMCs based on the MACHO ligand framework have shown versatile activity in catalyzed (de)hydrogenation reactions.71–76 Analyzing the chemical space of the Ru-MACHO catalytic scaffold can be a valuable asset for multiple applications. Next, the functionalization of Mn–pincer complexes as potential (de)hydrogenation catalysts is studied.61 With this application the chemical space of an earth-abundant alternative to RuPNP is explored. Manganese is known to be a cheap, abundant and biocompatible alternative to precious-metal catalysts.73,77–79 The quality of geometries generated by ChemSpaX is compared against higher-level DFT and GFN2-xTB methods.
Finally, the functionalization of a bipyridyl functionalized cobalt-porphyrin trapped in a M2L4 type cage complex (referred to as ‘M2L4 cage’ in the rest of this manuscript) is presented. This cage complex confines a Co porphyrin complex, which can lead to changed catalytic properties.60,80,81 The M2L4 cage is a challenging and cumbersome scaffold to functionalize manually. The quality of ChemSpaX generated M2L4 cage geometries is compared against semi-empirical and force-field based xTB optimization methods. This case shows how ChemSpaX can be used to functionalize diverse and challenging molecular scaffolds. We note here that while all our representative examples are TMC focused, ChemSpaX can be applied to other molecular scaffolds that do not necessarily contain a TM center as well.
2 Computational methods
2.1 Open Babel
Conversions between MDL Molfile and XYZ format were done using Open Babel.82,83 Open Babel was also used to perform Generalized Amber Force Field (GAFF), and the Universal Force Field (UFF) optimizations.84,852.2 Semiempirical tight-binding
Grimme lab's xTB package (version 6.3.3) was used for semi-empirical tight-binding calculations.86 The GFN2-xTB, and GFN-FF methods were used for geometry optimization.87–90 The GFNn-xTB methods are quantum chemistry based semiempirical methods which extend the original density functional tight binding model. GFN-FF is a nonelectronic, force-field version of the GFN approach. The M2L4 cage geometries were optimized using GFN2-xTB and GFN-FF. The GBSA solvation method as implemented in xTB was used with THF as solvent for most optimizations to implicitly account for solvent effects.91,92 Thermochemical parameters such as the Gibbs free energy were computed using the hessian matrix calculations. These GFNn (n = 2, FF) methods are denoted as GFNn-xTB(THF) or GFNn-xTB(GAS) depending on whether GBSA solvation was used.2.3 Density functional theory
The catalysts are denoted as M-L where M represents the metal center and L the ligand. Reactive adsorption of a H-X species (X = H, Br, OH, i-PrO) over M-L leads to the formation of M(X)-L(H) species. The thermodynamic stability of the M(X)-L(H) was estimated by computing the Gibbs free energy and total energy change under standard conditions upon addition of the H-X moiety.
| H-X + M-L → M(X)-L(H) | (1) |
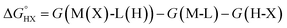 | (2) |
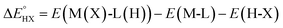 | (3) |
2.4 Root-mean-square deviation of atomic positions (RMSD)
The RMSD is used to compare two molecular structures. In this approach, the minimal difference between the positions of the same atom on both molecular structures is used. The cartesian heavy-atom (all elements except H) root-mean-square deviation (hRMSD) is an often used metric to compare molecular geometries produced from different methods.86 The RMSDs and hRMSDs were calculated using a Python program which uses the Kabsch or Quaternion algorithm to align the two molecular structures and calculate the minimum (h)RMSD over all possible alignments.105–107 If for example the two molecules p and q with n points (atoms) are compared, the RMSD is defined as: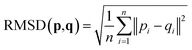 | (4) |
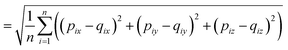 | (5) |
2.5 Machine learning methods
For the Mn–pincers, automated ML using the TPOT library in Python was applied to perform ML assisted HOMO–LUMO gap prediction.108–110 TPOT allows for optimization of machine learning pipelines using genetic programming. The molecular structure of each functionalized complex was represented as a Coulomb matrix generated using the qmlcode package.111 We used the generate_coulomb_matrix functionality of the qmlcode package with parameters size = 200 and sorting = “row-norm”. We used the GPU version of TPOT to search for a ML model using the coulomb matrix representation of the FF geometries. The ML pipeline from the first generation of TPOT run resulted in an XGBRegressor based ML model. The model with the related hyperparameters is provided in the ESI (see S12).† XGBRegressor uses the extreme gradient boosting algorithm which includes an ensemble of ML algorithms constructed via decision tree models. This ML model was used to learn the HOMO–LUMO gap for both FF and DFT geometries using the same hyperparameters and using the Coulomb matrix representation as a descriptor. The Pearson correlation coefficient (R2_score) was used as a metric for the optimization of the ML model. The dataset was split into the training and test sets (75–25 split). The ML model was trained on the training set and its performance was tested on a test set, which it had not seen before.3 Code implementation
An overview of the workflow of ChemSpaX is shown in Fig. 2. The user has to supply: a molecule that needs to be functionalized (skeleton), which sites on the skeleton should be functionalized (functionalization_list) and what substituent should be placed on the supplied site (substituent). The functionalization_list can contain several functionalizations. Each functionalization is an ordered pair of indices [b, a]. Here, a is the index of the atom bonded to the scaffold, and b corresponds to the atom which is replaced upon functionalization. This corresponds to indices b = 2 and a = 20 in Fig. 2. Substituents can be chosen from a pre-made database shipped with ChemSpaX or users can create new substituents in XYZ or MDL Molfile format.112 Information for the correct placement of a substituent is kept in a CSV file. The CSV file stores: (1) coordinates of the central atom of the substituent group which coordinates directly to the sites defined in the functionalization_list. (2) Coordinates of the centroid vector. A centroid vector, for a tetrahedral substituent such as CH3 is the vector connecting the central atom (C) to the centroid of the triangle formed by the three edges (hydrogens). For a planar substituent such as NH2 the centroid vector connects the center of the line joining the two hydrogen atoms to N (central atom).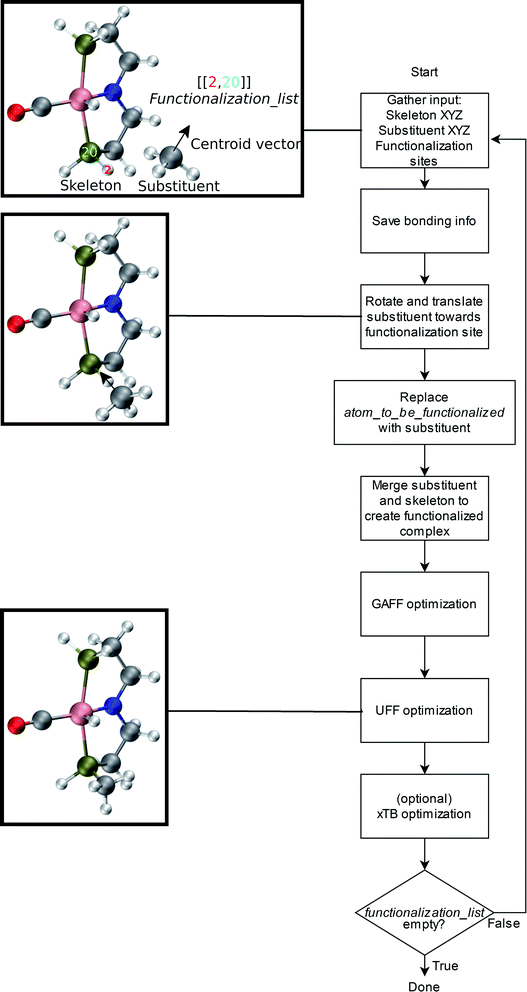 | ||
| Fig. 2 Overall workflow of ChemSpaX. (1) The user supplies the XYZ coordinates or MDL Molfile of a molecular skeleton, functionalization_list, and substituents. The atom_to_be_functionalized (index 2) and bonded_atom (index 20) are indicated in the skeleton's XYZ or MDL Molfile. (2) If XYZ files are supplied, they are converted to MDL Molfiles using Open Babel.113 If MDL Molfiles are already provided, they are used to conserve correct bonding info. This bonding info is used in step 5. (3) The central atom of the substituent group and the centroid vector are used to rotate and translate the substituent group towards the functionalization site. (4) atom_to_be_functionalized is replaced by the substituent group. (5) The skeleton and substituent group are merged in one MDL Molfile with correct bonding information from input MDL Molfiles. (6) GAFF optimization is done to prevent steric hindrance. (7) Additionally, UFF optimization is done to prevent GAFF related issues. (8) Optionally, xTB optimization can be used for further optimization of the full functionalized skeleton. (9) If there are no functionalizations left to do, the program exits and the functionalized skeleton is saved in MDL Molfile format. Else the functionalized skeleton will be used as input and the entire process repeats from step 1. | ||
The substituent group is first correctly oriented using rotation matrices and placed at a pre-defined distance from the substitution site. This process is described in more detail in the ESI.† Next, GAFF followed by UFF optimization methods from Open Babel were used to selectively optimize the newly placed substituent via a constrained optimization protocol while keeping the original molecular skeleton frozen.82,83 This combination of GAFF and UFF was found by trial-and-error (see ESI†). The correction in orientation of the substituent group prior to FF optimizations is needed to ensure a reasonable input geometry. The FF optimizations are based on MDL molfiles which contain the connectivity information between different atoms. When new substituents are placed the connectivity information is carefully updated to ensure that only desired connections are present. FF optimization using the MDL molfiles as input rectifies the geometry and removes any physical overlap between different atoms/functional groups. Optionally, an xTB optimization of the whole functionalized skeleton (including the new substituent) can be done.
It is recommended to use a DFT optimized geometry as input skeleton since the FF optimization only influences the newly placed functional group. This choice helps keep the core of the geometry as close to its DFT optimized input structure as possible upon serial functionalization, while preventing steric hindrance from newly placed substituents cheaply via force-field optimizations. ChemSpaX uses FF optimizations on newly placed substituent groups in each iteration. Therefore we name geometries generated directly by ChemSpaX as “FF geometries”.
4 Results and discussion
4.1 Co-porphyrin
Porphyrins are widely investigated, for example, for their applications in biocatalysis, organic photovoltaics, molecular wires and many more applications.2,114–116 This wide variety of applications has been enabled by the design and synthesis of structurally diverse porphyrins.2 PF has been widely used to tune the electronic and chemical properties of porphyrins, where functional groups and substituents are introduced after the construction of the porphyrin macrocycle. However, experimental exploration of the chemical space of porphyrins is limited by synthetic and economic feasibility. This is where computer-aided molecular design tools can be helpful.Apart from the chemical application perspective, investigating the functionalization of porphyrins is also of use for further refinement of our workflow. When functionalizing a structure as implemented in ChemSpaX (freezing the skeleton and performing FF optimization only on the newly placed substituents), errors can be introduced. Stretching or compression of the skeleton structure is not taken into account since the skeleton is frozen. By investigating a structure that is close to 2D instead of 3D, like porphyrins, the assessment of the introduced errors and their propagation through the workflow of ChemSpaX is simplified.
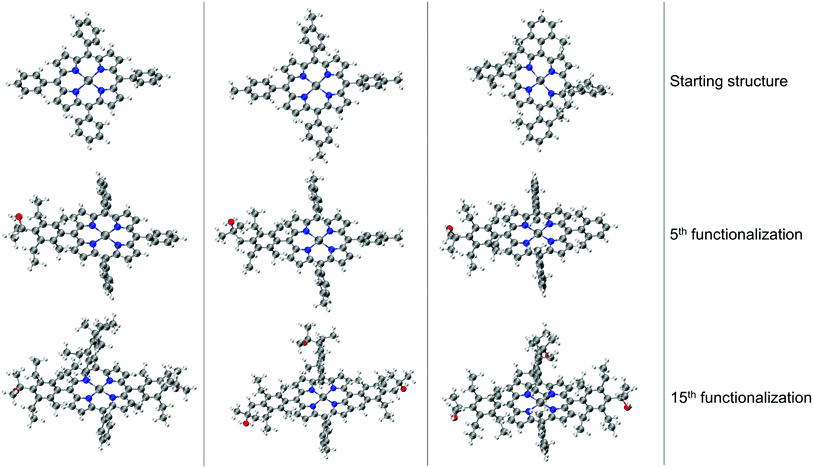
We performed functionalization of Co porphyrins following a serial functionalization strategy§ to create a database of ∼1100 complexes. Section 4.1.1 discusses the functionalization strategy. Subsequently, the propagation of errors introduced in geometries generated by ChemSpaX is investigated in Section 4.1.2.
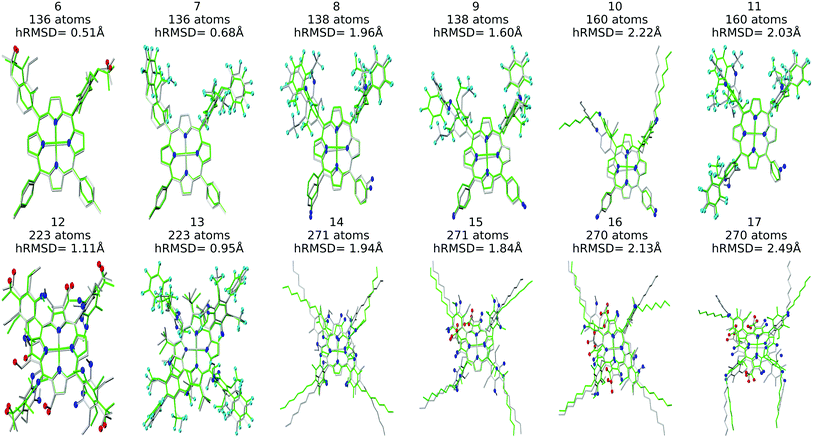
The resulting complexes are shown for 3 different skeletons in Fig. 4, where the skeleton, and Co-porphyrin complexes at the end of 5th, and 15th functionalization are shown in a column demonstrating the geometric complexity introduced upon functionalization.
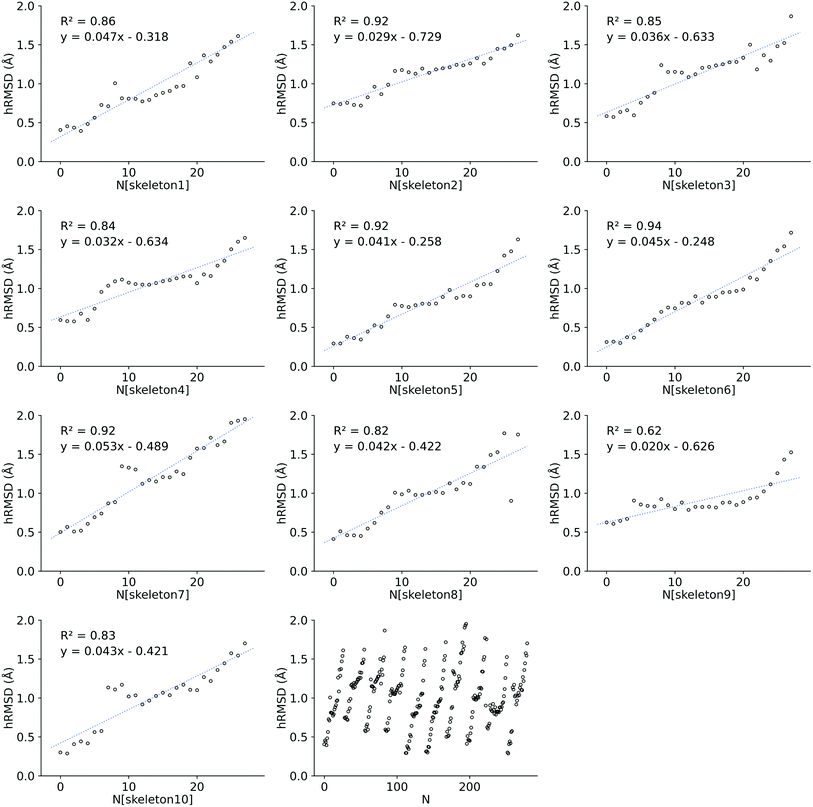
We also investigated the HOMO–LUMO gap of Co porphyrins within a serial functionalization run. DFT SP calculations on 28 GFN2-xTB optimized geometries and FF optimized geometries were done to calculate the HOMO–LUMO gap. These 28 geometries were obtained in a single serial functionalization run. The HOMO–LUMO gaps of GFN2-xTB optimized geometries and FF optimized geometries (see ESI†) showed a reasonable linear correlation (R2 = 0.68 RMSE = 0.10 eV). Consequently, in contrast to hRMSD, the difference in computed HOMO–LUMO gaps (GFN2-xTBHL-gap − FFHL-gap), did not show a growing trend within the functionalization run.
Structure overlay plots of the FF geometries (silver) and the GFN2-xTB optimized geometries (green) are shown in Fig. 6. The upper half of the figure shows structure overlay plots of complexes with <200 atoms while the lower half shows complexes with >200 atoms, and diverse hRMSDs. Large hRMSDs result from divergent orientation of long alkyl chain substituents, and fluorine containing groups.
4.2 Pincer complexes
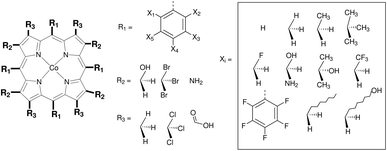
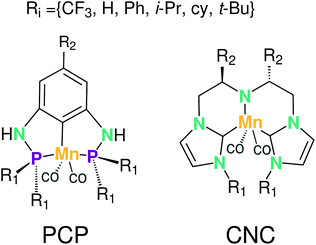
In this section the functionalization of the ligand scaffold of Ru and Mn based pincer complexes is described. In Section 4.2.1 the functionalization strategy for both types of pincer complexes is shown. Subsequently, the quality of geometries generated by ChemSpaX is compared to higher level methods in Section 4.2.2. Prediction of DFT computed HOMO–LUMO gap using a machine learning approach is presented in Section 4.2.3.Krieger and co-workers61 used an “under development” version of ChemSpaX to generate a database of 1225 Mn complexes based on five representative ligand scaffolds namely PNP-(bis(3-phosphaneylpropyl)amine)-¶, SNS (azanediylbis(ethane-1-thiol)), CNC (bis(2-(1H-3λ4-imidazol-3-yl)ethyl)amine), PNN (N1-(2-phosphaneylethyl)ethane-1,2-diamine), and PCP (N1,N3-bis(phosphaneyl)benzene-1,3-diamine).117–123 Out of these 1225 geometries, we chose 365 geometries containing the PCP and CNC ligand backbones for full DFT based optimization using BP86(GAS). This dataset of 365 complexes will be discussed further.
The functionalization strategy for PCP and CNC ligand based complexes is shown in Fig. 8. Functionalizations were performed symmetrically keeping all four R1 sites the same. Similarly both R2 sites (only 1 in case of PCP backbone) were functionalized with the same groups. However, R1 and R2 were not constrained to be the same.
| ΔΔEFF = ΔEDFT − ΔEFF//DFT-SP | (6) |
| ΔΔEGFN2-xTB = ΔEDFT − ΔEGFN2-xTB//DFT-SP | (7) |
Such a comparison allows us to estimate the range of error caused by the direct use of FF geometries by skipping computationally expensive DFT optimizations, for example in high-throughput screening (HTS) workflows. Geometries were also assessed along the spatial dimension where we computed the RMSD between FF-geometries against GFN2-xTB, and DFT optimized geometries.
For RuPNP complexes we chose the hydrogenation reaction (M-L + H2 → M(H)-L(H)) to investigate ΔΔEFF and ΔΔEGFN2-xTB. The corresponding mean (μ) and standard deviation (σ2) were also computed.|| We found μ(ΔΔEFF) = 7.20 ± 4.57 kcal mol−1; and μ(ΔΔEGFN2-xTB) = 4.77 ± 2.57 kcal mol−1. This indicates a qualitatively good agreement between the GFN2-xTB optimized structures and the structures generated by ChemSpaX.
For the Mn–pincer complexes we investigated reactive adsorption of H-X species (M-L + H-X → M(X)-L(H); X = H, Br, i-PrO, and OH) with the reaction energetics characterized by ΔE, and the respective FF geometries by ΔΔEFF respectively. FF geometries of Mn–PCP complexes were found to have the lowest ΔΔEFF in general, followed by the Mn–CNC complexes. For the formation of M(X)-L(H) adducts, ΔΔEFF were found to be lowest for the reactive adsorption of HBr and H2, and highest for i-PrOH and H2O. The reason for worse performance of i-PrOH and H2O can be attributed to the observed recombination of O–H bond in many geometries during DFT based optimization leading to M(H-X)-L type complexes, or non-adsorbed H-X adducts. We further observed that ΔΔEFF(HBr) and ΔΔEFF(H2) correlated well (Pearson correlation coefficient (R) = +0.87) opening up possibilities to reduce computational effort in screening through these intermediates. Krieger and co-workers had reported a similar albeit stronger correlation (R = 0.95) between ΔGHBr and ΔGH2.61 A detailed discussion of the effect of functionalization of the ligand scaffold on the ΔΔEFF values is presented in the ESI.†
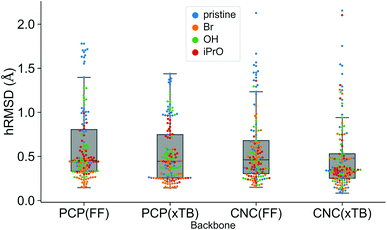
The quality of FF geometries along the spatial dimension was analyzed via hRMSD between the geometries produced by DFT or GFN2-xTB based optimizations.86 For the RuPNP complexes, both FF (0.67 ± 0.30 Å) and GFN2-xTB (0.41 ± 0.34 Å) structures had a similar average hRMSD when compared to DFT structures. A selection of the RuPNP geometries are visualized using structure overlay plots in Fig. 9. The comparisons in these structure overlay plots is done as follows: (a) the FF optimized structure (silver), generated by ChemSpaX, is compared to a DFT optimized structure (green) and (b) a GFN2-xTB optimized structure (silver) is compared to a DFT optimized structure (green).
A comparison using the hRMSD was done in a similar manner for the Mn–pincer complexes. It was again observed that both FF (0.60 ± 0.40 Å) and GFN2-xTB (0.51 ± 0.36 Å) structures had a similar average hRMSD when compared to DFT structures, albeit with moderately high standard deviations. It should be noted here that the GFN2-xTB optimizations were performed in the solvated phase (GBSA(THF)) while the DFT optimizations are in the gas phase. The hRMSD analysis was performed for PCP and CNC ligand backbones (see Fig. 10). For the CNC backbones it was observed that functionalization with electron donating substituents on the R1 site resulted in a higher hRMSD. For the PCP backbone it was observed that functionalization with t-Bu on the R1 site specifically gave a larger hRMSD. This observation is expected to have the following underlying causes: (1) electron donating groups like t-Bu are bulkier, have more number of atoms and a complex structure which increases the chance of accumulating an error (vide infra) (2) electron donating groups affect the electronic density in the entire complex and may elicit shearing of the skeleton which is kept frozen in FF calculations. When optimized with DFT, the skeleton would relax and this would lead to a higher hRMSD.
We would like to note here that all the FF geometries discussed above were generated using a serial functionalization scheme. For each complex a skeleton was chosen, functionalization sites were defined, and functional groups were placed on the skeleton one after another without any intermediate optimizations at a higher level of theory. Since the skeleton is not relaxed it is likely to accumulate errors (higher hRMSD; higher ΔΔEFF) as the size complexity increases. The hRMSD and ΔΔEFF values would be lower if intermediate optimizations are performed (vide supra).
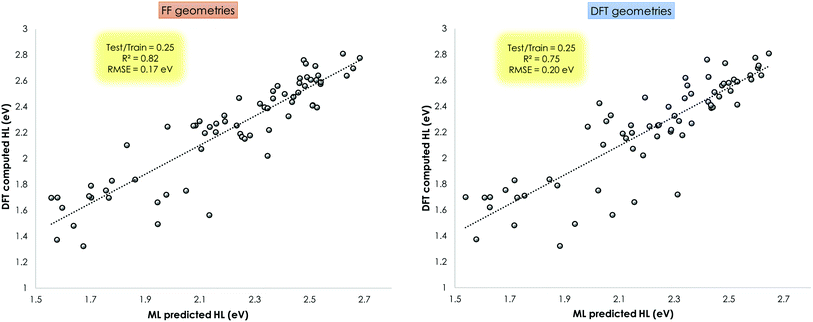
This ML assisted prediction of the HOMO–LUMO gap was done for the Mn–pincers with PCP and CNC ligands. The results are shown in Fig. 11. It is shown that for this small dataset, the ChemSpaX generated FF geometries can already give reasonable predictive power to a ML model (R2 = 0.82 RMSE = 0.17 eV) which is close to results obtained using DFT optimized geometries (R2 = 0.75 RMSE = 0.20 eV). It is noteworthy that the HOMO–LUMO gap computed on FF geometries weakly correlate with the HOMO–LUMO gap computed on DFT optimized geometries (R2 = 0.36; see ESI†). The linear regression fit results in a rather high RMSE of 0.6 eV to predict the HOMO–LUMO gap of DFT optimized geometries using the HOMO–LUMO gap computed for FF geometries. The ML model which uses the FF geometries as input, avoids additional DFT calculations, and provides a reasonably accurate prediction of HOMO–LUMO gaps, therefore directly reflects the usefulness of FF geometries (Fig. 11).
4.3 M2L4 cage
The versatility of ChemSpaX is shown by the automated placement of substituents without introducing steric hindrance on a geometry that is more complex. An M2L4 cage was functionalized at 16 sites with various substituent groups. The results are shown in Fig. 12. This serial functionalization yielded 16 structures and these were further optimized using GFN-FF and GFN2-xTB(GAS). The hRMSDs between FF geometries and those generated using the GFN-FF and GFN2-xTB optimization methods were calculated. The statistics shown for each optimization method in Table 1 revealed that the ChemSpaX generated FF geometries are closer to the GFN2-xTB optimized geometries compared to GFN-FF optimized geometries.| GFN-FF vs. GFN2-xTB | FF vs. GFN2-xTB | FF vs. GFN-FF | |
|---|---|---|---|
| μ | 2.54 Å | 2.14 Å | 0.83 Å |
| σ 2 | 0.34 Å | 0.25 Å | 0.26 Å |
| Max. hRMSD | 3.18 Å | 2.46 Å | 1.37 Å |
4.4 Remarks regarding ChemSpaX
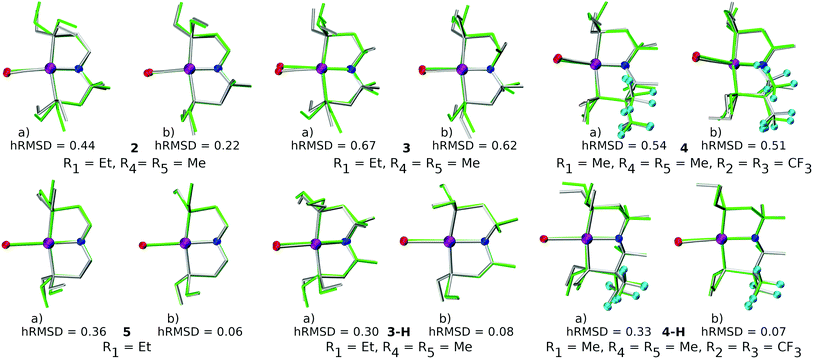
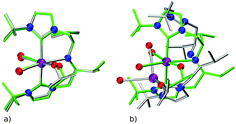
There are two key points of discussion related to the current work. First, it should be noted that (at least some of the) ChemSpaX generated geometries should be checked during serial functionalization. Such a check could be done by manual inspection of randomly selected geometries, or could be performed via descriptors such as a RMSD of the skeleton, and selected bond length and angle. Such checks are crucial since functionalization of the skeleton can significantly alter the geometry in some cases, for example, via ligand hemi-lability. In an early application of ChemSpaX, Krieger and co-workers found that some of the Mn–pincer complexes with a PNN backbone became hemi-labile upon functionalization.61 Such hemilability was only discovered after GFN2-xTB/DFT based geometry optimizations were performed on ChemSpaX generated geometries. This resulted in high hRMSDs and high ΔΔEFF. Note that Mn–PNN complexes also proved challenging for GFN2-xTB calculations and high hRSMDs and ΔΔEGFN2-xTB values were found. Structure overlay plots of a selected case of Mn–PNN demonstrating the challenges associated with hemi-labile PNN ligand are shown in Fig. 13. The comparison is again done as follows: (a) the FF optimized structure (silver), generated by ChemSpaX is compared to a DFT optimized structure (green) and (b) a GFN2-xTB optimized structure (silver) is compared to a DFT optimized structure (green). These complexes, before being subject to DFT based geometry optimizations, were pre-optimized using GFN2-xTB which yielded hemi-labile geometries, and biased the DFT optimizations to also converge to hemi-labile structures. Despite larger hRMSD values, it is noteworthy that majority of FF geometries still have hRMSD < 1 Å, and are overall lower than hRMSD values for the GFN2-xTB geometries (see ESI†).Another noteworthy point is that the purpose of ChemSpaX is to explore the local chemical space by placing functional groups on a given molecular scaffold. ChemSpaX is not designed for conformational search which can be important for exploration of the internal chemical space of a molecule. We recommend users to employ other software based solutions such as xTB's CREST simulations for this purpose.126–128
5 Summary and conclusions
In this work, an automated Python-based workflow for the exploration of local chemical space is presented. ChemSpaX can place substituents on specific sites of diverse molecular scaffolds based on initial user input and uses FF optimization to optimize newly placed substituents. Use cases were shown by using a data-augmented approach which utilized fast GFN2-xTB optimizations to compare structures generated by ChemSpaX. For selected use cases a comparison was also done against DFT optimized structures. Descriptors such as the HOMO–LUMO gap that can be used for HTS applications were studied in more detail for some of the presented use cases. Analysis of functionalized Co porphyrins generated by ChemSpaX showed that the hRMSD increased nearly linearly with the number of atoms in serial functionalization runs on a given skeleton. This observation paves the way for devising a strategy to optimally employ higher-level geometry optimizations in intermediate steps. For the pincer complexes the quality of geometries generated by ChemSpaX was assessed along the energy (ΔΔE) and spatial (hRMSD) dimensions. Generally FF geometries were found to be similar in quality compared to GFN2-xTB optimized geometries based on the hRMSDs, and ΔΔE. It was discovered that ChemSpaX generated FF geometries can be used to train a ML model which can predict the DFT calculated HOMO–LUMO gap with reasonable accuracy, which can be useful in accelerated property prediction and catalyst screening. Additionally, it has been demonstrated that diverse molecular scaffolds can be functionalized using ChemSpaX.To conclude, ChemSpaX can be used to generate satisfactory 3D geometric representations in the local chemical space of a given molecular scaffold, particularly including TM complexes. The generated structures, in conjunction with quantum chemical and statistical methods, can be used to generate structure–property databases enabling data-driven chemical design and discovery. We are working to further improve ChemSpaX along diverse research lines. Improved force-field methods can definitely help improve the accuracy of ChemSpaX. A data-informed approach to estimate the hRMSD based on the identity of the skeleton molecule and functional groups placed can improve the predictive capabilities for screening applications. Parallelization of the code for placing functional groups is work in progress. Additionally, we are working on implementing a more flexible approach where the user can choose the frequency of intermediate optimizations with a higher-level method based on a predicted hRMSD threshold, and also get recommendations about optimal strategies which balance speed and accuracy.
ChemSpaX is aimed at accelerating chemical space exploration and we hope that it will bolster and democratize the efforts of the catalysis and molecular modelling communities towards data-driven discovery. ChemSpaX is free, open-source and will soon be available with an introductory Google collaboratory notebook which can be immediately used by researchers.
Data availability
The ChemSpaX workflow is publicly available on our Github organization page: EPiCs-group (https://github.com/EPiCs-group). In addition to this manuscript, ESI† and all used datasets can be found via: DOI: 10.4121/14766345.• full_datasets.zip contains datasets per investigated complex in Excel workbook format.
• geometry_files.zip contains geometry files for all structures in MDL Molfiles or XYZ format.
• Coulomb_matrix_HL_gap_Mn_pincers.zip contains names, Coulomb matrix representations, and DFT computed HOMO–LUMO gaps of Mn–CNC and Mn–PCP complexes based on FF geometries, and DFT optimized geometries.
Author contributions
The code for ChemSpaX was written by A. V. K. and V. S. Generation of functionalized structures, the compilation of datasets, and execution and analysis of DFT & xTB calculations was performed by A. V. K. under supervision of V. S. Machine learning models were developed by V. S. E. A. P. and V. S. conceived the project. E. A. P. played an advisory role and directed the project. All the authors discussed the results and wrote the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
V. S. acknowledges the ARC-CBBC project 2016.008 for funding. E. A. P. acknowledges the financial support from the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Programme (grant agreement no. 725686). This work was sponsored by NWO Domain Science for the use of the national computer facilities, and made use of the resources and expertise offered by the SURF Open Innovation Lab. We acknowledge that the results of this research have been partially achieved using the DECI resource, Kay, based in Ireland at ICHEC with support from PRACE under the DECI16 call. The authors thank the PetaChem team for giving access to the TeraChem software package.References
- C. Y. Cheng, J. E. Campbell and G. M. Day, Evolutionary chemical space exploration for functional materials: computational organic semiconductor discovery, Chem. Sci., 2020, 11, 4922–4933, 10.1039/D0SC00554A , https://rsc.66557.net/en/content/articlehtml/2020/sc/d0sc00554a, https://rsc.66557.net/en/content/articlelanding/2020/sc/d0sc00554a.
- S. Hiroto, Y. Miyake and H. Shinokubo, Synthesis and Functionalization of Porphyrins through Organometallic Methodologies, Chem. Rev., 2017, 117(4), 2910–3043, DOI:10.1021/acs.chemrev.6b00427.
- M. Renom-Carrasco and L. Lefort, Ligand libraries for high throughput screening of homogeneous catalysts, Chem. Soc. Rev., 2018, 47, 5038–5060, 10.1039/C7CS00844A , https://rsc.66557.net/en/content/articlehtml/2018/cs/c7cs00844a, https://rsc.66557.net/en/content/articlelanding/2018/cs/c7cs00844a.
- J. H. Van Drie, Computer-aided drug design: the next 20 years, J. Comput.-Aided Mol. Des., 2007, 21(10), 591–601, DOI:10.1007/s10822-007-9142-y.
- S. Gregory, S. Kothiwale, J. Meiler and E. W. Lowe Jr, Computational methods in drug discovery, Pharmacol. Rev., 2013, 66(1), 334–395, DOI:10.1124/pr.112.007336 , https://pubmed.ncbi.nlm.nih.gov/24381236, https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3880464/.
- D. E. Clark, What has computer-aided molecular design ever done for drug discovery?, Expert Opin. Drug Discovery, 2006, 1(2), 103–110, DOI:10.1517/17460441.1.2.103.
- D. E. Clark, What has virtual screening ever done for drug discovery?, Expert Opin. Drug Discovery, 2008, 3(8), 841–851, DOI:10.1517/17460441.3.8.841.
- A. Jain, Y. Shin and K. A. Persson, Computational predictions of energy materials using density functional theory, Nat. Rev. Mater., 2016, 1(1), 15004, DOI:10.1038/natrevmats.2015.4.
- L. Cheng, R. S. Assary, X. Qu, A. Jain, S. P. Ong, N. N. Rajput, K. Persson and L. A. Curtiss, Accelerating Electrolyte Discovery for Energy Storage with High-Throughput Screening, J. Phys. Chem. Lett., 2015, 6(2), 283–291, DOI:10.1021/jz502319n DOI:10.1021/jz502319n.
- H. B. Dizaji and H. Hosseini, A review of material screening in pure and mixed-metal oxide thermochemical energy storage (TCES) systems for concentrated solar power (CSP) applications, Renewable Sustainable Energy Rev., 2018, 98, 9–26, DOI:10.1016/j.rser.2018.09.004 , http://www.sciencedirect.com/science/article/pii/S136403211830652X.
- J. Hachmann, R. Olivares-Amaya, S. Atahan-Evrenk, C. Amador-Bedolla, R. S. Sánchez-Carrera, A. Gold-Parker, L. Vogt, A. M. Brockway and A. Aspuru-Guzik, The Harvard Clean Energy Project: Large-Scale Computational Screening and Design of Organic Photovoltaics on the World Community Grid, J. Phys. Chem. Lett., 2011, 2(17), 2241–2251, DOI:10.1021/jz200866s.
- N. Fey, Lost in chemical space? maps to support organometallic catalysis, Chem. Cent. J., 2015, 9(1), 38, DOI:10.1186/s13065-015-0104-5.
- P. Kirkpatrick and C. Ellis, Chemical space, Nature, 2004, 432(7019), 823, DOI:10.1038/432823a.
- F. I. Saldívar-González, B. A. Pilón-Jiménez and J. L. Medina-Franco, Chemical space of naturally occurring compounds, Phys. Sci. Rev., 2018, 4(5) DOI:10.1515/psr-2018-0103 , https://www.degruyter.com/document/doi/10.1515/psr-2018-0103/html.
- C. Zhou, W. Grumbles, and T. Cundari, Using Machine Learning to Predict the pKa of C–H Bonds. Relevance to Catalytic Methane Functionalization, 2020, https://chemrxiv.org/articles/preprint/Using_Machine_Learning_to_Predict_the_pKa_of_C_H_Bonds_Relevance_to_Catalytic_Methane_Functionalization/12646772, https://chemrxiv.org/ndownloader/files/23820425 Search PubMed.
- O. A. von Lilienfeld, K.-R. Müller and T. Alexandre, Exploring chemical compound space with quantum-based machine learning, Nat. Rev. Chem., 2020, 4(7), 347–358, DOI:10.1038/s41570-020-0189-9.
- T. Fink and J.-L. Reymond, Virtual Exploration of the Chemical Universe up to 11 Atoms of C, N, O, F: Assembly of 26.4 Million Structures (110.9 Million Stereoisomers) and Analysis for New Ring Systems, Stereochemistry, Physicochemical Properties, Compound Classes, and Drug Discovery, J. Chem. Inf. Model., 2007, 47(2), 342–353, DOI:10.1021/ci600423u.
- L. C. Blum and J.-L. Reymond, 970 Million Druglike Small Molecules for Virtual Screening in the Chemical Universe Database GDB-13, J. Am. Chem. Soc., 2009, 131(25), 8732–8733, DOI:10.1021/ja902302h.
- L. Ruddigkeit, R. van Deursen, L. C. Blum and J.-L. Reymond, Enumeration of 166 Billion Organic Small Molecules in the Chemical Universe Database GDB-17, J. Chem. Inf. Model., 2012, 52(11), 2864–2875, DOI:10.1021/ci300415d.
- T. Sterling and J. J. Irwin, ZINC 15 – Ligand Discovery for Everyone, J. Chem. Inf. Model., 2015, 55(11), 2324–2337, DOI:10.1021/acs.jcim.5b00559.
- J. Arús-Pous, T. Blaschke, S. Ulander, J.-L. Reymond, H. Chen and O. Engkvist, Exploring the GDB-13 chemical space using deep generative models, J. Cheminf., 2019, 11(1), 20, DOI:10.1186/s13321-019-0341-z.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, T. Alexandre and K.-R. Müller, Machine learning force fields, Chem. Rev., 2021, 121(16), 10142–10186, DOI:10.1021/acs.chemrev.0c01111.
- F. Begnini, V. Poongavanam, B. Over, M. Castaldo, S. Geschwindner, P. Johansson, M. Tyagi, C. Tyrchan, L. Wissler, S. Peter, S. Schiesser and K. Jan, Mining natural products for macrocycles to drug difficult targets, J. Med. Chem., 2020, 64, 1054–1072, DOI:10.1021/acs.jmedchem.0c01569.
- J. Adrian, B. Sanchez-Lengeling, H. Ren, R. Harman and A. Aspuru-Guzik, A Mixed Quantum Chemistry/Machine Learning Approach for the Fast and Accurate Prediction of Biochemical Redox Potentials and Its Large-Scale Application to 315000 Redox Reactions, ACS Cent. Sci., 2019, 5(7), 1199–1210, DOI:10.1021/acscentsci.9b00297.
- R. A. Fernandes, A. K. Jha and P. Kumar., Recent advances in wacker oxidation: From conventional to modern variants and applications, Catal.: Sci. Technol., 2020, 10, 7448–7470, 10.1039/d0cy01820a , http://ether.chem.iitb.ac.in/rfernand/.
- M. L. Crawley and B. M. Trost, Applications of Transition Metal Catalysis in Drug Discovery and Development: An Industrial Perspective, John Wiley and Sons, 2012, ISBN 9780470631324, DOI:10.1002/9781118309872, http://www.wiley.com/go/permission.
- W. Keim, Concepts for the Use of Transition Metals in Industrial Fine Chemical Synthesis, Wiley-VCH Verlag GmbH, 2008, DOI:10.1002/9783527619405.ch1b.
- W. Kuriyama, T. Matsumoto, O. Ogata, Y. Ino, K. Aoki, S. Tanaka, K. Ishida, T. Kobayashi, N. Sayo and T. Saito, Catalytic hydrogenation of esters. development of an efficient catalyst and processes for synthesising (r)-1,2-propanediol and 2-(l-menthoxy)ethanol, Org. Process Res. Dev., 2012, 16, 166–171, DOI:10.1021/op200234j , https://pubs.acs.org/sharingguidelines.
- B. L. Tran, S. I. Johnson, K. P. Brooks and S. Tom Autrey, Ethanol as a liquid organic hydrogen carrier for seasonal microgrid application: Catalysis, theory, and engineering feasibility, ACS Sustainable Chem. Eng., 2021, 9(20), 7130–7138, DOI:10.1021/acssuschemeng.1c01513.
- J. Hagen, Industrial Catalysis: A Practical Approach, Wiley-VCH Verlag GmbH & Co. KGaA, 2015, chapter Homogeneously Catalyzed Industrial Processes, pp. 47–80, DOI:10.1002/9783527684625.ch3.
- G. d. P. Gomes, R. Pollice and A. Aspuru-Guzik, Navigating through the Maze of Homogeneous Catalyst Design with Machine Learning, Trends Chem., 2021, 3(2), 96–110, DOI:10.1016/j.trechm.2020.12.006 , https://www.sciencedirect.com/science/article/pii/S2589597420303166.
- R. Franke, D. Selent and A. Börner, Applied hydroformylation, Chem. Rev., 2012, 112, 5675–5732, DOI:10.1021/cr3001803 , https://pubs.acs.org/sharingguidelines.
- S. Gugler, J. Paul Janet and H. J. Kulik, Enumeration of de novo inorganic complexes for chemical discovery and machine learning, Mol. Syst. Des. Eng., 2020, 5, 139–152, 10.1039/C9ME00069K.
- J. J. Henle, A. F. Zahrt, B. T. Rose, W. T. Darrow, Y. Wang and S. E. Denmark, Development of a computer-guided workflow for catalyst optimization. descriptor validation, subset selection, and training set analysis, J. Am. Chem. Soc., 2020, 142, 11578–11592, DOI:10.1021/jacs.0c04715.
- J. G. Sobez and M. Reiher, Molassembler: Molecular graph construction, modification, and conformer generation for inorganic and organic molecules, J. Chem. Inf. Model., 2020, 60, 3884–3900, DOI:10.1021/acs.jcim.0c00503.
- D. J. Durand and N. Fey, Building a toolbox for the analysis and prediction of ligand and catalyst effects in organometallic catalysis, Acc. Chem. Res., 2021, 54, 837–848, DOI:10.1021/acs.accounts.0c00807.
- D. Balcells and B. B. Skjelstad, Tmqm dataset - quantum geometries and properties of 86k transition metal complexes, J. Chem. Inf. Model., 2020, 60, 6135–6146, DOI:10.1021/acs.jcim.0c01041.
- F. J. De Zwart, B. Reus, A. Annechien, H. Laporte, V. Sinha and B. De Bruin, Metrical oxidation states of 1,4-diazadiene-derived ligands, Inorg. Chem., 2021, 60, 3274–3281, DOI:10.1021/acs.inorgchem.0c03685.
- A. I. Green, C. P. Tinworth, S. Warriner, N. Adam and N. Fey, Computational mapping of dirhodium(ii) catalysts, Chem.–Eur. J., 2021, 27(7), 2402–2409, DOI:10.1002/chem.202003801.
- P. Friederich, G. d. P. Gomes, R. De Bin, A. Aspuru-Guzik and D. Balcells, Machine learning dihydrogen activation in the chemical space surrounding vaska's complex, Chem. Sci., 2020, 11, 4584–4601, 10.1039/D0SC00445F.
- K. C. Harper, E. N. Bess and M. S. Sigman, Multidimensional steric parameters in the analysis of asymmetric catalytic reactions, Nat. Chem., 2012, 4, 366–374, DOI:10.1038/nchem.1297 , http://www.nature.com/naturechemistry.
- J. P. Reid, R. S. J. Proctor, M. S. Sigman and R. J. Phipps, Predictive multivariate linear regression analysis guides successful catalytic enantioselective minisci reactions of diazines, J. Am. Chem. Soc., 2019, 141, 19178–19185, DOI:10.1021/jacs.9b11658 , https://pubs.acs.org/sharingguidelines.
- C. B. Santiago, J. Y. Guo and M. S. Sigman, Predictive and mechanistic multivariate linear regression models for reaction development, Chem. Sci., 2018, 9, 2398–2412, 10.1039/c7sc04679k , https://rsc.66557.net/en/content/articlehtml/2018/sc/c7sc04679k, https://rsc.66557.net/en/content/articlelanding/2018/sc/c7sc04679k.
- J. P. Reid and M. S. Sigman, Holistic prediction of enantioselectivity in asymmetric catalysis, Nature, 2019, 571, 343–348, DOI:10.1038/s41586-019-1384-z.
- D. Weininger, Smiles, a chemical language and information system: 1: Introduction to methodology and encoding rules, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36, DOI:10.1021/ci00057a005.
- C. A. James, R. Apodaca, N. M. O'Boyle, A. Dalke, J. H. Van Drie, P. Ertl, G. R. Hutchison, G. Landrum, C. Morley, E. Willighagen, H. De winter, T. Vandermeersch, and J. May, OpenSMILES specification, 2016, http://opensmiles.org/opensmiles.html Search PubMed.
- J. Jan, xyz2mol: Convert Cartesian coordinates to one or more molecular graphs, 2020, https://github.com/jensengroup/xyz2mol Search PubMed.
- M. Krenn, F. Häse, A. K. Nigam, P. Friederich and A. Aspuru-Guzik, Self-referencing embedded strings (SELFIES): A 100% robust molecular string representation, Mach. Learn., 2020, 1(4), 45024, DOI:10.1088/2632-2153/aba947.
- E. I. Ioannidis, T. Z. H. Gani and H. J. Kulik, molSimplify: A toolkit for automating discovery in inorganic chemistry, J. Comput. Chem., 2016, 37(22), 2106–2117, DOI:10.1002/jcc.24437.
- J. P. Janet, F. Liu, A. Nandy, C. Duan, T. Yang, S. Lin and H. J. Kulik, Designing in the Face of Uncertainty: Exploiting Electronic Structure and Machine Learning Models for Discovery in Inorganic Chemistry, Inorg. Chem., 2019, 58(16), 10592–10606, DOI:10.1021/acs.inorgchem.9b00109.
- A. Nandy, C. Duan, J. Paul Janet, S. Gugler and H. J. Kulik, Strategies and Software for Machine Learning Accelerated Discovery in Transition Metal Chemistry, Ind. Eng. Chem. Res., 2018, 57(42), 13973–13986, DOI:10.1021/acs.iecr.8b04015.
- J. Paul Janet, T. Z. H. Gani, A. H. Steeves, E. I. Ioannidis and H. J. Kulik, Leveraging Cheminformatics Strategies for Inorganic Discovery: Application to Redox Potential Design, Ind. Eng. Chem. Res., 2017, 56(17), 4898–4910, DOI:10.1021/acs.iecr.7b00808.
- J. P. Janet, Q. Zhao, E. I. Ioannidis and H. J. Kulik, Density functional theory for modelling large molecular adsorbate–surface interactions: a mini-review and worked example, Mol. Simul., 2017, 43(5–6), 327–345, DOI:10.1080/08927022.2016.1258465.
- V. M. Ingman, A. J. Schaefer, L. R. Andreola and S. E. Wheeler, Qchasm: Quantum chemistry automation and structure manipulation, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 11(4), e1510, DOI:10.1002/wcms.1510.
- L. Turcani, A. Tarzia, F. T. Szczypiński and K. E. Jelfs, stk: An extendable python framework for automated molecular and supramolecular structure assembly and discovery, J. Chem. Phys., 2021, 154(21), 214102, DOI:10.1063/5.0049708.
- molsimplify tutorials, 2016, http://hjkgrp.mit.edu/Tutorials Search PubMed.
- M. Goswami, C. Rebreyend and B. de Bruin, Porphyrin Cobalt(III) “Nitrene Radical” Reactivity; Hydrogen Atom Transfer from Ortho-YH Substituents to the Nitrene Moiety of Cobalt-Bound Aryl Nitrene Intermediates (Y = O, NH), Molecules, 2016, 21(2), 242, DOI:10.3390/molecules21020242.
- M. P. Doyle and D. C. Forbes, Recent Advances in Asymmetric Catalytic Metal Carbene Transformations, Chem. Rev., 1998, 98(2), 911–936, DOI:10.1021/cr940066a.
- S. Fantauzzi, A. Caselli and E. Gallo, Nitrene transfer reactions mediated by metallo-porphyrin complexes, Dalton Trans., 2009,(28), 5434–5443, 10.1039/B902929J.
- M. Otte, P. F. Kuijpers, T. Oliver, I. Ivanović-Burmazović, J. N. H. Reek and B. de Bruin, Encapsulated Cobalt–Porphyrin as a Catalyst for Size-Selective Radical-type Cyclopropanation Reactions, Chem.–Eur. J., 2014, 20(17), 4880–4884, DOI:10.1002/chem.201400055.
- A. Krieger, V. Sinha, A. V. Kalikadien and E. A. Pidko, Metal-ligand cooperative activation of HX (X=H, Br, OR) bond on Mn based pincer complexes, Z. Anorg. Allg. Chem., 2021, 647(14), 1486–1494, DOI:10.1002/zaac.202100078.
- V. Sinha, J. J. Laan and E. A. Pidko, Accurate and rapid prediction of pka of transition metal complexes: semiempirical quantum chemistry with a data-augmented approach, Phys. Chem. Chem. Phys., 2021, 23, 2557–2567, 10.1039/D0CP05281G.
- M. Bursch, A. Hansen and S. Grimme, Fast and reasonable geometry optimization of lanthanoid complexes with an extended tight binding quantum chemical method, Inorg. Chem., 2017, 56, 12485–12491, DOI:10.1021/acs.inorgchem.7b01950.
- M. Bursch, H. Neugebauer and S. Grimme, Structure optimisation of large transition-metal complexes with extended tight-binding methods, Angew. Chem., Int. Ed., 2019, 58, 11078–11087, DOI:10.1002/anie.201904021.
- M. Bursch, A. Hansen, P. Pracht, J. T. Kohn and S. Grimme, Theoretical study on conformational energies of transition metal complexes, Phys. Chem. Chem. Phys., 2021, 23, 287–299, 10.1039/D0CP04696E.
- S. Spicher and S. Grimme, Efficient computation of free energy contributions for association reactions of large molecules, J. Phys. Chem. Lett., 2020, 11, 6606–6611, DOI:10.1021/acs.jpclett.0c01930.
- L. Piccirilli, D. L. J. Pinheiro and M. Nielsen, Recent progress with pincer transition metal catalysts for sustainability, Catalysts, 2020, 10, 773, DOI:10.3390/catal10070773 , http://www.mdpi.com/journal/catalysts.
- G. Parkin, Special issue on pincer ligands, Polyhedron, 2018, 143, 1, DOI:10.1016/j.poly.2018.02.019.
- L. Maser, L. Vondung and R. Langer, The abc in pincer chemistry – from amine- to borylene- and carbon-based pincer-ligands, Polyhedron, 2018, 143, 28–42, DOI:10.1016/j.poly.2017.09.009.
- M. A. W. Lawrence, K. A. Green, P. N. Nelson and S. C. Lorraine, Review: Pincer ligands—tunable, versatile and applicable, Polyhedron, 2018, 143, 11–27, DOI:10.1016/j.poly.2017.08.017.
- S. Padmanaban, G. H. Gunasekar and S. Yoon, Direct heterogenization of the ru-macho catalyst for the chemoselective hydrogenation of α, β-unsaturated carbonyl compounds, Inorg. Chem., 2021, 60, 6881–6888, DOI:10.1021/acs.inorgchem.0c03681.
- P. A. Dub and J. C. Gordon, The role of the metal-bound n–h functionality in noyori-type molecular catalysts, Nat. Rev. Chem., 2018, 2, 396–408, DOI:10.1038/s41570-018-0049-z , http://www.nature.com/natrevchem.
- G. A. Filonenko, R. Van Putten, E. J. M. Hensen and E. A. Pidko, Catalytic (de)hydrogenation promoted by non-precious metals-Co, Fe and Mn: Recent advances in an emerging field, Chem. Soc. Rev., 2018, 47, 1459–1483, 10.1039/c7cs00334j , https://rsc.66557.net/en/content/articlehtml/2018/cs/c7cs00334j, https://rsc.66557.net/en/content/articlelanding/2018/cs/c7cs00334j.
- J. R. Cabrero-Antonino, R. Adam, V. Papa and M. Beller, Homogeneous and heterogeneous catalytic reduction of amides and related compounds using molecular hydrogen, Nat. Commun., 2020, 11, 1–18, DOI:10.1038/s41467-020-17588-5.
- J. Pritchard, G. A. Filonenko, R. Van Putten, E. J. M. Hensen and E. A. Pidko, Heterogeneous and homogeneous catalysis for the hydrogenation of carboxylic acid derivatives: History, advances and future directions, Chem. Soc. Rev., 2015, 44, 3808–3833, 10.1039/c5cs00038f , http://www.rsc.org/csr.
- R. v. Putten, T. Wissink, T. Swinkels and E. A. Pidko, Fuelling the hydrogen economy: Scale-up of an integrated formic acid-to-power system, Int. J. Hydrogen Energy, 2019, 44, 28533–28541, DOI:10.1016/j.ijhydene.2019.01.153.
- M. Garbe, K. Junge and M. Beller, Homogeneous Catalysis by Manganese-Based Pincer Complexes, Eur. J. Org. Chem., 2017, 2017(30), 4344–4362, DOI:10.1002/ejoc.201700376.
- W. Yang, I. Y. Chernyshov, R. K. A. van Schendel, M. Weber, C. Müller, G. A. Filonenko and E. A. Pidko, Robust and efficient hydrogenation of carbonyl compounds catalysed by mixed donor mn(i) pincer complexes, Nat. Commun., 2021, 12, 1–8, DOI:10.1038/s41467-020-20168-2.
- A. Lukas, M. Fritz and S. Schneider, First-row transition metal (de)hydrogenation catalysis based on functional pincer ligands, Chem. Rev., 2019, 119, 2681–2751, DOI:10.1021/acs.chemrev.8b00555 , https://pubs.acs.org/sharingguidelines.
- V. Mouarrawis, R. Plessius, J. I. van der Vlugt, and J. N. H. Reek, Confinement Effects in Catalysis Using Well-Defined Materials and Cages, 2018, https://www.frontiersin.org/article/10.3389/fchem.2018.00623 Search PubMed.
- M. Otte, P. F. Kuijpers, T. Oliver, I. Ivanović-Burmazović, J. N. H. Reek and B. de Bruin, Encapsulation of Metalloporphyrins in a Self-Assembled Cubic M8L6 Cage: A New Molecular Flask for Cobalt–Porphyrin-Catalysed Radical-Type Reactions, Chem.–Eur. J., 2013, 19(31), 10170–10178, DOI:10.1002/chem.201301411.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch, and G. R. Hutchison, The Open Babel Package, version 2.4.1, 2016, https://openbabel.org/ Search PubMed.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, Open Babel: An open chemical toolbox, J. Cheminf., 2011, 3(1), 33, DOI:10.1186/1758-2946-3-33.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations, J. Am. Chem. Soc., 1992, 114(25), 10024–10035, DOI:10.1021/ja00051a040.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25(9), 1157–1174, DOI:10.1002/jcc.20035.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Extended tight-binding quantum chemistry methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020,(n/a), e01493, DOI:10.1002/wcms.1493.
- P. Pracht, E. Caldeweyher, S. Ehlert and S. Grimme, A Robust Non-Self-Consistent Tight-Binding Quantum Chemistry Method for large Molecules, ChemRxiv, 2019 DOI:10.26434/chemrxiv.8326202.v1 , https://chemrxiv.org/articles/preprint/A_Robust_Non-Self-Consistent_Tight-Binding_Quantum_Chemistry_Method_for_large_Molecules/8326202, https://chemrxiv.org/ndownloader/files/15605534.
- S. Grimme, C. Bannwarth and P. Shushkov, A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86), J. Chem. Theory Comput., 2017, 13(5), 1989–2009, DOI:10.1021/acs.jctc.7b00118.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15(3), 1652–1671, DOI:10.1021/acs.jctc.8b01176.
- S. Spicher and S. Grimme, Robust Atomistic Modeling of Materials, Organometallic, and Biochemical Systems, Angew. Chem., Int. Ed., 2020, 59(36), 15665–15673, DOI:10.1002/anie.202004239.
- W. Clark Still, T. Anna, R. C. Hawley and T. Hendrickson, Semianalytical treatment of solvation for molecular mechanics and dynamics, J. Am. Chem. Soc., 1990, 112(16), 6127–6129, DOI:10.1021/ja00172a038.
- T. Ooi, M. Oobatake, G. Némethy and H. A. Scheraga, Accessible surface areas as a measure of the thermodynamic parameters of hydration of peptides, Proc. Natl. Acad. Sci. U. S. A., 1987, 84(10), 3086–3090, DOI:10.1073/pnas.84.10.3086 , http://www.pnas.org/content/84/10/3086.abstract.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16 Revision C.01, 2016 Search PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38(6), 3098–3100, DOI:10.1103/PhysRevA.38.3098.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305, 10.1039/B508541A.
- K. P. Jensen, B. O. Roos and U. Ryde, Performance of density functionals for first row transition metal systems, J. Chem. Phys., 2007, 126(1), 14103, DOI:10.1063/1.2406071.
- M. Bühl and H. Kabrede, Geometries of Transition-Metal Complexes from Density-Functional Theory, J. Chem. Theory Comput., 2006, 2(5), 1282–1290, DOI:10.1021/ct6001187.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113(18), 6378–6396, DOI:10.1021/jp810292n.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The pbe0 model, J. Chem. Phys., 1999, 110, 6158–6170, DOI:10.1063/1.478522.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, A generally applicable atomic-charge dependent London dispersion correction, J. Chem. Phys., 2019, 150(15), 154122, DOI:10.1063/1.5090222.
- I. S. Ufimtsev and T. J. Martínez, Quantum Chemistry on Graphical Processing Units. 1. Strategies for Two-Electron Integral Evaluation, J. Chem. Theory Comput., 2008, 4(2), 222–231, DOI:10.1021/ct700268q.
- I. S. Ufimtsev and T. J. Martinez, Quantum Chemistry on Graphical Processing Units. 2. Direct Self-Consistent-Field Implementation, J. Chem. Theory Comput., 2009, 5(4), 1004–1015, DOI:10.1021/ct800526s.
- I. S. Ufimtsev and T. J. Martinez, Quantum Chemistry on Graphical Processing Units. 3. Analytical Energy Gradients, Geometry Optimization, and First Principles Molecular Dynamics, J. Chem. Theory Comput., 2009, 5(10), 2619–2628, DOI:10.1021/ct9003004.
- P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg, J. Chem. Phys., 1985, 82(1), 270–283, DOI:10.1063/1.448799.
- J. C. Kromann, Calculate Root-mean-square deviation (RMSD) of Two Molecules Using Rotation, GitHub, v1.3.2, 2020, https://github.com/charnley/rmsd/releases/tag/rmsd-1.3.2 Search PubMed.
- W. Kabsch, A solution for the best rotation to relate two sets of vectors, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32(5), 922–923, DOI:10.1107/S0567739476001873.
- M. W. Walker, L. Shao and R. A. Volz, Estimating 3-D location parameters using dual number quaternions, CVGIP: Image Understanding, 1991, 54(3), 358–367, DOI:10.1016/1049-9660(91)90036-O , http://www.sciencedirect.com/science/article/pii/104996609190036O.
- R. S. Olson, R. J. Urbanowicz, P. C. Andrews, N. A. Lavender, L. C. Kidd, and J. H. Moore, Applications of Evolutionary Computation: 19th European Conference, EvoApplications 2016, Porto, Portugal, March 30 – April 1, 2016, Proceedings, Part I, chapter Automating Biomedical Data Science Through Tree-Based Pipeline Optimization, Springer International Publishing, 2016, pp. 123–137, ISBN 978-3-319-31204-0, DOI:10.1007/978-3-319-31204-0_9.
- R. S. Olson, B. Nathan, R. J. Urbanowicz, and J. H. Moore, Evaluation of a tree-based pipeline optimization tool for automating data science, in Proceedings of the Genetic and Evolutionary Computation Conference 2016, GECCO '16, New York, NY, USA, 2016, pp. 485–492, ACM, ISBN 978-1-4503-4206-3, DOI:10.1145/2908812.2908918.
- T. L. Trang, W. Fu and J. H. Moore, Scaling tree-based automated machine learning to biomedical big data with a feature set selector, Bioinformatics, 2020, 36(1), 250–256 CrossRef PubMed.
- A. S. Christense, F. A. Faber, B. Huang, L. A. Bratholm, A. Tkatchenko, K. R. Muller, and O. A. von Lilienfeld, Qml: A python toolkit for quantum machine learning, 2017, DOI:10.5281/Zeno.817331, https://github.com/qmlcode/qml.
- A. Dalby, J. G. Nourse, W. D. Hounshell, A. K. I. Gushurst, D. L. Grier, B. A. Leland and J. Laufer, Description of several chemical structure file formats used by computer programs developed at molecular design limited, J. Chem. Inf. Comput. Sci., 1992, 32, 244–255, DOI:10.1021/ci00007a012 , https://pubs.acs.org/sharingguidelines.
- Currently, Open Babel’s automated bond perception is used for this conversion which can miss longer metal-ligand bond lengths in TM complexes. Therefore, we strongly advise against using XYZ files for the skeleton. In a future version of ChemSpaX, the usage XYZ files as input will be deprecated.
- D. Dolphin, The Porphyrins V7: Biochemistry, Part B, Elsevier, 2012, ISBN 0323145612 Search PubMed.
- K. Kadish, K. M. Smith, and R. Guilard, The Porphyrin Handbook, Elsevier, 2000, vol. 3. ISBN 0123932033 Search PubMed.
- R. Grubbs, Handbook of Metathesis Volume 1: Catalyst Development and Mechanism, aug 2003, https://doi.org/10.1002/9783527619481 Search PubMed.
- P. G. Edwards and R. G. Jaouhari, Synthesis and characterization of complexes of nickel(ii), palladium(ii) and platinum(ii) with the new bifunctional aminodiphosphine ligand hn(ch2ch2ch2pme2)2, Polyhedron, 1989, 8(1), 25–28, DOI:10.1016/S0277-5387(00)86374-3 , https://www.sciencedirect.com/science/article/pii/S0277538700863743.
- D. Spasyuk, S. Smith and D. G. Gusev, Replacing phosphorus with sulfur for the efficient hydrogenation of esters, Angew. Chem., Int. Ed., 2013, 52(9), 2538–2542, DOI:10.1002/anie.201209218.
- S. Gründemann, M. Albrecht, J. A. Loch, J. W. Faller and R. H. Crabtree, Tridentate carbene ccc and cnc pincer palladium(ii) complexes: Structure, fluxionality, and catalytic activity, Organometallics, 2001, 20, 5485–5488, DOI:10.1021/om010631h , https://pubs.acs.org/sharingguidelines.
- G. A. Filonenko, E. Cosimi, L. Lefort, M. P. Conley, C. Copéret, M. Lutz, E. J. M. Hensen and E. A. Pidko, Lutidine-derived ru-cnc hydrogenation pincer catalysts with versatile coordination properties, ACS Catal., 2014, 4, 2667–2671, DOI:10.1021/cs500720y , https://pubs.acs.org/sharingguidelines.
- K. Z. Demmans, M. E. Olson and R. H. Morris, Asymmetric transfer hydrogenation of ketones with well-defined manganese(i) pnn and pnnp complexes, Organometallics, 2018, 37, 4608–4618, DOI:10.1021/acs.organomet.8b00625 , https://pubs.acs.org/sharingguidelines.
- M. Gagliardo, P. A. Chase, S. Brouwer, G. P. M. Van Klink and G. Van Koten, Electronic effects in pcp-pincer ru(ii)-based hydrogen transfer catalysis, Organometallics, 2007, 26, 2219–2227, DOI:10.1021/om060874f.
- S. Tang, N. Von Wolff, Y. Diskin-Posner, G. Leitus, Y. Ben-David and D. Milstein, Pyridine-based pcp-ruthenium complexes: Unusual structures and metal-ligand cooperation, J. Am. Chem. Soc., 2019, 141, 7554–7561, DOI:10.1021/jacs.9b02669 , https://pubs.acs.org/sharingguidelines.
- Y. Zhuo, A. M. Tehrani and J. Brgoch, Predicting the Band Gaps of Inorganic Solids by Machine Learning, J. Phys. Chem. Lett., 2018, 9(7), 1668–1673, DOI:10.1021/acs.jpclett.8b00124.
- T. L. Trang, W. Fu and J. H. Moore, Scaling tree-based automated machine learning to biomedical big data with a feature set selector, Bioinformatics, 2020, 36(1), 250–256 CrossRef PubMed.
- S. Grimme, Exploration of Chemical Compound, Conformer, and Reaction Space with Meta-Dynamics Simulations Based on Tight-Binding Quantum Chemical Calculations, J. Chem. Theory Comput., 2019, 15(5), 2847–2862, DOI:10.1021/acs.jctc.9b00143.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22(14), 7169–7192, 10.1039/C9CP06869D.
- P. Pracht and S. Grimme, Calculation of absolute molecular entropies and heat capacities made simple, Chem. Sci., 2021, 12(19), 6551–6568, 10.1039/D1SC00621E.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1dd00017a |
| ‡ Propagation of errors in this context means that complexes that are getting increasingly more complex are being compared to their DFT optimized ‘standard’. |
| § A serial functionalization strategy means that the functional groups were placed one after another, leading to functionalized structures that are increasingly getting more complex. |
| ¶ This is not the same PNP ligand as used for the Ru complexes. The PNP ligand used for Mn complexes contains a propyl bridge while the one used for Ru complexes contains an ethyl bridge. |
| || ΔΔEGFN2−xTB: 20 pairs; (ΔΔEFF) 25 pairs M–L/M(H)–L(H) geometries. |
| This journal is © The Royal Society of Chemistry 2022 |