SPA^HM: the spectrum of approximated Hamiltonian matrices representations

Abstract

Physics-inspired molecular representations are the cornerstone of similarity-based learning applied to solve chemical problems. Despite their conceptual and mathematical diversity, this class of descriptors shares a common underlying philosophy: they all rely on the molecular information that determines the form of the electronic Schrödinger equation. Existing representations take the most varied forms, from non-linear functions of atom types and positions to atom densities and potential, up to complex quantum chemical objects directly injected into the ML architecture. In this work, we present the spectrum of approximated Hamiltonian matrices (SPA^HM) as an alternative pathway to construct quantum machine learning representations through leveraging the foundation of the electronic Schrödinger equation itself: the electronic Hamiltonian. As the Hamiltonian encodes all quantum chemical information at once, SPA^HM representations not only distinguish different molecules and conformations, but also different spin, charge, and electronic states. As a proof of concept, we focus here on efficient SPA^HM representations built from the eigenvalues of a hierarchy of well-established and readily-evaluated “guess” Hamiltonians. These SPA^HM representations are particularly compact and efficient for kernel evaluation and their complexity is independent of the number of different atom types in the database.

---

1 Introduction

Modern machine learning (ML) techniques are at the forefront of an unprecedented methodological shift affecting virtually all fields of chemistry.^1–5 Regardless of the chosen application or algorithm, the predicting power of artificial intelligence in chemistry is ultimately related to the choice of a molecular representation, i.e. of a numerical descriptor encoding all the relevant information about the chemical system.^6–8

The crucial role of representations is mirrored by the intensive work that has been dedicated to finding ever more reliable and widely applicable fingerprints.^7,8 Although there are effectively infinite ways to input the information about a molecule into a machine learning algorithm, conceptually molecular representations could be subdivided into well-defined macro categories. Chemoinformatics descriptors are a comprehensive set of fingerprints that relies either on string-based fingerprints, such as SMILES^9,10 and SELFIES,¹¹ or on readily available and descriptive properties, such as the number of aromatic carbon atoms, the shape index of a molecule, and its size,^12–16 which are usually chosen using an a priori knowledge about their correlation with the specific target.¹⁷ A second class of chemical representations has been introduced very recently, relying on artificial neural networks (and no human input) to infer suitable descriptors for the learning exercise.¹⁸ Finally, physics-based or quantum machine learning (QML) representations include all those fingerprints inspired by the fundamental laws of physics that govern molecular systems, in particular, the laws of quantum mechanics and the basic laws of symmetry.

As physics-based representations are rooted in fundamental laws, they are directly applicable to any learning task, ranging from the regression of molecular properties to revealing the relationship between molecules in large chemical databases. Although existing quantum machine learning representations have drastically different mathematical forms and physical motivations, they all share the same starting point: the position (and often the type) of the atoms in real space. This choice is not arbitrary and it is intimately related to the connection between (static) molecular properties and the electronic Hamiltonian Ĥ.

For a fixed nuclear configuration, the information about all the electronic properties of a molecule is contained in the many-body electronic wavefunction Ψ(x₁, …, x_n), as defined by the Schrödinger equation. Since the electronic Hamiltonian defines Ψ(x₁, …, x_n), the molecular information necessary to fix Ĥ is in principle sufficient for a non-linear model to establish a one-to-one relationship with any electronic property. The expression for all the universal (i.e. non-molecule specific) terms of the Hamiltonian (e.g. kinetic energy) only requires the knowledge of the total number of electrons (N). In contrast, the external potential (the electron-nuclear attraction potential) also depends on the position of the nuclei {R_I} and their charges {Z_I}.¹⁹ Under the assumption of charge neutrality (i.e.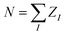), R_I and Z_I uniquely fix the form of the Hamiltonian and thus represent the only required information to characterize the electronic wavefunction and electronic properties.

Since no two different molecules have the same Hamiltonian, any representation that relies upon R_I and Z_I is guaranteed to satisfy the injectivity requirement of machine learning, i.e. there must be a one-to-one map between the representation of a molecule and its properties. Nonetheless, injectivity is not the only condition necessary for efficient and transferable learning. A representation must encode the same symmetries as the target property upon any transformation of real-space coordinates (equivariance): rotation, reflection, translation, and permutation of atoms of the same species.^6,20,21

To organize in separate groups all the existing physics-based representations, it is fundamental to define a metric for the classification. Among all the possibilities, it is useful for the purpose of this work to classify representations according to the way they use and transform their molecular inputs.

One well-established methodology is to build representations using atom-centered continuous basis functions from an input containing the type and the position of the nuclei. This choice is the common denominator of a series of representations such as the Behler–Parrinello symmetry functions,^22–24 the smooth overlap of atomic positions (SOAP),^6,21 the overlap fingerprint of Goedecker and coworkers,²⁵ the N-body iterative contraction of equivariant features (NICE),²⁶ and the atomic cluster expansion (ACE).^27–29

Other descriptors such as the many-body tensor representation (MBTR),³⁰ permutation invariant polynomials (PIPs),^31–35 and graph-based representations³⁶ rely on the transformation of the structural input into a system of internal coordinates and use directly this information to establish similarity measures.

A third possibility is to build representations as fingerprints of potentials. This family includes the Coulomb matrix (CM),^37,38 the bag of bonds (BoB),³⁹ (atomic) spectrum of London and Axilrod–Teller–Muto potential [(a)SLATM],⁴⁰ the long-distance equivariant (LODE) representation,⁴¹ FCHL18,⁴² and FCHL19.⁴³

More recently, sophisticated neural network architectures, such as OrbNet,^44,45 have shown that it is possible to use even more complex quantum chemical objects as input features, such as the tensor representation of quantum mechanical operators and their expectation values obtained from a converged semi-empirical computation.

In this work, we propose a different approach to designing physically motivated and efficient QML representations. The spectrum of approximated Hamiltonian matrices (SPA^HM) looks back at the common origin of physics-based representations and uses the electronic Hamiltonian as the central ingredient to generate an input for machine learning algorithms. In contrast to standard geometry-based descriptors, the Hamiltonian encodes all the relevant quantum chemical information at once and it is able not only to distinguish different molecules and conformations, but also different spin, charge, and electronic states. Importantly, SPA^HM representations do not require any self-consistent field (SCF) computation, as they all leverage the simplest, yet powerful, quantum chemical trick: the use of well-established, low-cost “guess” Hamiltonians, which are traditionally used to jump-start the SCF procedure. These matrices are cheaper to compute than a single SCF iteration (see Section 3.5 for more details on efficiency) and form a controlled hierarchy of increasing complexity and accuracy that is readily computed for any given molecular system. As a proof of concept, we focus in this work on SPA^HM representations built from the eigenvalues of the “guess” Hamiltonians. This choice is physically and chemically motivated, naturally invariant under the basic symmetries of physics, and, in contrast to existing QML representations, include seamlessly the information about the number of electrons and the spin state of a molecule. In addition, the choice of eigenvalues results in a small-size representation, which is particularly efficient for kernel construction and rather independent of the degree of chemical complexity in the databases. Eigenvalue-based SPA^HMs are global representations, which have the benefit to be rather accurate for molecular properties, but are not as transferable as local representations and are not applicable to regress local (atomic) targets (e.g. atomic partial charges).⁶ Nonetheless, the SPA^HM representations are not restricted to eigenvalues and could be constructed from other (atom-centered) properties, such as the “guess” Hamiltonian matrix elements, the eigenvectors, and their corresponding density matrices.

2 Computational methods

Each molecular set (described in the corresponding subsections of the Results and discussion) was randomly divided into the training and test sets (80–20% splits). To minimize the bias arising from the uneven distribution of molecular size and composition, the learning curves for each representation were averaged over 5 repetitions of sampling and prediction (error bars are additionally reported in the ESI†). While the atomization energies were taken as computed in the original QM7 reference (PBE0 in a converged numerical basis),³⁷ the other three properties (norm of dipole moment, HOMO energies and HOMO–LUMO gap) were computed at PBE0 (ref. 47)/cc-pVQZ^48,49 level. The structure and properties of the molecules in the L11 database were taken as computed in the original ref. 50. The hyperparameters for each representation were optimized with a grid search using a 5-fold cross-validation procedure and the learning curves were computed using random sub-sampling (5 times per point). The optimization and regression code was written in Python using the numpy⁵¹ and scikit-learn⁵² libraries. The QML⁵³ package was used to construct the CM and SLATM representations. The Gaussian kernel was used for the SLATM representation and the Laplacian kernel for CM and all the SPA^HMs.

The initial guesses were obtained in a minimal basis (MINAO⁴⁶). All quantum chemical computations were made with a locally modified version of PySCF.^54,55 The codes used in this paper are provided in a Github repository at https://github.com/lcmd-epfl/SPAHM and are included in a more comprehensive package called Q-stack (https://github.com/lcmd-epfl/Q-stack). Q-stack is a library and a collection of stand-alone codes, mainly programmed in Python, that provides custom quantum chemistry operations to promote quantum machine learning. The data and the model that support the findings of this study are freely available in Materials Cloud at https://archive.materialscloud.org/record/2021.221 (https://doi.org/10.24435/materialscloud:js-pz).

The CPU timings were recorded on 24-core CPU servers (2x Intel Xeon CPU E5-2650 v4@2.20 GHz), using one thread. The code was run with the packages from anaconda-5.2.0 (python-3.6) together with numpy-1.16.4, pyscf-2.0.0a, and qml-0.4.0. The user time was measured with the getrusage() system call and averaged over eight runs.

3 Results and discussion

3.1 Learning curves

To assess the ability of the SPA^HM representations to learn and their overall accuracy, we trained a kernel ridge regression (KRR) model on the QM7 database^37,56 to target four quantum chemical properties. Each of these quantities has been chosen as it is representative of a particular category. Atomization energies are both routinely used to assess the quality of ML models and represent a broader class of extensive (i.e. size-dependent) thermodynamic properties.^37,57 Dipole moments are traditionally used in quantum chemistry as proxies of the quality of the wavefunction. The HOMO energies are intensive (i.e. size-independent) quantities. Finally, the HOMO–LUMO gap allows probing the quality of both frontier orbitals and simultaneously tests the additivity of errors in the KRR models.

The QM7 dataset³⁷ was randomly divided into a training set of 5732 molecules and a test set containing the remaining 1433 compounds, corresponding to an 80–20% split. For each molecule, we constructed the SPA^HM representations by diagonalizing the different “guess” Hamiltonians in a minimal basis set (MINAO⁴⁶) and using the sorted occupied eigenvalues as the KRR fingerprint. The occupied orbital energies carry information about both the atom types (core-orbital eigenvalues), the general electronic structure of the molecule (core and valence), and the total number of electrons. In addition, the eigenvalues of a Hamiltonian are naturally invariant under all real-space transformations (permutation, translation, rotation) and the size of the occupied set is independent of the choice of the atomic orbital basis.

The learning curves for all the SPA^HM representations are reported in Fig. 1. In addition, we report the curves of the original version (eigenvalue) Coulomb matrix (CM)³⁷ and SLATM,⁴⁰ as the first has a similar size and diagonalization philosophy as SPA^HM and the second is an example of a widely-used global representation.

Fig. 1 (Left) Learning curves in logarithmic scale of (a) atomization energies, (b) dipole moments, (c) HOMO energies, and (d) HOMO–LUMO gaps. The color code reflects the different representations. (Right) Illustrative example of the sizes of the CM, SPA^HM, and SLATM representations. All the Hamiltonians were evaluated in the MINAO⁴⁶ minimal basis.

In Fig. 1, the SPA^HM representations are indicated by the type of approximate Hamiltonian used for their construction. Although it is rather complex to establish a definitive hierarchy of self-consistent-field guesses, it is always possible to provide a more qualitative trend based on the amount of physics that each guess includes. The diagonalization of the core (H_core) and the generalized Wolfsberg–Helmholz (GWH).⁵⁸ Hamiltonian matrices are the simplest approximations, as they do not try to model any two-electron term. Building on the GWH guess, the parameter-free extended Hückel method uses approximate ionization potentials as diagonal terms and it is generally more robust.^59,60 The superposition of atomic densities (SAD)^61–63 is another popular choice that however only produces a density matrix (DM). Nonetheless, it is rather straightforward to construct a complete Hamiltonian matrix (including the one- and two-electron terms) by contracting the SAD density matrix with a potential of choice (Hartree–Fock or any exchange-correlation density functional). We report the SAD learning curve in Fig. 1 using the PBE0 potential, as all the properties were computed with this functional. Finally, the superposition of atomic potentials (SAP)^60,64 and the Laikov–Briling (LB)⁶⁵ guesses use effective one-electron potentials to construct sophisticated, yet computationally lightweight, guess Hamiltonians.

Besides the internal hierarchy, the accuracy of all the SPA^HMs is always comprised between SLATM and the eigenvalues of the Coulomb matrix. While SLATM consistently outperforms the SPA^HM representations, the difference with the most robust guesses (LB and SAD) is usually much smaller than the accuracy of the functional itself (∼5 kcal mol⁻¹).⁶⁶ Importantly, SLATM is also three orders of magnitude larger than SPA^HM on QM7. The significant difference in the extent of the representation is crucial from an efficiency perspective, as the number of features dictates the computational effort of constructing the kernel matrix for an equal size of the training set. While lightweight, efficient, and naturally accounting for the charge state of molecules, we only tested a few well-known Hamiltonians for building SPA^HM. As the performance of SPA^HM is largely independent of the choice of the basis set or potential (see ESI†), it is necessary to consider alternative strategies to improve its accuracy. The heavy dependence of the learning on the quality of the parent Hamiltonian suggests that the construction of “better guesses” is the correct direction. Nonetheless, as discussed in Section 3.2, better guesses does not necessarily mean “improved quantum chemical approximate Hamiltonians” (i.e. closer to the converged Fock matrix), but rather the construction of simpler, systematic Hamiltonians specifically optimized for the learning task.

Besides the rather simple organic molecules of QM7, we tested the accuracy of the best performing SPA^HM representation (LB) on larger molecules, transition metal complexes, and conformers. Even in these more challenging chemical situations, SPA^HM shows the same relative performance with respect to existing representation as in QM7 (see ESI, Section II†).

3.2 Physics and noise

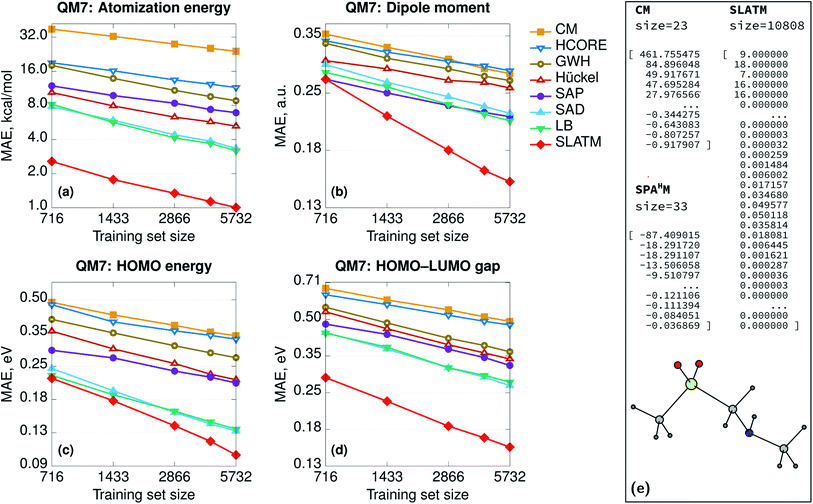
In general, the accuracy of the different SPA^HM representations (Fig. 1) follows the same trend as the complexity of the underlying SCF guess. This result seems to suggest that the more physics is included in the approximate Hamiltonian, the easier is the learning exercise for the corresponding SPA^HM representation. To test the robustness of this conclusion, we constructed a test representation using the converged PBE0 Hamiltonian matrix (Fig. 2, label PBE0). As already mentioned, any representation based on the converged Fock matrix is both too expensive and worthless for practical machine learning, since it is always possible to (upon diagonalization) use the converged wavefunction to compute any desired quantum chemical property. Nonetheless, this test is essential, as it pushes the physics of SPA^HM to the limit. Fig. 2 shows that PBE0 is not the best representation when regressing the atomization energies and even some SPA^HMs outperform its accuracy. As the SCF changes the eigenvalues of each molecule independently from the others, the relationship between the feature vectors also varies unconcertedly. This sparsification of the data in the representation space effectively decreases the correlation between the features and the target properties and worsens the learning.

Fig. 2 Learning curves (in logarithmic scale) of atomization energies for SPA^HM based on the converged PBE0 Fock matrix and on the LB Hamiltonian, with an increasing (pseudo-)random perturbation added to the representation vector. The perturbation max. magnitude is reflected in the legend. For comparison, a learning curve for a fully-random representation is shown. All the Hamiltonians (including converged PBE0) were evaluated in the MINAO⁴⁶ minimal basis.

The performance of the converged Fock matrix versus more approximated (and computationally cheaper) Hamiltonians shows that “more physics” is not necessarily the key to better learning. Yet, the relative ordering of the guess Hamiltonians suggests that higher-quality potentials correlate with the best representations. The question associated with the relevance of the physics could be generalized and one could ask if there is the need for any physics at all or random featurization could lead to the same (or better) results.⁶⁷ In addition, SPA^HM representations are so small (33 features for QM7) with respect to the size of the dataset (7165 molecules), that the learning could be the result of random correlations between the features and the target properties. Overall, it is still unclear if any random (i.e. not physically motivated) perturbation of SPA^HM could lead to better learning. To analyze the behavior of our most robust representation upon random perturbation, we modify SPA^HM-LB by adding an increasing (pseudo-)random perturbation sampled from a uniform distribution and testing its accuracy on the QM7 database.

Fig. 2 shows that, for the smallest perturbation tested (magnitude max. 0.001), the original and the modified learning curves are almost indistinguishable, except for a non-significant difference due to the shuffling of the training set. As the allowed random noise increases, we observe the systematic and progressive worsening of the learning exercise towards the limit of physically meaningless random numbers. As the magnitude of the perturbation increases, the physics in the representation fades, the error increases, and the learning curves become flatter. This demonstrates that the performance of SPA^HM is not just a consequence of a random correlation between the feature vectors and the properties.

3.3 Core and valence

Besides any consideration about the relative importance of physics, the SPA^HM representations are still the eigenvalues of (approximate) electronic Hamiltonians. As such, it is relevant to try to rationalize how the different parts of SPA^HM contribute to learning. As for any set of eigenvalues, it is always possible to divide any SPA^HM representation into its core and valence parts. The core orbital energies do not vary significantly for the same atom in different molecules and therefore naturally track the number and the types of nuclei across the database. In contrast, the valence set is a fingerprint of the chemistry and the bonding patterns proper to each molecule.

Fig. 3 shows the learning curves for the SPA^HMs based on the LB Hamiltonian with core, valence, and the full occupied eigenvalues sets taken as representation vectors. While the valence set results in consistently better learning than the core, both are necessary to achieve the overall accuracy of SPA^HM-LB with the exception of the HOMO energies. For the HOMO eigenvalues, the valence set can be considered an alternative type of Δ-learning,⁶⁸ where the approximate baseline (approximate HOMO energies) are the input of the kernel itself, rather than corrected a posteriori. Importantly, core orbital energies are not sufficient information to accurately regress the atomization energies, but the valence set error is also twice as large as the total SPA^HM. Therefore, while the information about the chemical bonding is more relevant for the general performance, the information about the number and the type of nuclei in the molecules is essential to improve learning.

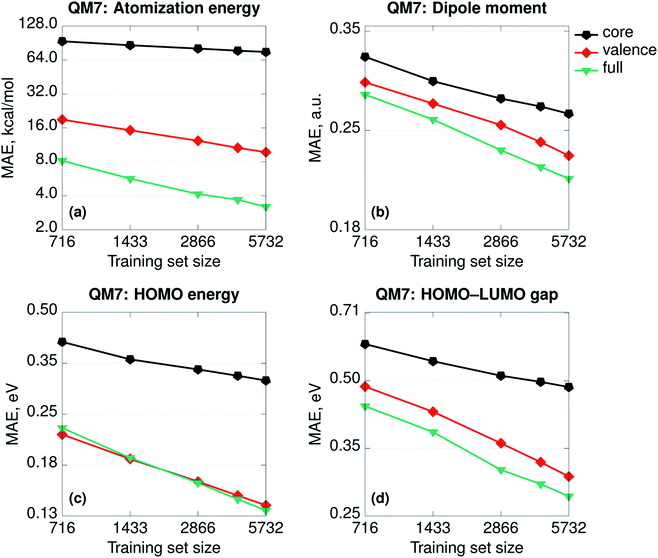Fig. 3 Learning curves (in logarithmic scale) for the SPA^HMs based on the LB Hamiltonian with core, valence, and the full occupied eigenvalues sets used as representations. All the Hamiltonians were evaluated in the MINAO⁴⁶ minimal basis.

3.4 Spin and charge

Existing QML representations such as SLATM are computed as non-linear functions of atom types and internal coordinates. However, from a quantum chemical perspective, this information is not sufficient to fix the (ground-state) wavefunction, which also requires knowledge of the number of electrons (N). Omitting the charge (and spin) information is not particularly problematic under the assumption of electroneutrality in the dataset, i.e. the number of electrons in each molecule is exactly equal to the sum of the nuclear charges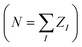 . Nonetheless, existing geometry-based representations are not suitable for datasets of molecular systems with different charges (spin states), since the injectivity rule is violated (the same geometry would correspond to multiple target properties) or, in the milder case of relaxed geometries, the representation-to-property mapping is not smooth. By construction and by choice of the electronic Hamiltonians as the key ingredient, SPA^HM representations include naturally both the structural (geometry and atom type) and the electronic (spin and charge) information and they are applicable with no modification to any molecular database.

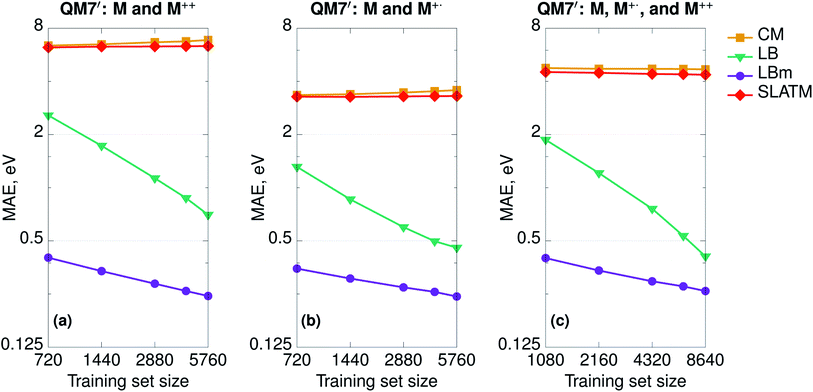
To demonstrate the difference in performance between geometry- and Hamiltonian-based representations on more complex databases, we randomly selected one-half of the QM7 set (3600 molecules) and computed at fixed geometries the properties of the double cations (M⁺⁺) and radical cations (M⁺˙). In this way, we constructed three additional sets: (a) neutral molecules and double cations (7200 molecules, 5760 in the training and 1440 in the test set); (b) neutral molecules and radical cations (7200 molecules, 5760 in the training and 1440 in the test set); and (c) neutral molecules, double cations, and radical cations (10 800 molecules, 8640 in the training and 2160 in the test set). We set the learning task to predict the HOMO (SOMO for radicals) orbital energies and report the learning curves in Fig. 4. As expected, CM and SLATM fail the learning exercise and the curves are flat for all three sets.

Fig. 4 Learning curves (in logarithmic scale) of HOMO energies for the SPA^HMs based on the LB Hamiltonian (LB and LBm) compared to CM and SLATM for the artificial sets including neutral molecules (M) taken from QM7 and their double cations (M⁺⁺) and/or radical cations (M⁺˙).

SPA^HM representations include the charge information on two separate levels. First, as we only include the occupied space, the length of the representation changes if we remove electrons. For instance, the SPA^HM representations of neutral molecules M and their double cations M⁺⁺ differ by one entry in length. Second, some of the approximate potentials at the origin of SPA^HM, e.g. LB, SAP, and SAD, are sensitive to electronic information and result in different Hamiltonian matrices when the number of electrons differs. For instance, the LB Hamiltonian relies on a constraint that fixes the charge corresponding to the effective Coulomb potential (LBm in Fig. 4). While both LB (with no modified potential) and LBm learn, it is evident from Fig. 4, that SPA^HM-LBm provides more robust predictions, resulting in errors one order of magnitude smaller than SPA^HM-LB at small training set sizes.

The spin-state information is also readily included in SPA^HMs by the same method used in traditional quantum chemistry: separating the α and β-spaces and concatenating α and β orbital energies in a matrix of size N_α × 2 (the β-orbitals column is padded with zeros). Using the Laplacian kernel function, this choice ensures that for closed-shell molecules the similarity measures are the same as described above when the fingerprint is a single vector of length N/2.

Hamiltonian-based representations such as SPA^HM outperform geometry-based representations in every database where electronic information is fundamental to distinguish molecules. The three sets proposed above are an example, but they are also quite peculiar since we do not allow geometries to relax. As a more realistic example of a database where electronic information is essential, we compare the overall performance of SPA^HM (LBm Hamiltonian) and SLATM on the L11 set.⁵⁰ L11 consists of 5579 small molecular systems (single atoms and atomic ions were excluded from the original set) characterized by a substantial diversity in terms of chemistry, charge, and spin states. From L11, 4463 molecules were randomly selected as the training set and the remaining 1116 – as the test set. To assess the accuracy of the representation, we set the norm of the dipole moment (for charged systems the origin is chosen to be the geometric center) as the learning target and report the learning curves in Fig. 5. Since there are no identical geometries in the set, the injectivity rule is not violated for SLATM, and the representation learns. However, even with relaxed structures, geometry-based representations struggle with a database containing mixed electronic information since they are not smooth with respect to the target property (similar geometries can correspond to significantly different values), and SPA^HM, incorporating seamlessly the electronic state information, performs better.

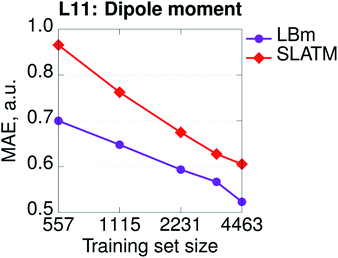Fig. 5 Learning curves (in logarithmic scale) of dipole moments for the SPA^HM based on the LB Hamiltonian (LBm) compared to SLATM for the set of ref. 50 (L11).

3.5 Efficiency

The efficiency and computational complexity of SPA^HM representations depend on the choice of the underlying guess Hamiltonian, the simplest guesses (core, GWH) being the fastest to evaluate. Formally, as the framework requires the diagonalization of a matrix, the overall complexity in big-O notation is O(N³) where N is a measure of the system size. SLATM, despite being a much larger representation (see Fig. 1e), also scales as O(N³), since it includes three-body interactions. Formal complexities for a single molecule are a useful analysis tool, but they are not always sufficient to characterize the efficiency of the representations on a full dataset. In this case, practical examples are a more compelling demonstration of the relative merits of the SPA^HM philosophy.

For this reason, we report in Fig. 6 the CPU timing for SLATM and SPA^HM-LBm on the QM7 and the L11 (ref. 50) databases (more details in the Computational methods). For both representations, we recorded the time for building the representation itself and the time for constructing the kernels.

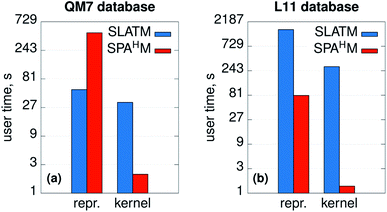Fig. 6 User times (in logarithmic scale) measured for computing the SLATM and SPA^HM representations and the molecular kernels on (a) the QM7 dataset³⁷ and (b) the database of ref. 50 (L11).

As SPA^HM representations based on occupied orbital eigenvalues are particularly compact, SPA^HM-LB is significantly more efficient than SLATM in the kernel construction for both databases. This result follows directly from the fact that, for a fixed dataset size, the complexity of the kernel construction depends only on the number of features (SLATM: 10 808 features on QM7 and 2 49 255 on L11; SPA^HM: 33 on QM7 and 64 on L11).

The relative efficiency of the construction of the representation itself is more sensitive to the dataset. To better understand the behavior of both SLATM and SPA^HM-LBm it is crucial to clarify the composition of each database. QM7 includes molecules up to 7 non-hydrogen atoms with a limited chemical complexity (H, C, N, O, S). In contrast, L11 contains all the elements hydrogen through bromine (noble gases excluded) and as such includes a significantly diverse chemistry. SLATM is faster to evaluate than SPA^HM-LB in the QM7 dataset, as the amount of different many-body types is very limited. However, on more complex databases with diverse chemistry and atom types, representations like SLATM become heavy in both computer time and memory (SLATM binary file occupies 11 GiB of memory vs. 5.5 MiB of SPA^HM). As the cost of the guess Hamiltonian does not depend on the number of different atom types, SPA^HM representations are extremely efficient for chemically complex molecular databases.

4 Conclusions

In this work, we proposed a lightweight and efficient quantum machine learning representation, capable of naturally accounting for the charge state of molecules by leveraging the information contained in standard quantum chemical “guess” Hamiltonians. Using the QM7 and the L11 databases, we tested the performance of a hierarchy of representations for a set of four representative quantum chemical properties. The performance of the SPA^HM representations follows the same qualitative trend as the one describing the amount of physics encoded in the parent approximate Hamiltonian. Nonetheless, we also find that the trend stops when pushing the physics to the limit and using the fully converged Fock matrices to construct the representation. Since increasingly adding physics is not the roadmap for the potential improvement of the SPA^HM representations, alternative strategies have to be analyzed. Sharing the same conceptual origin of this work, an alternative strategy for future improvement consists in representing molecules for ML using the approximate Hamiltonian matrix itself, its eigenvectors, or the resulting density matrices. Together with the SPA^HMs, these descriptors form a more comprehensive class of Hamiltonian-centered fingerprints leveraging the simplest, computationally efficient, and robust, quantum chemical trick: SCF guesses.

Data availability

The data that support the findings of this study are openly available in Materials Cloud at https://archive.materialscloud.org/record/2021.221. The code for SPAHM is available in Q-stack (https://github.com/lcmd-epfl/Q-stack) and as a separate Github repository at https://github.com/lcmd-epfl/SPAHM.

Author contributions

A. F. and K. R. B. performed the computations and developed the software. A. F. and C. C. designed the representations and conceptualized the project. All the authors contributed to the writing, reviewing and editing of the manuscript. C. C. is credited for funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge Ruben Laplaza and Puck van Gerwen for helpful discussion and critical propositions. The authors also acknowledge the National Centre of Competence in Research (NCCR) “Materials' Revolution: Computational Design and Discovery of Novel Materials (MARVEL)” of the Swiss National Science Foundation (SNSF, grant number 182892) and the European Research Council (ERC, grant agreement no. 817977).

References

1. B. Huang and O. A. von Lilienfeld, Chem. Rev., 2021, 121, 10001–10036.
2. P. O. Dral and M. Barbatti, Nat. Rev. Chem., 2021, 5, 388–405.
3. K. Jorner, A. Tomberg, C. Bauer, C. Sköld and P.-O. Norrby, Nat. Rev. Chem., 2021, 5, 240–255.
4. O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Chem. Rev., 2021, 121, 10142–10186.
5. M. Meuwly, Chem. Rev., 2021, 121, 10218–10239.
6. A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115.
7. B. Huang and O. A. von Lilienfeld, J. Chem. Phys., 2016, 145, 161102.
8. F. Musil, A. Grisafi, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Chem. Rev., 2021, 121, 9759–9815.
9. D. Weininger, J. Chem. Inf. Model., 1988, 28, 31–36.
10. D. Weininger, A. Weininger and J. L. Weininger, J. Chem. Inf. Comput. Sci., 1989, 29, 97–101.
11. M. Krenn, F. Häse, A. Nigam, P. Friederich and A. Aspuru-Guzik, Machine Learning: Science and Technology, 2020, 1, 045024.
12. M. Karelson, V. S. Lobanov and A. R. Katritzky, Chem. Rev., 1996, 96, 1027–1044.
13. M. Karelson, Molecular descriptors in QSAR/QSPR, Wiley-Interscience, New York, 2000.
14. R. Todeschini and V. Consonni, Handbook of molecular descriptors, Wiley, 2000, vol. 11.
15. R. Todeschini and V. Consonni, Molecular Descriptors for Chemoinformatics, Wiley, 2009, vol. 41.
16. L. David, A. Thakkar, R. Mercado and O. Engkvist, J. Cheminf., 2020, 12, 1–22.
17. L. M. Ghiringhelli, J. Vybiral, E. Ahmetcik, R. Ouyang, S. V. Levchenko, C. Draxl and M. Scheffler, New J. Phys., 2017, 19, 023017.
18. K. T. Schütt, O. T. Unke and M. Gastegger, 2021, arXiv:2102.03150.
19. A. Szabo and N. S. Ostlund, Modern quantum chemistry: introduction to advanced electronic structure theory, McGraw-Hill, New York, 1989.
20. A. Glielmo, P. Sollich and A. De Vita, Phys. Rev. B, 2017, 95, 214302.
21. A. Grisafi, D. M. Wilkins, G. Csányi and M. Ceriotti, Phys. Rev. Lett., 2018, 120, 036002.
22. J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401.
23. J. Behler, J. Chem. Phys., 2011, 134, 074106.
24. L. Zhang, J. Han, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2018, 120, 143001.
25. L. Zhu, M. Amsler, T. Fuhrer, B. Schaefer, S. Faraji, S. Rostami, S. A. Ghasemi, A. Sadeghi, M. Grauzinyte, C. Wolverton and S. Goedecker, J. Chem. Phys., 2016, 144, 034203.
26. J. Nigam, S. Pozdnyakov and M. Ceriotti, J. Chem. Phys., 2020, 153, 121101.
27. R. Drautz, Phys. Rev. B, 2019, 99, 014104.
28. R. Drautz, Phys. Rev. B, 2019, 100, 249901.
29. G. Dusson, M. Bachmayr, G. Csanyi, R. Drautz, S. Etter, C. van der Oord and C. Ortner, 2019, arXiv:1911.03550.
30. H. Huo and M. Rupp, 2017, arXiv:1704.06439.
31. A. Brown, A. B. McCoy, B. J. Braams, Z. Jin and J. M. Bowman, J. Chem. Phys., 2004, 121, 4105–4116.
32. B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577–606.
33. J. M. Bowman, B. J. Braams, S. Carter, C. Chen, G. Czakó, B. Fu, X. Huang, E. Kamarchik, A. R. Sharma, B. C. Shepler, Y. Wang and Z. Xie, J. Phys. Chem. Lett., 2010, 1, 1866–1874.
34. Z. Xie and J. M. Bowman, J. Chem. Theory Comput., 2010, 6, 26–34.
35. B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 054112.
36. F. Pietrucci and W. Andreoni, Phys. Rev. Lett., 2011, 107, 085504.
37. M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301.
38. M. Rupp, R. Ramakrishnan and O. A. von Lilienfeld, J. Phys. Chem. Lett., 2015, 6, 3309–3313.
39. K. Hansen, F. Biegler, R. Ramakrishnan, W. Pronobis, O. A. von Lilienfeld, K.-R. Müller and A. Tkatchenko, J. Phys. Chem. Lett., 2015, 6, 2326–2331.
40. B. Huang and O. A. von Lilienfeld, Nat. Chem., 2020, 12, 945–951.
41. A. Grisafi and M. Ceriotti, J. Chem. Phys., 2019, 151, 204105.
42. F. A. Faber, A. S. Christensen, B. Huang and O. A. von Lilienfeld, J. Chem. Phys., 2018, 148, 241717.
43. A. S. Christensen, L. A. Bratholm, F. A. Faber and O. A. von Lilienfeld, J. Chem. Phys., 2020, 152, 044107.
44. Z. Qiao, M. Welborn, A. Anandkumar, F. R. Manby and T. F. Miller, J. Chem. Phys., 2020, 153, 124111.
45. A. S. Christensen, S. K. Sirumalla, Z. Qiao, M. B. O'Connor, D. G. A. Smith, F. Ding, P. J. Bygrave, A. Anandkumar, M. Welborn, F. R. Manby and T. F. Miller, J. Chem. Phys., 2021, 155, 204103.
46. G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843.
47. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
48. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
49. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371.
50. D. N. Laikov, J. Chem. Phys., 2011, 135, 134120.
51. C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. Fernández del Río, M. Wiebe, P. Peterson, P. Gérard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Nature, 2020, 585, 357–362.
52. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, Journal of Machine Learning Research, 2011, 12, 2825–2830.
53. A. S. Christensen, F. A. Faber, B. Huang, L. A. Bratholm, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, QML: a Python toolkit for quantum machine learning, 2017, https://github.com/qmlcode/qml.
54. Q. Sun, J. Comput. Chem., 2015, 36, 1664–1671.
55. Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1340.
56. L. C. Blum and J.-L. Reymond, J. Am. Chem. Soc., 2009, 131, 8732–8733.
57. L. Ruddigkeit, R. Van Deursen, L. C. Blum and J. L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875.
58. M. Wolfsberg and L. Helmholz, J. Chem. Phys., 1952, 20, 837–843.
59. R. Hoffmann, J. Chem. Phys., 1963, 39, 1397–1412.
60. S. Lehtola, J. Chem. Theory Comput., 2019, 15, 1593–1604.
61. J. Almlöf, K. Faegri Jr and K. Korsell, J. Comput. Chem., 1982, 3, 385–399.
62. L. Amat and R. Carbó-Dorca, Int. J. Quantum Chem., 2001, 87, 59–67.
63. J. H. Van Lenthe, R. Zwaans, H. J. J. Van Dam and M. F. Guest, J. Comput. Chem., 2006, 27, 926–932.
64. S. Lehtola, L. Visscher and E. Engel, J. Chem. Phys., 2020, 152, 144105.
65. D. N. Laikov and K. R. Briling, Theor. Chem. Acc., 2020, 139, 17.
66. B. J. Lynch and D. G. Truhlar, J. Phys. Chem. A, 2003, 107, 3898–3906.
67. K. V. Chuang and M. J. Keiser, Science, 2018, 362, eaat8603.
68. R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096.

---

Footnotes

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d1dd00050k

‡ These authors contributed equally to this work.

---