Open Access Article
Open Access ArticleA transfer learning protocol for chemical catalysis using a recurrent neural network adapted from natural language processing†
Sukriti
Singh
*a and
Raghavan B.
Sunoj
 *ab
*ab
aDepartment of Chemistry, Indian Institute of Technology Bombay, Mumbai 400076, India. E-mail: sukriti243@gmail.com; sunoj@chem.iitb.ac.in
bCentre for Machine Intelligence and Data Science, Indian Institute of Technology Bombay, Mumbai 400076, India
First published on 11th April 2022
Abstract
Minimizing the time and material investments in discovering molecular catalysis would be immensely beneficial. Given the high contemporary importance of homogeneous catalysis in general, and asymmetric catalysis in particular, makes them the most compelling systems for leveraging the power of machine learning (ML). We see an overarching connection between the powerful ML tools such as the transfer learning (TL) used in natural language processing (NLP) and the chemical space, when the latter is described using the SMILES strings conducive for representation learning. We developed a TL protocol, trained on 1 million molecules first, and exploited its ability for accurate predictions of the yield and enantiomeric excess for three diverse reaction classes, encompassing over 5000 transition metal- and organo-catalytic reactions. The TL predicted yields in the Pd-catalyzed Buchwald–Hartwig cross-coupling reaction offered the highest accuracy, with an impressive RMSE of 4.89 implying that 97% of the predicted yields were within 10 units of the actual experimental value. In the case of catalytic asymmetric reactions, such as the enantioselective N,S-acetal formation and asymmetric hydrogenation, RMSEs of 8.65 and 8.38 could be obtained respectively, with the predicted enantioselectivities (%ee) within 10 units of its true value in ∼90% of the time. The method is highly time-economic as the workflow bypasses collecting the molecular descriptors and hence of direct implication to high throughput discovery of catalytic transformations.
Introduction
Chemical catalysis is a vibrant domain of research pursued alike in industry and academia owing to its importance in energy, automobile, fine chemicals, pharmaceuticals and so on.1,2 The drive to invent newer catalytic protocols or to impart superior efficiency to the known processes has been perpetual.3,4 The design of new catalysts, such as for homogeneous molecular catalysis, has remained in the forefront for decades.5,6 Such efforts are generally guided by chemical intuition and might even demand tiresome loops of trial and error.7 In recent years, the traditional approaches in catalysis were augmented by tools such as linear regression,8 machine learning (ML),9 active learning,10 and robotics;11,12 all seem to point to an emerging synergism in reaction discovery.13–15From a sustainability standpoint, it is high time that we endeavor to develop faster, reliable, and less resource intensive (e.g., time and material) invention workflows. To make this goal more realistic, ML driven protocols have a highly promising role to play.16,17 The yield and enantiomeric excess are countable indicators of how good a (asymmetric)catalytic method is, particularly in its developmental stage. One would inevitably encounter a high-dimensional chemical space composed of relevant molecular features of catalysts, substrates, solvent, additives, etc., for training ML models to predict the yields/ee of catalytic reactions.18,19 For instance, Rothenberg et al. built a classification and regression model for predicting the turnover number (TON) and turnover frequency (TOF) for 412 Heck reactions.20 A total of 74 physical organic descriptors were employed for the reaction components such as the substrate, ligand, solvent and so on in addition to the inclusion of reaction conditions (time, temperature, catalyst loading, etc.). The artificial neural networks were found to perform better than the linear regression techniques. The trained model was then utilized to predict the TON and TOF of a virtual library (in silico) of 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Heck reactions. In the recent years, there has been a visible increase in efforts in developing new molecular representations capable of improved performance and generalizability. Several approaches, other than those relying on quantum chemically derived molecular descriptors, have emerged. These methods primarily involve the use of various genres of structure-based representations.21–23
000 Heck reactions. In the recent years, there has been a visible increase in efforts in developing new molecular representations capable of improved performance and generalizability. Several approaches, other than those relying on quantum chemically derived molecular descriptors, have emerged. These methods primarily involve the use of various genres of structure-based representations.21–23
The representation learning methods such as the deep neural networks (DNNs) built on engineered features have found profound applications in chemical space.24,25 DNNs can also be trained on molecular representations, such as the SMILES (simplified molecular input line entry system) strings, to learn the feature representation involving minimal feature engineering.26 This approach can grasp the underlying patterns in atomic connectivity and capture the relationship between such features and molecular properties. During the developmental phase in catalysis research, only smaller or fragmented datasets are typically available, thereby necessitating a work-around, should one choose to deploy DNNs. It may be possible that tools from seemingly disparate domains become valuable for a task at hand, provided that shared or latent characteristics exist between them.
Natural language processing (NLP) is one of the most visible domains of artificial intelligence that provides computers the capability to generate and analyze text/speech.27 The large/labeled data requirements in NLP could be circumvented by using transfer learning methods,28 wherein the knowledge acquired from one task (source task) is retained and subsequently utilized for other related tasks (target task). Therefore, NLP could be deployed for those tasks that rely on the language or similar textual data. The SMILES representation of molecules can be considered analogous to a natural language. In fact, interesting applications of NLP-based methods to chemical reactions are now becoming available.29–31 The use of NLP-based models for accurate prediction of various properties of molecules is well-known.32,33 On the other hand, predicting the reaction outcome that is known to depend on the molecular attributes of catalysts, reactants, solvents and several other factors is challenging and has seldom been reported using language models.
Currently, most of the ML models for ee or yield predictions are custom-made for specific reactions, limiting their direct transferability to another reaction class. Further, such models are built on atomic/molecular descriptors as obtained through workflows involving time-consuming quantum chemical computations on a large library of molecules. We envisaged that NLP methods in conjunction with the SMILES representation of the molecular space could offer learning tools suitable for chemical catalysis. Such approaches could be transferable and time-economic. Herein, we design ML models that can predict both ee and yield of catalytic reactions. To demonstrate our ML protocol, a repertoire of transition metal-as well as organo-catalytic transformations of high recent interest, such as the (1) Buchwald–Hartwig reaction,34 (2) enantioselective N,S-acetal formation,35 and (3) asymmetric hydrogenation of alkenes/imines36 are chosen (Fig. 1a) (ESI Tables S1, S15, and S26†). It of importance to note that these reactions are of high contemporary importance owing primarily to their practical utility. For instance, reaction-1 finds broad applicability in pharmaceutical synthesis.37 The BINOL-derived chiral phosphoric acid catalysts, as employed in reaction-2, are valuable in a number of synthetically useful reactions.38 Reaction-3 and the catalyst families therein are employed in enantioselective synthesis of pharmaceuticals and agrochemicals.39 The trained ML model comprising these scaffolds would therefore be beneficial for reaction development. The availability of performance indices of various ML models on these reactions makes them the most suitable candidates as it enables us to place our NLP based transfer learning results vis-à-vis the reported benchmarks. In addition, the data distribution shown in Fig. 1b is representative of several pragmatic scenarios encompassing a (a) good number of samples (reaction-1) and their balanced distribution (reactions 1 and 2), or (b) fewer samples and unequal distribution (reaction-3) between the higher and lower ee/yield regions. Therefore, we believe that a unified TL model, applicable to all these types of data distributions, would find superior utility.
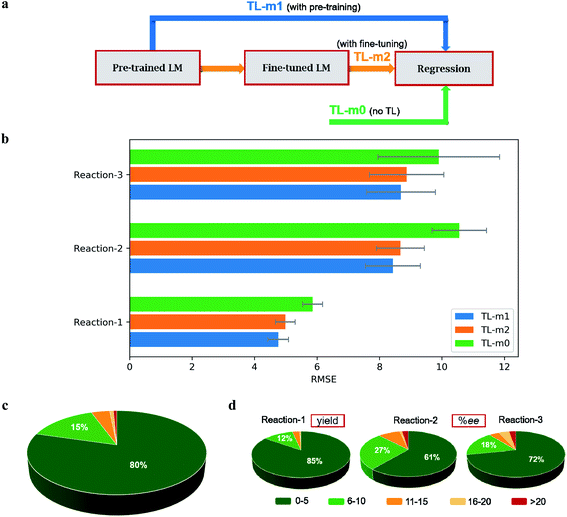
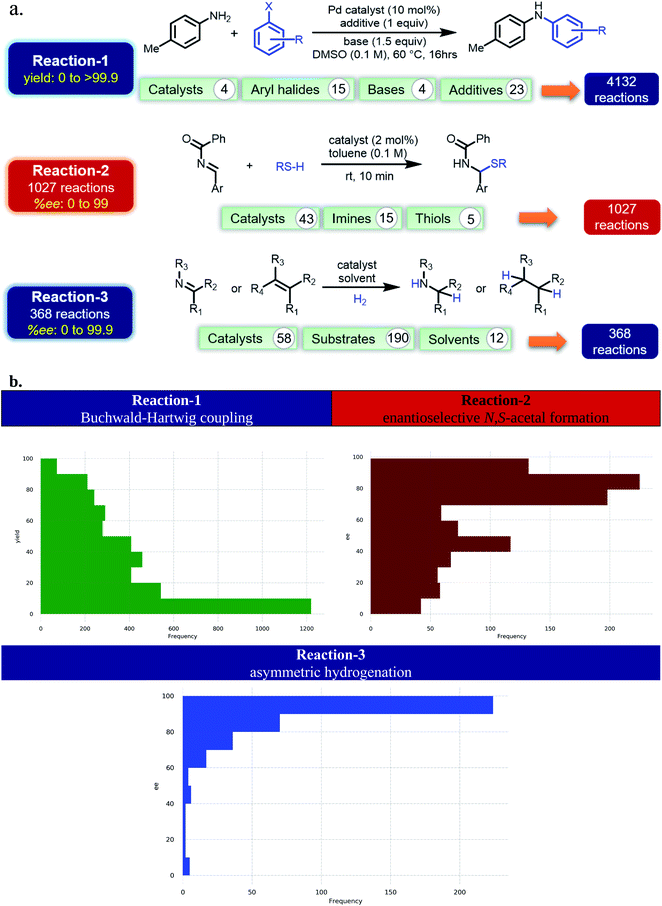 | ||
| Fig. 1 (a) The choice of reactions. (b) Distribution of the samples across various yield/ee regimes. | ||
Methods
Universal Language Model Fine-Tuning (ULMFiT) is a transfer learning method that can be applied for any NLP task. Here, the source task is a language model (LM) trained to predict the next word in a sentence, and the target task can be a classification/regression problem. A general overview of ULMFiT can be considered as involving three key steps as described below.(1) General domain language model (LM) pre-training: given a sequence, a trained LM can predict the probability of the next word. In the context of SMILES, a chemical LM is trained to predict the next character in a sequence of SMILES strings. To efficiently learn the characteristics of the SMILES representation, a large amount of data is required. For this purpose, we have pre-trained a general domain chemical LM using one million molecules from the ChEMBL database.40,41 This is known as the general domain LM as it is trained on a large set of diverse data to acquire a desirable level of learned representation that carries semantic or structural meanings of SMILES, beneficial for other downstream tasks. Different strategies are available for SMILES pre-training.42–44 For instance, in the ULMFiT method, the prediction of the next character in the SMILES string is the key task. In masked language modeling, some of the input tokens are masked, and the model is trained to predict such masked tokens.43 In the SMILES equivalence approach, given two SMILES strings, the task is to predict if they represent the same molecule.42 The generative strategy is also used for pre-training, wherein from a given input SMILES representation, the model is trained to generate valid and equivalent SMILES.44
(2) Target task LM fine-tuning: in the target task, we have chosen three reactions (Fig. 1a), which form a labeled dataset with reaction yield or ee as the output. Following the standard protocol in transfer learning, the knowledge acquired in the previous pre-training step is utilized for the target task. Consequently, the LM is fine-tuned on the target-task data to learn and predict the next character in a SMILES sequence. The key difference from the previously trained general domain LM is that the model has now learned the task-specific features of the SMILES language.
(3) Target task regressor: since the goal of our machine learning model is to predict the yield/ee of the reaction of interest, in the third step, the pre-trained or fine-tuned LM is accordingly expanded for the required regression task.
Fine-tuning the target regressor is crucial to transfer learning as an aggressive fine-tuning might even nullify the benefits of a trained LM. We examined the effect of two approaches in fine-tuning, depending on how the weights in the hidden layers are handled. In the first approach for fine-tuning, the model initialization with the pre-trained (or fine-tuned) weights and training the full model is done at once. In other words, the method employing a fixed learning rate and without frozen weights constitutes the first protocol. Another technique involving gradual unfreezing is also used for fine-tuning. In gradual unfreezing, we start with frozen weights first, and the layers are unfrozen step-by-step during training, and this process is repeated until the entire model is unfrozen and fine-tuned. The results presented in the manuscript are obtained by using the first protocol of fine-tuning without gradual unfreezing. However, the performance comparison employing both of these fine-tuning methods is also done (ESI sections 2 and 11†).
Dataset preparation
The reactions considered in this study consist of multiple chemical entities such as a catalyst, substrates, additives/solvents, etc., and the reaction outcome depends on the nature of these participating species. The SMILES strings of the individual reaction partners are therefore merged together, as shown in Fig. 2, for a representative reaction. The concatenated SMILES thus generated provides a composite representation for the desired reaction. To make these strings machine readable, the individual characters are generated through tokenization, wherein individual strings are split into tokens (e.g., ‘C’, ‘o’, ‘(’, ‘=’, ‘p’, etc.) separated by a dot (.). These tokens are then numericalized to integers. Based on the location of a token, a unique id is assigned to each token. The encoded token is then matched to the embedding vector via one-hot encoding (Fig. 2). The mapping of each of the tokens to their respective ids serves as an input for the deep learning model.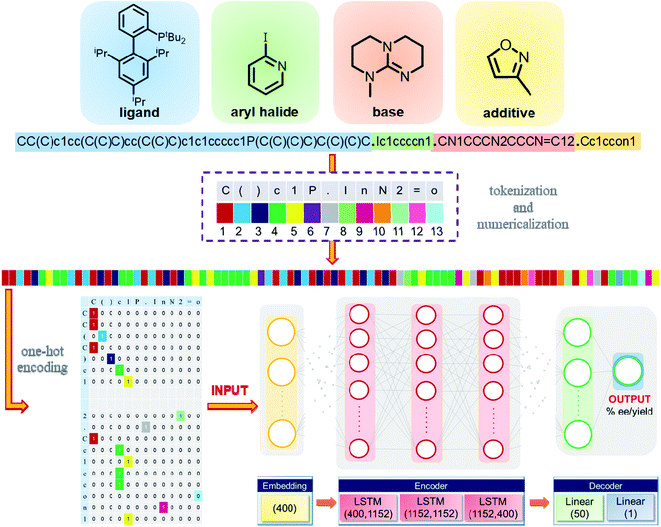 | ||
| Fig. 2 Illustration of the conversion of a representative sample from its SMILES strings to a machine-readable input, and a schematic diagram of the model architecture. More details on the model architecture are described in section 1.2† of the ESI. | ||
Exact splits are not readily available for all the reactions considered here. In the earlier report on reaction-1, only one 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 train-test split was used, while for reaction-2, ten different 600
30 train-test split was used, while for reaction-2, ten different 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 475 train-test splits were used. In the case of reaction-3, hundred different 80
475 train-test splits were used. In the case of reaction-3, hundred different 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 train-test splits were used. To ensure uniformity across all three reactions considered in this study, we have employed ten different 80
20 train-test splits were used. To ensure uniformity across all three reactions considered in this study, we have employed ten different 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 train-test splits. The full set of samples of a given reaction type was randomly split into a 70
20 train-test splits. The full set of samples of a given reaction type was randomly split into a 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 train-validation-test set. All the hyperparameter tuning was performed on the validation set, and the best set of hyperparameters thus obtained was used for prediction on the test set (ESI sections 12 and 13†).
20 train-validation-test set. All the hyperparameter tuning was performed on the validation set, and the best set of hyperparameters thus obtained was used for prediction on the test set (ESI sections 12 and 13†).
Results and discussion
First, an unambiguous naming of all molecules is done using a traversal 2D graph representation SMILES that carries more information than their respective chemical formula (ESI section 3†).45,46 In this text-based representation, a molecule is expressed as a linear string of characters with a linguistic construct, to render it conducive for language models (Fig. 2). The one unique SMILES representation for a molecule that satisfies a certain set of rules among all valid possibilities is known as the canonical SMILES. It is widely known that the deep learning models generally require large data for superior performance, and various data augmentation techniques have therefore been developed over the years.47 In the case of SMILES strings, a given molecule can be represented using multiple SMILES that differ in the starting atom and/or in the random directions chosen for traversing the graph (ESI Fig. S8 and S9†).48 The possibilities of SMILES generated through the randomization technique can be quite large. In the present context, we have selected the number of SMILES based on the requirement for each reaction type, instead of generating all possible SMILES. This procedure thus allows for desirable data augmentation and provides all valid SMILES. This is particularly beneficial for problems with a smaller data size. The ULMFiT (Universal Language Model Fine-tuning) is one of the state-of-the-art models that enable transfer learning for NLP tasks.49 Typically, a language model (LM) is first trained on a large dataset, and the pre-trained LM thus obtained is then fine-tuned on a target task (ESI Fig. S2 and S3†).In the present study, we endeavor to combine SMILES and ULMFiT to build a unified model that can predict (a) enantiomeric excess (%ee) in asymmetric catalysis and (b) yield (expressed in % of product formed) of catalytic reactions. Here, the source task is the chemical language modeling, and the target task is a regression problem to predict %ee or %yield (ESI Fig. S4†). The potential of this concept is evaluated on the reactions shown in Fig. 1a. The reported root mean square errors (i.e., RMSEs with respect to the corresponding experimental values) for reactions 1 and 3 were 7.8% and 8.4%, respectively, with the best performing RF algorithm built on quantum mechanically derived descriptors.34,36 In the case of reaction-2, the support vector machine (SVM) gave a mean absolute error (MAE, in terms of (ΔG‡R − ΔG‡S)) of 0.15 ± 0.005 kcal mol−1.35
We have pre-trained a language model with the ULMFiT architecture on the SMILES strings derived from 1 million molecules (ESI section 1†). This model is henceforth denoted as TL-m1 (i.e., with pre-training, Fig. 3a) and is used for predicting the %yield and %ee. The model performance, estimated in terms of the RMSE (in %yield or %ee) averaged over 30 independent runs, is provided in Fig. 3b (ESI sections 5.8, 6.6, and 7.6†). In this approach, we noticed that varying levels of SMILES augmentation, in the range of 25 (for reaction-1) to 100 (reaction-3), assures improved performance (ESI section 8†).50 It is discernible from the summary of results that the transfer learning returns better predictions. For instance, the most significant improvement is noted for reaction-1 with an RMSE of 4.89 ± 0.33 for our 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 train-test approach (ESI Table S13†). With a split of 70
20 train-test approach (ESI Table S13†). With a split of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30, we could obtain a performance of 5.11 ± 0.47 as compared to the earlier benchmark of 7.8. However, for reaction-3, the TL-m1 yielded a very similar result to that of the reported RF model (ESI Tables S30 and S35†). Similar RMSEs of 8.65 ± 0.80 and 8.38 ± 1.40 are noted respectively for reactions 2 and 3 (ESI Tables S19 and S25†).
30, we could obtain a performance of 5.11 ± 0.47 as compared to the earlier benchmark of 7.8. However, for reaction-3, the TL-m1 yielded a very similar result to that of the reported RF model (ESI Tables S30 and S35†). Similar RMSEs of 8.65 ± 0.80 and 8.38 ± 1.40 are noted respectively for reactions 2 and 3 (ESI Tables S19 and S25†).
At this juncture, in keeping with the standard practice in NLP, we wondered whether LM fine-tuning on the target-task might become beneficial (TL-m2, i.e., with fine-tuning, Fig. 3a). For all the three reactions, no improvement in the predictive capability of TL-m2 as compared to TL-m1 is noticed (Fig. 3b). The advantage of TL models can be evaluated by comparing the test performance of the ULMFiT architecture devoid of pre-training (TL-m1) and fine-tuning (TL-m2). An ablation study without using TL is carried out to evaluate the effect of transfer learning. Such a model, denoted as TL-m0 (i.e., with no TL, Fig. 3a), is found to be inferior to TL-m1/m2. In addition, the TL architecture can be used across different reaction classes (ESI sections 5.2, 5.4, 6.2, 6.4, 7.2 and 7.4†).
As discussed in the previous section, a second protocol involving the fine-tuning of the regressor using gradual unfreezing is also investigated. In this case, it is found that the TL is of no benefit to reaction-1, as can be seen from the corresponding performance metric of TL-m1 (6.02 ± 0.29), TL-m2 (6.69 ± 0.27), and TL-m0 (5.84 ± 0.49) (ESI sections 5.3 and 5.4†). However, in the case of reaction-3, TL is found to be more effective as evident from the performance of TL-m1 (8.56 ± 1.46), TL-m2 (8.61 ± 1.34), and TL-m0 (10.67 ± 2.54) models (ESI sections 7.3 and 7.4†). Similar results are obtained for reaction-2 as well, with TL-m1 (8.88 ± 0.96), TL-m2 (9.11 ± 1.15), and TL-m0 (11.83 ± 1.75) (ESI sections 6.3 and 6.4†). On comparing the results of fine-tuning the regressor, with or without gradual unfreezing, some interesting observations could be made. The largest performance boost is obtained for reaction-1 where the test RMSE for TL-m1/m2 reduced from 6.02 ± 0.29/6.69 ± 0.27 to 4.89 ± 0.33/5.27 ± 0.34 upon removing the gradual unfreezing. For reactions 2 and 3, no significant performance change is noted (ESI section 15†).
We noticed that there is no significant improvement with TL-m2 where the model is fine-tuned to a task-specific dataset (Fig. 3b). The fine-tuning is a delicate process as it may affect how much information learned from pre-training is retained. One of the ways to maintain this balance is the use of gradual unfreezing while fine-tuning. Therefore, fine-tuning using gradual unfreezing is also attempted to check whether the additional information with fine-tuning makes a notable difference. We noticed that the trend is same across all the three reactions when the model is fine-tuned with or without gradual unfreezing (ESI Table S43†).
Several intriguing aspects emerged through a comparison between the predictive capabilities for each reaction class and the nature of the corresponding data distribution as given in Fig. 3b and 1b. For instance, the best performance among all the reaction classes could be obtained with TL-m1 for reaction-1, which has rich and uniformly distributed output values. On the other hand, the most difficult system to predict in Fig. 4a is reaction-3, where both TL-m1/m2 results turned out to be very similar to the previously established RF performance. This can be attributed to low and sparse data along with class imbalance where the data are clustered around a high ee region. This may lead to a large deviation in the prediction of high ee samples with similar features. Another general strength of our TL-m1 can be gleaned on the basis of the overall quality of predictions of %yield and %ee; across all three reactions consisting of 1107 predictions in a typical test run (Fig. 3c) as well as for the individual reaction class (Fig. 3d). Of these, 95% of predictions were found to be within 10 units of the actual experimental value.
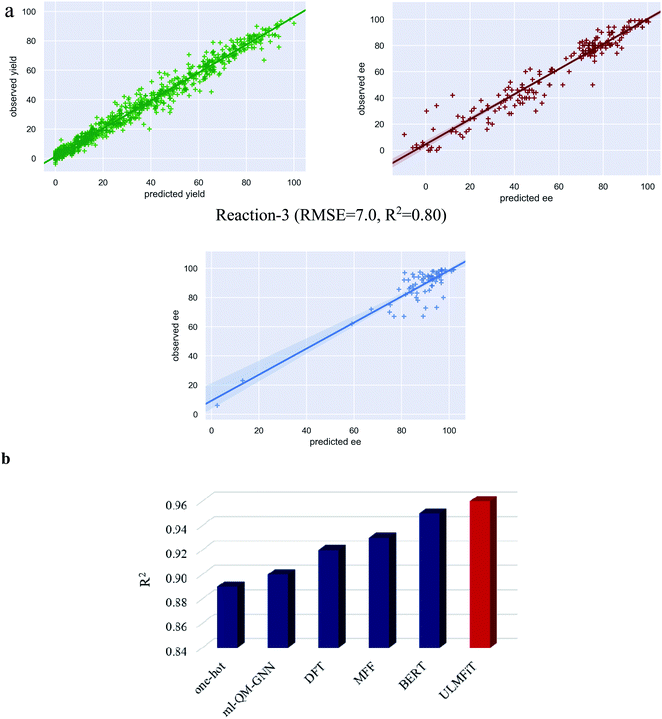 | ||
| Fig. 4 (a) The plots of predicted versus observed yields/ee for all three reactions. (b) Comparison of performance of different machine learning models for the yield predictions on the Buchwald–Hartwig cross-coupling dataset (reaction-1). The following acronyms are used; ml-QM-GNN: Quantum Mechanical descriptors and Graph Neural Network; DFT: Density Functional Theory; MFF: Multiple Fingerprint Features; BERT: Bidirectional Encoder Representations from Transformers; ULMFiT: Universal Language Model Fine-Tuning. It should be noted that the R2 values used here are exclusively for reaction-1 to enable a direct comparison with the previous reports, as it is the only performance metric available for this reaction across different ML protocols (ref. 21–23). | ||
To further analyze the model performance, we have plotted the predicted versus observed values for the best performing test set as a representative example for all the three reactions (Fig. 4a). The plot for reaction-1 is found to be most impressive with an R2 of 0.97 corresponding to an RMSE of 4.3. In the case of reaction-3, the data are clustered around the high ee region (Fig. 1b). Therefore, R2 may not be a good metric of the reaction performance. Nevertheless, the plot for reaction-3 is provided in Fig. 4a, with an R2 of 0.80 that corresponds to an RMSE of 7.0. In addition, we believe that the utility of TL-m0 should equally be acknowledged as it offers the most time economic performance for problems with uniform distribution of samples (as in reaction-1). In addition to the comparison between different transfer learning models, we have also undertaken an explicit performance comparison of our protocol with that of earlier approaches by taking the most well studied Buchwald–Hartwig cross-coupling reaction.
A comparison of performance between different ML methods on reaction-1
The Buchwald–Hartwig cross-coupling dataset34 has been used in multiple studies to evaluate the relative performance of various ML methods. Shown in Fig. 4b is a summary of the results expressed using the corresponding R-squared (R2) value as the measure of performance of different such ML protocols. The originally reported random forest model built on the DFT-based descriptors offered an R2 of 0.92.34 In another approach, wherein the molecular descriptors were replaced with one-hot encoded vector representations, an R2 of 0.89 was obtained.21,51 More recently, structure-based multiple fingerprint features (MFFs) were introduced as an alternative representation which yielded an improved R2 of 0.93.21 In another interesting approach for yield prediction, denoted as ml-QM-GNN, a combination of quantum mechanical descriptors and machine-learned representation (using the graph neural network, GNN) offered an R2 of 0.90.22 The transformer-based models have also been adopted for yield prediction tasks wherein the encoder of the transformer trained on the SMILES representation of molecules is subsequently augmented with a regression layer for yield prediction. This method with an R2 of 0.95 exceeds the performance of previous methods.23 Most importantly, we could obtain an R2 of 0.96 (obtained using TL-m1) with our transfer learning approach using the ULMFiT with SMILES strings (ESI section 5.6).52 In addition, the model generalizability is evaluated on non-random splits similar to that employed in previous studies.34,35,51 We have used the same out-of-samples splits for prediction using our language model (TL-m1) (ESI section 14†). We could obtain comparable performance with respect to the previous methods, thus demonstrating the utility of our protocol.Feature importance
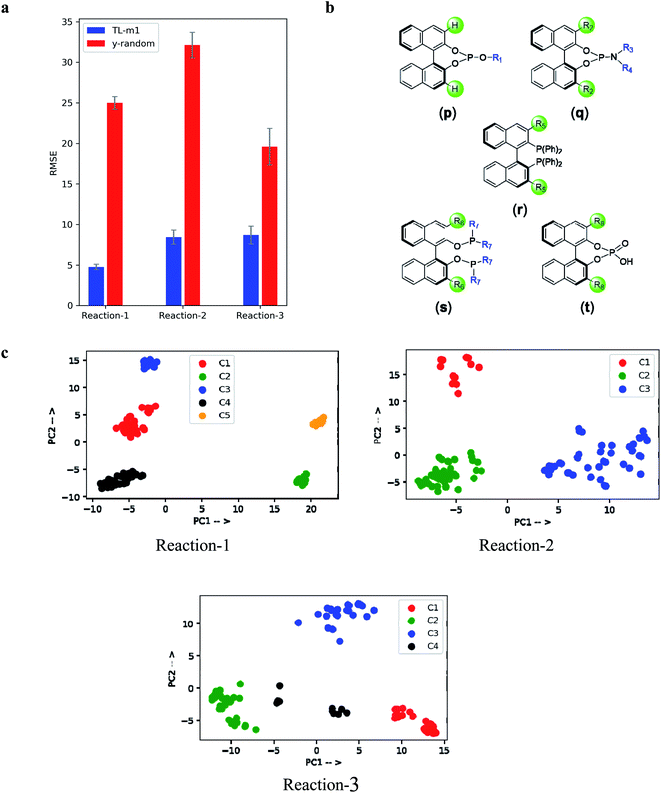
In view of some of the known concerns over chemical featurization as well as whether the ML model truly learns from the features provided or not,53 we have performed additional calculations as controls. First, the results of y-randomization of the output values were found to be abysmally off from both (a) the actual experimental values (ESI sections 5.5, 6.5, and 7.5†), and (b) the ones predicted using the correct SMILES (Fig. 5a). Second, the principal component analysis (PCA) of the encoder output revealed remarkably relevant chemical information. The presence of different clusters in each reaction class is readily discernible from Fig. 5c. While more discussion can be found in the ESI,† herein we wish to describe reaction-3 as a representative case. The clusters were primarily based on the similarity of the ligands (Fig. 5b) of the four distinct clusters, BINOL-phosphite (p) and BINOL-phosphoramidite (q) ligands get grouped together in cluster C2 (shown in green color), whereas BINOL-phosphoramidite appears exclusively in C4 (black). The similar ligands, such as BINAP (r) and BINAP-O (s), form C3 (blue). Interestingly, the only organocatalyst BINOL-phosphoric acid (t) forms a distinct cluster C1 (red). The relevant chemical information latently present in the encoder output could provide additional insights that in turn can be extrapolated to a newer chemical space. Third, the out-of-sample test set is considered for evaluating the model generalizability. We could obtain comparable performance on the non-random splits as originally used in the previous studies, thus demonstrating that our model does not simply fit to the structure in the dataset, but learns from the meaningful featurization of these reactions as provided. All these characteristics together convey that our TL model indeed learned certain reaction specific details from the SMILES representation (ESI sections 10, 14, and 15†).Now, consider a practically likely situation wherein one looks for a high yielding coupling partner, in the late-stage functionalization of a potential drug candidate, say using the Buchwald–Hartwig amination or via the asymmetric hydrogenation. Having equipped with the once-in-for-all trained TL-m1 model for these reactions, it is a straightforward task to predict whether or not the intended choice of substrate is likely to be successful. Here, the entire pipeline of feature extraction using quantum chemical computations can be bypassed through the generation of SMILES strings for the concerned substrates, just in a matter of a few minutes, thus making our protocol highly time-economic (ESI section 9†). In essence, when the initial batch of results (say, yield or ee) becomes available during the development of catalytic reactions, our transfer learning approach can be deployed for its training on the new data or augment the previous trained models with such new samples. A refined trained model, thus developed, would be able to quickly predict the outcome for unseen samples, i.e., the ones that are yet to be tested experimentally. This will help channelize time and resources on promising samples rather than trying out on a lot more additional samples.
In summary, our method directly uses SMILES strings as the input representation and thus doesn't require any additional step to convert SMILES to other frequently used alternate representations. This bypasses all the feature extraction steps and thus is highly time-economic. Our method can be used for both yield and ee predictions. We have demonstrated the ability of our protocol on three different catalytic reactions with varying data sizes (<400 to >4000) and data distribution (rich/balanced to sparse/imbalanced). One of the limitations in comparison to physical organic based descriptors is difficulty in gathering additional chemical or mechanistic insights from the trained model. The fine-tuning strategy seems to have an impact on the model performance. One method of fine-tuning, say using gradual unfreezing, may benefit a particular dataset, but not for another problem at the same time. Thus, the possible strategies could be to investigate the effect of fine-tuning on datasets of different sizes to understand how the reaction-specific information can be made more useful to learning. This can be especially of value for small datasets.
Conclusion
The NLP based transfer learning, as applied to the SMILES representation of the chemical space, has great potential for enabling a paradigm shift in ML deployments for homogeneous catalysis. In particular, a pre-trained model on a given reaction class can readily provide the first estimates on the likely success (%yield/enantioselectivity) for an intended set of new substrates for a given catalyst, just within a few minutes. The ability of our transfer learning model is demonstrated on three different catalytic reactions. For the Buchwald–Hartwig cross-coupling with well over 4000 reactions, the model was able to make accurate prediction of yields with an impressive RMSE of 4.89 ± 0.33, i.e., 97% of the time, the predicted yields were within 10 units of the actual experimental values. In the case of enantioselective N,S-acetal formation, comprising 1027 examples, and for asymmetric hydrogenation with as low as 368 examples, the model could obtain an RMSE in the predicted enantioselectivities (%ee) of 8.65 ± 0.80 and 8.38 ± 1.40, respectively, as compared to the corresponding experimentally known values. This indicates that ∼90% of the predicted %ee are within 10 units of its actual value. It is therefore assuring that our TL protocol is applicable for catalytic reactions with different data sizes as well as distribution within each such example. Furthermore, additional analyses (y-randomization and principal component analysis on the encoder output) showed that the model was able to capture the relevant chemical information, vindicating that it indeed learnt some important characteristics of these reactions from the SMILES representation. The preliminary data on a novel/emerging reaction, even bearing notable diversities in the catalyst/substrate structures, can also be quickly trained to build a transfer learning model. The protocol can be tailored as an effective time economic tool for high-throughput discovery of chemical reactions and hence might as well be a game changer toward realizing greater sustainability.Data availability
Data and codes related to this work are publicly available through Github at https://github.com/Sunojlab/Transfer_Learning_in_Catalysis.Conflicts of interest
The authors declare no conflicting financial interests.Acknowledgements
We acknowledge Prof. Preethi Jyothi (Department of Computer Science and Engineering, IIT Bombay) for valuable discussions during the course of this project.Notes and references
- A. Wang and L. Olsson, Nat. Catal., 2019, 2, 566–570 CrossRef.
- E. Roudner, Chem. Soc. Rev., 2014, 43, 8226–8239 RSC.
- J. G. Freeze, H. R. Kelly and V. S. Batista, Chem. Rev., 2019, 119, 6595–6612 CrossRef CAS PubMed.
- A. J. Neel, M. J. Hilton, M. S. Sigman and F. D. Toste, Nature, 2017, 543, 637–646 CrossRef CAS PubMed.
- M. Foscato and V. R. Jensen, ACS Catal., 2020, 10, 2354–2377 CrossRef CAS.
- L. Falivene, Z. Cao, A. Petta, L. Serra, A. Poater, R. Oliva, V. Scarano and L. Cavallo, Nat. Chem., 2019, 11, 872–879 CrossRef CAS PubMed.
- A. L. Dewyer, A. J. Arguelles and P. M. Zimmerman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1354 Search PubMed.
- J. P. Reid and M. S. Sigman, Nature, 2019, 571, 343–348 CrossRef CAS PubMed.
- M. I. Jordan and T. M. Mitchell, Science, 2015, 349, 255–260 CrossRef CAS PubMed.
- N. S. Eyke, W. H. Green and K. F. Jensen, React. Chem. Eng., 2020, 5, 1963–1972 RSC.
- C. W. Coley, D. A. Thomas, J. A. M. Lummiss, J. N. Jaworski, C. P. Breen, V. Schultz, T. Hart, J. S. Fishman, L. Rogers, H. Gao, R. W. Hicklin, P. P. Plehiers, J. Byington, J. S. Piotti, W. H. Green, A. H. Hart, T. F. Jamison and K. F. Jensen, Science, 2019, 365, eaax1566 CrossRef CAS.
- S. H. M. Mehr, M. Craven, A. I. Leonov, G. Keenan and L. Cronin, Science, 2020, 370, 101–108 CrossRef CAS.
- Y. Shi, P. L. Prieto, T. Zepel, S. Grunert and J. E. Hein, Acc. Chem. Res., 2021, 54, 546–555 CrossRef CAS PubMed.
- A.-C. Bedard, A. Adamo, K. S. Aroh, M. G. Russell, A. A. Bedermann, J. Torosian, B. Yue, K. F. Jensen and T. F. Jamison, Science, 2018, 361, 1220–1225 CrossRef CAS PubMed.
- M. Fitzner, G. Wuitschik, R. J. Koller, J.-M. Adam, T. Schindler and J.-L. Reymond, Chem. Sci., 2020, 11, 13085 RSC.
- F. Strieth-Kalthoff, F. Sandfort, M. H. S. Segler and F. Glorius, Chem. Soc. Rev., 2020, 49, 6154–6168 RSC.
- B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Nature, 2021, 590, 89–96 CrossRef CAS PubMed.
- L. C. Gallegos, G. Luchini, P. C. John, S. Kim and R. S. Paton, Acc. Chem. Res., 2021, 54, 827–836 CrossRef CAS PubMed.
- G. Skoraczyński, P. Dittwald, B. Miasojedow, S. Szymkuc, E. P. Gajewska, B. A. Grzybowski and A. Gambin, Sci. Rep., 2017, 7, 3582 CrossRef PubMed.
- E. Burello, D. Farrusseng and G. Rothenberg, Adv. Synth. Catal., 2004, 346, 1844–1853 CrossRef CAS.
- F. Sandfort, F. Strieth-Kalthoff, M. Kuhnemund, C. Beecks and F. Glorius, Chem, 2020, 6, 1379–1390 CAS.
- Y. Guan, C. W. Coley, H. Wu, D. Ranasinghe, E. Heid, T. J. Struble, L. Pattanaik, W. H. Green and K. F. Jensen, Chem. Sci., 2021, 12, 2198–2208 RSC.
- P. Schwaller, A. C. Vaucher, T. Laino and J.-L. Reymond, Mach. Learn.: Sci. Technol., 2021, 2, 015016 Search PubMed.
- E. Gawehn, J. A. Hiss and G. Schneider, Mol. Inf., 2016, 35, 3–14 CrossRef CAS.
- T. B. Hughes, N. L. Dang, G. P. Miller and S. Swamidass, ACS Cent. Sci., 2016, 8, 529–537 CrossRef.
- S. Zheng, X. Yan, Y. Yang and J. Xu, J. Chem. Inf. Model., 2019, 59, 914–923 CrossRef CAS.
- C. D. Manning, C. D. Manning and H. Schutze, Foundations of Statistical Natural Language Processing, MIT Press, 1999 Search PubMed.
- S. J. Pan and Q. Yang, IEEE Trans. Knowl. Data Eng., 2010, 22, 1345–1359 Search PubMed.
- G. Pesciullesi, P. Schwaller, T. Laino and J.-L. Reymond, Nat. Commun., 2020, 11, 4874 CrossRef CAS PubMed.
- X. Li and D. J. Fourches, J. Cheminf., 2020, 12, 27 CAS.
- S. Jiang, Z. Zhang, H. Zhao, J. Li, Y. Yang, B.-L. Lu and N. Xia, IEEE Access, 2021, 9, 85071–85083 Search PubMed.
- S. Wang, Y. Guo, Y. Wang, H. Sun and J. Huang, Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, 2019, pp. 429–436 Search PubMed.
- H. Kim, J. Lee, S. Ahn and R. L. Lee, Sci. Rep., 2021, 11, 11028 CrossRef CAS.
- D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Science, 2018, 360, 186–190 CrossRef CAS PubMed.
- A. F. Zahrt, J. J. Henle, B. T. Rose, Y. Wang, W. T. Darrow and S. E. Denmark, Science, 2019, 363, 1–11 CrossRef PubMed.
- S. Singh, M. Pareek, A. Changotra, S. Banerjee, B. Bhaskararao, P. Balamurugan and R. B. Sunoj, Proc. Natl. Acad. Sci. U.S.A., 2020, 117, 1339–1345 CrossRef CAS PubMed.
- P. Ruiz-Castillo and S. L. Buchwald, Chem. Rev., 2016, 116, 12564–12649 CrossRef CAS PubMed.
- D. Parmar, E. Sugiono, S. Raja and M. Rueping, Chem. Rev., 2017, 117, 10608–10620 CrossRef CAS PubMed.
- D. J. Ager, A. H. M. de Vries and J. G. de Vries, Chem. Soc. Rev., 2012, 41, 3340–3380 RSC.
- A. Gaulton, L. J. Bellis, A. P. Bento, J. Chambers, M. Davies, A. Hersey, Y. Light, S. McGlinchey, D. Michalovich, B. Al-Lazikani and J. P. Overington, Nucleic Acids Res., 2011, 40, D1100–D1107 CrossRef PubMed.
- The already curated one million SMILES were taken from 10.1186/s13321-020-00430-x for training the general-domain LM.
- B. Fabian, T. Edlich, H. Gaspar, M. Segler, J. Meyers, M. Fiscato and M. Ahmed, 2020, arXiv preprint arXiv:2011.13230.
- S. Chithrananda, G. Grand and B. Ramsundar, 2020, arXiv preprint arXiv:2010.09885.
- D. Xue, H. Zhang, D. Xiao, Y. Gong, G. Chuai, Y. Sun, H. Tian, H. Wu, Y. Li and Q. Liu, Sci. Bull., 2022 DOI:10.1016/j.scib.2022.01.029.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- Although stereochemical information is not present in the canonical SMILES as initially defined by Weininger, in the recent times many open-source programs (e.g., RDKit and OpenBabel) provide SMILES with stereochemical information, known as isomeric SMILES. In the case of reaction-1, the catalysts, aryl halides, bases, and additives are all achiral, whereas in reactions-2 and -3, the ligands are axially chiral. Since all the chiral ligands considered in our study bear the same axial configuration, consideration of this aspect is not directly relevant in the present context.
- M. Fadaee, A. Bisazza and C. Monz, 2017, arXiv preprint arXiv:1705.00440.
- E. J. Bjerrum, 2017, arXiv preprint arXiv:1703.07076.
- J. Howard and R. Sebastian, 2018, arXiv preprint arXiv:1801.06146.
- The data given in Table S36† are meant to convey the effect of data augmentation on predictive performance. However, the hyperparameter tuning has always been performed on the validation set.
- K. V. Chuang and M. J. Keiser, Science, 2018, 362, eaat8603 CrossRef PubMed.
- Besides the standard methods for generation of various test-train splits, for gauging the performance of ML models on the test sets, more challenging held-out sets (out-of-bag splits), same as reported in the original work (ref. 30), were also attempted. For eight different test splits consisting of additives, which were not present in the training set, an average RMSE of 10.0% was obtained, which is better than 11.3% with the random forest model built on quantum chemically derived molecular descriptors.
- K. V. Chuang and M. J. Keiser, ACS Chem. Biol., 2018, 13, 2819–2821 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d1dd00052g |
| This journal is © The Royal Society of Chemistry 2022 |