Open Access Article
Open Access ArticleParallel tempered genetic algorithm guided by deep neural networks for inverse molecular design†
AkshatKumar
Nigam‡
 abc,
Robert
Pollice‡
bc and
Alán
Aspuru-Guzik
*bcde
abc,
Robert
Pollice‡
bc and
Alán
Aspuru-Guzik
*bcde
aDepartment of Computer Science, Stanford University, USA
bDepartment of Computer Science, University of Toronto, Canada. E-mail: alan@aspuru.com
cDepartment of Chemistry, University of Toronto, Canada
dVector Institute for Artificial Intelligence, Toronto, Canada
eLebovic Fellow, Canadian Institute for Advanced Research (CIFAR), 661 University Ave, Toronto, Ontario M5G, Canada
First published on 3rd May 2022
Abstract
Inverse molecular design involves algorithms that sample molecules with specific target properties from a multitude of candidates and can be posed as an optimization problem. High-dimensional optimization tasks in the natural sciences are commonly tackled via population-based metaheuristic optimization algorithms such as evolutionary algorithms. However, often unavoidable expensive property evaluation can limit the widespread use of such approaches as the associated cost can become prohibitive. Herein, we present JANUS, a genetic algorithm inspired by parallel tempering. It propagates two populations, one for exploration and another for exploitation, improving optimization by reducing property evaluations. JANUS is augmented by a deep neural network that approximates molecular properties and relies on active learning for enhanced molecular sampling. It uses the SELFIES representation and the STONED algorithm for the efficient generation of structures, and outperforms other generative models in common inverse molecular design tasks achieving state-of-the-art target metrics across multiple benchmarks. As neither most of the benchmarks nor the structure generator in JANUS account for synthesizability, a significant fraction of the proposed molecules is synthetically infeasible demonstrating that this aspect needs to be considered when evaluating the performance of molecular generative models.
I. Introduction
Molecular design workflows usually consist of design-make-test-analyze cycles.1,2 Traditionally, the first step requires input from human scientists proposing molecules to be made and tested. In cheminformatics, powerful computer programs were constructed imitating human scientists designing molecules with desired properties. In recent years, the advent of machine learning (ML) in chemistry has reinvigorated these efforts and sparked the development of numerous data-driven tools for inverse molecular design.3–5Herein, we present JANUS, a genetic algorithm (GA) based on the SELFIES representation of molecules.6,7 It utilizes STONED8 for molecular generation, obviating structural validity checks. Inspired by parallel tempering,9,10 JANUS maintains two populations that exchange members and use distinct genetic operations. One population conducts a local (exploitative) search of the chemical space and uses molecular similarity as selection pressure. The other performs a global exploration and, optionally, uses a deep neural network (DNN) as selection pressure. While not requiring domain knowledge, we added the option to extract structure derivation rules from user-provided sets of molecules automatically. Comprehensive benchmarking shows that JANUS outperforms other generative models significantly in both fitness and number of fitness evaluations.
II. Background
Inverse molecular design creates structures with desired properties by inverting classical design that relies on structure first, property second. The idea is to specify target properties and explore the chemical space systematically to find structures optimizing them. Various approaches have been applied for that purpose including variational autoencoders (VAEs),11 generative adversarial networks (GANs),12 flow-based generative models,13 reinforcement learning (RL),14 sampling of Markov decision processes15 and metaheuristic optimization algorithms.16,17 Recent work about inverse molecular design based on deep learning methods is summarized in the ESI.† In the following, we will focus on metaheuristic optimization algorithms.GAs are population-based metaheuristic optimization algorithms and have a long-standing track record in the natural sciences for tackling complicated design problems.18,19 To the best of our knowledge, the first use of GAs for non-sequence-based de novo molecule design documented in the literature dates back to 1993. Two independent papers presented at the Molecular Graphics Society Meeting on Binding Sites at the University of York by researchers from the pharmaceutical industry described the application of GAs to problems related to drug design.20 One implementation made use of the SMILES molecular representation21,22 and was perhaps the first work to describe both the rediscovery of known molecules based on a molecular similarity metric and the use of a simplified ligand docking approach as benchmarks for molecular design.20 The other implementation demonstrated the optimization of molecular physical properties and was perhaps the first demonstration of designing log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P to probe the performance of molecular generative models.20
P to probe the performance of molecular generative models.20
In subsequent years, several implementations of GAs for molecular design in medicinal chemistry were published using various molecular representations and algorithms to perform structure generation. In 1995, PRO_LIGAND was the first detailed description of a GA for molecular design appearing in a scientific journal. Notably, it only made use of crossover operations. The algorithm identified suitable single bonds to break two parent molecules into two fragments each and subsequently recombine them randomly.23 Importantly, the 3D structure of the molecule was used directly as representation and the method was used to find mimics of the known drugs distamycin and methotrexate by comparing structural features.23 Almost simultaneously, another GA termed Chemical Genesis was described that used diverse mutation and crossover operations.24 Again, the 3D molecular structure was directly manipulated during molecular generation. Additionally, the algorithm implemented several molecular properties such as molecular weight, estimated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P and steric strain energy per atom as scalar constraints allowing to distinguish reasonable from unreasonable drug-like structures.24 Subsequently, this approach was tested designing ribose mimics and ligands for dihydrofolate reductase.24 Only a few years later, around the turn of the millennium, GAs gained significant popularity as molecular generative models and many implementations and case studies were published. Besides using the 3D structure of molecules directly for structure manipulation,25 molecular graphs,26–28 molecular strings,29 molecular fragments30–32 and chemical reactions33 were also employed. Importantly, all these approaches defined hand-crafted rules for mutation and crossover ensuring only valid structures to be generated.
P and steric strain energy per atom as scalar constraints allowing to distinguish reasonable from unreasonable drug-like structures.24 Subsequently, this approach was tested designing ribose mimics and ligands for dihydrofolate reductase.24 Only a few years later, around the turn of the millennium, GAs gained significant popularity as molecular generative models and many implementations and case studies were published. Besides using the 3D structure of molecules directly for structure manipulation,25 molecular graphs,26–28 molecular strings,29 molecular fragments30–32 and chemical reactions33 were also employed. Importantly, all these approaches defined hand-crafted rules for mutation and crossover ensuring only valid structures to be generated.
Early GA-based molecular design algorithms have been compared to alternative approaches for drug design in 2005,34 and, over the years, witnessing a host of new methods, more reviews and book chapters have been composed providing a comprehensive overview of that area.35–40 Accordingly, GAs have been applied to molecular design for decades, and they remain one of the most popular metaheuristic optimization algorithms for that purpose. The main difference between previously published approaches lies in the genetic operators, particularly mutation and crossover. Most prevalent are expert rules to ensure validity. Some recent examples of GAs implementing such expert rules include GB-GA,41 CReM,42 EvoMol43 and Molfinder.44 Alternatively, the robustness of SELFIES was exploited in GA + D7 allowing to rely on random string modifications for mutations. This obviates hand-crafted structure modification rules. In addition, GA + D makes use of a DNN discriminator driving molecular generation towards a reference distribution, or away from it. An alternative approach in the family of metaheuristic optimization algorithms is MSO,45 which uses particle swarm optimization in the continuous latent space of a VAE. Furthermore, mmpdb46 implements matched molecular pair analysis (MMPA47) and relies on structure modification rules explicitly derived from a dataset of molecule pairs. As the derived rules are applied stochastically, mmpdb can be considered a metaheuristic optimization algorithm.
III. Architecture
A Overview
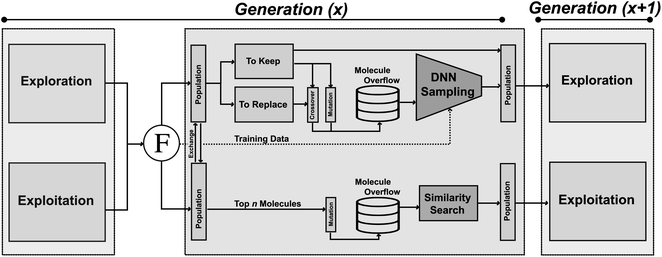
JANUS is a GA that is initiated either with random structures or with provided molecules. At every iteration, two molecule populations of fixed size are maintained. Members in each population compete against each other to proceed to the next generation. The quality of a molecule is determined by the fitness function. Between consecutive generations, JANUS uses elitist selection,59i.e., molecules with higher fitness survive, while structures with low fitness are replaced with new members generated via genetic operators. The genetic operators differ between the two populations, one being explorative and the other exploitative. Additionally, an overflow of potential children is produced from the parent molecules that is filtered using additional selection pressure. In the following, we will describe the components of JANUS (cf.Fig. 1) in more detail and highlight its differences to GA + D (cf. ESI Table 1†), a GA for molecular design developed previously.7B Genetic operators
Mutations and crossovers often require expert design. In contrast, JANUS relies on the STONED algorithm8 for efficient molecule generation. Namely, as demonstrated in ESI Fig. 2(a),† for mutating a molecule, random modifications (via character deletions, additions, or replacements) are performed on the corresponding SELFIES. To increase the diversity of the mutated structures, we use multiple reordered SMILES representations of the same molecule to generate numerous alternative SELFIES.8 Notably, GA + D uses the same mutation operator.7Starting from two molecules, an apt crossover resembles both parents. Hence, we form multiple paths between the two molecules (obtained via random string modifications of SELFIES, ESI Fig. 2(b)†), and select structures with high joint similarity (cf. Methods). Consideration of multiple SELFIES representations, multiple string modifications and the formation of numerous paths leads to the generation of many potential children. Importantly, GA + D does not use crossover operators.7
C Selection pressure
To deal with the molecule overflow, we add additional selection pressures when selecting children to be propagated to subsequent generations. Each generation, we train a DNN on molecules with known fitness. We explore training a DNN for both predicting the fitness function accurately (abbreviated as P) and for separating the good molecules (i.e., high fitness) from the bad (i.e., low fitness) with a classifier (abbreviated as C). The trained model evaluates the overflow molecules in the explorative population, and the most promising structures (i.e., highest estimated fitness) are added to the population. We also compare DNNs for applying selection pressure to randomly sampling the overflow molecules. For the exploitative population, additional selection pressure is added by only propagating the molecules most similar to the parents. GA + D does not use any additional selection pressure in the molecular generation.7D Parallel populations
Two populations of molecules are maintained. One explores the chemical space, the other exploits the regions possessing high fitness. New molecules in the exploration population are obtained using both mutation and crossover. Selection pressure is applied using a DNN upon the overflow molecules, establishing the next generation. Additionally, the explorative population is assigned an effective “temperature” parameter which determines what molecules are allowed to proceed to the genetic operators and the subsequent generation. This parameter is inspired by Fermi–Dirac statistics60,61 and gives molecules of lower fitness non-zero probabilities to be selected while still making it somewhat more likely to select molecules of higher fitness (details in ESI Section S3†). Consequently, the exploration population does not solely maintain high fitness solutions. This feature was implemented to allow for an escape of local optima. For the exploitation population, novel molecules are obtained using solely mutations. Subsequently, selection pressure is applied by picking molecules with high similarity to the parents from the overflow molecules. Furthermore, each generation, the two populations exchange members based on their fitness. Molecules of the explorative population with high fitness enter the exploitative population to investigate the corresponding structural regions more extensively. In turn, molecules from the exploitative population with high fitness enter the explorative population to investigate structural regions further away from current well-performing molecules. Notably, GA + D does not use parallel populations.7IV. Computational experiments
In the following, we compare JANUS against baseline methods in established molecular design benchmarks. In the ESI,† we present additional results including the constrained penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P optimization (cf. ESI Section S10†) and the GuacaMol suite of benchmarks65 without using additional DNN selection pressure (cf. ESI Section S13†). JANUS achieves state-of-the-art on most of these benchmarks. In particular, to the best of our knowledge, JANUS shows the second best performance of any generative model not relying on DNNs in GuacaMol.
P optimization (cf. ESI Section S10†) and the GuacaMol suite of benchmarks65 without using additional DNN selection pressure (cf. ESI Section S13†). JANUS achieves state-of-the-art on most of these benchmarks. In particular, to the best of our knowledge, JANUS shows the second best performance of any generative model not relying on DNNs in GuacaMol.
A Unconstrained penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) P optimization
P optimization
First, we investigated the performance of JANUS for maximizing the penalized logarithm of the octanol–water partition coefficient scores, referred to as penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P score J(m):66
P score J(m):66J(m) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(m) − SAscore(m) − RingPenalty(m) P(m) − SAscore(m) − RingPenalty(m) | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P scores can be generated by simply having longer SMILES. We compare both the averages of the best scores found in several independent runs and single best scores found within one particular run as both have been reported before.
P scores can be generated by simply having longer SMILES. We compare both the averages of the best scores found in several independent runs and single best scores found within one particular run as both have been reported before.
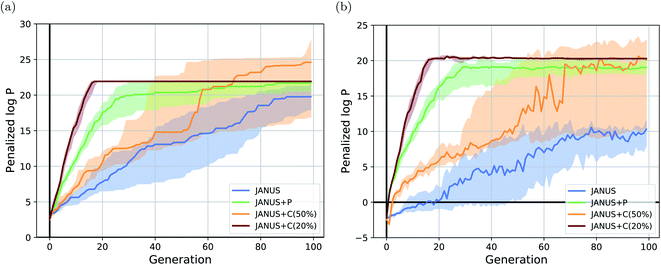
The corresponding results are summarized in Table 1. We run JANUS with four different variations of selection pressure, first without any additional selection pressure (i.e., randomly sampling the overflow) in the exploration population (“JANUS”), second with selection pressure from a DNN predictor trained to predict the molecular fitness (“JANUS + P”), and third with selection pressure from a DNN classifier trained to distinguish between high and low fitness molecules (“JANUS + C”). For the classifier, we also compare the performance of classifying the top 50% of all molecules as having a high fitness (“JANUS + C (50%)”) against only classifying the top 20% like that (“JANUS + C (20%)”). The optimization progress of JANUS with these four variations of selection pressure is depicted in Fig. 2.
| Algorithm | Average of best | Single best | Algorithm | Average of best | Single best |
|---|---|---|---|---|---|
a Average of 10 separate runs with 500 molecules of up to 81 SMILES characters per generation and 100 generations.
b Average of 5 separate runs with 500 molecules of up to 81 SMILES characters per generation and 1000 generations.
c Average of 5 separate runs with 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 molecules of up to 81 SMILES characters per generation and 200 generations.
d Average of 15 separate runs with 500 molecules of up to 81 SMILES characters per generation and 100 generations. 384 molecules of up to 81 SMILES characters per generation and 200 generations.
d Average of 15 separate runs with 500 molecules of up to 81 SMILES characters per generation and 100 generations.
|
|||||
| GVAE48 | 2.87 ± 0.06 | — | GA + Da7 | 13.31 ± 0.63 | 14.57 |
| SD-VAE49 | 3.60 ± 0.44 | — | GB-GAa41 | 15.76 ± 5.76 | — |
| ORGAN50 | 3.52 ± 0.08 | — | EvoMola43 | 17.71 ± 0.41 | 18.59 |
| CVAE + BO51 | 4.85 ± 0.17 | — | GA + Db7 | 20.72 ± 3.14 | 23.93 |
| JT-VAE52 | 4.90 ± 0.33 | — | GEGLc53 | 31.40 ± 0.00 | 31.40 |
| ChemTS54 | 5.6 ± 0.5 | — | |||
| GCPN55 | 7.87 ± 0.07 | — | JANUSd | 18.4 ± 4.4 | 20.96 |
| MRNN56 | — | 8.63 | JANUS + Pd | 21.0 ± 1.3 | 21.92 |
| MolDQN57 | — | 11.84 | JANUS + C (50%)d | 23.6 ± 6.9 | 34.04 |
| GraphAF58 | — | 12.23 | JANUS + C (20%)d | 21.9 ± 0.0 | 21.92 |
As seen in Table 1, JANUS outperforms all alternative approaches in terms of the single best molecule. GA + D merely reaches similarly high results after 10 times the number of generations. Only GEGL performs better on average than JANUS, but with double the number of generations and more than 30 times the number of structures per generation. While the average of the maximum penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P across independent runs does not show a large difference after 100 generations for the various selection pressure settings, both the optimization trajectory (cf.Fig. 2(a)) and the single best performing molecules found are significantly impacted. Using selection pressure via the DNN predictor (“JANUS + P′′) or the DNN classifier (“JANUS + C′′) results in populations with higher median fitness than without additional selection pressure (“JANUS”) (cf.Fig. 2(b)). Furthermore, selection pressure from the DNN predictor effects a fast fitness increase as the predictor learns the characteristics of molecules with a high penalized log
P across independent runs does not show a large difference after 100 generations for the various selection pressure settings, both the optimization trajectory (cf.Fig. 2(a)) and the single best performing molecules found are significantly impacted. Using selection pressure via the DNN predictor (“JANUS + P′′) or the DNN classifier (“JANUS + C′′) results in populations with higher median fitness than without additional selection pressure (“JANUS”) (cf.Fig. 2(b)). Furthermore, selection pressure from the DNN predictor effects a fast fitness increase as the predictor learns the characteristics of molecules with a high penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P score. The respective runs converge to the best-performing linear alkane with 81 carbon atoms, which corresponds to a local optimum. When selection pressure is applied via a DNN classifier, the optimization progress shows a large dependence on the fraction of molecules that are considered top-performing. When only the top 20% are considered top-performing, the respective runs converge to the best-performing linear alkane even faster than with the DNN predictor. However, the narrow fitness intervals of the generations indicate limited exploration of the chemical space leading to convergence to the same local optimum. When the top 50% are considered top-performing, exploration is significantly enhanced resulting in larger fitness variations across runs. This indicates that tuning classifier hyperparameters can be used to switch between exploration and exploitation.
P score. The respective runs converge to the best-performing linear alkane with 81 carbon atoms, which corresponds to a local optimum. When selection pressure is applied via a DNN classifier, the optimization progress shows a large dependence on the fraction of molecules that are considered top-performing. When only the top 20% are considered top-performing, the respective runs converge to the best-performing linear alkane even faster than with the DNN predictor. However, the narrow fitness intervals of the generations indicate limited exploration of the chemical space leading to convergence to the same local optimum. When the top 50% are considered top-performing, exploration is significantly enhanced resulting in larger fitness variations across runs. This indicates that tuning classifier hyperparameters can be used to switch between exploration and exploitation.
Finally, we also compare the number of property evaluations needed by JANUS and other models to reach three threshold fitness values (cf.Table 2). These results show that JANUS with the most exploitative classifier requires the lowest number of evaluations to reach penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values of 10, 15 and 20, respectively. The reduction in evaluations relative to JANUS without additional selection pressure corresponds to approximately 80%. We need to emphasize here that, as many of the other baselines were taken directly from the literature, detailed information about the number of property evaluations and the optimization trajectories were unavailable. We believe that it will be important for future comparisons of molecular generative models to provide detailed information about the number of property evaluations and the corresponding optimization trajectories. Nevertheless, among all the results and methods provided in the right column of Table 1, which correspond to the better-performing ones, JANUS uses the lowest total number of property evaluations to reach the corresponding results. However, despite a significant improvement, even the most aggressive method of selection pressure used requires 3500 property evaluations to surpass a penalized log
P values of 10, 15 and 20, respectively. The reduction in evaluations relative to JANUS without additional selection pressure corresponds to approximately 80%. We need to emphasize here that, as many of the other baselines were taken directly from the literature, detailed information about the number of property evaluations and the optimization trajectories were unavailable. We believe that it will be important for future comparisons of molecular generative models to provide detailed information about the number of property evaluations and the corresponding optimization trajectories. Nevertheless, among all the results and methods provided in the right column of Table 1, which correspond to the better-performing ones, JANUS uses the lowest total number of property evaluations to reach the corresponding results. However, despite a significant improvement, even the most aggressive method of selection pressure used requires 3500 property evaluations to surpass a penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P score of 10. This suggests that further work is needed for JANUS to be feasible for the direct optimization of more expensive molecular properties.
P score of 10. This suggests that further work is needed for JANUS to be feasible for the direct optimization of more expensive molecular properties.
To the best of our knowledge, JANUS identified the best-performing molecules ever found by molecular design algorithms that fulfill the 81 SMILES character limit, even outperforming GEGL. When JANUS (specifically “JANUS + C (50%)”) was allowed to run for more than 100 generations, a penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P value of 36.62 was achieved at generation 118 in one particular run. The fitness did not increase thereafter, but several isomers with identical fitness were discovered (cf.Fig. 3). It has been claimed that the unconstrained penalized log
P value of 36.62 was achieved at generation 118 in one particular run. The fitness did not increase thereafter, but several isomers with identical fitness were discovered (cf.Fig. 3). It has been claimed that the unconstrained penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P maximization task is not a useful benchmark as it has trivial solutions, molecules with ever longer chains.64 However, that is only true without enforcing a SMILES character limit. With the 81 character limit, the trade-off between log
P maximization task is not a useful benchmark as it has trivial solutions, molecules with ever longer chains.64 However, that is only true without enforcing a SMILES character limit. With the 81 character limit, the trade-off between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P and SAscore results in highly non-trivial solutions as evident from Fig. 3. Importantly, these structures are non-intuitive to design as the exact placement of the non-sulfur atoms in the chain affect the fitness considerably. Notably, JANUS even outperforms the human design demonstrated by Nigam et al.7 proposing a linear chain of sulfur atoms terminated by thiol groups with a penalized log
P and SAscore results in highly non-trivial solutions as evident from Fig. 3. Importantly, these structures are non-intuitive to design as the exact placement of the non-sulfur atoms in the chain affect the fitness considerably. Notably, JANUS even outperforms the human design demonstrated by Nigam et al.7 proposing a linear chain of sulfur atoms terminated by thiol groups with a penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P score of 31.79. In the ESI,† we also ran the benchmark where penalized log
P score of 31.79. In the ESI,† we also ran the benchmark where penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P scores are improved for select molecules with the constraint to keep the similarity to the initial structure high (cf. ESI Section S10†).
P scores are improved for select molecules with the constraint to keep the similarity to the initial structure high (cf. ESI Section S10†).
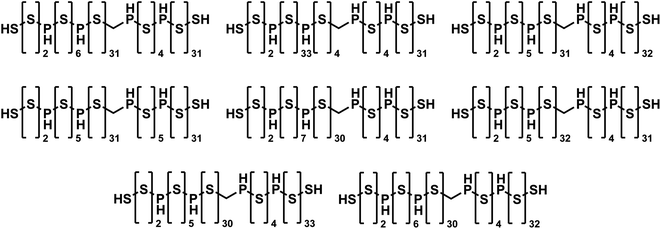 | ||
Fig. 3 Molecules discovered by JANUS with the highest penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P score of 36.62 that are within the 81 SMILES character limit. P score of 36.62 that are within the 81 SMILES character limit. | ||
B Imitated inhibition
Next, we tested JANUS in the imitated protein inhibition tasks introduced recently.62 The objective is generating 5000 molecules that inhibit either only GSK3β (A, Table 3), or only JNK3 (B, Table 3), or both (C, Table 3). A fourth task is to generate molecules that inhibit both GSK3β and JNK3, and also have high drug-likeness (i.e., QED ≥ 0.6)68 and a low synthetic accessibility score (SAscore ≤ 4.0).67 Inhibition is assessed via a random forest classifier that imitates docking62 wherein values above 0.5 indicate inhibition that is trained on a dataset taken from ChEMBL.69–71 Performance in these tasks is assessed via success, novelty and diversity metrics.62 The success metric is the fraction of the best 5000 molecules produced that fulfill the constraints. The novelty metric is based on the similarity of the generated molecules to a reference dataset. The diversity metric is based on the similarity among the generated molecules (cf. Section S8†).| Method | Success | Novelty | Diversity | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | A | B | C | D | A | B | C | D | |
| a Result obtained from using 500 molecules per generation and 278 generations in total. b Result obtained from using 500 molecules per generation and up to 100 generations in total. | ||||||||||||
| JTVAE52 | 32.2% | 23.5% | 3.3% | 1.3% | 11.8% | 2.9% | 7.9% | — | 0.901 | 0.882 | 0.883 | — |
| GCPN55 | 42.4% | 32.3% | 3.5% | 4.0% | 11.6% | 4.4% | 8.0% | — | 0.904 | 0.884 | 0.874 | — |
| GVAE-RL62 | 33.2% | 57.7% | 40.7% | 2.1% | 76.4% | 62.6% | 80.3% | — | 0.874 | 0.832 | 0.783 | — |
| REINVENT63 | 99.3% | 98.5% | 97.4% | 47.9% | 61.0% | 31.6% | 39.7% | 56.1% | 0.733 | 0.729 | 0.595 | 0.621 |
| RationaleRL62 | 100% | 100% | 100% | 74.8% | 53.4% | 46.2% | 97.3% | 56.8% | 0.888 | 0.862 | 0.824 | 0.701 |
| GA + Da64 | 84.6% | 52.8% | 84.7% | 85.7% | 100.0% | 98.3% | 100% | 100% | 0.714 | 0.726 | 0.424 | 0.363 |
| JANUS (no fragments)b | 90.6% | 86.4% | 90.4% | 90.2% | 57.9% | 15.9% | 74.9% | 22.8% | 0.850 | 0.807 | 0.681 | 0.728 |
| JANUSb | 100% | 100% | 100% | 100% | 80.9% | 40.6% | 77.9% | 32.4% | 0.821 | 0.894 | 0.876 | 0.831 |
| JANUS + Pb | 100% | 100% | 100% | 100% | 84.1% | 43.1% | 78.8% | 17.4% | 0.881 | 0.883 | 0.857 | 0.822 |
| JANUS + C (50%)b | 100% | 100% | 100% | 100% | 82.9% | 40.4% | 74.4% | 18.4% | 0.884 | 0.894 | 0.877 | 0.841 |
As this benchmark provides a training dataset, we initiated JANUS with these known inhibitors. Additionally, we derived mutation rules from the reference molecules (cf. ESI Fig. 1†). Importantly, this is not necessary and the benchmarks can be run without these custom genetic operators (cf. “JANUS (no fragments)” in Table 3). For these tasks, the fitness is a binary function assigning a value of 1 to molecules fulfilling all constraints. Our results are summarized in Table 3. JANUS achieves perfect, i.e., state-of-the-art, performance for all four tasks in terms of success. While the diversity is also high and comparable to literature baselines, novelty is significantly lower for some of the tasks. Particularly, JANUS shows a significantly decreased novelty when drug-likeness and synthesizability are included in the objective whereas diversity does not seem to be impacted (cf. Task D in Table 3). This suggests that exploration is considerably reduced with JANUS when synthesizability and other structural constraints are incorporated, which is not surprising. We believe that this can be improved by running JANUS for more generations, by implementing a discriminator into JANUS,7 and by seeding the algorithm with methane. Without the incorporation of mutation rules (cf. “JANUS (no fragments)” in Table 3), performance is slightly worse, which indicates that derived mutation rules can bias the results towards the provided set of molecules. However, it also suggests that the classifier is more likely to accept molecules sufficiently close to the training dataset. We were again interested in comparing the number of property evaluations needed by each method to get the corresponding results. However, as all the literature baselines were taken directly from other work, we could not find the corresponding numbers for most of them. Nevertheless, we can say that JANUS (≤50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 property evaluations) needs a significantly lower number of property evaluations to reach higher success rates in the imitated inhibition benchmarks than GA + D (139
000 property evaluations) needs a significantly lower number of property evaluations to reach higher success rates in the imitated inhibition benchmarks than GA + D (139![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 property evaluations).
000 property evaluations).
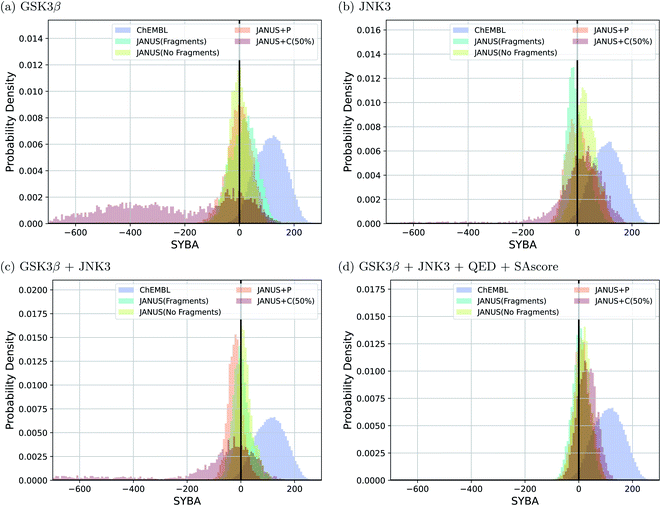
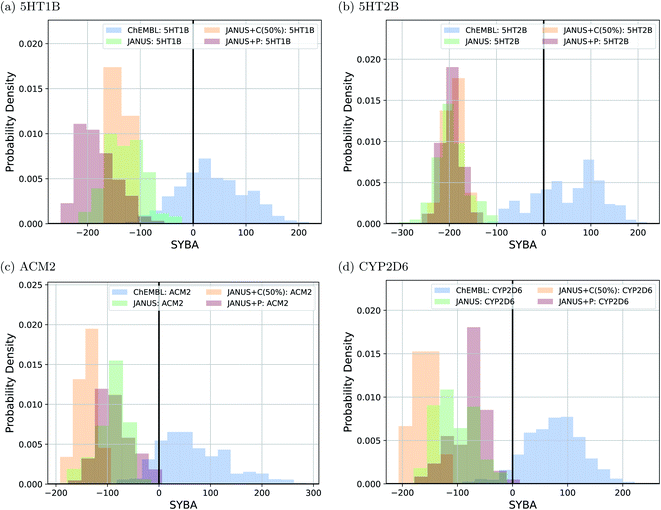
Interestingly, we observe that many molecules passing the constraints are very large and thus extremely hard to synthesize, indicating both problematic biases in some of these benchmark tasks and the fact that the current version of JANUS does not account for synthesizability during structure generation. A subset of the corresponding structures generated by JANUS using the classifier for additional selection pressure are depicted in ESI Fig. 9–12.† To investigate the synthesizabilities of the generated structures in this set of benchmarks more systematically, we compared the corresponding SYBA score72 distributions with the ones of the reference molecules62 taken from the ChEMBL database.69,70 The respective histograms are depicted in Fig. 4. We observe that the generated molecules have a systematically lower SYBA score compared to the reference, which indicates that these structures are more likely to be hard to synthesize.72 Importantly, using additional selection pressure from the classifier has a tendency to lead to molecules with very low SYBA scores (cf.Fig. 4(a–c)). However, when the SAscore is used explicitly as constraint to be passed in the benchmark, selection pressure through the classifier actually tends to provide molecules somewhat more likely to be easy to synthesize compared to the other selection pressure variations (cf.Fig. 4(d)). This demonstrates the importance of incorporating synthesizability evaluations explicitly in molecular design benchmarks when the molecular design algorithm employed does not account for it. Furthermore, our results show that a significant fraction of the proposed structures have synthesizabilities comparable to a significant fraction of the reference molecules. In addition to the results discussed above, we also compared histograms for the SAscore,67 the SCScore,73 and the RAscore74 based on the same structures, and they are provided in ESI Fig. 13–15.† The corresponding results agree qualitatively very well with the ones based on the SYBA score. As can be seen in ESI Fig. 9–12,† visual inspection of a subset of the structures generated by JANUS using the classifier for additional selection pressure confirms that the inclusion of the SAscore in this benchmark task leads to more synthetically feasible molecules. This demonstrates that the incorporation of synthesizability in the fitness function can compensate for a molecular design algorithm that does not account for it. Hence, we suggest that synthesizabilities should be explicitly compared in the imitated inhibition benchmark task in the future.
C Molecular docking
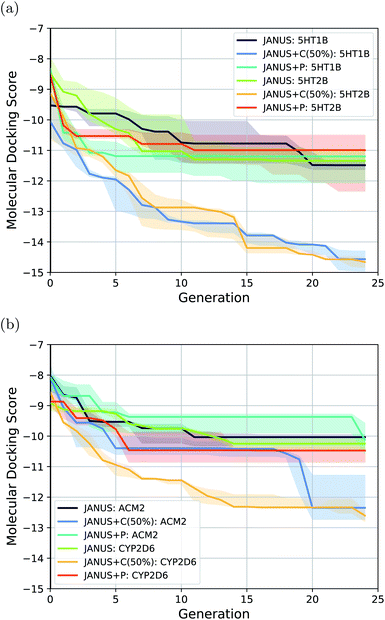
Better than imitating molecular docking with a classifier or using ML-based surrogate models,75–77 to approach the complexity of real-life drug discovery tasks, actual molecular docking has been proposed to benchmark generative models.78 Hence, we tackled the tasks introduced by Cieplinski et al.,78i.e., minimize the docking scores obtained from actual docking calculations to the protein targets 5HT1B, 5HT2B, ACM2 and CYP2D6. Our results in comparison to literature baselines are summarized in Table 4. We ran JANUS with three different variations of selection pressure. The optimization trajectories are illustrated in Fig. 5.| Method | 5HT1B | 5HT2B | ACM2 | CYP2D6 |
|---|---|---|---|---|
| a Result obtained from using 500 molecules per generation and 25 generations in total. | ||||
| ZINC (10%) | −9.894 (0.862) | −9.228 (0.851) | −8.282 (0.860) | −8.787 (0.853) |
| ZINC (1%) | −10.496 (0.861) | −9.833 (0.838) | −8.802 (0.840) | −9.291 (0.894) |
| Train (10%) | −10.837 (0.749) | −9.769 (0.831) | −8.976 (0.812) | −9.256 (0.869) |
| Train (1%) | −11.493 (0.849) | −10.023 (0.746) | −10.003 (0.773) | −10.131 (0.763) |
| CVAE66 | −4.647 (0.907) | −4.188 (0.913) | −4.836 (0.905) | — (—) |
| GVAE48 | −4.955 (0.901) | −4.641 (0.887) | −5.422 (0.898) | −7.672 (0.714) |
| REINVENT63 | −9.774 (0.506) | −8.657 (0.455) | −9.775 (0.467) | −8.759 (0.626) |
| GA + Da7 | −8.3 ± 0.5 (0.123) | −8.1 ± 0.9 (0.122) | −7.9 ± 0.3 (0.136) | −8.3 ± 0.5 (0.149) |
| JANUSa | −9.6 ± 0.9 (0.126) | −9.8 ± 0.7 (0.133) | −8.1 ± 0.5 (0.112) | −9.1 ± 0.4 (0.166) |
| JANUS + Pa | −9.9 ± 0.9 (0.132) | −9.8 ± 1.5 (0.166) | −8.0 ± 0.5 (0.125) | −9.3 ± 0.6 (0.194) |
| JANUS + C (50%)a | −13.8 ± 0.5 (0.366) | −13.8 ± 0.4 (0.331) | −9.9 ± 0.3 (0.235) | −11.7 ± 0.4 (0.363) |
The results show that JANUS readily proposes molecules with favorable docking scores for each target. In particular, it outperforms REINVENT significantly for all targets in terms of the docking scores, while only slightly for ACM2 when selection pressure is applied via a classifier, more significantly for all other targets. However, the diversities are significantly lower leaving room for improvement. Notably, we limited these runs to 25 generations, which likely contributes to the low diversities. We observe that selection pressure from the DNN classifier yields both significantly lower docking scores and higher diversities demonstrating its supremacy compared to the other selection pressure variations. Both JANUS and GA + D use 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 property evaluations to reach their respective docking scores, which implies that JANUS needs a lower number of evaluations to reach the same docking scores as GA + D. However, when property evaluations are more time-intensive than molecular docking, e.g., when binding free energies are simulated via molecular dynamics, 12
500 property evaluations to reach their respective docking scores, which implies that JANUS needs a lower number of evaluations to reach the same docking scores as GA + D. However, when property evaluations are more time-intensive than molecular docking, e.g., when binding free energies are simulated via molecular dynamics, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 is still a prohibitively high number of evaluations. Accordingly, we believe that further improvements are needed in future work. Notably, as all other literature baselines were taken directly from other work, we could not find the corresponding numbers of property evaluations used.
500 is still a prohibitively high number of evaluations. Accordingly, we believe that further improvements are needed in future work. Notably, as all other literature baselines were taken directly from other work, we could not find the corresponding numbers of property evaluations used.
Moreover, we observed that a significant fraction of the proposed molecules contain macrocyclic moieties. This is particularly relevant as the docking algorithm used in this benchmark cannot sample the conformations of macrocycles properly making the corresponding scores unreliable.79 Finally, the molecules produced by JANUS contain several structural features that would be infeasible in real drugs such as extended cummulenes or triple bonds inside small rings (cf. ESI Fig. 20†). Notably, this could be regarded as a problem of JANUS as it does not propose synthesizable structures by construction in contrast to alternative molecular generative models. However, JANUS is designed for the fitness function alone to guide the molecular design process. Hence, when stability or synthesizability are not incorporated in the fitness function, JANUS has no incentive to produce structures with these properties. When they are incorporated, as demonstrated in the imitated inhibition benchmarks, our results suggest that JANUS will propose structures with a high likelihood to be synthesizable. Thus, the problem can be attributed to the molecular design task definition or to the molecular generative model. These are two sides of the same coin. The molecules that are being proposed are not very synthesizable. To generate more synthesizable structures, either the algorithm is made to inherently produce synthesizable structures or the fitness function is modified to incorporate synthethic accessibility metrics, or both. Both approaches are a priori equally valid to reach the same goal. Nevertheless, we think that incorporating metrics to assess stability or synthesizability in molecular design benchmarks is beneficial regardless as it provides a better evaluation of the quality of proposed structures and allows for a more direct comparison of molecular generative models that account for synthesizability in the design process against ones that do not. Thus, we believe that future molecular design benchmarks should be developed in that context. This complicates the comparison of our results to alternative methods as it has been demonstrated to be harder to find molecules with both good docking scores and high synthesizabilities compared to only finding molecules fulfilling the former requirement.80 However, the original set of benchmarks did not incorporate an evaluation of synthesizability which would be required to that end.78 Importantly, this is a more general problem in the comparison of generative models as some of them have implicit structural constraints and biases for molecule generation that are largely absent in approaches like JANUS when not incorporated explicitly.
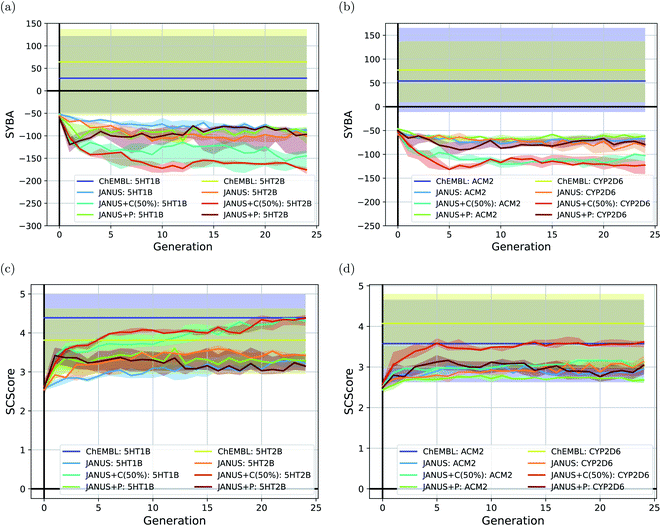
To follow synthesizabilities systematically along the optimizations, we computed four distinct metrics for that purpose, namely SAscore,67 SCScore,73 SYBA72 and RAscore,74 for all molecules generated in each generation, and compared them to the corresponding values of the reference molecules taken from the ChEMBL database69,70 provided by the benchmark developers.78 The corresponding results are depicted in Fig. 6 and ESI Fig. 16.† Additionally, we also inspected the histograms with respect to these four synthesizability metrics based on the 250 best molecules in each individual run, which is precisely the subset of generated structures used to derive the benchmark scores provided in Table 4. They are shown in Fig. 7 and ESI Fig. 17–19.†
Importantly, these four metrics do not quantify the same aspect of synthesizability which is directly reflected in our results. SYBA is solely based on fragment contributions determining whether a given molecule is hard or easy to be synthesized.72 The SAscore relies on a combination of conceptually comparable fragment contributions and a penalty accounting for, among others, the presence of uncommon moieties, the presence of large rings, and molecule size.67 The SCScore is designed to provide a measure for the estimated number of synthetic steps to make a molecule.73 The RAscore predicts whether or not AiZynthfinder,81 an open-source program for retrosynthesis, will be able to generate a planned synthesis for the structure in question and, hence, is directly related to synthetic feasibility. Both SYBA (cf.Fig. 6 and 7) and the SAscore (cf. ESI Fig. 16 and 17†) provide qualitatively equivalent results suggesting that the structures generated by JANUS are significantly less likely to be synthesizable compared to the reference molecules. Additionally, during the optimization, the molecules tend to get increasingly less likely to be synthetically accessible. While the RAscore (cf. ESI Fig. 16 and 19†) shows a similar trajectory for the molecules proposed by JANUS, i.e., the molecules are getting less likely for AiZynthfinder to find a synthesis plan, a considerable subset of the reference compounds taken from the ChEMBL database, which have all been synthesized before,69,70 are recognized as not retrosynthesizable by AiZynthfinder. Unexpectedly, the SCScore (cf.Fig. 6 and ESI Fig. 18†) gives somewhat different results as it suggests the structures generated by JANUS to be lower in synthetic complexity at the outset compared to the reference structures. Nevertheless, the trend of increasing synthetic complexities during the optimization is still reproduced but the new molecules only reach similar complexities compared to the reference molecules. Importantly, the results of the SYBA, SAscore and RAscore metrics agree well to our visual assessment of samples of the corresponding structures (cf. ESI Fig. 20†) suggesting them to be of poor quality and emphasizing the importance of explicitly accounting for synthesizability, either in the optimization target or in the molecular design algorithm. Accordingly, we propose to refine these docking benchmarks by incorporating the SYBA, SAscore or RAscore metrics in the final benchmark metric or by using stability filters to assess the generated structures so that the proposed molecules are overall more stable and have a higher chance of being synthetically accessible.
V. Conclusion and outlook
We present JANUS, a GA that propagates two populations, one explorative and one exploitative, which exchange members. JANUS relies on the SELFIES representation of molecular graphs and the STONED algorithm for efficient generation of molecules by string manipulations, requiring no domain knowledge. It can apply additional selection pressure via an on-the-fly trained DNNs that estimate the fitness of the generated molecules and propagate good members to subsequent generations, leading to faster optimization. Our model outperforms literature baselines in common molecular design benchmarks relevant to drug discovery and material design. Additionally, JANUS even outperforms previous computer-inspired human design in one of the benchmarks. Nevertheless, we see significant room for improvement. First, a considerable portion of the generated structures has low synthetic accessibility. This demonstrates that synthesizability needs to be considered when comparing the performance of molecular design algorithms in benchmarks. Additionally, it suggests that synthetic accessibility needs to be directly accounted for somewhere in the molecular design process, either already during structure generation or in the fitness evaluation, or both, in order for more feasible molecules to be generated. Second, we plan to refine the discriminator approach developed recently7 to avoid getting stuck in local optima and allow for more extensive structure exploration. Third, the current standard for multiobjective design is the (linear) combination of objectives into one superobjective. However, this requires tailoring the weights of each objective. To avoid that, we will explore more general frameworks that concatenate multiple objectives out of the box such as Chimera82 or alternative approaches.83VI. Methods
All standard cheminformatic operations, i.e., molecular similarity calculation, validity checks and conversion to canonicalized SMILES are performed using RDKit (version 2020.03.4).84 The property distributions of molecules generated from random SELFIES depend on the version of SELFIES used (cf. ESI Fig. 3†). The differences are caused by changes to the SELFIES alphabet. In all our experiments, we use SELFIES version 1.0.3, which leads to a slight decrease in performance but provides the fastest encoding and decoding. All parameters for running our code are provided in the file ‘params_init.py’ of the repository. A description of these parameters is provided in ESI Table 2.†The synthetic accessibility score (SAscore)67 was evaluated using the implementation in RDKit.84 The synthetic complexity score (SCScore)73 was evaluated using the standalone importable model, relying on the numpy package and employing the Morgan Fingerprint of radius 2 (ref. 85) folded to a length-1024 bit vector as input, that is provided in the corresponding GitHub repository (cf.https://github.com/connorcoley/scscore, master branch). The Synthetic Bayesian Accessibility (SYBA) metric72 was evaluated by fitting the default score based on the dataset provided in the corresponding GitHub repository via the ‘fitDefaultScore ()’ function of the ‘SybaClassifier’ object (cf.https://github.com/lich-uct/syba, master branch). The Retrosynthetic accessibility score (RAscore)74 was evaluated based on the Tensorflow-based model provided in the corresponding GitHub repository (cf.https://github.com/reymond-group/RAscore, master branch).
Mutation and crossover are based on the STONED algorithm8 (cf.https://github.com/aspuru-guzik-group/stoned-selfies). Mutations are performed using both the SMILES21,22 and SELFIES6 molecular string representations. SMILES are first reordered randomly and then converted to SELFIES. The obtained SELFIES are modified randomly via string point mutations. The resulting SELFIES after mutation represent the mutant structure. Crossover between two molecules is performed by interpolation between the corresponding SELFIES. Thus, paths are generated by successively matching characters of the two SELFIES and changing the character of one to the respective character of the other until completion. Multiple paths between two molecules are generated by changing the order of character matching and by converting the SELFIES of both molecules to SMILES, reordering the SMILES randomly and then converting them back to SELFIES. The final molecule accepted as crossover is chosen by maximizing the joint similarity of the generated structures to the initial structures. The input molecules for the crossover operation are kekulized prior to path formation. When performing mutation and crossover in JANUS, we ensure that the new molecule is different from any of the initial structures.
To find the best crossover molecule, we implement the joint similarity metric proposed previously.8 For the parent molecules M = {m1, m2, …}, a good crossover molecule (m) maximizes the following joint similarity:
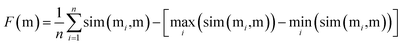 | (2) |
Similarity between two molecules is assessed using the Tanimoto similarity between the corresponding Morgan fingerprints.85 We use the default RDKit settings with a radius of size 2 and a 2048 bit restriction.
The architecture of all DNNs consists of two fully connected layers with 100 and 10 neurons, respectively. The DNN classifier is trained with the binary cross-entropy loss function, while the DNN property predictor is trained with the mean squared error loss function. Training is restricted to 4000 epochs, with a learning rate of 0.01 and a weight decay of 0.0001 using the entire set of molecules with known fitness as training set without the use of any test set. The Adam optimizer86 is employed and PyTorch (version 1.10.2) is used as backend.87 51 molecular structural descriptors obtained from RDKit,84 which are explicitly detailed in ESI Section S5,† are used as input features. For a particular generation, the DNN is trained on all molecules with known fitness values (i.e., all molecules with successful fitness calculations from all previous generations). All molecules from the current generation with yet unknown fitness are used for inference. We observe that training of the DNN takes approximately 170.9 ± 4.9 seconds (tested on 12 Intel i7-8750H threads, at 2.20 GHz, across five independent runs) in the 5th generation of JANUS when the number of training points is 2500. In the case of the DNN classifier, the labels for all molecules are reevaluated each generation based on the corresponding user-defined percentile of the training data. Hence, molecules with a fitness larger than the corresponding percentile each generation are assigned a label of one and all other molecules are assigned a label of zero. In this work, we tested percentiles of 0.50 (C50%, vide supra) and 0.80 (C20%, vide supra). We would like to note that, depending on the chosen percentile, this can lead to a systematic imbalance when training the DNN classifier. Thus, we recommend not to use too extreme percentiles.
Codes for the penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P experiments (Sections IVA and S6†) and the imitated inhibition task (Section IVB) were obtained from the master branches of the GitHub repositories at https://github.com/aspuru-guzik-group/GA and https://github.com/wengong-jin/multiobj-rationale, respectively. For the GuacaMol benchmarks (ESI Section S13†), we used the setup provided at https://github.com/BenevolentAI/guacamol. Docking scores in Section IVC are calculated using SMINA (Version: 9th November 2017, based on AutoDock Vina 1.1.2),88 with the default parameters of the corresponding code: https://github.com/cieplinski-tobiasz/smina-docking-benchmark.
P experiments (Sections IVA and S6†) and the imitated inhibition task (Section IVB) were obtained from the master branches of the GitHub repositories at https://github.com/aspuru-guzik-group/GA and https://github.com/wengong-jin/multiobj-rationale, respectively. For the GuacaMol benchmarks (ESI Section S13†), we used the setup provided at https://github.com/BenevolentAI/guacamol. Docking scores in Section IVC are calculated using SMINA (Version: 9th November 2017, based on AutoDock Vina 1.1.2),88 with the default parameters of the corresponding code: https://github.com/cieplinski-tobiasz/smina-docking-benchmark.
For the penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P experiment from Section IVA, JANUS is seeded with a population similar to the GA + D7 implementation, i.e., methane and 20 additional molecules obtained from random SELFIES. For the docking experiment in Section IVC, we use 20 random molecules. However, instead of methane, we add n-heptane because docking with extremely small molecules like methane can give meaningless results. EvoMol43 was run using the penalized log
P experiment from Section IVA, JANUS is seeded with a population similar to the GA + D7 implementation, i.e., methane and 20 additional molecules obtained from random SELFIES. For the docking experiment in Section IVC, we use 20 random molecules. However, instead of methane, we add n-heptane because docking with extremely small molecules like methane can give meaningless results. EvoMol43 was run using the penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P objective and the code from https://github.com/jules-leguy/EvoMol. Our results in Table 1 were obtained by setting the generation number to 100 (variable max_steps), the generation size to 500 (variable pop_max_size) and by replacing 400 (80%) of the least fit molecules between generations (via the parameter k_to_replace).
P objective and the code from https://github.com/jules-leguy/EvoMol. Our results in Table 1 were obtained by setting the generation number to 100 (variable max_steps), the generation size to 500 (variable pop_max_size) and by replacing 400 (80%) of the least fit molecules between generations (via the parameter k_to_replace).
In the imitated docking experiment (Section IVB), the first five rows of Table 2 were taken from the literature and all details are described therein.62 For molecular docking (Section IVC), all results displayed in Table 3, besides JANUS and GA + D, were taken from the literature78 and all details can be found in that work. GA + D was run using the code from https://github.com/aspuru-guzik-group/GA, by replacing penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P with the appropriate fitness functions, with otherwise identical settings as JANUS, i.e., same generation size and generation number. The training dataset provided with the benchmark in the corresponding GitHub repository (cf.https://github.com/cieplinski-tobiasz/smina-docking-benchmark), which was taken from the ChEMBL database,69,70 was used to estimate reference synthesizability scores.
P with the appropriate fitness functions, with otherwise identical settings as JANUS, i.e., same generation size and generation number. The training dataset provided with the benchmark in the corresponding GitHub repository (cf.https://github.com/cieplinski-tobiasz/smina-docking-benchmark), which was taken from the ChEMBL database,69,70 was used to estimate reference synthesizability scores.
Data availability
Results and code for running all the experiments are provided in our GitHub repository: https://github.com/aspuru-guzik-group/JANUS (DOI: https://doi.org/10.5281/zenodo.5711775). In addition, all datasets used in the course of this work are public (cf. Methods).Author contributions
AkshatKumar Nigam: conceptualization (supporting); data curation (lead); formal analysis (equal); investigation (lead); methodology (equal); project administration (equal); software (lead); validation (equal); visualization (equal); writing – original draft (equal); writing – review & editing (equal). Robert Pollice: conceptualization (lead); data curation (supporting); formal analysis (equal); funding acquisition (supporting); investigation (supporting); methodology (equal); project administration (equal); resources (supporting); software (supporting); supervision (lead); validation (equal); visualization (equal); writing – original draft (equal); writing – review & editing (equal). Alán Aspuru-Guzik: funding acquisition (lead); project administration (equal); resources (lead); supervision (supporting); writing – review & editing (supporting).Conflicts of interest
A. A.-G. is co-founder and Chief Visionary Officer of Kebotix, Inc.Acknowledgements
R. P. acknowledges funding through a Postdoc. Mobility fellowship by the Swiss National Science Foundation (SNSF, Project No. 191127). A. A.-G. thanks Anders G. Frøseth for his generous support. A. A.-G. also acknowledges the generous support of Natural Resources Canada and the Canada 150 Research Chairs program. Computations were performed on the Cedar supercomputer situated at the Simon Fraser University in Burnaby. In addition, we acknowledge support provided by Compute Ontario and Compute Canada.References
- S. S. Wesolowski and D. G. Brown, The strategies and politics of successful design, make, test, and analyze (dmta) cycles in lead generation, Lead Generation, 2016, pp. 487–512 Search PubMed.
- P. Schneider, W. P. Walters, T. P. Alleyn, S. Norman, J. Listgarten, R. A. Goodnow, J. Fisher, J. M. Jansen, J. S. Duca and T. S. Rush, et al., Rethinking drug design in the artificial intelligence era, Nat. Rev. Drug Discovery, 2020, 19(5), 353–364 CrossRef CAS PubMed.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Inverse molecular design using machine learning: Generative models for matter engineering, Science, 2018, 361(6400), 360–365 CrossRef CAS PubMed.
- R. Pollice, G. dos Passos Gomes, M. Aldeghi, R. J. Hickman, M. Krenn, C. Lavigne, M. Lindner-D’Addario, A. K. Nigam, C. Tian Ser and Z. Yao, et al., Data-driven strategies for accelerated materials design, Acc. Chem. Res., 2021, 54(4), 849–860 CrossRef CAS.
- A. K. Nigam, R. Pollice, M. F. D. Hurley, R. J. Hickman, M. Aldeghi, N. Yoshikawa, S. Chithrananda, V. A. Voelz and A. Aspuru-Guzik, Assigning confidence to molecular property prediction, Expert Opin. Drug Discovery, 2021, 16(9), 1009–1023 CrossRef.
- M. Krenn, F. Häse, A. K. Nigam, P. Friederich and A. Aspuru-Guzik, Self-referencing embedded strings (selfies): A 100% robust molecular string representation, Mach. Learn., 2020, 1(4), 045024 Search PubMed.
- A. K. Nigam, P. Friederich, M. Krenn, and A. Aspuru-Guzik, Augmenting genetic algorithms with deep neural networks for exploring the chemical space, in International Conference on Learning Representations, 2020 Search PubMed.
- A. K. Nigam, R. Pollice, M. Krenn, G. dos Passos Gomes and A. Aspuru-Guzik, Beyond generative models: superfast traversal, optimization, novelty, exploration and discovery (stoned) algorithm for molecules using selfies, Chem. Sci., 2021, 12, 7079–7090 RSC.
- D. J. Earl and M. W. Deem, Parallel tempering: Theory, applications, and new perspectives, Phys. Chem. Chem. Phys., 2005, 7(23), 3910–3916 RSC.
- U. HE Hansmann, Parallel tempering algorithm for conformational studies of biological molecules, Chem. Phys. Lett., 1997, 281(1–3), 140–150 CrossRef.
- D. P. Kingma and M. Welling, Auto-encoding variational bayes, 2013, arXiv, 1312.6114.
- I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, and Y. Bengio, Generative adversarial nets, in Advances in neural information processing systems, 2014, pp. 2672–2680 Search PubMed.
- D. P. Kingma and P. Dhariwal, Glow: Generative flow with invertible 1x1 convolutions, in Advances in Neural Information Processing Systems, ed. S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett. Curran Associates, Inc., 2018, vol. 31 Search PubMed.
- R. S. Sutton and A. G. Barto, Reinforcement learning: An introduction, MIT press, 2018 Search PubMed.
- R. A. Howard, Dynamic programming and markov processes, John Wiley, 1960 Search PubMed.
- M. Gendreau and P. Jean-Yves, Handbook of metaheuristics, Springer, vol. 2, 2010 Search PubMed.
- C. Blum and A. Roli, Metaheuristics in combinatorial optimization: Overview and conceptual comparison, ACM Comput. Surv., 2003, 35(3), 268–308 CrossRef.
- J. H. Holland, Genetic algorithms, Sci. Am., 1992, 267(1), 66–73 CrossRef.
- P. Willett, Genetic algorithms in molecular recognition and design, Trends Biotechnol., 1995, 13(12), 516–521 CrossRef CAS.
- T. Slater and D. Timms, Meeting on binding sites: Characterizing and satisfying steric and chemical restraints. University of York, 28–30 March 1993, J. Mol. Graph., 1993, 11(4), 248–251 CrossRef CAS.
- D. Weininger, Smiles, a chemical language and information system. 1. introduction to methodology and encoding rules, J. Chem. Inf. Comput. Sci., 1988, 28(1), 31–36 CrossRef CAS.
- D. Weininger, W. Arthur and L. Joseph, Weininger. Smiles. 2. algorithm for generation of unique smiles notation, J. Chem. Inf. Comput. Sci., 1989, 29(2), 97–101 CrossRef CAS.
- D. R. Westhead, D. E. Clark, D. Frenkel, J. Li, C. W. Murray, B. Robson and B. Waszkowycz, PRO_LIGAND: An approach to de novo molecular design. 3. A genetic algorithm for structure refinement, J. Comput.-Aided Mol. Des., 1995, 9(2), 139–148 CrossRef CAS.
- R. C. Glen and A. W. R. Payne, A genetic algorithm for the automated generation of molecules within constraints, J. Comput.-Aided Mol. Des., 1995, 9(2), 181–202 CrossRef CAS PubMed.
- R. Wang, Y. Gao and L. Lai, LigBuilder: A Multi-Purpose Program for Structure-Based Drug Design, Molecular Modeling Annual, 2000, 6(7), 498–516 CrossRef CAS.
- G. Al, J. Lawton and W. Todd, Automatic molecular design using evolutionary techniques, Nanotechnology, 1999, 10(3), 290–299 CrossRef.
- B. Robert, Nachbar. Molecular Evolution: Automated Manipulation of Hierarchical Chemical Topology and Its Application to Average Molecular Structures, Genet. Program. Evolvable Mach., 2000, 1(1), 57–94 Search PubMed.
- N. Brown, B. McKay, F. Gilardoni and J. Gasteiger, A Graph-Based Genetic Algorithm and Its Application to the Multiobjective Evolution of Median Molecules, J. Chem. Inf. Comput. Sci., 2004, 44(3), 1079–1087 CrossRef CAS PubMed.
- D. Dominique, E. Thoreau and G. Grassy, A genetic algorithm for the automated generation of small organic molecules: Drug design using an evolutionary algorithm, J. Comput.-Aided Mol. Des., 2000, 14(5), 449–466 CrossRef.
- G. Schneider, M.-L. Lee, M. Stahl and P. Schneider, De novo design of molecular architectures by evolutionary assembly of drug-derived building blocks, J. Comput.-Aided Mol. Des., 2000, 14(5), 487–494 CrossRef CAS.
- G. Schneider, O. Clément-Chomienne and L. Hilfiger, Petra Schneider, Stefan Kirsch, Hans-Joachim Böhm, and Werner Neidhart. Virtual Screening for Bioactive Molecules by Evolutionary De Novo Design, Angew. Chem., Int. Ed., 2000, 39(22), 4130–4133 CrossRef CAS PubMed.
- S. C.-H. Pegg, J. J. Haresco and I. D. Kuntz, A genetic algorithm for structure-based de novo design, J. Comput.-Aided Mol. Des., 2001, 15(10), 911–933 CrossRef CAS PubMed.
- H. Maarten Vinkers, M. R. de Jonge, F. F. D. Daeyaert, H. Jan, L. M. H. Koymans, J. H. van Lenthe, P. J. Lewi, H. Timmerman, K. Van Aken and A. Paul, J. Janssen. SYNOPSIS: SYNthesize and OPtimize System in Silico, J. Med. Chem., 2003, 46(13), 2765–2773 CrossRef PubMed.
- G. Schneider and U. Fechner, Computer-based de novo design of drug-like molecules, Nat. Rev. Drug Discovery, 2005, 4(8), 649–663 CrossRef CAS.
- M. Hartenfeller and G. Schneider, Enabling future drug discovery by de novo design, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2011, 1(5), 742–759 CrossRef CAS.
- M. Hartenfeller and G. Schneider, De Novo Drug Design, in Chemoinformatics and Computational Chemical Biology, Methods in Molecular Biology, ed, J. Bajorath, Humana Press, Totowa, NJ, 2011, pp. 299–323 Search PubMed.
- R. Vasundhara Devi, S. Siva Sathya and M. Selvaraj Coumar, Evolutionary algorithms for de novo drug design – A survey, Appl. Soft Comput., 2015, 27, 543–552 CrossRef.
- E. Habib Bechelane Maia, L. Cristina Assis, T. Alves de Oliveira, A. Marques da Silva and A. Gutterres Taranto, Structure-Based Virtual Screening: From Classical to Artificial Intelligence, Front. Chem., 2020, 8, 343 CrossRef.
- V. D. Mouchlis, A. Afantitis, A. Serra, M. Fratello, A. G. Papadiamantis, V. Aidinis, I. Lynch, D. Greco and G. Melagraki, Advances in De Novo Drug Design: From Conventional to Machine Learning Methods, Int. J. Mol. Sci., 2021, 22(4), 1676 CrossRef.
- X. Liu, A. P. IJzerman, and G. J. P. van Westen, Computational Approaches for De Novo Drug Design: Past, Present, and Future, in Artificial Neural Networks, Methods in Molecular Biology, ed. H. Cartwright, Springer US, New York, NY, 2021, pp. 139–165 Search PubMed.
- J. H. Jensen, A graph-based genetic algorithm and generative model/monte carlo tree search for the exploration of chemical space, Chem. Sci., 2019, 10(12), 3567–3572 RSC.
- P. Polishchuk, Crem: chemically reasonable mutations framework for structure generation, J. Cheminf., 2020, 12(1), 1–18 Search PubMed.
- J. Leguy, T. Cauchy, M. Glavatskikh, B. Duval and B. Da Mota, Evomol: a flexible and interpretable evolutionary algorithm for unbiased de novo molecular generation, J. Cheminf., 2020, 12(1), 1–19 Search PubMed.
- Y. Kwon and J. Lee, Molfinder: an evolutionary algorithm for the global optimization of molecular properties and the extensive exploration of chemical space using smiles, J. Cheminf., 2021, 13(1), 1–14 Search PubMed.
- R. Winter, F. Montanari, A. Steffen, H. Briem, F. Noé and D.-A. Clevert, Efficient multi-objective molecular optimization in a continuous latent space, Chem. Sci., 2019, 10(34), 8016–8024 RSC.
- A. Dalke, J. Hert and C. Kramer, mmpdb: An open-source matched molecular pair platform for large multiproperty data sets, J. Chem. Inf. Model., 2018, 58(5), 902–910 CrossRef CAS PubMed.
- P. W. Kenny and J. Sadowski, Structure modification in chemical databases, Chemoinformatics in Drug Discovery, 2005, pp. 271–285, vol. 23 Search PubMed.
- M. J. Kusner, B. Paige, and J. Miguel Hernández-Lobato, Grammar variational autoencoder, in Proceedings of the 34th International Conference on Machine Learning, JMLR, 2017, vol. 70, pp. 1945–1954 Search PubMed.
- H. Dai, Y. Tian, B. Dai, S. Skiena, and L. Song, Syntax-directed variational autoencoder for molecule generation, in Proceedings of the International Conference on Learning Representations, 2018 Search PubMed.
- G. Lima Guimaraes, B. Sanchez-Lengeling, C. Outeiral, P. Luis Cunha Farias, and A. Aspuru-Guzik, Objective-reinforced generative adversarial networks (organ) for sequence generation models, 2017, arXiv, 1705.10843.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. Miguel Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, Automatic chemical design using a data-driven continuous representation of molecules, ACS Cent. Sci., 2018, 4(2), 268–276 CrossRef PubMed.
- W. Jin, R. Barzilay, and T. Jaakkola, Junction tree variational autoencoder for molecular graph generation, in Proceedings of the 35th International Conference on Machine Learning, volume 80 of Proceedings of Machine Learning Research, ed. Jennifer Dy and Andreas Krause, PMLR, 10–15 Jul 2018, pp. 2323–2332 Search PubMed.
- S. Ahn, J. Kim, H. Lee, and J. Shin, Guiding deep molecular optimization with genetic exploration, in Advances in Neural Information Processing Systems, ed. H. Larochelle, M. Ranzato, R. Hadsell, M. F. Balcan, and H. Lin, Curran Associates, Inc., 2020, vol. 33, pp. 12008–12021 Search PubMed.
- X. Yang, J. Zhang, K. Yoshizoe, K. Terayama and K. Tsuda, Chemts: an efficient python library for de novo molecular generation, Sci. Technol. Adv. Mater., 2017, 18(1), 972–976 CrossRef CAS PubMed.
- J. You, B. Liu, Z. Ying, V. Pande, and J. Leskovec. Graph convolutional policy network for goal-directed molecular graph generation, in Advances in Neural Information Processing Systems, 2018, pp. 6410–6421 Search PubMed.
- M. Popova, M. Shvets, J. Oliva, and O. Isayev, Molecularrnn: Generating realistic molecular graphs with optimized properties, 2019, arXiv, 1905.13372.
- Z. Zhou, S. Kearnes, L. Li, R. N. Zare and P. Riley, Optimization of molecules via deep reinforcement learning, Sci. Rep., 2019, 9(1), 1–10 Search PubMed.
- C. Shi, M. Xu, Z. Zhu, W. Zhang, M. Zhang, and J. Tang, Graphaf: a flow-based autoregressive model for molecular graph generation, in International Conference on Learning Representations, 2020 Search PubMed.
- S. Baluja and R. Caruana, Removing the genetics from the standard genetic algorithm, in Machine Learning Proceedings, Elsevier, 1995, pp. 38–46 Search PubMed.
- P. Adrien Maurice Dirac, On the theory of quantum mechanics, Proc. R. Soc. Lond. - Ser. A Contain. Pap. a Math. Phys. Character, 1926, 112(762), 661–677 Search PubMed.
- E. Fermi, Sulla quantizzazione del gas perfetto monoatomic, Rend. Lincei., 1926, 3(3), 145–149 CAS.
- W. Jin, R. Barzilay, and T. Jaakkola. Multi-objective molecule generation using interpretable substructures, in International Conference on Machine Learning, PMLR, 2020, pp. 4849–4859 Search PubMed.
- O. Marcus, T. Blaschke, O. Engkvist and H. Chen, Molecular de-novo design through deep reinforcement learning, J. Cheminf., 2017, 9(1), 1–14 Search PubMed.
- Y. Xie, C. Shi, H. Zhou, Y. Yang, W. Zhang, Y. Yu, and L. Li. \{MARS\}: Markov molecular sampling for multi-objective drug discovery, in International Conference on Learning Representations, 2021 Search PubMed.
- N. Brown, M. Fiscato, M. H. S. Segler and A. C. Vaucher, Guacamol: benchmarking models for de novo molecular design, J. Chem. Inf. Model., 2019, 59(3), 1096–1108 CrossRef CAS PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. Miguel Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams, and A. Aspuru-Guzik. Automatic chemical design using a data-driven continuous representation of molecules, 2016, arXiv, 1610.02415v1.
- P. Ertl and A. Schuffenhauer, Estimation of synthetic accessibility score of drug-like molecules based on molecular complexity and fragment contributions, J. Cheminf., 2009, 1(1), 8 Search PubMed.
- G. Richard Bickerton, G. V. Paolini, J. Besnard, S. Muresan and A. L. Hopkins, Quantifying the chemical beauty of drugs, Nat. Rev. Chem, 2012, 4(2), 90–98 CrossRef.
- A. Gaulton, A. Hersey, Michał Nowotka, A. P. Bento, J. Chambers, D. Mendez, P. Mutowo, F. Atkinson, L. J. Bellis, E. Cibrián-Uhalte, M. Davies, N. Dedman, A. Karlsson, M. Paula Magariños, J. P. Overington, G. Papadatos, I. Smit and A. R. Leach, The ChEMBL database in 2017, Nucleic Acids Res., 2016, 45(D1), D945–D954 CrossRef PubMed.
- D. Mendez, A. Gaulton, A. P. Bento, J. Chambers, M. De Veij, E. Félix, M. P. Magariños, J. F. Mosquera, P. Mutowo, M. Nowotka, M. Gordillo-Marañón, F. Hunter, L. Junco, G. Mugumbate, M. Rodriguez-Lopez, F. Atkinson, N. Bosc, C. J. Radoux, A. Segura-Cabrera, A. Hersey and A. R. Leach, ChEMBL: towards direct deposition of bioassay data, Nucleic Acids Res., 2018, 47(D1), D930–D940 CrossRef PubMed.
- Y. Li, L. Zhang and Z. Liu, Multi-objective de novo drug design with conditional graph generative model, J. Cheminf., 2018, 10(1), 1–24 Search PubMed.
- M. Voršilák, M. Kolář, I. Čmelo and D. Svozil, Syba: Bayesian estimation of synthetic accessibility of organic compounds, J. Cheminf., 2020, 12(1), 1–13 Search PubMed.
- C. W. Coley, L. Rogers, W. H. Green and K. F. J. Scscore, Synthetic complexity learned from a reaction corpus, J. Chem. Inf. Model., 2018, 58(2), 252–261 CrossRef CAS PubMed.
- A. Thakkar, V. Chadimová, E. J. Bjerrum, O. Engkvist and J.-L. Reymond, Retrosynthetic accessibility score (rascore) – rapid machine learned synthesizability classification from ai driven retrosynthetic planning, Chem. Sci., 2021, 12, 3339–3349 RSC.
- F. Gentile, V. Agrawal, M. Hsing, A.-T. Ton, F. Ban, U. Norinder and E. Martin, Gleave, and Artem Cherkasov. Deep docking: A deep learning platform for augmentation of structure based drug discovery, ACS Cent. Sci., 2020, 6(6), 939–949 CrossRef CAS PubMed , PMID: 32607441..
- Y. Yang, K. Yao, M. P. Repasky, L. Karl, R. Abel, B. K. Shoichet and S. V. Jerome, Efficient exploration of chemical space with docking and deep learning, J. Chem. Theory Comput., 2021, 17(11), 7106–7119 CrossRef CAS PubMed , PMID: 34592101..
- J. Choi and J. L. V-dock, Fast generation of novel drug-like molecules using machine-learning-based docking score and molecular optimization, Int. J. Mol. Sci., 2021, 22(21), 11635 CrossRef CAS PubMed.
- T. Cieplinski, T. Danel, S. Podlewska, and S. Jastrzebski, We should at least be able to design molecules that dock well, 2020, arXiv, 2006.16955.
- J. Eberhardt, D. Santos-Martins, A. F. Tillack and S. Forli, Autodock vina 1.2.0: New docking methods, expanded force field, and python bindings, J. Chem. Inf. Model., 2021, 61(8), 3891–3898 CrossRef CAS PubMed , PMID: 34278794..
- C. Steinmann and J. H. Jensen, Using a genetic algorithm to find molecules with good docking scores, PeerJ Phys. Chem., 2021, 3, e18 CrossRef.
- S. Genheden, A. Thakkar, V. Chadimová and J.-L. Reymond, Ola Engkvist, and Esben Bjerrum. Aizynthfinder: a fast, robust and flexible open-source software for retrosynthetic planning, J. Cheminf., 2020, 12(1), 1–9 Search PubMed.
- F. Häse, L. M. Roch and A. Aspuru-Guzik, Chimera: enabling hierarchy based multi-objective optimization for self-driving laboratories, Chem. Sci., 2018, 9(39), 7642–7655 RSC.
- K. Abdullah, D. W. Coit and A. E. Smith, Multi-objective optimization using genetic algorithms: A tutorial, Reliab. Eng. Syst. Saf., 2006, 91(9), 992–1007 CrossRef.
- G. Landrum, et al., Rdkit: Open-source cheminformatics, 2006 Search PubMed.
- D. Rogers and M. Hahn, Extended-connectivity fingerprints, J. Chem. Inf. Model., 2010, 50(5), 742–754 CrossRef CAS PubMed.
- D. P. Kingma and J. Ba. Adam, A method for stochastic optimization, in ICLR (Poster), 2015 Search PubMed.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein and L. Antiga, et al., Pytorch: An imperative style, high-performance deep learning library, Adv. Neural Inf. Process. Syst., 2019, 32, 8026–8037 Search PubMed.
- D. R. Koes, M. P. Baumgartner and C. J Camacho, Lessons learned in empirical scoring with smina from the csar 2011 benchmarking exercise, J. Chem. Inf. Model., 2013, 53(8), 1893–1904 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2dd00003b |
| ‡ Equal contributions. |
| This journal is © The Royal Society of Chemistry 2022 |