Open Access Article
Open Access ArticleArtificial neural networks and data fusion enable concentration predictions for inline process analytics†
Peter
Sagmeister
 ab,
Robin
Hierzegger
ab,
Robin
Hierzegger
 ab,
Jason D.
Williams
ab,
Jason D.
Williams
 ab,
C. Oliver
Kappe
ab,
C. Oliver
Kappe
 *ab and
Stefan
Kowarik
*ab and
Stefan
Kowarik
 *b
*b
aCenter for Continuous Flow Synthesis and Processing (CCFLOW), Research Center Pharmaceutical Engineering (RCPE), Inffeldgasse 13, 8010 Graz, Austria
bInstitute of Chemistry, University of Graz, NAWI Graz, Heinrichstrasse 28, A-8010 Graz, Austria. E-mail: oliver.kappe@uni-graz.at; stefan.kowarik@uni-graz.at
First published on 9th May 2022
Abstract
Real-time process analytics enable an insight into chemical processes and are essential to implementing process optimization and control algorithms. However, the quantification of reaction species in complex mixtures can be difficult due to overlapping signals or low resolution data. Here we demonstrate the utilization of artificial neural networks (ANNs), as a technique for advanced data processing of nuclear magnetic resonance (NMR) and UV/vis spectra. The ANN training process was expedited by the generation and use of simulated training spectra. The output from multiple process analytical technology (PAT) instruments, in a continuous flow synthesis towards the active pharmaceutical ingredient (API) mesalazine, were fused by using ANNs. This allowed all relevant process intermediates and impurities to be monitored at two points in the process, effectively augmenting the UV/vis spectroscopy data. Approaches such as this will encourage increased uptake and usage of low-cost and accessible PAT instruments for multistep reaction monitoring.
Introduction
Digitalization and automation are key technologies to steer the pharmaceutical and fine chemical industries toward efficient, safe, and sustainable workflows.1 Continuous manufacturing plays a role in expediting this transformation, due to process intensification, the ease of automating unit operations and potential to improve batch quality.2 The vast majority of data to monitor critical quality attributes (CQAs) is still collected offline, manually processed, and analyzed. This time consuming exercise can be accelerated by using inline or online process analytical technology (PAT), which provides data in real time.3Regulatory agencies, such as the US Food and Drug Administration (FDA), are encouraging industrial process chemistry labs to integrate inline and online analytics, as part of continuous manufacturing.4 The large amount of recorded data must be stored, processed, and analyzed in a reliable automated workflow.5 Real-time data from automated continuous flow platforms enables, amongst others, the use of dynamic experimentation,6 automated self-optimization,7 kinetic model building,8 and feedback loops for process control.9
Process streams with multiple components, which are monitored with inline PAT, often result in spectra with overlapping signals. In such cases, the quantification of single components cannot be performed by following individual signals. Advanced data analysis models, such as indirect hard modelling (IHM)10 and partial least squares (PLS) regression11 are capable of deconvoluting complex spectra and providing precise concentration measurements. These techniques, however, are often limited by the commercial nature of the appropriate software and complexity of operation. Additionally, chemists are rarely trained in data science or programing during their education at university – a missed opportunity that is often not recognized in chemistry sub disciplines. Nevertheless, advanced data analysis could provide more confidence in experimental results and advance their research.
Artificial neural networks (ANNs) have become a powerful method for data processing in the PAT community.12 An ANN is a collection of different types of layers, comprised of neurons (Fig. 1).13 The input layer usually reflects the original input data. This can be, for example, a measured spectrum from the PAT, or other recorded process variables. The output layer is the last layer in the ANN and provides the output data. The output can be multiple different concentrations or molar ratios of reaction intermediates or products. The hidden layers define intermediate connections between the input and output layer. Different connectivities between hidden layers have been developed, such as fully dense, convolutional, locally connected, recurrent, and pooling layers. Neurons in a given layer take the weighted sum of inputs from the previous layer, process it with a non-linear activation function and pass it to the next layer or output. The numerical weighting factors are adjusted during training. The initial investment effort for using ANNs has been dramatically reduced by the use of open-source software, such as Tensorflow and PyTorch, embedded in python. Application programming interfaces allow non-specialist users to easily create ANNs with minimal coding experience.
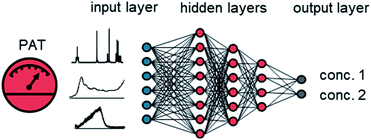 | ||
| Fig. 1 A graphical representation of an ANN. The input layer can consist of process data or spectra from PAT instruments, such as NMR, FTIR, UV/vis or Raman. | ||
Collection of training and validation data with concentration tags can be the most time consuming part in developing ANNs for data analysis. In an ideal case the training data consist of all possible concentration levels, spectral disturbances, and process variations, which may be experienced by the process itself. For a traditional PLS model, 5 to 10 concentration levels are recorded for calibration, yet ANNs require thousands of different levels for effective training. This time consuming part of manually recording the training spectra can be overcome by the simulation of synthetic spectra.12c,14
The utilization of multiple PAT instruments in single- or multistep continuous flow synthesis processes is rare.15 Incorporating these tools at different time points of the process can provide enhanced insight into the chemical transformations, compared to a single measurement at the end.16 Process deviations and faults can be observed more quickly, allowing for a faster response by the operator or control algorithm. Incorporating multiple high resolution PAT instruments generally comes with a high investment cost. The costs can be reduced by integration of simple PAT instruments, such as temperature, pressure, pH, conductivity probes, near-infrared spectroscopy or UV/vis spectroscopy. On the other hand, the recorded data often cannot be used to distinguish precisely between products and impurities. This complementary data can, however, be merged and exploited in data processing models. This approach can be referred to as data fusion, in which multiple inputs from different PAT instruments can be used for various predictions of output parameters.17 The combination of multiple PAT instruments or orthogonal techniques increase the model performance and robustness.
Herein we report the development of an easy to follow approach to simulating synthetic NMR spectra and showcase the capabilities of different ANNs on NMR data. Furthermore, we demonstrate an ANN, which is capable of fusing NMR and UV/vis spectra to provide precise predictions of process data on the synthesis pathway of an API.
Results and discussion
Studied reaction, flow process and placement of PAT
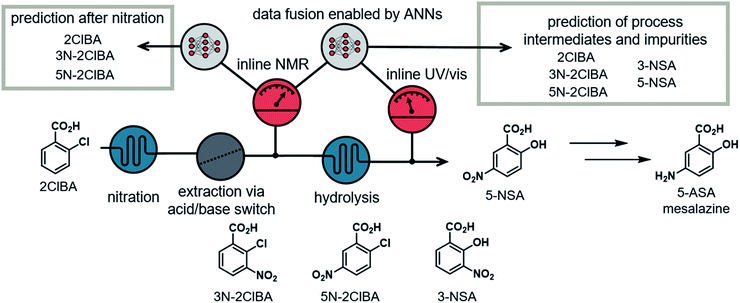
Our group previously described a continuous flow platform for the telescoped synthesis of 5-aminosalicylic acid (5-ASA) (Fig. 2).16b This API, known as mesalazine, is prescribed for treating colitis and Crohn's disease.18 The synthesis pathway starts with the nitration of 2-chlorobenzoic acid in a mixture of H2SO4 and HNO3. The nitration provides both isomers, the undesired 3-nitro-2-chlorobenzoic acid (3N-2ClBA) and desired 5-nitro-2-chlorobenzoic acid (5N-2ClBA). The next step in the linear synthesis pathway (hydrolysis) requires basic conditions, therefore an acid/base extraction was implemented. In the hydrolysis step the aryl chloride is displaced by hydroxide at 210 °C and elevated pressure. Both isomers from the previous step (3N-2ClBA and 5N-2ClBA) can be converted to 3-nitrosalicylic acid (3-NSA) and desired intermediate 5-nitrosalicylic acid (5-NSA), respectively.The nitration, and subsequent acid/base extraction, was monitored using an inline NMR (Magritek, Spinsolve Ultra 43 MHz). The NMR was placed after the extraction sequence, where the reaction mixture passed through a glass flow-through cell. The observed spectra provided the concentrations of the process intermediates (2ClBA, 3N-2ClBA, and 5N-2ClBA). This allowed for feedback control of the hydroxide equivalents for the hydrolysis step. A new spectrum was acquired every 10 to 12 s throughout the whole processing time (pulse angle = 90°, acquisition time = 6.4 s, repetition time = 10.0 s and number of scans = 1).
The hydrolysis was analyzed using inline UV/vis spectroscopy (fiber-coupled Avantes Starline AvaSpec-ULS2048 spectrometer). A home-made flow cell, constructed out of PFA tubing and a 4-way connector, provided chemical and pressure resistance.16b The observed spectra showed only minor spectral features and could only give insight into conversion of the reaction. The sampling time for each spectrum was 2 s (20 ms integration time and an averaged combination of 100 measurements per data point).
Development of neural network for NMR
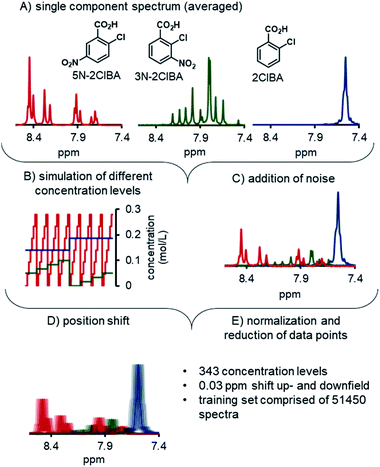
The development of the ANNs for NMR started with the preparation of synthetic training data. To achieve this, the single component spectra of 2ClBA, 3N-2ClBA, and 5N-2ClBA were recorded by recirculating stock solutions through the NMR. For each component 100 spectra were recorded and averaged (Fig. 3A). The pretreatment of the spectrum included phasing (auto, negative peak penalization) and spectral alignment of the highest peak (water) to 5.00 ppm. The global range was set from 7 to 9 ppm, to exclude parts of the spectrum with no relevant information.A python script generated a matrix of 343 different concentration levels from linear combinations of the 3 pure components (Fig. 3B). Each concentration level consisted of 50 simulated spectra, obtained from linear combinations of the 3 pure components. The synthetic spectra were compared to experimentally recorded spectra and low residuals were observed (see ESI†). Additionally, random noise was added to each spectrum, to simulate measuring noise in the training set (Fig. 3C). Noise was added to each point in the spectrum individually. The magnitude at each point was selected at random from a Gaussian distribution, centered at 1.0, with a standard deviation of 2. The center and standard deviation values were selected empirically, to mimic the level of noise observed in experimentally-measured spectra.
The synthetic spectra were triplicated and the position of the spectra were changed to simulate the influence of different pH values in the process (Fig. 3D). One part of the synthetic set was shifted by 0.03 ppm upfield, the other part was shifted downfield by the same distance, and final part was not shifted. In total, the synthetic training data set was comprised of 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 spectra. Prior to using the synthetic spectra for training the ANNs, each spectrum was reduced from 1148 data points to 600 (Fig. 3E). The spectra and the concentration tags were scaled between 0 and 1 to improve the stability and performance in the ANN training phase. The final training data set for the ANN was comprised of 7 experimentally measured concentration levels and the aforementioned synthetic training data.
450 spectra. Prior to using the synthetic spectra for training the ANNs, each spectrum was reduced from 1148 data points to 600 (Fig. 3E). The spectra and the concentration tags were scaled between 0 and 1 to improve the stability and performance in the ANN training phase. The final training data set for the ANN was comprised of 7 experimentally measured concentration levels and the aforementioned synthetic training data.
To obtain a dynamic validation data set, with transient concentration values, an automated concentration ramp was performed experimentally (see ESI†). Stock solutions of the pure components and a solvent solution were pumped with HPLC pumps and mixed prior to the NMR in a 5-way mixer. The concentration tags were calculated from the corresponding input flow rates. The final validation spectra were pretreated with the same phasing, spectral alignment, reduction of the global range and scaling.
The ANNs were coded in Python (v3.8), using Keras application programming interface (based on TensorFlow 2.0). The training of the ANNs was conducted either on an Intel i5-7200U (2.5 GHz) or AMD Ryzen 9 3950X (3.5 GHz) CPU. The initial attempts to develop an ANN to process NMR data used a fully dense architecture. In fully dense layers every neuron of one layer is directly connected to every neuron of its preceding layer. During the training process different numbers of layers and neurons were examined, but no satisfactory results could be obtained. Our attention was drawn to convolutional neural networks (CNNs), which have been previously applied for NMR data.12b,c,19
The convolutional layer in a CNN applies different filters to the input data. The filters have three adjustable parameters: the number of filters per layer, the kernel size (size of the filter) and strides (overlap of each filter). During the training process, an architecture of one convolutional layer followed by dense layers was investigated. The convolutional layer was either a conv1D layer or a locally connected 1D layer.
The weights of the different filters are shared for the conv1D layer, but are unshared for the locally connected 1D layer. Therefore, a different set of filters is applied to different sections of the input spectrum. The kernel size, strides, number of filters, architecture of the fully dense layers and batch size were optimized during the training process.
The training validation was performed on the continuous validation data set (described above). The result of the ANNs for NMR were benchmarked against partial least squares (PLS) regression, the current industry standard chemometric method, as well as indirect hard modelling (IHM), a more complex chemometric method that is not yet widely adopted (Table 1). The IHM and PLS regression models were trained with the 7 experimentally measured concentration levels (see ESI†). All investigated ANNs outperformed the PLS model. Additionally, it was found that ANNs comprised of convolutional layers had a lower root mean square error of validation for the continuous validation set (RMSEVcon, approximately 3 mM for each compound), compared to the ANN with fully dense layers only. Both convolutional ANNs had similar RMSEVcon values to the IHM approach. However, due to the relative simplicity of the ANN, the time taken to interpret a spectrum was significantly lower (∼2 ms vs. ∼2 s). This represents a clear advantage of ANNs, for example in low-power computing applications.
| Iterations | RMSEVcon | ||
|---|---|---|---|
| 2ClBA (mM) | 3N-2ClBA (mM) | 5N-2ClBA (mM) | |
| Indirect hard modelling (IHM) | 3.4 | 3.9 | 7.4 |
| PLS | 22.4 | 13.6 | 15.4 |
| ANN (fully dense) | 8.2 | 5.6 | 11.1 |
| ANN (locally connected 1D) | 6.2 | 2.9 | 8.2 |
| ANN (conv1D) | 3.9 | 3.1 | 6.8 |
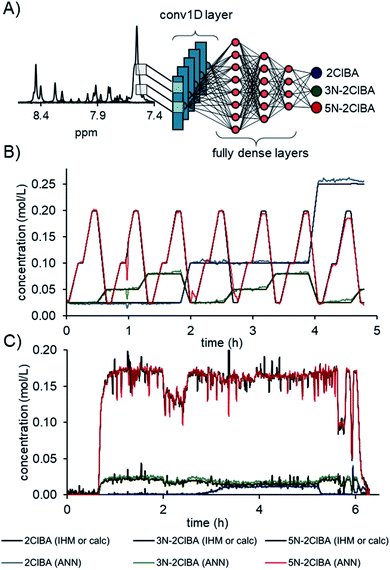
The best convolutional ANN model was comprised of a conv1D layer with 16 filters, kernel size of 9, and a stride size of 9. The output was flattened and followed by 3 fully dense layers of 27, 9, and 3 neurons, respectively (Fig. 4A). The activation function for the convolutional layer, fully dense layer, and output layer was a rectified linear unit (relu). A total number of 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 981 parameters could be adjusted during the training. The comparison of the ANN to the calculated concentration values from the continuous validation data shows an excellent fit (Fig. 4B). The root mean square error of the 7 experimentally measured concentration levels (RMSEVexp) was calculated to be 0.9 mM for 2ClBA, 1.1 mM for 3N-2ClBA, and 1.5 mM 5N-2ClBA for the locally connected 1D network.
981 parameters could be adjusted during the training. The comparison of the ANN to the calculated concentration values from the continuous validation data shows an excellent fit (Fig. 4B). The root mean square error of the 7 experimentally measured concentration levels (RMSEVexp) was calculated to be 0.9 mM for 2ClBA, 1.1 mM for 3N-2ClBA, and 1.5 mM 5N-2ClBA for the locally connected 1D network.
The concentration predictions from process data were in accordance for compounds 2ClBA, 3N-2ClBA, and 5N-2ClBA in relation to the previously published IHM concentrations (Fig. 4C).16b In sections where no compounds were present (start up and shutdown), the ANN predicted with less noise compared to IHM. Additional predictions on process data can be found in the ESI.†
Data fusion of NMR and UV/vis spectra
The hydrolysis step was monitored using UV/vis spectroscopy. Peaks corresponding to each of the reaction components are not separated (see ESI†), resulting in a relatively featureless UV/vis spectrum with nonlinear response to concentration changes. Analysis of these spectra alone did not allow quantification of the 5 process intermediates. Therefore, our focus was to fuse the information from the nitration step, quantified with NMR, with the information from the UV/vis spectrometer. By combining the output from both instruments, it should be possible to build a more detailed analytical model, essentially augmenting the usefulness of UV/vis measurements.16Deep learning modules with multiple inputs and outputs should allow the ANN to be fed with both the NMR and the UV/vis spectra. One output can be placed in the middle of the ANN to predict the values of 2ClBA, 3N-2ClBA, and 5N-2ClBA after the nitration step. Additionally, the concentrations of 3N-2ClBA, 5N-2ClBA, 3-NSA, and 5-NSA can be predicted as a final output. The concentration of 2ClBA was not predicted after the hydrolysis step, because experimental observations showed that its concentration did not change between the two measuring points.
Training data was generated by taking UV/vis spectra from dynamic experiments and prepared concentration levels (see ESI†). Additionally, a simulated baseline shift was added to the UV/vis spectra to cover spectral deviations in the process data. The concentration tags for the UV/vis spectra were mainly calculated by offline UHPLC measurements, taken directly after the process. Due to the difference in measuring frequency (2 s vs. 10–12 s), most of the UV/vis data did not have a corresponding NMR spectrum, therefore the NMR spectrum was synthetically simulated (as described and validated above).
A multidimensional dynamic experiment was conducted, using an automated concentration ramp for the nitration step and temperature ramp for the hydrolysis step. Stock solutions of pure components and solvent were pumped with HPLC pumps and mixed prior to the NMR in a 5-way mixer. The outlet of the NMR was collected in a buffer vessel and directly pumped with an HPLC pump through a stainless steel coil, which was placed on a coil heater. After passing through a back pressure regulator, the process mixture was analyzed with UV/vis and offline samples were taken (every 3 min) for UHPLC validation. The concentration tags were either calculated from the corresponding input flow rates (NMR) or the interpolated UHPLC measurements (UV/vis).
The pretreatment of NMR spectra included the reduction from 1148 data points to 600 data points and scaling of each spectrum. The UV/vis spectra were reduced from 2048 data points to 187, by averaging every 10 values (roughly 2–3 nm). Ranges without spectral information (below 250 nm and above 770 nm) were excluded from the UV/vis spectra. Additionally, the spectral intensities were scaled between 0 and 1. The concentration tags for the training output were also scaled between 0 and 1 to improve performance during training.
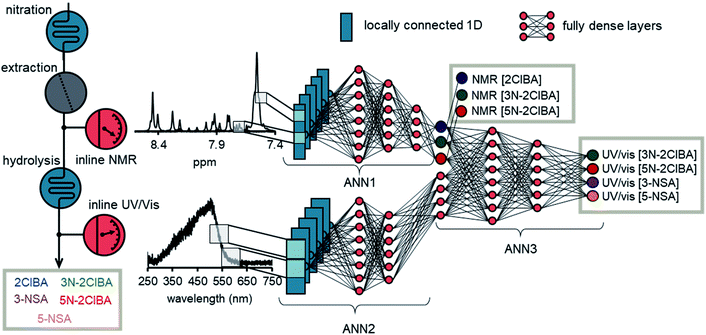
The basic structure of the ANN for data fusion was comprised of 3 different ANN parts (Fig. 5). ANN1 and ANN2 processed the NMR spectrum and the UV/Vis spectrum, respectively. The architecture of ANN1 was adopted from the previously developed ANN for NMR. During the training of the data fusion ANN, it was found that the 1D locally connected layer performed better than the conv1D layer (see ESI†). Therefore, ANN2 was comprised of a 1D locally connected layer followed by dense layers after flattening. The number of filters, kernel size, strides, number of dense layers, amount of neurons per layer, and activation functions were optimized during the training process.
The outputs of ANN1 and ANN2 were merged to provide the input for ANN3. This input was then connected with dense layers and one output layer. During the training the number of layers and the amount of neurons per layers were investigated. Typically, an epoch number of 1000 and a batch size of 1000 was used during training. The “Adam” optimizer was selected in the training process and reduced the mean square error on the validation data of the output of ANN1 and the output of ANN3. The data from the multidimensional dynamic experiment and selected process data were used as validation data. The duration of one epoch was roughly 2–3 seconds, which corresponds to roughly 30 to 50 minutes of training time. The root mean square error on the validation set (RSMEVfusion) was found to be <1.0 mM for 2ClBA (NMR), <1.0 mM for 3N-2ClBA (NMR), <2.0 mM for 5N-2ClBA (NMR), <1.0 mM for 3N-2ClBA (UV/vis), <1.0 mM for 5N-2ClBA (UV/vis), <1.0 mM for 3-NSA (UV/vis), and <2.0 mM for 5-NSA (UV/vis). The values obtained have to be carefully assessed, because the model was evaluated on these data during the training. Therefore, we also tested the ANN on process data.
Application of data fusion to process data
The final model was evaluated on real process data.16b First, the residence time between the two instruments (≈20 min) had to be accounted for. The difference in acquisition times between the NMR (10–12 s) and UV/vis (2 s) was resolved by interpolating the NMR data to the UV/vis time scale. Prior to feeding the spectra to the ANN model, the pretreatments for NMR and UV/vis were conducted, as detailed above. The prediction of the model was compared to offline or online UHPLC measurements after a moving average filter with a filter size of 30 (≈1 min).The model predictions for the multi-dimensional dynamic experiment show an excellent fit with the offline UHPLC data (Fig. 6A). The process data in a steady-state experiment revealed slight under prediction of 5-NSA and over prediction of 3-NSA during the whole run (Fig. 6B). The estimated error of prediction (compared to online UHPLC) of 5-NSA was ∼18 mM at the beginning of the run (0.5 to 2 h) and ∼8 mM at the middle and end. The over prediction of 3-NSA was roughly 12 mM throughout the run. The 3N-2ClBA and 5N-2ClBA were predicted with an error of less than 2 mM (compared to online UHPLC).
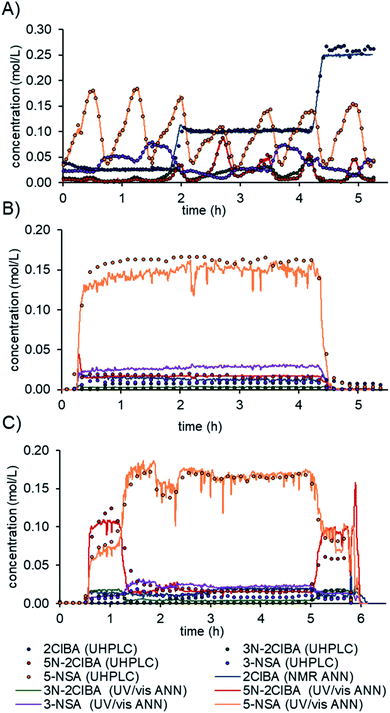 | ||
| Fig. 6 Predictions of the final data fusion ANN model from a multi-dimensional dynamic experiment (A), process data on a stability run (B) and a run with dynamic changes (C). | ||
Additionally, process data from a run with dynamic changes was analyzed (Fig. 6C). The predictions obtained for 2ClBA, 3N-2ClBA, 5N-2ClBA, and 5-NSA were in good agreement with the online UHPLC points. The results for 5N-2ClBA differed only at the end of the run (5 h to 6 h). A similar result, as in the stability run, of slight over prediction of 3-NSA was observed during the run with dynamic changes. This observation might be explained by an over prediction of 3N-2ClBA after ANN1 (see ESI†), which is fed forward in ANN3. In the future, the developed ANN could be further improved by refining and retraining it with process data.
The use of real-time data from inline PAT allows process deviations to be recognized more quickly compared to chromatographic methods. For example, a decrease in the separation efficiency after the nitration at around 1.5 hours could be detected and resolved faster using real-time data (Fig. 6C). The automation of the model can easily be utilized by implementing a simple folder watch system. The NMR and UV/vis spectra can be saved as a csv file locally or using cloud storage and automatically read in and analyzed by a python script. The developed and validated ANN allows one to monitor the synthesis process of mesalazine, which can yield significant improvements in terms of process control and quality by design (QbD) principles.
This successful application of ANNs demonstrates determination of seven species (3 after first reaction step and 4 after second reaction step) in a relatively complex process. It is envisaged that, based on the developed code, application to other processes will be relatively straightforward to implement. This will assist in bringing ANNs to the fore as a chemometric data processing method. Although there is no guarantee that the ANN architecture used here would be directly transferrable to other systems, it is likely that only minor changes (e.g., number of inputs, outputs, hidden layers) would be required, to suit the process to be monitored and desired species quantification.
Conclusions
In conclusion, we have developed an ANN for data fusion, which can be used to predict concentrations of process intermediates in the production of mesalazine. The use of information from multiple PAT instruments facilitated reliable concentration predictions for mixtures of intermediates, even though a simple sensor (UV/vis) was used. The lack of experimental training data was overcome by simulation of synthetic training data for NMR. This provides straightforward access to training data. Developments in the prediction of spectral data should further increase accessibility to synthetic training data for PAT in open data initiatives. Based on the techniques and workflows presented, we envision that more chemists will begin to use ANNs with their PAT data to develop powerful, low cost and accessible advanced data processing models.Data availability
The code developed during and used to carry out this study can be found at: https://github.com/SagmeisterPeter/ANN_Data_Fusion. The data used in this study can be found at: https://doi.org/10.5281/zenodo.6066166.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Austrian Research Promotion Agency FFG No. 871458, within the program “Produktion der Zukunft”. The INFRA FLOW project (Zukunftsfonds Steiermark No. 9003) is funded by the State of Styria (Styrian Funding Agency SFG). The CCFLOW Project (Austrian Research Promotion Agency FFG No. 862766) is funded through the Austrian COMET Program by the Austrian Federal Ministry of Transport, Innovation and Technology (BMVIT), the Austrian Federal Ministry for Digital and Economic Affairs (BMDW), and by the State of Styria (Styrian Funding Agency SFG).Notes and references
- For selected examples of integrated multistep flow systems, see: (a) A. Adamo, R. L. Beingessner, M. Behnam, J. Chen, T. F. Jamison, K. F. Jensen, J.-C. M. Monbaliu, A. S. Myerson, E. M. Revalor, D. R. Snead, T. Stelzer, N. Weeranoppanant, S. Y. Wong and P. Zhang, Science, 2016, 352, 61–67 CrossRef CAS; (b) C. W. Coley, D. A. Thomas, J. A. M. Lummiss, J. N. Jaworski, C. P. Breen, V. Schultz, T. Hart, J. S. Fishman, L. Rogers, H. Gao, R. W. Hicklin, P. P. Plehiers, J. Byington, J. S. Piotti, W. H. Green, A. J. Hart, T. F. Jamison and K. F. Jensen, Science, 2019, 365, eaax1566 CrossRef CAS; (c) A. Bédard, A. Adamo, K. C. Aroh, M. G. Russell, A. A. Bedermann, J. Torosian, B. Yue, K. F. Jensen and T. F. Jamison, Science, 2018, 361, 1–6 CrossRef; (d) S. Chatterjee, M. Guidi, P. H. Seeberger and K. Gilmore, Nature, 2020, 579, 379–384 CrossRef CAS PubMed; (e) S. Steiner, J. Wolf, S. Glatzel, A. Andreou, J. M. Granda, G. Keenan, T. Hinkley, G. Aragon-Camarasa, P. J. Kitson, D. Angelone and L. Cronin, Science, 2019, 363, eaav2211 CrossRef CAS PubMed.
- For reviews of flow chemistry for API synthesis, see: (a) M. B. Plutschack, B. Pieber, K. Gilmore and P. H. Seeberger, Chem. Rev., 2017, 117, 11796–11893 CrossRef CAS; (b) B. Gutmann, D. Cantillo and C. O. Kappe, Angew. Chem., Int. Ed., 2015, 54, 6688–6728 CrossRef CAS; (c) R. Porta, M. Benaglia and A. Puglisi, Org. Process Res. Dev., 2016, 20, 2–25 CrossRef CAS; (d) M. Baumann and I. R. Baxendale, Beilstein J. Org. Chem., 2015, 11, 1194–1219 CrossRef CAS; (e) S. Kobayashi, Chem.–Asian J., 2016, 11, 425–436 CrossRef CAS; (f) R. Gérardy, N. Emmanuel, T. Toupy, V.-E. Kassin, N. N. Tshibalonza, M. Schmitz and J.-C. M. Monbaliu, Eur. J. Org. Chem., 2018, 2018, 2301–2351 CrossRef.
- (a) T. Eifert, K. Eisen, M. Maiwald and C. Herwig, Anal. Bioanal. Chem., 2020, 412, 2037–2045 CrossRef CAS PubMed; (b) J. Workman, B. Lavine, R. Chrisman and M. Koch, Anal. Chem., 2011, 83, 4557–4578 CrossRef CAS PubMed.
- (a) S. L. Lee, T. F. O'Connor, X. Yang, C. N. Cruz, S. Chatterjee, R. D. Madurawe, C. M. V. Moore, L. X. Yu and J. Woodcock, Journal of Pharmaceutical Innovation, 2015, 10, 191–199 CrossRef; (b) C. J. Testa, C. Hu, K. Shvedova, W. Wu, R. Sayin, F. Casati, B. S. Halkude, P. Hermant, D. E. Shen, A. Ramnath, Q. Su, S. C. Born, B. Takizawa, S. Chattopadhyay, T. F. O'Connor, X. Yang, S. Ramanujam and S. Mascia, Org. Process Res. Dev., 2020, 24, 2874–2889 CrossRef CAS; (c) M. M. Nasr, M. Krumme, Y. Matsuda, B. L. Trout, C. Badman, S. Mascia, C. L. Cooney, K. D. Jensen, A. Florence, C. Johnston, K. Konstantinov and S. L. Lee, J. Pharm. Sci., 2017, 106, 3199–3206 CrossRef CAS; (d) A. Mesbah, J. A. Paulson, R. Lakerveld and R. D. Braatz, Org. Process Res. Dev., 2017, 21, 844–854 CrossRef CAS.
- K. Eisen, T. Eifert, C. Herwig and M. Maiwald, Anal. Bioanal. Chem., 2020, 412, 2027–2035 CrossRef CAS PubMed.
- For selected examples of dynamic experiments, see: (a) B. M. Wyvratt, J. P. McMullen and S. T. Grosser, React. Chem. Eng., 2019, 4, 1637–1645 RSC; (b) J. S. Moore and K. F. Jensen, Angew. Chem., Int. Ed., 2014, 126, 480–483 CrossRef; (c) C. A. Hone, N. Holmes, G. R. Akien, R. A. Bourne and F. L. Muller, React. Chem. Eng., 2017, 2, 103–108 RSC; (d) F. Florit, A. M. K. Nambiar, C. P. Breen, T. F. Jamison and K. F. Jensen, React. Chem. Eng., 2021, 6, 2306–2314 RSC.
- For selected examples of self-optimizations, see: (a) V. Sans and L. Cronin, Chem. Soc. Rev., 2016, 45, 2032–2043 RSC; (b) A. D. Clayton, J. A. Manson, C. J. Taylor, T. W. Chamberlain, B. A. Taylor, G. Clemens and R. A. Bourne, React. Chem. Eng., 2019, 4, 1545–1554 RSC; (c) M. Rubens, J. H. Vrijsen, J. Laun and T. Junkers, Angew. Chem., Int. Ed., 2019, 58, 3183–3187 CrossRef CAS PubMed; (d) M. Rubens, J. Van Herck and T. Junkers, ACS Macro Lett., 2019, 8, 1437–1441 CrossRef CAS; (e) C. Mateos, M. J. Nieves-Remacha and J. A. Rincón, React. Chem. Eng., 2019, 4, 1536–1544 RSC; (f) P. Sagmeister, F. F. Ort, E. C. Jusner, D. Hebrault, T. Tampone, G. F. Buono, J. D. Williams and C. O. Kappe, Adv. Sci., 2022, 9, 2105547 CrossRef.
- For selected examples of kinetic model building, see: (a) X. Duan, J. Tu, A. R. Teixeira, L. Sang, K. F. Jensen and J. Zhang, React. Chem. Eng., 2020, 5, 1751–1758 RSC; (b) C. Waldron, A. Pankajakshan, M. Quaglio, E. Cao, F. Galvanin and A. Gavriilidis, React. Chem. Eng., 2019, 4, 1623–1636 RSC.
- For selected examples of process control, see: (a) D. E. Fitzpatrick and S. V. Ley, Tetrahedron, 2018, 74, 3087–3100 CrossRef CAS; (b) R. J. Ingham, C. Battilocchio, D. E. Fitzpatrick, E. Sliwinski, J. M. Hawkins and S. V. Ley, Angew. Chem., Int. Ed., 2015, 54, 144–148 CrossRef CAS PubMed; (c) S. Sacher, I. Castillo, J. Rehrl, P. Sagmeister, R. Lebl, J. Kruisz, S. Celikovic, M. Sipek, J. D. Williams, D. Kirschneck, C. O. Kappe and M. Horn, Chem. Eng. Res. Des., 2022, 177, 493–501 CrossRef CAS.
- For selected examples of IHM, see: (a) S. Kern, K. Meyer, S. Guhl, P. Gräßer, A. Paul, R. King and M. Maiwald, Anal. Bioanal. Chem., 2018, 410, 3349–3360 CrossRef CAS PubMed; (b) M. Bornemann-Pfeiffer, J. Wolf, K. Meyer, S. Kern, D. Angelone, A. Leonov, L. Cronin and F. Emmerling, Angew. Chem., Int. Ed., 2021, 60, 23202–23206 CrossRef CAS; (c) M. Rößler, P. U. Huth and M. A. Liauw, React. Chem. Eng., 2020, 5, 1992–2002 RSC; (d) J. Meyer-Kirschner, M. Kather, A. Pich, D. Engel, W. Marquardt, J. Viell and A. Mitsos, Appl. Spectrosc., 2016, 70, 416–426 CrossRef CAS; (e) N. Zientek, C. Laurain, K. Meyer, A. Paul, D. Engel, G. Guthausen, M. Kraume and M. Maiwald, Magn. Reson. Chem., 2016, 54, 513–520 CrossRef CAS PubMed.
- For selected examples of PLS, see: (a) J. M. Amigo, J. Cruz, M. Bautista, S. Maspoch, J. Coello and M. Blanco, TrAC, Trends Anal. Chem., 2008, 27, 696–713 CrossRef CAS; (b) H. Winning, F. H. Larsen, R. Bro and S. B. Engelsen, J. Magn. Reson., 2008, 190, 26–32 CrossRef CAS PubMed; (c) S. B. Engelsen, F. Savorani and M. A. Rasmussen, eMagRes, 2013, 2, 267–278 CAS; (d) D. Patra and A. K. Mishra, TrAC, Trends Anal. Chem., 2002, 21, 787–798 CrossRef CAS; (e) M. Blanco and I. Villarroya, TrAC, Trends Anal. Chem., 2002, 21, 240–250 CrossRef CAS; (f) P. Sagmeister, D. Kaldre, J. Sedelmeier, C. Moessner, K. Püntener, D. Kummli, J. D. Williams and C. O. Kappe, Org. Process Res. Dev., 2021, 25, 1206–1214 CrossRef CAS; (g) P. Sagmeister, J. Poms, J. D. Williams and C. O. Kappe, React. Chem. Eng., 2020, 5, 677–684 RSC; (h) P. Ebrahimi, F. H. Larsen, H. M. Jensen, F. K. Vogensen and S. B. Engelsen, Metabolomics, 2016, 12, 77 CrossRef; (i) F. Tahir, E. Mercer, I. Lowdon and D. Lovett, Control Engineering Practice, 2018, 77, 225–234 CrossRef; (j) A. Balogh, A. Domokos, B. Farkas, A. Farkas, Z. Rapi, D. Kiss, Z. Nyiri, Z. Eke, G. Szarka, R. Örkényi, B. Mátravölgyi, F. Faigl, G. Marosi and Z. K. Nagy, Chem. Eng. J., 2018, 350, 290–299 CrossRef CAS; (k) E. Mercer, J. Mack, F. Tahir and D. Lovett, in Multivariate Analysis in the Pharmaceutical Industry, Elsevier, 2018, pp. 385–407 Search PubMed; (l) S. Wold, M. Sjöström and L. Eriksson, Chemom. Intell. Lab. Syst., 2001, 58, 109–130 CrossRef CAS.
- For selected examples of ANNs, see: (a) T. Väänänen, H. Koskela, Y. Hiltunen and M. Ala-Korpela, J. Chem. Inf. Comput. Sci., 2002, 42, 1343–1346 CrossRef PubMed; (b) E. C. Ferreira, D. M. B. P. Milori, E. J. Ferreira, R. M. Da Silva and L. Martin-Neto, Spectrochim. Acta, Part B, 2008, 63, 1216–1220 CrossRef; (c) S. Kern, S. Liehr, L. Wander, M. Bornemann-Pfeiffer, S. Müller, M. Maiwald and S. Kowarik, Anal. Bioanal. Chem., 2020, 412, 4447–4459 CrossRef CAS PubMed; (d) F. Fricke, M. Brandalero, S. Liehr, S. Kern, K. Meyer, S. Kowarik, R. Hierzegger, S. Westerdick, M. Maiwald and P. M. Hubner, IEEE Transactions on Emerging Topics in Computing, 2021, 1 Search PubMed; (e) J. R. Long, V. G. Gregoriou and P. J. Gemperline, Anal. Chem., 1990, 62, 1791–1797 CrossRef CAS; (f) J. Liu, M. Osadchy, L. Ashton, M. Foster, C. J. Solomon and S. J. Gibson, Analyst, 2017, 142, 4067–4074 RSC; (g) F. Despagne and D. Luc Massart, Analyst, 1998, 123, 157–178 RSC.
- C. M. Bishop, Rev. Sci. Instrum., 1994, 65, 1803–1832 CrossRef.
- For selected examples of ANNs trained with synthetic data for NMR analysis in biomolecular applications, see: (a) G. Karunanithy, H. W. Mackenzie and D. F. Hansen, J. Am. Chem. Soc., 2021, 143, 16935–16942 CrossRef CAS PubMed; (b) X. Qu, Y. Huang, H. Lu, T. Qiu, D. Guo, T. Agback, V. Orekhov and Z. Chen, Angew. Chem., Int. Ed., 2020, 59, 10297–10300 CrossRef CAS PubMed; (c) J. Luo, Q. Zeng, K. Wu and Y. Lin, J. Magn. Reson., 2020, 317, 106772 CrossRef CAS PubMed.
- M. A. Morin, W. Zhang, D. Mallik and M. G. Organ, Angew. Chem., Int. Ed., 2021, 60, 20606–20626 CrossRef CAS PubMed.
- (a) P. Sagmeister, J. D. Williams, C. A. Hone and C. O. Kappe, React. Chem. Eng., 2019, 4, 1571–1578 RSC; (b) P. Sagmeister, R. Lebl, I. Castillo, J. Rehrl, J. Kruisz, M. Sipek, M. Horn, S. Sacher, D. Cantillo, J. D. Williams and C. O. Kappe, Angew. Chem., Int. Ed., 2021, 60, 8139–8148 CrossRef CAS PubMed.
- (a) R. R. de Oliveira, C. Avila, R. Bourne, F. Muller and A. de Juan, Anal. Bioanal. Chem., 2020, 412, 2151–2163 CrossRef CAS PubMed; (b) N. O'Mahony, T. Murphy, K. Panduru, D. Riordan and J. Walsh, 2016 27th Irish Signals Syst. Conf., 2016, pp. 1–6 Search PubMed; (c) T. Casian, A. Farkas, K. Ilyés, B. Démuth, E. Borbás, L. Madarász, Z. Rapi, B. Farkas, A. Balogh, A. Domokos, G. Marosi, I. Tomută and Z. K. Nagy, Int. J. Pharm., 2019, 567, 1–13 CrossRef PubMed.
- (a) C. Vijaya Lakshmi, N. K. Katari and S. B. Jonnalagadda, Green Process. Synth., 2019, 8, 320–323 CAS; (b) O. Ø. Thomsen, A. Cortot, D. Jewell, J. P. Wright, T. Winter, F. T. Veloso, M. Vatn, T. Persson and E. Pettersson, N. Engl. J. Med., 1998, 339, 370–374 CrossRef CAS PubMed.
- D. Caramelli, J. M. Granda, S. H. M. Mehr, D. Cambié, A. B. Henson and L. Cronin, ACS Cent. Sci., 2021, 7, 1821–1830 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental procedures, python code, results with different ANNs and additional data. See https://doi.org/10.1039/d2dd00006g |
| This journal is © The Royal Society of Chemistry 2022 |