Open Access Article
Open Access ArticlePaRoutes: towards a framework for benchmarking retrosynthesis route predictions†
Samuel
Genheden
 * and
Esben
Bjerrum
* and
Esben
Bjerrum

Molecular AI, Discovery Sciences, R&D, AstraZeneca Gothenburg, SE-431 83 Mölndal, Sweden. E-mail: samuel.genheden@astrazeneca.com
First published on 12th July 2022
Abstract
We introduce a framework for benchmarking multi-step retrosynthesis methods, i.e. route predictions, called PaRoutes. The framework consists of two sets of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 synthetic routes extracted from the patent literature, a list of stock compounds, and a curated set of reactions on which one-step retrosynthesis models can be trained. PaRoutes also comes with scripts to compute route quality and route diversity, quantities that are important for comparing methods. As an illustration of the framework, we compare three template-based methods implemented in the AiZynthFinder software: Monte Carlo tree search (MCTS), Retro*, and a depth-first proof-number search (DFPN) algorithm. It is found that DFPN is inferior to both MCTS and Retro* and cannot be recommended in its current implementation. MCTS and Retro* are on a par with regard to search speed and the ability to find routes in which all starting material is in stock. However, MCTS outperforms Retro* when it comes to route quality and route diversity. MCTS more easily recovers the reference routes and tends to find a diverse set of solutions for a greater portion of the targets. Having showcased the benchmark for template-based methods, we discuss potential issues and caveats needed when adapting the framework for other methods,.e.g., template-free methods or expert systems. We will continue to update and expand the application of PaRoutes, and we also encourage practitioners and developers to adapt PaRoutes to their algorithms as we envisage that the framework could become the community standard to compare retrosynthesis route predictions. PaRoutes is available at https://github.com/MolecularAI/PaRoutes.
000 synthetic routes extracted from the patent literature, a list of stock compounds, and a curated set of reactions on which one-step retrosynthesis models can be trained. PaRoutes also comes with scripts to compute route quality and route diversity, quantities that are important for comparing methods. As an illustration of the framework, we compare three template-based methods implemented in the AiZynthFinder software: Monte Carlo tree search (MCTS), Retro*, and a depth-first proof-number search (DFPN) algorithm. It is found that DFPN is inferior to both MCTS and Retro* and cannot be recommended in its current implementation. MCTS and Retro* are on a par with regard to search speed and the ability to find routes in which all starting material is in stock. However, MCTS outperforms Retro* when it comes to route quality and route diversity. MCTS more easily recovers the reference routes and tends to find a diverse set of solutions for a greater portion of the targets. Having showcased the benchmark for template-based methods, we discuss potential issues and caveats needed when adapting the framework for other methods,.e.g., template-free methods or expert systems. We will continue to update and expand the application of PaRoutes, and we also encourage practitioners and developers to adapt PaRoutes to their algorithms as we envisage that the framework could become the community standard to compare retrosynthesis route predictions. PaRoutes is available at https://github.com/MolecularAI/PaRoutes.
1. Introduction
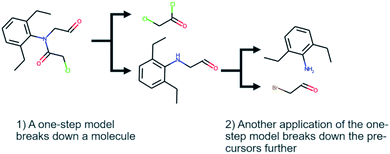
Computer-aided synthesis planning (CASP) is a field of intense research that can provide insight and accelerate the synthesis of novel compounds, both in early discovery and late-stage development.1,2 One particular area of CASP is retrosynthesis analysis in which the aim is to predict the necessary steps to synthesize a compound, i.e. a synthetic route (see Fig. 1). Such methods date back to the 60's and the early work of Corey,3 although the research has intensified in the last decade due to the increased interest in machine learning and artificial intelligence.4 At the heart of retrosynthesis analysis is a method that is capable of predicting disconnections on a compound and thereby producing precursors. Such methods are typically referred to as one-step retrosynthesis or single-step retrosynthesis. The precursors produced by the one-step retrosynthesis can then be further broken down recursively until a set of conditions are met. Such iterative methods are typically referred to as multi-step retrosynthesis. Typically, the stop conditions are that a precursor is found in a database of purchasable compounds, i.e. a stock, or that a maximum number of disconnections has been applied.One-step retrosynthesis methods have received the greatest amount of attention: there is a plethora of methods described in the literature that uses a diverse range of methods to extract synthesis rules, cheminformatic representations, neural network architectures, sampling techniques, etc. [see e.g.5–15]. For the practitioner that wants to use a method for predictions, or for a researcher developing a novel method, there are several comparisons for a subset of the available methods. In fact, once a novel method is developed it is customary to benchmark it against other methods using a common set of known reactions. The US patent office (USPTO) extracts provided by Lowe16 is the de-facto standard for comparing single-step retrosynthesis method, as it is one of few open-source datasets of chemical reactions. However, there are more than one curated subset of the dataset used,17,18 which is a complication. Furthermore, there has not been a survey published showing all one-step methods side by side, so it is still difficult to understand the range of available methods, although reading recent studies like19 could provide a good overview.
Multi-step retrosynthesis methods, or route prediction methods, have received less attention. To the practitioner, the pool of available solutions is dominated by commercial and closed-source alternatives,2 although a few complete, open-source packages have emerged, such as the ASKCOS suite from MIT20 and AiZynthFinder from AstraZeneca.21 An interesting tool is RXN for chemistry that not only predicts reactants but also reagents and is available through a free application programming interface.22 In addition, there have been a few algorithms described in the literature, which we will summarize in Section 4. What is lacking with regards to the route prediction methods is comparative studies. There is a lack of consensus on how to compare route predictions and what data one should do the comparison on. One reason for this could be that there is no public database of synthetic routes, as there is the USPTO data for single-step reactions. A further complication is that there is typically no unique way to synthesize a compound and several alternative routes could be used that are optimal for different scenarios. With regards to the data problem, there have been a few attempts to collect a set of routes on which one can perform a comparison: Heifets and Jurisica23 compiled a suite of routes from organic chemistry examinations that they then used to benchmark their approach. Unfortunately, the suite is extremely small, only 20 routes, and it is therefore difficult to make statistical analysis of the route predictions. Chen et al.24 extracted routes from the USPTO dataset to train a neural network for computing the cost of synthesizing a molecule. They found all compounds in the USPTO dataset that had a route to compounds in the eMolecules database,‡ and then performed further selections to arrive at a test set of size 189. Interestingly, they also used this to compare four different multi-step retrosynthesis methods (and variants thereof). They focused the comparison on computing time, the number of targets for which a route was found, and the length of the routes. Furthermore, Bradshaw et al. also extract routes from a cleaned sub-set of USPTO to train a deep generative model.25 Like in24 they also utilize a specification of building-blocks to define the reaction network and to find synthetic routes. Finally, Mo et al.26 also extracted routes from the USPTO dataset for training their neural network for predicting the human-likeness of routes. Instead of extracting routes from the full reaction network as in24,25 they extracted routes within a patent. Each patent consist of one or more reactions and a reaction network would have highly related reactions. Using a complete depth-first search of such networks for each patent, 238 K routes were extracted. This is an excellent number of routes for training a neural network model but is probably too excessive for benchmarking route prediction methods. However, we will build upon this methodology in Section 2 to extract routes suitable for benchmarking multi-step retrosynthesis tools. We will then proceed to discuss and suggest metrics to compute when comparing predictions on these routes in Section 3. Finally, we will apply this framework on an illustrative comparison of three kinds of search algorithms for template-based retrosynthesis implemented in the AiZynthFinder software in Sections 4 and 5.
2. A benchmark set for route predictions
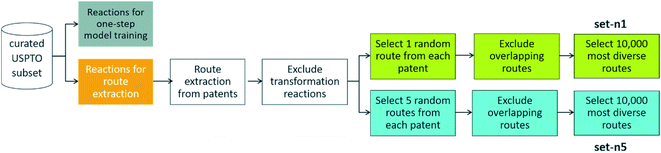
2.1 Route extraction
To extract routes, we started from the subset of the USPTO dataset prepared by Thakkar et al.,27 as this is a dataset that contains atom-mapped reactions and reaction templates, which is necessary for training a template-based one-step retrosynthesis model. We kept only reactions for which the template occurrence was four or more, i.e. all the reactions in the dataset are represented by a reaction template that occurs at least four times in the dataset. This amounts to 867![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620 reactions. When extracting the routes from this dataset, we left out 99
620 reactions. When extracting the routes from this dataset, we left out 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 093 reactions, three examples for each unique reaction template, to be able to have sufficient data to train a one-step model on (see below). We will now detail how routes were extracted from the 768
093 reactions, three examples for each unique reaction template, to be able to have sufficient data to train a one-step model on (see below). We will now detail how routes were extracted from the 768![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 527 remaining reactions, a procedure summarized in Fig. 2.
527 remaining reactions, a procedure summarized in Fig. 2.
 | ||
| Fig. 2 – Procedure to extract reference routes from a curated subset of the USPTO database. Details of the procedure is outlined in Section 2. | ||
We extracted 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 046
046![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 088 routes from 80
088 routes from 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 639 patents using the method of Mo et al.,26 provided as a script§ but with an increased timeout for finding a route from 6 to 10 s. The script puts all the reactions from a patent in a reaction network (see an example in Fig. 3), identifies molecules that only exist as a product as the starting point for synthetic routes, and then uses a depth-first search to extract the routes. After extracting the routes, we immediately discarded all routes with a single leaf, to avoid uninteresting transformation sequences, resulting in 158
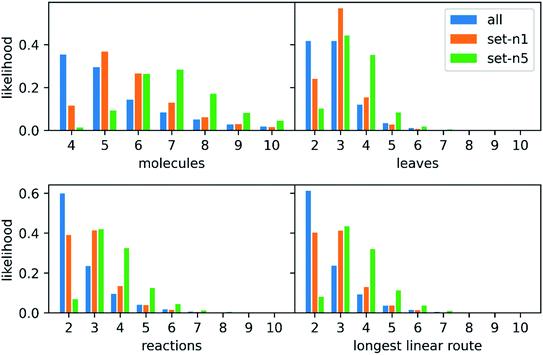
639 patents using the method of Mo et al.,26 provided as a script§ but with an increased timeout for finding a route from 6 to 10 s. The script puts all the reactions from a patent in a reaction network (see an example in Fig. 3), identifies molecules that only exist as a product as the starting point for synthetic routes, and then uses a depth-first search to extract the routes. After extracting the routes, we immediately discarded all routes with a single leaf, to avoid uninteresting transformation sequences, resulting in 158![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 698 routes. The distributions of the number of molecules, leaves, reactions, and longest linear route (LLR) are shown in Fig. 4. The dataset is tilted towards short routes with few leaves. Only 4.7% of the routes are convergent; the remainder are linear. We believe the 150 K routes are too extensive to benchmark route predictions and it is likely that many routes from the same patent are similar. Therefore, we processed the dataset further, although we acknowledge that the 150 K routes could be used in the future for e.g., machine learning tasks, and thus we provide them for downloading.
698 routes. The distributions of the number of molecules, leaves, reactions, and longest linear route (LLR) are shown in Fig. 4. The dataset is tilted towards short routes with few leaves. Only 4.7% of the routes are convergent; the remainder are linear. We believe the 150 K routes are too extensive to benchmark route predictions and it is likely that many routes from the same patent are similar. Therefore, we processed the dataset further, although we acknowledge that the 150 K routes could be used in the future for e.g., machine learning tasks, and thus we provide them for downloading.
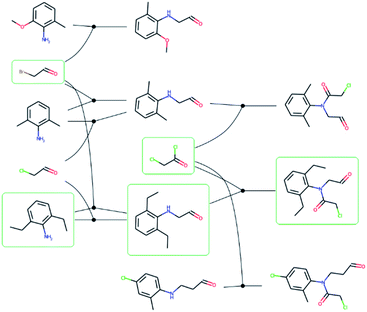 | ||
| Fig. 3 – Reaction network extracted from the US03983174 patent. Reactions are represented by solid circles and connects reactants to the left with the product to the right. The molecules with a green frame highlights one of the possible synthetic routes for 2-chloro-N-(2,6-diethylphenyl)-N-(2-oxoethyl)acetamide and corresponds to the route in Fig. 1. | ||
We randomly selected n routes from each patent and then we performed an overlap check: no route should have leaf molecules that exist in another route as intermediate precursors (non-leaves), and the target molecule should not exist as an intermediate in another route. The motivation behind this check will be explained below. We then discarded all routes with a depth of more than 10 reactions, to exclude a few really long routes that will require an extensive search (this excludes less than 100 out of the 150 K routes, possibly reflecting USPTOs patent oriented chemical scope without extensive coverage of complex syntheses). For the non-overlapping routes with a depth of at most 10 reactions, we selected the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 most diverse routes: the pair-wise distance matrix was computed using the machine learning approach previously described28 and then a greedy search with maxmin criteria was used to select the routes. We created two such sets of 10
000 most diverse routes: the pair-wise distance matrix was computed using the machine learning approach previously described28 and then a greedy search with maxmin criteria was used to select the routes. We created two such sets of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 routes one where either one or five routes were extracted from each patent before checking for overlap (n = 1 or n = 5). We will refer to these two sets as set-n1 and set-n5, respectively. The distributions of the number of leaves, molecules, reactions, and longest linear route (LLR) are shown in Fig. 4. For set-n1, the distributions are closer to the full set of routes: the number of molecules in the routes are typically small and the number of longer routes is quite small. On the contrary, in set-n5, the distributions are shifted to the right and there are more of the longer routes. There are 3.0% and 6.9% of convergent routes in set-n1 and set-n5, respectively. We classified the reactions in the reference routes using the NextMove software29 and analyzed the occurrences of the difference classes. This is shown in Fig. S1,† and we can see that the most common reaction classes are deprotections, n-acylation to amide, O-substitution and other functional group interconversions. It is clear that the reference routes contains predominately common chemistry, a reflection of the USPTO database. Furthermore, the reference routes represent similar chemistry as the reactions in the popular UPSTO-50 K subset,17 although we have not excluded reactions that cannot be classified by NextMove.
000 routes one where either one or five routes were extracted from each patent before checking for overlap (n = 1 or n = 5). We will refer to these two sets as set-n1 and set-n5, respectively. The distributions of the number of leaves, molecules, reactions, and longest linear route (LLR) are shown in Fig. 4. For set-n1, the distributions are closer to the full set of routes: the number of molecules in the routes are typically small and the number of longer routes is quite small. On the contrary, in set-n5, the distributions are shifted to the right and there are more of the longer routes. There are 3.0% and 6.9% of convergent routes in set-n1 and set-n5, respectively. We classified the reactions in the reference routes using the NextMove software29 and analyzed the occurrences of the difference classes. This is shown in Fig. S1,† and we can see that the most common reaction classes are deprotections, n-acylation to amide, O-substitution and other functional group interconversions. It is clear that the reference routes contains predominately common chemistry, a reflection of the USPTO database. Furthermore, the reference routes represent similar chemistry as the reactions in the popular UPSTO-50 K subset,17 although we have not excluded reactions that cannot be classified by NextMove.
2.2 Stock and reaction data
A set of routes is not sufficient to benchmark route prediction methods as there are other factors that determine the search. One such factor is the stock, the set of purchasable compounds that serves as the stop condition for the search. For creating the routes in24 the eMolecule database was used as stop criteria, and Genheden et al.21 created a stock from the ZINC database. Both of these alternatives are very extensive but we argue for not using such databases. Firstly, the extensiveness of the stocks could mask subtle differences between search algorithms as a route could be found by simply resorting to the stock rather than disconnecting molecules. Secondly, the quality and availability of the stock molecules are sometimes unclear, making the stop criteria arbitrary. Thirdly, databases such as eMolecules and ZINC are updated with time, making it hard to pick one representative snapshot of the database for the benchmark. We instead propose to simply use all the leaves of the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 routes as stock molecules. Because we added an overlap check when extracting the routes, we can be sure that an exhaustive search would be able to find the routes without prematurely stopping because of the extensiveness of the stock. There is a 48% overlap of the set-n1 and set-n5 stocks, and 3% of the leaves in the 150 K routes is covered by either the set-n1 or set-n5 stocks.
000 routes as stock molecules. Because we added an overlap check when extracting the routes, we can be sure that an exhaustive search would be able to find the routes without prematurely stopping because of the extensiveness of the stock. There is a 48% overlap of the set-n1 and set-n5 stocks, and 3% of the leaves in the 150 K routes is covered by either the set-n1 or set-n5 stocks.
Another factor affecting the search algorithm is of course the capability of the one-step retrosynthesis model. We have previously released a model trained on the entirety of the USPTO dataset,21,27 but this model was trained on reactions found in the reference routes, making it biased. Using this model in the search, or indeed any one-step model trained on the reactions in the reference routes will be a mix of neural network recommendations and what amounts to literature-lookup. However, we can train a new one-step model on the data that is not found in the reference routes, and because we left out three reactions per reaction template before extracting the routes, we have sufficient data to train a template-based one-step model. In Section 4, we will detail the training of such a model. If someone wants to extract another set of templates or train a template-free one-step model, one can always perform such modeling as well on the provided subset of USPTO. What could be interesting to consider in the future is to make a time-split of the original data, e.g., extract reference routes based on reactions dating before the cut-off year and then training one-step models on reactions after the cut-off year.
2.3 Framework summary
To summarize the created reference set for benchmarking:•A subset of the USPTO database with reactions that can be used to train a one-step model.
•∼150 K routes extracted from the USPTO database, which can be used for machine learning tasks.
•Set-n1 consisting of a diverse set of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 routes which show a similar distribution in the number of molecules and reactions as the 150 K routes.
000 routes which show a similar distribution in the number of molecules and reactions as the 150 K routes.
•Set-n5 consisting of a diverse set of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 routes that are longer and enriched in convergent routes.
000 routes that are longer and enriched in convergent routes.
•Stock-n1 consisting of the 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 633 leaves molecules in set-n1 and should be used as a stock together with set-n1.
633 leaves molecules in set-n1 and should be used as a stock together with set-n1.
•Stock-n5 consisting of the 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 783 leaves molecules in set-n5 and should be used as a stock together with set-n5.
783 leaves molecules in set-n5 and should be used as a stock together with set-n5.
The USPTO dataset, reference routes, and stocks are available as open-source together with the scripts used to create the reference routes.
We call the benchmarking set the PaRoutes (patent routes) framework. It is a framework for benchmarking route predictions because we acknowledge that not all methods are built the same. For instance, we have herein benchmarked algorithms using template-based one-step retrosynthesis methods, but there exist a plethora of alternatives. Therefore, researchers should be able to pick the parts of the framework that is applicable to their methods. For example:
•If your one-step retrosynthesis model is based on templates, you can re-train it using the provided USPTO subset, which includes RDChiral-derived templates.30
•If you want to derive templates yourself, or if you are using a template-free one-step model, you can use the atom-mapped reaction SMILES from the provided training set.
•If you have your own set of curated reactions that you want to train your one-step model on, you have to make sure to first exclude reactions that are also in the reference routes.
•If your one-step model is an expert system not derived from big-data extraction, you should be able to use the provided targets and stock, and not consider the provided reaction datasets.
Because many of the existing one-step models were trained on reactions included in the reference route, we acknowledge that many of those models need to be re-trained to fully exploit PaRoutes. However, some of the adaptions needed with the current version of PaRoutes would complicate the comparison, an issue we will discuss more extensively in Section 5.5.
3. Metrics for comparing route predictions
Several metrics for comparing route predictions are needed and should together form a consensus of how well a method is performing. Relying on a single metric would be vulnerable to adversarial strategies and therefore we will suggest a set of complementary evaluation metrics. Whenever route prediction methods have been compared in the literature the focus has been on computational speed and the number of solved targets,21,24,31i.e. the number of targets for which at least one route is found where all the starting material is in stock. It should be noted that a difference in a few seconds of search is not practically relevant, but speed is nevertheless an essential quantity for any computational method.Although speed and number of solved targets are interesting metrics, they tell nothing about the quality of the predictions. Sometimes the quality of the routes has been quantified as the length of the routes,24,31 the mean chemical complexity,32 or a metric based on the priors from the one-step model.24 Quantifying the quality of a route by simply the route length is particularly misleading as it is very easy to envisage a shorter alternative to a route by for instance removing all protection chemistry thus rendering the route chemically infeasible. An interesting approach taken by Shibukawa et al.32 was to sort the molecules in the routes by molecule weight and then compute the pairwise Tanimoto distances of a molecular fingerprint. Naturally, the sorting of the molecules destroys the order of the reactions in the route. We propose to use a tree edit distance (TED) method,33 which is a graph-theoretical method that recursively applies cheminformatic similarity calculations on a pair of routes to determine the similarity. By sorting the predicted routes and then computing the TED between the predictions and a reference route, one can find at what position the ground truth, i.e. the reference route is found. By doing this over all the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 targets in the reference set one can compute top-n accuracies, just as is standard when comparing one-step retrosynthesis methods. The top-n accuracies is a metric to show how well a search method is in recovering the reference route. Caveats with this definition of accuracy is discussed in Section 5.5.
000 targets in the reference set one can compute top-n accuracies, just as is standard when comparing one-step retrosynthesis methods. The top-n accuracies is a metric to show how well a search method is in recovering the reference route. Caveats with this definition of accuracy is discussed in Section 5.5.
In order to compute accuracies, we need to rank the predicted routes and we propose using the recursive route score by Badowski et al.34 with artificial costs of leaf molecules. For intermediate molecules in a route, the cost is defined recursively as
| cost(m) = minr∈pred(m)cost(r) | (1) |
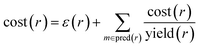 | (2) |
Finally, we propose a metric to quantify the diversity of the predictions. We argue that an algorithm producing more routes is not necessarily better than an algorithm producing fewer routes, because the routes can be highly similar. To compute the diversity, we compute the pairwise distance matrix of all the predicted routes using the fast machine learning method previously described28 that replaces the expensive TED calculations with a fast LSTM-based (long short-term memory) model, and then we use hierarchical clustering to group the routes. We optimize the number of clusters using the Silhouette method35 and the optimal number of clusters is viewed as a metric of diversity.
To summarize, we suggest applying the following metrics when comparing route prediction methods on the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 reference targets:
000 reference targets:
•Average search time to reach convergence in the number of solved targets.
•Number of solved targets.
•Top-1, top-5 and top-10 computed with the TED method.
•Number of route clusters.
Scripts to compute these route quality and diversity metrics are available open-source on GitHub and are considered to be part of the PaRoutes framework. We consider the calculation of timings and if targets are solved to be part of the software producing the routes. In order to compute the quality and diversity metrics, the routes need to be exported in a tree-like structure (in JSON format) with minimal features. Basically, the relationships between molecules and reactions need to be defined, molecules are defined by their SMILES string and reactions are featureless.
4. Example application of benchmarking framework
4.1 Route prediction methods
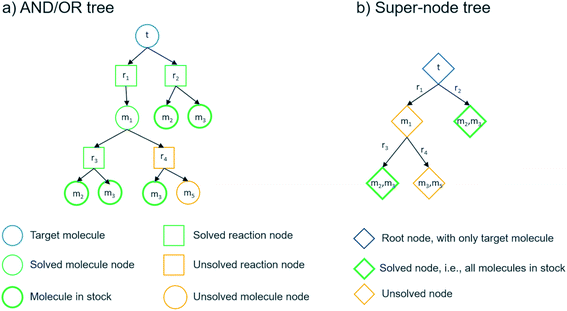
We can summarize the suggested multi-step retrosynthesis methods by dividing them into three categories: proof-number search (PNS),36 Monte Carlo tree search (MCTS),37 and A*-like algorithms.38 In PNS, the retrosynthesis is carried out in a directed bipartite graph consisting of molecule and reaction nodes, i.e. an AND/OR graph (see Fig. 5). The proof-number and disproof-number of each node, which is the number of children nodes necessary to prove and disprove a node, respectively, are used to guide the search. PNS-based retrosynthesis algorithms utilize these numbers differently and also add additional heuristics to increase the efficiency of the search.23,31,32 We implemented a depth-first PNS (DFPN) algorithm in the AiZynthFinder software that combines ideas from two different algorithms.31,32 In MCTS, the retrosynthesis is carried out in a different type of direct graph, where each node is a super-node consisting of one or more molecules that potentially can be extended. The search is typically guided by upper-bound confidence statistics that take into account how many times a node has been visited and a reward function for terminal nodes that can take different forms.20,27,39 We have previously described the MCTS implementation in the AiZynthFinder software,21 where the reward function is based on the depth of the terminal node and how many of the molecules represented by the node is in stock. Finally, several different A*-like algorithms have been described for retrosynthesis.24,40,41 The Chematica program carries out the search in a super-node tree and scores the node based on customizable molecule and reaction cost functions.40 In the Retro* algorithm, the search is carried out in an AND/OR graph and the search is guided by a molecule cost that is provided by a neural network trained on extracted routes.24 We have implemented the Retro* algorithm in the AiZynthFinder software.Although the algorithms that we will use the predict routes are representative of different classes of search algorithms, we acknowledge that our implementations are variants of the original implementations described in the literature. For instance, there are many hyper parameters settings that could be explored. As such, the benchmarks presented herein should serve as an illustration of the PaRoutes framework and provide an insight into the capabilities of the AiZynthFinder software.
4.2 Training a one-step model
We selected a subset of reactions from the USPTO dataset, excluding reactions used in the reference routes, to train one-step retrosynthesis models similar to the model trained by Thakkar et al.27 Atom-mapping was originally carried out with NextMove software.27,29 We trained one model that was used in the set-n1 experiments and one that was used in the set-n5 experiments, although we could have trained one model on the intersection of the two datasets with some reduction in the number of reactions. The dataset consists of 878![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 079 and 871
079 and 871![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001 reactions for the set-n1 and set-n5 routes respectively, distributed over 46
001 reactions for the set-n1 and set-n5 routes respectively, distributed over 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 092 unique reaction templates. The extracted templates were one-hot encoded as output to a neural network. The input was the extended connectivity fingerprints of the product molecules calculated by RDKit version 2020.09.5
092 unique reaction templates. The extracted templates were one-hot encoded as output to a neural network. The input was the extended connectivity fingerprints of the product molecules calculated by RDKit version 2020.09.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 using a radius of 2 and a length of 2048. The neural network was a simple feedforward network: 512 nodes with an ELU activation function, and L2 normalization, followed by a dropout later with a dropout rate of 0.4 and finally an output layer with a softmax activation function. The model was trained for 100 epochs and a batch size of 256. The Adam optimizer43 was used with a categorical cross-entropy loss. The learning rate was initially set to 0.001 and was halved upon a plateau of the validation loss after 5 epochs. The dataset was split by 90%/5%/5% into training, validation, and test set, respectively.
42 using a radius of 2 and a length of 2048. The neural network was a simple feedforward network: 512 nodes with an ELU activation function, and L2 normalization, followed by a dropout later with a dropout rate of 0.4 and finally an output layer with a softmax activation function. The model was trained for 100 epochs and a batch size of 256. The Adam optimizer43 was used with a categorical cross-entropy loss. The learning rate was initially set to 0.001 and was halved upon a plateau of the validation loss after 5 epochs. The dataset was split by 90%/5%/5% into training, validation, and test set, respectively.
4.3 Details of route prediction experiments
The target molecules of the reference routes were subjected to prediction by the AiZynthFinder software.21 As stock we used the reference stock detailed in Section 2, i.e. all the leaves of the reference routes. We used no filter policy and the expansion policy was the one detailed above. As the search algorithm, we use an MCTS algorithm detailed previously, an implementation of the Retro* algorithm, or a depth-first proof-number (DFPN) search. For Retro*, we used the official repository of the Retro* algorithm as a starting point,¶ and re-implemented it in AiZynthFinder. An extension we implemented was continuing the search after the first solutions has been found and extraction of routes using the CompRet algorithm.32 For the DFPN, we started with the algorithm suggested by Kishimoto et al.31 We used a constant unity edge cost, rewrote the algorithm to be iterative rather than recursive, and implemented logic similar to32 to continue the search after the first solution has been found. Routes were extracted using the CompRet algorithm32. Pseudo-code for all three search algorithms is provided in the ESI.† In all experiments, the search consisted of 500 iterations for MCTS and Retro*, 750 iterations for DFPN, and no time limits. The reported timings are wall-times using a single CPU. No GPUs were utilized in this study for route predictions.4.4 Validation metric computations
All routes found by either MCTS, Retro* or DFPN were scored by the route score of Badowski et al.:34 leaf molecules in stock were assigned a cost of 1, leaf molecules not in stock were assigned a cost of 10, and all reactions were assigned a cost of ε = 1. The top-1, top-5 and top-10 accuracies were calculated with the TED algorithm implemented in the route-distance repository. Clustering of the predicted routes was clustered using the publicly available model trained on routes for 10 K ChEMBL compounds.285. Results and discussion
The benchmark metrics listed in Section 3 are listed for all route prediction experiments in Tables 1 and 2. What follows is an analysis of those results.| Search method | Route set | Solved targets | Search timea | First solution timea | One-step model callsa | Template applicationsa |
|---|---|---|---|---|---|---|
a Averages over all targets. Each route set consist of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 targets. The times are wall-times of a single CPU. 000 targets. The times are wall-times of a single CPU.
|
||||||
| MCTS | Set-n1 | 9714 | 303.3 | 8.6 | 3355.6 | 8658.2 |
| Set-n5 | 9676 | 365.7 | 11.7 | 3615.3 | 8953.0 | |
| Retro* | Set-n1 | 9726 | 300.7 | 7.0 | 497.4 | 24281.1 |
| Set-n5 | 9703 | 349.2 | 10.5 | 498.0 | 24322.5 | |
| DFPN | Set-n1 | 8475 | 347.3 | 43.0 | 404.5 | 19503.2 |
| Set-n5 | 7382 | 297.9 | 53.2 | 414.5 | 19957.6 | |
5.1 Search timings
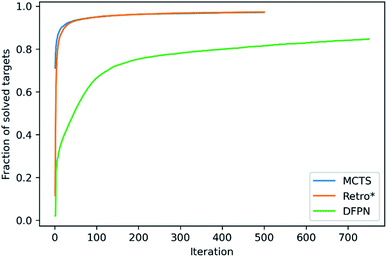
We will start with making an analysis of the overall search timings, and we will start with the predictions on the set-n1 routes. The retrosynthesis search was performed until 500 iterations had elapsed for MCTS and Retro*, but 750 iterations for DFPN. The reason for this is that much fewer retrosynthesis tasks, i.e. call to one-step model and template application, are done each iteration. For MCTS, the rollout implementation ensures that several calls to the one-step model and template applications are performed at each iteration. For Retro*, only a single call to the one-step model is performed each iteration. But on the other hand, one sub-tree is added to the search tree for each applicable template suggested by the one-step model, requiring several template applications. The DFPN implementation also only calls the one-step model once per iteration, but contrary to Retro* only a single sub-tree is added to the search tree, the one for the most promising template. These implementation differences are reflected in the average number of calls to the one-step model and the average number of template applications. MCTS makes on average 7 to 8 times as many calls to the one-step model as Retro* and DFPN, respectively, whereas Retro* and DFPN make 3 to 2 times as many template applications, respectively. However, more importantly, the difference in the amount of work performed in each iteration is reflected in the average search time shown in Table 1. The average search time is 303, 301, 347 s for MCTS, Retro* and, DFPN, respectively. Thus while using 1.5 times as many iterations, DFPN is not much slower than MCTS and Retro*, and the differences between the search methods are practically not important. Because of the relatively small amount of work done in each iteration, DFPN also requires more iterations to find solutions and the convergence in the number of solved targets is slower, as shown in Fig. 6. For MCTS and Retro*, the fraction of solved target is converged at 100 iterations, and thereafter the fraction increases only very slowly. However, for DFPN it is unclear if the fraction of solved targets has converged to the same degree even after 750 iterations.Because of the different amounts of one-step calls and template applications performed at each iteration, it is hard to benchmark the search methods based on the search time. However, when focusing on the time it takes to find a solution, DFPN is clearly outperformed by MCTS and Retro*. This can also be seen in the average time to find the first solution in Table 1, where one can observe that DFPN is approximately 6 times slower than MCTS and Retro* in finding the first solution. Analyzing the predictions on the set-n5 routes, we find that for these targets, the algorithms are generally slower finding the first solutions than searches on the set-n1, indicating that these compounds are more complex.
With respect to the comparison of MCTS and Retro*, there are some implementation details to consider. In the paper introducing Retro*, it was argued that Retro* was advantageous over MCTS because it made fewer calls to the one-step model.24 However, in our implementation of MCTS, the template application is deferred until it is necessary, heavily reducing the number of template applications. Thus for the template-based one-step models used herein, we observe that MCTS and Retro* are approximately equally fast to reach convergence in the number of solved routes. However, it is becoming more and more popular with template-free one-step retrosynthesis models, e.g. transformer-like architectures, that perform a translation task that effectively combines the template recommendation and template application tasks of a templated-based one-step model. Such machine learning (ML) models are typically much slower than the simple feed-forward architecture used in the template-based model. Therefore, using a more expensive ML model or template-free methods that do not need to apply a template would tip the speed advantage in the favor of Retro*.
5.2 Number of solved routes
The goal of any retrosynthesis algorithm is to find routes where all the starting material is known, i.e., solved routes. In Table 1, we list the number of targets for which at least one solution has been found. For the set-n1 routes, both MCTS and Retro* find solutions to about 97% of the targets, and the small difference is probably not statistically significant. However, DFPN only manages to find solutions for 85% of the targets, a significant decrease in performance. It is unclear how many iterations are necessary to reach the performance of MCTS and Retro*, but the extra search time is most likely not warranted.As discussed in Section 2, the distributions of the route shapes for the set-n1 follow closely the distributions for the full set of routes extracted from the patent data. However, we also extracted a set of routes that are enriched in longer and convergent routes, which presumable should be a greater challenge to the search algorithms. For all three search algorithms, we indeed observe a decrease in the number of solved targets when comparing the predictions made on the set-n1 routes and the set-n5 routes (see Table 1). Encouragingly, the decrease is typically rather small, between a fraction of percentage and a few percentages, for MCTS and Retro*. This shows that even though these algorithms require some more time to find a solution, they are capable of breaking down the compounds to starting material in stock. However, for DFPN, the decrease in the number of solved routes is on the order of 10%, a significant amount. This shows that DFPN not only is inferior to MCTS and Retro* in finding solutions but that its capabilities worsen with compound complexity.
In ESI, Table S1,† we make a cross-comparison of the different search methods on the set-n1 routes to find if they are complementary or not. We find that MCTS and Retro* find solutions to the same targets, and there is a practically negligible fraction of targets for which Retro* only finds a solution. Furthermore, DFPN solves no unique targets but both MCTS and Retro* find solutions to targets for which DFPN finds no solution.
5.3 Route quality
As argued in Section 3, finding routes is not a complete quality metric to assess different search methods. To be useful to a chemist, the predicted routes should be feasible, i.e. each step in the route should yield the predicted product under some reasonable conditions. We suggest computing top-n accuracies, similarly to what is typically done with a one-step model, using a tree edit distance (TED) method to compute the similarity between the predicted routes and a reference route. In Table 2, we list the top-1, top-5, and top-10 accuracies. Computing higher top-n accuracies are not particularly useful as there are very few lower-ranked routes because the route score used to rank the routes is rather indiscriminatory. Using MCTS on the set-n1, we arrive at a top-1 accuracy of 0.20, which means that for roughly 1/5 of targets, we find the reference ranked first. Top-10 accuracy is 0.61, implying just for a little bit more than half of the targets, the search finds the reference ranked in the top-10. Using Retro*, we consistently achieve lower accuracies on the set-n1 routes, with top-1 and top-10 of 0.17 and 0.54, respectively, a significant drop in accuracy. DFPN is on a par with MCTS on top-1 accuracies but is worse than both MCTS and Retro* on top-5 and top-10 accuracies. Furthermore, for DFPN there is no difference between top-5 and top-10 accuracies, highlighting again the convergence issue with DFPN.| Search method | Route set | Accuracy | Shorter routea | Leaves overlapb | Routes extractedc | Number of clustersc | ||
|---|---|---|---|---|---|---|---|---|
| Top-1 | Top-5 | Top-10 | ||||||
| a The average number of targets for which a shorter route than the reference route is found in top-1. b The average leaves overlap in top-1. The leaves overlap is the maximum overlap between the leaves in a predicted route and the leaves in the reference route. c Medians over all targets. | ||||||||
| MCTS | Set-n1 | 0.20 | 0.55 | 0.61 | 0.44 | 0.68 | 273 | 68 |
| Set-n5 | 0.09 | 0.34 | 0.42 | 0.59 | 0.62 | 272 | 77 | |
| Retro* | Set-n1 | 0.17 | 0.48 | 0.54 | 0.44 | 0.68 | 264 | 68 |
| Set-n5 | 0.08 | 0.30 | 0.38 | 0.61 | 0.63 | 149 | 39 | |
| DFPN | Set-n1 | 0.19 | 0.33 | 0.33 | 0.45 | 0.63 | 6 | 2 |
| Set-n5 | 0.08 | 0.14 | 0.14 | 0.65 | 0.55 | 6 | 2 | |
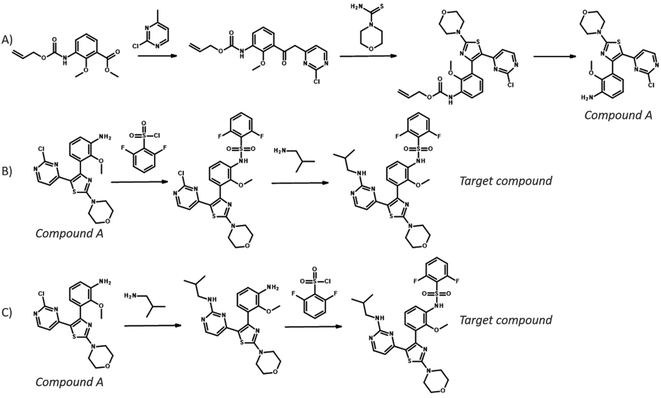
To compare the different search algorithms further, we performed a cross-comparison: given a pair of experiments: we calculated the percentage of targets for which the reference route was identified by both methods, by just one method or by neither of the method (see Table 3). Comparing MCTS and Retro*, we see that both find the reference for 48% of the targets, and for 29% of the targets, neither method is able to find the reference route. Interestingly, the methods are not entirely complementary because only MCTS finds the reference routes for 15% of the targets, whereas only Retro* finds the reference routes for 9% of the targets. Similar observations can be made when comparing the other pair of search methods: both MCTS and Retro* outperform DFPN in uniquely finding reference routes to varying degrees. In Fig. 7, we present the routes for a target for which the reference route is found by MCTS but not Retro*, and in ESI† we present a few similar analyses. In the routes presented in Fig. 7, we can see that the top-1 routes for both MCTS and Retro* start similar and share the first three steps. However, in the reference route, the final steps are a sulfonylation followed by an SNAr reaction. This is also among the extracted predictions from MCTS but not for Retro*. Instead, an alternative route is predicted with the SNAr first and the sulfonylation second, and this is the only top-1 route predicted by Retro*. This is a route also produced by MCTS, showing that this algorithm is able to extract both solutions. It is not clear why Retro* did not recover the reference route because the template corresponding to the SNAr was suggested by the one-step model as evident from the MCTS algorithm. However, something in the prioritization of nodes to expand deemed that path unpromising, continuing with the path following from the sulfonylation template.
| Method 1 | Method 2 | Found by | |||
|---|---|---|---|---|---|
| Both | Method 1 | Method 2 | Neither | ||
| MCTS | Retro* | 0.48 | 0.15 | 0.09 | 0.29 |
| MCTS | DFPN | 0.33 | 0.30 | 0.01 | 0.37 |
| Retro* | DFPN | 0.27 | 0.30 | 0.07 | 0.37 |
To further investigate the rather low accuracies, we did two additional analyses that are included in Table 2. First, we calculated the fraction of targets for which a shorter route than the reference route is found in top-1. For all three methods this fraction is around 0.45, showing that all methods were able to find alternative routes that are shorter for close to half of the targets. Second, we calculated the maximum leaves overlap between the leaves of the top-1 ranked routes and the leaves of the reference route. An overlap of 1.0 would imply that the predicted routes have exactly the same leaves as the reference route but the reactions are not necessarily in the same order. We observe that the average leaves overlap is between 0.63 and 0.68 for the different experiments, indicating a high overlap. In fact, the leaves overlap is one for approximately 1/3 of the targets in all experiments, which is significantly higher than the top-1 accuracies. This shows that the different search methods were able to identify routes similar to the reference routes, but with some of the steps interchanged.
The accuracies for the predictions on the set-n5 routes are significantly lower, with the best-observed top-1 around 0.10 and the best top-10 around 0.42 (see Table 2). This shows more than the fraction of solved routes that set-n5 is a challenging set for any route prediction method. MCTS slightly outperforms Retro*, but it is unclear if the differences are practically relevant. There is a trend that the fraction of targets for which a shorter route than the reference route was found in top-1 is greater than for the set-n1 routes. And it is also clear that the leaves overlap in top-1 is decreased compared to the set-n1 routes. What this analysis show is that all of the methods are in need of improvements when it comes to finding long and convergent routes. All of the three search methods can predict shorter routes, which in Table 1 is shown as a high fraction of solved targets, but they struggle to recover the human-like reference routes.
In the future it would be interesting to study the top-n accuracies as a function of search time, which would answer how long search one has to perform to find a good route. However, such a calculation would be more technically challenging to implement and therefore we did not include this in the first version of PaRoutes.
5.4 Route diversity
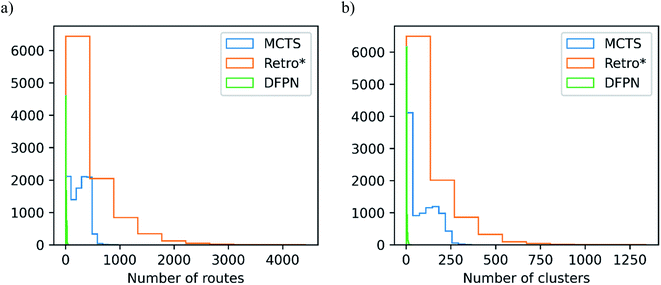
In Table 2, we list the median number of extracted routes and the median number of clusters they make. For the analysis, we extracted all predicted routes that are solved, but if a target is not solved, we extract at most 25 routes. We can observe that MCTS and Retro* produce roughly equal amounts of routes, the median number of produced routes are between 149 and 273. On the other hand, DFPN produces very few routes, the median is only 6 routes. Considering that it does find solutions for close to 85% of the targets, it seems the problem with DFPN lies in its ability to find alternative solutions. This is also reflected in the lower top-5 and top-10 accuracies discussed above. The CompRet implementation of a DFPN algorithm was able to find a considerably large number of routes for a rather small set of compounds,32 so it is possible that our implementation is inferior to CompRet in this regard. Finally, it should be noted that the distribution of the number of produced routes is heavily skewed for Retro* and DFPN, see Fig. 8, whereas it is comparatively uniform for MCTS.As argued in Section 3, it is not only the number of found routes that is important but rather the diversity of routes. To measure this, we find the optimal number of clusters formed by the predicted routes. MCTS seems to fare well in this comparison with a median of 68 for the set-n1 and 77 for the set-n5. Retro* is as successful in finding a diverse set of routes for set-n1, with a median of 68. However, for the set-n5 the diversity is lower with a median number of clusters of 39. Because DFPN gives a low number of routes it is not surprising to see that the median number of clusters is two for both sets of routes. As seen in Fig. 8 the distribution of the optimal number of clusters is also skewed. First, there is a sizable portion of the targets for which a relatively small number of clusters (<10) are found and this is true for all three search methods. Then there is a roughly equal portion of targets for which the number of clusters is more than 10 for MCTS and Retro*. Finally, for Retro* we find a few targets with more than 500 clusters.
5.5 Considerations for adaptation and future applications
In developing PaRoutes, we needed to strike a balance between being rigorous and allowing as many different retrosynthesis algorithms to be comparable with the benchmarking. We have deliberately constructed a narrow problem that the retrosynthesis algorithms should be able to solve, and we attempted to make it amenable to most type of algorithms. As such, PaRoutes is for instance vulnerable to adversarial strategies, currently incomplete in the treatment of alternative routes, and lacking in unusual chemistry. We will now discuss some of these issues and provide suggestions for future developments.With any benchmark using quantitative metrics, it is easy to construct adversarial strategies that artificially scores well. There is also the risk that the retrosynthesis methods starts to follow Goodhart's law that states that when a measure becomes a target, it ceases to be a good measure. For instance, one could train a one-step retrosynthesis on a set of reactions artificially made very similar to the reactions in the reference routes, and a multi-step retrosynthesis algorithm using such a one-step model would be artificially biased. We provide a defined subset of USPTO that is lacking the reactions in the reference routes. Of course there are similar reactions in the provided dataset, but it would be difficult to recover the reference route with a one-step model trained on a completely different part of reaction space, so some similarity is warranted. We therefore suggest to investigate reaction-space overlap and develop a robust metric for quantifying reaction dataset similarity. Furthermore, reinforcement learning could be used to overfit to the provided stock molecules and thus provide an advantage for the sake of the benchmark. In this scenario, PaRoutes could be used to measure how well the reinforcement would work, before retraining on the specific stock database of interest.
We focus PaRoutes on a narrow search problem: finding a single reference route for each target using a narrow set of stock molecules. Naturally, other routes could be as effective or feasible as the reference routes, but the only way to determine that is to perform the synthesis in the lab, which is not practically feasible for large numbers of routes. Because the routes are extracted from patents they incorporate human selection of feasible disconnections and the order of those steps, and thereby represent one possible route. We argue that an effective search algorithm should be able to find this one possible route and we therefore limit the search problem to recovering the one route for each target that we have knowledge about. Similarly, the definition of stock would naturally narrow the search scope and potentially prevent the finding of alternative, more creative, routes to alternative stock molecules. But because we cannot evaluate alternative routes, the narrow search is still meaningful. In the future, we could potentially extract more than one route for each target from USPTO, and extend the accuracy calculations to encompass these routes. However, these set of routes will still not be a complete set of feasible routes for each target.
We regard a limited reaction space; the selection of the routes were filtered to only consist of reactions that have a template extracted that are seen more than three times. This step was necessary as a noise filtering step to avoid having too many reactions with errors in the training and test-reactions, such as reactions with missing or wrongly extracted molecules or wrong atom-mappings. More robust template extraction or atom-mapping could be developed in the future, which would change the number of reactions possible to include. Nevertheless, PaRoutes would be biased towards this selection of reaction and therefore could favor retrosynthesis methods that is trained on these type of reactions and disfavor other methods. For instance, a template-free one-step retrosynthesis model could in principle be trained on the full reaction space and therefore could potentially predict a more diverse set of routes. However, as discussed above, we have no way to assess the feasibility of alternative routes and we have narrowed the search problem to a recover one known feasible route. Therefore, a potentially benchmarking scenario is to run two sets of retrosynthesis experiments, one where a template-free model trained on the full reaction space is used and one where a template-free model train on the limited subset of USPTO is used. In both set of experiments, the multi-step method would be the same and thus the benchmarking would reduce to a study of the effect the one-step model. On the other end of the scale of reaction space coverage, one could imagine an expertly curated one-step model with a limited coverage. In this scenario, the retrosynthesis method could fail in recovering the reference route because it doesn't have the necessary routes. We envisage that a metric showing how well the one-step model recovers the reactions in the reference routes can be added to PaRoutes in the future.
6. Conclusion and outlook
We have presented a framework for benchmarking multi-step retrosynthesis, i.e. route prediction, methods, and we call this framework PaRoutes (patent routes). PaRoutes consists of two sets of synthetic routes extracted from patent literature and corresponding compound stocks to be used as stop criteria for the retrosynthesis. Furthermore, it provides a curated set of reactions that can be used to train one-step retrosynthesis models. Finally, PaRoutes provides scripts to compute quality metrics: top-n accuracies and route diversity. The entire framework is provided open-source with detailed instructions on how to use it. The framework is available at https://github.com/MolecularAI/paroutes.To illustrate the use of PaRoutes, we have carried out route prediction experiments in order to benchmark three different search algorithms implemented in the AiZynthFinder software. We can draw some conclusions from these experiments: our implementation of DFPN is clearly inferior to MCTS and Retro*. DFPN finds fewer routes, solves fewer targets, and recovers to a lesser degree the reference routes. Further investigations are necessary to find the root cause of this, but it is clear in its current implementation, DFPN is not recommended. It should be mentioned that there are several implementations of proof-number search suggested in the literature, but all except one was designed to find a solution and then stop. The comparison of MCTS and Retro* is less clear-cut: both search algorithms solve roughly the same number of targets in roughly the same time. With respect to route quality, MCTS slightly outperforms Retro* especially for the set-n1 routes. Because both algorithms find approximately the same number of targets this shows that Retro* finds different solutions compared to MCTS. Which route would be the most chemically feasible is impossible to determine with certainty without doing experiments. Therefore, until we have a method that practically can evaluate multiple routes for a target, one can do what we are suggesting in here, which is to measure to accuracy of the search algorithms in finding the route there is knowledge about. It is worth emphasizing that all methods struggled with the set-n5 routes. Therefore, identifying and exploring human-like routes for complex targets that require longer synthetic routes seems to be an outstanding problem to solve.
PaRoute was developed and released open-source with the vision to create a community standard for benchmarking route predictions. One-step retrosynthesis is chiefly benchmarked using patent data, and we envisage that PaRoutes will be developed into the analog for multi-step methods. We believe that the lack of comparative studies of route predictions hampers the development and is detrimental to the transparency and reproducibility of published research. We acknowledge that PaRoutes in its current version does not solve all problems associated with comparing route predictions such as how to deal with multiple alternative routes or algorithms with different prerequisite for training data, but we argue that the framework targets an unmet need. Furthermore, we hope that PaRoutes can evolve with community contributions; for instance, we envisage that other quality metrics will be included in the framework when such methods are developed. By benchmarking our search algorithms with diverse metrics we can as a community truly understand the subtle differences and limits of the current state-of-the-art of computer-aided retrosynthesis planning and pave the way for novel developments that have the potential to impact molecular design campaigns.
Data availability
The AiZynthFinder software is available from https://github.com/MolecularAI/aizynthfinder, and the version of the code employed for this study is 3.3.0. The PaRoutes package is available from https://github.com/MolecularAI/PaRoutes, and the version of the code employed for this study is 1.0.0. Data for the PaRoutes framework can be found at Zenodo: https://www.doi.org/10.5281/zenodo.6275421.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Jason Shields is acknowledged with proof-reading and coming with valuable suggestions on the manuscript. Alexey Voronov is acknowledged with proof-reading the manuscript.References
- C. W. Coley, W. H. Green and K. F. Jensen, Machine Learning in Computer-Aided Synthesis Planning, Acc. Chem. Res., 2018, 51, 1281–1289, DOI:10.1021/acs.accounts.8b00087.
- S. Johansson, A. Thakkar and T. Kogej, et al. AI-assisted synthesis prediction, Drug Discov. Today Technol, 2020, 32, 65–72, DOI:10.1016/j.ddtec.2020.06.002.
- E. J. Corey and W. Todd Wipke, Computer-assisted design of complex organic syntheses, Science, 1969, 166, 178–192, DOI:10.1126/science.166.3902.178.
- P. Schwaller, A. C. Vaucher, R. Laplaza, C. Bunne, A. Krause, C. Corminboeuf and T. Laino, Machine Intelligence for Chemical Reaction Space WIREs, Comput. Mol. Biosci., 2022, e1604, DOI:10.1002/wcms.1604.
- M. H. S. Segler and M. P. Waller, Neural-Symbolic Machine Learning for Retrosynthesis and Reaction Prediction, Chem. – Eur. J., 2017, 23, 5966–5971, DOI:10.1002/chem.201605499.
- C. W. Coley, L. Rogers, W. H. Green and K. F. Jensen, Computer-Assisted Retrosynthesis Based on Molecular Similarity, ACS Cent. Sci., 2017, 3, 1237–1245, DOI:10.1021/acscentsci.7b00355.
- B. Liu, B. Ramsundar and P. Kawthekar, et al. Retrosynthetic Reaction Prediction Using Neural Sequence-to-Sequence Models, ACS Cent. Sci., 2017, 3, 1103–1113, DOI:10.1021/acscentsci.7b00303.
- S. Ishida, K. Terayama and R. Kojima, et al. Prediction and Interpretable Visualization of Retrosynthetic Reactions Using Graph Convolutional Networks, J. Chem. Inf. Model., 2019, 59, 5026–5033, DOI:10.1021/acs.jcim.9b00538.
- H. Dai, C. Li and C. W. Coley, et al. Retrosynthesis prediction with conditional graph logic network, Adv. Neural Inf. Process. Syst., 2019, 32, 8872–8882, DOI:10.5555/3454287.3455083.
- P. Karpov, G. Godin and I. V. Tetko, A Transformer Model for Retrosynthesis, in Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Springer, Cham, 2019, pp. 817–830, DOI:10.1007/978-3-030-30493-5_78.
- R. Sun, H. Dai, L. Li, et al., 2020, Energy-based View of Retrosynthesis, arXiv, 2007, 13437, DOI:10.48550/arXiv.2007.13437.
- M. E. Fortunato, C. W. Coley, B. C. Barnes and K. F. Jensen, Data Augmentation and Pretraining for Template-Based Retrosynthetic Prediction in Computer-Aided Synthesis Planning, J. Chem. Inf. Model., 2020, 60, 3398–3407, DOI:10.1021/acs.jcim.0c00403.
- C. Shi, M. Xu, H. Guo, et al., A graph to graphs framework for retrosynthesis prediction, in 37th International Conference on Machine Learning, ICML, 2020, pp. 8777–8786 Search PubMed.
- M. Sacha, M. Błaż and P. Byrski, et al. Molecule Edit Graph Attention Network: Modeling Chemical Reactions as Sequences of Graph Edits, J. Chem. Inf. Model., 2021, 61, 3273–3284, DOI:10.1021/acs.jcim.1c00537.
- P. Seidl, P. Renz and N. Dyubankova, et al., 2022, Modern Hopfield Networks for Few-and Zero-Shot Reaction Prediction, J. Chem. Inf. Model., 2022, 62(9), 2111–2120, DOI:10.1021/acs.jcim.1c01065.
- D. Lowe, Chemical reactions from US pat.510487, 1976–Sep 2016, https://figshare.com/articles/.
- N. Schneider, N. Stiefl and G. A. Landrum, What's What: The (Nearly) Definitive Guide to Reaction Role Assignment, J. Chem. Inf. Model., 2016, 56, 2336–2346, DOI:10.1021/acs.jcim.6b00564.
- W. Jin, C. W. Coley, R. Barzilay and T. Jaakkola, Predicting organic reaction outcomes with Weisfeiler-Lehman network. in Advances in Neural Information Processing Systems, 2017, pp. 2608–2617 Search PubMed.
- M. H. Lin, Z. Tu and C. W. Coley, Improving the Performance of Models for One-step Retrosynthesis through Re-ranking, J. Cheminf., 2022, 14, 15, DOI:10.1186/s13321-022-00594-8.
- C. W. Coley, D. A. Thomas and J. A. M. Lummiss, et al. A robotic platform for flow synthesis of organic compounds informed by AI planning, Science, 2019, 365, eaax1566, DOI:10.1126/science.aax1566.
- S. Genheden, A. Thakkar and V. Chadimová, et al. AiZynthFinder: a fast, robust and flexible open-source software for retrosynthetic planning, J. Cheminf., 2020, 12, 70, DOI:10.1186/s13321-020-00472-1.
- P. Schwaller, R. Petraglia, V. Zullo, V. H. Nair, R. A. Haeuselmann, R. Pisoni, C. Bekas, A. Iuliano and T. Laino, Predicting retrosynthetic pathways using transformer-based models and a hyper-graph exploration strategy, Chem. Sci., 2020, 11, 3316–3325, 10.1039/C9SC05704H.
- A. Heifets and I. Jurisica, Construction of New Medicines via Game Proof Search, in Twenty-Sixth AAAI Conference on Artificial Intelligence, 2012 Search PubMed.
- B. Chen, C. Li, H. Dai and L. Song, Retro*: Learning retrosynthetic planning with neural guided A* search, in 37th International Conference on Machine Learning, ICML, 2020, pp. 1586–1594 Search PubMed.
- J. Bradshaw, B. Paige, M. J. Kusner, et al., 2020, Barking up the right tree: An approach to search over molecule synthesis DAGs. arXiv:2012.1152 https://doi.org/10.48550/arXiv.2012.11522.
- Y. Mo, Y. Guan and P. Verma, et al. Evaluating and clustering retrosynthesis pathways with learned strategy, Chem. Sci., 2021, 12, 1469–1478, 10.1039/d0sc05078d.
- A. Thakkar, T. Kogej and J. L. Reymond, et al. Datasets and their influence on the development of computer assisted synthesis planning tools in the pharmaceutical domain, Chem. Sci., 2020, 11, 154–168, 10.1039/C9SC04944D.
- S. Genheden, O. Engkvist and E. J. Bjerrum, Fast Prediction of Distances Between Synthetic Routes with Deep Learning, Mach. Learn.: Sci. Technol., 2022, 3, 015018, DOI:10.1088/2632-2153/ac4a91.
- https://www.nextmovesoftware.com/namerxn.html .
- C. W. Coley, W. H. Green and K. F. Jensen, RDChiral: An RDKit Wrapper for Handling Stereochemistry in Retrosynthetic Template Extraction and Application, J. Chem. Inf. Model., 2019, 59, 2529–2537, DOI:10.1021/acs.jcim.9b00286.
- A. Kishimoto, B. Buesser, B. Chen and A. Botea Eaton, Depth-First Proof-Number Search with Heuristic Edge Cost and Application to Chemical Synthesis Planning, in Advances in Neural Information Processing Systems, 2019 Search PubMed.
- R. Shibukawa, S. Ishida and K. Yoshizoe, et al. CompRet: A comprehensive recommendation framework for chemical synthesis planning with algorithmic enumeration, J. Cheminf., 2020, 12, 52, DOI:10.1186/s13321-020-00452-5.
- S. Genheden, O. Engkvist and E. Bjerrum, Clustering of Synthetic Routes Using Tree Edit Distance, J. Chem. Inf. Model., 2021, 61, 3899–3907, DOI:10.1021/acs.jcim.1c00232.
- T. Badowski, K. Molga and B. A. Grzybowski, Selection of cost-effective yet chemically diverse pathways from the networks of computer-generated retrosynthetic plans, Chem. Sci., 2019, 10, 4640–4651, 10.1039/c8sc05611k.
- P. J. Rousseeuw, Silhouettes: A graphical aid to the interpretation and validation of cluster analysis, J. Comput. Appl. Math., 1987, 20, 53–65, DOI:10.1016/0377-0427(87)90125-7.
- L. V. Allis, M. van der Meulen and H. J. van den Herik, Proof-number search, Artificial Intelligence, 1994, 66, 91–124, DOI:10.1016/0004-3702(94)90004-3.
- C. Browne, E. Powley and D. Whitehouse, et al. A Survey of Monte Carlo Tree Search Methods, IEEE Trans Comput Intell AI GAMES, 2012, 4, 1–43, DOI:10.1109/TCIAIG.2012.2186810.
- P. E. Hart, N. J. Nilsson and B. Raphael, A Formal Basis for the Heuristic Determination of Minimum Cost Paths, IEEE Trans Syst Sci Cybern, 1968, 4, 100–107, DOI:10.1109/TSSC.1968.300136.
- M. H. S. Segler, M. Preuss and M. P. Waller, Planning chemical syntheses with deep neural networks and symbolic AI, Nature, 2018, 555, 604–610, DOI:10.1038/nature25978.
- T. Klucznik, B. Mikulak-Klucznik and M. P. McCormack, et al. Efficient Syntheses of Diverse, Medicinally Relevant Targets Planned by Computer and Executed in the Laboratory, Chem, 2018, 4, 522–532, DOI:10.1016/j.chempr.2018.02.002.
- J. Jeong, N. Lee, Y. Shin and D. Shin, Intelligent generation of optimal synthetic pathways based on knowledge graph inference and retrosynthetic predictions using reaction big data, J Taiwan Inst Chem Eng, 2022, 130, 103982, DOI:10.1016/j.jtice.2021.07.015.
- RDKit: Open-source cheminformatics, http://www.rdkit.org Search PubMed.
- D. P. Kingma and J. L. Ba, Adam: A method for stochastic optimization, in 3rd International Conference on Learning Representations, ICLR 2015 - Conference Track Proceedings. International Conference on Learning Representations, ICLR, 2015 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2dd00015f |
| ‡ https://downloads.emolecules.com/free/. |
| § https://github.com/moyiming1/Retrosynthesis-pathway-ranking. |
| ¶ https://github.com/binghong-ml/retro_star. |
| This journal is © The Royal Society of Chemistry 2022 |