Open Access Article
Open Access ArticleHow a quantum computer could accurately solve a hydrogen-air combustion model†
Alejandro
Becerra
abc,
Oscar Homero
Diaz-Ibarra
d,
Kyungjoo
Kim
d,
Bert
Debusschere
 d and
Eric A.
Walker
d and
Eric A.
Walker
 *ef
*ef
aInstitute for Artificial Intelligence and Data Science, The State University of New York at Buffalo, 14260, USA
bData Intensive Studies Center, Tufts University, Medford, MA 02155, USA
cDepartment of Mathematics, Tufts University, Medford, MA 02155, USA
dSandia National Laboratories, Livermore, CA 94551, USA
eDepartment of Chemical and Biological Engineering, The State University of New York at Buffalo, 14260, USA. E-mail: ericwalk@buffalo.edu; Tel: +1 716 645 2909
fLinde Plc, 175 E Park Dr, Tonawanda, NY 14150, USA
First published on 16th June 2022
Abstract
A quantum circuit method for modeling steady state behavior of homogeneous hydrogen-air combustion is presented. Extensive empirical testing has pinpointed the factor determining accuracy of quantum circuit calculations. Specifically, the accuracy of the Harrow, Hassidim and Lloyd (HHL) algorithm has been benchmarked using Qiskit simulations. For random linear systems that were constricted by various criteria, the quantum solution was compared to the classical solution. The criteria investigated include orthogonality, condition number, orthonormality, angle between vectors within the linear system, diagonality, and the angle between the solution vector and the right-hand side (RHS) vector. The results of these rigorous tests show that the single most powerful factor in accuracy is the angle between the solution vector and the RHS vector. This insight was used to inform the preconditioning of two reduced models of hydrogen-air combustion. These models have been compared in terms of accuracy and degree of utility in terms of the physical system. This application area could exploit a quantum advantage via the poly-logarithmic scaling of HHL.
Introduction
Currently, there is a great amount of interest in developing quantum computers, especially hardware and algorithms.1 Encryption2 and electronic structures of molecules are of particular interest because a quantum advantage has been shown in principle. Another area of research is quantum machine learning.3Mansouri, et al.,4 the authors of which have a start-up company affiliation, have published their perspective on the possible chemical industrial application of quantum computers. The perspective was on making chemical products. They explain, for example, the promise of a quantum computer exactly solving the Schrödinger equation for the caffeine molecule, limited currently by quantum hardware and its noise. They provide a background on the hardware development of quantum computers, beginning with a nuclear magnetic resonance system in 2001.
Durand, et al.5 applied a quantum algorithm for economic predictive control of a chemical process including an economic model. The quantum algorithm they use is Grover's Search Algorithm.6 Another work on quantum computing in industrial process systems was done by You, et al. of Cornell University.7
Other authors8,9 have used field programmable gate arrays (FPGAs) to emulate quantum circuits for modeling chemical phenomena. While one cannot execute quantum algorithms on classical structures in their natural time, FPGAs can be used to emulate quantum circuits and understand their potential speedups.
There currently exist a number of quantum algorithms for solving linear systems of equations,10 the most prominent of which is Harrow, Hassidim and Lloyd (HHL).11 Linear systems are fundamental in chemical kinetics,12 partial differential equations,13 back-propagation in neural networks,14 and graph theory analytics.15–17 So, the importance of a quantum speedup for solving linear systems cannot be understated.
Additionally, there are limitations to the accuracy of the approximate numerical solution provided by HHL.10,18 Previous efforts have been made toward obtaining accurate solutions to quantum linear systems arising from chemical kinetics models.19 One factor that was shown to influence the accuracy of HHL was the condition number of A (the ratio of the largest magnitude eigenvalue to the smallest magnitude eigenvalue of the matrix). Furthermore, preconditioners that restrict the condition number of A were previously known to be able to optimize for speed and accuracy.18
This work searches deeper in quantum accuracy and shows that the condition number of A is not the only control of accuracy. Many random linear systems were solved with the HHL algorithm as simulated by a Qiskit circuit. This extensive testing pinpointed a new criterion for linear systems to be accurately solved by a quantum computer. 2 versions of a reduced hydrogen-air combustion model were accurately solved by HHL with Qiskit circuit simulations that leveraged this new criterion. The criterion for high accuracy is that the angle between the true solution and the RHS vector is very small. TChem20 was used to compute the parameters for a Jacobian linearized model that solves for the steady state behavior of this reacting mixture. However, the full kinetic model has 9 species with 19 reversible reaction steps, and HHL can only guarantee a speedup if the linear system satisfies 4 strict criteria.18
The direction of this work is important because UQ encounters scaling problems which could be greatly alleviated by a quantum speedup. In particular, combustion models are known for high-dimensionality and strong non-linearity, both of which are challenging for effective UQ. While the examples presented are modest, the insights gained are critical for scaling up to larger applications of quantum computing to UQ. Furthermore, UQ is an entire field of its own,21 with many applications in the physical sciences.22 So, a quantum computing framework for UQ would have broad impact.
In the following sections, classical and quantum linear solvers are compared, a hydrogen-air combustion mechanism is outlined, preparation of a Jacobian linearized model is detailed, and methods for reducing the model are described. Subsequently, the results of many experiments with the Qiskit quantum circuit simulator are presented. For an accurate HHL solve, these experiments determined that the angle between the true solution and the RHS vector must be very small. Finally, this insight is leveraged for a combustion application, and directions for future work are discussed. All codes and data associated with this paper are hosted here: https://bitbucket.org/ericawalk/quantumcombustion/src/main/
Classical and quantum linear solvers
The fastest classical linear solver runs in O(Nκ) where N is the dimension of A and κ is the condition number of A. A runtime of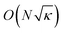 can be achieved with this algorithm for any positive semidefinite matrix A. Similar to HHL, this classical algorithm can only provide an approximation of the solution vector x. For comparison, Gaussian elimination can provide the exact solution vector x in O(N3) time (unless precision is lost due to floating point error). When considering precision, ε, the computational complexity becomes O(Nκ
can be achieved with this algorithm for any positive semidefinite matrix A. Similar to HHL, this classical algorithm can only provide an approximation of the solution vector x. For comparison, Gaussian elimination can provide the exact solution vector x in O(N3) time (unless precision is lost due to floating point error). When considering precision, ε, the computational complexity becomes O(Nκ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(1/ε)).
log(1/ε)).
When certain criteria are met (which are discussed in the following section), a runtime of O(κ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(N)1/ε) can be achieved with HHL. Certain advancements made by Ambainis23 as well as Childs, Kothari, and Somma24 can provide improvements in terms of the accuracy and condition number scaling, but not the scaling with respect to dimension. The runtime of HHL for systems with sparse matrices A (reaching O(κ
log(N)1/ε) can be achieved with HHL. Certain advancements made by Ambainis23 as well as Childs, Kothari, and Somma24 can provide improvements in terms of the accuracy and condition number scaling, but not the scaling with respect to dimension. The runtime of HHL for systems with sparse matrices A (reaching O(κ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log3
log3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κ
κ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N/ε3) and O(κ2
N/ε3) and O(κ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N
N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(1/ε)), respectively).24,25 Additionally, Wossnig, Zhao, and Prakash27 have provided a quantum linear solver for systems with dense matrices A that runs in
log(1/ε)), respectively).24,25 Additionally, Wossnig, Zhao, and Prakash27 have provided a quantum linear solver for systems with dense matrices A that runs in 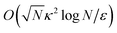 time. In comparison, HHL is only capable of solving systems with dense matrices A in O(Nκ2
time. In comparison, HHL is only capable of solving systems with dense matrices A in O(Nκ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N/ε) time.
N/ε) time.
Hydrogen-air combustion mechanism
For this context, we consider a system with 9 species and 19 reversible reactions as outlined by Yetter, et al.26 for the H2/O2 sub-mechanism with Ar. Here, Ar is inert and does not react, distinct from air. Air contains N2, which reacts with O2 to form NOx.27 For this mechanism, the reaction equations involved in H2–O2 chain reactions are shown in eqn (1a)–(1d). The reaction equations involved in H2–O2 dissociation and recombination are shown in eqn (2a)–(2d). The reaction equations involved in the formation and consumption of HO2 are shown in eqn (3a)–(3e). The reaction equations involved in the formation and consumption of H2O2 are shown in eqn (4a)–(4f).| H + O2 ⇌ O + OH | (1a) |
| O + H2 ⇌ H + OH | (1b) |
| OH + H2 ⇌ H + H2O | (1c) |
| OH + OH ⇌ O + H2O | (1d) |
| H2 ⇌ H + H | (2a) |
| O + O ⇌ O2 | (2b) |
| O + H ⇌ OH | (2c) |
| H + OH ⇌ H2O | (2d) |
| H + O2 ⇌ HO2 | (3a) |
| HO2 + H ⇌ H2 + O2 | (3b) |
| HO2 + H ⇌ OH + OH | (3c) |
| HO2 + O ⇌ OH + O2 | (3d) |
| HO2 + OH ⇌ H2O + O2 | (3e) |
| HO2 + HO2 ⇌ H2O2 + O2 | (4a) |
| H2O2 ⇌ OH + OH | (4b) |
| H2O2 + H ⇌ H2O + OH | (4c) |
| H2O2 + H ⇌ H2 + HO2 | (4d) |
| H2O2 + O ⇌ OH + HO2 | (4e) |
| H2O2 + OH ⇌ H2O + HO2 | (4f) |
Jacobian linearized ODE model
The chemical reactions in eqn (1a)–(4f) can be used to derive a first-order ordinary differential equation (ODE) model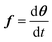 that relates the change in each species mass fraction (θi) with the reaction rates (ki).28–30 All of the species mass fractions can be denoted with a vector θ. Previously, a linear approximation of ordinary differential equations employed additional model constraints to remove nonlinearity.12 Here, we use a Jacobian linearization approach to approximate the steady-state solution.
that relates the change in each species mass fraction (θi) with the reaction rates (ki).28–30 All of the species mass fractions can be denoted with a vector θ. Previously, a linear approximation of ordinary differential equations employed additional model constraints to remove nonlinearity.12 Here, we use a Jacobian linearization approach to approximate the steady-state solution.
Given a vector of initial species mass fractions θ0, TChem20 was utilized to compute the Jacobian J0 and the RHS f0 for a Jacobian linearized model of a 0-dimensional homogenous gas reactor. Constant pressure was assumed. The entries of J0, f0, and θ0 for the mechanism outlined in eqn (1a)–(4f) are shown in Table S1, Table S2, and Table S3,† respectively. The approximate equality (≈) in eqn (5) and (6) arises due to the linearization method (it is like a Taylor series truncated after the first-order).
| f ≈ f0 + J0(θ − θ0) | (5) |
To solve eqn (5) for the steady state solution, we set f = 0. After a re-arrangement, we arrive at eqn (6) (which is a linear system Ax = b).
| J0θ ≈ J0θ0 − f0 | (6) |
Reduced models
H2/O2/Ar model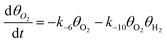 | (7a) |
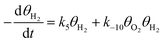 | (7b) |
This scenario above is known as a reduced kinetic model.19,31 In eqn (7a) and (7b), two reacting species and one inert species are modeled. H2 association is connected with the rate constant k5, and O2 dissociation is connected with the rate constant k−6. Eqn (3b) has the reverse rate constant k−10. The dimension of the model is 2 and the initial conditions are θAr = 0.5, θO2 = 0.45, θH2 = 0.05.
One constraint is that θAr is treated as constant. θH2 and θO2 can change, but an additional constraint is that they sum to a constant overall mass balance (θH2 + θO2 = 0.5). This is represented by the first row of eqn (8a). The second row of eqn (8a) essentially represents the dθtot/dt, which has been assumed to be zero. At the initial time, this would be a good approximation to the overall mechanism because all other species are zero. At steady state, however, it is not necessarily realistic. However, the answer will still balance H2 and O2.
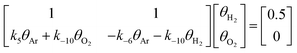 | (8a) |
Values inside the matrix in eqn (8a) can be retrieved from the Jacobian J0. Below, this is illustrated by eqn (8b):
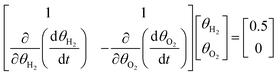 | (8b) |
The classical and quantum solutions to eqn (8b) are shown in Table 1.
| θ H2 | θ O2 | |
|---|---|---|
| Classical | 0.356 | 0.144 |
| Quantum | 0.491 | 0.009 |
| Preconditioned quantum | 0.354 | 0.146 |
H2/O2/H2O/Ar model
Another reduced kinetic model is elaborated below. The dimension is 4 and the initial conditions are the same as above. Once again, θAr cannot change. This is represented by the last row of eqn (9). θH2, θO2, and θH2O can change, but they sum to a constant overall mass balance (θH2 + θO2 + θH2O = 0.5). This is represented by the third row of eqn (9a). The first and second rows of eqn (9a) correspond to dθH2/dt and dθO2/dt, respectively. k−13 corresponds to the reverse rate constant of chemical eqn (3e).
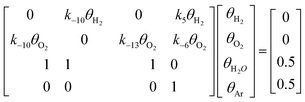 | (9a) |
Values inside the matrix in eqn (9a) can be retrieved from the Jacobian J0. Below, this is illustrated by eqn (9b):
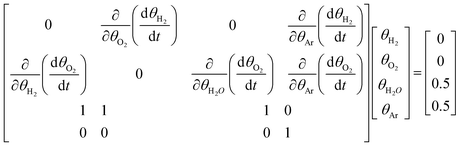 | (9b) |
The classical and quantum solutions to eqn (9b) are shown in Table 2.
| θ H2 | θ O2 | θ H2O | θ Ar | |
|---|---|---|---|---|
| Classical | 0.054 | 0.151 | 0.295 | 0.500 |
| Quantum | 0.000 | −0.015 | 0.583 | 0.421 |
| Preconditioned quantum | −0.032 | 0.168 | 0.304 | 0.553 |
Results of numerical HHL experiments
Condition number
What follows is a demonstration using an example calculation of why the condition number of a matrix is important for accuracy and why it is related to the number of qubits in the (compute) register. A subroutine that obtains eigenvalues of the matrix A in the HHL algorithm is quantum phase estimation (QPE).6,32–34 QPE requires that A is exponentiated as exp (2πiA). The purpose is to create a unitary gate. This transformation exponentiates the eigenvalues.One consequence of the above transformation is that a large condition number will require small intervals. This is because the precision of stored eigenvalues which can be stored is 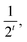 where t is the number of qubits in the (compute) register. The number of values that can be stored doubles with every qubit, and the t qubits store the eigenvalues around the complex unit circle.
where t is the number of qubits in the (compute) register. The number of values that can be stored doubles with every qubit, and the t qubits store the eigenvalues around the complex unit circle.
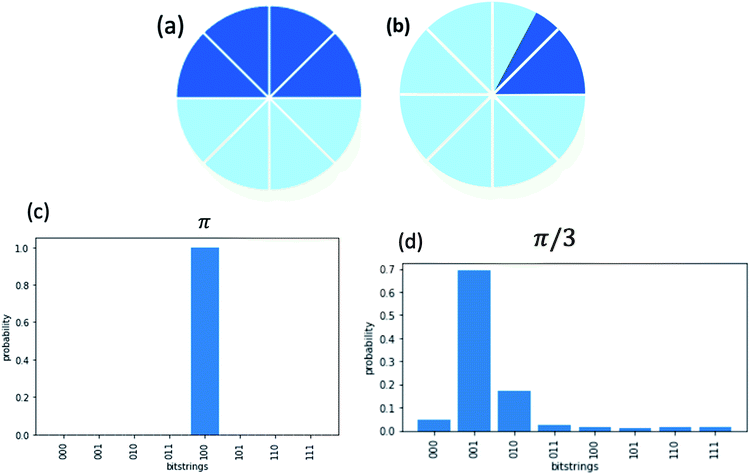
Fig. 1 illustrates eigenvalues on 1/8th intervals in the complex unit circle and off 1/8th intervals. By inference, the 1/8th intervals correspond to t = 3 qubits. A QPE circuit is run, and the results visualized. The matrix with the eigenvalues on the 1/8th intervals has a precise and accurate solution, but the matrix with the off-interval eigenvalues does not. QPE is a subroutine of HHL. In Fig. 1, parts (a) and (c) have the matrix,
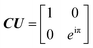 | (10) |
Parts (b) and (d) have the matrix:
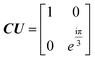 | (11) |
The respective shots histograms from statistical sampling of the quantum circuit are shown in parts (c) and (d). The height of a bitstring value is a probability mass. CU is the controlled unitary gate fed to the QPE for extracting eigenvalues.
Orthogonal tests
Orthogonal tests begin the series of tests searching for a criterion that controls the accuracy in quantum circuits solving linear systems. A Qiskit quantum circuit was used to simulate the HHL algorithm. The exact quantum state is revealed rather than the statistical shots which will be done on a real quantum computer.A computational experiment was performed by beginning with the identity matrix and rotating the second row vector by increments of 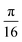 radians. Each system was solved with HHL as simulated by Qiskit. The accuracy of each simulation was evaluated using Qiskit's built-in metric: fidelity. The end results are shown in Fig. S1.† Fidelity is a measure of accuracy using the classical solution as a reference. Fidelity is the squared overlap between two quantum states. The classical analogy is the norm of the dot product of two vertical vectors. For these 2 × 2 matrices, the classical solution is expected to be accurate to machine precision. For each system, the vector b was
radians. Each system was solved with HHL as simulated by Qiskit. The accuracy of each simulation was evaluated using Qiskit's built-in metric: fidelity. The end results are shown in Fig. S1.† Fidelity is a measure of accuracy using the classical solution as a reference. Fidelity is the squared overlap between two quantum states. The classical analogy is the norm of the dot product of two vertical vectors. For these 2 × 2 matrices, the classical solution is expected to be accurate to machine precision. For each system, the vector b was 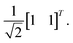
In (a), the first row of each matrix A was the vector 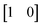 and the second row of each matrix A was a rotation of this vector by some angle θ (in increments of
and the second row of each matrix A was a rotation of this vector by some angle θ (in increments of 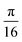 radians). For the blue points in (b), the first row of each matrix A was the vector
radians). For the blue points in (b), the first row of each matrix A was the vector 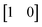 and the second row of each matrix A was a rotation of this vector by some angle θ (increments of
and the second row of each matrix A was a rotation of this vector by some angle θ (increments of 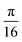 radians) but over a different domain than part (a). For the red points in (b), these rows are permuted. In other words, the first row and the second row are swapped. Thus, even though the blue and red points correspond to the same set of select linear systems of equations, the blue points use the diagonally dominant representation while the red points do not. These results appear to show that the closer to orthogonal a matrix is, the greater the accuracy obtained with HHL. However, these results are not proof, which is why the next test is conducted.
radians) but over a different domain than part (a). For the red points in (b), these rows are permuted. In other words, the first row and the second row are swapped. Thus, even though the blue and red points correspond to the same set of select linear systems of equations, the blue points use the diagonally dominant representation while the red points do not. These results appear to show that the closer to orthogonal a matrix is, the greater the accuracy obtained with HHL. However, these results are not proof, which is why the next test is conducted.
To further interrogate the orthogonality criterion for quantum accuracy, random orthogonal matrices were evaluated. Random orthogonal Q matrices were obtained from the QR decomposition of random matrices. The entries of the random matrices are random numbers over the interval [0,1) with a uniform probability distribution. The results are shown in Fig. S2.† In (a), each system has the vector 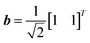 and each random orthogonal matrix A is 2 by 2. In (b), each system has the vector
and each random orthogonal matrix A is 2 by 2. In (b), each system has the vector 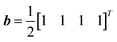 and each random orthogonal matrix A is 4 by 4. The results from Fig. S2† reveal that when the input matrix is perfectly orthogonal, HHL is not accurate.
and each random orthogonal matrix A is 4 by 4. The results from Fig. S2† reveal that when the input matrix is perfectly orthogonal, HHL is not accurate.
Orthonormal tests
It could be that the requirement for accuracy is that the vectors of the matrix be orthonormal. That is, beyond orthogonality, tested with negative results above, it could be necessary that those vectors also have unit length. So, in order to obtain the random orthonormal matrices used in this computational experiment, the Q matrices from the QR decomposition of random matrices were normalized by scaling the rows to be unit length. The results are shown in Fig. S3.† For two-dimensional systems with orthonormal matrices, the vector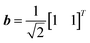 and each random orthonormal matrix A is 2 by 2. Random orthonormal tests did not yield accurate quantum solutions.
and each random orthonormal matrix A is 2 by 2. Random orthonormal tests did not yield accurate quantum solutions.
Diagonal tests
Diagonal matrices were constructed with random numbers on the diagonal from a uniform probability distribution over the interval [0, 1). Off-diagonal entries were set to zero. The results from the quantum accuracy tests are shown in Fig. S4.† In (a), each system has the vector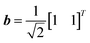 and each random diagonal matrix A is 2 by 2. In (b), each system has the vector
and each random diagonal matrix A is 2 by 2. In (b), each system has the vector 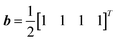 and each random diagonal matrix A is 4 by 4. These systems with random diagonal matrices exhibited higher accuracy, broadly speaking, than the ones with random orthogonal matrices. Still the accuracy is less than acceptable for UQ studies.
and each random diagonal matrix A is 4 by 4. These systems with random diagonal matrices exhibited higher accuracy, broadly speaking, than the ones with random orthogonal matrices. Still the accuracy is less than acceptable for UQ studies.
Angle of the true solution with the RHS vector
A foundational linear algebra principle of matrices is the concept of eigendecomposition. An interrogation of quantum accuracy criterion of linear systems would be incomplete without considering eigenvalues and eigenvectors. The eigendecomposition equation is:| Av = λv | (12) |
It was observed that higher accuracy with HHL was consistent with a smaller angle between the classical solution x and the vector b. This angle θ is shown on the x-axes in Fig. 2 and 3. In Fig. 2, each system has the vector 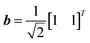 and each random diagonal matrix A is 2 by 2. The outlier at the low angle in Fig. 2 is likely due to using a limited number of qubits in simulating the quantum circuit with an HHL algorithm. In Fig. 3, each system has the vector
and each random diagonal matrix A is 2 by 2. The outlier at the low angle in Fig. 2 is likely due to using a limited number of qubits in simulating the quantum circuit with an HHL algorithm. In Fig. 3, each system has the vector 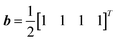 and each random diagonal matrix A is 4 by 4.
and each random diagonal matrix A is 4 by 4.
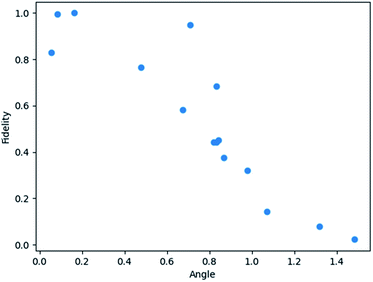 | ||
| Fig. 2 Fidelity of quantum solution to linear systems of equations (Ax = b) with random 2 by 2 matrices A. On the x-axis, the angle shown is between the true solution x and the RHS b. | ||
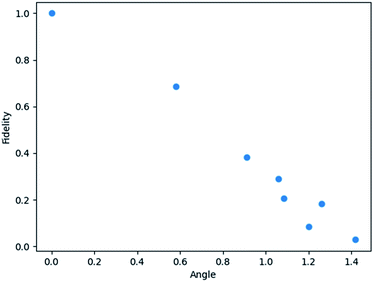 | ||
| Fig. 3 Fidelity of quantum solution to linear systems of equations (Ax = b) with random 4 by 4 matrices A. On the x-axis, the angle shown is between the true solution x and the RHS b. | ||
When θ = 0, near perfect accuracy can be obtained with HHL. One such case of when θ = 0 is when the system is Ax = λv for some eigenvalue λ and eigenvector v pair of A. This is shown in Fig. S5.† In (a), each matrix A is 2 by 2. In (b), each matrix A is 4 by 4. Another such case of when θ = 0 is when the system is Ax = v for some eigenvector v of A. This is shown in Fig. S6.† In (a), each matrix A is 2 by 2 and the vector 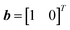 is an eigenvector of A. In (b), each matrix A is 4 by 4 and the vector
is an eigenvector of A. In (b), each matrix A is 4 by 4 and the vector 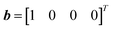 is an eigenvector of A. Creating this eigenvector is done by filling the first column with zeroes starting on the second row. Most generally, θ = 0 when b is any nonzero scalar multiple of an eigenvector of A. In this equation, λ and v are some eigenvalue and eigenvector pair of A. c can be any nonzero scalar.
is an eigenvector of A. Creating this eigenvector is done by filling the first column with zeroes starting on the second row. Most generally, θ = 0 when b is any nonzero scalar multiple of an eigenvector of A. In this equation, λ and v are some eigenvalue and eigenvector pair of A. c can be any nonzero scalar.
| Ax = (cλ)v | (13) |
The solution to this linear system is x = cv. Thus, xb = 1 and cos−1(1) = 0. Empirically, it has been seen in Fig. S1† that it is possible for θ = 0 when b is a linear combination of the eigenvectors of A. In this case, when the fidelity (accuracy) has peaked, the RHS vector can be written as an equal contribution of each of the two eigenvectors.
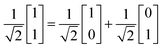 | (14) |
So, given a sufficient number of qubits for the condition number of the matrix, the key criterion for an accurate HHL solve is that the angle between the true solution with the RHS vector is very small. For practical scientific and engineering applications, this implies that most systems will have to be preconditioned to meet this criterion. In the next section, one way of preconditioning for this criterion is presented and applied to 2 reduced models of hydrogen-air combustion.
Results of combustion application
Combustion models
For the H2/O2/Ar model, eqn (8b) can be preconditioned with a 2D rotation matrix to maximize its accuracy. Due to both sides of the equations being multiplied by the rotation matrix, the x solution vector remains constant, while the RHS vector, b, is rotated.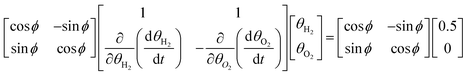 | (15) |
For this model, a rotation angle of 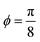 radians was used. This transformation makes the angle between the exact solution x and the RHS vector b less than 0.01 radians. After preconditioning, the HHL solution exhibits perfect accuracy (see Table 1). Further evidence of the small angle yielding an accurate quantum solution will be seen in the four-dimensional combustion model below. This new preconditioning method will greatly increase the cost of solving one linear system with HHL. However, in the context of UQ, this cost could be offset by leveraging the ability to apply one optimal preconditioner to many samples of the forward model.
radians was used. This transformation makes the angle between the exact solution x and the RHS vector b less than 0.01 radians. After preconditioning, the HHL solution exhibits perfect accuracy (see Table 1). Further evidence of the small angle yielding an accurate quantum solution will be seen in the four-dimensional combustion model below. This new preconditioning method will greatly increase the cost of solving one linear system with HHL. However, in the context of UQ, this cost could be offset by leveraging the ability to apply one optimal preconditioner to many samples of the forward model.
The H2/O2/H2O/Ar model can be preconditioned using a product of 4D rotation matrices,
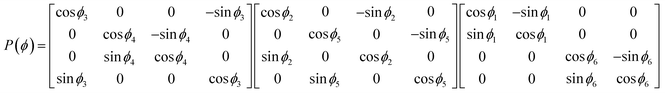 | (16) |
For this model, rotation angles of ϕ1 = 0 radians, 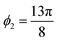 radians,
radians, 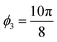 radians,
radians, 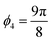 radians,
radians, 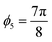 radians, and
radians, and 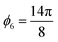 radians were used. This transformation makes the angle between the exact solution x and the vector b less than 0.06 radians. The results for the HHL quantum solution for this preconditioned system are presented in Table 2, along with the classical solution.
radians were used. This transformation makes the angle between the exact solution x and the vector b less than 0.06 radians. The results for the HHL quantum solution for this preconditioned system are presented in Table 2, along with the classical solution.
Conclusions
This paper identified a key criterion necessary for the accurate solution of linear systems of equations with HHL, which is a key element for incorporating this quantum algorithm into scientific computing. The criterion is that the angle between the solution vector and the RHS vector is small. A preconditioner in the form of a product of rotation matrices can optimize for this criterion. This method could be applied to any application of HHL. Therefore, the potential for cross-domain impact is vast.Using Qiskit to emulate an HHL circuit, we demonstrate the preparation and application of optimal preconditioners for obtaining accurate steady state solutions to simplified hydrogen-oxygen combustion models with 2 and 4 species.
In the context of UQ problems, we hypothesize that a single optimal preconditioner can be found once for the mean sample. Then, the same matrix could be used to precondition all samples. This way, quantum speedup could be maintained. Future work can test the accuracy of applying one optimized preconditioner to all samples. It is likely that this method has limitations to the amount of perturbation with a still-acceptable accuracy.
Future work also includes extracting statistics (namely mean and variance) pertaining to the entries of the quantum state containing the solutions to all of the samples. An oft-cited criticism of HHL is that the number of shots necessary to statistically extract the solution vector x is so large that it could cancel out a scaling advantage. However, UQ problems do not require knowing all entries of x; they only require information such as the mean or variance of x. So, if additional gate operations can be performed on x to prepare these statistics, then perhaps HHL can retain a quantum advantage in UQ applications.
Ultimately, this article is another small but necessary step on the path to achieving “quantum supremacy” in the area of UQ.
Data availability
All codes and data associated with this paper and the data that support the findings of this study will be made openly available upon publication at in https://bitbucket.org/ericawalk/quantumcombustion/src/main/.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Chemical Sciences, Geosciences and Biosciences Division, as part of the Computational Chemistry Sciences Program (Award Number:0000232253). Sandia National Laboratories is a multimission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International, Inc., for the U.S. Department of Energy's National Nuclear Security Administration under contract DE-NA0003525. The views expressed in the article do not necessarily represent the views of the U.S. Department of Energy or the United States Government. This work was supported in part by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, under the Accelerated Research in Quantum Computing program. Bert Debusschere would like to thank Habib Najm at Sandia National Laboratories for his helpful suggestions. Ojas Parekh of Sandia National Laboratories is acknowledged for the expert advice from a quantum computing mathematics perspective. Cosmin Safta of Sandia National Laboratories is acknowledged for the helpful discussions on combustion modeling and TChem.References
- National Academies of Sciences, E.; Medicine, Quantum Computing: Progress and Prospects, The National Academies Press, Washington, DC, 2019, p. 272 Search PubMed.
- P. W. Shor, in Algorithms for Quantum Computation: Discrete Logarithms and Factoring, Proceedings 35th Annual Symposium on Foundations of Computer Science, vol. 20–22, Nov. 1994, pp. 124–134 Search PubMed.
- J. Biamonte, P. Wittek, N. Pancotti, P. Rebentrost, N. Wiebe and S. Lloyd, Quantum Machine Learning, Nature, 2017, 549, 195–202 CrossRef CAS PubMed.
- M. P. Andersson, M. N. Jones, K. V. Mikkelsen, F. You and S. S. Mansouri, Quantum Computing for Chemical and Biomolecular Product Design, Curr. Opinion Chem. Eng., 2022, 36, 100754 CrossRef.
- K. Nieman, K. K. Rangan and H. Durand, On Probabilistic Input Selection: Utilizing a Quantum Algorithm in Selecting Inputs for Lyapunov-Based Economic Model Predictive Control Formulated as a Look-up Table, in American Institute of Chemical Engineers Annual Meeting, ed. M. Ellis, AIChE, Boston, MA, 2021 Search PubMed.
- J. D. Hidary, Quantum Computing: An Applied Approach, Springer International Publishing, 2019, XIX, p. 379 Search PubMed.
- A. Ajagekar and F. You, Quantum Computing Assisted Deep Learning for Fault Detection and Diagnosis in Industrial Process Systems, Comput. Chem. Eng., 2020, 143, 107119 CrossRef CAS.
- J. Pilch and J. Długopolski, An FPGA-Based Real Quantum Computer Emulator, J. Comput. Electron., 2019, 18, 329–342 CrossRef.
- J. M. Rodríguez-Borbón, A. Kalantar, S. S. R. K. C. M. Yamijala, B. Oviedo, W. Najjar and B. M. Wong, Field Programmable Gate Arrays for Enhancing the Speed and Energy Efficiency of Quantum Dynamics Simulations, J. Chem. Theory Comput., 2020, 16, 2085–2098 CrossRef PubMed.
- D. Dervovic, M. Herbster, P. Mountney, S. Severini, N. Usher and L. Wossnig, Quantum Linear Systems Algorithms: A Primer, arXiv Quantum Physics, 2018 Search PubMed.
- A. W. Harrow, A. Hassidim and S. Lloyd, Quantum Algorithm for Linear Systems of Equations, Phys. Rev. Lett., 2009, 103, 150502 CrossRef PubMed.
- E. A. Walker and S. A. Pallathadka, How a Quantum Computer Could Solve a Microkinetic Model, J. Phys. Chem. Lett., 2021, 12, 592–597 CrossRef CAS PubMed.
- E. Bueler, Petsc for Partial Differential Equations: Numerical Solutions in C and Python; SIAM, 2020, p xvi + 391 Search PubMed.
- R. J. Erb, Introduction to Backpropagation Neural Network, Computation. Pharm. Res., 1993, 10, 165–170 CrossRef CAS PubMed.
- E. A. Walker, M. M. Mohammadi and M. T. Swihart, Graph Theory Model of Dry Reforming of Methane Using Rh (111), J. Phys. Chem. Lett., 2020, 11, 4917–4922 CrossRef CAS PubMed.
- E. K. J. Walker, J. Goetz, M. T. Robo, A. Tewari and P. M. Zimmerman, Learning to Predict Reaction Conditions: Relationships between Solvent, Molecular Structure, and Catalyst, J. Chem. Inf. Model., 2019, 59, 3645–3654 CrossRef CAS PubMed.
- S. F. Muldoon, E. W. Bridgeford and D. S. Bassett, Small-World Propensity and Weighted Brain Networks, Sci. Rep., 2016, 6, 22057 CrossRef CAS PubMed.
- S. Aaronson, Read the Fine Print, Nat. Phys., 2015, 11, 291–293 Search PubMed.
- A. Becerra, A. Prabhu, M. S. Rongali, S. C. S. Velpur, B. Debusschere and E. A. Walker, How a Quantum Computer Could Quantify Uncertainty in Microkinetic Models, J. Phys. Chem. Lett., 2021, 12, 6955–6960 Search PubMed.
- K. Kim, O. Diaz-Ibarra, C. Safta and H. Najm, Tchem V2.0 – a Software Toolkit for the Analysis of Complex Kinetic Models, Sandia National Laboratories, 2020 Search PubMed.
- T. J. Santner, B. J. Williams and W. I. Notz, The Design and Analysis of Computer Experiments, Springer, 2003 Search PubMed.
- H. N. Najm, B. J. Debusschere, Y. M. Marzouk, S. Widmer and O. P. Le Maître, Uncertainty Quantification in Chemical Systems, Int. J. Numer. Methods Eng., 2009, 80, 789–814 CrossRef.
- A. Ambainis, Variable Time Amplitude Amplification and a Faster Quantum Algorithm for Solving Systems of Linear Equations, arXiv- quant-ph, 2010 Search PubMed.
- A. M. Childs, R. Kothari and R. D. Somma, Quantum Algorithm for Systems of Linear Equations with Exponentially Improved Dependence on Precision, SIAM J. Comput., 2017, 46, 1920–1950 CrossRef.
- L. Wossnig, Z. Zhao and A. Prakash, Quantum Linear System Algorithm for Dense Matrices, Phys. Rev. Lett., 2018, 120, 050502 CrossRef CAS PubMed.
- R. A. Yetter, F. L. Dryer and H. Rabitz, A Comprehensive Reaction Mechanism for Carbon Monoxide/Hydrogen/Oxygen Kinetics, Combust. Sci. Technol., 1991, 79, 97–128 CrossRef CAS.
- C.-H. Liu, K. Giewont, T. J. Toops, E. A. Walker, C. Horvatits and E. A. Kyriakidou, Non-Catalytic Gas Phase No Oxidation in the Presence of Decane, Fuel, 2021, 286, 119388 CrossRef CAS.
- K. Giewont, E. A. Kyriakidou and E. A. Walker, Investigation of Potential Catalytic Active Sites of Pd/SSZ-13: A DFT Perspective, J. Phys. Chem. C, 2021, 125(28), 15262–15274 CrossRef CAS.
- A. Savara and E. Walker, Chekipeuq Intro 1: Bayesian Parameter Estimation Considering Uncertainty or Error from Both Experiments and Theory, ChemCatChem, 2020, 12(21), 5385–5400 CrossRef CAS.
- S. Matera, W. F. Schneider, A. Heyden and A. Savara, Progress in Accurate Chemical Kinetic Modeling, Simulations, and Parameter Estimation for Heterogeneous Catalysis, ACS Catal., 2019, 9, 6624–6647 CrossRef CAS.
- E. A. Walker, K. Ravisankar and A. Savara, Chekipeuq Intro 2: Harnessing Uncertainties from Data Sets, Bayesian Design of Experiments in Chemical Kinetics, ChemCatChem, 2020, 12, 5401–5410 CrossRef CAS.
- G. M. D'Ariano, C. Macchiavello and M. F. Sacchi, On the General Problem of Quantum Phase Estimation, Phys. Lett. A, 1998, 248, 103–108 CrossRef.
- U. Dorner, R. Demkowicz-Dobrzanski, B. J. Smith, J. S. Lundeen, W. Wasilewski, K. Banaszek and I. A. Walmsley, Optimal Quantum Phase Estimation, Phys. Rev. Lett., 2009, 102, 040403 CrossRef CAS PubMed.
- T. E. O'Brien, B. Tarasinski and B. M. Terhal, Quantum Phase Estimation of Multiple Eigenvalues for Small-Scale (Noisy) Experiments, New J. Phys., 2019, 21, 023022 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Table of Jacobian values, Table of RHS values, table of initial state vector values, various figures showing fidelity of quantum solution. See https://doi.org/10.1039/d2dd00049k |
| This journal is © The Royal Society of Chemistry 2022 |