Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
What controls the observed size-dependency of the growth rates of sub-10 nm atmospheric particles?†
Jenni
Kontkanen
 *a,
Dominik
Stolzenburg
*a,
Dominik
Stolzenburg
 a,
Tinja
Olenius
a,
Tinja
Olenius
 b,
Chao
Yan
a,
Lubna
Dada
b,
Chao
Yan
a,
Lubna
Dada
 ac,
Lauri
Ahonen
ac,
Lauri
Ahonen
 a,
Mario
Simon
a,
Mario
Simon
 d,
Katrianne
Lehtipalo
d,
Katrianne
Lehtipalo
 ae and
Ilona
Riipinen
f
ae and
Ilona
Riipinen
f
aInstitute for Atmospheric and Earth System Research, University of Helsinki, Helsinki, Finland. E-mail: jenni.kontkanen@helsinki.fi
bSwedish Meteorological and Hydrological Institute, Norrköping, Sweden
cLaboratory of Atmospheric Chemistry, Paul Scherrer Institute, Villigen, Switzerland
dInstitute for Atmospheric and Environmental Sciences, Goethe University Frankfurt, Frankfurt am Main, Germany
eFinnish Meteorological Institute, Helsinki, Finland
fDepartment of Environmental Science (ACES), Bolin Centre for Climate Research, Stockholm University, Stockholm, Sweden
First published on 23rd March 2022
Abstract
The formation and growth of atmospheric particles involving sulfuric acid and organic vapors is estimated to have significant climate effects. To accurately represent this process in large-scale models, the correct interpretation of the observations on particle growth, especially below 10 nm, is essential. Here, we disentangle the factors governing the growth of sub-10 nm particles in the presence of sulfuric acid and organic vapors, using molecular-resolution cluster population simulations and chamber experiments. We find that observed particle growth rates are determined by the combined effects of (1) the concentrations and evaporation rates of the condensing vapors, (2) particle population dynamics, and (3) stochastic fluctuations, characteristic to initial nucleation. This leads to a different size-dependency of growth rate in the presence of sulfuric acid and/or organic vapors at different concentrations. Specifically, the activation type behavior, resulting in growth rate increasing with the particle size, is observed only at certain vapor concentrations. In our model simulations, cluster–cluster collisions enhance growth rate at high vapor concentrations and their importance is dictated by the cluster evaporation rates, which demonstrates the need for accurate evaporation rate data. Finally, we show that at sizes below ∼2.5–3.5 nm, stochastic effects can importantly contribute to particle population growth. Overall, our results suggest that interpreting particle growth observations with approaches neglecting population dynamics and stochastics, such as with single particle growth models, can lead to the wrong conclusions on the properties of condensing vapors and particle growth mechanisms.
Environmental significanceThe formation and growth of atmospheric particles involving sulfuric acid and organic vapors can significantly influence the climate, and thus the knowledge of the initial particle growth by these vapors is needed. Particle growth is commonly studied by assessing particle growth rates from measured particle size distributions. Here, we unravel the factors controlling the observed growth rates of sub-10 nm particles, by using cluster population simulations and chamber experiments. We find that particle growth rates are governed by (1) the concentrations and evaporation rates of vapors, (2) particle population dynamics, and (3) stochastic fluctuations. Thus, to get an unbiased view on particle growth mechanisms, observations should be interpreted with approaches able to consider these effects. |
1. Introduction
The formation and growth of aerosol particles from atmospheric vapors is predicted to produce a significant fraction of the global cloud condensation nuclei, estimates ranging from a few percent up to 80%.1–5 Therefore, there is a need for developing robust physical descriptions of this process, which can be implemented in large-scale models. For this, the correct interpretation of the observations on the initial growth of the particle population is necessary.According to the current understanding, the formation of the first nanometer-sized molecular clusters occurs by nucleation or barrier-less clustering of atmospheric vapors.6,7 In the case of nucleation, the molecular clusters on average decay by evaporation faster than grow by collisions of vapor molecules, but stochastic fluctuations enable some of them to reach the critical size regime, where the growth overcomes the evaporation.7,8 The stochastics-driven formation can be described by molecular-resolution cluster population models.9,10 After the initial formation of clusters, they can continue to grow to larger sizes by condensation of suitable vapors, which can be described by single-particle models that simulate the growth of particle diameter upon condensation.11,12 However, the mean size of the particle population is also affected by other population dynamics processes, including the collisions between different molecular clusters or particles and their losses due to coagulation scavenging or other sinks.13–15
Due to the limited knowledge of the thermodynamic properties of newly formed molecular clusters and particles, their high evaporation rates are commonly depicted with Kelvin effect, stating that the equilibrium vapor pressure of the compound over the surface of a spherical particle increases with increasing particle size. Therefore, only vapors i with low enough saturation vapor pressure (psat,i) (or in the case of mixtures, low enough equilibrium vapor pressure over the mixture) can reach high enough supersaturation to overcome the Kelvin barrier and condense on the smallest particles.16
Sulfuric acid is important in the initial steps of particle formation and growth in many environments,17 due to its low equilibrium vapor pressure over the mixture of sulfuric acid and bases, such as ammonia and amines.18 After the initial growth by sulfuric acid, organic compounds are considered to govern the growth of particles to larger sizes.19 Especially, highly-oxygenated organic molecules (HOMs), formed by autoxidation of volatile organic compounds (VOCs), such as monoterpenes, have been observed to participate in particle formation and growth in chamber experiments.12,20,21 Organic compounds are commonly divided into different groups based on their volatility.22 Extremely low volatility organic compounds (ELVOCs) have very low psat,i and can therefore contribute to particle growth even at the smallest, sub-3 nm, sizes.12 Low volatility organic compounds (LVOCs) have higher psat,i and can thus usually drive particle growth only after the particles have grown past a few nanometers.12,23
A common approach to study which compounds participate in particle growth based on atmospheric measurements is to (1) deduce the diameter growth rate of particles (in units nm h−1) in different size ranges from the time-evolution of particle size distribution24 and (2) determine if the observed growth rates can be explained by a condensation mass flux of some vapor (often sulfuric acid) on a single particle,25 using measured vapor concentrations. In most environments, particle growth rate is observed to increase with size between ∼1 and 25 nm,26 and the condensation of sulfuric acid is found insufficient to explain the growth rates, especially above ∼5 nm.27–30 This has been attributed to the important role of oxidized organic vapors, which can condense on particles with increasing efficiency as the particle size increases, due to the diminishing Kelvin barrier.31 The process has been proposed to be described by nano-Köhler theory, depicting the activation of particles to growth by organic vapors due to lowering of Kelvin barrier and the solute effect.32 However, the nano-Köhler theory can represent the complex dynamics of growing atmospheric particles only under certain ranges of condensable vapor concentrations and the saturation ratio of organic vapors.33 Also, comparing the observed particle growth rates with estimates from gas-phase vapors is challenging because of high uncertainties in the measurement of sub-10 nm particle size distribution (which growth rate is calculated from) and in the quantification of condensing vapors.34,35
In addition to atmospheric observations, particle growth rates have been studied using chamber experiments, such as the CLOUD (Cosmics Leaving OUtdoor Droplets) experiment at CERN.12,36,37 In the CLOUD experiments involving only sulfuric acid and ammonia, growth rate has been found to decrease with size.36 This can be explained by the decreasing vapor molecule size relative to particle size as particle size increases, causing the diameter growth rate to decrease with size when evaporation is negligible,25 as well as by the reduced influence of van der Waals forces at larger sizes.36 In experiments involving only organic vapors, sub-10 nm growth rate has been observed to increase with size.12,37,38 The strength of the increase has been shown to depend on the volatility distribution of the organic oxidation products and thus it is influenced for example by nitrogen oxides (NOx) concentrations,37,39 and the specific mixture of organics.40,41
In most parts of the atmosphere, sulfuric acid, ammonia, and organic vapors are all present and can be expected to participate in particle formation and growth.5,17 Although nucleation involving sulfuric acid, ammonia and HOMs has been investigated in the CLOUD experiment,42 the size-dependence of particle growth rate in the presence of all these vapors simultaneously has not been studied in detail.
Besides the properties of the vapors participating in condensation growth, observed sub-10 nm particle growth rates and their size-dependency can also be affected by other factors. These include population dynamics, such as cluster–cluster collisions, coagulation scavenging and the loss of particles onto chamber walls,13,43 as well as the time-dependent variation of condensable vapors.33,44 In addition, stochastic effects, which are often neglected, can significantly contribute to the growth of the particle population at the smallest sizes.8,45,46 The contributions of all these factors influencing observed particle growth rate cannot be separated solely based on measurements, or by using condensation growth models, where the deterministic mass flux of vapor on a single particle is studied. Thus, to interpret observations on sub-10 nm particle growth, modeling methods considering the evolution of the whole cluster or particle population are necessary.9,14,47
In this work, we investigate sub-10 nm particle growth by utilizing a combination of experimental data and molecular cluster population simulations. We analyze experiments from the CLOUD chamber involving sulfuric acid, ammonia, and/or oxidation products of monoterpenes,42 corresponding to conditions in the boreal forest where particle formation and growth is frequent.48 The CLOUD facility enables studying the formation and growth of particles from these vapors under well-controlled, atmospherically relevant conditions with negligible contaminations.49–51 To understand the behavior of observed growth rate, we perform molecular-resolution simulations of 1–6 nm cluster and particle population and compare growth rates from experiments to the corresponding simulations. We also apply a metric by Olenius et al.8 to both experimental and simulation data to assess the impact of stochastic collisions and evaporations on particle growth.
We aim to answer to the following questions: (1) what controls the variation in the observed growth rates of sub-10 nm particles in the presence of one or more condensable vapors, such as sulfuric acid and oxidized organic compounds, and (2) what does this imply in terms of how observed particle growth rates can be interpreted? Especially, we explore the impacts of condensable vapor properties (a) on the size-dependency of observed particle growth rate, (b) on the effects of particle population dynamics, such as cluster–cluster collisions, on particle growth, and (c) on the threshold size above which stochastic effects on particle growth can be neglected.
2. Methods
2.1 Experiments
For the sulfuric acid and ammonia experiments, sulfur dioxide, ammonia and ozone were added to the chamber. Sulfur dioxide and ozone were added up to 5 ppb and 30 ppb, respectively, while ammonia concentration was 41–45 ppt. The photo-oxidation of sulfur dioxide was induced by UV illumination of the chamber resulting in the formation of sulfuric acid and subsequent new particle formation and growth. The sulfuric acid concentration during the experiments was controlled by the UV intensity. For more details, see Stolzenburg et al.36
For the experiments involving organic vapors, alpha-pinene or a mixture of alpha-pinene and delta-3-carene were added to the chamber together with NOx. The experiments were typically initiated by switching between neutral and so-called galactic cosmic ray conditions, by switching off the electric field of the chamber and hence allowing ions to be produced in the chamber at an ion-pair production rate of ∼3 cm−3 s−1. This increases the nucleation rate in the system significantly42,52 and results in the formation of a new particle mode at rather constant gas-phase precursor concentrations. The new particle mode was used for growth rate calculations as described in Sect. 2.3. For more details on the experiments involving organic vapors, see Lehtipalo et al.42 and Yan et al.37
We also used ion size distributions measured with the NAIS (Neutral cluster and Air Ion Spectrometer). The NAIS measures the size distribution of positively and negatively charged ions with mobility diameters between 0.8 and 42 nm.54
The overall HOM volatility distribution can vary depending on NOx concentration37,39 and thus the volatility distribution of HOM was not identical in all the studied experiments. More specifically, with an increasing amount of NOx, the concentration of HOMnon-nit,dim is largely reduced, while the concentrations of nitrogen-containing HOMs, including HOMnit,mon and HOMnit,dim, are increased. From the perspective of HOM volatility, this causes a decrease in the concentrations of ELVOC compounds (saturation mass concentration Cmass,sat ≤ 10−4.5 μg m−3) and a slightly greater increase in the concentrations of LVOCs (10−4.5 μg m−3 < Cmass,sat ≤ 10−0.5 μg m−3).37
2.2 Cluster population simulations
In the model, the discrete General Dynamic Equation (GDE), including different processes where a cluster can be formed or lost, is numerically solved for each cluster composition i:
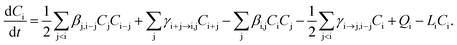 | (1) |
The collision rate coefficients βi,j were calculated as hard-sphere collisions. In reality, the collision-coefficients may exceed the hard-sphere collision rates, due to van der Waal forces. This enhancement has been shown to be approximately a factor of 2 for sub-5 nm particles in sulfuric acid system.36 However, estimates for the magnitude of enhancement do not exist for organic systems, or for the mixed organic–inorganic systems. To be able to compare the variation of growth rate in different systems with inorganic and organic vapors, we chose not to include the enhancement for any of the studied systems. This simplification can cause simulated growth rates to be underestimated, at least in the simulations involving only inorganic compounds.
The evaporation rate coefficients of vapor monomers from different clusters were in most simulations calculated from the Kelvin equation:
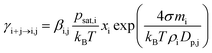 | (2) |
The loss coefficient Li in eqn (1) was set to represent losses in the CLOUD chamber, entailing a size-dependent wall loss and a size-independent dilution loss.60
In addition to performing simulations with a model system, where the largest clusters contain hundreds of molecules, we also performed a few simulations with a clearly smaller model system, including only clusters containing 0–6 sulfuric acid as well as ammonia molecules. In these simulations, sulfuric acid and ammonia were treated as separate model compounds instead of a quasi-unary substance (see the next section). This allowed us to assess quantum-chemistry-based evaporation rates for the large model system,61 and to investigate the effects of simplifying a binary sulfuric acid–ammonia system to a quasi-unary system.
One should note that ion processes are not included in our simulations. The presence of ions can affect particle dynamics, by modifying the collision and evaporation rates.14,49,62 The ions of opposite polarity can also form neutral particles in ion–ion recombination, influencing the growing mode used for growth rate calculations.15,63 While a charge enhancement in growth has been observed in CLOUD experiments for the smallest particles (<2 nm) in the presence of sulfuric acid and ammonia,14 no charge enhancement was observed with organic vapors.12 As the current understanding of the effects of ions on the growth dynamics in inorganic–organic mixtures is limited, and the charged fractions of growing particles in the studied experiments are low,36 we chose to omit ions in our simulations.
| Model substance | m (amu) | ρ (kg m−3) | σ (N m−1) | p sat (Pa) | C sat (cm−3) | C mass,sat (μg m−3) |
|---|---|---|---|---|---|---|
| SA | 142.6 | 1500.0 | 3.0 × 10−2 | 2.0 × 10−9 | 5.2 × 105 | 1.2 × 10−4 |
| LVOC | 345.0 | 1500.0 | 3.0 × 10−2 | 1.0 × 10−8 | 2.6 × 106 | 1.5 × 10−3 |
| ELVOC | 345.0 | 1500.0 | 3.0 × 10−2 | 1.0 × 10−10 | 2.6 × 104 | 1.5 × 10−5 |
The inorganic compound represents a quasi-unary sulfuric acid–ammonia mixture (abbreviated here as SA). The mass of the compound was obtained by summing up the masses of one sulfuric acid molecule, 1/2 ammonia molecules and two water molecules. The resulting acid–base molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is consistent with the experimental and theoretical studies suggesting that while cluster formation proceeds approximately by addition of acid–base pairs, the full neutralization of sulfuric acid by ammonia does not happen in small particles.64,65 The addition of water molecules is justified as sulfuric acid–ammonia particles are expected to contain some water.66 The value of psat for SA (2.0 × 10−9 Pa) was selected so that it resulted in test simulations in growth rates of the same order of magnitude with experimental values. It is also of the same order of magnitude with estimates of vapor pressure of sulfuric acid in partially neutralized solutions of sulfuric acid, ammonia and water.18
1 is consistent with the experimental and theoretical studies suggesting that while cluster formation proceeds approximately by addition of acid–base pairs, the full neutralization of sulfuric acid by ammonia does not happen in small particles.64,65 The addition of water molecules is justified as sulfuric acid–ammonia particles are expected to contain some water.66 The value of psat for SA (2.0 × 10−9 Pa) was selected so that it resulted in test simulations in growth rates of the same order of magnitude with experimental values. It is also of the same order of magnitude with estimates of vapor pressure of sulfuric acid in partially neutralized solutions of sulfuric acid, ammonia and water.18
The organic compounds represent atmospheric oxidized organic species with two volatilities, corresponding to a LVOC and an ELVOC. Their properties (see Table 1) were selected to reasonably reflect the properties of oxidation products of monoterpenes based on previous CLOUD experiments.38 The values of psat used for LVOC and ELVOC (1.0 × 10−8 and 1.0 × 10−10 Pa) are consistent with the volatility basis set classification of organic compounds,22 although psat of ELVOC is close to the upper limit of the volatility bin commonly used for ELVOCs. It should be noted that representing oxidized organic compounds with only two components is a very simplified approach, as the chemical complexity of organics is not considered. Furthermore, in the following, our definitions for LVOC and ELVOC monomers and dimers are not the same as for HOM monomers and dimers. In the case of LVOC and ELVOC, the monomer refers to a molecule of the model compound and the dimer is a cluster composed of two monomers, while for HOMs, the division to monomers and dimers is based on the HOM chemical properties (see Sect. 2.1.3).
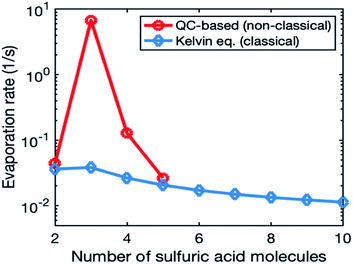
In most of the simulations, we calculated cluster evaporation rates from the Kelvin formula (eqn (2)) using psat values shown in Table 1. In reality, cluster evaporation rates are not expected to smoothly decrease with an increasing particle size as the Kelvin formula suggests but vary with the cluster composition. To study the effect of more realistic evaporation rates, we used quantum-chemistry-based evaporation rates for SA model compound in one simulation set. This was done as follows: (1) we retrieved from Besel et al.61 Gibbs free energies for the sulfuric acid–ammonia system, which had been obtained by applying a density functional theory (DFT) method for cluster structures and vibrational frequencies and the Domain based Local Pair Natural Orbital Coupled Cluster method (DLPNO-CCSD(T)) for single-point energy calculations. DLPNO-CCSD(T) is considered to be the best available quantum chemical method for atmospheric clusters.67 (2) We performed simulations with a cluster kinetics model treating sulfuric acid and ammonia as two separate model compounds. Sulfuric acid concentration was varied between 107 and 108 cm−3 and ammonia concentration was set to 43 ppt. Our model system included clusters containing 0–6 sulfuric acid and 0–6 ammonia molecules for which we calculated evaporation rates using Gibbs free energies by Besel et al.61 (3) From the model simulations, we determined the main cluster growth pathway (similar to Olenius et al.68). (4) We found the lowest evaporation rate (i.e., the evaporation rate of the most stable cluster) for each set of clusters with a certain number of sulfuric acid molecules on the growth pathway and used those for 2–5-mers in our quasi-unary sulfuric acid–ammonia simulations. For larger clusters, we calculated evaporation rates from the Kelvin formula (eqn (2)), like in other simulations.
Fig. 1 illustrates the evaporation rates obtained from quantum chemistry and the Kelvin equation for the smallest clusters (2–10-mers). In the quantum-chemistry-based evaporation rate profile, there is a clear maximum for trimer, while evaporation rates from the Kelvin equation decrease smoothly with an increasing number of molecules in the cluster. We do not use quantum-chemistry data for the organic system, as those data sets are currently very limited. This is because the relevant organic molecules have a high molecular mass and many possible rotamers, which makes quantum chemical calculations challenging.67
| Simulation set | Model compounds | Vapor concentrations (cm−3) | Method to retrieve evaporation rates |
|---|---|---|---|
| 1 | SA | C SA = 8.0 × 106, 2.0 × 107, 4.7 × 107, 1.1 × 108 | Kelvin eqn (classical evaporation rates) |
| 2 | SA | C SA = 2.0 × 107, 4.7 × 107, 1.1 × 108 | QC data and Kelvin eqn (non-classical evaporation rates) |
| 3 | LVOC | C LVOC = 5.0 × 107, 1 × 108 | Kelvin eqn (classical evaporation rates) |
| 4 | LVOC | C LVOC = 5.0 × 107, 1 × 108 | Kelvin eqn (classical evaporation rates) |
| ELVOC | C ELVOC = 1.0 × 107 | ||
| 5 | LVOC | C LVOC = 2.0 × 107, 5.0 × 107, 1 × 108 | Kelvin eqn (classical evaporation rates) |
| SA | C SA = 8.0 × 106 |
These simulations were chosen to elucidate how the presence of one or two condensable vapors with different evaporation rates and concentrations influences (1) the size-dependency of observed growth rates, and (2) the threshold size above which stochastics effects can be neglected. While cluster population simulations allow us to consider the impacts of population dynamics, including stochastic effects, on particle growth, the main drawback of this approach is high computational costs. For that reason, the number of model components was limited to two and the largest simulated particle size did not exceed 6 nm. For SA, we used similar vapor concentrations in the simulations to those observed in the corresponding experiments. However, for organic compounds, we did not exactly match the simulated vapor concentrations with the measured values, due to the limited number of different organic vapors in the simulations and high uncertainties in their evaporation rates. Instead, the simulated organic concentrations correspond to the approximate range of vapor concentrations in the studied experiments.
2.3 Determining particle growth rates
We determined particle growth rates from experimental and simulation data by using an appearance time method,69 which is a common approach to derive observed growth rates in the sub-5 nm size range from chamber experiments. The method is based on determining the times tapp,i when particle concentration in size bin with mean diameter Dp,i reaches 50% of the total increase in the concentration. For a discussion on the differences between this and other approaches used to determine particle growth rate, see Dada et al.70From experimental data we determined tapp,i by fitting a Sigmoid function to measured signal in each size channel. Then we determined particle growth rate and its uncertainty by using a Monte Carlo simulation.70 We obtained the uncertainty of tapp,i from the uncertainty of the Sigmoid fit and the uncertainty of Dp,i from the instrumental parameters and assumed that these uncertainties are normally distributed. Then we reproduced 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data sets by randomly selecting values for tapp,i and Dp,i from their estimated distributions and calculated growth rate from each data set using a total least squares method. We obtained the final value of growth rate as the median value of all calculated growth rates and its uncertainty as their standard deviation. We determined the growth rate for two size ranges: Dp = 1–3 nm (referred to as GR1–3) and Dp = 3–7 nm (GR3–7). We used both DMA-train and NAIS data to calculate growth rate in pure organic experiments and in mixed inorganic–organic experiments. In the experiments involving only sulfuric acid and ammonia, we used only DMA train data because in these experiments charged particles, measured with NAIS, grew faster than the total particle population, as also shown by Stolzenburg et al.36
000 data sets by randomly selecting values for tapp,i and Dp,i from their estimated distributions and calculated growth rate from each data set using a total least squares method. We obtained the final value of growth rate as the median value of all calculated growth rates and its uncertainty as their standard deviation. We determined the growth rate for two size ranges: Dp = 1–3 nm (referred to as GR1–3) and Dp = 3–7 nm (GR3–7). We used both DMA-train and NAIS data to calculate growth rate in pure organic experiments and in mixed inorganic–organic experiments. In the experiments involving only sulfuric acid and ammonia, we used only DMA train data because in these experiments charged particles, measured with NAIS, grew faster than the total particle population, as also shown by Stolzenburg et al.36
To treat the simulation data similarly to experimental data, we divided the simulated clusters in linearly spaced size bins of a width of 0.1 nm, based on their mobility diameter. Because the simulated concentrations do not fluctuate similarly to measurement data, we did not use Sigmoid fits but determined tapp,i for each size bin directly from simulated concentrations. Then we used a least square fitting to determine growth rate for two size ranges: Dp = 1–3 nm (GR1–3) and Dp = 3–5 nm (GR3–5). The larger size range extends only to 5 nm, because we wanted to be sure that boundary effects, which can be significant close to the upper limit of the simulation system, do not distort our results. In the simulations including SA and LVOC, the upper limit was set to 4.5 nm for the same reason. To assess the mechanisms driving particle growth in our simulations, we also investigated particle fluxes due to different collisions and evaporations past selected threshold sizes. We chose not to convert these to flux equivalent particle growth rates (see Kontkanen et al.43), as the resulting growth rates would not correspond to any observed particle growth rate and they would contain uncertainties related to the conversion.
2.4 Metric for determining the threshold size for stochastic effects
We applied a metric introduced by Olenius et al.8 to investigate the importance of stochastic effects in particle growth in different systems. The metric is based on studying the ratio of the absolute values of the second and first derivative of the particle size distribution: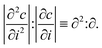 | (3) |
Olenius et al.8 showed that ∂2:∂ can be used to assess the size regime above which stochastic effects become negligible. Namely, at the particle size Dp,th where ∂2:∂ becomes very small (of the order of <5%), the relative difference between the growth rate due to only deterministic condensation and the growth rate including stochastic effects becomes negligible. Thus, Dp,th can be used as a threshold size above which the standard single-particle approach to interpret condensational growth (see Sect. 2.5) becomes valid. We determined Dp,th both from experimental data and simulations using the size distributions under steady-state condition, as the experimental data fluctuate less at the final state. We left out the experiments where the size distribution fluctuated too much, or simulated cluster concentrations became too low, for us to be able to determine Dp,th reliably.
2.5 Particle growth rate from deterministic condensation flux
To study the uncertainty of interpreting observed particle growth using a deterministic condensation model, which does not include stochastic effects or coagulational growth, we calculated particle growth rate based on deterministic condensation flux on a single particle according to:8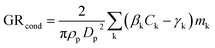 | (4) |
We calculated condensation growth rate from eqn (4) for 1–5 nm particles, considering the condensation of SA model compound at CSA = 1.0 × 107, 4.7 × 107 and 1.1 × 108 cm−3. We calculated βk as hard-sphere collisions and obtained γk from Kelvin equation (eqn (2)).
3. Results
3.1 Size-dependence of growth rate in experiments
We observe different size-dependency of the growth rate in different sets of experiments, depending on the precursor vapors present in the chamber (Fig. 2). Table 3 shows the particle growth rates in two studied size ranges and their ratio, as well as the concentrations of sulfuric acid and HOMs for each experiment (see Table S1† for more details). In the experiments with only sulfuric acid and ammonia, the growth rate decreases with size: the ratio between GR3–7 and GR1–3 is 0.7–0.8. A similar size-dependence of the growth rate has been reported previously for the same experiments.36 It can be explained by two mechanisms: (1) in collision-limited condensation, the growth rate decreases with size because the vapor molecule size relative to particle size decreases,25 and (2) collision enhancement due to van der Waals forces is reduced, when particle size increases.36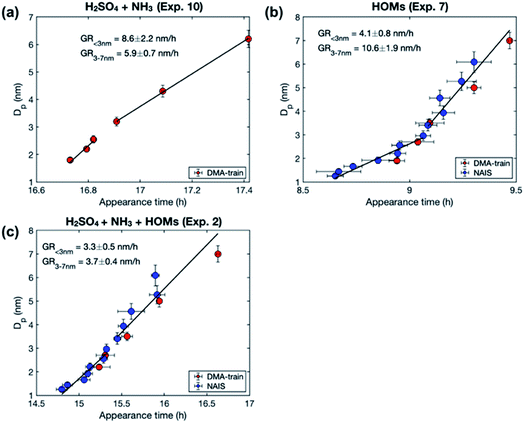 | ||
| Fig. 2 Examples of the size-dependency of growth rate in experiments involving different precursor vapors: (a) sulfuric acid (H2SO4) and ammonia (NH3). (b) HOMs, and (c) the mixture of H2SO4, NH3 and HOMs. The markers show particle diameters (Dp) as a function of the corresponding appearance times from different instruments and the error bars show their uncertainty. Solid black lines show the linear fits to the data points in two size ranges (1–3 and 3–7 nm). Growth rates (GR), obtained as slopes of the fits, are shown in the figures. For the vapor concentrations in each experiment, see Table 3. | ||
| Exp. no. | GR1–3 (nm h−1) | GR3–7 (nm h−1) | GR3–7/GR1–3 | H2SO4 (cm−3) | HOMmon (cm−3) | HOMdim (cm−3) | HOMnon-nit,tot/HOMnit,tot | D p,th (nm) |
|---|---|---|---|---|---|---|---|---|
| 1 | 4.2 ± 0.8 | 3.5 ± 0.6 | 0.8 | 7.8 × 106 | 2.5 × 107 | 3.2 × 106 | 1.0 | 2.9 |
| 2 | 3.3 ± 0.5 | 3.7 ± 0.4 | 1.1 | 7.9 × 106 | 2.2 × 107 | 2.9 × 106 | 1.1 | 3.0 |
| 3 | 8.4 ± 2.8 | 3.5 ± 0.4 | 0.4 | 9.7 × 106 | 2.2 × 107 | 2.8 × 106 | 1.0 | 2.9 |
| 4 | 4.4 ± 0.9 | 3.6 ± 0.4 | 0.8 | 8.3 × 106 | 1.5 × 107 | 3.0 × 106 | 1.0 | 3.0 |
| 5 | 9.8 ± 9.0 | 20.8 ± 5.7 | 2.1 | — | 2.6 × 107 | 7.8 × 106 | 1.7 | 3.5 |
| 6 | 4.5 ± 0.8 | 13.3 ± 3.6 | 3.0 | — | 1.9 × 107 | 5.0 × 106 | 3.4 | 3.5 |
| 7 | 4.1 ± 0.8 | 10.6 ± 1.9 | 2.6 | — | 1.9 × 107 | 5.1 × 106 | 3.5 | 3.5 |
| 8 | 3.4 ± 0.6 | 12.2 ± 4.2 | 3.6 | — | 1.8 × 107 | 4.8 × 106 | 3.5 | — |
| 9 | 3.5 ± 1.0 | 2.6 ± 0.3 | 0.7 | 2.0 × 107 | — | — | — | 2.6 |
| 10 | 8.6 ± 2.2 | 5.9 ± 0.7 | 0.7 | 4.7 × 107 | — | — | — | 2.5 |
| 11 | 17.0 ± 5.5 | 14.3 ± 1.7 | 0.8 | 1.1 × 108 | — | — | — | — |
In the experiments with only organic vapors in the chamber, growth rate increases with size: the ratio between GR3–7 and GR1–3 is 2.1–3.6. The increasing growth rate of sub-10 nm particles with increasing size has been previously observed in CLOUD experiments involving only biogenic vapors.12,38 It has been explained by decreasing Kelvin effect with increasing size, allowing a nano-Köhler type activation, where organic vapors with higher volatility can condense on particles when they grow.
In the experiments involving both sulfuric acid and organic vapors, one could also expect to see an increasing growth rate with the increasing size. However, in the experiments studied here, the growth rate either decreases with size or stays almost constant, the ratio between GR3–7 and GR1–3 varying between 0.4 and 1.1. The behavior of growth rate could be connected to the presence of sulfuric acid or to the volatility distribution of HOMs. As shown in Table 3, in the experiments involving both sulfuric acid and HOMs (Exp. 1–4), the ratio between the total concentrations of HOMs not containing nitrogen (HOMnon-nit,tot) and nitrogen containing HOMs (HOMnit,tot) is ∼1.0, while in the experiments with only HOMs (Exp. 5–8), this ratio is 1.7–3.5. This is mainly due to the difference in the ratio of NOx concentration to the monoterpene concentration (NOx/VOC) between the experiments – a lower NOx/VOC leads to a higher HOMnon-nit,tot/HOMnit,tot. With respect to the organic volatility distribution, low NOx/VOC leads to a higher ELVOC concentration and a lower LVOC concentration, compared to high NOx/VOC conditions.37,39 We will discuss the possible explanations for the size-dependency of growth rate in these experiments in Sect. 3.3, based on our modeling results. Generally, the observation that the growth rate does not increase with size in these experiments indicates that nano-Köhler type behavior, with clearly increasing growth rate with size, occurs only under specific constraints. This is consistent with our previous simulation results, suggesting that nano-Köhler type activation occurs in a system involving sulfuric acid and organics only when the saturation ratio of organic vapor and the ratio between organic and sulfuric acid concentrations are in a suitable range.33
3.2 Growth rate in simulations with sulfuric acid
Growth rate was found to decrease with size in the simulations involving only SA (Table 4), qualitatively similar to the experiments involving sulfuric acid and ammonia. The ratio between GR3–5 and GR1–3 is 0.8–0.9, which is close to the ratio observed in the experiments (see Table 3). Slightly higher values of the ratio in the simulations compared to the experiments (i.e. less strongly decreasing growth rate) could result from our simulations being quasi-unary, and not considering van der Waals forces.36 Another possible reason for the difference is that the upper limit of the larger size range for which growth rate is calculated extends to higher sizes (7 nm) in experiments than in the simulations (5 nm).| Simulation no. | Model compounds | C SA (cm−3) | C LVOC (cm−3) | C ELVOC (cm−3) | GR1–3 (nm h−1) | GR3–5 (nm h−1) | GR3–5/GR1–3 | D p,th (nm) |
|---|---|---|---|---|---|---|---|---|
| a Non-classical evaporation rates. | ||||||||
| 1 | SA | 8.0 × 106 | — | — | 0.8 | 0.6 | 0.8 | 3.6 |
| 2 | SA | 2.0 × 107 | — | — | 3.2 | 2.5 | 0.8 | 2.8 |
| 3 | SA | 4.7 × 107 | — | — | 21.4 | 19.5 | 0.9 | 2.8 |
| 4 | SA | 1.1 × 108 | — | — | 68.3 | 63.4 | 0.9 | 2.8 |
| 5 | SAa | 2.0 × 107 | — | — | 2.0 | 1.8 | 0.9 | 2.9 |
| 6 | SAa | 4.7 × 107 | — | — | 10.7 | 9.0 | 0.8 | 2.6 |
| 7 | SAa | 1.1 × 108 | — | — | 47.8 | 44.6 | 0.9 | 2.7 |
| 8 | LVOC | — | 5.0 × 107 | — | 3.5 | 2.0 | 0.6 | — |
| 9 | LVOC | — | 1.0 × 108 | — | 3.5 | 4.9 | 1.4 | — |
| 10 | LVOC, ELVOC | — | 5.0 × 107 | 1.0 × 107 | 2.1 | 4.5 | 2.1 | 3.7 |
| 11 | LVOC, ELVOC | — | 1.0 × 108 | 1.0 × 107 | 2.6 | 10.1 | 3.9 | 3.8 |
| 12 | LVOC, SA | 8.0 × 106 | 2.0 × 107 | — | 1.0 | 1.9 | 1.9 | 3.6 |
| 13 | LVOC, SA | 8.0 × 106 | 5.0 × 107 | — | 1.2 | 4.1 | 3.4 | 3.7 |
| 14 | LVOC, SA | 8.0 × 106 | 1.0 × 108 | — | 1.7 | 9.9 | 5.8 | 3.6 |
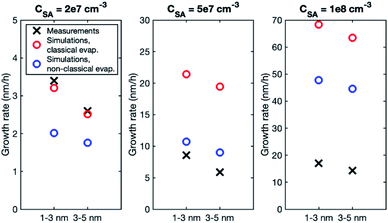
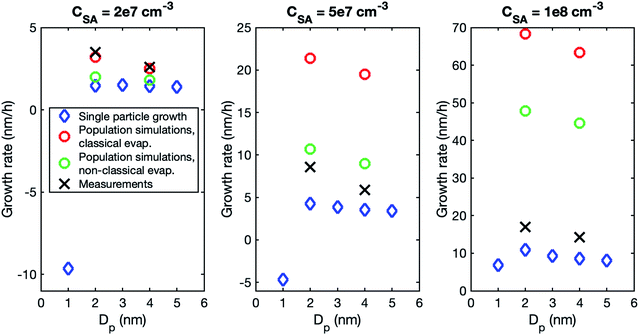
Although the size dependence of growth rate is rather similar in simulations and experiments, the absolute values of growth rate differ, especially at higher vapor concentrations. Fig. 3 shows the growth rates determined from simulations with classical and nonclassical evaporation rate profiles and the corresponding experimental values. At CSA = 2 × 107 cm−3, experimental growth rates are only slightly higher than simulated values, with the difference being larger for a nonclassical evaporation rate profile. However, at higher vapor concentrations, simulated growth rates become clearly higher than experimental growth rates. This is obvious especially in the simulations with a classical evaporation rate profile for which GR1–3 is by a factor of 2.5 and 4.0 higher than experimental values at CSA = 5 × 107 cm−3 and CSA = 1 × 108 cm−3, respectively. Thus, in the simulations, the growth rate increases with increasing sulfuric acid concentration clearly more than in the experiments.
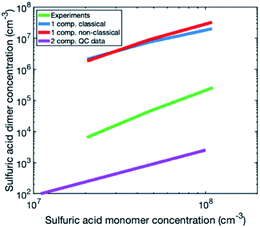
To investigate the reason for the differences between simulations and experiments, we compared sulfuric acid dimer concentrations in experiments and different simulations (Fig. 4): one-component simulations with a classical evaporation rate profile, one-component simulations with a nonclassical evaporation rate profile, and two-component simulations, where sulfuric acid and ammonia are separate model compounds and quantum chemical data is used for all the simulated clusters. In the one-component simulations, sulfuric acid dimer concentrations at certain monomer concentrations are similar with the two evaporation rate profiles and clearly higher (by two orders of magnitude) than dimer concentrations in the experimental data. However, in the two-component simulations, dimer concentrations are lower than in the experimental data (by one to two orders of magnitude). This comparison suggests that using one-component simulation system for sulfuric acid and ammonia results in unrealistically high dimer concentrations. Previously, one-component cluster population simulations have been used for describing particle formation involving sulfuric acid and dimethylamine and the measured and simulated cluster concentrations have been found to agree reasonably well.71 The better agreement for sulfuric acid–dimethylamine system can be explained by dimethylamine being a significantly stronger base than ammonia, making the first cluster consisting of one sulfuric acid molecule and one dimethylamine much more stable than the corresponding cluster with ammonia.72 The large difference between the dimer concentrations in the experiments and in the two-component simulations can result from the tendency of the used quantum chemistry method to slightly underestimate the cluster stability,61 illustrating the need to improve these methods (see Elm et al.67).
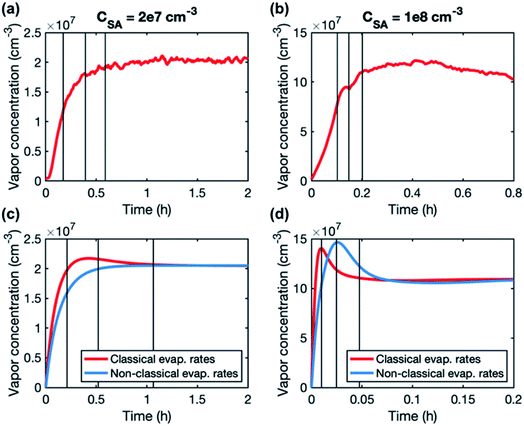
A higher contribution of clusters to particle growth can explain clearly higher growth rates in simulations than in experiments at high sulfuric acid concentrations. The time-dependence of vapor concentrations also suggests higher cluster concentrations in the simulations (Fig. 5). At CSA = 2 × 107 cm−3, simulated and measured vapor concentrations behave rather similarly, increasing until a steady state value is reached. However, at CSA = 1 × 108 cm−3, simulated vapor concentration has a clear maximum that is not observed in the experiments, and which can be explained by the interaction between vapor monomers and clusters. In the beginning of the simulation, cluster concentrations are still low and thus vapor concentration can reach its peak value. Then, the cluster concentrations increase, and the vapor is reduced due to collisions with the clusters, until a steady state is reached. A similar behavior is not observed in the experiments, because the concentrations of clusters are low and thus they do not act as a significant sink for the vapor. The time-dependent variation in the vapor concentration can also influence the size-dependence of growth rate.33 As shown in Fig. 5, the measured vapor concentration increases between the appearance times of 1.5 nm and 4 nm particles by a factor of ∼1.5. However, in the simulation with high SA concentration, vapor concentration decreases between these appearance times, which may enhance the reduction of growth rate with size.
To study the growth mechanisms in our simulations in more detail, we investigated the contributions of vapor monomers and clusters to particle fluxes past selected threshold sizes (Fig. 6). In line with the above, at low SA concentration, vapor monomer dominates the growth at sizes larger than 1.6 nm. Additionally, in the simulation with a classical evaporation rate profile, larger clusters have a non-negligible contribution to the growth at all sizes, while with a nonclassical evaporation rate profile, only dimer contributes to the growth besides vapor monomer. At high vapor concentrations, the difference between the classical and nonclassical cases becomes clearer: for the former, clusters larger than trimer dominate the particle growth at sizes above 1.6 nm while for the latter the growth mainly proceeds through monomers and dimers. Thus, the classical evaporation rate profile results in a more significant contribution of clusters to growth, leading to very high growth rates at high vapor concentrations.
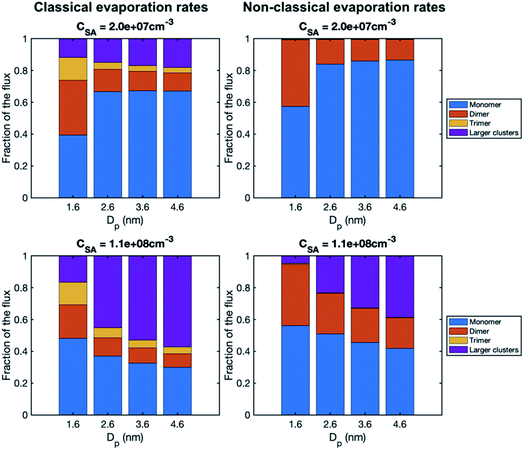 | ||
| Fig. 6 Contribution of vapor monomers and clusters to the particle flux past different threshold sizes in simulations with SA at two different concentrations (CSA = 2.0 × 107 and 1.1 × 108 cm−3). The values are at the steady state. The corresponding absolute fluxes are shown in Fig. S1.† | ||
Overall, in our simulations with a quasi-unary sulfuric acid–ammonia mixture, growth rate decreases with size, which is qualitatively similar to experimental observations, and can be explained by the decreasing vapor molecule size compared to particle size. Previous studies have found clusters to have a negligible contribution to particle growth in CLOUD experiments involving sulfuric acid and ammonia,36,73 which is consistent with our experimental results, but different from the simulation results for high vapor concentrations. The overestimation of the role of clusters in our simulations can result from using one-component model system and incorrect evaporation rate profiles, especially in the case of classical rates. This has implications also on the application of single-particle condensation models with classical evaporation rates: even if observed growth rates can be reproduced with such models, the modeled condensational growth rates are incorrect (even in the classical thermodynamics framework), as the classical rates lead to a significant contribution of clusters to particle growth. That is, applying Kelvin-based classical thermodynamics and assuming only vapor condensation is inconsistent at elevated vapor concentrations.
3.3 Growth rate in simulations involving organics
We studied growth rates in simulations including (1) only LVOC, (2) ELVOC and LVOC, and (3) SA and LVOC. The simulation results are summarized in Table 4. Fig. 7 shows the appearance times of different sized particles in a few selected simulations and Fig. S2† the corresponding behavior of growth rate as a function of particle size.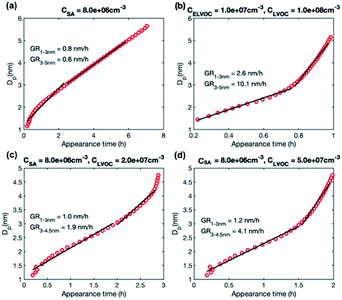 | ||
| Fig. 7 Particle diameter plotted as a function of appearance time in simulations with different model compounds: (a) SA at CSA = 8.0 × 106 cm−3, (b) LVOC and ELVOC at CLVOC = 1 × 108 and CELVOC = 1 × 107 cm−3 (c) SA and LVOC at CSA = 8 × 106 and CLVOC = 2 × 107 cm−3, (d) SA and LVOC at CSA = 8 × 106 and CLVOC = 5 × 107 cm−3. Growth rate (GR) values determined for two size ranges with a linear fit are shown in the figures, while growth rates obtained for each size as a slope of the curve are shown in Fig. S2.† | ||
In the simulations with only LVOC, the size-dependence of growth rate depends on LVOC concentration (shown only in Table 4). At CLVOC = 5 × 107 cm−3, growth rate decreases with size while at CLVOC = 1 × 108 cm−3, growth rate increases with size. The behavior of growth rate can be understood by studying the contribution of vapor monomers and clusters to particle flux (Fig. S3†). In both simulations, vapor monomer starts to dominate the growth flux above 3 nm, when its net flux becomes positive. When looking at the absolute values of the flux, at higher LVOC concentration, the partial flux due to vapor monomer barely decreases with the increasing particle size above 3 nm, despite the coagulation losses. This is due to the enhanced condensation of LVOC at these sizes, leading to the increase of growth rate with the increasing particle size.
In the simulations involving both LVOC and ELVOC, growth rate increases with size (see Table 4 and Fig. S2†), the ratio between GR3–5 and GR1–3 being 2.1 and 3.9 in the two simulations. This is qualitatively similar to the experiments involving only organics. Fig. 8a shows the comparison between growth rates in the experiments and simulations involving only organic vapors. In the simulation with CELVOC = 1 × 107 cm−3 and CLVOC = 1 × 108 cm−3 (Sim. 11), growth rate is within a factor of 2 of most of the experimental values in both studied size ranges. In one of the experiments (Exp. 5), growth rates are clearly higher at both sizes, likely due to higher HOM concentrations (see Table 3). Considering the simplifications of our model simulations, such as including only two organic compounds and using classical evaporation rates, the qualitative agreement between the simulated and experimental growth rates is good. In the simulations, the total concentration of organic compounds is higher than in the experiments with similar growth rate values, but the CI-APi-TOF is known to underestimate measured LVOC concentrations,12,36 which could partly explain this.
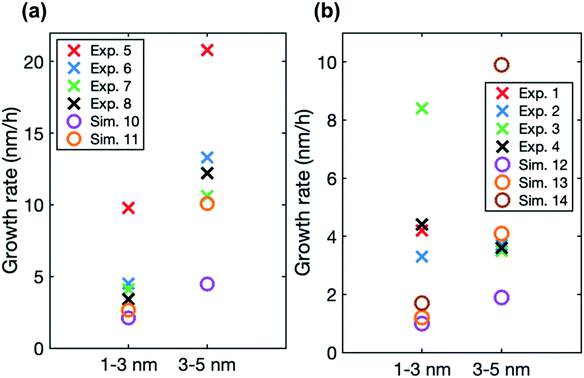 | ||
| Fig. 8 Particle growth rate in two size ranges in experiments (crosses) and in simulations (circles) with (a) LVOC and ELVOC and (b) LVOC and sulfuric acid. For the vapor concentrations in each case, see Tables 3 and 4. | ||
The increase of growth rate with size in the simulations with LVOC and ELVOC can be explained by the increasing contribution of more abundant LVOC to growth with the increasing size (Fig. 9 and S4†). In both simulations with LVOC and ELVOC, the net flux of vapor monomer is negative at the smallest size (1.6 nm), due to its high evaporation flux, and thus the growth flux is attributed mainly to ELVOC and LVOC dimers. Above that, the growth flux is caused by ELVOC and LVOC monomers, the contribution of LVOC monomer increasing with the increasing size, until at 4.6 nm it clearly dominates the flux in both simulations. The absolute values of the fluxes (Fig. S4†) show that the net flux due to LVOC monomer does not significantly decrease with the increasing particle size, despite coagulation losses, which can be explained by its increasing condensation efficiency.
 | ||
| Fig. 9 Contribution of vapor monomers and clusters to the particle flux past different threshold sizes in simulations with (a) LVOC and ELVOC at CELVOC = 107 cm−3 and CLVOC = 5 × 107 cm−3, (b) LVOC and ELVOC at CELVOC = 107 cm−3 and CLVOC = 108 cm−3, (c) SA and LVOC at CSA = 8 × 106 and CLVOC = 2 × 107 cm−3, (d) SA and LVOC at CSA = 8 × 106 and CLVOC = 5 × 107 cm−3. The values are at the steady state. The corresponding absolute fluxes are shown in Fig. S4.† | ||
In the simulations with LVOC and SA (CSA = 8 × 106 in all these simulations), growth rate increases with size, but the strength of the increase depends strongly on the LVOC concentration (see Table 4). At CLVOC = 2 × 107 cm−3, the ratio between GR3–5 and GR1–3 is 1.9. At higher LVOC concentrations, the increase of growth rate with size is more pronounced: the ratio between GR3–5 and GR1–3 is 3.4 and 5.8 (see Fig. 7 and S2†). Fig. 8b shows the comparison between growth rates in these simulations and in the experiments involving sulfuric acid and organic vapors. In the simulation with CLVOC = 2 × 107 cm−3 (Sim. 12), simulated GRs are lower than the experimental values in both size ranges. With higher LVOC concentrations (Sim. 13 and 14), GR1–3 is lower and GR3–5 higher in simulations than the corresponding values in the experiments.
The size dependence of growth rate in the simulations with SA and LVOC can be understood by studying particle fluxes (Fig. 9 and S4†). At the smallest size, the net flux of LVOC and SA monomers is negative, and the growth flux is attributed mainly to the dimers of SA and LVOC. Above 1.6 nm, the flux in both simulations is caused by SA and LVOC monomers, the contribution of LVOC monomer increasing with the increasing size and LVOC concentration. When studying the absolute fluxes (Fig. S4†), all the partial fluxes can be observed to clearly decrease with increasing particle size at CLVOC = 2 × 107 cm−3, due to coagulation losses. However, at higher LVOC concentration, the decrease of fluxes with size, especially that caused by LVOC monomer, is significantly smaller, due to more efficient condensation of LVOC. This corresponds to nano-Köhler type activation of particles to growth by an organic vapor32 and illustrates how the activation type behavior occurs only at specific vapor concentrations. Although LVOC significantly contributes to particle growth also in the simulation with CLVOC = 2 × 107 cm−3, a stronger increase in growth rate with size requires a higher LVOC concentration.
Our simulations suggest that the increase of growth rate with size is largely governed by LVOC concentration. The particle growth below 3 nm is almost solely due to SA and/or ELVOC (because they have low enough volatility), which is illustrated by GR1–3 being similar in the simulations with different LVOC concentrations (see Table 4). However, above 3 nm, the contribution of LVOC is important: increasing LVOC concentration enhances GR3–5 significantly in our simulations. Table 3 shows that in most experiments involving organics with or without sulfuric acid, GR1–3 are rather close to each other (∼3–4 nm h−1), while GR3–7 is clearly lower in the experiments with both sulfuric acid and organics. This could be explained by lower LVOC concentration, but as discussed in Sect. 3.1, the fractions of different HOMs in the two types of experiments indicate even higher LVOC concentration in the mixed organic–inorganic experiments compared to pure organic experiments. Another potential explanation to the different size-dependency in the experiments could be the difference in the time-dependence of vapor concentrations, but the vapor concentrations were kept constant in all the experiments involving organics. Thus, the reason for the growth rate not increasing with size in the experiments involving both sulfuric acid and organic vapors remains unresolved and needs further investigation.
3.4 Importance of stochastic effects in particle growth
To investigate the importance of stochastic effects in particle growth, we determined the threshold sizes Dp,th above which metric ∂2:∂ becomes less than 0.05 in different experiments (Table 3). In practice, these effects are mainly driven by evaporation and thus they extend to sizes at which evaporation rates are comparable to vapor collision rates. In terms of particle diameter, these sizes can be larger for larger molecules, as larger molecules result in a larger diameter for a given number of molecules in the particle.D p,th is lowest (2.5–2.6 nm) in the experiments involving only sulfuric acid and ammonia. This is expected because in these experiments vapor molecules are smallest, and evaporation can be assumed to be least significant. The result is consistent with Stolzenburg et al.36 who concluded that evaporation is negligible for particles larger than 2 nm in these experiments. In the experiments involving both sulfuric acid and HOMs, Dp,th is 2.9–3.0 nm. This suggests more significant evaporation than in the experiments with sulfuric acid and ammonia, due to the presence of HOMs with varying volatilities. As expected, Dp,th is highest (3.5 nm) in the experiments with only HOMs, which are larger than sulfuric acid molecules and have a wide range of volatilities.
To assess the sensitivity of the obtained Dp,th to the assumed vapor molecule size, which is needed for extracting ∂2:∂ from the size distribution function, we tested determining Dp,th using the mass of SA in the equation for ∂2:∂ (see eqn (11) in Olenius et al.8) for all the experiments. In this case, Dp,th is reduced by ∼0.3 nm in the experiments with sulfuric acid and HOMs and by ∼0.5 nm in the presence of only HOMs. Still, the values of Dp,th are slightly higher in the experiments involving organics than with only sulfuric acid and ammonia. This shows that Dp,th is not only determined by the vapor molecule size assumed in the calculations, but follows from the size distribution function, which is affected by both the true molecular size and the evaporation profile.
We also determined Dp,th from simulations involving different model compounds at different concentrations (Table 4). The simulation results are consistent with the experimental results: Dp,th is lowest (2.6–2.9 nm) in the simulations involving only SA, and higher with SA and LVOC (3.6–3.7 nm) and with ELVOC and LVOC (3.7–3.8 nm). The only exception is the simulation involving only SA at CSA = 8 × 106 cm−3, for which Dp,th is close to the values determined for simulations with ELVOC and LVOC. This indicates that in this simulation, vapor concentration is so low that evaporation is more significant than in other SA simulations. Generally, Dp,th in simulations and corresponding experiments are very close to each other, with Dp,th being only slightly (0.1–0.3 nm) higher in the simulations than in the experiments. The agreement is surprisingly good, considering the crude simplifications of the model simulations (e.g. the limited number of model compounds and classical evaporation rates). The good agreement may partly be explained by the effect of vapor molecule size on Dp,th, but it also indicates that the approximate size regime in which condensation overcomes evaporation is reasonably represented in the simulations.
Thus, our results show that stochastic effects are important in the growth of atmospheric particles by sulfuric acid and organic compounds below ∼2.5–3.5 nm. The stochastic effects cannot be considered with single particle growth models, which are based on studying the deterministic condensation mass flux on a particle surface. To demonstrate this, we calculated growth rate from a deterministic condensation flux (see Sect. 2.5), considering the condensation of SA model compound at different concentrations (Fig. 10). In Fig. 10, the single particle model is a valid representation of the growth when the single-particle results (blue diamonds) are close to the population model results with classical evaporation rates (red circles). One should note that in addition to the stochastic effects, the differences between the two approaches stem from other population dynamics effects (such as cluster–cluster collisions) influencing the growth rates derived from population simulations. This applies generally to appearance-time-based growth rates and is relevant to analysis of experimental growth rates in the presence of efficiently clustering chemical compounds.14
At CSA = 2 × 107 cm−3 and CSA = 5 × 107 cm−3, the growth rate predicted by the single particle growth model is negative for 1 nm particles and positive but lower than growth rate from cluster population simulations and experiments for 2–5 nm particles. This is because at 1 nm, the average cluster evaporation is faster than growth by collisions, and the growth is driven by stochastic effects. At CSA = 1 × 108 cm−3, growth rates from single particle model vary between 6.9 and 10.9 nm h−1 for 1–5 nm particles and are lower than experimental and cluster population simulation results. However, at this high vapor concentration, they are closer to experimental values than growth rates from cluster population simulations, as the latter ones are very high due to the high contribution of cluster–cluster collisions.
Overall, one should be cautious if using single particle growth models to interpret observations on the growth of atmospheric particle population below ∼3 nm. As single particle growth models do not include stochastic effects, they may underestimate the condensational growth at the smallest sizes. This can lead to wrong conclusions on, for example (1) thermodynamic properties of condensing vapors, (2) if the growth can be explained by the observed vapor concentrations or not, (3) if there exist a Kelvin barrier or not.8
3.5 Discussion
To correctly represent atmospheric particle formation and growth in large-scale models, the knowledge of the growth of sub-10 nm atmospheric particles is essential. Particle growth is commonly studied by assessing particle growth rate from the time-evolution of measured particle size distribution, and growth rates are then used to deduce particle growth mechanisms. In this study, we investigated the factors controlling sub-10 nm particle growth rates in the presence of inorganic and organic vapors, by comparing growth rates determined from chamber experiments to results from molecular-resolution cluster population simulations. The studied experiments involved sulfuric acid, ammonia and/or oxidation products of monoterpenes and our model simulations included either one or two model compounds, representing an inorganic vapor as well as organic vapors with two volatilities (LVOC and ELVOC). Especially, we focused on the size-dependency of particle growth rate, and on the effects of population dynamics and stochastic fluctuations on particle population growth in different atmospheric systems.In the experiments involving only inorganic vapors (sulfuric acid and ammonia), growth rate was found to decrease with size, similar to previous observations.36 Our simulations with a quasi-unary model compound (SA) reproduced this behavior, which is caused by the decreasing vapor molecule size relative to the particle size.25 Despite the similar size-dependence of the growth rate, the simulations overestimated the contribution of cluster–cluster collisions to the growth at high vapor concentrations, which results from the evaporation rate profiles assumed in the simulations. Using classical evaporation rates, derived from Kelvin equation, leads to a significant role of cluster–cluster collisions in the growth, which also implies that using these evaporation rates in single-particle condensation models for very small particles is inaccurate. In addition to uncertain evaporation rates, the disagreement between our simulations and the experiments is caused by the limitations of a quasi-unary model compound in representing a binary sulfuric acid–ammonia system. Overall, the sensitivity of particle growth dynamics to evaporation rates highlights the need for accurate estimates of cluster evaporation rates. Especially, there is a lack of quantum chemistry derived evaporation rates for clusters involving large organic molecules, such as HOMs (see Elm et al.67). In the future, the challenges in identifying and modeling individual organic compounds could be overcome by simulating the behavior of representative functional groups or by using data-driven machine learning approaches.74 In addition to computational chemistry methods, inversion modeling approaches can enable retrieving cluster rate constants from experimental data.75,76
In the experiments with only organic vapors, growth rate was observed to increase with size, consistently with previous studies.12 In the simulations involving two model compounds with different volatilities (LVOC and ELVOC), growth rate increased with size qualitatively similar to the experiments. The increase of growth rate resulted from the increasing contribution of abundant LVOC molecules to growth, which can be qualitatively depicted with nano-Köhler theory, describing the activation of particles to growth by oxidized organic vapors.32
In the experiments involving both sulfuric acid and organic vapors, growth rate either decreased with size or stayed close to constant. We were unable to reproduce this behavior with our simulations and thus it requires further investigation. In all the simulations involving SA and LVOC, growth rate increased with size, but the strength of the increase depended on LVOC concentration. These results illustrate that nano-Köhler type activation, with clearly accelerating growth rate, occurs only under specific vapor concentrations and saturation ratios. Previously, the acceleration of particle growth rate has been interpreted to show the size at which organic vapors start to contribute to growth.31 Our results indicate that while the increase of growth rate with size can be connected to the increasing contribution of organic vapors to the growth, oxidized organic vapors can also contribute to the growth in a situation where the growth rate does not increase with size.
To study the importance of stochastic collisions and evaporations in particle growth, we determined the threshold size Dp,th below which stochastic effects are nonnegligible8 in different experiments and simulations. We found that stochastic effects can be important in the growth of atmospheric particles by sulfuric acid and organic compounds below ∼3 nm, and the exact threshold size depends on the concentrations and properties (i.e. evaporation rates and molecule size) of the vapors. When the observed growth rates are interpreted using a condensation model, based on studying a vapor mass flux on a single particle, the limitations of this modeling approach should be recognized. Especially at particle sizes below 3 nm, stochastic collisions may enhance particle growth significantly. Thus, neglecting them can lead to wrong conclusions on particle growth mechanisms.
Generally, our results on the importance of the effects of particle-population dynamics on observed growth rates imply that particle growth rate should be viewed to describe the growth of the whole particle population, instead of a diameter growth rate of a single representative particle. When modeling particle growth, the stochastic fluctuations and population dynamics effects can be considered by using particle population simulations.9,10,73 Regarding measured growth rates, GDE-based methods29,77,78 to determine growth rate should be preferred over simpler ones, such as the appearance time method. This is because GDE-based methods can separate the effects of condensation and coagulation on particle growth rate, although they neglect stochastic effects. Moreover, they can retrieve both size- and time-dependence of growth rates, which makes it easier to evaluate the effect of vapor time-dependence on the behavior of the growth rate. Recently, Ozon et al.78 introduced a method based on applying a Kalman smoother to a finite difference solution of GDE that can also provide the uncertainty range for measured growth rate. The uncertainties of sub-10 nm particle size distribution measurements are significant,34 which propagates in the growth rate values and should thus be considered when interpreting particle growth observations.
In the broader view, our results suggest that instead of only investigating particle growth rates to understand the dynamics of a growing particle population, the focus should be shifted towards directly studying the evolution of particle size distribution and developing methods for this. For this, models accurately simulating the time-evolution of particle population and reliable measurements of the particle size distribution below 10 nm are also needed.
4. Conclusions
To represent atmospheric particle growth accurately in large-scale models, the observations on particle growth should be correctly interpreted. In this study, we unravel the factors controlling the observed growth rates of sub-10 nm atmospheric particles, using cluster population simulations and chamber experiments. Fig. 11 summarizes the different factors affecting the observed particle growth rates according to our results. They include the concentrations of condensable vapors, their evaporation rate profiles, their time-dependent variation as well as stochastic fluctuations and particle population dynamics effects, such as cluster–cluster collisions. Many approaches commonly used to interpret growth rate observations are unable to consider all these effects, which can lead to a biased view on the properties of condensing vapors and particle growth mechanisms. Therefore, to draw conclusions on observed particle growth rates, especially in the sub-10 nm size range, new data-analysis approaches and particle population modeling are needed.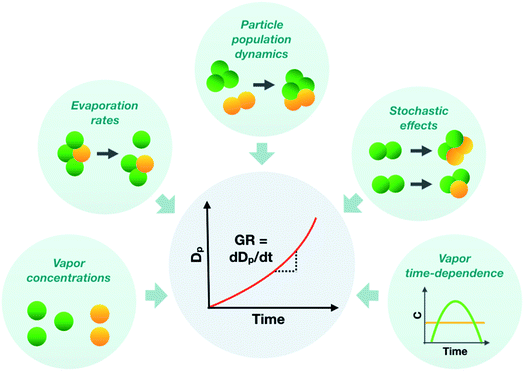 | ||
| Fig. 11 Schematic figure illustrating different factors influencing the observed sub-10 nm particle growth rate (GR). | ||
Author contributions
Conceptualization: JK, DS, TO, KL, IR; methodology: JK, TO, LA; formal analysis: JK, DS, CY; investigation: JK, DS, CY, LD, LA, MS, KL; writing – original draft preparation: JK, DS, TO, KL, IR; writing – review and editing: all authors; visualization: JK.Data availability
The particle size distributions measured with the DMA train are available at: https://doi.org/10.5281/zenodo.6362724 (Stolzenburg, 2022).79 The simulation data are available at: https://doi.org/10.5281/zenodo.6370141 (Kontkanen et al., 2022).80Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research has received funding from Academy of Finland Flagship funding (grant no. 337549), Academy of Finland Center of Excellence programme (grant no. 307331), Academy of Finland postdoctoral researcher funding (grant no. 316114), the Swedish Research Council VR (grant no. 2019-04853), the Swedish Research Council for Sustainable Development FORMAS (grant no. 2019-01433), German Federal Ministry of Education and Research, CLOUD-12 (01LK1222A) and CLOUD-16 (01LK1601A), and the European Union's Horizon 2020 Research and Innovation programme under the Marie Sklodowska-Curie grant agreement no. 895875 (“NPF-PANDA”). Financial support from the European Union's Horizon 2020 research and innovation programme (project FORCeS under grant agreement no. 821205), European Research Council (Consolidator grant INTEGRATE no. 865799), Knut and Alice Wallenberg foundation (Wallenberg Academy Fellowship project AtmoRemove no. 2015.0162), and from Max Planck society is also gratefully acknowledged.References
- M. Wang and J. E. Penner, Atmos. Chem. Phys., 2009, 9, 239–260 CrossRef CAS.
- D. V. Spracklen, K. S. Carslaw, M. Kulmala, V. M. Kerminen, S. L. Sihto, I. Riipinen, J. Merikanto, G. W. Mann, M. P. Chipperfield, A. Wiedensohler, W. Birmili and H. Lihavainen, Geophys. Res. Lett., 2008, 35, 1–5 Search PubMed.
- J. R. Pierce and P. J. Adams, Atmos. Chem. Phys., 2009, 9, 1339–1356 CrossRef CAS.
- D. M. Westervelt, J. R. Pierce and P. J. Adams, Atmos. Chem. Phys., 2014, 14, 5577–5597 CrossRef CAS.
- E. M. Dunne, H. Gordon, A. Kürten, J. Almeida, J. Duplissy, C. Williamson, I. K. Ortega, K. J. Pringle, A. Adamov, U. Baltensperger, P. Barmet, F. Benduhn, F. Bianchi, M. Breitenlechner, A. Clarke, J. Curtius, J. Dommen, N. M. Donahue, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, T. Jokinen, J. Kangasluoma, J. Kirkby, M. Kulmala, A. Kupc, M. J. Lawler, K. Lehtipalo, V. Makhmutov, G. Mann, S. Mathot, J. Merikanto, P. Miettinen, A. Nenes, A. Onnela, A. Rap, C. L. S. Reddington, F. Riccobono, N. A. D. Richards, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, K. Sengupta, M. Simon, M. Sipilä, J. N. Smith, Y. Stozkhov, A. Tomé, J. Tröstl, P. E. Wagner, D. Wimmer, P. M. Winkler, D. R. Worsnop and K. S. Carslaw, Science, 2016, 354, 1119–1124 CrossRef CAS PubMed.
- M. Kulmala, T. Petäjä, M. Ehn, J. Thornton, M. Sipilä, D. R. Worsnop and V.-M. Kerminen, Annu. Rev. Phys. Chem., 2014, 65, 21–37 CrossRef CAS PubMed.
- R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2012, 112, 1957–2011 CrossRef CAS PubMed.
- T. Olenius, L. Pichelstorfer, D. Stolzenburg, P. M. Winkler, K. E. J. Lehtinen and I. Riipinen, Sci. Rep., 2018, 1–11 CAS.
- T. Olenius and I. Riipinen, Aerosol Sci. Technol., 2017, 51, 397–408 CrossRef CAS.
- C. Li and R. Cai, J. Aerosol Sci., 2020, 150, 105615 CrossRef CAS.
- T. Yli-Juuti, K. Barsanti, L. Hildebrandt Ruiz, A. J. Kieloaho, U. Makkonen, T. Petäjä, T. Ruuskanen, M. Kulmala and I. Riipinen, Atmos. Chem. Phys., 2013, 13, 12507–12524 CrossRef.
- J. Tröstl, W. K. Chuang, H. Gordon, M. Heinritzi, C. Yan, U. Molteni, L. Ahlm, C. Frege, F. Bianchi, R. Wagner, M. Simon, K. Lehtipalo, C. Williamson, J. S. Craven, J. Duplissy, A. Adamov, J. Almeida, A. K. Bernhammer, M. Breitenlechner, S. Brilke, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, M. Gysel, A. Hansel, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, H. Keskinen, J. Kim, M. Krapf, A. Kürten, A. Laaksonen, M. Lawler, M. Leiminger, S. Mathot, O. Möhler, T. Nieminen, A. Onnela, T. Petäjä, F. M. Piel, P. Miettinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, K. Sengupta, M. Sipilä, J. N. Smith, G. Steiner, A. Tomè, A. Virtanen, A. C. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, K. S. Carslaw, J. Curtius, J. Dommen, J. Kirkby, M. Kulmala, I. Riipinen, D. R. Worsnop, N. M. Donahue and U. Baltensperger, Nature, 2016, 533, 527–531 CrossRef PubMed.
- C. Li and P. H. McMurry, Atmos. Chem. Phys., 2018, 18, 8979–8993 CrossRef.
- K. Lehtipalo, L. Rondo, J. Kontkanen, S. Schobesberger, T. Jokinen, N. Sarnela, A. Kürten, S. Ehrhart, A. Franchin, T. Nieminen, F. Riccobono, M. Sipilä, T. Yli-Juuti, J. Duplissy, A. Adamov, L. Ahlm, J. Almeida, A. Amorim, F. Bianchi, M. Breitenlechner, J. Dommen, A. J. Downard, E. M. Dunne, R. C. Flagan, R. Guida, J. Hakala, A. Hansel, W. Jud, J. Kangasluoma, V.-M. Kerminen, H. Keskinen, J. Kim, J. Kirkby, A. Kupc, O. Kupiainen-Määttä, A. Laaksonen, M. J. Lawler, M. Leiminger, S. Mathot, T. Olenius, I. K. Ortega, A. Onnela, T. Petäjä, A. Praplan, M. P. Rissanen, T. Ruuskanen, F. D. Santos, S. Schallhart, R. Schnitzhofer, M. Simon, J. N. Smith, J. Tröstl, G. Tsagkogeorgas, A. Tomé, P. Vaattovaara, H. Vehkamäki, A. E. Vrtala, P. E. Wagner, C. Williamson, D. Wimmer, P. M. Winkler, A. Virtanen, N. M. Donahue, K. S. Carslaw, U. Baltensperger, I. Riipinen, J. Curtius, D. R. Worsnop and M. Kulmala, Nat. Commun., 2016, 7, 11594 CrossRef CAS PubMed.
- J. Leppä, T. Anttila, V. M. Kerminen, M. Kulmala and K. E. J. Lehtinen, Atmos. Chem. Phys., 2011, 11, 4939–4955 CrossRef.
- H. Vehkamäki and I. Riipinen, Chem. Soc. Rev., 2012, 41, 5160–5173 RSC.
- V. M. Kerminen, X. Chen, V. Vakkari, T. Petäjä, M. Kulmala and F. Bianchi, Environ. Res. Lett., 2018, 13(10), 103003 CrossRef.
- J. Marti, A. Jefferson, X. P. Cai, C. Richert, P. H. McMurry and F. Eisele, J. Geophys. Res., 1997, 102, 3725–3735 CrossRef CAS.
- I. Riipinen, T. Yli-Juuti, J. R. Pierce, T. Petäjä, D. R. Worsnop, M. Kulmala and N. M. Donahue, Nat. Geosci., 2012, 5, 453–458 CrossRef CAS.
- S. Schobesberger, H. Junninen, F. Bianchi, G. Lönn, M. Ehn, K. Lehtipalo, J. Dommen, S. Ehrhart, I. K. Ortega, A. Franchin, T. Nieminen, F. Riccobono, M. Hutterli, J. Duplissy, J. Almeida, A. Amorim, M. Breitenlechner, A. J. Downard, E. M. Dunne, R. C. Flagan, M. Kajos, H. Keskinen, J. Kirkby, A. Kupc, A. Kürten, T. Kurtén, A. Laaksonen, S. Mathot, A. Onnela, A. P. Praplan, L. Rondo, F. D. Santos, S. Schallhart, R. Schnitzhofer, M. Sipilä, A. Tomé, G. Tsagkogeorgas, H. Vehkamäki, D. Wimmer, U. Baltensperger, K. S. Carslaw, J. Curtius, A. Hansel, T. Petäjä, M. Kulmala, N. M. Donahue and D. R. Worsnop, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17223–17228 CrossRef CAS PubMed.
- M. Ehn, J. A. Thornton, E. Kleist, M. Sipilä, H. Junninen, I. Pullinen, M. Springer, F. Rubach, R. Tillmann, B. Lee, F. Lopez-Hilfiker, S. Andres, I. H. Acir, M. Rissanen, T. Jokinen, S. Schobesberger, J. Kangasluoma, J. Kontkanen, T. Nieminen, T. Kurtén, L. B. Nielsen, S. Jørgensen, H. G. Kjaergaard, M. Canagaratna, M. D. Maso, T. Berndt, T. Petäjä, A. Wahner, V. M. Kerminen, M. Kulmala, D. R. Worsnop, J. Wildt and T. F. Mentel, Nature, 2014, 506, 476–479 CrossRef CAS PubMed.
- N. M. Donahue, J. H. Kroll, S. N. Pandis and A. L. Robinson, Atmos. Chem. Phys., 2012, 12, 615–634 CrossRef CAS.
- C. Mohr, J. A. Thornton, A. Heitto, F. D. Lopez-Hilfiker, A. Lutz, I. Riipinen, J. Hong, N. M. Donahue, M. Hallquist, T. Petäjä, M. Kulmala and T. Yli-Juuti, Nat. Commun., 2019, 10, 1–7 CrossRef PubMed.
- M. Kulmala, T. Petäjä, T. Nieminen, M. Sipilä, H. E. Manninen, K. Lehtipalo, M. Dal Maso, P. P. Aalto, H. Junninen, P. Paasonen, I. Riipinen, K. E. J. Lehtinen, A. Laaksonen and V. M. Kerminen, Nat. Protoc., 2012, 7, 1651–1667 CrossRef CAS PubMed.
- T. Nieminen, K. E. J. Lehtinen and M. Kulmala, Atmos. Chem. Phys., 2010, 10, 9773–9779 CrossRef CAS.
- H. E. Manninen, T. Nieminen, E. Asmi, S. Gagné, S. Häkkinen, K. Lehtipalo, P. Aalto, M. Vana, A. Mirme, S. Mirme, U. Hõrrak, C. Plass-Dülmer, G. Stange, G. Kiss, A. Hoffer, N. Töro, M. Moerman, B. Henzing, G. De Leeuw, M. Brinkenberg, G. N. Kouvarakis, A. Bougiatioti, N. Mihalopoulos, C. O'Dowd, D. Ceburnis, A. Arneth, B. Svenningsson, E. Swietlicki, L. Tarozzi, S. Decesari, M. C. Facchini, W. Birmili, A. Sonntag, A. Wiedensohler, J. Boulon, K. Sellegri, P. Laj, M. Gysel, N. Bukowiecki, E. Weingartner, G. Wehrle, A. Laaksonen, A. Hamed, J. Joutsensaari, T. Petäjä, V. M. Kerminen and M. Kulmala, Atmos. Chem. Phys., 2010, 10, 7907–7927 CrossRef CAS.
- I. Riipinen, J. R. Pierce, T. Yli-Juuti, T. Nieminen, S. Häkkinen, M. Ehn, H. Junninen, K. Lehtipalo, T. Petäjä, J. Slowik, R. Chang, N. C. Shantz, J. Abbatt, W. R. Leaitch, V. M. Kerminen, D. R. Worsnop, S. N. Pandis, N. M. Donahue and M. Kulmala, Atmos. Chem. Phys., 2011, 11, 3865–3878 CrossRef CAS.
- B. Wehner, T. Petäjä, M. Boy, C. Engler, W. Birmili, T. Tuch, A. Wiedensohler and M. Kulmala, Geophys. Res. Lett., 2005, 32, 1–4 CrossRef.
- C. Kuang, M. Chen, J. Zhao, J. Smith, P. H. McMurry and J. Wang, Atmos. Chem. Phys., 2012, 12, 3573–3589 CrossRef CAS.
- B. R. Bzdek, C. A. Zordan, M. R. Pennington, G. W. Luther and M. V. Johnston, Environ. Sci. Technol., 2012, 46, 4365–4373 CrossRef CAS PubMed.
- M. Kulmala, J. Kontkanen, H. Junninen, K. Lehtipalo, H. E. Manninen, T. Nieminen, T. Petäjä, M. Sipilä, S. Schobesberger, P. Rantala, A. Franchin, T. Jokinen, E. Järvinen, M. Äijälä, J. Kangasluoma, J. Hakala, P. P. Aalto, P. Paasonen, J. Mikkilä, J. Vanhanen, J. Aalto, H. Hakola, U. Makkonen, T. Ruuskanen, R. L. Mauldin, J. Duplissy, H. Vehkamäki, J. Bäck, A. Kortelainen, I. Riipinen, T. Kurtén, M. V. Johnston, J. N. Smith, M. Ehn, T. F. Mentel, K. E. J. Lehtinen, A. Laaksonen, V. M. Kerminen and D. R. Worsnop, Science, 2013, 339, 943–946 CrossRef CAS PubMed.
- M. Kulmala, V.-M. Kerminen, T. Anttila, A. Laaksonen and C. D. O’Dowd, J. Geophys. Res.: Atmos., 2004, 109(D4) DOI:10.1029/2003JD003961.
- J. Kontkanen, T. Olenius, M. Kulmala and I. Riipinen, Atmos. Chem. Phys., 2018, 18, 13733–13754 CrossRef CAS.
- J. Kangasluoma, R. Cai, J. Jiang, C. Deng, D. Stolzenburg, L. R. Ahonen, T. Chan, Y. Fu, C. Kim, T. M. Laurila, Y. Zhou, L. Dada, J. Sulo, R. C. Flagan, M. Kulmala, T. Petäjä and K. Lehtipalo, J. Aerosol Sci., 2020, 148, 1–29 CrossRef.
- A. Kürten, L. Rondo, S. Ehrhart and J. Curtius, J. Phys. Chem. A, 2012, 116, 6375–6386 CrossRef PubMed.
- D. Stolzenburg, M. Simon, A. Ranjithkumar, A. Kürten, K. Lehtipalo, H. Gordon, S. Ehrhart, H. Finkenzeller, L. Pichelstorfer, T. Nieminen, X. He, S. Brilke, M. Xiao, A. Amorim, R. Baalbaki, A. Baccarini, L. Beck, S. Bräkling, L. Caudillo Murillo, D. Chen, B. Chu, L. Dada, A. Dias, J. Dommen, J. Duplissy, I. El Haddad, L. Fischer, L. Gonzalez Carracedo, M. Heinritzi, C. Kim, T. K. Koenig, W. Kong, H. Lamkaddam, C. P. Lee, M. Leiminger, Z. Li, V. Makhmutov, H. E. Manninen, G. Marie, R. Marten, T. Müller, W. Nie, E. Partoll, T. Petäjä, J. Pfeifer, M. Philippov, M. P. Rissanen, B. Rörup, S. Schobesberger, S. Schuchmann, J. Shen, M. Sipilä, G. Steiner, Y. Stozhkov, C. Tauber, Y. J. Tham, A. Tomé, M. Vazquez-Pufleau, A. C. Wagner, M. Wang, Y. Wang, S. K. Weber, D. Wimmer, P. J. Wlasits, Y. Wu, Q. Ye, U. Zauner-Wieczorek, M. Baltensperger, K. S. Carslaw, J. Curtius, N. M. Donahue, R. C. Flagan, A. Hansel, M. Kulmala, J. Lelieveld, R. Volkamer, J. Kirkby and P. M. Winkler, Atmos. Chem. Phys., 2020, 20, 7359–7372 CrossRef CAS.
- C. Yan, W. Nie, A. L. Vogel, L. Dada, K. Lehtipalo, D. Stolzenburg, R. Wagner, M. P. Rissanen, M. Xiao, L. Ahonen, L. Fischer, C. Rose, F. Bianchi, H. Gordon, M. Simon, M. Heinritzi, O. Garmash, P. Roldin, A. Dias, P. Ye, V. Hofbauer, A. Amorim, P. S. Bauer, A. Bergen, A. K. Bernhammer, M. Breitenlechner, S. Brilke, A. Buchholz, S. B. Mazon, M. R. Canagaratna, X. Chen, A. Ding, J. Dommen, D. C. Draper, J. Duplissy, C. Frege, C. Heyn, R. Guida, J. Hakala, L. Heikkinen, C. R. Hoyle, T. Jokinen, J. Kangasluoma, J. Kirkby, J. Kontkanen, A. Kürten, M. J. Lawler, H. Mai, S. Mathot, R. L. Mauldin, U. Molteni, L. Nichman, T. Nieminen, J. Nowak, A. Ojdanic, A. Onnela, A. Pajunoja, T. Petäjä, F. Piel, L. L. J. Quéléver, N. Sarnela, S. Schallhart, K. Sengupta, M. Sipilä, A. Tomé, J. Tröstl, O. Väisänen, A. C. Wagner, A. Ylisirniö, Q. Zha, U. Baltensperger, K. S. Carslaw, J. Curtius, R. C. Flagan, A. Hansel, I. Riipinen, J. N. Smith, A. Virtanen, P. M. Winkler, N. M. Donahue, V. M. Kerminen, M. Kulmala, M. Ehn and D. R. Worsnop, Sci. Adv., 2020, 6, eaay4945 CrossRef CAS PubMed.
- D. Stolzenburg, L. Fischer, A. L. Vogel, M. Heinritzi, M. Schervish, M. Simon, A. C. Wagner, L. Dada, L. R. Ahonen, A. Amorim, A. Baccarini, P. S. Bauer, B. Baumgartner, A. Bergen, F. Bianchi, M. Breitenlechner, S. Brilke, S. B. Mazon, D. Chen, A. Dias, D. C. Draper, J. Duplissy, I. E. Haddad, H. Finkenzeller, C. Frege, C. Fuchs, O. Garmash, H. Gordon, X. He, J. Helm, V. Hofbauer, C. R. Hoyle, C. Kim, J. Kirkby, J. Kontkanen, A. Kürten, J. Lampilahti, M. Lawler, K. Lehtipalo, M. Leiminger, H. Mai, S. Mathot, B. Mentler, U. Molteni, W. Nie, T. Nieminen, J. B. Nowak, A. Ojdanic, A. Onnela, M. Passananti, T. Petäjä, L. L. J. Quéléver, M. P. Rissanen, N. Sarnela, S. Schallhart, C. Tauber, A. Tomé, R. Wagner, M. Wang, L. Weitz, D. Wimmer, M. Xiao, C. Yan, P. Ye, Q. Zha, U. Baltensperger, J. Curtius, J. Dommen, R. C. Flagan, M. Kulmala, J. N. Smith, D. R. Worsnop, A. Hansel, N. M. Donahue and P. M. Winkler, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9122–9127 CrossRef CAS PubMed.
- M. Schervish and N. Donahue, Atmos. Chem. Phys. Discuss., 2019, 1–29 Search PubMed.
- G. McFiggans, T. F. Mentel, J. Wildt, I. Pullinen, S. Kang, E. Kleist, S. Schmitt, M. Springer, R. Tillmann, C. Wu, D. Zhao, M. Hallquist, C. Faxon, M. Le Breton, Å. M. Hallquist, D. Simpson, R. Bergström, M. E. Jenkin, M. Ehn, J. A. Thornton, M. R. Alfarra, T. J. Bannan, C. J. Percival, M. Priestley, D. Topping and A. Kiendler-Scharr, Nature, 2019, 565, 587–593 CrossRef CAS PubMed.
- M. Heinritzi, L. Dada, M. Simon, D. Stolzenburg, A. C. Wagner, L. Fischer, L. R. Ahonen, S. Amanatidis, R. Baalbaki, A. Baccarini, P. S. Bauer, B. Baumgartner, F. Bianchi, S. Brilke, D. Chen, R. Chiu, A. Dias, J. Dommen, J. Duplissy, H. Finkenzeller, C. Frege, C. Fuchs, O. Garmash, H. Gordon, M. Granzin, I. El Haddad, X. He, J. Helm, V. Hofbauer, C. R. Hoyle, J. Kangasluoma, T. Keber, C. Kim, A. Kürten, H. Lamkaddam, T. M. Laurila, J. Lampilahti, C. P. Lee, K. Lehtipalo, M. Leiminger, H. Mai, V. Makhmutov, H. E. Manninen, R. Marten, S. Mathot, R. L. Mauldin, B. Mentler, U. Molteni, T. Müller, W. Nie, T. Nieminen, A. Onnela, E. Partoll, M. Passananti, T. Petäjä, J. Pfeifer, V. Pospisilova, L. L. J. Quéléver, M. P. Rissanen, C. Rose, S. Schobesberger, W. Scholz, K. Scholze, M. Sipilä, G. Steiner, Y. Stozhkov, C. Tauber, Y. J. Tham, M. Vazquez-Pufleau, A. Virtanen, A. L. Vogel, R. Volkamer, R. Wagner, M. Wang, L. Weitz, D. Wimmer, M. Xiao, C. Yan, P. Ye, Q. Zha, X. Zhou, A. Amorim, U. Baltensperger, A. Hansel, M. Kulmala, A. Tomé, P. M. Winkler, D. R. Worsnop, N. M. Donahue, J. Kirkby and J. Curtius, Atmos. Chem. Phys., 2020, 11809–11821 CrossRef CAS.
- K. Lehtipalo, C. Yan, L. Dada, F. Bianchi, M. Xiao, R. Wagner, D. Stolzenburg, L. R. Ahonen, A. Amorim, A. Baccarini, P. S. Bauer, B. Baumgartner, A. Bergen, A. K. Bernhammer, M. Breitenlechner, S. Brilke, A. Buchholz, S. B. Mazon, D. Chen, X. Chen, A. Dias, J. Dommen, D. C. Draper, J. Duplissy, M. Ehn, H. Finkenzeller, L. Fischer, C. Frege, C. Fuchs, O. Garmash, H. Gordon, J. Hakala, X. He, L. Heikkinen, M. Heinritzi, J. C. Helm, V. Hofbauer, C. R. Hoyle, T. Jokinen, J. Kangasluoma, V. M. Kerminen, C. Kim, J. Kirkby, J. Kontkanen, A. Kürten, M. J. Lawler, H. Mai, S. Mathot, R. L. Mauldin, U. Molteni, L. Nichman, W. Nie, T. Nieminen, A. Ojdanic, A. Onnela, M. Passananti, T. Petäjä, F. Piel, V. Pospisilova, L. L. J. Quéléver, M. P. Rissanen, C. Rose, N. Sarnela, S. Schallhart, S. Schuchmann, K. Sengupta, M. Simon, M. Sipilä, C. Tauber, A. Tomé, J. Tröstl, O. Väisänen, A. L. Vogel, R. Volkamer, A. C. Wagner, M. Wang, L. Weitz, D. Wimmer, P. Ye, A. Ylisirniö, Q. Zha, K. S. Carslaw, J. Curtius, N. M. Donahue, R. C. Flagan, A. Hansel, I. Riipinen, A. Virtanen, P. M. Winkler, U. Baltensperger, M. Kulmala and D. R. Worsnop, Sci. Adv., 2018, 4, 1–10 CrossRef PubMed.
- J. Kontkanen, T. Olenius, K. Lehtipalo, H. Vehkamäki, M. Kulmala and K. E. J. Lehtinen, Atmos. Chem. Phys., 2013, 13, 11391–11401 CrossRef.
- T. Olenius, I. Riipinen, K. Lehtipalo and H. Vehkamäki, J. Aerosol Sci., 2014, 78, 55–70 CrossRef CAS.
- V. Holten and M. E. H. Van Dongen, J. Chem. Phys., 2009, 130(1), 014102 CrossRef CAS PubMed.
- J. Wang, R. L. McGraw and C. Kuang, Atmos. Chem. Phys., 2013, 13, 6523–6531 CrossRef.
- A. Kürten, C. Li, F. Bianchi, J. Curtius, A. Dias, N. M. Donahue, J. Duplissy, R. C. Flagan, J. Hakala, T. Jokinen, J. Kirkby, M. Kulmala, A. Laaksonen, K. Lehtipalo, V. Makhmutov, A. Onnela, M. P. Rissanen, M. Simon, M. Sipilä, Y. Stozhkov, J. Tröstl, P. Ye and P. H. McMurry, Atmos. Chem. Phys., 2018, 18, 845–863 CrossRef.
- T. Nieminen, A. Asmi, P. P. Aalto, P. Keronen, T. Petäjä, M. Kulmala, V. M. Kerminen, T. Nieminen and M. Dal Maso, Boreal Environ. Res., 2014, 19, 191–214 Search PubMed.
- J. Kirkby, J. Curtius, J. Almeida, E. Dunne, J. Duplissy, S. Ehrhart, A. Franchin, S. Gagné, L. Ickes, A. Kürten, A. Kupc, A. Metzger, F. Riccobono, L. Rondo, S. Schobesberger, G. Tsagkogeorgas, D. Wimmer, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, A. Downard, M. Ehn, R. C. Flagan, S. Haider, A. Hansel, D. Hauser, W. Jud, H. Junninen, F. Kreissl, A. Kvashin, A. Laaksonen, K. Lehtipalo, J. Lima, E. R. Lovejoy, V. Makhmutov, S. Mathot, J. Mikkilä, P. Minginette, S. Mogo, T. Nieminen, A. Onnela, P. Pereira, T. Petäjä, R. Schnitzhofer, J. H. Seinfeld, M. Sipilä, Y. Stozhkov, F. Stratmann, A. Tomé, J. Vanhanen, Y. Viisanen, A. Vrtala, P. E. Wagner, H. Walther, E. Weingartner, H. Wex, P. M. Winkler, K. S. Carslaw, D. R. Worsnop, U. Baltensperger and M. Kulmala, Nature, 2011, 476, 429–435 CrossRef CAS PubMed.
- R. Schnitzhofer, A. Metzger, M. Breitenlechner, W. Jud, M. Heinritzi, L. P. De Menezes, J. Duplissy, R. Guida, S. Haider, J. Kirkby, S. Mathot, P. Minginette, A. Onnela, H. Walther, A. Wasem and A. Hansel, Atmos. Meas. Tech., 2014, 7, 2159–2168 CrossRef.
- J. Duplissy, J. Merikanto, A. Franchin, G. Tsagkogeorgas, J. Kangasluoma, D. Wimmer, H. Vuollekoski, S. Schobesberger, K. Lehtipalo, R. C. Flagan, D. Brus, N. M. Donahue, H. Vehkamäki, J. Almeida, A. Amorim, P. Barmet, F. Bianchi, M. Breitenlechner, E. M. Dunne, R. Guida, H. Henschel, H. Junninen, J. Kirkby, A. Kürten, A. Kupc, A. Määttänen, V. Makhmutov, S. Mathot, T. Nieminen, A. Onnela, A. P. Praplan, F. Riccobono, L. Rondo, G. Steiner, A. Tome, H. Walther, U. Baltensperger, K. S. Carslaw, J. Dommen, A. Hansel, T. Petäjä, M. Sipilä, F. Stratmann, A. Vrtala, P. E. Wagner, D. R. Worsnop, J. Curtius and M. Kulmala, J. Geophys. Res.: Atmos., 2016, 1752–1775 CrossRef CAS.
- J. Kirkby, J. Duplissy, K. Sengupta, C. Frege, H. Gordon, C. Williamson, M. Heinritzi, M. Simon, C. Yan, J. Almeida, J. Trostl, T. Nieminen, I. K. Ortega, R. Wagner, A. Adamov, A. Amorim, A. K. Bernhammer, F. Bianchi, M. Breitenlechner, S. Brilke, X. Chen, J. Craven, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, J. Hakala, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, J. Kim, M. Krapf, A. Kurten, A. Laaksonen, K. Lehtipalo, V. Makhmutov, S. Mathot, U. Molteni, A. Onnela, O. Perakyla, F. Piel, T. Petaja, A. P. Praplan, K. Pringle, A. Rap, N. A. D. Richards, I. Riipinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, C. E. Scott, J. H. Seinfeld, M. Sipila, G. Steiner, Y. Stozhkov, F. Stratmann, A. Tomé, A. Virtanen, A. L. Vogel, A. C. Wagner, P. E. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, X. Zhang, A. Hansel, J. Dommen, N. M. Donahue, D. R. Worsnop, U. Baltensperger, M. Kulmala, K. S. Carslaw and J. Curtius, Nature, 2016, 533, 521–526 CrossRef CAS PubMed.
- D. Stolzenburg, G. Steiner and P. M. Winkler, Atmos. Meas. Tech., 2017, 10, 1639–1651 CrossRef.
- S. Mirme and A. Mirme, Atmos. Meas. Tech., 2013, 6, 1061–1071 CrossRef.
- T. Jokinen, M. Sipilä, H. Junninen, M. Ehn, G. Lönn, J. Hakala, T. Petäjä, R. L. Mauldin, M. Kulmala and D. R. Worsnop, Atmos. Chem. Phys., 2012, 12, 4117–4125 CrossRef CAS.
- M. Heinritzi, M. Simon, G. Steiner, A. C. Wagner, A. Kürten, A. Hansel and J. Curtius, Atmos. Meas. Tech., 2016, 9, 1449–1460 CrossRef CAS.
- N. Hyttinen, O. Kupiainen-Määttä, M. P. Rissanen, M. Muuronen, M. Ehn and T. Kurtén, J. Phys. Chem. A, 2015, 119, 6339–6345 CrossRef CAS PubMed.
- M. J. McGrath, T. Olenius, I. K. Ortega, V. Loukonen, P. Paasonen, T. Kurtén, M. Kulmala and H. Vehkamäki, Atmos. Chem. Phys., 2012, 12, 2345–2355 CrossRef CAS.
- T. Olenius and I. Riipinen, Aerosol Sci. Technol., 2017, 51, 397–408 CrossRef CAS.
- A. Kürten, C. Williamson, J. Almeida, J. Kirkby and J. Curtius, Atmos. Chem. Phys., 2015, 15, 4063–4075 CrossRef.
- V. Besel, J. Kubečka, T. Kurtén and H. Vehkamäki, J. Phys. Chem. A, 2020, 124, 5931–5943 CrossRef CAS PubMed.
- J. Leppä, V. M. Kerminen, L. Laakso, H. Korhonen, K. E. J. Letinen, S. Gagné, H. E. Manninen, T. Nieminen and M. Kulmala, Boreal Environ. Res., 2009, 14, 559–575 Search PubMed.
- S. G. Gonser, F. Klein, W. Birmili, J. Gröβ, M. Kulmala, H. E. Manninen, A. Wiedensohler and A. Held, Atmos. Chem. Phys., 2014, 14, 10547–10563 CrossRef.
- T. Kurtén, L. Torpo, M. R. Sundberg, V. M. Kerminen, H. Vehkamäki and M. Kulmala, Atmos. Chem. Phys., 2007, 7, 2765–2773 CrossRef.
- S. Schobesberger, A. Franchin, F. Bianchi, L. Rondo, J. Duplissy, A. Kürten, I. K. Ortega, A. Metzger, R. Schnitzhofer, J. Almeida, A. Amorim, J. Dommen, E. M. Dunne, M. Ehn, S. Gagné, L. Ickes, H. Junninen, A. Hansel, V. M. Kerminen, J. Kirkby, A. Kupc, A. Laaksonen, K. Lehtipalo, S. Mathot, A. Onnela, T. Petäjä, F. Riccobono, F. D. Santos, M. Sipilä, A. Tomé, G. Tsagkogeorgas, Y. Viisanen, P. E. Wagner, D. Wimmer, J. Curtius, N. M. Donahue, U. Baltensperger, M. Kulmala and D. R. Worsnop, Atmos. Chem. Phys., 2015, 15, 55–78 CrossRef.
- H. Henschel, T. Kurtén and H. Vehkamäki, J. Phys. Chem. A, 2016, 120, 1886–1896 CrossRef CAS PubMed.
- J. Elm, J. Kubečka, V. Besel and M. J. Jääskeläinen, J. Aerosol Sci., 2020, 149, 105621 CrossRef CAS.
- T. Olenius, O. Kupiainen-Määttä, I. K. Ortega, T. Kurtén and H. Vehkamäki, J. Chem. Phys., 2013, 139(8), 084312 CrossRef CAS PubMed.
- K. Lehtipalo, J. Kontkanen, J. Kangasluoma, A. Franchin, D. Wimmer, S. Schobesberger, H. Junninen, T. Petäjä, M. Sipilä, D. R. Worsnop, M. Kulmala, K. Lehtipalo, J. Mikkilä, J. Vanhanen, J. Leppä and D. R. Worsnop, Boreal Environ. Res., 2014, 19(suppl. B), 215–236 Search PubMed.
- L. Dada, K. Lehtipalo, J. Kontkanen, T. Nieminen, R. Baalbaki, L. Ahonen, J. Duplissy, C. Yan, B. Chu, T. Petäjä, M. Kulmala and J. Kangasluoma, Nat. Protoc., 2020, 15, 1013–1040 CrossRef CAS PubMed.
- A. Kürten, T. Jokinen, M. Simon, M. Sipilä, N. Sarnela, H. Junninen, A. Adamov, J. Almeida, A. Amorim, F. Bianchi, M. Breitenlechner, J. Dommen, N. M. Donahue, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, J. Hakala, A. Hansel, M. Heinritzi, M. Hutterli, J. Kangasluoma, J. Kirkby, A. Laaksonen, K. Lehtipalo, M. Leiminger, V. Makhmutov, S. Mathot, A. Onnela, T. Petäjä, A. P. Praplan, F. Riccobono, M. P. Rissanen, L. Rondo, S. Schobesberger, J. H. Seinfeld, G. Steiner, A. Tomé, J. Tröstl, P. M. Winkler, C. Williamson, D. Wimmer, P. Ye, U. Baltensperger, K. S. Carslaw, M. Kulmala, D. R. Worsnop and J. Curtius, Proc. Natl. Acad. Sci., 2014, 111, 15019–15024 CrossRef PubMed.
- T. Olenius, R. Halonen, T. Kurtén, H. Henschel, O. Kupiainen-määttä, K. Ismael, C. N. Jen, H. Vehkamäki and I. Riipinen, J. Geophys. Res.: Atmos., 2017, 122, 7103–7118 CrossRef CAS.
- A. Kürten, Atmos. Chem. Phys., 2019, 19, 5033–5050 CrossRef.
- J. Elm, J. Phys. Chem. A, 2021, 125, 895–902 CrossRef CAS PubMed.
- O. Kupiainen-Määttä, Atmos. Chem. Phys., 2016, 16, 14585–14598 CrossRef.
- A. Shcherbacheva, T. Balehowsky, J. Kubečka, T. Olenius, T. Helin, H. Haario, M. Laine, T. Kurtén and H. Vehkamäki, Atmos. Chem. Phys., 2020, 20, 15867–15906 CrossRef CAS.
- L. Pichelstorfer, D. Stolzenburg, J. Ortega, T. Karl, H. Kokkola, A. Laakso, K. E. J. Lehtinen, J. N. Smith, P. H. McMurry and P. M. Winkler, Atmos. Chem. Phys., 2018, 18, 1307–1323 CrossRef CAS.
- M. Ozon, D. Stolzenburg, L. Dada, A. Seppänen and K. E. J. Lehtinen, Atmos. Chem. Phys., 2021, 21, 12595–12611 CrossRef CAS.
- D. Stolzenburg, Zenodo, 2022, https://doi.org/10.5281/zenodo.6362724.
- J. Kontkanen, T. Olenius, D. Stolzenburg, K. Lehtipalo and I. Riipinen, Zenodo, 2022, https://doi.org/10.5281/zenodo.6370141.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ea00103e |
| This journal is © The Royal Society of Chemistry 2022 |