Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Estimated timescales for wet deposition of organic compounds as a function of Henry's law constants†
Chenyang
Bi
 and
Gabriel
Isaacman-VanWertz
*
and
Gabriel
Isaacman-VanWertz
*
Department of Civil and Environmental Engineering, Virginia Tech, Blacksburg, Virginia 24060, USA. E-mail: ivw@vt.edu
First published on 11th October 2022
Abstract
Atmospheric organic compounds may deposit to Earth's surfaces via dry deposition, driven by concentration gradients, and wet deposition, driven by the scavenging of compounds by precipitation. Their removal by deposition has downstream impacts on concentrations of secondary organic aerosol by removing potential aerosol precursors that would otherwise oxidize to form particulate matter. The impact of deposition processes can consequently be considered as competition between rates of oxidation and deposition, but timescales for deposition are not well constrained. While timescales for dry deposition have been estimated and experimentally validated in the past, understanding of wet deposition of organics is still very limited. In this work, we estimate the wet deposition timescale for gas-phase organic compounds in the atmosphere as a function of Henry's law constants, H, using real-world precipitation frequency and size distributions at five globally-distributed sites. The wet deposition timescale decreases significantly with the increase of H until reaching a stable minimum for compounds with H > 105 M per atm. We estimate that the median wet deposition timescale for highly soluble gases is approximately 5 hours during a continuous rain event for all sites. However, median estimated timescales ranged from 80 to 200 hours, depending on location. Timescales are found to depend primarily on the frequency and duration of precipitation events rather than their intensity or size characteristics. Based on these data, we demonstrate that timescales for wet deposition of gases can be estimated at any given location using only basic precipitation information, without detailed or high-precision measurements.
Environmental significanceWet deposition (removal via rain or snow) of gaseous organic compounds can impact concentrations of secondary organic aerosol by removing aerosol precursors. However, timescales for wet deposition are not well constrained and consequently, their relative importance to other atmospheric removal processes of organics including dry deposition and oxidation is still unknown. In this work, we estimated the wet deposition timescale for gas-phase organic compounds using real-world precipitation data at five globally-distributed sites. We found that precipitation frequency and duration, rather than their intensity or size characteristics, drive most of the differences in wet deposition between sites. We demonstrate that timescales for wet deposition of gases can be estimated at any given location using only basic precipitation information, without high-precision measurements. |
Introduction
Organic gases may form particulate matter through oxidation, known as secondary organic aerosol (SOA),1–3 which may have significant influences on global climate4 and adversely impact human health.5,6 To understand the formation and fate of SOA, it is important to first investigate the evolution of atmospheric organic compounds including their removal pathways. Those gas-phase organics may deposit to Earth's surfaces via dry deposition, driven by concentration gradients, and wet deposition, driven by the scavenging of compounds by rain or snow.7 Deposition of gaseous species removes these compounds from subsequent processes in the atmosphere and determines their impact on the earth's ecosystems in many ways. Their removal by deposition may directly reduce the formation of SOA since these compounds are the fuel for chemical reactions that form SOA. Their removal may also volatilize particle-phase components by disrupting the equilibrium between gas- and particle-phases for “semi-volatile” gases.8 However, the oxygenated gases produced in the first generations of atmospheric oxidation are relatively short-lived, reacting on timescales of only a few hours to form SOA and longer-lived volatile gases.9 Therefore, the mass and composition of the formed aerosol depend critically on whether dry and wet removal of oxygenated gases efficiently compete with oxidation. Consequently, it is important to estimate the timescale for deposition of atmospheric organics to examine the competition between deposition and other processes. Unfortunately, timescales for wet deposition, in particular, are not well constrained and could vary significantly by ecosystem and region.Models of dry and wet deposition of a gas are typically governed by Henry's law constant, H, the main parameter describing uptake to water. For simplicity, H is often referred to in this study as “solubility”, though it is more accurately the ratio of solubilities in water and air and is thus also correlated to vapor pressure, at least for oxygenated gases.10,11 The modeled estimates of the impact of deposition on SOA formation are very sensitive to solubility across the range expected for semi-volatile atmospheric oxidation products (H = 105 to 108 M per atm),10 in large part because these compounds comprise a substantial fraction of “potential aerosol formation” (i.e., the extent to which a compound's oxidation is expected to yield aerosol).12 However, estimation of Henry's law constant may have orders of magnitude uncertainties, particularly for semi-volatile organic compounds.11 It is not necessarily clear the extent to which uncertainty in Henry's law constants propagates through to real-world atmospheric impacts, in part due to a relative dearth of studies on the timescales for deposition. Hodzic et al.10 found that deposition is insensitive to increases in Henry's law constants beyond ∼108 M per atm, but a direct relationship between Henry's law constants and deposition timescales is lacking. Examining this relationship would improve understanding generally of how physicochemical properties modulate concentrations of atmospheric gases, and more specifically how high uncertainties in H impact our understanding of deposition. Wet deposition in particular is complex because, in addition to Henry's law constant, it is dependent on meteorological parameters such as precipitation intensity, frequency, and duration, and droplet size distribution. Those rain characteristics may vary significantly depending on locations and climatic conditions. Therefore, it is critical to examine the real-world spatial heterogeneity of wet deposition timescales to understand the regional and global impacts of deposition.
Previous studies on wet removal mostly focused on inorganics13–15 and limited categories of organics such as organic nitrogen and phosphorus15,16 and persistent organic pollutants.17,18 Estimation of wet deposition timescale for atmospheric organics, particularly semi-volatiles and oxygenated gases that may serve as efficient aerosol precursors, is still limited. Therefore, the goal of this work is to more broadly estimate the wet deposition of gas-phase organic compounds in the atmosphere as a function of Henry's law constants and quantitatively understand the factors governing wet deposition. Our specific goals are to (1) estimate the H-dependent wet deposition timescale for gaseous organic compounds using real-world precipitation data; (2) analyze the influences of precipitation intensity, frequency, and duration on the wet deposition timescale at five geographically different sites; and (3) demonstrate a simplified, computationally-light approach for estimating global wet deposition timescale.
Methodology
Data sources
This work is based on precipitation-associated data (e.g., droplet number density, precipitation rate, and precipitation type) collected by laser disdrometer in the Department of Energy – Atmospheric Radiation Measurement (DOE-ARM) network at five globally distributed sites: Lamont, Oklahoma, USA (site code: SGP); Manacapuru, Brazil (MAO); Cordoba, Argentina (COR); Houston, Texas, USA (HOU); and Graciosa Island, Portugal (ENA). The date ranges are SGP: January 2019 to December 2020, COR: September 2018 to April 2019, MAO: September 2014 to December 2015, HOU: October 2021 to May 2022, and ENA: January 2019 to December 2020. This study uses data at the time resolution of the raw files, 1 min intervals. Because the determination of droplet size by disdrometer may have large inaccuracy from the observations of snowflakes and scavenging by snow involves separate processes than that by rain, data with snow and hail are excluded from the analysis. Sanity checking was performed to ensure that the data were being accurately processed, including: matching reported precipitation rates to those calculated from droplet number densities (to confirm proper understanding of rates and densities), matching reported droplet number densities to those calculated from raw reported spectra (to confirm proper understanding of densities and spectra), and matching calculated scavenging rates for an assumed monodisperse particle distribution to those calculated for a single particle size (to verify the correctness of calculations using full-size distributions).Calculation of scavenging coefficients
During rain, soluble gaseous species below clouds may dissolve into rain droplets and consequently be partially or completely washed out during the process. The first-order scavenging coefficient, Λi (cm3 s−1) for one droplet can be described as a function of chemical solubility, which can be determined using Henry's law constants, rain characteristics (e.g., fall height), and droplet physical properties (e.g., size and velocity) as follows:7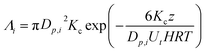 | (1) |
H (M per atm) is the Henry's law constant; T (K) is the droplet temperature; R (L atm mol−1 K−1) is the molar gas constant; Dp,i (cm) is the droplet diameter; z (cm) is precipitation height; Ut (cm s−1) is the droplet velocity; and Kc (cm s−1) is the mass transfer coefficient calculated as:7
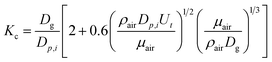 | (2) |
In the rain, the droplets usually cover a range of sizes and therefore the overall scavenging coefficient, Λ (s−1), is the summation of scavenging rates for droplets of different sizes:
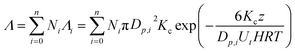 | (3) |
| F = ΛCg | (4) |
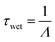 | (5) |
Estimation of wet deposition timescales
Using measurements of precipitation size distributions collected by laser disdrometer at 1-minute intervals, scavenging coefficients can be calculated as a function of Henry's law constants for each minute of data using eqn (3). However, rain characteristics typically change over time, resulting in varying scavenging coefficients that make eqn (5) an inaccurate approach to estimating real-world timescales. To include the impact of varying scavenging over time, we define the wet deposition timescale as the time taken for a unit mass of a compound to decay to 1/e mass; this follows the same mathematical definition as the first-order kinetics implicit in eqn (5). To estimate wet deposition timescales, a Monte Carlo approach is used, in which the scavenging of a unit mass of each compound is simulated using eqn (4) until the 1/e threshold is reached; 2000 scavenging simulations are performed for each surrogate compound having a prescribed value of Henry's law constant. The median timescale of all simulations for each compound is taken as the wet deposition timescale for that compound. This approach treats wet deposition as an approximately continuous first-order process; while this approach has some limitations (discussed later), it has the significant benefit of enabling direct comparisons between competing atmospheric processes such as oxidation, dry deposition, and advection, which are often treated as similarly first-order though they are not always continuous processes.Timescales during continuous rain events are estimated from simulations by randomly sampling 1 minute scavenging rates excluding periods without rain. More general wet deposition timescales are calculated by including both periods with and without rain. However, instead of using randomly sampled minutes of scavenging, the effects of frequency and duration are included by using only continuous data. In each simulation, a random minute is sampled as a starting point and scavenging is simulated forward in time until the 1/e threshold is reached. In all simulations, scavenging is the only loss process considered, so minutes with no rain are assumed to have zero scavenging coefficient. In simulations that reach the end of a dataset before reaching the 1/e threshold, the sequence is redirected to the beginning of the dataset.
We note that, in addition to Henry's law constant, diffusivity in air is compound-dependent. However, the variability of this parameter is only from 0.04 to 0.08 cm2 s−1 (calculated in the ESI†) for compounds with the approximate molecular weights of oxygenated atmospheric gases. Uncertainty in this parameter affects only the most soluble gases and has a relatively minor impact on less soluble species. Therefore, to simplify the analysis, we assign the diffusivity of α-pinene, 0.06 cm2 s−1,19 for all compounds in subsequent analysis and then discuss the influence of diffusivity in the ESI (Fig. S1†). Additionally, the precipitation height is assumed to be 1500 m in this study; the effects of this assumption impact only less soluble gases, but are generally relatively minor compared to the impact of H (Fig. S2†).
Estimation of dry deposition timescale
For comparison with wet deposition, dry deposition timescales as a function of Henry's law constants are also estimated in this study for products in α-pinene oxidation reactions from the Master Chemical Mechanism (MCM).20 We consider dry deposition to plant stomatal or non-stomatal components such as leaf cuticles using the surface deposition model described by Weseley,21 assuming the in-series coupling of aerodynamic, molecular diffusion, and surface resistance. Deposition to non-leaf surfaces is not considered in this model, as it is intended here only to provide context, not a globally useful representation of dry deposition. Since dry deposition timescales may vary significantly depending on multiple factors such as location, atmospheric conditions, and characteristics of the surfaces, we apply parameters used by Nguyen et al.22 for the southeastern U.S. as a representative case to compare with wet deposition, though this environment likely represents relatively rapid dry deposition due to high leaf area. Additionally, we include sensitivity analysis of dry deposition timescales to critical variable parameters, including friction velocity, leaf area index, and characteristic leaf thickness, to estimate a possible uncertainty or range of the dry deposition timescales. We emphasize that the estimation of dry deposition timescales is not the focus of this work, and actual competition between deposition processes requires a more detailed analysis and the possible inclusion of deposition on other surfaces.Results and discussion
Unlike dry deposition, which for gases is driven by concentration gradients and occurs constantly, wet deposition occurs intermittently and only happens during rainy periods. Consequently, wet deposition must be a function of both characteristics and frequency of rain. Therefore, we investigate the influence of rain characteristics and frequency separately by estimating the wet deposition timescale during rainy periods first and then studying the timescale during all periods.Wet deposition timescales during rain events
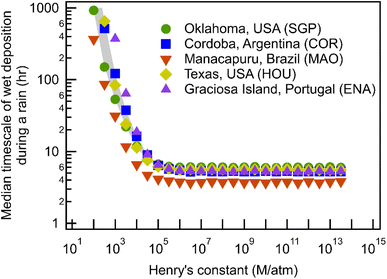
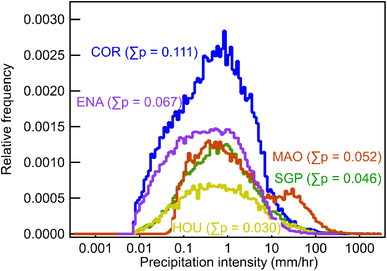
As shown, during a continuous rain event, the wet deposition timescale decreases exponentially with the increase of solubility, represented by the Henry's constant (Fig. 1), and plateaus at a minimum of 4–6 hours when H > 105 M per atm. Although the five sites represent significantly different geographic regions and climatic conditions, the differences in timescales are minimal. For highly soluble gases, the minimum timescales are 6.0, 5.4, 3.7, 5.5, and 5.2 hours, for SGP, COR, MAO, HOU, and ENA, respectively. Differences between deposition timescales for less soluble gases are somewhat larger, up to nearly an order of magnitude for the least soluble gases, but timescales are so long for the least soluble compounds studied (weeks to months) that wet deposition is unlikely to be the dominant loss process.The similarity between timescales at each site suggests that, despite the theoretical impacts of precipitation size and number on scavenging, the overall characteristics of precipitation at each site are sufficiently similar to produce only minor changes in deposition timescales. Distributions of precipitation intensity show that SGP, COR, HOU, and ENA have a similar distribution in precipitation intensity (Fig. 2), which helps explain the closer wet deposition timescales between the four sites. Note that the total frequency of rain at each site does not affect the timescales shown in Fig. 1 because only periods of precipitation are included in this analysis; impacts of frequency and duration will be discussed later. However, MAO, a site located near the Amazon Forest, has more frequent heavy rainfalls (i.e., high frequency of rain from 10 to 100 mm h−1 in Fig. 2), which contributes to slightly higher scavenging rates thus resulting in lower wet deposition timescales than other sites in Fig. 1. The small differences in timescales between MAO and the other four sites in Fig. 1 suggest that higher precipitation intensities may have some effects on wet deposition timescales, but the differences in precipitation intensity between sites are not big enough to have substantial influences on the wet deposition timescales.
Influence of droplet size on scavenging
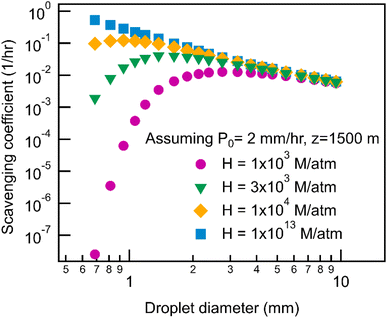
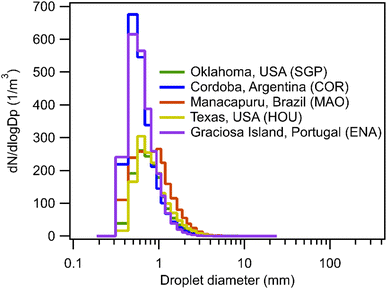
Scavenging rate during rain depends not only on the precipitation intensity but also on the size distribution of droplets. Fig. 3 shows the calculated scavenging coefficient as a function of droplet size for monodisperse droplets assuming the same precipitation intensity, 2 mm h−1, across a range of Henry's law constant. At low H (<∼104 M per atm), scavenging via large droplets is more efficient, while small droplets are more efficient at wet removal when the solubility of compounds is relatively high. Once solubility increases beyond a certain threshold, the exponential term in the scavenging equation describing air–water partitioning no longer constrains the mass transfer thus making the increase in surface-to-volume ratio (i.e., more small droplets with the same total volume) drive the increase of the scavenging coefficient. Beyond this solubility threshold, the impact of droplet size is the same for all Henry's law constants and scavenging is a function only of properties that are not H-dependent (e.g., precipitation intensity), resulting in the observed plateau (Fig. 1) in wet deposition timescales for H > 105 M per atm.The orders of magnitude impacts of droplet size on the scavenging coefficient suggest that the distribution of droplet size, in addition to precipitation intensity, should influence the wet removal rate during a continuous rain event; though site-to-site variability is not actually substantial, there are some differences for less soluble compounds. The impact of particle size explains the steeper decrease of wet deposition timescales with increasing H for COR and ENA compared to SGP and MAO (Fig. 1) because precipitation in COR and ENA have, on average, smaller droplets than SGP and MAO (Fig. 4). For the reasons discussed above, these differences in droplet size distributions do not impact the scavenging of more soluble gases. However, as in the case of precipitation rates (Fig. 2), differences in size distributions are relatively minor (Fig. 4), with all sites peaking between 0.5 and 1 mm, resulting in the low observed variance in the estimated wet deposition timescales between the five geographically distant sites.
Overall timescales for wet deposition
Estimation of wet deposition timescale during a rain event provides insight into the effects of precipitation characteristics, but is not enough to understand the overall impact of the wet removal process due to the intermittent nature of precipitation. The frequency and duration of rain events must have a strong effect on the timescale (e.g., there is no wet deposition in a desert). As described in the methods, the average timescale for wet deposition is examined by selecting random starting points in the real-world precipitation datasets and simulating scavenging by advancing forward in the time series. This approach inherently accounts for the frequency and duration of precipitation events by using continuous real-world data that preserve these features.As expected based on scavenging efficiency, wet deposition timescales decrease with the increasing solubility and plateau at a minimum for compounds with H > 105 M per atm (Fig. 5). The timescales for wet deposition of the most soluble gases range from 80–200 hours depending on location, specifically 182, 85, 100, 222, and 105 hours for SGP, COR, MAO, HOU, and ENA, respectively. In general, wet deposition during all periods follows the same trend as those during rainy periods but removes gases substantially slower due to periods of no wet deposition during non-precipitation periods. Some differences due to the influence of frequency and duration of rain are observed. For example, although compounds are scavenged in rain events slower in COR compared to MAO (Fig. 1), those chemical species deposit faster in COR than MAO because the precipitation frequency in COR is higher (i.e., probability of rain is 11% vs. 5% as shown in Fig. 2). However, while the overall wet deposition timescales strongly depend on the frequency and duration of precipitation events, differences in timescales between sites are again relatively minor.
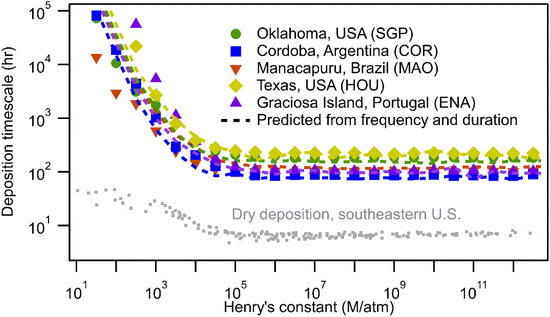 | ||
| Fig. 5 Overall timescale for wet deposition as a function of Henry's law constants using rain characteristics collected from five sites: SGP, COR, MAO, HOU, and ENA. Dashed lines are predicted median timescales based on rain frequency and duration, and global average timescale during rainy period (this approach is described in the text). Grey dots are modeled dry deposition timescales for α-pinene oxidation products estimated using parameters described by Nguyen et al.22 | ||
Rapid approach for estimation of wet deposition timescale at any location
Despite substantial differences in geographic locations, the analysis so far has shown that wet deposition timescales during rainy periods for a given compound are relatively similar across locations. Timescales of wet deposition for compounds with H > 105 M per atm during rain events are roughly 5 hours and impacts of Henry's law constants on lower solubility gases are comparable across sites. These low cross-site variance of wet deposition timescale during rainy period indicates that the differences in precipitation intensity and droplet size distributions are not sufficient to yield substantial differences in deposition. We therefore hypothesize that the wet deposition timescale at any site can be inferred based primarily on the frequency and duration of precipitation, assuming global average timescales for wet deposition during precipitation.To validate this hypothesis, we measure the time taken to reach the cumulative number of hours of rain that is equal to the average wet deposition timescale at each Henry's constant level (e.g., 5 hours for compounds with H > 105 M per atm). This approach is independent of rain intensity or size distributions, relying only on the most basic precipitation data from all five sites (i.e., whether or not it rains). As in the other estimation approach, randomly selected starting points are chosen in each dataset stepped forward until the number of hours of the in-rain timescale is reached (1000 simulations of each compound at each site). For compounds with H > 105 M per atm, timescales predicted using this size- and intensity-blind approach are within 20% of the more accurate approach using the complete precipitation information (Fig. 5). For compounds with H between 103 and 105 M per atm, the simplified approach still yields less than 20% errors at sites that tend more toward the central tendency (SGP, COR, and HOU), but can lead to somewhat higher uncertainties at other sites (at the most extreme end, a factor of 3 at ENA for H = 103 M per atm). For this simplified estimation approach, uncertainty gets significantly higher for compounds with H < 103 M per atm. However, for most of these less soluble compounds, wet deposition timescales on the order of months to years suggest that other processes such as dry deposition and oxidation will dominate atmospheric removal, making accuracy less important. This novel approach allows rapid estimations of wet deposition timescales for more soluble compounds at any site for which the presence or absence of precipitation is known with reasonable time resolution. We note that using a site-specific value for timescales during precipitation instead of global values can improve accuracy to be within 5% for compounds with H > 105 M per atm and within 20% for compounds with H between 103 and 105 M per atm (Fig. S3†), but this approach negates much of the advantage of the approach as it would still require a detailed analysis of precipitation size distribution and intensity at each site. Since the shapes of the predictions (dashed lines in Fig. 5) are similar across sites, we further simplify the approach and provide a fitted equation of the curves as eqn (S1).† While the details of the fit are described in the ESI, in Fig. S4,† we demonstrate that the estimation of wet deposition timescales as a function of Henry's law constants can be achieved by calculating only the timescales for compounds with H > 105 M per atm and fitting the timescales for less soluble species as an exponential curve.
The agreement between size- and intensity-blind predictions and estimated wet deposition timescales suggests that frequency and duration, not the precipitation characteristics, drive the site-to-site differences in wet deposition timescales. The global average timescales for wet deposition as a function of Henry's constant during precipitation can be reasonably representative of in-rain timescales at all sites. In other words, differences in precipitation intensity and droplet size distribution between sites are not sufficient to drive real differences in wet deposition timescales, at least in an average sense.
To examine the applicability and feasibility of this novel approach, we further downgrade the quality of the data, from DOE-ARM laser disdrometer data to relatively rough yet more accessible precipitation data from airports in the Automated Surface Observing System (ASOS) network. Basic precipitation data collected from nearby airports (KSWO, ∼80 km away from SGP, and KHOU, ∼24 km away from HOU) are applied to compare the estimated overall wet deposition timescales. The frequency and duration of rain are determined only by the airport weather code data at 1 min intervals obtained from the ASOS network. Minutes coded as “P”, “P?”, “R−“, “R”, and “R+” are treated as rainy periods while the rest are considered non-rainy periods. By using frequency and duration of rain from laser disdrometer data vs. from weather code data at nearby airports (i.e., SGP vs. KSWO and HOU vs. KHOU) with the same site-specific values for timescales during precipitation (i.e., same approach as in Fig. S3†), as shown in Fig. S5,† we find that the estimated overall wet deposition timescales are relatively close between DOE-ARM sites and nearby airports with relative differences less than 30%. The findings show that the estimation of overall wet deposition timescales can be achieved with relatively basic weather code data, which are widely available at airports in the US and globally.
Comparison with dry deposition
To consider wet deposition in the context of competition between different removal processes, we further compare the estimated wet deposition timescales with dry deposition timescales estimated for the southeastern U.S. following Nguyen et al.22 Dry deposition timescales for predicted α-pinene oxidation products exhibit a similar trend with Henry's law constants, reaching a relative minimum for compounds with H > 105 M per atm. The dry deposition timescales of more soluble compounds are about 7 hours in the case of the heavily forested summertime southeastern U.S. (assuming the same 1500 m boundary layer height used for wet deposition), which is about one order of magnitude faster than wet deposition. However, dry deposition timescale may vary significantly with seasonally-dependent variables (e.g., leaf area index (LAI) and characteristic leaf thickness) and weather-dependent variables (e.g., friction velocity). The rapid dry deposition estimated in this case is likely relatively fast compared to many environments, so a more thorough examination of dry deposition timescales is necessary to actually quantify competition between loss processes. Nevertheless, to understand the likely range of global dry deposition timescale, we examine the dry deposition timescale using Monte-Carlo style simulations with ranges of these parameters, as shown in Fig. S6.† Uncertainty of dry deposition timescales is approximately half an order of magnitude considering possible values of characteristic leaf thickness and friction velocity. Furthermore, timescales are nearly linearly sensitive to LAI; a value of 4.7 is used for the southeastern summertime U.S., while a value of 0.47 increases dry deposition timescales to 20–60 hours, lower but comparable to some wet deposition. This suggests that dry deposition likely outcompetes wet deposition in general, but may be competitive depending on season and ecosystem. Nevertheless, we note that dry deposition is not the focus of this study and the brief analysis here is to provide context for comparisons between dry and wet deposition. A more thorough global investigation is warranted to better constrain this competition.Conclusion
In this work, we estimate the wet deposition timescale for gas-phase organic compounds in the atmosphere as a function of Henry's law constants, H, using real-world precipitation data collected from globally-distributed sites. Wet deposition timescales decrease significantly with the increase of Henry's law constants and become constant for compounds with H > 105 M per atm, which have wet deposition timescales of approximately 5 hours during a continuous rain event for all sites. Most importantly, we find that characteristics of precipitation events (i.e., intensity and droplet size distributions) are sufficiently similar across sites to yield only minor differences in scavenging during precipitation. Estimated overall timescales for soluble gases range from 80 to 200 hours across sites, with similar increases at each site for less soluble gases. We conclude, therefore, that precipitation frequency and duration drive most of the differences in wet deposition between sites.The strong dependence on frequency and duration of precipitation allows us to propose a rapid, computationally-light approach to estimate wet deposition timescales for any compounds at any location as long as basic precipitation data is available. The overall timescale for wet deposition can be predicted as simply the length of time it takes to reach a cumulative number of minutes of precipitation equal to the global average timescale for in-rain scavenging. We demonstrate that this approach can yield accuracy within 20% of error for most sites and most compounds with H > 103 M per atm, though uncertainty in the most extreme case for compounds with H between 103 and 105 M per atm can be a factor of 3. This approach could be applied to rapidly estimate the global wet deposition timescales in the future.
It is worth noting that wet deposition is by nature sporadic, so describing the process as occurring with a first-order timescale has inherent imprecision. For instance, because wet deposition acts only during precipitation events, it is possible that competing processes are somewhat more important than implied by a comparison of first-order timescales, as other processes are available to act unperturbed between events. Similarly, wet deposition occurs in bursts, which can cause downstream effects (e.g., intermittent periods of rapid influx of compounds to an ecosystem). However, understanding the approximate first-order timescales of wet deposition, even if not fully precise, carries significant value by enabling comparisons between sites and between atmospheric processes. The global understanding of wet deposition provided by the analyses here, coupled with the novel approach to develop a more spatially and temporally detailed measurement of the process, shines new light on the process and its potential role in atmospheric processes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the United States Department of Energy Office of Biological & Environmental Research (DE-SC0022020).References
- A. H. Goldstein and I. E. Galbally, Known and unexplored organic constituents in the earth's atmosphere, Environ. Sci. Technol., 2007, 41, 1514–1521 CrossRef CAS.
- J. L. Jimenez, M. R. Canagaratna, N. M. Donahue, A. S. H. Prevot, Q. Zhang, J. H. Kroll, P. F. DeCarlo, J. D. Allan, H. Coe, N. L. Ng, A. C. Aiken, K. S. Docherty, I. M. Ulbrich, A. P. Grieshop, A. L. Robinson, J. Duplissy, J. D. Smith, K. R. Wilson, V. A. Lanz, C. Hueglin, Y. L. Sun, J. Tian, A. Laaksonen, T. Raatikainen, J. Rautiainen, P. Vaattovaara, M. Ehn, M. Kulmala, J. M. Tomlinson, D. R. Collins, M. J. Cubison, E. J. Dunlea, J. A. Huffman, T. B. Onasch, M. R. Alfarra, P. I. Williams, K. Bower, Y. Kondo, J. Schneider, F. Drewnick, S. Borrmann, S. Weimer, K. Demerjian, D. Salcedo, L. Cottrell, R. Griffin, A. Takami, T. Miyoshi, S. Hatakeyama, A. Shimono, J. Y. Sun, Y. M. Zhang, K. Dzepina, J. R. Kimmel, D. Sueper, J. T. Jayne, S. C. Herndon, A. M. Trimborn, L. R. Williams, E. C. Wood, A. M. Middlebrook, C. E. Kolb, U. Baltensperger and D. R. Worsnop, Evolution of organic aerosols in the atmosphere, Science, 2009, 326, 1525–1529 CrossRef CAS.
- J. H. Kroll and J. H. Seinfeld, Chemistry of secondary organic aerosol: formation and evolution of low-volatility organics in the atmosphere, Atmos. Environ., 2008, 42, 3593–3624 CrossRef CAS.
- M. Hallquist, J. C. Wenger, U. Baltensperger, Y. Rudich, D. Simpson, M. Claeys, J. Dommen, N. M. Donahue, C. George, A. H. Goldstein, J. F. Hamilton, H. Herrmann, T. Hoffmann, Y. Iinuma, M. Jang, M. E. Jenkin, J. L. Jimenez, A. Kiendler-Scharr, W. Maenhaut, G. McFiggans, T. F. Mentel, A. Monod, A. S. H. Prévôt, J. H. Seinfeld, J. D. Surratt, R. Szmigielski and J. Wildt, The formation, properties and impact of secondary organic aerosol: current and emerging issues, Atmos. Chem. Phys., 2009, 9, 5155–5236 CrossRef CAS.
- R. T. Burnett, C. A. Pope, M. Ezzati, C. Olives, S. S. Lim, S. Mehta, H. H. Shin, G. Singh, B. Hubbell, M. Brauer, H. R. Anderson, K. R. Smith, J. R. Balmes, N. G. Bruce, H. Kan, F. Laden, A. Prüss-Ustün, M. C. Turner, S. M. Gapstur, W. R. Diver and A. Cohen, An integrated risk function for estimating the global burden of disease attributable to ambient fine particulate matter exposure, Environ. Health Perspect., 2014, 122, 397–403 CrossRef PubMed.
- C. A. Pope and D. W. Dockery, Health effects of fine particulate air pollution: lines that connect, J. Air Waste Manage. Assoc., 2006, 56, 709–742 CrossRef CAS PubMed.
- J. H. Seinfeld and S. N. Pandis, Atmospheric chemistry and physics : from air pollution to climate change, 3rd edn, 2016 Search PubMed.
- C. Knote, A. Hodzic and J. L. Jimenez, The effect of dry and wet deposition of condensable vapors on secondary organic aerosols concentrations over the continental US, Atmos. Chem. Phys., 2015, 15, 1–18 CrossRef.
- G. Isaacman-Vanwertz, P. Massoli, R. O'Brien, C. Lim, J. P. Franklin, J. A. Moss, J. F. Hunter, J. B. Nowak, M. R. Canagaratna, P. K. Misztal, C. Arata, J. R. Roscioli, S. T. Herndon, T. B. Onasch, A. T. Lambe, J. T. Jayne, L. Su, D. A. Knopf, A. H. Goldstein, D. R. Worsnop and J. H. Kroll, Chemical evolution of atmospheric organic carbon over multiple generations of oxidation, Nat. Chem., 2018, 10, 462–468 CrossRef CAS PubMed.
- A. Hodzic, B. Aumont, C. Knote, J. Lee-Taylor, S. Madronich and G. Tyndall, Volatility dependence of Henry's law constants of condensable organics: application to estimate depositional loss of secondary organic aerosols, Geophys. Res. Lett., 2014, 41, 4795–4804 CrossRef CAS.
- G. Isaacman-VanWertz and B. Aumont, Impact of organic molecular structure on the estimation of atmospherically relevant physicochemical parameters, Atmos. Chem. Phys., 2021, 21, 6541–6563 CrossRef CAS.
- J. F. Hunter, D. A. Day, B. B. Palm, R. L. N. Yatavelli, A. W. H. Chan, L. Kaser, L. Cappellin, P. L. Hayes, E. S. Cross, A. J. Carrasquillo, P. Campuzano-Jost, H. Stark, Y. Zhao, T. Hohaus, J. N. Smith, A. Hansel, T. Karl, A. H. Goldstein, A. Guenther, D. R. Worsnop, J. A. Thornton, C. L. Heald, J. L. Jimenez and J. H. Kroll, Comprehensive characterization of atmospheric organic carbon at a forested site, Nat. Geosci., 2017, 10, 748–753 CrossRef CAS.
- M. G. Vivanco, M. R. Theobald, H. Garcia-Gomez, J. L. Garrido, M. Prank, W. Aas, M. Adani, U. Alyuz, C. Andersson, R. Bellasio, B. Bessagnet, R. Bianconi, J. Bieser, J. Brandt, G. Briganti, A. Cappelletti, G. Curci, J. H. Christensen, A. Colette, F. Couvidat, C. Cuvelier, M. D'Isidoro, J. Flemming, A. Fraser, C. Geels, K. M. Hansen, C. Hogrefe, U. Im, O. Jorba, N. Kitwiroon, A. Manders, M. Mircea, N. Otero, M. T. Pay, L. Pozzoli, E. Solazzo, S. Tsyro, A. Unal, P. Wind and S. Galmarini, Modeled deposition of nitrogen and sulfur in Europe estimated by 14 air quality model systems: evaluation, effects of changes in emissions and implications for habitat protection, Atmos. Chem. Phys., 2018, 18, 10199–10218 CrossRef CAS PubMed.
- H. Rodhe, F. Dentener and M. Schulz, The global distribution of acidifying wet deposition, Environ. Sci. Technol., 2002, 36, 4382–4388 CrossRef CAS PubMed.
- R. Vet, R. S. Artz, S. Carou, M. Shaw, C.-U. Ro, W. Aas, A. Baker, V. C. Bowersox, F. Dentener, C. Galy-Lacaux, A. Hou, J. J. Pienaar, R. Gillett, M. C. Forti, S. Gromov, H. Hara, T. Khodzher, N. M. Mahowald, S. Nickovic, P. S. P. Rao and N. W. Reid, A global assessment of precipitation chemistry and deposition of sulfur, nitrogen, sea salt, base cations, organic acids, acidity and pH, and phosphorus, Atmos. Environ., 2014, 93, 3–100 CrossRef CAS.
- S. M. Calderón, N. D. Poor and S. W. Campbell, Estimation of the particle and gas scavenging contributions to wet deposition of organic nitrogen, Atmos. Environ., 2007, 41, 4281–4290 CrossRef.
- L. Melymuk, M. Robson, M. L. Diamond, L. E. Bradley and S. Backus, Wet deposition loadings of organic contaminants to Lake Ontario: assessing the influence of precipitation from urban and rural sites, Atmos. Environ., 2011, 45, 5042–5049 CrossRef CAS.
- E. Jurado, F. Jaward, R. Lohmann, K. C. Jones, R. Simó and J. Dachs, Wet deposition of persistent organic pollutants to the global oceans, Environ. Sci. Technol., 2005, 39, 2426–2435 CrossRef CAS PubMed.
- ARChem, SPARC, ARChem's physicochemical calculator, http://www.archemcalc.com/sparc.html, accessed 2022/06/15 Search PubMed.
- S. M. Saunders, M. E. Jenkin, R. G. Derwent and M. J. Pilling, Protocol for the development of the Master Chemical Mechanism, MCM v3 (Part A): tropospheric degradation of non-aromatic volatile organic compounds, Atmos. Chem. Phys., 2003, 3, 161–180 CrossRef CAS.
- M. L. Weseley, Parameterization of Surface Resistances to Gaseous Dry Deposition in Regional-Scale Numerical Models, Atmos. Environ., 1989, 23, 1293–1304 CrossRef.
- T. B. Nguyen, J. D. Crounse, A. P. Teng, J. M. St Clair, F. Paulot, G. M. Wolfe and P. O. Wennberg, Rapid deposition of oxidized biogenic compounds to a temperate forest, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E392–E401 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ea00091a |
| This journal is © The Royal Society of Chemistry 2022 |