Computational framework for evaluating risk trade-offs in costs associated with legionnaires' disease risk, energy, and scalding risk for hospital hot water systems†
Ashley
Heida
ab,
Alexis
Mraz
c,
Mark T.
Hamilton
de,
Mark H.
Weir
 f and
Kerry A.
Hamilton
f and
Kerry A.
Hamilton
 *bg
*bg
aSchool for Engineering of Matter, Transport and Energy, Arizona State University, 502 E Tyler Mall, Tempe, AZ 85287, USA
bThe Biodesign Institute Center for Environmental Health Engineering, Arizona State University, 1001 S. McAllister Ave, Tempe, AZ 85281, USA. E-mail: kerry.hamilton@asu.edu
cSchool of Nursing, Health, and Exercise Science, The College of New Jersey, PO BOX 7718, 2000 Pennington Rd, Ewing, NJ 08628, USA
dComputer Science & Artificial Intelligence Lab, Massachusetts Institute of Technology, 32 Vassar St, Cambridge, MA 02139, USA
eNew England Research and Development Center, Microsoft, 1 Memorial Drive, Cambridge, MA 02139, USA
fDivision of Environmental Health Sciences and Sustainability Institute, The Ohio State University, Columbus, OH 43210, USA
gSchool of Sustainable Engineering and the Built Environment, Arizona State University, Tempe, AZ 85281, USA
First published on 7th October 2021
Abstract
Legionella pneumophila are bacteria that when inhaled cause Legionnaires' disease (LD) and febrile illness Pontiac fever. As of 2014, LD is the most frequent cause of waterborne disease outbreaks due to drinking water exposure in the United States. The optimal temperature for the bacteria's growth is between 25–45 °C, and water heaters that are set within this range can become an environment for L. pneumophila to grow. The recommended water heater temperature varies across organizations, from 60 °C to kill L. pneumophila bacteria to 49 °C to prevent scalding and minimize energy costs. To evaluate these trade-offs, we have developed a computational framework for evaluating an optimal water heater temperature set point for reducing cost and health risks. This framework uses a quantitative microbial risk assessment (QMRA) to assess the risk of infection from a single shower aerosol exposure in terms of disability-adjusted life years (DALY) and costs. The model demonstrated that the optimal water heater temperature set point for reducing cost and health risks was 55 °C or 48 °C for a common configuration of an electric water heater used in a hospital setting, using a subclinical infection or clinical severity infection dose response model, respectively. Based on these preliminary results, we expect this modeling framework will be able to provide useful insight into the optimal water heater temperature set point for hospitals based on their specific premise plumbing system configurations and constraints and can inform computational tools used to make site-specific decisions.
Water impactThe importance of understanding risk trade-offs in hospital plumbing systems is significant to minimize the risk of infection or scalding to building inhabitants while reducing energy costs. Models that can help provide less discrepancy among governmental organizations for recommended water heater temperatures would greatly benefit building owners in the design and ongoing operation of their buildings to keep inhabitants safe. |
1. Introduction
Legionella pneumophila (L. pneumophila) is a species of bacteria that can cause the pulmonary disease known as Legionnaires' disease (LD) or the febrile illness, Pontiac fever. LD can be contracted when a person is exposed to bacteria-laden bioaerosols,1 most commonly generated by devices such as water fixtures, cooling towers, spa pools, or other sources.2,3 In 2017, there were 7400 reported cases in the United States, which corresponded to 2.29 cases/100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 persons.4,5 LD is the most frequently identified cause of waterborne disease outbreaks involving drinking water in the United States and is known to be found in building plumbing systems where they can be aerosolized by numerous water fixtures to cause disease.6,7 Outbreaks can also result from non-potable exposures to contaminated aerosols originating from other sources.2 Together, biofilm-associated waterborne pathogens nontuberculous mycobacteria, Pseudomonas, and Legionella cost the US $2.39 billion annually in hospitalizations and deaths.8
000 persons.4,5 LD is the most frequently identified cause of waterborne disease outbreaks involving drinking water in the United States and is known to be found in building plumbing systems where they can be aerosolized by numerous water fixtures to cause disease.6,7 Outbreaks can also result from non-potable exposures to contaminated aerosols originating from other sources.2 Together, biofilm-associated waterborne pathogens nontuberculous mycobacteria, Pseudomonas, and Legionella cost the US $2.39 billion annually in hospitalizations and deaths.8
Over 60 different species of Legionella spp. have been described,9 with the most commonly implicated species being L. pneumophila serogroup 1, which grows at elevated temperatures between 25–45 °C.10 For this reason, a water heater can act as a source or amplifier of L. pneumophila in indoor environments. Existing management guidance, including that of the World Health Organization (WHO), and the National Academies of Sciences, Engineering and Medicine (NASEM) recommend setting water heater temperatures (the water heater “set point”) at 60 °C to kill L. pneumophila bacteria.5,11 However, scalding is a concern at these temperatures.12 Additionally, concerns for increasing sustainability would dictate that the energy cost associated with high water heater temperatures should be minimized. The Consumer Product Safety Commission (CPSC) and the US Department of Energy (DOE) recommend setting water heater temperatures to 49 °C to prevent scalding in addition to minimizing energy costs.13,14 A review by Singh et al. (2020) highlighted values from several national and international guidance documents which covered multiple set point recommendations in this range.15 Subsequently, a debate continues over what the recommended set point temperature(s) is to prevent L. pneumophila growth, reduce scalding risks, and increase energy savings. A quantitative and systematic framework is needed for evaluating these tradeoffs for different plumbing systems and scenarios to support guidance efforts.
Due to its public health importance, regulatory and guidance efforts have focused on LD prevention,16–18 with a focus on healthcare premise plumbing environments19 as they are the setting for transmission of a large portion of LD cases.2 Hospital and residential premise plumbing systems can differ substantially in design, with hospital systems having larger, more complex water systems that can promote Legionella spp. growth if not maintained properly, and also serve susceptible populations who are more likely to contract LD due to underlying health conditions.20 The focus of this work will be primarily on a simplified hospital water system.
The financial burden associated with LD has many contributing factors that can vary greatly between cases. In addition to the loss of life experienced from LD, the infection has a significant cost associated with medical treatment, outbreak investigation, and business closures. It is estimated that $434 million is paid by insurers for medical treatment of LD each year,21 with individual costs varying greatly.22 In addition to the costs of medical treatment, the cost of investigating a suspected outbreak must be considered as it often requires a great deal of effort to locate and confirm the source of an outbreak.22 The economic cost from lost productivity due to business closures at suspected outbreak locations also contributes to the total cost associated with LD, although specific estimates of the dollar value of this cost are not available.21,22
Tap water scalds are a potential public health concern and have been well documented in residential settings.23–26 Approximately 1500 hospital admissions and 50 deaths from scalding due to excessively hot tap water are reported annually in the United States.27 The majority of these cases affect children under 5, people with disabilities, and people over age 65. Patients with a disability and geriatric patients are often unable to remove themselves from excessively hot water, and when grouped with young children account for 85% of hot tap water burns.28 Scalds can be particularly concerning when elderly populations are exposed to showers and bathtubs where prolonged exposure to elevated temperatures can cause significant damage but go unnoticed initially due to their decreased sensitivity to high temperatures.5,28 Specific cases of this have been documented and can result in extended hospitalization or death.24 It is acknowledged that the exact circumstances and causes of a scald injury cannot be fully ascertained based on the available scalding data due to factors such as the abuse of children. In a study where families were questioned about the nature of a child's burn, 15 out of 17 cases were assumed to be accidental and not due to child abuse.24 This aligns with a 2005 study from the UK that found approximately 90% of pediatric burn cases were accidental.29 Public health initiatives have been implemented over the years to reduce preset water heater temperatures in residential settings to lower the risk associated with tap water scalding but were deemed unsuccessful24 or had a statistically significant but small (4%) change in risk reduction while increasing the risk of L. pneumophila.30 Passing legislation to reduce water heater temperatures upon installation in residential settings has been shown to decrease average water heater temperature in some settings,31 decreasing water scalds. A study of hot water scalds after a change in Ontario, Canada building codes to require residential water heaters in new or renovated buildings to be set at 49 °C resulted in a significant decrease in the age-standardized monthly ambulatory scald cases per 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 population of 0.01055 and long-term decrease of 0.19 per 100
000 population of 0.01055 and long-term decrease of 0.19 per 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, but the number of hospitalized cases did not significantly change.32 These residential cases emphasize the importance of considering scalding risk while determining optimal water heater temperature set points to reduce L. pneumophila in both residential and hospital or healthcare settings.
000, but the number of hospitalized cases did not significantly change.32 These residential cases emphasize the importance of considering scalding risk while determining optimal water heater temperature set points to reduce L. pneumophila in both residential and hospital or healthcare settings.
There is a lack of federal laws and regulations around balancing the risk of scalding with the risk of LD. This is described in the NASEM (2019) report highlighting some ambiguity regarding water temperature control guidance.5 The Center for Medicare & Medicaid Services (CMS), which has regulatory authority over hospitals, states that patients should not be in “immediate jeopardy” concerning hot water scalds, which is defined as “access to hot water of sufficient temperature to cause tissue injury”.33 This is interpreted by individual states to correspond to a variety of temperatures. However, this varied interpretation is not inconsistent with true variation in the range of temperatures that can cause tissue damage. Experimental studies on skin burns are understandably rare; using skin from pigs, second degree burns can be achieved in temperatures as low as 44 °C if the skin is exposed for extended periods.34
Globally, various approaches have been taken regarding scalding and Legionella spp. tradeoffs. The Canadian government recommends that residential water heater temperatures be reduced to 49 °C to reduce the risk of scalding and lower energy costs.35 Singh et al. (2020) summarizes findings from 15 guidance documents and interviews of 22 premise plumbing subject matter experts, including nine documents (from the World Health Organization [WHO], US CDC, USEPA, NASEM, Department of Veterans Affairs, European Guidelines, and International Plumbing Code) with recommendations for hot water temperatures >50 °C and most hot water heater temperature recommendations greater than 60 °C for Legionella spp. control.15
In addition to direct health risks like LD and scalding, sustainability has risen as a priority for the built environment. Consequently, there are national efforts to increase water and energy efficiency that can have unintended consequences for public health. As the popularity of green buildings increases, green certification programs such as Leadership in Energy and Environmental Design (LEED) encourage the minimization of water usage. Decreasing water usage is commonly implemented by installing low-flow fixtures or eliminating the use of potable water for landscaping purposes. While decreasing the use of potable water is generally encouraged, it can increase the residence time of the water in the premise plumbing system. These increases in water age have been found to have consequences for the water chemistry, temperature, and microbial growth which can leave energy-efficient buildings more susceptible to L. pneumophila contamination.36,37 One factor contributing to increased microbial concentrations is the rapid loss of disinfectant residual in green buildings. For example, it has been found that 60–91% of the chloramine residual is lost after a stagnation time of only six hours in copper pipes.38,39
Due to competing objectives for managing water in buildings, trade-offs can exist. The current work focuses on hospital premise plumbing systems, with the intention of applying the modeling framework beyond hospital systems with modified input parameters. To evaluate trade-offs in microbial quality (specifically L. pneumophila growth and subsequent risks), energy cost, and scalding risks, we have developed a computational framework for evaluating an optimal water heater temperature set point. The overall risk management goals are to reduce the burdens of illness, injury, and death associated with building water supplies while maintaining an economically viable approach that conserves energy. Weighing these objectives is not always straightforward and a model is designed to provide a framework for judgment by building designers and analysts. The model is not designed to be used as a direct risk communication tool but rather an in silico testbed for evaluating tradeoffs. The goal is for this model is therefore to be able to provide useful insight into the optimal water heater temperature set point for hospitals based on their specific premise plumbing system configurations and constraints. As a result, our objectives are: (1) to develop a conceptual model which incorporates the risk of Legionella infection, the risk of scalding, and the cost of energy associated with a specific water heater set point; (2) to demonstrate the utility of applying such a model using a test case of a premise plumbing system from a design that would be representative of a section of the type of system seen in a hospital; and (3) to identify influential factors and data gaps for making recommendations for optimal water heater set points that balance public health and energy sustainability.
2. Methods
2.1 Model framework
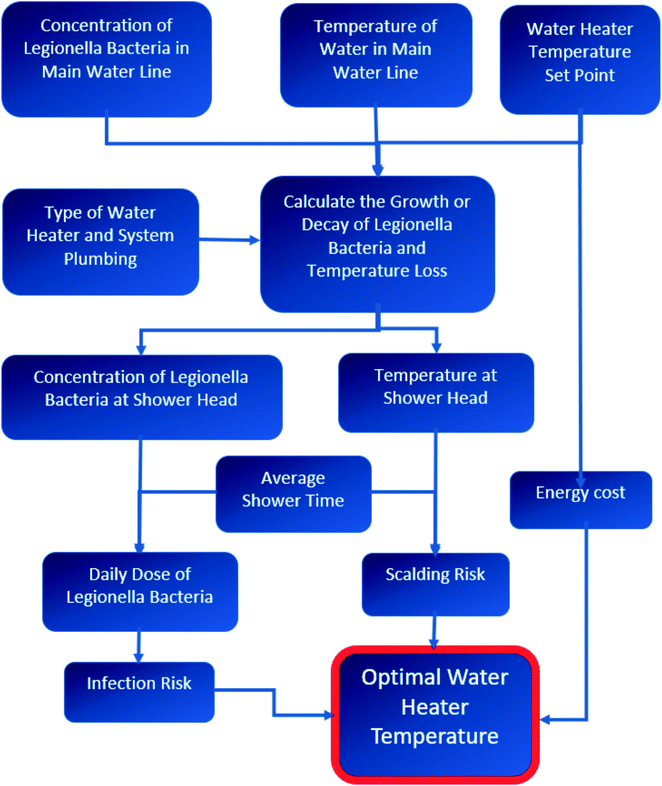
As a starting point, a use-case was developed for a hypothetical hospital room located in the United States that would serve a susceptible hospitalized population, however the generalized model proposed here is not currently regionally- or geographically-specific (although a site- or region-specific model could be adapted from this framework). Our computational framework is composed of three sub-models that are expressed in final terms of daily cost (2020 US dollars per day): (1) L. pneumophila bacteria growth, decay, health risk, and subsequent cost of infection and disease; (2) scalding risk and subsequent cost of burn injuries; and (3) energy cost. All models are normalized to “per day” costs. All models rely upon water temperature calculations throughout a premise plumbing system. The water temperature and concentration of L. pneumophila being dispensed at the showerhead are calculated for various water heater set points scenarios, from 48 °C to 63 °C at intervals of 1 °C. This range was chosen to include a setting lower than the recommended temperature from the DOE and the CPSC, to the highest temperature that Legionella spp. has been isolated from water.40 However, the water heater used as an exemplar in this model is advertised to deliver a temperature range from 43.3 °C to 76.7 °C.41 A conceptual flow chart of the described methods is shown in Fig. 1 to help guide the reader through the model.2.2 Simplified hot water plumbing system chosen for analysis
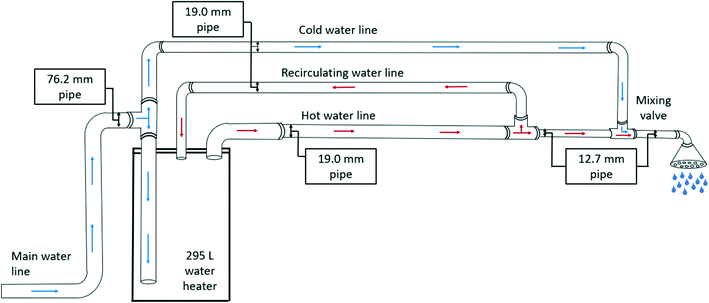
Building plumbing systems are extremely heterogeneous, therefore it is not possible to designate a single system that is representative of every situation in this analysis. The example chosen premise plumbing system represents a simplified section of what might exist in the patient rooms of a hospital that will provide patients with hot water for bathing and showering.42 It is common in the healthcare setting to have at least two large water heaters to meet the building's peak demand. This model is comprised of a single 316 L water heater with a 295 L storage rating41 and a hot water outlet pipe 3/4′′ in diameter. Subsequent branches that lead to the outlet at the showerhead are 1/2′′ diameter.41,43 Only one branching pipe leading to a showerhead is considered in this model, any other branching pipes are ignored. A full recirculating line 3/4′′ in diameter is assumed at the junction of the 1/2′′ branching pipe to continually carry water back to the water heater. A cold-water line leading to a mixing valve before the showerhead would also be expected but is excluded for this model. A schematic of the selected system layout can be seen in Fig. 2.Large hospitals might choose a steam system instead of water heaters.44 The size of the water heaters and the quantity needed to meet peak demand varies for each building and is calculated on a case by case basis.45 A water heater of the size chosen (295 L) would serve approximately five showers of 59 L each to meet peak demand. This would not be considering other fixtures on the floor such as sinks or dishwashers. Two of these water heaters would be optimal for a small hospital floor. Water heaters of this size commonly have 3/4′′ diameter pipe outlets to disperse the hot water throughout the building, so that is why this diameter was chosen.41 This water heater and pipe system is large enough to meet peak demand for a floor with 5–10 showers. The sections below describe heat loss throughout the premise plumbing system and water heater, with an assumption made that heat is not lost through the walls of the water heater.
2.3 Water temperature in the water heater
A one-dimensional, multi-node model was selected to approximate the temperature change throughout different sections of the premise plumbing system.46 This method divides the water heater into twelve equal nodes (i = 1–12) stacked on top of each other vertically (Fig. 3). This aligns with standing water heater models (a common configuration in the US) and the stratification experienced will be replicated by the nodes that are assumed to be completely mixed at each timestep.47 This model for the water heater is similar to a one-dimensional plug flow model with the exception that there is an assumed percentage of mixing between nodes and intermittent flow is ignored. In this water heater, water enters the system from the mainline at the lowest node, and water exits to the hot water line from the highest node. eqn (1) represents the temperature of each node based on the flow of water at each timestep. These equations were modified from their original form in Kleinbach et al. (1993)46 as discussed in ESI† section 1 to allow for implementation in Python.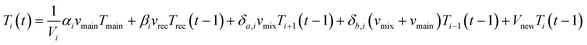 | (1) |
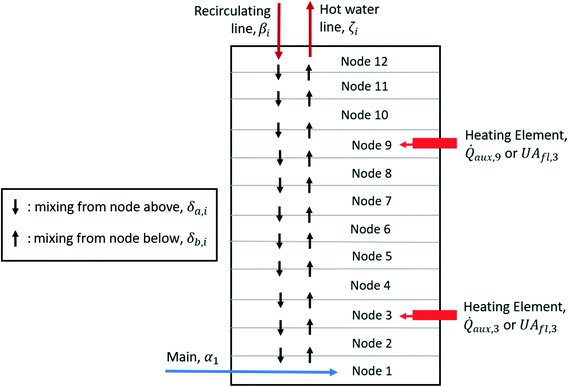 | ||
| Fig. 3 Water heater schematic divided into nodes for temperature calculations following methods used in Kleinbach et al. (1993).46 | ||
Once the temperature in each node has been calculated, the average temperature in the tank is measured to determine whether the heating element is on at each timestep. This water heater has two heating elements of equal power placed at the third and ninth nodes. Both are either fully on or fully off. When the heating elements are on, they add 5500 J of heat to the node at each timestep. This energy input is represented by Qi in eqn (2) and is equivalent to a 0.05 °C rise in temperature for a 26.33 L node. This is equivalent to 5500 W at that node.41 When the heating elements are off, it is assumed that a small amount of heat is lost through the elements.46 UAi is the heat loss equal to a 0.005 °C drop in temperature, or 550 W (ESI† section 1). The change in the node temperature described by eqn (2) is accounted for at each timestep after the initial temperature calculation. It is assumed that no heat is lost through the walls of the water heater.
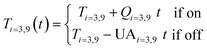 | (2) |
2.4 Water temperature in the premise plumbing pipes
Heat loss as water flows through the pipes is modeled using one-dimensional plug flow where heat loss occurs radially. Each pipe was divided into 1 m sections for calculations at each time step and complete mixing within each section of the pipe is assumed. The pipes will experience turbulent flow when water is not stagnant due to their Reynolds number being greater than 4000. Water exiting the water heater is distributed to the pipe system and flows at a constant velocity of 3.04 m s−1 (ESI† section 2). The hot water line 3/4′′ in diameter is assumed to have rubber pipe insulation with a thickness of 1/2′′. The branching pipe will have rubber pipe insulation with a thickness of 1/2′′ for cases where branching pipe insulation is present as specified in Table 1. The 1/2′′ rubber insulation has a thermal conductivity 0f 0.16 W mK−1.50 Insulation thickness on the recirculating pipe is sufficient enough that the temperature loss is not greater than 3.3 °C for a pipe length of 24 m.51,52 The water velocity and insulation are changed during the scenario analysis described in section 3.4.| Scenarios | Decision analysis result | Results at optimum set point | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Case number | Branch insulation | Pipe length | Water velocity | Dose response parameter | Optimal temperature set point | Energy cost USD (5th, 50th, 95th) | Microbial risk cost USD (5th, 50th, 95th) | Median scald cost USD (5th, 50th, 95th) | Total cost USD (5th, 50th, 95th) | Median microbial risk (5th, 50th, 95th) | Scald risk (no injury, injury, necrosis)a |
| a Proportion of scald model iterations that fall within the injury category. | |||||||||||
| Case 0 | Yes | 26 m | 3.04 m s−1 | Subclinical | 56 °C | 2.50 | 3.69 | 0.00 | 7.54 | 1.58 × 10−5 | 1.00 |
| 3.82 | 84.43 | 0.00 | 88.31 | 2.82 × 10−4 | 0.00 | ||||||
| 5.83 | 7356.96 | 0.00 | 7360.23 | 3.64 × 10−3 | 0.00 | ||||||
| Case 1 | Yes | 52 m | 3.04 m s−1 | Subclinical | 56 °C | 4.76 | 3.70 | 0.00 | 11.19 | 1.61 × 10−5 | 1.00 |
| 7.26 | 82.89 | 0.00 | 90.13 | 2.78 × 10−4 | 0.00 | ||||||
| 11.08 | 6912.72 | 0.00 | 6917.08 | 3.80 × 10−3 | 0.00 | ||||||
| Case 2 | Yes | 26 m | 1.52 m s−1 | Subclinical | 55 °C | 2.43 | 7.78 | 0.00 | 11.76 | 3.46 × 10−5 | 1.00 |
| 3.66 | 185.37 | 0.00 | 188.62 | 6.30 × 10−4 | 0.00 | ||||||
| 5.68 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 060.44 060.44 |
0.00 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 063.78 063.78 |
9.06 × 10−3 | 0.00 | ||||||
| Case 3 | Yes | 26 m | 1.90 m s−1 | Subclinical | 56 °C | 2.50 | 5.97 | 0.00 | 9.80 | 2.64 × 10−5 | 1.00 |
| 3.81 | 141.37 | 0.00 | 145.33 | 4.69 × 10−4 | 0.00 | ||||||
| 5.82 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 694.75 694.75 |
0.00 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 698.88 698.88 |
6.35 × 10−3 | 0.00 | ||||||
| Case 4 | Yes | 52 m | 0.30 m s−1 | Subclinical | 55 °C | 4.30 | 118.85 | 0.00 | 126.03 | 5.15 × 10−4 | 1.00 |
| 6.49 | 2903.31 | 0.00 | 2911.33 | 9.95 × 10−3 | 0.00 | ||||||
| 10.08 | 210![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 791.99 791.99 |
0.00 | 210![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 798.13 798.13 |
1.24 × 10−1 | 0.00 | ||||||
| Case 5 | Yes | 52 m | 1.52 m s−1 | Subclinical | 55 °C | 4.59 | 8.08 | 0.00 | 15.35 | 3.45 × 10−5 | 1.00 |
| 6.92 | 185.23 | 0.00 | 192.59 | 6.31 × 10−4 | 0.00 | ||||||
| 10.76 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 313.66 313.66 |
0.00 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327.57 327.57 |
8.95 × 10−3 | 0.00 | ||||||
| Case 6 | Yes | 26 m | 0.30 m s−1 | Subclinical | 56 °C | 2.42 | 125.61 | 0.00 | 129.21 | 5.26 × 10−4 | 1.00 |
| 3.69 | 2897.83 | 0.00 | 2902.13 | 9.83 × 10−3 | 0.00 | ||||||
| 5.63 | 195![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685.96 685.96 |
0.00 | 195![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 690.37 690.37 |
1.18 × 10−1 | 0.00 | ||||||
| Case 7 | No | 26 m | 3.04 m s−1 | Subclinical | 59 °C | 2.72 | 3.62 | 0.00 | 7.83 | 1.55 × 10−5 | 1.00 |
| 4.17 | 82.05 | 0.00 | 86.25 | 2.83 × 10−4 | 0.00 | ||||||
| 6.39 | 8068.23 | 0.00 | 8071.15 | 3.69 × 10−3 | 0.00 | ||||||
| Case 8 | Yes | 26 m | 3.04 m s−1 | Clinical | 48 °C | 1.88 | 0.02 | 0.00 | 2.14 | 8.17 × 10−8 | 1.00 |
| 2.87 | 0.31 | 0.00 | 3.46 | 8.02 × 10−7 | 0.00 | ||||||
| 4.42 | 13.52 | 0.00 | 16.65 | 7.78 × 10−6 | 0.00 | ||||||
| Case 9 | Yes | 52 m | 3.04 m s−1 | Clinical | 48 °C | 3.56 | 0.03 | 0.00 | 3.93 | 9.63 × 10−8 | 1.00 |
| 5.44 | 0.35 | 0.00 | 6.21 | 9.38 × 10−7 | 0.00 | ||||||
| 8.40 | 13.92 | 0.00 | 19.53 | 8.03 × 10−6 | 0.00 | ||||||
| Case 10 | Yes | 26 m | 1.52 m s−1 | Clinical | 48 °C | 1.87 | 0.04 | 0.00 | 2.25 | 1.38 × 10−7 | 1.00 |
| 2.86 | 0.64 | 0.00 | 3.84 | 1.67 × 10−6 | 0.00 | ||||||
| 4.40 | 27.50 | 0.00 | 30.18 | 1.70 × 10−5 | 0.00 | ||||||
| Case 11 | Yes | 26 m | 1.90 m s−1 | Clinical | 48 °C | 1.87 | 0.04 | 0.00 | 2.21 | 1.14 × 10−7 | 1.00 |
| 2.86 | 0.49 | 0.00 | 3.68 | 1.28 × 10−6 | 0.00 | ||||||
| 4.41 | 23.18 | 0.00 | 26.43 | 1.37 × 10−5 | 0.00 | ||||||
| Case 12 | Yes | 52 m | 0.30 m s−1 | Clinical | 55 °C | 4.21 | 0.20 | 0.00 | 5.71 | 6.32 × 10−7 | 1.00 |
| 6.49 | 4.66 | 0.00 | 11.78 | 1.18 × 10−5 | 0.00 | ||||||
| 9.97 | 229.80 | 0.00 | 238.22 | 1.34 × 10−4 | 0.00 | ||||||
| Case 13 | Yes | 52 m | 1.52 m s−1 | Clinical | 48 °C | 3.53 | 0.05 | 0.00 | 4.08 | 1.59 × 10−7 | 1.00 |
| 5.40 | 0.68 | 0.00 | 6.65 | 1.81 × 10−6 | 0.00 | ||||||
| 8.33 | 31.33 | 0.00 | 36.82 | 1.82 × 10−5 | 0.00 | ||||||
| Case 14 | Yes | 26 m | 0.30 m s−1 | Clinical | 56 °C | 2.42 | 0.21 | 0.00 | 3.51 | 6.63 × 10−7 | 1.00 |
| 3.69 | 4.55 | 0.00 | 8.51 | 1.17 × 10−5 | 0.00 | ||||||
| 5.62 | 299.61 | 0.00 | 302.36 | 1.34 × 10−4 | 0.00 | ||||||
| Case 15 | No | 26 m | 3.04 m s−1 | Clinical | 48 °C | 1.88 | 0.02 | 0.00 | 2.14 | 8.23 × 10−8 | 1.00 |
| 2.87 | 0.31 | 0.00 | 3.45 | 8.01 × 10−7 | 0.00 | ||||||
| 4.42 | 13.75 | 0.00 | 16.98 | 7.91 × 10−6 | 0.00 | ||||||
As the water moves through the pipes, heat is lost through radial convection. The new temperature is calculated using Newton's law of cooling (eqn (3)) and the formula for heat capacity (eqn (4)), as discussed in ESI† section 3. Q is the heat transfer [W], U is the heat transfer coefficient for a multi-layer pipe [W m−2 K−1] (ESI† section 4), T(x) is the temperature of the section being analyzed [°C], and Tenv is the air temperature inside the building of interest surrounding the premise plumbing system, assumed to be a uniform distribution ranging from 20 °C to 27 °C.53,54cp is the specific heat of water [J kg−1 K−1] and m is the mass of water inside the pipe section [kg].
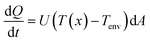 | (3) |
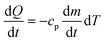 | (4) |
Solving for the temperature in pipe section n (Tpipe,n) results in eqn (5). ρ is the density of water [kg m−3], ν is water velocity [m s−1], and D is the diameter of the pipe [m]. The values for these parameters are summarized in Table S2.†
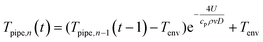 | (5) |
2.5 Free chlorine residual concentrations throughout the system
The free chlorine concentration is first calculated in the nodes of the water heater based on the fluid dynamics of the system and water temperature. The concentration is calculated at each timestep using eqn (6).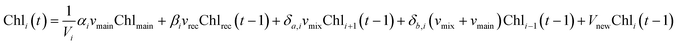 | (6) |
Chli is the free chlorine concentration in each node (i = nodes 1–12) [mg L−1], and Chlrec is the free chlorine concentration of the water in the recirculating line [mg L−1]. Chlmain is the free chlorine concentration in the water entering the system from the main line ranging from 0.01 to 4 mg L−1 of chlorine.55
Assuming first-order kinetics, the chlorine concentration throughout the plumbing system (Chl) will decay due to temperature and is calculated at each point using eqn (7). The decay rate of chlorine due to temperature (kChl) is calculated using the Arrhenius equation, which considers total organic carbon concentrations in the system that were estimated to be between 1 and 3 mg L−1 (ESI† section 5). Chl0 is the initial chlorine concentration [mg L−1].
| Chl(t) = Chl0e−kchlt | (7) |
2.6 Legionella pneumophila concentration throughout the system
L. pneumophila concentrations are modeled as a function of fluid flow, chlorine concentration, temperature, and time throughout the system (ESI† section 6). The L. pneumophila concentration is first calculated in the nodes of the water heater based on the fluid flow of the system at each timestep using eqn (8).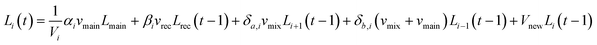 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 CFU per L, the maximum culturable concentration observed in an experiment where L. pneumophila was allowed to remain in stagnant water for 21 days, to avoid a scenario of unrealistic unconstrained growth.56 This information was combined with kinetic constants (ESI† section 7) as a function of chlorine residual, time, and temperature in eqn (9). Cp is the concentration of planktonic L. pneumophila [CFU per L], ktemp is the rate of growth or inactivation due to water temperature for both planktonic and sloughed L. pneumophila [s−1], and kp,Chl is the rate of inactivation for planktonic L. pneumophila due to the chlorine concentration [s−1]. Cp,0 is the initial concentration of planktonic L. pneumophila [CFU per L].
17 CFU per L, the maximum culturable concentration observed in an experiment where L. pneumophila was allowed to remain in stagnant water for 21 days, to avoid a scenario of unrealistic unconstrained growth.56 This information was combined with kinetic constants (ESI† section 7) as a function of chlorine residual, time, and temperature in eqn (9). Cp is the concentration of planktonic L. pneumophila [CFU per L], ktemp is the rate of growth or inactivation due to water temperature for both planktonic and sloughed L. pneumophila [s−1], and kp,Chl is the rate of inactivation for planktonic L. pneumophila due to the chlorine concentration [s−1]. Cp,0 is the initial concentration of planktonic L. pneumophila [CFU per L].| Cp(t) = Cp,0e(ktemp+kp,chl)t | (9) |
2.7 Modeling the biofilm sloughing throughout the system
The amount of L. pneumophila in the system due to biofilm sloughing at the time that the shower is turned on (ts) is calculated by eqn (10) and (11).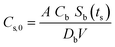 | (10) |
| Cs(t) = Cs,0e(ks+kb,ChlChl+ktemp)ts | (11) |
These equations collectively allowed for computation of the temperature, chlorine residual concentration, decay rate of chlorine due to temperature, inactivation rate of L. pneumophila due to temperature and chlorine, and final L. pneumophila concentration from planktonic and sloughed biofilm to be simulated at all points throughout the system at each timestep (1 s). The temperature, chlorine concentration, planktonic L. pneumophila, and biofilm L. pneumophila were initialized for a 24 hour period prior to the Monte Carlo for cost analysis (ESI† section 8).
2.8 QMRA model
The temperature and L. pneumophila concentration at the showerhead is used in a quantitative microbial risk assessment (QMRA). QMRA is a computational method for assessing the risk associated with different conditions of exposure to infectious microorganisms.61 The QMRA model used here assesses the daily risk of infection from shower aerosol exposure in terms of monetary cost, as determined in the case of health risks through a relationship to disability-adjusted life years (DALYs). This is then combined with models to assess the cost associated with water heater energy consumption and the cost associated with different outcomes related to scalding risk.A previously derived QMRA model for L. pneumophila was used from Hamilton et al. (2018).62 The dose is calculated using the concentration of L. pneumophila at the showerhead and the shower time (eqn (12)–(14)).
| Lair(ts) = CLeg(ts)∑10i=1CaeroVaero∑10i=1FD | (12) |
| Lacc(ts) = Lair(ts − 1)e−dits + Lair(ts) | (13) |
| dose = ∑LaccBts | (14) |
The total L. pneumophila concentration at the fixture, CLeg, is the sum of the planktonic L. pneumophila Cp and the sloughed L. pneumophila Cs over the duration of the shower. The dose is calculated using equations by multiplying the L. pneumophila concentration CLeg [CFUs per L s], the concentration of aerosols Caero [# aerosols per m2] (i.e. the number of water droplets of diameter i in each respirable size bin 1–10 μm, with the majority of respirable droplets falling in the 1–5 μm range), the volume of aerosols Vaero [L per # aerosols], the fraction of L. pneumophila that partition to each of the aerosol diameters, F, the alveolar deposition efficiency, D, the rate of inhalation, B [m3 min−1], the aerosol removal rate, di,60 and the duration of the shower (ESI† section 9), ts [s].63 The L. pneumophila concentration released into the air, Lair (ts), is used to calculate an air concentration assuming accumulation of aerosols, Lacc (ts), and removal due to ventilation at a rate of di which was found using a weighted average of aerosol size63 and aerosol decay rate.60 The accumulated concentration of aerosols is used with the average breathing rate to determine the accumulating dose that is inhaled at each timestep.
Two dose response models have been previously used to describe L. pneumophila subclinical infection or clinical severity infection, where a subclinical infection would be a case not requiring seeking of medical attention or potentially Pontiac fever, and a clinical severity infection would be a case requiring seeking of healthcare resources.64,65 The dose response parameter for subclinical infection (ks) and clinical severity infection (kc) were used and were modeled as lognormal distributions. For subclinical infection, the risk of infection (Riskinf) can be calculated with eqn (15). The risk of illness from subclinical infection can be calculated from the risk of infection modified to be the risk of illness using the morbidity ratio for elderly individuals (MRe) in eqn (16).66 For the clinical dose response, the risk of illness can be calculated directly from the dose response parameter for clinical severity infection (kc) and the dose of L. pneumophila with eqn (17). The use of the clinical severity endpoint as representative of illness is supported by an analysis that used a dose response model with the same order of magnitude median effective dose (N50) used to reproduce epidemic curves that aligned with well-documented LD outbreaks.67
| Riskinf = 1 − e−ks dose | (15) |
| Riskill = Riskinf MRe | (16) |
| Riskill = 1 − e−kc dose | (17) |
The cost associated with the risk of illness for each daily showering event, Cillness, was calculated in eqn (18) and (19). An approach to monetizing a DALY was taken as described in Robinson and Hammitt (2019),68 making use of the value of a statistical life year (VSLY). A VSLY is derived from the value of a statistical life (VSL), which is not the value that is placed on saving an identified life with certainty but rather is indicative of an individuals' willingness to exchange money for a small change in their own risk.68 A recent (2020) estimate for the United States VSL corrected for inflation and changes in real income with a low, central, and high estimate of 5.3 M, 11.4 M, and 17.4 M USD, respectively was used.69 In order to calculate a VSLY from a VSL, the VSL must be divided by an estimate of the remaining life years (remaining life expectancy) used to estimate the underlying VSL estimate, not the remaining years applicable to the impact of the policy since the idea is to convert a VSL to an equivalent VSLY. A simplifying assumption was made that a constant VSLY was applicable and therefore that the value of mortality risk reduction increases with life expectancy, i.e. decreases with age, averaging health status over future life years; the limitations of this assumption are discussed further elsewhere.68,70,71 The estimates for VSL derived by the US Department of Health and Human Services69 were derived from a meta-analysis of VSL values published in the literature,72 and therefore, it was not possible to ascertain a single life expectancy value. To compute a remaining life expectancy, the difference was taken between the US average life expectancy in the year the meta-analysis was performed (2013) with a point estimate of 78.8 years73 and a normal distribution computed for the age of the living adult (>18 years) population in December 2013 with a mean of 36.0 years and standard deviation of 18.7 years.74 The disability adjusted life year for LD (DALY) of 0.97 years was used from a study of a Netherlands population and assumed to be representative of a US population.62 QMRA parameters are summarized in Table S10.†
| Cillness = Riskill × DALY × VSLY | (18) |
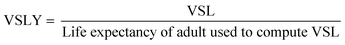 | (19) |
2.9 Scalding model
A set of simple linear regressions for scalding risk as a function of water temperature and shower time were developed based on data from Moritz and Henriques (1947) (ESI† section 10). Burns from Moritz and Henriques (1947) were categorized by epidermal injury and epidermal necrosis for humans and pigs. Human data were used, and the regressions were employed to define temperature–time combinations that resulted in each injury type (no injury, injury, or necrosis). Based on the temperature computed at the point of use (at the showerhead) and the shower duration, an injury category was assigned along with a corresponding cost. The range of temperatures considered in this model ranged from 48 °C to 63 °C. The shower times were modeled as a truncated normal distribution with a mean of 7.8 minutes and a standard deviation of 1.2 minutes.75 The reaction time, i.e., the time an elderly person would be exposed to scalding hot water before moving away from the water, was modeled as a uniform distribution from one to five seconds.The daily scalding costs (Cscalding) were approximated as uniform distributions in 2020 US dollars (USD) that ranged from 142–222 USD for a clinical visit for an injury, and from 629–863 USD for an emergency room visit (necrosis injury category).76 There is uncertainty associated with these values as they can vary based on insurance types, geographic region, individual susceptibilities, and the care provider.
2.10 Energy cost model
The daily energy cost (Cenergy) used in this model was calculated in USD per day for a storage tank water heater using the Department of Energy's (DOE) method for estimating costs and efficiency of water heaters.77 This was done by first calculating the amount of water used and multiplying by the difference in water temperature from the desired set point (Qdegree) as shown in eqn (20) [L per day per K]. The average water use per capita was estimated as the national average of 291.47 L (77 gallons) per day.78 However, this includes both cold and hot water. The U.S. Geological Survey estimates that the low end of shower water usage to be two gallons of water per minute.79 Assuming an average shower time of 7.8 minutes, the average hot water usage for showering (Qin) is approximately 59 L per day. Therefore, an additional 59 L per day will need to enter the water heater from the main line to replenish the water used for the shower. This quantity is multiplied by the difference between the temperature set point (Setpt) and the main line temperature (Tmain). The cost to heat the water that has cooled in the recirculating line was also considered. The volume of water that needed to be reheated was calculated from the flow rate in the recirculating line over 24 hours (Qrec). The difference in temperature that the water needed to be reheated was calculated from the difference between the set point and the water temperature at the end of the recirculating line (Tend).The cost to heat a liter of water by one degree (cdegree liter) is calculated in eqn (21). The price per kW h (PkW h) varies by region across the US for residential energy usage with the average from the US Energy Information Administration (EIA) being 13.04 cents per kW h in 2019.80 The energy factor (EF) is a standardized metric used for the energy efficiency of different appliances. It is calculated as a ratio of the theoretical energy use required during a 24 hour period over the actual energy use of the appliance. For water heater tanks this varies between 0.904 and 0.95, with some manufacturers of electric heaters claiming higher values.81 A higher EF corresponds to a more efficient water heater. For this model, the EF was modeled as a uniform distribution ranging from 0.904 to 0.95. cp is the specific heat of water in J kg−1 K−1 and is multiplied by the conversion factor from Joules to kilowatt hours [2.77 × 10−7 kW h J−1] to reach cp units of kW h kg−1 K−1.
The daily energy cost (Cenergy) is calculated in eqn (22) with the cost to heat a liter of water by one degree (cdegree liter) multiplied by the amount of water used with temperature difference (Qdegree).This temperature will vary based on the geographical region the premise plumbing system is in, thus, the energy cost will change greatly based on the difference between the main water line and the water heater set point. Energy parameters are summarized in Table S12.†
| Qdegree = Qin(Setpt − Tmain) + Qrec(Setpt − Tend) | (20) |
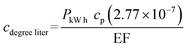 | (21) |
| Cenergy = cdegree literQdegree | (22) |
2.11 Integration of infection risk, scalding risk, and energy cost models
The total cost for each water heater setpoint was calculated with eqn (23). Once the total cost for each set point was calculated, the minimum cost was selected from the array.| Ctotal = Cinfection + Cscalding + Cenergy | (23) |
2.12 Scenario analysis and sensitivity analysis
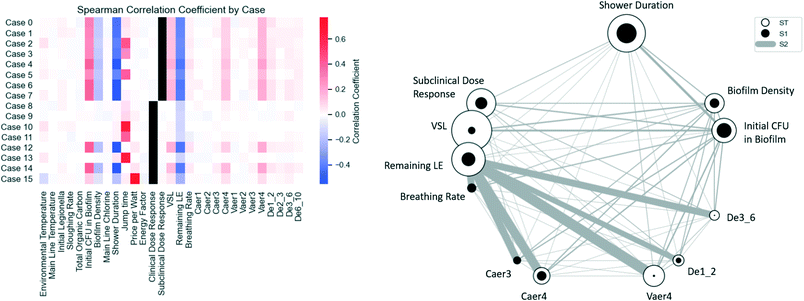
To investigate various scenarios for varying the branching pipe insulation, pipe length, water velocity, and dose response parameter, 15 additional test cases were considered (Table 1). A sensitivity analyses was conducted to examine the impact of individual variables (input–output correlations using Spearman rank correlation coefficients) for all cases. Additionally, for case 0 (insulation of the branch pipe, 26 m long recirculating line, 3.04 m s−1 velocity of water, and subclinical dose response parameter), interactions between variables and their impact on the model output was analyzed using a global Sobol sensitivity analysis. The Spearman rank correlation coefficient was calculated using the Spearmanr function from the stats package in Python. A Spearman rank correlation coefficient ranges from −1 to 1, indicating that parameters closer to these limits have a strongly negative or positive correlation in ranks whereas a value of zero would indicate no meaningful relationship. Parameters with p values less than 0.05 were determined to be statistically significant. The Sobol global sensitivity analysis was performed with the SALib package in Python.82 For each variable that was represented as a distribution on the model, the total, first-order, and second-order indices were calculated. Total-order indices (ST) account for the influence of a single variable as well as higher-order effects over the entire parameter space. First-order indices (S1) measures the influence of a single variable on the output and are displayed by the filled circles near each variable name. Second-order indices (S2) measures the contribution of interactions to the output as displayed by the thickness of the gray connecting line between two variables. Higher values of sensitivity indices represent a greater influence of the parameter(s) on the model output. Variables below the threshold value of 0.005 in the SALib package were considered non-influential and were not displayed.2.13 Computational specifications
All simulations were conducted in Python v 3.6.8. Monte Carlo simulations were conducted with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations, a 24 hour model initialization period, and using random sampling. Several Python libraries were used including torch, torch.nn, torchdiffeq (odeint), matplotlib, pyplot, matplotlib.patches (patch, math), torch.distributions, time, typing, pickle, numpy, pandas, seaborn, os, scipy, SALib.sample (saltelli), SALib.analyze (sobol), SALib.tesst_functions (Ishigami), itertools, math (pi), and matplotlib.legend_handler (HandlerPatch) (see https://github.com/Hamilton-Lab-ASU/Water-Heater).
000 iterations, a 24 hour model initialization period, and using random sampling. Several Python libraries were used including torch, torch.nn, torchdiffeq (odeint), matplotlib, pyplot, matplotlib.patches (patch, math), torch.distributions, time, typing, pickle, numpy, pandas, seaborn, os, scipy, SALib.sample (saltelli), SALib.analyze (sobol), SALib.tesst_functions (Ishigami), itertools, math (pi), and matplotlib.legend_handler (HandlerPatch) (see https://github.com/Hamilton-Lab-ASU/Water-Heater).
Differential equations were solved using the 5th order Dormand–Prince method, an adaptive step ODE solver with a relative tolerance limit of 0.0001 and absolute tolerance limit 0.01.83 We implement ODE equations using PyTorch and solve these equations using the “torchdiffeq” package.84 This architecture allows for parallel processing of thousands of simulations at once, GPU acceleration, and end-to-end differentiability. In particular, our system's differentiability allows users to tune simulation parameters to real-world data using gradient descent. This enables integration and joint optimizations with other machine learning systems and neural differential equations.85
3. Results
3.1 Simulation of conditions throughout the premise plumbing system
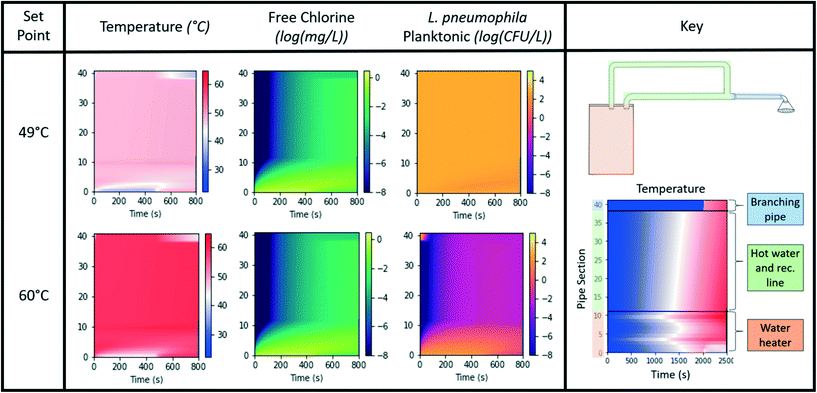
The temperature, chlorine, planktonic L. pneumophila concentration, sloughed (biofilm-associated) L. pneumophila concentration, and remaining L. pneumophila in the biofilm were calculated throughout the system for all simulated time points for a base case (case 0) as well as different combinations of system parameters (case 1–15) (ESI† section 13). The values for the temperature, chlorine, and planktonic L. pneumophila concentration were displayed over time in the heatmaps in Fig. 4 for case 0 for select water heater set points to demonstrate trends. As the water heater temperature set point was increased, the temperatures throughout the system increase. Despite the variation in set point from 48 °C to 63 °C, free chlorine residual concentrations throughout the system were all at low concentrations until chlorinated water from the main line entered as the shower turned on (ts = 1). The manufacturer-reported lower limit of the analytical range for some commonly used spectrophotometric methods for free and/or total chlorine in practice is approximately 0.02 mg L−1 (low range kits) to 0.2 mg L−1 (high range kits), with measurements below this range having a greater associated error and therefore indicating some potential challenges with measuring very low chlorine concentrations in practice.86 The concentration of L. pneumophila in both the planktonic form and within the biofilm decreased as the water heater set point was increased over the range of set points. The planktonic L. pneumophila concentrations remain relatively constant at a set point between 48 °C and 54 °C, but will decrease rapidly in the heated regions ≥60 °C. Similarly, the concentration in the biofilm also rapidly decreases with an increase in temperature. The majority of the L. pneumophila in the system is originating from the biofilm rather than the planktonic state (the ratio of planktonic to biofilm ranges from ∼1.6% to 2.4% in the current model), consistent with estimates of about only 5% of microbial cells thought to exist in the planktonic state in a pipe.87 The branching pipe will be stagnant until the shower is turned on and consequently, the temperature in the branch is more isolated and consequently less impacted by the set point temperature until the shower is turned on. The biofilm residing on the inner surfaces of the water heater was not considered due to a high degree of heterogeneity and complexity related to biofilms within the water heater.3.2 Identification of optimal water heater set point
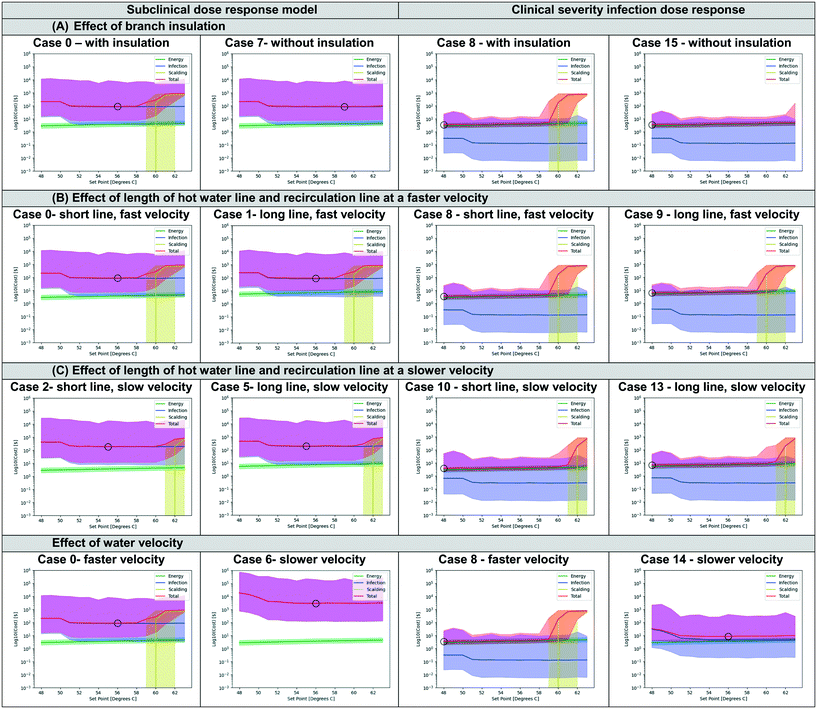
The parameters of the plumbing system calculated throughout the model were used to calculate the costs of infection, energy usage, and scalding per showering event as shown in Fig. 5 for an elderly hospital room occupant for each scenario. The total cost was calculated from the sum of these values for subclinical and clinical dose response parameter scenarios. The optimal water heater set point corresponds to the minimum total cost for each set of conditions. The optimal water heater temperature set point based on the minimum total cost for each case is shown in Table 1. Optimum set points ranged from 48 °C to 59 °C for all cases.A large difference in optimal set point was observed depending on the choice of dose response model (subclinical or clinical severity infection) (Fig. 5). The use of a subclinical infection dose response model generally resulted in higher optimal setpoints (55–59 °C) due to a more conservative treatment of the health endpoint (any infection vs. an infection requiring clinical attention) and therefore in the cost calculations will result in a prioritization of infection risks compared to the other considerations. Therefore, for the case of subclinical dose response, the infection cost is the driver of the total cost, whereas the energy cost is the driver of total cost in the scenario where the clinical dose response parameter is used. For the base case scenario (case 0), optimum set points were determined to be 56 °C if using a subclinical dose response model and 48 °C if using a clinical severity dose response model (case 8). These had median cost values of 88.31 USD and 3.47 USD respectively. The costs for the subclinical dose response parameter ranged from 86.25–2902 USD while the costs for clinical dose response ranged from 3.47–11.73 USD. This is expected due to the more conservative treatment costs associated with subclinical infection and emphasizes the importance of the choice of dose response parameter for the scenario of interest.
3.3 Scenario analysis for multiple cases and sensitivity analysis for case 0
3.4 Scenario analysis
The scenario analysis varied several parameters determined to be uncertain (Table 1) including the branch insulation (insulated vs. not insulated), length of the recirculating line (26 or 52 m), the velocity of water in the pipes (0.30 to 3.04 m s−1), and dose response model (subclinical or clinical severity infection). A comparison of select scenarios is shown in Fig. 5 for effects of changing the branch pipe insulation (Fig. 5A), varying the length of the hot water line and recirculating line (Fig. 5B and C), and varying the water velocity (Fig. 5D).Insulation on the branching pipe leading to the shower has the greatest effect on the scalding cost. Removing the insulation from the branch will drastically decrease the scalding risk for the proposed model (Fig. 5A). The length of the pipe and the recirculating line will also influence the energy cost. As the water in the pipe has increasing time to cool down, the water heater must use more energy to heat the recirculated water back to the set point temperature (Fig. 5B). At slower water velocities, the infection cost increases in addition to the energy cost for longer pipes (Fig. 5C). Slower water velocity increases the time water spends in the pipe and recirculating line and the water can reach lower temperatures that are better for L. pneumophila growth. The increased L. pneumophila growth increases the infection cost (Fig. 5D). As noted in section 3.2, the dose response parameter chosen will have the greatest impact on determining which variable has the greatest influence over the optimal set point. The selection of a subclinical dose response parameter increases the cost of infection, which will be greater than the energy cost and unaffected by the risk of scalding until temperatures of 59 °C. Using the clinical dose response parameter lowers the cost of infection to be at the same order of magnitude or lower than the energy cost, making energy cost the most influential variable. As a result, it is recommended that the dose response chosen should be carefully considered prior to conducting a decision analysis. The importance of considering multiple dose response models has previously been emphasized for QMRA of other pathogens.88
4. Discussion
The physical system modeled was a simplified model of what might be found in a hospital plumbing system leading to a patent room. A water heater, hot water line, recirculating line, and branching pipe were included for analysis. The cold water line and any mixing valves were excluded from this model as a simplifying assumption but will be necessary for a full consideration of risk; incorporating mixing would also presumably lower the scalding risk even at higher temperatures but could present opportunities for growth on the surfaces of valve components or the introduction of zones of stagnation into the system that will vary depending on the placement of the valve.89–91 The branching pipe from the hot water line to the shower was the only branching pipe considered, although many other lines leading to other showers, sinks, and equipment would also be present in a real building. The water heater chosen is large and could be used in a hospital setting, although many buildings will have more than one large water heater in service to meet peak demand. Additionally, some hospitals may use point-of-use heating devices or thermostatic devices that limit temperature ranges to below scalding temperatures. The impact of different water heater types, valves, and pipe materials was not considered. However, with additional information, this model can presumably be scaled up and applied to a more complete hospital premise plumbing configuration but requires validation in order to do so. Demand information from a residential setting was used for describing individual patient water demand in this model and may not fully describe hospital water demand; water demand can be modified if specific information is available for a particular hospital or other setting.Sufficient information is not yet available to quantitatively predict concentrations of L. pneumophila as a combination of water quality factors. It is presumed that different water qualities such as soft vs. hard water, warm vs. cold water, or surface water vs. groundwater sources would impact quality and therefore the propensity for Legionella growth. In areas where hard water is an issue, water softeners may also be employed which will affect water chemistry as well. Investigation of the effects of softeners was beyond the scope of the current modeling effort, but recent data from an Arizona study of a commercial building indicated potential removal of free chlorine residual by a water softener system, which could impact Legionella spp. growth.92 Water quality factors such as high organic carbon (e.g. total organic carbon [TOC] or assimilable organic carbon [AOC]) may also lead to the growth of opportunistic pathogens.93–96 The relative composition of AOC and TOC may play a role in Legionella spp. growth and differ between hot and cold water.97 TOC was addressed in the L. pneumophila kinetic parameters based on available experimental data,55 however more detailed analysis of the relationship between the type of organic carbon present and L. pneumophila could be accounted for in a more detailed model.
Hard water caused by the presence of multivalent cations can cause scaling.98 Scaling in the plumbing system was not considered for this model despite its potential to influence the lifetime of the water heater, add regular maintenance costs, and increase energy cost because buildup on the heating elements will decrease heat transfer efficiency.99 Different methods for scaling prediction have been proposed, but the complexity of scaling leads to many limitations that are acknowledged.100,101 New methods have recently been developed to calculate the calcium carbonate saturation in drinking water that can be explored in future iterations of this model if a chemical assessment of the water entering the premise plumbing system is conducted.102
The scalding model used in this decision analysis evaluated the endpoints of epidermal injury or epidermal necrosis defined in Moritz and Henriques (1947) to be a 1st degree reaction with hyperemia without loss of the epidermis or a 2nd or 3rd degree reaction with complete epidermal necrosis. Using regression equations fit to data from Moritz and Henriques (1947), we used three injury categories for scalding (no injury, injury, or necrosis). However, different assumptions regarding how scalding data are pooled can result in slightly different values for optimum set point (ESI† section 10). The scalding severity was determined by using data from human skin experimentation from Moritz and Henriquez,34 which was performed using a running stream of hot water brought into direct contact with the skin using a metal cup covered with a pad of closed-cell sponge rubber to insure a watertight contact. This situation produced time–temperature–injury curves but may be slightly conservative due to the stringent contact conditions. A reaction time of five seconds was assumed the maximum time the model for removing a hot stimulus, and this may be overly optimistic given that some elderly populations in hospital care may have reduced reaction times to injuries or other conditions. Scalding and infection injuries were considered only from showers; however, sinks and toilets may also be a source of LD or Pontiac fever infections,62 and scalding could reasonably occur at sinks or bathtubs as well. Bathtubs were not considered in the current model.
For the purposes of this model, a clinical visit cost was assumed if the time of exposure and water temperature was above the epidermal injury threshold but below the epidermal necrosis threshold. An emergency room visit cost was assumed if the time of exposure and water temperature was above the epidermal necrosis threshold. This may be a conservative estimate due to 1st degree or epidermal burns being categorized as burns with minimal damage, whereas 2nd degree or dermal burns extend past the epidermal layer causing damage in the dermal layer, and 3rd degree or subdermal burns are complete destruction of the dermis.103 However, a great number of factors can affect the severity of a burn. Location of the burn on the body is expected to vary in severity due to the variation of skin thickness throughout the body. Skin thickness is also impacted by age and underlying disease. After burn care can also greatly affect the severity of a burn. All these variables should be considered on an individual basis, making a generalizable burn model very difficult to achieve.103
Numerous challenges exist for verification and/or validation of this model and similar premise plumbing models. Validation of health risk predictions would involve comparison with disease outcome statistics which in most cases would not be possible at the desired level of granularity and therefore our focus here will be on verification. Calibrating the concentration portion of this model will involve operating premise plumbing systems at multiple scales with well-developed, representative biofilms and conducting frequent sampling of L. pneumophila, free chlorine, temperature, and other meta-data. A variety of disparate laboratory scale experimental models exist for monitoring L. pneumophila growth within various plumbing system schematics that are challenging to integrate with a full-scale, decision-relevant mechanistic model as has been done here. While several bench- and pilot scale laboratory studies36,104,105 and some studies at the building-scale106,107 have informed the knowledge base for Legionella spp. growth, these concepts have not yet been linked in a quantitative way to predict the “trouble spots” in real buildings for informing interventions before an outbreak arises and significant barriers exist to integrating this information across multiple scales. Full-scale plumbing systems that include both the water heater and the pipes have been analyzed,37 along with the effects of the pipe orientation within the premise plumbing system.111 A variety of simulated water heaters scaled to a benchtop size have also been investigated.112,113 The simulated water heater allows for controlled environments where microbial growth can be closely monitored in response to changing water temperatures, pipe material, and initial water chemistry. Models using software packages such as EPANET or others have been proposed for modeling lead in premise plumbing108 or temperature109 for various aspects of hot and cold water systems but have not integrated these approaches for modeling Legionella spp. specifically. Stone et al. (2019) addressed Legionella growth and infection risks in a horizontal water heater using the advanced computational fluid dynamics (CFD) software ANSYS.114 However, these models exclude the pipes leading to the shower and the recirculating lines in their computational analysis, and do not consider health risks.
A quantitative relationship for L. pneumophila growth in operational premise plumbing systems has not yet been proposed, and few computational models have assessed L. pneumophila growth in plumbing systems. The goal is therefore to use this model as a basis for proposing additional work and identifying the drivers of the model so that information collection can be more judiciously targeted toward high-impact parameters during a calibration effort. The generalized framework presented here could also be easily adapted for a variety of building situations and configurations. This approach also allows for a greater degree of complexity to be added if such information were available for a particular building. Therefore, prior to application of this model in practice, verification is needed (1) at the pilot scale; and (2) at the full building-scale for a variety of pipe materials and configurations, operational strategies, and exposure scenarios. Ideally, information on pathogens in both biofilm and bulk water could be collected along with a rich set of meta-data to support such an effort. In contrast, Saetta et al. (2021)110 used a data-driven approach to chlorine residuals without accounting for mechanistic aspects of the system using gradient-boosting machine models, indicating that in the future either mechanistic models with learned parameters or purely data-driven models could provide improved predictive power for L. pneumophila.
The quantity of L. pneumophila in the biofilm and in sloughing events will vary greatly due to the fluid dynamics within the pipes, stagnation, chlorine residual, and the available nutrients in the local water among other things. All the parameters used to calculate the biofilm contributions to this model were taken from scenario-specific cases at the bench scale, and more information would be needed to be integrated to reflect the type of heterogeneity expected in a full-scale system. A simple modified plug-flow approach with axial dispersion in the water heater only was taken for modeling flow dynamics in the system due to simplicity in this framework. However, with additional system-specific information, a more complex approach such as CFD or similar methods could be used for a more nuanced consideration of flow within the system. In the current work, a planktonic concentration upper-bound limit of 104.17 CFU L−1 after 21 days of incubation at 37 °C in tap water was used for constraining the simulated 24 h stagnation period prior to a shower event, as this was the highest concentration observed in a study of L. pneumophila stagnation,56 however the authors noted that the plate count may be an underestimation of viable L. pneumophila present due to differences between laboratory stock strains and those adapted to growing in water. Additionally, uncertainty regarding the net impacts of stagnation and other water quality factors on L. pneumophila concentrations remains uncertain,115 and additional sensitivity analysis on the impact of this constraining variable is warranted.
The model made use of a large literature of disparate kinetic information for L. pneumophila behavior in the planktonic and biofilm-associated forms in the presence of free chlorine disinfectant as well as different temperatures. Many of these experiments were performed at the bench scale under various conditions for solute concentrations and reactor setup, indicating the need for more information to reliably fill out this parameter space. To calculate kinetic constants beyond the observed ranges of information for chlorine inactivation at various temperatures, the Arrhenius equation was used. However, the authors cautioned against extrapolating their results beyond 25 °C, which in this case was required due to a lack of additional experimental information for all required temperatures needed for the model. Chlorine demand due to other water quality aspects aside from TOC were not considered, resulting in conservative estimates for the concentration of chlorine in the modeled system. Recent studies have added to the literature on kinetic information,116 and additional kinetic information would improve the robustness of this model. It is also noted that the water heater set point may not always be fully accurate or fully encompass temperature variations. Consideration of temperature and disinfection kinetics in the context of stagnation time, nutrient availability, and other considerations is also needed. A disinfectant dose-dependent variability in disinfection efficacy for L. pneumophila was not considered and a more rigorous meta-analysis of disinfection models for L. pneumophila is recommended as an outcome of this work.
Several uncertainties to address involve the selection of dose response models and morbidity ratios for LD infection. Two dose response parameters were used in the case studies to calculate the risk of infection which influences the optimal water heater temperature set point, with terminologies of “subclinical” vs. “clinical severity infection” used from prior QMRA work.64,65 A morbidity ratio specific to elderly populations66 was used in addition to DALYs, VSL, and life expectancy to calculate the cost of infection. A DALY estimate from the Netherlands was used that did not differentiate between clinical and subclinical cases. Overall, there is a lack of information on DALY estimates from the US for LD or Pontiac fever, and US-based estimates would be needed to update this estimate in the model. The same morbidity ratio, DALYs, VSL, and life expectancy was applied for both dose response scenario and the VSL was not corrected for age. Therefore, the health-associated parameters would not apply to all populations as the focus here was on an elderly hospital vulnerable population. However, these data could be included if other populations were to be considered. Future efforts for dose response model validation could be made to examine the implications of subclinical infections and account for these costs more explicitly in the calculation for a DALY.
Perhaps counterintuitively, the clinical severity dose response results in a lower cost of infection despite having a greater severity due to the fact that the dose response relationship results in a lower likelihood of illness using the clinical severity dose response relationship compared to multiplying the probability of infection generated with the subclinical infection dose response model by a morbidity ratio. While the clinical severity infection relationship aligns with efforts to use QMRA to re-produce epidemic curves,67 additional validation of dose response and morbidity ratio relationships would be useful for identifying specific modulating factors in susceptibility and modifying the currently developed model to other scenarios and populations of interest. Further validation efforts for dose–response datasets would be useful for clarifying the interpretation of the outcomes of subclinical infection and clinical severity infection as distinct independent versus conditional outcomes.
The type of susceptible subpopulation considered could also impact the exposure factors chosen; in this case, a 1.0 to 5.0 second reaction time was conservatively chosen for an elderly person removing themselves from a water temperature that could pose a danger of scalding. Reaction times to a stimuli can be shorter than 1 s.117 However, while contact heat pain thresholds may not differ between the elderly and other populations,118 actual duration of contact with the hot water of up to 5 seconds is assumed to be reasonable as elderly individuals can have co-occurring conditions and decreased mobility compared to younger, healthy individuals.119–122
Cost assumptions were made for the risk of infection, risk of scalding, and energy cost. The predicted costs will vary regionally according to local energy costs, medical costs, as well as costs of illness and can be discounted or have uncertainty accounted for accordingly in a more detailed consideration of situation-specific costs. This model was limited to only a small section of a clinical plumbing system, the average daily water use per capita was estimated to be the use for a single patient. The average was used to calculate the approximate energy cost to heat the used and recirculating water. This value inherently has a lot of uncertainty, as a patient might need a lot more or a lot less water depending on the reason for hospitalization. For example, patients with scalding might require that they have baths multiple times a day, whereas other patients might not require a bath for 24 hours. The cost of heating the water will also depend on the location of the patient room relative to the water heater. The further the room is from the water heater, the more the water will cool down and the more energy will be required to heat it again. The model did not account for variations beyond a single day of operation and exposure, and therefore future models could account for the dynamics of the costs over a more comprehensive timeframe, including construction and operation, health risks, and scalding risks during a longer time-frame, accounting for discounting or weighting preferences for these attributes.
Choosing appropriate time horizons will be needed for applying discount rates and estimating the effects of decision-making over a more realistic operational timeline. To this end, it would be complex to consider the dynamics of pathogen growth over a longer time range without additional kinetic information and quantitative relationships between performance, stagnation, and occurrence of L. pneumophila in the biofilms and bulk water. Presumably if an issue such as an outbreak or scalding episode were to occur, changes would be made to water operation that would impact the putative risks. More mechanistic understanding of these relationships would allow for implementation of such a model. Importantly, the costs associated with remediating a system after a L. pneumophila contamination event and the role an initial colonization an event can play in re-seeding the system were not considered but presumably would further elevate the importance of infection risk as a driving factor in the model. The current model is initialized over a 24 h period but could be modified to allow for different stagnation periods. While systematic studies of the costs of remediation are not currently available, follow-up studies of Legionella spp. after colonization events indicate that long-term measures such as building-level disinfection may be necessary to control colonization and would incur additional costs,123 in addition to sampling costs, maintenance, legal, and personnel costs. Recolonization after disinfection, heat treatment, or UV treatment may occur on a timeframe of weeks to months in water distribution systems and/or premise plumbing.37,124–126 Only direct costs were considered for infection and scalding and did not account for example, for lost wages due to missed work or other costs such as lawsuits resulting from a case of illness or injury, pain and suffering, or long-term impacts and associated future costs from infection and/or scalding. Additional cost evaluation methodology such as cost-benefit or cost-effectiveness approaches could also be used.
5. Conclusion
A computational framework is presented for evaluating an optimal water heater temperature set point for reducing energy costs and health risks for a single showering exposure event. This framework uses a quantitative microbial risk assessment (QMRA) model to assess the risk of infection from shower aerosol exposure in terms of disability-adjusted life years and daily costs. The cost associated with the risk of scalding was evaluated, along with the cost of energy used to heat the water for a variety of uncertain assumptions related to the system design, operation, and risk assumptions. As a starting point, a use-case was developed for a hypothetical hospital room located in the United States that would serve a susceptible hospitalized population.The model provides a valuable means of exploring the impact of interactions between the assumptions and evaluated tradeoffs between infection risk for LD, scalding risk, and energy costs. Overall, the model was most sensitive to assumptions regarding the system configuration and dose response model chosen for analysis. In all cases, the scalding risk was not a driver of total cost until the higher set points, assuming no thermostatic mixing valve in use (≥59 °C). The use of a subclinical infection vs. a clinical severity infection dose response model dictated the rank order of infection and energy costs, with the more conservative (subclinical) model resulting in a prioritization of infection considerations over the other (energy cost or scalding) considerations. The sensitivity analyses indicated that biofilm dynamics drove risk estimates, as well as assumptions regarding energy price. Limitations and additional considerations for the model were discussed.
The approach proposed in this work should be a companion tool to other simple, direct evidence-based approaches and a complex model may not be warranted in every situation. The uncertainties identified in this work could also be reduced with the use of site-specific information regarding building design and operation. With further validation, this model could be used by building owners and architects to assess the cost associated with the risk of infection or scalding, as well as the energy cost to heat different plumbing configurations in different climates. Ideally, architects will be able to use this tool to minimize total costs for different scenarios by evaluating pipe materials, pipe lengths, pipe sizes, stagnant dead ends, or insulation prior to the construction phase. Building owners can use this tool for existing plumbing systems to make operational improvements by determining the optimal water heater temperature set point, adding or removing insulation, or taking regular preventative measures to mitigate L. pneumophila growth. This model contributes to the mechanistic understanding of system dynamics within premise plumbing systems and serves as a good base for the addition of other pathogens like mycobacteria, disinfection byproducts, or the cost of emissions for fossil fuel usage. As such, the current analysis could constitute a piece in a larger consideration of more holistic building design and operational decision support tools.
Conflicts of interest
There are no conflicts to declare.References
- K. D. Beer, J. W. Gargano, V. A. Roberts, V. R. Hill, L. E. Garrison and P. K. Kutty, et al. Surveillance for Waterborne Disease Outbreaks Associated with Drinking Water - United States, 2011-2012, Morb. Mortal. Wkly. Rep., 2015, 64(31), 842–848 CrossRef.
- K. A. Hamilton, A. J. Prussin, W. Ahmed and C. N. Haas, Outbreaks of Legionnaires' Disease and Pontiac Fever 2006–2017, Curr. Environ. Health Rep., 2018, 5(2), 263–271 CrossRef CAS PubMed.
- E. van Heijnsbergen, J. A. C. Schalk, S. M. Euser, P. S. Brandsema, J. W. den Boer and A. M. de Roda Husman, Confirmed and Potential Sources of Legionella Reviewed, Environ. Sci. Technol., 2015, 49(8), 4797–4815 CrossRef CAS PubMed.
- CDC, Legionella(Legionnaires' Disease and Pontiac Fever), CDC, 2018, Available from: https://www.cdc.gov/legionella/about/history.html Search PubMed.
- NASEM, Water Science and Technology Board, Board on Life Sciences, Board on Population Health and Public Health Practice, Division on Earth and Life Studies, Health and Medicine Division, et al.Management of Legionella in Water Systems, National Academies Press, Washington, D.C., 2019, [cited 2019 Nov 27], Available from: https://www.nap.edu/catalog/25474 Search PubMed.
- NASEM, Drinking Water Distribution Systems: Assessing and Reducing Risks, National Academies Press, Washington, D.C., 2006, [cited 2020 Jan 13], Available from: http://www.nap.edu/catalog/11728 Search PubMed.
- CDC, A. Barskey, A. Binder, C. Edens, S. Lee and J. Smith, et al., Legionnaires' Disease Surveillance Summary Report, United States- 2014 and 2015, Center for Disease Control and Prevention, 2015, Available from: https://www.cdc.gov/legionella/health-depts/surv-reporting/2014-15-surv-report-508.pdf Search PubMed.
- S. A. Collier, L. Deng, E. A. Adam, K. M. Benedict, E. M. Beshearse and A. J. Blackstock, et al., Estimate of Burden and Direct Healthcare Cost of Infectious Waterborne Disease in the United States, Emerging Infect. Dis., 2021, 27(1), 140–149 CrossRef.
- L. Gomez-Valero and C. Buchrieser, Intracellular parasitism, the driving force of evolution of Legionella pneumophila and the genus Legionella, Microbes Infect., 2019, 21(5–6), 230–236 CrossRef.
- K. Paranjape, É. Bédard, L. G. Whyte, J. Ronholm, M. Prévost and S. P. Faucher, Presence of Legionella spp. in cooling towers: the role of microbial diversity, Pseudomonas, and continuous chlorine application, Water Res., 2020, 169, 115252 CrossRef CAS PubMed.
- WHO, in Legionella and the prevention of legionellosis, ed. J. Bartram, World Health Organization, Geneva, 2007, p. 252 Search PubMed.
- B. Lévesque, M. Lavoie and J. Joly, Residential Water Heater Temperature: 49 or 60 Degrees Celsius?, Can. J. Infect. Dis., 2004, 15(1), 11–12 Search PubMed.
- DOE, Savings Project: Lower Water Heating Temperature, DOE, 2016, Available from: https://www.energy.gov/energysaver/services/do-it-yourself-energy-savings-projects/savings-project-lower-water-heating Search PubMed.
- W. C. Shields, E. McDonald, S. Frattaroli, E. C. Perry, J. Zhu and A. C. Gielen, Still Too Hot: Examination of Water Temperature and Water Heater Characteristics 24 Years After Manufacturers Adopt Voluntary Temperature Setting, J. Burn Care Res., 2013, 34(2), 281–287 CrossRef PubMed.
- R. Singh, K. A. Hamilton, M. Rasheduzzaman, Z. Yang, S. Kar and A. Fasnacht, et al., Managing Water Quality in Premise Plumbing: Subject Matter Experts' Perspectives and a Systematic Review of Guidance Documents, Water, 2020, 12(2), 347 CrossRef.
- ASHRAE, ANSI/ASHRAE Standard 188: Legionellosis: Risk Management for Building Water Systems, 2018, Available from: https://ashrae.iwrapper.com/ViewOnline/Standard_188-2018 Search PubMed.
- CDC, Developing a Water Management Program to Reduce Legionella Growth & Spread in Buildings, 2017, Available from: https://www.cdc.gov/legionella/downloads/toolkit.pdf Search PubMed.
- A. Parr, E. A. Whitney and R. L. Berkelman, Legionellosis on the Rise: A Review of Guidelines for Prevention in the United States, J. Public Health Manag. Pract., 2015, 21(5), E17–E26 CrossRef.
- CMS and Centers for Medicare and Medicaid Services, SUBJ: Requirement to Reduce Legionella Risk in Healthcare Facility Water Systems to Prevent Cases and Outbreaks of Legionnaires' Disease(LD), Revised to Clarify Expectations for Providers, Accrediting Organizations, and Surveyors, Memorandum, 2018, Available from: https://www.cms.gov/Medicare/Provider-Enrollment-and-Certification/SurveyCertificationGenInfo/Downloads/QSO17-30-HospitalCAH-NH-REVISED-.pdf Search PubMed.
- CDC, Legionella: Healthcare Water Management Program FAQs, 2021, [cited 2021 Sep 25], Available from: https://www.cdc.gov/legionella/wmp/healthcare-facilities/healthcare-wmp-faq.html Search PubMed.
- S. A. Collier, L. J. Stockman, L. A. Hicks, L. E. Garrison, F. J. Zhou and M. J. Beach, Direct healthcare costs of selected diseases primarily or partially transmitted by water, Epidemiol. Infect., 2012, 140(11), 2003–2013 CrossRef CAS.
- K. Lock, C. Millett, R. Heathcock, C. A. Joseph, T. G. Harrison and J. V. Lee, et al. Public health and economic costs of investigating a suspected outbreak of Legionnaires' disease, Epidemiol. Infect., 2008, 136(10), 1306–1314 CrossRef CAS PubMed.
- R. Hockey, Safe hot tap water and the risk of scalds and legionella infection, Inj. Prev., 2002, 8(2), 170 CrossRef CAS PubMed.
- M. L. Katcher, Scald Burns From Hot Tap Water, JAMA, 1981, 245(11), 1219–1222 CrossRef.
- G. Lowell, K. Quinlan and L. J. Gottlieb, Preventing Unintentional Scald Burns: Moving Beyond Tap Water, Pediatrics, 2008, 122(4), 799–804 CrossRef PubMed.
- M. D. E. Potter, P. K. M. Maitz, P. J. Kennedy and D. Goltsman, Perineal tap water burns in the elderly: at what cost?: Perineal tapster burns in the elderly, ANZ J. Surg., 2017, 87(11), E188–E192 CrossRef PubMed.
- M. Peck, A. Chang Brewer, M. Pressman, E. Blank and A. Mickalide, Hot Tap Water Legislation in the United States, J. Burn Care Res., 2010, 31(6), 918–925 CrossRef PubMed.
- P. L. Graitcer and J. E. Sniezek, HOSPITALIZATIONS DUE TO TAP WATER SCALDS, 1978–1985, Public Health Surveill 1990 Inj Control Object Nation, 1988, Feb, vol. 37, p. 4 Search PubMed.
- D. L. Chester, R. M. Jose, E. Aldlyami, H. King and N. S. Moiemen, Non-accidental burns in children—Are we neglecting neglect?, Burns, 2005, 32(2), 222–228 CrossRef.
- G. P. Barnsley and S. E. Barnsley, Rate of pediatric tap water scald injuries in eastern Ontario, Can. J. Plast. Surg., 2007, 15(1), 33–37 CrossRef.
- T. C. Erdmann, K. W. Feldman, F. P. Rivara, D. M. Heimbach and H. A. Wall, Tap Water Burn Prevention: The Effect of Legislation, Pediatrics, 1991, 88(3), 572–577 CAS.
- E. Clouatre, R. Pinto, J. Banfield and M. G. Jeschke, Incidence of Hot Tap Water Scalds After the Introduction of Regulations in Ontario, J. Burn Care Res., 2013, 34(2), 243–248 CrossRef PubMed.
- CMS, State operations manual Appendix Q. Guidelines for determining immediate jeopardy. Rev. 102, 2000, Available from: file:///C:/Users/ashle/Dropbox/Ashley%20Heida/Water%20heater%20project/Water%20Heater%20Papers/CMS_2014.pdf Search PubMed.
- A. R. Moritz and F. C. Henriques, Studies of Thermal Injury: II. The Relative Importance of Time and Surface Temperature in the Causation of Cutaneous Burns, Am. J. Pathol., 1947, 23(5), 695–720 CAS.
- Government of Canada, Water Temperature and Burns/Scalds, 2011, Available from: https://www.canada.ca/en/public-health/services/water-temperature-burns-scalds.html Search PubMed.
- W. J. Rhoads, P. Ji, A. Pruden and M. A. Edwards, Water heater temperature set point and water use patterns influence Legionella pneumophila and associated microorganisms at the tap, Microbiome, 2015, 3(1), 1–13 CrossRef.
- W. Rhoads, A. Pruden and M. Edwards, Convective Mixing in Distal Pipes Exacerbates Legionella pneumophila Growth in Hot Water Plumbing, Pathogens, 2016, 5(1), 29 CrossRef PubMed.
- C. Nguyen, C. Elfland and M. Edwards, Impact of advanced water conservation features and new copper pipe on rapid chloramine decay and microbial regrowth, Water Res., 2012, 46(3), 611–621 CrossRef CAS.
- Y. Zhang and M. Edwards, Accelerated chloramine decay and microbial growth by nitrification in premise plumbing, J. - Am. Water Works Assoc., 2009, 101(11), 51–62 CrossRef CAS.
- P. Borella, M. T. Montagna, V. Romano-Spica, S. Stampi, G. Stancanelli and M. Triassi, et al., Legionella Infection Risk from Domestic Hot Water, Emerging Infect. Dis., 2004, 10(3), 457–464 CrossRef.
- Westinghouse, Westinghouse Grid-Enabled Electric Water Heaters, 2020, p. 2 Search PubMed.
- J. Reiling, R. G. Hughes and M. R. Murphy, Chapter 28, The Impact of Facility Design on Patient Safety, Patient Saf., 2008, vol. 2, p. 26 Search PubMed.
- IAPMO, 2015 Minnesota Plumbing Code Water Pipe Sizing Workshop, IAPMO, 2016 Search PubMed.
- Watts, Aerco, PVI, Powers, Healthcare Solutions F-WWT-Healthcare 1826, MF10448, 2018, [cited 2021 Sep 25], Available from: http://media.wattswater.com/f-wwt-healthcare.pdf Search PubMed.
- M. Scruggs, How to select a commercial water heater, Consulting - Specifying Engineer, 2020, [cited 2021 Sep 25], Available from: https://www.csemag.com/articles/how-to-select-a-commercial-water-heater/ Search PubMed.
- E. M. Kleinbach, W. A. Beckman and S. A. Klein, Performance study of one-dimensional models for stratified thermal storage tanks, Sol. Energy, 1993, 50(2), 155–166 CrossRef CAS.
- R. H. Brazeau and M. A. Edwards, Role of Hot Water System Design on Factors Influential to Pathogen Regrowth: Temperature, Chlorine Residual, Hydrogen Evolution, and Sediment, Environ. Eng. Sci., 2013, 30(10), 617–627 CrossRef CAS PubMed.
- E. J. M. Blokker and E. J. Pieterse-Quirijns, Modeling temperature in the drinking water distribution system, J. - Am. Water Works Assoc., 2013, 105(1), E19–E28 CrossRef.
- A. Chmielewska, Fluctuating temperature of the mains water throughout the year and its influence on the consumption of energy for the purposes of DHW preparation, ed. B. Kaźmierczak, M. Kutyłowska, K. Piekarska and P. Jadwiszczak, E3S Web Conf., 2018, vol. 44, p. 00017 Search PubMed.
- Fundamentals of heat and mass transfer, ed. F. P. Incropera, D. P. Dewitt, T. L. Bergman and A. S. Lavine, John Wiley, Hoboken, NJ, 6th edn, 2007, p. 997 Search PubMed.
- ASHRAE, ANSI/ASHRAE/IES Standard 90.1–2019 -- Energy Standard for Buildings Except Low-Rise Residential Buildings, 2019, [cited 2021 Sep], p. 424, Report No.: D-86270, 86270, Available from: https://www.ashrae.org/technical-resources/bookstore/standard-90-1 Search PubMed.
- J. P. Guyer, An Introduction to Hospital Domestic Water Systems, 2016, vol. 36 Search PubMed.
- EPA, Indoor Air Quality Tools for Schools Reference Guide, EPA, 2009, Available from: https://www.epa.gov/sites/production/files/2014-08/documents/reference_guide.pdf Search PubMed.
- ASHRAE, M. Brian, B. M. Lynch and E. A. Arens, ANSI/ASHRAE Standard 55: Thermal Environmental Conditions for Human Occupancy, ASHRAE, 2010, Available from: http://arco-hvac.ir/wp-content/uploads/2015/11/ASHRAE-55-2010.pdf Search PubMed.
- AWWA, 2017 Water Utility Disinfection Survey Report, American Water Works Association, 2018, Available from: https://www.awwa.org/Portals/0/AWWA/ETS/Resources/2017DisinfectionSurveyReport.pdf?ver=2018-12-21-163548-830 Search PubMed.
- R. B. Yee and R. M. Wadowsky, Multiplication of Legionella pneumophila in Unsterilized Tap Water, Appl. Environ. Microbiol., 1982, 43, 5 CrossRef.
- J. M. Thomas, The Risk to Human Health from Free-Living Amoebae Interaction with Legionella in Drinking and Recycled Water Systems, University of New South Wales, 2012 Search PubMed.
- K. Garny, T. R. Neu and H. Horn, Sloughing and limited substrate conditions trigger filamentous growth in heterotrophic biofilms—Measurements in flow-through tube reactor, Chem. Eng. Sci., 2009, 64(11), 2723–2732 CrossRef CAS.
- W. J. Rhoads and F. Hammes, Growth of Legionella during COVID-19 lockdown stagnation, Environ. Sci.: Water Res. Technol., 2021, 7(1), 10–15 RSC.
- C. Huang, Y. Shen, R. L. Smith, S. Dong and T. H. Nguyen, Effect of disinfectant residuals on infection risks from Legionella pneumophila released by biofilms grown under simulated premise plumbing conditions, Environ. Int., 2020, 137, 105561 CrossRef.
- C. N. Haas, J. B. Rose and C. P. Gerba, Quantitative Microbial Risk Assessment, John Wiley & Sons, Inc., 1999 Search PubMed.
- K. Hamilton, M. T. Hamilton, W. Johnson, P. Jjemba, Z. Bukhari and M. LeChevallier, et al. Risk-Based Critical Concentrations of Legionella pneumophila for Indoor Residential Water Uses, Environ. Sci. Technol., 2019, 53(8), 4528–4541 CrossRef CAS PubMed.
- K. Hamilton, M. T. Hamilton, W. Johnson, P. Jjemba, Z. Bukhari and M. LeChevallier, et al. Health risks from exposure to Legionella in reclaimed water aerosols: Toilet flushing, spray irrigation, and cooling towers, Water Res., 2018, 134, 261–279 CrossRef CAS PubMed.
- T. W. Armstrong and C. N. Haas, A Quantitative Microbial Risk Assessment Model for Legionnaires' Disease: Animal Model Selection and Dose-Response Modeling: A Quantitative Microbial Risk Assessment Model for Legionnaires' Disease, Risk Anal., 2007, 27(6), 1581–1596 CrossRef CAS PubMed.
- T. W. Armstrong and C. N. Haas, Legionnaires' disease: evaluation of a quantitative microbial risk assessment model, J. Water Health, 2008, 6(2), 149–166 CrossRef.
- M. H. Weir, A. L. Mraz and J. Mitchell, An Advanced Risk Modeling Method to Estimate Legionellosis Risks Within a Diverse Population, Water, 2019, 12(1), 43 CrossRef.
- B. Prasad, K. A. Hamilton and C. N. Haas, Incorporating Time-Dose-Response into Legionella Outbreak Models, Risk Anal., 2017, 37(2), 291–304 CrossRef PubMed.
- L. A. Robinson, J. K. Hammitt, M. Cecchini, K. Chalkidou, K. Claxton and P. H.-V. Eozenou, et al., Reference Case Guidelines for Benefit-Cost Analysis in Global Health and Development, Bill & Melinda Gates Foundation, 2019, p. 126 Search PubMed.
- US Department of Health and Human Services, Guidelines for Regulatory Impact Analysis Appendix D: Updating Value per Statistical Life(VSL) Estimates for Inflation and Changes in Real Income, ASPE, 2021, [cited 2021 Sep 14], Available from: https://aspe.hhs.gov/reports/updating-vsl-estimates Search PubMed.
- W. Viscusi, The value of life, The Harvard John M. Olin Discussion Paper Series, Report No.: Discussion paper No. 517, Harvard Law School, Cambridge, MA, 2005 Search PubMed.
- W. K. Viscusi, How to value a life, J. Econ. Finan., 2008, 32(4), 311–323 CrossRef.
- L. A. Robinson and J. K. Hammitt, Valuing Reductions in Fatal Illness Risks: Implications of Recent Research: Valuing Reductions in Fatal Illness Risks, Health Econ., 2016, 25(8), 1039–1052 CrossRef.
- E. Arias, M. Heron and J. Xu, United States Life Tables, 2013, NVSS, 2017, vol. 66, 3, p. 64 Search PubMed.
- US Census Bureau, National Population by Characteristics: 2010–2019, The United States Census Bureau, [cited 2021 Sep 24], Available from: https://www.census.gov/data/tables/time-series/demo/popest/2010s-national-detail.html Search PubMed.
- W. B. DeOreo, P. W. Mayer, B. Dziegielewski, J. Kiefer, B. Dziegielewski and B. Dziegielewski, Residential End Uses of Water, version 2, Water Res Found., 2016, vol. 18 Search PubMed.
- B. C. B. Shield, Typical Costs for Common Medical Services, Blue Cross and Blue Shield of Massachusetts, 2009 Search PubMed.
- DOE, Estimating Costs and Efficiency of Storage, Demand, and Heat Pump Water Heaters, DOE, [cited 2020 Feb 7]. Available from: https://www.energy.gov/energysaver/estimating-costs-and-efficiency-storage-demand-and-heat-pump-water-heaters Search PubMed.
- C. A. Dieter, M. A. Maupin, R. R. Caldwell, M. A. Harris, T. I. Ivahnenko and J. K. Lovelace, et al., Estimated Use of Water in the United States in 2015: U.S. Geological Survey Circular 1441, U.S. Geological Survey, 2018 Search PubMed.
- USGS. Per capita water use: How much water do you use at home? [Internet], 2021, [cited 2021 Sep 25], Available from: https://water.usgs.gov/edu/activity-percapita.php.
- U.S. Energy Information Administration, Electric Power Monthly, U.S. Energy Information Administration, Available from: https://www.eia.gov/electricity/monthly/epm_table_grapher.php?t=epmt_5_6_a Search PubMed.
- ENERGY STAR, ENERGY STAR Residential Water Heaters: Final Criteria Analysis, ENERGY STAR, 2008, Available from: https://www.energystar.gov/ia/partners/prod_development/new_specs/downloads/water_heaters/waterheateranalysis_final.pdf Search PubMed.
- J. Herman, W. Usher, C. Mutel, B. Trindade, D. Hadka and M. Woodruff, et al., SALib, MIT, 2017, [cited 2020 Nov 24], Available from: https://salib.readthedocs.io/en/latest/license.html Search PubMed.
- J. R. Dormand and P. J. Prince, A family of embedded Runge-Kutta formulae, J. Comput. Appl. Math., 1980, 6(1), 19–26 CrossRef.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga and A. Desmaison, PyTorch: An Imperative Style, High-Performance Deep Learning Library, Advances in Neural Information Processing Systems, 2019, vol. 32, pp. 8026–8037 Search PubMed.
- R. T. Chen, Y. Rubanova, J. Bettencourt and D. Duvenaud, Neural ordinary differential equations, arXiv, 2018, preprint, arXiv:1806.07366, https://arxiv.org/abs/1806.07366 Search PubMed.
- Hach, Chlorine, Free and Total, Low Range: USEPA DPD Method 8021 (Free) 8167 (Total) DOC316.53.01450, 2018, Available from: https://www.hach.com/asset-get.download-en.jsa?code=163953 Search PubMed.
- H.-C. Flemming, S. L. Percival and J. T. Walker, Contamination potential of biofilms in water distribution systems, Water Supply, 2002, 2(1), 271–280 CrossRef CAS.
- N. Van Abel, M. E. Schoen, J. C. Kissel and J. S. Meschke, Comparison of Risk Predicted by Multiple Norovirus Dose-Response Models and Implications for Quantitative Microbial Risk Assessment: Comparison of Risk Predicted by Multiple Norovirus Dose-Response Models, Risk Anal., 2017, 37(2), 245–264 CrossRef.
- A. Brûlet, M.-C. Nicolle, M. Giard, F.-E. Nicolini, M. Michallet and S. Jarraud, et al. Fatal Nosocomial Legionella pneumophila Infection Due to Exposure to Contaminated Water From a Washbasin in a Hematology Unit, Infect. Control Hosp. Epidemiol., 2008, 29(11), 1091–1093 CrossRef PubMed.
- P. J. Hugo Johansson, K. Andersson, T. Wiebe, C. Schalén and S. Bernander, Nosocomial transmission of Legionella pneumophila to a child from a hospital's cold-water supply, Scand. J. Infect. Dis., 2006, 38(11–12), 1023–1027 CrossRef.
- M. Rasheduzzaman, R. Singh, C. N. Haas and P. L. Gurian, Required water temperature in hotel plumbing to control Legionella growth, Water Res., 2020, 182, 115943 CrossRef CAS.
- R. Richard, K. A. Hamilton, P. Westerhoff and T. H. Boyer, Tracking copper, chlorine, and occupancy in a new, multi-story, institutional green building, Environ. Sci.: Water Res. Technol., 2020, 6(6), 1672–1680 RSC.
- M. W. LeChevallier, N. J. Welch and D. B. Smith, Full-scale studies of factors related to coliform regrowth in drinking water, Appl. Environ. Microbiol., 1996, 62(7), 2201–2211 CrossRef CAS PubMed.
- M. W. LeChevallier, N. E. Shaw, L. A. Kaplan and T. L. Bott, Development of a Rapid Assimilable Organic Carbon Method for Water, Appl. Environ. Microbiol., 1993, 59(5), 1526–1531 CrossRef CAS PubMed.
- D. van der Kooij, Assimilable Organic Carbon(AOC) in Drinking Water, in Drinking Water Microbiology, ed. G. A. McFeters, Springer New York, New York, NY, 1990, [cited 2021 Ar 19], pp. 57–87, (Brock TD, editor. Brock/Springer Series in Contemporary Bioscience). Available from: http://link.springer.com/10.1007/978-1-4612-4464-6_3 Search PubMed.
- C. Volk, K. Bell, E. Ibrahim, D. Verges, G. Amy and M. LeChevallier, Impact of enhanced and optimized coagulation on removal of organic matter and its biodegradable fraction in drinking water, Water Res., 2000, 34(12), 3247–3257 CrossRef CAS.
- D. van der Kooij, H. R. Veenendaal, E. J. van der Mark and M. Dignum, Assessment of the microbial growth potential of slow sand filtrate with the biomass production potential test in comparison with the assimilable organic carbon method, Water Res., 2017, 125, 270–279 CrossRef CAS.
- B. Van der Bruggen, H. Goossens, P. A. Everard, K. Stemgée and W. Rogge, Cost-benefit analysis of central softening for production of drinking water, J. Environ. Manage., 2009, 91(2), 541–549 CrossRef CAS PubMed.
- J. Hofman, J. P. V. D. Hoek, M. Nederlof and M. Groenendijk, Twenty years of experience with centralised softening in the Netherlands: Water quality, environmental benefits, and costs, 2007, Feb 1 [cited 2021 Apr 21]; Available from: https://researchportal.bath.ac.uk/en/publications/twenty-years-of-experience-with-centralised-softening-in-the-neth Search PubMed.
- H. Brink, P. G. G. Slaats and M. W. M. van Eekeren, Scaling in domestic heating equipment: getting to know a complex phenomenon, Water Sci. Technol., 2004, 49(2), 129–136 CrossRef CAS.
- Innovation and integration - impact on desalination and water reuse costs: IDA International Water Forum, ed. International Desalination Association, Dubai, UAE, March 5–6, 2006, Topsfield, Mass: IDA; 2006, p. 100, Available from: https://www.researchgate.net/profile/Hamza-Elfil/publication/323615931_A_New_Index_for_Scaling_Assessment/links/5aa02af60f7e9badd9a0ba07/A-New-Index-for-Scaling-Assessment.pdf Search PubMed.
- P. J. de Moel, A. W. C. van der Helm, M. van Rijn, J. C. van Dijk and W. G. J. van der Meer, Assessment of calculation methods for calcium carbonate saturation in drinking water for DIN 38404-10 compliance, Drinking Water Eng. Sci., 2013, 6(2), 115–124 CrossRef.
- N. A. Martin and S. Falder, A review of the evidence for threshold of burn injury, Burns, 2017, 43(8), 1624–1639 CrossRef CAS PubMed.
- C. R. Proctor, Effect of Various Water Chemistry Factors on Legionella Proliferation and the Premise Plumbing Microbiome Composition, Doctoral dissertation, Virginia Tech, 2014 Search PubMed.
- W. J. Rhoads, A. Pruden and M. K. Edwards, Interactive Effects of Corrosion, Copper, and Chloramines on Legionella and Mycobacteria in Hot Water Plumbing, Environ. Sci. Technol., 2017, 51(12), 7065–7075 CrossRef CAS PubMed.
- M. Salehi, M. Abouali, M. Wang, Z. Zhou, A. P. Nejadhashemi and J. Mitchell, et al., Case study: Fixture water use and drinking water quality in a new residential green building, Chemosphere, 2018, 195, 80–89 CrossRef CAS PubMed.
- C. J. Ley, C. R. Proctor, K. Jordan, K. Ra, Y. Noh and T. Odimayomi, et al., Impacts of Municipal Water–Rainwater Source Transitions on Microbial and Chemical Water Quality Dynamics at the Tap, Environ. Sci. Technol., 2020, 54(18), 11453–11463 CrossRef CAS PubMed.
- J. B. Burkhardt, H. Woo, J. Mason, F. Shang, S. Triantafyllidou and M. R. Schock, et al., Framework for Modeling Lead in Premise Plumbing Systems Using EPANET, J. Water Resour. Plan. Manag., 2020, 146(12), 04020094 CrossRef.
- B. Hillebrand and E. M. Blokker, Modeling the Influence of District Heating Systems on Drinking Water Temperatures in Domestic Drinking Water Systems within Domestic Properties, in World Environmental and Water Resources Congress, 2021, vol. 3, pp. 961–968 Search PubMed.
- D. Saetta, R. Richard, C. Leyva, P. Westerhoff and T. H. Boyer, Data-mining methods predict chlorine residuals in premise plumbing using low-cost sensors, AWWA Water Sci., 2021, 3(1), e1214 CAS.
- W. J. Rhoads, P. Ji, A. Pruden and M. A. Edwards, Water heater temperature set point and water use patterns influence Legionella pneumophila and associated microorganisms at the tap, Microbiome, 2015, 3(1), 67 CrossRef PubMed.
- C. R. Proctor, D. Dai, M. A. Edwards and A. Pruden, Interactive effects of temperature, organic carbon, and pipe material on microbiota composition and Legionella pneumophila in hot water plumbing systems, Microbiome, 2017, 5(1), 130 CrossRef PubMed.
- M. Shaheen, C. Scott and N. J. Ashbolt, Long-term persistence of infectious Legionella with free-living amoebae in drinking water biofilms, Int. J. Hyg. Environ. Health, 2019, 222(4), 678–686 CrossRef PubMed.
- W. Stone, T. M. Louw, G. K. Gakingo, M. J. Nieuwoudt and M. J. Booysen, A potential source of undiagnosed Legionellosis: Legionella growth in domestic water heating systems in South Africa, Energy Sustainable Dev., 2019, 48, 130–138 CrossRef.
- W. J. Rhoads and F. Hammes, Growth of Legionella during COVID-19 lockdown stagnation, Environ. Sci.: Water Res. Technol., 2021, 7(1), 10–15 RSC.
- S. D. Papagianeli, Z. Aspridou, S. Didos, D. Chochlakis, A. Psaroulaki and K. Koutsoumanis, Dynamic modelling of Legionella pneumophila thermal inactivation in water, Water Res., 2021, 190, 116743 CrossRef CAS PubMed.
- E. Brenner and J. B. J. Smeets, How Can You Best Measure Reaction Times?, J. Mot. Behav., 2019, 51(5), 486–495 CrossRef PubMed.
- H. El Tumi, M. I. Johnson, P. B. F. Dantas, M. J. Maynard and O. A. Tashani, Age-related changes in pain sensitivity in healthy humans: A systematic review with meta-analysis, Eur. J. Pain, 2017, 21(6), 955–964 CrossRef CAS PubMed.
- M. A. Durand, J. Green, P. Edwards, S. Milton and S. Lutchmun, Perceptions of tap water temperatures, scald risk and prevention among parents and older people in social housing: A qualitative study, Burns, 2012, 38(4), 585–590 CrossRef PubMed.
- A. Hewitt, C. Macarthur and P. Raina, The Role of Evidence in Public Health Policy: An Example of Linkage and Exchange in the Prevention of Scald Burns, Healthc. Policy, 2007, 3(2), 59–66 Search PubMed.
- D. W. Huyer and S. H. Corkum, Reducing the incidence of tap-water scalds: strategies for physicians, Can. Med. Assoc. J., 1997, 156(6), 841–844 CAS.
- M. Stone, J. Ahmed and J. Evans, The continuing risk of domestic hot water scalds to the elderly, Burns, 2000, 26(4), 347–350 CrossRef CAS PubMed.
- M. A. Coniglio, M. Ferrante and M. H. Yassin, Preventing Healthcare-Associated Legionellosis: Results after 3 Years of Continuous Disinfection of Hot Water with Monochloramine and an Effective Water Safety Plan, Int. J. Environ. Res. Public Health, 2018, 15(8), 1594 CrossRef PubMed.
- Y. E. Lin, R. D. Vidic, J. E. Stout and V. L. Yu, Legionella in water distribution systems, J. AWWA, 1998, 90(9), 112–122 CrossRef CAS.
- Z. Liu, J. Stout, L. Tedesco, M. Boldin, C. Hwang and V. Lu, Efficacy of ultraviolet light in preventing Legionella colonization of a hospital water distribution system, Water Res., 1995, 29(10), 2275–2280 CrossRef CAS.
- Z. Liu, J. E. Stout, M. Boldin, J. Rugh, W. F. Diven and V. L. Yu, Intermittent Use of Copper-Silver Ionization for Legionella Control in Water Distribution Systems: A Potential Option in Buildings Housing Individuals at Low Risk of Infection, Clin. Infect. Dis., 1998, 26(1), 138–140 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ew00397f |
| This journal is © The Royal Society of Chemistry 2022 |