Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the energy gap determination of organic optoelectronic materials: the case of porphyrin derivatives†
Rian E.
Aderne
a,
Bruno Gabriel A. L.
Borges
b,
Harold C.
Ávila
c,
Fredrik
von Kieseritzky
d,
Jonas
Hellberg
e,
Marlus
Koehler
 f,
Marco
Cremona
f,
Marco
Cremona
 a,
Lucimara S.
Roman
a,
Lucimara S.
Roman
 f,
C. Moyses
Araujo
f,
C. Moyses
Araujo
 gh,
Maria Luiza M.
Rocco
gh,
Maria Luiza M.
Rocco
 *b and
Cleber F. N.
Marchiori
*b and
Cleber F. N.
Marchiori
 *h
*h
aDepartamento de Física, Pontifícia Universidade Católica do Rio de Janeiro – PUC-Rio, 22453-900, Rio de Janeiro-RJ, Brazil
bInstituto de Química, Universidade Federal do Rio de Janeiro-UFRJ, 21941-909, Rio de Janeiro-RJ, Brazil. E-mail: luiza@iq.ufrj.br
cDepartment of Physics, University of Atlantic, Puerto Colombia, Atlántico, Colombia
dDepartment of Neurobiology, Care Sciences and Society, Karolinska Institutet, Stockholm, Sweden
eChemtronica AB, Bergkällavägen 37C, 192 79 Sollentuna, Sweden
fDepartamento de Física, Universidade Federal do Paraná-UFPR, 81531-980, Curitiba-PR, Brazil
gMaterials Theory Division, Department of Physics and Astronomy, Uppsala University, Box 516, 75120 Uppsala, Sweden
hDepartment of Engineering and Physics, Karlstad University, 65188 Karlstad, Sweden. E-mail: cleber.marchiori@kau.se
First published on 5th January 2022
Abstract
The correct determination of the ionization potential (IP) and electron affinity (EA) as well as the energy gap is essential to properly characterize a series of key phenomena related to the applications of organic semiconductors. For example, energy offsets play an essential role in charge separation in organic photovoltaics. Yet there has been a lot of confusion involving the real physical meaning behind those quantities. Experimentally the energy gap can be measured by direct techniques such as UV-Vis absorption, or indirect techniques such as cyclic voltammetry (CV). Another spectroscopic method is the Reflection Electron Energy Loss Spectroscopy (REELS). Regarding data correlation, there is little consensus on how the REELS’ energy gap can be interpreted in light of the energies obtained from other methodologies such as CV, UV-Vis, or photoemission. In addition, even data acquired using those traditional techniques has been misinterpreted or applied to derive conclusions beyond the limits imposed by the physics of the measurement. A similar situation also happens when different theoretical approaches are used to assess the energy gap or employed to explain outcomes from experiments. By using a set of porphyrin derivatives as model molecules, we discuss some key aspects of those important issues. The peculiar properties of these porphyrins demonstrate that even straightforward measurements or calculations performed in a group of very similar molecules need a careful interpretation of the outcomes. Differences up to 660 meV (∼190 meV) are found comparing REELS (electrochemical) measurements with UV-Vis energy gaps, for instance. From the theoretical point of view, a reasonable agreement with electrochemical measurements of the IP, EA, and the gap of the porphyrins is only obtained when the calculations involve the full thermodynamics of the redox processes. The purpose of this work is to shed light on the differences and similarities of those aforementioned characterization methods and provide some insight that might help one to develop a critical analysis of the different experimental and theoretical methodologies.
1. Introduction
For a couple of decades, organic semiconductors (OS) have been extensively investigated as candidate materials for optoelectronic devices such as field-effect transistors (OFETs),1–4 light-emitting devices (OLEDs),5–10 photovoltaics (OPVs)11–17 and more recently for solar-fuel production18–23 and energy storage such as Lithium-ion batteries (LIB).24–29 OS are very appealing thanks to several intrinsic characteristics of organic materials viz. processability from solution, mechanical flexibility enabling integration to curved or flexible substrates, easy functionalization leading to the possibility to fine-tune their optoelectronic properties. In what concerns the easier synthesis and/or functionalization one remarkable feature is the possibility of adjusting the energy levels which, to some extent, will control the charge transfer mechanism in the redox-like reactions as well as the optical absorption. This tailoring can be done by combining electron-rich and electron-withdrawing moieties forming the so-called Donor–Acceptor (D–A) molecules or copolymers.30–33 This strategy was one of the driving forces for the impressive development of OPVs, which now are reaching the market as an alternative for clean energy generation.In fact, for all the mentioned application, a proper assessment of the ionization potential (IP) and electron affinity (EA) as wells as the energy gap is crucial, not only as a basic characterization of newly synthesized materials but also to conceive the combination of materials to be used to assemble the device. To cite an example, the energy offsets play a key role in the charge separation in OPVs.34–37 Since the advent of the new electron acceptors, commonly called non-fullerene acceptor (NFA), an intense debate is taking place regarding the need (or not) of an IP offset between the donor and acceptor materials for the charge transfer process when the acceptor is excited by the absorption of a photon.37–41 Additionally, a simplistic comparison of energy levels measured for the isolated materials cannot fully describe the charge transfer process.42 Concerning the energy gap, different techniques are used to measure it both as a direct measurement, such as UV-Vis absorption, or as an indirect measurement, such as cyclic voltammetry (CV). In CV measurements both the reduction and oxidation processes are accessible so that the energy gap will be defined as the difference between the reduction and oxidation potentials multiplied by the fundamental electron charge. Finally, the energy gap can be evaluated by spectroscopic measurements if one has access to ultraviolet photoelectron spectroscopy (UPS)43 to directly measure the HOMO energy and inverse photoemission spectrocopy44,45 to probe the LUMO energy (then the energy gap is determined by the HOMO–LUMO difference).
Another spectroscopic technique that could be used to probe the energy gap is the Reflection Electron Energy Loss Spectroscopy (REELS). A REELS spectrum is obtained by firing monochromatic electrons at the surface of the analyte. After interacting through elastic and inelastic scattering, the reflected electrons are collected by an electron energy analyzer, which records their reminiscent kinetic energy. One of the advantages of REELS lies in the elastically backscattered portion of a REELS spectrum as it allows to quantify hydrogen atoms at the surface of the samples.46 Furthermore, the study of the inelastic peaks helps towards chemical characterization of materials as they hold information about valence and inner-shell excitations. That is the main reason why this technique can also be used to estimate the energy gap.47,48 Additionally, the REELS spectrum can be acquired combined with the UPS measurement in the same experimental setup and most important, in the same sample spot. Although most of the works reported in the literature are still focused on inorganics, the energy gap is undeniably a very important parameter for semiconducting organic molecules and indeed there are several examples of successful applications of REELS into organic systems.49–52
Regarding data correlation, there is little consensus in the literature on how the energy gap determined through REELS is physically related to the ones determined through other methodologies, such as CV, UV-Vis, or photoemission. In optical measurements, for instance, the energy gap is the lowest incident energy for photon absorption, i.e., the onset of the absorption band. In this case, there is an additional information due to the interaction between the electron and the hole (exciton), which should affect the gap obtained through this method. The exciton binding energy may range from few meV to 1.5 eV depending on the material.53 Vos et al.49 have pointed out these energy gap discrepancies and suggested that the gap obtained by REELS could be higher than those obtained through UV-Vis and closer to the actual energy separation between valence and conduction bands (obtained through the combination of direct and inverse photoemission). On the other hand, Y. R. Denny et al. reported gaps determined by REELS for oxide thin films that were consistent and comparable to the ones obtained by UV-Vis spectroscopy.48 Furthermore, the surface sensitivity of REELS is expected to be higher when compared to photon-based measurements since it is well-known that electrons have less penetration depth into solids.54 Consequently, surface effects may not be completely discharged when analyzing energy gap values obtained through REELS. In the event of a more conventional method such as CV measurements involving organic materials, several approximations are inevitable to correlate the electrochemical potentials with orbital energies, as described by C. M. Cardona et al. in their report.55 Moreover, in spectroscopic measurement of energy gaps, such as UV-Vis and REELS, the electronic transitions take place in a very fast rate, in comparison with the nuclei relaxation, resulting in the so-called vertical energy gap, while in the CV measurement the redox reaction are slow (at least when compared to the characteristic time for photon absorption) allowing structural relaxation providing an adiabatic energy gap. Because of all those peculiarities, energy gap evaluations in organic semiconductors (especially when derived employing different experimental techniques) must be interpreted with caution.
Theoretical estimation of energy gaps also has challenges of its own. It can be determined as an energy difference between the frontier orbitals (HOMO and LUMO), which is analog to the photoemission assessment of the gap. It can also be determined by the difference between the calculated redox potential obtained by properly preparing the ionic states and computing all the thermodynamic contributions to the Gibbs free energy,56–58 which should be more comparable to CV based measurements. Another way is to calculate the energy of the first electronic excitation via time-dependent calculation which is the theoretical analog of a UV-Vis measurement. According to our experience, a comparative analysis of these quantities is not often seeing in the literature.
Besides the non-trivial correlation of those different techniques commonly used to probe the energy gap, a lack of standardized nomenclature is also a clear issue. Usually, the terminology bandgap is used, perhaps borrowed from the inorganic semiconductor field. This sounds inappropriate for organic semiconductors as for most of them the intermolecular interaction is rather weak, resulting in more molecular-like electronic structure without the formation of bands. In those cases, the term energy gap is more appropriated. Another point is the proliferation of many specifications associated to the term “gap” like transport gap, optical gap, and electrochemical gap, which raises an important question on which of them should be used to describe a general physical process or what is the meaning of them. That is a crucial discussion since those terms do not denote simple nomenclature differences, but they represent distinct physical concepts that are related to specific information about the energetics of the material. These subtle differences should be considered for a sound interpretation of the desired physical/chemical phenomena.
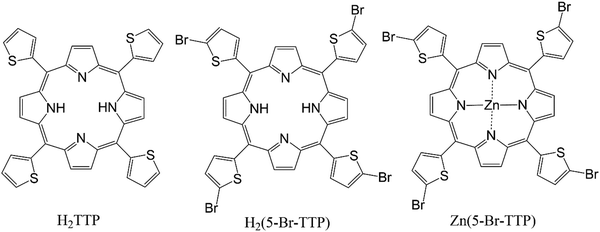
To shed some light on this discussion we present here a comparative study of different experimental and theoretical assessments of energy gaps for a set of porphyrin derivatives, viz.H2TTP – 5,10,15,20-tetra(thiophen-2-yl)porphyrin, H25BrTTP – 5,10,15,20-tetrakis(5-bromothiophen-2-yl)porphyrin and Zn5BrTTP – 5,10,15,20-tetrakis(5-bromothiophen-2-yl)porphyrin; Zn(II) complex (see Scheme 1). The chosen porphyrins display interesting features showing clearly that even straightforward measurements or calculations carried out in a group of similar molecules need to be carefully analyzed to have the proper interpretation of the outcomes. For instance, the REELS determination of the energy gap can lead to a difference up to 600 meV in comparison to UV-Vis since the first absorption peak has very low intensity being difficult to resolve in the REELS spectra. Additionally, the optical and electrochemical energy gaps displayed a difference up to 100 meV because of the different nature of these two measurements. From the theoretical perspective, the need for a proper assessment of the redox potentials is clear when one compares the HOMO–LUMO energy gap and the gap estimated considering the ionic states and the full thermodynamics of the redox processes. The critical analysis of those different methodologies to determine the energy gap can contribute to the debate regarding the real meaning of these quantities and how to properly interpret them.
2. Experimental and computational methods
As mentioned before, three porphyrin derivatives were considered in this study as shown in Scheme 1.59 We restricted our discussion to a narrow number of strongly related molecules to avoid further confusions and complexities associated to variations in the chemical structure of the OS. It is worth to mention that, among several interesting properties, these materials were shown to be very good π-stackers, a behavior which can explain the results discussed in Section 4. For the three materials, the energy gap was determined using both experimental and theoretical approaches whose methods are described below.All the measurements describe bellow were performed in solution and/or thin film deposited from solution.
2.1. Reflection electron energy loss spectroscopy (REELS)
Reflection Electron Energy Loss Spectroscopy (REELS) spectra were carried out using the Thermo Escalab 250Xi spectrometer. The pressure inside the vacuum chamber was maintained below 5 × 10−9 mbar. REELS spectra were measured using a primary electron beam with energy of 1000 eV and spot size of 150 μm, an electron current of 5 nA and a constant analyzer pass energy of 12 eV. The full-width at half-maximum (FWHM) of the elastic peak in this experimental condition was 0.6 eV.2.2. Cyclic voltammetry
The redox potential and the ionization energy (IP) and electron affinity (EA) associated with the potentials were achieved through cyclic voltammetry measurements. The equipment used, a CompactStat from Ivium technologies, consists essentially in a set of a controller module, a sealed electrochemical cell with an atmosphere controlled by a constant flow of nitrogen and a set of three electrodes, which setup is composed by: (a) a graphite electrode as working electrode (where the redox process occurs), (b) an Ag–AgCl as reference electrode and (c) a platinum wire as a counter electrode.In order to setup the optimal measurements condition, an initial electrochemical cell composed of a solution of 10 mL of anhydrous dichloromethane (CH2Cl2) and 193.7 mg of tetrabutylammonium hexafluorophosphate (TBAPF6) as electrolyte support55 was prepared, to check the quality of the solvent and identify the potential presence of contaminants. After that, ferrocene Fe(C5H5)2, whose voltammogram profile is well known by IUPAC (International Union of Pure and Applied Chemistry),60 was used as a reference and to calibrate the system.
The solution of the three porphyrins (H2TTP, H25BrTTP and Zn5BrTTP) were prepared separately at a concentration of 10−3 M in 10 mL of CH2Cl2 plus 193.7 mg of TBAPF6, then transferred to different pre-cleaned electrochemical cells. Each measure was performed between the pivoting points (−1.5 V to 1.5 V) with a step of 50 mV s−1 during 3 cycles.
2.3. UV-Vis measurements
The linear absorption spectra were measured using the PerkinElmer Lambda 950 UV-Vis spectrophotometer equipped with deuterium and halogen lamps. The samples, which consist in thin solid film and solutions were measured in the range of 300–800 nm at room temperature. Thin films were manufactured through the spin-coating method from a concentration of 4 mg mL−1 in THF and then spin cast at 900 rpm for 60 s with average thickness in the order of 20–25 nm on quartz substrate. For liquid measurements, the spectra were measured for samples with concentrations ranging from 10−4 to 10−7 M in THF solution into a quartz cuvette.2.4. Computational methods
The redox potential and the Gibbs free energies associated to oxidation and reduction processes were also assessed theoretically by means of Density Functional Theory (DFT). The procedure to obtain the Gibbs free energy variation, associated to the oxidation and reduction reactions for the redox pair P+/P0(Eox) and P0/P−(Ered) was as follow. First the structures were optimized using M0661 as exchange–correlation functional and 6-311++G(d,p) as basis-set,62–64 followed by frequency calculations to get the Gibbs free energies for the neutral and ionic species. The Gibbs free energy was calculated as| Gsolv = Eelect + EZPE + PV + U298 – TS298, | (1) |
| EECalcG = Ered – Eox. | (2) |
Additionally, the HOMO–LUMO energy gaps (EESCFG) were obtained directly from self-consistent field DFT calculations.
Finally, the electronic transitions were calculated within the TD-DFT framework, by considering the first 100 singlet electronic transitions at the same theory level described before. These calculations provided the optical energy gap (OECalcG) by considering the energy of the first electronic transition. All the calculations were performed using the Gaussian16 code.65
3. Results
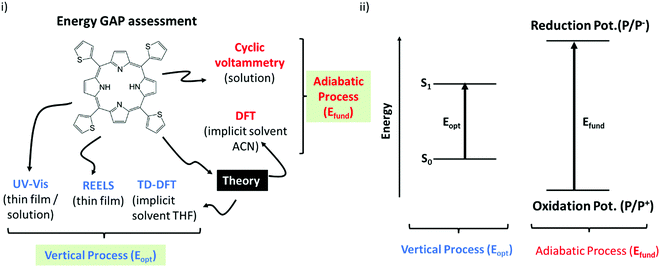
Before going to the results, it is important to consider Scheme 2. Essentially it classifies the gaps in two major groups:66 (i) The first group is formed by the techniques that quantifies the optical gaps (Eopt). Here it corresponds to the experimental gaps given by REELS and UV Vis and the theoretical gap calculated by TD-DFT (OECalcG). The methods in this group are characterized by very fast electronic transitions so that the geometry of the molecules is essentially frozen (vertical transition) during the gap quantification. (ii) The second group is constituted by the techniques that evaluate the fundamental gap (Efund). Here it corresponds to the cyclic voltammetry measurements and the theoretical gap (EECalcG). The methods in this group are characterized by slow adiabatic processes that allow nuclear relaxation.Scheme 2 can be used as a guide to clarify the basic physics behind each kind of energy gap, and it will be very helpful for the discussions below. The basic distinction illustrated in this scheme should always be remembered before any direct inference from the numerical results reported in the next section.
3.1. REELS measurements
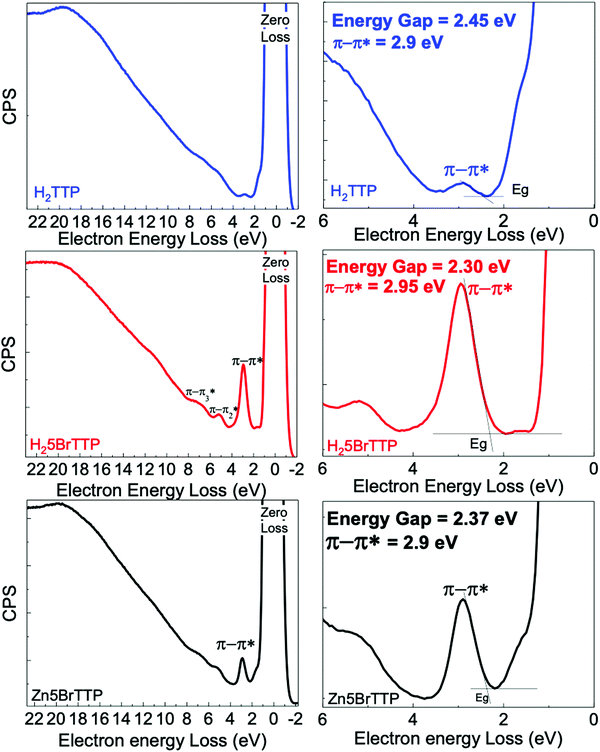
Fig. 1 presents REELS measurements for samples deposited onto ITO/glass substrate. The most intense peak of all REELS spectra has 0 eV of electron energy loss and therefore it is also called the zero-loss peak. This peak is related to the elastically backscattered electrons from the surface of the thin films.67,68However, the more energetic and less intense peaks observed emerge from inelastic scattering between the electrons and the surface. In particular, the low-loss energy region contains useful information about valence electronic transitions of the material.68 In this specific region, depending on the analyzed sample, an inelastic peak emerges between 2.70 eV and 2.95 eV, which usually can be attributed to the less energetic π–π* transitions. Thus, we have used the onset of this particular peak to obtain the electronic energy gap for each sample as shown in Table 1. All samples presented electronic energy gaps in the 2.00–2.50 eV energy range. The highest gap was derived for the H2TTP. When brominated, it was observed a small decrease in the electronic energy gap. Another interesting finding is that the presence of Zinc in the porphyrin ring slightly increased the electronic energy gap.
| Onset energy − Eonset (eV) | Maximun energy − Emax (eV) | |
|---|---|---|
| H2TTP | 2.45 | 2.90 |
| H25BrTTP | 2.30 | 2.95 |
| Zn5BrTTP | 2.37 | 2.90 |
3.2. Cyclic voltammetry measurements
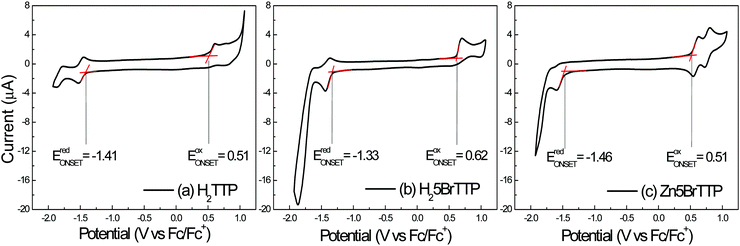
Fig. 1 shows the voltammograms obtained for the three porphyrin derivatives by using cyclic voltammetry. The three porphyrin derivatives displayed quasi-reversible oxidation and reduction processes. The redox potentials for the compounds were determined by considering the onset of the oxidation and reduction peaks, respectively. Ferrocene (Fc/Fc+), which presents the well-defined and characteristic voltammogram (see Fig. S1 in the ESI†), was the reference sample. Two peaks of oxidation and reduction were observed at 0.55 V and 0.46 V, respectively. The potential obtained through the onset methodology is located at 0.43 V, when using a similar experimental setup as reported by Cardona.55In Fig. 2a) the H2TTP voltammogram shows the main oxidation peak at 0.60 V and the main reduction peaks at −1.52 V, with the onset potentials obtained at 0.51 V and −1.41 V, respectively. For negative bias this molecule presents a reversible local reduction process and oxidation peaks at −1.52 V and −1.44 V, respectively. For a positive applied bias, an irreversible process was noticed, showing a peak at 0.60 V.
A similar behavior was observed for the H25BrTTP molecule, as shown in Fig. 2b). The main oxidation peak is localized at 0.69 V and the main reduction peak at −1.44 V. The oxidation onset is located at 0.62 V while the reduction onset was obtained at −1.33 V. Reversible processes were observed when negative voltage was applied.
For the Zn5BrTTP molecule, present in the Fig. 2c), two reversible processes were observed with oxidation peaks at 0.62 V and 0.80 V and reduction peaks at 0.54 V and 0.73 V. In the negative voltage bias, it was observed one single reduction peak at −1.59 V and a one tiny oxidation peak at −1.55 V. The onset values were 0.51 V and −1.46 V for oxidation and reduction potentials, respectively.
The energy gaps obtained from the electrochemical measurements (EEG) are 1.92 eV for H2TTP, 1.95 eV for H25BrTTP and 1.97 eV for Zn5BrTTP.
The results discussed up to now reveals a major disagreement for energy gaps obtained from REELS and CV measurements. Following the classification in Scheme 2, the first is an optical gap while the second is a fundamental gap so that a fair agreement between these two quantities is highly unexpected. Yet the details behind this discrepancy will be better rationalized in the Discussion section.
3.3. UV-Vis measurements
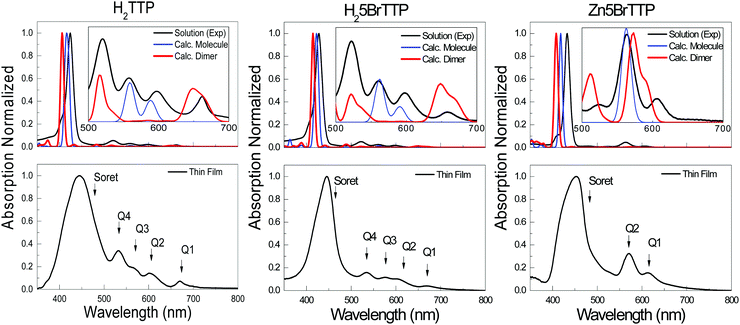
Aiming to address further fundamental variations between the energy gaps measured by spectroscopic or electrochemical techniques, we recurred to a second experimental technique to measure Eopt, viz. UV-Vis absorption. In addition, we also performed theoretical assessment of the optical and electrochemical properties that will be presented and discussed later.Fig. 3 shows the spectra for H2TTP, H25BrTTP and Zn5BrTTP which were measured in a THF solution at 10−5 M as well as in thin films. The spectra exhibit the main absorption peak centered at around 435 nm, labeled as the Soret band and also minors bands, commonly called Q-bands,69 located at higher wavelengths (530–670 nm).
Different procedures to determine the UV-Vis optical gap were considered, such as the onset absorption edge70–72 and Tauc plot.73–75 (To check other procedures, see Table S2, ESI†). When using the absorption onset edge method, the UV-Vis optical gap (OEG) can be achieved from the offset wavelength (λedge) derived at a low energy absorption band, estimated according to:
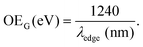 | (3) |
By using the Tauc plot method, the OEG is determined through a linear extrapolation of the observed trend in the spectral dependence of (αhν)1/2 which intercepts the abscissa axis giving by the photon energies hν following the relation:76
| (αhν)1/2 ∝ (hν − OEG), | (4) |
| Onset absorption edge | Tauc plot | |||
|---|---|---|---|---|
| Solution (eV) | Thin film (eV) | Solution (eV) | Thin film (eV) | |
| H2TTP | 1.84 | 1.79 | 1.81 | 1.77 |
| H25BrTTP | 1.82 | 1.76 | 1.80 | 1.70 |
| Zn5BrTTP | 1.97 | 1.85 | 1.85 | 1.86 |
As expected, the thin film spectra displayed a redshift in the absorption, when compared to the spectra measured in solution, as well as broadening of the peaks (see Fig. 3) because of solid-state effects associated to π-stacking and formation of aggregates. For this reason, the OEG is lower for the films than in solution. Regarding the two different methods (absorption onset and Tauc plot), one can see that they are equivalent since their application only result in minor variations of OEG.
As one could anticipate, the OEG is slightly smaller than the EEG. As a matter of fact, this is one important point to be discussed. The EEG and OEG are two different quantities in essence since the first is an optical gap whereas the second is a fundamental gap. However, sometimes these two concepts are mixed or referred in the literature as the same property. A more detailed discussion regarding this topic will be conducted in Section 4.
3.4. Redox potentials and UV-Vis assessment from DFT and TD-DFT calculation
Theoretical determination of energy levels and optical properties are nowadays quite common practice thanks to advances in computational resources and the dissemination of quantum mechanics packages. Here, we present the evaluation of the energy gaps (the calculated analogs to EEG and OEG) from a perspective of atomic-scale modeling.Table 3 summarizes the main results of our calculations. It shows the energies of the HOMO and LUMO orbitals and the calculated free energies for the reduction and oxidation reactions together with the respective energy gaps for the three porphyrin derivatives considered in this study. ESCFG is the HOMO–LUMO gap obtained directly from the Self-Consistent Field (SCF) calculation and EECalcG is the gap derived from the difference between the Eox and Ered free energies. It is clear the discrepancy between the values of energy gaps obtained directly from the SCF calculation and the values obtained from a more elaborated methodology which considers variations of the Gibbs free energy for the redox process.
| HOMO (eV) | LUMO (eV) | E SCFG (eV) | E ox (eV) | E red (eV) | EECalcG (eV) | |
|---|---|---|---|---|---|---|
| H2TTP | −5.73 | −2.69 | 3.04 | −5.06 | −3.27 | 1.79 |
| H25BrTTP | −5.98 | −2.98 | 3.00 | −5.46 | −3.38 | 2.08 |
| Zn5BrTTP | −6.02 | −2.89 | 3.13 | −5.41 | −3.22 | 2.19 |
It is commonly acknowledged in the literature that the discrepancy between the experimental and calculated LUMO energy has its origin in the fact that DFT calculations are not suitable to describe unoccupied orbitals. Indeed, this is one of the reasons behind the bad description of LUMO energies estimated using this method. However, there are more to be considered if one aims for a proper theoretical description of the redox potential or other characteristic energies like IP and EA. One strong indication of that is the clear difference between the HOMO energy and the Eox in Table 3, revealing that the HOMO energy assessed from SCF calculations is not directly comparable to the oxidation energy. This is equally valid if one wants to compare the calculated HOMO energy in Table 3 with experimental values. This result raises an important discussion on how significant a simple DFT calculation is to explain certain properties of organic materials. Of course, the DFT method is of great relevance to estimate electronic properties of organic semiconductors. Yet one needs to be meticulous and (in most of the cases) go beyond a simple geometry optimization or single-point calculations to address some key features of these materials. For instance, a more sophisticated approach might be fundamental to get relevant information about redox potentials which is essential to properly characterize processes involving charge transfer. The comparison between experimental and theoretical energy gaps will be left to Section 4.
Regarding the optical absorption, it is well known that TD-DFT is a powerful tool to describe the UV-Vis absorption profile as well as to provide important information about the nature of the electronic transitions which contribute to each absorption band.
Fig. 3 shows the comparison of experimental UV-Vis and the calculated spectra. Although the fair agreement regarding the main absorption peak, the Soret band, and even the overall shape, when zoom out one can see that some features are not captured by a single molecule calculation (see the inset in Fig. 3). To properly explain the Q bands, it was necessary to perform calculation for dimers aiming to model the presence of complex molecular agglomerates which might be formed even in solution. As depicted in the insets of Fig. 3, two of the Q bands sound to have an intrinsic origin while two of them only appear when an aggregate model is considered. This effect results in two different energies for the first singlet electronic transition which here has been called OECalcG, being the dimer energy gap lower in ∼0.25 – 0.15 eV in comparison to the gap calculated considering an isolated molecule (see Table 3).
4. Discussion
After showing several values of energy gaps obtained with different experimental and theoretical methodologies, it is worth rationalizing those results. The idea is to instigate a necessary discussion on the meaning of those quantities and their respective conceptual basis. In addition, it is also worth to promote a critical analysis on how simplistic and uncareful interpretations of experimental and theoretical data can influence the validity of conclusion drawn from those measurements. Table 4 summarizes all the relevant outcomes that were discussed separately in the previous sections. It compiles the different energy gaps obtained experimentally and theoretically and how they are arranged in the two groups of Scheme 2.| Experimental | |||||
|---|---|---|---|---|---|
| EEG (eV) | OEG,sol (eV) | OEG,film (eV) | REELS Eonset (eV) | REELS Emax (eV) | |
| H2TTP | 1.92 | 1.84 | 1.79 | 2.45 | 2.90 |
| H25BrTTP | 1.95 | 1.82 | 1.76 | 2.30 | 2.95 |
| Zn5BrTTP | 1.97 | 1.97 | 1.85 | 2.37 | 2.90 |
| Theoretical | ||||
|---|---|---|---|---|
| EECalcG (eV) | OECalcG single molecule (eV) | OECalcG dimer (eV) | E λmax (eV) | |
| H2TTP | 1.79 | 2.10 | 1.87 | 2.92 |
| H25BrTTP | 2.08 | 2.10 | 1.85 | 2.94 |
| Zn5BrTTP | 2.19 | 2.20 | 2.05 | 2.93 |
One striking result in Table 4 is the great contrast among the energy gaps measured by REELS relative to the other measurements, especially to the UV-Vis. In principle both techniques should lead to equivalent results since they belong to the group of optical gaps in Scheme 2. But before further discuss this issue, it is worth highlighting the main aspects underlying the REELS technique. Primarily, the raise of the inelastic peak to the left side of the highly intense zero-loss (or elastic) peak is related to the energy transfer from the incident electrons to the valence electrons enabling the electronic transitions. This process would be REELS’ analog to photon absorption in UV-Vis absorption measurement. In this sense one may suggest that the REELS spectrum, at least in the energy range close to the material's gap, should resemble the standard optical spectrum. Following this assumption, the REELS spectrum may carry information regarding the energy gap that would agree with OEG. However, the validity of this assumption is arguable for low energy gap materials when the spectrum features associated to OEG are close to the zero-loss peak (becoming indistinguishable from the hydrogen loss peak at 1.8 eV) and/or when there are weaker electronic excitations associated to the HOMO–LUMO transition. Both undesirable characteristics seems to be present in the REELS measurements of the porphyrin derivatives considered in this study since the Q's bands of the UV-Vis spectra are completely masked by the hydrogen loss peak. Yet one can see from Fig. S2 and Table S2 (ESI†), the onset of the Soret band is in quite good agreement with the energy onset obtained from REELS spectrum, showing unambiguously that the electron energy loss technique is indeed able to detect the most intense band of photon absorption. If one defines the energy gap as the first electronic transition involving the HOMO and LUMO orbitals, the porphyrins are an example on how uncareful comparisons between experimental data measured using different techniques (in this case UV-Vis and REELS) can be confusing.
Regarding the electrochemical and optical measurements, a small divergence in the energy gaps was observed despite the different basic nature of those gaps (see Scheme 2). However, there are key aspects regarding the physical processes involved in those measurements that it is worth discussing. Even when an apparent match between the electrochemical and optical gap are achieved caution must be taken when comparing these values as the similar values can be an artifact of terms cancelation (viz. adiabatic or vertical, solvation, exciton binding energy, etc…).
Contrary to the UV-Vis technique, electrochemical determination of the redox potentials (that gives EEG) quantifies a fundamental gap which involves slow adiabatic charge transfer processes. Consequently, the final reduced or oxidized species may have enough time to relax its structure in order to accommodate the excess charge. This relaxation is followed by a stabilization of the charge state by the dielectric environment and the charge compensation by interaction with the respective counter-ions. The optical (UV-Vis spectroscopy) measurement, on the other hand, probes an optical gap which depends on the electronic transitions promoted by the absorption of a photon that excites electrons from occupied electronic states to unoccupied ones. In principle it does not produce a net charge on the excited molecule and is usually fast compared to any structural relaxation (vertical transition). In addition, the intensity of this absorption depends on the energy of the incident photon and on the symmetry of the states involved in the electronic excitation. Due to these distinctions, the assessment of the HOMO–LUMO energy, as usually this gap is assumed to be in the literature, can be quite tricky and even misleading.
Another point is that the fundamental and optical gap tends to be different for a solvated isolated molecule or molecules in the solid-state because of enhanced intermolecular interactions as well as variations in the dielectric screening. Such effects might add additional caution when comparing gaps measured in solution or in thin films as highlighted in the commentaries about Table 2.
Two important facts cannot be ignored for a sound estimative of the gap using optical measurements:
(i) First, the HOMO → LUMO transition leads to a state in which the excited electron is experiencing an electrostatic interaction with the net coulombic potential generated by the positive charges of N nuclei and the negative charges of the N − 1 electrons that remains in the occupied states. The absence of the excited electron from the HOMO can then be modeled as a hole (effective positive charge equivalent to the net charge between N nuclei and the N − 1 electrons). This interaction gives rise to a bounded state called exciton (or electron–hole pair). In this sense, the value of OEG brings the influence of the exciton binding energy which contributes to the difference between this value and the energy gaps measured by assessing IP and EA either through spectroscopic (UPS and IPES) or electrochemical (CV) techniques. In this sense OEG tends to underestimate the gap given by the difference between IP and EA as can be verified in Table 4.
(ii) Second, for highly symmetric molecules the HOMO → LUMO transition can be forbidden by selection rules due to the parity of the orbitals. In this case, the OEG obtained might not correspond exactly to the HOMO–LUMO energy difference. Indeed, the absorption spectrum of porphyrins is again an example of this fact. This spectrum has been explained in terms of the “four-orbital” (two degenerated highest occupied π orbitals and two degenerated lowest unoccupied π* orbitals). This oversimplified picture well reproduces the major feature of these systems. The Q and Soret bands arise from a linear combination of these one-electron transitions. For the lower Q band, the transition dipoles nearly cancel producing a weak absorption in the visible region. For the Soret band, the transition dipoles reinforce, resulting in the very intense absorption in the UV region.77 Hence, even though the S band involves a HOMO → LUMO transition, it corresponds to a slightly higher energy compared to the lowest energy necessary to excite an electron between these two states.
Having these concepts in mind, one should acknowledge that the use of OEG to estimate the missing potential (or energy level) can be, for some materials, a very rough approximation, and any conclusion based on these measurements (viz. energy levels offset, …) should take those aspects into account. For instance, if the OEG was used to estimate the EA of the porphyrins reported in this study, the deviation would be between 80 meV and 130 meV (considering the UV-Vis measured in solution). This difference is more than enough to eventually mislead a discussion for which the determination of the EA position is crucial, as it is the case of charge separation or charge injection processes in organic electronics.
Finally, regarding the theoretical assessment of energy gaps, the outcomes of our calculations make clear the need for a proper treatment of the redox processes aiming to achieve a good description of the redox potentials. A reasonable theoretical estimate of the energy gap (that can be compared to the EEG obtained by CV measurements) is found only after computing the entire free energies for the oxidation and reduction processes. Considering the H25BrTTP molecule for instance, a large discrepancy was observed between the HOMO (LUMO) energy taken directly from SCF calculations and the IP (EA) determined by the electrochemical method (a deviation of 590 meV for IP/HOMO and 460 meV for EA/LUMO). On the other hand, the IP and EA are in reasonable agreement with the respective calculated redox potentials showing a deviation of 70 meV for the oxidation potential (IP/ΔGP+/P0) and 60 meV for the reduction potential (EA/ΔGP0/P−). For further details regarding these values, see Table 3 and Table S1 from the ESI.† Actually, one important consideration is needed at this point. Although the energies obtained from CV measurements (when converting the redox potentials to absolute values of energy against vacuum) are commonly called HOMO and LUMO energies, they do not correspond to the molecular eigenvalues or, in other words, orbital energies. They bring much more information than only quantities related to electronic states. As mentioned before, a whole thermodynamic process is probed by these measurements, and the energies associated to redox potentials are, in essence, free energy variations of the oxidation/reduction electrochemical reaction. Those variations involve entropic contributions and structural relaxation. Hence the energies assessed by those techniques are more suitable to describe adiabatic charge transfer reactions. In contrast, the “real” HOMO and LUMO energies (that play a key role in ultrafast charge transfer dynamics) are more likely to be assessed by UPS and IPES measurements, respectively. It is important to acknowledge that the redox free energies and the orbitals energies might be close for systems characterized by small contributions of thermal and reorganization energies. However, even in these cases, the meaning of these two quantities is still different.
Regarding the calculated OEG, a good theoretical–experimental agreement can be achieved when considering the proper level of theory (DFT exchange–correlation functional and basis set), as well as the appropriate molecular model. The latter is the main source of inaccuracy for the molecules considered here since single molecule calculations cannot fully reproduce the experimental absorption. As shown in Table 4, a remarkable agreement between theory and experiment is obtained when considering a dimer of molecules as the primary molecular model. Using this approach, the calculate OEG in solution differs only 30 meV from the experimental value for H2TTP and H25BrTTP, and 80 meV for Zn5BrTTP. This is an indication that these porphyrins are prone to form aggregates (which increases intermolecular interactions) even in low concentration solutions (see Fig. S3, ESI†).
5. Conclusions
By using three porphyrin derivatives as model compounds, we attempt to reconcile experimental and theoretical methodologies for the determination of the energy gap. Different assessments of the gap are a source of divergences and even controversies in the literature which may eventually lead to misleading conclusions. The situation can be specially confusing when comparing gaps obtained by methods that involves adiabatic processes (fundamental gap, Efund) with the ones obtained involving fast electronic transitions (optical gap, Eopt). A clear distinction between those two general types of energy gaps is essential towards finding a wide accepted and sound conceptual framework to this important physical quantity.In more specific terms, REELS is a particularly useful spectroscopic tool that, among other applications, can aid in the determination of the optical gap. This technique can be particularly useful when UPS measurements are performed to assess the IP of a given material. In principle REELS measurements are expected to closely match the UV-Vis absorption profile (another technique to measure Eopt). Yet the absorption onset obtained by REELS might not correspond to the Eopt for low energy gap materials and/or for those materials with a low-intensity first electronic HOMO → LUMO transition, which is the case of the porphyrin derivatives. In this sense, a previous knowledge of the material's electronic transitions is highly desirable for a proper interpretation of the REELS spectrum (at least in what concerns the energy gap determination). For this task, the theoretical calculation of the electronic transitions is a convenient tool.
TD-DFT calculations of the UV-Vis spectrum can also have their challenges, as observed in our model materials. When the intermolecular interaction is not negligible, the single molecule approach is not enough to fully describe the absorption features. In these cases, a cluster model (or at least dimer models as proposed here to the porphyrins) should be considered. This result highlights the importance of calibrating both the theoretical level and the molecular model against experimental data when the aim is to perform a joint experimental–theoretical study. This criterion procedure ensures the proper assignment of the photophysics/photochemistry underlying the target phenomena.
Regarding the theoretical determination of the IP and EA, attention must be paid to what indeed is aimed to be calculated. Simple DFT calculations, from which the HOMO and LUMO energies are obtained, are commonly used to address questions as energy offsets for charge transfer. This is a rough approximation since accurate values of energies for the charge transfer reaction, like the ones measured in a CV experiment for instance, can be significantly different from orbital energies of single molecules. Depending on the experimental technique, a better theoretical description of the measured data can be obtained only if thermal contributions and structural relaxation are not ignored during calculations.
Another source of misinterpretation is the common practice of using the optical gap to estimate the missing potential when the material cannot be reduced/oxidized. As these two quantities are unlike in essence, one needs to keep in mind the implications of those intrinsic differences on conclusions derived following such approximation.
The main conclusion one can learn from these simple model systems we discussed here is that even the most standard and well-established measurements as CV, spectroscopies as UV-Vis and REELS, and DFT calculations should be used having in mind the physics behind them and as consequence, how to properly interpret and use the outcomes of those measurements. Otherwise, the full comprehension of the system and the interpretation of the results can be compromised.
Author contributions
Rian E. Aderne and Harold C. Ávila were responsible for cyclic voltammetry and UV-Vis measurements, processing of experimental data. Bruno G. A. L. Borges was responsible for REELS measurements, Fredrik von Kieseritzky and Jonas Hellberg synthesized the molecules, contributed to the discussion, and revised the article. Marlus Koehler contributed to the discussion on how to interpret some of the experimental results. He also helped to revise and write some parts of the manuscript's text. Marco Cremona and Lucimara S. Roman provided assistance for data acquisition and analysis and revised the article. C. Moyses Araujo provided assistance for theoretical data acquisition and analysis as well as discussion and revised the article. Maria Luiza M. Rocco and Cleber F. N. Marchiori contributed to the conception, analysis, and substantial part of the writing process. Cleber F. N. Marchiori also performed the DFT calculation and theoretical data analysis. All authors approved the final manuscript.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
CFNM and CMA thank the Swedish National Infrastructure for Computing (SNIC) at the PDC Center for High-Performance Computing and National Supercomputer Center at Linköping University (NSC), The Swedish Research Council (VR) (grant no. 2020–05223), Swedish Energy Agency (grant no. 45420-1) and STandUP for Energy collaboration. MK, LSR, MC and MLMR thanks CNPq. MLMR and MC thanks FAPERJ and FINEP. MC thanks MCT-INEO and MLMR thanks CT-INFRA for financial support.References
- G. Horowitz, Adv. Mater., 1998, 10, 365–377 CrossRef CAS.
- J. Zaumseil and H. Sirringhaus, Chem. Rev., 2007, 107, 1296–1323 CrossRef CAS PubMed.
- M. Małachowski and J. Żmija, Opto-Electron. Rev., 1989, 91, 1062–1065 Search PubMed.
- H. Sirringhaus, Adv. Mater., 2005, 17, 2411–2425 CrossRef CAS.
- P. A. Levermore, R. Jin, X. Wang, J. C. de Mello and D. D. C. Bradley, Adv. Funct. Mater., 2009, 19, 950–957 CrossRef CAS.
- J. Ràfols-Ribé, P.-A. Will, C. Hänisch, M. Gonzalez-Silveira, S. Lenk, J. Rodríguez-Viejo and S. Reineke, Sci. Adv., 2018, 4, eaar8332 CrossRef PubMed.
- R. A. K. Yadav, D. K. Dubey, S.-Z. Chen, T.-W. Liang and J.-H. Jou, Sci. Rep., 2020, 10, 9915 CrossRef CAS PubMed.
- R. Isci, E. Tekin, K. Kaya, S. Piravadili Mucur, S. F. Gorkem and T. Ozturk, J. Mater. Chem. C, 2020, 8, 7908–7915 RSC.
- X. Zheng, Y. Liu, Y. Zhu, F. Ma, C. Feng, Y. Yu, H. Hu and F. Li, Opt. Mater., 2020, 101, 109755 CrossRef CAS.
- D. Chen, W. Li, L. Gan, Z. Wang, M. Li and S. J. Su, Mater. Sci. Eng., R, 2020, 142, 100581 CrossRef.
- C. D. Canestraro, P. C. Rodrigues, C. F. N. Marchiori, C. B. Schneider, L. Akcelrud, M. Koehler and L. S. Roman, Sol. Energy Mater. Sol. Cells, 2011, 95, 2287–2294 CrossRef CAS.
- H. Yao, L. Ma, H. Yu, J. Yu, P. C. Y. Chow, W. Xue, X. Zou, Y. Chen, J. Liang, L. Arunagiri and F. Gao, Adv. Energy Mater., 2020, 2001408, 1–6 Search PubMed.
- Q. Fan, Q. An, Y. Lin, Y. Xia, Q. Li, M. Zhang, W. Su, W. Peng, C. Zhang, F. Liu, L. Hou, W. Zhu, D. Yu, M. Xiao, E. Moons, F. Zhang, T. D. Anthopoulos, O. Inganäs and E. Wang, Energy Environ. Sci., 2020, 13, 5017–5027 RSC.
- H. Bin, L. Gao, Z. G. Zhang, Y. Yang, Y. Zhang, C. Zhang, S. Chen, L. Xue, C. Yang, M. Xiao and Y. Li, Nat. Commun., 2016, 7, 13651 CrossRef CAS PubMed.
- K. Cnops, B. P. Rand, D. Cheyns, B. Verreet, M. A. Empl and P. Heremans, Nat. Commun., 2014, 5, 3406 CrossRef PubMed.
- W. Zhao, D. Qian, S. Zhang, S. Li, O. Inganäs, F. Gao and J. Hou, Adv. Mater., 2016, 28, 4734–4739 CrossRef CAS PubMed.
- L. C. Wouk de Menezes, W. Renzi, C. Fabianodo Nascimento Marchiori, C. Karla BritesQueiroz Martins de Oliveira, F. von Kieseritzky, J. Leonil Duarte and L. Stolz Roman, J. Phys. Chem. C, 2018, 122, 5796–5804 CrossRef CAS.
- C. M. Aitchison, R. S. Sprick and A. I. Cooper, J. Mater. Chem. A, 2019, 37–39 Search PubMed.
- L. Wang, R. Fernández-Terán, L. Zhang, D. L. A. Fernandes, L. Tian, H. Chen and H. Tian, Angew. Chem., Int. Ed., 2016, 55, 12306–12310 CrossRef CAS PubMed.
- P. B. Pati, G. Damas, L. Tian, D. L. A. Fernandes, L. Zhang, I. B. Pehlivan, T. Edvinsson, C. M. Araujo and H. Tian, Energy Environ. Sci., 2017, 10, 1372–1376 RSC.
- D. J. Woods, R. S. Sprick, C. L. Smith, A. J. Cowan and A. I. Cooper, Adv. Energy Mater., 2017, 7, 1700479 CrossRef.
- M. Sachs, R. S. Sprick, D. Pearce, S. A. J. Hillman, A. Monti, A. A. Y. Guilbert, N. J. Brownbill, S. Dimitrov, X. Shi, F. Blanc, M. A. Zwijnenburg, J. Nelson, J. R. Durrant and A. I. Cooper, Nat. Commun., 2018, 9, 4968 CrossRef PubMed.
- A. Liu, C.-W. Tai, K. Holá and H. Tian, J. Mater. Chem. A, 2019, 7, 4797–4803 RSC.
- S. Renault, V. A. Oltean, C. M. Araujo, A. Grigoriev, K. Edström and D. Brandell, Chem. Mater., 2016, 28, 1920–1926 CrossRef CAS.
- T. B. Schon, B. T. McAllister, P. F. Li and D. S. Seferos, Chem. Soc. Rev., 2016, 45, 6345–6404 RSC.
- J. Wu, X. Rui, C. Wang, W.-B. Pei, R. Lau, Q. Yan and Q. Zhang, Adv. Energy Mater., 2015, 5, 1402189 CrossRef.
- N. Casado, D. Mantione, D. Shanmukaraj and D. Mecerreyes, ChemSusChem, 2020, 13, 2464–2470 CrossRef CAS PubMed.
- P. Acker, L. Rzesny, C. F. N. Marchiori, C. M. Araujo and B. Esser, Adv. Funct. Mater., 2019, 29, 1906436 CrossRef CAS.
- J. J. Samuel, V. K. Karrothu, R. K. Canjeevaram Balasubramanyam, A. A. Mohapatra, C. Gangadharappa, V. R. Kankanallu, S. Patil and N. P. B. Aetukuri, J. Phys. Chem. C, 2021, 125, 4449–4457 CrossRef CAS.
- H. Zhou, L. Yang, S. Stoneking and W. You, ACS Appl. Mater. Interfaces, 2010, 2, 1377–1383 CrossRef CAS PubMed.
- H. Zhou, L. Yang and W. You, Macromolecules, 2012, 45, 607–632 CrossRef CAS.
- Z. Cai, N. Zhang, M. A. Awais, A. S. Filatov and L. Yu, Angew. Chem., Int. Ed., 2018, 57, 6442–6448 CrossRef CAS PubMed.
- X. Wan, C. Li, M. Zhang and Y. Chen, Chem. Soc. Rev., 2020, 49, 2828–2842 RSC.
- J. Liu, S. Chen, D. Qian, B. Gautam, G. Yang, J. Zhao, J. Bergqvist, F. Zhang, W. Ma, H. Ade, O. Inganäs, K. Gundogdu, F. Gao and H. Yan, Nat. Energy, 2016, 1, 16089 CrossRef CAS.
- N. A. Ran, J. A. Love, M. C. Heiber, X. Jiao, M. P. Hughes, A. Karki, M. Wang, V. V. Brus, H. Wang, D. Neher, H. Ade, G. C. Bazan and T.-Q. Nguyen, Adv. Energy Mater., 2018, 8, 1701073 CrossRef.
- S. Li, L. Zhan, C. Sun, H. Zhu, G. Zhou, W. Yang, M. Shi, C.-Z. Li, J. Hou, Y. Li and H. Chen, J. Am. Chem. Soc., 2019, 141, 3073–3082 CrossRef CAS PubMed.
- Y. Liu, J. Zhang, G. Zhou, F. Liu, X. Zhu and F. Zhang, J. Phys. Chem. C, 2020, 124, 15132–15139 CrossRef CAS.
- L. Perdigón-Toro, H. Zhang, A. Markina, J. Yuan, S. M. Hosseini, C. M. Wolff, G. Zuo, M. Stolterfoht, Y. Zou, F. Gao, D. Andrienko, S. Shoaee and D. Neher, Adv. Mater., 2020, 32, 1906763 CrossRef PubMed.
- A. Karki, J. Vollbrecht, A. J. Gillett, P. Selter, J. Lee, Z. Peng, N. Schopp, A. L. Dixon, M. Schrock, V. Nádaždy, F. Schauer, H. Ade, B. F. Chmelka, G. C. Bazan, R. H. Friend and T. Nguyen, Adv. Energy Mater., 2020, 10, 2001203 CrossRef CAS.
- Y. Cai, H. Zhang, L. Ye, R. Zhang, J. Xu, K. Zhang, P. Bi, T. Li, K. Weng, K. Xu, J. Xia, Q. Bao, F. Liu, X. Hao, S. Tan, F. Gao, X. Zhan and Y. Sun, ACS Appl. Mater. Interfaces, 2020, 12, 43984–43991 CrossRef CAS PubMed.
- Y. Zhong, M. Causá, G. J. Moore, P. Krauspe, B. Xiao, F. Günther, J. Kublitski, R. Shivhare, J. Benduhn, E. BarOr, S. Mukherjee, K. M. Yallum, J. Réhault, S. C. B. Mannsfeld, D. Neher, L. J. Richter, D. M. DeLongchamp, F. Ortmann, K. Vandewal, E. Zhou and N. Banerji, Nat. Commun., 2020, 11, 833 CrossRef CAS PubMed.
- S. Alam, V. Nádaždy, T. Váry, C. Friebe, R. Meitzner, J. Ahner, A. Anand, S. Karuthedath, C. S. P. De Castro, C. Göhler, S. Dietz, J. Cann, C. Kästner, A. Konkin, W. Beenken, A. M. Anton, C. Ulbricht, A. Sperlich, M. D. Hager, U. Ritter, F. Kremer, O. Brüggemann, U. S. Schubert, D. A. M. Egbe, G. C. Welch, V. Dyakonov, C. Deibel, F. Laquai and H. Hoppe, J. Mater. Chem. C, 2021, 40, 14463–14489 RSC.
- Y. Nakayama, S. Kera and N. Ueno, J. Mater. Chem. C, 2020, 8, 9090–9132 RSC.
- C. Deibel, D. Mack, J. Gorenflot, A. Schöll, S. Krause, F. Reinert, D. Rauh and V. Dyakonov, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085202 CrossRef.
- C. Arantes, M. Scholz, R. Schmidt, V. Dehm, M. L. M. Rocco, A. Schöll, F. Reinert and F. Würthner, Appl. Phys. A: Mater. Sci. Process., 2012, 108, 629–637 CrossRef CAS.
- F. Yubero and K. Tőkési, Appl. Phys. Lett., 2009, 95, 084101 CrossRef.
- B. P. Silva Santos, J. J. Rubio Arias, L. S. Albuquerque, A. G. da Veiga, J. G. de Melo Furtado, A. de Castro Ribeiro, L. A. F. da Silva, E. V. Bendinelli, M. L. M. Rocco, R. Valaskiand and M. d. F. Vieira Marques, J. Electron Spectrosc. Relat. Phenom., 2019, 234, 27–33 CrossRef CAS.
- Y. R. Denny, H. C. Shin, S. Seo, S. K. Oh, H. J. Kang, D. Tahir, S. Heo, J. G. Chung, J. C. Lee and S. Tougaard, J. Electron Spectrosc. Relat. Phenom., 2012, 185, 18–22 CrossRef CAS.
- M. Vos, S. W. King and B. L. French, J. Electron Spectrosc. Relat. Phenom., 2016, 212, 74–80 CrossRef CAS.
- B. Lesiak, J. Zemek, J. Houdkova, P. Jiricek and A. Jóźwik, J. Electron Spectrosc. Relat. Phenom., 2011, 184, 360–365 CrossRef CAS.
- D. Tahir and S. Tougaard, J. Phys.: Condens. Matter, 2012, 24, 175002 CrossRef PubMed.
- D. Mandal, K. Henkel, K. Müller and D. Schmeißer, Bull. Mater. Sci., 2010, 33, 457–461 CrossRef CAS.
- M. Knupfer, Appl. Phys. A: Mater. Sci. Process., 2003, 77, 623–626 CrossRef CAS.
- S. Tanuma, C. J. Powell and D. R. Penn, Surf. Interface Anal., 1991, 17, 911–926 CrossRef CAS.
- C. M. Cardona, W. Li, A. E. Kaifer, D. Stockdale and G. C. Bazan, Adv. Mater., 2011, 23, 2367–2371 CrossRef CAS PubMed.
- G. Damas, C. F. N. Marchiori and C. M. Araujo, J. Phys. Chem. C, 2018, 122, 26876–26888 CrossRef CAS.
- G. B. Damas, C. F. N. Marchiori and C. M. Araujo, J. Phys. Chem. C, 2019, 123, 25531–25542 CrossRef CAS.
- G. B. Damas, F. von Kieseritzky, J. Hellberg, C. F. N. Marchiori and C. M. Araujo, J. Phys. Chem. C, 2019, 123, 30799–30808 CrossRef CAS.
- R. Friedlein, F. Von Kieseritzky, S. Braun, C. Linde, W. Osikowicz, J. Hellberg and W. R. Salaneck, Chem. Commun., 2005, 1974–1976 RSC.
- R. R. Gagne, C. A. Koval and G. C. Lisensky, Inorg. Chem., 1980, 19, 2854–2855 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- K. Raghavachari and G. W. Trucks, J. Chem. Phys., 1989, 91, 1062–1065 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, 2009 Search PubMed.
- J. L. Bredas, Mater. Horiz., 2014, 1, 17–19 RSC.
- Z. L. Wang and J. M. Cowley, Surf. Sci., 1988, 193, 501–512 CrossRef CAS.
- F. Hofer, F. P. Schmidt, W. Grogger and G. Kothleitner, IOP Conf. Ser.: Mater. Sci. Eng., 2016, 109, 012007 Search PubMed.
- P. J. Spellane, M. Gouterman, A. Antipas, S. Kim and Y. C. Liu, Inorg. Chem., 1980, 19, 386–391 CrossRef CAS.
- J. C. S. Costa, R. J. S. Taveira, C. F. R. A. C. Lima, A. Mendes and L. M. N. B. F. Santos, Opt. Mater., 2016, 58, 51–60 CrossRef CAS.
- H. Liu, P. Chen, D. Hu, X. Tang, Y. Pan, H. Zhang, W. Zhang, X. Han, Q. Bai, P. Lu and Y. Ma, Chem. – Eur. J., 2014, 20, 2149–2153 CrossRef CAS PubMed.
- H. Ajie, M. M. Alvarez, S. J. Anz, R. D. Beck, F. Diederich, K. Fostiropoulos, D. R. Huffman, W. Kraetschmer and Y. Rubin, et al. , J. Phys. Chem., 1990, 94, 8630–8633 CrossRef CAS.
- J. Tauc, Mater. Res. Bull., 1968, 3, 37–46 CrossRef CAS.
- M. E. Sánchez-Vergara, J. C. Alonso-Huitron, A. Rodriguez-Gómez and J. N. Reider-Burstin, Molecules, 2012, 17, 10000–10013 CrossRef PubMed.
- A. R. Zanatta, Sci. Rep., 2019, 9, 11225 CrossRef CAS PubMed.
- T. M. Mok and S. K. O’Leary, J. Appl. Phys., 2007, 102, 113525 CrossRef.
- T. Hashimoto, Y.-K. Choe, H. Nakano and K. Hirao, J. Phys. Chem. A, 1999, 103, 1894–1904 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00652e |
| This journal is © The Royal Society of Chemistry 2022 |