Open Access Article
Open Access ArticleMitigating mass transport limitations: hierarchical nanoporous gold flow-through electrodes for electrochemical CO2 reduction
Zhen
Qi
 *,
Steven A.
Hawks
*,
Steven A.
Hawks
 ,
Corie
Horwood
,
Corie
Horwood
 ,
Juergen
Biener
,
Juergen
Biener
 and
Monika M.
Biener
and
Monika M.
Biener
 *
*
Materials Science Division, Physical and Life Sciences Directorate, Lawrence Livermore National Laboratory, 7000 East Ave., Livermore, CA 94550, USA. E-mail: qi2@llnl.gov; biener3@llnl.gov
First published on 1st November 2021
Abstract
The reaction rates for electrochemical CO2 reduction in aqueous electrolytes can be limited by the low concentration and diffusion rate of the reactant CO2. To overcome this limitation, we fabricated and tested hierarchical nanoporous gold (hnpAu) flow-through electrodes that enable pumping CO2 saturated potassium bicarbonate electrolyte directly through the macropores of hnpAu. The hnpAu flow-through electrode was fabricated by ink casting followed by annealing and dealloying to generate a bimodal pore distribution where macropores (5–10 μm) act as flow channels and nanopores (∼40 nm) provide high surface area. To minimize local CO2 depletion at the electrolyte–electrode interface we selected flow rates that warranted diffusion lengths exceeding the macropore diameter dimensions. We observed that the CO2 reduction rate increases with increasing flow rate through the electrode, but even for the highest overpotentials and flow rates, less than 20% of the dissolved CO2 was utilized despite the absence of diffusion limitations. We find that the competing hydrogen evolution reaction becomes increasingly suppressed with increasing flow rate, specifically in the low overpotential regime. These observations suggest that, beyond diffusion limitations, the CO2 reduction rate in aqueous electrolytes may become limited by the availability of free reaction sites, and that flowing the electrolyte through the electrode increases the CO2 reduction rate by facilitating the removal of the CO product.
Introduction
Utilization of CO2via electrochemical reduction using renewable energy has become a promising technology to close the anthropic CO2 emission cycle.1–6 As a consequence, much work has been devoted to developing more efficient catalysts for electrochemical CO2 reduction (ECR), but despite much progress in the field both catalyst energy efficiency and product selectivity still need to be improved.7–11 The majority of mechanistic studies on metal and metal alloy ECR catalysts have been performed in aqueous bicarbonate solutions,12–15 and often it has been found that the catalyst performance is limited by the availability of the reactant CO2 at the catalyst surface. At higher current densities, the low solubility and slow diffusion rate of CO2 in aqueous electrolytes lead to localized CO2 depletion at the electrode/electrolyte interface. ECR is operated in the potential region where the hydrogen evolution reaction (HER) and ECR are competing processes. Local pH gradients created by both HER and ECR further complicate catalyst evaluation by affecting the dissolved CO2/bicarbonate equilibrium. Thus, to investigate the intrinsic catalyst reactivity, it would be beneficial to develop test conditions where diffusion limitations can be reduced or at least be controlled.Early work revealed that mass transport, controlled by stirring, affects the ECR product distribution.16,17 More recently, inverse opal templated copper structures have been used to study the effect of mass transport in more detail,18 and it has been shown that thicker samples had a higher FE for HER due to mass transport limitations. Using copper nanowire catalyst coatings with different thickness as an example, Raciti et al.13 pointed out that mass transport effects need to be considered in the design of advanced ECR electrocatalysts. However, a rotating cylinder electrode study on Cu catalyzed ECR19 challenges the idea that the ECR faradaic efficiency (FE) can be improved by facilitating mass transport to reduce interfacial pH and CO2 gradients. Specifically, the observation that the HER becomes more predominant at higher rotation speeds has been explained by faster removal of CO adsorbed at the solid interface. By contrast, a more recent rotating ring disk electrode study on Au catalysed ECR20 suggests that the FE of the CO2-to-CO reduction increases with enhanced mass transport which in this study was attributed to the suppression of HER. Clearly, more work is needed to understand the various effects of mass transport on ECR. Here, a recently developed inverse rotating disk electrode21 that enables the use of gas chromatography may enable more detailed studies on the effect of mass transport. But regardless of these controversial results with regard of the effect of mass transport on ECR, it is generally accepted that the transport of the reactant CO2 limits the ECR current density that can be achieved in liquid electrolytes. Today the most promising approach to overcome this limitation is the use of gas diffusion electrodes (GDEs)22–28 that take advantage of the six orders of magnitude higher diffusivity of gas phase CO2 compared to CO2 dissolved in aqueous electrolytes.29 A variation of this concept are flow-through gas diffusion electrodes that recently have attracted increased attention as modelling and experimental studies on flow-through gas diffusion electrodes for ECR30 and N2 reduction31 demonstrated significant electrolyzer performance improvements. Specifically, the flow-through concept further improves mass transport and enables suppression of HER through control of the water content in the catalyst layer. Specifically, a reduction of the boundary layer thickness, for example by increasing the flow-through rate, can dramatically increase the limiting current density. However, as promising as the GDE technology is, it may have limitations connected to efficient removal of lower volatility or ionic products which may lead to GDE flooding and/or catalyst degradation.32 This can be true even for microfluidic GDE electrolyzer designs with a catholyte flow field where it has been shown that lower volatility products such as ethanol can change the wetting behavior of the GDE leading to electrolyte penetration causing mass transport limitations.33
In this work, we explore the use of hierarchical nanoporous gold (hnpAu) liquid phase flow-through electrodes to control and eliminate the effects of diffusion limitations on ECR as outlined above. A gold catalyst was used for its well-known high selectivity for CO2-to-CO reduction which simplifies the gas product analysis.15,34–36 In our previous work on ERC in ionic liquids we demonstrated that implementing a liquid phase flow-through electrode approach can increase current density and faradaic efficiency for CO2-to-CO reduction by 7000% and 700%, respectively.37 For the present study, we developed and tested hnpAu electrodes in a flow-through configuration in the well-defined environment of an H-cell (please refer to the experimental section for details of the testing setup). The hnpAu electrodes were fabricated by a combination of metallic ink casting and dealloying using our previously developed Ag–Au inks.38 Decomposition of the polymeric binder of the Ag–Au particle inks during heating the casted green body to 850 °C for 12 hours generates the macroporosity required for the flow-through electrode configuration; dealloying then introduces the characteristic nanoscale porosity of npAu that provides the macroporous walls with high surface area. We observe that the effect of flow via pumping a CO2 saturated electrolyte through the electrode improves the ECR selectivity upon application of higher flow rates, especially in the low overpotential region.
Results and discussion
Electrode fabrication and structure characterization of flow-through hierarchical nanoporous gold
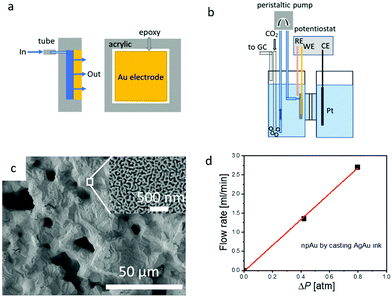
A schematic diagram of the liquid flow-through electrode and its integration into the H-cell setup is shown in Fig. 1a and b. More details regarding the fabrication and integration of the flow-through electrode into the H-cell setup the can be found in the experimental section, and additional information about the microstructure of hnpAu fabricated by our Ag–Au ink technology can be found in our previous work.38 Because the hnpAu electrodes (Fig. 1c) used in this work were cast instead of 3D printed they have only two characteristic length scales: micron-sized pores, resulting from the removal of the polymeric binder and water in the Au–Ag ink during drying and annealing, and nanoscale porosity formed by dealloying. During the annealing step, the micron-sized Ag and Au particles of the Au–Ag ink form a homogeneous AgAu alloy through solid state diffusion resulting in a micron-scale facetted monolithic surface morphology (Fig. 1c). Subsequent dealloying in concentrated nitric acid selectively leached Ag from the AgAu alloy resulting in the formation of a uniform nanoporosity (Fig. 1c, inset) with a characteristic pore/ligament length scale of ∼40 nm. The micro-scale porosity of this hierarchical morphology enables flow-through rates in the ml min−1 range at sub-atmospheric pressure gradients across the hnpAu electrode (see below); the integrated nanoscale porosity provides high surface area for high catalytic activity. Based on the gold oxidation/reduction surface area measurement reported in our previous work,38 the electrochemically active surface area of our npAu flow-through electrode is 4.7 m2 g−1.The permeability of the hnpAu electrode was evaluated through the pressure drop measurements (Fig. 1d) described in the experimental section. It was observed that the pressure drop increases linearly with the flow rate confirming the interconnected nature of the macropores of the casted hnpAu. The flow rate through our one-square-centimeter footprint and one-millimeter-thick hnpAu flow-through electrode was 3.25 ml min−1 at 1 atm pressure drop across the electrode (Fig. 1d). This gives an approximate fluid permeability of 5.4 using Darcy's law. Despite using a ∼10× larger pressure drop across the hnpAu membrane, the highest flow rate is about 10 times smaller than the highest flow rate used in previous experiments with 3D printed hnpAu membranes.38 We attribute the lower conductance of the ink-cast hnpAu membranes to the absence of the printed 100 micron-scale porosity in 3D printed hnpAu which reduces the macroscale porosity to ∼0.3 compared to ∼0.9 for 3D printed hnpAu.
Electrochemical CO2 reduction under different flow rates
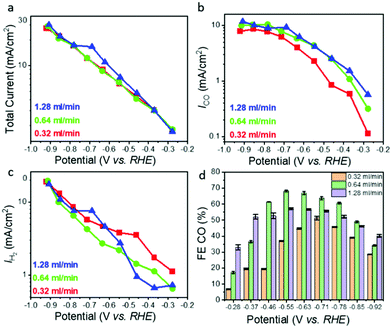
Based on the pressure drop measurements described above, we chose three different flow rates, 0.32, 0.64, and 1.28 ml min−1, to study the effect of pressure gradient driven mass transport on ECR performance (Fig. 2). The following trends were observed: (i) for all flow rates, the total current density as well as the CO and H2 specific current densities increase as expected with increasing overpotential. The total current density was relatively independent of the flow rate, with less than 20 percent variation between the different flow rates for any given overpotential (Fig. 2a); (ii) the CO2-to-CO specific current density (Fig. 2b) increased for all overpotentials with increasing flow rate (from 0.32 to 1.28 ml min−1) but seems to saturate at high overpotentials; and (iii) the HER related current density increased exponentially with increasing overpotential but decreased with increasing flow rate (Fig. 2c). The effect of flow rate is more pronounced in the low overpotential region (below −0.6 V vs. RHE) where the CO specific current density at highest flow rate of 1.28 ml min−1 is up to 5 times higher than that measured the lowest flow rate of 0.32 ml min−1 (Fig. 2b). The corresponding H2 specific current density (Fig. 2c) shows the opposite trend revealing suppression of HER with increasing flow rate. At higher overpotentials (above −0.6 V vs. RHE) the CO and H2 specific current densities show a much weaker dependence on the flow rate than in the low overpotential region (Fig. 2b and c) although the trends remain the same, that is, the CO specific current density increases while the H2 specific current density decreases with increasing flow rate. For the highest overpotentials the CO specific current density increases only by ∼50% if the flow rate (and thus the reactant CO2 supply) is increased by a factor of 4. The trends described above are very stable and reproducible, with less than 1% variation (in terms of current densities) between repeat experiments performed with the same hnpAu flow-through electrode assembly after several weeks. Finally, it is interesting to note that the hnpAu catalyst flow-through electrode studied in this work shows lower CO FEs compared to those observed on very similar npAu catalyst surfaces in previous ECR studies.15,39 Especially oxide derived npAu catalysts with its smaller feature size nanoporosity provided CO FEs near 100% over a wide range of applied potentials.15 Higher CO FEs up to 80%@100 mA cm−2 were also observed on npAu coated GDEs.39 The lower CO FEs as shown in Fig. 2d (maximum FE for CO of ∼70%@5 mA cm−2) observed in the present study thus seem to be a consequence of the flow-through operation modus rather than reflecting the activity and selectivity of the npAu catalyst surface itself, most likely related to the different microenvironment created by the flow-through operation.Discussion of the effect of flow on electrochemical CO2 reduction
Neglecting pH induced changes in the CO2/HCO3− equilibrium, the concentration of the reactant CO2 dissolved in the electrolyte at the electrode exit, and corresponding average CO2 depletion while passing through the flow-through electrode, can be calculated from the residence time τ of the electrolyte in the electrode and the measured CO specific current (Fig. 3a and b). Here, the residence time τ is defined as the ratio of the macropore volume (only the macropores contribute to flow) to the flow rate (0.34–1.28 ml min−1). The macropore volume is the macropore porosity times the electrode volume (0.3 × 0.1 ml = 0.03 ml in the present case). For the flow rate range used in this work, the residence time thus is between 1.3 s (1.28 ml min−1) and 5.3 s (0.32 ml min−1). Neglecting additional CO2 consumption by ECR and HER induced pH changes, the calculated CO2 depletion is less than 10% for the highest flow rate (Fig. 3b), even at the highest overpotential where the CO specific current density is the highest. For the lowest flow rate, the CO2 depletion reaches a maximum of about 24%, but stays below 10% in the low overpotential region. While this calculation demonstrates that the global CO2 depletion in the electrolyte stayed moderately low for most operating conditions, it does not capture local CO2 depletion at the electrode/electrolyte interface. The assumption that CO2 consumption by ECR and HER induced pH changes can be neglected seems to be reasonable in view of the slow rate of the first step of the CO2 to bicarbonate reaction under near pH neutral conditions where the CO2 hydrogenation is at least 4 times slower compared to even the longest electrolyte residence time in our hnpAu flow-through electrode (∼20 s vs. 5 s).40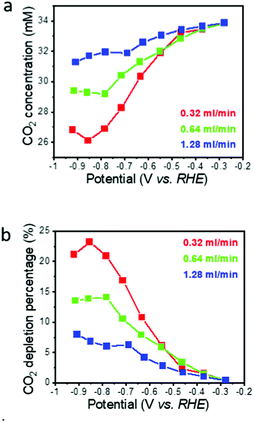 | ||
| Fig. 3 Calculated CO2 concentration (a) and corresponding CO2 depletion (b) on the flow through electrode exit side as a function of potential and electrolyte flow rate. | ||
The degree of local CO2 depletion at the macropore surface, again neglecting pH induced changes of the CO2/HCO3− equilibrium, can be estimated from the diffusion length with respect to the macropore dimension. The diffusion length, L, is given by Fick's law, 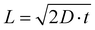 , where D is the diffusion coefficient (0.0016 mm2 s−1 for CO2 in aqueous solution),29 and t is diffusion time. Inserting the residence times τ (1.3–5.3 s) calculated above yields diffusion lengths of 130, 91, and 65 μm for 0.32, 0.64, and 1.28 ml min−1, respectively. Thus, even for the shortest residence time (highest flow rate) the diffusion length is larger than the typical macropore dimension in our hnpAu flow-through electrodes (Fig. 1c). This indicates that radial diffusion within the macropores is fast on the residence time scale thus avoiding concentration gradients and local CO2 depletion zones within the macropores. The tortuous morphology of the macroporous system is expected to further facilitate mixing of the electrolyte thus mitigating any remaining concentration gradients while passing through the flow-through electrode. Such a beneficial effect of a tortuous, branching pore morphology on transport properties has been recently demonstrated by fluid dynamics simulations on various heat exchanger designs.41 However, even though diffusion limitations in the flow-through electrode can be ruled out under the chosen operation conditions, the ECR related current density seems to saturate in the limit of high overpotentials indicating operation in a limiting current regime. As the current density in the limit of high overpotentials depends only weakly on the flow rate, the current density does not seem to be limited by the CO2 supply but rather by the reaction rate. In this context it is important to note that the npAu morphology is generally highly active for ECR as CO FEs up to 80%@100 mA cm−2 have been observed on npAu coated GDE's.39 NpAu catalysts have a nanoscale morphology consisting of high-surface-curvature Au ligaments which provide a high density of low-coordination number step-edge and kink sites that are more reactive than terrace sites characteristic for planar Au electrodes.42
, where D is the diffusion coefficient (0.0016 mm2 s−1 for CO2 in aqueous solution),29 and t is diffusion time. Inserting the residence times τ (1.3–5.3 s) calculated above yields diffusion lengths of 130, 91, and 65 μm for 0.32, 0.64, and 1.28 ml min−1, respectively. Thus, even for the shortest residence time (highest flow rate) the diffusion length is larger than the typical macropore dimension in our hnpAu flow-through electrodes (Fig. 1c). This indicates that radial diffusion within the macropores is fast on the residence time scale thus avoiding concentration gradients and local CO2 depletion zones within the macropores. The tortuous morphology of the macroporous system is expected to further facilitate mixing of the electrolyte thus mitigating any remaining concentration gradients while passing through the flow-through electrode. Such a beneficial effect of a tortuous, branching pore morphology on transport properties has been recently demonstrated by fluid dynamics simulations on various heat exchanger designs.41 However, even though diffusion limitations in the flow-through electrode can be ruled out under the chosen operation conditions, the ECR related current density seems to saturate in the limit of high overpotentials indicating operation in a limiting current regime. As the current density in the limit of high overpotentials depends only weakly on the flow rate, the current density does not seem to be limited by the CO2 supply but rather by the reaction rate. In this context it is important to note that the npAu morphology is generally highly active for ECR as CO FEs up to 80%@100 mA cm−2 have been observed on npAu coated GDE's.39 NpAu catalysts have a nanoscale morphology consisting of high-surface-curvature Au ligaments which provide a high density of low-coordination number step-edge and kink sites that are more reactive than terrace sites characteristic for planar Au electrodes.42
The conclusion that depletion zones are not the root cause of the limiting current behavior is further supported by the theoretically predicted limiting current density iL that can be calculated from the depletion layer thickness δ43 which, per definition, for our flow-through electrode cannot be thicker than the average macropore radius (∼10 μm for hnpAu):
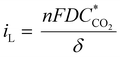 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 As mol−1), D is the diffusion constant (1.6 × 10−5 cm2 s−1),44 and
485 As mol−1), D is the diffusion constant (1.6 × 10−5 cm2 s−1),44 and 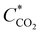 is the CO2 bulk concentration (30 mM). According to eqn (2), the limiting current density of 20 μm diameter pores under flow-through conditions is approximately 90 mA cm−2. As the projected macropore surface area of our npAu electrode is ∼60 cm2 (assuming that straight cylindrical 20 μm-diameter pores account for the macropore porosity of 0.3), the theoretically predicted limiting current density of our 3D hnpAu flow-through electrode is ∼5 A per square centimeter footprint of the flow-through electrode, many times larger than maximum current density of 0.12 A cm−2 electrode footprint area calculated for the highest flow rate (1.28 ml min−1) assuming 100% CO2-to-CO conversion.
is the CO2 bulk concentration (30 mM). According to eqn (2), the limiting current density of 20 μm diameter pores under flow-through conditions is approximately 90 mA cm−2. As the projected macropore surface area of our npAu electrode is ∼60 cm2 (assuming that straight cylindrical 20 μm-diameter pores account for the macropore porosity of 0.3), the theoretically predicted limiting current density of our 3D hnpAu flow-through electrode is ∼5 A per square centimeter footprint of the flow-through electrode, many times larger than maximum current density of 0.12 A cm−2 electrode footprint area calculated for the highest flow rate (1.28 ml min−1) assuming 100% CO2-to-CO conversion.
Thus, neither global nor local (at the electrode/electrolyte interface) CO2 depletion can explain relatively small effect of flow rate on the observed ECR/HER current densities in the limit of high over potentials. For example, the CO specific current density for the highest flow rate/highest overpotential combination increases by only 50% with respect to the corresponding lowest flow rate and global CO2 depletion decreases to 10%. The question remains why only a small fraction of the 4× higher CO2 supply is utilized even when diffusion limitations can be ruled out? The analysis above seems to rule out that the CO specific current density and selectivity are limited by the diffusion of the reactant CO2.
Besides diffusion limitations, the experimentally observed flow-rate dependent changes in the CO and HER specific current densities can potentially be caused by local pH changes. Both ERC (CO2 + 2H+ + 2e− → CO + H2O) and HER (2H+ + 2e− → H2) consume protons which, especially for higher current densities, increases the local pH at the electrode/electrolyte interface. A higher pH value can affect the ECR process by (i) shifting the CO2/HCO3−/CO32− equilibrium towards HCO3− and CO32− thus effectively consuming of free CO2 which reduces the selectivity towards ECR;45,46 (ii) by affecting the surface coverages of adsorbed *CO and *H intermediates; and (iii) by suppressing HER.47 Indeed, the highest calculated CO2 depletion of 24% at the lowest flow rate (0.32 ml min−1) and highest overpotentials (Fig. 3a) could significantly increase if the pH increases above the equilibrium value of 6.8.13 The pH effects should become more pronounced for the combination of high overpotentials and low flow rates where ECR and HER current densities are high and the electrolyte exchange is slow. However, as discussed above, in view of the slow rate of the first step of the CO2 to bicarbonate reaction under near pH neutral conditions40 and the short electrolyte residence times under our experimental conditions, CO2 consumption by local pH changes does not seem to be an important factor. This conclusion is further corroborated by the observation that the effect of flow rate on ECR and HER rates is most pronounced in the low overpotential region where the current densities are small, and the pH can thus be expected to be more stable. Thus, while it is tempting to attribute the suppression of HER to an increase of the local pH, the counter intuitive flow rate dependency hints towards a more complicated picture where the rate also depends on the availability of free catalytic sites. Au is an excellent catalyst for electrochemical CO2-to-CO reduction due to its low CO adsorption energy which facilitates the desorption of the product CO which is a known catalyst poison.48 We hypothesize that higher flow-rates facilitate the removal of the product and catalyst poison CO thus increasing the number of free reaction sites available for ECR.
One electron ferricyanide reduction
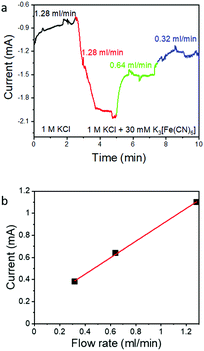
To further test the effectiveness of the flow-through electrode approach, we explored the effect of flow rate on ferricyanide reduction, which is a simple one-electron inner sphere electrode reaction49 without the complications of the ECR system that arise from pH-induced changes of the CO2/HCO3−/CO32− equilibrium or catalyst poisoning by the reaction product CO. Thus, ferricyanide reduction is frequently used in the field to assess cell hydrodynamics such as boundary layer thickness versus flow rate.50 We used a 30 mM potassium ferricyanide in 1 M KCl supporting electrolyte solution to mimic the solubility of CO2 in aqueous solution. The flow rate dependence of the reduction current was tested in the diffusion limited regime at a constant potential at −0.3 V vs. Ag/AgCl (Fig. 4a). The K3[Fe(CN)6] reduction current increases as expected with increasing flow rate as more ferricyanide becomes available. The current density increases linearly with the flow rate, but only ∼2% of the available K3[Fe(CN)6] is consumed in a single pass (Table 1). The lower utilization of Fe(CN)63− compared to CO2 may be caused by a weaker interaction of Fe(CN)63− with the Au surface compared to CO2 (inner sphere electrode reactions require strong interaction with the electrode) and the lower diffusion constant of the ferricyanide ion in aqueous solution (0.0007 mm2 s−1)51 which makes this system more prone to local depletion.| Flow rate (ml min−1) | Average current measured (mA) | Ferricyanide consumed (mol s−1) | Ferricyanide available (mol s−1) | Consumption (%) |
|---|---|---|---|---|
| 0.32 | 0.38 | 3.93 × 10−9 | 1.68 × 10−7 | 2.3 |
| 0.64 | 0.64 | 6.63 × 10−9 | 3.37 × 10−7 | 1.9 |
| 1.28 | 1.10 | 1.13 × 10−8 | 6.75 × 10−6 | 1.7 |
But independent from the lower utilization of ferricyanide compared to CO2, the linear increase of the ferricyanide reduction current with increasing flow rate (as shown in Fig. 4b) confirms that the flow through electrode approach can indeed be used to increase electrochemical conversion currents. In case of ECR at high overpotentials, the CO specific current does not increase linearly with the flow rate even though the combination of residence time (controlled by the flow rate) and the characteristic macropore dimensions of hnpAu should have prevented even local depletion at the electrolyte/electrode interface. So while the 50% increase in the CO2 reduction rate (from 8 mA cm−2 at 0.32 ml min−1 to 12 mA cm−2 at 0.128 ml min−1) at the highest overpotential (−0.925 V) can be attributed to the improved mass transport, ECR seems to be a much more complex reaction; in addition to CO2 supply, the overall reaction rate depends on the availability of free reaction sites, competition between ERC and HER, and the equilibrium between CO2 and the bicarbonate solution, all of which are interconnected and pH dependent. The current results suggest that understanding and controlling the interplay among CO2 concentration, pH, and CO2/HCO3−/CO32− equilibrium is the key to maintain high CO FEs. By using a flow through electrode and conditions which result in diffusion lengths much greater than the macropore dimensions, we can rule out global and local depletion as a limitation. Furthermore, the flow rate dependency on the ECR–HER competition seems to rule out local pH changes as deciding factor. We also can rule out that the activity of npAu prepared by dealloying too low to sustain higher CO2-to-CO specific current densities as high CO FEs up to 80%@100 mA cm−2 were observed in previous work on npAu coated GDEs.39 This leaves the availability of free reaction sites as a dominating factor limiting the ECR rate beyond diffusion limitations.
Conclusion
We fabricated, integrated, and tested a hnpAu catalyst liquid phase flow-through electrode for electrochemical CO2-to-CO reduction. The results demonstrate that the flow-through configuration can improve the faradaic efficiency of the CO2-to-CO reduction, but also shows that the increase in the CO2 reduction rate lacks behind the increase in reactant supply with increasing flow rate despite carefully matching flow rate, pore size and diffusion length to rule out global and local CO2 depletion as well as diffusion limitations. The effect of flow rate is most pronounced in the low overpotential region (below −0.6 V vs. RHE) where the CO specific current density at highest flow rate (1.28 ml min−1) is up to 2–5 times higher compared to that measured at the lowest flow rate (0.32 ml min−1) although the low ECR and HER rates in this potential region are not expected to cause local CO2 depletion or pH changes, even at the lowest flow rate. The HER related current density shows the opposite trend and decreases with increasing flow rate. At higher overpotentials (above −0.6 V vs. RHE) the CO specific current density increases more slowly with increasing flow rate despite the much higher reaction rates in this potential region. CO2 depletion can be ruled out as limiting factor as it remains below 10% for the highest flow rate/overpotential combination leaving plenty of room for higher ECR rates. While ECR and HER induced pH changes are expected to affect the ECR performance, the more pronounced HER suppression in the low overpotential region seems to indicate that the ECR performance is dominated by other effects. Here, we speculate that besides increasing the CO2 supply, an increase in the flow rate benefits the ECR performance by facilitating the removal of the product CO thus increasing the number of available catalytic sites. More broadly, the effectiveness of CO removal might be a more important factor than generally assumed in determining the performance of an ECR electrolyzer configuration. Specifically, it might explain why npAu coated GDEs39 can sustain much higher ECR current densities than the flow-through ECR electrode configuration described in this work as our analysis shows that, like a GDE, our flow-through ECR electrode is very effective in supplying CO2. In absence of bubble formation, the CO removal in a flow-through electrode requires that the produced CO dissolves in the electrolyte which is limited by the 40 times lower solubility of CO in water compared to that of CO2.52 By contrast, the GDE configuration allows transport of CO through the gas phase thus making this process much more efficient. We note that we also tested thick metal foam electrodes in a GDE environment and observed poor performance due to insufficient water management (unpublished results). Finally, a related but different reason for the lower-than-expected ECR current density of our flow-through electrode design in the absence of CO2 transport limitations might be the presence of electrolyte related strongly adsorbed species like carbonate or bicarbonate anions that can poison the active sites but are not present in the GDE configuration.Despite the lower-than-expected ECR related current density, accompanying tests with the simple one-electron transfer ferricyanide reduction reaction show the expected linear increase in current density with the flow rate, thus confirming the validity of the liquid phase flow-through electrode design concept and further demonstrating that factors other than the CO2 supply control the ECR rate in aqueous electrolytes at high current densities and flow rates.
In conclusion, we believe that this work provides new insight into ECR under flow-through conditions and will help to improve the design of ECR reactors. While we studied the ECR performance of flow-through electrodes on the CO2-to-CO reaction because of its simplicity regarding product analysis, the flow through electrode technology is geared towards ECR products that are less volatile (C2–C3 products or higher) or less soluble (formate) where operation in a liquid electrolyte may become advantageous over GDE technologies.
Experimental
Ag–Au ink preparation
As previously reported,38 Ag–Au inks with a ∼2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Ag to Au atomic ratio were prepared by mixing 5 g of Ag clay [90 wt% silver powder + 10 wt% water and organic binder, precious metal clay (PMC), Mitsubishi Materials] with 5 g of Au clay (91.7 wt% pure gold + 8.3 wt% organic binder, water, and silver; PMC, Mitsubishi Materials) and 0.5 to 1.0 g of water (Millipore). In this work we explored a casting technique thus avoiding the more time-consuming 3D printing process used in previous work: the ink was directly casted into a laser cut mold (10 × 10 × 1 mm3), and a gold wire with a diameter of 1 mm was imbedded in the ink to serve as a current collector. The green body, obtained by drying the cast ink at room temperature for one day, was heated in a muffle furnace at 850 °C for 12 hours to form a uniform AgAu alloy while simultaneously removing the remaining polymeric binders and water. Dealloying was performed in concentrated (68 wt%) HNO3 (ACS, VWR) for 5 days. Scanning Electron Microscopy (Jeol 7410 with lower secondary electron detector, accelerating voltage of 5 keV and a working distance of 8 mm) confirmed the hierarchical porosity generated by the ink casting/dealloying approach.
1 Ag to Au atomic ratio were prepared by mixing 5 g of Ag clay [90 wt% silver powder + 10 wt% water and organic binder, precious metal clay (PMC), Mitsubishi Materials] with 5 g of Au clay (91.7 wt% pure gold + 8.3 wt% organic binder, water, and silver; PMC, Mitsubishi Materials) and 0.5 to 1.0 g of water (Millipore). In this work we explored a casting technique thus avoiding the more time-consuming 3D printing process used in previous work: the ink was directly casted into a laser cut mold (10 × 10 × 1 mm3), and a gold wire with a diameter of 1 mm was imbedded in the ink to serve as a current collector. The green body, obtained by drying the cast ink at room temperature for one day, was heated in a muffle furnace at 850 °C for 12 hours to form a uniform AgAu alloy while simultaneously removing the remaining polymeric binders and water. Dealloying was performed in concentrated (68 wt%) HNO3 (ACS, VWR) for 5 days. Scanning Electron Microscopy (Jeol 7410 with lower secondary electron detector, accelerating voltage of 5 keV and a working distance of 8 mm) confirmed the hierarchical porosity generated by the ink casting/dealloying approach.
Flow-through electrode assembly and pressure drop test
The hnpAu disks were glued with epoxy (Torr Seal) into a sealed acrylic frame. A tube on the backside of the acrylic frame allows flowing of the electrolyte through the hnpAu sample (Fig. 1a). A spacer between the hnpAu sample and the acrylic back plate of the frame ensured a uniform flow field within this flow-through electrode assembly. The transport properties of this setup were assessed by measuring the pressure drop across the cell using a pressure transducer (Omega, PX209, 200g5v, detection range of 0 to 103.4 kPa) connected to the cell inlet while pumping (Watson-Marlow 120, pumping speed up to 27 ml min−1) the aqueous electrolyte at different flow rates through the cell.ECR test
ECR tests were performed in a customized H-cell (80 ml volume per chamber, Adams & Chittenden Scientific Glass) with a low-profile Ag/AgCl (6 mm in diameter, Pine research) reference electrode. An anion exchange membrane (Fumasep, FKS-PET-75) was used to separate the cathode and anode compartments. 60 ml of 0.1 M KHCO3 (ACS grade, Sigma-Aldrich) solution was filled into each chamber leaving 20 ml headspace. The electrolyte was pumped through the inserted flow-through electrode assembly described above using a peristaltic pump (Fig. 1b). All experiments were performed at ambient temperature (∼21 °C). Applied potentials were converted to the reversible hydrogen electrode (RHE) scale using E(RHE) = E(Ag/AgCl) + 0.2 V + 0.0591 × pH unless otherwise specified in the paper and the Biologic software was used to correct for 85% of the ohmic drop (iRu) of about 40 Ω (as determined by impedance measurements) with the remainder being manually corrected. After each experiment, the impedance measurement was repeated to check for changes of the resistance. Under all circumstances, the resistance change was negligible. The cathode compartment was constantly purged with CO2 at a flow rate of 30 sccm, and the exhaust gases were directly purged into the inlet of a GC. All current density values are reported with respect to the geometrical area of working electrode.Gas product analysis
Gas products formed during the CO2 electrolysis were analyzed using an in-line gas chromatograph (SRI Instruments, Multi-Gas Analyzer #5) equipped with a thermal conductivity detector (TCD) for hydrogen, and a flame ionization detector (FID) for carbon monoxide. Argon was used as a carrier gas to collect hydrogen signals. Molecular Sieve 5A and HayeSep D were used in series for gas separations. The partial current density of CO production was calculated from GC peak area as follows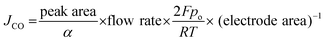 | (2) |
Ferricyanide reduction test
Ferricyanide reduction tests were carried out using 30 mM K3[Fe(CN)6] (99%, Sigma Aldrich) in 1 M KCl (ACS, Sigma Aldrich) supporting electrolyte using the same flow-through electrode assembly and electrolyte flow rates used for the electrochemical CO2 reduction tests, and a Pt mesh counter electrode. The potential was held constant at −0.3 V vs. Ag/AgCl in the diffusion limited regime while recording the current response as a function of flow rate. A baseline current measurement was performed in 1 M KCl at a flow rate of 10 rpm; once the current stabilized the inlet was switched to the ferricyanide electrolyte reservoir, and the effect of flow rate on the ferricyanide reduction current was measured.Author contributions
Z. Qi: conceptualization, investigation, validation writing – original draft. S. Hawks and C. Horwood: investigation, writing – original draft. J. Biener: conceptualization, writing – review & editing. M. Biener: conceptualization, writing – review & editing, funding acquisition, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
IM release number: LLNL-JRNL-818910. Funding: The authors are grateful for the support of this research under the auspices of the U.S. Department of Energy under Contract DE-AC52-07NA27344, through LDRD award 17-LW-013.Notes and references
- E. E. Benson, C. P. Kubiak, A. J. Sathrum and J. M. Smieja, Chem. Soc. Rev., 2009, 38, 89–99 RSC.
- R. Kortlever, J. Shen, K. J. Schouten, F. Calle-Vallejo and M. T. Koper, J. Phys. Chem. Lett., 2015, 6, 4073–4082 CrossRef CAS PubMed.
- Z.-L. Wang, C. Li and Y. Yamauchi, Nano Today, 2016, 11, 373–391 CrossRef CAS.
- M. Dunwell, Q. Lu, J. M. Heyes, J. Rosen, J. G. Chen, Y. Yan, F. Jiao and B. Xu, J. Am. Chem. Soc., 2017, 139, 3774–3783 CrossRef CAS.
- L. Wang, S. Nitopi, A. B. Wong, J. L. Snider, A. C. Nielander, C. G. Morales-Guio, M. Orazov, D. C. Higgins, C. Hahn and T. F. Jaramillo, Nat. Catal., 2019, 2, 702–708 CrossRef CAS.
- L. Wang, D. C. Higgins, Y. F. Ji, C. G. Morales-Guio, K. Chan, C. Hahn and T. F. Jaramillo, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 12572–12575 CrossRef CAS PubMed.
- X. Feng, K. Jiang, S. Fan and M. W. Kanan, J. Am. Chem. Soc., 2015, 137, 4606–4609 CrossRef CAS PubMed.
- X. Feng, K. Jiang, S. Fan and M. W. Kanan, ACS Cent. Sci., 2016, 2, 169–174 CrossRef CAS PubMed.
- H. A. Hansen, C. Shi, A. C. Lausche, A. A. Peterson and J. K. Norskov, Phys. Chem. Chem. Phys., 2016, 18, 9194–9201 RSC.
- Q. Lu and F. Jiao, Nano Energy, 2016, 29, 439–456 CrossRef CAS.
- W. Luc, C. Collins, S. Wang, H. Xin, K. He, Y. Kang and F. Jiao, J. Am. Chem. Soc., 2017, 139, 1885–1893 CrossRef CAS PubMed.
- D. Raciti, K. J. Livi and C. Wang, Nano Lett., 2015, 15, 6829–6835 CrossRef CAS PubMed.
- D. Raciti, M. Mao, J. H. Park and C. Wang, Catal. Sci. Technol., 2018, 8, 2364–2369 RSC.
- D. Raciti, M. Mao and C. Wang, Nanotechnology, 2018, 29, 044001 CrossRef.
- Z. Qi, J. Biener and M. Biener, ACS Appl. Energy Mater., 2019, 2, 7717–7721 CrossRef CAS.
- J. J. Kim, D. P. Summers and K. W. Frese, J. Electroanal. Chem., 1988, 245, 223–244 CrossRef CAS.
- K. Hara, A. Tsuneto, A. Kudo and T. Sakata, J. Electrochem. Soc., 1994, 141, 2097–2103 CrossRef CAS.
- H. Song, M. Im, J. T. Song, J. A. Lim, B. S. Kim, Y. Kwon, S. Ryu and J. Oh, Appl. Catal., B, 2018, 232, 391–396 CrossRef CAS.
- C. F. C. Lim, D. A. Harrington and A. T. Marshall, Electrochim. Acta, 2017, 238, 56–63 CrossRef CAS.
- A. Goyal, G. Marcandalli, V. A. Mints and M. T. M. Koper, J. Am. Chem. Soc., 2020, 142, 4154–4161 CrossRef CAS PubMed.
- P. Moreno-Garcia, N. Kovacs, V. Grozovski, M. D. Galvez-Vazquez, S. Vesztergom and P. Broekmann, Anal. Chem., 2020, 92, 4301–4308 CrossRef CAS.
- J. B. Vennekoetter, R. Sengpiel and M. Wessling, Chem. Eng. J., 2019, 364, 89–101 CrossRef CAS.
- T. Burdyny and W. A. Smith, Energy Environ. Sci., 2019, 12, 1442–1453 RSC.
- D. Higgins, C. Hahn, C. X. Xiang, T. F. Jaramillo and A. Z. Weber, ACS Energy Lett., 2019, 4, 317–324 CrossRef CAS.
- B. Endrődi, E. Kecsenovity, A. Samu, F. Darvas, R. V. Jones, V. Török, A. Danyi and C. Janáky, ACS Energy Lett., 2019, 4, 1770–1777 CrossRef PubMed.
- L.-C. Weng, A. T. Bell and A. Z. Weber, Energy Environ. Sci., 2019, 12, 1950–1968 RSC.
- M. de Jesus Gálvez-Vázquez, P. Moreno-García, H. Xu, Y. Hou, H. Hu, I. Z. Montiel, A. V. Rudnev, S. Alinejad, V. Grozovski, B. J. Wiley, M. Arenz and P. Broekmann, ACS Catal., 2020, 10, 13096–13108 CrossRef.
- Z. Qi, M. M. Biener, A. R. Kashi, S. Hunegnaw, A. Leung, S. C. Ma, Z. Y. Huo, K. P. Kuhl and J. Biener, J. CO2 Util., 2021, 45, 101454, DOI:10.1016/j.jcou.2021.101454.
- D. M. Weekes, D. A. Salvatore, A. Reyes, A. X. Huang and C. P. Berlinguette, Acc. Chem. Res., 2018, 51, 910–918 CrossRef CAS.
- Y. K. Chen, N. S. Lewis and C. X. Xiang, J. Electrochem. Soc., 2020, 167, 114503 CrossRef CAS.
- N. C. Kani, A. Prajapati, B. A. Collins, J. D. Goodpaster and M. R. Singh, ACS Catal., 2020, 10, 14592–14603 CrossRef CAS.
- K. Liu, W. A. Smith and T. Burdyny, ACS Energy Lett., 2019, 4, 639–643 CrossRef CAS PubMed.
- D. Corral, J. T. Feaster, S. Sobhani, J. R. DeOtte, D. U. Lee, A. A. Wong, J. Hamilton, V. A. Beck, A. Sarkar, C. Hahn, T. F. Jaramillo, S. E. Baker and E. B. Duoss, Energy Environ. Sci., 2021, 14, 3064–3074 RSC.
- J. J. L. Humphrey, D. Plana, V. Celorrio, S. Sadasivan, R. P. Tooze, P. Rodriguez and D. J. Fermin, ChemCatChem, 2016, 8, 952–960 CrossRef CAS.
- M. Clark and C. Kubiak, Abstr. Pap. Am. Chem. Soc., 2016, 252, 54 Search PubMed.
- C. Z. Chen, B. Zhang, J. H. Zhong and Z. M. Cheng, J. Mater. Chem. A, 2017, 5, 21955–21964 RSC.
- V. Vedharathinam, Z. Qi, C. Horwood, B. Bourcier, M. Stadermann, J. Biener and M. Biener, ACS Catal., 2019, 10605–10611, DOI:10.1021/acscatal.9b03201.
- C. Zhu, Z. Qi, V. A. Beck, M. Luneau, J. Lattimer, W. Chen, M. A. Worsley, J. C. Ye, E. B. Duoss, C. M. Spadaccini, C. M. Friend and J. Biener, Sci. Adv., 2018, 4, eaas9459 CrossRef CAS.
- Z. Qi, M. M. Biener, A. R. Kashi, S. Hunegnaw, A. Leung, S. C. Ma, Z. Y. Huo, K. P. Kuhl and J. Biener, Mater. Res. Lett., 2021, 9, 99–104 CrossRef CAS.
- K. G. Schulz, U. Riebesell, B. Rost, S. Thoms and R. E. Zeebe, Mar. Chem., 2006, 100, 53–65 CrossRef CAS.
- W. Li, G. Yu and Z. Yu, Appl. Therm. Eng., 2020, 179, 115686 CrossRef CAS.
- J. Biener, A. Wittstock, L. A. Zepeda-Ruiz, M. M. Biener, V. Zielasek, D. Kramer, R. N. Viswanath, J. Weissmuller, M. Baumer and A. V. Hamza, Nat. Mater., 2009, 8, 47–51 CrossRef CAS.
- A. J. Martín, G. O. Larrazábal and J. Pérez-Ramírez, Green Chem., 2015, 17, 5114–5130 RSC.
- D. M. Weekes, D. A. Salvatore, A. Reyes, A. X. Huang and C. P. Berlinguette, Acc. Chem. Res., 2018, 51, 910–918 CrossRef CAS PubMed.
- M. R. Singh, E. L. Clark and A. T. Bell, Phys. Chem. Chem. Phys., 2015, 17, 18924–18936 RSC.
- M. R. Singh, Y. Kwon, Y. Lum, J. W. Ager and A. T. Bell, J. Am. Chem. Soc., 2016, 138, 13006–13012 CrossRef CAS PubMed.
- K. J. P. Schouten, E. P. Gallent and M. T. M. Koper, J. Electroanal. Chem., 2014, 716, 53–57 CrossRef CAS.
- J. Qiao, Y. Liu, F. Hong and J. Zhang, Chem. Soc. Rev., 2014, 43, 631–675 RSC.
- W. T. E. van den Beld, M. Odijk, R. H. J. Vervuurt, J.-W. Weber, A. A. Bol, A. van den Berg and J. C. T. Eijkel, Sci. Rep., 2017, 7, 45080 CrossRef CAS PubMed.
- E. L. Clark, J. Resasco, A. Landers, J. Lin, L. T. Chung, A. Walton, C. Hahn, T. F. Jaramillo and A. T. Bell, ACS Catal., 2018, 8, 6560–6570 CrossRef CAS.
- S. J. Konopka and B. McDuffie, Anal. Chem., 1970, 42, 1741–1746 CrossRef CAS.
- G. W. C. Kaye and T. H. Laby, Tables of Physical and Chemical Constants, Longman Publishing Group, New York, 15th edn, 1986 Search PubMed.
| This journal is © The Royal Society of Chemistry 2022 |