Towards understanding photon absorption and emission in MgAl layered double hydroxide

Abstract

The use of layered double hydroxides (LDHs) in advanced photoactive applications requires tailoring their light absorption, the stabilisation of separated charges and the manipulation of charge recombination behaviour. However, understanding of these processes in LDHs is mostly lacking. Here, we dissect the UV-to-mid-infrared absorption and UV-visible luminescence (at 83 K to 298 K) of MgAl-LDH and discuss plausible charge recombination pathways with the aid of Mg(OH)₂, Al(OH)₃ and calcined MgAl-LDH (373 K to 673 K). Excitation of electrons into the conduction band (CB) is accompanied by prominent intragap absorption: excitation of fundamental vibrations and their overtones to 1.7 eV, and a long band tail to the CB edge, from which a bandgap of 3.12 eV was determined. Luminescence spectra reveal strong, broad, overlapping, multi-band emission between 2 eV and 4.5 eV dependent on temperature. Removal of adsorbed water increases luminescence. At 83 K, nearly 50% is emitted above the CB edge—contradicting common behaviour. Luminescence occurs mainly from the band edge at 298 K, or with the removal of hydroxyl- and carbonate groups by calcination. The temperature dependence reveals competition between radiative and non-radiative deactivation pathways, indicating meta-stable CB states and possible polaron formation. Below-band-edge luminescence is believed to be dominated by the effects of vibrational broadening, coordination defects, access to band-tail states, and exciton formation and its binding to defects/Al³⁺ islands in addition to the interlayer carbonate facilitating charge separation.

---

1 Introduction

As complex structures that house a variety of bond- and interaction types (ionic, dipolar/ionic, dipolar, hydrogen bonds and van der Waals forces) and consist of cationic layers held together by anions, LDHs have, over the past decade, established themselves as promising materials in advanced applications for use in photocatalysis,¹ solar cells,² supercapacitors^3–5 and sensors^6,7 due to their high modification potential. This structure—consisting of octahedrally hydroxyl-coordinated metals (M(OH)₆) summarised by the formula [M^II_1−xM^III_x(OH)₂][X^q−_x/q·nH₂O], where M^II and M^III are di- and trivalent cations and X^q−_x/q the interlayer anion with charge q balanced with x, the molar fraction of trivalent to total cations in the layer⁸—allows them to act as semiconductors housing metal ions of different valency with an array of modification options.

One LDH, MgAl-LDH—commonly known in two forms as hydrotalcite (3Mg : 1Al) and quintinite (2Mg : 1Al)—is particularly well-known and forms the basis of many modifications of its structure and composition for advanced applications. While there are many interesting applications of LDHs, current interest in renewable energy alternatives involving sunlight makes specifically the interaction of these materials with light important to study and understand. MgAl-LDH is known to be a semiconductor with a wide bandgap quoted to range between 5.45 eV and 3.5 eV experimentally (somewhat dependent on the synthesis method used^9–13) and is often seen as a material with little advanced functionality in photo-applications without further modification. However, being the parent structure for many transition-metal-modified LDHs, it is interesting to study the fundamentals of charge excitation and recombination, which would be very difficult to study in the more complex transition-metal-modified forms due to luminescence quenching.

MgAl-LDH is an even more interesting material when considering the theoretically possible bandgaps between 1.6 eV and 5.6 eV, dependent on the crystal structure.¹⁴ This considerable span of bandgap values could provide an interesting starting point to modify this inexpensive material for applications in water-splitting or solar cells, absorbing in the visible light region. However, at present there is a strong limitation in doing so, since fundamental knowledge on the interaction of LDHs with light is lacking; two of the most important questions being what the frequently observed broad, undefined absorption below the band edge^9–15 (resulting in materials with a range of bandgap values determined although prepared compositionally identical and with the same reported crystal structure) and complex overlapping spectra in absorption¹⁵ and luminescence⁷ result from.

At present, very little is known about the pathways to charge separation and -recombination in LDHs. The most valuable study of their separation has arguably been achieved through density-functional-theory (DFT) approaches,¹⁴ but recombination mechanisms are not yet properly understood. This has been claimed to the contrary,^13,16 but the studies were based on materials not directly related to the LDH structure and can thus only be an extrapolation. Most understanding has been gained through application of these materials as photocatalysts and luminescent materials. Here, beneficial charge-stabilisation has been attributed to the use of a charge stabilising-anions (such as CO₃²⁻),¹⁷ orderedness in the structure,¹⁸ and surface and oxygen defects.^18,19 It has also been discovered that the bulk-material properties can be very different to those of exfoliated nano-sheets,^7,20 in addition to the ratio of di- and trivalent metals being able to influence the luminescence intensity.²⁰ But recent work⁷ shows that this knowledge is not yet sufficient to properly identify recombination mechanisms, yielding the hypothesis of very interesting effects (such as the coupling of excitons and phonons, excitonic rather than defect-related transitions, possible similarities to processes in polar semiconductors and the interaction of optical and acoustic phonons) that deem LDHs worthy of more thorough study.

With this work we aim to narrow this gap in understanding by analysing in depth the UV-Vis-NIR-MIR (ultraviolet-visible-near-infrared-mid-infrared) absorption and UV-Vis luminescence of MgAl-CO₃²⁻-LDH (in quintinite form (2 : 1), the most commonly used elemental ratio in materials modified for advanced applications) in bulk form with the aid of the two structurally related materials Mg(OH)₂ and Al(OH)₃. These three materials are different in the types of bonding present—the LDH being an anionic clay with carbonate anions balancing the charge difference of the cationic layers and hydrogen bonds linking interlayer water molecules to layer hydroxyl groups and the carbonate, while the hydroxides are held together only through hydrogen bonds—but retain great similarity as a result of octahedrally hydroxyl-coordinated Mg and Al ions present in all three materials. Their comparison thus allows insight into the role of each of the metals as well as that of the anion in absorption and luminescence. To gain insight specifically into the lesser-studied recombination mechanisms, this study was focused heavily on luminescence, with the advantage that this also aided in describing the very complex absorption results. Luminescence spectra were obtained as a function of temperature to reveal radiative-recombination-pathway selectivity, the MgAl-LDH was calcined at temperatures between 373 K and 673 K to study dependence on each of the lattice constituents, and excitation spectra were used to determine luminescence dependence on the excitation energy—comprehensively describing the luminescence of MgAl-LDH. Together, it was possible to gain appreciation of the importance of the bandgap region (making available a multitude of sub-band-edge states that contribute to absorption and luminescence spectra), discover a significant contribution to absorption bands through vibrational overtones, and question the meaning of traditional bandgap measurements.

2 Experimental

2.1 Synthesis

The MgAl-LDH, Mg(OH)₂ and Al(OH)₃ were prepared using co-precipitation synthesis at identical conditions, allowing for the preparation of materials with close compositional control and the necessary comparability. For this, chemically pure (CP, 99% purity) or analytical grade (AR, 99.5% purity) reactants were used for all experiments. AlCl₃·6H₂O (CP), MgCl₂·6H₂O (CP), NaOH (AR) and Na₂CO₃ (AR) were sourced from ACE Chemicals. Deionised water was used for all experiments. The LDH was synthesised according to our previous method²¹ by creating a 2.5 M salt solution of MgCl₂·6H₂O and AlCl₃·6H₂O (stoichiometric to a Mg : Al ratio of 2 : 1) and adding this dropwise to a solution of 0.4 M Na₂CO₃ while maintaining a pH of 11.0 ± 0.3 through the addition of 10 M NaOH solution as required. The hydroxides were prepared in the same manner (leaving out the relevant cation), but with dropwise addition of the salt solution to de-ionised water instead of a Na₂CO₃ solution. The resulting slurry was stirred vigorously throughout the reaction and the precipitated structures were recovered through vacuum filtration. The materials were subsequently washed with ample deionised water, and dried at 60 °C overnight (18 h).

2.2 Characterisation

X-ray powder diffraction (XRD) measurements were performed on a Panalytical X'Pert PRO X-ray diffractometer in θ–θ configuration, equipped with Fe-filtered Co-Kα radiation (1.789 Å) and an X'Celerator detector and variable-divergence- and fixed receiving slits. Samples were prepared according to the standardised Panalytical backloading system, which facilitates nearly random distribution of the particles. Data were collected in the angular range 5° ≤ 2θ ≤ 80°, with a step size of 0.008° 2θ and a 13 s scan step time. The phases were identified using X'Pert HighScore Plus software. The spectra were converted from variable slit to fixed slit prior to phase identification. The detection limit for the crystalline phases was 2%.

Scanning electron microscopy (SEM) micrographs were taken on a Zeiss Gemini 2 Crossbeam 540 FEG SEM and Zeiss Ultra Plus. The samples were distributed on carbon tape and coated with two layers of carbon using a sputter coater (Zeiss Ultra Plus: sputter coated with 3 nm of platinum). The micrographs were taken at 1 keV (Zeiss Ultra Plus: 4 keV, SE2 filter).

Attenuated total reflectance Fourier-transform infrared (ATR-FTIR) spectra were obtained using a PerkinElmer 100 Spectrophotometer. Spectra of sample wafers were obtained between 4000 cm⁻¹ and 550 cm⁻¹ each with 32 scans at a resolution of 2 cm⁻¹. Spectra were deconvoluted using Origin Pro 2016 and Gaussian line profiles.

Inductively coupled plasma optical emission spectroscopy (ICP-OES) was used to verify the elemental ratio of Mg : Al and identify impurities in MgAl-LDH.

Absorption spectroscopy in the UV-Vis-NIR range was carried out using an Agilent Technologies Cary 6000i UV-Vis-NIR Spectrophotometer with a DRA-1800 (diffuse reflectance) attachment. The scans were recorded using a 5 mm slit width and an integration time of 0.2 s. Sample pellets were prepared by mixing the LDHs with KBr (30% LDHs and 70% KBr) and grinding the mixture for 60 s. The mixture was pressed into 300 mg, 1 mm thick pellets using a weight of 8 t that was applied for 2 min.

Photoluminescence spectra of MgAl-LDH, Mg(OH)₂ and Al(OH)₃ were recorded on a Deep UV miniPL 5.0 between 260 nm and 650 nm with a stepsize of 2 nm and using an excitation wavelength of 248 nm (spot size 70 μm). Excitation spectra were obtained using a Horiba QuantaMaster 8075-22 Spectrofluorometer with a 3 nm slit width, integration time of 0.3 s and stepsize of 1 nm. Light from a Xe lamp was filtered through a double excitation monochromator using 1200 lines per mm gratings blazed at 300 nm (for UV excitation). The emission was filtered through a double emission monochromator with 1200 lines per mm gratings blazed at 500 nm and the signal was detected with a Hamamatsu R2658 Photomultiplier Tube. Data resulting from both techniques were transformed from wavelength- to energy-dependence using the formula I(E) = I(λ) × λ².²² Spectra were deconvoluted using Origin Pro 2016 and Gaussian line profiles.

The X-ray photoelectron spectrum of the O 1s binding energy region was acquired in a ultra-high vacuum (UHV) chamber with a base pressure of 2 × 10⁻¹⁰ mbar at room temperature. The UHV chamber was equipped with a SPECS XR 50M monochromatised X-ray source with an Al anode (Al-Kα excitation line, hv = 1486.71 eV) and a SPECS PHOIBOS 150 hemispherical electron energy analyser. The overall energy resolution of the combined analyser and photon source system was set to 0.6 eV. Surface charging was compensated by illuminating the samples with a low-energy electron beam generated by a flood gun set to operate at: electron energy = 2.5 eV, electron flux = 20 μA.

3 Results

3.1 Structure and morphology

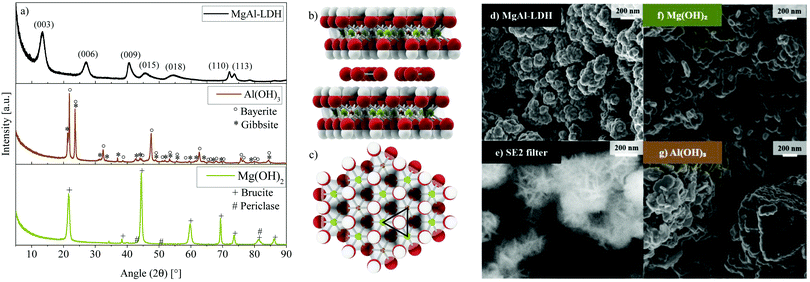
The quintinite-type MgAl-LDH under consideration in this work was shown to crystallise in the frequently-found rhombohedral polytype (3R),^23,24 which is the expected result considering the ambient synthesis conditions used.²⁴ This polytype shows characteristic (003), (006), (009), (110) and (113) reflections indicative of the R3̄m̄ space group that are visible in Fig. 1(a).

Fig. 1 (a) XRD results for the 3R MgAl-LDH polytype with an Mg : Al ratio of 2 : 1, Mg(OH)₂ and Al(OH)₃. (b) Side view (left) of 2 layers and the carbonate-containing interlayer and (c) top view (right) of a single LDH layer of MgAl-LDH with a Mg : Al ratio of 2 : 1 (green = Mg, brown = Al, red = O and white = H). (d) Morphology of MgAl-LDH showing intertwined, ball-like-shape-producing agglomerated platelets (1 keV). (e) Representative twinning of the LDH structure, producing star-like shapes within the ball-like shapes (SE2, 4 keV). (f) Morphology of Mg(OH)₂ showing agglomerated individual plate-like structures. (g) Al(OH)₃, comprising of crystals of mixed morphologies.

A, for co-precipitation, well-crystallised LDH was obtained—a result of the elevated pH synthesis method.^21,25 The pattern obtained for MgAl-LDH in this work is very similar to that obtained experimentally and modelled with DIFFaX,²⁶ where the XRD pattern resulted from the intergrowth of two polytypes of LDH, 3R₁ and 3R₂ (60% and 40%). In conjunction with stacking faults, these led to broadened 01l reflections.²⁶ In contrast, MgAl-LDH does not show as well-defined (110) and (113) reflections. This is expected to be a result of cation vacancies and/or turbostraticity and interstratification that are known to broaden reflection (110).²⁶ The ratio of the (003) and (006) reflection intensities in MgAl-LDH is less than expected for the 3R₁ polytype, which can (along with a slight c-parameter increase) be explained by a higher amount of water present in the interlayer region.^21,26

The XRD results for Mg(OH)₂ and Al(OH)₃—synthesised at identical conditions to the MgAl-LDH to better understand the impact of each metal ion on absorption and luminescence characteristics—are also shown in Fig. 1. At these conditions, Al(OH)₃ precipitated as a mixture of bayerite (77.4%, d₀₀₁ = 4.719 Å) and gibbsite (22.6%, d₀₁₀ = 4.845 Å) (determined through Rietveld refinement, see Fig. S1, ESI†). Mg(OH)₂ precipitated as brucite (d₀₀₁ = 4.775 Å) with small impurities of an unidentifiable phase and periclase (MgO). The formation of MgAl-LDH stands in competition with the formation of Mg(OH)₂, Al(OH)₃ and other related species. At the chosen synthesis conditions, MgAl-LDH formation was found to be favourable with no crystalline impurities detectable. Any such phases would have had to exceed the crystalline phase detection limit of 2%. Due to no amorphous halos being present on the XRD scans and the SEM micrographs not indicating appreciable amounts of amorphous phases either, this material is expected to contain low amounts of amorphous and crystalline impurities. ICP analysis verified that the desired Mg : Al ratio of 2 : 1 was achieved almost exactly (2.079) and that only minor (Ca: 0.637 mass%) or trace (Ni: 0.006 mass%, Cu: 0.012 mass%, Fe: 0.050 mass%, Co: 0.007 mass%, Zn: 0.013 mass%, and Na: 0.052 mass%) contaminants were present, stemming from the chemicals used for the synthesis. Chlorine contamination could not be detected (verified using X-ray fluorescence spectroscopy). The layered structure of the MgAl-LDH with carbonate in the interlayer is shown in Fig. 1(b) from the side and Fig. 1(c) from the top (1 layer) based on the d-spacing calculated for this material (d₀₀₃ = 7.676 Å)²¹ and bond-length data for the 3R polytype.²³ Calculations of the crystallite size using the Scherrer equation²⁷ with a shape factor of 0.89^21,28 yielded an in-plane crystallite size of 17 nm and crystallite thickness of 5 nm. A similar aspect ratio was also observable on the SEM micrographs of MgAl-LDH in Fig. 1(d) and (e), showing crystallisation into globularly agglomerated structures (d) with platelet intertwinement (e) (approximately 200 nm in diameter) as a precursor to a sand-rose morphology often observed in LDHs. Fig. 1(f) and (g) show the micrographs of Mg(OH)₂ and Al(OH)₃, respectively. The Al(OH)₃, hereby, shows a mix of crystallised phases comprising of an interesting pillared platelet structure with rough platelet edges and smaller particles. The Mg(OH)₂ displays platelet agglomerates.

3.2 Photon absorption of MgAl-LDH, Mg(OH)₂ and Al(OH)₃ in the UV-Vis-NIR and MIR region

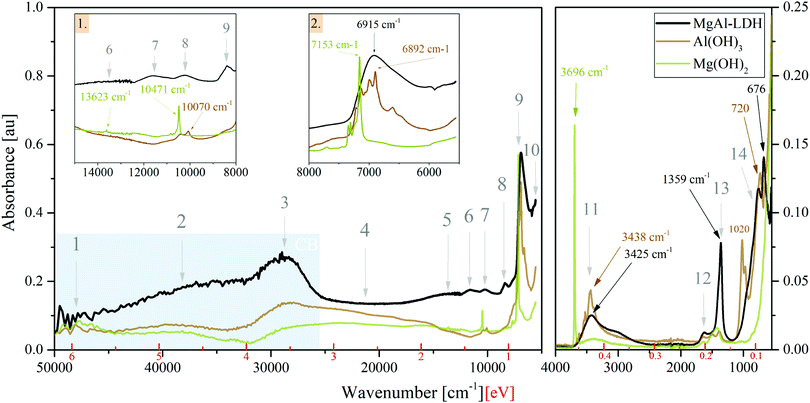
Absorption spectra (Fig. 2) in the UV-Vis-NIR range and ATR-FTIR spectra in the MIR range show that there exists great similarity between the spectra of MgAl-LDH, Mg(OH)₂ and Al(OH)₃, showing clear features in the

Fig. 2 UV-Vis-NIR absorption and FTIR spectra of MgAl-LDH, Mg(OH)₂ and Al(OH)₃ prepared using co-precipitation at identical conditions. Insets 1. and 2. show excerpts of the UV-Vis-NIR spectrum with the overtone positions of the hydroxides indicated. Points 1–14 refer to points of interest discussed further in the text. In the FTIR spectrum, important vibrations of the MgAl-LDH are labelled with their peak position. The shading indicates the CB with its edge at 3.12 eV.

• UV range (Points 1 to 3): broad bands comprising multiple overlapping bands;

• Vis range (Point 4): a broad continuum with little structure for all compounds;

• NIR range (Points 5 to 10): sharp features are visible in the hydroxides, whereas the features of the MgAl-LDH are broad, indicating some variability in the local environment and interaction of the vibrating groups; and the

• MIR range (Points 11 to 14): multiple sharp bands in the hydroxides and broader bands in the LDH with a small shift between peaks.

Unexpectedly, these three materials thus show significant absorption over the entire spectral range investigated (50 000 cm⁻¹ to 5555.55 cm⁻¹ and 4000 cm⁻¹ to 550 cm⁻¹) and, more importantly, no clearly defined band edge as a result of the broad continuum in the visible light range.

The optical bandgap was graphically determined to be 3.12 eV for MgAl-LDH (under the assumption of a direct bandgap material, see Fig. S2, ESI†) based on the prominent band in Point 3. The hydroxides did not allow accurate application of such methods. For a 3R polytype MgAl-LDH (chloride intercalated) with a Mg : Al ratio of 2 : 1, a bandgap of 2.76 eV was previously estimated using plane-wave DFT calculations.¹⁴ The graphically determined value thus matches the theoretical one closely.

The bandgap region has generally received very little attention in LDH literature. Often, absorption spectra are cut off at 800 nm or 1000 nm (1.55 eV, 1.24 eV) and thus do not offer insight into absorption past the visible light region. In this region, we, however, observe a multitude of overlapping bands. Through the comparison between the LDH and the hydroxides it is clear that these are not a background (as sometimes thought), but that they indicate states available for absorption. The bandgap region can hereby be split into two: the visible light region (absorption in this region is subject to interpretation and will be discussed later on) and the NIR/MIR regions. Studies of LDHs in the MIR region and assignment of features has been executed a multitude of times in literature with the aid of vibrational spectroscopy (Raman microprobe spectroscopy in combination with infrared spectroscopy) and without too much debate. In the NIR region, we found overtones of fundamental vibrations in the MIR region to dominate. Assignment of the relevant fundamental vibrations is discussed below:

• Point 11 contains the MO–H str. (stretching) vibrations related to Al and Mg in the LDH at 3437 cm⁻¹ (present as M–OH (1): 3437 cm⁻¹ and M–OH (2): 3566 cm⁻¹ bands), the CO₃²⁻—H₂O-br. (bridging) vibration at 3062 cm⁻¹, and the H₂O⋯H-bond vibration/H₂O-str. vibration at 3264 cm⁻¹.^29–31 Further details can be extracted from Fig. S3(a) (ESI†). The carbonate v_3a + v_3b combination band and 1st overtone of the carbonate v₃ band is believed to be seen at 2771 cm⁻¹ and 2610 cm⁻¹. The bands have not been reported prior, although the fit in this region has been imperfect and could accommodate such bands. For MgAl-LDH, the bands are necessary to obtain a good deconvolution fit. In contrast to the fine-structured bands seen in this region for the metal hydroxides, the LDH shows no fine structure due to broadening by hydrogen bonding. The sharpness of the absorption of Mg(OH)₂ at 3696 cm⁻¹ indicates that the group is not as strongly involved in hydrogen bonding.

• Point 12 at 1634 cm⁻¹ corresponds to the bending of water molecules associated with interlayer anions in the LDH.³² This vibration is also visible in the hydroxides, indicating that these likely contain some interlayer water to better stabilise the layers with hydrogen bonding.

• Point 13 represents the characteristic v₃ mode of the carbonate anion in LDHs and is typically observed as a twin peak at 1365/1400 cm⁻¹, due to symmetry breaking.^30,31 Here it is observed at 1358 cm⁻¹/1372 cm⁻¹ (see Fig. S3, ESI†) and—in combination with the other vibrational modes—confirms the desired carbonate intercalation of the MgAl-LDH. Splitting of this vibration indicates lower-than-three-fold site symmetry and interaction between the carbonate and the water molecues/hydroxide groups through hydrogen bonding (as also visible in Peak 11).^29,31,33 The hydroxides and LDH show a small band between Point 12 and 13 (Fig. S3b, ESI†) of unknown origin. We believe it to be linked to Al–OH str. vibration overtones. The small band of the hydroxides in Point 13 is expected to be related to a small amount of adsorbed CO₂³⁴ (previously having been reasoned as a source for carbonate contamination in LDHs³⁵).

• Point 14 houses Al–OH vibrations (approximately 550 cm⁻¹ and 759 cm⁻¹), Mg–OH vibrations (approximately 635 cm⁻¹) and Al–OH deformation vibrations (approximately 930 cm⁻¹) of the MgAl-LDH,^29,31 as well as water librational modes (theoretically observable at 776 cm⁻¹, 841 cm⁻¹, 866 cm⁻¹ and 949 cm⁻¹ in quintinite).³¹ Water in LDHs is strongly hydrogen bonded to the anions and layer hydroxides.³¹ Comparison between the LDH and Al(OH)₃ vibrations confirms the presence of these vibrations, although the pure hydroxide vibrations are shifted with respect to those of the LDH. In this range, Mg(OH)₂ showed no characteristic bands. In addition to these vibrational bands, this region also houses the v₁, v₂ and v₄ vibrational modes of the carbonate anion at 1030 cm⁻¹, 850 cm⁻¹ and 676 cm⁻¹, respectively, of which v₂ and v₄ are clearly visible in Fig. 2 at positions which agree mostly with previous accounts.^30,31 Due to symmetry, v₁ is infra-red-forbidden and is thus only weakly observed.

Strong vibrational overtones in the NIR region have previously been shown for LDHs³⁶ up to approximately 11 000 cm⁻¹ (1.3 eV). In our work, we observe these overtones up to approximately 14 000 cm⁻¹ (1.7 eV). The responsible vibrations for these overtones are MO–H str., CO₂-br., H-bonding between interlayer H₂O and CO₃²⁻, and H₂O-str.^36,37 The strongest impact is made by the first overtones of the bands listed above and present in Point 11, which together form Point 9 in the LDH. The other points indicated in Fig. 2 can thus be assigned to the 1st overtone of the carbonate v_3a + v_3b combination band (Point 10), the 2nd overtones of the carbonate combination band (Point 8), the MO–H str. 2nd overtone band (Point 7—likely a combination of the other vibrations similar to Point 9), the 3rd carbonate combination band overtones (Point 6), and the 3rd overtone of the MO–H str. vibration (Point 5). The fundamental carbonate combination band falls within the MIR range and is situated next to the 1st overtones of the v₃ carbonate vibration (Fig. S3(a), ESI†). Past 1.7 eV, the influence of these vibrational overtones dwindles. For the higher-energy bands, it is believed that other states are superimposed in this region in the LDH due to the flat region that is not present to the same extent in the hydroxides.

Table 1 lists the vibrations in the MIR region and the corresponding expected overtones in the harmonic approximation, while Table 2 shows the experimental band positions and the calculated anharmonicity of these overtones. Taking into consideration anharmonicity, as accounted for by the Morse potential of diatomic oscillators,³⁸ the position of the experimental bands fits the theoretical overtones very well. Anharmonicity of Mg(OH)₂ vibrations is greater than that of Al(OH)₃ and MgAl-LDH. But since the band in the LDH is a superposition of many vibrations, it might be higher than calculated (considering the strong overtone vibrations visible). The relatively large intensities of the overtones demonstrates that the anharmonicity is sufficiently large in all compounds to render forbidden transitions appreciably allowed.

Table 1 Theoretical overtones (ν = 1 to ν = 5) of the experimental fundamental vibration (ν = 0) of MgAl-LDH in the MIR region based on harmonic oscillation (H-b = H-bond and c. = combination band)

	Vib. band	ν = 0	ν = 1	ν = 2	ν = 3	ν = 4	ν = 5
[cm^−1]	MO–H	3437	6874	10 311	13 748	17 185	20 622
	H2O-str./H-b	3264	6528	9792	13 056	16 320	19 584
	H2O-CO3^2− br.	3062	6124	9186	12 248	15 310	18 372
	v 3a CO3^2−	1373	2745	4118	5490	6863	8236
	v 3b CO3^2−	1358	2716	4074	5432	6790	8148
	v 3 CO3^2− c.	2731	5461	8191	10 922	13 653	16 384
[eV]	MO–H	0.43	0.85	1.28	1.70	2.13	2.56
	H2O-str./H-b	0.40	0.81	1.21	1.62	2.02	2.43
	H2O-CO3^2− br.	0.38	0.76	1.14	1.52	1.90	2.28
	v 3a CO3^2−	0.17	0.34	0.51	0.68	0.85	1.02
	v 3b CO3^2−	0.17	0.34	0.51	0.67	0.84	1.01
	v 3 CO3^2− c.	0.34	0.68	1.02	1.35	1.69	2.03

---

Table 2 The experimentally determined fundamental vibrations (ν = 0) and overtones of the MO–H str. vibrations in MgAl-LDH, Mg(OH)₂ and Al(OH)₃ (points 9, 7 and 5), and the corresponding ratios of the overtones (ν = n) to the fundamental vibration (ν = 0)

ν = n	MgAl-LDH			Mg(OH)2			Al(OH)3
	[cm^−1]	[eV]	ν n /ν0	[cm^−1]	[eV]	ν n /ν0	[cm^−1]	[eV]	ν n /ν0
ν = 0	3437	0.42	1	3696	0.46	1	3438	0.43	1
ν = 1	6916	0.86	2.01	7158	0.89	1.94	6897	0.86	2.01
ν = 2	10 235	1.27	2.98	10 482	1.30	2.84	10 070	1.25	2.93
ν = 3				13 624	1.69	3.69

---

3.3 Luminescence of MgAl-LDH, Mg(OH)₂ and Al(OH)₃ in the UV-Vis region

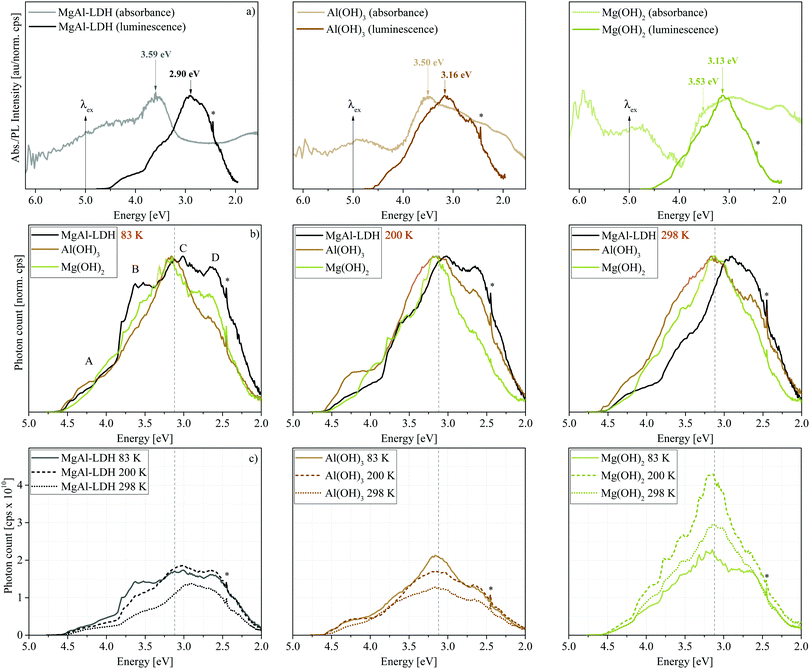
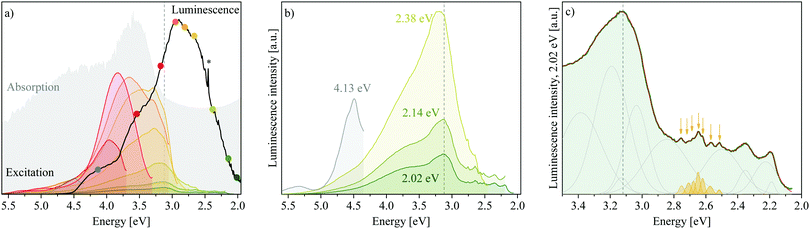
Luminescence results presented in Fig. 3 show that MgAl-LDHs and the hydroxides are possible to manufacture with high luminescence intensity and with clearly defined luminescence bands. These materials were not dehydrated prior to analysis and yet exhibit considerable luminescence intensity and fine structure/band resolution at all temperatures and in their native hydrated state. This is unusual, because LDHs in the bulk have so far not shown any appreciable fine structure,^7,20 and it stands in contrast to findings in ZnAl-LDHs, where luminescence quenching was prominent in the hydrated form.⁷ The luminescence behaviour seen here is more similar to that of exfoliated LDH nanosheets⁷ (a 2D material) than other bulk materials prepared. The bands observed are also unprecedentedly broad, covering an emission range of more than 2 eV, but show an overlap of multiple bands within this region; a complicated spectrum, expected for the complicated structure of LDHs.

Fig. 3 (a) Comparison between absorption and luminescence spectra for MgAl-LDH, Mg(OH)₂ and Al(OH)₃ at 298 K. All luminescence data was corrected and normalised. Absorption intensities were adjusted to properly depict overlapping luminescence bands. (b) Normalised luminescence spectroscopy results for MgAl-LDH, Mg(OH)₂ and Al(OH)₃ showing temperature-dependent (83 K, 200 K and 298 K) changes in band intensity and placement with an excitation wavelength (λ_ex) of 248 nm (5.0 eV). (c) Absolute temperature-dependent luminescence of MgAl-LDH, Al(OH)₃ and Mg(OH)₂ at 83 K, 200 K and 298 K. * = artefact at double excitation energy. - - - = 3.12 eV band edge of MgAl-LDH.

Fig. 3(a) shows that the excitation energy (5.0 eV) used in this work falls within the band at Point 2. Emission, which was only significant below approximately 4.5 eV, hereby, indicates that excited electrons relax to a high-energy CB state before taking part in radiative charge recombination pathways. The band maximum occurs 2 eV lower than the excitation energy, overlapping with the graphically obtained CB edge (3.12 eV).

In Fig. 3(b) and (c) we can observe the dependence of the luminescence spectra on temperature. All materials display four distinct bands (Bands A–D). However, Bands B and D are more prominent in the LDH than in the hydroxides. At 83 K, the MgAl-LDH spectrum is especially fine-structured and broad. With an increase in temperature, the width of the hydroxide spectra remains similar, while the LDH spectrum narrows, intensity of Bands A and B is reduced, and Band C redshifts. The intensity, fine-structure and breadth of the bands above the band-edge is rather unexpected. Typically, one would expect excited charges to non-radiatively relax to the CB edge and, from there, to radiatively (or non-radiatively) relax to the ground state and recombine with the hole. Here, however, 47% of the luminescence of MgAl-LDH occurs at an energy above the lower CB edge at 83 K (50% at 100 K, 45% at 150 K, 41% at 200 K, 40% at 250 K and 37% at 298 K).

Another noteworthy aspect to be extracted from Fig. 3(c) is that the luminescence intensity of MgAl-LDH and Mg(OH)₂ goes through a maximum at 200 K. This is an unexpected result, since increased lattice vibration amplitudes at higher temperatures usually allow excited electrons to access non-radiative relaxation pathways, returning to the ground electronic state through a release of heat, thermally quenching luminescence intensity in turn.²² A more detailed temperature sweep of the MgAl-LDH in 50 K steps is shown in Fig. 4(a).

Fig. 4 (a) Luminescence temperature-dependence of MgAl-LDH showing results at 83 K, 100 K, 150 K, 200 K, 250 K and 298 K. (b) Luminescence spectroscopy repeatability results for MgAl-LDH at 83 K. The standard stepsize was 2 nm (36.41 meV to 5.89 meV). Luminescence of MgAl-LDH rep 2 was recorded with a stepsize of 0.5 nm (9.15 meV at 260 nm to 1.47 meV at 650 nm). (c) Luminescence changes upon calcination of MgAl-LDH at 373 K to 673 K (spectra acquired at 83 K) * = artefact at double excitation energy. - - - = 3.12 eV band edge of MgAl-LDH.

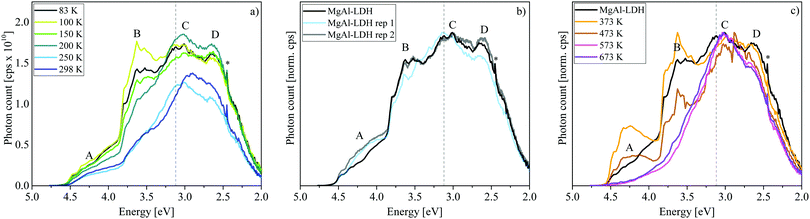
Here we can observe that not only Band C is affected by this temperature dependence but also especially Band B, which reaches its maximum intensity at 100 K. In this more detailed temperature-sweep, it can be observed that 100 K allows more photons to be emitted than any other temperature (area ≈ 2.6 × 10¹⁰ cps eV), the lowest number being emitted at 250 K (area ≈ 1.5 × 10¹⁰ cps eV). We can also observe that at 200 K a redistribution of luminescence occurs in comparison to that observed at 83 K, favouring luminescence in Bands C and D rather than Band B.

Luminescence of the MgAl-LDH was tested in triplicate (with different sample portions) at 83 K, 200 K and 298 K (see Fig. 4(b) for results at 83 K and Fig. S4, ESI,† for a comparison of results at all temperatures). Especially at 83 K, the reproducibility was very closely achieved. Using a smaller step size (0.5 nm instead of 2 nm) at 83 K revealed that fine-structure in the bands is reproducible.

Further, we determined luminescence changes upon calcination of the MgAl-LDH between 373 K and 673 K. These results are depicted in Fig. 4(c). Upon heating, an LDH undergoes several stages of transformation. First, it loses loosely adsorbed species and surface adsorbed water up to 373 K. Interlayer water is more stable and is lost at approximately 473 K. Heating the LDH further leads to the loss of carbonate interlayer anions and the hydroxyl groups in either a 2-step or 1-step process.^8,24,32 For the MgAl-LDH, this was found to be a 2-step process with the main loss of the hydroxyl groups (first those bound to Al) at 573 K and main loss of interlayer carbonate (and hydroxyl groups bound to Mg) at 673 K.²¹ Of course, these two latter steps are not discrete and some of both species will be lost at either temperatures, even in a 2-step process. Water-loss would decrease hydrogen bonding in the material, while the loss of the interlayer carbonate leads to the expulsion of CO₂ and the loss of the hydroxyls to the expulsion of H₂O.

Annealing at successively higher temperatures leads to band narrowing and a shift in the percentage of above- and below-band-edge luminescence (above-band-edge emission at 83 K: 47% untreated, 52% at 373 K, 43% at 473 K, 34% at 573 K, and 37% at 673 K). At 373 K the removal of surface water yields better defined, more intense bands, as also found in ZnAl-LDH upon dehydration.⁷ Interestingly, removal of interlayer water leads to a loss of some luminescence intensity. The luminescence dependence on hydration substantiates previous suggestions^7,9 of a non-radiative relaxation mechanism through the interaction with water (water-oxidation on the photogenerated hole on the OH groups⁹)—a good indication of their suitability for photocatalytic water-splitting.

Loss of the hydroxyl groups and re-arrangement/loss of the interlayer carbonate due to a lack of H₂O and hydroxyl bonding partners at 573 K and 673 K leads to a loss of Bands A and B as well as a small depression of Band D. It has been shown that this process of carbonate and hydroxyl-group removal can lead to the grafting of oxide anions to the LDH layers.³⁹ While typically little attention is given to the electrons during the conversion process, these are quite important for luminescence characteristics. Expulsion of one carbonate anion leaves behind an O²⁻ anion and the expulsion of two hydroxide groups an O⁻ anion and an oxygen vacancy (upon the loss of a water molecule). The material thus changes in oxygen content and the availability of “free” electrons while retaining charge neutrality. It is hereby expected that remaining carbonate ions would preferentially arrange themselves into places that stabilise possible defects in the structure and interact more closely with the LDH layers (metal ions).⁴⁰

3.4 Excitation spectra of MgAl-LDH

Excitation spectra obtained monitoring luminescence in the LDH at 298 K at nine points along the spectrum reveal that a multitude of excitable states above and below the graphically determined band edge contribute to the luminescence observed (Fig. 5(a)). Hereby, luminescence below the band edge results almost entirely from a multitude of excitable states above it (although luminescence is observed up to 1 eV below the band edge) and the contribution of each of these states to the different luminescence energies varies. Highest luminescence intensity of all bands is obtained through excitation between 4.5 eV and 3.0 eV. Below 3.0 eV, states able to yield luminescence fall sharply in intensity but are nevertheless able to contribute. This correlates well with the absorption spectrum, but with more resolution, achieving the highest luminescence intensity with excitation in regions of optimal absorption (an expected result). Combined with the luminescence results through excitation at 5.0 eV, these results give us complementary insight into the charge recombination behaviour in the LDH: excitation at 5.0 eV leads to observation of the “trickling pathway” of excited carriers to the band edge releasing luminescence on its way, while the excitation spectra give us insight to which states contribute most to each band of luminescence observed.

Fig. 5 (a) Excitation spectrum of MgAl-LDH between 5.6 eV and 2.0 eV, monitoring luminescence at 4.13 eV, 3.54 eV, 3.18 eV, 2.95 eV, 2.82 eV, 2.67 eV, 2.38 eV, 2.14 eV and 2.02 eV. (b) Close-up of the excitation scans monitoring emission at 4.13 eV, 2.38 eV, 2.14 eV and 2.02 eV to expose below-band-edge fine structure and that far above the band edge. (c) Deconvoluted excerpt of the 2.02 eV excitation spectrum showing defect states below the band edge and the distinct feature of overlapping sharp bands between 2.75 eV and 2.5 eV (yellow). * = artefact at double excitation energy. - - - = 3.12 eV band edge of MgAl-LDH.

In Fig. 5(b) we can observe that luminescence monitored at 2.38 eV, 2.14 eV and 2.02 eV forms almost identical excitation patterns whereby the luminescence intensity depression is similar to the excitation spectra intensity. It is interesting that these three spectra correlate so beautifully, considering that the luminescence spectrum was obtained through excitation at 5.0 eV and excited charge carriers had to relax to the band edge first before partaking in radiative relaxation. The correlation indicates that processes yielding luminescence of energies lower than the bandgap energy are similar, whereas luminescence at higher energies has differing origins. Particularly, the scans at 2.14 eV and 2.02 eV are identical (apart from intensity) while the scan at 2.38 eV shows a higher energy contribution (3.24 eV) to luminescence that is not as prevalent in the (lower energy scans). In addition, it indicates that states above the valence band (VB) edge must be available that roughly match the ΔE of the observed luminescence (roughly 0.24 eV and 0.12 eV between the three green scans) to yield luminescence at different energies although the excitation spectra are almost identical. Fundamental vibrations available at these energies are those involving the carbonate anion, the ν_3a,3b str. and H₂O–CO₃²⁻ br. vibrations (Table 2), which suggests an interaction of this anion in relaxation pathways involving luminescence far below the band edge. Further, the strongly favoured luminescence from excitation of states within the CB indicates that the conversion of absorbed- into emitted light is more efficient than excitation of states below the band edge. A larger fraction of excitation of these lower energies must thus be converted to heat, i.e. non-radiative relaxation. Excitation of MgAl-LDH at 3.8 eV is shown in Fig. S5 (ESI†) and shows that the luminescence spectrum remains similar, but has increased counts. A 1.4-fold increase in luminescence is expected if corrected for the higher absorbance at 3.8 eV. A 10.5-fold increase in luminescence at 3.12 eV is observed though. This shows that excitation so far above the band edge is not ideal and leads to increased recombination through non-radiative means above the band edge. Generally, the luminescence efficiency of MgAl-LDH is expected to be low, since it reflects a large portion of incident photons and, in powdered form, does not luminesce visible to the naked eye.

Finally, some of the excitation scans show similar features, such as the triple band state in the grey, yellow and dark green scans (Fig. 5(b)) and the distinct sharper feature at 3.24 eV present in the orange and yellow scans. One of the scans (red, monitoring at 3.18 eV, close to the band edge), is also noticeably less complex and of higher intensity. Deconvolution revealed each scan to be reconstructible with bands at the same positions. Thus, although luminescence of each band is favoured from excitation at different energies, the underlying states and thus the pathways to radiative relaxation may be overlapping to a degree. At present, this deconvolution cannot be taken as absolute, but it is encouraging to learn that excitation spectra can aid in uncovering available states in LDHs with more resolution than absorption spectra can. An excerpt is shown in Fig. 5(c), showing the rich and reproducible structure below the band edge that exists in scans monitored at 2.38 eV, 2.14 eV and 2.02 eV. Further, the fine-structure below the band edge shows a distinct accumulation of sharp bands between 2.5 eV and 2.75 eV indicated in yellow in Fig. 5(c)—a special defect state. It also shows that overlapping states exist between 2.0 eV and 2.9 eV that may be less delocalised than this special state. The fine-structured region—and particularly the existence of the special state—is the first observation of its kind in LDHs.

4 Discussion

4.1 What we can learn from comparing the absorption spectra of MgAl-LDH, Mg(OH)₂ and Al(OH)₃

DFT studies of MgAl-LDH¹⁴ and the hydroxides^41,42 have revealed that the same kinds of transitions are predominant in the LDH and the hydroxides: O 2p → Mg/Al 3p and O 2p → Mg/Al 3s, O 2p states forming the VB edge and the metal states contributing to the CB. Contrary to previous explanations,^7,9 Al definitely contributes to the available states in the CB, as visible in the absorption and luminescence results (and the computational results⁴²). These transitions are expected to feature especially prominently in Points 2 and 3 and Bands A and C as a result of the strong overlap. Interestingly, Band A can be exactly replicated through linear combination of the hydroxide spectra in the 2Mg : 1Al ratio, Band C very closely (less broad) (Fig. S6, ESI†)—a strong indicator that these bands are a more direct result of contributions by the metal ions.

In all three materials, these transitions dictate—in part—the size of the bandgap. As previously stated, the predicted bandgap of MgAl-LDH (2.76 eV) is close to our graphically determined value (3.12 eV). Ab inito calculations⁴¹ of Mg(OH)₂ predicted, however, that its theoretical bandgap is significantly larger (7.70 eV). This extremely large bandgap does not agree with our findings, where the hydroxides show significant absorption, overlapping with that of the LDH. Interestingly, the calculated bandgaps also do not always correspond to those obtained experimentally in literature, where low bandgap values in the range of 2.6 eV to 3.5 eV have been observed for Mg(OH)₂.^43–45 We believe these differences to be a result of the limitations of computational approaches (complexity and size of the structures necessary for accurate predictions) and different computational methods used.

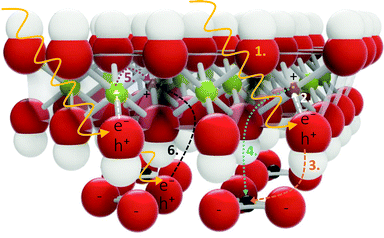
Other types of transitions are also expected in LDHs. These could involve the carbonate anion (which has been suggested to contribute to bandgap narrowing in ZnCr-LDH⁴⁶) or be the result of oxygen and interstitial defects (in sufficient concentration), aliovalent or isovalent impurities (such as the small amount of Ca present, 0.637 mass%), structural disorder, and strain and stress in the crystal. These are known to contribute to bandgap narrowing in other semiconductors,^47,48 particularly making states available for excitation close to or below the CB edge where exciton formation can also contribute.⁴⁹ In addition, it is possible that electrons situated within the VB be excited into the CB with sufficient energy. Such excitation would broaden the bands and could introduce new ones above the band edge. Another LDH-specific effect that could contribute to band broadening/bandgap narrowing is the effect we have termed “islanding”. LDHs (especially of the 2 : 1 ratio type) are generally considered globally ordered instead of the cations being randomly distributed within the lattice.⁵⁰ Mg₂AlOH clusters are expected to dominate.^50,51 It can thus be broadly assumed that the Al³⁺ ions in the LDH lattice are mainly surrounded by Mg²⁺ ions, forming a charge deficient island in their midst (see Fig. 1(b)), which could be responsible for the formation of an inhomogeneous density of states in the CB/near the CB edge. Dependent on the overlap of localised wavefunctions and the proximity to the CB, the above-mentioned defects could thus form an impurity band below the band edge, which could merge with band states if the Anderson-Mott limit is exceeded,⁴⁹—thus becoming accessible—and present with an Urbach energy (band tail) in absorption spectra.^49,52 We believe this impurity-band-formation below the band edge to be responsible for the continuum in the absorption spectra.

4.2 Relaxation to states within the CB and recombination yielding photons of energies exceeding the bandgap energy

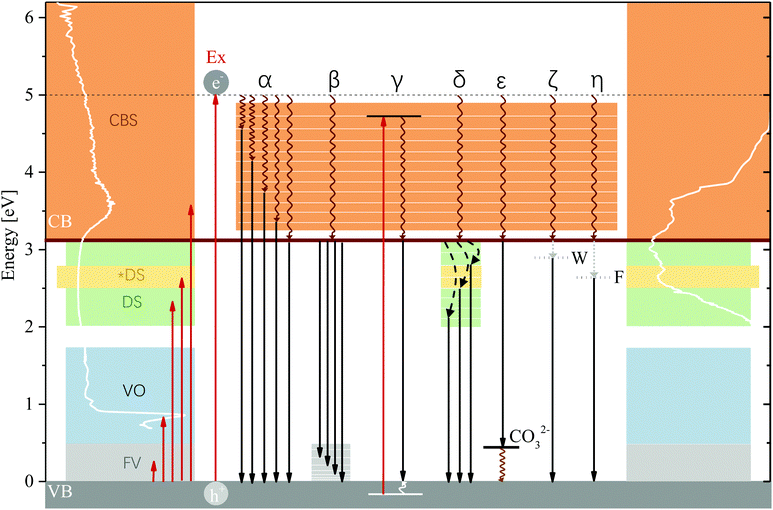
As has been described in the Results section, 47% of luminescence (at 83 K) occurs at energies exceeding the bandgap energy—a considerable fraction and an unexpected result considering that the typical assumption is that excited electrons relax to the band edge before radiatively recombining with the hole. Emission of photons of energies exceeding the bandgap energy are plausible only as a result of radiative relaxation from states within the CB, excitation of electrons within the VB or radiative relaxation to high-energy states above the upper VB edge. In the excitation spectra of MgAl-LDH, we can observe a multitude of excitable states above the lower CB edge which contribute in different strengths to emission of photons with energies exceeding the bandgap energy. These states (shown in Fig. S7 as a result of deconvolution, ESI†) show us that there exist plausible levels within the CB to which an excited electron could relax non-radiatively (Pathway α) and from which emission could subsequently occur. Coupled with non-radiative relaxation from vibrational levels above the band edge to the VB edge (Pathway β), these recombinations could give rise for the extremely broad and complex part of the luminescence spectrum observed above the band edge; the most plausible cause. In addition, some of the luminescence band-breadth could have resulted from excitation of electrons within the VB as has been observed, e.g. in SiO₂.⁵³ Coupled with relaxation of the hole to the VB edge, luminescence energy would be lowered by the difference between the VB state and the VB edge (Pathway γ). The excited electron can also again engage in Pathways α and β which would further lower the emitted-photon energy. While plausible due to the complexity of the LDH structure and thus density of states in the VB, this mechanism requires deeper investigation. High-energy states above the VB edge could not be clearly identified due to the strong contribution of the overtones, but could be present at around 1 eV and above, considering the strong absorption in that region causing a flat absorption band.

4.3 Temperature dependence of radiative recombination pathway selection

Emission of photons above and below the bandgap energy was found to be significantly affected by the measurement temperature. Raising the measurement temperature leads to an increase in lattice vibration amplitudes, which usually encourages non-radiative relaxation.²² This can be observed in our results by comparing the area of the spectra of MgAl-LDH at 83 K and 298 K (radiative emission reduction of 38%) yielding an increase (19%) in below-band-edge emission at 298 K. This dependence on the temperature indicates that there exists a competition between radiative and non-radiative deactivation from meta-stable CB states, and especially an influence on the efficiency of non-radiative relaxation of excited charges to the band edge before recombination. This path dependence is solidified by the repeatability results, which show that even though repeatability is closely achieved at 83 K, some differences exist at higher temperatures (see Fig. S4, ESI†), indicating the thermal activation/deactivation of some radiative relaxation pathways.

The band structure of complex materials like these can contain a multitude of local energy minima in addition to the absolute minimum that would be used for the calculation of the bandgap in theoretical work because of the inhomogeneity of the material (the distribution of metals, different bond types, the presence of the anion or of defects). Should these minima be favourably positioned energetically, it could be possible for excited electrons to get trapped in them (especially at low temperatures). With suitably large vibrational coupling, higher temperatures could then aid in overcoming potential barriers and allow relaxation to the band edge (this is the predominant emission point at all temperatures other than 100 K, as seen in Fig. 4(a)). This vibrational coupling, or electron–phonon coupling (polaron formation), we believe to be especially prominent in LDHs due to their polar-ionic nature and the loss of symmetry that allows, e.g. the vibrational overtones observed in our results to be strongly visible although they should actually be forbidden. This coupling would require the presence of local defects and impurities to locally deform the lattice upon phonon emission⁵⁴—both are expected to be present. We believe that this kind of activation causes the increase in luminescence at 200 K for MgAl-LDH and Mg(OH)₂. In Table 1 we showed that the anharmonicity of Al(OH)₃ is much lower than that of Mg(OH)₂, giving an explanation as to why this luminescence increase at 200 K is not seen in Al(OH)₃. Unfortunately, as a result of the spectral complexity, it is not possible to quantify the electron–phonon coupling. The strength of this coupling can be related to the Stokes shift and the Huang Rhys parameter, but they require clearly identifiable transitions to monitor redshift,⁵⁵ which are not available.

4.4 Effects causing luminescence below the band edge

From the luminescence results it is clear that emission resulting in the formation of Band D presents important mechanisms taking place in the LDH to recombine the excited electron with the hole at sub-bandgap energies. Band D is present in the LDH and the hydroxides and must thus present an effect that is at least in part related to them all. Confirmation of the exact recombination pathways being utilised in LDHs would be premature. However, there exist several plausible reasons for this below band-edge emission, it likely being a superposition of equally/similarly energetic photons released due to different mechanisms. These options are discussed in the following paragraphs.

Vibrational broadening. Radiative relaxation of excited electrons from the band edge to vibrational states of the electronic ground state (Pathway β) is the expected default cause of luminescence broadening, especially at higher measurement temperatures. This is very strongly observed in the MgAl-LDH compared to the hydroxides by a strong shift in the peak luminescence intensity. Three prominent groupings of vibrational states exist in MgAl-LDH (visible in Fig. S7, ESI†)—from 0.32 to 0.44 eV, 0.17 eV to 0.2 eV, and 0.12 eV to the VB edge. Relaxation, especially to the higher energy levels, would, hereby, broaden the luminescence spectrum and complicate the observation of individual pathways of recombination from different states within the CB and from the CB edge.

Coordination defects. The prevalent interpretation concerning luminescence in LDHs is that it occurs mainly as a result of surface^7,16 or coordination⁵⁶ defects. Defects are often encountered in LDHs, be they as a result of stacking faults, cation or oxygen vacancies, or edge and surface sites;⁵⁷ usually as a synthesis by-product. The luminescence origin proposed in LDHs hereby follows a similar interpretation to luminescence in Mg(OH)₂ and MgO, where it has been found that the type of oxygen coordination site has a great influence on absorption and emission properties, being the cause of very complex spectra in the UV-Vis region below the CB edge.^44,58–61 Specifically, the lower the metal coordination, the lower the absorption bands resulting from them, the immediate environment of the site playing a crucial role.⁵⁸ Luminescence at an energy overlapping with Band D has previously been postulated to be linked to such hydroxyl groups in specific low-coordination sites in Mg(OH)₂, the band disappearing upon full calcination.⁴⁴ In Fig. 4(c), we can observe that calcination at 673 K is not enough to remove this band. Since excitation occurred at 5.0 eV (far above the band edge), for this luminescence to be caused by such a low-coordination defect, the excited electron (or an exciton formed at the band edge) would need to be able to bind to the defect to lower the luminescence energy sufficiently or be able to access states of such a type below the band edge.

In an attempt to observe whether significant oxygen defects are present in MgAl-LDH, we analysed the material with X-ray photoelectron spectroscopy, which is able to pick up percentages upward of 0.1 at% (atomic percent).⁶² It was revealed that the O 1s band contains a secondary band (see Fig. S8, ESI†) that indicates a defect percentage of up to 16 at%. This type of analysis can be used as an indication of oxygen defects.⁶³ However, due to this method not having been applied to LDHs prior, it is uncertain whether this is a true reflection of oxygen defects in the structure or also of, for example, compression of the lattice.⁶⁴ Nevertheless, we do expect some oxygen defects in the LDH, which are expected to be contributing to the broadened XRD reflections visible in Fig. 1(a). Visibility of these in XRD indicates their concentration to exceed 1 at%.⁶² Considering our results, we do not agree with assigning all luminescence to these oxygen/coordination-type defects as often simplified, but believe that they do play a role in broadening the CB and emission from above the bande egde as well as being involved in below-band-edge emission through defect binding. The use of X-ray absorption studies would be a good addition for future studies to better characterise these effects.

Accessing defect states below the band edge. In our results, Band D overlaps with the fine-structured state in the excitation spectra found between 2.75 eV and 2.5 eV (indicated in yellow in Fig. 5(c)). At present, it is not known what the exact origin of this fine-structured band and the surrounding states is. In the first section of the discussion, it was explored how impurity-band-formation as a result of structural, oxygen and interstitial defects, aliovalent or isovalent impurities, disorder, and strain and stress could cause the formation of an impurity band, should the wavefunctions of these states sufficiently overlap. Further, if they overlap sufficiently with the CB, some of these states might become accessible in the recombination pathway, causing below-band-edge luminescence (Pathway δ). The fine structure visible in the excitation spectra indicates that some of these states overlap with the CB and also each other. Some connectivity is thus plausible, facilitating access to these states.

Exciton formation and related effects. Excitonic effects have been postulated in LDHs⁷ and in Mg(OH)₂^41,44 to contribute to below-band-edge emission, but their exact nature (and the types of excitons present) has not yet been determined. A cause of below-band-edge emission in related materials (halide perovskites and transition-metal dichalcogenides, 2D and sometimes 3D) has shown to be, for example, exciton trapping/binding, producing very broad white-light emission.^65–70

LDHs are unique layered structures as a result of the way that the octahedral units are connected and thus exhibit a multi-sandwich structure where metal ions form one layer, enveloped by oxygen and hydrogen and the interlayer region. This is different to, for example, perovskites, which still contain octahedrally-coordinated clusters but where the metals and bonded halide groups fall within the same layer. It is possible that this kind of structure also allows for the generation of interlayer and intralayer excitons as separate or linked processes. As a result of the structure and bonding types in the LDH it could be plausible to find Frenkel excitons as a result of polar-ionic bonding in the layers. Upon recombination, this kind of exciton with a high binding energy could release luminescence of more than 0.5 eV lower than the bandgap energy (Pathway η). This binding energy would match with luminescence beyond Band C and could potentially be the cause of excitation in the broad bands of the fine-structured region. Another alternative could be the formation of Wannier excitons. Wannier excitons are frequently observed in semiconductors,^22,49 contributing significantly to just-below-band-edge absorption at low temperatures⁴⁹ and forming more stable forms in dimensionally confining materials at higher temperatures.⁴⁹ LDHs, as a result of the thin metal hydroxide sheets, are dimensionally confining perpendicular to the c-axis. Wannier excitons have a far lower binding energy than Frenkel excitons, thus theoretically releasing higher energy photons upon recombination (Pathway ζ). But, as the most flexible of the excitons, they can exceed multiple lattice constants in size²² and could thus extend over different layers (also interacting with the interlayer region, forming an interlayer exciton), and their luminescence energy lowered if, additionally, they bind to defect states. This type of exciton could allow for some interesting effects to be observed in the LDH. Specifically, these excitons could make use of electron/hole stabilisation sites in the layer (such as the Al³⁺) and interlayer (such as the carbonate), which could contribute to their stability at higher temperatures. Further, trapping of electrons and excitons might be facilitated in the LDH by islanding through attraction to Al³⁺ in the lattice in addition to attraction to defects, causing self-trapping as a result of strong phonon coupling—a prevalent effect in polar semiconductors⁷¹ and expected to be amplified here due to the presence of local defects and impurities⁵⁴ and the 2D-material-like behaviour of MgAl-LDH.

4.5 The role of the anion

Through the comparison of the hydroxides and the LDH, we wished to gain insight into the role of the carbonate in absorption and recombination processes, since the presence of the carbonate has, for example, been shown to broaden absorption bands⁴⁶ and it is credited with greater separated charge stabilisation in photocatalysts.¹⁷ Bands B and D are significantly more prominent in the LDH than in the hydroxides and both bands are believed to carry some impact of the carbonate anion. In Band B this luminescence is strongly affected by calcination, removal of most hydroxide groups causing a depression in this band. Band D is also somewhat affected by this removal, showing some luminescence depression. If the carbonate does contribute to these bands, we expect the re-arrangement of the carbonate ion as a result of structural changes, rendering this relaxation route unfavourable. In Band D, a plausible interaction would also be for the carbonate to act as a charged hole acceptor state (A⁻, CO₃²⁻, Pathway ε) above the VB edge (this could result in the greater charge separation and support previous findings¹⁷) or that the particular vibrational states forming Point 11 in the MIR region (Fig. 2) create a particularly important vibrational level in the LDH to which radiative relaxation is favoured (it is at the same energy as the difference between the band edge and Band D). The latter would match with observations of the calcined materials (573 K and 673 K), which show a successively lower red-shift measured at 298 K (Fig. S9, ESI†). It would also match with the results obtained from the almost identical excitation spectra below the band edge, separated by ΔE = 0.24 eV and 0.12 eV, roughly the energetic distance between the carbonate vibrational levels and the VB edge, giving a very strong indication that the carbonate is involved in radiative relaxation pathways far below the band edge.

Considering the spatial separation of the carbonate from the layer, we thought it necessary to consider how the involvement of the carbonate in charge separation/stabilisation could be facilitated. In the first section of the discussion, it was described that the predominant contribution of density of states in the CB is a result of the excitation of an electron in the O 2p orbital of the M–OH bonds.¹⁴ Involvement of the carbonate ion in the relaxation process could, hereby, be facilitated by stabilising the hole (which would decrease its energy and lower the energy of emission) through triangular shuffling. This mechanism is depicted in Fig. 6.

Fig. 6 Involvement of the carbonate ion in the relaxation mechanism through triangular shuffling of excited electrons and holes. 1. Excitation of an electron in the O 2p orbital partaking in the layer M—OH bonds. 2. Separation of the excited electron to a neighbouring M 3s/3p orbital. 3. Stabilisation of the hole on the carbonate anion. 4. Recombination of the electron with the hole. 5. Attraction of the excited electron to a near-by Al³⁺ ion (or to an impurity/defect). 6. Excitation of an O 2p orbital in the carbonate ion.

However, because the carbonate is spatially separated from the layer, this kind of mechanism would predicate the existence of Wannier excitons, facilitating access between the layer and interlayer. It is expected that this kind of process would lead to broadened bands in the presence of e.g. coordinational defects that lower the energy of excitation and subsequently emission.

More generally, the presence of the carbonate ion is believed to be enhancing the much more significant redshift of Band C at higher measurement temperatures. This redshift is almost negligible in the hydroxides and is expected to be caused mainly by the availability of vibrational states that contribute to levels above the VB edge. These are particularly broad in the LDH compared to the hydroxides as visible in Fig. 2. In Fig. 7 all radiative recombination pathways discussed are summarised.

Fig. 7 Summary of excitation and and plausible charge recombination pathways. Excitation can occur to fundamental vibrations (FV), vibrational overtones (VO), defect states (DS, an *DS = special defect state overlapping with band D) and CB states (CBS). Luminescence results of this study were obtained through excitation at 5 eV (Ex), far above the CB edge. (α) Non-radiative relaxation to a variety of states within the CB and subsequent radiative relaxation to the VB edge. This process can precede any of the following pathways and occurs in conjunction with the radiative relaxation to vibrational states above the VB edge and subsequent non-radiative relaxation to the ground state (β). These vibrational levels are also accessed in all following pathways (radiative relaxation to the band edge shown as a simplification). (γ) Excitation of an electron in the VB and subsequent relaxation of the hole to the VB edge, lowering emission energy. (δ) Defect binding of excited electrons above the CB edge. (ε) Interaction with a charged hole acceptor (CO₃²⁻) decreasing the hole energy. (ζ) Formation of a Wannier exciton. (η) Formation of a Frenkel exciton. These excitons can lower emission energy by binding to impurity/defect states/Al³⁺ islands. Absorption spectrum: 298 K, Emission spectrum: 83 K.

4.6 The effect of calcination

Because the LDH structure “collapses” and partially amorphitises with the loss of water, the hydroxides and the carbonate to form layered double oxides and, eventually, (irreversibly) spinels,⁴⁰ because the loss of the hydroxides leaves an O⁻ anion and an oxygen vacancy, and because the carbonate re-arranges in this process, there are many convoluted factors contributing to changes in the luminescence behaviour of heat-treated materials.

Luminescence changes as a result of calcination at as high temperatures as in our work, have, to our knowledge, not been reported before. However, luminescence of LiAl-LDH has been tested in the calcined form at 573 K, with some interesting results obtained.⁵⁶ There, it resulted in strengthened blue-light emission (blue shift from the uncalcined material), thought to be as a result of the creation of Al sites with 5-fold-oxygen-coordination.⁵⁶ Particularly, this blue-light emission was attributed to vacancy acceptor and donor states (it is uncertain how these could act as the same state). In our results, we see a similar, slight blue shift in the calcined materials. But instead of this being attributed to these defect states—which in our opinion should reduce the luminescence energy by creating a state below the band edge akin to MgO results,^58,59,72 such a band is also seen in their results around 650 nm (1.9 eV) but was not observed for MgAl-LDH, which showed no significant luminescence below 2 eV (Fig. S10, ESI†)—we believe these to be a function of a reduction in vibrational states available due to the reduction in the number of hydroxyl and carbonate groups in the LDH structure/the rearrangement of the carbonate to defect sites (Fig. S9, ESI†). In future work, the calcination results will need to be supplemented by targetedly altered materials, especially concerning defects, to draw definite conclusions on the effect of each constituent of the LDH lattice on luminescence.

4.7 The importance of correct bandgap determination and its effect on absorption and luminescence interpretation

The most frequently applied methods for optical bandgap determination of LDHs are graphical (like the Tauc plot method, or as used here, the absorption spectrum fitting method). A concern with these methods is that they are strongly dependent firstly, on accurate fitting of a tangent line and secondly, that more complex parts of the spectrum which fall below the main band are often ignored. In MgAl-LDHs, for example, low-definition absorption bands are visible in all spectra^9–13 and the clean absorption edge as predicted from calculations^9,14 has never been observed in practice. Yet, these bands did not form part of the discussion in any of the works. In one work, multiple bandgaps were even reported for ZnAl-LDH⁷ (and excitonic effects predicted above what would be the lowest band edge), yielding the questions of which one of the bandgaps is “correct” and which the correct interpretation of complex absorption spectra with many overlapping bands in LDHs—as they are also visible in our work—is.

In this work, we graphically determined the bandgap of MgAl-LDH to be 3.12 eV (Fig. S2, ESI†). This matched well with the excitation spectra findings. However, depending on the connection of impurity states to this band, the true bandgap could be significantly lower. Since the interpretation of luminescence is dependent on the relative placement of the CB edge, our work should inspire the careful application of graphical bandgap determination methods and subsequent interpretation. Furthermore, the presence of absorption over the entire spectral range in the absorption spectrum (Fig. 2) questions, to some extent, the discussion of the material as a semiconductor with a well-defined bandgap. Should the bandgap be significantly smaller as a result of access to band-tail states, this could be a positive discovery, one that might accelerate the much desired bandgap-narrowing of semiconductors used in photocatalytic, photoelectrochemical or photovoltaic applications. However, due to their likely impurity/defect nature, their exact origin, their tailorability, and their impact on charge separation has to be better understood. This is especially important in consideration of the fact that defects can both be productive, e.g. yielding active sites in photocatalysis, but also contribute to charge recombination, thus lowering efficiency. Thus, to better understand the tailoring options of LDHs, it must be elucidated what the possible functional contribution of below-band-edge states to facilitate charge separation is and whether they can be productively used in the desired applications.

5 Conclusion

In this work, we have shown that MgAl-LDH achieves full-spectrum absorbance (UV-Vis-NIR-MIR) to varying degrees, forming a CB with a significant low-energy band tail and showing a strong contribution to absorption through the excitation of fundamental vibrations and their overtones. The band tail holds important information on impurity/defect states below the band edge and should receive more consideration, rather than omission in discussion as is currently common practice. Once excited to above the CB edge, excited charges can use multiple pathways to recombine with the hole in the VB, 47% of which ended in emission of photons with energies greater than the bandgap energy at 83 K in MgAl-LDH (37% at 298 K), highly dependent on the measurement temperature and calcination (the presence of surface water, hydroxyl groups and interlayer carbonate). Temperature dependence revealed a strong competition between non-radiative and radiative relaxation from meta-stable CB states before reaching the CB edge, as well as possible polaron formation, increasing non-radiative relaxation to the band edge. Pathways contributing to below-band-edge luminescence are believed to be relaxation to excited vibrational states above the VB edge, coordination defects, access to band-tail-states, possible relaxation of a hole to the VB edge upon excitation of electrons in the VB, and exciton formation (Wannier and Frenkel) and their binding to impurities/defects/Al³⁺ islands in addition to the carbonate facilitating charge separation through a triangular shuffling mechanism.

LDHs find frequent application in photo-applications such as photocatalysis, photoelectrochemistry, photovoltaics and light-emitting diodes. To increase their efficiency in these applications, our work has revealed a pressing need for the study of the productive contribution of band-tail states to charge separation, the impact of exciton generation and their luminescence as a result of possible self-trapping or binding/trapping, the mechanism for access of/mechanism of tailoring access to states below the band edge, the exact types of defects causing the formation of the impurity band, what the role of coordination defects is, and untangling the effects contributing to the strong luminescence in Band D. In addition, since the anionic layered structure of LDHs adds to their uniqueness, the role of the carbonate (or more generally, the anion) in radiative relaxation requires deeper study. For this, DFT studies would be especially helpful and should be combined with experimental results where careful determination of the bandgap is matched to careful interpretation of the full absorption spectrum and luminescence.

Author contributions

The idea for this manuscript, synthesis, experimental work and initial draft writing were conceived and conducted by B. R. G. B. R. G. and E. R. analysed and interpreted the data together and prepared the final version of the manuscript. F. J. W. J. L. provided funding and contributed to the review and editing of the document. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors extend particular thanks to Prof. Reinhardt Botha (SA National Laser Centre) from the Department of Physics at the Nelson Mandela University, South Africa, and Dr Rudolph Erasmus (NRF NEP Grant 116179) from the Department of Physics at the University of the Witwatersrand, South Africa, for their generosity and time to allow the use of their equipment and assistance to obtain luminescence and excitation spectra. The authors also thank Prof.s Bryan Doyle and Emanuela Carleschi from the Department of Physics, University of Johannesburg (South Africa) for the measurements and analysis of the O 1s core level spectrum (NRF Grant No.: 93205, 90698, 119314). Further, they thank the Leibniz-Institut für Polymerforschung Dresden, e.V. (Dr Andreas Leuteritz and Mr Sajid Naseem) for the absorption spectra as extension of Bianca's visit to the institute and Mrs Wiebke Gröte from the Department of Geology, University of Pretoria, for the Rietveld refinement. David Viljoen is thanked for language-checking the document. Bianca expresses particular thanks to Prof. Johan Labuschagné for her funding and the encouragement to pursue independent research as part of her PhD work. Finally, Bianca would like to thank the L'Oréal-UNESCO Foundation for her PhD grant as part of the L'Oréal-UNESCO For Women in Science South African National Young Talents Programme encouraging and making possible her independent work, as well as the University of Pretoria for her doctoral scholarship. This work was funded by Techsparks (Pty) Ltd, the Technology and Human Resources for Industry Programme (THRIP) (Grant No: THRIP/133/31/03/2016) and the Technology and Innovation Agency (TIA) (2019 Seed Fund).

References

1. M. Wu, J. Wu, J. Zhang, H. Chen, J. Zhou, G. Qian, Z. Xu, Z. Du and Q. Rao, Catal. Sci. Technol., 2018, 8, 1207–1228.
2. S. Naseem, B. R. Gevers, F. J. W. J. Labuschagné and A. Leuteritz, Materials, 2020, 13, 4384.
3. X. Long, Z. Wang, S. Xiao, Y. An and S. Yang, Mater. Today, 2016, 19, 213–226.
4. M. Shao, R. Zhang, Z. Li, M. Wei, D. G. Evans and X. Duan, Chem. Commun., 2015, 51, 15880–15893.
5. C. Coluccini, I. Sporer, A. Leuteritz, I. Kuehnert and D.-Y. Wang, Nanomater. Energy, 2014, 3, 177–191.
6. W. Shi, M. Wei, D. G. Evans and X. Duan, J. Mater. Chem., 2010, 20, 3901–3909.
7. G. Prestopino, G. Arrabito, A. Generosi, A. Mattoccia, B. Paci, G. Perez, G. Verona-Rinati and P. Medaglia, Sci. Rep., 2019, 9, 1–12.
8. C. Forano, T. Hibino, F. Leroux and C. Taviot-Guého, Developments in Clay Science in Handbook of Clay Science, ed. F. Bergaya, B. K. Theng and G. Lagaly, Elsevier, 2006, vol. 1, pp. 1021–1095.
9. S. M. Xu, T. Pan, Y. B. Dou, H. Yan, S. T. Zhang, F. Y. Ning, W. Y. Shi and M. Wei, J. Phys. Chem. C, 2015, 119, 18823–18834.
10. K. Parida, M. Satpathy and L. Mohapatra, J. Mater. Chem., 2012, 22, 7350–7357.
11. G. Carja, E. Husanu, C. Gherasim and H. Iovu, Appl. Catal., B, 2011, 107, 253–259.
12. J. S. Valente, F. Tzompantzi, J. Prince, J. G. Cortez and R. Gomez, Appl. Catal., B, 2009, 90, 330–338.
13. C.-H. Lin, H.-L. Chu, W.-S. Hwang, M.-C. Wang and H.-H. Ko, AIP Adv., 2017, 7, 125005.
14. H. Yan, M. Wei, J. Ma, D. G. Evans and X. Duan, J. Phys. Chem. A, 2010, 114, 7369–7376.
15. B. Gevers, S. Naseem, C. Sheppard, A. Leuteritz and J. Labuschagne, ChemRxiv, 2020, 1–25.
16. K. Xu, Z. Zhang, G. Chen and J. Shen, RSC Adv., 2014, 4, 19218–19220.
17. L. Mohapatra and K. Parida, J. Mater. Chem. A, 2016, 4, 10744–10766.
18. Y. Zhao, P. Chen, B. Zhang, D. S. Su, S. Zhang, L. Tian, J. Lu, Z. Li, X. Cao, B. Wang, M. Wei, D. G. Evans and X. Duan, Chem. – Eur. J., 2012, 18, 11949–11958.
19. Y. Zhao, B. Li, Q. Wang, W. Gao, C. J. Wang, M. Wei, D. G. Evans, X. Duan and D. O'Hare, Chem. Sci., 2014, 5, 951–958.
20. Z. Zhang, G. Chen and K. Xu, Ind. Eng. Chem. Res., 2013, 52, 11045–11049.
21. B. R. Gevers, S. Naseem, A. Leuteritz and F. J. Labuschagné, RSC Adv., 2019, 9, 28262–28275.
22. I. Pelant and J. Valenta, Luminescence Spectroscopy of Semiconductors, Oxford University Press, Oxford, 2012, pp. 160–204.
23. E. S. Zhitova, S. V. Krivovichev, V. N. Yakovenchuk, G. Y. Ivanyuk, Y. A. Pakhomovsky and J. A. Mikhailova, Mineral. Mag., 2018, 82, 329–346.
24. V. Rives, Layered Double Hydroxides: Present and Future, Nova Science Publishers, 2001, pp. 39–92.
25. A. Seron and F. Delorme, J. Phys. Chem. Solids, 2008, 69, 1088–1090.
26. G. S. Thomas, M. Rajamathi and P. V. Kamath, Clay Miner., 2004, 52, 693–699.
27. A. Patterson, Phys. Rev., 1939, 56, 978–982.
28. Y. Zhao, F. Li, R. Zhang, D. G. Evans and X. Duan, Chem. Mater., 2002, 14, 4286–4291.
29. J. Kloprogge and R. L. Frost, J. Solid State Chem., 1999, 146, 506–515.
30. J. T. Kloprogge, D. Wharton, L. Hickey and R. L. Frost, J. Solid State Chem., 2002, 87, 623–629.
31. F. Theiss, A. López, R. L. Frost and R. Scholz, Spectrochim. Acta, Part A, 2015, 150, 758–764.
32. F. Cavani, F. Trifirò and A. Vaccari, Catal. Today, 1991, 11, 173–301.
33. F. Labajos, V. Rives and M. Ulibarri, Spectrosc. Lett., 1991, 24, 499–508.
34. K. Coenen, F. Gallucci, B. Mezari, E. Hensen and M. van Sint Annaland, J. CO2 Util., 2018, 24, 228–239.
35. B. R. Gevers and F. J. W. J. Labuschagné, Crystals, 2020, 10, 672.
36. M. Mora, M. I. López, C. Jiménez-Sanchidrián and J. R. Ruiz, Solid State Sci., 2011, 13, 101–105.
37. R. L. Frost, H. J. Spratt and S. J. Palmer, Spectrochim. Acta, Part A, 2009, 72, 984–988.
38. P. M. Morse, Phys. Rev., 1929, 34, 57–64.
39. V. Rives, Mater. Chem. Phys., 2002, 75, 19–25.
40. W. Yang, Y. Kim, P. K. Liu, M. Sahimi and T. T. Tsotsis, Chem. Eng. Sci., 2002, 57, 2945–2953.
41. A. Pishtshev, S. Z. Karazhanov and M. Klopov, Solid State Commun., 2014, 193, 11–15.
42. J. Frenzel, A. F. Oliveira, H. A. Duarte, T. Heine and G. Seifert, ZAAC, 2005, 631, 1267–1271.
43. D. Y. Zhang, P. Yang, Z. Du, Q. H. Yuan, S. H. Song, X. Z. Ren and P. X. Zhang, Trans. Nonferrous Met. Soc. China, 2015, 25, 4080–4088.
44. W. W. Duley, J. Chem. Soc., Faraday Trans. 1 F, 1984, 80, 1173–1179.
45. H. Yoshida, T. Tanaka, T. Funabiki and S. Yoshida, J. Chem. Soc., Faraday Trans., 1994, 90, 2107–2111.
46. K. Parida and L. Mohapatra, Dalton Trans., 2012, 41, 1173–1178.
47. P. Van Mieghem, Rev. Mod. Phys., 1992, 64, 755–793.
48. J. Wong, S. T. Omelchenko and H. A. Atwater, ACS Energy Lett., 2021, 6, 52–57.
49. K. W. Böer and U. W. Pohl, Excitons, Springer International Publishing, Cham, 2018, pp. 485–525.
50. P. J. Sideris, U. G. Nielsen, Z. Gan and C. P. Grey, Science, 2008, 321, 113–117.
51. S. Cadars, G. Layrac, C. Gérardin, M. Deschamps, J. R. Yates, D. Tichit and D. Massiot, Chem. Mater., 2011, 23, 2821–2831.
52. I. Studenyak, M. Kranj and M. Kurik, Int. J. Opt. Appl., 2014, 4, 76–83.
53. T. Bakos, S. Rashkeev and S. Pantelides, Phys. Rev. Lett., 2003, 91, 1–4.
54. Y. Zhang, J. Semicond., 2019, 40, 091102.
55. M. De Jong, L. Seijo, A. Meijerink and F. T. Rabouw, Phys. Chem. Chem. Phys., 2015, 17, 16959–16969.
56. S. H. Huang, S. J. Liu and J. Y. Uan, J. Mater. Chem. C, 2019, 7, 11191–11206.
57. Y. Zhao, X. Jia, G. I. Waterhouse, L.-Z. Wu, C.-H. Tung, D. O'Hare and T. Zhang, Adv. Energy Mater., 2016, 6, 1501974.
58. C. Chizallet, G. Costentin, H. Lauron-Pernot, J.-M. Krafft, M. Che, F. Delbecq and P. Sautet, J. Phys. Chem. C, 2008, 112, 16629–16637.
59. C. Chizallet, G. Costentin, H. Lauron-Pernot, J. M. Krafft, M. Che, F. Delbecq and P. Sautet, J. Phys. Chem. C, 2008, 112, 19710–19717.
60. N. Pathak, P. S. Ghosh, S. K. Gupta, R. M. Kadam and A. Arya, RSC Adv., 2016, 6, 96398–96415.
61. V. Avdeev and G. Zhidomirov, J. Struct. Chem., 2003, 44, 918–926.
62. F. Gunkel, D. Christensen, Y. Chen and N. Pryds, Appl. Phys. Lett., 2020, 116, 120505.
63. J. Marco, J. Gancedo, M. Gracia, J. Gautier, E. Ríos and F. Berry, J. Solid State Chem., 2000, 153, 74–81.
64. D. E. Haycock, M. Kasrai, C. J. Nicholls and D. S. Urch, Dalton Trans., 1978, 1791–1796.
65. M. D. Smith and H. I. Karunadasa, Acc. Chem. Res., 2018, 51, 619–627.
66. S. Kahmann, E. K. Tekelenburg, H. Duim, M. E. Kamminga and M. A. Loi, Nat. Commun., 2020, 11, 1–8.
67. Y. Lekina and Z. X. Shen, J. Sci. Adv. Mater. Devices, 2019, 4, 189–200.
68. J. Li, H. Wang and D. Li, Front. Optoelectron., 2020, 13, 225–234.
69. J. G. Kim, W. S. Yun, S. Jo, J. Lee and C. H. Cho, Sci. Rep., 2016, 6, 1–7.
70. X. Zheng and X. Zhang, in Advances in Condensed-Matter and Materials Physics - Rudimentary Research to Topical Technology, ed. J. Thirumalai, IntechOpen, 2019, ch. 2, p. 13.
71. Z. Guo, X. Wu, T. Zhu, X. Zhu and L. Huang, ACS Nano, 2016, 10, 9992–9998.
72. A. Kumar and J. Kumar, J. Phys. Chem. Solids, 2008, 69, 2764–2772.

---

Footnote

† Electronic supplementary information (ESI) available: The Rietveld refinement, the bandgap determination, the deconvolution of the MIR spectrum, more information on the MgAl-LDH luminescence reproducibility, the comparison of luminescence intensity with excitation at 5.0 eV and 3.8 eV, the linear combination of luminescence spectra, a thorough description of deconvoluted excitable states, the X-ray photoelectron analysis of MgAl-LDH (O 1s), additional data on the calcined MgAl-LDH (luminescence at 298 K and MIR spectra), and the full spectrum luminescence of MgAl-LDH to 1000 nm. See DOI: 10.1039/d1ma00893e

---