Open Access Article
Open Access ArticleSulfide glass solid-state electrolyte separators for Li metal batteries: using an interlayer to increase rate performance and reduce stack pressure†
Thomas A.
Yersak
 *a,
Chansoon
Kang
b,
James R.
Salvador
a,
Nicholas P. W.
Pieczonka
a and
Mei
Cai
a
*a,
Chansoon
Kang
b,
James R.
Salvador
a,
Nicholas P. W.
Pieczonka
a and
Mei
Cai
a
aChemical and Materials Systems Laboratory, General Motors Global R&D, 30500 Mound Rd., Warren, MI 48092-2031, USA. E-mail: thomas.yersak@gm.com; Tel: +01-586-320-8889
bOptimal, Inc., 47802 W. Anchor Ct., Plymouth, MI 48170, USA
First published on 16th March 2022
Abstract
We report on the solubility of (Li2S)60(SiS2)x(P2S5)40−x, (0 ≤ x ≤ 40) sulfide glass solid-state electrolytes in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) DME
1 (v/v) DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL solvent mixture, a popular choice for lithium metal battery liquid electrolytes. SiS2-rich glasses within the compositional range of (Li2S)60(SiS2)x(P2S5)40−x (28 ≤ x ≤ 40) were found to be functionally insoluble in DME
DOL solvent mixture, a popular choice for lithium metal battery liquid electrolytes. SiS2-rich glasses within the compositional range of (Li2S)60(SiS2)x(P2S5)40−x (28 ≤ x ≤ 40) were found to be functionally insoluble in DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL. Hybrid symmetric test cells with a thin liquid electrolyte layer (0.6 M LiTFSI + 0.4 M LiNO3 in 1
DOL. Hybrid symmetric test cells with a thin liquid electrolyte layer (0.6 M LiTFSI + 0.4 M LiNO3 in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) DME
1 (v/v) DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL) at the interface between lithium metal electrodes and an insoluble (Li2S)60(SiS2)28(P2S5)12 glass wafer were tested. Hybrid test cells delivered a critical current density of 3.0 mA cm−2 at 25 °C and 0.1 MPa, which is nearly double the CCD of comparable dry symmetric test cells cycled at 10× higher stack pressure.
DOL) at the interface between lithium metal electrodes and an insoluble (Li2S)60(SiS2)28(P2S5)12 glass wafer were tested. Hybrid test cells delivered a critical current density of 3.0 mA cm−2 at 25 °C and 0.1 MPa, which is nearly double the CCD of comparable dry symmetric test cells cycled at 10× higher stack pressure.
1. Introduction
Solid-state electrolytes (SSE) are under investigation to enable Li metal anodes. Fully dense, defect free sulfide glasses have been shown to block Li metal dendrites.1,2 However, one of the major challenges associated with solid-state batteries (SSBs) is the ability to obtain and maintain a low junction resistance at the SSE/Li interface. Recent work has shown that the mechanics of Li metal creep dictate that Li metal SSBs should be cycled under a stack pressure of > 1 MPa to achieve practical areal capacity and rates at room temperature.3–5 In fact, Samsung's recently reported SSB utilized a 10 MPa stack pressure.6 For comparison, conventional Li-ion pouch cells are cycled at <0.1 MPa stack pressure7 and from the perspective of battery pack design it may be desired for SSBs to operate with similar specifications to those of conventional Li-ion batteries.Fortunately, SSEs may be used in conjunction with other materials to alleviate the stack pressure requirement. For example, we previously integrated a (Li2S)60(SiS2)28(P2S5)12 sulfide glass separator into a single layer Li–S pouch cell with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) 1,2 dimethoxyethane (DME): 1,3 dioxolane (DOL) + 1 M LiTFSI liquid electrolyte (LE). The Li–P–Si–S glass was chosen for its low melt volatility and adequate stability versus lithium.1 The cell was cycled under a stack pressure of <0.05 MPa.8 Similar hybrid cells, containing both LE and SSE, have also been reported with other SSEs such as Li1.3Al0.3Ti1.7(PO4)3 (LATP), Li1+xYxZr2−x(PO4)3 (LYZP), Li1.5Al0.5Ge1.5(PO4)3 (LAGP), and Li7La3Zr2O12 (LLZO).9–12 Though the cells in these examples were flooded with LE, a small volume LE interlayer may sufficiently change the physics of Li stripping and plating to eliminate the >1 MPa stack pressure requirement.
1 (v/v) 1,2 dimethoxyethane (DME): 1,3 dioxolane (DOL) + 1 M LiTFSI liquid electrolyte (LE). The Li–P–Si–S glass was chosen for its low melt volatility and adequate stability versus lithium.1 The cell was cycled under a stack pressure of <0.05 MPa.8 Similar hybrid cells, containing both LE and SSE, have also been reported with other SSEs such as Li1.3Al0.3Ti1.7(PO4)3 (LATP), Li1+xYxZr2−x(PO4)3 (LYZP), Li1.5Al0.5Ge1.5(PO4)3 (LAGP), and Li7La3Zr2O12 (LLZO).9–12 Though the cells in these examples were flooded with LE, a small volume LE interlayer may sufficiently change the physics of Li stripping and plating to eliminate the >1 MPa stack pressure requirement.
At first glance, it is non-obvious that the (Li2S)60(SiS2)28(P2S5)12 sulfide glass would be stable in an ether-based LE. In fact, there have been at least two reports of sulfide SSEs precipitated from precursor solutions with ether-based solvents.13,14 These SSE formulations, (Li2S)75(P2S5)25 and Li10GeP2S12, were also found to be soluble in trigylme.15 Nonetheless, an ether-based LE was desired for two reasons. First, conventional Li-ion carbonate-based LEs are not compatible with the Li–S chemistry because sulfur may react with carbonates.16 Second, LiNO3 is an electrolyte additive that creates an effective SEI on Li metal that promotes efficient cycling.17–19 Ether-based solvents are preferable because LiNO3 has low solubility in carbonate solvents.20
In this study, we present a range of sulfide glass SSE compositions that are insoluble in ether based solvents. We then calculate glass weighted average bond dissociation enthalpies to predict each glass’ relative solubility. We expect that our approach may inform the compatibility of a wide range of sulfide glass SSEs compositions with other solvents. Using this result we then show that a LE interlayer can concomitantly reduce the stack pressure requirement and increase critical current density (CCD).
2. Experimental
2.1 Glass synthesis, material characterization and solubility measurement
All precursors and products described in this work are hygroscopic so work was carried out in an argon-filled glovebox with a moisture level of <1 ppm. Glass precursors include P2S5 (Sigma-Aldrich, 99.9% powder), SiS2 (American Elements, 99.0% powder), GeS2 (American Elements, 99.0% powder), GeO2 (American Elements, 99.0% powder) and Li2S (Sigma-Aldrich, 99.8% powder). A range of glass compositions were prepared according to the equation, (Li2S)60(SiS2)x(P2S5)40−x, where x = 0, 4, 8, 12, 16, 20, 28, 40. The glass with composition (Li2S)50(GeS2)45(GeO2)5 was also synthesized. To synthesize each glass electrolyte sample, 4 g of precursor powders were mixed in the appropriate stoichiometric ratios and pressed into 1 inch diameter pellets. Glasses were obtained by using one of two melt quenching methods chosen based on the volatility of each glass melt. In the first method the precursor pellet was loaded into a boron nitride (BN) crucible, capped with a quartz watch glass to minimize material loss by volatilization, and heated to 800–1000 °C for 30 minutes in a box furnace. Glass wafers of approximately 1 mm thickness were then formed by quenching the melt between a quartz glass and an agate anvil. The first method was used to synthesize glass compositions with low melt volatility; namely, (Li2S)60(SiS2)x(P2S5)40−x (x = 28, 40) and (Li2S)50(GeS2)45(GeO2)5. In the second method, precursor pellets were broken into pieces and loaded into carbon coated quartz ampoules (outer diameter = 8 mm). After flame sealing, the ampoules were heated to 800 °C for 30 minutes in a box furnace and quenched in oil. Using this method small ingots of approximately 5 mm diameter were obtained. The second method was used to synthesize glass compositions with high melt volatility; namely, (Li2S)60(SiS2)x(P2S5)40−x (x = 0, 4, 20), (Li2S)70(P2S5)30 and (Li2S)75(P2S5)25. SSEs with composition (Li2S)60(SiS2)x(P2S5)40−x (x = 8, 12, 16) were also synthesized by the second melt quenching method, but had poor glass formability. For this reason, these compositions are not included in this study. The (Li2S)60(SiS2)x(P2S5)40−x (x = 28, 40) compositions could not be synthesized by the second method because the melt was too corrosive to the quartz ampoule. The ionic conductivity of (Li2S)60(SiS2)x(P2S5)40−x glasses was previously reported.34Samples were characterized to determine long range and short range order by X-ray diffraction (XRD, D8 Advance, Bruker, Cu-Kα (1.5406 Å) at room temperature) and Raman spectroscopy (Renishaw), respectively. X-Ray samples were prepared by sealing glass powder with Kapton film and Raman samples were prepared by loading glass powder in sealed quartz capillary tubes. The actual composition of splat quenched SiS2-rich glasses was measured by energy dispersive spectroscopy (EDS, EDAX). We characterized the bulk composition of the glass by measuring 5 spots at the center of the glass’ fracture surface.
The solubility of glass electrolyte samples was evaluated by immersing 150 mg of glass electrolyte in a 5 ml mixture of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) 1,2 dimethoxyethane (DME) (BASF) and 1,3 dioxolane (DOL) (BASF) and observing the change in color. Solvated species and the degree of solubility was quantified by Raman spectroscopy (Renishaw). Post processing of Raman spectra was carried out in the range of 330–520 cm−1. The DOL
1 (v/v) 1,2 dimethoxyethane (DME) (BASF) and 1,3 dioxolane (DOL) (BASF) and observing the change in color. Solvated species and the degree of solubility was quantified by Raman spectroscopy (Renishaw). Post processing of Raman spectra was carried out in the range of 330–520 cm−1. The DOL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DME 1
DME 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) spectrum was used as a baseline for all spectra.
1 (v/v) spectrum was used as a baseline for all spectra.
2.2 Solubility calculation
Whether a solute dissolves in a solvent at constant pressure and temperature is determined by eqn (1) where ΔGsol is the Gibb's free energy of solution, ΔHsol is the enthalpy of solution, T is temperature, and ΔSsol is the entropy of solution. The enthalpy of solution and entropy of solution are described by eqn (2) and (3), respectively. The subscripts in each of these two equations refer to the three steps that take place in the formation of a solution; namely, (1) expanding the solute, (2) expanding the solvent, and (3) solvation.33 The aim of this work was not treat the full free energy of solution, but rather to compare the relative solubility of glasses by deriving an expression that trends with the enthalpic term that varies the most with glass composition, namely, the enthalpy of solute expansion, ΔH1.This simplified treatment of solubility to explain experimental trends is reasonable since the other thermodynamic terms are expected to have a lesser impact as a function of glass composition. We acknowledge that there may be difference in the enthalpy of solvation between the SiSx and PXx and the ether based solvents. It is likely, based on Pauling electronegativities that Si–S bond would have a higher dipole moment compared to that of the P–S bond and we may therefore expect that SiSx species to interact more strongly with polar groups of the ether solvents and be more exothermic in terms of solvation. Secondly, the bond lengths of Si–S and P–S are 192 and 212 pm, respectively, suggesting a larger and positive enthalpic contribution to solvent expansion for PSx as compared to SiSx units. With both of these considerations we might expect that SiS2 rich species would be more soluble if the solute/solvent interactions and solute separation enthalpies dominated the resulting solubility behavior. However, since we will show that the more SiS2 rich glasses are insoluble, we conclude that solute expansion and the interatomic interactions of the solute are principal contribution to the observed solubility behavior. We therefore expect the variation of ΔH2 and ΔH3 to be small compared to that of ΔH1.
| ΔGsol = ΔHsol−TΔSsol | (1) |
| ΔHsol = ΔH1−ΔH2 +ΔH3 | (2) |
| ΔSsol = ΔS1 + ΔS2 + ΔS3 | (3) |
Two approaches were used for approximating the relative enthalpy of solute expansion, ΔH1, by calculating the glass weighted average bond dissociation enthalpy (BDEwa). The first approach is to simply use the mole fractions of the nominal glass composition and assume that each metalloid species (M) in the glass former constituent (M = P, Si or Ge) are all tetrahedrally coordinated by sulfur atoms thus forming 4 M–S bonds while each Li2S contributes 2 Li–S bonds. This simplification neglects contributions from Si, P and Ge homoatomic interactions. This approach is summarized in eqn (1) where mi is the mole fraction of glass former, co-former and modifier. Furthermore, ni is the number of bonds formed for each molecule of former, co-former and modifier. Literature values for the bond dissociation enthalpies (BDE) are taken from a variety of sources and listed in Table 1.21–24 In the case of (PS4)−3 based moieties there are 3 single P–S bonds and 1 P–S double bond. The difference in BDE between P–S single and double bond is only 1 kJ mol−1 so are treated as equivalent. The denominator in eqn (1) reduces the expression to the weighted average of a single “composite bond” and allows the expression to be applied to any glass composition. This allows the comparison of bond strength over widely varying compositions within and across phase diagrams.
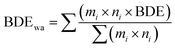 | (4) |
| Glass constituent | Bond | BDE (kJ mol−1) | Number of bonds (n) |
|---|---|---|---|
| P2S5 | P–S | 346 | 8 |
| GeS2 | Ge–S | 551 | 4 |
| SiS2 | Si–S | 619 | 4 |
| GeO2 | Ge–O | 658 | 4 |
| Li2S | Li–S | 312 | 2 |
The second method of calculating the BDEwa is to determine the mole fraction of each short-range order (SRO) structural moiety present in the glass, account for the number and type of bonds in each moiety and then use eqn (4) to calculate the BDEwa. In this case, mi is the mole fraction of the moiety and ni is the number of M–S and M–M bonds within the moiety. This approach accounts for the homoatomic interactions but requires a great deal of structural detail of the glass in question. For this study we use a previously reported structural analysis for a similar glass compositional range (Li2S)60(SiS2)x(P2S5)30–0.75x.25,26
2.3 Critical current density measurement
A Li/SSE/Li symmetric test cell was assembled to measure the critical current density (CCD) of a dense sulfide glass separator with liquid electrolyte interlayers at the Li electrolyte interfaces. The glass electrolyte composition of (Li2S)60(SiS2)28(P2S5)12 was chosen based on the results of the solubility evaluation and unpolished glass wafer discs with about 1 mm thickness were prepared as described above. The liquid electrolyte was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) DME
1 (v/v) DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL + 0.6 M bis(trifluoromethanesulfonyl)imide (LiTFSI) + 0.4 M lithium nitrate (LiNO3). When soaked in this liquid electrolyte, a (Li2S)60(SiS2)28(P2S5)12 glass wafer showed no evidence of dissolution after 2 years (Fig. S1, ESI†). The test cell housing consists of a modified ½′′ PTFE union fitting (Swagelok, PFA-820-6) and two ½′′ diameter PEEK rods with 13/64′′ diameter stainless steel inserts. The stack pressure was measured using a force sensor as previously described.27 The cell was assembled by stacking a glass electrolyte wafer between two 13/64′′ diameter Li metal foil discs (Honjo, 100 μm thick on stainless steel). 6 μL of liquid electrolyte was applied to each electrode interface; enough to wet the interface, but not enough to flood the cell. 6. In dry cells, Li metal was applied to glass wafer surface by applying pressure to the stainless steel foil backing. In the hybrid cell, Li metal was simply stacked on top of the wetted glass wafer surface. The test cell was then cycled under progressively higher current densities (Arbin LBT-21084) until shorting failure was observed. Total cell resistance was calculated using Ohm's law. AC impedance could not be used to measure the relative values of bulk and interfacial impedance since equivalent circuits could not be fitted to the data due to significant hardware inductance at higher frequencies.
DOL + 0.6 M bis(trifluoromethanesulfonyl)imide (LiTFSI) + 0.4 M lithium nitrate (LiNO3). When soaked in this liquid electrolyte, a (Li2S)60(SiS2)28(P2S5)12 glass wafer showed no evidence of dissolution after 2 years (Fig. S1, ESI†). The test cell housing consists of a modified ½′′ PTFE union fitting (Swagelok, PFA-820-6) and two ½′′ diameter PEEK rods with 13/64′′ diameter stainless steel inserts. The stack pressure was measured using a force sensor as previously described.27 The cell was assembled by stacking a glass electrolyte wafer between two 13/64′′ diameter Li metal foil discs (Honjo, 100 μm thick on stainless steel). 6 μL of liquid electrolyte was applied to each electrode interface; enough to wet the interface, but not enough to flood the cell. 6. In dry cells, Li metal was applied to glass wafer surface by applying pressure to the stainless steel foil backing. In the hybrid cell, Li metal was simply stacked on top of the wetted glass wafer surface. The test cell was then cycled under progressively higher current densities (Arbin LBT-21084) until shorting failure was observed. Total cell resistance was calculated using Ohm's law. AC impedance could not be used to measure the relative values of bulk and interfacial impedance since equivalent circuits could not be fitted to the data due to significant hardware inductance at higher frequencies.
3. Results and discussion
3.1 Solubility
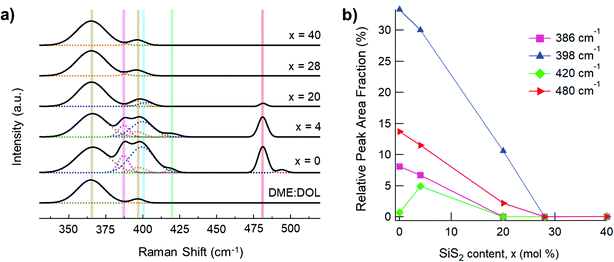
Prior to conducting the solubility experiment the long and short range structures of the samples with compositions (Li2S)60(SiS2)x(P2S5)40−x (x = 0, 4, 20, 28, 40) were characterized. All samples were determined to be amorphous according to pXRD measurement provided in Fig. 1. The short range structure for the glasses was characterized by Raman spectroscopy and the data are provided in Fig. 2. In agreement with the literature, the glasses were composed primarily of Si2S52− (362 cm−1), SiS44− (385 cm−1), Si2S64− (408 cm−1), P2S64− (396 cm−1), P2S74− (404 cm−1), and PS43− (420 cm−1) structural units.25,26 For compositions (Li2S)60(SiS2)x(P2S5)40−x (x = 0, 4, 20) the actual composition is equivalent to the nominal composition because the precursors were melt quenched inside a sealed quartz ampoule. In this case, the samples lost zero mass during synthesis because melt vapors were confined within the ampoule. On the other hand, the (Li2S)60(SiS2)x(P2S5)40−x (x = 28, 40) samples experienced mass loss of 15.0% and 4.9%, respectively. A mass loss of 15% for the (Li2S)60(SiS2)28(P2S5)12 composition is similar to that reported by a previous study.1 The actual compositions for (Li2S)60(SiS2)x(P2S5)40−x (x = 28, 40) as determined by EDS are provided in Table 2 and only deviate slightly from the actual composition.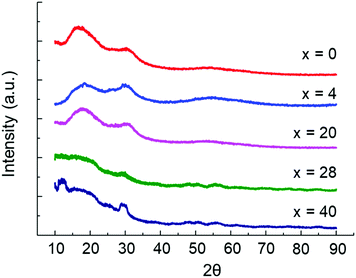 | ||
| Fig. 1 pXRD of (Li2S)60(SiS2)x(P2S5)40−x (x = 0, 4, 20, 28, 40) samples indicate all compositions are amorphous. | ||
| Sample, (Li2S)60(SiS2)x(P2S5)40−x | Method | P (%) | S (%) | Si (%) |
|---|---|---|---|---|
| x = 28 | Calc. | 10.5 | 77.2 | 12.3 |
| EDS | 9.0 | 74.3 | 16.7 | |
| x = 40 | Calc. | — | 77.8 | 22.2 |
| EDS | — | 75.4 | 24.6 |
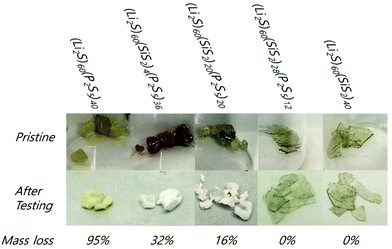
The results of the solubility experiment are provided in Fig. 3. After only 1 hour, the P2S5-rich glasses, (Li2S)60(SiS2)x(P2S5)40−x (x = 0, 4), partially dissolved as evidenced by the DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL solvent's yellow color. After two weeks, the (Li2S)60(SiS2)20(P2S5)20 composition also showed evidence of dissolution. On the other hand, the DME
DOL solvent's yellow color. After two weeks, the (Li2S)60(SiS2)20(P2S5)20 composition also showed evidence of dissolution. On the other hand, the DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL solvent for the SiS2-rich glasses, (Li2S)60(SiS2)x(P2S5)40−x (x = 28, 40), remained clear for the entire testing period. After two weeks, the remaining solids were collected from each solution and weighed (Fig. 4). The color of the (Li2S)60(P2S5)40 sample changed from dark yellow to light yellow and the (Li2S)60(SiS2)x(P2S5)40−x (x = 4, 20) samples turned white. On the other hand, the (Li2S)60(SiS2)x(P2S5)40−x (x = 28, 40) samples were completely intact. While the x = 0, 4, and 20 samples experienced mass loss of 95%, 32%, and 16%, respectively, the x = 28, 40 samples had zero mass loss. It was concluded that P2S5-rich compositions were susceptible to dissolution in a DME
DOL solvent for the SiS2-rich glasses, (Li2S)60(SiS2)x(P2S5)40−x (x = 28, 40), remained clear for the entire testing period. After two weeks, the remaining solids were collected from each solution and weighed (Fig. 4). The color of the (Li2S)60(P2S5)40 sample changed from dark yellow to light yellow and the (Li2S)60(SiS2)x(P2S5)40−x (x = 4, 20) samples turned white. On the other hand, the (Li2S)60(SiS2)x(P2S5)40−x (x = 28, 40) samples were completely intact. While the x = 0, 4, and 20 samples experienced mass loss of 95%, 32%, and 16%, respectively, the x = 28, 40 samples had zero mass loss. It was concluded that P2S5-rich compositions were susceptible to dissolution in a DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL co-solvent. In addition, the solubilities of two other SSEs were tested in DME
DOL co-solvent. In addition, the solubilities of two other SSEs were tested in DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL. A glass ingot of (Li2S)50(GeS2)45(GeO2)5, prepared as previously described,28 was insoluble while Li10GeP2S12 (NEI Corporation) was slightly soluble.
DOL. A glass ingot of (Li2S)50(GeS2)45(GeO2)5, prepared as previously described,28 was insoluble while Li10GeP2S12 (NEI Corporation) was slightly soluble.
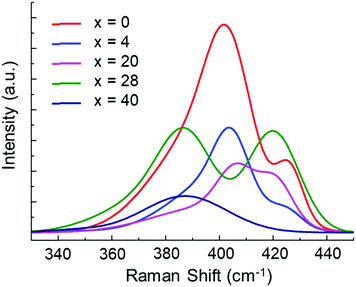
The solubility of each glass composition was further quantified with Raman spectroscopy and the data are provided in Fig. 5. Fig. 5a provides the Raman spectra of all samples and neat 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) DME
1 (v/v) DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL in the range of 100–500 cm−1. The spectra are normalized to a strong C–O vibrational mode from DOL
DOL in the range of 100–500 cm−1. The spectra are normalized to a strong C–O vibrational mode from DOL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DME mixture at 940 cm−1 (not shown).29,30 Generally, the vibrational modes below 200 cm−1 and around 450 cm−1 are attributable to sulfur species,31 while the vibrational modes in the 350–450 cm−1 range are attributable to solvated glass structural units (P2S6)4−, (P2S7)4−, and (PS4)3−.25,26 A vibrational mode of DME, centered at 365 cm−1, is minorly convolved with the structural units’ vibrational modes, but does not impact analyses. Since several unidentified vibrational modes are observed in the 220–330 cm−1 range, our analysis therefore focuses on the range of 330–520 cm−1. The peaks at 387, 398, 420 and 480 cm−1 are attributed to vibrational modes of (P2S6)4−, (P2S7)4−, (PS4)3−, and S8, respectively.25,26,31 P2S5-rich glasses, (Li2S)60(SiS2)x(P2S5)40−x (x = 0, 4), showed the highest prevalence of (P2S6)4−, (P2S7)4−, (PS4)3−, and S8 species. On the other hand, the spectra for the SiS2-rich glasses, (Li2S)60(SiS2)x(P2S5)40−x (x = 28, 40), were indistinguishable from the spectrum for neat 1
DME mixture at 940 cm−1 (not shown).29,30 Generally, the vibrational modes below 200 cm−1 and around 450 cm−1 are attributable to sulfur species,31 while the vibrational modes in the 350–450 cm−1 range are attributable to solvated glass structural units (P2S6)4−, (P2S7)4−, and (PS4)3−.25,26 A vibrational mode of DME, centered at 365 cm−1, is minorly convolved with the structural units’ vibrational modes, but does not impact analyses. Since several unidentified vibrational modes are observed in the 220–330 cm−1 range, our analysis therefore focuses on the range of 330–520 cm−1. The peaks at 387, 398, 420 and 480 cm−1 are attributed to vibrational modes of (P2S6)4−, (P2S7)4−, (PS4)3−, and S8, respectively.25,26,31 P2S5-rich glasses, (Li2S)60(SiS2)x(P2S5)40−x (x = 0, 4), showed the highest prevalence of (P2S6)4−, (P2S7)4−, (PS4)3−, and S8 species. On the other hand, the spectra for the SiS2-rich glasses, (Li2S)60(SiS2)x(P2S5)40−x (x = 28, 40), were indistinguishable from the spectrum for neat 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) DME
1 (v/v) DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL suggesting the complete absence of solvated SSE species. With the exception of PS43−, solvated SSE species decrease linearly with increasing SiS2, x (Fig. 5b). The non-linear prevalence of PS43− with respect to x can be explained by the structural composition of the pristine glass samples (Fig. 2) wherein PS43− is not present in the (Li2S)60(P2S5)40 (x = 0) composition. With this result we show that the (Li2S)60(SiS2)28(P2S5)12 glass is functional insoluble in DME
DOL suggesting the complete absence of solvated SSE species. With the exception of PS43−, solvated SSE species decrease linearly with increasing SiS2, x (Fig. 5b). The non-linear prevalence of PS43− with respect to x can be explained by the structural composition of the pristine glass samples (Fig. 2) wherein PS43− is not present in the (Li2S)60(P2S5)40 (x = 0) composition. With this result we show that the (Li2S)60(SiS2)28(P2S5)12 glass is functional insoluble in DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL. It is possible that this glass composition exhibits a small degree of solubility, however, it was below the detection limit or our equipment.
DOL. It is possible that this glass composition exhibits a small degree of solubility, however, it was below the detection limit or our equipment.
3.2 BDEWA calculation
As discussed in the Methods section, solubility is governed in part by the enthalpy of solute expansion, ΔH1, which is a measure of the solute's interatomic bond strength. To that end, we conjecture that the relative insolubility of glasses can be estimated by calculating a weighted average bond dissociate energy, BDEwa, for each glass composition. As outlined in the Methods section we take two approaches to compute the BDEwa. The first approach calculates an approximate BDEwa using only the nominal glass composition, while the second approach is more exact since it uses the glass SRO structural moiety composition. To calculate BDEwa with the second approach, we use a SRO dataset for Li2S–SiS2–P2S5 glasses previously reported by Aguilar.26 The glass compositions explored by Aguilar differ slightly from this study as shown in the ternary phase diagram presented in Fig. 6. Nonetheless, we chose to use the Aguilar's SRO dataset because it was compiled using both Raman, IR, and NMR Spectroscopy, whereas this study's SRO dataset is incomplete since it was compiled with only Raman Spectroscopy. Using this previously reported SRO dataset, we will first show that there is not a significant difference between the two BDEwa calculation methods.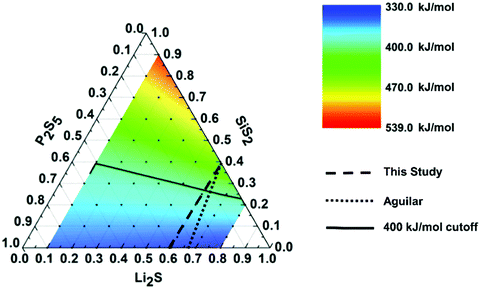 | ||
Fig. 6 Ternary phase diagram with BDEwa mapping. The solid line represents the 400 kJ mol−1 cutoff line, below which, the compositions are predicted to be soluble in DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL. The dashed line depicts the (Li2S)60(SiS2)x(P2S5)40−x compositions used in this study while the dotted line depicts the previously reported (Li2S)60(SiS2)x(P2S5)30–0.75x compositions.25,26 DOL. The dashed line depicts the (Li2S)60(SiS2)x(P2S5)40−x compositions used in this study while the dotted line depicts the previously reported (Li2S)60(SiS2)x(P2S5)30–0.75x compositions.25,26 | ||
Aguilar26 identifies seven SRO moieties present in glass compositions described by the formula, (Li2S)60(SiS2)x(P2S5)30–0.75x, (0 ≤ x ≤ 40). Table 3 summarizes the approximate relative abundance (%) for each of these seven SRO units for compositions in the range (Li2S)60(SiS2)x(P2S5)30–0.75x.26 The BDEwa for each glass composition was calculated using the values in Table 3 and eqn (4). For the calculations we assume that each Li2S contributes 2 Li–S bonds and so the mole fraction of the modifier is multiplied by 2 and by the BDE of the Li–S bond. The calculated SRO BDEwa's are provided in the second column of Table 4. As expected, the SRO BDEwa increases with increasing SiS2 content since the Si–S bond is comparatively stronger than the P–S bond.
| Composition/SRO | (SiS4)4− | (Si2S4)2− | (SiS4)2− | (Si2S6)−6 | (P2S7)4− | (P2S6)4− | (PS4)3− |
|---|---|---|---|---|---|---|---|
| (Li2S)60(SiS2)40 | 59 | 12 | 17 | 12 | 0 | 0 | 0 |
| (Li2S)61.86(SiS2)28.87(P2S5)9.28 | 25 | 20 | 15 | 5 | 5 | 5 | 25 |
| (Li2S)63.16(SiS2)21.05(P2S5)15.79 | 10 | 20 | 10 | 5 | 5 | 10 | 40 |
| (Li2S)65.93(SiS2)4.40(P2S5)29.67 | 0 | 5 | 3 | 2 | 70 | 15 | 5 |
| (Li2S)67(P2S5)33 | 0 | 0 | 0 | 0 | 85 | 15 | 0 |
| Nominal glass composition (mol%) | BDEwa (kJ mol−1) SRO composition | BDEwa (kJ mol−1) Nominal composition |
|---|---|---|
| (Li2S)60(SiS2)40 | 487 | 489 |
| (Li2S)61.86(SiS2)28.87(P2S5)9.28 | 433 | 431 |
| (Li2S)63.16(SiS2)21.05(P2S5)15.79 | 408 | 412 |
| (Li2S)65.93(SiS2)4.40(P2S5)29.67 | 347 | 348 |
| (Li2S)67(P2S5)33 | 336 | 335 |
| (Li2S)60(SiS2)28(P2S5)12 | N/A | 427 |
| (Li2S)60(SiS2)20(P2S5)20 | N/A | 395 |
| (Li2S)60(SiS2)4(P2S5)36 | N/A | 347 |
| (Li2S)60(P2S5)40 | N/A | 339 |
| (Li2S)50(GeS2)45(GeO2)5 | 479 | 479 |
| Li10GeP2S12 | 375 | N/A |
Despite the diversity of the SRO units that comprise chalcogenide glasses, the number of M–S bonds (M = P, Si, Ge) is fixed at 4 per metalloid/chalcogenide center with the exception of P2S6 and Si2S6 SRO units. We can therefore compute the BDEwa by using the nominal glass composition of modifier, former, and co-formers. This approach ignores the P–P bonds in P2S6 and the Si–Si bonds in Si2S6 since the contribution of these bonds to the BDEwa is small. Specifically, the relative abundances of the P2S6 and Si2S6 units in most glasses is low and the M–M bond is only 1 part in 7 bonds within each unit. The nominal BDEwa's for all glass compositions are provided in the third column of Table 4. There is good agreement between the SRO BDEwa and nominal BDEwa.
Having established that the nominal glass composition is adequate for the calculation of BDEwa using Aguilar's similar glass system, we then computed the BDEwa for our glass system, (Li2S)60(SiS2)x(P2S5)40−x. The BDEwa for this study's glass compositions are listed in the third column of Table 4. The same trend emerges in that the BDEwa increases as the SiS2 content increases. The results listed in Table 4 combined with those of the solubility study would seem to indicate that a BDEwa threshold value of > 400 kJ mol−1 is associated with glass compositions that are insoluble in DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL. Using the nominal composition allows for the calculation of BDEwa for an entire phase diagram so that one can locate a compositional space in which formulations are likely to be insoluble in DME
DOL. Using the nominal composition allows for the calculation of BDEwa for an entire phase diagram so that one can locate a compositional space in which formulations are likely to be insoluble in DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL without laboriously identifying and quantifying all SRO units for each composition. Fig. 6 presents a contour ternary phase diagram for Li2S·SiS2·P2S5 glasses. The color mapping visualizes the BDEwa for each ternary composition allowing us to visualize the compositional regions where the BDEwa is > 400 kJ mol−1 and therefore anticipated to be compatible with DME
DOL without laboriously identifying and quantifying all SRO units for each composition. Fig. 6 presents a contour ternary phase diagram for Li2S·SiS2·P2S5 glasses. The color mapping visualizes the BDEwa for each ternary composition allowing us to visualize the compositional regions where the BDEwa is > 400 kJ mol−1 and therefore anticipated to be compatible with DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL solvents.
DOL solvents.
Next, we extend our approach to GeS2-based glasses28 and the LGPS (Li10GeP2S12) ceramic superionic SSE.32 We find that the BDEwa for (Li2S)50(GeS2)45(GeO2)5, a formulation we know to be insoluble in DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL (Fig. S2, ESI†), has a very high BDEwa of 479 kJ mol−1. This is based on the fact that (Li2S)50(GeS2)45(GeO2)5 is composed exclusively of (GeS4)2− SROs with O atoms mixed on the sulfur sites.28 This result is consistent with our insolubility selection criteria of BDEwa > 400 kJ mol−1. The LGPS ceramic, which is known to be composed of a network of one (GeS4)4− and two (PS4)3− tetrahedral units, has a BDEwa of 375 kJ mol−1. We note that the BDEwa calculated for LGPS and (Li2S)60(SiS2)20(PsS5)20 are within 20 kJ mol−1 of each other and that both SSEs are weakly soluble in DME-DOL solutions.
DOL (Fig. S2, ESI†), has a very high BDEwa of 479 kJ mol−1. This is based on the fact that (Li2S)50(GeS2)45(GeO2)5 is composed exclusively of (GeS4)2− SROs with O atoms mixed on the sulfur sites.28 This result is consistent with our insolubility selection criteria of BDEwa > 400 kJ mol−1. The LGPS ceramic, which is known to be composed of a network of one (GeS4)4− and two (PS4)3− tetrahedral units, has a BDEwa of 375 kJ mol−1. We note that the BDEwa calculated for LGPS and (Li2S)60(SiS2)20(PsS5)20 are within 20 kJ mol−1 of each other and that both SSEs are weakly soluble in DME-DOL solutions.
Recent work by Oh et al. examined the dual solid–liquid electrolyte systems of (Li2S)75(P2S5)25 (LPS) or LGPS in combination with a highly concentrated solution of LiTFSI in triglyme, which is an ether based solvent.15 Here, it was found that both LPS and LGPS were soluble in neat triglyme but that the solubility could be decreased by increasing the concentration of LiTFSI. Oh et al. argue that the Li+ of the TFSI− coordinated with the O atoms in the glyme and therefore reduced the propensity for nucleophilic attack on the P-atoms in the SSE. Lower LiTFSI concentrations were required to stabilize the LGPS in the glyme and the authors argued that hard-soft acid base theory favored stronger nucleophilic attack on the P sites in LPS glass by O as compared to the Ge sites in LGPS glass. We argue here that the differences in solubility observed in their work may also be explained by the average strength of the bonds in the solute. By our method, LPS has a BDEwa of 331 kJ mol−1, which is ∼13% lower than LGPS’ BDEwa of 375 kJ mol−1. Consistent with Oh et al.'s observations, our method predicts that both SSEs are soluble in ethers, but that LGPS will have a lower solubility since it has the higher BDEwa.
In our compositions, the nucleophilic centers (Si and P) are both hard acids and therefore should be more amenable to attack by O in the ether solvents. Instead, we find that certain SiS2 rich glasses are functionally insoluble in DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL. Based on these observations we argue that the difference in solubility behavior is due to the average bond strength of the solute and not just its hard or soft acidic nature. Further supporting this argument is the observation that glass formulations with BDEwa less than, but close to, 400 kJ mol−1 dissolve far more slowly than those with BDEwa well below 400 kJ mol−1. We believe that this approach is generally applicable to other glass former systems and that it can be used as a criterion for selecting glass and ceramic compositions that are insoluble in ether based solvent systems often used in Li–S battery chemistries.
DOL. Based on these observations we argue that the difference in solubility behavior is due to the average bond strength of the solute and not just its hard or soft acidic nature. Further supporting this argument is the observation that glass formulations with BDEwa less than, but close to, 400 kJ mol−1 dissolve far more slowly than those with BDEwa well below 400 kJ mol−1. We believe that this approach is generally applicable to other glass former systems and that it can be used as a criterion for selecting glass and ceramic compositions that are insoluble in ether based solvent systems often used in Li–S battery chemistries.
3.3 Critical current density measurement
Having established the functional insolubility of a range of sulfide glass, we then sought to demonstrate a practical use for our findings. For this work, the (Li2S)60(SiS2)28(P2S5)12 glass composition was carried forward due to its functional insolubility, its high ionic conductivity of 1.8 mS cm−1, and the availability of a baseline dataset.1,8 As previously discussed, recent work establishes the need for a high stack pressure (>1 MPa) to maintain the integrity of the SSE/Li metal interface.1,3–5 When cycled under a stack pressure of 0.1 MPa at 25 °C, the voltage response of a dry symmetric Li/SSE/Li test cell increased rapidly at an applied current density of 600 μA cm−2 (Fig. 7a).1 The rapidly increasing voltage response may be explained by contact failure. Mechanical creep is the predominant mechanism for the mass transport of Li metal to the SSE interface and contact failure occurs when the rate of Li stripping outpaces the rate of interfacial Li replenishment by mechanical creep.3,4 As a result, voids form at the SSE interface causing the eventual detachment of the electrode and an increase in cell resistance. The rate of creep is influenced both by temperature and applied pressure. When the stack pressure is increased to 3.0 MPa, but the temperature kept at 25 °C, the CCD of a similar Li/SSE/Li test cells increases to ≥ 1400 μA cm−2 (Fig. 7b) with failure attributed to shorting.1 While higher stack pressures allow for practical current densities, battery packs with conventional Li-ion pouch cells apply stack pressures of <0.1 MPa.7 From the perspective of pack design, it may therefore be desired for advanced batteries with SSE to operate under similarly low stack pressure specifications.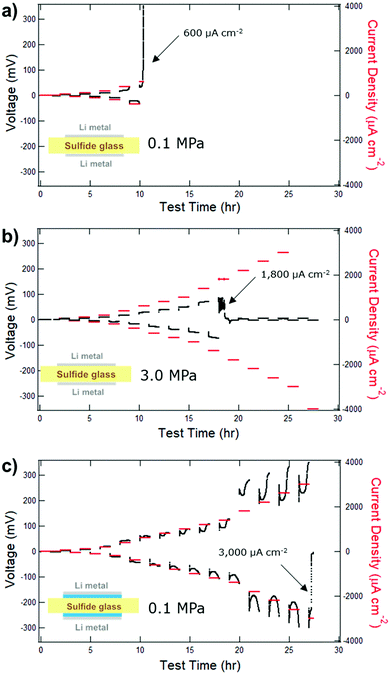 | ||
| Fig. 7 CCDs of symmetric Li/SSE/Li test cells with or without a liquid electrolyte interlayer and a different stack pressures at 25 °C. The SSE separators are (Li2S)60(SiS2)28(P2S5)12 glass wafers of approximately 600 μm thickness. (a) A test cell with direct Li/SSE contact and 0.1 MPa stack pressure experiences electrode contact failure at a CCD of 600 μA cm−2.1 (b) A test cell with direct Li/SSE contact and 3 MPa stack pressure experiences shorting failure at a CCD of 1800 μA cm−2.1 (c) A hybrid test cell with liquid electrolyte Li/SSE interlayer and a 0.1 MPa stack pressure experiences shorting failure at a CCD of 3000 μA cm−2. Note: the test was paused for two days at 20 hours due to a planned facility power outage. | ||
In this study, a small amount of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) DME
1 (v/v) DME![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL + 0.6 M LiTFSI + 0.4 M LiNO3 liquid electrolyte (LE) was applied to the Li/SSE interfaces (blue layer, Fig. 7c – inset). A hybrid symmetric Li/LE/SSE/LE/Li test cell cycled with a stack pressure of only 0.1 MPa at 25 °C had a CCD of 3000 μA cm−2. A second test cell (Fig. S3, ESI†) had a CCD of 2600 μA cm−2, thus confirming the repeatability of our experiment. With these data, it is understood that a liquid electrolyte interlayer concomitantly decreases the stack pressure requirement and increases the CCD. Pictures of a glass wafer separator post-mortem (Fig. S4, ESI†) show that the wafer surface is the same color and transparency as a pristine, uncycled wafer. A short is evident along a fracture surface of the wafer suggesting that sulfide glass separator fracture toughness should be improved.
DOL + 0.6 M LiTFSI + 0.4 M LiNO3 liquid electrolyte (LE) was applied to the Li/SSE interfaces (blue layer, Fig. 7c – inset). A hybrid symmetric Li/LE/SSE/LE/Li test cell cycled with a stack pressure of only 0.1 MPa at 25 °C had a CCD of 3000 μA cm−2. A second test cell (Fig. S3, ESI†) had a CCD of 2600 μA cm−2, thus confirming the repeatability of our experiment. With these data, it is understood that a liquid electrolyte interlayer concomitantly decreases the stack pressure requirement and increases the CCD. Pictures of a glass wafer separator post-mortem (Fig. S4, ESI†) show that the wafer surface is the same color and transparency as a pristine, uncycled wafer. A short is evident along a fracture surface of the wafer suggesting that sulfide glass separator fracture toughness should be improved.
Conclusions
In this work we demonstrated that sulfide glass SSE separators can be paired with an ether-based liquid electrolyte interlayer to increase critical current density while concomitantly decreasing stack pressure. Future work involves understanding the cycle life and safety of similarly designed hybrid test cells and investigating other liquid electrolyte formulations. Furthermore, we presented the BDEwa calculation as a method to predict the compatibility of sulfide SSEs with organic solvents. As the solid-state battery community shifts its focus from the laboratory to the development of large scale manufacturing processes, our method may also hold value for predicting how sulfide SSEs interact with solvents used for carrying slurries or dissolving binders.Conflicts of interest
The authors have no external funding sources or competing interests to declare.Acknowledgements
This work was funded by Department of Energy (DOE) Energy Efficiency and Renewable Energy (EERE) Vehicle Technologies Office (VTO) grant number DE-EE0008857.References
- T. A. Yersak, J. R. Salvador, N. P. W. Pieczonka and M. Cai, Dense, Melt Cast Sulfide Glass Electrolyte Separators for Li Metal Batteries, J. Electrochem. Soc., 2019, 166(8), A1535–A1542 CrossRef.
- L. Porz, T. Swamy, B. W. Sheldon, D. Rettenwander, T. Frömling, H. L. Thaman, S. Berendts, R. Uecker, W. C. Carter and Y.-M. Chiang, Mechanism of lithium metal penetration through inorganic solid electrolytes, Adv. Energy Mater., 2017, 20, 1701003 CrossRef.
- W. S. LePage, Y. Chen, E. Kazyak, K.-H. Chen, A. J. Sanchez, A. Poli, E. M. Arruda, M. D. Thouless and N. P. Dasgupta, Lithium Mechanics: Roles of Strain Rate and Temperature and Implications for Lithium Metal Batteries, J. Electrochem. Soc., 2019, 166(2), A89 CrossRef CAS.
- A. Masias, N. Felten, R. Garcia-Mendez, J. Wolfenstine and J. Sakamoto, Elastic, Plastic, and Creep Mechanical Properties of Lithium Metal, J. Mater. Sci., 2019, 54(3), 2585–2600 CrossRef CAS.
- J. Kasemchainan, S. Zekoll, D. Spencer Jolly, Z. Ning, G. O. Hartley, J. Marrow and P. G. Bruce, Critical Stripping Current Leads to Dendrite Formation on Plating in Lithium Anode Solid Electrolyte Cells, Nat. Mater., 2019, 18(10), 1105–1111 CrossRef CAS PubMed.
- Y.-G. Lee, S. Fujiki, C. Jung, N. Suzuki, N. Yashiro, R. Omoda, D.-S. Ko, T. Shiratsuchi, T. Sugimoto and S. Ryu, High-Energy Long-Cycling All-Solid-State Lithium Metal Batteries Enabled by Silver–Carbon Composite Anodes, Nat. Energy, 2020, 5(4), 299–308 CrossRef CAS.
- Y. C. Zhang; O. Briat; J.-Y. Deletage; C. Martin; G. Gager and J.-M. Vinassa Characterization of External Pressure Effects on Lithium-Ion Pouch Cell. In 2018 IEEE International Conference on Industrial Technology (ICIT); IEEE, 2018; pp. 2055–2059.
- T. Yersak, J. R. Salvador, R. D. Schmidt and M. Cai, Hybrid Li-S Pouch Cell with a Reinforced Sulfide Glass Solid-State Electrolyte Film Separator, Int. J. Appl. Glas. Sci., 2021, 12(1), 124–134 CrossRef CAS.
- L. Wang, Y. Wang and Y. Xia, A High Performance Lithium-Ion Sulfur Battery Based on a Li2S Cathode Using a Dual-Phase Electrolyte, Energy Environ. Sci., 2015, 8(5), 1551–1558 RSC.
- X. Yu, Z. Bi, F. Zhao and A. Manthiram, Hybrid Lithium − Sulfur Batteries with a Solid Electrolyte Membrane and Lithium Polysulfide Catholyte, ACS Appl. Mater. Interfaces, 2015, 7, 16625–16631 CrossRef CAS PubMed.
- Q. Wang, Z. Wen, J. Jin, J. Guo, X. Huang, J. Yang and C. Chen, A Gel-Ceramic Multi-Layer Electrolyte for Long-Life Lithium Sulfur Batteries, Chem. Commun., 2016, 52(8), 1637–1640 RSC.
- X. Yu, Z. Bi, F. Zhao and A. Manthiram, Polysulfide-Shuttle Control in Lithium-Sulfur Batteries with a Chemically/Electrochemically Compatible NaSICON-Type Solid Electrolyte, Adv. Energy Mater., 2016, 1601392 CrossRef.
- H. Lim, H. Lim, X. Xing, B. Lee, H. Liu, C. Coaty, H. Kim and P. Liu, Solid Electrolyte Layers by Solution Deposition, Adv. Mater. Interfaces, 2018, 5(8), 1701328 CrossRef.
- Q. Xiao, M. Cai, J. R. Salvador, L. Yang and D. A. I. Fang Electrolyte and Electrode Structure. Google Patents June 16, 2016.
- D. Y. Oh, Y. J. Nam, K. H. Park, S. H. Jung, S. Cho, Y. K. Kim, Y. Lee, S. Lee and Y. S. Jung, Excellent Compatibility of Solvate Ionic Liquids with Sulfide Solid Electrolytes: Toward Favorable Ionic Contacts in Bulk-Type All-Solid-State Lithium-Ion Batteries, Adv. Energy Mater., 2015, 5(22), 1500865 CrossRef.
- J. Gao, M. A. Lowe, Y. Kiya and H. D. Abruna, Effects of Liquid Electrolytes on the Charge–Discharge Performance of Rechargeable Lithium/Sulfur Batteries: Electrochemical and in-Situ X-Ray Absorption Spectroscopic Studies, J. Phys. Chem. C, 2011, 115(50), 25132–25137 CrossRef CAS.
- Y. V. Mikhaylik Electrolytes for Lithium Sulfur Cells. Google Patents April 8, 2008.
- S. S. Zhang, Role of LiNO3 in Rechargeable Lithium/Sulfur Battery, Electrochim. Acta, 2012, 70, 344–348 CrossRef CAS.
- B. D. Adams, E. V. Carino, J. G. Connell, K. S. Han, R. Cao, J. Chen, J. Zheng, Q. Li, K. T. Mueller and W. A. Henderson, Long Term Stability of Li-S Batteries Using High Concentration Lithium Nitrate Electrolytes, Nano Energy, 2017, 40, 607–617 CrossRef CAS.
- Z. L. Brown, S. Heiskanen and B. L. Lucht, Using Triethyl Phosphate to Increase the Solubility of LiNO3 in Carbonate Electrolytes for Improving the Performance of the Lithium Metal Anode, J. Electrochem. Soc., 2019, 166(12), A2523 CrossRef CAS.
- T. L. Cottrell, The Strengths of Chemical Bonds, Butterworth, London, 2nd edn, 1958 Search PubMed.
- B. Darwent deB. Bond Dissociation Energies in Simple Molecules, National Standard Reference Data Series; Washington, 1970.
- S. W. Benson, III-Bond Energies, J. Chem. Educ., 1965, 42(9), 502 CrossRef CAS.
- J. A. Kerr, Bond Dissociation Energies by Kinetic Methods, Chem. Rev., 1966, 66(5), 465–500 CrossRef CAS.
- R. Zhao, S. Kmiec, G. Hu and S. W. Martin, Lithium Thiosilicophosphate Glassy Solid Electrolytes Synthesized by High-Energy Ball-Milling and Melt-Quenching: Improved Suppression of Lithium Dendrite Growth by Si Doping, ACS Appl. Mater. Interfaces, 2019, 12(2), 2327–2337 CrossRef PubMed.
- M. A. P. Aguilar, Characterization of Lithium Thiosilicophosphate Glasses Prepared by High Energy Ball Milling, Dissertation, Iowa State University, 2018.
- T. Yersak, J. R. Salvador, R. D. Schmidt and M. Cai, Hot Pressed, Fiber-Reinforced (Li2S)70(P2S5)30 Solid-State Electrolyte Separators for Li Metal Batteries, ACS Appl. Energy Mater., 2019, 2(5), 3523–3531 CrossRef CAS.
- Y. Kim, J. Saienga and S. W. Martin, Anomalous Ionic Conductivity Increase in Li2S + GeS2 + GeO2 Glasses, J. Phys. Chem. B, 2006, 110(33), 16318–16325 CrossRef CAS PubMed.
- V. Mohaček-Grošev, K. Furić and H. Ivanković, Observed Bands in Raman and Infrared Spectra of 1,3-Dioxolane and Their Assignments, Vib. Spectrosc., 2013, 64, 101–107 CrossRef.
- P. J. Victor, B. Das and D. K. Hazra, A Study on the Solvation Phenomena of Some Sodium Salts in 1,2-Dimethoxyethane from Conductance, Viscosity, Ultrasonic Velocity, and FT-Raman Spectral Measurements, J. Phys. Chem. A, 2001, 105(24), 5960–5964 CrossRef CAS.
- W. Zhu, A. Paolella, C. S. Kim, D. Liu, Z. Feng, C. Gagnon, J. Trottier, A. Vijh, A. Guerfi, A. Mauger, C. M. Julien, M. Armand and K. Zaghib, Investigation of the Reaction Mechanism of Lithium Sulfur Batteries in Different Electrolyte Systems by: In Situ Raman Spectroscopy and in Situ X-Ray Diffraction, Sustainable Energy Fuels, 2017, 1(4), 737–747 RSC.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama and K. Kawamoto, A Lithium Superionic Conductor, Nat. Mater., 2011, 10(9), 682–686 CrossRef CAS PubMed.
- S. S. Zumdahl, Chemical Principles, Houghton Mifflin Co., Boston, 5th edn, 2005 Search PubMed.
- J. H. Kennedy and Z. Zhang, Preparation and Electrochemical Properties of the SiS2–P2S5–Li2S Glass Coformer System, J. Electrochem. Soc., 1989, 136(9), 2441 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00926e |
| This journal is © The Royal Society of Chemistry 2022 |