Open Access Article
Open Access ArticleEnhancing the catalytic activity of CdX and ZnX (X = S, Se and Te) nanostructures for the hydrogen evolution reaction via transition metal doping†
Feifei
Xia
 *,
Li
Shu
,
Yingpin
Wen
,
Fengli
Yang
and
Chunzhi
Zhen
*,
Li
Shu
,
Yingpin
Wen
,
Fengli
Yang
and
Chunzhi
Zhen
School of Chemical and Environmental Engineering, Jiangsu University of Technology, Changzhou 213001, Jiangsu, P. R. China. E-mail: ffxia@jsut.edu.cn
First published on 26th May 2022
Abstract
Exploring stable and non-precious electrocatalysts for the hydrogen evolution reaction (HER) is the key to electrochemical water splitting. Herein, the catalytic activity of CdX and ZnX (X = S, Se and Te) nanostructures for the HER was systematically evaluated. Our calculations reveal that pristine CdX and ZnX (X = S, Se and Te) have a higher hydrogen adsorption free energy (ΔG*H) in the range of 1.07–2.00 eV, indicating very weak *H adsorption and inefficient electrocatalytic activity for the HER. However, it is found that the HER activity of CdX and ZnX (X = S, Se and Te) nanostructures can be effectively enhanced by doping with transition metal (TM) atoms (Fe, Co, Ni, Cu, Pd and Pt). In particular, Ni-doped CdS and ZnTe, and Cu-doped CdSe, CdTe, ZnS and ZnSe have ΔG*H values in the range of −0.03 to 0.09 eV, which is ideally near to zero, indicating their efficient catalytic activity. These results suggest that our work introduces Ni-doped CdS and ZnTe, and Cu-doped CdSe, CdTe, ZnS and ZnSe nanostructures as promising HER catalysts for future energy applications.
Introduction
Electrochemical water splitting offers an essential strategy to resolve the environmental and energy problems of using fossil fuels for hydrogen production.1–3 As a fundamental step in electrochemical water splitting, the hydrogen evolution reaction (HER) always requires a favourable catalyst to achieve fast kinetics for practical applications.1–4 It is well known that the noble metal Pt is the most effective electrocatalyst for the HER in acidic media due to its near-zero overpotential, low Tafel slope and high stability,5–9 but the scarcity and high cost of Pt hinder its commercial applications as an industry-level electrocatalyst. So, the discovery of highly active, low-cost and Earth-abundant alternatives is a crucial challenge for the development of efficient hydrogen technologies. Many types of promising HER electrocatalysts have been explored,10–19 including transition-metal dichalcogenides (TMDs),10,11 transition-metal phosphides,12,13 carbon-based layered nanomaterials,14,15 and MXenes,16,17 which are currently regarded as potential candidates to replace Pt as HER electrocatalysts. However, the HER-inert basal plane exists in these two-dimensional (2D) catalysts, which limits their large-scale application. Therefore, it is of great significance to seek new efficient electrocatalysts for the HER that are of high electrocatalytic activity and stability.It has been reported that transition metal (TM) atom doping can provide an active site for the HER, which can significantly reduce the Gibbs free energy change (ΔG*H) value.18–23 For example, Jiang et al.18 discovered that the HER activity of 1T MoS2 can be further increased via substitutional doping of the Mo atom with transition metal atoms (e.g., Mn, Cr, Cu, Ni, and Fe). These results offer useful insights for understanding and improving the HER activity of the 1T phase of MoS2 and other 2D TMD nanosheets. In addition, Pathak et al.19 observed that all of the TMs (Fe, Co, Ni, Cu, Ag, Au, Pd, Pt, Os, Ir, Ru and Rh) are efficient for reducing the ΔG*H values of pure CdS nanotubes; in particular, Ni- and Ru-doped CdS nanotubes are the best HER catalysts with the smallest ΔG*H values, suggesting that TM doping is an efficient way to improve the performance of CdS nanotubes toward electrocatalytic hydrogen evolution.
II–VI nanostructures CdX and ZnX (X = S, Se, and Te) have drawn tremendous research interest in photocatalytic fields24–26 due to their remarkable electronic and optical properties. These reported studies show that CdX and ZnX (X = S, Se and Te) can be used as semiconductor photocatalysts for hydrogen generation from water splitting. However, their use in the area of electrocatalysis has clearly been lacking. The limiting factor that has conventionally bound electrocatalytic water splitting to either alkaline or acidic media is simply inappropriate for the use of II–VI nanostructures due to the high observed overpotentials. Moreover, the electrocatalytic hydrogen evolution reaction, much like any catalytic process, is a surface phenomenon, and the importance of surface modulation lies in the induced local surface electronic changes. Thus, tuning the surface properties of the catalyst can lead to significant activity enhancement.
To improve the catalytic hydrogen production activity of pristine CdX and ZnX (X = S, Se and Te) nanostructures, transition metal (TM) atom doping was introduced to change their local surface electronic properties. Moreover, the stability and HER activity of these nanostructures were systematically explored based on density functional theory (DFT)27,28 in this work. Firstly, the structural parameters and dynamic stabilities of pristine CdX and ZnX (X = S, Se and Te) were predicted using hybrid DFT calculations. Furthermore, the hydrogen adsorption free energy (ΔG*H) and the corresponding catalytic activities for the HER were evaluated by computationally screening II–VI nanostructures for doping with different TM atoms (Fe, Co, Ni, Cu, Pd and Pt). Our results demonstrate that pristine CdX and ZnX (X = S, Se and Te) have a higher ΔG*H in the range of 1.07–2.00 eV, indicating very weak *H adsorption and easy product desorption, which are unfavorable for the electrocatalytic HER. However, TM doping can significantly reduce the ΔG*H values of pristine CdX and ZnX (X = S, Se and Te) nanostructures, especially for Ni-doped CdS and Cu-doped ZnS, which show the smallest ΔG*H values of −0.03 and 0.01 eV, respectively. These results are a clear indication of the enhanced electrocatalytic HER activity from TM doping. The findings provide clear evidence that TM doping has great potential for significantly enhancing the catalytic activity of CdX and ZnX (X = S, Se and Te) nanostructures for the HER, thus opening a new avenue towards replacing noble metals with broader alternatives in a wide variety of applications.
Computational methods
All the calculations were performed using density functional theory (DFT) as implemented in the Vienna ab initio simulation package.29 The projector augmented-wave method was adopted to describe the ion–electron interactions, and the electron exchange–correlation was depicted with the form of Perdew, Burke, and Ernzerhof (PBE) in the generalized gradient approximation (GGA).30–34 It is well known that the GGA usually underestimates the band gap, so the Heyd–Scuseria–Ernzerhof (HSE06)35,36 hybrid functional was also used for band-structure calculations. The energy cutoff for plane-wave expansion was set to 550 eV. And the Vanderbilt ultrasoft pseudopotential37 was used to describe the interactions between the valence electrons and the ionic core. Brillouin zone sampling was performed using Monkhorst–Pack special k-point meshes,38 and the 6 × 6 × 1 k-grid was chosen for geometry optimization of the CdX and ZnX (X = S, Se and Te) nanostructures. Both the cutoff energy and k-grid were tested to be converged in the total energy. The geometry was optimized until the total energy converged to 10−6 eV and the forces of all atoms were smaller than 0.01 eV Å−1.The change in Gibbs free energy of hydrogen atom adsorption (ΔG*H) was used to describe and predict the HER activity on the surface of the CdX and ZnX (X = S, Se, Te) nanostructures. The equation to calculate ΔG*H is shown as follows:39,40
| ΔG*H = ΔE*H + ΔEZPE − TΔS | (1) |
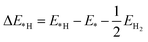 | (2) |
Results and discussion
To assess the dynamical stabilities of pristine CdX and ZnX (X = S, Se and Te), the phonon dispersions were computed along the high-symmetry lines in the first Brillouin zone (Fig. 1), which provides useful information for the experimental feasibility. It can be noted that pristine CdX and ZnX (X = S, Se and Te) have similar phonon spectra, and the absence of imaginary frequencies in the whole Brillouin zone demonstrates the dynamical stability of these corresponding structures (Fig. 1), agreeing well with previous reports.41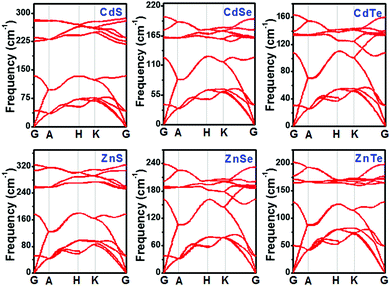 | ||
| Fig. 1 Phonon band structures of pristine CdX and ZnX (X = S, Se and Te) in the bulk phase at the HSE06 level. | ||
As discussed above, pristine CdX and ZnX (X = S, Se and Te) are dynamically stable, and we calculated their bond length and lattice parameters (shown in Table 1) based on the GGA-PBE and HSE06 methods, which were compared with the experimental data.41 The lattice constants of CdX and ZnX increase with the increase in the Cd–X and Zn–X (X = S, Se, Te) bond length. Moreover, it is interesting that the bond length and lattice parameters of ZnX are slightly smaller than those of CdX and increase when S is replaced by Se and Se by Te in the bulk phase. This phenomenon indicates that the unit cell volumes of ZnX and CdX are probably related to the size of the component atoms with some adjustment for bonding in the solid. In addition, it can be noted that the calculated lattice constants of pristine CdX and ZnX (X = S, Se and Te) using the GGA-PBE and HSE06 methods are in good agreement with the experimental data, with deviations of roughly 1–2%. Furthermore, the band structure and partial density of states (PDOS) of pristine CdX and ZnX (X = S, Se and Te) were calculated using the GGA-PBE and HSE06 methods and compared with the experimental values (in Table S1 and Fig. S1, ESI†). Our calculated results are in good agreement with the reported work41 and experimental data,42 which reveals that our calculated method is reliable.
| Nanostructure | Bond length (Å) | Lattice parameters (Å) | ||||||
|---|---|---|---|---|---|---|---|---|
| GGA/PBE | HSE06 | GGA/PBE | HSE06 | Expt42 | ||||
| Cd–X or Zn–X | a | c | a | c | a | c | ||
| CdS | 2.58 | 2.61 | 4.22 | 6.83 | 4.27 | 6.90 | 4.19 | 6.66 |
| CdSe | 2.67 | 2.71 | 4.36 | 7.12 | 4.43 | 7.19 | 4.29 | 7.01 |
| CdTe | 2.88 | 2.89 | 4.71 | 7.69 | 4.71 | 7.69 | 4.55 | 7.45 |
| ZnS | 2.34 | 2.44 | 3.85 | 6.29 | 3.98 | 6.49 | 3.89 | 6.20 |
| ZnSe | 2.46 | 2.54 | 4.02 | 6.57 | 4.15 | 6.78 | 3.99 | 6.62 |
| ZnTe | 2.68 | 2.72 | 4.37 | 7.15 | 4.44 | 7.26 | 4.37 | 7.18 |
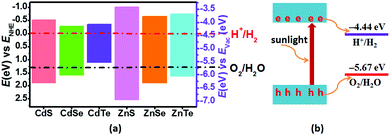
As known, the primary requirement to realize photocatalytic water splitting is that the redox potential of water must lie between the bandgap of the photocatalyst, i.e., the conduction band minimum (CBM) should be higher than the reduction potential of H+/H2, and the valence band maximum (VBM) should be lower than the oxidation potential of H2O/O2 simultaneously. Therefore, the theoretical bandgap of the photocatalyst should be larger than 1.23 eV, which is the minimum value of energy demanded to split water into hydrogen and oxygen. However, because there will inevitably be energy loss during the electron-transfer process, and the barriers of the hydrogen evolution reaction and the oxygen evolution reaction will also be overcome by the kinetic overpotential, the bandgap of the photocatalyst should usually be larger than 1.8 eV.43 Therefore, to evaluate the redox ability of pristine CdX and ZnX (X = S, Se, Te), the band edge potentials of the valence band (EVB) and conduction band (ECB) of these structures were calculated according to the following equations:44
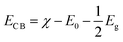 | (3) |
| EVB = ECB + Eg | (4) |
The calculated band gaps at the HSE06 level for pristine CdS, CdSe, CdTe, ZnS, ZnSe and ZnTe are 2.41, 1.86, 1.47, 3.56, 2.55 and 2.39 eV, respectively (Table S1 and Fig. S1, ESI†). On the basis of eqn (3) and (4), the band edge positions of the CBM for CdS and ZnS are −0.515 and −1.019 eV, while the band edge positions of the VBM are 1.895 and 2.54 eV, respectively (shown in Fig. 2a), versus the normal hydrogen electrode (NHE). These have band edges located at energetically favorable positions for water splitting, suggesting that both pristine CdS and ZnS are suitable as photocatalysts. Similarly, the band edge positions of the CBM and VBM for CdSe, CdTe, ZnSe and ZnTe were obtained versus the NHE, as also illustrated in Fig. 2a. It can be noted that the calculated band edge positions of the CBM and VBM for these structures also encompass the redox potentials of water, suggesting their applicability for photocatalytic water splitting. Moreover, the calculated band edge of the CBM for CdTe is located at an energetically favorable position only for hydrogen evolution from water splitting. All these results indicate that pristine CdX and ZnX (X = S, Se and Te) are applicable for photocatalytic hydrogen evolution from water splitting, although their catalytic activity for hydrogen evolution is not fully clear.
It has been reported that TM doping can accelerate the efficiency of catalysts toward the electrochemical HER, examples of which include C2N,15 1T-MoS2,18 silicone20 and so on.21–23 Therefore, a series of DFT calculations for the electrochemical HER on TM-doped CdX and ZnX (X = S, Se and Te) surfaces were carried out for gaining insight into the effect of the TM atoms on the HER activity. The overall HER pathway can be described using a three-state diagram comprising the initial state H+ + e−, an intermediate absorbed *H, and the final product 1/2H2 (Fig. 3 and 4). In this work, the Volmer–Heyrovský mechanism39,46 was used for the electrochemical HER on TM-doped CdX and ZnX (X = S, Se and Te), which involves proton adsorption along with electron deduction and the formation of *H, followed by the generation of molecular hydrogen in the next step. Hence, the possible HER mechanism is as follows:47
| * + H+ + e− → *H | (5) |
| *H + H+ + e− → H2 + * | (6) |
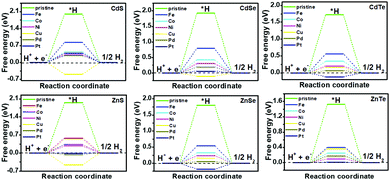 | ||
| Fig. 3 Gibbs free-energy (ΔG*H) diagram for the HER on pristine and TM-doped CdX and ZnX (X = S, Se and Te) surfaces, with the TM active site at the potential U = 0. | ||
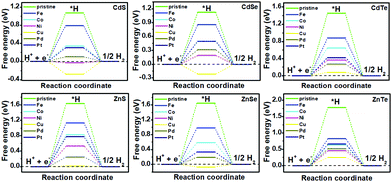 | ||
| Fig. 4 Gibbs free-energy (ΔG*H) diagram for the HER on pristine and TM-doped CdX and ZnX (X = S, Se and Te) surfaces, with the X (S, Se, Te) active site at the potential U = 0. | ||
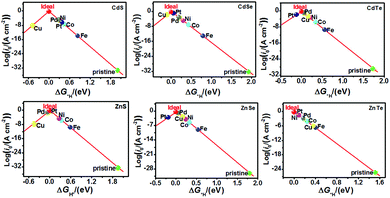
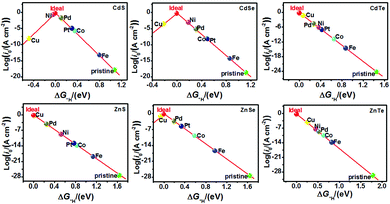
The catalytic efficiency of TM-doped CdX and ZnX (X = S, Se and Te) for the HER was examined using the ΔG*H values of *H formation on the different TM–CdX and TM–ZnX (X = S, Se and Te) surfaces. The ΔG*H values for hydrogen adsorption on pristine CdX and ZnX and on the CdX and ZnX (X = S, Se and Te) surfaces doped with TM atoms (Fe, Co, Ni, Cu, Pd and Pt) are shown in Fig. 3 and 4. In comparison with the ΔG*H value of pristine CdX or ZnX (X = S, Se and Te), TM doping leads to an obvious decrease in ΔG*H for hydrogen adsorption both on the metal active site and the X active site, suggesting that doping is efficient for reducing the reaction overpotential of the HER. It can be noted that the ΔG*H value of Ni-doped CdS and Cu-doped ZnS at the S active site is close to zero (Fig. 4 and Table S2, ESI†), indicating they are the most active HER catalysts and are efficient for enhancing the HER activity. Moreover, for noble metal (Pt and Pd) doping, the Pt–CdSe, Pd–CdTe, Pd–ZnSe, and Pt–ZnTe nanostructures show ΔG*H values of 0.06, 0.06, 0.05, and 0.01, respectively (Table S1, ESI†), which are nearer to zero than the value for the well-known highly efficient Pt catalyst (ΔGPt*H ≈ 0.09 eV),38 implying their better electrocatalytic activity. In addition, although Fe and Co doping decreases the energy barrier of ΔG*H for pristine CdX and ZnX (X = S, Se and Te), these doped nanostructures are not efficient enough for the HER.
In this work, the exchange current density (i0) is calculated as a function of ΔG*H for further depiction of the volcano curve, on the basis of the assumption by Nørskov et al.38 The exchange current density can be expressed as:
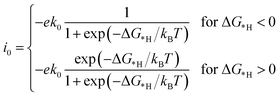 | (7) |
As shown in Fig. 5 and 6, the H atom is weakly adsorbed on the surface of pristine CdX and ZnX (X = S, Se and Te) with a very positive ΔG*H value of 1.07–2.00 eV, which is located at the bottom right of the volcano curve with a very low i0 value (highlighted in green). This suggests that pristine CdX and ZnX (X = S, Se and Te) are not favourable electrocatalysts for the HER. However, this situation can be significantly improved upon doping the surface with TM atoms. Interestingly, it can be noted that the adsorption of a H atom on Ni-doped CdS and Cu-doped ZnS at the S active site becomes significantly weakened with ΔG*H values (−0.03 and 0.01 eV) close to zero (around the volcano peak, as shown in Fig. 6), which is favorable for the HER. Moreover, this behavior balances the adsorption and release of hydrogen, resulting in a much higher exchange current i0. Moreover, the ΔG*H values of Cu-doped CdSe, CdTe and ZnSe, and Ni-doped ZnTe are, respectively, −0.09, 0.08, −0.06, and 0.09 (also close to zero), much lower than those of pristine surfaces, indicating that the electrocatalytic activity of CdX and ZnX (X = S, Se and Te) is significantly improved upon doping with Ni and Cu atoms. Furthermore, doping with the novel metal atoms (Pd and Pt) also improved the electrocatalytic activity of CdX and ZnX (X = S, Se and Te). In addition, Pd-doped CdTe and ZnSe, and Pt-doped CdSe and ZnTe can change the ΔG*H value of these pristine nanostructures to be close to zero (0.06, 0.05, 0.06 and 0.01 eV, respectively), suggesting doping with Pd and Pt is efficient for the HER. Thus, the doping with Ni and Cu is an effective method of enhancing the electrocatalytic activity of pristine CdX and ZnX (X = S, Se and Te) nanostructures.
Conclusions
In summary, we have systematically investigated the stability and electrocatalytic activity of CdX and ZnX (X = S, Se and Te) nanostructures for the HER, and screened Ni- or Cu-doped CdX and ZnX (X = S, Se and Te) as efficient electrocatalysts for the HER. The calculated phonon band structures show that pristine CdX and ZnX (X = S, Se and Te) are dynamically stable, which provides useful information for their experimental feasibility. Our calculations indicate that the H atom is weakly adsorbed on the pristine surface of CdX and ZnX (X = S, Se and Te) with a very positive ΔG*H value of 1.07–2.00 eV, indicating that pristine CdX and ZnX (X = S, Se and Te) are not appropriate electrocatalysts for the HER. However, the ΔG*H values of CdX and ZnX (X = S, Se and Te) doped with a TM (Fe, Co, Ni, Cu, Pd and Pt) show a clear decrease in ΔG*H compared with that of pristine structures, showing an efficient enhancement of their HER activity. All these results provide a theoretical basis for the design and synthesis of efficient HER electrocatalysts that could be verified via future experiments.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 21703087).Notes and references
- J. A. Turner, Science, 2004, 305, 972–974 CrossRef CAS PubMed.
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. X. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6673 CrossRef CAS PubMed.
- S. Chu and A. Majumdar, Nature, 2012, 488, 294–303 CrossRef CAS PubMed.
- Y. M. Xu, K. C. Fan, Y. Zhou, H. Q. Fu, M. Y. Dong, Y. H. Dou, Y. Wang, S. Chen, H. J. Yin, M. Al-Mamun, P. R. Liu and H. J. Zhao, Nanoscale, 2021, 13, 20324–20353 RSC.
- R. Subbaraman, D. Tripkovic, D. Strmcnik, K. C. Chang, M. Uchimura, A. P. Paulikas, V. Stamenkovic and N. M. Markovic, Science, 2011, 334, 1256–1260 CrossRef CAS PubMed.
- A. L. Goff, V. Artero, B. Jousselme, P. D. Tran, N. Guillet, R. Métayé, A. Fihri, S. Palacin and M. Fontecave, Science, 2009, 326, 1384–1387 CrossRef PubMed.
- R. Guo, X. Xu, Y. Xia, W. Huang, Z. Li and B. Teng, J. Catal., 2018, 368, 379–388 CrossRef CAS.
- D. Bernsmeier, R. Sachse, M. Bernicke, R. Schmack, F. Kettemann, J. Polte and R. Kraehnert, J. Catal., 2019, 369, 181–189 CrossRef CAS.
- Y. Jiao, Y. Zheng, M. Jaroniec and S. Z. Qiao, Chem. Soc. Rev., 2015, 44, 2060–2086 RSC.
- Y. Zhang, X. S. Chen, Y. Huang, C. Zhang, F. Li and H. B. Shu, J. Phys. Chem. C, 2017, 121, 1530–1536 CrossRef CAS.
- X. Hai, W. Zhou, S. Wang, H. Pang, K. Chang, F. Ichihara and J. Ye, J. Nano Energy, 2017, 39, 409–417 CrossRef CAS.
- E. J. Popczun, J. R. McKone, C. G. Read, A. J. Biacchi, A. M. Wiltrout, N. S. Lewis and R. E. Schaak, J. Am. Chem. Soc., 2013, 135, 9267–9270 CrossRef CAS PubMed.
- E. J. Popczun, C. G. Read, C. W. Roske, N. S. Lewis and R. E. Schaak, Angew. Chem., Int. Ed., 2014, 53, 5427–5430 CrossRef CAS PubMed.
- J. Duan, S. Chen, M. Jaroniec and S. Z. Qiao, ACS Nano, 2015, 9, 931–940 CrossRef CAS PubMed.
- X. Zhang, A. Chen, Z. Zhang, M. Jiao and Z. Zhou, J. Mater. Chem. A, 2018, 6, 11446–11452 RSC.
- G. Gao, A. P. O’Mullane and A. Du, ACS Catal., 2016, 7, 494–500 CrossRef.
- Y. W. Cheng, J. Dai, Y. M. Zhang and Y. Song, J. Phys. Chem. C, 2018, 122, 28113–28122 CrossRef CAS.
- Q. Tang and D. E. Jiang, ACS Catal., 2016, 6, 4953–4961 CrossRef CAS.
- P. Garg, A. S. Nair, K. S. Rawat and B. Pathak, J. Phys. Chem. C, 2019, 123, 13419–13427 CrossRef CAS.
- Y. X. Sun, A. J. Huang and Z. G. Wan, RSC Adv., 2019, 9, 26321–26326 RSC.
- J. Pan, R. Wang, X. Xu, J. Hu and L. Ma, Nanoscale, 2019, 11, 10402–10409 RSC.
- M. D. Sharma, C. Mahala, B. Modak, S. Pande and M. Basu, Langmuir, 2021, 37, 4847–4858 CrossRef CAS PubMed.
- I. S. Kwon, I. H. Kwak, S. Ju, S. Kang, S. Han, Y. C. Park, J. Park and J. Park, ACS Nano, 2020, 14, 12184–12194 CrossRef CAS PubMed.
- Z. B. Fang, S. X. Weng, X. X. Ye, W. H. Feng, Z. Y. Zheng, M. L. Lu, S. Lin, X. Z. Fu and P. Liu, ACS Appl. Mater. Interfaces, 2015, 7, 13915–13924 CrossRef CAS PubMed.
- F. Cao, W. Shi, L. Zhao, S. Song, J. Yang, Y. Lei and H. Zhang, J. Phys. Chem. C, 2008, 112, 17095–17101 CrossRef CAS.
- J. J. Wang, J. Meng, Q. X. Li and J. L. Yang, Phys. Chem. Chem. Phys., 2016, 18, 17029–17036 RSC.
- P. Hohenberg and W. Kohn, Phys. Rev. B, 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. H. T. Philipsen, G. teVelde and E. J. Baerends, Chem. Phys. Lett., 1994, 226, 583–588 CrossRef CAS.
- A. Zupan, K. Burke, M. Ernzerhof and J. P. J. Perdew, Chem. Phys., 1997, 106, 10184–10193 CAS.
- B. Hammer, K. W. Jacobsen and J. K. Norskov, Phys. Rev. Lett., 1993, 70, 3971–3974 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- J. K. Noerskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23–J26 CrossRef.
- X. P. Xu, H. X. Xu and D. J. Cheng, Nanoscale, 2019, 11, 20228–20237 RSC.
- G. Petretto, S. Dwaraknath, H. P. C. Miranda, D. Winston, M. Giantomassi, M. J. van Setten, X. Gonze, K. A. Persson, G. Hautier and G. M. Rignanese, Sci. Data, 2018, 5, 180065 CrossRef CAS PubMed.
- Z. J. Nourbakhsh, J. Alloy. Compd., 2010, 505, 698–711 CrossRef CAS.
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446 CrossRef CAS PubMed.
- J. J. Liu, X. L. Fu, S. F. Chen and Y. F. Zhu, Appl. Phys. Lett., 2011, 99, 191903 CrossRef.
- R. G. Pearson, Inorg. Chem., 1988, 27, 734–740 CrossRef CAS.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Nat. Mater., 2006, 5, 909–913 CrossRef CAS PubMed.
- Y. Li, H. Wang, L. Xie, Y. Liang, G. Hong and H. Dai, J. Am. Chem. Soc., 2011, 133, 7296–7299 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma00007e |
| This journal is © The Royal Society of Chemistry 2022 |