Open Access Article
Open Access ArticleModeling ionization quenching in organic scintillators†
Thibault A.
Laplace
 *a,
Bethany L.
Goldblum
*a,
Bethany L.
Goldblum
 ab,
Joshua A.
Brown
a,
Glenn
LeBlanc
a,
Tianyue
Li
a,
Juan J.
Manfredi‡
a and
Erik
Brubaker
ab,
Joshua A.
Brown
a,
Glenn
LeBlanc
a,
Tianyue
Li
a,
Juan J.
Manfredi‡
a and
Erik
Brubaker
 c
c
aDepartment of Nuclear Engineering, University of California, Berkeley, CA 94720, USA. E-mail: lapthi@berkeley.edu
bNuclear Science Division at Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. E-mail: bethany@lbl.gov
cSandia National Laboratories, Livermore, CA 94550, USA
First published on 16th June 2022
Abstract
Recoil nuclei produce high ionization and excitation densities in organic scintillators leading to reduced light yield via ionization quenching. To improve understanding of the relationship between organic scintillator specific luminescence and the characteristics of the recoil particle, this work evaluates proton and carbon light yield data using ionization quenching models over an energy range of tens of keV to several MeV for protons and 1–5 MeV for carbon ions. Previously-measured proton and carbon light yield data were examined for a variety of commercial and novel organic scintillating media: EJ-309, a liquid with pulse shape discrimination (PSD) properties; EJ-204, a fast plastic; EJ-276, a PSD-capable plastic; and a custom organic glass scintillator developed by Sandia National Laboratories. The canonical model of Birks did not adequately describe the ionization quenching behavior. Models proposed by Yoshida et al. and Voltz et al. provided a reasonable description of the proton light yield of a variety of organic scintillators over a broad energy range, but additional work is needed to extend the models to carbon ions. The impact of stopping power data was also investigated by comparing model predictions using SRIM and PSTAR/MSTAR libraries, and the results show a significant discrepancy for carbon ions. This work enhances understanding of ionization quenching and facilitates the accurate modeling of scintillator-based neutron detection systems relevant for medical physics, nuclear security and nonproliferation, and basic science studies.
1 Introduction
When protons or other heavy charged particles deposit energy in organic scintillators, high excitation and ionization densities result in a reduction in scintillation efficiency—a phenomenon known as ionization quenching. While extensive research has been conducted on the response of organic scintillators to recoil nuclei,1–13 there remains disagreement regarding the impact of the nature of the ionizing particle on the specific luminescence. The canonical Birks model is often used to describe the ionization quenching effect though it has failed to predict the scintillation response at low recoil energies and for particles of different charge.14 For example, von Krosigk et al. performed a simultaneous measurement of α particle and proton quenching in a linear alkylbenzene scintillator and showed that the measured α and proton light yield relations cannot be well described using the same Birks parameter.15 Yoshida et al. observed a similar phenomenon, where the Birks model failed to describe the measured proton and carbon quenching factors of the KamLAND liquid scintillator over the energy range of 424 keV to 10.5 MeV.16 A variety of extensions of the Birks formalism have been proposed to address this challenge: the addition of a bimolecular quenching term in the manner of Chou,17 separate consideration of the electronic and nuclear components of the stopping power by Hong et al.,18 and a model from Yoshida et al. wherein both effects are considered in tandem.16 Voltz et al. further posed a theoretical expression for the specific luminescence that differs notably from prior approaches, introducing a dependence on the charge number of the ion.19 The Voltz et al. approach features separate consideration of the prompt and delayed components of the scintillation light with specialized treatment of δ rays.In a recent study by Norsworthy et al.,20 the Birks law, an adapted formulation of Voltz, and other empirical models were used to fit measured proton light yield data of EJ-309, a liquid organic scintillator with pulse shape discrimination (PSD) properties. While agreement was obtained between the models and measured data in the energy range of 1.15 to 5.15 MeV, the extrapolated proton light yield relations diverged wildly at low energies.20 Using a proton beam with energies of 30 to 100 MeV, Pöschl et al. recently measured ionization quenching in two different plastic scintillating fibers, SCSF-78 and BC-408.21 Several ionization quenching models were tested, including those of Birks, Chou, and Voltz et al. examined in this work. The authors concluded that none of the models provided an accurate description of the data for both scintillating materials over the full energy range. Studies of multiple ions in different scintillating media have further led to disparate conclusions regarding the validity of theoretical models of specific luminescence.16,18,22 Additional research is needed to understand and describe the response of organic scintillators to recoil nuclei over a broad energy range, important for scintillation physics and applications.
The goal of this work is to evaluate the performance of specific luminescence models for a variety of classes of organic scintillating media and recoil ions over the fission neutron energy range. Model parameters were obtained with covariance to facilitate the use of these data for detector response modeling, neutron spectrum unfolding, kinematic neutron imaging, and scintillation studies. Section 2 provides an overview of the ionization quenching models examined in this work. In Section 3, the Monte Carlo method for model parameter estimation and uncertainty quantification is described. Though no measurements were performed as a part of this study, an overview of the evaluated experimental data and approach is provided for context. Model parameter constraints and inputs are also addressed. Section 4 shows the results of the models applied to proton light yield data for the liquid EJ-309,23 the fast plastic EJ-204,24 the PSD-capable plastic EJ-276,25 and an organic glass scintillator.26,27 Using proton and carbon light yield data for EJ-309 and EJ-204, the models were further interrogated with regard to their behavior as a function of the charge, showcasing the first simultaneous fit of the proton and carbon light yield data of the EJ-309 and EJ-204 organic scintillators. Additionally, the impact of stopping power libraries on the model output was assessed. Concluding remarks are given in Section 5.
2 Models
The first model of ionization quenching in organic scintillators was proposed by Birks14,28 and remains widely used today. In the Birks model, the specific luminescence, defined as the light output per unit path length of the recoil particle, is given by: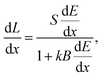 | (1) |
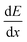 is the specific energy loss. The absolute scintillation efficiency, S, represents the fraction of energy deposited by the particle that is converted to light in the absence of quenching, and kB is collectively referred to as the Birks parameter, a constant characteristic of ionization quenching. This approach treats ionization quenching as a unimolecular phenomenon arising from temporary molecular damage and neglects the potential effects of interactions between neighboring excited and ionized molecules.14
is the specific energy loss. The absolute scintillation efficiency, S, represents the fraction of energy deposited by the particle that is converted to light in the absence of quenching, and kB is collectively referred to as the Birks parameter, a constant characteristic of ionization quenching. This approach treats ionization quenching as a unimolecular phenomenon arising from temporary molecular damage and neglects the potential effects of interactions between neighboring excited and ionized molecules.14
The model of Chou17 extends the Birks relation to include a bimolecular quenching term:
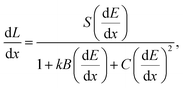 | (2) |
As an ion traverses the scintillating medium, energy loss may occur through electronic and nuclear processes. Electronic stopping (collisions between the heavy charged particle and electrons in the stopping medium) leads to excitation and ionization of scintillating molecules, whereas nuclear stopping (collisions between the heavy charged particle and target nuclei) leads primarily to energy loss and change of the direction of the ion.30 The nuclear stopping power becomes significant at low energy where electronic excitation channels close.31 Hong et al.18 provided an additional extension of the Birks model in which electronic and nuclear interactions (denoted by the subscripts e and n, respectively) are treated separately:
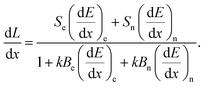 | (3) |
In this approach, energy deposited via electronic and nuclear stopping may contribute differently to quenching effects or the absolute scintillation efficiency. As the velocity of the heavy charged particle goes to zero, there is a continual reduction in the ionic charge. That is, there is some probability of charge exchange with the medium, whereby the heavy charged particle will capture and lose electrons. When atomic projectiles suffer hard (wide deflection angle, small impact parameter) collisions with other atoms, the electron shells deeply interpenetrate allowing for electronic excitation and ionization.32 This mechanism motivates the Sn term in eqn (3). The kBn term can be understood, e.g., as energy transfer being sufficiently large in a nuclear collision to cause an atom to be displaced from its normal site resulting in a damaged molecule.33 In 2010, Yoshida et al.16 expanded upon the Hong et al.18 model to include the bimolecular quenching term:
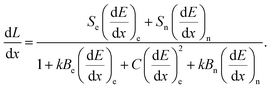 | (4) |
While the above models provide extensions of the Birks formalism, an alternate description from Voltz et al.19 was introduced that separately addresses the prompt and delayed components of the scintillation light. According to amorphous track structure theory (Fig. 1), the heavy charged particle track is comprised of a narrow core of high ionization and excitation density. In this central zone, prompt fluorescence occurs through the de-excitation of singlet states. Delayed fluorescence arises via triplet–triplet annihilation, the bimolecular interaction of triplet excitons resulting in the production of an excited singlet state and a singlet in the ground state.34,35 The core of the particle track is surrounded by the penumbra, a peripheral region wherein energy deposition occurs primarily via δ rays, secondary electrons with sufficient energy to leave the track core. In the model of Voltz et al.,
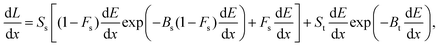 | (5) |
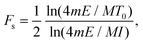 | (6) |
 | ||
| Fig. 1 Illustration of a heavy charged particle track showing the core (region of high ionization and excitation density) and penumbra (peripheral region where energy deposition occurs via δ rays). | ||
3 Methods
3.1 Experimental data
Specific luminescence models were fit to previously measured proton and carbon light yield data, summarized in Table 1. For the EJ-309, EJ-204, and the organic glass scintillator, the proton light yield data evaluated in this work were derived from multiple independent experimental measurements for each material with different dynamic ranges. The light yield measurement approach employed a double time-of-flight (TOF) technique.10,36 A representative experimental setup is shown in Fig. 2. In brief, a broad spectrum neutron beam is made incident on a target scintillator, which is surrounded by an array of observation detectors. The incoming and outgoing neutron energies are measured using TOF and the particle recoil energy is obtained via elastic scattering kinematics. Given the known scattering angle, this approach provides a kinematically over-constrained system by which to obtain the proton and carbon light yield on an event-by-event basis over a broad range of energies.3.2 Light output unit
Given the challenges associated with accurate measurement of the absolute photon yield of organic scintillators,38,39 it is common practice to report the scintillator light output relative to the light produced by a recoil electron of known energy.40 This is often accomplished using one or more sealed γ-ray sources and a MeV electron-equivalent (MeVee) light unit, where the electron light yield is assumed to be linear above a given threshold.41 However, recent studies have shown a nonproportionality in the electron response of organic scintillators over a broad energy range.42–44 As such, the measured light output for the various datasets examined in this work was expressed relative to the light produced by a 477 keV electron. The responses of the photomultiplier tubes used for the presented measurements were also measured and scintillation signals were corrected for any observed nonlinearity.3.3 Parameter constraints
The absolute scintillation efficiency, S, in eqn (1) and (2) represents the fraction of energy deposited by an unquenched particle that is converted to light, where the remainder of the energy deposited is dissipated through non-radiative processes. For a light unit defined relative to the light produced by a 0.477 MeV electron, S would equal 1/0.477 if the electron were an unquenched particle. Given contributions from Cherenkov light45 and observations of electron light quenching in organic scintillators at low recoil energies,42–44 the S parameter in the Birks and Chou models was allowed to vary about the nominal value by a conservative 20%. Cases for which the bound was reached will be discussed in further detail. For the Hong et al. and Yoshida et al. models given in eqn (3) and (4), respectively, both Se and Sn were bounded about the nominal value. The Sn bound is motivated by electron-nucleus collisions that give rise to excitation and ionization via resonant electron scattering and attachment at low energy and pseudo-photoabsorption/ionization at high energy.46 For the model of Voltz et al., the absolute scintillation efficiency, S, was bounded. Here, S is given by the sum of the prompt singlet and triplet scintillation efficiencies (i.e., S = Ss + St in eqn (5)). To facilitate model fitting, the triplet scintillation efficiency was represented as St = RdS, where Rd corresponds to the fraction of the total absolute scintillation efficiency represented by the delayed component.In the Voltz et al. model, the free parameter T0 (see eqn (6)) corresponds to the minimum energy required for an electron to escape the core of the particle track. As singlet excitation in the penumbra does not occur for T0 ≥ 4mE/M, the model is insensitive to increases in T0 above this threshold. To constrain parameter uncertainty, an upper bound was placed on the T0 parameter at 1 keV above the threshold. The bound was determined independently for each material examined in this work using the highest measured recoil energy.
3.4 Mean excitation energy
The mean excitation energy of the scintillating medium, I, is used in the Voltz et al. model (see eqn (6)) to calculate the fraction of singlet excitation produced outside of the particle track. Values for this parameter were obtained using the Particle Data Group library.47,48 For EJ-204, EJ-276, and the organic glass scintillator, the mean excitation energy of polyvinyltoluene (PVT) was used (I = 64.7 eV). For EJ-309, the value for xylene was taken (I = 61.8 eV).3.5 Stopping power libraries
Stopping power values (in units of MeV cm2 per mg) were obtained using the Stopping and Range of Ions in Matter (SRIM) software package.49 For each material, the stopping power of the compound is given by the linear combination of the stopping power of its atomic constituents.50 The atomic composition of the organic glass was specified by the designer51 and that of the commercial scintillating media were obtained from manufacturer specification sheets.23–25 For the PVT-based plastic EJ-204, stopping power tables were also generated using the PSTAR52 and MSTAR53 libraries. In this case, the material definition was specified using ICRU-216, a vinyltoluene-based plastic scintillator studied in the International Commission on Radiation Units and Measurements (ICRU) Report 49.54A compound correction factor can be included in the SRIM calculation to account for the effects of molecular bonding and orbital and excitation structure. No compound correction is suggested by SRIM for ICRU-216 or Pilot B (a commercial plastic scintillator). As such, compound correction factors were not applied for the stopping power libraries used in this work.
3.6 Parameter estimation and uncertainty quantification
Model parameter estimation was performed via χ2 minimization using the SIMPLEX and MIGRAD algorithms from the ROOT Minuit2 package.55 To propagate covariance arising from analysis parameter uncertainties, model parameter estimation was accomplished via Monte Carlo sampling of the analysis parameters with N = 2000 trials. The analysis parameters included the detector locations, TOF calibration constants, and light output calibration constant.10 Each analytic parameter was sampled from a normal distribution with the standard deviation given by the estimated parameter uncertainty. For each sample of analysis parameters, the mean proton recoil energy and mean light yield, Mi, were recalculated for each of the i data points. The reduced light yield data from each Monte Carlo trial were fit using a given quenching model via χ2 minimization to obtain the model parameters and goodness-of-fit in the form of the χ2 statistic: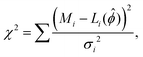 | (7) |
![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) .
.
The recommended model parameters were then calculated using the method of Birge.56 That is, for each model parameter, a weighted mean was obtained over the ensemble of fitted parameters:
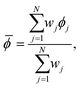 | (8) |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) is the weighted mean model parameter estimate and ϕj is the model parameter estimate of the jth trial. The weight of the jth trial, wj, is given by:
is the weighted mean model parameter estimate and ϕj is the model parameter estimate of the jth trial. The weight of the jth trial, wj, is given by: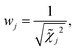 | (9) |
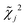 is the reduced chi-square statistic (i.e., χ2 per degrees of freedom) characterizing the goodness-of-fit of the jth trial. Similarly, the weighted covariance of the model parameters was also computed:
is the reduced chi-square statistic (i.e., χ2 per degrees of freedom) characterizing the goodness-of-fit of the jth trial. Similarly, the weighted covariance of the model parameters was also computed: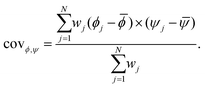 | (10) |
4 Results and discussion
In Section 4.1, the specific luminescence models were applied to describe the proton light yield of a variety of liquid, plastic, and glass organic scintillators. Section 4.2 explores model behavior as a function of the charge of the ionizing particle, showcasing simultaneous fits of the EJ-204 and EJ-309 proton and carbon light yield relations. The status of stopping power data for protons and carbon ions in organic scintillating media and the associated impact on model inquiry is explored in Section 4.3.4.1 Proton quenching
Fig. 3a shows the EJ-204 proton light yield data11 along with model fits obtained using the SRIM stopping power tables. Fig. 3b shows the deviation of the measured datapoints with respect to the model prediction. Distributions of model parameters were generated by sampling a multivariate Gaussian distribution constructed from the recommended model parameters and the associated covariance matrix using the ROOT RooFit package with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trials.57 For the proton energy corresponding to each of the measured data points, the light yield predicted from the distribution of model parameters was histogrammed. The median light yield value was used to represent the model prediction and the error bars represent the boundary within which 68.27% of the model predictions lie. The Birks and Hong et al. models exhibit significant deviation from the data at low energy; the S, Se, and Sn parameters reached the upper bound of the parameter range discussed in Section 3.2. If these parameters are allowed to vary beyond physically-reasonable values, the goodness-of-fit remains poor relative to the other models (see Table S1 in the ESI†). The models of Chou, Yoshida et al., and Voltz et al. provide a better prediction of the EJ-204 proton light yield data over the full energy range, although only the Yoshida et al. model reproduces the data within uncertainty below 100 keV.
000 trials.57 For the proton energy corresponding to each of the measured data points, the light yield predicted from the distribution of model parameters was histogrammed. The median light yield value was used to represent the model prediction and the error bars represent the boundary within which 68.27% of the model predictions lie. The Birks and Hong et al. models exhibit significant deviation from the data at low energy; the S, Se, and Sn parameters reached the upper bound of the parameter range discussed in Section 3.2. If these parameters are allowed to vary beyond physically-reasonable values, the goodness-of-fit remains poor relative to the other models (see Table S1 in the ESI†). The models of Chou, Yoshida et al., and Voltz et al. provide a better prediction of the EJ-204 proton light yield data over the full energy range, although only the Yoshida et al. model reproduces the data within uncertainty below 100 keV.
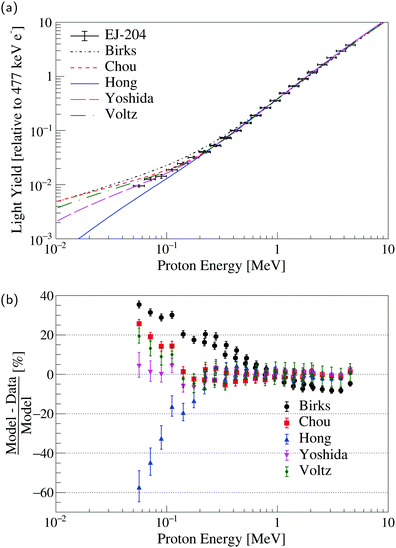 | ||
| Fig. 3 (a) Specific luminescence models applied to EJ-204 proton light yield data from Laplace et al.11 (b) Percent difference of the measured data with respect to the model prediction. The error bars represent the 68.27% confidence interval. | ||
Model fits of the EJ-309, EJ-276, and organic glass proton light yield are shown in Fig. S1–S3, respectively (ESI†). Table 2 provides the median reduced χ2 statistic from the Monte Carlo distribution (see Section 3.6) along with the median absolute deviation for each model and material. For all of the scintillating media examined in this work, the Birks and Hong et al. models fail to provide an adequate description of the proton light yield over the full energy range. The Chou and Yoshida et al. models explicitly include a bimolecular quenching term and perform notably better than the Birks and Hong et al. models where this term is absent.
| Scintillator | Birks | Chou | Hong et al. | Yoshida et al. | Voltz et al. |
|---|---|---|---|---|---|
| EJ-204 | (24202 ± 2980)/31 | (1878 ± 674)/30 | (3219 ± 1039)/29 | (1282 ± 701)/28 | (1411 ± 671)/28 |
| EJ-309 | (52655 ± 8844)/46 | (2114 ± 1618)/45 | (3459 ± 1788)/44 | (1954 ± 1549)/43 | (1645 ± 1412)/43 |
| EJ-276 | (9926 ± 1777)/21 | (156 ± 56)/20 | (1238 ± 300)/19 | (204 ± 76)/18 | (90 ± 16)/18 |
| Organic glass | (6725 ± 1732)/52 | (741 ± 206)/51 | (1042 ± 311)/50 | (342 ± 152)/49 | (371 ± 145)/49 |
For the proton recoil energies examined in this study, the amount of energy lost through nuclear stopping represents a small fraction of the total energy loss (e.g., approximately 1.4% for a 56 keV proton in EJ-204). As the contribution to the specific energy loss from nuclear stopping decreases with increasing recoil energy, the impact of nuclear stopping is even less significant in the energy ranges covered by the EJ-309 and EJ-276 proton light yield datasets, which extend to 200 keV and 170 keV, respectively (where the energy lost through nuclear stopping represents approximately 0.5% of the total energy loss). This low contribution from nuclear stopping hinders interrogation of the validity of the Hong et al. and Yoshida et al. models.
Nonetheless, the Yoshida et al. and Voltz et al. models consistently provide a reasonable description of the proton light yield and exhibit physically-plausible behavior in the low-energy extrapolation region. Model parameters along with their covariances matrices are provided for EJ-204, in Tables S2 and S3 (ESI†); for EJ-309, in Tables S4 and S5 (ESI†); for EJ-276, in Tables S6 and S7 (ESI†); and for the organic glass, in Tables S8 and S9 (ESI†).
4.2 Impact of the nature of the heavy charged particle
For the EJ-204 and EJ-309 scintillators, carbon light yield data are also available.36 These data enable testing of the models for high stopping power values and with a higher relative contribution from nuclear stopping in comparison with proton recoils. For example, a 1 MeV carbon recoil in EJ-204 loses approximately 5% of its energy through nuclear stopping. The results of a simultaneous fit of the proton and carbon light yield data are given in Fig. 4 and 5 for EJ-204 and EJ-309, respectively. The goodness-of-fit for each model in the form of the median reduced χ2 statistic from the Monte Carlo distribution (see Section 3.6) along with the median absolute deviation for each model and material is provided in Table 3. Model parameters and covariances matrices are provided for EJ-204 in Tables S10 and S11 (ESI†) and for EJ-309, in Tables S12 and S13 (ESI†).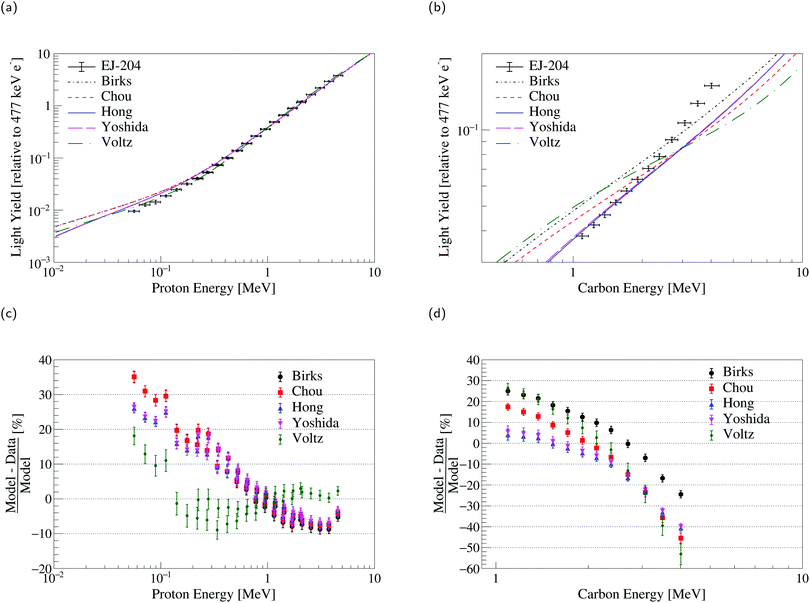 | ||
| Fig. 4 Simultaneous fit of EJ-204 (a) proton and (b) carbon light yield data. Comparison of the models to the measured EJ-204 (c) proton and (d) carbon light yield data. | ||
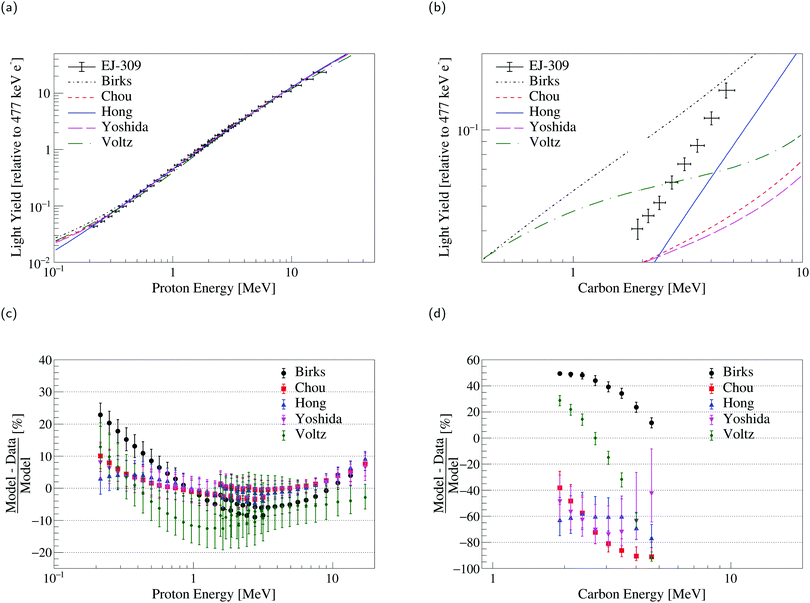 | ||
| Fig. 5 Simultaneous fit of EJ-309 (a) proton and (b) carbon light yield data. Comparison of the models to the measured EJ-309 (c) proton and (d) carbon light yield data. | ||
| Scintillator | Birks | Chou | Hong et al. | Yoshida et al. | Voltz et al. |
|---|---|---|---|---|---|
| EJ-204 | (30446 ± 2968)/43 | (27630 ± 2768)/42 | (22885 ± 2733)/41 | (29093 ± 3482)/40 | (13171 ± 1272)/40 |
| EJ-309 | (78778 ± 10502)/54 | (18727 ± 3395)/53 | (16913 ± 3960)/52 | (15778 ± 2957)/51 | (14720 ± 3178)/51 |
For the EJ-204 proton and carbon light yield data, none of the models examined in this work provide a reasonable description of both datasets simultaneously. The statistical uncertainty on the proton measurements considered is significantly smaller than that of the carbon measurements. This leads to model predictions that agree significantly better with the proton data than with the carbon data. For both the Birks and Chou models, the S parameter reached the upper bound discussed in Section 3.2. For the Hong et al. and Yoshida et al. models, the Se parameter reached the upper bound (as well as the Sn parameter in the case of Yoshida et al.). For Voltz et al., the total scintillation efficiency reached the lower bound. The results are similar for EJ-309, with a more significant disagreement with the carbon light yield data driven by the relatively larger statistical uncertainties. In this case, the S parameter reached the upper bound for the Birks model. Likewise, the Sn parameter reached the upper bound for the Hong et al. and Yoshida et al. models. If freed, the parameters converge towards unphysical values and provide only marginally better agreement with the data (see Table S14 in the ESI†).
Model improvements are needed to provide a reasonable description of the specific luminescence of different recoil ions and build confidence in extrapolations to both high and low energies, and other heavy charged particles. The models of Hong et al. and Yoshida et al. provide extensions of Birks and Chou with separate treatment of the nuclear and electronic stopping power, though they still do not fully describe the data presented. Even at the lowest energies covered by the datasets presented in this work, the contribution of nuclear stopping to the total specific energy loss remains small. In consequence, the parameters associated with nuclear stopping in the Hong et al. and Yoshida et al. models act as perturbations to improve the goodness of fit.
While Voltz et al. offers a more physically-motivated description of the specific luminescence of organic scintillators, the model does not adequately describe the data as a function of the charge of the ionizing particle. Specifically, there may be limitations in the approach with regard to the treatment of δ rays and delayed light. In the case of the former, the light produced by δ rays in the Voltz et al. model is treated as unquenched (see eqn (5)). However, significant electron light nonlinearity has been observed for liquid and plastic organic scintillators suggesting quenching of the electron response in the energy range relevant for these measurements.42–44,58 For example, a 5 MeV proton can transfer a maximum of 11 keV to an electron in a head-on collision. Assuming a proportional electron response at 477 keV, electron light nonproportionality measurements from Payne et al.42 suggest that an 11 keV electron produces only 69% of the amount of light that would be generated by an unquenched electron in EJ-204. With regard to the delayed light, in the Voltz et al. approach, the amount of delayed light decreases with increasing stopping power. However, the increased excitation and ionization density associated with increased stopping power is expected to give rise to increased delayed light—the mechanism underlying n/γ pulse shape discrimination. That is, delayed fluorescence is produced via triplet–triplet annihilation, whereby the interaction of two triplet excitons results in a molecule populated in a singlet state and one left in the ground state. The probability for this bimolecular interaction to occur increases with increasing excitation density. In addition, the probability of triplet state population through rapid ion recombination increases in likelihood with increasing ionization density through the Onsager effect.42,59 Given this, a more sophisticated treatment of the delayed light taking into account the excitation and ionization density distributions in the medium is required to accurately describe the specific luminescence. Recent advances in track structure modeling60–64 provide a potential path forward.
4.3 Impact of stopping power libraries
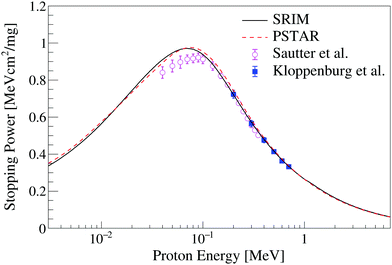
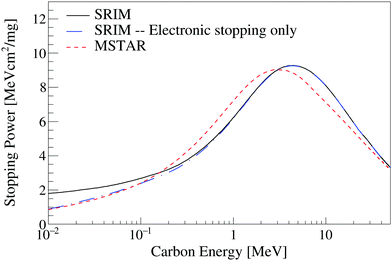
Stopping power data are required input for the ionization quenching models examined in this work. Fig. 6 shows the stopping power of protons in PVT, a common plastic scintillator base used in the EJ-204 formulation, obtained using the SRIM49 and PSTAR52 packages. The only two measurements available in the literature for proton stopping in PVT below 10 MeV are also shown.65,66 The SRIM and PSTAR calculations are less than 3% discrepant over the full energy range and within 2σ of the measurement of Sautter et al.66 For the proton light yield data examined in this work, the influence of the choice of stopping power library on the model parameters is less than the estimated parameter uncertainty.Fig. 7 shows the stopping power calculation for carbon ions in PVT from the MSTAR53 and SRIM49 packages. The MSTAR calculation includes only the electronic component of the stopping power whereas the SRIM calculation provides both electronic and nuclear stopping. The electronic component of the stopping power, taken from the SRIM49 library, is also shown in Fig. 7. No measurements of the carbon stopping power in PVT are available in the literature. The models predict Bragg peak positions for carbon ions in PVT at approximately 3 MeV and 4.5 MeV for MSTAR and SRIM, respectively. The discrepancy between the two stopping power models introduces significant uncertainty in the adjudication of ionization quenching models of the scintillation response to carbon recoils.
Despite the large discrepancy in the carbon stopping power data, use of the MSTAR stopping power tables did not provide improved agreement in the simultaneous fit of the EJ-204 and EJ-309 proton and carbon light yield data relative to models generated using the SRIM library. For example, the model of Voltz et al. was further examined in a simultaneous fit of the EJ-204 proton and carbon light yield data using the PSTAR and MSTAR libraries. Fig. 8 provides a plot the EJ-204 carbon light yield data along with Voltz et al. models generated using the SRIM and PSTAR/MSTAR libraries. The model goodness of fit using PSTAR/MSTAR (![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) 2 = (15223 ± 1208)/40) is worse than that obtained using the SRIM stopping power tables (
2 = (15223 ± 1208)/40) is worse than that obtained using the SRIM stopping power tables (![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) 2 = (13171 ± 1272)/40) when the total scintillation efficiency is constrained. In both cases, the model does not provide reasonable agreement with the data, which introduces challenges in the comparison of the stopping power libraries.
2 = (13171 ± 1272)/40) when the total scintillation efficiency is constrained. In both cases, the model does not provide reasonable agreement with the data, which introduces challenges in the comparison of the stopping power libraries.
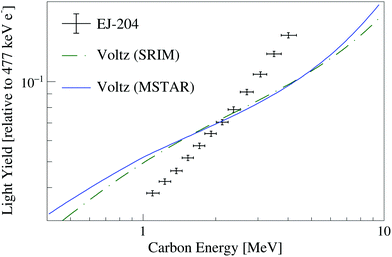 | ||
| Fig. 8 EJ-204 carbon light yield data along with Voltz et al. models obtained via a simultaneous fit of EJ-204 proton and carbon light yield using the SRIM and PSTAR/MSTAR stopping power tables. | ||
5 Conclusions
The ionization quenching effect was explored via the application of specific luminescence models to measured organic scintillator proton and carbon light yield data. The canonical Birks model and the model of Hong et al. failed to describe the proton light yield data over a broad energy range, whereas the models of Yoshida et al. and Voltz et al. consistently provided a reasonable description of the proton light yield. Simultaneous fits of the EJ-204 and EJ-309 proton and carbon light yield data demonstrated poor generalization of the models for carbon ions, suggesting that a more sophisticated treatment of the excitation and ionization density distributions is required. Improvements to the Voltz et al. model taking into account electron light nonlinearity and addressing the dependence of the delayed scintillation component on excitation and ionization density may provide a path forward. Track structure based models also hold promise for future work. The lack of experimental stopping power data in common scintillating media, particularly for carbon ions, and discrepancies in the carbon stopping power calculations from the SRIM49 and PSTAR/MSTAR52,53 libraries also introduces uncertainties in probing ionization quenching model performance. This work showcases the limitations of commonly used specific luminescence models and provides recommendations on a path forward for organic scintillator response modeling in basic science and a broad range of applications.Author contributions
Thibault Laplace: conceptualization, data curation, formal analysis, investigation, methodology, software, visualization, writing – original draft, and writing – reviewing & editing. Bethany Goldblum: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, supervision, writing – original draft, and writing – reviewing & editing. Joshua Brown: conceptualization, methodology, and writing – reviewing & editing. Glenn LeBlanc: formal analysis, methodology, software, and writing – reviewing & editing. Tianyue Li: formal analysis, investigation, software, and writing – reviewing & editing. Juan Manfredi: conceptualization, formal analysis, methodology, and writing – reviewing & editing. Erik Brubaker: funding acquisition, project administration, and writing – reviewing & editing.Conflicts of interest
The authors declare no commercial or associative interests that represent a conflict of interest in connection with the submitted work.Acknowledgements
The authors are grateful for discussions and expert advice from the Single Volume Scatter Camera collaboration. This work was performed under the auspices of the US Department of Energy by Lawrence Berkeley National Laboratory under Contract DE-AC02-05CH11231 and through the Nuclear Science and Security Consortium under Award Numbers DE-NA0003180 and DE-NA0003996. The project was funded by the US Department of Energy, National Nuclear Security Administration, Office of Defense Nuclear Nonproliferation Research and Development (DNN R&D). Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International Inc., for the US Department of Energy's National Nuclear Security Administration under contract DE-NA0003525. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the US Department of Energy or the United States Government.References
- C. J. Taylor, W. K. Jentschke, M. E. Remley, F. S. Eby and P. G. Kruger, Phys. Rev., 1951, 84, 1034–1043 CrossRef CAS.
- E. J. Zimmerman, Phys. Rev., 1955, 99, 1199–1203 CrossRef CAS.
- V. V. Verbinski, W. R. Burrus, T. A. Love, W. Zobel, N. W. Hill and R. Textor, Nucl. Instrum. Methods, 1968, 65, 8–25 CrossRef CAS.
- D. Smith, R. Polk and T. Miller, Nucl. Instrum. Methods, 1968, 64, 157–166 CrossRef CAS.
- M. Takada, K. Yajima, S. Kamada, H. Yasuda and T. Nakamura, Prog. Nucl. Sci. Technol., 2011, 2, 274–279 CrossRef.
- L. Reichhart, D. Akimov, H. M. Araújo, E. J. Barnes, V. A. Belov, A. A. Burenkov, V. Chepel, A. Currie, L. DeViveiros, B. Edwards, V. Francis, C. Ghag, A. Hollingsworth, M. Horn, G. E. Kalmus, A. S. Kobyakin, A. G. Kovalenko, V. N. Lebedenko, A. Lindote, M. I. Lopes, R. Lüscher, P. Majewski, A. J. Murphy, F. Neves, S. M. Paling, J. Pinto da Cunha, R. Preece, J. J. Quenby, P. R. Scovell, C. Silva, V. N. Solovov, N. J. T. Smith, P. F. Smith, V. N. Stekhanov, T. J. Sumner, C. Thorne and R. J. Walker, Phys. Rev. C: Nucl. Phys., 2012, 85, 065801 CrossRef.
- C. C. Lawrence, M. Febbraro, T. N. Massey, M. Flaska, F. Becchetti and S. A. Pozzi, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 759, 16–22 CrossRef CAS.
- F. Pino, L. Stevanato, D. Cester, G. Nebbia, L. Sajo-Bohus and G. Viesti, Appl. Radiat. Isot., 2014, 89, 79–84 CrossRef CAS PubMed.
- J. Iwanowska, L. Swiderski, T. Krakowski, M. Moszynski, T. Szczesniak and G. Pausch, Nucl. Instrum. Methods Phys. Res., Sect. A, 2015, 781, 44–49 CrossRef CAS.
- J. Brown, B. L. Goldblum, T. Laplace, K. Harrig, L. Bernstein, D. Bleuel, W. Younes, D. Reyna, E. Brubaker and P. Marleau, J. Appl. Phys., 2018, 124, 045101 CrossRef.
- T. Laplace, B. Goldblum, J. Brown, D. Bleuel, C. Brand, G. Gabella, T. Jordan, C. Moore, N. Munshi, Z. Sweger, A. Sweet and E. Brubaker, Nucl. Instrum. Methods Phys. Res., Sect. A, 2020, 954, 161444 CrossRef CAS.
- J. J. Manfredi, B. L. Goldblum, T. A. Laplace, G. Gabella, J. Gordon, A. O'Brien, S. Chowdhury, J. A. Brown and E. Brubaker, IEEE Trans. Nucl. Sci., 2020, 67, 434–442 CAS.
- R. Weldon, J. Mueller, P. Barbeau and J. Mattingly, Nucl. Instrum. Methods Phys. Res., Sect. A, 2020, 953, 163192 CrossRef CAS.
- J. Birks, The Theory and Practice of Scintillation Counting, Pergamon Press, New York, 1964, pp. 185–234 Search PubMed.
- B. von Krosigk, M. Chen, S. Hans, A. R. Junghans, T. Kögler, C. Kraus, L. Kuckert, X. Liu, R. Nolte, H. M. O'Keeffe, H. W. C. Tseung, J. R. Wilson, A. Wright, M. Yeh and K. Zuber, Eur. Phys. J. C, 2016, 76, 1–13 CrossRef CAS.
- S. Yoshida, T. Ebihara, T. Yano, A. Kozlov, T. Kishimoto, I. Ogawa, R. Hazama, S. Umehara, K. Mukaida, K. Ichihara, Y. Hirano, I. Murata, J. Datemichi and H. Sugimoto, Nucl. Instrum. Methods Phys. Res., Sect. A, 2010, 622, 574–582 CrossRef CAS.
- C. N. Chou, Phys. Rev., 1952, 87, 904–905 CrossRef CAS.
- J. Hong, W. Craig, P. Graham, C. Hailey, N. Spooner and D. Tovey, Astropart. Phys., 2002, 16, 333–338 CrossRef.
- R. Voltz, J. L. da Silva, G. Laustriat and A. Coche, J. Chem. Phys., 1966, 45, 3306–3311 CrossRef CAS.
- M. A. Norsworthy, A. Poitrasson-Rivière, M. L. Ruch, S. D. Clarke and S. A. Pozzi, Nucl. Instrum. Methods Phys. Res., Sect. A, 2017, 842, 20–27 CrossRef CAS.
- T. Pöschl, D. Greenwald, M. J. Losekamm and S. Paul, Nucl. Instrum. Methods Phys. Res., Sect. A, 2021, 988, 164865 CrossRef.
- J. B. Christensen and C. E. Andersen, Radiat. Meas., 2019, 124, 158–162 CrossRef CAS.
- Eljen Technology, Neutron/Gamma PSD Liquid Scintillator EJ-301, EJ-309, 2021.
- Eljen Technology, General Purpose Plastic Scintillator EJ-200, EJ-204, EJ-208, EJ-212, 2021.
- Eljen Technology, PSD Plastic Scintillator EJ-276 & EJ-276G, 2021.
- J. S. Carlson and P. L. Feng, Nucl. Instrum. Methods Phys. Res., Sect. A, 2016, 832, 152–157 CrossRef CAS.
- J. S. Carlson, P. Marleau, R. A. Zarkesh and P. L. Feng, J. Am. Chem. Soc., 2017, 139, 9621–9626 CrossRef CAS PubMed.
- J. B. Birks, Phys. Rev., 1951, 84, 364–365 CrossRef CAS.
- R. P. Steer, Can. J. Chem., 2017, 95, 1025–1040 CrossRef CAS.
- H. Paul, AIP Conf. Proc., 2013, 1525, 309–313 CrossRef CAS.
- P. Sigmund, in Nuclear Stopping, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 85–94 Search PubMed.
- W. Lichten, Phys. Rev., 1967, 164, 131–142 CrossRef CAS.
- S. G. Prussin, in Nuclear Physics for Applications, Wiley-VCH Verlag, 2007, ch. 14, pp. 525–538 Search PubMed.
- P. E. Gibbons, D. C. Northrop and O. Simpson, Proc. Phys. Soc., 1962, 79, 373–382 CrossRef CAS.
- F. Brooks, Nucl. Instrum. Methods, 1979, 162, 477–505 CrossRef CAS.
- T. A. Laplace, B. L. Goldblum, J. J. Manfredi, J. A. Brown, D. L. Bleuel, C. A. Brand, G. Gabella, J. Gordon and E. Brubaker, Phys. Rev. C: Nucl. Phys., 2021, 104, 014609 CrossRef CAS.
- T. Laplace, B. Goldblum, J. Bevins, D. Bleuel, E. Bourret, J. Brown, E. Callaghan, J. Carlson, P. Feng, G. Gabella, K. Harrig, J. Manfredi, C. Moore, F. Moretti, M. Shinner, A. Sweet and Z. Sweger, J. Instrum., 2020, 15, P11020–P11020 CrossRef CAS.
- J. de Haas, P. Dorenbos and C. van Eijk, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 537, 97–100 CrossRef CAS.
- J. T. M. de Haas and P. Dorenbos, IEEE Trans. Nucl. Sci., 2008, 55, 1086–1092 Search PubMed.
- G. Dietze and H. Klein, Nucl. Instrum. Methods Phys. Res., 1982, 193, 549–556 CrossRef CAS.
- J. Nattress and I. Jovanovic, Nucl. Instrum. Methods Phys. Res., Sect. A, 2017, 871, 1–7 CrossRef CAS.
- S. A. Payne, W. W. Moses, S. Sheets, L. Ahle, N. J. Cherepy, B. Sturm, S. Dazeley, G. Bizarri and W. S. Choong, IEEE Trans. Nucl. Sci., 2011, 58, 3392–3402 CAS.
- L. Swiderski, R. Marcinkowski, M. Moszynski, W. Czarnacki, M. Szawlowski, T. Szczesniak, G. Pausch, C. Plettner and K. Roemer, J. Instrum., 2012, 7, P06011–P06011 Search PubMed.
- A. Nassalski, M. Moszyński, A. Syntfeld-Każuch, L. Świderski and T. Szcześniak, IEEE Trans. Nucl. Sci., 2008, 55, 1069–1072 CAS.
- H. Wan Chan Tseung, J. Kaspar and N. Tolich, Nucl. Instrum. Methods Phys. Res., Sect. A, 2011, 654, 318–323 CrossRef.
- S. Trajmar, Science, 1980, 208, 247–255 CrossRef CAS PubMed.
- Particle Data Group, Atomic and Nuclear Properties of Materials for more than 350 materials, https://pdg.lbl.gov/2021/AtomicNuclearProperties/, 2021, Accessed: 2022-03-16.
- S. M. Seltzer and M. J. Berger, Int. J. Appl. Radiat. Isot., 1982, 33, 1189–1218 CrossRef CAS.
- J. F. Ziegler, M. D. Ziegler and J. P. Biersack, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1818–1823 CrossRef CAS.
- W. H. Bragg and R. Kleeman, London, Edinburgh Dublin Philos. Mag. J. Sci., 1905, 10, 318–340 CrossRef CAS.
- P. Feng, Private communcation.
- M. Berger, J. Coursey and M. Zucker, ESTAR, PSTAR, and ASTAR: Computer Programs for Calculating Stopping-Power and Range Tables for Electrons, Protons, and Helium Ions, https://physics.nist.gov/Star, 1999.
- H. Paul and A. Schinner, At. Data Nucl. Data Tables, 2003, 85, 377–452 CrossRef CAS.
- M. J. Berger, M. Inokuti, H. H. Andersen, H. Bichsel, D. Powers, S. M. Seltzer, D. Thwaites and D. E. Watt, J. ICRU, 1993, os25, 3 Search PubMed.
- R. Brun and F. Rademakers, Nucl. Instrum. Methods Phys. Res., Sect. A, 1997, 389, 81–86 CrossRef CAS.
- R. T. Birge, Phys. Rev., 1932, 40, 207–227 CrossRef.
- W. Verkerke and D. Kirkby, Statistical Problems in Particle Physics, Astrophysics and Cosmology, World Scientific, 2006, pp. 186–189 Search PubMed.
- J. F. Williamson, J. F. Dempsey, A. S. Kirov, J. I. Monroe, W. R. Binns and H. Hedtjärn, Phys. Med. Biol., 1999, 44, 857–871 CrossRef CAS PubMed.
- L. Onsager, Phys. Rev., 1938, 54, 554–557 CrossRef CAS.
- T. Ogawa, T. Yamaki and T. Sato, PLoS One, 2018, 13, 1–19 Search PubMed.
- T. Ogawa, Y. Hirata, Y. Matsuya and T. Kai, Sci. Rep., 2021, 11, 24401 CrossRef CAS PubMed.
- S. Kikuta, D. Sakata and S. Fukuda, Phys. Med., 2021, 89, 258–264 CrossRef PubMed.
- Y. Matsuya, T. Kai, T. Sato, T. Ogawa, Y. Hirata, Y. Yoshii, A. Parisi and T. Liamsuwan, Int. J. Radiat. Biol., 2022, 98, 148–157 CrossRef CAS PubMed.
- J. B. Christensen and C. E. Andersen, Phys. Med. Biol., 2018, 63, 195010 CrossRef PubMed.
- J. Kloppenburg and A. Flammersfeld, Z. Phys., 1966, 196, 424–432 CrossRef CAS.
- C. Sautter and E. Zimmerman, Phys. Rev., 1965, 140, A490 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma00388k |
| ‡ Present address: Department of Engineering Physics, Air Force Institute of Technology, Wright Patterson Air Force Base, OH, 45433, USA. |
| This journal is © The Royal Society of Chemistry 2022 |