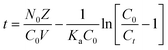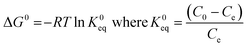DOI:
10.1039/D2MA00392A
(Paper)
Mater. Adv., 2022,
3, 8544-8556
Sol–gel synthesis of alumina gel@zeolite X nanocomposites for high performance water defluoridation: batch and column adsorption study†
Received
7th April 2022
, Accepted 27th September 2022
First published on 27th September 2022
Abstract
Fluoride content in groundwater above the permissible limit is a major concern worldwide due to its detrimental effects toward human beings. The development of a suitable adsorbent for water defluoridation with high efficiency still remains a great challenge. In this work, an alumina gel@zeolite X nanocomposite was prepared by modification of rice husk ash derived zeolite X with sol–gel derived alumina sol at 70 °C/2 h. The crystallinity of zeolite X and the presence of the Si–O–Al vibrational band in the nanocomposite material were confirmed by X-ray diffraction (XRD) and Fourier transform infrared spectroscopy (FTIR), respectively. The presence of the adsorbed hydroxyl (OH−) group was confirmed by an X-ray photoelectron spectroscopy (XPS) study indicating the binding energy (BE) at 533.2 eV of the O 1s spectra. During the adsorption process an electrostatic force of attraction and ion exchange mechanism occur between protonated hydroxyl/surface hydroxyl groups and fluoride ions (F−). The nanocomposite with a BET surface area of 257 m2 g−1 shows ≥99% fluoride removal for a 1–2 g L−1 adsorbent dose. In the batch study, the Langmuir model was found to be the best fitted adsorption isotherm showing the maximum adsorption capacity of 103.6 mg g−1 for the adsorbent doses of 0.5 g L−1, while in the column study, the bed depth service time (BDST) model shows an adsorption capacity of 2933.55 mg L−1.
Introduction
Fluoride levels in groundwater are due to the dissolution of rocks as well as hydrogeological and geothermal factors. Based on the concentration level, fluoride has both beneficial and detrimental effects on the human body. Fluoride concentration in the range of 0.8–1 mg L−1 as a micronutrient helps to prevent dental caries particularly in children. However, a fluoride level above a certain limit (>1.5 mg L−1) as prescribed by the World Health Organization (WHO) causes dental and skeletal fluorosis. Apart from this, fluoride toxicity has harmful effects on human beings causing headaches, joint pains, non-ulcer dyspepsia, polyuria, polydipsia, fatigue, anemiaetc, etc.1 Defluoridation of groundwater is becoming essential worldwide in terms of health concerns.
For fluoride remediation from groundwater, different methods are reported like coagulation and flocculation,2 precipitation using calcium containing ore,3 anion exchange resin,4 electrodialysis,5 membrane based technology,6,7 electrolysis,8 adsorption,9etc. Among all these processes, the adsorption technique is widely acceptable in terms of cost effectiveness, relatively low sludge disposal, technological viability and better efficiency. Selection of an effective adsorbent material is another key issue for defluoridation via the adsorption technique. The adsorbents are chosen based on their physico-chemical properties like porosity, surface area, favourable kinetic and transport properties, thermo-chemical stability, regenerative capacity and low cost. Ceramic based metal oxides (alumina, magnesia, calcia, iron oxide, etc.),10 layered double hydroxides,11–14 activated alumina,15,16 alumina dispersed charcoal,17 porous alumina,18etc. are generally used for water defluoridation.19 Zeolite can be used as a potential adsorbent for the removal of heavy metals. It is worth mentioning that zeolite without any modification shows a nominal adsorption efficiency within the range 25–50 mg g−1 towards the removal of heavy metals.20 Therefore, prior modification using different materials is needed towards water decontamination applications. Recently, Angaru et al. reported the removal of industrial effluents using sodium alginate (SA) and carboxymethylcellulose (CMC) entrapped with bimetallic magnetic (nano zero valent iron and nickel) fly ash zeolite (ZFN) with the composition of SA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CMC
CMC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ZFN at 1
ZFN at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (weight ratio).21,22 The adsorption capacities for Cu(II) and Cr(VI) were found to be 63.29 and 10.15 mg g−1, respectively. For defluoridation of water different modified zeolites as adsorbents have also been reported.23,24 Recently Rita et al. reported alum modified zeolite and its efficiency toward fluoride removal with a maximum adsorption capacity of 2.43 mg g−1.25 Yang et al. prepared Mn–Ti modified zeolite for water defluoridation resulting in a maximum adsorption capacity of 2.17 mg g−1.26 Aluminum coated natural zeolite was also found to be effective toward fluoride removal.27 However, the preparation of a zeolite based composite adsorbent via a simple route with a high adsorption capacity still remains a great challenge.
1 (weight ratio).21,22 The adsorption capacities for Cu(II) and Cr(VI) were found to be 63.29 and 10.15 mg g−1, respectively. For defluoridation of water different modified zeolites as adsorbents have also been reported.23,24 Recently Rita et al. reported alum modified zeolite and its efficiency toward fluoride removal with a maximum adsorption capacity of 2.43 mg g−1.25 Yang et al. prepared Mn–Ti modified zeolite for water defluoridation resulting in a maximum adsorption capacity of 2.17 mg g−1.26 Aluminum coated natural zeolite was also found to be effective toward fluoride removal.27 However, the preparation of a zeolite based composite adsorbent via a simple route with a high adsorption capacity still remains a great challenge.
With the above motivating factors, in the present study we have synthesized alumina gel@zeolite X nanocomposites using a sol–gel process followed by its structural and surface textural properties analysis. The synthesized material was utilized to investigate its fluoride ion uptake capacity from water by a batch and fixed bed column study. In a batch process, the performance of the adsorbent was studied by varying the adsorbate and adsorbent concentration, pH, temperature and competing ions effect, whereas in a column adsorption process breakthrough study was performed in terms of initial fluoride concentration, flow rate and bed height of the column. The adsorption behavioural pattern of the adsorbent for the removal of fluoride was accomplished by applying different kinetic models.
Materials and methods
Materials
Aluminium nitrate nonahydrate (>98%), ammonia solution (25 wt%), sodium hydroxide pellet (>97%), and sodium fluoride (>97%) were purchased from Merck, India while sodium aluminate (45% Na2O + 55% Al2O3) was procured from Sigma-Aldrich. Rice husk ash (95% SiO2) was collected from J. M. Biotech Pvt. Ltd, India.
Synthesis of alumina gel@zeolite X nanocomposite
Zeolite X was prepared from rice husk ash (RHA) as a silica source mentioned in our previous report.28 In a typical process, 7 g of RHA was digested in the presence of 5.25 M NaOH solution (50 mL) under stirring at 85 °C for 2 h. Sodium aluminate powder (4.4 g) in 20 mL water was introduced in the above digested dispersion followed by stirring for 20 min. The whole dispersion was hydrothermally treated at 90 °C for 6 h to obtain zeolite X powder. Alumina sol was prepared by slow addition of ammonia solution into 1 M aluminium nitrate solution under stirring at 60 °C for 8–10 h until a translucent sol was obtained at a pH value around 4–5. For the synthesis of the alumina gel@zeolite X composite, 5 g of as-prepared zeolite X was added into 100 mL of alumina sol under stirring at 70 °C for 2 h, and the pH was maintained at around 7 by the addition of ammonia solution yielding a viscous slurry mass. It was then dried at around 100 °C for 4–6 h to obtain an alumina gel@zeoliteX nanocomposite.
The synthesis procedure for the alumina gel@zeolite X nanocomposite is shown schematically in Fig. 1. In the first step, zeolite X was synthesized by digestion of rice husk ash (RHA) in the presence of sodium hydroxide and sodium aluminate. Under hydrothermal reaction at 90 °C for 6 h, the silicate of RHA extract interacts with sodium aluminate yielding zeolite X with the formation of an Al–O–Si network in which negatively charged AlO4 and SiO4 species are counterbalanced by non-bridging Na+ ions in the network structure. In the second step for the preparation of alumina sol, aluminium nitrate solution undergoes a hydrolysis and polymerization reaction in the presence of NH3 solution at 60 °C/8–10 h rendering alumina sol with an Al–O–Al network structure. At pH 4–5, the sol particles are protonated and interact with the Al–O–Si network of zeolite X particles through hydrogen bonding resulting in an alumina sol-zeolite X suspension. By adding further NH3 solution at 70 °C/2 h up to pH ∼ 7, a slurry viscous mass composing of alumina sol and zeolite X particles is formed. After heat treatment at 100 °C, the slurry is transformed into an alumina gel@zeolite X nanocomposite composed of adhered alumina nanoparticles surrounding micron sized zeolite X particles.
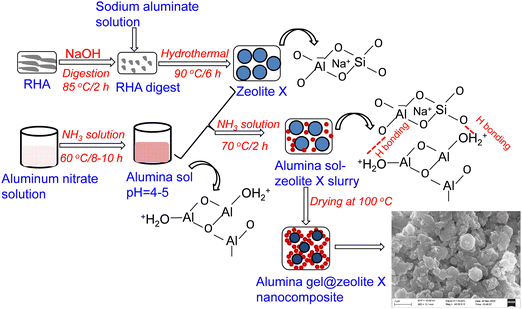 |
| | Fig. 1 A schematic diagram for the synthesis of alumina gel@zeolite X nanocomposites. | |
Characterization
The synthesized alumina gel@zeolite X nanocomposite was characterized by X-ray diffraction (XRD) operating with Philips X’Pert Pro (XRD, PW 3050/60) using CuKα radiation, X-ray photoelectron spectroscopy (XPS,ULVAC-PHI), Fourier Transform Infrared, FTIR (Spectrum two, PerkinElmer), N2 adsorption–desorption isotherms (Quantachrome (ASIQ MP)), field emission scanning electron microscopy (FESEM, Zeiss, SupraTM 35VP, Oberkochen, Germany) and transmission electron microscopy (TEM, Tecnai G2 30ST (FEI)). The particle size of a nanocomposite was also evaluated using a dynamic light scattering (DLS) method (Zetasizer, ZEN 3600, Malvern, UK).
Batch adsorption study
For fluoride ion adsorption in a batch study, different experimental parameters like adsorbate and adsorbent concentrations, contact time, pH, temperature and competing ions were varied. For recyclability and competing ions effect, an adsorbent dose of 2 g L−1 was used. Adsorption kinetic studies were performed by varying the initial fluoride concentration for each of the adsorbent dose i.e., 0.5, 1 and 2 g L−1. Fluoride measurement was carried out using an Ion Selective Electrode, ISE (Orion Versa Star 90). The amount of qe (mg g−1) was calculated using the following equation.where, C0 and Ce represent the initial and final concentration of adsorbate (mg L−1), respectively, whereas V and m are the solution volume (L) and mass (g) of the adsorbent, respectively.
For the regeneration study, 2 g L−1 of adsorbent after adsorption treatment with 5 mg L−1 fluoride (F−) solution for 120 min at pH 6.5, was treated with 0.1 M Na2CO3 solution under stirring conditions for 20 h. It was then filtered and washed with DI water followed by drying to obtain the regenerated sample.
Column adsorption study
A continuous column adsorption study was performed in a glass column of 3 cm ID and 60 cm height (Fig. S1, ESI†). Glass wool of 0.5 mm size was placed above the adsorbent. For the column study, different concentrations of influent fluoride solution (2, 5 and 8 mg L−1) were used for the downward flow. The flow rates were adjusted to 5, 10 and 15 mL min−1 and the bed heights were maintained as 5, 10 and 15 cm. At regular time intervals, the samples were collected from the exit of the column and fluoride ion concentrations were measured by ISE. It is worth noting that for the column study, downward flow was chosen because it helps prevent bed lifting of the column.
For operational and dynamic behaviour of the adsorption column, the breakthrough time and shape of the breakthrough curve was studied. For the breakthrough curve, Ct/C0 was plotted as a function of time, where C0 and Ct are the influent and effluent fluoride concentrations at time t, respectively. The amount of fluoride concentration adsorbed (qtotal) by the alumina gel@zeolite X nanocomposite in the column was determined from the area under the breakthrough curve of Cads (mg L−1) vs time (t) multiplied by the flow rate using the following equation:
| | 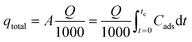 | (2) |
where,
Q (mL min
−1) is the flow rate,
A is the area under the breakthrough curve,
t is the total flow time and
Cads (mg L
−1) is the adsorbed concentration (
C0 −
Ct).
The amount of total fluoride ions introduced as influent in the column (mtotal) was determined by the following equation:
| | 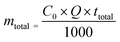 | (3) |
The removal percentage (
X%) of fluoride ions is calculated as follows:
| | 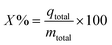 | (4) |
The desorption experiment was carried out by passing 0.1 M NaOH solution at a flow rate of 2 mL min−1 followed by washing with DI water until the pH of the effluent reached ∼6.5.
Results and discussion
Characterization of alumina gel@zeolite X nanocomposites
Fig. 2(a) shows the XRD pattern of the alumina gel@zeolite X nanocomposite with the appearance of characteristic peaks of zeolite X at 2θ values of 6.1, 11.7, 15.4, 20.1, 23.3, 26.6, 30.9 and 33.6 corroborating the hkl values of (111), (311), (331), (440), (533), (642), (157) and (664), respectively (JCPDF File # 39-218). However, no characteristic peaks of crystalline alumina polymorphs were noticed indicating its amorphous gel stage in the synthesized material which was confirmed by comparing with pure zeolite X crystalline peak obtained from our previous study.28 The FTIR spectrum of the material is shown in Fig. 2(b). The appearance of absorption bands at 3440 and 1640 cm−1 is due to OH stretching and bending vibrations, respectively. The Si–O–Si stretching and bending vibrations are located at 990 and 460 cm−1, respectively; whereas the Si–O–Al bending vibration is confirmed at 580 cm−1.29 The shifting of the stretching vibration of Si–O–Si to a lower wavenumber is attributed to a decrease in bond strength with internal hydrogen bonding as Si–O⋯HO–Si and Si–O⋯HO–Al.24 The absorption bands at 662 and 735 cm−1 are the signature of Si–O/Al–O S4R symmetric bending and stretching vibrations of zeolite X, respectively.30 It is to be noted that the sharp absorption peak at 1385 cm−1 is due to the presence of NO3− ions accumulated during the synthesis of alumina sol from an aluminium nitrate precursor.
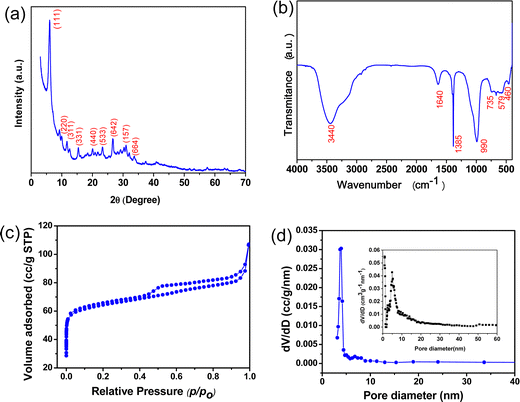 |
| | Fig. 2 (a) XRD pattern, (b) FTIR, (c) BET isotherm and (d) BJH pore size distribution (inset: pore size distribution by NLDFT) of the alumina gel@zeolite X nanocomposite. | |
The BET surface area of the alumina gel@zeolite X composite was calculated from a N2 adsorption–desorption isotherm (Fig. 2(c)). The total surface area was found to be 257 m2 g−1 comprising of a micropore surface area of 198 m2 g−1 and mesopore surface area of 59 m2 g−1. The BET isotherm shows typical IV type with a H3 hysteresis loop signifying mesopore characteristics above a relative pressure (p/p0) of 0.4. However, the horizontal plateau at the lower p/p0 range indicates the zeolitic micropores. The total pore volume of the sample was estimated to be 0.166 cm3 g−1. Fig. 2(d) shows the BJH pore size distribution curve with a pore size of 3.9 nm from the desorption data, and the inset corresponds to the pore size distribution obtained from the NLDFT method revealing cylindrical pores with pore sizes of 0.98, 2.6 and 4.8 nm. It is to be pointed out that unmodified zeolite X shows a surface area of 703 m2 g−1 with micropore and mesopore surface area values of 623 and 80 m2 g−1, respectively.28 Interestingly, the surface area decreased after modification of zeolite X with alumina gel. However, the adsorption efficiency of alumina gel modified zeolite X is higher than that of unmodified zeolite X (discussed in the next section). It is inferred that for adsorption of fluoride ions, the surface area of the adsorbent is not the sole factor but the presence of alumina gel with an abundance of surface hydroxyl ions plays a significant role.
XPS of the sample was performed to study the surface chemical analysis i.e., chemical and electronic states of the elements, binding energy of the specific element and the composition of the elements present in the sample. Fig. 3 shows the XPS results of the alumina gel@zeolite X nanocomposite: (a) full scan survey and (b) Al 2p, (c) Si 2p, (d) Na 1s and (e) O 1s deconvoluted spectra. The Al 2p spectrum is centred at 74.18 eV associated with the BE of the Al–O bond while the BE for Na 1s is found at 1072 eV. The deconvoluted Si 2p3/2 spectra with BE at 101.8 and 102.8 eV correspond to Si–O− (non-bridging) and Si–O–Si (bridging) bonds, respectively.31 Interestingly, the O 1s deconvoluted spectra show the BE at 530.2, 531.6 and 533.2 eV which signify the presence of lattice oxygen (42.4%), surface oxygen defects (49.2%) and adsorbed hydroxyl (OH−) groups (8.4%), respectively.32 The elemental composition (atomic%) of Al, Si, Na and O was found to be 19.15, 5.84, 0.33 and 74.67%, respectively. The Al and O contents are contributed from both the zeolite X and alumina gel components in the nanocomposite while Si and Na originate from zeolite X.
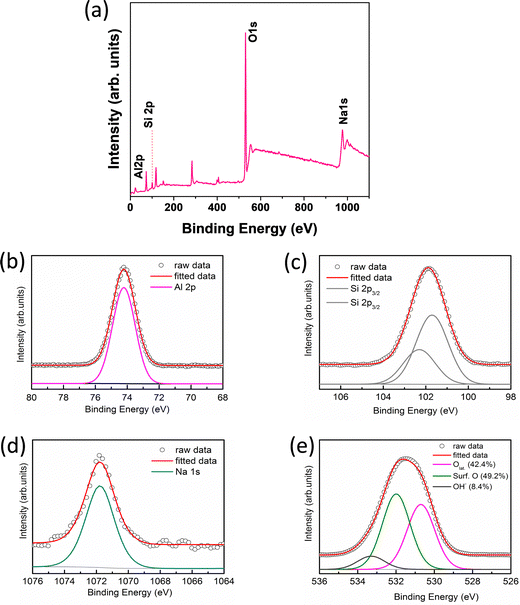 |
| | Fig. 3 XPS of (a) full scan survey, (b) Al 2p, (c) Si 2p, (d) Na 1s and (e) O 1s spectra of the alumina gel@zeolite X nanocomposite. | |
A microstructural study of the synthesized material is carried out by FESEM and TEM. Fig. 4a and b show FESEM micrographs with low and high magnification images. It is noticed that nanometer sized alumina gel particles (50–100 nm) with a high surface charge are aggregated surrounding the zeolite X particles. The gel particles with Al–O–Al linkage interacts with zeolite X via hydrogen bonding and/or electrostatic interaction. The TEM image of the alumina gel@zeolite X nanocomposite also confirms the adherence of nanometer sized aggregated alumina gel particles around the spheroid shaped zeolite X particles of size around 0.5–1 μm (Fig. 4c). The adhered alumina gel particles are indicated with a dotted red line. The particle size of the nanocomposite was also determined by a dynamic light scattering (DLS) method indicating an average particle size of 1.2 μm (Fig. S2, ESI†). The atomic% composition of the element present in the material is determined from EDS analysis (Fig. 4(d)). It reveals Al, Si, Na and O atomic% as 20.82, 11.30, 1.15 and 66.73%, respectively.
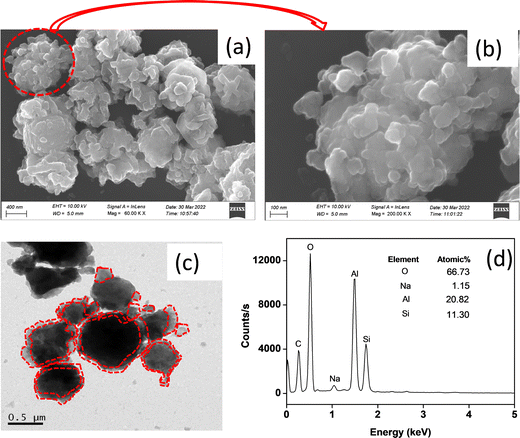 |
| | Fig. 4 (a) FESEM (low mag.), (b) FESEM (high mag.), (c) TEM images and (d) EDS analysis of the alumina gel@zeolite X nanocomposite. | |
Batch adsorption experiment
Effect of contact time.
Fig. 5(a) shows the % removal of F− ions with the contact time keeping the initial concentration of 5 mg L−1 (pH ∼ 6.5) at 30 °C for different adsorbent doses of 0.5, 1 and 2 g L−1. It is clear that at 120 min of adsorption, equilibrium is reached with a % adsorption of 96.2, 99 and 99.7% for adsorbent dosages of 0.5, 1 and 2 g L−1, respectively. Fig. S3(a) (ESI†) shows the change in adsorption capacity (qt) with time. It reveals that adsorption capacity is maximum for 0.5 g L−1 of the adsorbent dose which is in decreasing order with increasing the dose concentration.
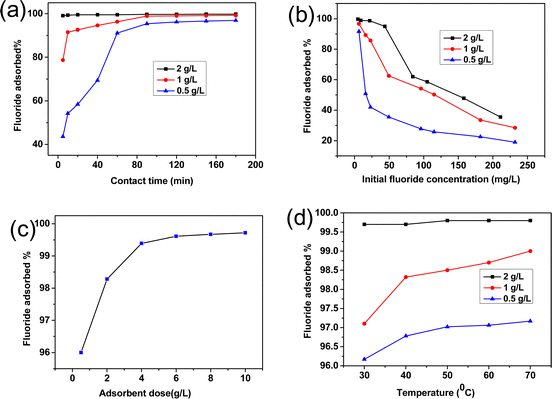 |
| | Fig. 5 Effect of (a) contact time, (b) initial fluoride ion concentration, (c) adsorbent dose and (d) temperature on the adsorption of F−ions by the alumina gel@zeolite X nanocomposite. | |
Effect of initial F− ion concentration.
Fig. 5(b) shows that with an increase in the initial F− concentration (pH ∼ 6.5), % adsorption decreases for different adsorbent dosages of 0.5, 1 and 2 g L−1 for 120 min contact time at 30 °C. The decreasing trend can be explained by the fact that with increasing F− ions, the adsorption sites get more screened by the accumulated adsorbate species with the saturation of co-ordination sites rendering less adsorption.33 Fig. S3(b) (ESI†) shows that the adsorption capacity (qe) increased sharply with adsorbate dose. The adsorption capacity becomes higher with decreasing adsorbent dose.
Effect of adsorbent dose.
Fig. 5(c) reveals that with an increase in adsorbent dose, the % removal increased sharply up to 4 g L−1 followed by reaching a saturation limit after 8 g L−1. It is worth noting that with an increase in adsorbent dose, the accessible adsorption sites are increased rendering a larger amount of fluoride uptake.34 However, the fluoride uptake capacity becomes saturated after a certain adsorbent dosage. The % adsorption is >99% for an adsorbent dose in the range of 4–10 g L−1. Fig. S3(c) (ESI†) shows that the adsorption capacity (qe) decreased with increasing adsorbent dose.
To compare the adsorption capacity (mg g−1) of alumina gel@zeolite X nanocomposite with respect to zeolite X for the removal of fluoride, the same experiment was carried out for 120 min with different adsorbent dosages (0.5, 1, 2 g L−1). The adsorption capacities for both the zeolite X and alumina gel@zeolite X were measured (Table S1, ESI†). It was found that the adsorption capacity values for zeolite X were 2.6, 0.70 and 0.55 mg g−1 for adsorbate dosages of 0.5, 1, and 2 g L−1, respectively, whereas those were 9.75, 5.02 and 2.40 mg g−1 for alumina gel@zeolite X nanocomposites, respectively. It is worth noting that modified zeolite (alumina gel@zeolite X) enhances the adsorption capacity for fluoride ion removal.
Effect of temperature.
To study the temperature effect on adsorption, the initial F− concentration was maintained at 5 mg L−1 for 120 min contact time at pH 6.5. Fig. 5(d) shows that the % adsorption increases significantly with an increase in temperature for 0.5 g L−1 to 2 g L−1 adsorbent dose. The increasing trend with temperature is attributed to the endothermic nature of the process, therefore showing better fluoride removal efficiency. Fig. S3(d) (ESI†) shows that adsorption capacity (qe) increased slightly with increasing temperature.
Effect of pH.
The pH of an aqueous solution plays a pivotal role in adsorption because positively charged hydrogen ions and negatively charged hydroxyl ions on the adsorbent surface interact with F− ions during adsorption. Fig. 6(a) shows that for a 0.5 g L−1 adsorbent dose, the % adsorption drastically falls after neutral pH. On the other hand, for 1–2 g L−1 adsorbent doses no significant change of % adsorption occurs through a wide range of pH. It is obvious that at higher pH, particularly for lower adsorbent doses (0.5 g L−1), the affluence of hydroxyl ions diminishes the adsorption of negatively charged fluoride ions rendering a decreasing trend in adsorption. However, pH has a minimal effect for a higher concentration of adsorbent which is important for practical applications. Fig. S3(e) (ESI†) shows the change in adsorption capacity (qe) with pH. The adsorption capacity is maximum for an adsorbent dose of 0.5 g L−1; however, it decreased significantly after pH ∼ 6.5. For an adsorbent dose of 1–2 g L−1, the adsorption capacity remains almost the same throughout a wide range of pH (3–10).
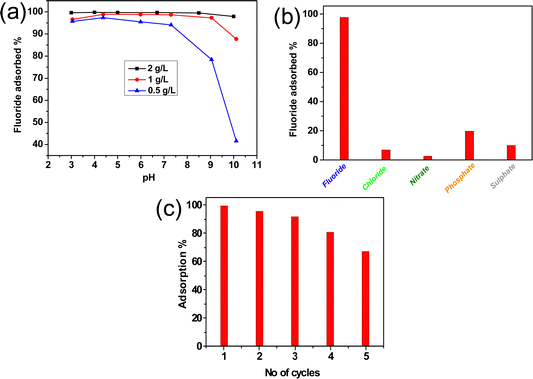 |
| | Fig. 6 Effect of (a) pH, (b) co-existing ion and (c) recyclability study for the adsorption of F−ions by the alumina gel@zeolite X nanocomposite. | |
Effect of co-existing anions.
The presence of various co-existing anions in natural groundwater may challenge the removal efficiency of the adsorbent material during adsorption of fluoride ions. The effect of co-existing anions like sulphate (SO42−), chloride (Cl−), nitrate (NO3−), and phosphate (PO43−) was studied. Fig. 6(b) reveals that the % adsorption of F− becomes 97.7% in the presence of Cl−, NO3−, PO43− and SO42− ions which contributed 6.9%, 2.6%, 19.7% and 9.88% adsorption, respectively. It is to be noted that the lyotropic series of different anions for Al3+ is in the order of F− > SO42− > Cl− > NO3− which reflects the adsorption affinities of these anions with the adsorbent containing Al3+.35 Due to the larger hydrated ionic radius of the phosphate ion compared to other competing ions, the phosphate ion has the tendency to form outer sphere complexes held by a long range electrostatic force rendering higher adsorption.36 Moreover, PO43− ions are readily hydrolyzed in solution rendering more hydroxyl ions, and the adsorption sites become negative. This causes electrostatic repulsion with F− ions. Thus, a negative effect is the result for adsorption of F− ions in the presence of PO43−ions.37
Regeneration study
To study the effectivity of the adsorbent, the regeneration study is one of the most important processes to be performed and generally an alkaline solution is chosen to fulfil this purpose as the hydroxyl ions show the ion exchange ability with fluoride ions. The regeneration process was continued for up to five cycles and the F− adsorption run was continued for each cycle. It is found that >90% adsorption is noticed up to the 3rd cycle followed by a gradual decrease in fluoride removal efficiency for the 4th and 5th cycles (Fig. 6(c)). During regeneration, the fluoride ions are desorbed by the adsorption of the hydroxyl ion. This is attributed to the fact that after regeneration with some cycles, some hydroxyl groups are entrapped at the adsorbent surface which could not be removed completely by washing with water. It inhibits to some extent further adsorption of fluoride ions due to anion–anion repulsion between entrapped OH− ions of the adsorbent and F− ions of adsorbate. Thus, removal efficiency starts decreasing gradually after the 4th cycle.
Adsorption kinetics
Pseudo first-order and pseudo-second order kinetics models were applied for an adsorption study. Table S2 (ESI†) presents the mathematical expressions and kinetic parameters obtained from the above models. For first order kinetics, qe and k1 (first order rate constant) can be determined from the intercept and slope, respectively obtained from the linear plot of ln(qe − qt) vs. t, while for second order kinetics, by plotting t/qtvs. t, the values of qe and k2 (second order rate constant) can be obtained from the intercept and slope, respectively. The linear fitting curves with the kinetic data are shown in Fig. S4(a) and (b) (ESI†) for pseudo-first-order and pseudo-second-order models, respectively. From the curves it is clear that pseudo-second-order model is best fitted with correlation co-efficient (R2) values close to unity, signifying chemisorption process of the adsorption. It is obvious that for different adsorbent doses, F− adsorption decreased with increasing adsorbent doses (Table S2, ESI†).
Adsorption isotherms
The equilibrium adsorption data for different adsorbent doses of 0.5, 1 and 2 g L−1 were fitted with Langmuir and Freundlich isotherm models. Table S3 (ESI†) represents the linear form of the two models along with the parameters calculated from the two isotherm curves. For the Langmuir Isotherm, the linear plot of Ce/qevs. Ce, the maximum adsorption capacity (qm(mg g−1)) and Langmuir adsorption constant (KL) can be determined from the slope and intercept, respectively (Fig. 7(a)); whereas, for the Freundlich isotherm, by plotting log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qevs. log
qevs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce, the adsorption intensity (nF) and KF (Freundlich constant) can be determined from the slope and intercept of the linear plot, respectively (Fig. 7(b)). The higher correlation coefficient R2 obtained from the Langmuir isotherm curve indicates the best fitting for the adsorption of F− removal. It is clear that there is an increasing trend of adsorption capacity with a decrease in adsorbent dose rendering a maximum adsorption of 104.16 mg g−1 for the adsorbent dose of 0.5 g L−1. Comparative data on maximum adsorption capacity, kinetics and rate constant for fluoride ion adsorption by alumina gel@zeolite X nanocomposite and reported adsorbents is presented in Table S4, (ESI†), which shows a better adsorption capacity of the present synthesized nanocomposite.
Ce, the adsorption intensity (nF) and KF (Freundlich constant) can be determined from the slope and intercept of the linear plot, respectively (Fig. 7(b)). The higher correlation coefficient R2 obtained from the Langmuir isotherm curve indicates the best fitting for the adsorption of F− removal. It is clear that there is an increasing trend of adsorption capacity with a decrease in adsorbent dose rendering a maximum adsorption of 104.16 mg g−1 for the adsorbent dose of 0.5 g L−1. Comparative data on maximum adsorption capacity, kinetics and rate constant for fluoride ion adsorption by alumina gel@zeolite X nanocomposite and reported adsorbents is presented in Table S4, (ESI†), which shows a better adsorption capacity of the present synthesized nanocomposite.
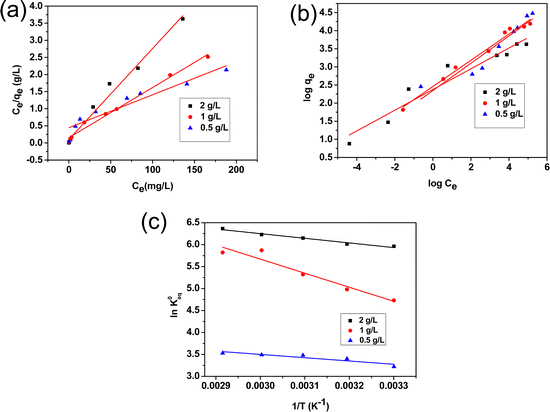 |
| | Fig. 7 (a) Langmuir and (b) Freundlich isotherms, and (c) plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K0eqversus 1/T for fluoride ions adsorption. K0eqversus 1/T for fluoride ions adsorption. | |
Thermodynamic parameters
The thermodynamic parameters such as Gibbs free energy (ΔG°), enthalpy (ΔH°) and entropy (ΔS°) were calculated using the following equations.38
| | 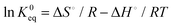 | (5) |
where K0eq is the equilibrium constant,39–41R represents the universal gas constant (8.314 J mol−1 K−1) and T is the temperature in Kelvin scale. The Gibb's free energy (ΔG°) values obtained for the adsorption process at all temperatures are listed in Table 1. ΔH° and ΔS° were determined from the slope and intercept of the plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K0eqvs. 1/T (Fig. 7(c)). The positive values of ΔH° indicate the adsorption process to be endothermic which was observed for all three adsorbent doses 0.5, 0.1 and 2 g L−1, and the value of ΔS° was also found to be positive for all three cases indicating the increasing trend of randomness of the adsorption process. The negative value of ΔG°indicates the process is spontaneous which in turn was found to be more negative with increasing temperature.42
K0eqvs. 1/T (Fig. 7(c)). The positive values of ΔH° indicate the adsorption process to be endothermic which was observed for all three adsorbent doses 0.5, 0.1 and 2 g L−1, and the value of ΔS° was also found to be positive for all three cases indicating the increasing trend of randomness of the adsorption process. The negative value of ΔG°indicates the process is spontaneous which in turn was found to be more negative with increasing temperature.42
Table 1 Thermodynamic parameters of fluoride adsorption for different adsorbent doses
| Adsorbent dose (g L−1) |
ΔH° (kJ mol−1) |
ΔS° (J mol−1 K−1) |
ΔG° (kJ mol−1) |
| 0.5 |
+6.225 |
+47.772 |
−8.249 at 303 K |
|
|
|
|
−8.726 at 313 K |
|
|
|
|
−9.204 at 323 K |
|
|
|
|
−9.682 at 333 K |
|
|
|
|
−10.160 at 343 K |
| 1.0 |
+26.603 |
+126.870 |
−11.575 at 303 K |
|
|
|
|
−12.835 at 313 K |
|
|
|
|
−14.095 at 323 K |
|
|
|
|
−15.355 at 333 K |
|
|
|
|
−16.615 at 343 K |
| 2.0 |
+8.878 |
+78.310 |
−14.840 at 303 K |
|
|
|
|
−15.629 at 313 K |
|
|
|
|
−16.413 at 323 K |
|
|
|
|
−17.196 at 333 K |
|
|
|
|
−17.979 at 343 K |
Adsorption mechanism
Fig. 8 shows schematically a proposed mechanism for the adsorption of F− ions by the alumina gel@zeolite X nanocomposite. Two possible routes for fluoride adsorption onto the adsorbent surface could take place: (i) electrostatic attraction between protonated hydroxyl groups and fluoride ions and (ii) ion exchange of fluoride ions with surface hydroxyl groups. To understand the adsorption mechanism, the point of zero charge (pHpzc) of the nanocomposite was studied varying pH conditions. The pHpzc was calculated by the familiar mass titration method43 varying different adsorbent concentrations (0.005 to 4 g) which were added to 10 mL of 0.01 N NaCl solution. The pH of the solution was plotted with the respective mass of the adsorbent. An asymptomatic value of pH was reached with increasing the mass of the adsorbent and the equilibrium pH was considered to be the pHpzc which was found to be around 5.7 (Fig. S5, ESI†). Nanoporous zeolite X with a high surface area enhances the adherence of nanometer size alumina gel particles in the adsorbent. Alumina gel contains a plethora of hydroxyl groups on its surface. In acidic medium, below the pHpzc, these hydroxyl groups are protonated which helps facilitate the adsorption of fluoride ions. However, in alkaline medium where the solution pH is greater than pHpzc some of the hydroxyl groups could be exchanged with fluoride ions, the rest of the hydroxyl groups take part in electrostatic repulsion with negatively charged fluoride ions. Thus, at higher pH the electrostatic repulsion prevails over the exchange capability between negatively charged hydroxyl and fluoride ions. It is worth mentioning that nanoporous zeolite with a high surface area and surface hydroxyl groups (protonated and non-protonated) of alumina gel play a significant role for the adsorption of fluoride ions from aqueous solution.
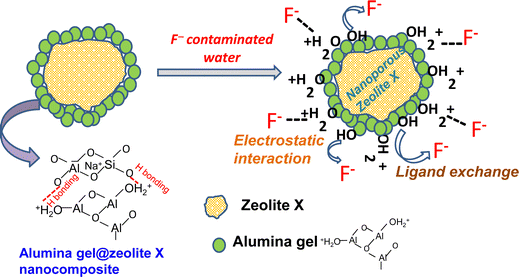 |
| | Fig. 8 A proposed mechanism for the adsorption of F− ions by the alumina gel@zeolite X nanocomposite. | |
Column adsorption study
Effect of initial fluoride concentration.
To study the effect of influent concentration on the breakthrough curve, the initial fluoride concentration was varied from 2 to 8 mg L−1 keeping the bed height at 10 cm and flow rate at 10 mL min−1. Fig. 9(a) shows the breakthrough curve obtained at different fluoride concentrations. This illustrates that the time taken for bed saturation was longer for a low initial fluoride concentration. At a lower concentration gradient, the required amount of fluorinated water was higher due to slower transportation with an increase in mass transfer interface causing a decrease in the mass transfer coefficient. As the initial fluoride concentration increases, the slope of the breakthrough curve becomes steeper, giving rise to a smaller breakthrough and exhaustion time. It was found that breakthrough time (Ct/C0 = 0.05) occurred after 94, 59 and 36 h for fluoride concentrations of 2, 5 and 8 mg L−1, respectively. This phenomenon could be explained by the fact that with increasing fluoride concentration, the number of available fluoride ions increases rendering rapid saturation of the bed column within a particular time span. At the saturation stage, the excess fluoride ions remain unadsorbed, and the uptake capacity of the column is reduced. It is worth mentioning that the mass diffusion process is affected by the concentration gradient of fluoride ions. The higher concentration gradient with higher driving force renders maximum mass transfer.
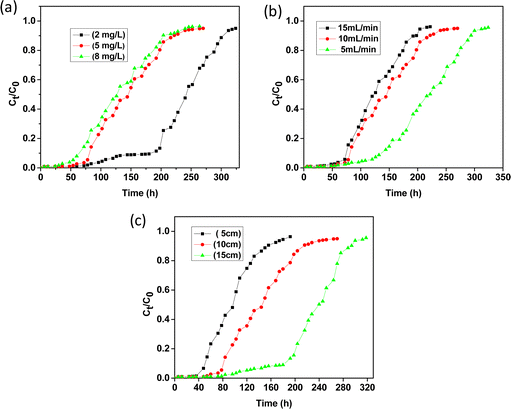 |
| | Fig. 9 Breakthrough curves for the adsorption of fluoride (a) at different initial concentrations, (b) at different flow rates and (c) at different bed heights. | |
Effect of flow rate.
The effect of flow rate was studied at 5, 10 and 20 mL min−1 keeping the bed height at 10 cm and the initial feed concentration at 5 mg L−1. The breakthrough curves at different flow rates are shown in Fig. 9(b). At a lower flow rate, the adsorption process was found to be very effective initially due to the availability of more adsorption sites which gradually decreases with time leading to less effective adsorption. It was observed that with increasing flow rate, the breakthrough curve becomes steeper giving rise to decreasing breakthrough time as well as adsorbed ion concentration. At a faster flow rate the solute could not reside in the column for a longer time and the fluoride ions leave the column before the adsorption equilibrium can be reached.44,45 Thus, at a lower flow rate, the contact time of the fluoride ions with the adsorbent materials becomes greater with high interparticle diffusion which causes the removal efficiency to be higher leading to a higher breakthrough and exhaustion time. The interparticle diffusion is the rate of diffusion after the early stages of adsorption determined by various parameters like mass of adsorbent, initial concentration of adsorbate and particle size.
Effect of bed height.
Fig. 9(c) shows the breakthrough curves obtained for the adsorption of fluoride ions with bed heights of 5, 10 and 15 cm in which 30, 60 and 90 g of adsorbent were loaded, respectively in the column, keeping the flow rate at 10 mL min−1 and initial feed concentration at 5 mg L−1. From the breakthrough profile it is observed that the curve for 5 cm bed height is steeper compared to 10 and 15 cm i.e., the breakthrough time and exhaustion time increase with increasing bed height. With increasing bed volume the adsorption sites also increase which leads to greater mass-transfer interface with a larger amount of fluoride ion adsorption. It is reported that with an increase in adsorbent volume in the column the diffusive mass-transfer overrides the axial dispersion of the adsorbate. Therefore, efficient removal of contaminants can be achieved by increasing the bed height which in turn will furnish more active sites for considerable adsorption.
Kinetic models on breakthrough curves
For evaluating the adsorption efficiency, an adsorption study on a fixed bed column is advantageous over the batch mode. An effective study of breakthrough curves could be explained by different mathematical models. In this study, the adsorption behavioural pattern of alumina gel@zeoliteX nanocomposites for the removal of fluoride was accomplished by applying different models like Adams–Bohart,46 Thomas,47 Yoon–Nelson48 and bed depth service time (BDST)49 for ascertaining the individual factors of the column along with the extrapolation of breakthrough curves.
Adams–Bohart model
The adsorption capacity of the adsorbent as well as the initial part of breakthrough curves can be predicted by the Adams–Bohart model. It also helps to predict the saturation concentration of the adsorbate. This model considers surface reaction theory by defining a relationship between Ct/C0 and t in a continuous arrangement in which instantaneous equilibrium is not attained. The mathematical expression of this model can be written as| | 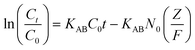 | (6) |
where, Ct and C0 indicate effluent and influent adsorbate concentration at time t, KAB (L mg−1 h−1) represents the Adams–Bohart rate constant, and N0 (mg L−1), Z (cm) and F (cm min−1) refer to the sorption capacity of the bed, bed height and linear velocity, respectively. By plotting ln(Ct/C0) against time (t), line fitting curves are obtained. The values of N0 and KAB are obtained from the slope and intercept of the linear plots, respectively. Fig. S6 (ESI†) shows linear regression analysis of the breakthrough curves using an Adams–Bohart model at different (a) concentrations, (b) flow rates and (c) bed heights. Table S5(a) (ESI†) summarizes the calculated parameters obtained from linear regression analysis. It is noticed that kinetic constant KAB increases with increasing flow rate and decreases with increasing initial fluoride concentration and bed height. It is to be noted that at the initial stages of the column adsorption study the entire system was occupied by the external mass transfer.50 Interestingly, the adsorption capacity N0 increases with increasing influent concentration and flow rate, but a reverse trend is observed for bed height which has been found to be similar by Mukherjee et al. in their study of biosorption of fluoride by an immobilized bead of NaA zeolite.51
Thomas model
Thomas model is one of the most acceptable and widely used models for the interpretation of performance theory of the adsorption process in fixed bed columns. The assumptions of this model mainly hold as: (1) the adsorption–desorption process follows Langmuir kinetics, (2) pseudo-second order reversible reaction kinetics and (3) negligible axial dispersion. The Thomas model is applicable where external resistance and intraparticle diffusion become insignificant throughout the mass transfer process.52 The linearized form of the Thomas model is shown in the following equation.| | 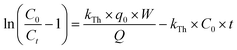 | (7) |
where, C0 (mg L−1) and Ct (mg L−1) correspond to inlet and outlet fluoride concentrations, respectively, kTh (L mg−1 h−1) is the Thomas rate constant, q0 (mg g−1) refers to equilibrium fluoride uptake per gm of adsorbent, W (g) indicates the mass of the adsorbent, Q (mL min−1) is the flow rate and t is the flow time. By plotting 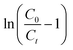 vs. time t, line fitting curves are obtained. The values of kTh and q0 can be obtained from the slope and intercept of the linearized plot, respectively. Fig. 10 shows linear regression analysis of the breakthrough curves using the Thomas model at different (a) concentrations, (b) flow rates and (c) bed heights. Table S5(b), ESI,† summarizes the calculated parameters obtained from linear regression analysis of the Thomas model. The Thomas rate constant kTh increases with increasing flow rate and decreases with influent fluoride concentration and bed height. It is attributed to mass transport resistance which decreases with an increase in flow rate and a decrease in the initial fluoride concentration and bed height of the packed column. The adsorption capacity, q0 (mg g−1) increases with increasing initial fluoride concentration and flow rate; however, it decreases with bed height. The higher regression coefficient (R2) values obtained from the Thomas model compared to other models fit well with the experimental data. It demonstrates that internal and external diffusions are not the rate limiting step.53
vs. time t, line fitting curves are obtained. The values of kTh and q0 can be obtained from the slope and intercept of the linearized plot, respectively. Fig. 10 shows linear regression analysis of the breakthrough curves using the Thomas model at different (a) concentrations, (b) flow rates and (c) bed heights. Table S5(b), ESI,† summarizes the calculated parameters obtained from linear regression analysis of the Thomas model. The Thomas rate constant kTh increases with increasing flow rate and decreases with influent fluoride concentration and bed height. It is attributed to mass transport resistance which decreases with an increase in flow rate and a decrease in the initial fluoride concentration and bed height of the packed column. The adsorption capacity, q0 (mg g−1) increases with increasing initial fluoride concentration and flow rate; however, it decreases with bed height. The higher regression coefficient (R2) values obtained from the Thomas model compared to other models fit well with the experimental data. It demonstrates that internal and external diffusions are not the rate limiting step.53
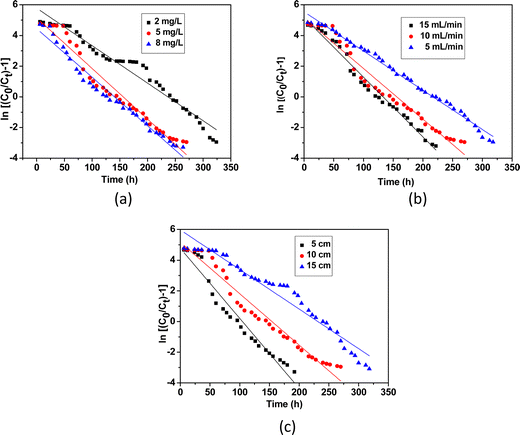 |
| | Fig. 10 Linear regression analysis of the breakthrough curves using the Thomas model at different (a) concentrations, (b) flow rates and (c) bed heights. | |
Yoon–Nelson model
A simple model was established by Yoon and Nelson for analysing the breakthrough performance of the column. The Yoon and Nelson model indicates that the decrease rate of adsorption probability for each adsorbate molecule is proportional to the adsorbate adsorption probability and adsorbate breakthrough probability. It is a simple model because it does not require any detailed data regarding the characteristics of the adsorbate, type of adsorbent or physical properties of the adsorption bed. The mathematical expression of this model is given as follows:| | 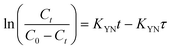 | (8) |
where, KYN represents the Yoon–Nelson rate constant, τ corresponds to the time required for 50% breakthrough, Ct (mg L−1) and C0 (mg L−1) are the effluent and initial fluoride concentrations, respectively and t (h) is the flow time. By plotting 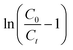 vs. time t, line fitting curves are obtained. The values of KYN and τ can be obtained from the slope and intercept of the linearized plot, respectively. Fig. S7 (ESI†) shows linear regression analysis of the breakthrough curves using the Yoon–Nelson model at different (a) concentrations, (b) flow rates and (c) bed heights. Table S5(c), ESI,† summarizes the calculated parameters obtained from linear regression analysis of the Yoon–Nelson model. The Yoon–Nelson rate constant KYN increases with increasing flow rate and initial fluoride concentration while it decreases with increasing bed height. It is to be noted that the values of KYN were found to decrease with increasing τ values upon increasing bed height which indicates that the adsorbate breakthrough was taking longer with increasing bed height. Meanwhile KYN was found to increase with increasing flow rate and initial fluoride concentration while their corresponding τ value shows a decreasing trend.
vs. time t, line fitting curves are obtained. The values of KYN and τ can be obtained from the slope and intercept of the linearized plot, respectively. Fig. S7 (ESI†) shows linear regression analysis of the breakthrough curves using the Yoon–Nelson model at different (a) concentrations, (b) flow rates and (c) bed heights. Table S5(c), ESI,† summarizes the calculated parameters obtained from linear regression analysis of the Yoon–Nelson model. The Yoon–Nelson rate constant KYN increases with increasing flow rate and initial fluoride concentration while it decreases with increasing bed height. It is to be noted that the values of KYN were found to decrease with increasing τ values upon increasing bed height which indicates that the adsorbate breakthrough was taking longer with increasing bed height. Meanwhile KYN was found to increase with increasing flow rate and initial fluoride concentration while their corresponding τ value shows a decreasing trend.
Bed depth service time (BDST) Model
The BDST model holds a simple relationship between bed depth and service time. This model helps anticipate the sustainability of the removal capacity of a certain amount of adsorbent material before the revival is required. The assumptions of this model are that the adsorption rate is proportional to the residual capacity of adsorbent as well as the concentration of the adsorbing solute. The BDST model neglects both the external and internal mass transfer resistance. A linear relationship between bed height (Z) and service time (t) was proposed by Hutchins49 which is as follows:| | 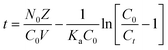 | (9) |
where Ka (L mg−1 h−1) is the rate constant, N0 (mg L−1) is the sorption capacity, C0 is the initial fluoride concentration (mg L−1), Cb is the effluent concentration (mg L−1) and V (cm h−1) corresponds to the linear velocity. The service time was selected as the time when Ct/C0 attains the value 0.05. By plotting service time (t) vs. bed depth (Z) at a flow rate of 19 mL min−1, the values of N0 and Ka can be calculated from the slope and the intercept of the plot, respectively (Fig. S8, ESI†). The linear plot with regression co-efficient (R2) 0.9974 indicates the validity of the BDST model with this column experiment. The BDST model parameters are shown in Table S5(d) (ESI†). The adsorption capacity (N0) and rate constant (Ka) were calculated as 2933.55 mg L−1 and 0.0430 L mg−1 h−1, respectively. The rate constant signifies the transfer rate from fluid to solid phases. For avoidance of breakthrough a short bed height is required for high Ka, and for a low Ka value the bed depth should be high.
Among various kinetic models for the column study, a better correlation with experimental data (R2) ranging from 0.95 to 0.99 is fitted for the Thomas, Yoon–Nelson and BDST models. The Thomas model with no external and internal dispersion limits is dependent on Langmuir adsorption–desorption energy following second-order reversible reaction kinetics. The Yoon–Nelson model is based on the assumption that adsorption rate is proportional to the rate of decrease in adsorption. The BDST model signifies that the rate of adsorption is maintained by the surface reaction between the adsorbate and unused capacity of the adsorbent.
Desorption and regeneration study
After the exhaustion point is reached in the fixed bed column experiment, the adsorbent alumina gel@zeolite X nanocomposite is regenerated by desorption of the adsorbed fluoride ions. Fig. S9 (ESI†) shows the desorption–regeneration cycle for fluoride removal. It was observed that the % removal of fluoride ions decreases as 99%, 90%, 78% and 69% for the 1st, 2nd, 3rd and 4th cycle, respectively. The adsorption capacity of the regenerated adsorbent decreased in each cycle which is attributed to the fact that a quantity of fluoride ions was trapped into the pores of the adsorbent and was difficult to remove during the desorption process, deactivating the adsorption of fluoride ions to some extent.
Conclusions
Alumina gel@zeolite X nanocomposites were prepared via a sol–gel process using alumina sol and hydrothermally synthesized zeolite X particles. A microstructural study confirmed that alumina gel particles (50–100 nm) are aggregated surrounding the micron sized (0.5–1 μm) zeolite X particles. The synthesized material was utilized for the adsorption of F− ions via batch and column studies. In a batch study, the % adsorption increases with contact time, adsorbent doses and temperature while it decreases with initial F− ion concentrations. pH has a minimal effect for adsorbent doses of 1–2 g L−1. Langmuir isotherm shows the best fitting for the adsorption of F− rendering a maximum adsorption of 104.16 mg g−1. The adsorption process is endothermic with a negative value of ΔG° indicating the spontaneity of the process. In the column study, the Thomas model fitted well with the experimental data and breakthrough curve prediction, demonstrating that internal and external diffusions are not the rate limiting step. The adsorption capacity, q0 (mg g−1) increased with increasing initial fluoride concentration and flow rate; however, it decreased with bed height. The present work is significant for the development of nanocomposite-based materials toward the removal of different contaminants from water.
Conflicts of interest
The authors have no conflicts of interest.
Acknowledgements
The authors would like to thank Science and Engineering Research Board (SERB), Government of India for funding the project (Sanction No. CRG/2020/00722) under the project No. GAP 0176. Dr. Suman Kumari Mishra, Director, CSIR-CGCRI is kindly acknowledged for giving permission to pursue the above work.
References
- S. Royand and G. Dass, Resour. Environ., 2013, 3, 53–58 Search PubMed.
- S. Dubey, M. Agrawal and A. B. Gupta, J. Mol. Liq., 2018, 266, 349–360 CrossRef CAS.
- L. Wang, Y. Zhang, N. Sun, W. Sun, Y. Hu and H. Tang, Minerals, 2019, 9, 511 CrossRef CAS.
- S. Singh, M. German, S. Chaudhari and A. K. Sengupta, J. Environ. Manage., 2020, 263, 110415 CrossRef CAS.
- Z. Amor, B. Bariou, N. Mameri, M. Taky, S. Nicolas and A. Elmidaoui, Desalination, 2001, 133, 215–223 CrossRef CAS.
- J. Shen and A. Schäfer, Chemosphere, 2014, 117, 679–691 CrossRef CAS.
- M. M. Damtie, Y. C. Woo, B. Kim, R. H. Hailemariam, K. D. Park, H. K. Shon, C. Park and J.-S. Choia, J. Environ. Manage., 2019, 251, 109524 CrossRef CAS.
- M. Aliaskari and A. I. Schafer, Water Res., 2021, 190, 116683 CrossRef CAS PubMed.
- A. Bhatnagar, E. Kumar and M. Sillanpaa, Chem. Eng. J., 2011, 171, 811–840 CrossRef CAS.
- P. Loganathan, S. Vigneswaran, J. Kandasamy and R. Naidu, J. Hazard. Mater., 2013, 1, 248–249 Search PubMed.
- P. Cai, H. Zheng, C. Wang, H. Ma, J. Hu, Y. Pu and P. Liang, J. Hazard. Mater., 2012, 100, 213–214 Search PubMed.
- S. Kundu and M. Naskar, J. Chem. Eng. Data, 2019, 64, 1594–1604 CrossRef.
- A. V. Radha, G. S. Thomas, V. Kamath, C. A. Antonyraj and S. Kannan, Bull. Mater. Sci., 2010, 33, 319–324 CrossRef.
- S. Kundu and M. K. Naskar, Mater. Adv., 2021, 2, 3600–3612 RSC.
- S. I. Alhassan, L. Huang, Y. He, L. Yan, W. Bichao and H. Wang, Crit. Rev. Environ. Sci.Technol., 2021, 51, 2051 CrossRef.
- M. L. Camacho, A. Torres, D. Sahaand and S. Deng, J. Colloid Interface Sci., 2010, 349, 307–313 CrossRef PubMed.
- E. Tchomgui-Kamga, V. Alonzo, C. P. Nanseu-Njiki, N. Audebrand, E. Ngameni and A. Darchen, Carbon, 2010, 48, 333–343 CrossRef.
- P. Singh, P. K. Maiti and K. Sen, Bull. Mater. Sci., 2020, 43, 56 CrossRef.
- S. Kundu, I. Hazra Chowdhuri, P. K. Sinha and M. K. Naskar, J. Chem. Eng. Data, 2017, 62, 2067–2074 CrossRef.
- L. F. Magalhães, G. R. da Silva and A. E. C. Peres, Adsorp. Sci. Technol., 2022, 4544104 Search PubMed.
- G. K. R. Angaru, Y. L. Choi, L. P. Lingamdinne, J. R. Koduru, J.-K. Yang, Y.-Y. Chang and R. R. Karri, Sci. Rep., 2022, 12, 3430 CrossRef PubMed.
- G. K. R. Angaru, L. P. Lingamdinne, Y. L. Choi, J. R. Koduru, J.-K. Yang and Y.-Y. Chang, Mater. Today Chem., 2021, 22, 100577 CrossRef.
- P. Ghomashi, A. Charkhi, M. Kazemeini and T. Yusefi, J. Water. Environ.
Nanotechnol., 2020, 5, 270–282 Search PubMed.
- M. K. Naskar, J. Asian Ceram. Soc., 2020, 8, 437–447 CrossRef.
- R. N. Tabi, F. O. Agyemang, K. M-Darkwa, E. K. Arthur, E. Gikunoo and F. Momade, Mater. Chem. Phys., 2021, 261, 124229 CrossRef.
- B. Yang, G. Sun, B. Quan, J. Tang, C. Zhang, C. Jia, Y. Tang, X. Wang, M. Zhao, W. Wang and B. Xiao, Water, 2021, 13(23), 3343 CrossRef.
- Y. D. Wirtu, F. Melak, M. Yitbarek and H. Astatkie, Groundwater Sustain. Dev., 2021, 12, 100525 CrossRef.
- A. Kumar and M. K. Naskar, J. Asian Ceram. Soc., 2019, 7, 355–360 CrossRef.
- B. Yan, S. Liu, M. L. Chastain, S. Yang and J. Chen, Sci. Rep., 2021, 11, 3316 CrossRef PubMed.
- K. Byrappa and B. V. Suresh Kumar, Asian J. Chem., 2007, 19(6), 4933–4935 Search PubMed.
- J. Abenojar, I. Colera, M. A. Martínez and F. Velasco, J. Adhes. Sci. Technol., 2010, 24, 1841–1854 CrossRef.
- M. Roy, S. Basak and M. K. Naskar, Phys. Chem. Chem. Phys., 2016, 18, 5253–5263 RSC.
- A. Teimouri, S. G. Nasab, S. Habibollahi, M. Fazel-Najafabadi and A. N. Chermahini, RSC Adv., 2015, 5, 6771–6781 RSC.
- N. Thakur, S. A. Kumar, D. N. Wagh, S. Das, A. K. Pandey, S. D. Kumara and A. V. R. Reddy, J. Hazard. Mater., 2012, 201–202, 193–201 CrossRef.
- C. Y. Hu, Sl Lo and W. H. Kuan, Water Res., 2003, 37, 4513–4523 CrossRef.
- M. S. Onyango, Y. Kojima, O. Aoyi, E. C. Bernardo and H. Matsuda, J. Colloid Interface Sci., 2004, 279, 341–350 CrossRef.
- P. Pillai, S. Dharaskar and M. Khalid, Chemosphere, 2021, 284, 131317 CrossRef PubMed.
- K. Narasimharao, L. P. Lingamdinne, S. Al-Thabaiti, M. Mokhtar, A. Alsheshri, S. Y. Alfaifi, Y.-Y. Chang and J. R. Koduru, J. Water Process Eng., 2022, 47, 102746 CrossRef.
- P. S. Kumar, P. S. A. Fernando and R. T. Ahmed, Chem. Eng. Commun., 2014, 201(11), 1526–1547 CrossRef.
- A. Rahmani-Sani, A. Hosseini-Bandegharaei, S. H. Hosseini, K. Kharghani, H. Zarei and A. Rastegar, J. Hazard. Mater., 2015, 286, 152–163 CrossRef PubMed.
- A. Saravanan, S. Jeevanantham, P. S. Kumar, S. Varjani, P. R. Yaashikaa and S. Karishma, Ind. Crops. Prod., 2020, 153, 112613 CrossRef.
- J. He, X. Cai, K. Chen, Y. Li, K. Z. Jin, F. Meng, N. Liu, X. Wang, L. Kong, X. Huang and J. Liu, J. Colloid Interface Sci., 2016, 484, 162–172 CrossRef PubMed.
- J. S. Noh and J. A. Schwarz, J. Colloid Interface Sci., 1989, 130, 157–162 CrossRef.
- P. G. Hiremath and T. Theodore, Periodica. Polytechnol. Chem. Eng., 2017, 61, 188–199 CrossRef.
- S. Kudari, Int. J. Adv. Res. Pub., 2017, 1, 174–178 Search PubMed.
- G. C. Bohart and E. Q. Adams, J. Am. Chem. Soc., 1920, 42(3), 523–544 CrossRef.
- H. C. Thomas, J. Am. Chem. Soc., 1944, 66, 1664–1666 CrossRef CAS.
- Y. N. Yoon and J. H. Nelson, J. Am. Ind. Hyg., 1984, 45, 509 CrossRef CAS.
- R. A. Hutchins, Chem. Eng., 1973, 80, 133 CAS.
- M. Jaroniec, Surf. Sci., 1975, 50, 553–564 CrossRef CAS.
- S. Mukherjee, A. A. Khan, S. Barman and G. Halder, Environ. Prog. Sustain. Energy, 2020, 39, e13456 Search PubMed.
- A. A. Ahmad and B. H. Hameed, J. Hazard. Mater., 2010, 175, 298–303 CrossRef CAS.
- C. Murutu, M. S. Onyango, A. Ochieng and F. Otieno, Water. S.A., 2012, 38(2), 279–286 CAS.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Milan Kanti
Naskar
and
Milan Kanti
Naskar
 *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CMC
CMC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ZFN at 1
ZFN at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (weight ratio).21,22 The adsorption capacities for Cu(II) and Cr(VI) were found to be 63.29 and 10.15 mg g−1, respectively. For defluoridation of water different modified zeolites as adsorbents have also been reported.23,24 Recently Rita et al. reported alum modified zeolite and its efficiency toward fluoride removal with a maximum adsorption capacity of 2.43 mg g−1.25 Yang et al. prepared Mn–Ti modified zeolite for water defluoridation resulting in a maximum adsorption capacity of 2.17 mg g−1.26 Aluminum coated natural zeolite was also found to be effective toward fluoride removal.27 However, the preparation of a zeolite based composite adsorbent via a simple route with a high adsorption capacity still remains a great challenge.
1 (weight ratio).21,22 The adsorption capacities for Cu(II) and Cr(VI) were found to be 63.29 and 10.15 mg g−1, respectively. For defluoridation of water different modified zeolites as adsorbents have also been reported.23,24 Recently Rita et al. reported alum modified zeolite and its efficiency toward fluoride removal with a maximum adsorption capacity of 2.43 mg g−1.25 Yang et al. prepared Mn–Ti modified zeolite for water defluoridation resulting in a maximum adsorption capacity of 2.17 mg g−1.26 Aluminum coated natural zeolite was also found to be effective toward fluoride removal.27 However, the preparation of a zeolite based composite adsorbent via a simple route with a high adsorption capacity still remains a great challenge.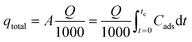
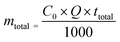
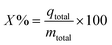



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qevs. log
qevs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce, the adsorption intensity (nF) and KF (Freundlich constant) can be determined from the slope and intercept of the linear plot, respectively (Fig. 7(b)). The higher correlation coefficient R2 obtained from the Langmuir isotherm curve indicates the best fitting for the adsorption of F− removal. It is clear that there is an increasing trend of adsorption capacity with a decrease in adsorbent dose rendering a maximum adsorption of 104.16 mg g−1 for the adsorbent dose of 0.5 g L−1. Comparative data on maximum adsorption capacity, kinetics and rate constant for fluoride ion adsorption by alumina gel@zeolite X nanocomposite and reported adsorbents is presented in Table S4, (ESI†), which shows a better adsorption capacity of the present synthesized nanocomposite.
Ce, the adsorption intensity (nF) and KF (Freundlich constant) can be determined from the slope and intercept of the linear plot, respectively (Fig. 7(b)). The higher correlation coefficient R2 obtained from the Langmuir isotherm curve indicates the best fitting for the adsorption of F− removal. It is clear that there is an increasing trend of adsorption capacity with a decrease in adsorbent dose rendering a maximum adsorption of 104.16 mg g−1 for the adsorbent dose of 0.5 g L−1. Comparative data on maximum adsorption capacity, kinetics and rate constant for fluoride ion adsorption by alumina gel@zeolite X nanocomposite and reported adsorbents is presented in Table S4, (ESI†), which shows a better adsorption capacity of the present synthesized nanocomposite.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K0eqversus 1/T for fluoride ions adsorption.
K0eqversus 1/T for fluoride ions adsorption.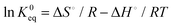
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K0eqvs. 1/T (Fig. 7(c)). The positive values of ΔH° indicate the adsorption process to be endothermic which was observed for all three adsorbent doses 0.5, 0.1 and 2 g L−1, and the value of ΔS° was also found to be positive for all three cases indicating the increasing trend of randomness of the adsorption process. The negative value of ΔG°indicates the process is spontaneous which in turn was found to be more negative with increasing temperature.42
K0eqvs. 1/T (Fig. 7(c)). The positive values of ΔH° indicate the adsorption process to be endothermic which was observed for all three adsorbent doses 0.5, 0.1 and 2 g L−1, and the value of ΔS° was also found to be positive for all three cases indicating the increasing trend of randomness of the adsorption process. The negative value of ΔG°indicates the process is spontaneous which in turn was found to be more negative with increasing temperature.42

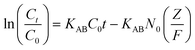
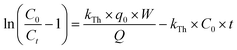
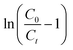 vs. time t, line fitting curves are obtained. The values of kTh and q0 can be obtained from the slope and intercept of the linearized plot, respectively. Fig. 10 shows linear regression analysis of the breakthrough curves using the Thomas model at different (a) concentrations, (b) flow rates and (c) bed heights. Table S5(b), ESI,† summarizes the calculated parameters obtained from linear regression analysis of the Thomas model. The Thomas rate constant kTh increases with increasing flow rate and decreases with influent fluoride concentration and bed height. It is attributed to mass transport resistance which decreases with an increase in flow rate and a decrease in the initial fluoride concentration and bed height of the packed column. The adsorption capacity, q0 (mg g−1) increases with increasing initial fluoride concentration and flow rate; however, it decreases with bed height. The higher regression coefficient (R2) values obtained from the Thomas model compared to other models fit well with the experimental data. It demonstrates that internal and external diffusions are not the rate limiting step.53
vs. time t, line fitting curves are obtained. The values of kTh and q0 can be obtained from the slope and intercept of the linearized plot, respectively. Fig. 10 shows linear regression analysis of the breakthrough curves using the Thomas model at different (a) concentrations, (b) flow rates and (c) bed heights. Table S5(b), ESI,† summarizes the calculated parameters obtained from linear regression analysis of the Thomas model. The Thomas rate constant kTh increases with increasing flow rate and decreases with influent fluoride concentration and bed height. It is attributed to mass transport resistance which decreases with an increase in flow rate and a decrease in the initial fluoride concentration and bed height of the packed column. The adsorption capacity, q0 (mg g−1) increases with increasing initial fluoride concentration and flow rate; however, it decreases with bed height. The higher regression coefficient (R2) values obtained from the Thomas model compared to other models fit well with the experimental data. It demonstrates that internal and external diffusions are not the rate limiting step.53

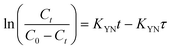
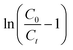 vs. time t, line fitting curves are obtained. The values of KYN and τ can be obtained from the slope and intercept of the linearized plot, respectively. Fig. S7 (ESI†) shows linear regression analysis of the breakthrough curves using the Yoon–Nelson model at different (a) concentrations, (b) flow rates and (c) bed heights. Table S5(c), ESI,† summarizes the calculated parameters obtained from linear regression analysis of the Yoon–Nelson model. The Yoon–Nelson rate constant KYN increases with increasing flow rate and initial fluoride concentration while it decreases with increasing bed height. It is to be noted that the values of KYN were found to decrease with increasing τ values upon increasing bed height which indicates that the adsorbate breakthrough was taking longer with increasing bed height. Meanwhile KYN was found to increase with increasing flow rate and initial fluoride concentration while their corresponding τ value shows a decreasing trend.
vs. time t, line fitting curves are obtained. The values of KYN and τ can be obtained from the slope and intercept of the linearized plot, respectively. Fig. S7 (ESI†) shows linear regression analysis of the breakthrough curves using the Yoon–Nelson model at different (a) concentrations, (b) flow rates and (c) bed heights. Table S5(c), ESI,† summarizes the calculated parameters obtained from linear regression analysis of the Yoon–Nelson model. The Yoon–Nelson rate constant KYN increases with increasing flow rate and initial fluoride concentration while it decreases with increasing bed height. It is to be noted that the values of KYN were found to decrease with increasing τ values upon increasing bed height which indicates that the adsorbate breakthrough was taking longer with increasing bed height. Meanwhile KYN was found to increase with increasing flow rate and initial fluoride concentration while their corresponding τ value shows a decreasing trend.