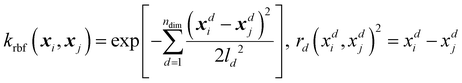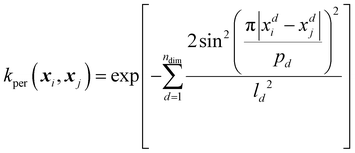Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
ICHOR: a modern pipeline for producing Gaussian process regression models for atomistic simulations†
Matthew J.
Burn
and
Paul L. A.
Popelier
 *
*
Department of Chemistry, The University of Manchester, Manchester, M13 9PL, UK. E-mail: pla@manchester.ac.uk; Tel: +44 161 3064511
First published on 24th October 2022
Abstract
Current practical use of machine learning is more involved than model architecture and the optimisation technique itself. It is very important that the modern machine learning method is supported with a robust set of tools for the creation and manipulation of data sets. ICHOR is one such tool designed for the purpose of creating fast and accurate atomistic Gaussian process regression (GPR) models through the use of active learning. ICHOR operates in the context of FFLUX, a fully polarisable force field based on the energies and multipole moments of quantum topological atoms. ICHOR interacts with the in-house GPR program FEREBUS for training, and with DL_FFLUX (derived from DL_POLY) for geometry optimisation and molecular simulation. ICHOR utilises the latest technologies in HPC cluster management to produce GPR models reliably at scale.
1. Introduction
Machine learning (ML) has become a vital part of computational chemistry across a range of disciplines from studying the properties of materials1–3 to generating new drug candidates.4–6 Throughout the years, ML has increased in popularity and complexity, and provides a wide range of chemists with a diverse toolset for tackling some of the most difficult problems faced today.One field within computational chemistry in which ML is becoming ever more commonplace is the design of new force fields.7–12 Traditionally, force fields have consisted of equations derived from classical mechanics and parameterised using empirical or ab initio data.13–21 It is known that the classical equations used in common classical force fields have common downfalls when it comes to nuclear quantum effects22,23 as well as many-body effects.24–28 ML is perfectly suited to combat these issues by learning such phenomena from the data itself whilst maintaining the speed we have come to expect from modern day force fields.
A ML model generally consists of a series of inputs and outputs known as the training set. The quality of the training set, combined with the architecture of the ML model, determines the performance of the model. How these data are generated and manipulated is a domain-specific problem but becomes an essential step when dealing with larger and larger models. A ML pipeline is the name given to the process of creating a ML model from start to finish. It is generally an automated process enabling the production of large and complex ML models.
ML pipelines are a vital stage within the design process of making models suitable for use in simulations. A pipeline, and furthermore a pipelining application, enables the production of reliable models in a reproducible way due to the standardisation of how each data point is produced and processed. Automating such an application removes the likelihood of user error and allows for data acquisition and manipulation at much greater scales than manual processes would allow. There are many examples of pipeline automation applications within the machine learning literature, both within chemistry and beyond.29–32
Past studies33–36 from our group have used the pipelining tool called GAIA,12 which is a Perl program written to automate the generation and manipulation of Quantum Theory of Atoms in Molecules (QTAIM)37,38 data (i.e. atomic energies and multipole moments) to produce atomistic Gaussian process regression39 (GPR) models although we initially constructed40 neural net models, now some time ago. GAIA was an essential tool for creating such atomistic models enabling pioneering research within the molecular simulation domain.11,41,42 Whilst GAIA was instrumental in outlining the pipeline for the creation of atomistic models, the models produced by GAIA were performed statically. In other words, if the predictive performance of the model produced was not accurate enough, there was little that could be done other than regenerating more data and retrain a new model. For this reason, a new pipelining application was developed called ICHOR, which was designed from the ground up with active learning in mind.43
Active learning is a broad term used in ML to describe an algorithm designed to iteratively improve a training set using unlabelled data. Active learning44 provides a pathway to improve a model if the current model does not meet the expected accuracy. ICHOR implements several active learning methods alongside its automation tools necessary to generate such large amounts of data in a time-efficient manner.
This paper outlines the features implemented in ICHOR to allow for the reliable creation of robust GPR models, validated for use in atomistic simulations. ICHOR is a comprehensive toolkit providing interfaces to many external programs enabling novice users to create models quickly and providing tools to experienced users to enhance their productivity.
2. Point generation
2.1 Initial point generation
The first step in producing an atomistic GPR model is to generate a set of points that describes the system to be modelled. ICHOR implements an interface to several point generation methods, the three most common being: (i) ab initio MD (AIMD), (ii) classical MD, or (iii) normal mode sampling. Each method has benefits and drawbacks: AIMD sampling produces chemically accurate (given its first principle nature) geometries but at great computational cost,45–47 classical MD simulations reduces the chemical accuracy (given its force field nature) of the geometries produced but decreases the computational cost allowing for more geometries to be produced, while normal mode sampling is even faster still.ICHOR provides interfaces to three external programs intended for point generation:
• CP2K48 – AIMD Software.
• AMBER49 – Classical Force Field.
• Tyche50 – Normal Mode Sampler.
Full details on the interfaces to each of these programs may be found in the ESI.† Note that any point generation method may be used with ICHOR and the programs detailed here are only those that are included in ICHOR's automated workflow.
2.2 Training set production
Once the initial set of (input) geometries has been produced it needs to be split into a training, sample and test set. Creating a good training set is a difficult task because it is important to describe the entire space in order to get good predictions from your model. It is also important to keep the number of training points to a minimum in order to limit (i) the amount of time spent calculating the true values for each training point, (ii) the time spent to train the model, and (iii) the time taken to predict values using the model in a production setting.ICHOR allows for several methods of set generation to be defined and combined. When initialising the training set, a common method is to combine the so-called min–max–mean method with a number of random points. The min–max–mean method takes a set of input geometries and calculates the features of the training set using the methods described in Section 3.2. Subsequently the points corresponding to the minimum, maximum and (closest to the) mean value for each feature (i.e. in each dimension) are added to the training set. If the number of features is denoted nf then the resulting training set will have an initial size of 3nf, which scales linearly with respect to the number of features. For smaller molecules, which have relatively few features, the min–max–mean method alone suffices for training set initialisation. However, when moving to larger molecules, there is much more space to be filled in between the minimum and maximum of each feature. For this reason, for larger systems, random points are added to partially fill the void producing an improved initial training set for active learning. After generating the training set, it is common practice to initialise the sample set and test set from the remaining points selected at random from the initial set of geometries.
3. Generating training data
3.1 ALF determination
The geometries in the training set are often represented as a set of Cartesian coordinates. Cartesian coordinates are a N × 3 set of points that are described with respect to a global axis system. This means that translating and rotating the geometry will affect the coordinates without changing the system's geometry. Because this is undesirable for a set of machine learning features we convert the Cartesian coordinates to a set of features expressing internal geometry before inputting them to the GPR model. The features used by the ICHOR pipeline are calculated using the Atomic Local Frame51 (ALF). The ALF replaces the global axis system with one that is local to the atom the features are being calculated for. Given an origin atom A, the ALF is defined by two atoms, Ax and Axy. Ax is the atom defining the x-axis for the ALF and Axy is the atom defining the xy-plane. The z-axis is then defined using a right-handed axis system.To define Ax and Axy given A, the Cahn–Ingold–Prelog rules are used, setting Ax to the highest priority atom and Axy to the atom with the second highest priority. To implement the Cahn–Ingold–Prelog rules, first the connectivity of the system must be defined, which is done by ICHOR using an adjacency matrix. The calculation of the adjacency matrix D is carried out with eqn (1),
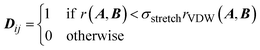 | (1) |
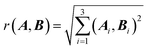 | (2) |
| rVDW(A, B) = dVDW(A) + dVDW(B) | (3) |
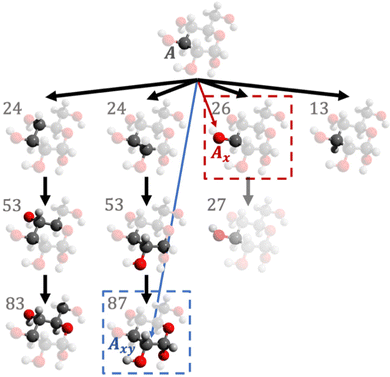
The adjacency matrix enables the construction of a molecular graph and the determination of an ALF. Previous work utilised a recursive algorithm to determine the ALF for a given atom. An iterative approach was designed for ICHOR to remove some of the potential problems with stack overflow errors deriving from recursive routines. ICHOR's ALF determination algorithm is an implementation of the breadth-first search (BFS) algorithm designed to implement the Cahn–Ingold Prelog rules. Fig. 1 shows an example of the BFS algorithm in practice.
As can be seen from Fig. 1, the BFS algorithm iteratively increases the depth of the search once all atoms connected to the previous search level have been investigated and priorities calculated. The priority of a particular atom is the sum of the atomic masses for each atom in the molecular graph within a certain depth assigned by the current iteration of the BFS algorithm,
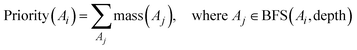 | (4) |
The result of the first search (shown in red in Fig. 1) assigns the Ax atom. The same BFS algorithm is used to assign the second highest priority atom (shown in blue) by removing the highest priority atom from the search and assigning the second highest priority to the highest priority atom of this second search. If the origin atom only has a single connected atom (and is therefore already assigned as the highest priority atom), the origin of the second BFS is set to the connected atom, and again the second highest priority atom is set to the highest priority of this second BFS.
A final point concerns the stability of the adjacency matrix in response to small perturbations of the atomic positions. In fact, one test case was encountered, during the development of the ALF determination algorithm, of a highly branched system where a small rotation of a methyl group led to a change in the ALF. However, to protect the user against this scenario they must specify a reference geometry that will produce the desired adjacency matrix or explicitly define the ALF directly. The ALF is then used for every geometry rather than recalculating the ALF for each geometry, which could lead to issues with inconsistent adjacency matrices. The ALF that is used for feature calculation is then written to the model file to be used for future calculations. The model file contains all hyperparameters and training data used for prediction. It is important for the current algorithm to be robust because thousands and thousands of ALFs typically need to be calculated, and this should be done correctly.
3.2 ALF feature calculation
Once the ALF for each atom in a system has been determined, the ALF can be used on any configuration of the same system in order to calculate the input features for the GPR models. The features used in the force field FFLUX are geometric features deriving only from the Cartesian coordinates of the original system. The first three features correspond to the atoms in the ALF for a given atom (A, Ax and Axy). The first feature (Ax) is the distance between the origin atom (A) and the atom defining the x-axis (Ax). The second feature (Axy) is the distance from the origin atom and the atom defining the xy-plane (Axy). The third feature (χA) is the angle subtending the atom defining the x-axis (Ax), the origin atom (A) and the atom defining the xy-plane (Axy). The remaining features are calculated as spherical polar coordinates of every non-ALF atom with respect to the axis system defined by the ALF. Formally we can express the above as follows,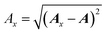 | (5) |
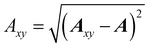 | (6) |
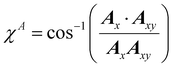 | (7) |
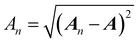 | (8) |
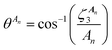 | (9) |
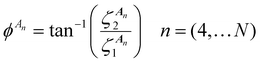 | (10) |
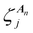 is the jth local atomic Cartesian coordinate of atom An calculated by rotating the global atomic Cartesian coordinate
is the jth local atomic Cartesian coordinate of atom An calculated by rotating the global atomic Cartesian coordinate 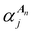 using the rotation matrix C. As mentioned previously, the ALF spherical features are calculated using the ALF axis system. Therefore the Cartesian coordinates, ai, must first be rotated from the global frame to the atomic local frame resulting in the ALF Cartesian coordinates, ζj. The rotation is performed using a rotation matrix C, the rows of which (Ci) are calculated using
using the rotation matrix C. As mentioned previously, the ALF spherical features are calculated using the ALF axis system. Therefore the Cartesian coordinates, ai, must first be rotated from the global frame to the atomic local frame resulting in the ALF Cartesian coordinates, ζj. The rotation is performed using a rotation matrix C, the rows of which (Ci) are calculated using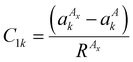 | (11) |
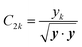 | (12) |
| C3 = C1 × C2 | (13) |
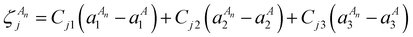 | (14) |
3.3 Calculating atomic properties
Once a training set has been generated, the true values for each training point are required to make a GPR model. For atomistic GPR models, the property we want to use in our models is an atomic property. These atomic properties can be energy values or multipole moments and are calculated using quantum mechanics. The first step in calculating the atomic properties for a geometry is generating a wavefunction. In ICHOR this is performed by an external quantum chemistry program such as GAUSSIAN52 or PySCF.53 ICHOR is required to interface with these programs to generate a wavefunction for any geometry at any level of theory and basis set. From the wavefunction for a given geometry atomic properties can be calculated according to QTAIM. Much like calculating the wavefunction, ICHOR interfaces with an external QTAIM program such as AIMAll54 or MORPHY55 in order to calculate the atomic properties. ICHOR is then able to use the atomic properties to make a GPR model.For each atomic property to be learnable by the GPR model, it must be possible to describe the behaviour of the property by the input features only. The input features of the GPR model are in the ALF and therefore the atomic properties must also be expressed in this ALF. This affects directional properties such as atomic dipole moments and higher moments. The interacting quantum atoms (IQA)56 energy is an atomic property defined by only the self-energy (i.e. intra-atomic) of the atom and the interaction energy between the atom and every other atom in the system,
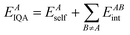 | (15) |
So long as the input features to the machine learning method describes each B atom relative to atom A, the IQA energy of atom A will be a learnable atomic property. For example, AIMAll outputs the multipole moments in the global frame as opposed to the atomic local frame. This means that the multipole moment is not described with respect to the ALF but instead with respect to the global frame. Therefore, to transform the multipole moments into a property defined in the ALF (and hence a learnable property) the moments must first be rotated.
To rotate the multipole moments into the ALF, the C matrix from the previous section is used. The C matrix describes the rotation necessary for a set of Cartesian coordinates to rotate from the global frame into the ALF. Unfortunately, the multipole moments outputted by AIMAll (i.e. the multipole moments that will be trained) are in the spherical harmonic representation. Therefore, to rotate the moments provided by AIMAll, it is necessary to convert the spherical moments into the Cartesian format. Subsequently, we rotate these Cartesian moments using the C matrix before converting the rotated Cartesian moments back to the spherical representation. The equations for the conversions and rotations are taken from Stone et al.57 and can be found in the ESI.†
4. Gaussian process regression
ICHOR calculates features and parses data files from quantum chemistry programs to generate a training set for FEREBUS.58 FEREBUS is an in-house program that has been designed to work alongside ICHOR and DL_FFLUX to generate models quickly with a highly detailed model file output. ICHOR has two roles when interacting with FEREBUS: (i) produce the input files for FEREBUS and (ii) interpret the model files outputted from FEREBUS.FEREBUS has two input files: a config file and a training set file. The config file is a TOML file that specifies how to perform the optimisation of the GPR model. It contains information such as: system information, the mean function to use, the kernel function to use and optimiser parameters. ICHOR is responsible for generating the config file with the parameters specified by the user, an example of which can be found in the ESI.† The training set file is simply a comma-separated value (csv) file containing the inputs and outputs calculated previously, where the inputs are the ALF features of the training set, and the outputs are the atomic properties that are to be trained. Full details on the FEREBUS input files can be found in the ESI.†
The benefit of using an external program to generate the GPR models, as opposed to producing the models internally in ICHOR, is that the GPR engine implementation may be changed without needing any modification to ICHOR. If the new GPR implementation can parse the standard FEREBUS inputs and output standard model files then the GPR implementation may be changed at will.
With the optimised GPR model, ICHOR is required to use the model for analysis and active learning. ICHOR makes no assumptions on the GPR model and requires all information to come from the model file itself. For this reason, ICHOR must implement the full model file standard including non-standard ALFs, universal mean functions and composite kernels. Full details may be found in the ESI.†
To begin with, let us look at making a prediction with an arbitrary GPR model,
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) (x*) = μ(x*) + r′R−1(y − μ(X)) (x*) = μ(x*) + r′R−1(y − μ(X)) | (16) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) (x*) is the model prediction of arbitrary point x*, μ is the mean function, y is the training output, X is the training input, r is the covariance vector (with the prime representing the transpose) and R is the covariance matrix given by
(x*) is the model prediction of arbitrary point x*, μ is the mean function, y is the training output, X is the training input, r is the covariance vector (with the prime representing the transpose) and R is the covariance matrix given by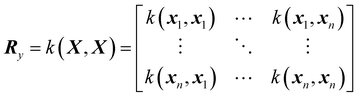 | (17) |
| R = Ry + Iσ | (18) |
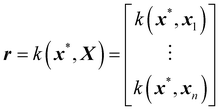 | (19) |
From eqn (16)–(19), ICHOR must implement a variety of mean (μ) and kernel (k) functions as well as enable the formation of composite kernels to fully satisfy the FEREBUS model file standard. Currently ICHOR implements the mean functions listed in Table 1.
| Function name | Mean function |
|---|---|
| Zero | μ(x) = 0 |
| Constant | μ(x) = c |
| Linear | μ(x) = (x − xmin)β + ymin |
| Quadratic | μ(x) = (x − xmin)2β + ymin |
The zero mean function is the simplest and merely returns 0 regardless of the input. The constant mean is similar to the zero mean but instead of returning 0, returns a constant value, c, defined by the model file. The linear and quadratic mean functions with coefficients, β, are scaled based upon the values of xmin while ymin is introduced to remove the requirement of the function of passing through the origin. It is a trivial task to implement new mean functions in ICHOR because new mean functions are supported by GPR engines such as FEREBUS. Currently ICHOR does not implement composite mean functions as the current FEREBUS model file standard has no support for this feature although there are no restrictions on this feature being added within ICHOR's architecture.
Alongside the standard kernels shown in Table 2, the GPR engine FEREBUS implements a domain-specific kernel known as the RBF-cyclic kernel. The standard RBF kernel models the difference between two points as a Gaussian scaled by the lengthscale parameter l. For many situations, this kernel function is suitable except for angular features leading to the RBF-cyclic kernel. For ALF features, every third feature is an angular feature with a potential value range of [−π,π]. Importantly, this range allows for the difference between two features to exceed π radians leading to the necessity of a cyclic feature correction. FEREBUS performs this correction using this RBF-cyclic kernel,
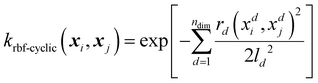 | (20) |
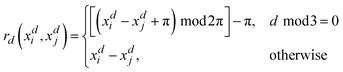 | (21) |
As can be seen from eqn (20), the RBF-cyclic kernel is identical to the RBF kernel (see Table 2) with the modification of the distance function used every third feature, whereby the standard distance metric is replaced by a metric modified to ensure the difference between the two points never exceeds π radians. Full details can be found in the ESI.†
Note that the kernels in Table 2 do not contain a constant prefactor in front of the typical exponential function acting as another hyperparameter. Some texts use this prefactor while others do not. We have chosen the route of not including the prefactor as we have not noticed any significant detriment when not including this parameter. However, the user has the option to define a constant prefactor using a product of the constant kernel and the kernel of choice.
Aside from modifying existing kernels, new kernels may be produced by combining simpler kernels such as the ones shown in Table 2 to produce a composite kernel. Composite kernels can be very complex but the most used composite kernel used by ICHOR is the RBF-periodic kernel because this kernel solves the same problem as the RBF-cyclic kernel shown in eqn (20). The RBF-periodic kernel combines the RBF and periodic kernels by multiplying the output of each kernel on a subset of the input features, where the RBF uses only non-cyclic features whilst the periodic kernel uses only cyclic features. The dimensions used by a kernel function are known as the kernel's active dimensions,
| krbf-per(x) = krbf(xnon-cyclic) × kper(xcyclic) | (22) |
The optimisation of the hyperparameters of the GPR model is undertaken by FEREBUS through maximising the marginal log-likelihood,
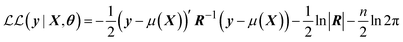 | (23) |
5. Active learning
ICHOR was primarily written to implement active learning, which was deemed infeasible with the preceding program GAIA. Active learning is the process of iteratively improving a machine learning model's training set by adding points that will optimise some metric. For ICHOR's and FFLUX's GPR models, a model describes the potential energy surface of an atom. Hence, the model's success can be defined by minimising the prediction error of molecular geometries, which may come up while using the model in a molecular dynamics simulation. A naïve approach would be to construct a set of points to sample from, calculate the true atomic property for each point and then calculate the prediction error of each point using the current model. We can then add the point with the maximum prediction error to the training set and retrain to improve the model. Repeating this process would minimise the prediction error of the model overall.The issue with the above active learning method is that t requires the true value of all sample points to be known prior to calculating the prediction error, which can be very expensive. Active learning methods are generally designed to also minimise prediction error without the requirement that the true value for each sample point is known. GPR models are useful in this regard because a prediction not only provides a value for the prediction but the prediction also comes with an uncertainty value because each point is a modelled Gaussian. This uncertainty in the prediction is an invaluable tool used by most active learning methods implemented in ICHOR. We now discuss five active learning methods.
5.1 Random method
The simplest active learning method implemented in ICHOR is the random active learning method. The random active learning method acts as a baseline method to compare with other active learning methods in terms of performance. The random active learning method simply selects a point at random from the sample set and adds it to the training set,| xrand = xi ∈RX* | (24) |
5.2 Variance method
A more sophisticated active learning method implemented in ICHOR is the variance method. This method calculates the variance (also called the uncertainty in the prediction) of each sample point and selects the point with the maximum variance to add to the training set. The idea is that points with a large variance are far away from the points in the training set and are therefore not modelled very well. The variance59 is denoted by s2(x*) and given by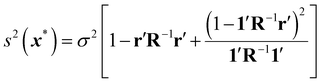 | (25) |
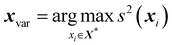 | (26) |
As the variance active learning method is explorative, the method may fail to properly sample space that is close to the training set, which is known as exploitation. The magnitude of this downfall depends on the surface being sampled because a surface that has many small details will likely benefit from an exploitative active learning method, as opposed to a surface that varies over large distances where the lack of exploitation is a non-issue.
5.3 SigMu
At the other end of the exploration versus exploitation scale is an active learning method known as SigMu. SigMu is an active learning method designed to place points at the peaks and troughs of a function by selecting the point with the largest SigMu value. SigMu is therefore highly exploitative by nature. The SigMu value is calculated by multiplying the predictive variance (s2) by the predicted mean60 (![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) ),
),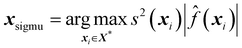 | (27) |
The SigMu method is designed to find the local optima of a surface by combining the variance and predicted mean. The larger the absolute predicted value, the more likely the sample point, xi, will be chosen. Similarly, the larger the variance of the parameter, the higher the likelihood of the sample point that is chosen. By combining the variance and the prediction, the active learning method will continually sample both optima that are known and potential unsampled optima. This behaviour is most favourable when the objective of the model is to predict well points around optimum values because the SigMu active learning method exploits such regions of space.
5.4 Uncertainty query
Another active learning method, alternative to SigMu and the variance one, is the uncertainty query method. The uncertainty metric balances exploration and exploitation by dividing the predictive mean by the predictive variance. This is in contrast to the SigMu strategy because the goal of balancing exploration and exploitation is achieved by balancing the exploitative predictive mean with the explorative predicted variance,61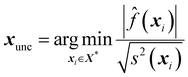 | (28) |
5.5 Maximum expected prediction error method
Currently the maximum expected prediction error62 (MEPE) active learning method is the most sophisticated active learning method implemented in ICHOR. The MEPE method contains three terms: (i) an explorative term, (ii) an exploitative term, and (iii) a term to balance the exploration versus exploitation. As the name suggests, the MEPE method calculates the expected prediction error (EPE), which approximates the true prediction error (PE). The objective of an active learning method is to minimise the PE (maximise accuracy) of the model over an area of space that the model will be expected to work within. The best method for achieving this objective would be to use the true PE and select the sample points with the lowest PE,PEtrue(x*) = |f(x*) − ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) (x*)| (x*)| | (29) |
Calculating the true prediction error requires the computation of the unknown true value of the objective function for each sample point. Often the objective function is expensive to calculate. For this reason, an approximation of the prediction error is required and the MEPE method solves this problem using the EPE,
| EPE(x*) = αPEcv(x*)2 + (1 − α)s2(x*) | (30) |
As mentioned previously, EPE is a trade-off between exploration and exploitation: the variance represents the explorative term while the cross-validation prediction error, PEcv, represents the exploitative term and both terms are balanced by the balance factor α. Because the true prediction error is not known, the cross-validation prediction error is used as an approximation. This is achieved by calculating the cross-validation error for each training point and then assigning the cross-validation error of the arbitrary point to the closest training point. The definition of the approximate cross-validation error is
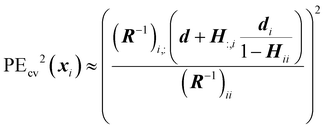 | (31) |
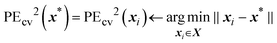 | (32) |
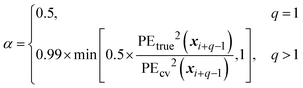 | (33) |
6. HPC cluster management
ICHOR is designed for high-throughput data and model generation on the order of 107 data points. However, IQA data are too expensive to be scaled at this small. In order to compute the volume of data required for a high-accuracy, high-dimensional GPR model, the use of a HPC cluster becomes a necessity. ICHOR implements several interfaces to such systems, making full use of batch systems such as Sun Grid Engine (SGE) and SLURM.Using the glycine example shown in Table 3, it would take almost 250 days to perform the active learning run on a single machine running each calculation in series. ICHOR's utilisation of HPC clusters and batch systems reduces this time down to just 8 days (wall clock time including time to queue each job). The optimisation achieved through the use of batch systems is one of ICHOR's greatest strengths. The cluster interface is explained in detail in the ESI.†
| Atom | AIMALL | FEREBUS | GAUSSIAN | ICHOR | Total time |
|---|---|---|---|---|---|
| C1 | 298:57:01 | 60:16:21 | 34:44:08 | 22:36:20 | 416:33:50 |
| N2 | 335:02:20 | 58:36:21 | 35:28:00 | 25:05:59 | 454:12:40 |
| H3 | 108:51:20 | 70:08:44 | 36:50:28 | 22:22:37 | 238:13:09 |
| C4 | 296:34:53 | 62:22:12 | 35:27:03 | 23:48:53 | 418:13:01 |
| H5 | 100:33:15 | 55:34:25 | 35:28:58 | 20:44:28 | 212:21:06 |
| C6 | 291:31:36 | 61:02:56 | 35:56:38 | 24:35:22 | 413:06:32 |
| O7 | 320:10:12 | 57:24:18 | 35:46:04 | 23:36:11 | 436:56:45 |
| N8 | 314:14:23 | 55:28:14 | 35:54:32 | 22:31:36 | 428:08:45 |
| C9 | 268:20:38 | 58:30:40 | 36:22:04 | 25:10:57 | 388:24:19 |
| O10 | 282:41:44 | 63:07:39 | 35:10:15 | 31:34:02 | 412:33:40 |
| C11 | 257:25:41 | 54:26:51 | 34:18:08 | 20:38:13 | 366:48:53 |
| H12 | 103:59:01 | 63:14:18 | 35:25:21 | 21:24:42 | 224:03:22 |
| H13 | 108:09:52 | 62:59:18 | 34:45:25 | 20:44:26 | 226:39:01 |
| H14 | 107:40:36 | 58:05:12 | 35:24:46 | 23:51:40 | 225:02:14 |
| H15 | 104:47:12 | 59:39:40 | 35:11:10 | 23:26:28 | 223:04:30 |
| H16 | 104:33:19 | 66:57:42 | 34:54:19 | 23:28:37 | 229:53:57 |
| H17 | 104:10:28 | 62:55:10 | 34:40:09 | 23:24:42 | 225:10:29 |
| H18 | 127:56:17 | 55:24:42 | 34:29:42 | 22:45:42 | 240:36:23 |
| H19 | 98:58:09 | 59:11:22 | 33:53:10 | 23:43:23 | 215:46:04 |
| Total time | 3734:37:57 | 1145:26:05 | 670:10:20 | 445:34:18 | 5995:48:40 |
7. Conclusions
ICHOR has grown to become an invaluable tool, providing the novice user with the tools necessary to make GPR models quickly, and the expert user with access to a library of functions to tackle typical “computational chemistry tasks”. ICHOR has been designed as both an application and a library, allowing experienced users to take advantage of ICHOR's file handling, program interfaces and high-level abstractions. ICHOR is a feature-rich and easily expandable computational chemistry suite that has enabled cutting edge research in machine learning, active learning, quantum chemistry and force field design.Modern machine learning models have grown to a point that requires a substantial amount of infrastructure behind them, providing data in a clean and reliable way in order to produce accurate models. ICHOR bridges the gap between computational chemistry and machine learning in an easy-to-use, robust manner as is required to produce machine learning models in the present day. The implementation of interfaces, not only to external programs, but also to HPC clustering systems enable computation at a scale that otherwise would not be possible within a reasonable timeframe running on a single node. ICHOR provides a solid foundation for future work to build upon, with a design based upon modularity and ease of expansion. ICHOR thus removes the need to solve already solved problems, instead allowing solutions to new problems to be implemented within a production-ready application.
Data-access
Data not included in the ESI† is available from the authors on reasonable request.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
M. J. B. acknowledges the MRC DTP for the award of a PhD studentship.References
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine learning for molecular and materials science, Nature, 2018, 559, 547–555 CrossRef CAS PubMed
.
- J. Westermayr, M. Gastegger, K. T. Schuett and R. J. Maurer, Perspective on integrating machine learning into computational chemistry and materials science, J. Chem. Phys., 2021, 154, 230903 CrossRef CAS
.
- O. V. Prezhdo, Advancing physical chemistry with machine learning, Chem. Phys. Lett., 2020, 11, 9656–9658 CrossRef CAS
.
- L. Zhao, H. L. Ciallella, L. M. Aleksunes and H. Zhu, Advancing computer-aided drug discovery (CADD) by big data and data-driven machine learning modeling, Drug Discovery Today, 2020, 25, 1624–1638 CrossRef CAS PubMed
.
- D. A. Dobchev, G. G. Pillai and M. Karelson,
In silico machine learning methods in drug development, Curr. Top. Med. Chem., 2014, 14, 1913–1922 CrossRef CAS PubMed
.
- L. Patel, T. Shukla, X. Huang, D. W. Ussery and S. Wang, Machine learning methods in drug discovery, Molecules, 2020, 25, 5277 CrossRef CAS PubMed
.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Machine learning force fields, Chem. Rev., 2021, 121, 10142–10186 CrossRef CAS
.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Gaussian process regression for materials and molecules, Chem. Rev., 2021, 121(16), 10073–10141 CrossRef CAS PubMed
.
- J. Behler, Four generations of high-dimensional neural network potentials, Chem. Rev., 2021, 121(16), 10037–10072 CrossRef CAS PubMed
.
- F. Musil, A. Grisafi, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Physics-inspired structural representations for molecules and materials, Chem. Rev., 2021, 121(16), 9759–9815 CrossRef CAS
.
- F. Zielinski, P. I. Maxwell, T. L. Fletcher, S. J. Davie, N. Di Pasquale, S. Cardamone, M. J. L. Mills and P. L. A. Popelier, Geometry optimization with machine trained topological atoms, Sci. Rep., 2017, 7(1), 12817 CrossRef PubMed
.
- P. L. A. Popelier, QCTFF: On the construction of a novel protein force field, Int. J. Quant. Chem., 2015, 115, 1005–1011 CrossRef CAS
.
- S. Patel and C. L. Brooks III, CHARMM fluctuating charge force field for proteins: I parameterization and application to bulk organic liquid simulations, J. Comput. Chem., 2004, 25(1), 1–15 CrossRef CAS PubMed
.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Comparison of multiple amber force fields and development of improved protein backbone parameters, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725 CrossRef CAS
.
- P.-O. Norrby and P. Brandt, Deriving force field parameters for coordination complexes, Coord. Chem. Rev., 2001, 212(1), 79–109 CrossRef CAS
.
- K. M. Visscher and D. P. Geerke, Deriving force-field parameters from first principles using a polarizable and higher order dispersion model, J. Chem. Theory Comput., 2019, 15(3), 1875–1883 CrossRef CAS PubMed
.
- B. Chen, J. Xing and J. I. Siepmann, Development of polarizable water force fields for phase equilibrium calculations, J. Phys. Chem. B, 2000, 104(10), 2391–2401 CrossRef CAS
.
- S. K. Burger, P. W. Ayers and J. Schofield, Efficient parameterization of torsional terms for force fields, J. Comput. Chem., 2014, 35, 1438–1445 CrossRef CAS PubMed
.
- C. Kramer, P. Gedeck and M. Meuwly, Multipole-based force fields from ab initio interaction energies and the need for jointly refitting all intermolecular parameters, J. Chem. Theory Comput., 2013, 9(3), 1499–1511 CrossRef CAS PubMed
.
- D. M. Ferguson, Parameterization and evaluation of a flexible water model, J. Comput. Chem., 1995, 16(4), 501–511 CrossRef CAS
.
- J. B. Lim, B. Rogaski and J. B. Klauda, Update of the Cholesterol Force Field Parameters in CHARMM, J. Phys. Chem. B, 2012, 116(1), 203–210 CrossRef CAS
.
- M. Ceriotti, J. Cuny, M. Parrinello and D. E. Manolopoulos, Nuclear quantum effects and hydrogen bodn fluctuations in water, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15591–15596 CrossRef CAS
.
- L. Pereyaslavets, I. Kurnikov, G. Kamath, O. Butin, A. Illarionov, I. Leontyev, M. Olevanov, M. Levitt, D. Kornberg Roger and B. Fain, On the importance of accounting for nuclear quantum effects in ab initio calibrated force fields in biological simulations, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8878–8882 CrossRef CAS PubMed
.
- A. van der Vaart, B. D. Bursulaya, C. L. Brooks, III and K. M. Merz, Jr., Are many-body effects important in protein folding?, J. Phys. Chem. B, 2000, 104(40), 9554–9563 CrossRef CAS
.
- S. Rybak, B. Jeziorski and K. Szalewicz, Many-body symmetry-adapted perturbation theory of intermolecular interactions. H2O and HF dimers, J. Chem. Phys., 1991, 95, 6576–6601 CrossRef CAS
.
- S. K. Reddy, S. C. Straight, P. Bajaj, C. H. Pham, M. Riera, D. R. Moberg, M. A. Morales, C. Knight, A. W. Gotz and F. Paesani, On the accuracy of the MB-pol many-body potential for water: Interaction energies, vibrational frequencies, and classical thermodynamic and dynamical properties from clusters to liquid water and ice, J. Chem. Phys., 2016, 145, 194504 CrossRef
.
- A. Konovalov, B. C. B. Symons and P. L. A. Popelier, On the many-body nature of intramolecular forces in FFLUX and its implications, J. Comput. Chem., 2021, 42, 107–116 CrossRef CAS PubMed
.
- A. Otero-de-la-Roza, L. M. LeBlanc and E. R. Johnson, What is “many-body” dispersion and should I worry about it?, Phys. Chem. Chem. Phys., 2020, 22(16), 8266–8276 RSC
.
- I. Drori, Y. Krishnamurthy, R. Rampin, R. Lourenço, J. Ono, K. Cho, C. Silva and J. Freire, AlphaD3M: Machine Learning Pipeline Synthesis ICML 2018 AutoML Workshop 2018.
- S. O. Randal and H. M. Jason,
Proceedings of Machine Learning Research
, 2016, 64, 66–74 Search PubMed
.
- G. Imbalzano, A. Anelli, D. Giofré, S. Klees, J. Behler and J. Ceriotti, J. Chem. Phys., 2018, 148, 241730 CrossRef PubMed
.
- C. Rosenbrock, E. Homer, G. Csányi and G. Hart, npj Comput. Mater., 2017, 3, 1–7 CrossRef CAS
.
- T. L. Fletcher and P. L. A. Popelier, Multipolar electrostatic energy prediction for all 20 natural amino acids using kriging machine learning, J. Chem. Theory Comput., 2016, 12(6), 2742–2751 CrossRef CAS
.
- J. L. McDonagh, A. F. Silva, M. A. Vincent and P. L. A. Popelier, Machine learning of dynamic electron correlation energies from topological atoms, J. Chem. Theory Comput., 2018, 14, 216–224 CrossRef CAS
.
- Z. E. Hughes, J. C. R. Thacker, A. L. Wilson and P. L. A. Popelier, Description of potential energy surfaces of molecules using FFLUX machine learning models, J. Chem. Theory Comput., 2019, 15, 116–126 CrossRef CAS PubMed
.
- T. L. Fletcher, S. J. Davie and P. L. A. Popelier, Prediction of intramolecular polarization of aromatic amino acids using kriging machine learning, J. Chem. Theory Comput., 2014, 10, 3708–3719 CrossRef CAS
.
-
R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Oxford Univ. Press, Oxford, Great Britain, 1990 Search PubMed
.
-
P. L. A. Popelier, Atoms in Molecules. An Introduction, Pearson Education, London, Great Britain, 2000 Search PubMed
.
-
C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, The MIT Press, Cambridge, USA, 2006 Search PubMed
.
- C. M. Handley and P. L. A. Popelier, A dynamically polarizable water potential based on multipole moments trained by machine learning, J. Chem. Theory Comput., 2009, 5, 1474–1489 CrossRef CAS
.
- J. C. R. Thacker, A. L. Wilson, Z. E. Hughes, M. J. Burn, P. I. Maxwell and P. L. A. Popelier, Towards the simulation of biomolecules: Optimisation of peptide-capped glycine using FFLUX, Mol. Simul., 2018, 44, 881–890 CrossRef CAS
.
- B. C. B. Symons and P. L. A. Popelier, Application of quantum chemical topology force field FFLUX to condensed matter simulations: Liquid water, J. Chem. Theory Comput., 2022, 18(9), 5577–5588 CrossRef CAS
.
- M. J. Burn and P. L. A. Popelier, Creating Gaussian process regression models for molecular simulations using adaptive sampling, J. Chem. Phys., 2020, 153, 054111 CrossRef CAS
.
- Y. Xie, J. Vandermause, L. Sun, A. Cepellotti and B. Kozinsky, Bayesian force fields from active learning for simulation of inter-dimensional transformation of stanene, npj Comput. Mater., 2021, 7, 40 CrossRef CAS
.
- M. E. Tuckerman,
Ab initio molecular dynamics: Basic concepts, current trends and novel applications, J. Phys.: Condens. Matter, 2002, 14, R1297–R1355 CrossRef CAS
.
-
D. Marx and J. Hutter, Ab initio molecular dynamics: Theory and implementation, Modern methods and algorithms of quantum chemistry, 2000, vol. 1, pp. 301–449 Search PubMed
.
- P. Carloni, U. Rothlisberger and M. Parrinello, The role and perspective of ab initio molecular dynamics in the study of biological systems, Acc. Chem. Res., 2002, 35, 455–464 CrossRef CAS PubMed
.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, CP2K: An electronic structure and molecular dynamics software package – Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152(19), 194103 CrossRef
.
-
D. A. Case, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham III, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, D. Ghoreishi, M. K. Gilson, H. Gohlke, A. W. Goetz, D. Greene, R. Harris, N. Homeyer, Y. Huang, S. Izadi, A. Kovalenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, D. J. Mermelstein, K. M. Merz, Y. Miao, G. Monard, C. Nguyen, H. Nguyen, I. Omelyan, A. Onufriev, F. Pan, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, J. Smith, R. SalomonFerrer, J. Swails, R. C. Walker, J. Wang, H. Wei, R. M. Wolf, X. Wu, L. Xiao, D. M. York and P. A. Kollman, AMBER, 2018, University of California, San Francisco, 2018 Search PubMed
.
- T. J. Hughes, S. Cardamone and P. L. A. Popelier, Realistic sampling of amino acid geometries for a multipolar polarizable force field, J. Comput. Chem., 2015, 36, 1844–1857 CrossRef PubMed
.
- M. J. L. Mills and P. L. A. Popelier, Intramolecular polarisable multipolar electrostatics from the machine learning method Kriging, Comput. Theor. Chem., 2011, 975, 42–51 CrossRef
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, F. O. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Wallingford, CT, 2016 Search PubMed
.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova and S. Sharma, PySCF: The Python-based simulations of chemistry framework, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1340 Search PubMed
.
-
T. A. Keith, AIMAll TK Gristmill Software, Overland Park, Kansas, USA, 2019 Search PubMed
.
- P. L. A. Popelier, MORPHY, a program for an automated “atoms in molecules” analysis, Comput. Phys. Commun., 1996, 93(2–3), 212–240 CrossRef
.
- M. A. Blanco, A. Martín Pendás and E. Francisco, Interacting quantum atoms:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A correlated energy decomposition scheme based on the quantum theory of atoms in molecules, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef
A correlated energy decomposition scheme based on the quantum theory of atoms in molecules, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef .
-
A. J. Stone, The Theory of Intermolecular Forces, Clarendon Press, Oxford, 2nd edn, 2013, vol. 32, p. 264 Search PubMed
.
- N. Di Pasquale, M. Bane, S. J. Davie and P. L. A. Popelier, FEREBUS: Highly parallelized engine for kriging training, J. Comput. Chem., 2016, 37, 2606–2616 CrossRef PubMed
.
- D. R. Jones, M. Schonlau and W. J. Welch, Efficient global optimization of expensive black-box functions, J. Glob. Optim., 1998, 13, 455–492 CrossRef
.
- Y. K. Wakabayashi, T. Otsuka, Y. Taniyasu, H. Yamamoto and H. Sawada, Machine-learning-assisted thin-film growth: Bayesian optimization in molecular beam epitaxy of SrRuO3 thin films, Appl. Phys. Express, 2018, 11, 112401 CrossRef
.
- A. Kapoor, K. Grauman, R. Urtasun and T. Darrell, Gaussian processes for object categorization, Int. J. Comput. Vis., 2010, 88, 169–188 CrossRef
.
- H. Liu, J. Cai and Y.-S. Ong, An adaptive sampling approach for Kriging metamodeling by maximizing expected prediction error, Comput. Chem. Eng., 2017, 106, 171–182 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: (1) ICHOR interface: 1.1 terminal user interface, 1.2 command line interface, 1.3 library interface; (2) external program interfaces: 2.1 molecular dynamics software, 2.2 quantum chemistry program interfaces, 2.3 quantum chemical topology interfaces, 2.4 FEREBUS; (3) high performance computing cluster interface: 3.1 batch system interface, 3.2 submission script, 3.3 datafiles, 3.4 error handling, 3.5 submission queues; (4) machines: 4.1 environment modules, 4.2 node privileges, 4.3 parallel environments, 4.4 precompiled binaries; (5) per-value; (6) model analysis: 6.1 model reading, 6.2 S-curves, 6.3 RMSE curve; (7) analysis tools: 7.1 geometry analysis, 7.2 rotate-mol, 7.3 DL_FFLUX analysis; (8) multipole rotation and (9) atomic constants. See DOI: https://doi.org/10.1039/d2ma00673a |
| This journal is © The Royal Society of Chemistry 2022 |