Data-driven approach for the prediction of mechanical properties of carbon fiber reinforced composites

Abstract

Fiber-reinforced composite materials are integral to aerospace, automotive, and military industries. In manufacturing, these composites are subjected to certain curing cycles, which are known to have a significant impact on the mechanical properties of the material. Many studies have focused on predicting these mechanical properties of composites, but environmental conditions and curing cycles are often not considered. In this work, supervised machine learning techniques are applied to experimental data obtained from the National Center for Advanced Materials Performance (NCAMP) for various unidirectional carbon fiber laminates to predict the mechanical properties of composite materials. These techniques holistically consider the effects of environmental conditions and curing cycles, factors frequently overlooked in analytical approaches. Results show that recurrent neural network models can accurately predict the modulus of these materials, achieving R² values up to 0.98. This work establishes a statistical framework to analyze complex empirical data for advanced materials design.

---

Introduction

Composites have demonstrated several advantages over traditional materials, including longevity, strength, and low weight, and have influenced several fields such as biomedical,¹ naval,² structural,^3–8 and aerospace,^9,10 among many others.^11–14 Carbon fiber reinforced polymers (CFRPs) are of particular interest in aerospace applications: unlike metals, CFRPs do not corrode and are less susceptible to fatigue cracking. Additionally, carbon fiber yields significant weight reduction when compared to other load-bearing materials. There exist many factors in the design process that affect the strength of the resulting CFRP. A common manufacturing method involves a layup process in which individual laminae are stacked at varying angles in a repeating pattern; selecting a certain pattern can exploit desirable properties of both the polymer and fiber in multiple directions. The laminae are subject to a set of curing conditions, which include temperature, humidity, and cycle time, and these factors can also affect the strength of the resulting composite. Post curing, the surrounding environmental conditions also have a significant effect on material performance; these conditions are often studied to understand the long-term behavior of the material in varying temperatures and humidity.

The effects of curing conditions, environmental temperature, lamina orientation, and environmental moisture on CFRPs have been studied extensively. Various studies demonstrate that strength development is dependent on curing time and temperature, though no quantitative relationship has been established between these variables.¹⁵ In structural applications, bond joint strength has been shown to decrease with increased curing temperature, although ultimate strain increased with high-temperature curing; additionally, curing CFRPs at 120 °C may not improve their strength at room temperature, but it can significantly increase their ultimate tensile strength at an environmental temperature of 50 °C.^16,17 Some environmental studies have demonstrated that short-term exposure to extremely low temperature (−28 °C) does not have significant effects on the flexural behavior of CFRPs, and others have shown increased flexural strength and energy absorption at lower (−60 °C, −100 °C) temperatures,^18,19 which is advantageous for high-altitude aviation applications. Extreme high-temperature exposure (177 °C) yields considerable reductions in the ultimate tensile strength of fiber-epoxy composites. A fatigue-focused study has shown increased fatigue strength with increased temperature (125 °C), and different layup patterns have resulted in different failure modes in transverse and longitudinal directions; tensile and compressive strength have been maximized along the direction of fiber orientation.^20,21 Humid environmental conditions, often referred to as wet conditions, also result in significant reduction of ultimate tensile strengths, tensile shear strengths, and compressive strengths; these reductions are generally attributed to the weakening of the matrix at high moisture content.^22–24 Ultimately, the following general conclusions can be drawn from the extensive literature at hand: polymer composite strength decreases with increasing curing temperature, increasing environmental temperature, and increasing ambient humidity, and its strength is maximized along the direction of fiber orientation.

Given these trends, researchers have developed increasingly accurate models over decades to predict the properties of CFRPs. Early models, including the rule of mixtures,²⁵ the Reuss model,²⁶ and the Halpin–Tsai equations²⁷ all provide relatively accurate estimates of ultimate strength and Young's modulus. While these models provide useful measures, they often make assumptions about the material that are difficult to achieve in practice such as homogeneity and perfect adhesion. In recent years, computational approaches have increased in popularity for their robustness and ability to incorporate several factors into predictions. Studies have shown the potential of machine learning (ML) techniques in materials design.^28–34 Neural networks are commonly used as a computational tool in ML and have been used to predict the mechanical properties of several materials and optimize the microstructures of materials.^35–39

In this paper, supervised ML techniques are applied to empirical data gathered from thousands of physical material samples to predict the modulus of elasticity of novel CFRPs in various directions. The results and methods presented in this paper differ greatly from the existing literature due to the real-world holistic dataset and the efficient computational models, offering significant novel avenues for exploration. Beyond the overhead incurred in training, predicting the properties of a composite using the ML models presented in this paper only requires knowledge of a small set of variables representing the material constituents, their ordering, curing and environmental conditions, and the direction of loading. The models explored here are relatively computationally inexpensive and can be implemented to incorporate a large subset of potential materials. Moreover, this work explicitly demonstrates the potential for regressive ML techniques in the composite design space.

Methods

Data collection

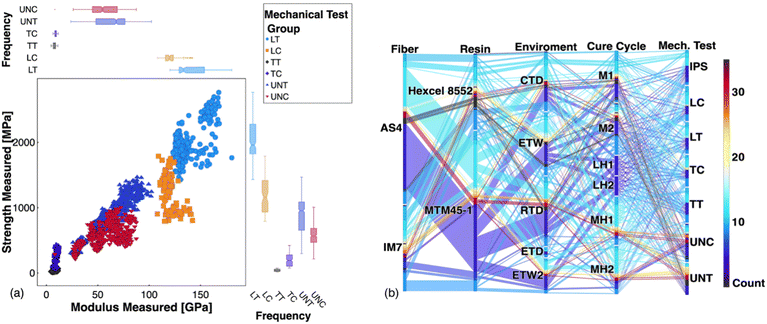
The following data has been collected by the National Center for Advanced Materials Performance (NCAMP), a research program funded by the Federal Aviation Administration that collaborates with industry manufacturers to qualify advanced aerospace materials. From their extensive database, four CFRPs have been selected for analysis: Solvay MTM45-1 with 12K AS4 unidirectional carbon fiber, Solvay MTM45-1 with IM7 unidirectional carbon fiber, Hexcel 8552 with 12K AS4 unidirectional carbon fiber, and Hexcel 8552 with IM7 unidirectional carbon fiber.^40–45 Solvay MTM45-1 and Hexcel 8552 are both toughened epoxy resins. Note that the four selected materials are unique combinations of the two fibers and two resins; this selection is exploited and discussed in the following section. Properties of the material such as fiber type, resin type, curing conditions, environmental conditions, and fiber orientation are used as inputs for the models later presented.

The composite material data of interest are publicly available on the NCAMP website.⁴⁶ Just over 6,500 data points are obtained across all four materials, and each point is described by of one of two fibers, one of two resins, one of five environmental conditions, one of seven curing conditions, and one of seven general mechanical tests. Each point is also described by the orientation of the fibers in each layer of the laminate. Fig. 1b provides a simplified visualization of some of the features that go into manufacturing and testing a carbon fiber specimen. The various design parameters lead to hundreds of thousands of potential combinations, each of which correspond to a unique material. It is important to note that although fiber orientation is excluded from the figure to aid visualization, it is not disregarded in the model. Including the orientation in the dataset increases the number of possible combinations to the millions.

Fig. 1 Exploratory data analysis. (a) Maximum strain scatter plots reveal direction-dependent properties of carbon fiber composites. Box plots visualize the distributions of the properties of each mechanical test group in one dimension. Note that the IPS strength data is unavailable, so it is not shown. (b) Sankey diagram illustrates the count of different combinations of carbon fiber specimens that have been collected. It is important to note that the true design space is significantly larger than what is displayed in the figure, as fiber orientation has been removed from the figure for simplicity and size. Mechanical test variations have also been grouped for visualization purposes.

Of these numerous combinations within the data set, each requires multiple test specimens to obtain an accurate measure of the mechanical properties in varying directions. This orientation-dependent behavior is demonstrated in Fig. 1a, which shows the relationship between modulus and strength. Clusters formed by the mechanical tests reinforce the significance of composites’ direction-dependent properties. Data on specimens that have not been tested on both strength and modulus are excluded in this figure. To reduce data loss and enforce consistency, the modulus is chosen as the sole output for all models. The abbreviations for the variables used throughout this paper are defined in Table 1. Each environmental condition is specified by a temperature and humidity condition; CTD, for example, corresponds to −65 ± 5 °F in dry conditions. Note that ‘wet’ indicates equilibrium moisture content. Each mechanical test follows an ASTM standard; LT, for example, follows ASTM D3039. Each cure cycle follows an NCAMP Process Specification (NPS); M, for example, follows NPS 81228. The reader is referred to the material property reports for additional information on mechanical test and cure cycle specifications.^40–45

Table 1 Definitions of acronyms in NCAMP dataset

Acronym	Definition
CTD	Cold temperature dry (−65 ± 5 °F, dry)
RTD	Room temperature dry (70 ± 10 °F, dry)
ETD	Elevated temperature dry (200 ± 5 °F, dry)
ETW	Elevated temperature wet (200 ± 5 °F, wet)
ETW2	Elevated temperature wet 2 (250 ± 5 °F, wet)
LT	Longitudinal tension (ASTM D3039)
LC	Longitudinal compression (ASTM D6641)
TT	Transverse tension (ASTM D3039)
TC	Transverse compression (ASTM D6641)
IPS	In-plane shear (ASTM D3518)
UNC [#]	Unnotched compression [#]
UNT [#]	Unnotched tension [#]
M [#]	Cure cycle M [#]
MH [#]	Cure cycle MH [#]
LH [#]	Cure cycle LH [#]

---

Statistical analysis

Statistical analyses have been conducted to compare the mean and variance of material mechanical properties between the test environments. A common statistical experiment for such a study is an ANOVA, which assesses the equality of means and assumes an approximately normal distribution of data and equal variances across test groups. Prior to conducting this test, Levene's test of homogeneity of variances has been conducted to assess the equality of the variances across environments for a given mechanical property. For material properties that have satisfied Levene's test, an ANOVA has been conducted. For material properties that have failed Levene's test, Welch's ANOVA, which does not rely upon an equal variance assumption, has been conducted as an alternative to an ANOVA.

ANOVA and Welch's ANOVA are omnibus tests; they do not indicate which groups differ the most from the others, but instead show whether there exists a statistically significant difference between the means of test groups. Thus, for material properties that have yielded statistically significant results from the omnibus test, a post hoc test has been conducted to determine the test group (namely, the environment) that differs most from the others. For material properties that have satisfied Levene's test, Tukey's honestly significant difference (HSD) test has been conducted; for material properties that have not satisfied Levene's test, a Tamhane T multi comparison test has been conducted as an alternative post hoc test. All tests have been conducted with p = 0.01.

Model development

The NCAMP data provide several attributes for each mechanical test and material. To consolidate the dataset and ensure uniformity, a certain subset of features has been selected as model inputs; these include resin, fiber, cure cycle, environment, mechanical test, and laminate orientation. Most of these inputs are one-hot encoded variables; from the one-hot encoded data matrix, the correlation matrix has been generated to gain a better understanding of the relationships between these variables. These relationships are summarized in Fig. 2. More detailed correlation heatmaps are available in the ESI† (Fig. S1 and S2). As shown, modulus values correlate most strongly with mechanical tests, closely followed by laminate orientations. There also exist small correlations between modulus and resin, as well as between modulus and environment. Thus, these correlations justify the chosen inputs and model types.

Fig. 2 Correlation between input variables and modulus. The correlation plot reveals the correlation between each input variable and modulus. Significantly small correlations have been filtered out.

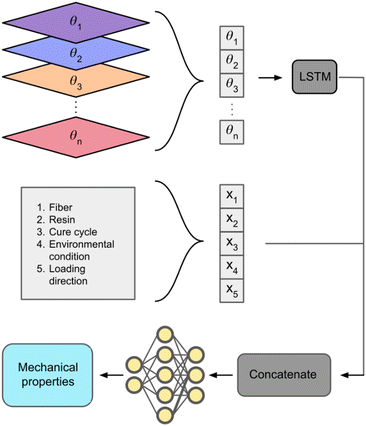
This work studies the use of four ML models: ridge regression, random forests, a multi-layer perceptron (MLP) neural network, and a bimodal recurrent neural network. All inputs to the ridge regression, random forest, and neural network models are one-hot encoded discrete variables. For the bimodal model, all inputs are one-hot encoded except for laminate orientation, which is represented as an array of normalized values. Each entry in the array corresponds to the fiber angle orientation of that layer of the laminate. The arrays are of length 24, which is the maximum number of layers any sample in the dataset has; these arrays are front padded with a −1 for materials that have less than 24 layers to create uniform arrays for the LSTM branch of the bimodal model. The sole output of all models is the modulus.

Linear regression is generally used as a benchmark to compare the performance of other ML models. Due to the nature of our data splits, a regularization term is desired to desensitize trained models to predict similar but unseen material properties without overfitting. Least absolute shrinkage and selection operator (LASSO) is not desirable as it could disregard critical features, so ridge regression is chosen as a suitable alternative. Due to the discrete nature of our dataset, decision trees are potentially a simple and efficient solution; however, they often have high variance and low bias on training data. Random forest models accommodate for this bias and variance tradeoff by building hundreds of decision trees and taking the weighted average across all of them, so random forest models are utilized in this work. Ridge regression and random forest models have all been trained, tested and compared using the Python module scikit-learn.⁴⁷

Artificial neural networks are powerful functional approximators that have shown tremendous success in several applications and are thus also studied in this work. Finally, the bimodal neural network consists of a standard neural network and a recurrent neural network. Recurrent neural networks (RNNs) are a type of artificial neural network that have shown significant success in temporal settings, including text prediction, speech recognition, and translation, where individual units, such as letters or words, must be interpreted in the context of those preceding and succeeding them. Long short-term memory (LSTM) is an RNN-based architecture that overcomes some of the disadvantages of traditional RNN implementations.⁴⁸ Given the success of LSTM models in other ordering-dependent applications,^49,50 LSTMs are used to model the fiber orientations of each layer in a laminate. The laminate orientation array is passed into the LSTM component. The output from the LSTM branch is concatenated with the one-hot encoded variable input and passed into an MLP network. All neural network models have been created, trained and tested using TensorFlow Keras functional API.⁵¹ The neural network model contains two dense layers with batch normalizations and dropout layers. A similar construction is used for the bimodal model, with the exception that the laminate orientation first passes through an LSTM layer, as depicted in Fig. 3.

Fig. 3 Bimodal recurrent neural network model. θ_i represents the fiber orientation angle of the ith layer of the material. The variables x₁ to x₅ represent the five variables listed in the light grey box. The circles connected by lines represent a standard MLP network. The top branch depicts how the fiber orientation is input to the LSTM, and the middle branch depicts how the remaining one-hot encoded variables are input to the first MLP network. The outputs of these separate branches are then concatenated and passed into a second MLP network to produce a property value.

With the collected data, two different data splits have been applied. Given a set of four similar materials, the first split leaves three materials for training and the last for training, following an approximate 3 : 1 test-train split. For example, AS4 MTM45-1 would be kept for testing, and IM7 MTM45-1, IM7 Hexcel 8552, and AS4 Hexcel 8552 would be trained on. The second split leaves two dissimilar materials with unique fiber-resin combinations for training and the remaining two for testing, following an approximate 2 : 2 test-train split. For example, AS4 Hexcel 8552 and IM7 MTM45-1 would be kept for testing, and IM7 Hexcel 8552 and AS4 MTM45-1 would be trained on. This data split is different from a traditional 70 : 30 test-train split, as an entire material is left out for testing as opposed to a randomly selected set of data. For each split, the material that is left out shares similar features with the training data but in different combinations. This situation simulates the prediction of properties for an unseen but similar material for potential new designs. Additionally, it is important to note that several high-precision tests are available for each material combination in the dataset. Thus, a randomly shuffled test-train split would not assess the ability of the model to predict new designs, as any testing point would likely have several nearly identical representatives in the training dataset.

With the data encoded and split, all models and their respective parameters are cross-validated with 3 folds on the training data using grid search across the hyperparameters. The regularization strength parameter has been searched in the range from 0.5 to 6.5 with increments of 0.25. The random forest depth parameter and the number of estimators have been searched in the ranges from 11 to 14 and 300 to 600, respectively. Regarding the deep learning models, both the standard neural network and bimodal model have the same architectures except for the initial LSTM layer that differentiates the bimodal model. Each of the deep learning models consists of two repeating blocks of dense layers with leaky ReLU⁵² activation functions, dropout,⁵³ and batch normalization layers. The number of nodes in each layer and the Adam⁵⁴ optimizer learning rate have been searched in the ranges from 80 to 150 and 0.0001 to 0.01, respectively. The dropout layer value has been searched across the values of 0.05, 0.1, and 0.15. Lastly, the bimodal model has an additional LSTM layer as the input; for this model, the number of LSTM units have been searched in the range from 1 to 3. Both the standard neural net and the bimodal model have been trained for a maximum of 50 epochs with early stopping criteria set with a patience of 3. The final set of hyperparameters that have been used are provided in the ESI.†

Results and discussion

Statistical analysis results

After conducting statistical analyses, the following results are obtained. For most mechanical tests and materials, the null hypothesis of equal variance for Levene's test is failed to be rejected. This indicates that generally, testing environmental conditions do not have a statistically significant effect on the variance of mechanical properties; all of the environments provide similarly consistent results. However, for most mechanical tests and materials, the null hypothesis of equal means for the omnibus test is generally rejected. This indicates that generally, testing environmental conditions have a statistically significant effect on the mean values of mechanical properties; certain environments yield stronger and weaker materials.

The results of Levene's test can be attributed to the high-quality nature of the data. These samples have been developed and tested in highly controlled environments, and thus minimal variation in modulus values is expected across all environments. The results of the omnibus tests are explained by the results obtained from correlation analysis. As shown in Fig. 2, there is a small correlation between modulus and environmental conditions. Causally, this is a result of the fact that temperature and humidity affect the elastic modulus of the resin, and thus play a significant role in its macroscopic properties. It is also worth noting that Levene's test is more often failed for properties of materials manufactured with the MTM45-1 resin than it is for properties of materials manufactured with the Hexcel 8552 resin. This suggests that Hexcel 8552 demonstrates more consistent behavior across temperatures, whereas MTM45-1 is more likely to vary.

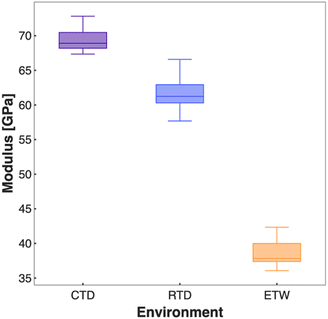
For materials manufactured with Hexcel 8552 as the constituent resin, a statistically significant difference is observed between ETW, RTD, and CTD environments; additionally, average modulus values decrease with temperature for all properties except tensile and compressive longitudinal modulus. For materials manufactured with MTM45-1 as the constituent resin, a statistically significant difference is generally observed between ETW2, ETW, RTD, and CTD environments; again, average modulus values decrease with temperature for all properties except longitudinal and unnotched properties. An example of this trend is shown in Fig. 4.

Fig. 4 Modulus distribution across environmental conditions. Box and whisker plot illustrating the difference in longitudinal tensile modulus between various environmental conditions for Hexcel 8552 IM7 unitape.

The relationship between environmental conditions and modulus is explained by the direct relationships between humidity and modulus and temperature and modulus. CTD, a cold, dry environment, yields high modulus values; RTD, a room temperature, dry environment, yields lower modulus values; ETW, a warm, wet environment, yields the lowest modulus values. Note, however, that the overall decreased modulus is attributed to the resin, not the fiber; this explains the observation that average modulus values decrease with temperature for all properties except tensile and compressive longitudinal modulus. Longitudinal modulus is a fiber-dominated property, whereas the modulus in the remaining directions is a matrix-dominated property. Thus, a decrease in modulus is observed in all directions except for longitudinal as temperature increases.

Model results

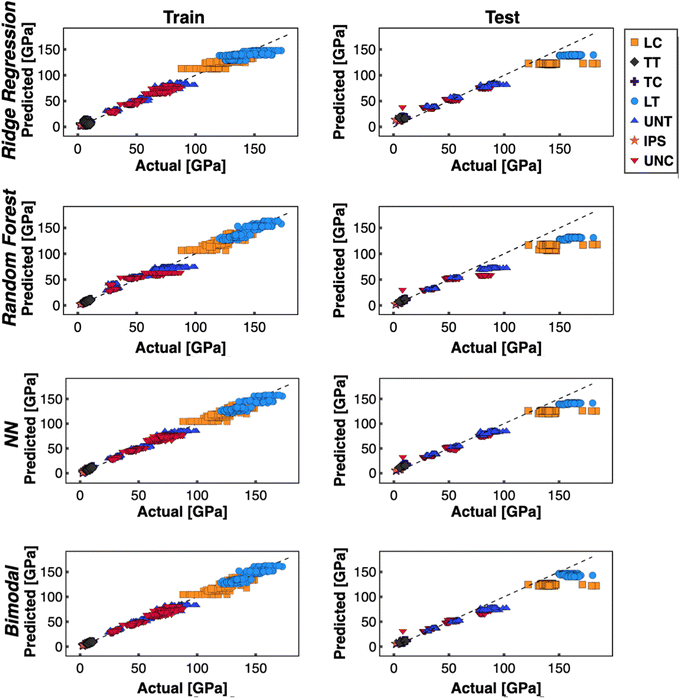
After models are trained, cross-validated and tested, the following results are obtained. Fig. 5 visualizes the training and testing results across all models using the 3 : 1 data split with IM7 MTM45-1 as the material left for testing. Additional visualizations for other splits are available in the ESI† (Fig. S3–S6). One critical observation is the striation of results across models within individual mechanical test groups, which can be attributed to the categorical nature of the input data. In turn, providing any of the models' multiple inputs with the exact same set of manufacturing conditions will yield similar outputs. This contrasts with the nature of the actual experimental data, where similar manufacturing conditions will yield slightly different results due to material imperfections, testing inconsistencies, and other stochastic influences. Additionally, there are bands within each of the test groups, each of which corresponds to different environmental conditions. This indicates that environments are either overly weighted in the model, or that the other variables are not weighted heavily enough to dissipate the banding behavior.

Fig. 5 Training and testing results for all models. Modulus predicted by model is plotted against true modulus value across all models. For these data, the IM7 Hexcel 8552 material has been left for testing.

When discussing the influence of each input on the results of the model, it is important to interpret these results with the context of the correlation analysis presented in Fig. 2. The mechanical test variable, which dictates the direction and type of loading, displays the greatest correlation with modulus, followed closely by fiber orientation in certain directions; the environmental condition variable displays a low correlation with modulus. Mechanically, this is expected, as the elastic modulus of the material is highly dependent upon the alignment between fiber orientation and the loading direction, whereas environmental conditions contribute minimal, yet non-negligible, perturbations to the final modulus value. Given that the mechanical test and fiber orientation variables correlate with modulus far more than the environmental condition variable, it is then of considerable interest that the aforementioned banding behavior occurs along the lines of environmental condition. This behavior is attributed to the fact that while nearly all the materials are tested in all the studied environmental conditions, most materials are only constructed using a limited set of fiber orientation profiles, and the fiber orientation variable is thus interpreted by the models as an indicator of the material type.

Four different models are trained and tested on six data splits, totaling twenty-four models. The average R² and RMSE values across all models and data splits are 0.992 and 4.222 GPa, respectively, for the training data. The average R² and RMSE values are 0.934 and 12.103 GPa, respectively, for the testing data. For the 3 : 1 data split, among the four models, the bimodal model yields the most accurate results, with average testing R² and RMSE values of 0.953 and 10.293 GPa, respectively, whereas the standard neural network yields the least accurate results, with average R² and RMSE values of 0.925 and 12.940 GPa, respectively. For the 2 : 2 data split, among the four models, the bimodal model yields the most accurate results, with average testing R² and RMSE values of 0.949 and 10.919 GPa, respectively, whereas the standard neural network yields the least accurate results, with average R² and RMSE values of 0.907 and 14.737 GPa, respectively. As shown in Table 2, on average, the bimodal model outperforms the other models across all data splits; however, for certain splits, the random forest outperforms the bimodal model. The standard neural network also outperforms the bimodal model for one data split. The results of the bimodal model across various data splits are visualized in Fig. 6. The results of the bimodal model and the standard neural network visualized side-by-side are available in the ESI† (Fig. S7).

Table 2 R ² and RMSE values for modulus across all models and data splits. RMSE values are computed across all mechanical tests and are given in gigapascals. The best testing metrics for each data split are shown in bold

		RF train	RF test	Ridge train	Ridge test	NN train	NN test	RNN train	RNN test
Without IM7 MTM45-1	RMSE	3.112	8.200	5.786	14.344	4.210	17.310	5.828	9.558
	R ^2	0.996	0.975	0.986	0.925	0.992	0.895	0.985	0.968
Without AS4 MTM45-1	RMSE	2.959	6.192	5.665	12.484	4.207	12.241	5.705	11.667
	R ^2	0.996	0.982	0.987	0.929	0.993	0.932	0.987	0.938
Without IM7 Hexcel 8552	RMSE	2.858	15.870	4.596	12.572	3.824	10.696	3.474	11.200
	R ^2	0.996	0.915	0.990	0.947	0.993	0.962	0.994	0.958
Without AS4 Hexcel 8552	RMSE	3.404	14.074	4.981	10.617	5.297	11.511	4.003	8.748
	R ^2	0.996	0.870	0.991	0.926	0.989	0.913	0.994	0.950
Without IM7 MTM45-1 and AS4 Hexcel 8552	RMSE	2.676	13.547	3.363	14.715	5.047	12.969	5.397	9.774
	R ^2	0.997	0.928	0.995	0.915	0.990	0.922	0.989	0.955
Without AS4 MTM45-1 and IM7 Hexcel 8552	RMSE	3.192	10.911	4.368	12.706	3.943	16.505	3.426	12.065
	R ^2	0.996	0.944	0.993	0.925	0.993	0.893	0.995	0.943
Average across all data splits	RMSE	3.033	11.466	4.793	12.906	4.421	13.539	4.639	10.502
	R ^2	0.996	0.936	0.990	0.928	0.992	0.919	0.990	0.952

---

Fig. 6 Performance of bimodal recurrent neural network model across different data splits. (a) R² values for bimodal model across each data split. (b) RMSE values for bimodal model across each data split.

All models are capable of predicting the modulus of unseen materials considering the relatively minute difference between R² and RMSE values between testing and training datasets. Moreover, the models perform well across both types of test-train splits, implying that even with sparse training data, the models continue to demonstrate their generalizability. With a higher R² coefficient and lower RMSE on average, the bimodal model outperforms the rest, likely because of the continuous nature of the laminate orientation input. This suggests that the LSTM successfully interprets various features of the laminate input, including the number of layers, the fiber orientation of each layer, and most importantly, the ordering of these layers, properties that were not represented by the one-hot encoded input provided to other models. However, it is important to note that this model did not significantly outperform the others, suggesting that the less computationally expensive models perform comparably well.

In the future, the benefits of machine learning in composite design can be extended to the prediction of other material properties, such as strength and Poisson's ratio. Additionally, other inputs to the model can be represented in other ways to increase generalizability. Cure cycles can also be modeled as sequential variables of temperature and pressure, and thus can be similarly provided as an input to an additional LSTM branch. Finally, in this work, data is obtained for a limited number of materials; the NCAMP database encompasses dozens of other CFRPs, and other manufacturers may provide similar information. As opposed to artificially randomized computer-generated data, experimental data describes the inherent stochasticity of the manufacturing process; though mean values are predicted in this work, real-world data can be exploited to predict a more useful distribution of values instead.

Conclusions

The following conclusions can be drawn from the results of this work. Firstly, from the statistical explorations, there is no statistically significant difference between the variances of the moduli across environments, but there is a statistically significant difference between their means, implying that the increased modulus in certain environments can be exploited without increasing its variability. For fiber-dominated properties, namely those in the longitudinal direction, warmer environmental conditions yield higher modulus values, whereas for matrix-dominated properties, cooler environmental conditions yield higher modulus values. The results of the ML models yield the following conclusions. Firstly, all the models yield highly accurate results, demonstrating significant potential for regressive analysis of CFRPs using ML techniques; nevertheless, these models have room for improvement, especially regarding distribution prediction. Secondly, the highly accurate results across both unconventional data splits speak strongly to the models’ ability to predict unseen material combinations, which has several implications for accelerating material design. Finally, these results demonstrate the success of recurrent neural network architectures in modeling the features and ordering of lamina in laminate composites. Ultimately, advancing these models will reduce the number of experiments that need to be conducted to achieve desired properties, paving the way for a faster analysis of new laminate composite designs.

Author contributions

Vade Shah: conceptualization, methodology, software, formal analysis, investigation, writing – original draft, writing – review & editing Steven Zadourian: conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing – review & editing, visualization Charles Yang: methodology, resources, writing – review & editing Zilan Zhang: writing – review & editing Grace Gu: resources, writing – review & editing, supervision, project administration.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank General Motors for supporting this research. Additionally, the authors would like to acknowledge support from the Office of Naval Research (Fund Number: N00014-21-1-2604).

References

1. S. Ramakrishna, J. Mayer, E. Wintermantel and K. W. Leong, Compos. Sci. Technol., 2001, 61, 1189–1224.
2. A. P. Mouritz, E. Gellert, P. Burchill and K. Challis, Compos. Struct., 2001, 53, 21–42.
3. G. X. Gu, M. Takaffoli and M. J. Buehler, Adv. Mater., 2017, 29, 1700060.
4. P. K. Mallick, Fiber-reinforced composites: materials, manufacturing, and design, CRC press, 2007.
5. F. Libonati, G. X. Gu, Z. Qin, L. Vergani and M. J. Buehler, Adv. Eng. Mater., 2016, 18, 1354–1363.
6. J. W. C. Dunlop and P. Fratzl, Annu. Rev. Mater. Res., 2010, 40, 1–24.
7. S. Budhe, M. D. Banea, S. de Barros and L. F. M. da Silva, Int. J. Adhes. Adhes., 2017, 72, 30–42.
8. S. N. A. Safri, M. T. H. Sultan, M. Jawaid and K. Jayakrishna, Composites, Part B, 2018, 133, 112–121.
9. P. D. Mangalgiri, Bull. Mater. Sci., 1999, 22, 657–664.
10. M. Maria, Incas Bull., 2013, 5, 139–150.
11. F. L. Matthews and R. D. Rawlings, Mater. Des., 1995, 16, 119–120.
12. J. Bauer, S. Hengsbach, I. Tesari, R. Schwaiger and O. Kraft, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 2453–2458.
13. C.-T. Chen, F. J. Martin-Martinez, S. Ling, Z. Qin and M. J. Buehler, Nano Futures, 2017, 1, 11003.
14. B. G. Compton and J. A. Lewis, Adv. Mater., 2014, 26, 5930–5935.
15. C. Czaderski, E. Martinelli, J. Michels and M. Motavalli, Composites, Part B, 2012, 43, 398–410.
16. E. R. K. Chandrathilaka, J. C. P. H. Gamage and S. Fawzia, Compos. Struct., 2019, 207, 471–477.
17. T. C. Nguyen, Y. Bai, X. L. Zhao and R. Al-Mahaidi, Constr. Build. Mater., 2013, 40, 899–907.
18. E.-H. Raafat, W. R. Gordon and M. F. Green, J. Compos. Constr., 2004, 8, 3–13.
19. Z. Jia, T. Li, F. Pen Chiang and L. Wang, Compos. Sci. Technol., 2018, 154, 53–63.
20. S. Mortazavian and A. Fatemi, Composites, Part B, 2015, 72, 116–129.
21. S. Mortazavian and A. Fatemi, Int. J. Fatigue, 2015, 77, 12–27.
22. C.-H. Shen and G. S. Springer, J. Compos. Mater., 1977, 11, 2–16.
23. O. K. Joshi, Composites, 1983, 14, 196–200.
24. C. Soutis and D. Turkmen, J. Compos. Mater., 1997, 31, 832–849.
25. W. Voigt, Lehrbuch der Kristallphysik, Vieweg+Teubner Verlag, Wiesbaden, 1966, vol. 962.
26. A. Reuss, ZAMM - J. Appl. Math. Mech./Zeitschrift für Angew. Math. und Mech, 1929, 9, 49–58.
27. J. C. H. Affdl and J. L. Kardos, Polym. Eng. Sci., 1976, 16, 344–352.
28. Y. Liu, T. Zhao, W. Ju and S. Shi, J. Mater, 2017, 3, 159–177.
29. K. J. Callahan and G. E. Weeks, Compos. Eng., 1992, 2, 149–160.
30. G. X. Gu, C.-T. Chen, D. J. Richmond and M. J. Buehler, Mater. Horiz., 2018, 5, 939–945.
31. G. X. Gu, C. T. Chen and M. J. Buehler, Extrem. Mech. Lett., 2018, 18, 19–28.
32. A. Paul, P. Acar, W. Liao, A. Choudhary, V. Sundararaghavan and A. Agrawal, Comput. Mater. Sci., 2019, 160, 334–351.
33. G. Pilania, C. Wang, X. Jiang, S. Rajasekaran and R. Ramprasad, Sci. Rep., 2013, 3, 1–6.
34. C. Yang, Y. Kim, S. Ryu and G. X. Gu, Mater. Des., 2020, 189, 108509.
35. K. Hornik, M. Stinchcombe and H. White, Neural Networks, 1989, 2, 359–366.
36. G. V. Seretis, G. N. Kouzilos, D. E. Manolakos and C. G. Provatidis, SAE Int. J. Mater. Manuf., 2018, 11, 193–204.
37. F. Khademi, M. Akbari, S. M. Jamal and M. Nikoo, Front. Struct. Civ. Eng., 2017, 11, 90–99.
38. S. Tiryaki and A. Aydın, Constr. Build. Mater., 2014, 62, 102–108.
39. C.-T. Chen and G. X. Gu, Adv. Sci., 2020, 7, 1902607.
40. National Center for Advanced Materials Performance, Hexcel 8552 IM7 Unidirectional Prepreg 190 gsm & 35%RC Qualification Material Property Data Report, https://www.wichita.edu/industry_and_defense/NIAR/Documents/Qual-CAM-RP-2009-015-Rev-B-Hexcel-8552-IM7-MPDR-04.16.19.pdf.
41. National Center for Advanced Materials Performance, Hexcel 8552 AS4 Unidirectional Prepreg 190 gsm & 35%RC Qualification Material Property Data Report, https://www.wichita.edu/industry_and_defense/NIAR/Research/hexcel-8552/AS4-Unitape-2.pdf.
42. National Center for Advanced Materials Performance, SOLVAY MTM45-1/IM7-145 32%RW 12k IM7 Unidirectional 145 gsm Qualification Material Property Data Report, https://www.wichita.edu/industry_and_defense/NIAR/Research/cytec-mtm45-1/CAM-RP-2008-007-Rev-B-ACG-IM7-Uni-3.28.2018-FINAL-MPDR.pdf.
43. National Center for Advanced Materials Performance, MTM45-1 AS4 Data MH Cure Cycle, https://www.wichita.edu/industry_and_defense/NIAR/Research/cytec-mtm45-1/12K-AS4-Unidirectional-2.pdf.
44. National Center for Advanced Materials Performance, MTM45-1 AS4-145 CPT Normal Data M Cure Cycle Values Only, https://www.wichita.edu/industry_and_defense/NIAR/Research/cytec-mtm45-1/MTM45-1-AS4-145-CPT-Normal-Data-LH-Cure-Cycle-Values-Only-2-1-08.pdf.
45. National Center for Advanced Materials Performance, MTM45-1 AS4-145 CPT Normal Data LH Cure Cycle Values Only, https://www.wichita.edu/industry_and_defense/NIAR/Research/cytec-mtm45-1/MTM45-1-AS4-145-CPT-Normal-Data-LH-Cure-Cycle-Values-Only-2-1-08.pdf.
46. Wichita State University, National Center for Advanced Materials Performance, https://www.wichita.edu/research/NIAR/Research/ncamp.php, (accessed 8 May 2022).
47. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830.
48. S. Hochreiter and J. Schmidhuber, Neural Comput., 1997, 9, 1735–1780.
49. K. Greff, R. K. Srivastava, J. Koutník, B. R. Steunebrink and J. Schmidhuber, IEEE Trans. neural networks Learn. Syst., 2016, 28, 2222–2232.
50. M. Sundermeyer, R. Schlüter and H. Ney, in Thirteenth annual conference of the international speech communication association, 2012.
51. M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mane, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viegas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, 2016, arXiv:1603.04467.
52. A. F. Agarap, 2018, arXiv:1803.08375.
53. S. Park and N. Kwak, Asian conference on computer vision, Springer, 2016, pp. 189–204.
54. D. P. Kingma and J. Ba, 2014, arXiv:1412.6980.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma00698g

‡ These authors contributed equally to this work.

---