Open Access Article
Open Access ArticleZinc-doped hydroxyapatite and graphene oxide composites for bone and teeth implants: a theoretical understanding
Oliver
Song
 and
Xuan
Luo
and
Xuan
Luo
 *
*
National Graphene Research and Development Center, Springfield, Virginia 22151, USA. E-mail: xluo@ngrd.org
First published on 14th September 2022
Abstract
Recently, bone and teeth implants have relied on Hydroxyapatite (HA) benefits to mediate bone restoration, but its weak antibacterial and mechanical properties limit its usage. Research to address these properties has shown that Zinc-doped HA (ZnHA) and Graphene Oxide (GO) composites have the potential to address both limitations. The interaction behavior of these ZnHA and GO composites is crucial and yet to be understood. Here, we used density functional theory (DFT) to investigate the interaction mechanisms of GO and ZnHA composites. Our results show that the calcium of ZnHA was found to have interactions with neighboring epoxy atoms in GO. ZnHA was selective and showed energetically favorable interactions with GO at a 6.25% oxygen concentration. Charge transfer, projected density of states, and band structures support the design and synthesis of future ZnHA/GO composites, improving their interfacial binding strength and interaction mechanisms. This study provides a theoretical basis for the potential applications of ZnHA/GO composites in bone and teeth applications.
1 Introduction
Hydroxyapatite (HA) is an inorganic bioceramic component of bone and teeth. Researchers first used HA in regenerative sciences during the 1950s as an inert scaffold for filling bone defects and grafting, which held little interaction with surrounding living tissues.1 Gradually, the usage of HA expanded after the milestone discoveries of HA's high bioactivity,2 biocompatibility,3 osteoconductivity, and osteointegrative4 properties. Now HA is used as implant coatings to encourage bioactivity and fixation in restorative bone procedures. To succeed in bone and teeth applications, HA requires robust antibacterial and mechanical properties. Researchers have explored doping trace elements such as Zn2+, Ag+, Mn2+, Mg2+, Sr2+, and Ce3+ into HA to address these limitations.5–8 Zn stands out as it holds unique properties such as facilitating enzyme function, osteoclast differentiation, and bone formation, given HA's weak antibacterial properties.9–11 With these properties, doping Zn ions into HA is a point of interest for experimental and theoretical research.4Recently, researchers have investigated the difference between HA and Zn-doped Hydroxyapatite (ZnHA) and discovered that ZnHA has advanced performance. Anwar et al. found that ZnHA showed significant antibacterial activity against both Gram-positive and Gram-negative bacterial growth.12 Furko et al. further established that ZnHA showed better osteoblast responses when compared to HA.13 Wang et al. found that Zn tends to occupy the Ca2 location symmetrically.14 In addition to these properties, mechanical properties also play an essential role in bone and teeth applications. Researchers have explored improving ZnHA's elastic modulus and hardness using polymers, graphene materials, carbon nanotubes, and titanium alloys.15–17
Previous research has shown that graphene materials can overcome weak mechanical properties in HA due to its hardness18–20 and have demonstrated high biocompatibility and osteogenic properties.21 Graphene oxide (GO) is even better due to its many functional groups, such as epoxy, hydroxyl, carboxyl, and carbonyl.16,22,23 These chemically active oxygen functional groups can strongly affect the electronic, mechanical, and electrochemical properties of GO,24 allowing for additional interactions between molecules.25 Li et al. found that GO could reduce HA's surface cracks and increase coating adhesion strength.26 Liu et al. found that GO increased the Young's modulus and reduced cracking of HA.27 HA and GO are thus quite compatible for orthopedic applications with clear advantages over pure HA.28,29
With the advantages HA/GO composites hold, it is of interest to create ZnHA/GO composites that retain high antibacterial activity and mechanical properties. Maleki-Ghaleh et al. investigated the antibacterial and biocompatibility properties of a ZnHA/graphene nanocomposite and found that it had 3.4 times better antibacterial properties than HA.30 Furthermore, Chopra et al. discovered that ZnHA/GO has excellent biocompatibility, antimicrobial properties, and supported vascularization, which is critical to supporting the long-term survival of scaffold grafts.31 With these benefits, the effect of Zn doping and graphene functional groups on the interface between ZnHA and GO should be explored on the theoretical level. This study could provide a fundamental theory to effectively explore interfacial interaction between functional groups in GO and ZnHA.
Our research employs Density Functional Theory (DFT) to investigate the effect of different oxygen concentrations in GO on the interfacial bonding strength of ZnHA. Binding energy was calculated to determine the energetically favorable composites. In Section 2, we detail our methods to perform first-principle calculations. Section 3 presents our results on ZnHA and GO, compares our results to experimental and theoretical research, and discusses future applications.
2 Methods
We use electronic structure methods to analyze ZnHA interfaced with GO to discover new properties about ZnHA/GO composites.2.1 Computational details
First-principles calculations based on Density Functional Theory (DFT) were performed within the Generalized Gradient Approximation (GGA)32 in the format of Perdew–Burke–Ernzerhof (PBE) as implemented in the ABINIT33,34 package. The Projected Augmented Wave (PAW) method35–37 was used to generate the pseudopotentials with the ATOMPAW code.38 The cut-off radii are 1.0, 1.4, 1.9, 1.9, 2.3, 1.5 a.u. and the valence electrons are 1s1, [He]2s22p4, [Ar]4s2, [Ne]3s23p3, [Ar]4s23d10, and [He]2s22p2 for H, O, Ca, P, Zn, and C, respectively.In total energy calculations, self-consistent field (SCF) iterations were considered converged when the total energy difference was less than 1.0 × 10−10 hartree twice consecutively. The kinetic energy cutoff and Monkhorst–Pack k-point grid was considered converged when the total energy difference between datasets was less than 1.0 × 10−4 hartree twice consecutively.
Atomic structure optimizations were performed with the Broyden–Fletcher–Goldfarb–Shanno algorithm. In each step of optimization, the SCF iterations were terminated when the difference between forces of each atom was less than 2.0 × 10−5 hartree bohr−1 twice consecutively. The optimization was terminated when the maximal absolute force on each atom was less than 2.0 × 10−4 hartree bohr−1 (about 0.01 eV Å−1).
2.2 Electronic structure
The electronic structure of the composites was analyzed through band structure calculations, projected density of states (PDOS), and charge transfer. Because DFT calculations are well known to underestimate band gaps,39 our research will primarily focus on binding trends.The electronic band structure of HA/GO and ZnHA/GO was analyzed and plotted by using the high symmetry k-points Γ(0,0,0), M(1/2,0,0), K(2/3,1/3,0), and Γ(0,0,0).
The PDOS was performed using the tetrahedron method for the GO and HA or ZnHA complexes. The atoms chosen for projections were the atoms in the ZnHA complexes closest to the epoxy groups in GO.
The interactions between the GO and HA or ZnHA complexes were further analyzed using charge transfer. The charge transfers between HA or ZnHA and GO complexes were obtained using the following equation:
| Δρ(r) = ρHA−GO(r) − ρHA(r) − ρGO(r) | (1) |
| Δρ(r) = ρZnHA−GO(r) − ρZnHA(r) − ρGO(r) | (2) |
2.3 Binding energy
HA or ZnHA were placed above GO in different configurations to analyze binding behavior.Binding energies of GO and HA or ZnHA complexes were obtained using the following equation:
| Ebind = EHA−GO − EHA − EGO | (3) |
| Ebind = EZnHA−GO − EZnHA − EGO | (4) |
Binding energy is essential in determining the viability of the HA/GO or ZnHA/GO composites. Negative binding energy indicates the interaction is energetically favorable, with more negative binding energies indicating stronger interactions. Positive binding energy indicates that the interaction is repulsive or not energetically favorable.
3 Results and discussion
Here, ZnHA interfaced with varying oxygen concentrations of GO substrates was systematically studied. Band structure, PDOS, charge transfer, and binding energy were evaluated.3.1 Graphene oxide
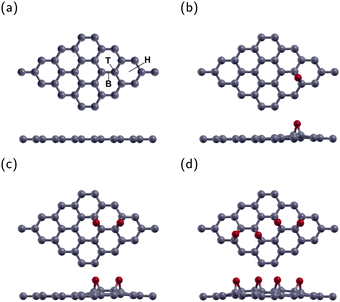
The current research investigated a 4 × 4 graphene supercell with one, two, or four epoxies. These correspond to oxygen concentrations of 3.125% (GO1), 6.25% (GO2), and 12.5% (GO4), respectively. There are three typical adsorption sites. These sites were the top site directly above a C atom (T site), the bridge site above the bond between two C atoms (B site), and the hexagonal site above the center of the graphene hexagon (H site). Fig. 1(a) displays the B, T, and H sites on a 4 × 4 graphene sheet. After optimization, the O atoms in all three configurations remained roughly in their original sites. The energy of the B site was the lowest one, in agreement with previous research.40,41 The lowest energy configuration for GO1 is shown in Fig. 1(b).The lowest energy configuration for GO2 is shown in Fig. 1(c) with two O atoms placed one bond away from each other. After relaxation, the epoxies remain in their original position and tilt slightly away from each other. This configuration is the most stable location for two epoxies, in agreement with previous research.42–44
The configuration for GO4 is shown in Fig. 1(d) with two epoxies in the GO2 position and two more across the diagonal of the graphene sheet.
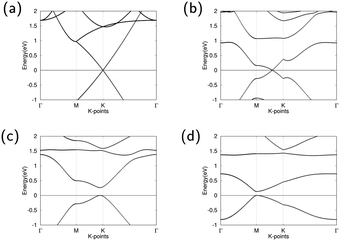
The band structures of pure graphene, GO1, GO2, and GO4 are illustrated in Fig. 2. For GO1, the Dirac point shifts between high symmetry point M and K. The minor influence of the epoxy on band structure can be attributed to the weak effects that the epoxy has on the overall graphene structure. GO2 opens the Dirac point and has a direct band gap of 0.264 eV between high symmetry k-points M and K, demonstrating that GO2 is a semiconductor. The direct band gap of GO4 is at high symmetry k-point M and is 0.133 eV wide, demonstrating that GO4 is also a semiconductor. With increasing oxygen concentrations, this band gap shrinkage is similar to the previous observed result by Huang et al.45
3.2 Hydroxyapatite and zinc-doped hydroxyapatite
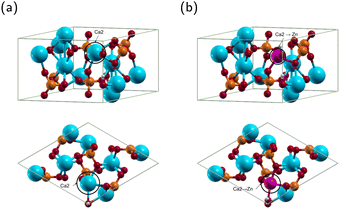
HA exists in monoclinic and hexagonal structures. The monoclinic structure contains 88 atoms, and the hexagonal 44 atoms.46,47 The two structures have minimal energy difference, with the hexagonal structure being only 22 meV per cell higher than the monoclinic.48,49 Most theoretical calculations use the hexagonal phase because it is computationally efficient without losing the accuracy of results.49 Therefore, we will use the hexagonal phase. The structure of hexagonal HA is displayed in Fig. 3(a) and the optimized lattice constants in Table 1.Convergence calculations for HA yielded a kinetic energy cutoff of 20 Hartree and a Monkhorst–Pack k-point grid of 2 × 2 × 4. The optimized HA lattice constants a, b and c were 9.548 Å and 6.921 Å, respectively, in good agreement with other theoretical results using the projector augmented wave method and the generalized gradient approximation.50,51 Notably, Yuan et al. obtained lattice parameters a, b and c of 9.545 Å and 6.892 Å, respectively, compared to experimental results of 9.424 Å and 6.879 Å.50 Our results are thus within 1.3% and 0.6% of experimental results for the a, b and c lattice constants, respectively.52 The above results confirm that our method is reliable.
For ZnHA, previous research has demonstrated that Ca2 is the most stable site for Zn substituting Ca in HA12,53–56 as shown in Fig. 3(b). Convergence calculations for ZnHA yielded a kinetic energy cutoff of 23 Hartree and a Monkhorst–Pack k-point grid of 2 × 2 × 4. The structure of ZnHA is shown in Fig. 3(b). The optimized ZnHA lattice constants a, b and c were 9.520 Å and 6.901 Å, respectively. Compared with the lattice constants of HA, the a, b and c lattice constants of ZnHA decreased. Fig. 3(b) shows that Zn bonds with the nearest hydroxyl group, pulling it off the c axis. Additionally, the interatomic distance between the Zn atom and the surrounding O atoms decreases. The reduction is in agreement with Wang et al., who concluded that the smaller atomic radius of Zn2+ compared to that of Ca2+ would result in a decrease in lattice constants.14 The current calculated Zn–O(OH) distance is 2.058 Å, in agreement with Tang et al. They obtained a distance of 2.020 Å,54 demonstrating that our method is consistent with previous theoretical calculations.
3.3 Hydroxyapatite and graphene oxide composites
In this subsection, the interactions between HA and GO molecules were investigated. The current research will investigate the interface and binding trends of HA and GO superlattice configurations.| Configuration | a, b (Å) | c (Å) | E Bind (eV) |
|---|---|---|---|
| HA/GO1 | 9.792 | 12.873 | −1.078 |
| ZnHA/GO1 | 9.787 | 12.845 | 0.097 |
| HA/GO2 | 9.819 | 12.358 | −1.144 |
| ZnHA/GO2 | 9.814 | 12.856 | −0.299 |
| HA/GO4 | 9.816 | 12.813 | −1.611 |
| ZnHA/GO4 | 9.844 | 12.829 | 0.119 |
The calculated Ca–O atomic distance was 2.329 Å, which is less than the sum of the covalent radii of O (0.73 Å) and Ca (1.74 Å),57 indicating a probable bond formation. Compared with the isolated HA and GO1 molecules, the HA/GO1 complex retains much of its counterparts' features. The GO1 molecule remains continuous, and the epoxy remains in the bridge position. Compared to GO1, the C–O bond length in HA/GO1 increases from 1.458 Å to 1.506 Å, demonstrating that the Ca has an attractive force on the epoxy. The hydroxyl in HA shifts off the c axis, likely due to interactions with neighboring images. The lattice constants of HA were smaller than those of GO1, leading to HA/GO1 having larger lattice parameters than HA.
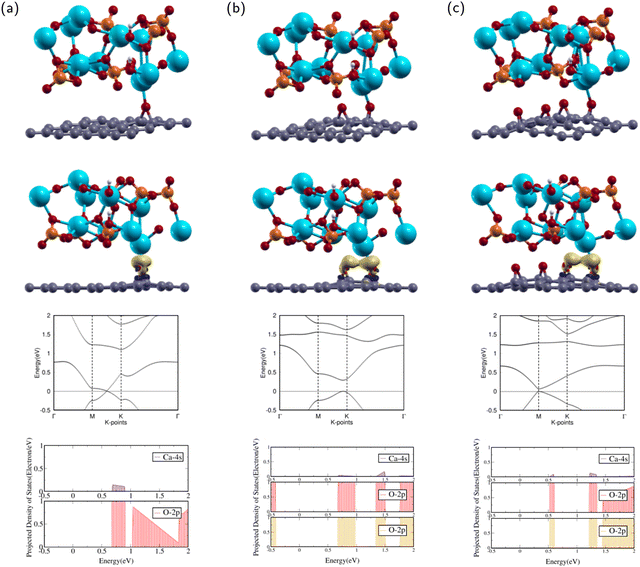
After optimization, the band structure and the PDOS of HA/GO1 were calculated as shown in rows three and four of Fig. 4(a). The band structure contains a Dirac point meeting between high symmetry k-points M and K, as the valence band maximum (VBM) meets the conduction band minimum (CBM) at the Fermi level. This means that HA/GO1 is a zero band gap semi-metal material, similar to the electronic properties of GO1. Since the two structures are similar, it can be shown that the addition of HA does not affect the band structure of GO1 significantly.
The PDOS of the 2p orbitals in O and the 4s orbital in Ca show overlapping regions from 0.6–1.0 eV. The overlap between PDOS peaks of interacting O and Ca atoms indicates the formation of chemical bonds between the atoms.
The attractions between HA and GO1 were confirmed through charge transfer and binding energy analysis of the HA/GO1 composite. As shown by the yellow regions in the second row of Fig. 4(a), there is significant charge accumulation from the O in GO1 towards the Ca atom in HA.
The binding energy was analyzed by using eqn (3). The binding energy of HA/GO1 is −1.078 eV. The negative binding energy means the interaction is energetically favorable, and the small binding energy denotes physisorption.41,58 Since the binding energy of this composite was negative, HA/GO1 is a suitable composite for bone and teeth applications.
The calculated Ca–O atomic distances with the epoxies were 2.275 Å and 2.647 Å. The closest epoxy is within the sum of the covalent radii of O and Ca,57 indicating a probable bond formation. Compared with the isolated HA and GO2 molecules, the HA/GO2 complex retains much of its counterparts' features. The GO2 molecule remains continuous, and both epoxies remain in the bridge position. The epoxy closest to the Ca has C–O bond lengths of 1.460 Å and 1.497 Å, while the epoxy further away has bond lengths 1.453 Å and 1.494 Å. The epoxy closest to the Ca has longer C–O bonds than the other epoxy, demonstrating that the Ca has an attractive force on the closest epoxy. The hydroxyl in HA shifts off the c axis, likely due to interactions with neighboring images.
After optimization, the band structure and the PDOS of HA/GO2 were calculated as shown in rows three and four of Fig. 4(b). The band structure has a direct band gap, as the VBM and the CBM are at the same high symmetry k-point near K. The direct band gap means that HA/GO2 is a semiconductor with a band gap of 0.292 eV, similar to the electronic properties of GO2. Since the two structures are similar, it can be shown that the addition of HA does not affect the band structure of GO2 significantly.
The PDOS of the 2p orbitals in both epoxies and the 4s orbital in Ca show overlapping regions from 0.7–1.0 eV, 1.3–1.5 eV, and 1.75–2 eV. The overlap between PDOS peaks of interacting O and Ca atoms indicates the formation of chemical bonds between the atoms.
The attractions between HA and GO2 were confirmed through charge transfer and binding energy analysis of the HA/GO2 composite. As shown in the second row of Fig. 4(b), there is significant charge accumulation from both epoxies in GO2 towards the Ca atom in HA.
Using eqn (3), the binding energy of HA/GO2 is −1.144 eV. This value is less than that of HA/GO1, demonstrating that an additional epoxy increased binding between the two complexes. The negative binding energy means the interaction is energetically favorable, and the small binding energy denotes physisorption,41,58 which indicates it is a suitable composite for bone and teeth applications.
The calculated Ca–O atomic distances with the two closest epoxies were 2.449 Å and 2.739 Å. The closest epoxy is within the sum of the covalent radii of O and Ca,57 indicating a probable bond formation. HA/GO4 retains much of the structural properties of its counterparts' features. The GO4 molecule remains continuous, and all four epoxies remain in the bridge position. The epoxy closest to the Ca has bond lengths 1.479 Å and 1.500 Å, while the epoxy second closest has bond lengths 1.483 Å and 1.450 Å. The hydroxyl in HA shifts off the c axis, likely due to interactions with neighboring images.
After optimization, the band structure and the PDOS of HA/GO4 were calculated as shown in rows three and four of Fig. 4(c). The band structure has a direct band gap, as the VBM and the CBM are at the same k-point at M. The band gap means that HA/GO4 is a semiconductor with a band gap of 0.067 eV, similar to the electronic properties of GO4. This band gap is much smaller than that of HA/GO2. Since the two structures are similar, it can be shown that adding HA does not affect the band structure of GO4 significantly.
The PDOS of the 2p orbitals in both epoxies and the 4s orbital in Ca show overlapping regions from 0.5–0.6 eV, 1.2–1.4 eV, and 1.5–2 eV. The overlap between PDOS peaks of interacting O and Ca atoms indicates the formation of chemical bonds between the atoms.
The attractions between HA and GO4 were confirmed through charge transfer and binding energy analysis of the HA/GO4 composite. As shown in the second row of Fig. 4(c), there is significant charge accumulation from the two closest epoxies in GO4 towards the Ca atom in HA.
Using eqn (3), the binding energy of HA/GO4 is −1.611 eV. Two additional epoxies had a favorable effect on decreasing the binding energy between the two complexes. The negative binding energy means the interaction is energetically favorable, and the small binding energy denotes physisorption.41,58
Since HA/GO4 showed the most robust interactions out of the three HA composites, HA/GO4 is the most suitable composite for bone and teeth applications. Li et al. studied a HA/GO composite and found that HA is uniformly decorated on the GO surface through van der Waals bonding. These findings are thus consistent with our results that indicate physisorption for HA/GO1, HA/GO2, and HA/GO4.26
3.4 Zinc-doped hydroxyapatite composites
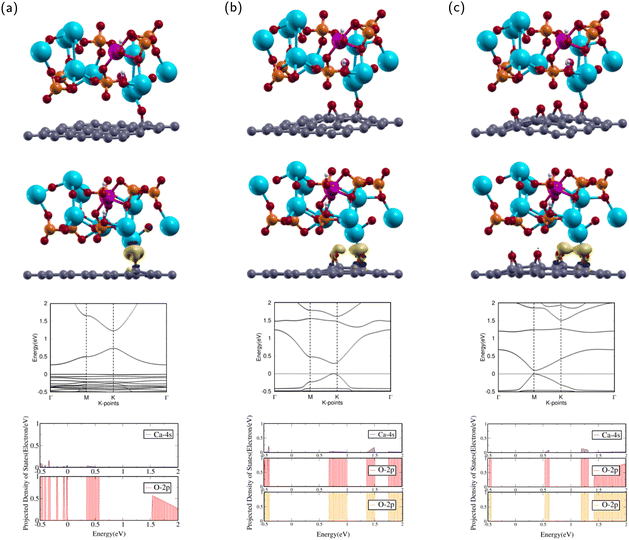
In this subsection, the interactions between ZnHA and GO molecules were investigated. The current research will investigate the interface and binding trends of ZnHA and GO superlattice configurations.The calculated Ca–O interatomic distance was 2.176 Å, which is smaller than that of HA/GO1. This value is less than the sum of the covalent radii of O and Ca,57 indicating a probable bond formation. Compared with the isolated ZnHA and GO1 molecules, the ZnHA/GO1 complex retains some of its counterparts' features. The GO1 molecule remains continuous, but the epoxy breaks away from the bridge position. The C–O bond length is 1.417 Å, which is smaller than that of HA/GO1. The hydroxyl in ZnHA remains shifted off the c axis, with a slight rotational tilt towards the Zn atom.
After optimization, the band structure and the PDOS of ZnHA/GO1 were calculated as shown in rows three and four of Fig. 5a. The band structure is very different from that of GO1. The CBM occurs at high symmetry k-point while the VBM is constant throughout, which means that ZnHA/GO1 is a semiconductor, different from the electronic properties of GO1. Since the two structures are not similar, it can be shown that the addition of ZnHA affects the band structure of GO1 significantly.
The PDOS of the 2p orbitals in O and the 4s orbital in Ca show overlapping regions from −0.5 to 0.0 and 0.4–0.6 eV. The overlap between PDOS peaks of interacting O and Ca atoms indicates the formation of chemical bonds between the atoms.
The interactions between ZnHA and GO1 were confirmed through charge transfer and binding energy analysis of the ZnHA/GO1 composite. As shown in the second row of Fig. 5(a), there is significant charge accumulation from the O in GO1 towards the Ca atom in ZnHA and slight depletion from the Ca towards the O.
The binding energy was analyzed by using eqn (4). The binding energy of ZnHA/GO1 is 0.097 eV. The positive binding energy denotes an energetically unfavorable interaction between ZnHA and GO1, which indicates it is not a suitable composite for bone and teeth applications.
The calculated Ca–O interatomic distance with neighboring epoxies was 2.320 Å and 2.934 Å. The closest epoxy is within the sum of the covalent radii of O and Ca,57 indicating a probable bond formation. Compared with the isolated ZnHA and GO2 molecules, ZnHA/GO2 retains much of its counterparts' features. The GO2 molecule remains continuous and bends slightly upwards. Both epoxies remain in the bridge position. The epoxy closest to the Ca has bond lengths 1.458 Å and 1.499 Å, while the epoxy further away has bond lengths 1.449 Å and 1.487 Å. The hydroxyl remains shifted from the c axis.
After optimization, the band structure and the PDOS of ZnHA/GO2 were calculated as shown in rows three and four of Fig. 5(b). The band structure has a direct band gap, as the VBM and the CBM are at the same high symmetry k-point near K. The direct band gap means that ZnHA/GO2 is a semiconductor with a band gap of 0.288 eV, similar to the electronic properties of GO2. Since the two structures are similar, it can be shown that the addition of HA does not affect the band structure of GO2 significantly.
The PDOS of the 2p orbitals in both epoxies and the 4s orbital in Ca show overlapping regions from 0.6–1.0 eV, 1.3–1.5 eV, and 1.75–2 eV. The overlap between PDOS peaks of interacting O and Ca atoms indicates the formation of chemical bonds between the atoms.
The attractions between ZnHA and GO2 were confirmed through charge transfer and binding energy analysis of the ZnHA/GO2 composite. As shown in the second row of Fig. 5(b), there is significant charge accumulation from both epoxies in GO2 towards the Ca atom in ZnHA. This behavior is similar to that of HA/GO2.
Using eqn (4), the binding energy of ZnHA/GO2 is −0.299 eV. This value is greater than the binding energy of ZnHA/GO1, demonstrating that an additional epoxy had a favorable effect on decreasing the binding energy between the two complexes. The negative binding energy means the interaction is energetically favorable, and the small binding energy denotes physisorption.41,58 Because ZnHA/GO2 has negative binding energy, it is a suitable composite for bone and teeth applications.
The calculated Ca–O bond lengths with neighboring epoxies were 2.380 Å and 2.735 Å. The closest epoxy is within the sum of the covalent radii of O and Ca,57 demonstrating a probable bond. As with ZnHA/GO2, ZnHA/GO4 retains much of the structural properties of its counterparts' features. The GO4 molecule remains continuous, and all four epoxies remain in the bridge position. The epoxy closest to the Ca has bond lengths 1.446 Å and 1.466 Å, while the epoxy second closest has bond lengths 1.450 Å and 1.486 Å. The hydroxyl in HA shifts off the c axis, likely due to interactions with neighboring images. ZnHA/GO4 has the largest a, b lattice constant of the six composites.
After optimization, the band structure and the PDOS of ZnHA/GO4 were calculated as shown in rows three and four of Fig. 5(c). The band structure has a direct band gap, as the VBM and the CBM are at the same high symmetry k-point at M. This band gap means that ZnHA/GO4 is a semiconductor with a band gap of 0.095 eV, similar to the electronic properties of GO4. The band structures of HA/GO4 and ZnHA/GO4 are also similar, which means that doping Zn into HA does not change the electronic properties of the composite. The PDOS of the 2p orbitals in both epoxies and the 4s orbital in Ca show overlapping regions from 0.5–0.6 eV, 1.2–1.3 eV, and 1.4–2 eV. The overlap between PDOS peaks of interacting O and Ca atoms indicates the formation of chemical bonds between the atoms.
The attractions between ZnHA and GO4 were confirmed through charge transfer and binding energy analysis of the ZnHA/GO4 composite. As shown in the second row of Fig. 5(c), there is significant charge accumulation from the two closest epoxies in GO4 towards the Ca atom in HA.
Using eqn (4), the binding energy of ZnHA/GO4 is 0.119 eV. The positive binding energy means the interaction is energetically unfavorable, demonstrating that two additional epoxies negatively impacted binding. Lower binding energies are necessary for ZnHA/GO4 to be a strong composite.
Out of the three ZnHA composites, ZnHA/GO2 showed the most substantial interactions. Zn decreases the binding capability between GO and ZnHA. This result agrees with Yuan et al., who found that increasing amounts of Zn doping decreased interfacial interactions between ZnHA and Graphene due to lower crystallinity.59 ZnHA boasts beneficial properties for selective O concentrations.
Future research may explore the interactions between different surfaces of HA and ZnHA and other functional groups and the impact of higher amounts of oxygen concentration on the interfacial interactions. The impact of the experimental ratio of Zn and O on the interaction strength between ZnHA and GO is a point of investigation.
4 Conclusions
In this study, the interactions between GO and HA or ZnHA were investigated using DFT calculations. HA, ZnHA, and different oxygen concentrations were investigated. With increasing amounts of oxygen, the binding between HA and GO was stronger, while for ZnHA, the strongest binding energy was observed for 6.25% oxygen concentration. ZnHA is selective towards specific graphene oxide oxygen concentrations, and doping Zn decreases binding strength between ZnHA and GO.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Dr Geifei Qian for his technical support throughout our research.Notes and references
- V. S. Kattimani, S. Kondaka and K. P. Lingamaneni, Bone Tissue Regener. Insights, 2016, 7, 9–19 CrossRef.
- M. Šupová, Ceram. Int., 2015, 41, 9203–9231 CrossRef.
- V. Saxena, I. Shukla and L. M. Pandey, Mater. Biomed. Eng.: Nanobiomater. Tissue Eng., 2019, 205–249 CAS.
- D. Arcos and M. Vallet-Regí, J. Mater. Chem. B, 2020, 8, 1781–1800 RSC.
- M. S. Gezaz, S. M. Aref and M. Khatamian, Mater. Chem. Phys., 2019, 226, 169–176 CrossRef.
- I. R. de Lima, G. G. Alves, C. A. Soriano, A. P. Campaneli, T. H. Gasparoto, E. S. R. Jr, L. A. de Sena, A. M. Rossi and J. M. Granjeiro, Soc. Biomater., 2011, 98, 351–358 Search PubMed.
- A. Garley, S. E. Hoff, N. Saikia, S. Jamadagni, A. Baig and H. Heinz, J. Phys. Chem. C, 2019, 123, 16982–16993 CrossRef CAS.
- F. Ren, R. Xin, X. Ge and Y. Leng, Acta Biomater., 2009, 5, 3141–3149 CrossRef CAS.
- G. Meng, Z. Wu, R. Yao, J. He, W. Yao and F. Wu, Regener. Biomater., 2019, 349–359 CAS.
- R. J. Friederichs, H. F. Chappell, D. V. Shepherd and S. M. Best, Interface, 2015, 12, 20150190 Search PubMed.
- Y. Huang, X. Zhang, H. Mao, T. Li, R. Zhao, Y. Yan and X. Pang, RSC Adv., 2015, 5, 17076–17086 RSC.
- A. Anwar, S. Akbar, A. Sadiqa and M. Kazmi, Inorg. Chim. Acta, 2016, 453, 16–22 CrossRef CAS.
- M. Furko and C. Balázsi, Materials, 2020, 13, 4690 CrossRef CAS PubMed.
- J. Wang, R. Wang, M. Yang and D. Xu, J. Mater. Chem. B, 2022, 10, 1281–1290 RSC.
- H. Shi, Z. Zhou, W. Li, Y. Fan, Z. Li and J. Wei, Crystals, 2021, 11, 149 CrossRef CAS.
- M. Li, P. Xiong, F. Yan, S. Li, C. Ren, Z. Yin, A. Li, H. Li, X. Ji, Y. Zheng and Y. Cheng, Bioactive Mater., 2018, 3, 1–18 CrossRef PubMed.
- H. Nosrati, R. Sarraf-Mamoory, D. Q. S. Le, A. H. Ahmadi, M. C. Perez and C. Bünger, Ceram. Int., 2020, 46, 20081–20087 CrossRef CAS.
- M. A. Rafiee, J. Rafiee, Z. Wang, H. Song, Z.-Z. Yu and N. Koratkar, ACS Nano, 2009, 2, 12 Search PubMed.
- A. K. Pathak and S. R. Dhakate, J. Polym. Sci., 2021, 59, 84–99 CrossRef CAS.
- L. Zhang, W. Liu, C. Yue, T. Zhang, P. Li, Z. Xing and Y. Chen, Carbon, 2013, 61, 105–115 CrossRef CAS.
- M. Z. Nizami, S. Takashiba and Y. Nishina, Appl. Mater. Today, 2020, 19, 100576 CrossRef.
- K. Zhou, P. Yu, X. Shi, T. Ling, W. Zeng, A. Chen, W. Yang and Z. Zhou, ACS Nano, 2019, 13, 9595–9606 CrossRef CAS PubMed.
- J. H. Lee, Y. C. Shin, S.-M. Lee, O. S. Jin, S. H. Kang, S. W. Hong, C.-M. Jeong, J. B. Huh and D.-W. Han, Sci. Rep., 2015, 5, 18833 CrossRef CAS PubMed.
- A. T. Lawal, Biosens. Bioelectrics, 2019, 141, 111384 CrossRef CAS.
- I. Maity, K. Ghosh, H. Rahaman and P. Bhattacharyya, IEEE Trans. Device Mater. Reliab., 2018, 17, 738–745 Search PubMed.
- M. Li, Q. Liu, Z. Jia, X. Xu, Y. Cheng, Y. Zheng, T. Xi and S. Wei, Carbon, 2014, 67, 185–197 CrossRef CAS.
- Y. Liu, J. Huang, M. Niinomi and H. Li, Ceram. Int., 2016, 42, 11248–11255 CrossRef CAS.
- H. Nosrati, R. S. Mamoory, D. Q. S. Le and C. Bünger, Diamond Relat. Mater., 2019, 100, 107561 CrossRef CAS.
- H. Nosrati, R. Sarraf-Mamoory, D. Q. S. Le, R. Z. Emameh, M. C. Perez and C. E. Bünger, Sci. Rep., 2020, 10, 8552 CrossRef CAS PubMed.
- H. Maleki-Ghaleh, M. Siadati, A. Fallah, B. Koc, M. Kavanlouei, P. Khademi-Azandehi, E. Moradpur-Tari, Y. Omidi, J. Barar, Y. Beygi-Khosrowshahi, A. P. Kumar and K. Adibkia, Int. J. Mol. Sci., 2021, 22, 9564 CrossRef CAS PubMed.
- V. Chopra, J. Thomas, A. Sharma, V. Panwar, S. Kaushik, S. Sharma, K. Porwal, C. Kulkarni, S. Rajput, H. Singh, K. Jagavelu, N. Chattopadhyay and D. Ghosh, ACS Biomater. Sci. Eng., 2020, 6(12), 6710–6725 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- X. Gonze, G.-M. Rignanese, M. Verstraete, J.-M. Beuken, Y. Pouillon, R. Caracas, F. Jollet, M. Torrent, G. Zerah, M. Mikami, P. Ghosez, M. Veithen, J.-Y. Raty, V. Olevano, F. Bruneval, L. Reining, R. Godby, G. Onida, D. R. Hamann and D. C. Allan, Zeitschrift für Kristallographie, 2005, 220, 558–562 CrossRef CAS.
- X. Gonze, B. Amadon, P. Anglade, J. Beuken, F. Bottin, P. Boulanger, F. Bruneval, D. Caliste, R. Caracas, M. Côté, T. Deutsch, L. Genovese, P. Ghosez, M. Giantomassi, S. Goedecker, D. Hamann, P. Hermet, F. Jollet, G. Jomard, S. Leroux, M. Mancini, S. Mazevet, M. Oliveira, G. Onida, Y. Pouillon, T. Rangel, G. Rignanese, D. Sangalli, R. Shaltaf, M. Torrent, M. Verstraete, G. Zerah and J. Zwanziger, Comput. Phys. Commun., 2009, 180, 2582–2615 CrossRef CAS.
- P. Blöch, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- A. R. Tackett, N. A. W. Holzwarth and G. E. Matthews, Comput. Phys. Commun., 2001, 135, 348–376 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- N. Holzwarth, A. Tackett and G. Matthews, Comput. Phys. Commun., 2001, 135, 329–347 CrossRef CAS.
- P. Borlido, J. Schmidt, A. W. Huran, F. Tran, M. A. L. Marques and S. Botti, npj Comput. Mater., 2020, 6, 96 CrossRef CAS.
- H. T. Larijani, M. D. Ganji and M. Jahanshanhi, RSC Adv., 2015, 5, 92843–92857 RSC.
- A. C. Rossi-Fernández, N. Villegas-Escobar, D. Guzmán-Angel, S. Gutiérrez-Oliva, R. M. Ferullo, N. J. Castellani and A. Toro-Labbé, J. Mol. Model., 2020, 26, 33 CrossRef PubMed.
- M. D. Esrafili and L. Dinparast, J. Mol. Graphics Modell., 2018, 80, 25–31 CrossRef CAS PubMed.
- W. Liu and G. Speranza, ACS Omega, 2021, 2021(6), 6195–6205 CrossRef PubMed.
- C. Liu and X. Luo, J. Mater. Chem. B, 2021, 9, 2736 RSC.
- H. Huang, Z. Li, J. She and W. Wang, J. Appl. Phys., 2012, 054317, 111 Search PubMed.
- N. Y. Mostafa and P. W. Brown, J. Phys. Chem. Solids, 2007, 68, 431–437 CrossRef CAS.
- V. S. Bystrov, E. Costa, S. Santos, M. M. Almeida, A. L. Kholkin, Y. D. Dekhtyar, A. V. Bystrova, S. Kopyl and E. Paramonova, Proc. ISAF-ECAPD-PFM 2012, 2005, 1–3 Search PubMed.
- A. Slepko and A. A. Demkov, Phys. Rev., 2011, 84, 134108 CrossRef.
- V. Bystrov, Mat. Biolog. Bioinform., 2017, 12, 14–54 CrossRef CAS.
- Z. Yuan, S. Li, J. Liu, X. Kong and T. Gao, Int. J. Hydrogen Energy, 2018, 43, 13639–13648 CrossRef CAS.
- J. Sun, Y. Song, G. Wen, Y. Wang and R. Yang, Mater. Sci. Eng., C, 2012, 33, 1109–1115 CrossRef PubMed.
- K. Sudarsanan and R. Young, Acta Cryst., 1969, 25, 1534 CrossRef CAS.
- W. Hu, J. Ma, J. Wang and S. Zhang, Mater. Sci. Eng., C, 2012, 32, 2404–2410 CrossRef CAS.
- Y. Tang, H. F. Chappell, M. T. Dove, R. J. Reeder and Y. J. Lee, Biomaterials, 2009, 30, 2864–2872 CrossRef CAS PubMed.
- M. Matos, J. Terra and D. Ellis, J. Phys.: Condens. Matter, 2010, 22, 145502 CrossRef CAS PubMed.
- H. Murata, K. Shitara, I. Tanaka, A. Nakahira, T. Mizoguchi and K. Matsunaga, J. Phys.: Condens. Matter, 2010, 22, 384213 CrossRef.
- Periodic Table – Ptable, https://ptable.com, accessed: 2022-07-15.
- S. Ayissi, P. A. Charpentier, N. Farhangi, J. A. Wood, K. Palotás and W. A. Hofer, J. Phys. Chem. C, 2013, 117, 25424–25432 CrossRef CAS.
- Q. Yuan, J. Wu, C. Qin, A. Xu, Z. Zhang, Y. Lin, Z. Chen, S. Lin, Z. Yuan, X. Ren and P. Zhang, Mater. Chem. Phys., 2017, 199, 122–130 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |