Open Access Article
Open Access ArticleA combined experimental and molecular simulation study on stress generation phenomena during the Ziegler–Natta polyethylene catalyst fragmentation process†
Antonio
De Nicola
 a,
Vasileios
Touloupidis
c,
Vasileios
Kanellopoulos
c,
Alexandra R.
Albunia‡
*c and
Giuseppe
Milano‡
*b
a,
Vasileios
Touloupidis
c,
Vasileios
Kanellopoulos
c,
Alexandra R.
Albunia‡
*c and
Giuseppe
Milano‡
*b
aScuola Superiore Meridionale, Largo San Marcellino 10, 80132 Napoli, Italy
bDipartimento di Ingegneria Chimica dei Materiali e della Produzione Industriale, Università degli Studi di Napoli Federico II, Piazzale V. Tecchio 80, 80125 Napoli, Italy. E-mail: giuseppe.milano@unina.it
cInnovation & Technology, Borealis Polyolefine GmbH, St. Peter Strasse 25, 4021 Linz, Austria. E-mail: alexandra.albunia@borealisgroup.com
First published on 17th October 2022
Abstract
The morphology of particles obtained under different pre-polymerization conditions has been connected to the stress generation mechanism at the polymer/catalyst interface. A combination of experimental characterization techniques and atomistic molecular dynamics simulations allowed a systematic investigation of experimental conditions leading to a certain particle morphology, and hence to a final polymer with specific features. Atomistic models of nascent polymer phases in contact with magnesium dichloride surfaces have been developed and validated. Using these detailed models, in the framework of McKenna's hypothesis, the pressure increase due to the polymerization reaction has been calculated under different conditions and is in good agreement with experimental scenarios. This molecular scale knowledge and the proposed investigation strategy would allow the pre-polymerization conditions to be better defined and the properties of the nascent polymer to be tuned, ensuring proper operability along the whole polymer production process.
Introduction
Polyolefins (PO) have contributed to shaping the modern world. Being very versatile, they are used in a wide range of applications and their demand is still expected to increase in volume and applications in the next few decades, imposing an urgent need for sustainable production processes and for improving end-of-life management.1,2The target of all polyolefin manufacturing businesses is to design a process to promote polymer chain growth. For industrial applications, polyethylene (PE) can be produced with both free coordination catalysts (i.e., low pressure PO production technologies) and radical initiators (i.e., high pressure PO production technologies). Coordination catalysts have the huge advantage of fine control of the polymer molecular microstructure leading to the production of polyolefins with a wide range of properties unimaginable before their discovery. The reason for the success of modern industrial polymerization processes is largely due to the evolution of catalyst technologies and to their achieved level of sophistication towards producing multi-modal grades. Academic and industrial olefin catalytic processes have been developed and implemented since the original discoveries of Ziegler and Natta,3 and Hogan and Banks (Phillips catalysts).4 Nowadays, huge volume plants are run in a very cost competitive way. Still, there is margin to optimize production processes and make them more efficient and sustainable, for example in terms of energy efficiency, smooth and controlled operations and optimal product design.5–10
Most low pressure olefin polymerization processes utilize heterogeneous catalysts in multi-stage reactor configurations consisting of two- or three-phase reactors connected in series. An optimal process design must take into account different aspects influencing the final properties of the produced polymer. As an example, the mass and heat transfer phenomena occurring during the process may affect the polymerization rate and the polymer molecular microstructure. The evolution of the catalyst (synthesized using MgCl2 or silica to impregnate a variable quantity of active sites) internal morphology on polymer particle growth during the early stage of polymerization is another striking example. Indeed, the way the nascent polymer induces the fragmentation of the catalyst particles determines the internal and external morphological properties of the polymer particles which in turn, affect the operability of the plant, its productivity, and the final polymer properties.4 All these phenomena mentioned above take place during the dynamic operation of the polymerization reactor, while all aspects controlling those phenomena have a significant impact on both economic and environmental costs. A standard industrial catalytic polymerization process is schematized below (Scheme 1).
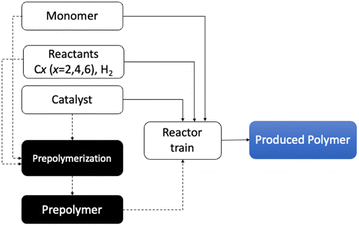 | ||
| Scheme 1 Industrial flow-chart process of a typical fourth-generation plant for polyethylene polymerization. | ||
In a typical catalytic olefin polymerization process the catalyst is continuously fed to the reactor train together with the addition of a co-catalyst, monomer, comonomer, diluent, and chain transfer agents. The pre-polymerization process involves injecting the catalyst into a slurry reactor that usually operates under relatively mild conditions.1 In this step, 10–100 grams of polymer per gram of catalyst is produced. Then, the pre-polymerized powder (prepolymer) is injected into the main reactor. The purpose of the pre-polymerization is to improve the control of catalyst particle morphology and obtain an appropriate size of the catalyst particle as well as nascent polymer for the injection into the main reactor train. This is needed since the process conditions in the main reactor are such that the local reaction rates are quite high, and “virgin” catalyst particles would not maintain their integrity without pre-polymerization. In other words, the pre-polymerization step allows just enough polymer to be generated, which means that the catalyst particles fragment but not so much and not too quickly that they disintegrate. For simplicity, we will refer to the term “particle” as the catalyst particle plus a small fraction of polymer which is produced in the pre-polymerization step and can trigger the fragmentation of catalyst particles. It has to be noted that smooth initial fragmentation of the catalyst particle contributes to lessening of the internal heat and mass transfer limitations.11
The reaction taking place in the main reactor train is the chain propagation, in the sense of the addition of new monomer (or comonomer) building blocks in the polymeric chain initiated at the catalyst active sites. Hydrogen is added into the reactor to control the molecular weight distribution (MWD), since it acts as the transfer agent causing the break of the developed chain and controlling the length of the produced polymer. Comonomer addition, apart from the apparent increase of its content of the developed polymer, further reduces the crystallization potential of the nascent polymer, increases the possibility of diffusion of the monomer and comonomer within the catalyst particle, and affects the solubility behaviour of the monomer too (co-solubility effect).12–16 Usually, a monomer/diluent recycle step precedes the storage of the product.
It is well known that the particle morphology controls the rate at which the reactive species reach the active sites and, hence, the molecular properties of the produced polymer like MWD, the copolymer composition distribution (CCD) and the concentration of the polymer branches. It is worth noting that poor particle morphology (defined, e.g., by shape, bulk density, roughness) would lead to risks of agglomeration, sheeting and chunking phenomena, which largely affect the reactor's operability. Optimal control of particle morphology is directly related to: (i) the growth rate of the catalyst particles during the process. (ii) The selection of the pre-polymerization and polymerization conditions such as the temperature, pressure and the component composition in the reactor.8,17–19 (iii) How the nascent polymer accumulates in the catalyst particles during the polymerization reaction leading to the particle fragmentation. Based on the above considerations, it is clear that the fragmentation phenomena are pivotal in the particle morphology evolution. A deep understanding of that phenomena would lead to further optimization of the process.5–10 Indeed, even smaller variation of the properties of the fragmented particles in the early stages of polymerisation can be amplified during the successive polymerization steps and lead to very different morphologies. In practice, control of the initial fragmentation in the plants is mainly handled based on experience and best practices. Besides temperature, monomer and diluent, the particle morphology is adjusted by adding hydrogen (known to improve the flowability) and comonomers, e.g. 1-butene or 1-hexene (known to improve productivity, and at the same time decreasing the polymer crystallinity till the point to lead to particle stickiness).
Generally speaking, fragmentation can be seen as the first step of the polymerization process where the accumulated polymer causes the rupture of the local catalyst support material.11 More specifically, the accumulation of mechanical stresses on the walls of the pores of the catalyst particles causes the fragmentation (see Scheme 2). The mechanism of particle break-up and the evolution of the internal morphology are the result of a trade-off between the rate of polymerization (rate of stress generation), the structural arrangement of the catalyst particle (distribution and structure of the pores) and the polymer properties at the point of stress. As an example, the MgCl2 support used in the Ziegler–Natta catalysts has been shown to be more friable compared to the silica support,20–23 resulting in a faster fragmentation process.
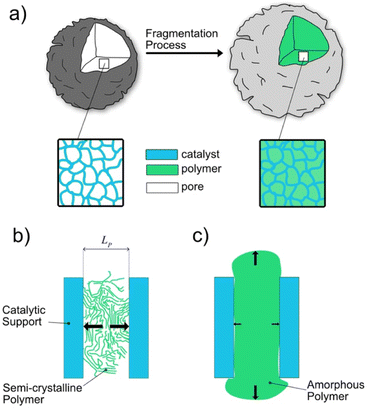 | ||
| Scheme 2 (a) Schematic representation of the fragmentation process. On the left a particle with no active polymerization reaction is shown. When the polymerization takes place, from the catalyst surface, the polymer starts to fill the pore more and more. The stress is accumulated up to fragmentation (particle on the right). Limiting scenarios for the catalytic support fragmentation proposed by McKenna: (b) crystalline polymer cannot flow out of pores and large stress is accumulated on the walls (black arrows). (c) Amorphous polymer flowing out (most of the stress is released laterally, black arrows). A bi-dimensional finite pore is considered for simplicity.11 | ||
From the experimental point-of-view, it is rather difficult to track the early stages of fragmentation. Recently, a combination of X-Ray ptychography and fluorescence nano-tomography has been used to get a 3D-spatial resolution of titanium atoms (Ziegler–Natta catalyst family) involved in the early stage of olefin polymerization.24 The authors revealed a coexistence of different mechanisms, involving the core of the particle and the diffusion of monomers thought it, which contribute to the fragmentation process.25
To the best of our knowledge, a description at the molecular level (∼10 nm, the typical length-scale of atomistic modelling) and a fundamental understanding of the interfacial phenomena controlling the early stage of fragmentation is still missing from the scientific literature of heterogeneous catalysis.
As for microscopic modelling, most of the molecular mechanics and quantum chemical studies in the field of Ziegler–Natta catalysis focus on the nature and properties of Ti-species: active site formation and the energetic pathways of the polymerization reaction,26–34 and understanding of the role of Lewis bases in the support morphology and active site polymerization behaviour, as well as in the MgCl2 surface morphology.35,36 On the other hand, macroscopic modelling approaches focus on the selection of the operation conditions of reactors to perform optimization studies.5,17–19,37–44 There are two examples of this class of modeling approaches: Polymer Flow (PF) models are a typical example of modeling aimed to predict the final polymer properties like MWD, CCD and reaction rate;8,45 morphology models (MF) based on experimental information, like porometer data,17–19 are used to describe how the fragmentation takes place during the polymerization reaction.17,40,41,45,46 However, though they can well describe the fragmentation mechanism, they are not predictive “a priori” because experimental morphology information is needed at different stages of the process. Moreover, a connection between microscopic atomic and macroscopic modeling approaches is still missing. A full integration of these two classes of approaches is amenable, because this would be a powerful tool to gain a fundamental understanding of the phenomena involved in the polymerization process.
Herein, we provide an unprecedented contribution to the field by linking the morphologies of particles obtained under different conditions to the stress generation mechanism at the polymer/catalyst wall interface by combining experimental characterization and atomistic molecular dynamics (MD) simulations. The paper is organized as follows: in the Results section, a systematic investigation of experimental conditions leading to a certain particle morphology, and hence to a final polymer with specific characteristics, is discussed. The modelling strategy, purposely designed to investigate the stress generation at the atomic level, is then reported and discussed. Effect of crystallinity of PE and then of additives on the stress generation is evaluated through MD simulations and compared with experiments. Finally, in the Conclusion section the main results are summarized. Both, experimental and computational methods are briefly reported in the Experimental method section.
Results
Polymer particle morphologies produced under different conditions
Since the particle morphology is a direct consequence of the fragmentation pattern,8,11,47,48 we have experimentally investigated the morphologies obtained under a relatively broad range of conditions. In Fig. 1 a series of SEM images are shown for PE samples produced with a MgCl2 supported catalyst at different temperatures (from 313 K to 353 K), or with different compositions (samples B and C: at the same temperature 323 K and different monomer (C2) concentrations; sample D: at 323 K with H2; sample F: at 343 K with comonomer (C6)). SEM images show minor but important differences between all morphologies. For instance, the samples A and E, at 313 and 353 K respectively, show significant differences in the surface roughness. While for the samples A–C the differences in terms of roughness are minor, sample F exhibits a smoother surface, and samples D and E are comparable. An empirical correlation between the particle morphology and the nascent polymer properties can be gained by linking the bulk density with the heat of fusion and the melting temperature of the nascent polymer (collected by DSC during the first heating scan).In Fig. 1H–I, a dataset of melting temperature, heat of fusion and bulk density is reported. From this figure it is clear that high heats of fusion and melting temperatures correspond to a low bulk density indicating a high degree of crystallinity of the nascent polymer. Keeping constant the temperature of polymerization, the addition of a third component, like H2, or a higher C2 concentration, alters the physical state of the produced polymer. This effect can be seen by comparing the samples B and D (see the samples labelled with B and D in the panels G and H of Fig. 1). Both are produced at 323 K, with the difference that sample B contains only C2, and sample D is produced in the presence of H2.
In particular, the addition of hydrogen reduces the lamellar length leading to a polymer with a lower melting temperature and higher bulk density. More in general, a low melting temperature leads to a high bulk density. The reported empirical correlations agree with the two extreme scenarios proposed by McKenna.11 In his hypothesis the particle morphology is controlled by the physical state of the nascent polymer.
In Scheme 2, a representation of the fragmentation process is provided. Cartoons showing particles before and after the polymerization reaction are compared in Scheme 2a. While in Scheme 2b and c, both scenarios hypothesized by McKenna for the stress generation mechanism are depicted. Depending on experimental conditions, the nascent polymer can be in the semicrystalline or amorphous state. In the first case, local mechanical stress starts to accumulate quickly on catalyst walls since when the nascent polymer just covers the pore dimension Lp (see Scheme 2b). Due to the rigidity of crystal domains the accumulated stress is not released, causing a rapid fragmentation of the catalyst walls with a consequential lowering of the bulk density. This scenario is compatible with a polymer morphology reported in Fig. 1A in which the nascent polymer has a high overall crystallinity. In contrast, if the polymer is in the amorphous state, or possesses a low crystallinity, the stress is released by the polymer squeezing out from the pore (Scheme 2c and panel E of Fig. 1).
Molecular dynamics simulations
The MD technique is used to study PE semi-crystalline or amorphous phases in contact with the MgCl2 surface (the inert crystalline support of the Ziegler–Natta catalyst). The adopted detailed atomistic models allow the chemical structures of species, the composition, and physical states of the systems (semicrystalline or amorphous, temperature conditions, presence of additives, etc.) to be connected to their thermodynamic properties. We designed two systems representing the extreme scenarios discussed above. We aimed to study the phenomena occurring at the interface between the MgCl2 surface and amorphous or semi-crystalline phases of PE.Crystallization of PE at the interface with MgCl2: structural properties and crystalline domain stability
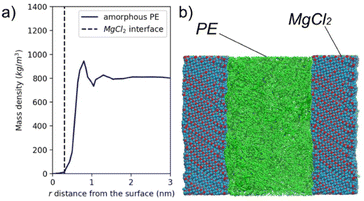
The crystalline phase of PE is obtained by using the TraPPE-UA (transferable potentials for phase equilibria, united atom) force-field, developed by Siepmann49 and parameterized to match the equilibrium properties of linear and branched alkanes and for different properties relevant to the present study. In addition to the PE model, an atomistic model of an MgCl2 crystal surface is employed. A detailed description of the models and of their validations are reported in the Method and ESI sections.† In the following, we report MD simulations of PE/MgCl2 interfaces and interphases of systems composed of 111 PE chains in contact with the surface (110) of MgCl2.The amorphous PE, simulated at 500 K, shows a significant structuration at the interface with MgCl2, due to the presence of a solid surface (Fig. 2a). In particular, the PE mass density profile averaged by collecting atomic positions shows a maximum value at ∼0.6 nm from the surface, corresponding to an increase of 20% of mass density with respect to the bulk value of 780 kg m−3. The highest peak is at a distance roughly equal to the close contact distance between PE atoms and the crystalline surface (i.e. sum of the van der Waals radii of the CH2 group and Mg and Cl atoms, see the ESI† for the model parameters). After some further structuring (an oscillation weaker than the previous first peak), at a distance beyond 1.5 nm, the density attains an average almost constant value equal to the bulk one. Similar density profiles were observed in several computational studies on confined systems by investigating the polymer/solid interfaces with either atomistic50–52 or coarse-grained models.53,54 The behavior of density of a liquid phase confined between walls is mainly determined by the entropic effect, moreover net attractive interactions between the liquid phase and the wall can contribute to its enhancement.55
Fig. 3a shows the mass density temporal evolution of PE during the quenching procedure (from 500 to 280 K). It can be observed that after ∼25 ns of induction time, there is a sudden increase of the density, which reaches, at the end, a plateau of about 946 kg m−3. The observed trend is typical of a first order liquid–solid transition. In the time interval 25–100 ns, density fluctuations promote the nucleation and the growth of crystal domains. A more detailed picture of crystalline domain formation can be gained by having a look at the sequence of density isosurfaces shown in Fig. 3b. The reported isosurfaces, computed at different times of crystalline domain formation, represent spatial regions where the PE density is 1.3 times larger than the average density of the last semicrystalline configuration. The presence of a source of heterogeneities, in our case the interface with the MgCl2 surface, induces the crystallization of PE. This is a well-known effect used in many technological applications.56–60 We observe a typical case of heterogeneous nucleation in which regions with higher probability of nucleation (higher PE density) are found at the MgCl2 surface, see the isosurfaces at 25, 50 and 80 ns in Fig. 3b. The effect of unidimensional confinement in the crystallization process has been computationally studied, via MD or MC (Monte Carlo), for a variety of polymers and substrates.61–67 In particular, Frenkel et al. investigated the structure and free energy landscape of a semiflexible lattice polymer during the crystallization occurring in the presence of an interface.61 More recently, Yamamoto has shown that even the fast crystallization obtained in computer modelling can reproduce morphologies and lamellae orientation in agreement with those experimentally observed from ultrafast undercooling of a PE melt.64 Rutledge and co-workers deeply studied the crystallization of PE under several conditions,68–72 focusing on the nucleation at the crystalline/melt interface.73
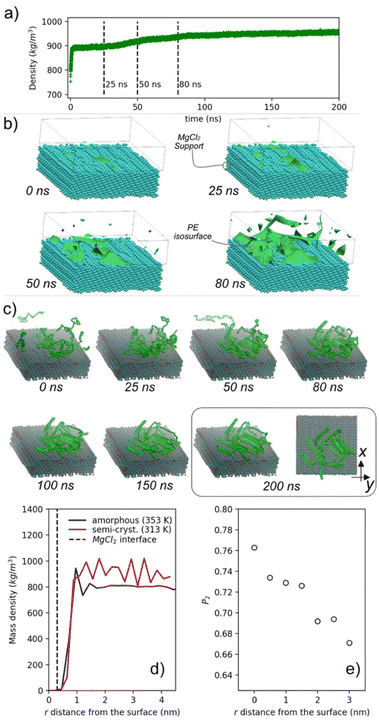 | ||
| Fig. 3 (a) Temporal variation of PE mass density, for the system PE in contact with a crystalline slab of MgCl2, during the first 100 ns of the fast quenching procedure. (b) Density isosurfaces of PE (in green) at different stages of simulation. The MgCl2 bead support is reported together with the isosurfaces. (c) Snapshot sequence of selected chains. Selected chains belong to spatial regions with a mass density 1.3 times larger than the average density of the last configuration. (d) Mass density profiles of amorphous (blue line) and semi-crystalline (red line) phases of PE in contact with a crystalline slab of MgCl2 (black discontinuous line). Profiles in panels (d) and (e) are calculated in the direction normal to the MgCl2 surface and time averaged over the last 50 ns of NPT production runs. (e) Orientational order parameter P2 as a function of the distance r from the surface. The final configuration has a degree of crystallinity of ∼68%, like those obtained from the homogeneous melt using the same quenching procedure (see the ESI† for further details). | ||
The typical lamellar morphology starts to appear after about 10 ns, reaching in ∼200 ns a well-defined structuration. A snapshot sequence of PE crystalline domain formation is shown in Fig. S13.† Lateral and top views of the snapshot at 200 ns show a disordered orientation of the lamellae with respect to the MgCl2 surface. In Fig. 3c, the conformations assumed by a selection of representative PE chains, in contact with the MgCl2 surface, are reported at different stages of the crystallization. At the starting time (t = 0 ns), chain segments in contact with the MgCl2 surface start to order themselves forming a crystalline stem (nucleus). Then, the addition/formation of further crystalline stems leads to a growth of the initial nucleus (see the snapshot sequence at 25, 50, 80 and 200 ns in Fig. 3c). In experiments, it has been observed that a confined environment contributes to modifying the growth and crystal orientation.59 In particular, the crystal domain orientation depends on both the polymer film thickness and polymer/substrate interactions.74,75 A thin film of the order of 100 nm shows a preferential parallel orientation of lamellae with respect to the substrate, while ultrathin films, <100 nm but higher than the average random coil chain size can induce both edge-on (perpendicular) or flat-on (parallel) orientation of the lamellae with respect to the substrate. In a quasi-two dimensional ultrathin film, where the thickness approaches the average size of random coil chains, the observed crystalline morphologies have low orientation, resembling seaweed and dendrites.76,77 Typical examples are reported for PET,78 PEO75 and PE.79 In our simulated systems we found, in agreement with experimental observations, both parallel and perpendicular orientations of lamellar domains.
The stability and structural properties of both systems have been tested at 353 and 313 K, respectively. In Fig. 3d, the mass density profiles of amorphous and semi-crystalline PE in contact with MgCl2 are reported. The profiles unveil the different polymer structuration at the interface. Specifically, the semi-crystalline phase of PE exhibits a series of regularly spaced peaks showing long range order typical of a semicrystalline phase. Conversely, for the amorphous PE only a short distance order (up to ∼2 nm from the interface) is preserved. The relatively long-order structuration of semi-crystalline PE is further confirmed by the orientational order parameter (P2) calculated as a function of the distance from the MgCl2 surface, Fig. 3e. see Section 1.3 of ESI† for the definition of P2. The highest P2 value (∼0.76) is found at the highest density peak. However, the P2 is considerably high (∼0.66) even at ∼3 nm from the surface. We expect that the different mobilities of the amorphous and crystalline phases, which affects the stress accumulation mechanism, is a physical behaviour that can be represented by atomistic simulations.
Molecular view of the stress generation mechanism
Molecular simulations, beside structural properties, give access to the thermodynamics of the simulated systems. The pressure P can be directly calculated from MD simulations by the virial theorem of Clausius (eqn (1)), where the virial is defined as the product of the particle position vectors and forces acting on them (eqn (2)):| PV = NkBT + 〈W〉 | (1) |
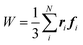 | (2) |
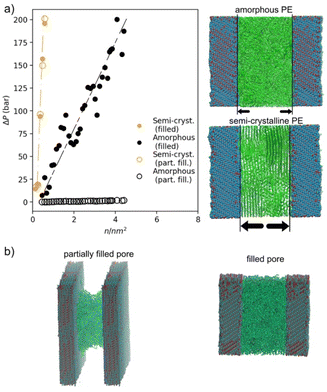
Because the PE is industrially produced in the presence of additives, we investigated how a load of low MW molecules (including H2, C2 and C6) alters the ΔP response in the case of a semi-crystalline PE (see Fig. 5). The amorphous case is not considered since the ΔP increment is very low (Fig. 4a, open black circles).
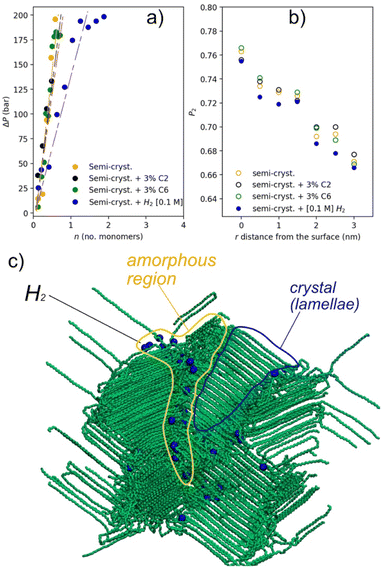
This is a crucial aspect to explore since the final properties of the produced polymer are controlled in the industrial processes by regulating the load of reactants.4 The MD simulations revealed a significant difference between the behavior of PE with a load of [0.1 M] H2 and all the remaining samples (with 3% w/w of C2 and with 3% w/w of C6). Only in the case of hydrogen load, the increase of pressure is slower than that in the semi-crystalline case (see blue points in Fig. 5a). Conversely, for the other simulated systems the pressure increase is almost unchanged by addition of C2 or C6. It is well expected that the increase of the C2 concentration will lead to an increase of the catalyst activity. However, the morphology and the crystallinity of the nascent polymers are comparable, as can be seen by comparing samples 1 and 2 in Table S3,† and panels B and C of Fig. 1. Even if the polymer chains are growing at a much faster rate, the fragmentation pattern is practically unchanged (similar bulk densities, high surface roughness, leading to no particle flowability). This behavior is well predicted by our simulation results, showing a negligible difference in the ΔP increase when C2 is added to the PE bulk (Fig. 5a).
In contrast, if a tiny amount of H2 is added, namely a few ppm, the influence on the morphology is immediately observed (higher bulk density and the powder flows) resulting in enhanced reactor operability and acceptable flowability. By adding H2 it is well known that the molecular weight of the polymer chains will be shifted to lower chain lengths, while the polymerization rate should not be considerably affected.80 Consequently, it is further expected that the lower MW would affect crystallization behaviour; however, this is not applicable to the nascent polymer (the increase of crystallinity due to the lower MW will be seen only after melting and re-crystallization). Under the selected polymerization conditions (T = 323 K), the chains start crystallizing before being terminated. In the presence of H2 the nascent polymer exhibits less long-range order, i.e. shorter lamellae, than the polymer produced only with C2, as indicated by the lower melting temperature (Tm1 first melting point) when comparing samples 2 and 3 in Table S3 of ESI.† A similar trend is also found from MD simulations. In fact, the P2 order parameter, calculated as a function of the distance from the interface with the support wall, indicates a lower P2 value for the system loaded with hydrogen (Fig. 5b). Simulation results suggested that H2 acts as a plasticizer, thus partially increasing the polymer mobility and the possibility of stress release. At the molecular level, the hydrogen molecules, mainly located in the amorphous regions of the semicrystalline model (see the snapshots in Fig. 5c), contribute to enhancing the mobility of the amorphous regions. In practice the hydrogen molecules increase the free volume between polymer chains letting them move and rotate more freely. The increase of the bulk density is a consequence of the improved chain mobility, leading to more efficient expansion/filling of the available pore volume and a smoother increase of stress on the support walls. Interestingly, simulation indicates that the same plasticizing effect is not found in the presence of a comonomer. Indeed, although by adding a comonomer (C6 or C4) there is again a reduction of the MW and of the crystallinity (this time both in the nascent and in the recrystallized polymer) and the particle morphology improves (see Fig. 1F), only a minor change of the pressure behaviour is calculated. The higher amount of amorphous phase produced when the comonomer is present, indicated by the lower ΔH1, for example when comparing samples 2 and 4 in Table S3 of ESI,† is contributing to the higher bulk density. The effect is noticeable already at very low comonomer concentration values. At higher concentrations, when incorporation of defects inhibits more the in situ crystallization, much higher bulk densities can be achieved (Fig. 1H) because of the high content of amorphous phase. Vice versa, by dosing only H2, a crystalline material is always produced, and the bulk density will be lower.
Conclusions
A systematic study, connecting the morphology of particles obtained under different polymerization conditions and the possible different stress generation mechanisms at the PE/MgCl2 support interface, has been presented. In particular, experimental characterization of the particles in terms of microscopy, heat of fusion, melting temperature and bulk density of the polymer produced under different pre-polymerization conditions has been compared with pressure increases perpendicular to the PE/MgCl2 interface calculated by atomistic MD under the same conditions.Two limiting scenarios, corresponding to the McKenna hypothesis, in which different flowabilities of totally amorphous or semicrystalline PE phases have been considered. In the case of amorphous PE phases, very flat behaviors of pressure increases have been calculated. In contrast, for all considered models, in the presence of semicrystalline PE phases, a steep behavior of pressure increase as a function of inserted monomers has been registered. Crystallinity of the nascent PE phase is confirmed as a dominant factor in the stress mechanism generation.
Atomistic MD simulations allowed a straightforward extension to models where additives are present. In particular, a load of low MW molecules such as H2, C2 and C6 has been considered for the simulation of stress behavior for both semicrystalline and amorphous PE phases. Interestingly, in agreement with experiments, hydrogen molecules alter the ΔP response in the case of a semi-crystalline PE, while, in the same case, C2 and C6 do not alter the stress behavior. These results open the possibility, employing the proposed models, of a systematic investigation and rational design of reactants composition. More in general, the proposed approach, focused on a length-scale (∼10 nm) intermediate between microscopic and macroscopic modelling of the polymerization process, can open the way to a fruitful bridging of modelling, experiments, and product design.
Experimental methods
SEM/EDS
Prepolymerised catalyst samples are analysed using a FEI Quanta 200F Scanning Electron Microscope (SEM) equipped with an Energy Dispersive Spectrometer (EDS). In this method, the pre-polymerised catalyst particles are cut with a microtome blade and attached to a sample holder with a carbon conductive adhesive. The cut specimens are sputter coated with Pd/Au in a Polaron sputter coater to make them conductive.Bulk density
For the bulk density measurement a 100 mL cylinder is placed on the balance and tared. Afterwards the cylinder is positioned concentric under the funnel. The funnel is closed by turning the fastener plate. Then the granules or powder is filled quickly in the closed funnel. After the filling the fastener plate is opened. The overrun of the sample above the upper edge of the cylinder is wiped off in a 45° angle with a straight-sharp-edged corner. The cylinder filled with the sample is reweighed to calculate the weight. This determination is performed two times. Resulting weight [g 100 mL−1] × 10 = bulk density [kg m−3]. The result is given as the arithmetic mean of the double determination.DSC
A TA Instruments Q2000 Differential Scanning Calorimeter calibrated with indium, zinc, and tin and operating under 50 mL min−1 of nitrogen flow was used. The employed thermal program consisted of a first heating step from 0 to453 K, followed by a cooling step and a second heating scan from 0 to 423 K. The heating/cooling rate was always 10 K min−1. The DSC trace was integrated from 303 K to the end of the melting peak to evaluate the melting enthalpy.Computational methods and details
TraPPE-UA has been demonstrated to better reproduce, against experiments, the mass density, thermal expansion coefficient, gyration radius of PE chains, diffusion coefficient, and the early stage of crystallization of an entangled PE without the use of a pre-oriented amorphous melt,81,82 needed in the case of the PYS force-field.71 We choose a PE chain of C150H300 (from now C150) since it is long enough to display chains folded (lamellae) in the crystal domains.83 In Section 1 of ESI,† a description and a validation (where needed) of all models used in this paper are reported. In the same section, a procedure to build a stable crystal slab of (110) cut of MgCl2, considered in the current literature as the most representative surface for the polymerization reaction,84,85 is reported. Moreover, since we are going to perform simulations under conditions close to experimental ones, the thermal stability of the crystal slab is also checked (see Section 1.5 of ESI†). The initial well equilibrated PE bulk configuration has been obtained, using the hybrid particle-field approach,86,87 by following the procedure reported by De Nicola et al.,88,89 and using the OCCAM MD package.90Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to offer our special thanks to Dr Dusan Jeremic and Harald Herbst for useful discussions. “The computing resources and the related technical support used for this work have been provided by CRESCO/ENEAGRID High Performance Computing infrastructure and its staff. CRESCO/ENEAGRID High Performance Computing infrastructure is funded by ENEA, the Italian National Agency for New Technologies, Energy and Sustainable Economic Development and by Italian and European Research Programmers, see http://www.cresco.enea.it/english for information”.Notes and references
- I. Vollmer, M. J. F. Jenks, M. C. P. Roelands, R. J. White, T. Harmelen, P. Wild, G. P. Laan, F. Meirer, J. T. F. Keurentjes and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2020, 59, 15402–15423 CrossRef CAS PubMed
.
- A. Rahimi and J. M. García, Nat. Rev. Chem., 2017, 1, 0046 CrossRef
.
- D. Sauter, M. Taoufik and C. Boisson, Polymers, 2017, 9, 185 CrossRef PubMed
.
-
J. B. P. Soares, T. F. L. McKenna, Polyolefin Reaction Engineering, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2012, pp. 87–129, ISBN: 978-3-527-31710-3 Search PubMed
.
- Y. Zhou, A. Alizadeh, B. Liu and J. B. P. Soares, Macromol. React. Eng., 2021, 15, 2000043 CrossRef CAS
.
- Y. Zhou, R. Zhang, H. Ren, X. He, B. Liu, N. Zhao and B. Liu, J. Organomet. Chem., 2020, 908, 121066 CrossRef CAS
.
- B. Jiang, J. Ye, Z. Liao, X. Shi, Z. Huang, J. Wang and Y. Yang, J. Appl. Polym. Sci., 2018, 135, 46589 CrossRef
.
- A. Alizadeh and T. F. L. McKenna, Macromol. React. Eng., 2018, 12, 1700027 CrossRef
.
- S. Lee and K. Y. Choi, Macromol. React. Eng., 2017, 11, 1600027 CrossRef
.
- K.-J. Chu, J. B. P. Soares and A. Penlidis, J. Polym. Sci., Part Polym. Chem., 2000, 38, 1803–1810 CrossRef CAS
.
- T. F. L. McKenna, A. Di Martino, G. Weickert and J. B. P. Soares, Macromol. React. Eng., 2010, 4, 40–64 CrossRef CAS
.
- M. A. Bashir, M. Al-haj Ali, V. Kanellopoulos and J. Seppälä, Fluid Phase Equilib., 2013, 358, 83–90 CrossRef CAS
.
- M. A. Bashir, V. Monteil, V. Kanellopoulos, M. A.-H. Ali and T. McKenna, Macromol. Chem. Phys., 2015, 216, 2129–2140 CrossRef CAS
.
- A. Krallis and V. Kanellopoulos, Ind. Eng. Chem. Res., 2013, 52, 9060–9068 CrossRef CAS
.
- A. Alizadeh, V. Touloupidis and J. B. P. Soares, Macromol. React. Eng., 2021, 15, 2100006 CrossRef CAS
.
-
J. B. P. Soares and V. Touloupidis, in Multimodal Polymers with Supported Catalysts, Springer, New York, 2019 Search PubMed
.
- M. A. Ferrero and M. G. Chiovetta, Polym. Eng. Sci., 1987, 27, 1436–1447 CrossRef CAS
.
- M. A. Ferrero and M. G. Chiovetta, Polym. Eng. Sci., 1987, 27, 1448–1460 CrossRef CAS
.
- M. A. Ferrero and M. G. Chiovetta, Polym. Eng. Sci., 1991, 31, 886–903 CrossRef CAS
.
- X. Zheng, M. Smit, J. C. Chadwick and J. Loos, Macromolecules, 2005, 38, 4673–4678 CrossRef CAS
.
- X. Zheng, M. S. Pimplapure, G. Weickert and J. Loos, Macromol. Rapid Commun., 2006, 27, 15–20 CrossRef
.
- S. Knoke, D. Ferrari, B. Tesche and G. Fink, Angew. Chem., Int. Ed., 2003, 42, 5090–5093 CrossRef CAS PubMed
.
- M. A. Ferrero, E. Koffi, R. Sommer and W. C. Conner, J. Polym. Sci., Part Polym. Chem., 1992, 30, 2131–2141 CrossRef CAS
.
- K. W. Bossers, R. Valadian, S. Zanoni, R. Smeets, N. Friederichs, J. Garrevoet, F. Meirer and B. M. Weckhuysen, J. Am. Chem. Soc., 2020, 142, 3691–3695 CrossRef CAS PubMed
.
- K. W. Bossers, R. Valadian, J. Garrevoet, S. van Malderen, R. Chan, N. Friederichs, J. Severn, A. Wilbers, S. Zanoni, M. K. Jongkind, B. M. Weckhuysen and F. Meirer, JACS Au, 2021, 1, 852–864 CrossRef CAS PubMed
.
- P. Corradini, V. Barone, R. Fusco and G. Guerra, Eur. Polym. J., 1979, 15, 1133–1141 CrossRef CAS
.
- M. Boero, M. Parrinello and K. Terakura, J. Am. Chem. Soc., 1998, 120, 2746–2752 CrossRef CAS
.
- G. Monaco, M. Toto, G. Guerra, P. Corradini and L. Cavallo, Macromolecules, 2000, 33, 8953–8962 CrossRef CAS
.
- M. Boero, M. Parrinello, H. Weiss and S. Hüffer, J. Phys. Chem. A, 2001, 105, 5096–5105 CrossRef CAS
.
- M. Seth, P. M. Margl and T. Ziegler, Macromolecules, 2002, 35, 7815 CrossRef CAS
.
- T. Taniike and M. Terano, Macromol. Rapid Commun., 2008, 29, 1472 CrossRef CAS
.
- M. D'Amore, R. Credendino, P. H. M. Budzelaar, M. Causá and V. Busico, J. Catal., 2012, 286, 103 CrossRef
.
- E. Breuza, G. Antinucci, P. H. M. Budzelaar, V. Busico, A. Correa and C. Ehm, Int. J. Quantum Chem., 2018, 118, e25721 CrossRef
.
- A. Piovano, M. Signorile, L. Braglia, P. Torelli, A. Martini, T. Wada, G. Takasao, T. Taniike and E. Groppo, ACS Catal., 2021, 11, 9949–9961 CrossRef CAS
.
- M. D'Amore, G. Takasao, H. Chikuma, T. Wada, T. Taniike, F. Pascale and A. M. Ferrari, J. Phys. Chem. C, 2021, 125, 20048–20058 CrossRef
.
- G. Takasao, T. Wada, A. Thakur, P. Chammingkwan, M. Terano and T. Taniike, ACS Catal., 2019, 9, 2599 CrossRef CAS
.
- Z. Grof, J. Kosek, M. Marek and P. M. Adler, AIChE J., 2003, 49, 1002–1013 CrossRef CAS
.
- B. Horáčková, Z. Grof and J. Kosek, Chem. Eng. Sci., 2007, 62, 5264–5270 CrossRef
.
- M. Najafi, M. Parvazinia, M. H. R. Ghoreishy and C. Kiparissides, Macromol. React. Eng., 2014, 8, 29–45 CrossRef CAS
.
- P. Kittilsen, T. F. McKenna, H. Svendsen, H. A. Jakobsen and S. B. Fredriksen, Chem. Eng. Sci., 2001, 56, 4015–4028 CrossRef CAS
.
- A. Di Martino, G. Weickert, F. Sidoroff and T. F. L. McKenna, Macromol. React. Eng., 2007, 1, 338–352 CrossRef CAS
.
- M. Najafi and M. Parvazinia, Macromol. Theory Simul., 2015, 24, 28–40 CrossRef CAS
.
- V. Touloupidis, G. Rittenschober and C. Paulik, Macromol. React. Eng., 2020, 14, 2000028 CrossRef CAS
.
- V. Touloupidis, Macromol. React. Eng., 2014, 8, 508–527 CrossRef CAS
.
- T. F. McKenna and J. B. P. Soares, Chem. Eng. Sci., 2001, 56, 3931–3949 CrossRef CAS
.
-
Polymer Reaction Engineering: Influence of Reaction Engineering
on Polymer Properties; proceedings of the Berlin International Workshop on Polymer Reaction Engineering, ed. K.-H. Reichert and W. Geiseler, Hanser, Munich Vienna New York, 1983 Search PubMed
.
- V. W. Buls and T. L. Higgins, J. Polym. Sci., Part A-1: Polym. Chem., 1970, 8, 1037–1053 CrossRef CAS
.
- P. Ingram and A. Schindler, Makromol. Chem., 1968, 111, 267–270 CrossRef CAS
.
- M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577 CrossRef CAS
.
- K. Ch. Daoulas, V. Harmandaris and V. G. Mavrantzas, Macromolecules, 2005, 38, 5780–5795 CrossRef CAS
.
- T. K. Xia, J. Ouyang, M. W. Ribarsky and U. Landman, Phys. Rev. Lett., 1992, 69, 1967–1970 CrossRef CAS PubMed
.
- O. Borodin, G. D. Smith, R. Bandyopadhyaya and O. Byutner, Macromolecules, 2003, 36, 7873–7883 CrossRef CAS
.
-
K. Binder, Monte Carlo and Molecular Dynamics Simulations in Polymer Science, Oxford University Press, New York, 1995 Search PubMed
.
- S. Caputo, V. Hristov, A. D. Nicola, H. Herbst, A. Pizzirusso, G. Donati, G. Munaò, A. R. Albunia and G. Milano, J. Chem. Theory Comput., 2021, 17, 1755–1770 CrossRef CAS PubMed
.
-
W. Krauth, Statistical Mechanics: Algorithms and Computations, Oxford University Press, Oxford, 2006 Search PubMed
.
- H. Li and S. Yan, Macromolecules, 2011, 44, 417–428 CrossRef CAS
.
- C. Y. Li, Polymer, 2020, 211, 123150 CrossRef CAS
.
- A.-K. Flieger, M. Schulz and T. Thurn-Albrecht, Macromolecules, 2018, 51, 189–194 CrossRef CAS
.
- R. M. Michell and A. J. Müller, Prog. Polym. Sci., 2016, 54–55, 183–213 CrossRef CAS
.
- P. F. Green, C. J. Palmstrom, J. W. Mayer and E. J. Kramer, Macromolecules, 1985, 18, 501–507 CrossRef CAS
.
- J. P. K. Doye and D. Frenkel, J. Chem. Phys., 1998, 109, 10033–10041 CrossRef CAS
.
- W. Mao, X. Yang and E. Nies, J. Phys. Chem. B, 2008, 112, 6753–6761 CrossRef CAS PubMed
.
- C. Luo, M. Kröger and J.-U. Sommer, Polymer, 2017, 109, 71–84 CrossRef CAS
.
- T. Yamamoto, J. Chem. Phys., 2013, 139, 054903 CrossRef PubMed
.
- T. Shimizu and T. Yamamoto, J. Chem. Phys., 2000, 113, 3351–3359 CrossRef CAS
.
- H. Yang, X. J. Zhao and M. Sun, Phys. Rev. E, 2011, 84, 011803 CrossRef PubMed
.
- J. H. Jang and W. L. Mattice, Macromolecules, 2000, 33, 1467–1472 CrossRef CAS
.
- J. L. Wilhelmi and G. C. Rutledge, J. Phys. Chem., 1996, 100, 10689–10695 CrossRef CAS
.
- N. Waheed, M. J. Ko and G. C. Rutledge, Polymer, 2005, 46, 8689–8702 CrossRef CAS
.
- G. C. Rutledge, J. Chem. Phys., 2009, 131, 134902 CrossRef PubMed
.
- P. Yi, C. R. Locker and G. C. Rutledge, Macromolecules, 2013, 46, 4723–4733 CrossRef CAS
.
- A. Ghazavizadeh, G. C. Rutledge, A. A. Atai, S. Ahzi, Y. Rémond and N. Soltani, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 1228–1243 CrossRef CAS
.
- A. Bourque, C. R. Locker and G. C. Rutledge, Macromolecules, 2016, 49, 3619–3629 CrossRef CAS
.
- H. Wang, K. Keum Jong, A. Hiltner, E. Baer, B. Freeman, A. Rozanski and A. Galeski, Science, 2009, 323, 757–760 CrossRef CAS PubMed
.
- J.-P. Yang, Q. Liao, J.-J. Zhou, X. Jiang, X.-H. Wang, Y. Zhang, S.-D. Jiang, S.-K. Yan and L. Li, Macromolecules, 2011, 44, 3511–3516 CrossRef CAS
.
- G. Reiter and J.-U. Sommer, J. Chem. Phys., 2000, 112, 4376–4383 CrossRef CAS
.
- J.-U. Sommer and G. Reiter, J. Chem. Phys., 2000, 112, 4384–4393 CrossRef CAS
.
- Y. Sakai, M. Imai, K. Kaji and M. Tsuji, J. Cryst. Growth, 1999, 203, 244–254 CrossRef CAS
.
- F. Zhang, J. Liu, H. Huang, B. Du and T. He, Eur. Phys. J. E, 2002, 8, 289–297 CrossRef CAS PubMed
.
-
Multimodal Polymers with Supported Catalysts: Design and Production, ed. A. R. Albunia, F. Prades and D. Jeremic, Springer International Publishing, Cham, 2019 Search PubMed
.
- J. Ramos, J. F. Vega and J. Martínez-Salazar, Macromolecules, 2015, 48, 5016–5027 CrossRef CAS
.
- J. Ramos, J. F. Vega and J. Martínez-Salazar, Eur. Polym. J., 2018, 99, 298–331 CrossRef CAS
.
- G. Ungar, J. Stejny, A. Keller, I. Bidd and M. C. Whiting, Science, 1985, 229, 386–389 CrossRef CAS PubMed
.
- A. Correa, F. Piemontesi, G. Morini and L. Cavallo, Macromolecules, 2007, 40, 9181–9189 CrossRef CAS
.
- A. Andoni, J. Chadwick, H. Niemantsverdriet and P. Thune, J. Catal., 2008, 257, 81–86 CrossRef CAS
.
- G. Milano and T. Kawakatsu, J. Chem. Phys., 2009, 130, 214106 CrossRef PubMed
.
- G. Milano and T. Kawakatsu, J. Chem. Phys., 2010, 133, 214102 CrossRef PubMed
.
- A. De Nicola, T. Kawakatsu and G. Milano, J. Chem. Theory Comput., 2014, 10, 5651–5667 CrossRef CAS PubMed
.
- A. De Nicola, G. Munaò, N. Grizzuti, F. Auriemma, C. De Rosa, A. Sevink and G. Milano, Soft Mater., 2020, 18, 228–241 CrossRef CAS
.
- Y. Zhao, A. De Nicola, T. Kawakatsu and G. Milano, J. Comput. Chem., 2012, 33, 868–880 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Description of the united-atom PE model and parameters, validation of the model in the reproduction of polymer amorphous and crystalline bulk phases. Fine tuning of MgCl2 atomistic model parameters. Additional analyses and data of the semi-crystalline PE phase. Short movie showing the crystallization of PE chains, in contact with MgCl2, during the quenching procedure (Movie_1.mpeg). Short movie showing the typical PE lamellae on the MgCl2 surface (Movie_2.mpeg). See DOI: https://doi.org/10.1039/d2na00406b |
| ‡ These authors contributed equally |
| This journal is © The Royal Society of Chemistry 2022 |

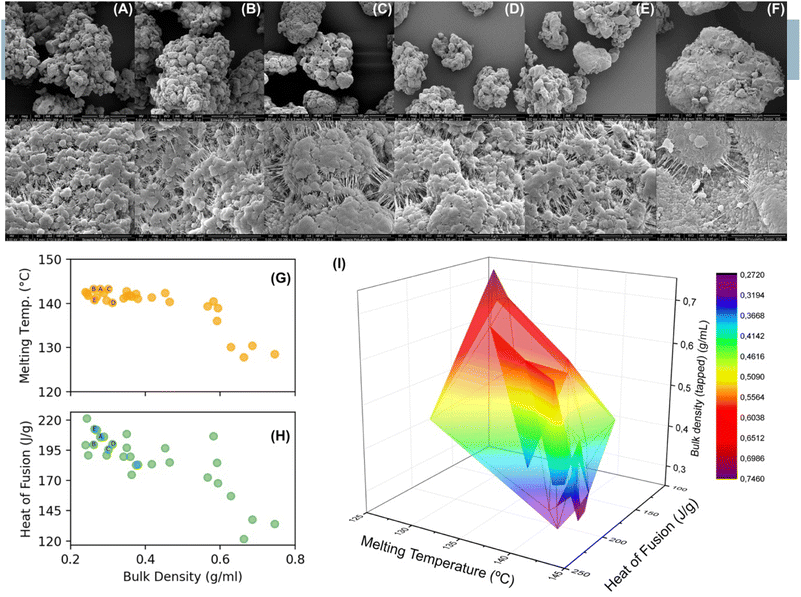
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 00×). Melting temperature (G) and heat of fusion (H) of the produced polymer as a function of the bulk density. The DSC technique has been used to measure the melting temperature and heat of fusion of the polymer (first heating scan). (I) 3D plot correlating the bulk density and both the properties of the polymer produced, heat of fusion (crystallinity degree of PE) and melting temperature (lamella dimension).
00×). Melting temperature (G) and heat of fusion (H) of the produced polymer as a function of the bulk density. The DSC technique has been used to measure the melting temperature and heat of fusion of the polymer (first heating scan). (I) 3D plot correlating the bulk density and both the properties of the polymer produced, heat of fusion (crystallinity degree of PE) and melting temperature (lamella dimension).