Open Access Article
Open Access ArticleNon-contact friction energy dissipation via hysteretic behavior on a graphite surface
Chong
Wang
a,
Huixian
Liu
a,
Jiangcai
Wang
a,
Yishu
Han
a,
Zejun
Sun
a,
Haowen
Xu
b,
Huan
Liu
*a,
Dameng
Liu
 *a and
Jianbin
Luo
*a
*a and
Jianbin
Luo
*a
aState Key Laboratory of Tribology, Tsinghua University, Beijing 100084, China. E-mail: liuhuansklt@163.com; ldm@tsinghua.edu.cn; luojb@mail.tsinghua.edu.cn
bInstitue for Advanced Materials and Technology, University of Science and Technology Beijing, Beijing 100083, China
First published on 29th September 2022
Abstract
For non-contact friction, energy is usually dissipated through phonon excitation, Joule dissipation and van der Waals friction. Although some new dissipation mechanisms related to the quantum phenomenon have been discovered, the contribution of hysteretic behavior to non-contact friction energy dissipation is lacking in research. In this paper, the distance dependence of non-contact friction on the graphite surface is studied by using a quartz tuning fork with lateral vibration in the atmosphere. It is found that energy dissipation begins to increase when the distance is less than 2 nm, showing the form of phonon dissipation. However, when the distance is further decreased, the dissipation deviates from phonon dissipation and presents a huge friction energy dissipation peak, which is caused by the hysteretic behavior between the vibration of the surface atoms and the oscillation of the tip. This work expands the understanding of the energy dissipation mechanism of non-contact friction.
Introduction
About 30% of the world's primary energy is consumed by friction, and 80% of mechanical parts fail due to wear and tear.1,2 It is a key problem to explore the mechanism of energy dissipation in friction and control the energy dissipation channel from the source. Normally, friction occurs between two surfaces that are in contact. Interestingly, when two objects separated by a few nanometers move relative to each other, there is still little resistance, which is called non-contact friction.3,4 Non-contact friction is a common phenomenon which has been observed in conductors, semiconductors and insulators, and the associated energy dissipation is closely related to phonons, electrons, defects and structural phase transitions.5–18 The study of non-contact friction is of great significance to explore the origin of friction and break the detection limit of precision instruments.19 At present, the tuning fork non-contact lateral force microscope can detect lateral non-contact friction sensitively at a very small tip-sample distance with the help of a high-quality factor quartz tuning fork, and it has become a powerful tool to study the energy dissipation mechanism of non-contact friction.20–26There are three typical dissipation forms of non-contact friction, which are phonon excitation, Joule dissipation and van der Waals friction.27 Recently, a number of new dissipation mechanisms have been discovered, which induce striking non-contact friction energy dissipation peaks. For instance, due to the disturbance of the tip, phase slip of the charge-density-wave (CDW) occurs on the surface of NbSe2 at a low temperature, which produces hysteretic behavior of the CDW phase and introduces huge dissipation peaks at a certain tip-sample distance and bias.28 Similarly, at a low temperature, the oscillation of the tip can induce charge and spin state transitions of oxygen vacancy defects on the SrTiO3 surface, leading to significant mechanical dissipation peaks.29 In addition, a new mechanism due to single electron resonance tunneling to image potential states has also been observed on the Bi2Te3 topological insulator surface.30 However, friction exists not only in extreme environments such as an ultra-high vacuum and ultra-low temperature, but also in atmospheric environments more widely. Although some quantum phenomena related to non-contact dissipation vanish in the atmospheric, phonon excitation and lattice deformation which may have hysteretic behavior with the oscillation of the tip still exist on the sample surface, whose significance is poorly explored.
In this paper, we detect a large non-contact friction energy dissipation peak on the surface of graphite by using a homebuilt tuning fork non-contact lateral force microscope in the atmosphere. We speculate that the dissipation peak is due to the hysteretic behavior between the vibration of the surface atoms and the oscillation of the tip. This work helps to better understand the non-contact friction energy dissipation mechanism.
Results and discussion
Experimental setup and sample characterization
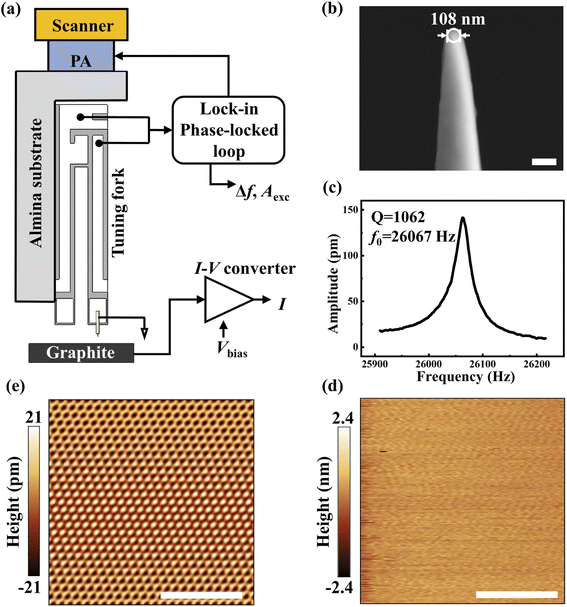
Fig. 1(a) shows the schematic diagram of the homebuilt tuning fork non-contact lateral force microscope. The microscope uses a piezoelectric scanning tube to drive the tip while the sample remains stationary. Below the scanning tube is a piezo actuator (PA) that vibrates horizontally to excite the quartz tuning fork to oscillate. The quartz tuning fork acts as a force sensor. One of its cantilevers is fixed to an alumina substrate by high-strength epoxy adhesive, while an electrochemically etched tungsten tip is glued to the front end of the other free cantilever to increase the quality factor. To extract the tunneling current while detecting the lateral interaction, a soft gold wire with a diameter of 12.5 μm and a length of approximately 1 mm is used to ground the tip, and bias is applied on the sample surface. This method can detect the tunneling current between the tip and sample without affecting the vibration of the quartz tuning fork to the greatest extent. Before the experiment, the sensor has been calibrated by analyzing the thermal noise spectrum31 (see Methods). The OC4 module of a commercial Nanonis controller is applied to control PA which excites the quartz tuning fork to vibrate at a certain frequency and amplitude through a lock-in phase-locked loop (PLL) feedback system, and maintain a constant amplitude A = 300 pm. The cantilever of the quartz tuning fork is placed perpendicular to the sample, so the tip oscillates parallelly to the sample surface, allowing direct detection of the lateral interaction between the tip and the sample.The tip used in the experiment was obtained by electrochemically etching 75 μm tungsten wire in 2 mol L−1 KOH solution. As shown in Fig. 1(b), a field emission scanning electron microscope (HITACHI SU8220) was used to image the tip, and the tip radius was about 54 nm. The elastic constant of the quartz tuning fork is approximately 104 N m−1. After installing the tungsten tip and gold wire, we measured the response of the sensor's amplitude to excitation frequency in the atmosphere with the help of an OC4 module. By Gaussian function fitting, we obtained the intrinsic frequency f0 = 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 067 Hz and the quality factor of sensor Q = 1062, as shown in Fig. 1(c).
067 Hz and the quality factor of sensor Q = 1062, as shown in Fig. 1(c).
The sample was fresh, atomically flat, commercial highly oriented cleaved graphite crystals (HOPG) that had been mechanically cleaved. Using tunneling current as the feedback signal, the surface morphology of the sample was measured in constant current mode. As shown in Fig. 1(d), the surface of the sample is atomically flat with a surface roughness of Ra = 0.13 nm, and no obvious contaminant or other structural defects are found. Fig. 1(e) shows the atomic lattice diagram of Fig. 1 (d) filtered by FFT. On this basis, we carried out non-contact friction measurements.
Tip oscillation induced phonon dissipation on a graphite surface
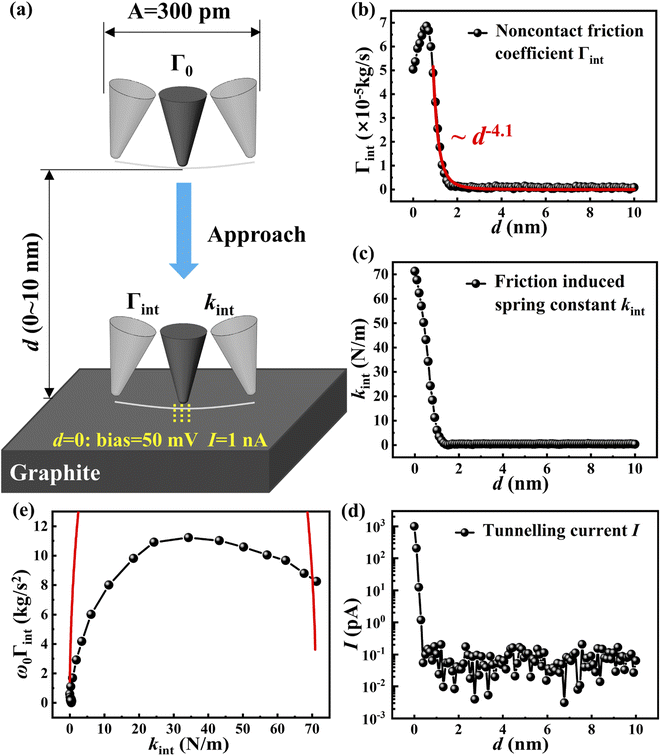
Under the open-loop control, the variation of the non-contact friction coefficient Γint and the friction-induced elastic constant kint with the tip-sample distance d were investigated. As shown in Fig. 2(a), the probe always oscillates at the intrinsic frequency and constant amplitude, and we control the tip to approach the sample surface gradually from a large separation until it stops when the tunneling current reaches a preset value. At a large distance (>100 nm), the oscillation of the tip is not affected by the sample and the damping comes only from the internal friction Γ0 of the cantilever. In the process of approaching, energy dissipation occurs due to the interaction. In order to maintain the constant amplitude of the quartz tuning fork, PLL must increase the excitation amplitude Aexc. Therefore, Aexc directly reflects the non-conservative interaction, while the frequency offset Δf reflects the conservative interaction.22,32 Here, the non-conservative interaction refers to the interaction which causes energy dissipation in the tip-sample junction, while the conservative interaction on the contrary, refers to those that do not cause energy dissipation. Γint and kint can be calculated using Aexc and Δf:5,33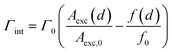 | (1) |
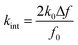 | (2) |
Fig. 2(b) and (c) show that Γint and kint on the graphite surface gradually increase with the decrease of the tip-sample distance at d < 2 nm. The order of magnitude of Γint is 10−5 kg s−1. Unlike kint which increases monotonically as d decreases, Γint shows a huge peak at d ∼0.6 nm. At the same time, when it reaches its peak, no tunneling current is detected [Fig. 2(d)], indicating that the tip does not form a physical contact with the sample at this time, that is, the maximum of the friction coefficient is not from the collision with the sample surface. Similar results were also observed by Saitoh et al.20 The difference was that they observed the dissipation peak at a low temperature, while we observed the dissipation peak at room temperature. In addition, the non-contact friction observed by us increased significantly at d < 2 nm, while the friction observed by them began to increase at d < 15 nm. We have observed a more localized non-contact interaction in space.
Volokitin et al. found that for a spherical tip oscillating parallel to the elastic surface, the non-contact friction coefficient is proportional to F2(d) which is the static force resulting from the interaction between the tip and the sample surface.35 According to Lifshitz theory, the elastic stress F(d) caused by van der Waals interaction gives rise to the static force to be proportional to d−2, and therefore the phonon friction coefficient to be proportional to d−4.36 By fitting the data in Fig. 2(b) with power exponents, we find that the non-contact friction coefficient is proportional to d−4.1±0.1 within the range 1 nm < d < 10 nm, which is in good agreement with the above prediction, indicating that phonon friction is the main dissipation mechanism at this time. However, when the tip gets closer to the sample, the dissipation increases further and then decreases gradually, deviating from the phonon dissipation. Therefore, a new dissipation mechanism appears at closer separation.
Possible reasons for the maximum of Γint as the tip-sample distance decreases are discussed below. First of all, surface contaminants and structure defects can induce dissipation.37 However, the STM topography shows that the sample surface is atomically smooth and clean, and no obvious contaminants and structure defects are found. In addition, the effect of a water film and adsorbed contamination on dissipation has been discussed in previous studies where the dissipation started to increase at d > 15 nm, whose distance is much larger than that observed in our experiment.23,24 Therefore, the influence of the water film and adsorbed contamination on dissipation may be ruled out. Secondly, the formation of chemical bonds between the atoms of the tip and sample surface will also cause huge dissipation, but such short–range interactions require that the tip-sample distance is very small enough to form chemical bonds.21,22 However, in our experiment, friction began to increase at d ∼2 nm, and there was no tunneling current when the maximum value appeared, indicating that there was no physical contact and chemical bond formation between the tip and the sample. Karrai et al. found that if a long probe was used, when the tip-sample distance was very small, a huge lateral interaction will make the tip bend elastically, thus generating restoring force and modulating the observed dissipation.24 Therefore, the frequency offset will gradually stabilize as the distance decreased. The stiffness of the force sensor we used was 6 times higher than theirs, and the frequency offset detected by us maintained an increasing trend at small tip-sample separation, instead of stabilizing as observed by Karrai et al. Therefore, the effect of tip bending can be ruled out. Similar results can be observed in different areas of the graphite surface, excluding the influence of tip deformation on experimental results, indicating that this phenomenon is determined by the intrinsic properties of the graphite surface.
Many relaxation processes exist at the friction interface
In the equation of cantilever motion, Γint and kint are expressed as20| Γintẋ + kintx = (kint + iωΓint)x ≅ (kint + iω0Γint)x ≡ G(ω0)x | (3) |
The dissipation peak is caused by the hysteretic behavior of tip oscillation and the relaxation process
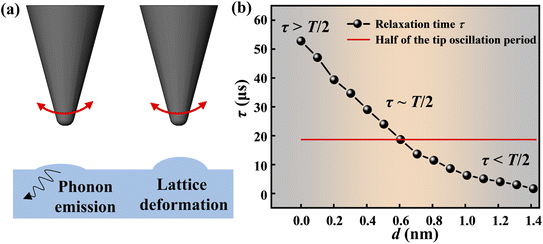
To further explore the relaxation mechanism, we established the following model. The oscillation of the tip can induce some relaxation processes like atomic vibration which excites phonons and even cause lattice deformation, as shown in Fig. 3(a). Therefore, it is natural to assume that as d decreases, it becomes much easier for the atoms on the sample surface to vibrate, which can explain the dependence of non-contact friction on d. Based on this idea, we can describe the lateral interactions with a dashpot γf connected in series with a spring kf. Γint and kint can be expressed as20| ω0Γint = kfω0τ/(1 + ω20τ2) | (4) |
| kint = kfω20τ2/(1 + ω20τ2) | (5) |
According to the expression of ω0Γint and kint in the model, we can solve the expression of the average relaxation time τ as
| τ = kint/ω20Γint | (6) |
Fig. 3(b) shows the mean relaxation time τ increase with the decrease of d with an order of tens of microseconds. Surprisingly, when the average relaxation time increases to 19 μs which is about half of the tip oscillation period, it corresponds to the position where the maximum non-contact friction occurs (d ∼0.6 nm), which indicates that the energy dissipation is closely related to the mean relaxation time τ.
We propose that the non-contact friction phenomenon in the experiment can be attributed to the hysteretic behavior between the oscillation of the tip and the vibration of the surface atoms. When the tip-sample distance is large, the interaction between the tip and sample surface atoms is weak, which makes the surface atoms vibrate slightly, showing the form of phonon dissipation. Meanwhile, the average relaxation time is smaller than the oscillation period of the tip and almost no hysteretic behavior occurs. Therefore, the coupling of the two motions is weak, and the non-contact friction is also small. However, with the decrease of the distance, the vibration of the surface atoms gradually intensifies leading to a longer relaxation time. When the average relaxation time increases to half of the oscillation period of the tip, it will induce a phase shift between the oscillation of the tip and the surface atomic deformation which causes significant hysteretic behavior resulting in a huge non-contact friction peak.39,40 As the distance decreases further, the relaxation time exceeds half of the oscillation period of the tip. The hysteretic behavior disappears and the two motions change from strong coupling to weak coupling. The smaller the distance, the weaker the coupling of the two motions and the dissipation becomes small. This hypothesis explains our experimental phenomenon very well.
Conclusions
We have studied the relationship between the energy dissipation of non-contact friction and the tip-sample distance on the graphite surface with a homebuilt tuning fork non-contact lateral force microscope in the atmosphere. It is found that energy dissipation begins to increase when the distance is less than 2 nm, which is proportional to d−4.1±0.1, showing the form of phonon dissipation. However, when the distance is further reduced, the dissipation deviates from the phonon dissipation and presents a huge dissipation peak. The oscillation of the tip above the surface induces the vibration of the surface atoms, and the relaxation time of the vibration of surface atoms increases with the decrease of the tip-sample distance. At the peak position, the mean relaxation time of the surface atomic vibration has the same scale as half of the oscillation period of the tip, which induces significant hysteretic behavior and strong coupling of the two motions. However, before and after the peak position, due to the different time scales of the two motions, the hysteretic behavior and coupling is weak and the friction is small. This work provides new insights into the mechanism of non-contact friction energy dissipation.Methods
Calibration process of the sensor
The sensor has been calibrated by analyzing the thermal noise spectrum. Sensitivity is defined as the ratio of the actual amplitude of the free cantilever of the tuning fork to the amplitude of the AC voltage signal output by the pre-amplifier. When there is no specific frequency driving signal, the free cantilever exhibits random thermal vibration, which satisfies the relation: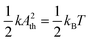 , where k is the spring constant; Ath is the amplitude of the thermal vibration of the cantilever; kB is the Boltzmann's constant. The frequency spectrum of the voltage signal corresponding to the thermal vibration can be obtained by connecting the pre-amplifier with a spectrum analyzer. By calculating the root mean square Vth of the signal peak, the sensitivity can be calculated as Ath/Vth.
, where k is the spring constant; Ath is the amplitude of the thermal vibration of the cantilever; kB is the Boltzmann's constant. The frequency spectrum of the voltage signal corresponding to the thermal vibration can be obtained by connecting the pre-amplifier with a spectrum analyzer. By calculating the root mean square Vth of the signal peak, the sensitivity can be calculated as Ath/Vth.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 52075284, 52105195, 51527901, and 11890672) and Postdoctoral Research Foundation of China (No. 2020M680528 and BX2021151).References
- O. Hod, E. Meyer, Q. Zheng and M. Urbakh, Nature, 2018, 563, 485–492 CrossRef CAS PubMed.
- J. Luo, Chin. Sci. Bull., 2020, 65, 2966–2978 CrossRef.
- J. B. Pendry, J. Phys.: Condens. Matter, 1997, 9, 10301–10320 CrossRef CAS.
- A. I. Volokitin, B. N. J. Persson and H. Ueba, Phys. Rev. B, 2006, 73, 165423 CrossRef.
- M. Kisiel, E. Gnecco, U. Gysin, L. Marot, S. Rast and E. Meyer, Nat. Mater., 2011, 10, 119–122 CrossRef CAS PubMed.
- B. C. Stipe, H. J. Mamin, T. D. Stowe, T. W. Kenny and D. Rugar, Phys. Rev. Lett., 2001, 87, 096801 CrossRef CAS PubMed.
- T. D. Stowe, T. W. Kenny, D. J. Thomson and D. Rugar, Appl. Phys. Lett., 1999, 75, 2785–2787 CrossRef CAS.
- S. Kuehn, R. F. Loring and J. A. Marohn, Phys. Rev. Lett., 2006, 96, 156103 CrossRef PubMed.
- M. Kisiel, F. Pellegrini, G. E. Santoro, M. Samadashvili, R. Pawlak, A. Benassi, U. Gysin, R. Buzio, A. Gerbi, E. Meyer and E. Tosatti, Phys. Rev. Lett., 2015, 115, 046101 CrossRef CAS PubMed.
- F. Federici Canova, S. Kawai, C. de Capitani, K. Kan'no, T. Glatzel, B. Such, A. S. Foster and E. Meyer, Phys. Rev. Lett., 2013, 110, 203203 CrossRef PubMed.
- X. Tan, D. Guo and J. Luo, Friction, 2022, 10, 748–761 CrossRef.
- S. Kuehn, J. A. Marohn and R. F. Loring, J. Phys. Chem. B, 2006, 110, 14525–14528 CrossRef CAS PubMed.
- S. Kuehn, R. F. Loring and J. A. Marohn, Phys. Rev. Lett., 2006, 96, 156103 CrossRef PubMed.
- A. J. Weymouth, J. Phys.: Condens. Matter, 2017, 29, 323001 CrossRef CAS PubMed.
- J. H. She and A. V. Balatsky, Phys. Rev. Lett., 2012, 108, 136101 CrossRef PubMed.
- A. Siria, T. Barois, K. Vilella, S. Perisanu, A. Ayari, D. Guillot, S. T. Purcell and P. Poncharal, Nano Lett., 2012, 12, 3551–3556 CrossRef CAS PubMed.
- Z. Xu, Z. Jacob and T. Li, Nanophotonics, 2021, 10, 537–543 Search PubMed.
- R. Luthi, E. Meyer, M. Bammerlin, A. Baratoff, L. Howald, C. Gerber and H. J. Guntherodt, Surf. Rev. Lett., 1997, 4, 1025–1029 CrossRef CAS.
- D. Rugar, R. Budakian, H. J. Mamin and B. W. Chui, Nature, 2004, 430, 329–332 CrossRef CAS PubMed.
- K. Saitoh, K. Hayashi, Y. Shibayama and K. Shirahama, Phys. Rev. Lett., 2010, 105, 236103 CrossRef PubMed.
- A. J. Weymouth, D. Meuer, P. Mutombo, T. Wutscher, M. Ondracek, P. Jelinek and F. J. Giessibl, Phys. Rev. Lett., 2013, 111, 126103 CrossRef CAS PubMed.
- F. J. Giessibl, M. Herz and J. Mannhart, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12006–12010 CrossRef CAS PubMed.
- M. Lee, B. Kim, J. Kim and W. Jhe, Nat. Commun., 2015, 6, 7359 CrossRef CAS PubMed.
- K. Karrai and I. Tiemann, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 13174–13181 CrossRef CAS.
- A. Laine, A. Vanossi, A. Nigues, E. Tosatti and A. Siria, Nanoscale, 2021, 13, 1955–1960 RSC.
- A. Nigues, A. Siria, P. Vincent, P. Poncharal and L. Bocquet, Nat. Mater., 2014, 13, 688–693 CrossRef CAS PubMed.
- B. Gotsmann, Nat. Mater., 2011, 10, 87–88 CrossRef CAS PubMed.
- M. Langer, M. Kisiel, R. Pawlak, F. Pellegrini, G. E. Santoro, R. Buzio, A. Gerbi, G. Balakrishnan, A. Baratoff, E. Tosatti and E. Meyer, Nat. Mater., 2014, 13, 173–177 CrossRef CAS PubMed.
- M. Kisiel, O. O. Brovko, D. Yildiz, R. Pawlak, U. Gysin, E. Tosatti and E. Meyer, Nat. Commun., 2018, 9, 2946 CrossRef PubMed.
- D. Yildiz, M. Kisiel, U. Gysin, O. Gurlu and E. Meyer, Nat. Mater., 2019, 18, 1201–1206 CrossRef CAS PubMed.
- F. J. Giessibl, Appl. Phys. Lett., 2000, 76, 1470–1472 CrossRef CAS.
- B. Gotsmann, C. Seidel, B. Anczykowski and H. Fuchs, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 11051–11061 CrossRef CAS.
- C. Loppacher, R. Bennewitz, O. Pfeiffer, M. Guggisberg, M. Bammerlin, S. Schar, V. Barwich, A. Baratoff and E. Meyer, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 13674–13679 CrossRef CAS.
- G. Rubio-Bollinger, P. Joyez and N. Agrait, Phys. Rev. Lett., 2004, 93, 116803 CrossRef CAS PubMed.
- A. I. Volokitin, B. N. J. Persson and H. Ueba, J. Exp. Theor. Phys., 2007, 104, 96–110 CrossRef CAS.
- I. E. Dzyaloshinskii, E. M. Lifshitz and L. P. Pitaevskii, Adv. Phys., 1961, 10, 165–209 CrossRef.
- A. I. Volokitin and B. N. Persson, Phys. Rev. Lett., 2005, 94, 086104 CrossRef CAS PubMed.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351 CrossRef CAS.
- P. M. Hoffmann, S. Jeffery, J. B. Pethica, H. O. Ozer and A. Oral, Phys. Rev. Lett., 2001, 87, 265502 CrossRef CAS PubMed.
- L. N. Kantorovich, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 245409 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |