Controlling the rotation modes of hematite nanospindles using dynamic magnetic fields

Abstract

The magnetic field-induced actuation of colloidal nanoparticles has enabled tremendous recent progress towards microrobots, suitable for a variety of applications including targeted drug delivery, environmental remediation, or minimally invasive surgery. Further size reduction to the nanoscale requires enhanced control of orientation and locomotion to overcome dominating viscous properties. Here, control of the coherent precession of hematite spindles via a dynamic magnetic field is demonstrated using nanoscale particles. Time-resolved small-angle scattering and optical transmission measurements reveal a clear frequency-dependent variation of orientation and rotation of an entire ensemble of non-interacting hematite nanospindles. The different motion mechanisms by nanoscale spindles in bulk dispersion resemble modes that have been observed for much larger, micron-sized elongated particles near surfaces. The dynamic rotation modes promise hematite nanospindles as a suitable model system for field-induced locomotion in nanoscale magnetic robots.

---

1 Introduction

Field-driven actuation on magnetic particles builds the foundation of various intriguing applications, including self-propelling particles in active matter,^1,2 mixers in microfluidics,³ swarms of magnetic rollers,⁴ and viscosity probes in nanorheology,⁵ and also aspects based on structure formation, such as field-induced self-organization^6–9 and smart fluids.^10,11 Biological microorganisms such as magnetotactic bacteria are inspiring model systems for magnetic microswimmers¹² operating at low Reynolds numbers, but also large enough so that their movement and dynamics can be tracked by optical techniques. The development of artificial magnetically-driven micro- and nanorobots has received tremendous attention in the last few years,^2,13,14 leading to advanced applications including magnetic two-arm nanoswimmers¹⁵ or the combination of magnetic hyperthermia and magnetically driven propulsion for local pollutant remediation.¹⁶

Achieving a remotely controlled, sustained translational motion for active Brownian particles in a viscous fluid is a challenging endeavour. This is typically approached by an advanced synthesis of complex, chiral structures,¹⁷ such as helical structures for magnetically actuated propulsion in dynamic, rotating or oscillating magnetic fields.¹⁸ A rich variety of motion mechanisms has been achieved using achiral, elongated objects with perpendicular magnetization.^19–22 Even random shapes based on nanoparticle aggregates have been shown to succeed as fast magnetic micropropellers.²³ All these particles propel when stirred by a relatively weak rotating uniform magnetic field of the order of a few mT. The motion mechanism in the vicinity of a planar wall is tunable from tumbling through precessing to rolling motion via the frequency of the rotating magnetic field,²² ultimately fading into the step-out behavior associated with declining propulsion velocity at the highest frequencies.²⁴ These examples emphasize the great potential of dynamic magnetic fields for the controlled locomotion of mesoscopic magnetic particles in a viscous medium and the design of magnetoresponsive soft matter.

If the particle size is reduced to the nanoscale, thermal effects dominate, and stochastic motion of the particles due to random collisions (i.e., Brownian motion) complicates controlled steering of magnetic nanoparticles in viscous fluids.²⁵ One of the rare examples of successfully synthesized propellers with dimensions below 1 μm was demonstrated with carbon-coated aggregates of nanoparticles involving a post-synthesis selection process.²⁶ Hematite nanospindles represent a peculiar case of anisometric nanoparticles that promise to progress magnetohydrodynamics to an even smaller length scale. Hematite nanospindles are achiral, elongated nanoparticles that fulfill the IUPAC definition of nanoscale (i.e., particles with at least one dimension between 1 and 100 nm)²⁷ and intrinsically exhibit a magnetization perpendicular to the long axis. This geometry is similar to the microwires with artificially engineered perpendicular magnetization^20,22 and therefore promising for locomotion of nanoscale objects in dynamic magnetic fields. As the particle moments align parallel with an applied magnetic field, hematite nanospindles in dilute dispersion orient with their long spindle axis perpendicular to a static field direction.^28,29 Within this plane perpendicular to the field the long spindle axis fluctuates randomly. There are two different characteristic relaxation frequencies associated with (1) a rotation of the spindle along the long rotational axis and (2) a rotation along the minor axes.

Here we demonstrate that by application of a rotating magnetic field in a suitable frequency range, the dynamic reorientation of nanoscale hematite spindles can be forced into a synchronized spinning mode. Using time-resolved small-angle X-ray scattering (SAXS), we reveal how the orientation of an ensemble of water-dispersed hematite nanospindles can be tuned between coherent precession and a collinear alignment by suppression of one of the two distinct rotation directions. The time-resolution of stroboscopic SAXS is pivotal to track our nanoscale particles and provides information on the dynamic particle orientation of a large number (in the order of 10⁹) of independently moving nanospindles while applying an alternating or rotating magnetic field. Our results are supported with complementary optical transmission measurements and agree with theoretical estimates of the rotational diffusion constant. The observations demonstrate that hematite nanospindles hold out the key features for future application as nanoscale propellers.

2 Results and discussion

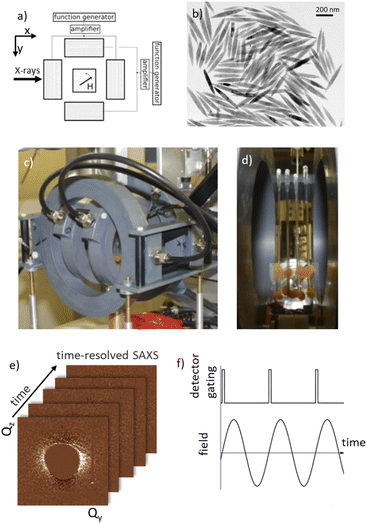
To achieve well-separated relaxation time scales, a large aspect ratio between the length and diameter of the hematite spindles is required. We therefore synthesized hematite nanospindles according to the hydrolysis method developed by Matijević and co-workers that allows the aspect ratio to be tuned.³⁰ TEM analysis reveals an average diameter of 51.5 nm and a particle length of 374 nm along with normal size distributions in the range of 13–20%, corresponding to an aspect ratio of around 7.3 (Fig. S1†). Small-angle X-ray scattering (SAXS) of the colloidal suspension of nanospindles in water was performed at the instrument ID13 (ESRF). To avoid interparticle interactions, the nanospindle concentration was kept low, <0.1 vol%, corresponding to ∼10¹² particles per mL solution, i.e. ∼10⁹ particles studied simultaneously in the scattering volume of the SAXS experiment. Refinement of the data using the form factor of an ellipsoid of revolution confirms the average particle diameter of 49.9 nm with an intermediate lognormal size distribution of 9.6% (Section S3.1†). The quasi-static magnetization measurement of the colloidal suspension further confirms the weakly ferromagnetic behavior of hematite above the Morin transition by the pseudo-superparamagnetic field dependence typically observed for magnetically blocked nanoparticles in dispersion (Fig. S2†). Refinement of the Langevin behavior reveals an integral nanoparticle moment of 7.643 × 10⁻¹⁹ J T⁻¹, corresponding to 82414(705) μ_B. Along with the morphological particle volume of 5.19 × 10⁻²² m³ as determined from TEM and SAXS analysis, a spontaneous magnetization of 1473 A m⁻¹ is derived. The obtained spontaneous magnetization represents only 74% of the bulk value for hematite of ∼ 2000 A m⁻¹,³¹ in agreement with earlier reports.^28,32 From this follows that the particles are not interacting and hence can freely rotate in suspension when applying external magnetic fields.

The anisotropy of the relaxation frequencies for rotation around the principal and minor spindle axes is confirmed by a combination of depolarized dynamic light scattering (DDLS, Fig. S3†) and AC magnetic susceptometry (ACMS, Fig. S4†). DDLS is sensitive to the orientational diffusion of the particles in dilute dispersion, and hence uniquely senses the rotation around the minor spindle axis. The rotational diffusion constant D_R = 149(7) s⁻¹ derived from DDLS analysis agrees well with its theoretical estimate of 179 s⁻¹ for an ellipsoid of revolution of the same dimensions^33,34 and corresponds to a characteristic frequency of ν_⊥ = D_R/π = 47(2) Hz. In contrast, ACMS probes the field-induced orientation of the spindle magnetization, including contributions of both rotation around the minor and principal axes. The characteristic frequency for rotation around the principal spindle axis is therefore not unambiguously accessible from ACMS, and will lie well beyond the experimentally observed ν_ACMS = 278 Hz. The significant difference between the characteristic frequencies for rotation around principal and minor spindle axes is an important prerequisite for a tunable motion control: we expect that for a magnetic field rotating with a frequency between both characteristic frequencies, a transition between coherent precession and synchronized spinning of nanospindles in dispersion is achievable.³⁵

Small-angle scattering is the most suitable technique to probe inhomogeneities on the nanoscale, with suitable spatial resolution to address the orientation distribution of a large ensemble of nanoparticles,^36–38 whereas time-resolved approaches give versatile opportunities to study in situ nanoparticle dynamics.^39–41 Stroboscopic SAXS provides the necessary time resolution to monitor changes in the orientation distribution near the characteristic frequencies of our nanoscale particles. We therefore performed time-resolved SAXS at the microfocus beamline ID13 (ESRF) to monitor the dynamic field-dependent orientation of hematite spindles driven by a custom-made set of Helmholtz coils. The two Helmholtz coils can each generate alternating magnetic fields, and together a magnetic field rotating in the horizontal plane if both applied fields have the same amplitude and frequency with a 90° phase shift (Fig. 1a). The magnetic field period was divided into 20 frames by synchronizing the coil setup with the detector to obtain the time-resolved scattering patterns as shown in Fig. 1f. The Maxipix detector allowed stroboscopic measurements up to 300 Hz. To emphasize the scattering anisotropy caused by the particle alignment in the applied field, all the following scattering images will be presented as the difference pattern with respect to the isotropic scattering pattern in zero field (see Fig. S6†).

Fig. 1 Experimental setup for stroboscopic SAXS at the ID13 beamline (ESRF). (a) Schematic drawing of two Helmholtz coils placed parallel and perpendicular to the X-ray beam. (b) TEM by hematite nanospindles. (c) Helmholtz coil set. (d) A colloidal dispersion of nanospindles and reference samples, mounted in quartz capillaries in the center of the field setup. (e) Time-resolved acquisition of SAXS. Detector images show a large beam stop in the center, surrounded by the SAXS signal. Detector images are presented as the difference scattering pattern with respect to the isotropic scattering pattern in zero field. (f) Detector gating with respect to the magnetic field phase.

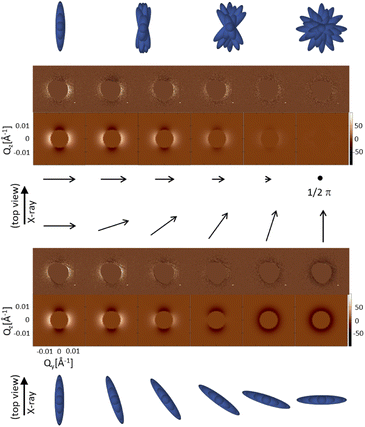
At frequencies of up to 25 Hz, where the moments of the entire nanospindle ensemble follow the applied field, a periodic variation of the anisotropic scattering intensities is observed for both alternating and rotating magnetic fields (Fig. 2, full period shown in Fig. S7†). In the alternating magnetic field, the time-resolved variation of scattering intensities indicates a dynamic interplay of order and disorder. Whereas the SAXS intensity is isotropic at times near the zero-field condition (1/2 π and 3/2 π), corresponding to the random nanoparticle orientation in the absence of a magnetic field, a clear scattering anisotropy is observed at a maximum field of 10 mT (0 and π). This scattering anisotropy results from the orientation of the spindles perpendicular to the inducing field, where the degree of alignment corresponds well to the Langevin parameter of 1.85, estimated for the integral nanospindle moment in the maximum applied field of 10 mT. We confirm this by computing the expected scattering pattern for a spindle ensemble using the spindle dimensions, integral particle moment, and average applied field for each frame according to the corresponding expected Boltzmann statistics of the particle distribution.²⁹ As shown in Fig. 2, the computed scattering pattern is in excellent agreement with the measured pattern. In the case of a rotating magnetic field of 10 mT, the easy magnetic axes of the nanospindles will maintain their orientation towards the applied field and the nanoparticle ensemble may fulfill a complete turn within one period of the applied field as long as thermal motion and fluid friction are subsidiary effects. We identify this behavior in a low frequency rotating magnetic field as coherent precession: the spindle ensemble fulfills precession around the field normal with a coherent phase behavior, albeit different precession angles. The difference between the two cases of alternating and rotating magnetic fields becomes very clear at the 1/2 π and 3/2 π time frames. In these time frames the applied rotating field is oriented parallel to the X-ray beam, resulting in isotropic scattering patterns. However, the difference in scattering intensity against the zero-field state is negative (shown in detail in Fig. S8†). The computed scattering pattern (Fig. 2) confirms that the nanospindle ensemble is oriented parallel to the detector plane, whereas for the alternating field these time frames correspond to an isotropic, disordered ensemble at nearly zero field and hence vanishing difference scattering intensities. The excellent agreement of the experimental scattering patterns with those computed based on the Boltzmann statistics of the particle distribution further confirms that the nanospindles orient independently from each other. Such an independent, interaction-free motion of a large ensemble of nanospindles is possible because the low magnetization of hematite and the small particle size combine into a very low magnetic moment of the individual particles.

Fig. 2 Stroboscopic SAXS by hematite nanospindles in alternating (top) and rotating (bottom) magnetic fields of 25 Hz. Field configuration is depicted by black arrows (center). The SAXS difference detector images are shown for a quarter period (0–1/2 π). Computed scattering patterns according to the expected orientation of the nanospindle ensemble are shown below the respective data. The average, time-resolved nanospindle orientation is depicted schematically showing the overlayed configurations of several particles (shapes in blue).

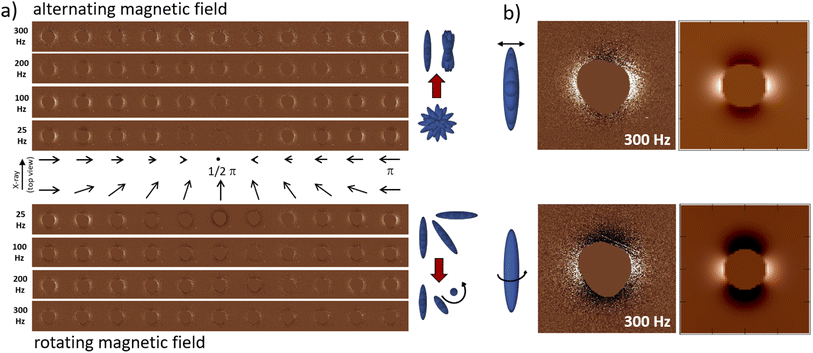
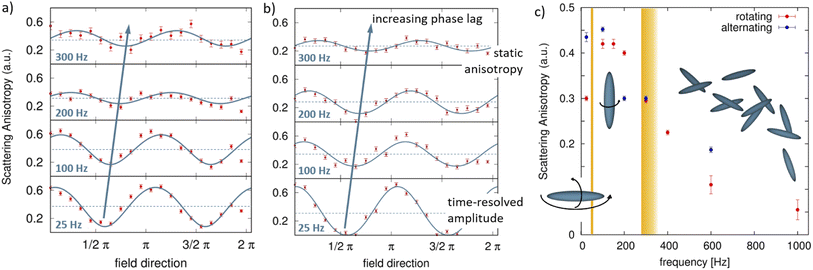
The evolution of difference scattering patterns with increasing frequency for both the alternating and rotating fields (Fig. 3) reveals how the time-dependent fluctuation of the scattering intensities disappears, while the scattering anisotropy remains. This is a clear signal of a transition from the dynamic particle reorientation observed at low frequency towards a confined particle arrangement. A more quantitative picture is established by analysis of the time- and frequency-dependent scattering anisotropy of the two field configurations (Fig. 4a and b), derived as the difference between scattering intensity in horizontal and vertical directions (see ESI†). Whereas in the low frequency case (25 Hz) a clear time-resolved fluctuation between maximum and vanishing scattering anisotropies is evident, the increasing magnetic field frequency is accompanied by a significant phase lag of the scattering anisotropy. This is a strong indication that there is a dissipative process acting such that the nanospindles cannot follow the dynamic magnetic field anymore at elevated frequencies. The time-dependent amplitude in scattering anisotropy decreases, corresponding to a more and more static orientation of the ensemble of nanospindles. However, there is a strong scattering anisotropy even at the highest investigated stroboscopic frequency of 300 Hz at all times. This indicates that the average orientation of a significant portion of the nanospindle ensemble is not isotropic.

Fig. 3 (a) Stroboscopic SAXS data by hematite nanospindles in alternating (top) and rotating (bottom) magnetic fields up to 300 Hz. Field configuration is depicted by black arrows (center) next to the SAXS difference detector images for half a period. (b) Time-integrated SAXS for alternating (top) and rotating (bottom) magnetic fields with 300 Hz (left) along with computed scattering patterns (right).

Fig. 4 Time-resolved SAXS by hematite nanospindles in a dynamic magnetic field with varying frequencies. Extracted scattering anisotropies for all time frames measured at the different frequencies of the (a) alternating and (b) rotating magnetic fields. (c) Frequency-dependent scattering anisotropy derived from time-averaged SAXS measurements in alternating (blue) and rotating (red) fields. The characteristic frequencies for rotation around the minor (47(2) Hz) and major axis (beyond 278 Hz) are indicated by orange bars.

For higher frequencies beyond 300 Hz, only time-averaged scattering anisotropies, corresponding to the dotted lines in Fig. 4a and b, are accessible from time-averaged SAXS data. Over the complete frequency range, these illustrate the transitions between different types of collective motion (Fig. 4c). For a rotating magnetic field, a maximal scattering anisotropy occurs for 150–200 Hz, i.e. in between the characteristic frequencies for rotation around the minor axis (47 Hz as determined from DDLS) and principal axis (beyond 278 Hz as estimated from ACMS and DDLS). In this frequency range, rotation around the principal axis is still allowed while rotation around the minor axis is inhibited. Beyond the characteristic frequencies for rotation around both principal and minor axes, the spindles do not follow the field variation anymore. Consequently, the scattering anisotropy decreases continuously, indicating an increasingly isotropic orientation of the nanoparticle ensemble.

A different spindle orientation distribution for alternating and rotating magnetic fields at intermediate frequency is inferred from the scattering intensities shown in Fig. 3b. The differential scattering patterns correspond well to those computed for orientation distributions with the long spindle axis either confined to the plane perpendicular to the alternating magnetic field or to the direction perpendicular to the rotating field plane (Fig. 3b). In the case of the alternating field, the time-independent but anisotropic scattering intensity indicates that the long axes of the spindles stabilize permanently with an orientational spread in the plane perpendicular to the field direction. We understand this such that beyond the characteristic frequency for rotation around the minor axis, the average field-induced angular moment is strong enough and reorientation of the magnetic moment in the fields occurs on time-scales much faster than rotational diffusion of the long axis that disordering Brownian rotational motion is suppressed in the field direction. In effect, the spindles become confined in the plane perpendicular to the field and fulfill random rotation on this 2D plane.⁴² In the rotating case, on the other hand, a particle experiences a constant torque produced by the rotating magnetic field that increases with frequency and eventually becomes significantly larger than Brownian random fluctuation within the 2D plane. A self-stabilizing rotational motion is favored as the viscous friction is reduced in a rotation around the long axis as compared to precessing motion involving rotation around the short axis. As a result, the spindle long axis stabilizes permanently in the direction perpendicular to the rotating field plane such that the magnetic moments can follow the rotating field on the shortest path of least action. We understand this as a synchronized spinning: the ensemble of collinearly aligned nanospindles rotates synchronously around their major spindle axes.

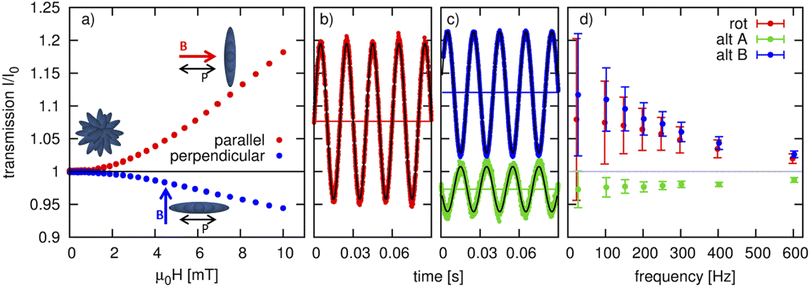
The field-induced, frequency-dependent reorientation variation observed by time-resolved SAXS is strongly supported by optical transmission measurements (Fig. 5). The optical transmission of linearly polarized laser light through a dilute suspension of elongated nanoparticles depends directly on the relative orientation of laser light polarization and the principal nanoparticle axis. For hematite nanospindles in a static magnetic field, an increase in optical transmission with an applied static field parallel to the polarization direction and a decrease in optical transmission for a magnetic field applied perpendicular to the polarization direction are consequently observed (Fig. 5a). The time-resolved optical transmission recorded in a rotating magnetic field of 25 Hz (Fig. 5b) oscillates exactly between the maximum and minimum static transmission, confirming that the entire nanoparticle ensemble follows the applied field. Similarly, in an alternating magnetic field of 25 Hz (Fig. 5c) the time-resolved optical transmission oscillates between the transmission extrema and 1, indicating considerable orientation of the nanospindles in the maximum applied field and isotropic orientation in zero field. With increasing frequency of both rotating and alternating magnetic fields (Fig. 5d), the full orientational order of the static or nearly-static case is not reached anymore. This is indicated by the decrease of the time-resolved amplitudes as well as by the center of the relative optical transmission approaching 1. However, the time-averaged anisotropy remains high, so that the full rotation amplitudes move above the isotropic case (I/I₀ = 1, grey line in Fig. 5d), indicating that a new, ordered state is achieved. The baseline of the rotation amplitude above 1 indicates that in the characteristic frequency range (with a maximum at 200–250 Hz), a significant portion of the spindles must be aligned perpendicular to the polarization direction at all times, which can only be the case if the spindles are aligned perpendicular to the rotating field plane. Likewise, the oscillation amplitudes in the alternating field do not reach the fully isotropic state at elevated frequencies, supporting the anisotropic nanospindle orientation observed with SAXS.

Fig. 5 Optical transmission measurements: (a) field-dependent relative optical transmission in a DC magnetic field along with time-resolved optical transmission for (b) rotating and (c) alternating magnetic fields of 25 Hz and 10 mT, (d) frequency dependence of the relative optical transmission (•) with error bars representing the time-resolved amplitude.

To summarize the response of the nanospindle ensemble in rotating fields: At low frequencies below the characteristic relaxation frequencies, rotation around both major and minor particle axes is enabled. In consequence, the nanospindles follow the magnetic field and remain quasi-statically oriented with their major axis perpendicular to the inducing magnetic field, corresponding to coherent precession around the field normal. For intermediate magnetic field frequencies between the two relaxation time scales, rotation around the minor particle axis becomes suppressed, resulting in a decreasing precession angle. In consequence, the particles are driven into a collinearly aligned orientation of the major particle axis with synchronized spinning around the normal to the rotation plane. At high frequencies beyond the characteristic frequencies of rotation around both axes, the spindle ensemble disorients toward isotropic disorder.

3 Conclusions

We have elucidated the frequency-dependent reorientation behavior of a large ensemble of non-interacting nanoscale hematite spindles in dynamic magnetic fields. The study emphasizes the potential of dynamic fields to control the rotation modes of shape anisotropic magnetic nanoparticles with perpendicular magnetic anisotropy.

Stroboscopic SAXS resolves signatures of different types of motion with a clear enhancement of the particle orientation in the intermediate frequency range between the characteristic relaxation time scales. The orientational behavior of the spindles strikingly differs between alternating or rotating magnetic fields. Time-resolved SAXS is a valuable tool to investigate this type of dynamic self-organization in situ towards a nearly collinear alignment of nanospindles perpendicular to the rotating magnetic field. The peculiar behavior of the spindle particle ensemble in a rotating magnetic field from coherent precession to synchronized spinning is understood in analogy to the frequency-dependent variation of motion mechanisms of individual microwires near a surface boundary, ranging from tumbling and precessing to a rolling motion with increasing frequency.²² With further increasing frequency, the effective field that aligns the nanospindle upwards reduces due to the increasing phase lag of the spindle magnetization towards the rotating magnetic field. For dynamic frequencies well above the characteristic frequencies for rotation around the major axis, the synchronized rotational motion of the spindle ensemble ceases. This corresponds well to the step-out behavior observed as a decay in the propulsion velocity of helical objects in a rotating field with increasing frequency.^24,43 The characteristic frequencies for rotational diffusion of hematite nanospindles are adjustable by the solvent viscosity and by variation of the spindle length and aspect ratio through synthetic considerations. This will enable direct tuning of the frequency range needed to control the different rotation modes. The ability to control the dynamic reorientation of large ensembles (in the order of 10⁹) independently moving nanoscale magnetic particles establishes an important step to progressing field-driven actuation and locomotion to the nanoscale. With this prerequisite, oriented locomotion of a swarm of nanoscale particles may become accessible using complex magnetic field geometries, such as combined rotating and static magnetic fields.⁴⁴

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the ESRF for the provision of synchrotron radiation facilities at the Microfocus beamline ID13. This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. SasView contains code developed with funding from the European Union's Horizon 2020 research and innovation program under the SINE2020 project, grant agreement no. 654000. We thank Stefan Roitsch for the acquisition of TEM micrographs. Financial support from the German Research Foundation (DFG: Emmy Noether Grant DI 1788/2-1) is gratefully acknowledged. We acknowledge support for the Article Processing Charge from the DFG (German Research Foundation, 491454339).

Notes and references

1. G. Z. Lum, Z. Ye, X. Dong, H. Marvi, O. Erin, W. Hu and M. Sitti, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E6007–E6015.
2. H. Zhou, C. C. Mayorga-Martinez, S. Pané, L. Zhang and M. Pumera, Chem. Rev., 2021, 121, 4999–5041.
3. N.-T. Nguyen, Microfluid. Nanofluid., 2012, 12, 1–16.
4. G. Kokot and A. Snezhko, Nat. Commun., 2018, 9, 2344.
5. V. L. Calero-DdelC, D. I. Santiago-Quiñonez and C. Rinaldi, Soft Matter, 2011, 7, 4497.
6. S. Disch, E. Wetterskog, R. P. Hermann, G. Salazar-Alvarez, P. Busch, T. Brückel, L. Bergström and S. Kamali, Nano Lett., 2011, 11, 1651–1656.
7. E. Wetterskog, A. Klapper, S. Disch, E. Josten, R. P. Hermann, U. Rücker, T. Brückel, L. Bergström and G. Salazar-Alvarez, Nanoscale, 2016, 8, 15571–15580.
8. M. Kapuscinski, P. Munier, M. Segad and L. Bergström, Nano Lett., 2020, 20, 7359–7366.
9. A. Pal, C. A. De Filippo, T. Ito, M. A. Kamal, A. V. Petukhov, C. De Michele and P. Schurtenberger, ACS Nano, 2022, 16, 2558–2568.
10. R. Stanway, Mater. Sci. Technol., 2004, 20, 931–939.
11. J. de Vicente, D. J. Klingenberg and R. Hidalgo-Alvarez, Soft Matter, 2011, 7, 3701.
12. K. Bente, A. Codutti, F. Bachmann and D. Faivre, Small, 2018, 14, 1704374.
13. X.-Z. Chen, B. Jang, D. Ahmed, C. Hu, C. D. Marco, M. Hoop, F. Mushtaq, B. J. Nelson and S. Pané, Adv. Mater., 2018, 23, 1705061.
14. Q. Cao, Q. Fan, Q. Chen, C. Liu, X. Han and L. Li, Mater. Horiz., 2020, 7, 638–666.
15. T. Li, J. Li, K. I. Morozov, Z. Wu, T. Xu, I. Rozen, A. M. Leshansky, L. Li and J. Wang, Nano Lett., 2017, 17(8), 5092.
16. P. Dhar, S. Narendren, S. S. Gaur, S. Sharma, A. Kumar and V. Katiyar, Int. J. Biol. Macromol., 2020, 158, 1020–1036.
17. P. Tierno, Phys. Chem. Chem. Phys., 2014, 16, 23515–23528.
18. P. Mandal, G. Patil, H. Kakoty and A. Ghosh, Acc. Chem. Res., 2018, 51, 2689–2698.
19. P. Dhar, C. D. Swayne, T. M. Fischer, T. Kline and A. Sen, Nano Lett., 2007, 7, 1010–1012.
20. L. O. Mair, B. A. Evans, A. Nacev, P. Y. Stepanov, R. Hilaman, S. Chowdhury, S. Jafari, W. Wang, B. Shapiro and I. N. Weinberg, Nanoscale, 2017, 9, 3375–3381.
21. F. Martinez-Pedrero, E. Navarro-Argemí, A. Ortiz-Ambriz, I. Pagonabarraga and P. Tierno, Sci. Adv., 2018, 4, eaap9379.
22. B. Jang, A. Hong, C. Alcantara, G. Chatzipirpiridis, X. Martí, E. Pellicer, J. Sort, Y. Harduf, Y. Or, B. J. Nelson and S. Pané, ACS Appl. Mater. Interfaces, 2019, 11, 3214–3223.
23. P. J. Vach, P. Fratzl, S. Klumpp and D. Faivre, Nano Lett., 2015, 15, 7064–7070.
24. F. Bachmann, J. Giltinan and A. Codutti, Appl. Phys. Lett., 2021, 118, 174102.
25. S. P. Jang and S. U. Choi, Appl. Phys. Lett., 2004, 84, 4316–4318.
26. P. J. Vach, N. Brun, M. Bennet, L. Bertinetti, M. Widdrat, J. Baumgartner, S. Klumpp, P. Fratzl and D. Faivre, Nano Lett., 2013, 13, 5373–5378.
27. ISO/TR 14786:2014(En), Nanotechnologies — Considerations for the Development of Chemical Nomenclature for Selected Nano-Objects, https://www.iso.org/obp/ui/#iso:std:iso:tr:14786:ed-1:v1:en.
28. M. Reufer, H. Dietsch, U. Gasser, B. Grobety, A. M. Hirt, V. K. Malik and P. Schurtenberger, J. Phys.: Condens. Matter, 2011, 23, 065102.
29. D. Zákutná, Y. Falke, D. Dresen, S. Prévost, P. Bender, D. Honecker and S. Disch, Nanoscale, 2019, 11, 7149–7156.
30. M. Ozaki, S. Kratohvil and E. Matijević, J. Colloid Interface Sci., 1984, 102, 146–151.
31. F. Bødker, M. F. Hansen, C. B. Koch, K. Lefmann and S. Mørup, Phys. Rev. B, 2000, 61, 6826–6838.
32. D. Hoffelner, M. Kundt, A. M. Schmidt, E. Kentzinger, P. Bender and S. Disch, Faraday Discuss., 2015, 181, 449–461.
33. F. Perrin, J. Phys. Radium, 1934, 5, 497–511.
34. S. B. Dubin, N. A. Clark and G. B. Benedek, J. Chem. Phys., 1971, 54, 5158–5164.
35. A. Ghosh, D. Dasgupta, M. Pal, K. I. Morozov, A. M. Leshansky and A. Ghosh, Adv. Funct. Mater., 2018, 28, 1705687.
36. T. Li, A. J. Senesi and B. Lee, Chem. Rev., 2016, 116, 11128–11180.
37. C. M. Jeffries, J. Ilavsky, A. Martel, S. Hinrichs, A. Meyer, J. S. Pedersen, A. V. Sokolova and D. I. Svergun, Nat. Rev. Methods Primers, 2021, 1, 70.
38. D. Honecker, M. Bersweiler, S. Erokhin, D. Berkov, K. Chesnel, D. A. Venero, A. Qdemat, S. Disch, J. K. Jochum, A. Michels and P. Bender, Nanoscale Adv., 2022, 4, 1026.
39. T. Narayanan, M. Sztucki, P. Van Vaerenbergh, J. Léonardon, J. Gorini, L. Claustre, F. Sever, J. Morse and P. Boesecke, J. Appl. Crystallogr., 2018, 51, 1511–1524.
40. C. Glinka, M. Bleuel, P. Tsai, D. Zákutná, D. Honecker, D. Dresen, F. Mees and S. Disch, J. Appl. Crystallogr., 2020, 53, 598–604.
41. D. Zákutná, K. Graef, D. Dresen, L. Porcar, D. Honecker and S. Disch, Colloid Polym. Sci., 2021, 299, 281–288.
42. K. I. Morozov, Y. Mirzae, O. Kenneth and A. M. Leshansky, Phys. Rev. Fluids, 2017, 2, 044202.
43. D. Schamel, M. Pfeifer, J. G. Gibbs, B. Miksch, A. G. Mark and P. Fischer, J. Am. Chem. Soc., 2013, 135, 12353–12359.
44. K. I. Morozov and A. M. Leshansky, Phys. Chem. Chem. Phys., 2020, 22, 16407.

---

Footnote

† Electronic supplementary information (ESI) available: Details of nanoparticle synthesis and characterization. See https://doi.org/10.1039/d2na00522k

---