Photonic band structure calculation of 3D-finite nanostructured supercrystals

Abstract

Computational modeling of plasmonic periodic structures are challenging due to their multiscale nature. On one hand, nanoscale building blocks require very fine spatial discretization of the computation domain to describe the near-field nature of the localized surface plasmons. On the other hand, the microscale supercrystals require large simulation domains. To tackle this challenge, two approaches are generally taken: (i) an effective medium approach, neglecting the nanoscale effects and (ii) the use of a unit cell with periodic boundary conditions, neglecting the overall habit of the supercrystal. The latter, which is used to calculate the photonic band structure of these supercrystals, fails to describe the photonic properties arising from their finite-size such as Fabry-Pérot modes (FPMs), whispering gallery modes (WGMs), and decrease of the photonic mode lifetime. Here, we developed a computational approach, based on the finite-difference time-domain method to accurately calculate the photonic band structures of finite supercrystals. We applied this new approach to 3D periodic microstructures of Au nanoparticles with cubic, spherical, and rhombic dodecahedral habits and discuss how their photonic band structures differ from those of infinite structures. Finally, we compared the photonic band structures to reflectance spectra and describe phenomena such as FPMs, WGMs, and polaritonic bandgaps.

---

Introduction

Coherent, collective oscillations of the conduction electron gas, known as localized surface plasmon resonances (LSPRs), are sustained by nanostructures composed of noble metals.^1,2 Due to their unique optical properties, valuable applications have been found for these elementary excitations in photocatalysis,^3–5 surface-enhanced spectroscopies,^6–8 drug delivery, cancer therapy and theranostics,^9–11 imaging,^12,13 sensing,^12,14,15 active light manipulation/circuitry,^16–18 and solar applications.^19–21 However, plasmonic materials also exhibit limiting physical effects associated with their materials composition, such as inherent losses.^22–24 A route to overcoming these limitations and achieving sustainable materials with improved optical properties consists of structuring the plasmonic building blocks in a well-organized manner,²⁵ forming one-dimensional (1D) chains,^26–28 two-dimensional (2D) arrays,^28–32 or three-dimensional (3D) superlattices.^8,28,33–42 These supercrystals possess the unique ability to retain the intrinsic properties of their building blocks but also display unique collective properties originating from interparticle coupling effects. In recent years, DNA-linked 3D superlattices composed of metallic NPs have been investigated.^{33,35,37,39,42–45} In their pioneering work, Mirkin and Schatz have shown that such 3D supercrystals exhibit strong novel optical behaviors resulting from the coexistence of plasmonic and photonic modes.^28,35,46,47 By continuously varying the NPs orientation, periodicity, spacing, size, and shape, as well as the crystal habit, an enormous set of fundamentally interesting metamaterials can be designed. With the countless superlattices now synthetically realizable,³⁸ computational methods and theoretical models play a crucial role in identifying the supercrystals that exhibit the most exciting properties (Fig. 1).^34,48 When the supercrystal lattice parameter is much smaller than the wavelength, the medium usually behaves like a uniform, continuous material, characterized by an effective dielectric permittivity and magnetic permeability, which are modeled using an effective medium theory such as the Maxwell-Garnett^49,50 and Bruggeman⁵¹ models. However, when the lattice parameter is comparable to the optical wavelength, the photonic band structure plays a key role. In such assemblies, the interparticle distance becomes the critical parameter that governs the collective optical properties. When the distance is larger than the wavelength of optical excitation the NPs are uncoupled and the collective optical response is the incoherent summation of individual responses of each NP constituting the assemblies. Additional photonic behaviors arise when the interparticle distance satisfies Bragg's law (e.g., Rayleigh anomalies) or when multipolar interactions are involved. Finally, geometrical aspects such as the dimensionality and the habit of the supercrystal, the lattice parameter in each spatial direction, and the morphology of the NPs composing the supercrystal play a key role in defining their optical properties including (an)isotropy/birefringence,^47,48 the emergence of Fabry-Pérot resonances and whispering gallery modes (WGM),³⁴ and decrease of the photonic mode lifetime.

Fig. 1 Approaches to calculate the properties of photonic crystals, i.e., infinite lattice for band structure calculations, effective medium theory for optical properties like reflectance, and proposed FDTD simulation for finite supercrystals.

Understanding the optical properties of realistic, experimentally fabricated nanostructures require a deep understanding of the morphological defects,^52–54 size distributions,⁵⁵ materials inhomogeneity, size effects,⁵⁶ and finite-size effects.^57–59 Computationally, periodic systems are very often regarded as infinite via the use of periodic boundary conditions applied to the simulation domain^9,47,60 or effective medium approaches.^34,35,61 Only a few studies have focuses on finite-size effects in 1D linear chains of nanoparticles,⁶² and 2D periodic arrays.^58,59 All of these studies focused on very specific optical properties such as scattering, absorption, transmission, or reflection. With the recent advances in nanoscale and microscale fabrication techniques, plasmonic superlattices and their optical properties have rapidly become an interesting platform of novel optical properties. While semiconductor superlattices have been well-studied and theoretical tools have been developed to study their optical properties,⁶³ the field of Plasmonics lacks computational models and methods to investigate these finite-size effects.⁶⁴ On one hand, the nanoscale nature of the building blocks requires very fine spatial discretization of the computation domain to describe the near-field nature of the LSPRs. On the other hand, the microscale nature of the superlattice requires a very large simulation domain.⁶⁴ To tackle this challenge, two approaches are generally taken: (i) an effective medium theory approach which neglects the nanoscale effects and periodicity to focus on the overall optical properties of the supercrystal, and (ii) the use of a unit cell with periodic boundary conditions which neglects the overall habit of the supercrystal to focus on nanoscale behaviors. While the former fails to account for local effects such as interparticle coupling and anisotropy effects as shown by Mirkin and co-workers,^34,47 the latter approach, which is used for the calculation of the photonic band structures, fails to describe the photonic properties rising from finite-size and microscopic effects.^34,65

Here, we theoretically investigate the photonic properties of 3D periodic micron-scale arrangements of plasmonic nanoparticles that form supercrystals, also known as plasmonic supercrystals, 3D superlattices, or plasmonic photonic crystals. We propose a theoretical and computational approach for calculating the photonic band structures of finite supercrystals and investigate the effect of the habit (i.e., crystal shape) and size on its photonic properties and conduct a detailed comparison with standard electrodynamic simulations of the optical properties (reflectance) of these finite superlattices. We also conduct a direct comparison with photonic band structure calculations of truly infinite superlattices. Although we applied this new approach to 3D Au-NPs supercrystals, this method is far more general and can straightforwardly be applied to finite 1D and 2D periodic structures of many kinds of building-block materials.

Methods

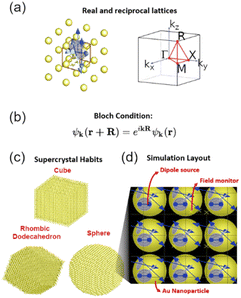
In order to calculate the optical properties of the supercrystals, we use the finite-difference time-domain (FDTD) method from Ansys-Lumerical.⁶⁶ We have considered multiple cases: infinite and finite crystals, different crystal habits (for the finite case), lattice parameters, and building blocks (nanospheres and nanorods) to determine the photonic band structure and the reflectance of each case. Different methods were used depending on the system and are described below. For all these cases, the cubic unit cell (see Fig. 2a, real lattice) has been chosen because it is the simplest lattice to analyze. However, it is important to note right away that the proposed method also applies to other unit cell symmetries. In this work, we used an optical excitation in the UV-vis-NIR region (0.83–3.3 eV in energy or 375–1500 nm in wavelength), and which includes the LSPR frequency of the Au NPs (∼2.3 eV or 550 nm for Au NPs of 80 nm in size). For calculating the band diagram, only the first-order Brillouin zone is considered. We defined 80 different wavevectors within the first Brillouin zone of the cubic reciprocal lattice (Fig. 2a) running over the high symmetry path described by the high symmetry points (Table S1, ESI†): Γ (center of the Brillouin zone), X (center of a face), M (center of an edge), and R (corner point); thus, requiring one simulation per k-vector. The crystal building blocks are taken as either Au NPs of 80 nm in diameter or Au nanorods with a size of 40 × 80 nm immersed in an aqueous medium. Gold is modeled with a frequency-dependent refractive index taken from Johnson and Christy's experimentally-tabulated data,⁶⁷ and the aqueous medium with a constant refractive index n_m = 1.33. Two lattice parameters, a, were considered: 100 and 130 nm, corresponding to interparticle distances of 20 and 50 nm, respectively. These lengths, NPs sizes, and interparticle distances, were selected in order to maintain the computational resources relatively low without compromising the main goal of the present contribution which is to demonstrate the new approach to calculate the photonic band structure.

Fig. 2 (a) Real-space simple cubic lattice (left) formed with Au NPs showing the dipole sources (blue arrows) and field monitors (red crosses) within the unit cell used for the infinite-case simulation and the first Brillouin zone of the reciprocal cubic lattice (right) showing the high symmetric path (Γ–X–M–R–Γ) used for the band structure calculations. (b) Block condition. (c) Supercrystals with cubic, rhombic dodecahedral, and spherical habits, used in the finite-case simulations made up of Au NPs. (d) Simulation layout of the finite supercrystal (9 unit cells are shown) consisting in Au NPs (yellow spheres), electric dipoles (blue arrows), and field monitors (red crosses).

Infinite case

Infinite cubic superlattices of Au NPs (Fig. 2a) were simulated to determine their photonic band structures. The unit cell was defined by Bloch boundary conditions in x-, y-, and z-directions, used to define the periodicity of the system copying the fields at one edge of the simulation region and re-injecting them at the other edge, ensuring the phase correction of the fields via the Bloch conditions (Fig. 2b). The simulation domain (i.e., unit cell) was discretized with a uniform mesh of 2.5 × 2.5 × 2.5 nm. Twenty electric dipole sources were randomly distributed within the unit cell, each one with a random phase and a random spatial orientation (defined by the angles θ and ϕ) to excite all possible photonic modes within the system. This approach will ensure that all modes are excited even if one dipole is located at a node. We also randomly distribute twenty electric field monitors within the cell to record the time evolution of the electromagnetic field. Using multiple time monitors at different locations ensures all modes are captured. Convergence was assured via the auto-shutoff parameter in the Ansys-Lumerical software, which was set at 10⁻⁷ to allow for the electromagnetic fields to propagate for 500 fs. Finally, the photonic band structure was determined from the photonic density of states by applying the fast Fourier transformation (FFT) to the collected electric field in the time domain for each k-vector, where the intensity refers to the squared amplitude of the electric field. The optical signal was previously filtered by a Gaussian function centered at 250 fs and width of 65 fs to ignore initial and final effects.

Finite case

Many of the parameters described for the infinite case were used for the present one and are, therefore, omitted here. Three supercrystal structures of different habits were simulated to obtain their photonic band structure and reflectance spectra: cube, rhombic dodecahedron, and sphere; all of them were structured with Au NPs and ordered in a simple cubic lattice arrangement (Fig. 2c). The dimensions of each supercrystal, L, were 2 and 3.5 μm (for a = 100 and 130 nm, respectively) in length for the cube, face-to-face length for rhombic dodecahedron, and diameter for the sphere. The simulation domain was delimited with standard perfectly matched layers (PMLs, 12 layers) to absorb the electromagnetic fields at the boundaries in the x-, y-, and z-directions. The simulation domain was taken with a size equal to the length of the supercrystal, L, plus the maximum source wavelength, i.e., 3.5 μm (for a = 100 nm) and 5 μm (for a = 130 nm) and was discretized with a non-uniform mesh. A refined mesh of 4 × 4 × 4 nm was applied to the Au NPs. For the photonic band structure calculations, 6 electric dipole sources were randomly distributed and oriented within a unit cell and distributed to the other unit cells by applying the Bloch conditions (Fig. 2b) to the dipole phase in order to couple all these sources within the crystal lattice depending on their spatial positions (Fig. 2d). A thousand electric field monitors were also randomly distributed within the entire supercrystals. The photonic band structures were also determined following the same process as for the infinite case. For the reflectance calculations, the supercrystal was excited using an optical plane wave source (total-field scattered-field, TFSF source) with normal incidence at one end and a planar monitor was located at the other end of the supercrystal to record the reflected signal during the simulation.

Effective medium model

Maxwell-Garnett theory⁴⁹ was used to calculate the effective refractive index (N_eff = ε^1/2_eff) of a simple-cubic superlattice (a = 100 and 130 nm) composed of Au NPs (80 nm in diameter) in an aqueous medium. Briefly, the effective dielectric permittivity, was defined as ε_eff = ε_m(2αF + 1)/(1 − αF), where α = (ε_Au – ε_m)/(ε_Au + 2ε_m) and F = V_NP/V_cell is the filling factor (i.e., volume fraction; Table S2, ESI†). ε_Au and ε_m = n²_m are the dielectric permittivities of Au and the surrounding medium, respectively, and V_NP and V_cell are the volumes of the Au NPs and the unit cell, respectively. The resulting N_eff (Fig. S1, ESI†) was used to determine the dispersion relation, ω = kc/N_eff, of light in this medium, and for a slab of 2 μm of thickness using FDTD in order to compare them with that obtained from the finite supercrystal method.

Results and discussion

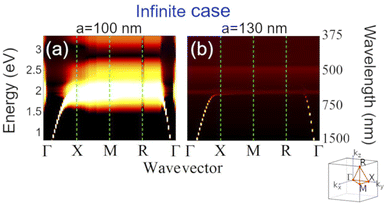
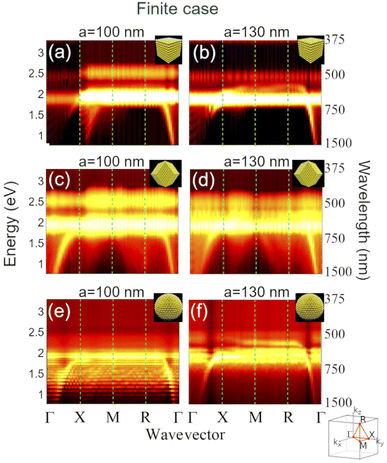
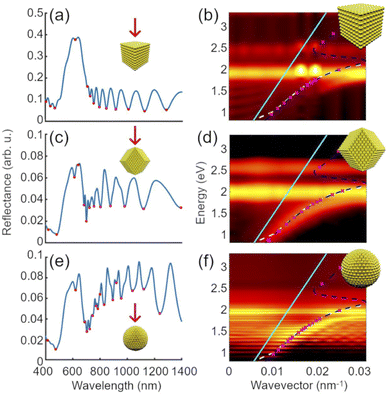
First, we calculated the photonic band structure of an infinite cubic lattice for two different lattice parameters, a, of 100 nm (interparticle distance of 20 nm, Fig. 3a) and 130 nm (interparticle distance of 50 nm, Fig. 3b) in order to compare them with the finite cases (different habits). We can see that the thin band coming from zero energy at the Γ point along the symmetry line Δ (between Γ and X), which is the light dispersion line in the lattice, is bent at ∼2.3 eV (i.e., 550 nm) forming a wide band, in the case of a = 100 nm. This frequency corresponds to the LSPR of the 80 nm Au NPs, which is confirmed by a simple Mie theory calculation.⁶⁸ Due to the proximity of the NPs, plasmon hybridization occurs, thus producing that broad and intense band in the photonic band structure.⁶⁹ When the interparticle distance increases (a = 130 nm, Fig. 3b), the coupling between NPs rapidly decreases, and the light is almost completely absorbed by the individual NPs, resulting in a fading of the photonic band observed in the former band structure (Fig. 3a). In both cases, there is a bandgap at higher energies due to the absorption of light mediated by electronic interband transitions in gold. Using an effective medium approximation (Maxwell-Garnett theory), we have calculated the relation dispersion of the Au NP lattice (a = 100 nm) to better visualize the coupling effect of the LSPR and the light (see Fig. S2, ESI†).

Fig. 3 Photonic band structures of an infinite cubic lattice composed of 80 nm Au NPs and with a lattice parameter of (a) 100 nm and (b) 130 nm. The interparticle distances are 20 and 50 nm, respectively.

Now that the photonic band structure of an infinite Au-NPs lattice has been introduced, let us turn our focus to finite-size supercrystals with cubic, rhombic dodecahedral, and spherical habits (Fig. 4). In general, it is noted that, in all the cases, the photonic band structures seem to qualitatively resemble that of the infinite supercrystal: i.e., exhibiting an intense photonic band around 2 eV due to the light-plasmon coupling and the formation of the collective, hybridized plasmon response. However, we note that new features arise as a result of the supercrystal finite size, and which clearly depend on the supercrystal habit. The first thing to notice is a significant broadening of the various photonic bands calculated for the finite-size supercrystals. Because we are now working outside of the bandgap, the characteristics of a finite periodic structure are a non-monotonous function of the number of periods, which results in surface (i.e., interface) scattering. These losses, in turn, translate into a decrease of the photonic mode lifetime (i.e., increased damping). While these effects have not been investigated for plasmonic-based superlattices, there have been studied in dielectric photonic crystals.^70,71

Fig. 4 Photonic band structures of the finite cubic-lattice supercrystals with (a and b) cubic, (c and d) rhombic dodecahedral, and (e and f) spherical habits. The supercrystals are composed of 80 nm Au NPs with lattice parameters of 100 nm (left panels) and 130 nm (right panels).

Centering now our attention on the cubic supercrystal with a = 100 nm (Fig. 4a), it is appreciated that multiple dispersion lines are generated at low energies along the symmetry line Δ and replicated along the symmetry line Z(between X and M). These new features correspond to Fabry-Pérot photonic modes (FPM), which occur from the interference of the reflected waves between the parallel surfaces forming two opposite faces of the cubic supercrystal.³³ In order to confirm the formation of FPM, we calculated the reflectance of the cubic supercrystal for normal incidence (red arrow in Fig. 5a inset), i.e., k = k_X (X point in the photonic band diagram). The reflectance spectrum, which is shown in Fig. 5a, exhibits well defined FPMs patterns, previously observed in backscattering measurements in similar nanoparticle assemblies.³⁴ These FPMs are also plotted in the dispersion diagram (Fig. 5b, magenta crosses) to clarify their connection with the aforementioned bands along the symmetry line Δ. It is worth noting that the FPMs are also coupled to the LSPR (bending and almost complete suppression around the plasmon band). Thanks to this coupling, a bandgap is formed between the two branches approximately at the Au-NPs LSPR, termed polaritonic bandgap (PBG).³⁴ The upper branch is quenched due to the electronic interband transitions of gold. This PBG is not formed in the case of an infinite lattice because of the lack of FPM (see Fig. 5b and S2†). In the vis-NIR region, the skin-depth of metals such as gold and silver is typically below 25 nm. In Fig. S3† we can see that the incident electric field penetrates into the cubic supercrystal up ∼100–150 nm from the face, where the wave is impinging at the frequency of the upper branch (490 nm, Fig. S3a and d†). This penetration is due to the absorption from the interband transitions, highly absorbed at the PBG (539 nm, Fig. S3b and e†) and reflected at the lower branch (650 nm, Fig. S3c and f†). The same behavior is observed when the supercrystal is rotated by 90° with respect to the incident electric field, i.e., when k is at the high symmetric point M (see Fig. S4†). This behavior is in excellent agreement with previous theoretical work by Ross et al.⁴⁸

Fig. 5 Reflectance at the X point (k = k_X, left panels) with the FPMs indicated by red markers (the red arrow in the inset indicates the incident wavevector orientation relative to the supercrystal). Dispersion relation (right panels) of Au-NPs supercrystals with a lattice parameter of 100 nm. (a and b) Cubic, (c and d) rhombic dodecahedral, and (e and f) spherical habits. In the dispersion relations are included the light dispersion in water (cyan solid line), dispersion relation calculated with FDTD of a slab with effective refractive index of the supercrystal (white dashed line), and dispersion relation of the light in the effective medium (blue dashed line) with the FPMs obtained from the reflectance spectrum and applying the resonant condition of a Fabry-Pérot cavity, to find the k value, k_N = ω_nRe[N_eff(ω)]/c (magenta crosses).

Going back to the photonic band structures of the cubic supercrystal (Fig. 4a,b), we can see that by increasing the interparticle distance from 20 to 50 nm (Fig. 4b), the LSPR remains present but the FPMs are no longer coupled to it; thus leading to the disappearance of the PBG. In Fig. S5,† we show a direct comparison of the reflectance spectra with a cross-section of the photonic band structure taken at the X point for both the infinite lattice and the finite cubic supercrystal. What this figure shows is that, for both analyzed lattice parameters, the FPM patterns decrease in intensity as they approach to the LSPR (around 600 nm). It can also be noted how the PBG is formed around 550 nm in the band structure of the finite supercrystal, in contrast with the continuous band in the infinite case. Additionally, we calculated the dispersion relation for a slab with the effective refractive index N_eff of a Au-NP supercrystal with a lattice parameter a = 100 nm and in aqueous medium (Fig. S6†). This calculation allows us to verify the formation and evolution of the FPM bands, which are the only modes present in the slab configuration. This dispersion relation is to be compared with the photonic band structures shown in Fig. 4 and which contain a richer variety of photonic features. For this, the FPMs found in the reflectance spectra calculated for the three supercrystals (Fig. 5a,c,e) were verified by taking their frequency positions (ω = 2πc/λ) and applying the resonance condition of a Fabry-Pérot cavity to find the corresponding wavenumber, k = ωRe[N_eff(ω)]/c.³⁴ These FPMs fit with the photonic features as showed with the magenta crosses in the dispersion relations (Fig. 5b, d and f). Interestingly, at lower energies (i.e., longer wavelengths), the FPM positions calculated with the effective medium theory (Fig. S6†) slightly deviate from those calculated with the full model (Fig. 5). This deviation, which has already been observed by Park et al.,³⁴ is attributed to the decreased size parameter, πLN_eff(λ)/λ, and is due to the low refractive index and small size-to-wavelength ratio at longer wavelengths. This further illustrates the limitations of the effective medium approach for a quantitative description of finite-size effects such as Fabry-Pérot resonances.

We have also calculated the mode splitting energy (ħΩ_R) defined as the energy difference between the upper and lower polaritonic bands, in order to quantify the FPM-LSPR coupling. In Fig. S7a† we show the intensity of the bands at the X point of the cubic supercrystal with a lattice parameter a = 100 nm, to better visualize the mode splitting, which we determined to be ħΩ_R = 0.55 eV. Although the upper polaritonic band is almost vanished when a = 130 nm, as seen in Fig. S7b,† it is still possible to determine the mode splitting energy to be ħΩ_R = 0.55 eV. Considering the LSPR energy to be ω₀ = 2.3 eV, the corresponding normalized coupling strength is η = Ω_R/ω₀ ≈ 0.24. While these coupling strengths are much smaller than these obtained in the ultra-strong coupling regime achieved by Mueller et al. for Au NP,⁴¹ it is important to also notice that the gap-to-diameter ratio they have is 0.02–0.12 as opposed to 0.25–0.63 in our work).

The photonic band structure of a rhombic dodecahedral supercrystal (Fig. 4c and d) is slightly different from that of a cubic supercrystal. While this supercrystal habit appears more complex, it is nonetheless a system which can be experimentally fabricated.^34,40 It is, therefore, a very relevant morphology to look at. Similarly to the cubic supercrystal, it also exhibits a PBG, as well as lower and upper polaritonic branches due to the FPM-LSPR coupling, with a splitting energy ħΩ_R = 0.55 eV (Fig. S7c†) which is comparable to the values reported by Park et al.³⁴ This coupling almost disappears when the lattice parameter is increased from 100 to 130 nm (Fig. S7d†); however, the splitting energy could be determined to be ħΩ_R = 0.53 eV. These splitting energies are similar to those obtained for the cubic supercrystals because the filling fraction is the same for both supercrystals (F = 0.268). However, the main difference arises from the emergence of FPM bands along the other symmetry lines, and not only along Δ and Z as in the cubic supercrystal. The other directions which sustain these FPM are the symmetry lines T (between M and R) and Λ (between R and Γ). These characteristic FPM bands are also apparent since the rhombic dodecahedron has parallel surfaces not only along the X direction, but also along the diagonals of the lattice (R direction; i.e., k = k_R) causing Fabry-Pérot interferences. However, it is worth noting that the contrast between these FPMs and the plasmon band is much smaller than in the cubic supercrystal. The rhombic dodecahedral supercrystal does not have faces along k = k_M and, therefore, it does not exhibit Fabry-Pérot interferences at the M point. The FPM bands are less intense in the dispersion diagram of the rhombic dodecahedral supercrystal (Fig. 5d) than in the cubic supercrystal because the Fabry-Pérot interferences occur three times along the same symmetry line as opposed to only once in the rhombic dodecahedron.

Finally, the photonic band structure (Fig. 4e and f) and reflectance spectrum (Fig. 5e) for the case of a spherical supercrystal exhibits oscillating patterns similar to those observed in the cubic and rhombic dodecahedral supercrystals. However, since the sphere does not have any parallel flat faces which could sustain FPM, these oscillations are associated with whispering gallery modes.^72,73 One can also notice that the spectral features observed in the sphere are narrower than those observed for the FPM in the cube and rhombic dodecahedron, which is another characteristic of WGMs. When considering a spherical optical resonator, such as our sphere supercrystal, characterized by its diameter, L, and effective refractive index N_eff, the expected spectral positions of the WGM resonances can be found analytically;⁷³ however, this is beyond the scope of the present study. As it can be seen from the band structure, these bands are present along the entire symmetry path (Γ–X–M–R–Γ) indicating that these WGM occur independently of the light direction (isotropic), which should come as no surprise considering the spherical symmetry of the supercrystal. Interestingly, the PBG does not appear as clearly in the photonic band structure compared to the two previous cases (Fig. 5f), although the reflectance shows the coupling between the WGMs and the LSPR (decrease of the WGMs intensity near the plasmon resonance). While the reason remains unclear, it could be related to the small number of Au NPs from the supercrystal surface that are resonating and coupling to the WGMs.

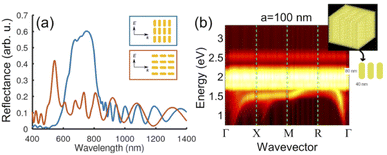
Lastly, we calculated the reflectance spectra (Fig. 6a) and photonic band structure (Fig. 6b) of a cubic supercrystal composed of isotropically-oriented nanorods with an aspect ratio of 2 (80 nm long and 40 nm wide) to highlight the versatility of the method. These nanorods are also arranged in a simple cubic lattice with lattice parameter a = 100 nm, where the long axis of the nanorods is oriented along the symmetry line Δ (between Γ and X), as shown in the inset of Fig. 6b. Supercrystals composed of elongated nanoparticles have previously been shown to display interesting optical anisotropy/birefringence and polarization-dependent properties.^38,47,48 The reflectance spectra calculated for two different polarizations (Fig. 6a), clearly illustrate the polarization dependence of the optical properties of these nanorod supercrystals. Because of the difference in effective refractive index along the two directions, the Fabry-Pérot resonances along these directions are at different wavelengths. From the band structure (Fig. 6), we can clearly see the formation of the PBG between 2.25 eV (longitudinal LSPR) and 2.35 eV (transverse LSPR). More interestingly, we now observe the formation of a new low-dispersion photonic band at lower energy (i.e., longer wavelengths) along the symmetry lines Δ and Z (i.e., Γ–X–M) that returns to the lower polaritonic branch along the symmetry lines T and Λ (i.e., M–R–Γ). The appearance of this photonic branch, which dispersion strongly depends on the incident k-vector clearly illustrates the optical anisotropy of such supercrystal, which has previously been studied by Ross et al.⁴⁸ The strong optical anisotropy of the Au nanorods directly impacts the coupling of the FPMs with the longitudinal and transverse LSPRs, thus leading to coupling/decoupling phases along the various symmetry paths of the photonic band diagram.⁶⁴ Another clear effect of this anisotropic coupling is the presence of FPM features along the symmetry line Δ.

Fig. 6 (a) Reflectance spectra calculated for an incident polarization along the nanorods long axis (blue) and short axis (red) of a finite supercrystal with cubic habit composed of Au nanorods with a length of 80 nm and a width of 40 nm, arranged in a simple cubic lattice with a lattice parameter of 100 nm. (b) Photonic band structure of the same finite supercrystal.

Conclusions

Plasmonic-based 3D supercrystals with well-defined habits and with lattice parameters in the deep sub-wavelength regime behave as plasmonic cavity and have, therefore, a strong potential for studies and applications in cavity quantum electrodynamics (QED). While these structures have been shown to have significant optical ability and structural flexibility, the full understanding of their complex optical properties is conditioned by the availability of multiscale computational tools. In this work, we developed a computational approach, based on the finite-difference time-domain (FDTD) method that is capable of simultaneously describing nanoscale effects, interparticle coupling, periodicity, and microscale photonic properties associated with the supercrystal morphology. Our approach allows for accurately calculating the photonic band structures from finite-size 3D superlattices of various habits (cubic, spherical, rhombic dodecahedral) and building blocks (spheres and rods). We showed that they differ from the photonic band structures computed for infinite supercrystal and encompass phenomena such as the Fabry-Pérot interferences, whispering gallery modes, a decrease in photonic mode lifetime, and the formation of polaritonic bandgaps.

It is important to notice that although this approach was applied to 3D supercrystals, it is far more general and versatile. Not only it applies to other morphologies, compositions, and sizes of the building blocks (e.g., cubes, prisms …), but also to other unit cell symmetries (e.g., fcc, bcc …), supercrystal habits (e.g., ellipsoidal, pyramidal …), and dimensionalities of the periodic structures (e.g., 1D chains, 2D arrays).

We anticipate that this new approach will serve as a platform for the study of other types of finite-size periodic structures, such as multi-composition periodic superlattices for the study of exciton-photon coupling,⁶⁵ and novel magneto-optical properties,⁴⁶ thus opening the door to new directions in QED and quantum optics.³² Finally, this approach opens up new opportunities since it does not only compare to optical spectroscopy results but also to electron energy-loss spectroscopy (EELS)⁷⁴ and zero index materials.⁷⁵

Author contributions

J. L. M.-P. developed the methodology, performed the computational simulations, analysis, and interpretation. N. L. conceptualized the project and methodology, performed the analysis and interpretation, managed the whole project, and acquired the funding. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

The authors declare no conflicts of interest regarding this article.

Acknowledgements

This material is based upon research supported by the Thomas Jefferson Fund managed by the Office for Science and Technology of the Embassy of France in the United States and the FACE Foundation under grant number Large-TJF 19_092. This work received computational support from UTSA's HPC cluster SHAMU, operated by Tech Solutions.

References

1. R. H. Ritchie, Phys. Rev., 1957, 106, 874–881.
2. C. J. Powell and J. B. Swan, Phys. Rev., 1959, 115, 869–875.
3. S. Mukherjee, F. Libisch, N. Large, O. Neumann, L. V. Brown, J. Cheng, J. B. Lassiter, E. A. Carter, P. Nordlander and N. J. Halas, Nano Lett., 2013, 13, 240–247.
4. H. Jing, Q. Zhang, N. Large, C. Yu, D. A. Blom, P. Nordlander and H. Wang, Nano Lett., 2014, 14, 3674–3682.
5. C. Zhang, H. Zhao, L. Zhou, A. E. Schlather, L. Dong, M. J. McClain, D. F. Swearer, P. Nordlander and N. J. Halas, Nano Lett., 2016, 16, 6677–6682.
6. M. Moskovits, Rev. Mod. Phys., 1985, 57, 783–826.
7. H. Maekawa, E. Drobnyh, C. A. Lancaster, N. Large, G. C. Schatz, J. S. Shumaker-Parry, M. Sukharev and N.-H. Ge, J. Phys. Chem. C, 2020, 124, 20424–20435.
8. N. S. Mueller, E. Pfitzner, Y. Okamura, G. Gordeev, P. Kusch, H. Lange, J. Heberle, F. Schulz and S. Reich, ACS Nano, 2021, 15, 5523–5533.
9. S. Manrique-Bedoya, M. Abdul-Moqueet, P. Lopez, T. Gray, M. Disiena, A. Locker, S. Kwee, L. Tang, R. L. Hood, Y. Feng, N. Large and K. M. Mayer, J. Phys. Chem. C, 2020, 124, 17172–17182.
10. C. M. García-Rosas, L. A. Medina, P. Lopez, N. Large and A. Reyes-Coronado, J. Nanopart. Res., 2021, 23, 144.
11. S. Mondal, J. Luis Montaño-Priede, V. Tu Nguyen, S. Park, J. Choi, V. Hoang Minh Doan, T. Mai Thien Vo, T. Hung Vo, N. Large, C.-S. Kim and J. Oh, J. Adv. Res. DOI:10.1016/j.jare.2022.1002.1006.
12. K.-S. Lee and M. A. El-Sayed, J. Phys. Chem. B, 2006, 110, 19220–19225.
13. S. Kawata, Y. Inouye and V. Prabhat, Nat. Photon., 2009, 3, 388.
14. K. A. Willets and R. P. Van Duyne, Annu. Rev. Phys. Chem., 2007, 58, 267–297.
15. J. N. Anker, W. P. Hall, O. Lyandres, N. C. Shah, J. Zhao and R. P. Van Duyne, Nat. Mater., 2008, 7, 442–453.
16. N. Large, M. Abb, J. Aizpurua and O. L. Muskens, Nano Lett., 2010, 10, 1741–1746.
17. T. Ebbesen, C. Genet and S. I. Bozhevolnyi, Phys. Today, 2008, 61, 44–50.
18. J. A. Schuller, E. S. Barnard, W. Cai, Y. C. Jun, J. S. White and M. L. Brongersma, Nat. Mater., 2010, 9, 193–204.
19. J. Lee, S. Mubeen, X. Ji, G. D. Stucky and M. Moskovits, Nano Lett., 2012, 12, 5014–5019.
20. O. Neumann, A. S. Urban, J. Day, S. Lal, P. Nordlander and N. J. Halas, ACS Nano, 2013, 7, 42.
21. H. A. Atwater and A. Polman, Nat. Mater., 2010, 9, 205–213.
22. J. B. Khurgin and A. Boltasseva, MRS Bull., 2012, 37, 768–779.
23. M. Bosman, E. Ye, S. F. Tan, C. A. Nijhuis, J. K. W. Yang, R. Marty, A. Mlayah, A. Arbouet, C. Girard and M.-Y. Han, Sci. Rep., 2013, 3, 1312.
24. C. A. Thibodeaux, V. Kulkarni, W.-S. Chang, O. Neumann, Y. Cao, B. Brinson, C. Ayala-Orozco, C.-W. Chen, E. Morosan, S. Link, P. Nordlander and N. J. Halas, J. Phys. Chem. B, 2014, 118, 14056–14061.
25. F. Schulz, O. Pavelka, F. Lehmkühler, F. Westermeier, Y. Okamura, N. S. Mueller, S. Reich and H. Lange, Nat. Comm., 2020, 11, 3821.
26. A. Teulle, M. Bosman, C. Girard, K. L. Gurunatha, M. Li, S. Mann and E. Dujardin, Nat. Mater., 2015, 14, 87–94.
27. L. S. Slaughter, L.-Y. Wang, B. A. Willingham, J. M. Olson, P. Swanglap, S. Dominguez-Medina and S. Link, Nanoscale, 2014, 6, 11451–11461.
28. M. B. Ross, C. A. Mirkin and G. C. Schatz, J. Phys. Chem. C, 2016, 120, 816–830.
29. D. Wang, A. Yang, A. J. Hryn, G. C. Schatz and T. W. Odom, ACS Photonics, 2015, 2, 1789–1794.
30. W. Wang, M. Ramezani, A. I. Väkeväinen, P. Törmä, J. G. Rivas and T. W. Odom, Mater. Today, 2018, 21, 303–314.
31. A. Yang, Z. Li, M. P. Knudson, A. J. Hryn, W. Wang, K. Aydin and T. W. Odom, ACS Nano, 2015, 9, 11582–11588.
32. W. Zhou, M. Dridi, J. Y. Suh, C. H. Kim, D. T. Co, M. R. Wasielewski, G. C. Schatz and T. W. Odom, Nat. Nanotechnol., 2013, 8, 506–511.
33. C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoff, Nature, 1996, 382, 607–609.
34. D. J. Park, C. Zhang, J. C. Ku, Y. Zhou, G. C. Schatz and C. A. Mirkin, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 977–981.
35. M. B. Ross, J. C. Ku, B. Lee, C. A. Mirkin and G. C. Schatz, Adv. Mater., 2016, 28, 2790–2794.
36. M. B. Ross, J. C. Ku, V. M. Vaccarezza, G. C. Schatz and C. A. Mirkin, Nat Nano, 2015, 10, 453–458.
37. K. L. Young, M. B. Ross, M. G. Blaber, M. Rycenga, M. R. Jones, C. Zhang, A. J. Senesi, B. Lee, G. C. Schatz and C. A. Mirkin, Adv. Mater., 2014, 26, 653–659.
38. D. García-Lojo, S. Núñez-Sánchez, S. Gómez-Graña, M. Grzelczak, I. Pastoriza-Santos, J. Pérez-Juste and L. M. Liz-Marzán, Acc. Chem. Res., 2019, 52, 1855–1864.
39. S. Wang, X. Xie, Z. Chen, N. Ma, X. Zhang, K. Li, C. Teng, Y. Ke and Y. Tian, Int. J. Mol. Sci., 2021, 22, 7558.
40. C.-W. Liao, Y.-S. Lin, K. Chanda, Y.-F. Song and M. H. Huang, J. Am. Chem. Soc., 2013, 135, 2684–2693.
41. N. S. Mueller, Y. Okamura, B. G. M. Vieira, S. Juergensen, H. Lange, E. B. Barros, F. Schulz and S. Reich, Nature, 2020, 583, 780–784.
42. D. J. Lewis, D. J. D. Carter and R. J. Macfarlane, J. Am. Chem. Soc., 2020, 142, 19181–19188.
43. M. S. Lee, D. W. Yee, M. Ye and R. J. Macfarlane, J. Am. Chem. Soc., 2022, 144, 3330–3346.
44. D. J. Lewis, L. Z. Zornberg, D. J. D. Carter and R. J. Macfarlane, Nat. Mater., 2020, 19, 719–724.
45. P. J. Santos, P. A. Gabrys, L. Z. Zornberg, M. S. Lee and R. J. Macfarlane, Nature, 2021, 591, 586–591.
46. M. B. Ross, M. R. Bourgeois, C. A. Mirkin and G. C. Schatz, J. Phys. Chem. Lett., 2016, 7, 4732–4738.
47. L. Sun, H. Lin, D. J. Park, M. R. Bourgeois, M. B. Ross, J. C. Ku, G. C. Schatz and C. A. Mirkin, Nano Lett., 2017, 17, 2313–2318.
48. M. B. Ross, M. G. Blaber and G. C. Schatz, Sci. Rep., 2014, 5, 4090.
49. J. C. Maxwell-Garnett, Philos. Trans. R. Soc. London, 1904, 203, 385–420.
50. J. C. Maxwell-Garnett, Philos. Trans. R. Soc. London, 1906, 205, 237–288.
51. D. A. G. Bruggeman, Ann. Phys., 1935, 416, 636–664.
52. N. Large, J. Aizpurua, S. Lang Teo, V. Kaixin Lin, R. Marty, S. Tripathy and A. Mlayah, Opt. Express, 2011, 19, 5587–5595.
53. N. Large, L. Saviot, J. Margueritat, J. Gonzalo, C. N. Afonso, A. Arbouet, P. Langot, A. Mlayah and J. Aizpurua, Nano Lett., 2009, 9, 3732.
54. H. Wang, G. P. Goodrich, F. Tam, C. Oubre, P. Nordlander and N. J. Halas, J. Phys. Chem. B, 2005, 109, 11083–11087.
55. S. Link, M. B. Mohamed and M. A. El-Sayed, J. Phys. Chem. B, 1999, 103, 3073–3077.
56. J. Zuloaga, E. Prodan and P. Nordlander, ACS Nano, 2010, 4, 5269–5276.
57. M. Nakayama, K. Kubota, H. Kato and N. Sano, J. Appl. Phys., 1986, 60, 3289.
58. L. Zundel and A. Manjavacas, J. Phys., 2018, 1, 015004.
59. V. I. Zakomirnyi, A. E. Ershov, V. S. Gerasimov, S. V. Karpov, H. Ågren and I. L. Rasskazov, Opt. Lett., 2019, 44, 5743–5746.
60. V. Kuzmiak and A. A. Maradudin, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 7427–7444.
61. E. Simsek, PIERS Online, 2009, 5, 629–632.
62. D. S. Citrin, Nano Lett., 2005, 5, 985–989.
63. N. Large, J. R. Huntzinger, J. Aizpurua, B. Jusserand and A. Mlayah, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 075310–075318.
64. D. M. Solís, J. M. Taboada, F. Obelleiro, L. M. Liz-Marzán and F. J. García de Abajo, ACS Nano, 2014, 8, 7559–7570.
65. F. Davoodi, M. Taleb, F. K. Diekmann, T. Coenen, K. Rossnagel and N. Talebi, ACS Photonics, 2022, 9, 2473–2482.
66. Ansys-Lumerical, Inc, https://www.lumerical.com/.
67. P. B. Johnson and R. W. Christy, Phys. Rev. B: Solid State, 1972, 6, 4370–4379.
68. G. Mie, Ann. Phys. Vierte Folge, Band, 1908, 25, 377–445.
69. D. W. Brandl, N. A. Mirin and P. Nordlander, J. Phys. Chem. B, 2006, 110, 12302–12310.
70. E. Sauer, J. P. Vasco and S. Hughes, Phys. Rev. Res., 2020, 2, 043109.
71. W. Ogaerts, P. Bienstman, D. Taillaert, R. Baets and D. D. Zutter, IEEE Photonics Technol. Lett., 2001, 13, 565–567.
72. E. Marino, H. Bharti, J. Xu, C. R. Kagan and C. B. Murray, Nano Lett., 2022, 22, 4765–4773.
73. A. Chiasera, Y. Dumeige, P. Féron, M. Ferrari, Y. Jestin, G. Nunzi Conti, S. Pelli, S. Soria and G. C. Righini, Laser Photonics Rev., 2010, 4, 457–482.
74. F. J. García de Abajo and L. A. Blanco, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 125108.
75. H. Zhang, Y. Li, X. Long, J. Luo, Y. Zhang, M. Song, J. Fang, C. Guan, Y. Cheng and H. Liu, J. Mater. Chem. C, 2020, 8, 12876–12885.

---

Footnotes

† Electronic supplementary information (ESI) available: (Table S1) High symmetry points and lines of the simple cubic reciprocal lattice. (Table S2) Key physical parameters for each system. (Fig. S1) Complex effective refractive index (N_eff) of a superlattices composed by 80 nm Au NPs arranged in a simple cubic lattice with a = 100 and 130 nm. (Fig. S2) Dispersion relation of an infinite Au-NPs supercrystal with a lattice parameter of 100 nm. (Fig. S3) Real part of the x-component of the electric field and logarithm of the electric field intensity of a cubic supercrystal nm excited with a plane wave k = k_X. (Fig. S4) real part of the x-component of the electric field and logarithm of the electric field intensity of a cubic supercrystal nm excited with a plane wave k = k_M. (Fig. S5†) Photonic band structures at the X point (k = k_X) and reflectance spectra of cubic Au NPs supercrystals with lattice parameters of 100 and 130 nm. (Fig. S6) Dispersion relation of slab with effective refractive index representing a Au-NPs supercrystal with a lattice parameter of 100 nm in water. (Fig. S7) Polaritonic mode splitting and normalized coupling constants at the X point for the finite supercrystals with cubic and rhombic dodecahedral habits. See https://doi.org/10.1039/d2na00538g

‡ Present Address: Department of Electricity and Electronics, FCT-ZTF, UPV-EHU, Bilbao, 48080, Spain.

---