Tailoring the interaction between a gold nanocluster and a fluorescent dye by cluster size: creating a toolbox of range-adjustable pH sensors

Abstract

We present a novel strategy for tailoring the fluorescent azadioxatriangulenium (KU) dye-based pH sensor to the target pH range by regulating the pK_a value of the gold nanoclusters. Based on the correlation between the pK_a and surface curvature of ligand-protected nanoparticles, the pK_a value of the gold nanoclusters was controlled by size. In particular, three different-sized para-mercaptobenzoic acid (p-MBA) protected gold nanoclusters, Au₂₅(p-MBA)₁₈, Au₁₀₂(p-MBA)₄₄, and Au_210–230(p-MBA)_70–80 were used as the regulator for the pH range of the KU response. The negatively charged gold nanoclusters enabled the positively charged KU to bind to the surface, forming a complex and quenching the fluorescence of the KU by the energy transfer process. The fluorescence was restored after adjusting the surface charge of the gold nanocluster by controlling the solution pH. In addition, the KU exhibited a significantly different pH response behaviour for each gold nanocluster. Au_210–230(p-MBA)_70–80 showed a higher pH response range than Au₁₀₂(p-MBA)_44, which was intuitive. However, Au₂₅(p-MBA)₁₈ showed an unexpectedly high pH response behaviour. pK_a titration measurement, molecular dynamics simulations, and essential dynamics analysis showed that small nanoclusters do not follow the scaling between the curvature and the pK_a value. Instead, the behaviour is governed by the distribution and interaction of p-MBA ligands on the nanocluster surface. This work presents an effective design strategy for fabricating a range adjustable pH sensor by understanding the protonation behaviour of the ultrasmall gold nanoclusters in an atomic range.

---

Introduction

Due to the connection between the pH and many chemical processes, pH measurement plays a vital role in a broad range of applications, such as environmental, industrial, chemical, and biomedical fields.^1–4 For that reason, enhancing the accuracy of the pH measurement and fabricating a suitable pH sensor has become an essential task in scientific research. Especially for intracellular pH measurements, it is crucial to develop a highly sensitive method to measure the small pH changes in a wide pH range. Intracellular pH controls cellular processes such as cell metabolism, apoptosis, and proliferation, making it extremely important to be strictly regulated in organelles.^5–10 Even a small pH change could dramatically trigger an inappropriate cell function, as observed in some common diseases such as cancer and Alzheimer's.^11,12

Optical pH sensors have many advantageous properties, such as ease of transport, need for low concentration of the pH indicator, high sensitivity and spatial resolution, and the non-invasive nature. Fluorescence-based indicators such as organic dyes have been the most studied materials for optical sensors because of their high sensitivity and brightness.^13–16 However, despite these merits, they suffer from poor solubility, low photobleaching resistance, and a lack of understanding of the behaviour towards harsh environments.^17,18 Moreover, the pH detection range for the pH-sensitive fluorophore only covers two pH units. This range depends on the acid dissociation constant (K_a), which gives a sigmoidal curve in a pH range of pK_a ±1. Because of these limitations, the pH-sensitive fluorophores are not ideal for general pH measurements alone, and additional modifications are needed for further use.

There have been some attempts to overcome these limitations by modifying the structure of the dye to adjust the pH range^19,20 or functionalizing various pH indicators (e.g., using large nanoparticles as carriers), which have different pH detection ranges to widen the pH range of the sensor.^21,22 For example, Benjaminsen et al. have formed a triple-labeled sensor with a pH measurement range of 3.2–7.0, composed of two pH-sensitive fluorophores with different pK_a values and a nanoparticle as a carrier.²² These pH sensors have a more extensive pH detection range, brighter fluorescence signals, higher photostability, and easier functionalization, which provides the opportunity to introduce various strategies to fabricate fluorescent pH sensors. However, there were still drawbacks to this method. The water solubility of the dye-functionalized nanoparticles would decrease with an increasing number of aromatic dyes, and thus the level of functionalization has to be a compromise between the function and the solubility. Moreover, the fabrication method differs for each dye which will intricate the synthesis steps, lower the yield, and reproducibility of the final product with the exact composition of the dyes. Therefore, it is crucial to distinctly understand the materials' properties before and after forming the sensors when designing a pH sensor. Furthermore, developing a method to freely control the pH range of the sensor with the least number of ingredients is significantly needed.

In our previous report,²³ we fabricated a fluorescent pH sensor by covalently binding a pH-independent dye (azaoxotriangulenium dye, KU) with an atomically precise and a water-soluble gold nanocluster (Au₁₀₂(p-MBA)₄₄; p-MBA = para-mercaptobenzoic acid) to create a functional hybrid material for intracellular pH imaging in live cells. The gold nanoclusters act as both nanocarriers and regulators of the fluorescence intensity in the targeted live cells. In acidic conditions, the dye-nanocluster hybrid is dissociated via hydrolysis of the ester bond. However, the dye and the nanocluster form a complex by weak interactions, which leads to quenching of fluorescence via Förster type of energy transfer. Simultaneously, local pH changes also influence the surface charge of the p-MBA ligand of the gold nanoclusters, which modifies the strength of the electrostatic interaction between the dye and the nanocluster, adjusting the extent of fluorescence quenching. Furthermore, the pH dependency behaviour of the dissociated KU dye and gold nanoclusters follows the gold nanoclusters' protonation behaviour, showing a more comprehensive pH range than other pH indicators. In other words, the functionality of the KU response on pH is tailored by nanoclusters with a different protonation behaviour.

In this report, we present a novel strategy for regulating the nanocluster's pK_a value to tailor the KU dye-based pH sensor to the target pH range. As a starting point, the pK_a value is known to be dependent on the surface curvature of the nanoclusters.^24–26 Large-sized nanoclusters have a low curvature surface, leading to a more densely packed ligand distribution. Because of the negative charge of the ligands and the short distance between the ligands, electrostatic repulsion between the ligands grows stronger. To reduce the repulsion between the ligands, the acid–base equilibrium of the ligands tends to shift to a higher pH and protonate the natively charged groups. Consequently, the pK_a of the large-size nanocluster shifts to a higher pH.

We used Au₂₅(p-MBA)₁₈, Au₁₀₂(p-MBA)₄₄, and Au_210–230(p-MBA)_70–80 (referred further on as Au₂₅₀(p-MBA)_n)²⁷ as the regulator for the pH range of the KU response. First, a complex of gold nanocluster and the KU dye was formed in an alkaline solution. Then the pH response of the KU was measured by lowering the pH by adding an acid. Three different nanoclusters showed significantly different response behaviours. Furthermore, the pK_a of each nanocluster was measured by the acid–base titration measurement. The Au₁₀₂(p-MBA)₄₄ and Au₂₅₀(p-MBA)_n showed an intuitively correct difference in the pK_a value, while Au₂₅(p-MBA)₁₈ exhibited an unexpected pK_a value. Therefore, to understand the unique pK_a shift behaviour of Au₂₅(p-MBA)₁₈, molecular dynamics (MD) simulations and essential dynamics (ED) analysis were carried out to compare the structural difference of the ligand surface between the small and large nanoclusters. The results showed that small nanoclusters do not follow the scaling between the curvature and the pK_a but the behaviour is governed by the distribution and interaction of p-MBA ligands on the nanocluster surface. This is the first study attempting to analyse the pK_a value of ultrasmall nanoclusters and pinpoint what regulates the protonation behaviour in an atomic range. By understanding the pK_a trend of each nanocluster, it is possible to easily design or modify the pH sensor by tailoring the nanocluster size. Furthermore, the use of atomically precise nanoclusters facilitates synergy between theory and experiments toward paving the way for the rational design of new probes.

Experimental

Materials

Gold(III)chloride trihydrate (HAuCl₄·3H₂O, ≥99.9%), para-mercaptobenzoic acid (p-MBA, 99%), sodium borohydride (NaBH₄, 99%), and ammonium persulfate (APS, ≥98%) were purchased from Sigma-Aldrich (Merck). Hydrochloric acid (HCl, 37%) and methanol (MeOH, 99.9%) were purchased from Honeywell. Acrylamide/bisacrylamide (bio reagent, 30%) was purchased by Bio-Rad. Sodium hydroxide (NaOH, ≥98.5%) was purchased from VWR Internationals, and etax Aa (anhydrous ethanol, 99.5%) was purchased from Anora Industrial. Glycerol (99.5%) was purchased from VWR BDH Prolabo. Carbon monoxide (CO, 99.9%) was purchased from Messer Griesheim. The 10× TBE (Tris–borate–EDTA) buffer for the PAGE separation was homemade with Trizma base (≥99%), borate (99%), and ethylenedinitrilotetraacetic acid (EDTA, pH 8.0). The solution was sterilized before use. Water was purified by using a Millipore Elix Essential 3 UV water purification system (15 MΩ cm). The azaoxotriangulenium dye (KU) used in the complex studies was obtained as a courtesy of Thomas Just Sørensen and Bo W. Larsen from the University of Copenhagen and was used without further modifications. All the chemicals were used as received without further purification.

Methods

UV-vis absorption and photoluminescence spectra of the synthesized gold nanoclusters and KU dye were collected with Horiba AquaLog spectrophotometer. Sample solutions were measured at ambient conditions using quartz fluorescence cuvettes from Hellma. Fluorescence emission spectra were measured after exciting the sample at 500 nm wavelength.

Transmission electron microscopy (TEM) samples were prepared by drop-casting 2 μL of the aqueous solution of clusters on a glow discharged 400 mesh lacey carbon copper grid (01824, Ted Pella). The solution was let to adsorb for 10 min, after which the excess sample was removed and washed with water and methanol. The grids were allowed to dry for more than 2 h at room temperature before imaging. Au₂₅(p-MBA)₁₈ was measured with 120 kV high voltage, Au₁₀₂(p-MBA)₄₄ and Au₂₅₀(p-MBA)_n were measured with 80 kV high voltage. All samples were imaged with JEOL electron microscope (JEM-1400). The size of the nanoclusters was analysed by using ImageJ. The isolated gold nanoclusters were run through polyacrylamide gel electrophoresis (PAGE) by Mini-PROTEAN Tetra Cell (Bio-Rad) to verify the purity of the prepared samples. The PAGE was run on homemade 15% polyacrylamide gel (29 : 1 acryl-amide : bisacrylamide) using a 1× TBE run buffer at 130 V for 2 h. The PAGE gel was imaged using an iPhone 13 pro camera.

Synthesis of gold nanoclusters (Au₂₅(p-MBA)₁₈, Au₁₀₂(p-MBA)₄₄, Au₂₅₀(p-MBA)_n)

Au₁₀₂(p-MBA₄₄) and Au₂₅₀(p-MBA)_n were obtained by following a previously published procedure.^27,28 Au₂₅(p-MBA)₁₈ was synthesized by a reported protocol with minor modifications.²⁹ In a typical synthesis, 50 mM HAuCl₄·3H₂O (5 mL) and 50 mM p-MBA aqueous solution (in 10 mL of 150 mM NaOH) were added into 235 mL of ultrapure water in a 500 mL Erlenmeyer flask during vigorous stirring. After stirring for 10 min, the pH of the solution was adjusted to 11.0 by adding 1 M NaOH aqueous solution, which made the solution turn clear yellow. After stirring for 30 min, CO gas was bubbled into the reaction mixture for 2 min (1 bar) for reduction. The reaction was kept air-tight for more than 3 days under stirring until the solution showed a reddish-brown colour. Before further process, the bulk solution was observed with UV-vis spectra to verify the existence of Au₂₅(p-MBA)₁₈ in the solution. The product solution was then rotary evaporated to near dryness (water bath 40 °C). After that, 15 mL water was added to dissolve the dried product. Then 15 mL of ethanol was added to induce precipitation of large-sized nanoclusters. After transferring the solution to a 50 mL conical tube, the precipitant was collected by centrifugation (3500 rpm for 3 min), and more ethanol (10 mL) was added to the supernatant to induce additional precipitation of Au₂₅(p-MBA)₁₈. This process was repeated until the supernatant was clear, and each collected products were washed with ethanol and dried in air. The fraction containing Au₂₅(p-MBA)₁₈ cluster was further purified by PAGE separation.

KU fluorescence quenching measurement

To observe the effect of the bound gold nanoclusters on the KU dye, the fluorescence intensity of the KU dye was measured while adding gold nanoclusters to the KU solution. In detail, 1.5 mL of KU dye (0.41 μM) and 1 mL of Au₂₅(p-MBA)₁₈ solution (18 μM) were prepared in pH 10 solution. A small volume of gold nanoclusters (<10 μL) was carefully added to the KU solution and thoroughly mixed with a glass pipette. The solution was excited at 500 nm wavelength, and the fluorescence intensity was read at 554 nm. The gold nanocluster was added until the KU intensity was quenched completely. The mole of the nanocluster was calculated based on the added volume. The mole amount of Au₂₅(p-MBA)₁₈ was divided by the KU mole to calculate the molar ratio. The KU intensity measurement for Au₁₀₂(p-MBA)₄₄ and Au₂₅₀(p-MBA)_n was performed by a similar procedure. The KU dye concentration was prepared lower than 3 μM to avoid quenching behaviour by the high concentration. Moreover, to avoid the effect of the concentration changes by the added nanocluster solution, the gold nanocluster was prepared in a very high concentration.

Preparation of the gold nanocluster and KU complex

Based on the concentration of the KU dye, the gold nanocluster was added to the solution, and the concentration of the KU dye was calculated by using the extinction coefficient value. 2 mL of 1.0 μM KU dye solution and 2 mL of 0.5 μM of Au₂₅(p-MBA)₁₈ solution were prepared in pH 10 aqueous solution. 1 mL of each solution was mixed to form a complexation. ([mol_Au]/[mol_KU] = 2) KU complex with Au₁₀₂(p-MBA)₄₄ and Au₂₅₀(p-MBA)_n was prepared with the same method. The concentration for the KU dye was less than 3 μM.

Acid–base titration measurement of Au₂₅(p-MBA)₁₈ and Au₂₅₀(p-MBA)_n nanoclusters

The protonation–deprotonation behaviour of the gold nanoclusters was studied using regular acid–base pH titration. Titration curves were measured in pure H₂O with the purified and precipitated gold nanoclusters. The nanocluster was dissolved in pH 4–5 water and centrifuged to remove any precipitating nanoclusters. In addition, the pK_a was extracted from the titration data by evaluating the titration curve's first and second derivative plots.

First derivative:

dpH/dV

where, dpH is the change in pH between successive additions of titrant and dV is the volume of the added titrant.

Second derivative:

d(dpH/dV)/dV

Molecular dynamics simulations and essential dynamics analysis

Initial coordinates of Au₂₅(p-MBA)₁₈ nanocluster were obtained from a previous model²⁹ based on the reported crystal structure of Au₂₅(PET)₁₈ (PET = phenylethylthiolate),^30,31 while Au₁₀₂(p-MBA)₄₄ was obtained from the published X-ray crystal structure.³² Simulations were performed with GROMACS 2020 (ref. 33) using an AMBER-compatible force field for thiolate-protected nanoclusters.³⁴ The fully deprotonated³⁵p-MBA-protected gold nanoclusters were placed in a periodic cubic box with TIP3P water molecules³⁶ using the SETTLE algorithm to constrain their internal degrees of freedom.³⁷ Sodium and chloride ions (0.15 M NaCl) were added to neutralize the systems. Energy minimizations were carried out by using the steepest descent algorithm, followed by a short equilibration consisting of 10 ns NVT ensemble (constant number of particles, volume, and temperature) at 300 K and 10 ns NPT (constant number of particles, pressure, and temperature) at 300 K and 1 bar pressure with position restraints on the heavy atoms of the nanoclusters. The velocity-rescale thermostat was used to keep the temperature constant at the desired value with a coupling time constant of 0.1 ps.³⁸ Berendsen barostat with a reference pressure of 1 bar and coupling time constant of 1.0 ps³⁹ was used in the NPT equilibration. Afterward, 100 ns of production MD were performed for each system removing all the position restraints. The velocity-rescale thermostat was used to keep the temperature at 300 K, and pressure was kept constant at 1 bar using Parrinello–Rahman barostat with relaxation times of 2.0 ps.⁴⁰ A leapfrog Verlet integrator was used with a 1.0 fs time step. Lennard–Jones interactions were truncated at 1.0 nm, and the particle-mesh Ewald (PME) method with a real-space cutoff of 1.0 nm and 0.12 nm grid spacing was used to model Coulomb interactions.⁴¹ The lengths of covalent bonds containing hydrogens were constrained with the LINCS algorithm⁴² for improved performance. All trajectories were visualized in VMD⁴³ and analysed by using the utility toolkits of GROMACS such as gmx rdf to obtain the pair correlation functions between the carbon atoms of the carboxylate groups of the ligands. The pair correlation function was calculated over the whole MD-trajectory. Pair correlation function was also solved for the phenyl rings of the ligands as a running average over 40 snapshots for the apex- and core-ligands and is reported here per phenyl ring per frame. Distances were determined from the centre of the apex/core phenyl ring to all other phenyl rings in the system. There are six apex-ligands in Au₂₅ and two in Au₁₀₂ being located at the centre of the longer SR–Au–SR–Au–SR (SR = p-MBA) protecting units.

ED analysis was carried out to extract the dominant modes in the overall molecular motion of the gold nanoclusters.^44,45 Covariance matrices were constructed using all the atoms of the nanoclusters and removing the rotation and translational movements. The calculated eigenvectors and eigenvalues of the covariance matrices were then projected along with the first two (most important) principal components. The trajectories were analysed by using the GROMACS utilities gmx covar and gmx anaeig. The data from ED analysis was plotted in two ways: first, as a time evolution scatter plot and second, as a configurational free energy plot. The first was plotted directly using the projection data of individual MD-snapshot structures by using colour scale dependent on the snapshot frame index 0–500. The second plot was formed by collecting the principal component analysis (PCA) projection data of all 500 MD-snapshots into equally distributed bins on the two principal axes based on the closest distance producing a 200 × 200 grid. The number of hits on bins directly gives the statistical probability distribution when correlated to the total number of snapshots in analysis. Finally, configurational free energy of the bins was solved from the probabilities using Boltzmann distribution. The minimum of the free energy was set to zero. Only the energy range between 0 kJ mol⁻¹ and 5 kJ mol⁻¹ was shown in the coloured contour plots. Gaussian distribution was applied to smoothen the data on the discrete grid with broadening parameter of 0.05 nm. For both studied clusters, Au₂₅(p-MBA)₁₈ and Au₁₀₂(p-MBA)₄₄, the last structure of the MD-simulations was used in structure visualizations. VMD symmetry tools were used to analyse the symmetries of the metal core of Au₂₅(p-MBA)₁₈ structures.

Results and discussion

Synthesis of highly pure gold nanoclusters

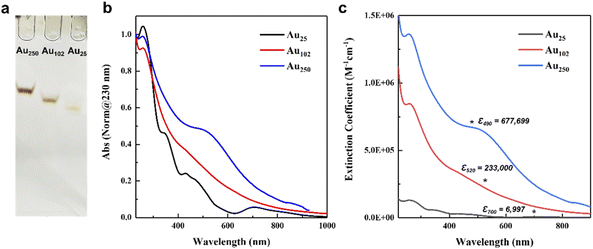
The three p-MBA protected gold nanoclusters with the composition of Au₂₅(p-MBA)₁₈, Au₁₀₂(p-MBA)_44, and Au₂₅₀(p-MBA)_n were synthesized according to the reported methods.^27–29 The composition of the largest gold nanoclusters was predicted to be Au_210–230(p-MBA)_70–80 by experimental analysis and computationally aided prediction, based on the structurally known reference gold nanoclusters.²⁷ This large-size gold nanoclusters will be abbreviated as Au₂₅₀ further on, as was defined by Sokołowska et al.²⁷ In addition, Au₂₅(p-MBA)₁₈ and Au₁₀₂(p-MBA)₄₄ will be abbreviated as Au₂₅ and Au₁₀₂, respectively.

It is imperative to obtain highly pure gold nanoclusters to prevent any interference between the residues and the functionality of the pH sensor. The synthesis we followed is known to form only one size of the targeted nanoclusters. However, the bulky separated fractions could still carry excess counterions or a small portion of different size nanoclusters. In order to acquire highly purified gold nanoclusters, the fraction of each sample was separated once more through PAGE, and the targeted clusters were collected from the gel. After the distinct separation of the bands, they were cut out and extracted in water overnight. The extracted samples were purified by precipitating the nanoclusters using 100 μL 0.1 M NaCl and 0.1 M HCl (pH 2). The precipitant was thoroughly washed with clean water to remove excess salt or residue from the gel and air-dried for a day. The products were stored in the refrigerator and were re-dissolved with 0.01 M NaOH before use. The electrophoresis was run once more to evaluate the purity and stability of the separated nanoclusters. As shown in Fig. 1a, a single narrow band was observed for each nanocluster, indicating the high stability and purity of the prepared nanoclusters. The distinct difference in each band position shows that the size of the nanoclusters is relatively different, which is apposite to our comparison. The TEM results were also used to verify the purity of Au₂₅, Au₁₀₂, and Au₂₅₀ nanoclusters (Fig. S1; see Experimental section† for more details). Each nanocluster showed a monodisperse nature with a spherical shape. The size of Au₂₅, Au₁₀₂, and Au₂₅₀ was 1.1 nm, 1.3 nm, and 1.56 nm, respectively, and the values correspond to the sizes reported elsewhere.^27,29,46,47

Fig. 1 Characterization of synthesized p-MBA protected gold nanocluster. (a) Image of PAGE separation of the purified Au₂₅₀ (left), Au₁₀₂ (middle), and Au₂₅ (right). (b) Normalized UV-vis absorption spectra and (c) extinction coefficient spectra in water.

Optical measurements of the gold nanoclusters

UV-vis absorption spectra and the extinction coefficient values of the isolated gold nanoclusters in water are presented in Fig. 1b and c. The merit of using gold nanoclusters is that the electronic structure of the nanoclusters changes by the size and shape of their metallic core, which is reflected in their UV-vis spectra. For smaller sizes, the spectrum is continuous with distinctive peaks, while for larger sizes, a clear localized surface plasmon resonance (LSPR) is observed.^48,49 These unique, distinctive absorbance features provide a convenient tool for identifying the isolated nanoclusters. As shown in Fig. 1b, the gold nanoclusters exhibit size-dependent absorption spectra with the same absorption peak around 200–300 nm, consistent with the hybridized transitions localized on the p-MBA ligand.⁵⁰ Au₂₅ nanocluster displays characteristic absorption peaks at 701, 470, and 430 nm, corresponding to the Au₂₅ characteristic optical transitions.²⁹ Larger nanoclusters show more featureless optical spectra than Au₂₅. Therefore, the optical spectra of the larger nanoclusters were compared with the reported spectra for evaluation. Au₁₀₂ has a weak peak around 423 nm,²³ and Au₂₅₀ exhibits weak LSPR around 530 nm.²⁷ These isolated large-size nanoclusters were identified as Au₁₀₂ and Au₂₅₀, respectively.

We measured the extinction coefficients of the gold nanoclusters to determine the molar concentration of the dilute gold nanocluster solution for further observations. The extinction coefficient was calculated using the Beer–Lambert equation (see ESI† for details). As shown in Fig. 1c, the differences in the extinction coefficient vales for each nanocluster followed qualitatively the number of gold atoms. To avoid any interference by absorbance of the residues, such as salt and p-MBA (absorbance at ∼200–300 nm), the extinction coefficient values of Au₂₅, Au₁₀₂ and Au₂₅₀ were read at 700, 520, and 490 nm, respectively. The molar extinction coefficient values of Au₂₅ (6997 M⁻¹ cm⁻¹), Au₁₀₂ (233 000 M⁻¹ cm⁻¹), and Au₂₅₀ (677 699 M⁻¹ cm⁻¹) (Fig. 1c) were further utilized to calculate the molar ratio between the gold nanoclusters and the KU dye.

pH response measurements of the Au + KU complex

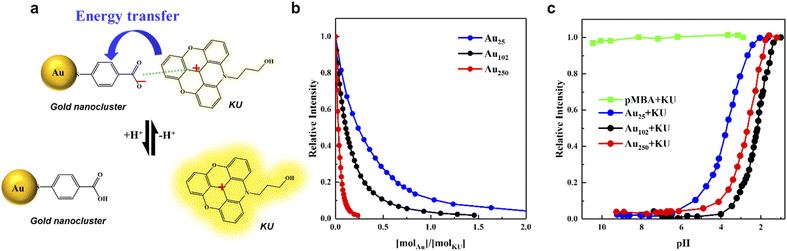
The steady-state fluorescent intensity of the KU dye at different pH was measured in the presence of three different-sized gold nanoclusters protected with the same type of ligand, to understand the size effect on the functionality of the fluorescent pH sensor. The fluorescence of the positively charged (+1) KU dye is quenched when they are bound to the negatively charged (–COO⁻) p-MBA protected gold nanoclusters, leading to an energy transfer process from the KU dye to the gold nanocluster²³ (Fig. 2a). This behaviour allows the fluorescence of the KU dye to quench and it is dependent on the surface charge of the nanocluster, which could be regulated by the amount of the nanoclusters or the number of charged ligands. It is worth noting that, based on the 8 electron superatom model, Au₂₅ is known to have a −1 charge state, but it is mainly localized in the metal core, not affecting its surface charge. Thus, in our studies, this extra charge was not considered a factor affecting the interaction between the KU dye and the p-MBA ligands. Moreover, the only possible counterion to stabilize the cluster charge is Na⁺, which, due to its small steric size, cannot considerably affect the accessibility of the dye to the cluster surface. As shown in Fig. 2b, Au₂₅, Au₁₀₂, and Au₂₅₀ were added to the KU solution (pH 10) having the same concentration in each case, which triggered the KU intensity to drop rapidly (see Experimental section for more details). Moreover, the trend of the quenching curves differed by the nanoclusters. In detail, Au₂₅₀ shows the fastest quenching characteristic, followed by Au₁₀₂ and Au₂₅. Due to the abundance of the KU molecule in the solution and the availability of multiple ligands on each cluster, the complexation involves several KU dyes interacting with one gold nanocluster. To determine how many KU dyes tend to bound to the nanoclusters in a low concentration region ([mol_Au]/[mol_KU] < 0.1), the initial slope of the titration curve was determined. As shown in Fig. S2,† approximately 2, 5, and 19 KU dyes were bound to Au₂₅, Au₁₀₂, and Au₂₅₀, respectively. This result indicates that more than one KU dye molecules are bound to larger nanoclusters because of the highly negative surface charge and more p-MBA groups available for binding per clusters. Furthermore, the fluorescence for all three nanoclusters is almost totally quenched when the [mol_Au]/[mol_KU] ratio reaches 2, indicating nearly all the KU dyes formed a complex with the nanoclusters.

Fig. 2 (a) Schematic diagram illustrating electrostatic interaction and energy transfer process between the p-MBA protected gold nanoclusters (AuNC) and KU dye in different pH conditions. (b) Relative intensity of KU emission as function of [mol_Au]/[mol_KU] molar ratio in pH 10 solution (excitation wavelength 500 nm). (c) Relative intensity of KU emission as function of pH. The molar ratio of the solution was [mol_Au]/[mol_KU] = 2.

The pH dependence measurements of the Au + KU complexes were carried out to observe the effect of the different gold nanoclusters on the response. In order to accurately compare how the KU fluorescence properties change according to the size of the gold nanocluster, it is essential to fix the other conditions carefully. Therefore, in the subsequent pH experiment, the concentrations for the gold nanocluster and KU were fixed to [mol_Au]/[mol_KU] = 2, where the KU fluorescence quenches with all nanoclusters (see Experimental section for more details). The pH titration curve of the Au + KU complex was measured by gradually adding 0.01 M HCl to the Au + KU complex solution. As the HCl is added, the fluorescence of the KU dye dramatically starts to increase around pH 4–6 and saturates around pH 1 (Fig. 2c). On the other hand, the fluorescence of p-MBA + KU complex did not change during pH adjustments, which indicates that the pH dependence properties of the KU are exhibited only in the presence of the gold nanoclusters. Moreover, a distinct shift of the titration curve for each complex was observed. These significant changes in the titration curves lead us to determine the approximate half-point pH of each curve for further comparison. The pH values were read at the 0.5 relative intensity point. The half-point pH was 2.11, 2.66, and 3.70 for Au₂₅₀, Au₁₀₂, and Au₂₅, respectively. This result clearly shows that the pH response of the KU dye can be regulated by varying the size of the nanocluster as predicted. Moreover, this is the first experimental result on tuning the pH sensor properties by tailoring the size of the nanoclusters.

In detail, the pH titration curve for the Au₂₅₀ + KU complex was shifted to a higher pH region than the Au₁₀₂ + KU complex, indicating the correlation between the surface curvature and the pK_a value of the nanoclusters, assuming that the pH dependence of fluorescence is related to the surface charge of the cluster. On the other hand, the Au₂₅ + KU complex exhibited an unexpectedly high pK_a trend compared to the other larger nanocluster-based complexes. Based on previous research,²⁴ Au₂₅ was expected to have the lowest pH response range owing to its highest surface curvature among the nanoclusters. However, as shown in Fig. 2c, the Au₂₅ + KU complex shows the highest pH response range, followed by Au₂₅₀ and Au₁₀₂. To understand the grounds for the unexpected behaviour of the Au₂₅ nanocluster, it is crucial to comprehend the fundamental nature of the nanoclusters. As shown in Fig. 2a, the KU dye's fluorescence intensity depends on the surface negativity of the gold nanoclusters. In other words, the pK_a of the nanoclusters will be one of the factors in regulating the effective pH range. Therefore, it was important to measure the protonation–deprotonation behaviour of the Au₂₅, Au₁₀₂, and Au₂₅₀ nanoclusters by the acid–base pH titration method.

Acid–base titration of the gold nanoclusters

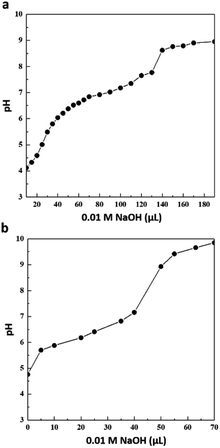
The titration curves were measured in pure H₂O, where the clusters were diluted and dispersed in the lowest pH solution that did not fully precipitate the nanoclusters (pH ∼ 4–5, see Experimental section for more details). The titration studies for Au₁₀₂ were referred to in our previous report.³⁵ As shown in Fig. 3, a single pK_a is observed in both Au₂₅ and Au₂₅₀, and the pK_a values were extracted from the second derivative curve, as shown in Fig. S3 and Table S1.† The pK_a values for Au₂₅ and Au₂₅₀ nanoclusters were 6.82 and 6.29, respectively. The pK_a values for the nanoclusters had similar order compared to the Au + KU complex half-point pH. The difference in the apparent pK_a of the nanoclusters and the response pH of the Au + KU complex could be explained by the effect of the positively charged KU dye. In the presence of a positively charged counterion, the interaction between the neighbouring weak acid groups is reduced, thus decreasing the pK_a value as in our experimental results.^51–53 Moreover, the intermolecular interactions, i.e., π–π stacking of the ligands, could affect the complexation between the gold nanocluster and the KU dye; thus, the pH response range and the acid–base titration will not follow each other in a one-to-one correlation. Even though we still have to understand the unexpected result from Au₂₅, the results indicate that the pK_a value of the nanocluster is controlled by the size, and by these pK_a values, the KU response range is regulated. Moreover, the consistency of the trends between the nanoclusters makes it possible to exhibit the probability of strategizing how to design and regulate the pH sensor with precision.

Fig. 3 Acid–base titration curve of (a) Au₂₅ and (b) Au₂₅₀ nanoclusters in water.

Surface structure analysis of Au₂₅(p-MBA)₁₈

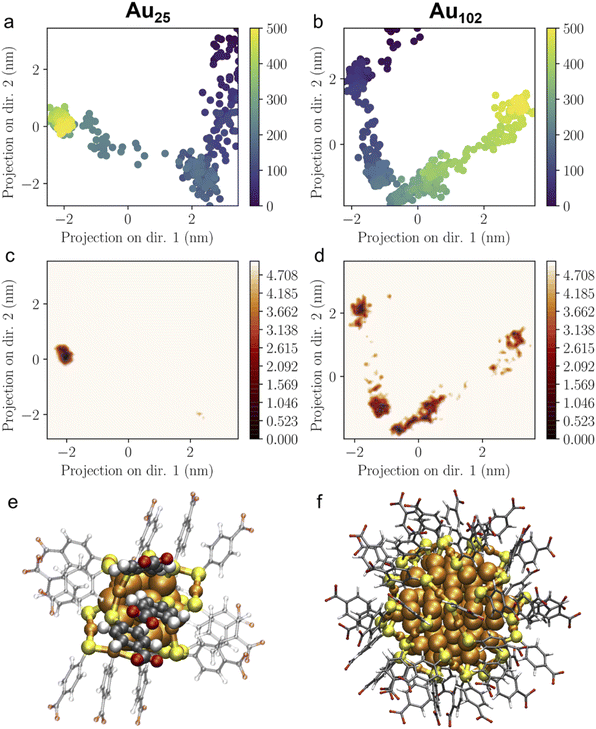
The pK_a of the nanoclusters is regulated by their curvature, which will, in turn, determine the distance at which the ligand–ligand interaction occurs. The closer the negatively charged ligands are, the higher the equilibrium shifts to a higher pH, enhancing the pK_a. Therefore, analysing and comparing the intermolecular packing of the nanocluster ligand layer is needed to understand the unique pK_a shift behaviour of Au₂₅. Fig. 4 shows the calculated pair correlation functions g(r) between carbon atoms of p-MBA carboxylate groups (–COO⁻) from MD simulations of Au₂₅ and Au₁₀₂ nanoclusters in water. For Au₂₅, a very sharp main peak is observed at 0.4 nm with broader but still well-defined minor peaks at longer distances. While, for Au₁₀₂, the first peak is observed at 0.5 nm with a remarkable difference in intensity compared to Au₂₅ and minor oscillations above this distance. The g(r) peaks for Au₂₅ suggest a highly structured ligand layer, which is governed by the packing of phenyl rings of the p-MBA ligands and the multiple π–π stacking interactions. Computed g(r) for phenyl–phenyl rings during 100 ns MD simulation (Fig. S4†) show how the highly ordered ligand layer of Au₂₅ is established as the simulation time increases. This feature is exhibited in a sharp increase in the peaks related to the average nearest and second nearest neighbour distances between the π–π stacked groups. In contrary, Au₁₀₂ shows considerably less structural ordering in the ligand layer and the characteristics are different compared to Au₂₅ (see Fig. S5†). For Au₁₀₂ a higher peak appears during the simulation at 0.5 nm distance which is typical for neighbouring T-stacked phenyl rings. It is known that parallel stacked phenyl rings have a higher pK_a compared to the T-stacked phenyl rings because of their higher repulsive behaviour. Therefore, Au₂₅ is eligible to have a higher pK_a than Au₁₀₂.⁵⁴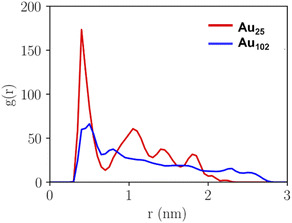

Fig. 4 Pair correlation function g(r) of carbon atoms of the carboxylic groups of ligands of Au₂₅ and Au₁₀₂ clusters as calculated from MD-trajectory.

The flexibility and structural stability of the Au₂₅ and Au₁₀₂ ligand layer was also studied by ED analysis (Fig. 5a and b). ED analysis can be used to solve the principal collective modes of the atomic fluctuations and statistically analyse the most prominent conformations as projected to them. Here, the first two principal components were selected to analyse the projection of MD-trajectories in the conformational phase space. Au₂₅ covered a smaller region of phase space with only one major basin (Fig. 5a and c), while Au₁₀₂ showed several conformational basins distributed on a larger region (Fig. 5b and d), which demonstrates a higher ordered arrangement of p-MBA ligands on Au₂₅ over Au₁₀₂ nanoclusters. Time evolution in Fig. 5 shows that the structure of Au₂₅ gets stabilized in 60 ns (after 300 snapshot frames) after which the conformation is frozen at the major basin of the phase space. The same kind of stabilization is not seen for Au₁₀₂. In terms of structural features, Au₂₅ and Au₁₀₂ exhibit a different gold–sulfur interface. Au₂₅ has an icosahedral Au₁₃ core protected by six long SR–Au–SR–Au–SR units, while Au₁₀₂ has 19 short SR–Au–SR units and only two long SR–Au–SR–Au–SR units protecting the Au₇₉ core.^31,32,55,56 Based on this composition, the Au₂₅ ligand layer is expected to be more flexible due to the long units attached to an ultrasmall core with a high curvature. Hence, the flexibility allows Au₂₅ cluster to adjust itself better for changed conditions than Au₁₀₂ and find a highly ordered and stable ligand layer arrangement, although the relative distribution of the ligands in Au₂₅ and Au₁₀₂ was initially qualitatively the same (see Fig. S4 and S5†). Fig. 5e and f illustrates the multiple π–π stacking interactions formed between the locally densely packed phenyl rings of p-MBA ligands as observed in the final snapshot of 100 ns MD simulation of Au₂₅ nanocluster in comparison to the final snapshot of Au₁₀₂. The point group symmetry of the metal core of the averaged structure of last 200 snapshots of Au₂₅ MD-trajectory is D_2d with root mean square deviation (RMSD) of 0.054 Å from the ideal which resembles the structure distortions that are seen for the neutral and cationic experimental clusters as compared to the nearly ideal icosahedral metal core of experimental anionic cluster.⁵⁷ Our results indicate that Au₂₅ has a more organized ligand layer orientation than Au₁₀₂, which can explain the singular pK_a shift observed.

Fig. 5 a) and (b) Show the time evolution of the conformations, and (c) and (d) show the conformational free energies of the MD-trajectories of Au₂₅ and Au₁₀₂ in the essential dynamics analysis. Minimum of the free energy is set to zero and the colour scale is fixed to the energy scale from 0 kJ mol⁻¹ to 5 kJ mol⁻¹. The data above 5 kJ mol⁻¹ is not distinguished and is shown in the unified solid pale background. Projection is done based on the two main principal component eigenvector directions. (e) and (f) Show the final structure of Au₂₅ and Au₁₀₂ cluster taken from the same 100 ns MD simulation. Formation of six separate π–π stacked groups of three ligands is highlighted for Au₂₅.

Conclusions

We have shown a robust strategy for regulating the pH response range by tailoring the size of the gold nanoclusters. For different-sized gold nanoclusters, Au₂₅, Au₁₀₂, and Au₂₅₀ were synthesized and formed a complex with the KU dye for pH measurements. The pH titration measurement of the Au_n + KU complex (n = 25, 102, 250) showed that the pH response range of the KU dye was evidently shifted, which matched well with the order of the pK_a value measured by the acid–base titration measurement. Au₂₅₀ exhibited a higher pH response range than Au₁₀₂ based on the surface curvature effect. However, Au₂₅ showed an unexpectedly high pK_a value compared to the larger size nanoclusters. This behaviour was understood by performing the MD simulations and ED analysis. The results showed that small nanoclusters do not follow the scaling between the curvature and the pK_a. Instead, the behaviour is more controlled by the distribution and interaction of the p-MBA ligands on the nanocluster surface. This is the first study attempting to analyse the pK_a value of ultrasmall nanoclusters and understand the factor that regulates the protonation behaviour in an atomic range. Understanding the relationship between the ligands orientation and the pK_a trend of each nanocluster on an atomic scale makes it possible to create a toolbox for efficiently designing or modifying the pH sensor by tailoring the size of the nanoclusters. Furthermore, the use of atomically precise nanoclusters facilitates synergy between theory and experiments toward paving the way for the rational design of new probes.

Author contributions

Kyunglim Pyo: conceptualization, investigation, validation, visualization, writing – original draft. María Francisca Matus: formal analysis, visualization, writing – review & editing. Sami Malola: formal analysis, visualization, writing – review & editing. Eero Hulkko: resources, supervision. Johanna Alaranta: resources. Tanja Lahtinen: Resources, supervision. Hannu Häkkinen: conceptualization, funding acquisition, supervision, writing – review & editing. Mika Pettersson: conceptualization, funding acquisition, supervision, writing – review & editing. All authors discussed the results.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Academy of Finland (grants 292352, 319208), the post-doctoral program of the NSC, and by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2021R1A6A3A03038668). The computations were made at the Finnish National Supercomputing Centre CSC. We thank Marta Monti for discussions on the analysis of the dynamics of the nanoclusters' ligand layer.

Notes and references

1. B. A. Webb, et al., Dysregulated pH: a perfect storm for cancer progression, Nat. Rev. Cancer, 2011, 11, 671–677.
2. M. Stubbs, et al., Metabolic consequences of a reversed pH gradient in rat tumors, Cancer Res., 1994, 54, 4011–4016.
3. M. I. Khan, et al., A review on pH sensitive materials for sensors and detection methods, Microsyst. Technol., 2017, 23, 4391–4404.
4. R. Avolio, et al., Review of pH sensing materials from macro- to nano-scale: recent developments and examples of seawater applications, Crit. Rev. Environ. Sci. Technol., 2022, 52, 979–1021.
5. J. R. Casey, S. Grinstein and J. Orlowski, Sensors and regulators of intracellular pH, Nat. Rev. Mol. Cell Biol., 2010, 11, 50–61.
6. W. F. Boron, Regulation of Intracellular pH, Adv. Physiol. Educ., 2004, 28, 160–179.
7. Y. Liu, K. A. White and D. L. Barber, Intracellular pH regulates cancer and stem cell behaviors: a protein dynamics perspective, Front. Oncol., 2020, 10, e1401.
8. D. Lagadic-Gossmann, L. Huc and V. Lecureur, Alterations of intracellular pH homeostasis in apoptosis: origins and roles, Cell Death Differ., 2004, 11, 953–961.
9. R. A. Gottlieb, et al., Apoptosis induced in jurkat cells by several agents is preceded by intracellular acidification, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 654–658.
10. A. Ishaque and M. Al-Rubeai, Use of intracellular pH and annexin-V flow cytometric assays to monitor apoptosis and its suppression by bcl-2 over-expression in hybridoma cell culture, J. Immunol. Methods, 1998, 221, 43–57.
11. H. Izumi, et al., Cellular pH regulators: potentially promising molecular targets for cancer chemotherapy, Cancer Treat. Rev., 2003, 29, 541–549.
12. T. A. Davies, et al., Non-age related differences in thrombin responses by platelets from male patients with advanced Alzheimer's disease, Biochem. Biophys. Res. Commun., 1993, 194, 537–543.
13. J. Han and K. Burgess, Fluorescent indicators for intracellular pH, Chem. Rev., 2010, 110, 2709–2728.
14. J. Dakin and B. Culshaw, Optical Fiber Sensors, Artech House, Boston-London, 1997, vol. 15, ch. 8, pp. 53–107.
15. S. Schutting, et al., New highly fluorescent pH indicator for ratiometric RGB imaging of pCO₂, Methods Appl. Fluoresc., 2014, 2, e024001.
16. N. Boens, V. Leen and W. Dehaen, Fluorescent indicators based on BODIPY, Chem. Soc. Rev., 2012, 41, 1130–1172.
17. A. P. Demchenko, Photobleaching of organic fluorophores: quantitative characterization, mechanisms, protection, Methods Appl. Fluoresc., 2020, 8, 022001.
18. P. Reineck, et al., Brightness and photostability of emerging red and near-IR fluorescent nanomaterials for bioimaging, Adv. Opt. Mater., 2016, 4, 1549–1557.
19. A. Praetorius, et al., Design of a fluorescent dye for indicator displacement from cucurbiturils: a macrocycle-responsive fluorescent switch operating through a pKa shift, Org. Lett., 2008, 10, 4089–4092.
20. K. N. More, et al., Molecular design of fluorescent pH sensors based on reduced rhodol by structure-pKa relationship for imaging of lysosome, Dyes Pigm., 2021, 184, 108785.
21. D. R. Wilson, et al., A triple-fluorophore-labeled nucleic acid pH nanosensor to investigate non-viral gene delivery, Mol. Ther., 2017, 25, 1697–1709.
22. R. V. Benjaminsen, et al., Evaluating nanoparticle sensor design for intracellular pH measurements, ACS Nano, 2011, 5, 5864–5873.
23. E. Hulkko, et al., Covalent and non-covalent coupling of a Au102 nanocluster with a fluorophore: energy transfer, quenching and intracellular pH sensing, Nanoscale Adv., 2021, 3, 6649–6658.
24. D. Wang, et al., How and why nanoparticle's curvature regulates the apparent pKa of the coating ligands, J. Am. Chem. Soc., 2011, 133, 2192–2197.
25. D. A. Walker, et al., Geometric curvature controls the chemical patchiness and self-assembly of nanoparticles, Nat. Nanotechnol., 2013, 8, 676–681.
26. J. Lin, et al., Understanding the synergistic effect of physicochemical properties of nanoparticles and their cellular entry pathways, Commun. Biol., 2020, 3, 205.
27. K. Sokołowska, et al., Towards controlled synthesis of water-soluble gold nanoclusters: synthesis and analysis, J. Phys. Chem. C, 2019, 123, 2602–2612.
28. K. Salorinne, et al., Solvation chemistry of water-soluble thiol-protected gold nanocluster Au₁₀₂ from DOSY NMR spectroscopy and DFT calculations, Nanoscale, 2014, 6, 7823–7826.
29. Y. Cao, et al., Reversible isomerization of metal nanoclusters induced by intermolecular interaction, Chem, 2021, 7, 2227–2244.
30. M. W. Heaven, et al., Crystal Structure of the Gold Nanoparticle [N(C₈H₁₇)₄][Au₂₅(SCH₂CH₂Ph)₁₈], J. Am. Chem. Soc., 2008, 130, 3754–3755.
31. M. Zhu, et al., Correlating the crystal structure of a thiol-protected Au₂₅ cluster and optical properties, J. Am. Chem. Soc., 2008, 130, 5883–5885.
32. P. D. Jadzinsky, et al., Structure of a thiol monolayer-protected gold nanoparticle at 1.1 Å resolution, Science, 2007, 318, 430–433.
33. D. Van Der Spoel, et al., GROMACS: Fast, flexible, and free, J. Comput. Chem., 2005, 26, 1701–1718.
34. E. Pohjolainen, et al., A unified AMBER-compatible molecular mechanics force field for thiolate-protected gold nanoclusters, J. Chem. Theory Comput., 2016, 12, 1342–1350.
35. J. Koivisto, et al., Acid−base properties and surface charge distribution of the water-soluble Au₁₀₂(pMBA)₄₄ nanocluster, J. Phys. Chem. C, 2016, 120, 10041–10050.
36. W. L. Jorgensen, et al., Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935.
37. S. Miyamoto and P. A. Kollman, Settle: an analytical version of the SHAKE and RATTLE algorithm for rigid water models, J. Comput. Chem., 1992, 13, 952–962.
38. G. Bussi and M. Parrinello, Stochastic thermostats: comparison of local and global schemes, Comput. Phys. Commun., 2008, 179, 26–29.
39. H. J. C. Berendsen, et al., Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690.
40. M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: a new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190.
41. T. Darden, D. York and L. Pedersen, Particle mesh Ewald: an N log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092.
42. B. Hess, et al., LINCS: a linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 18, 1463–1472.
43. W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graph. Model., 1996, 14, 33–38.
44. A. Amadei, A. B. M. Linssen and H. J. C. Berendsen, Essential dynamics of proteins, Proteins: Struct., Funct., Bioinf., 1993, 17, 412–425.
45. M. Monti, M. Stener and M. Aschi, A computational approach for modelling Electronic Circular Dichroism of solvated chromophores, J. Comput. Chem., 2022 DOI:10.1002/jcc.27001.
46. T. Lahtinen, et al., Covalently linked multimers of gold nanoclusters Au₁₀₂(p-MBA)₄₄ and Au_∼250(p-MBA)_n, Nanoscale, 2016, 8, 18665–18674.
47. Z. Wu, J. Suhan and R. Jin, One-pot synthesis of atomically monodisperse, thiol-functionalized Au₂₅ nanoclusters, J. Mater. Chem., 2009, 19, 622–626.
48. Y. Negishi, et al., A critical size for emergence of nonbulk electronic and geometric structures in dodecanethiolate-protected Au clusters, J. Am. Chem. Soc., 2015, 137, 1206–1212.
49. C. Yi, et al., Nanometals: identifying the onset of metallic relaxation dynamics in monolayer-protected gold clusters using femtosecond spectroscopy, J. Phys. Chem. C, 2015, 119, 6307–6313.
50. M. Walter, et al., A unified view of ligand-protected gold clusters as superatom complexes, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9157–9162.
51. C. N. Pace, G. R. Grimsley and J. M. Scholtz, Protein ionizable groups: pK values and their contribution to protein stability and solubility, J. Biol. Chem., 2009, 284, 13285–13289.
52. S. Mafé, V. Garcia-Morale and P. Ramirez, Estimation of pKa shifts in weak polyacids using a simple molecular model: effects of strong polybases, hydrogen bonding and divalent counterion binding, Chem. Phys., 2004, 296, 29–35.
53. P. Ramirez, et al., Donnan equilibrium of ionic drugs in pH-dependent fixed charge membranes: theoretical modeling, J. Colloid Interface Sci., 2002, 253, 171–179.
54. A. Olasz, et al., Effect of the π-π stacking interaction on the acidity of phenol, Chem. Phys. Lett., 2005, 407, 504–509.
55. H. Häkkinen, The gold–sulfur interface at the nanoscale, Nat. Chem., 2012, 4, 443–455.
56. M. Zhu, W. T. Eckenhoff, T. Pintauer and R. Jin, Conversion of anionic [Au₂₅(SCH₂CH₂Ph)₁₈]⁻ cluster to charge neutral cluster via air oxidation, J. Phys. Chem. C, 2008, 112, 14221–14224.
57. M. A. Tofanelli, et al., Jahn–Teller effects in Au₂₅(SR)₁₈, Chem. Sci., 2016, 7, 1882–1890.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2na00487a

---