Open Access Article
Open Access ArticleA first-principles study on atomic-scale pore design of microporous carbon electrodes for lithium-ion batteries†
Young Chul
Lee
 and
Sung Chul
Jung
and
Sung Chul
Jung
 *
*
Department of Physics, Pukyong National University, Busan 48513, Republic of Korea. E-mail: scjung@pknu.ac.kr
First published on 1st November 2022
Abstract
Porous carbon materials are considered attractive lithium storage media because their large specific surface areas and pore volumes provide high adsorption capacity. This first-principles study elucidates the atomic-scale mechanisms of lithium storage and diffusion in microporous carbon. Microporous carbon structures with initial densities of 1.5, 2.0, and 2.5 g cm−3 store up to 7.5–8.2 Li ions per C6 corresponding to the capacities of 2783–3032 mA h g−1, which are 7–8 times higher than that for graphite. Fully lithiated microporous carbon has about 62% of Li ions inside the pore cavity and on the pore surface, responsible for reversible capacity, and about 38% of Li ions inside the pore wall, responsible for irreversible capacity. As lithiation proceeds, microporous carbon structures with different total pore volumes evolve to have similar total pore volumes but different average pore volumes. The average pore volume has a great influence on Li ion conductivity, as evidenced by the highest conductivity of 103.5 mS cm−1 for the largest average pore diameter of 9.3 Å. Inside large pore cavities, Li ions diffuse rapidly without encountering carbon atoms that impede Li diffusion, suggesting that a high Li-to-C ratio around Li causes fast Li ion motion. This study offers not only a comprehensive understanding of the lithiation of microporous carbon but also design directions for developing efficient microporous carbon electrodes for lithium-ion batteries.
1. Introduction
Carbon is a versatile material used in a variety of energy and environmental applications.1–3 One of the most important applications is rechargeable lithium-ion batteries (LIBs), in which graphitic carbon is used as the anode material. The graphite anode has been the primary choice for commercial LIBs to date, but its theoretical capacity of 372 mA h g−1 (LiC6) is insufficient to meet the ever-increasing energy demand. Instead of graphite, high-capacity anode materials such as Si, SiO, Sn, and SnO2 have been intensively studied for the development of advanced LIBs.4,5 Carbon is electrochemically less active than these anode materials. Nevertheless, carbon is still an important material because it has been widely used as a coating, composite, and matrix material in candidate electrode systems for advanced LIBs or next-generation batteries, such as Na-ion, Li–S, Li–O2, and all-solid-state batteries.6–8 In particular, high-capacity anode materials embedded or encapsulated in carbonaceous additives such as carbon nanotubes, reduced graphene oxide, and pyrolyzed carbon exhibit enhanced capacity and cycling stability because the additives can effectively alleviate large volume expansion and improve electronic conductivity.9–12Porous carbon has unique properties of various pore sizes, large specific surface areas, variable morphologies, and good thermal, chemical, and mechanical stabilities.13,14 Due to these characteristics, porous carbon has been used in applications such as energy storage and conversion, hydrogen storage, electrocatalysis, water purification, gas adsorption, separation, and catalyst support.15–18 Porous carbon has been used as an active material or stabilizing matrix in LIBs because it offers superior lithium-ion storage ability, enhanced cycle stability, sufficient void space accommodating large volume changes, and reasonable electronic conductivity provided by interconnected carbon walls.13,19,20
According to the pore size, porous carbons are classified into microporous (pore size of <2 nm), mesoporous (pore size of 2–50 nm), and macroporous (pore size of >50 nm) carbons. Despite their significant irreversible capacities, porous carbons, such as hierarchically porous (micro–meso–macroporous) carbons, have exhibited much higher reversible capacities of 550–1550 mA h g−1 than graphite.21–27 These high capacities appear to come mainly from micropores, because mesopores and macropores promote efficient mass transport, whereas micropores provide an abundance of accessible active sites.15,22,28,29 Indeed, Kwon et al.21 reported that zeolite-templated ordered microporous carbon with a pore size of 0.92 nm delivered a remarkable initial capacity of 2950 mA h g−1 and reversible capacity of 1550 mA h g−1. Furthermore, microporous carbon provided not only a higher capacity but also a higher rate capability than reduced graphene oxide.30 The high lithium storage ability of microporous carbon is attributed to the adsorption of a large amount of Li ions on the pore wall surface of uniformly ordered micropores.21 Thus, highly ordered microporous carbon structures are very attractive in terms of the electrochemical performance of LIBs. However, the mechanisms of Li ion storage and diffusion in microporous carbon remain veiled because of the disordered amorphous structure of porous carbon.
This study investigated the lithiation of microporous carbon structures with initial densities of 1.5, 2.0, and 2.5 g cm−3 using density functional theory (DFT) calculations and ab initio molecular dynamics (AIMD) simulations. The lithiation of microporous carbon proceeds until carbon accommodates up to 7.5–8.2 Li ions per C6 corresponding to high capacities of 2783–3032 mA h g−1. In fully lithiated microporous carbon, about 17%, 45%, and 38% of Li ions are stored inside the pore cavity, on the pore surface, and inside the pore wall, respectively. During lithiation, microporous carbon structures with different total pore volumes tend to have similar total pore volumes but different average pore volumes. The lithiated microporous carbon structure with the largest average pore volume exhibits the highest Li ion conductivity of 103.5 mS cm−1 in the Li7.8C6 composition, showing that the abundance of large individual pores is important for fast Li ion diffusion. In lithiated microporous carbon, Li ions inside the pore cavity have few or no carbon atoms around them and diffuse rapidly without being disturbed by carbon atoms, suggesting that a high Li-to-C ratio around Li leads to rapid Li ion motion.
2. Computational details
We performed DFT calculations using the Vienna ab initio simulation package (VASP).31 The projector augmented wave (PAW) method32 and the Perdew–Burke–Ernzerhof (PBE) functional33 were used. Grimme's DFT-D2 method34 was employed to describe the long-range van der Waals interactions of carbon atoms. The electronic wave functions were expanded in a plane-wave basis set with an energy of 624 eV. The 1s22s1 and 2s22p2 orbitals for Li and C, respectively, were treated as valence electron configurations. The microporous amorphous LixC6 structures were simulated using periodic cubic (x = 0) and triclinic (0.3 ≤ x ≤ 10.2) supercells containing (160/6) × x Li atoms and 160 C atoms. The total number of atoms used in the supercells was 160–432 for x = 0, 0.3, 0.6, 1.2, 1.8, 2.4, 3.6, 5.4, 6.6, 7.8, 8.4, 9.0, 9.6, and 10.2. Brillouin zone integrations were done using a 1 × 1 × 1 k-point mesh. The atomic positions were optimized until the residual forces were less than 0.02 eV Å−1.AIMD simulations were used to generate amorphous structures. The equations of motion were integrated with the Verlet algorithm using a time step of 1 fs. The temperature was controlled by velocity rescaling and canonical ensemble using a Nosé–Hoover thermostat. The amorphous carbon structures with initial densities of 1.5, 2.0, and 2.5 g cm−3 were constructed using the liquid-quench method, in which heating, equilibration, and cooling were performed as a series of steps using the AIMD simulations. Initially, for a given carbon density, 160 C atoms were randomly distributed in a cubic supercell with a size corresponding to the density. This structure was heated up to 8000 K at a heating rate of 1 K fs−1, equilibrated for 3 ps at 8000 K, and then quenched to 0 K at a cooling rate of 0.5 K fs−1. The quenched structure was fully optimized with respect to the atomic position using static DFT calculations. The (160/6) × x Li atoms were added to the constructed carbon structure with the given density to generate amorphous LixC6 structures using the same liquid-quench method. For amorphous LixC6, the quenched structure was fully optimized with respect to atomic position, cell volume, and cell shape using static DFT calculations, resulting in an amorphous structure with a triclinic supercell. The AIMD method used can accurately describe carbon bonds with different degrees of sp, sp2, and sp3 hybridization states. In terms of describing chemical bonds, the high accuracy of AIMD is superior to classical molecular dynamics using empirical potentials.35 Although AIMD can handle a much smaller number of atoms than classical molecular dynamics, the number (160–432) of atoms used in this study is significantly larger than those (64–70) used in a previous AIMD study of amorphous lithiated carbon structures.36 The pore structures of amorphous LixC were analyzed using Zeo++ software.37 Coordination numbers (CNs), radial distribution functions (RDFs), and angle distribution functions (ADFs) of amorphous LixC were analyzed by rigorous investigation of networks generated using the simulation (RINGS) code.38 The generation of amorphous structures using the liquid-quench method has been successfully used in our previous AIMD studies of amorphous KxSi,39 MgxSi,40 CaxSi,40 and NaxSn4P3.41
3. Results and discussion
3.1 Pristine microporous carbon
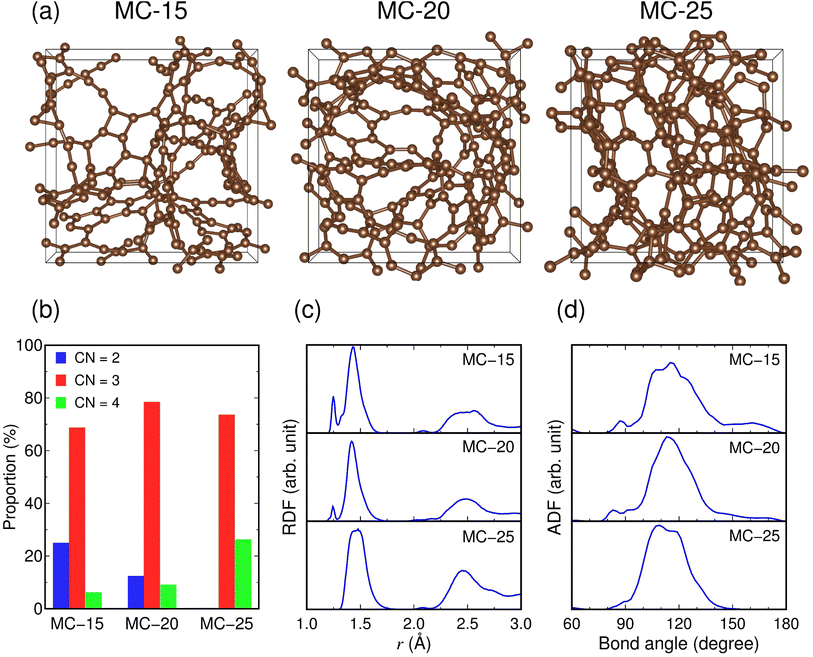
We constructed microporous carbon structures with carbon densities of 1.5, 2.0, and 2.5 g cm−3 (hereinafter referred to as MC-15, MC-20, and MC-25, respectively) (Fig. 1a). The carbon densities were chosen, taking into account the experimental densities (0.9–3.2 g cm−3) reported for amorphous or glassy carbon.42–44 Note that the density of graphite is 2.3 g cm−3.45,46 The calculated average pore diameters are 0.62, 0.38, and 0.28 nm for MC-15, MC-20, and MC-25, respectively, showing a decrease in pore size with increasing carbon density. The microporous carbon structures have two-, three-, and four-fold coordinated carbon atoms. The average coordination numbers (CNs) of the carbon atoms are CNC–C = 2.81, 2.97, and 3.26 for MC-15, MC-20, and MC-25, respectively, with CNα–β, representing the number of β atoms around an α atom. This indicates that CNC–C increases with increasing carbon density. The proportions of two-, three-, and four-fold coordination are 0–25%, 69–78%, and 6–26%, respectively (Fig. 1b), revealing that the three-fold coordination dominates the three microporous carbon structures. The proportions of two- and four-fold coordination decrease and increase, respectively, with increasing carbon density.The RDF of the C–C pair in MC-15 shows that the C–C bonds are formed at r = 1.25 and 1.43 Å, as shown in the satellite and main peaks, respectively, for the first-nearest neighbors (Fig. 1c). In the RDF for MC-20, these C–C bond peaks remain unchanged in position and shape, except for attenuation of the satellite peak. In the RDF for MC-25, the satellite peak disappears, and the main peak splits into two peaks: r = 1.44 and 1.48 Å. The changes in the RDF peak indicate that the C–C bond length increases with increasing carbon density; thus, the C–C bond strength weakens with increasing coordination number. The ADFs of the C–C–C bond show the main peaks at 115°, 113°, and 109° for MC-15, MC-20, and MC-25, respectively, with some shoulder peaks (e.g., a second peak at 117° for MC-25) (Fig. 1d). Given the bond angles of 180°, 120°, and 109° for ideal two-, three-, and four-fold coordination, respectively, the decrease in the main peak position from 115° (MC-15) to 109° (MC-25) is consistent with the increasing coordination number with increasing carbon density.
3.2 Lithiation of microporous carbon
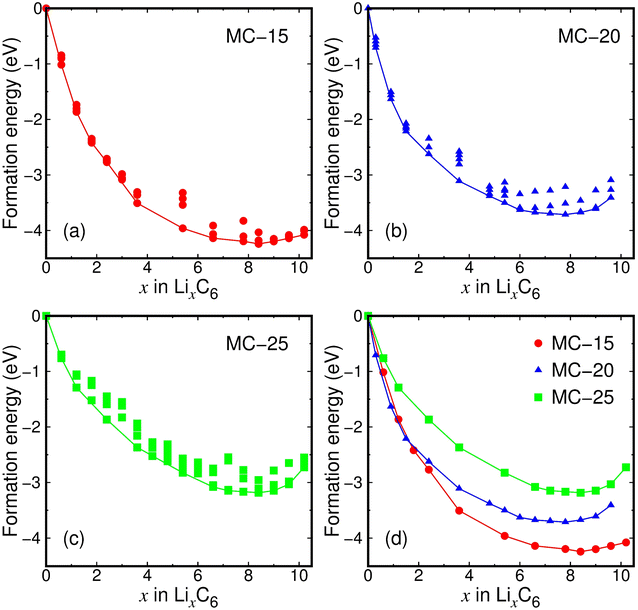
The lithiation of microporous carbon was investigated by calculating the formation energies of 3–6 lithiated microporous carbon structures (LixC6) with different Li configurations at each x (0.3 ≤ x ≤ 10.2). The total number of investigated LixC6 structures in the entire range of x was 171. All the calculated formation energies of lithiated MC-15, MC-20, and MC-25 structures are shown in Fig. 2a–c, and the formation energies of the lowest-energy structures at each x for lithiated microporous carbon are separately shown in Fig. 2d. The most stable LixC6 compositions of the lithiated MC-15, MC-20, and MC-25 structures were determined to be x = 8.15, 7.48, and 8.08, respectively, by a least-square fit to the calculated formation energies around x = 8.0. The Li8.15C6, Li7.48C6, and Li8.08C6 compositions correspond to the specific capacities of 3032, 2783, and 3006 mA h g−1, respectively. Despite the difference in the average pore diameter of microporous carbon between this study (0.28–0.62 nm) and a previous experimental study (0.92 nm),17 the determined capacities of 2783–3032 mA h g−1 are in good agreement with the initial capacity of 2950 mA h g−1 (Li7.9C6) for zeolite-templated microporous carbon.17 The determined capacities are 7.5–8.2 times higher than that (372 mA h g−1 for LiC6) for graphite and 2.1–5.8 times higher than the initial capacities of state-of-the-art carbon-based anode materials for LIBs, such as silicon-coated graphite (525 mA h g−1),47 NiO@CNT (824 mA h g−1),48 and carbon-based composite nanosheets (1327 mA h g−1).49 This shows that microporous carbon has excellent lithium storage ability. To the best of our knowledge, no carbon materials for LIBs have offered capacities comparable to microporous carbon.The fitted x values of 7.48–8.15 in Fig. 2 are in a narrow range of Δx = 0.67 over the entire interval of x = 0.0–10.2, implying that the initial density of microporous carbon has little to do with lithium storage ability. The calculated lowest formation energies are −7.07, −6.19, and −5.31 eV for MC-15 (Li8.4C6), MC-20 (Li7.8C6), and MC-25 (Li8.4C6), respectively, exhibiting that the lower the initial carbon density, the lower the formation energy. This result indicates that less dense microporous carbon is relatively less stable due to the lack of coordination numbers and therefore reacts more strongly with Li ions.
The fully lithiated microporous carbon structures with the lowest formation energies are displayed in Fig. 3a. Despite their similar Li contents (x = 7.8–8.4), the three fully lithiated microporous carbon structures have carbon pores of different sizes. Whereas the fully lithiated MC-15 and MC-25 structures have small carbon pores, the fully lithiated MC-20 structure has relatively large carbon pores (Fig. 3b).
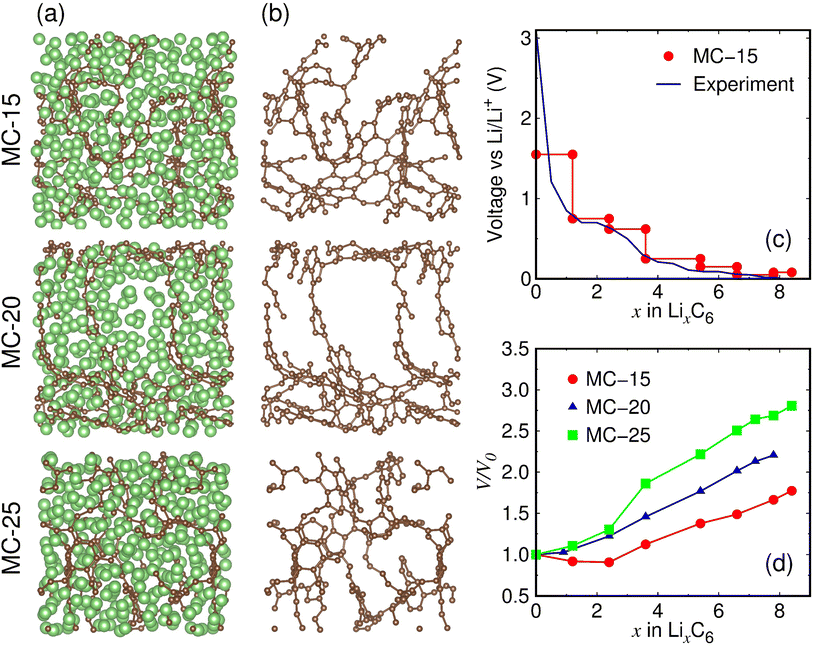 | ||
| Fig. 3 (a) Fully lithiated MC-15 (Li8.4C6), MC-20 (Li7.8C6), and MC-25 (Li8.4C6) structures. The green and brown balls represent the Li and C atoms, respectively. (b) Carbon pore structures with Li atoms removed in (a). (c) Calculated average voltage of lithiated MC-15, defined as V(x) = −[Etot(Lix+ΔxC6) − Etot(LixC6)]/Δx + Etot(Li). The experimental voltage was measured at the first discharge.21 (d) Volume expansion ratios of lithiated microporous carbon structures. V0 and V represent the volumes of pristine and lithiated structures, respectively. | ||
The average voltage of lithiated MC-15 structures with the initial pore size closest to that of the experimental sample17 was calculated based on the formation energies (Fig. 3c). The calculated voltage curve is in reasonable agreement with the experimentally measured first discharge curve,17 showing the validity of our simulation model for lithiated microporous carbon. The calculated and measured voltage curves appear close to a sloping shape with no distinct plateau, reflecting nonequivalent ion storage sites provided by microporous carbon.
During lithiation, the volumes of microporous carbon structures increase almost linearly with increasing x, except that the volumes of MC-15 decrease in the range of x = 0.0–2.4 and that of MC-25 increase sharply in the range of x = 2.4–3.6 (Fig. 3d). Considering the linear volume expansion over the entire range of x for MC-20, the nonlinear volume changes of MC-15 and MC-25 in the early stages of lithiation appear to be due to the initial carbon densities of MC-15 and MC-25, which are lower and higher than MC-20, respectively. The volume expansion ratio of fully lithiated microporous carbon, defined as (V − V0)/V0 × 100%, is calculated to be 77.3%, 120.5%, and 180.6% for MC-15 (Li8.4C6), MC-20 (Li7.8C6), and MC-25 (Li8.4C6), respectively, revealing that the lower the initial carbon density, the smaller the volume expansion during lithiation.
3.3 Structural properties of lithiated microporous carbon
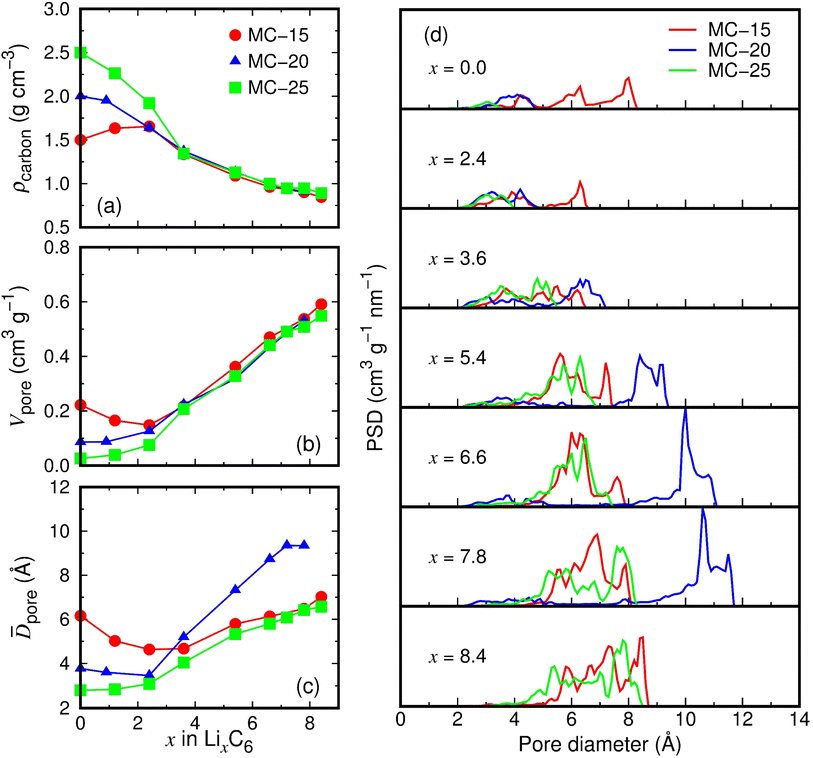
Structural changes in microporous carbon during lithiation were investigated. We analyzed the lithiated microporous carbon structures with Li atoms removed, as shown in Fig. 3b. Due to volume expansion during lithiation, the carbon densities of MC-15, MC-20, and MC-25 decrease with increasing x (Fig. 4a). Interestingly, the MC-15, MC-20, and MC-25 structures have almost the same carbon densities in the range of x ≥ 3.6. Consequently, despite their different initial carbon densities, the three microporous carbon structures have a carbon density of about 0.9 g cm−3 upon full lithiation. Similarly, the total pore volumes of MC-15, MC-20, and MC-25 become similar as lithiation proceeds (Fig. 4b). The total pore volumes of the fully lithiated MC-15 (Li8.4C6), MC-20 (Li7.8C6), and MC-25 (Li8.4C6) structures are 0.59, 0.53, and 0.55 cm3 g−1, respectively. However, the average pore diameter behaves differently from the total pore volume. Whereas MC-15 and MC-25 have similar average pore diameters in the range of x > 3.6, MC-20 has significantly larger pore diameters in the same range of x (Fig. 4c). The average pore diameters of the fully lithiated MC-15 (Li8.4C6), MC-20 (Li7.8C6), and MC-25 (Li8.4C6) structures are 7.0, 9.3, and 6.6 Å, respectively. The average pore volumes (![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) pore), calculated from the average pore diameter (
pore), calculated from the average pore diameter (![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) pore) using a simple relation
pore) using a simple relation ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) pore = 4π(
pore = 4π(![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) pore/2)3/3, are 181.1, 426.6, and 148.5 Å3 for the fully lithiated MC-15, MC-20, and MC-25, respectively, which is consistent with the carbon pores of different sizes shown in Fig. 3b. Therefore, as lithiation proceeds, the average pore volumes of microporous carbon structures may evolve differently for each structure, even if their total pore volumes become similar.
pore/2)3/3, are 181.1, 426.6, and 148.5 Å3 for the fully lithiated MC-15, MC-20, and MC-25, respectively, which is consistent with the carbon pores of different sizes shown in Fig. 3b. Therefore, as lithiation proceeds, the average pore volumes of microporous carbon structures may evolve differently for each structure, even if their total pore volumes become similar.
Fig. 4d shows the pore size distributions (PSDs) of lithiated microporous carbon structures. The pores of MC-15 with a diameter of 2.0–8.2 Å at x = 0.0 decrease in diameter with increasing x but increase in diameter in the range of x > 3, reaching a diameter of 2.4–8.6 Å at x = 8.4. The pore size decrease in the range of x < 3 is probably due to small amounts of Li ions attracting the pore walls while partially filling the pores, which explains the volume decrease of MC-15 in the range of x = 0.0–2.4 (Fig. 3d). The pores of MC-20 increase in diameter from 1.9–4.7 Å at x = 0.0 to 2.1–11.5 Å at x = 7.8, and those of MC-25 increase in diameter from 1.4–3.5 Å at x = 0.0 to 2.8–8.4 Å at x = 8.4. Compared to the pores of MC-15 and MC-25, those of MC-20 show a much larger increase in diameter in the range of x > 3. As a result, the maximum PSD peak for MC-20 at x = 7.8 is 10.6 Å in diameter, which is much larger than those (6.9 and 7.6 Å) for MC-15 and MC-25, respectively. This accounts for the larger average pore diameters of MC-20 than MC-15 and MC-25 in the range of x > 3.6 (Fig. 4c). The evolution of pores of different sizes appears to depend not on the initial carbon density of microporous carbon, but on the number of carbon bonds locally broken by Li ions during lithiation.
The carbon network changes in microporous carbon structures during lithiation were investigated. CNC–C increases in the order of MC-15 (2.81) < MC-20 (2.97) < MC-25 (3.26) at x = 0, whereas the order is MC-25 (2.33) < MC-15 (2.65) < MC-20 (2.77) at x = 7.8–8.4 (Fig. S1a†). The increasing order in CNC–C upon full lithiation is the same as that in average pore diameter upon full lithiation (Fig. 4c), suggesting that the larger the pore, the larger CNC–C. The proportions of two-, three-, and four-fold coordinated carbon atoms were further analyzed, as shown in Fig. S1b–S1d.† In the fully lithiated MC-20 (Li7.8C6) structure, the three-fold coordination accounts for the highest proportion, with 44.1%. However, in the fully lithiated MC-15 (Li8.4C6) and MC-25 (Li8.4C6) structures, the two-fold coordination accounts for the highest proportions, with 40.1% and 49.5%, respectively. The predominance of three-fold coordination in the fully lithiated MC-20 structure seems to be related to the largest average pore volume in this structure. This is because the larger the pores, the more carbon atoms are concentrated inside the pore walls (see MC-20 in Fig. 3b).
3.4 Lithium storage in microporous carbon
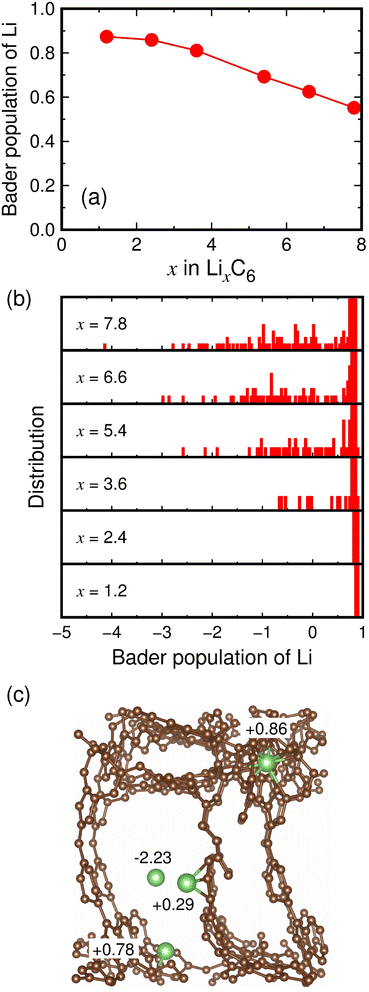
We investigated where Li ions are stored in microporous carbon to deliver high capacities of 2783–3032 mA h g−1 (Li7.5–8.2C6). Lithium storage sites can be inferred from the charge states of Li ions in microporous carbon. The Bader charge analyses of lithiated MC-20 structures show that Li ions have an average charge state of +0.87 at x = 1.2, and this charge state decreases to +0.55 at x = 7.8 as x increases, mitigating the increasing electrostatic repulsion between Li cations (Fig. 5a). The decrease in the Li charge state with increasing x is due to the appearance of various charge states below approximately +0.7, as shown in the distribution histograms of the Li charge state (Fig. 5b). In the histograms, the main charge states in the range of +0.72 to +0.96 remain almost unchanged as x increases, but additional charge states ranging from −4.12 to +0.68 appear at x ≥ 3.6. The main charge states result from Li ions embedded in the pore wall or adsorbed on the pore surface, as shown in Fig. 5c, where two Li ions have charge states of +0.86 and +0.78. However, the additional charge states originate from Li ions inside the pore cavity or adsorbed on the pore surface, as shown in Fig. 5c, where two Li ions have charge states of −2.23 and +0.29.The Li storage sites in lithiated microporous carbon were quantitatively analyzed using the charge states and coordination numbers of Li. As shown in Table 1, Li ions have 0–14 nearest carbon atoms (i.e., CNLi–C = 0–14) in the fully lithiated MC-20 (Li7.8C6) structure. Depending on CNLi–C, the storage sites of Li ions can be classified as follows: (1) Li ions with CNLi–C = 0 exist inside the pore cavity and have an average charge state of +0.36. (2) Li ions with CNLi–C = 1–3 exist on the pore surface and have average charge states ranging from +0.38 to +0.40. (3) Li ions with CNLi–C = 4–9 exist on the pore surface or inside the pore wall and have average charge states ranging from +0.44 to +0.77. (4) Li ions with CNLi–C = 10–14 exist inside the pore wall and have average charge states ranging from +0.84 to +0.86. Li ions with CNLi–C = 4–9 can exist both on the pore surface and inside the pore wall. Using the data in Table 1, the average charge state of all the Li ions with CNLi–C = 1–3 on the pore surface is +0.38, and that of all the Li ions with CNLi–C = 10–14 inside the pore wall is +0.84. Therefore, we assumed that the average charge state (q) of Li ions with CNLi–C = n (n is one of 4, 5, 6, 7, 8, and 9) is equivalent to q = 0.38 × y + 0.84 × (1 − y), where y is the proportion of Li ions on the pore surface, and 1 − y is the proportion of Li ions inside the pore wall. For the Li ions with CNLi–C = 4–9, the proportions y and 1 − y can be determined by substituting the q values in Table 1 into the above equation. As a result, we estimated that about 17%, 45%, and 38% of total Li ions exist inside the pore cavity, on the pore surface, and inside the pore wall, respectively (Table 1). This suggests that about 62% of Li ions contribute to the reversible capacity because they could move relatively freely inside the pore cavity and on the pore surface, whereas about 38% of Li ions contribute to the irreversible capacity because they are virtually trapped inside the pore wall. In zeolite-templated ordered microporous carbon, the reported irreversible capacity (1400 mA h g−1) accounts for 47% of the maximum capacity (2950 mA h g−1).17 We therefore speculate that a large portion of the irreversible capacity reported in the experimental study17 was due to Li ions trapped inside the pore walls in the first cycle.
| CNLi–C | Q | P | P1 | P2 | P3 | Site |
|---|---|---|---|---|---|---|
| a CNα–β represents the number of β atoms around an α atom. The atomic bond is connected when the Li–C distance is within 2.9 Å. q(e) represents the average charge state. P (%) represents the proportion of Li ions. P1 (%), P2 (%), and P3 (%) represent the proportions of Li ions inside the pore cavity, on the pore surface, and inside the pore wall, respectively. The numbers in the last row represent the sum of the values in each column (P, P1, P2, and P3). | ||||||
| 0 | +0.36 | 16.9 | 16.9 | 0 | 0 | Pore cavity |
| 1 | +0.40 | 2.4 | 0 | 2.4 | 0 | Pore surface |
| 2 | +0.38 | 8.7 | 0 | 8.7 | 0 | |
| 3 | +0.38 | 10.1 | 0 | 10.1 | 0 | |
| 4 | +0.44 | 12.0 | 0 | 10.3 | 1.7 | Pore surface + pore wall |
| 5 | +0.59 | 8.9 | 0 | 4.8 | 4.1 | |
| 6 | +0.67 | 8.7 | 0 | 3.3 | 5.4 | |
| 7 | +0.69 | 9.6 | 0 | 3.2 | 6.5 | |
| 8 | +0.76 | 7.9 | 0 | 1.4 | 6.5 | |
| 9 | +0.77 | 5.9 | 0 | 0.9 | 5.0 | |
| 10 | +0.84 | 3.5 | 0 | 0 | 3.5 | Pore wall |
| 11 | +0.84 | 2.9 | 0 | 0 | 2.9 | |
| 12 | +0.85 | 1.7 | 0 | 0 | 1.7 | |
| 13 | +0.86 | 0.7 | 0 | 0 | 0.7 | |
| 14 | +0.86 | 0.1 | 0 | 0 | 0.1 | |
| 100 | 16.9 | 45.1 | 38.0 | |||
The Li storage behaviors of MC-15 and MC-25 are expected to be similar to that of MC-20, because the Bader charge analyses of lithiated MC-15 and MC-25 structures exhibit similar characteristics to those of lithiated MC-20 structures (Fig. S2 and S3†). It is worth noting that the capacity is related to the total pore volume rather than the average pore volume. In the fully lithiated microporous carbon structures, the increasing order of the capacity, that is, MC-20 (2783 mA h g−1) < MC-25 (3006 mA h g−1) < MC-15 (3032 mA h g−1), is in good agreement with the increasing order of the total pore volume, that is, MC-20 (0.53 cm3 g−1) < MC-25 (0.55 cm3 g−1) < MC-15 (0.59 cm3 g−1). By contrast, the increasing order of the capacity is irrelevant to the increasing order of the average pore volume, that is, MC-25 (148.5 Å3) < MC-15 (181.1 Å3) < MC-20 (426.6 Å3). The average pore volume is not related to the total capacity but is related to the reversible capacity. As the average pore volume increases, the amount of Li ions stored in the pore cavities increases, thereby increasing the reversible capacity.
3.5 Diffusion properties of lithiated microporous carbon
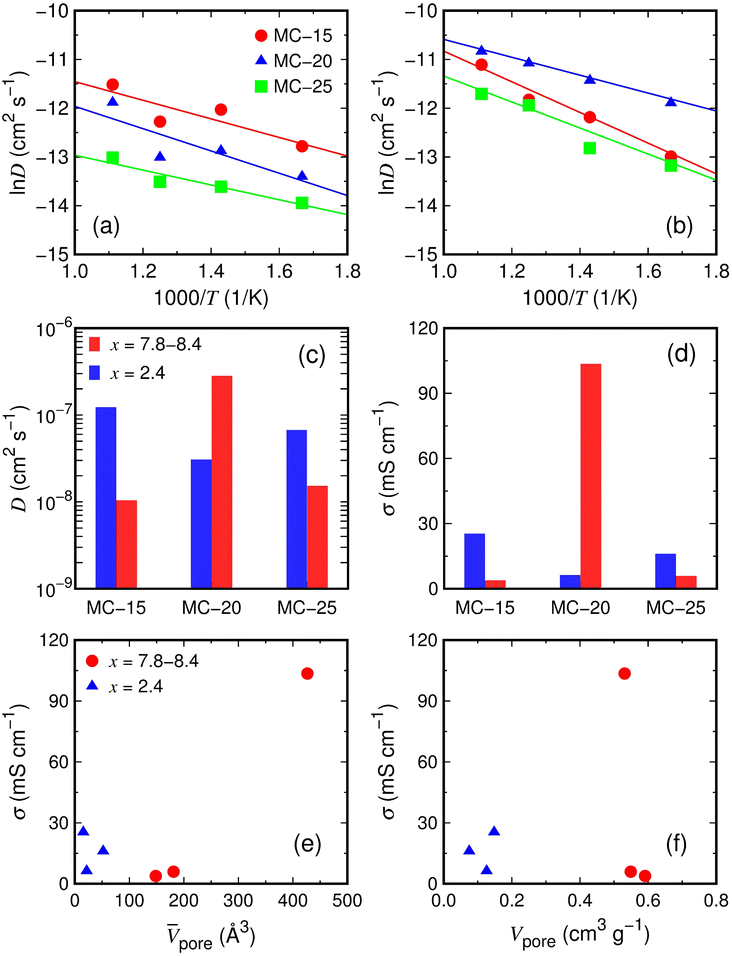
The Li ion transport in lithiated microporous carbon at T = 300 K was examined using AIMD simulations. The Li ion diffusivity (D) at T = 300 K was determined by simulating the partially and fully lithiated microporous carbon structures with the Li2.4C6 and Li7.8–8.4C6 compositions, respectively, for 40 ps at T = 600, 700, 800, and 900 K. The mean-square displacement (dms) of Li ions was calculated as a function of time t at T = 600, 700, 800, and 900 K. The dms curves are almost linear for all structures at these temperatures (Fig. S4 and S5†). The D values at T = 600–900 K were determined using the Einstein relation D = 〈r2(t)〉/6t, where D is the diffusivity, and 〈r2(t)〉 is the mean-square displacement. The D values at T = 600–900 K were used to extrapolate the D value at T = 300 K using the Arrhenius law D = D0 exp(−ED/kBT), where D0 is the pre-exponential factor, ED is the activation energy for diffusion, and kB is the Boltzmann constant. The Arrhenius plots exhibit linear ln(D) variations against the inverse temperature for all structures (Fig. 6a and b).The calculated Li ion diffusivities at T = 300 K are D = 1.23 × 10−7, 3.07 × 10−8, and 6.71 × 10−8 cm2 s−1 for the partially lithiated MC-15 (Li2.4C6), MC-20 (Li2.4C6), and MC-25 (Li2.4C6) structures, respectively (Table 2). The Li ion diffusivities at T = 300 K were used to estimate the Li ion conductivities (σ) based on the Nernst–Einstein relation σ = DNq2/kBT, where N is the carrier density, and q is the carrier charge. The Li ion conductivities are σ = 25.4, 6.3, and 16.0 mS cm−1 for MC-15 (Li2.4C6), MC-20 (Li2.4C6), and MC-25 (Li2.4C6), respectively (Table 2). The Li ion diffusivities at T = 300 K for the fully lithiated MC-15 (Li8.4C6), MC-20 (Li7.8C6), and MC-25 (Li8.4C6) structures are D = 1.04 × 10−8, 2.82 × 10−7, and 1.53 × 10−8 cm2 s−1, respectively (Table 2). The corresponding Li ion conductivities are σ = 3.8, 103.5, and 5.9 mS cm−1 for MC-15 (Li8.4C6), MC-20 (Li7.8C6), and MC-25 (Li8.4C6), respectively (Table 2). The calculated Li ion diffusivities of about 10−8–10−7 cm2 s−1 at x = 2.4 and 7.8–8.4 are generally higher than those for recently reported anode materials for LIBs, such as SiOx/hard carbon nanocomposites (about 10−10–10−9 cm2 s−1),50 P-doped Si (about 10−14–10−13 cm2 s−1),51 and NiNb2O6 (about 10−12 cm2 s−1).52 The Li ion diffusivities and conductivities shown in Fig. 6c and d, respectively, reveal that the diffusivity and conductivity in lithiated microporous carbon do not have a clear dependence on the Li concentration.
| Structure | x | D 0 | D | E D | σ | |
|---|---|---|---|---|---|---|
| a D 0 (cm2 s−1) is the pre-exponential factor, D (cm2 s−1) is the diffusivity at T = 300 K, ED (eV) is the activation energy for diffusion, and σ (mS cm−1) is the conductivity at T = 300 K. | ||||||
| Partially lithiated | MC-15 | 2.4 | 7.14 × 10−5 | 1.23 × 10−7 | 0.16 | 25.4 |
| MC-20 | 2.4 | 6.28 × 10−5 | 3.07 × 10−8 | 0.20 | 6.3 | |
| MC-25 | 2.4 | 1.07 × 10−5 | 6.71 × 10−8 | 0.13 | 16.0 | |
| Fully lithiated | MC-15 | 8.4 | 4.88 × 10−4 | 1.04 × 10−8 | 0.28 | 3.8 |
| MC-20 | 7.8 | 1.66 × 10−4 | 2.82 × 10−7 | 0.16 | 103.5 | |
| MC-25 | 8.4 | 1.95 × 10−4 | 1.53 × 10−8 | 0.24 | 5.9 | |
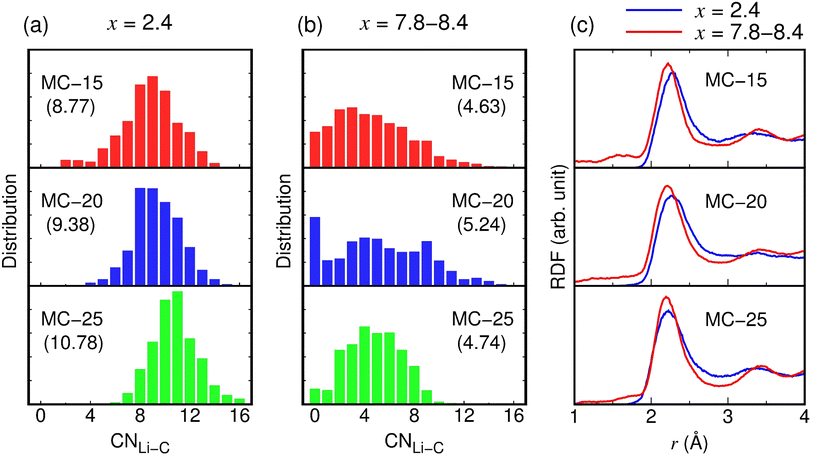
The conductivity (103.5 mS cm−1) of the fully lithiated MC-20 (Li7.8C6) structure is considerably higher than those (3.8–25.4 mS cm−1) of other MC (Li2.4C6 and Li8.4C6) structures. The high conductivity of the MC-20 (Li7.8C6) structure is partly due to the high Li concentration of x = 7.8 but primarily due to the average pore volume of 426.6 Å3, which is much larger than those (15.5–181.1 Å3) of other MC structures with x = 2.4 and 8.4 (Fig. 6e). Although the conductivity is not linearly proportional to the average pore volume (Fig. 6e), the large average pore volume of the MC-20 structure with x = 7.8 significantly contributes to the high conductivity. If individual pores are large, some Li ions in the pore cavities can move freely and rapidly because they are not in contact with carbon atoms on the pore wall surface and skip the process that has to break bonds with carbon atoms during diffusion. This scenario is supported by the distribution histograms of CNLi–C (Fig. 7a and b). In the MC structures with x = 2.4 and 7.8–8.4, Li ions have CNLi–C = 0–16. Fig. 7a shows that Li ions with CNLi–C = 9, 8, and 11 are most abundant in the MC-15, MC-20, and MC-25 structures with x = 2.4, respectively, and Fig. 7b shows that those with CNLi–C = 3 and 4 are most abundant in the MC-15 and MC-25 structures with x = 8.4, respectively. By contrast, Li ions with CNLi–C = 0 are most abundant in the MC-20 structure with x = 7.8 (Fig. 7b), implying that they exist in the middle of the large pores and diffuse rapidly without being disturbed by carbon atoms. The high conductivity of the MC-20 (Li7.8C6) structure appears to be irrelevant to the total pore volume, because the total pore volume (0.53 cm3 g−1) of the MC-20 (Li7.8C6) structure is slightly lower than those (0.55–0.59 cm3 g−1) of the MC-15 (Li8.4C6) and MC-25 (Li8.4C6) structures exhibiting much lower conductivities (Fig. 6f).
As shown in Fig. 6e, despite having larger average pore volumes, the MC-15 and MC-25 structures with x = 8.4 show slightly lower conductivities than the MC-15, MC-20, and MC-25 structures with x = 2.4. This result seems to be related to the Li–C bond strength. Due to the smaller average CNLi–C in x = 8.4 than in x = 2.4 (see parentheses in Fig. 7a and b), Li ions in the MC structures with x = 8.4 have shorter Li–C bond lengths than those in the MC structures with x = 2.4. In the RDFs of the Li–C pair, the first-peak positions of 2.20–2.22 Å in the MC structures with x = 8.4 are lower by 0.01–0.09 Å than those of 2.23–2.29 Å in the MC structures with x = 2.4 (Fig. 7c), indicating stronger Li–C bonds in the MC structures with x = 8.4. The strong Li–C bonds are detrimental to fast Li ion diffusion, as Li ions diffuse by breaking bonds with the surrounding carbon atoms.
3.6 Motion of individual Li ions in lithiated microporous carbon
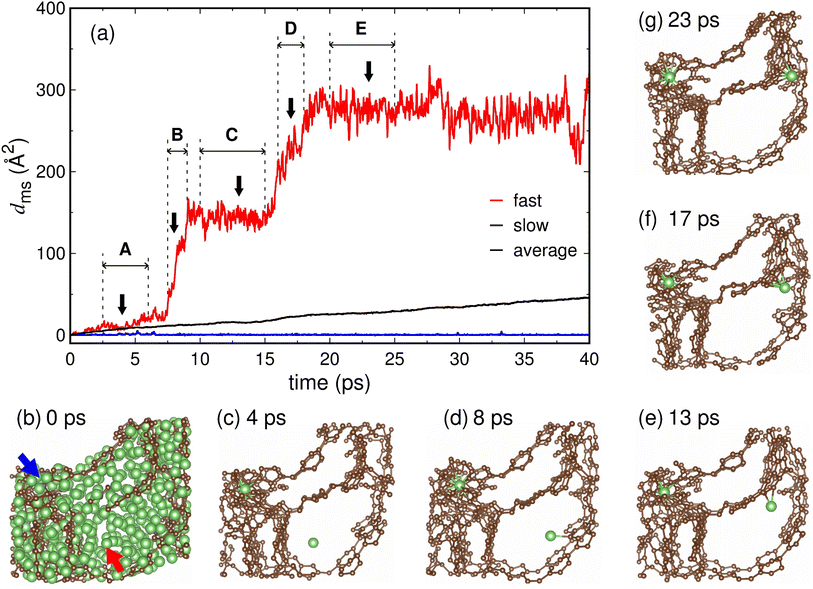
We examined in detail the movement of individual Li ions in the fully lithiated MC-20 (Li7.8C6) structure. The dms curves of fast- and slow-moving Li ions obtained from the AIMD simulation of MC-20 for 40 ps at T = 900 K are shown in Fig. 8a. Whereas the curve of the slow Li ion is virtually flat over time and shows dms values of less than 6 Å2, the curve of the fast Li ion has a step-like shape with dms values of up to about 330 Å2. The fast and slow Li ions exist inside the pore cavity and wall, respectively, at 0 ps (see the red and blue arrows in Fig. 8b). The Li ion inside the pore wall hardly moves over time (Fig. 8b–g), thus responsible for the flat dms curve of the slow Li ion in Fig. 8a. By contrast, the Li ion inside the pore cavity travels a much greater distance than that inside the pore wall (Fig. 8b–g). Thus, the high Li ion conductivity of the fully lithiated MC-20 structure results mainly from the movement of Li ions in the pore cavities. This is evidenced by the average dms curve of all Li ions, which is much closer to the dms curve of the slow Li ion inside the pore wall than the fast Li ion inside the pore cavity (Fig. 8a). Fig. 8 demonstrates that mobile Li ions inside the pore cavities and immobile Li ions inside the pore walls are responsible for the reversible and irreversible capacities of microporous carbon, respectively.The dramatic difference in Li ion motion between the pore cavity and wall is associated with the coordination numbers. Whereas the Li ion inside the pore wall has CNLi–Li = 5.15 and CNLi–C = 12.52, that inside the pore cavity has CNLi–Li = 10.41 and CNLi–C = 3.32 (Table 3). The Li ions inside the pore cavity and wall have Li-to-C ratios of 3.14 and 0.41, respectively, in their surrounding atomic environments (Table 3). The Li ion inside the pore wall has a C-rich environment and should break bonds with attractive carbon atoms to escape from the pore wall, whereas the Li ion inside the pore cavity has a Li-rich environment and is relatively free to move. The Li ion inside the pore cavity has a Li–C bond length of dLi–C = 2.36 Å, which is shorter by 0.07 Å than that (2.43 Å) for the Li ion inside the pore wall (Table 3). The short (and therefore strong) Li–C bonds hinder fast Li ion diffusion, as discussed in Section 3.5, but Li–C bonds are formed when the Li ion approaches the pore wall. The Li ion initially present in the pore cavity rarely encounters carbon atoms until it approaches the pore wall; thereby, its diffusion is not prevented by carbon atoms while present in the pore cavity.
| X | Fast Li (pore cavity) | Slow Li (pore wall) | |
|---|---|---|---|
| a The atomic bonds are connected when the Li–Li and Li–C distances are within 3.4 and 2.9 Å, respectively. Values in parentheses indicate Li-to-C ratios. | |||
| CNLi–X | Li | 10.41 | 5.15 |
| C | 3.32 | 12.52 | |
| (3.14) | (0.41) | ||
| d Li–X (Å) | Li | 2.79 | 2.73 |
| C | 2.36 | 2.43 | |
The motion of the Li ion in the pore cavity was closely observed during different periods A, B, C, D, and E (Fig. 8a). During the period of A (2.5–6.0 ps), the Li ion moves inside the pore cavity without forming bonds with carbon atoms (Fig. 8c and Table 4). During period B (7.5–9.0 ps), the Li ion moves suddenly to the pore wall by the attraction of carbon atoms, resulting in a steep slope in the dms curve (Fig. 8a), and begins to form bonds with carbon atoms on the pore wall surface (Fig. 8d and Table 4). During period C (10.0–15.0 ps), the Li ion adsorbed on the pore wall surface forms two bonds with carbon atoms (Fig. 8e and Table 4) and vibrates strongly on the surface (Fig. 8a). During period D (16.0–18.0 ps), the Li ion begins to enter the pore wall, forming five or six bonds with the carbon atoms (Fig. 8f and Table 4). This process occurs rapidly because many carbon atoms strongly attract the Li ion, resulting in a sharp increase in the dms curve (Fig. 8a). During period E (20.0–25.0 ps), the Li ion remains in the subsurface region of the pore wall and vibrates violently while maintaining four or five bonds with the carbons (Fig. 8g and Table 4). The calculated Li-to-C ratios in periods B, C, D, and E are 13.54, 5.57, 1.53, and 2.22, respectively (Table 4), indicating that the Li-to-C ratio generally decreases as the Li ion moves from the pore cavity to the pore wall. The Li ion during periods D and E has low Li-to-C ratios of 1.53 and 2.22, but these values are still higher than that (0.41) for the slow Li ion embedded in the pore wall (see the blue arrow in Fig. 8b). Our analyses in Fig. 8 and Table 3 and 4 suggest that the Li-to-C ratio around Li is an important factor affecting the movement of individual Li ions. As the Li-to-C ratio increases, Li ions move freely and contribute to the conductivity, but as the Li-to-C ratio decreases, Li ions become immobile Li ions (or kinetically lost Li ions).
| X | A | B | C | D | E | |
|---|---|---|---|---|---|---|
| a Values in parentheses indicate Li-to-C ratios. | ||||||
| CNLi–X | Li | 11.77 | 11.24 | 11.19 | 8.77 | 10.12 |
| C | — | 0.83 | 2.01 | 5.74 | 4.55 | |
| (13.54) | (5.57) | (1.53) | (2.22) | |||
| d Li–X (Å) | Li | 2.81 | 2.75 | 2.78 | 2.77 | 2.79 |
| C | — | 2.48 | 2.17 | 2.36 | 2.36 | |
3.7 Discussion
This study of the lithiation of microporous carbon suggested that a large total pore volume could increase the total capacity and that a large average pore volume could increase the reversible capacity and conductivity. Therefore, a microporous carbon structure composed of large and uniform micropores is expected to deliver superior performance in terms of lithium storage and transport. However, too large pore size may be detrimental to thermal stability at high current densities as it can promote the growth of lithium dendrites and eventually lead to thermal runaway.53,54 The optimal size of uniform micropores needs to be determined through elaborate experimental investigations. Our microporous carbon structures with initial densities of 1.5–2.5 g cm−3 showed volume expansion ratios of 77.3–180.6% upon full lithiation, and the volume expansion ratio decreased with decreasing initial density. It is thus desirable that the initial density of the microporous carbon structure be less than 1.5 g cm−3, because large volume expansion of the electrode can decrease the cycle stability. The observed difficult diffusion of the Li ions embedded inside the pore walls suggests that they are responsible for irreversible capacities. To minimize the amount of Li ions entering the pore walls during lithiation, it is necessary to prepare a microporous carbon structure with stable pore surfaces that exhibit low reactivity toward Li ions. In the end, the factors affecting the reversibility of lithium storage in microporous carbon are the storage sites of Li ions, the average pore size, and the reactivity between Li ions and the pore surface.4. Conclusion
The present first-principles study has demonstrated that microporous carbon provides excellent lithium storage ability and fast lithium-ion transport. Microporous carbon structures with initial densities of 1.5, 2.0, and 2.5 g cm−3 deliver considerably high capacities of 3032, 2783, and 3006 mA h g−1, respectively. In fully lithiated microporous carbon, about 62% of Li ions are present inside the pore cavity and on the pore surface, responsible for reversible capacity, and about 38% of Li ions are present inside the pore wall, responsible for irreversible capacity. The total pore volume and average pore volume of lithiated microporous carbon are related to total capacity and reversible capacity, respectively. During lithiation, the total pore volumes of microporous carbon structures with different initial densities become similar, but their average pore volumes can grow differently depending on the extent to which Li ions locally disrupt the carbon network. The calculated Li ion conductivities are as high as 6.3–25.4 and 3.8–103.5 mS cm−1 for the Li2.4C6 and Li7.8–8.4C6 compositions, respectively. The highest conductivity of 103.5 mS cm−1 is achieved for the largest average pore volume, and thereby, the average pore volume is related to the conductivity. Li ions can diffuse rapidly inside Li-rich pore cavities, suggesting that the Li-to-C ratio around Li is an important factor influencing Li ion motion. Our discussion of the pore structure, pore size, carbon density, and pore surface of microporous carbon will serve as a useful guide for experimental researchers in developing efficient microporous carbon electrodes for lithium-ion batteries.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by a research grant of Pukyong National University (2021).References
- S. Chen, L. Qiu and H. M. Cheng, Chem. Rev., 2020, 120, 2811–2878 CrossRef CAS PubMed.
- M. M. Titirici, R. J. White, N. Brun, V. L. Budarin, D. S. Su, F. Del Monte, J. H. Clark and M. J. MacLachlan, Chem. Soc. Rev., 2015, 44, 250–290 RSC.
- Z. Peng, X. Liu, W. Zhang, Z. Zeng, Z. Liu, C. Zhang, Y. Liu, B. Shao, Q. Liang, W. Tang and X. Yuan, Environ. Int., 2020, 134, 105298 CrossRef CAS PubMed.
- J. Duan, X. Tang, H. Dai, Y. Yang, W. Wu, X. Wei and Y. Huang, Electrochem. Energy Rev., 2020, 3, 1–42 CrossRef CAS.
- X. Li, X. Sun, X. Hu, F. Fan, S. Cai, C. Zheng and G. D. Stucky, Nano Energy, 2020, 77, 105143 CrossRef CAS.
- M. S. Balogun, Y. Luo, W. Qiu, P. Liu and Y. Tong, Carbon, 2016, 98, 162–178 CrossRef CAS.
- L. Chen, H. Yu, W. Li, M. Dirican, Y. Liu and X. Zhang, J. Mater. Chem. A, 2020, 8, 10709–10735 RSC.
- P. Wang, Y. Ren, R. Wang, P. Zhang, M. Ding, C. Li, D. Zhao, Z. Qian, Z. Zhang, L. Zhang and L. Yin, Nat. Commun., 2020, 11, 1576 CrossRef CAS PubMed.
- J. Wu, Y. Cao, H. Zhao, J. Mao and Z. Guo, Carbon Energy, 2019, 1, 57–76 CrossRef CAS.
- S. Zhao, Y. He, Z. Wang, X. Bo, S. Hao, Y. Yuan, H. Jin, S. Wang and Z. Lin, Adv. Energy Mater., 2022, 12, 2201015 CrossRef CAS.
- S. Zhao, C. D. Sewell, R. Liu, S. Jia, Z. Wang, Y. He, K. Yuan, H. Jin, S. Wang, X. Liu and Z. Lin, Adv. Energy Mater., 2020, 10, 1902657 CrossRef CAS.
- S. Zhao, Z. Wang, Y. He, H. Jiang, Y. W. Harn, X. Liu, C. Su, H. Jin, Y. Li, S. Wang, Q. Shen and Z. Lin, Adv. Energy Mater., 2019, 9, 1901093 CrossRef.
- A. D. Roberts, X. Li and H. Zhang, Chem. Soc. Rev., 2014, 43, 4341–4356 RSC.
- X. Zheng, J. Luo, W. Lv, D. W. Wang and Q. H. Yang, Adv. Mater., 2015, 27, 5388–5395 CrossRef CAS PubMed.
- W. Tian, H. Zhang, X. Duan, H. Sun, G. Shao and S. Wang, Adv. Funct. Mater., 2020, 30, 1909265 CrossRef CAS.
- Y. He, X. Zhuang, C. Lei, L. Lei, Y. Hou, Y. Mai and X. Feng, Nano Today, 2019, 24, 103–119 CrossRef CAS.
- J. Yin, W. Zhang, N. A. Alhebshi, N. Salah and H. N. Alshareef, Small Methods, 2020, 4, 1–31 Search PubMed.
- G. Singh, K. S. Lakhi, S. Sil, S. V. Bhosale, I. Y. Kim, K. Albahily and A. Vinu, Carbon, 2019, 148, 164–186 CrossRef CAS.
- H. Liu, X. Liu, W. Li, X. Guo, Y. Wang, G. Wang and D. Zhao, Adv. Energy Mater., 2017, 7, 1–24 Search PubMed.
- K. Zhang, Z. Hu and J. Chen, J. Energy Chem., 2013, 22, 214–225 CrossRef CAS.
- Y. Kwon, K. Kim, H. Park, J. W. Shin and R. Ryoo, J. Phys. Chem. C, 2018, 122, 4955–4962 CrossRef CAS.
- J. Hu, Z. Xu, X. Li, S. Liang, Y. Chen, L. Lyu, H. Yao, Z. Lu and L. Zhou, J. Power Sources, 2020, 462, 228098 CrossRef CAS.
- Y. Xi, S. Huang, D. Yang, X. Qiu, H. Su, C. Yi and Q. Li, Green Chem., 2020, 22, 4321–4330 RSC.
- Y. Lu, Q. Zhang, S. Lei, X. Cui, S. Deng and Y. Yang, ACS Appl. Energy Mater., 2019, 2, 5591–5599 CrossRef CAS.
- Y. E. Miao, Y. Huang, L. Zhang, W. Fan, F. Lai and T. Liu, Nanoscale, 2015, 7, 11093 RSC.
- L. Shi, Y. Chen, G. Chen, Y. Wang, X. Chen and H. Song, Carbon, 2017, 123, 186–192 CrossRef CAS.
- L. Wang, J. Ju, N. Deng, B. Cheng and W. Kang, Mater. Lett., 2019, 240, 39–43 CrossRef CAS.
- T. Yang, R. Zhou, D. W. Wang, S. P. Jiang, Y. Yamauchi, S. Z. Qiao, M. J. Monteiro and J. Liu, Chem. Commun., 2015, 51, 2518–2521 RSC.
- M. E. Suss, T. F. Baumann, M. A. Worsley, K. A. Rose, T. F. Jaramillo, M. Stadermann and J. G. Santiago, J. Power Sources, 2013, 241, 266–273 CrossRef CAS.
- K. Kim, T. Lee, Y. Kwon, Y. Seo, J. Song, J. K. Park, H. Lee, J. Y. Park, H. Ihee, S. J. Cho and R. Ryoo, Nature, 2016, 535, 131–135 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 2020, 54, 11169–11186 CrossRef PubMed.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B, 1994, 49, 16223–16233 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- X. Li, A. Wang and K. R. Lee, Comput. Mater. Sci., 2018, 151, 246–254 CrossRef CAS.
- F. Legrain, J. Sottmann, K. Kotsis, S. Gorantla, S. Satori and S. Manzhos, J. Phys. Chem. C, 2015, 119, 13496–13501 CrossRef CAS.
- M. Pinheiro, R. L. Martin, C. H. Rycroft, A. Jones, E. Iglesia and M. Haranczyk, J. Mol. Graphics Modell., 2013, 44, 208–219 CrossRef CAS PubMed.
- S. Le Roux and P. Jund, Comput. Mater. Sci., 2010, 49, 70–83 CrossRef CAS.
- S. Lee, S. C. Jung and Y. K. Han, J. Power Sources, 2019, 415, 119–125 CrossRef CAS.
- S. Lee, M. Ko, S. C. Jung and Y. K. Han, ACS Appl. Mater. Interfaces, 2020, 12, 55746–55755 CrossRef CAS PubMed.
- S. C. Jung, J. H. Choi and Y. K. Han, J. Mater. Chem. A, 2018, 6, 1772–1779 RSC.
- G. M. Pharr, D. L. Callahan, S. D. McAdams, T. Y. Tsui, S. Anders, A. Anders, J. W. Ager, I. G. Brown, C. S. Bhatia, S. R. P. Silva and J. Robertson, Appl. Phys. Lett., 1995, 68, 779 CrossRef.
- J. Robertson, Adv. Phys., 1986, 35, 317–374 CrossRef CAS.
- A. C. Ferrari, A. Libassi, B. K. Tanner, V. Stolojan, J. Yuan, L. M. Brown, S. E. Rodil, B. Kleinsorge and J. Robertson, Phys. Rev. B, 2000, 62, 11089–11103 CrossRef CAS.
- X. Du, S. W. Tsai, D. L. Maslov and A. F. Hebard, Phys. Rev. Lett., 2005, 94, 166601 CrossRef PubMed.
- R. Sengupta, M. Bhattacharya, S. Bandyopadhyay and A. K. Bhowmick, Prog. Polym. Sci., 2011, 36, 638–670 CrossRef CAS.
- N. Kim, S. Chae, J. Ma, M. Ko and J. Cho, Nat. Commun., 2017, 8, 812 CrossRef PubMed.
- B. Ng, X. Peng, E. Faegh and W. E. Mustain, J. Mater. Chem. A, 2020, 8, 2712–2727 RSC.
- H. Pang, P. Yu, F. Xu, W. Zhang, J. Peng, H. Hu, M. Zheng, Y. Xiao, Y. Liu and Y. A. Liang, J. Mater. Chem. A, 2020, 8, 25382–25389 RSC.
- J. K. Dora, D. Nayak, S. Ghosh, V. Adyam, N. Yelda and T. K. Kundu, Energy Fuels, 2020, 4, 6054–6065 CAS.
- B. Long, Y. Zou, Z. Li, Z. Ma, W. Jiang, H. Zou and H. Chen, ACS Appl. Energy Mater., 2020, 3, 5572–5580 CrossRef CAS.
- R. Xia, K. Zhao, L. Y. Kuo, L. Zhang, D. M. Cunha, Y. Wang, S. Huang, J. Zheng, B. Boukamp, P. Kaghazchi, C. Sun, J. E. Elshof and M. Huijben, Adv. Energy Mater., 2022, 12, 2102972 CrossRef CAS.
- M. Zhu, J. Wu, W. H. Zhong, J. Lan, G. Sui and X. Yang, Adv. Energy Mater., 2018, 8, 1702561 CrossRef.
- Y. Wang, S. Wang, J. Fang, L. X. Ding and H. Wang, J. Membr. Sci., 2017, 537, 248–254 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2na00621a |
| This journal is © The Royal Society of Chemistry 2022 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)