Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Machine learning in electron microscopy for advanced nanocharacterization: current developments, available tools and future outlook
Marc
Botifoll
 a,
Ivan
Pinto-Huguet
a and
Jordi
Arbiol
a,
Ivan
Pinto-Huguet
a and
Jordi
Arbiol
 *ab
*ab
aCatalan Institute of Nanoscience and Nanotechnology (ICN2), CSIC and BIST, Campus UAB, Bellaterra, 08193 Barcelona, Catalonia, Spain. E-mail: arbiol@icrea.cat
bICREA, Pg. Lluís Companys 23, 08010 Barcelona, Catalonia, Spain
First published on 14th October 2022
Abstract
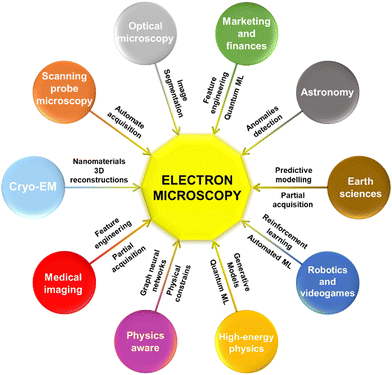
In the last few years, electron microscopy has experienced a new methodological paradigm aimed to fix the bottlenecks and overcome the challenges of its analytical workflow. Machine learning and artificial intelligence are answering this call providing powerful resources towards automation, exploration, and development. In this review, we evaluate the state-of-the-art of machine learning applied to electron microscopy (and obliquely, to materials and nano-sciences). We start from the traditional imaging techniques to reach the newest higher-dimensionality ones, also covering the recent advances in spectroscopy and tomography. Additionally, the present review provides a practical guide for microscopists, and in general for material scientists, but not necessarily advanced machine learning practitioners, to straightforwardly apply the offered set of tools to their own research. To conclude, we explore the state-of-the-art of other disciplines with a broader experience in applying artificial intelligence methods to their research (e.g., high-energy physics, astronomy, Earth sciences, and even robotics, videogames, or marketing and finances), in order to narrow down the incoming future of electron microscopy, its challenges and outlook.
1. Introduction
Machine Learning (ML) has been a core partner for the scientific and technical breakthroughs of the last decade in multiple fields, ranging from the less obvious finances to the fundaments of robotics. It is ubiquitous in a huge variety of scientific fields, providing both tools for automating processes and knowledge-revealing algorithms exploitable without a deep computer science background. Among many others, Electron Microscopy (EM) is a valuable example of how ML is and will be providing a solid framework for the upcoming advances. This review intends to compile and highlight the most important and recent advances in Transmission Electron Microscopy (TEM) in which ML has had a key role in the scientific discussion. Additionally, we discuss the future perspectives of ML in EM and how the cross-fertilization with other fields can expand the experimental setups to a yet unexplored domain. From astrophysics, where imaging distant galaxies or searching for black matter generates terabytes per second, to high-energy physics, where the particle colliders can hide particle interactions in a noisy background. From cryo-TEM to the broad window of optical microscopy techniques, to even geological sciences, robotics, epidemiology dynamics or finances. For already many years, these fields have in common that they have fed from machine learning to solve manifold scientific and technical challenges. Therefore, the potential of EM to mirror the progress done in these fields to solve its own future challenges is real, straightforward, and worth a review. This reading is mainly intended for the broad EM and materials science communities, although general microscopy or even data analysis communities may also find useful and mind-broadening approaches to their hurdles. Next section details the progress of ML applied to imaging techniques ranging from traditional parallel-beam TEM or Scanning TEM (STEM) to more recent breakthroughs such as 4D-STEM. TEM spectroscopies and their ML-based applications are discussed in this section as well. After this first part, the section that follows is intended as a pragmatic guide for the community newcomers to provide them with useful (mostly open-source) tools and state-of-the-art computational frameworks developed to apply ML to experimental datasets in a general and less case-dependant basis. Finally, the last part of this review correlates EM with other fields by exploring experiments and data analysis routines that could easily be transferred from one to another to enrich both tackled ecosystems, therefore revealing an accurate scope of the direction ML applied to EM is going to follow in the next few years.2. Electron microscopy advances with machine learning
2.1. Most important imaging developments: from 2D images to 4D-STEM
Nevertheless, just recently more complex supervised methods are emerging and showing their potential to push the current methods forward.18–20 Generally, supervised ML, specially Deep Learning (DL), aims to mimic human-level operation by finding complex regressions that adapt to the data. Instead, unsupervised ML is the preferred choice when an exploratory approach based on unveiling the internal data structure is needed, although it is still useful for application engineering to provide a more versatile but typically less general performance than supervised solutions. The pros and cons of each approach are more detailed in the next section and extensively throughout the review. In fact, the denoising ideas tackled by unsupervised approaches are being explored from the supervised perspective and beyond. C. Lee et al. could increase the Signal-to-Noise Ratio (SNR) in an annular dark-field STEM image of a single-atom defect and measure the strain field around it by training a Fully Convolutional Neural Network (FCNN) on different defect types.21 Then, the initially hidden-by-noise but theoretically predicted strain field could only be measured after this key postprocessing step. This was because FCNN are primarily designed to find shared patterns in image sets.
The successful proofs of concept made additional denoising alternatives arise, including a denoising–noising Generative Adversarial Network (GAN) for the active denoising of STEM data (Fig. 2 GAN)22–24 or case-independent denoising models that successfully outperformed classical restoration filters for both TEM and STEM.23,25–31 Interestingly J. Vincent et al. studied the latent features learned by the DL model to unveil the nature of the trained denoising dependencies to shine light on what is typically left as a black box. They showed that the FCNN learns to adapt its filtering strategies depending on the structural properties of every particular region in the image.26–28 Importantly, ML-based noise reduction methods also reached niche EM experimental approaches such as electron holography. This latest example highlights the significance that the ML-based methodology may eventually have in the field and how broad it might be. Electron holography has also benefited from ML-based noise reduction methods. For instance, ML has been used to obtain the accurate phase estimation at low SNR, which flattened the path towards the low-dose holography analysis of beam-sensitive materials by training a sparse coding model on simulations.32–34
On the other hand, computer vision routines for automating the electron microscope alignments have already been reported in order to fine-tune the (S)TEM acquisition process. The first approaches, mainly lead by microscope manufacturers, were based on automating the column (fine) alignments through. For instance, solutions for the automatic aberration correction, or the aberration-free converge angle maximisation are available both through manufacturers and in the literature (Fig. 1a).35–37 In fact, recent results exploit these provided tools to automate the detection of features of interest in the TEM and their online classification by Few-Shot Learning (FSL).38 FSL is a sub-area of supervised ML, where new data is classified, despite models are trained with only a few training samples. Meaningfully, K. Roccapriore et al. could automate the dynamic STEM exploration and EELS acquisition, through training a deep kernel capable of actively distinguishing physically-significant regions.39 However, acquisition and alignment automation are not limited to experiment optimisation, and was key to open unprecedented experimental setups impossible otherwise. In that sense, E. Rotunno et al. trained a CNN to align an orbital angular momentum sorter in the context of beam shaping experiments. The authors demonstrated a high accuracy and computational speed in estimating the aberrations induced by the sorter. Such a performance opened the possibility to implement this methodology to every optical system and aberration corrector in the electron microscope for real-time self-alignment.40–44 Parallelly, optical microscopy on, for example, the real-time estimation of the wavefront aberration, and Scanning Probe Microscopies (SPM) on thoroughly autonomous experimental setups, are setting the basis for the automation of more complex microscopy setups.43–51 These meaningful results, though, constitute nothing but baby steps towards an eventual and highly anticipated fully automated TEM, which is where ML is called to play a pilar role in skyrocketing its advances in the next decade.52,53 To achieve this, the industry-science cross-fertilisation will be mandatory to open the microscopes up for implementing the research community advances in a user-friendly manner. Moreover, it is our community's duty to validate open and universal data formats to push their support by the companies.54,55
 | ||
| Fig. 1 The two main trends of Machine Learning (ML) for Electron Microscopy (EM): (a) representing the automation of the microscope tuning and data acquisition, and (b) showing the potential of ML in advanced data analysis. (a) Research work from JEOL devoted to the automatic measurement and correction of aberrations through Ronchigram ML analysis. Each column is linked to a different defocus. The top and bottom rows display simulated Ronchigrams with aberrations determined manually (top) or by a Convolutional Neural Network (CNN) (bottom), while the mid row corresponds to the experimentally equivalent ones.37 R. Sagawa et al., Microsc. Microanal., 2021, 27, 814–816, reproduced with permission. (b) Diagram of a CNN trained to count the atoms of an atomic column in gold nanoparticles. The CNN admits both single images and focal series as inputs to classify every atomic column by setting, in the depicted case, a probability (PX) of containing from 1 (P0) to 6 (P5) atoms.66 Reproduced with permission of J. Madsen et al., Adv. Theory Simulat., 2018, 1, 1–12 Copyright 2018 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
However, the current bottleneck of the workflow lies in the analysis of the acquired data, not in the acquisition itself. Therefore, most of the current efforts are pushing towards the automated analysis and ML-based knowledge extraction. For instance, CNNs have widely emerged as excellent tools for the identification, classification, and quantification of defects in EM data. In this way, there is an abundant and successful enough literature to constitute a strong enough basis to conglomerate a starting unitary and general Artificial Intelligence (AI) model that would replace the human intervention in this specific characterisation task. The first studies faced the preliminary complexity of 2D materials in STEM, which allowed the direct correlation between image and structure.56–58 M. Ziatdinov et al. trained an encoder–decoder FCNN to detect the atomic coordinates of Si-doped graphene. Importantly, the trained model proved its ability to adapt to another 2D system, Mo1−xWxSe2, showing a generalised performance. Moreover, the authors converted the outputted atomic coordinates into graphs (i.e., atoms as the graph nodes, with the chemical bonds being the links) for the automated classification of the Si dopants (namely, point defects) based on their bonding with neighbouring Si and C atoms (Fig. 2 CNN).59,60 This idea has extensively been reproduced in further research in similar 2D systems by taking advantage of the monotonic (with the atomic weight and thickness) dark-field STEM signal.21,61–64 On the other hand, tackling harder to interpret signal, J. Madsen et al. trained a similar FCNN architecture65 on High-Resolution TEM (HRTEM) simulated micrographs, including focal series and therefore phase information, to identify the atomic coordinates of graphene and count atoms in gold nanoparticles (Fig. 1b).66 This core idea extended the analysis of HRTEM defects data further to surface contaminants on more complex graphene configurations or to quantitative atom counting in Au nanoparticles.2,4,66,67
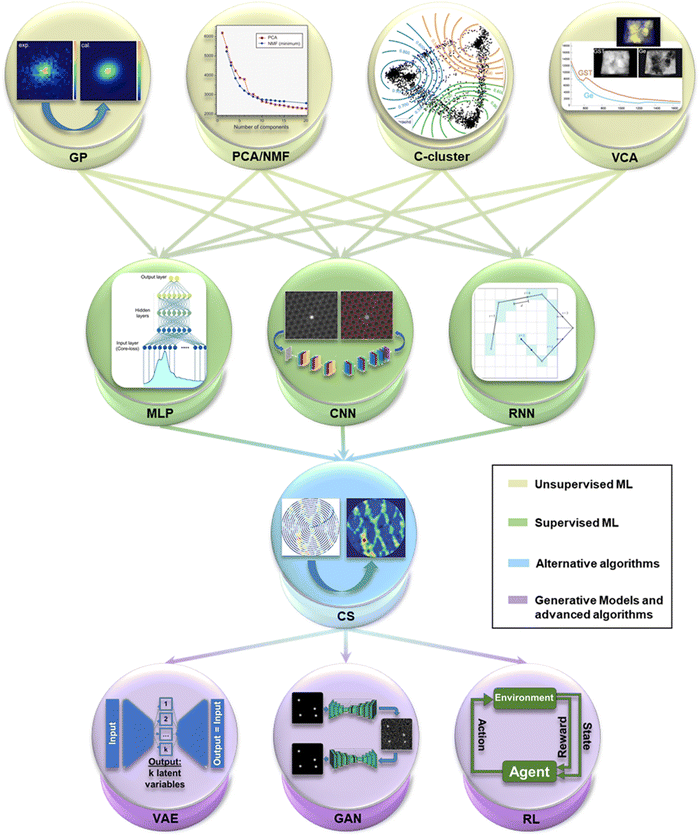 | ||
| Fig. 2 A selection of the key Machine Learning (ML) methods most recurrently employed in Electron Microscopy (EM) imaging and spectroscopy. The first layer contains the first ML techniques that arose in EM, unsupervised methods, consisting of Gaussian Processing14 (GP), Principal Component Analysis and Non-negative Matrix Factorisation100 (PCA/NMF) (reprinted from F. Uesugi et al., Ultramicroscopy, 2021, 221, 113168 Copyright 2021 with permission from Elsevier), fuzzy c-clustering78 (C-cluster), Vertex Component Analysis101 (VCA) (M. Jacob et al., Microsc. Microanal., 2019, 25(suppl. 2), 156–157, reproduced with permission), among others. The evolution in complexity leads to the second layer of supervised techniques, with MultiLayer Perceptron102 (MLP), and Convolutional Neural Networks59 (CNN) (adapted with permission from M. Ziatdinov et al., ACS Nano, 2017, 11(12), 12742–12752 Copyright 2017 American Chemical Society) and Recurrent NN103 (RNN). The third layer stands for Compressed Sensing104 (CS) (reproduced with permission of K. Kelley et al., Small, 2020, 2002878 Copyright 2020 Willey-VCH GmbH), a group of alternative algorithms with powerful compatibility with ML. Finally, the last layer outputs the future of ML in EM in the use of generative models like Variational AutoEncoders (VAE) and Generative Adversarial Networks22 (GAN), and more complex learning paradigms such as Reinforcement Learning (RL). | ||
The next step in complexity comprises the defect detection in 3D systems. For this, the available research is sparser and mostly presenting a theoretical scope. The proofs of concept are in relatively simple systems such as zinc blende GaAs, and for seeing its future steps it will certainly be of interest to resemble the progress lastly achieved in SPM with more complex 3D systems, just as expected with the self-driven experiments.68–70 As a result, we see an outstanding opportunity for pushing the state-of-the-art defect detection to a broader spectrum of 3D systems. To achieve this, CNN combined with unsupervised clustering or anomaly detection methods seem to be the way to go. We envision that this general model will also include the identification of planar defects and dislocations, both in an atomistic nature, and in a more macroscopic or industrially-oriented basis.71–73
2.1.2.1 Unsupervised exploratory routines. As mentioned earlier, the path of unsupervised ML in EM started with the multivariate analysis of EELS spectra, mainly aimed for noise reduction.11,12,16 Since the very first nearest neighbour algorithm that aimed to find the shortest path to interconnect data points, unsupervised learning has rapidly grown in popularity in manifold ways and fields. Its strongest virtue is the absence of training process, making its easy access and implementation its key to success. Although the main drawback of unsupervised routines is their lack of robustness when aiming for general models, they can provide an excellent platform for exploring specific imaged systems.
Unsupervised ML on imaging techniques followed the logical path started by the multivariate analysis of spectra. Principal Component Analysis (PCA) constitutes the most straightforward dimensionality reduction and data decomposition available, allowing both data cleaning and classification. Nevertheless, it can also be key in the core of more intricate routines. PCA can map the crystal phases and defects, such as twins or phase boundaries, in encoded dichalcogenide (i.e., MoSe2 and WS2) micrographs with rotational-invariance (i.e., independently of their in-(image) plane rotation).56,75 The main drawback of PCA is its pure mathematical nature and the inability to directly correlate the obtained results with a physical interpretation. This is why alternative physically-constrained methods arose. For instance, ensuring every component is thoroughly positive in its domain with Non-negative Matrix Factorisation (NMF). For instance, R. Kannan et al. tested NMF in spectral data generated by multimodal STEM and X-ray Diffraction (XRD).58 The authors generated a hyperspectral dataset from the sliding window Fast Fourier Transform (FFT) of a single atomically resolved STEM image. Then, they mapped the crystallographic phase by assigning a phase to each meaningful NMF component extending the previous PCA approach further.58,73,76,77 Similarly, B. Martineau et al. also applied NMF, combining it with fuzzy c-means clustering (i.e., assigning each datum a probability of being in each cluster), to overcome the effects of sample bending on the diffraction patterns obtained in precession mode while scanning twinned GaAs nanowires (Fig. 2 C-cluster).78
The outstanding balance between the ease of implementation and the remarkable results obtained by PCA or NMF raised the interest to explore higher-complexity unsupervised routines.63,79–81 Variational AutoEncoders (VAEs) are emerging as a powerful dimensionality reduction tool able to extract physically meaningful information (Fig. 2 VAE). Although they are catalogued as unsupervised processes, they require the manual specification of the features of interest of the data for that study. For example, in a crystal phase classifier, the mapping of the phases throughout the micrograph should be manually given a priori as input. Then, by specifying the features of interest in the micrographs, the data is compressed and decompressed in an encoder–decoder architecture that generates a few latent variables that “simply” explain the variability of the original image.82–84 These compressed latent variables can further go through complementary clustering or refinement routines to eventually be correlated with physically meaningful features, such as local crystallography, defects, or subtler sample-dependent identifiers.85–87 Relevantly, S. Kalinin et al. used rotationally invariant VAEs (rVAEs) to explore the evolution of Si on graphene under the electron beam. To achieve so, the authors encoded the variability of this model system in just three latent variables: rotations, and x and y translations. The latest proved the robustness of VAEs to track time-resolved data, outperforming traditional unmixing methods by capturing the rotation information in just a single latent variable and clarifying the origin of the remaining variability in other independent variables.88 As indicated by their name, rVAEs are phenomenal tools to evaluate features that are susceptible to suffer in-plane rotations, which may be particularly advantageous for ferroelectric, ferromagnetic or generally polar materials. In that sense, S. Kalinin et al. applied rVAEs to correlate the rotation latent variable with the orientation of ferroic variants, directly locating the unit cell deformations through the sample, independently of the structural and chemical variability and under non-ideal imaging conditions.89
2.1.2.2 Supervised exploratory routines. Mimicking the intricate neural structure of the human brain, and even building new neuromorphic hardware architectures, is the latest revolutionary idea in computer science, together with quantum computing, to overcome the computing capabilities of classical algorithmics. Since the very first perceptron proposed by W. Pitts and W. McCulloch, to the explosion of DL, neural networks and other supervised algorithms have systematically outperformed classical classification and regression tasks.90,91
Supervised routines, and paradigmatically DL, are based on a training process that requires the preparation of a large dataset representing the statistical variability of the problem data. The key idea is that after engineering a model (i.e. the neural network) capable of recognising the statistical variability and descriptors of the data (i.e. training process), any data lying within these statistical limits could be automatically and robustly analysed. Thus, in the same way a linear regression would adapt to data following a linear trend, neural networks generate complex non-linear multi-dimensional regressions that can adapt, in theory, to any data structure. However, the main drawback relies on the resource-consuming model set-up, which essentially consists of generating and getting the training data ready, and tailoring the model architecture to the problem. Nevertheless, recent results elucidated that the automatic AI-based architecture and hyperparameter fine-tuning (i.e. the supervised model properties) is currently possible for EM problems and datasets.92–95
Currently, the main trend of DL in the field has been the finding of atomic positions and their correlation with mathematical graphs, as stated before, for defect identification59–61,66,67,70 and quantification,96 or image denoising.21,26–28 Nevertheless, the extraction of further properties with physical meaning can be envisioned from this idea, such as atom counting or quantitative TEM in a broader sense.3,4,66 Interestingly, the atomic positions identification started with FCNN on 2D systems and model 3D systems. However, FCNN extended their reach to higher complexity systems, therefore exhibiting their generalisation capabilities. For example, M. Ziatdinov et al. trained a FCNN to detect the atomic positions of a La-doped BiFeO3 system to extract local descriptors of the lattice such as the polarisation.97 Importantly, local descriptors coming from supervised networks can be post-processed by unsupervised means to group them in physically equivalent categories. Indeed, the authors compressed the supervised output with PCA and grouped it by k-means clustering. As a result, they could map back the distribution of the lattice distortions in the original image.97,98 Multimodal approaches, as the former example, mostly introduced in atomic column finding and phase mapping, are of huge importance nowadays to go through the intrinsic limitations of standalone models. These methodologies are common for dealing with data outputted from neural networks, as their formats are susceptible to being further simplified by classical unsupervised routines or by more complex algorithms such as VAEs.85,89,99 In fact, most of the DL-based studies available in the literature for atomic column-positioning routines interact with similar data (roughly, atomic columns “always” appear as rounded dots in micrographs). Thus, the first step towards a universal model could be a shared transfer learning-based starting point, which would save time and resources in updating and tailoring it for any specific or individual need. And for that, the attention paid to these multimodal approaches would perfectly fit in the intercommunication of the specific models towards a more general and beneficial model.
The next complexity stage for supervised algorithms was shifting to the reciprocal space analysis. Fortunately, ML methods are sensitive to geometry to easily detect symmetry constraints. This makes them excellent options for dealing with crystals and their reciprocal space description. In order to simplify the electron diffraction data and reduce the computational pressure, the 2D diffractograms can be turned into 1D spectra. In that sense, as J. Aguiar et al. proposed, a CNN can be trained on electron diffraction data or equivalently, FFTs obtained on atomic resolution STEM micrographs, to identify the space group of a given unit cell.105 The key idea relies on the azimuthal integration of diffraction patterns (or FFTs) to generate a line profile containing the whole information in a simplified encoding. The authors used a huge dataset with 571.340 crystals to reach a classification confidence of 95% in regular SNR scenarios, and of the 70% in noisier data. Similarly, and by directly tackling 2D diffraction data, R. Vasudevan et al. worked on a CNN capable of determining the Bravais lattice of both experimental and simulated Scanning Tunnelling Microscopy (STM) and STEM images. Indeed, the authors mapped this Bravais symmetry distribution within a time-resolved set of images of electron beam-damaged WS2.61,106,107 Interestingly, these constitute preliminary signs highlighting the interest to apply supervised methods, and generally ML, to evolving systems or in situ setups. This idea is reviewed in detail a few paragraphs below.
The high versatility of supervised methods confirmed their ease to handle manifold experimental data productively. Nonetheless, the ML practitioners in the community attempted the ML implementation in microscopy simulations, too. Simulations are key in EM to facilitate the interpretation of micrographs taken under complex conditions, and also allow for virtual experiments on the characterised structures. In this direction, R. Pennington et al. combined Density Functional Theory (DFT) calculations and a neural network-based optimisation algorithm both to improve TEM simulations and to retrieve properties along the beam propagation dimension (properties like ferroelectric polarisation domains and strain). In this latter case, this methodology was tested with simulated Convergent-Beam Electron Diffraction (CBED) patterns, although it should be comparable to the available imaging and spectroscopic modes.103,108 Indeed, literature extensively showed that features learnt by DL may extrapolate to data which a priori had no relation with the training data. Interestingly, the way DL models learn these complex routines is still mostly unknown to date in a general basis. The generated weights of the networks are task-specific, which hampers distilling general and common patterns. J. Horwath et al. carefully checked the learned convolutional filters of a U-Net architecture intended to segment TEM images of rounded gold nanoparticles.109 They learnt that the kernels filters could be easily engineered by combinations of traditional filters (i.e., Laplacian, Gaussian, etc.), emphasising the importance of tailoring the model architecture for a task.26,109–112 At this point, it is important not only to clarify the nature of DL applied to (materials) science, from a computer science perspective, but also to extract individual filters repeatedly observed in networks sharing objectives and apply them to simplify specific data treatment problems.
As reviewed, in EM the typical research workflow involving supervised ML consists of tackling a specific problem and generating a supervised model that fits into the target information. However, the solutions to these tailored research problems are meant to converge into broader unified models with a customisable or modular nature gathering all the developed features at once. In fact, the latest EM hardware evolutions and their software assistance were meaningfully based on automation. It was fundamental for cryo-TEM and its autonomous particle search and analysis, and also played a role in delivering intuitive parallelisation capabilities to the newest microscopes and focused ion beam machines. Therefore, it is important to emphasise the effort led by the computational EM community towards the open software and its easy accessibility and centralisation. This idea should make the next incoming hardware and software evolution of EM and materials science be deeply based on ML. Initiatives such as sharing public codes, libraries and repositories, or “papers with code” (i.e., Jupyter notebooks, Google Colab notebooks) to straightforwardly reproduce the data analysis shown in the publications, foresee a new format for the papers that journals will need to embrace from now.89,97,105 Interestingly, these paradigmatic tendencies confirm that this new incoming evolution is already here.
Ptychography is a promising technique based on the mathematical reconstruction of the electron phase information (i.e. the inverse problem) based on the acquired experimental signal. It has recently proven its high value achieving the current spatial resolution record in EM, 16 pm, only limited by lattice vibrations.114–118 Whilst it is still an early technique, the community has identified the need to enhance the computations assisting the reconstructions. For that, ML applied to ptychography is currently relying on optimising the phase retrieval routines.119 For instance, M. Schloz et al. combined the multislice formalism (interestingly, implemented with a multilayer perceptron, which is a fully-connected neural network) with gradient descent regularised optimisation to perform the reconstruction. The multislice formalism accounting for multiple scattering improved the resolution, and the regularisation allowed to diminish the oversampling requirements and still reconstruct the experimental data under noisy conditions.120
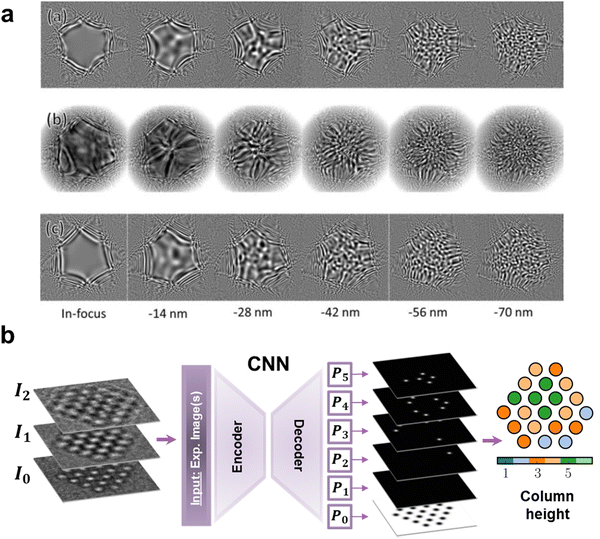
After improving the reconstruction mechanisms and relaxing its constraints, the ML practitioner's aim is to make ptychography an end-to-end process. In this way, M. Cherukara et al. trained a FCNN (named PtychoNN) to retrieve both the amplitude and phase from diffraction data. The authors claimed to achieve a fast, sub-sampling tolerant and computationally-friendly method to solve the inverse problem in real time, in a single step (Fig. 3a and b).121 The computational speed of the FCNN opened real-time ptychography, which could be potentially used to apply ptychography in dose-sensitive and thick samples. Consequently, ML pushed even more the relaxation of the required electron dose with advanced methods. DL, specifically deep Reinforcement Learning (RL), was used for this purpose. RL learns by rewarding the behaviours or patterns we are interested in, while penalising the rest. For that, RL was studied to generate real-time adaptive scanning paths that benefited the relaxation of the overdetermination constraints towards low dose experiments (Fig. 2 RL). For that, a Recurrent Neural Network (RNN) rewarded the most physically meaningful diffraction patterns (i.e., highest phase dynamic range) and automatically engineered the most optimal scanning path for the reconstruction.122,123 This example of ptychography expanding its target materials to beam-sensitive and thick devices is a paradigmatic victory of ML. It accentuates that even in refined techniques capable of leading to super resolution, ML can still play a role improving the classical approach. Nevertheless, the acquisition of diffraction patterns to generate a 4D dataset is more general and goes beyond ptychography. Nanobeam diffraction patterns of very wide fields of view can be obtained by means of 4D-STEM nanodiffraction (generally just 4D-STEM for simplicity). In order to collect the 4D-STEM 2D diffraction patterns, pixelated detectors are a cornerstone that also received the attention of ML practitioners.124–128 In fact, so far, we have reviewed how close the ML software development can be with the progress of the actual hardware receiving the signals. Despite that, it is not common in the bibliography to directly face the hardware, or as in the following case, the capabilities of the before mentioned detectors. Interestingly enough, G. Correa and D. Muller exceptionally pushed the performance of these detectors by training a CNN on Monte Carlo electron beam trajectories. The idea was the prediction of experimental beam paths and detector hitting spots to achieve sub-pixel super-resolution.129 Again, similar research is currently scarce in the literature, but certainly illustrates what we were referring to as the next coupled software–hardware evolution in EM.
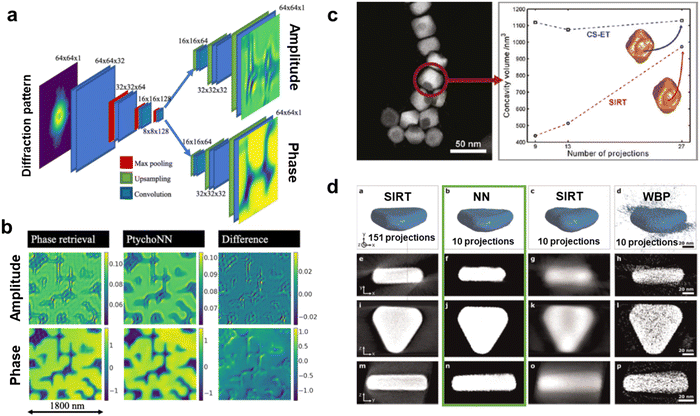 | ||
| Fig. 3 Machine Learning (ML) applied to Electron Microscopy (EM) high-dimensionality data analysis. (a) An encoder–double decoder convolutional neural network dubbed PtychoNN designed for the ptychography reconstruction of the amplitude and phase information out of single diffraction patterns. PtychoNN allowed (b) to reconstruct the wave information with higher fidelity than traditional iterative phase retrieval algorithms, and up to 300 times faster.121 Reprinted from M. J. Cherukara et al., Appl. Phys. Lett., 2020, 117, with the permission of AIP Publishing. (c) Comparison of the accuracy of the Electron Tomography (ET) reconstruction of an iron oxide nanoparticle with a concavity between the SIRT algorithm and a compressed sensing (CS)-based one. The CS algorithm reproducibly estimated the concavity size independently of the number of acquired projections while the SIRT approximation was strongly affected by that.148 Reprinted with permission from Z. Saghi et al., Nano Lett., 2011, 11, 4666–4673. Copyright 2011 American Chemical Society. (d) ET reconstruction by, from left to right, the SIRT algorithm with 151 acquired projections, and a Neural Network (NN), SIRT and WBP algorithms with 10 projections, and their orthoslices in the three bottom rows. The NN overwhelmingly improved the 10 projections SIRT and WBP reconstruction, but also the reference 151-projections SIRT. The NN orthoslices clarified its superior performance highlighting the potential for low-dose ET.154 Reprinted from E. Bladt et al., Ultramicroscopy, 2015, 158, 81–88, Copyright (2015), with permission from Elsevier. | ||
It is currently much more common to find ML on 4D-STEM focusing on facilitating the extraction of physical properties of huge datasets. To do so, traditional algorithms would inevitably take ages. A common approach, as happens with regular atomically-resolved (S)TEM data, is to employ unsupervised methods to give a physical origin to a mathematical component, such as assigning each NMF/PCA component a characteristic diffraction pattern. Its recent success unveils unsupervised techniques as a standard for the processing of high-dimensional datasets, resembling the multimodal crystal phase mapping we described for regular STEM.130–135 Indeed, the mapping of crystal phases and their relative rotations was tested with success in complex oxide systems (e.g., Ti0.87O2vs. Ti2O3) and in dichalcogenide multilayers, such as MoS2 bilayers.100,136
Supervised ML has also been proven beneficial for 4D-STEM, as regarded in ptychography. Nonetheless, its mere consideration can become thoroughly more time-consuming than in regular (S)TEM, given the higher dimensionality of the former and the consequent higher-complexity network-architectures required.137 Explicitly, the high dimensionality engineering of training data would nowadays become the main implementation barrier. Therefore, unsupervised methods would constitute the best starting point for newcomers diving into the smart processing of 4D datasets. Nevertheless, the preparation of useful 4D training sets is still possible as showed by the 3D-CNN trained on simulated diffraction patterns arising from a LaAlO3–SrTiO3 heterostructure.138 In this case, the capability of the resulting model was to distil whether the interface presented atomically sharp steps or a chemically diffuse nature, a task often complicated even for trained microscopists. The necessary tools for reproducing this and the previous cases, as well as to deploy custom models on 4D data are described in detail in Section 3.
As mentioned earlier, the research on CS applied to tomography mostly tries to improve the current tomogram reconstruction schemes. Virtually every experimental setup would benefit from having its total dose reduced. For that, CS pointed towards a dose-reduced but also real-time and shape-independent tomography.143–147 This idea provided extra sensitivity to morphological features difficult to resolve, such as surface rugosity and porosity, also allowing the tomography of challenging shapes. For example, Z. Saghi et al. could both quantitatively evaluate the concavities of iron oxide nanoparticles and to reconstruct additional challenging biological needle-shaped tomograms by means of CS (Fig. 3c).146,148 Besides, the promising achievements of CS in the field opened the tendency of ML to emulate these algorithms and make their implementation more agile. This played a substantial role after involving DL in the equation.149–153 For instance, E. Bladt et al. went beyond CS with the implementation of a multilayer perceptron capable of automatically reconstructing the sample upon a sparse tilt series, without the user-defined prior knowledge of the sample typically required in traditional reconstruction algorithms (Fig. 3d).154–156 Interestingly, as it happens with ML mimicking DFT and multislice, ML copying CS enforces the future of ML overwriting classical algorithms and making them worth a try when contemplating a scientific problem.
Beyond tomography, CS burst in with the development of non-rectangular scanning paths in STEM, which promise faster and lower dose STEM experiments.157,158 The idea lies in the measurement of (random) sparse pixels and the mathematical inference of the unsampled signal. This approach was successful for practical scenarios such as undersampled lattice distortions like point defects, in both STEM imaging and EELS.159 However, as indicated, the velocity boost is not the main attraction. Its application for beam-sensitive nanostructures as a way to ensure not surpassing the maximum allowed dose was also corroborated experimentally. X. Li et al. could perform real-time CS-based reconstructions on beam-sensitive materials (i.e., graphene) with nonrectangular spiral and Lissajous scans.160 Interestingly, the scanning path optimisations were parallelly extended in SPM following this same logic.104,160,161 It is not surprising, then, that as happened with CS-tomography, DL also emulated the goodness of CS in STEM path optimisation. For that, J. Ede and R. Beanland modelled a GAN to automatically reconstruct nonrectangular scan paths. Based on this, J. Ede additionally created a sample-aware adaptive scan path learned by reinforcing a RNN that scores the reconstruction of the GAN from the previous study (Fig. 2 RNN).162,163 This research piece constitutes one of the most sophisticated examples of ML applied to EM currently available. Nonetheless, it unveils that the expertise in a wide ML toolset is key for bringing the applications into a next level. Indeed, it is the shown stacking of complementary ML tools (referred previously as multimodal ML) what would lead to general ML models for EM. In favour of this, in Section 3 we review the currently available ML toolset for easily transferring this knowledge into helpful algorithms, in a practical and easy-going way.
CS has also showed potential for compressing the data volume associated to time series in in situ experiments.164 As introduced before, this shines light on the important role ML can play when dealing with in situ experimental setups, topic that will conclude this first section of the review.165–168 In the previous paragraphs we have already reviewed some examples in which the effect of the beam, mainly on 2D materials, was carefully considered. Specifically, the potential reproducer of these experiments would find value in the evaluation of changing defects or phase distributions.26,29,61,88,109 For instance, T. Patra et al. studied MoS2 in different time scales by combining ML-enhanced dynamic simulations of defects with time-resolved HRTEM. They found that the long-time scale displacement of the defects could lead to rapid (up to picoseconds) 2H to 1T phase transitions.62 Remarkably, ML unlocked the required time resolution to capture this ultrafast phase transitions invisible to classical in situ data analysis.
The current investigations involving ML on in situ experiments are only on preliminary stages, fundamentally facing relatively simple systems such as nanoparticles, and their evolution in size and morphology. For these primary applications, the methodology to deploy is not advanced either, which makes it even more accessible to newcomer ML practitioners. Some of these works rely on combining traditional computer vision routines (i.e., thresholding and edge detection) with unsupervised clustering to draw the contours and central positions of the particles.169,170 In this context, the clustering could be understood as a sample-aware thresholding that better adapts to the changing conditions of time series or dynamic stimuli. In that sense, Y. Qian et al. developed an unsupervised segmentation routine that is representative of what can be obtained by taking advantage of relatively simple clustering routines. The authors pooled the k-means clustering (intensity evaluation) with the edge detection (gradient evaluation) to extract complete statistics from videos of silica nanoparticles.171,172 Interestingly, the authors achieved a robust method that was tested on more complex situations such as the environmental TEM study of the formation of Fe nanoparticles after the dewetting of a Fe thin film.173
The previous example remarked that evolving systems may find in simple algorithms the best ally to capture their dynamics without the need to deploy complex codes. However, abrupt intensity changes in the micrographs coming from, for instance, thickness variations, or compositional changes can make unsupervised routines miss. If this case is identified, it would probably require a supervised approach specifically trained for these observed image variations. This may allow to push the conditions of the tolerated in situ experiments and still get robustness, at the cost model-design resources. For example, supervised routines based on the CNN U-Net architecture successfully segmented and tracked the statistics of nanoparticles. As U-Net was the first notorious DL model for dealing with scientific images (i.e. segmentation of cells), most of the currently available CNN for microscopy are fine tunings of U-Net.65 Then, before the time-consuming neural network architecture design, it is always worth to try first with U-Net as a reliable supervised proof of concept. In fact, meaningful results were obtained just with U-Net both in liquid and gas phases, and under temperature changes, surpassing the former traditional and unsupervised approaches.174–176 In any case, it is clear that ML has much more to say in in situ EM, and it will surely explode as soon as the in situ machinery becomes a much wider standard within the community. For instance, we envision the use of CS to reduce the required frame rate, similarly to CS-tomography, further allowing the chemical and physical tracking of beam-sensitive materials. Furthermore, we envisage the use of VAEs to encode time-dependent meaningful descriptors for its direct correlation with actual materials dynamics. At the same time, the computing efficiency of ML and the advent of fast detectors could open the real-time correlation of in situ experiments with parallel simulations that automatically record and explain the evolution of materials in a limitless scenario of knowledge extraction.
As a final comment for this first section devoted to imaging, we cannot forget about those technical fields in which ML has extensively helped to push the limits of the achievable. In fact, as this review is mainly intended for the materials science community, we have not covered ML on cryo-TEM, in which the problems solved are mainly bio-related. However, it is important to keep it in mind when trying to apply ML to materials science (or to any other field), as similar routines might have already been developed, for instance, within the mentioned cryo-TEM community.177–192 The cross-fertilization with not only other microscopy techniques, but other scientific and technical disciplines is of capital importance and is deeply discussed in the fourth section of this review.
2.2. Most important advances in spectroscopy
The previous section highlights the latest ML developments in the EM community to extract information from images. Even though we have seen strategies for dealing with high-dimensionality data such as 4D-STEM related techniques, most of the processes tackle 2D signals (mainly images). In fact, this is because computer vision has evolved fast in fields such as autonomous driving or macroscopic pattern recognition, in which the way to communicate the information to the computer is through digital imaging. Therefore, the processing of more complex data, such as the generated by Electron Spectroscopy (ES), still remains a challenge even more arduous than the previously reviewed EM image analysis.193 This section shines light on whether the advances on spectroscopy can compare to the imaging ones, and in which situations the employed methods can share convenience. In the process, we pinpoint suggestions to push the development of these data types, trying to imitate the ascending trend observed in EM image processing. Indeed, opposed to ML for imaging, the reader may find, both in this review and in an autonomous literature research, a substantially smaller number of ML-related research works devoted to ES. By now, ES has mainly received a much simpler ML modelling, the architectures of which head the following subsections.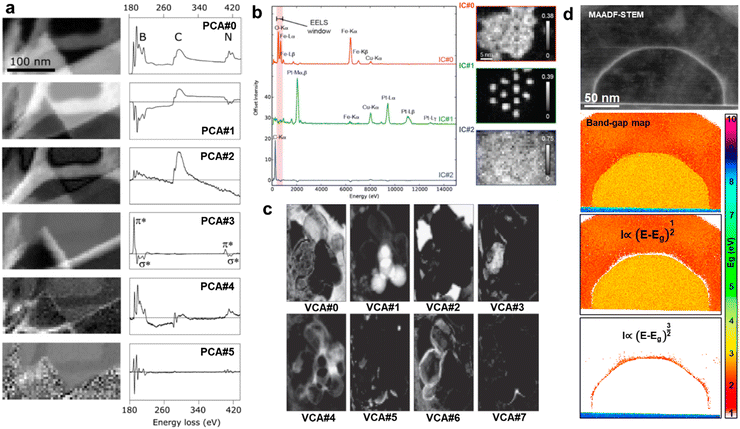 | ||
| Fig. 4 Unsupervised unmixing methods for hyperspectral analysis. (a) Principal Component Analysis (PCA) of a BN Electron Energy Loss Spectroscopy (EELS) Spectrum Image (SI) and the first six components, from top to bottom, with higher statistical significance. The presence of peaks and features of interest diminishes as going down in significance, where background or noise is the main feature. PCA does not physically constrain the components, as regarded by the negative losses.13 Reprinted from M. Bosman et al., Ultramicroscopy, 2006, 106, 1024–1032 Copyright (2006), with permission from Elsevier. (b) Independent Components Analysis (ICA) of an Energy Dispersive X-Ray (EDX) SI of Fe-based core–shell nanoparticles with the three main independent components. The independence of the components mapped the cores (IC#1), the shells (IC#0), and the C background (IC#2).249 Reproduced with permission of D. Rossouw et al., Part. Part. Syst. Charact., 2016, Copyright 2016 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. (c) Vertex Component Analysis (VCA) of an EELS SI of BN/BOx nanoparticles, displaying the eight more important components. As the components were from the original SI, VCA was capable of mapping physically meaningful variations for each component such as particle edges vs. particle centres.250 Reprinted from N. Dobigeon and N. Brun, Ultramicroscopy, 2012, 120, 25–34 Copyright (2012), with permission from Elsevier. (d) Band-gap map of a ZnSe–ZnTe core–shell nanowire separating the areas where a direct or indirect band type was found. PCA was used on the low-loss SI to isolate the interfacial pixels between core and shell where the strain was accumulated, as visible in the Middle-Angle Annular Dark-Field (MAADF) micrograph.204 | ||
As described previously, the first contact of ML with ES was precisely in the denoising of spectra via unsupervised unmixing methods. As a result, the examples in the literature highlighting the benefits, limits, associated handicaps, and mostly the direct routinary application of (mostly) PCA to ES data is really manifold.16,17,212–224 The idea behind unmixing is the simplification of the spectral features and its description as a function of key physical properties such as material type or spatial distribution. Most of the unsupervised unmixing methods are variations or inspirations of SVD, which is currently an incredibly well-documented and accessible method that is worth relying on.225–227 Its use decomposes the data into components that can be weighted in importance and reconstructed to dismiss any noise or inconsequential information (Fig. 4a). For example, SVD and its alternative methods can be used to clean atomic resolution EDX and EELS maps without significative distortions of the spectral fine structure.228,229 Importantly, the chosen word “significative” is indeed significative, as special care must be taken when unmixing signals and choosing the components to reconstruct. For that, P. Potapov and A. Lubk published a guide on how to automatically choose the meaningful PCA components.230 It was based on an initial smoothing of the data followed by the evaluation of the anisotropy of the generated scree plot and its components. Finally, only those components not exhibiting the characteristic isotropy of noise are selected for the reconstruction. Related to this, the introduced statistical bias as a function of the truncated portion of the scree plot, total pixels and total energy channels was also extensively studied, facilitating the correct adoption of the method.225,226
We previously introduced that despite all the advantages of PCA, its main limitation is the lack of physical interpretability for its resulting components. To overcome so, alternatives physically constraining PCA became popular and demonstrated extended capabilities. In fact, the addition of physical constraints to ML is the logic evolution to follow in the coming years, both in the unsupervised and supervised domains. Among others, as introduced in the imaging section, we can find NMF, which forces the components to be positive, mimicking in this case the measured energies in ES; Independent Component Analysis (ICA), which only extracts statistically independent features assuming, for instance, that the spectral peaks for each element are not correlated; while contrarily, Gaussian Mixture Modelling (GMM) assumes that all the sources are governed by Gaussian distributions and separates the signals into a finite combination of these distributions; or Vertex Component Analysis (VCA), which assumes the presence of pure spectral signals, for instance, coming from pure materials, and evaluates their distribution through the hyperspectral dataset.231,232
Again, the literature referring unmixing methods for ES is bast. Specially from articles comparing, for a single application or for a similar purpose, some of these methods and confronting them towards finding the best performer.233–244 In a general basis, NMF was the preferred way to proceed when the major goal lied beyond denoising or data inspection. That is because it can admit not only the direct physical significance of the extracted components, but to add additional constraints with ease. In this way, M. Shiga et al. broadened NMF by adding extra physical constraints that better imitate the statistical nature of both EDX and EELS. The constraints were the automatic prior-based component relevance and soft orthogonality determination, although these constraints can be tailored to more complex setups such as simultaneously acquired multimodal spectroscopy (multidetector imaging, EELS, EDX, cathodoluminescence,…).245,246
Nevertheless, alternative unmixing methods do not necessarily need to substitute PCA or SVD, but to complement them. This is the case for ICA. After the pioneer work of N. Bonnet and D. Nuzillard on applying ICA to simulated EELS, ICA has been mainly used to complement PCA. In fact, N. Bonnet and D. Nuzillard claimed that ICA was a complementary technique to the standard unmixing methods, not a substitute, given that EELS does not fulfil the condition of statistical independence.247 This complementarity can make use of PCA to avoid overfitting and next ICA can be used to spatially map crystal phases or elements.248 Following this direction, D. Rossouw et al. developed a compositional quantification routine based on dual-PCA + ICA and dual-EDX + EELS. To prove it, the authors tested their method on FePt@Fe3O4 core–shell nanoparticles. Interestingly, they solved the quantification of the spatially overlapping core and shell phases with the complementary spectral unmixing, and the mapping of both light and heavy atoms with the complementary spectroscopy (Fig. 4b).249
The mixed use of PCA/ICA allowed to directly distinguish phases which would require an exhaustive and tedious least-squares fitting to be reproduced. However, the ICA assumption of independence between spectral peaks might cause artefacts when dealing with similar phases (e.g. sharing elements or oxidation states). This is where VCA can make a difference, as it succeeds at identifying the individual spectral profiles (i.e. combination of peaks) of distinguishable phases. VCA should then be used when the expected components already appear in isolated hyperspectral pixels representing a physically/chemically independent structure. This idea was validated in a comparative study carried out by, N. Dobigeon and N. Brun, who confronted PCA and ICA, least-square fitting and VCA. By requiring gentler statistical assumptions, the authors claimed the superior interpretability of VCA versus both PCA/ICA for the finer analysis of high-complexity sample configurations (Fig. 4c).250 From this analysis we may get spatial information from the mapping of spectral components that are extracted by just looking at the energy domain. Therefore, spatial correlations, if present, may be ignored by just searching for similarities between spectra and not caring where the probe was. Alternatively, and in order to further account for spatial correlations within the SI, S. Kalinin et al. proposed an unmixing method based on spatial Gaussian kernels. These kernels were based on traditionally unmixed components that reduced the complexity of the energy domain and democratised the computational needs of the GP. The process can be understood as the convolution of the unmixed spectral features through the spatial dimension, leading into higher-fidelity reconstructions and mapping.251 Interestingly, the authors demonstrate the ease to tune and adapt the kernels to a combination of unmixed components or to engineer them based on the physical characteristics we want to find from the hyperspectral dataset. As a result, this methodology was proposed as the preferred way to go if we handle highly spatially-correlated data (e.g., core–shell nanoparticles, nanoparticle clusters, compositional gradients,…).
The main unsupervised routines used for ES, as commented, rely on unmixing methods. The decomposition in statistical components can be oriented to spectra denoising or cleaning, for unlocking a smoother post-processing, or even to map and quantify crystal phases and their stoichiometries. However, more intricate processes have been devoted to solve unattended matters such as spectral classification or the analysis of finer features such as the Energy Loss Near Edge Structure (ELNES). For this purpose, unsupervised clustering methods may represent an strategy worth relying on.252–256 The idea behind spectral clustering is to automatically detect fine spectral changes and group them accordingly. As it is an unsupervised method, it would require the manual tuning of a hyperparameter referring (somehow) to the number of final groups we want to have (for instance, the total number of different crystal phases in a Spectrum Image (SI)). For example, we can create a cluster for each spectra representing the different ELNES oxygen K edges. In fact, this kind of reasoning can act as the building block for elaborating models further. Representatively, S. Kiyohara et al. generated a decision tree (supervised learning) that dealt with the clusters representing the ELNES oxygen K edges.257,258 As its name points, a decision tree is a supervised model capable of acting differently on its reference data depending on the way these reference data are structured. Interestingly, in this case, the reference data are directly the clusters representing the ELNES information. From that, the authors managed to, on the one hand, unveil the oxidation nature of oxides given their spectral description, and on the other hand, predict the spectra of a known oxide-based nanostructure.
The idea behind clustering is not far from unmixing, as we identify common patterns from spectra. Indeed, we can combine both to improve the identification of materials, either by applying PCA before clustering, or by applying it to segment each individual cluster.259 In addition, this approach can be combined with non-linear least squares fitting for a deeper ELNES analysis that not only classifies the data, but unveils finer ELNES features such as valence, oxidation and coordination states. These options are available online in the software solution dubbed WhatEELS, the use of which can be complemented with many other practical tools described in detail in the third section of this review.260 In fact, clustering and unmixing are not exclusive for core losses and can also be applied to low-loss EELS, for instance, to map plasmons or even in the future to map with high accuracy the electronic properties of nanomaterials such as the topology of the band structure.204,261
Independently on the spectral range in which it was applied, the complexity of the ML reviewed so far for ES was standard. It is a good signal that in most of the cases this basic stage it is just enough. For the rest, more sophisticated routines are arising and will appear as the methodology reaches broader audiences. For that, a fruitful approach would be mimicking the progress done in EM imaging, where developing ML-based solutions might be more intuitive. In that sense, S. Kalinin et al. brought the idea of autoencoders from imaging to spectroscopy.82–85,88 In a paradigmatic case, they deployed 1D convolutional autoencoders to unsupervisedly represent each spectral pixel into a set of only two latent variables. Afterwards, they grouped these outputted variables by GMM to distil the spectrally distinguishable regions of an heterogenous array of nanoparticles, in this case, composed of fluorine and tin-doped indium oxide (Fig. 5c and d).262–264 Importantly, as happened on imaging, this research work and related265 might draw the future of spectral analysis, and point it towards the implementation of more complex autoencoder-based routines, soft supervision, and the use of GAN architectures. Furthermore, this important last example from S. Kalinin et al. highlighted how different unsupervised (i.e., the commented autoencoder) and semi-supervised (discussed below) approaches can lead to the same spectral analysis. For that, we discuss this revealing complementary approach further in the next section about supervised ES.
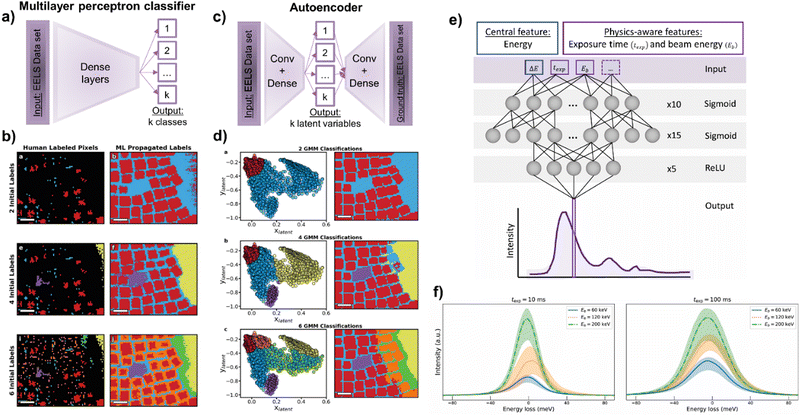 | ||
| Fig. 5 (a–d) Representations of S. Kalinin et al.'s work,262 comparing two learning paradigms to unveil physically-distinguishable Electron Energy-Loss Spectroscopy (EELS) components. The authors suggested: (a) a supervised approach based on a multilayer perceptron capable of (b) extrapolating the partially manually labelled pixels of (b.a and b) two, (b.e and f) four and (b.i and j) six physically-different classes. On the other hand, (c) the authors proposed an unsupervised approach based on an autoencoder. (d) The autoencoder reduced the EELS dataset into two latent variables, which after being Gaussian clustered in (d.a) two, (d.b) four and (d.c) six classes, produced comparable maps to the supervised approach (b and d, reproduced with permission of S. Kalinin et al., Adv. Opt. Mater., 2021, 9, 2001808 Copyright 2021 Wiley-VCH GmbH). (e) L. Roest et al.'s work,296 represents the training of a physically-aware multilayer perceptron capable of (f) modelling a zero-loss peak and its uncertainty under different exposure times and beam energies. | ||
| Software solution | Level of theory | Programmatic interface | Accessibility | Ref. | |
|---|---|---|---|---|---|
| Electron microscopy (imaging) | abTEM | Multislice, ab initio DFT bonding information + PRISM approximation | Yes, Python-based | Open | 343–345 |
| Bloch wave simulations | Bloch wave formulation | No | Open | 330 and 331 | |
| Cerius2, Molecular Simulations Inc. | Multislice, molecular dynamics | No | Paid | 346 | |
| cudaTEM → clTEM | Multislice, independent atomic potential | Yes, command line | Open | 347 and 348 | |
| Dr. Probe | Multislice, independent atomic potential | Yes, command line | Open | 349 | |
| Electron direct methods (EDM) | Multislice, independent atomic potential + kinematic scattering | No | Open | 350 | |
| Multis | Multislice, independent atomic potential | No | Open | 330 | |
| Multivariate polynomial fit | Multislice, independent atomic potential | Yes, Python-based | Open | 337 | |
| Prismatic | Multislice, independent atomic potential + PRISM approximation | Yes, Python (PyPrismatic), C++ | Open | 351–353 | |
| QSTEM | Multislice, independent atomic potential | Yes, Python (PyQSTEM) | Open | 354 and 355 | |
| scikit-ued | Multislice, independent atomic potential + Kinematic scattering | Yes, Python-based | Open | 356 | |
| STEM_CELL | Multislice, independent atomic potential + linear image approximation | No | Open | 357 and 358 | |
| Tempas | Multislice, independent atomic potential + kinematic scattering + Bloch wave formulation | Yes, digital micrograph-like scripting | Paid | 359 | |
| Electron spectroscopy | Bloch wave simulations | Bloch wave formulation | No | Open | 284–286 |
| DTSA-II (NIST) | EDX (characteristic and Bremsstrahlung) → Monte Carlo + φ(ρz) + XPP | Yes, command line | Open | 289 | |
| Electrodynamics | Classical relativistic (faster) → quantum (more accurate) | Yes, command line | Upon request | 269–271 | |
| FEFF | Ab initio, projector-augmented wave | Yes, command line | Paid | 281 | |
| LEEPS (and variations) | Monte Carlo + classical relativistic cross sections (faster) → quantum (more accurate) | Yes, command line | Upon request | 272–275 | |
| PENELOPE | Monte Carlo + classical relativistic cross sections (faster) → quantum (more accurate) | Yes, Python (pyPENELOPE) | Open | 360 and 361 | |
| Prismatic | PRISM approximation | Yes, Python (PyPrismatic), C++ | Open | 351–353 | |
| Semi-empirical calculations | Experimental cross-sections or dielectric functions | Yes, command line | Upon request | 222 and 276–280 | |
| WIEN2k | Ab initio, projector-augmented wave | Yes, command line | Paid | 194–196, 198, 209, 210, 282 and 283 |
Anyhow, these approximations can still be too computationally demanding for generating training data for 3D and 4D CNN. Promisingly, ML has already offered alternatives to EM simulation, such as the potential propagation through slices via the forward propagation of a trained neural network.120 In this case, each slice in the multislice approach can be modelled with a layer of the neural network, as if the propagated weights were the actual propagated potential. This ML-based acceleration, together with the most efficient alternatives suggested could be enough to generate enough data for 1D analyses. Unfortunately, spatial correlations in SI would be majorly lost in this way, although the community already found ways to circumvent that.251 Indeed, there is already research using 1D convolutions for dealing with SI, but 3D convolutions have solely tackled ptychography so far.138,262,290,291 Importantly, the unsupervised example from S. Kalinin et al. would perfectly fill the gap of the simulated 1D data to emulate the spatial correlation of SI.251 Therefore, this would dramatically reduce the costs of data engineering and model training while mirroring the expected advantages of 3D CNN (i.e. direct spatial correlations). Moreover, ML could still make the simulation scene evolve to reach simulation efficiencies that could unlock 3D hyperspectral datasets. For example, taking advantage of new ML paradigms such as graph neural networks (i.e., supervised models for dealing with mathematical graphs). One idea is deconvolving the electron probe with the electrostatic potential encoded in trained graph neural networks, associating the atoms with the nodes and the bonding with the edges of these graphs. This inspiration from the multislice neural network may not be immediate, that is why more practical approaches resembling the discussed generative models are called to play a key role in the next years. Eventually, the desired paired data would be rapidly generated by these trained but tuneable generative models. A more complete picture about simulation and generation of data is found in Section 3 about the practical ML deployment for EM.
As reviewed, the ease of application and reliability of unsupervised methods in ES has hitherto left supervised routines to a second plane. Nevertheless, novel supervised ideas have been introduced to face more challenging cases, or even to have their performance compared with equivalent unsupervised methods.235,258 At this point, it is very interesting to go back to S. Kalinin et al.'s work on autoencoders for categorising low-loss EELS.262 A few paragraphs above we present an autoencoder plus GMM approach capable of mapping spectrally distinct regions in an SI (Fig. 5c and d). In the same manuscript, the authors presented a multilayer perceptron obtaining comparable results to the autoencoder. The idea behind this supervised model was the partial labelling of some pixels (spectra) of the SI and to base its training on the labelled pixels to infer the non-labelled ones. This labelling was done by assigning a class (element type and even chemical surrounding) to a fraction of the pixels belonging to this class. The authors evaluated the percentage of pixels that needed to be manually labelled for the correct supervised classification of the remaining unlabelled pixels. Surprisingly, they found that the well-chosen labelling of only a 0.31% of representative pixels led to an output comparable to the unsupervised autoencoder, validating the outstanding generalisation capabilities of DL (Fig. 5a and b). Remarkably, this approach facilitated the labour of training a supervised model for ES. Any microscopist wondering whether to invest resources on engineering a supervised model might just label a key fraction of the data to see how well an eventual model may generalise. It is excellent, then, to gradually put resources on model design and avoid massive resource investments unless it is mandatory.
This juicy research piece is not the only supervised approximation in ES. FCNN and support vector machines were also applied for automatic mapping and elemental identification, for ELNES characterisation, for instrument-independent spectral calibration, etc.290,292,293 Nonetheless, these applications essentially resembled the reviewed unsupervised methods and their achievements. To be fair, the scenarios were more challenging, but the main workflow remained essentially unchanged. Indeed, the extra energy dimension that spectroscopy introduced, unlocks the in most cases missed opportunity to actively physically constrain the ML used. As happened with NMF versus PCA, where we force the maths to behave under some physical logic, we want to directly make the ML aware of the science it would eventually represent. This is known as physics-aware ML and is currently scarcer than standalone supervised ML. However, it is called to be the next breakthrough in scientific ML. Interestingly, there are already some examples that are worth to comment and guide the reader on what can be achieved by following this path. L. Roest et al. tried to answer the repeatedly assessed universal modelling of the Zero-Loss Peak (ZLP) with a neural network trained on Monte Carlo simulations.294,295 They generated a physics-aware model by adapting the regression model describing the ZLP (and its uncertainty) with the physical conditions of the acquisition, namely the exposure time and the beam energy (Fig. 5e and f).296 This means that the input data the model received was the ZLP curve with the exposure time and beam energy, making these variables constitute individual dimensions within the parametric space of the model. Typically, the science awareness arises from directly inputting the physical conditions, although similar effects can be achieved with physically aware labels. For instance, one could use different unit cells, jointly simulate spectra and some physical properties, and train a model where the input is the spectra and the label is the simulated physical property. This is what S. Kiyohara et al. did with a MultiLayer Perceptron (MLP) on core-loss spectra (i.e., each neuron represented each energy channel) for the extraction of up to six properties (Fig. 2 MLP).102 The training was performed on 1171 spectra, simulated by DFT from 188 different silicon oxides, and the labels were also simulated by DFT. Therefore, they eventually engineered a ML-based DFT simulator from experimental EELS spectra. From the input spectra, they were capable of extracting the physical properties they chose to generate the labels: properties such as average bond length and angle, Voronoi volume, bond overlap population, Mulliken charge and excitation energy.
Until now, the physics-aware approaches are based on simulations as the best way to directly link curves or images with a specific physical property. However, its implementation on experimental datasets would start with the reproducible and systematic acquisition of the metadata accompanying the experiment. In microscopy, the acquisition conditions and microscope parameters would be an already vast starting point. The works of L. Roest et al. and S. Kiyohara et al. shined light on the promising future of physics-aware ML in EM/ES.102,296 Indeed, these are two of the few physics-guided ML models we can currently find among the EM literature. The importance of adding scientific constraints to ML not only does it turn in more general models, but can remarkably reduce the required training volume (similarly to rVAEs).88 For instance, S. Kiyohara et al.'s work could be extended by training high-complexity DL models on full databases of spectra if a systematic spectra-property correlation was done. In addition, related to L. Roest et al., a plural scattering remover could be trained with a dataset of dual EELS SI and then applied to correct only the core-loss spectral region of interest. Similarly, the energy resolution post-acquisition could be effectively improved by training a neural network on sets of the same spectra but acquired with different resolutions. Moreover, L. Roest et al.'s work highlighted the importance of the cross-fertilization with other scientific and technical fields, as the ML methodology the authors followed was inspired by equivalent solutions in particle physics. This cross-fertilization is further discussed in the final section of the review.
On the other hand, EDX, EELS and even Energy-Filtered TEM (EFTEM) tomography skyrocketed its progress in the last two decades.301–307 Both qualitatively and quantitatively.308–311 Even though its major advances in reconstruction algorithmics were not CS/ML-based, classic data processing established a starting point to which apply these new methodologies for refinement (majorly for EDX and EELS). As happened in imaging, the use of CS-based reconstructions overcame the effects of traditional reconstructions in managing the missing wedge. Even more given the additional energy channel and the requirement of DualEELS to avoid multiple scattering artefacts in ST.312
Interestingly, tomography may also benefit from CS-enabled multimodal approximations, namely STEM-HAADF and EDX with total generalized variation. The combination of complementary signals and their simultaneous regularisation (i.e. signal balancing) might be helpful for research cases where the separated techniques cannot reach the desired level of detail. For example, R. Huber et al. explored this method for the 3D reconstruction of nanostructures with both sharp edges and gradual compositional changes.313 Despite the benefits of multimodal approaches, it can often be a time-consuming or dose-demanding methodology, even with the support of CS algorithms. Then, it may be even more interesting the use of unmixing methods as a pre-reconstruction step, following the leading work of L. Yedra et al.314 PCA, ICA and VCA can be used to prepare the data for the posterior CS reconstruction. This initial unmixing step allows to reduce the reconstruction computational cost and its complexity by relaxing the prior assumptions, both for EDX and EELS, and under challenging sample configurations (Fig. 2 VCA).101,315,316 Nevertheless, the ST processing is not limited to the pre-reconstruction and reconstruction steps. In fact, meaningful post-processing and cleaning routines might be applied after a reconstruction that has already met the benefits of the reviewed strategies. In the same way as DL was a successful tool used to denoise micrographs, it was also used to denoise EDX tomography reconstructions, following the original development in X-ray computed tomography.317 To do so, A. Skorikov et al. trained a U-Net architecture on a set of 850 noisy EDX maps obtained on nanoparticles.318 The DL denoising of the 2D maps outperformed traditional denoising methods and proved to be cumulative for 3D reconstructions of both simulated and experimental tilt series of metallic nanoparticles. As a result, EDX tomography was rewarded with a much gentler trade-off between dose management and SNR.
Ultimately, this section reviewed the manifold ML techniques already used in ES. Nonetheless, its preliminary stage is stressed if compared with the variety presented in the imaging section. Therefore, the opportunities for applying the already developed methodologies to EDX or EELS are huge, but not only to these two techniques, but to EFTEM or even cathodoluminescence (CL). We were astonished to find absolutely no bibliographical match with ML for EFTEM or CL. In fact, the experimental similarities between EFTEM and, especially EELS, result in a theoretically straightforward implementation of its methods for energy-filtered imaging (despite its lately decreasing popularity), or differently, the use of CS for adding sparsity in the temporal axis of analytical tomography. Nonetheless, one of the most important ideas this section showed us is the potential of the inter-collaboration between different fields, as shown in the multidisciplinary work of L. Roest et al., in this case towards physics-aware modelling.296 Indeed, we cannot stress enough the importance of investing towards deeper physically-aware models aimed to simplify the nowadays too often unaffordable human and computational costs of developing complex ML models.
3. Tools to deploy machine learning in electron microscopy
The resources for applying ML to research are nowadays countless. For this reason, the present section is intended to be pragmatic. In the following we will discuss on the different resources concerning ML the reader interested in EM and ES may have access to. This includes software packages and code snippets which relax not only the required knowledge in coding, but in all the steps of the workflow. These steps consist of the (training) data preparation, the renting of high-performance computing time to run the models, the availability of already trained models or either the design of optimised architectures for a given problem, and even the final benchmarking. Therefore, those EM users willing to start applying ML methodologies to their research but also those more advanced willing to optimise their case-specific bottlenecks or barriers, may find useful resources in the following paragraphs. In fact, we will show that it is possible to develop a ML-based application for EM data analysis without an advanced knowledge on ML and not even with a big funding/infrastructure investment.3.1 Preparation of the training set
On one hand, we should closely evaluate the problem to solve and classify it. The possible categories can be data analysis or data acquisition automation, knowledge extraction, modelling and experiment optimisation, among other possibilities. Afterwards we should decide whether to go for an unsupervised, supervised or a semi-supervised approach. The decision will be mainly dependent on the ease to generate labelled data (e.g., data accompanied with the ground truth of the expected classification), the data structure and its orthogonality (correlations between variables), the task, and even the computational resources available. In the previous sections we have reviewed the major pros and cons of each approach, and the scenarios in which they better shine.319 For example, in case we opt to follow a supervised approach to challenge the data preparation step, as previously emphasised, we should carefully plan the labelling step and not just rely on human workforce for doing this repetitive and tedious task. Therefore, as the first approximation to follow, we should self-engineer the dataset by using model-based methods or simulations to allow the automatic generation of the labels. In addition, special attention should be initially paid to the data format, and the current trends towards open and universal ML-intended data formats, such as the Universal Spectroscopy and Imaging Data (USID), based on hierarchical data formats like HDF5 or NumPy's native file type.320–323 These formats are designed to intuitively store paired data and any metadata that could be used either to physically constrain our models or to be used as labels.Data can be generated by means of very complex simulations but also through extremely simple ones. For instance, it is possible to simulate an atom image by calculating its electric potential by DFT and then deconvolving an electron probe to generate a micrograph. However, it is also possible to generate a circular feature (like a 2D Gaussian curve) and add some Poisson noise to have a simpler and cheaper (in computational terms) representation of the same atom.97 Even further, although a bit circular, a properly trained generative model should be capable of outputting tones of synthetic atoms with the accuracy used for its training.324–326 Of course, the utility of the latter would lie in having the generative model ready, thanks to someone else's previous efforts. In any case, the physical accuracy between these three approaches is incomparable, but the rudimentary model might be enough if it can represent the variability of the data of interest. At the end, ML can be seen as just an esoteric regression representing the variability of a dataset. If higher-complexity simulations are required, the resources available are manifold. Importantly, the label generation must always accompany the simulation, either with the same software or with a complementary custom script. In fact, this parallel automatic labelling is key to minimise the bias of a human labelling. For example, the pixelwise labelling of the compositional distribution of a qualitative EELS map will find pixelwise discrepancies if two different microscopists label them. Specially at the interface, the contrast and intensity of a pixel might be interpreted differently by two different expert microscopists. However, if a model was built and this interface was perfectly defined by a mathematical curve or function, the pixelwise labelling would be completely objective. Another example is the labelling of the central position of the atom we have previously simulated to create a model for atom finding. If it is an experimental STEM atom, the scan distortions may generate an odd intensity distribution. On the other hand, for a simulated atom, the central position is just the pixel closer to the spatial coordinate where we placed the atom in our model. Fortunately, this is independent on how we paint the intensities within this atom. In other words, we are free to generate as much variability as we want.
The following simulation resources are precise but time-consuming. As a result, in these cases, the optimisation of the simulated volume is a priority. For instance, a handful of unit cells might be simulated and artificially spatially translated, rather than simulating a large area of the same repeated unit cell. For imaging, the multislice approximation is the most adopted and adapted solution: from the first formulation by J. Cowley and A. Moodie,327 and E. Kirkland's first adaptation to STEM,268,328,329 there are many solutions currently available, as summarised in Table 1, Electron microscopy (imaging). Most of these multislice solutions and Bloch wave codes perform similarly in terms of computing time and accuracy, thus the final choice mainly depend on our own interface implementation preferences.330,331 Nevertheless, the Python-based codes might be more suitable for customising the parallel labelling step. For this purpose, existing Python packages can thoroughly facilitate the communication with atomistic models and crystallographic analysis.332–336 Interestingly, STEM_CELL and Prismatic offer simplified versions of the multislice algorithm with higher speed but reducing the precision (linear imaging, and combined Bloch wave-multislice, respectively). We can even find a multivariate polynomial fit trained on multislice simulations to provide a comparable accuracy in an up to six orders of magnitude faster algorithm than a CPU-parallelized multislice.337 In addition, fast neural network-based computations mimicking ab initio calculations could be implemented in a more sophisticated approach for computing the specimen potential with existing solutions.338–342 The same applies for the ES simulation (Table 1, Electron spectroscopy). The solutions and their particularities are presented in the previous section devoted to ML for ES, for which the labelling process would also demand a parallel script.
In case the application of interest cannot benefit from model-based labelling, we could instead take advantage of the already existing images or crystal databases. The goal will be finding the datasets in which the data structure resembles as much as possible our targeted data. Regarding images, this means having (or forcing) the same number of information channels (typically single, grayscale), number of pixels representing edges (learnt convolutional filters may not detect edges or features represented by a different number of pixels), similar histograms and contrast/brightness descriptions, total number of pixels, the image calibration or resolution (if accounting for a physics-aware model), or the materials and morphologies illustrated. In these cases, the starting point can be the transfer learning of models trained on habitual and general computer vision databases (Table 2, General digital images). The idea is to exploit transfer learning with the datasets that resemble our data the most and provide a better starting point in the model training than just initialising the weights randomly or with the Xavier method.362 In fact, despite the disparity between mainstream digital imaging and electron micrographs, this procedure reported advantageous results when training an ImageNet-initialised VGG-16 architecture used for the classification of HRTEM images of carbon nanomaterials.95 However, EM databases may constitute an even better starting transferable knowledge given the proximity of the variance of the data. The most interesting EM databases to initially use or work with are depicted in Table 2, Databases for electron microscopy images and spectra, where both unlabelled and labelled datasets are available free of charge. Complementarily, these micrograph databases could also be linked with crystal structures (e.g., encoded .cif files as the labels) for a rapid and automated crystallographic phase identification. This idea is represented in Fig. 6, where the development of this hypothetical application is schematically represented, requiring no specific coding ability nor extraordinary computing resources. The available crystallography databases to complete similar tasks are huge and are updated regularly. A summary of the available crystallography databases can also be found in Table 2. These databases thoroughly store the structural crystallographic information of manifold crystal phases. Interestingly, its format is suitable for encoding physically meaningful information in our models, such as cell parameters, space groups, chemical bonding and valence states, among others.
| Database | Data amount (images) | Content | Data type | Accessibility | Ref. | |
|---|---|---|---|---|---|---|
| General digital images | ImageNet | >14.000.000 | Multiple categories of digital images (animals, vehicles, objects…) | Labelled | Open | 363 and 364 |
| MNIST | 70.000 | Handwritten digits | Labelled | Open | 365 and 366 | |
| LabelMe | >4.000 | City landscapes showing people, vehicles, objects… | Multi-labelled | Open | 367 and 368 | |
| ESP | >350.000 | All kinds of digital images and increasing | Multi-labelled | Upon request | 369 | |
| Lotus Hill | >636.000 | Multiple categories of digital images (animals, vehicles, objects…) | Multi-labelled | Upon request | 369 | |
| Caltech101 | >9.000 | Multiple categories of digital images (animals, vehicles, objects…) | Labelled | Open | 370 | |
| Caltech 256 | >30.000 | Multiple categories of digital images (animals, vehicles, objects…) | Labelled | Open | 371 | |
| MSRC kinect gesture dataset | >719.000 | Human movements and gestures | Labelled | Open | 371 | |
| PASCAL | >19.000 | Multiple categories of digital images (animals, vehicles, objects, gestures…) | Multi-labelled | Open | 372 | |
| Electron microscopy images and spectra | TEM ImageNet | 14.000 | – Simulated atomically-resolved STEM | Multi-labelled | Open | 373 |
| – Multiple materials and orientations | ||||||
| EPFL EM dataset | 1.065 | Cell biology, experimental | Labelled | Open | 374 | |
| Freiburg University | 637 | Cell biology, experimental | Labelled | Open | 375 | |
| ImageJ | Multiple sources >30 TB in images | Cell biology, experimental | Labelled and unlabelled | Open | 376 | |
| CNR – IOM SEM dataset | 22.000 | – Experimental images | Labelled | Open | 377 | |
| – Low-dimensionality nanostructures | ||||||
| – MEMS | ||||||
| Zelinsky Institute of Organic Chemistry SEM dataset | 1.000 | Simulated images of nanoparticles | Labelled | Open | 378 | |
| DeCost – Holm SEM dataset | 2.048 | Simulated images of nanoparticles | Labelled | Open | 379 | |
| Warwick EM dataset | 135.375 | – 19769 experimental STEM | Unlabelled | Open | 380 | |
– 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 266 experimental TEM 266 experimental TEM |
||||||
– 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 simulated exit wavefunctions 340 simulated exit wavefunctions |
||||||
| EELS DB | >200 spectra | Experimental EELS + XRD | Unlabelled, but with metadata | Open | 266 | |
| EELS.info | Sample spectra for every element | Experimental EELS | Unlabelled, but with metadata | Open | 381 | |
| Crystallography databases | Crystallography open database | >490.000 crystal structures | Complete crystallography of inorganic, organic, minerals and metal–organic compounds | Unlabelled, but with metadata | Open | 382 and 383 |
| – Both experimental and theoretical studies | ||||||
| Inorganic crystal structure database, ICSD | 60.000 crystal structures | Complete crystallography of inorganic structures | Unlabelled, but with metadata | Paid | 384 and 385 | |
| – Both experimental and theoretical studies | ||||||
| NIST crystal database | – 220.000 crystal structures | Complete crystallography of inorganic, organic, minerals and metal–organic compounds | Unlabelled, but with metadata | Paid | 386 | |
| – 81.000 electron diffractograms | – Both experimental and theoretical studies |
 | ||
| Fig. 6 Example of the hypothetical development of a Deep Convolutional Neural Network (DCNN) model to correlate Annular Dark-Field Scanning Transmission Electron Microscopy (ADF-STEM) images with the crystal phase and zone axis displayed. The Machine Learning (ML) workflow is thoroughly based on open software and resources, and requires almost zero ML-specific knowledge and funding/infrastructure. The ADF-STEM micrographs are taken from the TEM ImageNet open database,373 with 14.364 images of multiple crystal structures. The images metadata correlates them with a class defined by the crystal phase and the zone axis (labels). The complete crystallographic information of the crystal phases is extracted from the free Crystallography Open Database.382,383 Next, a VGG396-like architecture is used from an open-source397,398 repository like GitHub,399 almost eliminating the coding. The training can be done either in a PC or in a cloud service such as Microsoft Azure,400 Google Cloud401/Colab,402 IBM Cloud,403 among others. Eventually, the model can be tested and used, allowing the user to identify the crystal phases and orientations of different micrographs. | ||
If we cannot either label via modelling or thoroughly rely on existing databases, we have no other option than labelling the data manually. After carefully planning the necessary training volume, one solution is the trivial manual labelling done by the researcher. However, it is not recommended, as the researchers’ time is such a valuable resource that should not be spent in this repetitive task with no intrinsic nor transferable value. Alternatively, one may opt for a company specialised in preparing datasets for ML as another valid purchasable resource, as can be reagents, human talent or computing time. These companies excel in optimally augmenting and labelling the data of interest. Nonetheless, scientific labelling may require a trained eye. As a result, the labelling instructions should be clarified to reduce biases as much as possible, with a regular supervision of the results. Companies offer both tools for an optimised and intuitive manual labelling, and the labelling service itself: Amazon's mechanical Turk,387 appen,388 TrainingSet.AI,389 Superb AI,390 iMerit,391 Clickworker,392 ImageLabeller in MATLAB,393 Sama,394 or LabelMe Annotation tool,395 among others.
3.2 Model design
As a matter of fact, the data generation step should always be accompanied with a decision on the model architecture. The description and purposes of the available unsupervised algorithms, models, supervised networks and architectures is out of the scope of this review article. There is plenty of information about it in the literature, and we summon the attentive reader to the review by J. Ede, which described in detail the most widely used architecture types in EM.92 Generally speaking, CNN will be the preferred option for the EM data that can easily be structured as a vector, matrix or tensor (line spectra, images, SI…). Anyhow, assuming the architecture choice is appropriate, we can search for its code implementation, and preferably open source. One of the key intrinsic concerns of the Python language and specifically of the AI community, is the will towards open science. Gladly, this is translated into huge sources of open code for implementing any imaginable ML model. Fortunately, the EM community has followed this democratisation trend and has already provided open tailored solutions. Interestingly, these solutions come along with tutorials and intuitive guides both for newcomers searching for basic implementations and for experts wanting to carefully fine tune well-established models. For example, Pycroscopy (and its sub packages like AICrystallographer,404 AtomAI,405,406 GPax,407 pyTEMlib408) offers a centralised platform of ML/DL pretrained models and raw architectures, among other analytical functionalities.320,405,409 It provides a straightforward way to call and train models like U-Net or VAEs, as well as having their weights initialised on EM/materials data (for transfer learning). On the other hand, the Materials Simulation Toolkit for ML (MAST-ML) provides a broader platform to boost materials-related research with ML.410,411 DeepImageJ is its equivalent for biosciences, although the network architectures and weights might be exploited universally.412 In a similar way, and despite it was originally intended for particle tracking in optical microscopy, DeepTrack 2.0 offers a pythonic solution to easily call ML/DL models.413,414 This is why this might be the preferred choice for optical microscopy or biosciences applications. In this case, it also displays a user-friendly graphical interface, with which newcomers will thank the interpretability of the deployable tools. Additionally, CDeep3M and ZeroCostDL4Mic work similarly, while offering the added possibility to run the code directly on cloud computers via notebooks.415,416 The comprehensible tutorial format of these notebooks makes the implementation of the provided methods even more direct.417 In addition, for those looking for CS tools, they can also be easily implemented with open codes like CSET418 and RTSSTEM,160 tailored for EM and its tomography.The previous software packages are the formal answer to the community's need for straightforward and centralised ML/DL tools. However, if a given publication is inspiring us a specific architecture, one possibility is to directly dig into the article material. In this way, most of the papers developing a certain ML model contribute further with the code (and even datasets) towards reproducibility and for it to be applied in complementary research. Seldom do the authors protect their codes with private intellectual property. The proof is that most of the articles reviewed in the imaging and spectroscopy sections provide a GitHub or Zenodo link to freely download the represented code.399,419 Indeed, these repositories, among others like OSDN,420 Bitbucket421 or GitLab,422 have become powerful search engines to intermediary-free get open software and code snippets. Representatively, searching for “U-Net” in GitHub results in 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 732 resources (Search date: July 2022) that could be used instead of coding U-Net from scratch. Similar results are obtained by searching for the most well-known network architectures in image analysis, VGG,396–398 AlexNet423,424 or YOLO9000,425 among many others.426–431 The use of one or another network will depend on the final application: we would use U-Net if we want a pixelwise classification of our image, but VGG-like architectures for classifying the whole image into a category. Alternatively, in case the research project demands a ML model not yet programmed nor shared, it could be coded from scratch. Obviously, this approach demands a higher understanding of coding and of the ML scheme. Nevertheless, the Python packages indicated in Table 3 offer intuitive programmatic interfaces to easily implement from the simplest unsupervised model to the most complex neural network. The most interesting or exploitable features of each are indicated in Table 3, although in a general basis, the beginner user would find a better ally in high-level APIs such as Keras, while the advanced user looking for further fine-tuning will benefit from low-level APIs like TensorFlow.
732 resources (Search date: July 2022) that could be used instead of coding U-Net from scratch. Similar results are obtained by searching for the most well-known network architectures in image analysis, VGG,396–398 AlexNet423,424 or YOLO9000,425 among many others.426–431 The use of one or another network will depend on the final application: we would use U-Net if we want a pixelwise classification of our image, but VGG-like architectures for classifying the whole image into a category. Alternatively, in case the research project demands a ML model not yet programmed nor shared, it could be coded from scratch. Obviously, this approach demands a higher understanding of coding and of the ML scheme. Nevertheless, the Python packages indicated in Table 3 offer intuitive programmatic interfaces to easily implement from the simplest unsupervised model to the most complex neural network. The most interesting or exploitable features of each are indicated in Table 3, although in a general basis, the beginner user would find a better ally in high-level APIs such as Keras, while the advanced user looking for further fine-tuning will benefit from low-level APIs like TensorFlow.
| Package | Used for | Programming interface/language/APIs | Key feature | Accessibility | Ref. |
|---|---|---|---|---|---|
| Caffe/Caffe2 | Supervised | Python, C++ | DL performance and cross-platform deployment → features migrated to PyTorch | Open | 432 and 433 |
| Ctypes | Un- and supervised | C/C++ → Python | Use C/C++ libraries in Python | Open | 434 |
| Cython | Un- and supervised | C/C++ → Python | Use C/C++ libraries in Python | Open | 435 |
| Dask | Un- and supervised | Python | Scalability, parallelisation | Open | 436 |
| DL Toolkits | Supervised | Wolfram Mathematica | Multifunction and interpretability | Paid | 437 |
| Gensim | Un- and supervised | Python | For natural language processing | Open | 438 |
| GNU Octave | Un- and supervised | Octave | Flexibility | Open | 439 |
| Hadoop | Un- and supervised | Apache | Scalability, big data and parallel computing | Open | 440 |
| Keras | Supervised | Python | Easy implementation of DL | Open | 441 |
| Mahout | Un- and supervised | Apache | Scalability | Open | 442 |
| MATLAB | Un- and supervised | MathWorks | Flexibility | Paid | 443 |
| Matplotlib | Un- and supervised | Python | Visualization and plotting | Open | 444 |
| MXNet | Supervised | Apache (integration with Python, Java, C++, R, Scala, Julia, Clojure, Perl) | Scalability and interpretability | Open | 445 |
| Numba | Un- and supervised | Python | Code parallelisation | Open | 446 |
| Numpy | Un- and supervised | Python | Flexibility | Open | 321 |
| OpenCV | Un- and supervised | Windows, Android, Linux, MacOS, FreeBSD, OpenBSD – C/C++, Python, Java, Android | Computer vision and image processing | Open | 447 and 448 |
| Pandas | Un- and supervised | Python | Tabular data processing | Open | 449 |
| Pattern | Un- and supervised | Python | Web mining | Open | 450 |
| Pillow, Python Imaging Library | Un- and supervised | Python | General image processing | Open | 451 |
| PyTorch | Supervised | Python, C++, Java | DL flexibility and rapid prototyping | Open | 452 |
| scikit-image | Unsupervised | Python | ML image processing | Open | 453 |
| scikit-learn | Unsupervised | Python | Flexible ML built-in tools for data analysis | Open | 454 |
| SciPy | Unsupervised | Python | Flexible general built-in tools for data science | Open | 455 |
| Shogun | Unsupervised | Python, JavaScript, C/C++, R, Ruby, Octave, Java, Scala | Multi-language support, ML data science | Open | 456 |
| MLlib | Un- and supervised | Apache Spark (integration with Python, Java, Scala and R) | Fast general ML | Open | 457 |
| TensorFlow | Un- and supervised | Python, Java, C++, Swift | Highest flexibility, low-level DL | Open | 458 |
| Theano | Un- and supervised | Python | DL flexibility and rapid prototyping | Open | 459 |
3.3 Training and testing
Once the (training, validation and test) data and the model are ready, the question is where to train the model. Generally, in DL the training volume is of about the 90–95% of the total data, while the test and validation set equally share the remaining 5–10%. This assumes that our data volume is large (i.e. 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 images or more). Nonetheless, these numbers are nothing but a guide towards best practises that can be modified depending on the total data volume. For instance, if our data volume is scarce because it is difficult to generate it, we will decrease the training percentage in favour of test and validation. At the end, these percentages could even be considered as hyperparameters to tune and will eventually be defined to maximise the overall performance. Practically, if the model and training volume is reasonable (i.e., around 106–107 trainable parameters and from 10
000 images or more). Nonetheless, these numbers are nothing but a guide towards best practises that can be modified depending on the total data volume. For instance, if our data volume is scarce because it is difficult to generate it, we will decrease the training percentage in favour of test and validation. At the end, these percentages could even be considered as hyperparameters to tune and will eventually be defined to maximise the overall performance. Practically, if the model and training volume is reasonable (i.e., around 106–107 trainable parameters and from 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 15
000 to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 512 × 512 images), the training time should mostly be a few hours in a regular PC with a GPU. Larger models, and even the generation of larger data volumes would require a larger computing infrastructure. For that, the ideal case scenario would be a partner institution placing computing systems at the researcher's disposal. In case this requirement is not met, then online and cloud computing services would instead be suggested. The following are the most established services for renting high-performance computing time, which most of them provide specific solutions for ML projects: Alibaba Cloud,460 Amazon Web Services,461 Microsoft Azure,400 Deepnote,462 Genesis Cloud,463 Google Cloud401 and Colab,402 IBM Cloud,403 OVHcloud,464 and Paperspace CORE.465 Whilst accessing powerful computing solutions is key to speed up the training-tuning cycle, the huge hyperspace susceptible to be modified can be overwhelming to face. To cope with that, we can nowadays find intuitive and powerful interfaces providing insight and suggestions to optimise the training and hyperparameter tuning of our models (Weights & Biases,466 and PerceptiLabs467). In fact, these solutions are not only intended for ML newcomers, as anyone looking for the effects entailed by the hyperparameter tuning of their models will benefit from these visualisation tools.
000 512 × 512 images), the training time should mostly be a few hours in a regular PC with a GPU. Larger models, and even the generation of larger data volumes would require a larger computing infrastructure. For that, the ideal case scenario would be a partner institution placing computing systems at the researcher's disposal. In case this requirement is not met, then online and cloud computing services would instead be suggested. The following are the most established services for renting high-performance computing time, which most of them provide specific solutions for ML projects: Alibaba Cloud,460 Amazon Web Services,461 Microsoft Azure,400 Deepnote,462 Genesis Cloud,463 Google Cloud401 and Colab,402 IBM Cloud,403 OVHcloud,464 and Paperspace CORE.465 Whilst accessing powerful computing solutions is key to speed up the training-tuning cycle, the huge hyperspace susceptible to be modified can be overwhelming to face. To cope with that, we can nowadays find intuitive and powerful interfaces providing insight and suggestions to optimise the training and hyperparameter tuning of our models (Weights & Biases,466 and PerceptiLabs467). In fact, these solutions are not only intended for ML newcomers, as anyone looking for the effects entailed by the hyperparameter tuning of their models will benefit from these visualisation tools.
After training the model, the ML workflow is almost complete. The only step remaining would be the testing or benchmarking of the resulting trained model. At this point is when the dataset division into test and validation sets play a role. The test set will be used to iterate into the hyperparameter tuning till the test metric is maximised. Only then, the validation set is evaluated to output a final metric on the performance of the model on this dataset. This split into test and validation is not mandatory but recommended. With this, we reduce the bias of the final metric by avoiding the tuning of the model with the information that must serve the final metric. Apart from testing with our own data, it is recommended to evaluate the performance of the model with a standardised benchmarking dataset. Each community can formalise a dataset intended for a given purpose and make it the benchmark to follow when creating similar applications. For example, EM for cell biology received formal segmentation benchmark standards with a platform dubbed EM-stellar.326 Nevertheless, the feature complexity of the materials science EM data, along with the early stage in which ML/DL is currently in the field, turns into the absence of formal benchmarking tools. As reviewed, the applications achievable by ML methods are manifold, and each would require a specific benchmark routine. As a result, and until task-specific (or even more general task-agnostic) benchmark tools are standardised in EM, the best practice can be the strict evaluation of a representative test/validation set, by the most suitable metric given the aim of the model. Eventually, the model should be tested with the experimental data for which it was originally aimed. Complementarily, existing ML or general data processing tools can be useful to crosscheck the performance of our trained model. This can be both a substitute for absent benchmarks and a validation tool for successfully benchmarked models. For instance, if our model is devoted to crystallographic analysis or phase identification, we can use the powerful CrysTBox for a quick validation.468 If our model is for 4D-STEM data processing, we may additionally use Py4DSTEM469 or Pyxem470–472 for corroboration. In case our developed model tries to automate a particular step of the TEM data acquisition, maybe combining it with the ANIMATED-TEM toolbox allows us to reach the next level of overall automation.473 On the other hand, if our application is intended for image or spectra analysis, it may benefit from double-checking the results manually in one of the many data processing software available, among which we highlight the broad capabilities and open philosophy of gempa,474 LiberTEM475 and HyperSpy.476,477 More specifically, if the goal of the trained model is general STEM strain analysis, we can crosscheck it with Fourier-space phase analysis and with real-space atomic position determination, or even with Moiré fringe imaging or the simulation of lattice elasticity relaxation.7,8,478 For instance, among the real-space analysis we find traditional and well-stablished methods such as Atomap,99,479 ranger,1,10 qHAADF,480,481 iMtools,482 StatSTEM2, or oxygen octahedra picker,483 but also ML/DL-based methods (e.g., atomic column finding), which can be even more indicative of the state of the art for comparison purposes.6,15,59,97
The tools and resources reviewed in this section are meant to make the electron microscopists’ life easier. In fact, ML routines can be fully developed thanks to them, requiring little resources to make brand new models come true, as depicted in Fig. 6. Nevertheless, these are the tools that are currently being used or have been developed or adapted mostly by the EM community. Therefore, there is plenty of room at the bottom for introducing new models and architectures yet unexplored in EM. For instance, the need for rapid and trustworthy dynamical simulations has catapulted the popularity of graph neural networks.484–488 Interestingly, the structure of the EM data could perfectly fit these flexible networks, allowing to point towards dimensionality-independent models. Even (deep) RL (already reviewed for a couple of applications107,122,163), key in robotics and in videogames design, could be the major breakthrough for the complete TEM automation.489,490 These and many other ML developments not yet implemented in EM are reviewed with further attention in the next section.
4. Inspirations from other fields for future developments
The previous sections described manifold EM applications and how the numerous available ML methodologies pushed towards thrilling advances in the field. Nevertheless, the reviewed potential of ML is just the tip of the iceberg of everything ML has to offer. The best way to realise this fact is by the examination of the significance of ML in other fields where it is not a complementary resource but a keystone. As promised, this section is intended to evaluate the ML-based case studies in these other fields and the way they could be beneficial to EM in order to solver materials science questions in the near future. Importantly, it is easy to repeatedly consider the following results as robust starting points for tailoring specific experiments to the materials/EM community. Or the other way around, the previously reviewed developments could be extrapolated to these fields to strengthen them even more. In fact, both the electron microscopists and materials science researchers, but also domain experts from the specified fields may benefit from the ideas discussed below. The ideas and findings discussed throughout the section have been schematised as a guide in Fig. 8.4.1 Microscopies and imaging
Moreover, autoencoders were also used to detect those single particles orientation and help with the optimisation of the 3D reconstruction step, similarly to S. Kalinin et al.'s work.84,88,497 In fact, ML and DL was used to improve the reconstruction of the tilt series. Remarkably, this ML-based improvement unlocked new fidelity landmarks allowing to decipher the secondary structure of proteins.180,498,499 To achieve it, D. Si et al. used support vector machines, while R. Li et al. used a CNN instead, obtaining comparable results.191,500 As happened with region-finding automation, these approaches can be used to improve the resolution of materials ET, and to make it gentler, as observed with CS.142,146,148 In fact, CS, which was extensively used for materials science, is just testimonial in cryo-EM. Therefore, CS may be a way to improve the biomolecule reconstruction further, even with ML algorithms mimicking CS, by relaxing the total dose and data necessary to complete these reconstructions.
 | ||
| Fig. 7 Segmentation of optical microscopy images of cells, 2D materials and steels. The cells were imaged with fluorescence microscopy and segmented using a neural network trained on synthetic 3D models of cells simulating the imaging conditions.511 The optical microscopy of stacks of 2D materials like MoS2 were unsupervisedly segmented and classified to map the number of stacked layers.513 The same applies to optical images of steels and its different phases. This case is a combination of the previous two: the authors segmented the images with a trained convolutional neural network and classified the steel phases with an unsupervised clustering algorithm.514 | ||
Specifically for biosciences, contouring and drawing the cells area is of paramount importance for multiple studies such as the cell division and the cell cycle, or cell dynamics and the interactions with substrates. Doing it in an automated way is therefore a requirement to obtain representative results over large populations of cells.501 One of the main challenges is that cellular and subcellular features are complex and diverse in morphologies and textures. This problem would hamper the implementation of a robust unsupervised solution. As a result, supervised (mostly CNN) approaches are excelling in this job in contrast, fluorescence, and super-resolution microscopy, among others.502–510 For that, the idea we have widely reviewed on simulating data that resembles the variability of our target micrographs is also valid here. For instance, A. Sekh et al. followed the idea of physics-based labelling by simulating fluorescence microscopy images out of the simulated 3D geometries of organelles (Fig. 7).511 The authors proved the viability to train a subcellular DL segmenting tool on simulated data with a workflow that faithfully resembles most of the supervised routines reviewed in atomic resolution STEM. At the end, it is important to remember that the original U-Net was designed for cell segmentation!65,512
The reach of ML-based segmentation in optical microscopy is broadened when applied to materials science. For instance, in metallurgy it is a common practise to image steels and locate and quantify the spatial extension of their phases and grains. Furthermore, it is common to extract statistics on the total area synthesised when optimising the growth of 2D materials, the automation of which is welcomed. In these cases, the complexity of the imaged features perishes in comparison to those imaged in biosciences. Therefore, these simpler features allow unsupervised routines to succeed. For example, the number of layers of stacked graphene or dichalcogenide sheets and the micrograins of steel can be automatically counted and mapped with clustering-based segmentation (Fig. 7).513 In addition, postprocessing can be applied to the segmented data if an end-to-end application is sought. An example of this is the semi-supervised approach followed by H. Kim et al., who mixed a CNN-based segmentation and simple linear iterative clustering to firstly, identify, and afterwards classify the microstructure of experimental optical images of steel (up to fields of view of about 1 mm) (Fig. 7).514–516 This example highlighted that, as mentioned, the automation makes the statistics extraction and the handling of large regions of interest realistic. Nevertheless, its application to EM and materials science might not be so straightforward. The idea of segmentation is a bit more abstract in EM, as the features presented strongly depend on the magnification, and there are multiple magnification intervals providing meaningful information. Thus, the techniques to be used for segmenting the atoms in an atomically resolved micrograph will differ from the segmentation of a large field of view where no atoms appear. Consequently, the reviewed segmentation approaches for optical microscopy could be beneficial for EM experimental setups exploring the morphology of nanostructures and nanodevices, as in the case of SEM and low magnification (S)TEM. This is because these would be the EM situations that better mimic the scenarios handled by optical microscopy, with immense fields of view being analysed. Indeed, both industrial processes and other tedious counting steps would take valuable advantage from it. Importantly, the sparsity of the EM features would likely demand a supervised model to attain robustness. Hypothetically, the first step towards this time-saving model could be transferring the learned weights from the optical microscopy models reviewed here. Unfortunately, the additional generation of the necessary meaningful ground truths to complete the training remains an open challenge, by now.
The studies augmenting the feature space are abundant, but all share the emphasis on capturing the images texture.527–529 By texture the researchers refer to different ways to deal with the pixels intensity to convert it into potential features.524,530,531 For instance, the intensity histogram and the segmentation of the images and its resulting shapes could be considered as additional straightforward features. Moreover, not as direct local descriptors such as the grey-level co-occurrence matrix or the neighbourhood grey-level dependence matrix proved helpful.525 Indeed, the powerful idea of adding meaningful extra features to the EM data is a synergy that it is worth exploring. This is because most of the explored articles just relied on the intensity as “the feature”, and only occasionally was it accompanied by additional channels of information. Being careful about the statistical significance of the added features to avoid overfitting, this approach could potentially benefit especially unsupervised routines in EM. This approach could start with the simple stacking of, for example, multiple edge detection filters as fake channels of the original image. Furthermore, we could even add multiple DL segmentation routines or higher-complexity image processing as the added features. Interestingly, within an interactive exploratory workflow, additional features could be progressively added till the model is found to overfit, and then to progressively constrain these features towards a more robust eventual unsupervised model.
A similar idea is recurrent in Atomic Force Microscopy (AFM), although most of its ML studies are devoted to optimise the extremely time-consuming analysis of force–distances curves.545,546 These curves arise when testing the proteins superstructure in tension/elasticity experiments, with the binding/unbinding of proteins or macromolecules that interact with each other, after the indentation of the tip into cellular and subcellular structures, or into organic molecules and inorganic materials. The typical workflow is then to fit these curves into a possible model that explains the (bio)physics behind the interaction. Of course, this may end up in a time-consuming iterative process guessing the most close-fitting assumption. Nevertheless, the advances in ML allow to automate its analysis by fitting the data with trained models. In fact, this process was automated by training neural networks both to fit the curves and to generate test models, therefore accelerating the model-experiment correlation.547–549
Interestingly, the tackled experimental setups of atomic force microscopy share the fact that they induce some degree of modification to the sample, either by digging a topological hole in a wafer or by stretching the ternary structure of a protein. Therefore, these time or effect-resolved analyses would fit properly in the framework of in situ EM experiments. The conversion of the acquired in situ datasets into a data format equivalent to force–distance curves would allow the immediate exploitation of these already built-in model validation tools. As a result, EM experiments correlating time and beam-damaged area, voltage and domain orientation, or gas pressure and growth ratio, would instantly have their analysis automated when matched with the workflow provided by atomic force microscopy and its accessory techniques.
4.2 Big data and physics
The detection of a priori hidden features or patterns in data is of outmost relevance in the characterisation of the outer space.554–557 Finding new galaxies, black holes, dark matter and even dark energy is driving astronomers mad, and the ML tools are helpful on this crusade.558–560 For example, neural networks and decision trees proved useful for detecting black holes in globular clusters, dark matter in strong-lensing systems, and even for gravitational wave sensing.561–563 These examples could fit into the category of anomaly detection, which has not been formally explored in detail in EM yet. The concept of anomaly detection is quite self-explanatory, being key in multiple scientific, technical or business fields, as finding and understanding outliers is inevitably a source of knowledge. Besides, as ML excels in finding patterns or regressions in data, just by complementarity so does it to find data that deviates from those found regressions. Other astronomy applications that also shine light on the potential of ML anomaly detection are the spotting of extragalactic transient astronomic events (e.g., supernovae), the refinement of supernovae simulation through anomaly detection and correction, or even the general searching for any anomaly in any dataset in the so-called “Systematic serendipity”, among others.564–567 Moreover, an especially interesting field of application is the detection of exoplanets or near-Earth objects watch (e.g., asteroids and comets), and the premature detection of those having orbits with potential impact hazard to the Earth.568–571 Not surprisingly, CNN excelled in the detection of both exoplanets and asteroids, again confirming their versatility.572–575
Importantly, these ideas closely bonded to anomaly detection would fit in the EM framework with ease. Some would say that some of the applications reviewed would fit in the anomaly detection category, but as said, the truth is that the concept hardly ever appeared formalised in EM studies. At least not until P. Cho et al. developed an anomaly detection method combining PCA and CNN for detecting point defects in atomically resolved micrographs.68 Interestingly, the authors could generate heatmaps highlighting the image regions in which the presence of defects (i.e., anomalies) was more likely. As mentioned, so far, we have reviewed a few EM studies that operated similarly, but none performed as maturely as the surveyed examples in astronomy. It is not about being picky about the wording given to every application, but to have the anomaly detection routines in mind as tailored solutions for problems like the point defects example. For instance, the astronomy example holding the comparative and cooperative training between anomaly-free and anomaly-full datasets would not even be thinkable unless the anomaly detection concept was deeply implanted in the researcher mindset.567 Indeed, the defects detection idea could be opened up further to interpret any lattice distortion or strain: a model trained on a perfect regular atomic lattice (anomaly-free), complemented with a model trained on a distorted lattice labelling the strain and the defects (anomaly-full). On the other hand, in an EELS edge identification model, the anomaly-free set could be represented by a smooth background, with the anomalies being the core-loss edges themselves. Or even subtler with the edges acting as the main signal and the anomalies being the edge shifts or near-edge variations, in a finer chemical analyser.
4.2.2.1 Classical methodologies. The idea of doing a final fourth section comparing the state of the art of ML in EM with its state in other fields has its roots in astronomy, but also in high-energy physics. Since its origins, the uninterrupted massive data flow coming from particle colliders demanded special data processing tools, as in astronomy. Again, ML embraced this labour fitting well for necessities such as the adoption of generative models to provide a real-time answer to simulations on the detector response, to accelerate the exploration of parameters based on the matrix element method, or to allow the analysis of the rawest data, such as raw detector hits, in end-to-end models.576–580 These cases constitute narrow field-specific problems with a hard to stablish equivalence to EM. However, the aspect that receives most of the attention, and that is also easier to link, is the analysis, identification, discrimination and classification of the collisions themselves and the resulting particle jets and showers.581,582
Generally, the main goal is finding rare events deviating from a standard model background (i.e. the main theoretical model describing the elemental particles and their interactions). Importantly, most of these works are centralised in the Large Hadron Collider (LHC), which the foremost hub to be inspired by.583,584 Either by a centralised acquisition and processing in the same LHC, or by acquiring in LHC and processing in collaborating centres, or vice versa, hardly ever is the LHC not involved in one way or another. In fact, it conducted the main advances in ML for finding these rare events in data. The huge amount of available data and the ease to accurately simulate it made that mainly supervised models were used since the beginning. These were typically based on both CNN and RNN to distinguish between different types of particles in traces of jets (e.g., quarks vs. gluons) or to directly discriminate actual data from background.585,586 A particularly interesting example representing this trend came from P. Komiske et al.'s work, in the framework of physics-aware models.585 The authors used a CNN in which the input was a multichannel image and the output the subtle features and patterns (e.g. particles) to detect. The novelty lied in that the first channel of the input image represented the image itself, but every additional one represented a different measured physical property. In this way, the authors made sure the model would treat differently two images if obtained under different experimental conditions, consequently making the model aware of the experimental setup employed. The idea introduced here is of paramount importance for ML-based EM and will be developed a few subsections ahead. Also of great importance is the use of generative models in the field. In fact, we could find multiple studies exploiting the goodness of GANs, specially for simulating particle showers, as reviewed above.587–589 The advances and examples in EM using GANs are not scarce, but as mentioned, they have only just scratched the surface of what is possible. Again, and in a general basis, the EM community should slowly push towards embracing generative models over supervised ones, even if it may seem intimidating. This is why, the imitation of the progress done in the previous jet-simulator GANs studies may serve us to simplify an otherwise titanic task.
4.2.2.2 Quantum machine learning. The outstanding level of the ML practitioners in high-energy physics allowed the field to reach the next level of complexity: quantum ML (QML). While the quantum computing researchers strenuously battle to profile the problems and algorithms that can benefit from quantum mechanics, the research on particle physics has already applied some solutions based on this new paradigm.590 In any case, the end-to-end QML is currently a chimera, although intermediate steps such as algebra, linear differential equations solving, or pattern recognition have been implemented.591,592 Excitingly, the literature referring to quantum advantage in this field is vast, although we want to specifically highlight the next piece of work given its potential (direct) applicability to EM. S. Chen et al. proposed a quantum CNN to classify multiple high-energy physics events.593 In the model, the convolution operations were performed by a variational quantum circuit, which is a set of quantum states and parameters that can be optimised iteratively and classically. In this case, the network consisted of only two quantum convolutional kernels, but already learned and tested faster than the classical analogue (Fig. 9a).594 Therefore, we cannot help seeing this exact same quantum kernel learning the patterns from EM images, as the workflow is exactly the same as the multiple times reviewed along this contribution.
 | ||
| Fig. 9 Future perspectives of advanced Machine Learning (ML) for Electron Microscopy (EM) data analysis and automation. (a) Quantum Convolutional Neural Networks (QCNN) in high-energy physics already provided quantum advantage versus classical CNN even with just two convolution kernels. However, there are no research examples of quantum ML in EM yet.594 Reprinted by permission from Springer Nature, I. Cong et al., Nat. Phys., 2019, 15, 1273–1278, Copyright (2019). (b) Schematic of a Reinforcement Learning (RL) CNN designed to autonomously play videogames. The convolutional layers allowed to get information from the videogame frames and to translate that into actions (joystick + buttons) that would maximise the score in a given game. Instead of a joystick, we can think of the microscope control panel in a RL approach that seeks to maximise the image quality.642 Reprinted by permission from Springer Nature, V. Mnih et al., Nature, 2015, 518, 529–533 Copyright (2015). (c) RL used to train an autonomous surgical robot. The RL trained the robot to take the elements on the table one upon the other as in a surgical intervention. The algorithm would reward putting the objects together and penalise any other action that would not end up in this result.627 We can imagine a similar robot that takes a lamella or a grid to a holder and afterwards inserts it into the electron microscope. Furthermore, if we concatenate this autonomous holder loader/inserter with the joystick-like approach, we obtain the fully automated microscope! | ||
Interestingly enough, two of the main hot topics in the current quantum computing/quantum ML research could be of direct concern for EM. These are quantum Fourier transforms and quantum image processing.595–597 This increasing interest is based on the belief of the eventual supremacy of quantum computing for these applications.594,598–600 As a result, it is easy to get overexcited with the perspectives QML would promise in these two routinary processes in EM. Nevertheless, as reviewed through the entire text, the path classical ML must follow is still huge, and QML should only be thought as a complementary and exploratory tool, by now. For instance, it would make sense to explore the advantages of QML for well-established applications such as DL-based atomic-column finding. Even to just prepare the equivalent algorithms for the highly-anticipated establishment of quantum computers, or for testing them in quantum simulators or tensor networks, just like the quantum computing practitioners do. On the other hand, exploring the new horizons of the ML functionalities in EM, directly stepping through quantum algorithms might be detrimental given the additional implementation barriers.
Quantum algorithms are thought to transform the modelling of physical systems in which quantum physics have a primordial role. As nanostructures are typically ruled by quantum laws, the access to these machines should enhance its simulation fidelity. In the case of EM, as commented, the required level of theory to build large datasets for ML applications is not too strict. However, using quantum circuits to force a physical constrain in our ML models would be amazing. It would allow our models to encode certain complex behaviours that otherwise would be extremely difficult to learn. For instance, an image dataset on classical atomic columns could be immediately converted into an ab initio dataset with the following idea: we could train a neural network on classically simulated atoms but adding a quantum circuit forcing quantum mechanical interactions between them. This idea lies within the science-aware experiment planning, treated in more detail below.
Overall, the image processing and CNN usage of most of these examples only exhibited the first degrees of complexity if compared to EM. This is why, (imaging-based) Earth sciences would leverage the previously reviewed image processing techniques. The trivial example is on crystallography, which is key for geology. Oppositely, as evaluated, Earth sciences excel in forecasting tasks. As a result, EM could take advantage of similar predictive decision-tree algorithmics to work, for instance, in conjunction with CS. Thus, they could fill missing data gaps through predictions, after being trained on pairs of partial-complete datasets. These data gaps could be either time-resolved for an efficient and low-dose in situ setup, 3D-correlated to overcome the missing wedges in tomography, or for partial scans in STEM, as happened with CS. Another application of interest would include the prediction of events such as spontaneous crystallisation or phases transitions during in situ experiments.
4.3 Artificial human-like systems: the path towards automation?
As discussed, the ultimate goal of AI in EM is the total automation of the electron microscope. In other words, we dream of a TEM to autonomously behaving as if it was operated by a human expert. With this major goal in mind, the close examination of technological fields devoted to automating human actions can be highly beneficial. Obviously, the major methodology breakthroughs are linked to the fundamental research on pure computer science and AI. Unfortunately, though, these are occasionally difficult to abstract to practical cases. Nevertheless, there are some fields closer to the application development the strategies of which might be even more useful for the practical purposes to which our community is devoted: robotics and videogames. These disciplines rapidly come to mind when thinking on complex automated behaviours and continuous interactions with human beings, similarly to voice-assistant services. For EM, the main automation challenge is in the reproduction of domain-specific knowledge rather than in the development of complex methodologies. At the end, the microscope automation would just demand the tuning of the lenses, which is translated as modifying a value in a software. In a second stage of complexity, the most exotic automation step would be sample mounting and holder insertion/extraction. Indeed, robotics and videogames present manifold automation routines oriented to multiple processes of comparable or even higher complexity in their mechanics.623–625 For instance, ML was used in more critical situations such as the training of surgical robots both to precisely respond to the inputs of surgeons, and to perform key interventions in the absence of human supervisors (Fig. 9c).626,627 More closely related to materials science, robotics already proved the autonomous ML-guided discovery of materials and nanostructures.628,629 Therefore, the technology that should unlock the autonomous TEM is already here, “only” requiring the community's effort for guiding it to the longing goal.Interestingly, one of the challenges in the nowadays robotics is the better identification and representation of the elements present in the robots environment.630 Equivalently, we have reviewed many examples of identification of these features in EM micrographs and spectra, mainly by CNN. However, EM could take extra advantage of a trend in robotics called perceptual learning, which aims to optimise the feedback with the environment.631 Bioinspired, perceptual learning modifies the nature of signals before reaching the traditional learning algorithms to enhance the interpretability. As if electron micrographs were abstracted and encoded (e.g., through simple processes like downsampling, filtering, (e.g., Fourier transforming) before the main processing through the deep convolutional filters of a CNN. Particularly, this idea is becoming key in the development of mobile robots.632,633 The TEM cannot be considered a mobile robot, although the constantly changing interaction with the environment (i.e., changing magnification and sample position) is comparable and could surely benefit from perceptual pre-processing. Even the holder handling and loading could be directly tackled with the mobile robot perspective!
Another learning paradigm that is being and will be a primary breakthrough for robotics is RL.489,634 Surprisingly, its applicability to robotics is mainly motivated by its reach and research in videogames. From the well-known Deep Blue that defeated the chess world champion Garry Kasparov, and DeepMind's AlphaGo that beat the Go world champion Lee Sedol, to recent algorithms capable to beat much more complex game mechanics, the AI in videogames has constantly evolved since its simple origins. It was capable of remarkable milestones even if it was not actually based on AI algorithms: Deep Blue relied on a traditional brute-force decision tree while AlphaGo was based on Monte Carlo tree search. In summary, these algorithms are based on the so-called behaviour trees, an evolution of predefined states reacting to certain stimuli, following a heuristic logic. It was only recently when videogames incorporated AI to generate human-behaving game engines, but also to self-challenge these same games.635 RL, together with evolutionary algorithms and automated ML burst into the field to answer the need of adaptability.636–639 Meaning that a supervised model will perform great to a given data but cannot be adapted to new data unless it is trained with it. These new paradigms act as if they were continuously trained with the new data they may end up facing. The main idea behind these new learning paradigms is the iterative maximisation of a score or fitness metric that encodes whether the model performed well or not in a given task. Thanks to this, powerful RL algorithms such as deep Q-Network or Go-Explore surpassed the human performance in multiple videogames (Fig. 9b).640–642 Interestingly, the mechanics of some of these games implied hundreds of actions that required optimisation depending on the in-game situation. Astonishingly, some learned action trees (i.e., the decisions of the RL algorithm) could go beyond the preestablished rules of the game in favour of the score maximisation.643 Yes, the AI learned to cheat in these games! In terms of implementation, importantly, the main companies developing these algorithms, such as OpenAI or DeepMind, provide RL solutions for free to academia that constitute optimal starting points for introducing newcomers to these new learning paradigms.644–646
Going back to the microscope automation, the correlation with the proposed research is direct, and the cross-fertilisation, welcome. As indicated, a robotic electron microscope would autonomously change the power of the electromagnetic lenses to improve the image quality. In this case, the image quality would represent the score whilst the modifiable lenses are the interactable parameters. Therefore, the problem is reduced to the optimal chose of the score metric based on the data to acquire. Defocus and higher-order aberrations, artifacts, and the different regions of interest in our nanodevices should be encoded in this metric, assessing the quality of the data and the complete scanning of the nanostructure. More precisely, this problem would lie in the sparse-reward framework of RL, in which a positive reward might depend on multiple consecutive and correct actions. Importantly, the identification of the features defining the score metric was mostly automated by the reviewed examples.35–38,40–44,473 Then, the goal would be to reduce this sparsity or make it less meaningful. One option could be linking each tuneable parameter with a score modification, which would imply a hard encoding of the score. In addition, this score or metric could be further guided as well by recorded microscopy sessions capturing the variation of the tuneable parameters and the resulting transient image quality. Alternatively, and mimicking the research on videogames, multiagent training could enhance the creativity of the algorithms in modifying the interactable parameters towards a top score.642,643 Thus, training competing agents on the same problem to force unexpected behaviour trees. This could be translated into many microscopy sub-routines or entire microscopes parallelly competing with each other to maximise the sparse score based on the image quality. Excitingly, this could potentially mean just leaving the microscopes being trained alone (i.e., trial and error to maximise the score) for a week to retrieve a fully operative autonomous entity afterwards. Even more excitingly, this could lead to innovative ways to operate the microscopes that we, as trained humans, could have never thought before, in the same way a reinforced AI can break the game designers’ rules.
4.4 Other fields of research
Beyond the discussed learning paradigms like RL, automated ML, or evolutionary algorithms, complementary constraints can also add extra value to the more traditional supervised and unsupervised approaches. We have briefly stated through this review the importance of adding knowledge constraints to ML algorithms. Interestingly, this can simplify our model in terms of necessary training volume and architecture complexity. Moreover, if adequately planned, the response of the models against the constrained physical parameters should be more general and easier to achieve and interpret.The first way to explore physics constraints and also the typical way to introduce them in our models is by guiding the algorithms as steps with a physically logical sequence.647 This is the workflow of the 99% of works in any scientific field and is just processing the data differently based on the science ruling the phenomena. Indeed, the concept we want to communicate is the natural inclusion of this logic in end-to-end ML models that overwrite the manual steps. A great starting point is to use models the architecture of which explicitly carry a physical constraint. In this case, approaches like the previously reviewed rVAEs are capable of extracting some latent variables with physical constraints like rotations or translations as output.84,87 Furthermore, in the formal science-guided approach, we a priori set a physical constraint forcing the ML model to have this predefined condition or consideration as part of its nature.648,649 A straightforward implementation can just be the addition of accessory channels to EM images, each of which accounts for an experimental parameter of the acquisition. For instance, adding the defocus in a focal series for its automated reconstruction, or adding a channel per independent aberration in a digital post-acquisition aberration corrector. A clear example already reviewed doing this was the work of L. Roest et al. for modelling the ZLP in different experimental conditions.296 Another option to physically constrain models is the modification of the architecture of a priori unphysical models to capture these restrictions. Although it is not strictly EM, the following inspirational example in the framework of X-ray coherent diffraction imaging represents this idea. Moreover, it would be equivalent to EM as it provides a 3D reciprocal reconstruction similar to electron diffraction tomography. In this way, H. Chan et al. built a 3D autoencoder with a single encoder-double decoder architecture trained to invert 3D X-ray diffraction patterns into real space information of nanostructures.650 The innovation lied in the multiple-decoder architecture that allowed to split the training and the output in different physically distinctive information: in the present case, the predicted shape of the nanostructure (retrieved amplitude) and its strain through (retrieved phase). The authors named this architecture AutoPhaseNN and proved its inverse reconstruction to be about one hundred times faster than other phase retrieval methods.651 This work is an equivalent approach to the reported PtychoNN for EM ptychography reconstructions.121 Nonetheless, the main inherent drawback of doubling the outputs is the consequent doubling of the required labels for training. Therefore, this would almost deny the possibility to train this kind of models with experimental data. Oppositely, when using synthetic simulated data, the obtention of extra labels will not cost additional computing resources, making it the preferred choice (i.e., in simulations, we get simultaneously the phase and the amplitude, both useable as double labels). In conclusion, this application further highlighted the potential of physics-aware modelling to enhance the research in more general reverse engineering EM scenarios.652–655 Unfortunately, similar instances in EM are not yet common, certainly displaying a knowledge gap yelling to be filled.
Quite related, the physics-aware architecture design might be intuitively represented by the recent advances in graph neural networks.656 As mentioned, the properties of EM datasets should allow a direct transformation of their formats into graph representations. The easiest example would apply for an image in which each pixel represents a node and connects with as many edges as neighbouring pixels. There is an absence of EM bibliography referring to the potential benefits of graph networks for image processing, although more general computer vision applications have already benefited from them.657,658 Indeed, multiple physically constraining strategies can be followed at once to improve the generalisation capabilities of the final model. Indeed, a fatal error would be to limit the thinkable possibilities of the reviewed tools to just the reviewed cases and the resembling. Interestingly, general digital imaging benefited from combining a 3D CNN with graph neural networks and the distance channel (i.e. physical constrain) of RGB-D data to automatically segment images.659 The addition of the D channel (in-depth distance) allowed to, by graph representations, encode and refine geometric information otherwise impossible to extract only with intensity-based channels. Conveniently, this simple constraining of digital images consolidated the previous discussion on the benefits that even a simple physics guiding may have.
Nonetheless, when graph-like systems were allowed to evolve in time under a certain physical constraint, graph networks showed the most outstanding and promising results. For example, when they were used to simulate dynamical systems for providing trustworthy digital twins of complex physical behaviours like mass-springs, rigid bodies (e.g., to be applied in a videogames physics engine, closing the previous sections loop), molecules, or to encode finite element simulations, among others.485,486,488 Again, the previous examples would better fit into pure AI research, but the versatility these graph neural networks have shown are worth the exploration. As briefly pointed through the document, the properties of graph networks could be applied to EM, for instance, to follow the evolution of features changing along an in situ stimuli. Either by the pixelwise evolution of node-per-pixel graphs, or by the identification of features and its posterior encoding into connected nodes. We would like to warn the reader, not to forget that complementarily, this already scientific and technical encoding could be further assisted by adding extra information channels to the micrographs with the mentioned stimuli: time frame of a sequence, voltage, gas pressure, beam intensity, the discussed distance-to-camera, etc.659
To conclude this section, we want to briefly go through a vast and distant field of knowledge specially experienced in the parallel optimisation of huge multivariate systems: marketing and finances. Both marketing and finances automated most of their routinary tasks by using ML.660–662 On one hand, marketing seeks to turn into a variable every action a customer may do, first, before deciding to buy a product, and then to actually buy it. As a result, monitoring and statistically linking these variables for all the potential customers would represent a titanic task in which ML has already provided insight.663,664 On the other hand, the automation of small stock transactions avoiding cognitive biases, or the creation of optimised portfolios given an investor's profile, count as ML-based daily-life operations.665–667 The common pattern in both fields lies behind the assignation and optimisation of the variables, typically numerous and with intricate data structures. For EM, this expertise might help in experiment planning and decision-making refinement in autonomous EM, through a set of predefined goals and sample features constituting the variables space. Additionally, the optimisation of financial and trading problems has undergone through meaningful improvements with quantum computing, and more precisely with QML.668–670 Therefore, as introduced by the research in high-energy physics leading to the consequent possibilities of QML in EM, quantum finances strike to reiterate the likely future of EM with QML.
5. Conclusions and final remarks
Through this document, we have reviewed in detail the advances that ML has introduced to the broad field of EM. By unavoidably sliding to the domains of materials science, the main electron-based imaging and spectroscopy techniques have revealed important scenarios in which ML is shown to be essential to decipher new physical phenomena, to model nanostructures or for advanced micrograph and multidimensional data processing, among many others. From traditional parallel-beam TEM and STEM imaging to the possibilities of 4D STEM, and from spectrum profiles to fully 3D compositional maps, the variability of unsupervised, supervised, semi-supervised, generative and RL, or even CS, have extensively showed their goodness. Nevertheless, we have also shown and discussed the current ML challenges, still open due to the early stage of the ML journey into the EM community.This early stage and the recent motivating discoveries will likely turn into an avalanche of (electron) microscopists wanting to become ML practitioners. Consequently, we have tried to provide an easy step-by-step guide for microscopists and materials scientists to start with ML despite their initial level. Our scope was not the review of the algorithms and algebra behind ML, as there are endless resources covering this, but to present a sorted set of tools that may make the (new) practitioners’ life much easier. At least in the first stages, applications, or prototypes. Relatedly, the guide aimed to schematically educate about the possibilities of ML in EM applied to materials science. Ideally, its application should be accompanied by the deepest possible understanding of the mathematical models behind to avoid falling into the comfortable but dangerous void of the black boxes.
Finally, the exploration of the ML literature around other scientific fields, revealed an enormous source of refined methodologies and successful implementations of AI into science. From neighbouring microscopies to high-energy physics and astronomy, and even from apparently unrelated fields such as videogames or finances. From all of them we have been able to extract valuable insight to draw the future in which the EM/materials science points to. Interestingly enough, while surfing this literature some of the unanswered challenges presented for EM started receiving a preliminary treatment. As we frequently wrote, the slight adaptation and fine tuning of certain reviewed methodologies would instantly mean solving or improving a lack in EM. It could be a data-format transformation, or just a direct exchange between physical properties, but rarely a logistically prohibitive process. Moreover, the reviewed technical and scientific fields outlined the learning paradigms that must rule the progress of the next decade, with RL and generative modelling being the most promising ones. In addition, special care and attention must be paid to QML as a future insurance, but specially to physically-aware AI as a present guarantee. In conclusion, we wanted to foster the habit of browsing through other fields to seek for new ideas to implement in the readers’ own community. The idea of intercommunicating scientific fields is rich and global and adds value to one of the most beautiful aspects of ML being the amazing community devoted to open science and knowledge transfer.
Abbreviations
| AFM | Atomic force microscopy |
| AI | Artificial intelligence |
| CL | Cathodoluminescence |
| CBED | Convergent-beam electron diffraction |
| CNN | Convolutional neural network |
| CS | Compressive sensing |
| DFT | Density functional theory |
| DL | Deep learning |
| DPC | Differential phase contrast |
| EDX | Energy dispersive X-ray spectroscopy |
| EELS | Electron energy loss spectroscopy |
| EFTEM | Energy-filtered transmission electron microscopy |
| ELNES | Energy loss near edge structure |
| EM | Electron microscopy |
| ES | Electron spectroscopy |
| ET | Electron tomography |
| FCNN | Fully convolutional neural network |
| FFT | Fast Fourier transform |
| FSL | Few-shot learning |
| GAN | Generative adversarial network |
| GMM | Gaussian mixture modelling |
| GP | Gaussian processing |
| HAADF | High-angle annular dark-field |
| HRTEM | High-resolution transmission electron microscopy |
| ICA | Independent component analysis |
| LHC | Large hadron collider |
| ML | Machine learning |
| MLP | Multilayer perceptron |
| MRI | Magnetic resonance imaging |
| NMF | Non-negative matrix factorisation |
| PCA | Principal component analysis |
| QML | Quantum machine learning |
| RL | Reinforcement learning |
| RNN | Recurrent neural network |
| rVAEs | Rotationally invariant Variational AutoEncoders |
| SEM | Scanning electron microscopy |
| SI | Spectrum image |
| SNR | Signal-to-noise ratio |
| SPM | Scanning probe microscopies |
| ST | Spectral tomography |
| STEM | Scanning transmission electron microscopy |
| STM | Scanning tunnelling microscopy |
| SVD | Singular value decomposition |
| TEM | Transmission electron microscopy |
| VAEs | Variational autoencoders |
| VCA | Vertex component analysis |
| XRD | X-ray diffraction |
| ZLP | Zero-loss peak |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding from Generalitat de Catalunya 2017 SGR 327. ICN2 is supported by the Severo Ochoa programme from the Spanish Ministry of Economy (MINECO) (grant no. SEV-2017-0706) and is funded by the CERCA Programme/Generalitat de Catalunya. The authors thank support from the project NANOGEN (PID2020-116093RB-C43), funded by MCIN/AEI/10.13039/501100011033/and by “ERDF A way of making Europe”, by the “European Union”. Part of the present work has been performed within the framework of the Universitat Autònoma de Barcelona Materials Science PhD programme. We acknowledge support from CSIC Interdisciplinary Thematic Platform (PTI+) on Quantum Technologies (PT-QTEP+). M. B. acknowledges funding from SUR Generalitat de Catalunya and the EU Social Fund; project ref. 2020 FI 00103. This study was supported by MCIN with the funding form European Union NextGenerationEU (PRTR-C17-I1) and Generalitat de Catalunya. This study was supported by EU HORIZON INFRA TECH 2022 project IMPRESS (Ref.: 101094299).References
- L. Jones, et al., Smart Align—a new tool for robust non-rigid registration of scanning microscope data, Adv. Struct. Chem. Imaging, 2015, 1, 8 CrossRef.
- A. De Backer, K. H. W. van den Bos, W. Van den Broek, J. Sijbers and S. Van Aert, StatSTEM: An efficient approach for accurate and precise model-based quantification of atomic resolution electron microscopy images, Ultramicroscopy, 2016, 171, 104–116 CrossRef CAS PubMed.
- A. De Backer, S. Van Aert, P. D. Nellist and L. Jones, Procedure for 3D atomic resolution reconstructions using atom-counting and a Bayesian genetic algorithm, arXiv, 2021, preprint, arXiv.2105.05562, DOI:10.48550/arXiv.2105.05562.
- A. De Backer, G. T. Martinez, A. Rosenauer and S. Van Aert, Atom counting in HAADF STEM using a statistical model-based approach: Methodology, possibilities, and inherent limitations, Ultramicroscopy, 2013, 134, 23–33 CrossRef CAS PubMed.
- M. Vatanparast, et al., Strategy for reliable strain measurement in InAs/GaAs materials from high-resolution Z-contrast STEM images, J. Phys. Conf. Ser., 2017, 902, 012021 CrossRef.
- J. M. Zuo, et al., Lattice and strain analysis of atomic resolution Z-contrast images based on template matching, Ultramicroscopy, 2014, 136, 50–60 CrossRef CAS PubMed.
- M. J. Hÿtch, J.-L. Putaux and J.-M. Pénisson, Measurement of the displacement field of dislocations to 0.03
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Å by electron microscopy, Nature, 2003, 423, 270–273 CrossRef PubMed.
Å by electron microscopy, Nature, 2003, 423, 270–273 CrossRef PubMed. - M. J. Hÿtch, E. Snoeck and R. Kilaas, Quantitative measurement of displacement and strain fields from HREM micrographs, Ultramicroscopy, 1998, 74, 131–146 CrossRef.
- S. Bals, S. Van Aert, G. Van Tendeloo and D. Ávila-Brande, Statistical estimation of atomic positions from exit wave reconstruction with a precision in the picometer range, Phys. Rev. Lett., 2006, 96, 096106 CrossRef PubMed.
- L. Jones and P. D. Nellist, Identifying and correcting scan noise and drift in the scanning transmission electron microscope, Microsc. Microanal., 2013, 19, 1050–1060 CrossRef CAS PubMed.
- N. Bonnet, Multivariate statistical methods for the analysis of microscope image series: Applications in materials science, J. Microsc., 1998, 190, 2–18 CrossRef CAS.
- N. Bonnet, E. Simova, S. Lebonvallet and H. Kaplan, New applications of multivariate statistical analysis in spectroscopy and microscopy, Ultramicroscopy, 1992, 40, 1–11 CrossRef.
- M. Bosman, M. Watanabe, D. T. L. Alexander and V. J. Keast, Mapping chemical and bonding information using multivariate analysis of electron energy-loss spectrum images, Ultramicroscopy, 2006, 106, 1024–1032 CrossRef CAS PubMed.
- K. Aso, K. Shigematsu, T. Yamamoto and S. Matsumura, Detection of picometer-order atomic displacements in drift-compensated HAADF-STEM images of gold nanorods, Microscopy, 2016, 65, 391–399 CrossRef CAS PubMed.
- K. Aso, J. Maebe, T. Yamamoto and S. Matsumura, Lattice Tetragonality and Local Strain Depending on Shape of Gold Nanoparticles, Microsc. Microanal., 2019, 25, 2122–2123 CrossRef.
- P. Trebbia, EELS elemental mapping with unconventional methods I. Theoretical basis: image analysis with multivariate statistics and entropy concepts, Ultramicroscopy, 1990, 34, 165–178 CrossRef CAS PubMed.
- N. Bonnet, N. Brun and C. Colliex, Extracting information from sequences of spatially resolved EELS spectra using multivariate statistical analysis, Ultramicroscopy, 1999, 77, 97–112 CrossRef CAS.
- C. Tian, et al., Deep learning on image denoising: An overview, Neural Networks, 2020, 131, 251–275 CrossRef PubMed.
- S. V. Kalinin, et al., Lab on a beam-Big data and artificial intelligence in scanning transmission electron microscopy, MRS Bull., 2019, 44, 565–575 CrossRef.
- M. Shen, et al., Multi defect detection and analysis of electron microscopy images with deep learning, Comput. Mater. Sci., 2021, 199, 110576 CrossRef CAS.
- C. H. Lee, et al., Deep learning enabled strain mapping of single-atom defects in two-dimensional transition metal dichalcogenides with sub-picometer precision, Nano Lett., 2020, 20, 3369–3377 CrossRef CAS PubMed.
- F. Wang, T. R. Henninen, D. Keller and R. Erni, Noise2Atom: unsupervised denoising for scanning transmission electron microscopy images, Appl. Microsc., 2020, 50, 23 CrossRef PubMed.
- J. M. Ede and R. Beanland, Improving electron micrograph signal-to-noise with an atrous convolutional encoder-decoder, Ultramicroscopy, 2019, 202, 18–25 CrossRef CAS PubMed.
- T. M. Quan, et al., Removing imaging artifacts in electron microscopy using an asymmetrically cyclic adversarial network without paired training data, in Proc. – 2019 Int. Conf. Comput. Vis. Work. ICCVW 2019, 2019, pp. 3804–3813 DOI:10.1109/ICCVW.2019.00473.
- J. P. Buban and S.-Y. Choi, Auto-encoders for Noise Reduction in Scanning Transmission Electron Microscopy, Microsc. Microanal., 2017, 23, 130–131 CrossRef.
- J. L. Vincent, et al., Developing and Evaluating Deep Neural Network-Based Denoising for Nanoparticle TEM Images with Ultra-Low Signal-to-Noise, Microsc. Microanal., 2021, 27, 1431–1447 CrossRef CAS.
- S. Mohan, Adaptive Denoising via GainTuning, Adv. Neural Inf. Process. Syst., 2021, 34, 23727–23740 Search PubMed.
- S. Mohan, Deep Denoising For Scientific Discovery: A Case Study In Electron Microscopy, IEEE Trans. Comput. Imaging, 2022, 8, 585–597 Search PubMed.
- R. Manzorro, et al., A Deep Learning Approach to Retrieving 3D Structure Information from High Resolution Time-Resolved TEM Images, Microsc. Microanal., 2021, 27, 464–465 CrossRef.
- J. Lee, Y. Lee, J. Kim and Z. Lee, Contrast transfer function-based exit-wave reconstruction and denoising of atomic-resolution transmission electron microscopy images of graphene and cu single atom substitutions by deep learning framework, Nanomaterials, 2020, 10, 1977 CrossRef CAS PubMed.
- A. Suveer, A. Gupta, G. Kylberg and I. M. Sintorn, Super-resolution reconstruction of transmission electron microscopy images using deep learning, Proc. Int. Symp. Biomed. Imaging, 2019, 548–551 Search PubMed.
- S. Anada, Y. Nomura, T. Hirayama and K. Yamamoto, Simulation-Trained Sparse Coding for High-Precision Phase Imaging in Low-Dose Electron Holography, Microsc. Microanal., 2020, 26, 429–438 CrossRef CAS PubMed.
- S. Anada, Y. Nomura, T. Hirayama and K. Yamamoto, Sparse coding and dictionary learning for electron hologram denoising, Ultramicroscopy, 2019, 206, 112818 CrossRef CAS PubMed.
- Y. Midoh and K. Nakamae, Accuracy improvement of phase estimation in electron holography using noise reduction methods, Microscopy, 2020, 69, 123–131 CrossRef CAS PubMed.
- N. Schnitzer, S. H. Sung and R. Hovden, Maximal Resolution from the Ronchigram: Human vs. Deep Learning, Microsc. Microanal., 2019, 25, 160–161 CrossRef.
- C. Zhang, et al., Aberration Corrector Tuning with Machine-Learning-Based Emittance Measurements and Bayesian Optimization, Microsc. Microanal., 2021, 27, 810–812 CrossRef.
- R. Sagawa, F. Uematsu, K. Aibara, T. Nakamichi and S. Morishita, Aberration Measurement and Correction in Scanning Transmission Electron Microscopy using Machine Learning, Microsc. Microanal., 2021, 27, 814–816 CrossRef.
- M. Olszta, et al., An Automated Scanning Transmission Electron Microscope Guided by Sparse Data Analytics, Microsc. Microanal., 2022, 1611–1621 CAS.
- K. Roccapriore, S. V. Kalinin and M. Ziatdinov, Physics discovery in nanoplasmonic systems via autonomous experiments in Scanning Transmission Electron Microscopy, arXiv, 2021, preprint, arXiv:2108.03290, DOI:10.48550/arXiv.2108.03290.
- E. Rotunno, et al., Alignment of electron optical beam shaping elements using a convolutional neural network, Ultramicroscopy, 2021, 228, 113338 CrossRef CAS PubMed.
- E. Rotunno, et al., Convolutional neural network as a tool for automatic alignment of electron optical beam shaping devices, Microsc. Microanal., 2021, 27, 822–824 CrossRef.
- E. F. Rauch, et al., Automated nanocrystal orientation and phase mapping in the transmission electron microscope on the basis of precession electron diffraction, Z. Kristallogr., 2010, 225, 103–109 CrossRef CAS.
- Y. Jin, et al., Machine learning guided rapid focusing with sensor-less aberration corrections, Opt. Express, 2018, 26, 30162 CrossRef PubMed.
- Y. Xu, et al., An improved method of measuring wavefront aberration based on image with machine learning in free space optical communication, Sensors, 2019, 19, 3665 CrossRef PubMed.
- B. P. Cumming and M. Gu, Direct determination of aberration functions in microscopy by an artificial neural network, Opt. Express, 2020, 28, 14511 CrossRef PubMed.
- B. Huang, Z. Li and J. Li, An artificial intelligence atomic force microscope enabled by machine learning, Nanoscale, 2018, 10, 21320–21326 RSC.
- S. V. Kalinin, B. G. Sumpter and R. K. Archibald, Big-deep-smart data in imaging for guiding materials design, Nat. Mater., 2015, 14, 973–980 CrossRef CAS PubMed.
- S. V. Kalinin, et al., Automated and Autonomous Experiments in Electron and Scanning Probe Microscopy, ACS Nano, 2021, 15, 12604–12627 CrossRef CAS PubMed.
- R. K. Vasudevan, et al., Autonomous Experiments in Scanning Probe Microscopy and Spectroscopy: Choosing Where to Explore Polarization Dynamics in Ferroelectrics, ACS Nano, 2021, 15, 11253–11262 CrossRef CAS PubMed.
- A. Ghosh, B. G. Sumpter, O. Dyck, S. V. Kalinin and M. Ziatdinov, Ensemble learning-iterative training machine learning for uncertainty quantification and automated experiment in atom-resolved microscopy, npj Comput. Mater., 2021, 7, 100 CrossRef.
- C. Ophus, H. I. Rasool, M. Linck, A. Zettl and J. Ciston, Automatic software correction of residual aberrations in reconstructed HRTEM exit waves of crystalline samples, Adv. Struct. Chem. Imaging, 2016, 2, 15 CrossRef PubMed.
- O. Dyck, S. Jesse and S. V. Kalinin, A self-driving microscope and the Atomic Forge, MRS Bull., 2019, 44, 669–670 CrossRef.
- S. R. Spurgeon, et al., Towards data-driven next-generation transmission electron microscopy, Nat. Mater., 2021, 20, 274–279 CrossRef CAS PubMed.
- GitHub – PyJEM/PyJEM.
- Gatan Microscopy Suite (GMS), 2021.
- J. Dan, et al., A hierarchical active-learning framework for classifying structural motifs in atomic resolution microscopy, arXiv, 2020, preprint, arXiv:2005.11488, DOI:10.48550/arXiv.2005.11488.
- H. I. Rasool, C. Ophus and A. Zettl, Atomic Defects in Two Dimensional Materials, Adv. Mater., 2015, 27, 5771–5777 CrossRef CAS PubMed.
- R. Kannan, et al., Deep data analysis via physically constrained linear unmixing: universal framework, domain examples, and a community-wide platform, Adv. Struct. Chem. Imaging, 2018, 4, 6 CrossRef CAS PubMed.
- M. Ziatdinov, et al., Deep Learning of Atomically Resolved Scanning Transmission Electron Microscopy Images: Chemical Identification and Tracking Local Transformations, ACS Nano, 2017, 11, 12742–12752 CrossRef CAS PubMed.
- M. Ziatdinov, O. Dyck, S. Jesse and S. V. Kalinin, Deep Learning for Atomically Resolved Imaging, Microsc. Microanal., 2018, 24, 60–61 CrossRef.
- A. Maksov, et al., Deep learning analysis of defect and phase evolution during electron beam-induced transformations in WS2, npj Comput. Mater., 2019, 5, 12 CrossRef.
- T. K. Patra, et al., Defect dynamics in 2-D MoS2 probed by using machine learning, atomistic simulations, and high-resolution microscopy, ACS Nano, 2018, 12, 8006–8016 CrossRef CAS PubMed.
- R. K. Vasudevan, et al., Investigating phase transitions from local crystallographic analysis based on statistical learning of atomic environments in 2D MoS2-ReS2, Appl. Phys. Rev., 2021, 8, 011409 CAS.
- Z. Maxim, S. Jesse, B. G. Sumpter, S. V. Kalinin and O. Dyck, Tracking atomic structure evolution during directed electron beam induced Si-atom motion in graphene via deep machine learning, Nanotechnology, 2021, 32, 035703 CrossRef CAS PubMed.
- O. Ronneberger, P. Fischer and T. Brox, U-Net: Convolutional Networks for Biomedical Image Segmentation. Med. Image Comput. Comput. Interv. – MICCAI 2015. MICCAI 2015, Lect. Notes Comput. Sci., 2015, 9351, 1–8 Search PubMed.
- J. Madsen, et al., A Deep Learning Approach to Identify Local Structures in Atomic-Resolution Transmission Electron Microscopy Images, Adv. Theory Simulat., 2018, 1, 1–12 Search PubMed.
- R. Sadre, C. Ophus, A. Butko and G. H. Weber, Deep Learning Segmentation of Complex Features in Atomic-Resolution Phase-Contrast Transmission Electron Microscopy Images, Microsc. Microanal., 2021, 27, 804–814 CrossRef CAS PubMed.
- P. Cho, A. Wood, K. Mahalingam and K. Eyink, Defect detection in atomic resolution transmission electron microscopy images using machine learning, Mathematics, 2021, 9, 1209 CrossRef.
- W. Lin, et al., Local crystallography analysis for atomically resolved scanning tunneling microscopy images, Nanotechnology, 2013, 24, 415707 CrossRef PubMed.
- M. Ziatdinov, U. Fuchs, J. H. G. Owen, J. N. Randall and S. V. Kalinin, Robust multi-scale multi-feature deep learning for atomic and defect identification in Scanning Tunneling Microscopy on H-Si(100) 2x1 surface, arXiv, 2020, preprint, arXiv:2002.04716, DOI:10.48550/arXiv.2002.04716.
- G. Roberts, et al., DefectNet – A Deep Convolutional Neural Network for Semantic Segmentation of Crystallographic Defects in Advanced Microscopy Images, Microsc. Microanal., 2019, 25, 164–165 CrossRef.
- C. Kunka, A. Shanker, E. Y. Chen, S. R. Kalidindi and R. Dingreville, Decoding defect statistics from diffractograms via machine learning, npj Comput. Mater., 2021, 7, 67 CrossRef.
- J. Dan, X. Zhao and S. J. Pennycook, A machine perspective of atomic defects in scanning transmission electron microscopy, InfoMat, 2019, 1, 359–375 CrossRef CAS.
- J. Yi, Z. Yuan and J. Peng, Adversarial-Prediction Guided Multi-Task Adaptation for Semantic Segmentation of Electron Microscopy Images, Proc. – Int. Symp. Biomed. Imaging, 2020, 1205–1208 Search PubMed.
- Q. Li, et al., Quantification of flexoelectricity in PbTiO3/SrTiO3 superlattice polar vortices using machine learning and phase-field modeling, Nat. Commun., 2017, 8, 1468 CrossRef CAS PubMed.
- D. Daniel and L. H. Sebastian, Learning the parts of objects by non-negative matrix factorization, Nature, 1999, 401, 788–791 CrossRef PubMed.
- B. R. Jany, A. Janas and F. Krok, Automatic microscopic image analysis by moving window local Fourier Transform and Machine Learning, Micron, 2020, 130, 102800 CrossRef PubMed.
- B. H. Martineau, D. N. Johnstone, A. T. J. Van Helvoort, P. A. Midgley and A. S. Eggeman, Unsupervised machine learning applied to scanning precession electron diffraction data, Adv. Struct. Chem. Imaging, 2019, 5, 3, DOI:10.1186/s40679-019-0063-3.
- E. Winter, M. N-FINDR: an algorithm for fast spectral endmember determination in hyperspectral data, Int. Geosci. Remote Sens. Symp., 1999, 3753, 266–275 Search PubMed.
- M. Ziatdinov, et al., Causal analysis of competing atomistic mechanisms in ferroelectric materials from high-resolution scanning transmission electron microscopy data, npj Comput. Mater., 2020, 6, 127 CrossRef CAS.
- R. K. Vasudevan, M. Ziatdinov, S. Jesse and S. V. Kalinin, Phases and Interfaces from Real Space Atomically Resolved Data: Physics-Based Deep Data Image Analysis, Nano Lett., 2016, 16, 5574–5581 CrossRef CAS PubMed.
- P. Baldi, Autoencoders, Unsupervised Learning, and Deep Architectures, ICML Unsupervised Transf. Learn., 2012, 37–49, DOI:10.1561/2200000006.
- W. H. Lopez Pinaya, S. Vieira, R. Garcia-Dias and A. Mechelli, Autoencoders, Mach. Learn. Methods Appl. Brain Disord., 2019, 193–208, DOI:10.1016/B978-0-12-815739-8.00011-0.
- M. A. Ziatdinov and S. V. Kalinin, Robust Feature Disentanglement in Imaging Data via Joint Invariant Variational Autoencoders: from Cards to Atoms, arXiv, 2021, preprint, arXiv:2104.10180, DOI:10.48550/arXiv.2104.10180.
- S. V. Kalinin, O. Dyck, A. Ghosh, Y. Liu, R. Proksch, B. G. Sumpter and M. Ziatdinov, Unsupervised Machine Learning Discovery of Chemical and Physical Transformation Pathways from Imaging Data, arXiv, 2020, preprint, arXiv:2010.09196, DOI:10.48550/arXiv.2010.09196.
- L. Vlcek, et al., Learning from Imperfections: Predicting Structure and Thermodynamics from Atomic Imaging of Fluctuations, ACS Nano, 2019, 13, 718–727 CrossRef CAS PubMed.
- M. P. Oxley, et al., Probing atomic-scale symmetry breaking by rotationally invariant machine learning of multidimensional electron scattering, npj Comput. Mater., 2021, 7, 65 CrossRef CAS.
- S. V. Kalinin, O. Dyck, S. Jesse and M. Ziatdinov, Exploring order parameters and dynamic processes in disordered systems via variational autoencoders, Sci. Adv., 2021, 7, eabd5084 CrossRef CAS PubMed.
- S. V. Kalinin, C. T. Nelson, M. Valleti, J. J. P. Peters, W. Dong, R. Beanland, X. Zhang, I. Takeuchi and M. Ziatdinov, Unsupervised learning of ferroic variants from atomically resolved STEM images, arXiv, 2021, preprint, arXiv:2101.06892, DOI:10.48550/arXiv.2101.06892.
- W. S. McCulloch and W. Pitts, A logical calculus of the ideas immanent in nervous activity, Bull. Math. Biol., 1990, 52, 99–115 CrossRef CAS PubMed.
- Y. Lecun, Y. Bengio and G. Hinton, Deep learning, Nature, 2015, 521, 436–444 CrossRef CAS PubMed.
- J. M. Ede, Deep learning in electron microscopy, Mach. Learn. Sci. Technol., 2021, 2, 011004 CrossRef.
- A. Garcia-Garcia, S. Orts-Escolano, S. Oprea, V. Villena-Martinez and J. Garcia-Rodriguez, A Review on Deep Learning Techniques Applied to Semantic Segmentation, arXiv, 2017, preprint, arXiv:1704.06857, DOI:10.48550/arXiv.1704.06857.
- R. M. Patton, et al., 167-PFlops deep learning for electron microscopy: From learning physics to atomic manipulation, in Proc. - Int. Conf. High Perform. Comput. Networking, Storage, Anal. SC 2018, 2019, pp. 638–648 DOI:10.1109/SC.2018.00053.
- Q. Luo, E. A. Holm and C. Wang, A transfer learning approach for improved classification of carbon nanomaterials from TEM images, Nanoscale Adv., 2021, 3, 206–213 RSC.
- S. Yang, et al., Deep Learning-Assisted Quantification of Atomic Dopants and Defects in 2D Materials, Adv. Sci., 2021, 2101099 CrossRef CAS PubMed.
- M. Ziatdinov, C. Nelson, R. K. Vasudevan, D. Y. Chen and S. V. Kalinin, Building ferroelectric from the bottom up: The machine learning analysis of the atomic-scale ferroelectric distortions, Appl. Phys. Lett., 2019, 115, 052902 CrossRef.
- M. Ziatdinov, A. Maksov and S. V. Kalinin, Learning surface molecular structures via machine vision, npj Comput. Mater., 2017, 3, 31 CrossRef.
- M. Nord, P. E. Vullum, I. MacLaren, T. Tybell and R. Holmestad, Atomap: a new software tool for the automated analysis of atomic resolution images using two-dimensional Gaussian fitting, Adv. Struct. Chem. Imaging, 2017, 3, 9 CrossRef PubMed.
- F. Uesugi, et al., Non-negative matrix factorization for mining big data obtained using four-dimensional scanning transmission electron microscopy, Ultramicroscopy, 2021, 221, 113168 CrossRef CAS PubMed.
- M. Jacob, et al., Statistical Machine Learning and Compressed Sensing Approaches for Analytical Electron Tomography – Application to Phase Change Materials, Microsc. Microanal., 2019, 25, 156–157 CrossRef.
- S. Kiyohara, M. Tsubaki, K. Liao and T. Mizoguchi, Quantitative estimation of properties from core- loss spectrum via neural network, J. Phys. Mater., 2019, 2, 024003 CrossRef CAS.
- R. S. Pennington, C. Coll, S. Estradé, F. Peiró and C. T. Koch, Neural-network-based depth-resolved multiscale structural optimization using density functional theory and electron diffraction data, Phys. Rev. B, 2018, 97, 024112 CrossRef CAS.
- K. P. Kelley, et al., Fast Scanning Probe Microscopy via Machine Learning: Non-Rectangular Scans with Compressed Sensing and Gaussian Process Optimization, Small, 2020, 16, 2002878 CrossRef CAS PubMed.
- J. A. Aguiar, M. L. Gong, R. R. Unocic, T. Tasdizen and B. D. Miller, Decoding crystallography from high-resolution electron imaging and diffraction datasets with deep learning, Sci. Adv., 2019, 5, aaw1949 CrossRef PubMed.
- R. K. Vasudevan, et al., Mapping mesoscopic phase evolution during E-beam induced transformations via deep learning of atomically resolved images, npj Comput. Mater., 2018, 4, 30 CrossRef.
- R. K. Vasudevan, A. Ghosh, M. Ziatdinov and S. V. Kalinin, Exploring Electron Beam Induced Atomic Assembly via Reinforcement Learning in a Molecular Dynamics Environment, Nanotechnology, 2021, 33, 115301 CrossRef PubMed.
- R. S. Pennington, W. Van den Broek and C. T. Koch, Third-dimension information retrieval from a single convergent-beam transmission electron diffraction pattern using an artificial neural network, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205409 CrossRef.
- J. P. Horwath, Understanding important features of deep learning models for segmentation of high-resolution transmission electron microscopy images, npj Comput. Mater., 2020, 6, 1–9, DOI:10.1038/s41524-020-00363-x.
- G. Benton, M. Finzi, P. Izmailov and A. G. Wilson, Learning invariances in neural networks from training data, Adv. Neural Inf. Process. Syst., 2020, 33, 17605–17616 Search PubMed.
- M. Ziatdinov, A. Maksov and S. V. Kalinin, Deep data analytics in structural and functional imaging of nanoscale materials. Springer Series in Materials Science, Springer International Publishing, 2018, vol. 280 Search PubMed.
- M. Finzi, S. Stanton, P. Izmailov and A. G. Wilson, Generalizing convolutional neural networks for equivariance to lie groups on arbitrary continuous data, in 37th Int. Conf. Mach. Learn. ICML 2020 PartF16814, 2020, pp. 3146–3157 Search PubMed.
- T. Zhou, M. Cherukara and C. Phatak, Differential programming enabled functional imaging with Lorentz transmission electron microscopy, npj Comput. Mater., 2021, 7, 141 CrossRef.
- Z. Chen, et al., Electron ptychography achieves atomic-resolution limits set by lattice vibrations, Science, 2021, 372, 826–831 CrossRef CAS PubMed.
- S. Kandel, et al., Using automatic differentiation as a general framework for ptychographic reconstruction, Opt. Express, 2019, 27, 18653–18672 CrossRef PubMed.
- S. Ghosh, Y. S. G. Nashed, O. Cossairt and A. Katsaggelos, ADP: Automatic differentiation ptychography, in IEEE Int. Conf. Comput. Photogr. ICCP 2018, 2018, pp. 1–10 DOI:10.1109/ICCPHOT.2018.8368470.
- W. Hoppe, Trace structure analysis, ptychography, phase tomography, Ultramicroscopy, 1982, 10, 187–198 CrossRef.
- B. A. R. Lupini, M. P. Oxley and S. V. Kalinin, Pushing the limits of electron ptychography, Science, 2018, 362, 399–400 CrossRef PubMed.
- M. Cao, et al., Machine Learning for Phase Retrieval from 4D-STEM Data, Microsc. Microanal., 2020, 26, 2020–2021 CrossRef.
- M. Schloz, et al., Overcoming information reduced data and experimentally uncertain parameters in ptychography with regularized optimization, Opt. Express, 2020, 28, 28306 CrossRef CAS PubMed.
- M. J. Cherukara, et al., AI-enabled high-resolution scanning coherent diffraction imaging, Appl. Phys. Lett., 2020, 117, 044103 CrossRef CAS.
- M. Schloz, J. Müller, T. Pekin, W. Van den Broek and C. Koch, Adaptive Scanning in Ptychography through Deep Reinforcement Learning, Microsc. Microanal., 2021, 27, 818–821 CrossRef.
- X. Huang, et al., Optimization of overlap uniformness for ptychography, Opt. Express, 2014, 22, 12634 CrossRef PubMed.
- C. Ophus, Four-Dimensional Scanning Transmission Electron Microscopy (4D-STEM): From Scanning Nanodiffraction to Ptychography and Beyond, Microsc. Microanal., 2019, 563–582, DOI:10.1017/S1431927619000497.
- G. W. Paterson, et al., Fast Pixelated Detectors in Scanning Transmission Electron Microscopy. Part II: Post-Acquisition Data Processing, Visualization, and Structural Characterization, Microsc. Microanal., 2020, 26, 944–963 CrossRef CAS PubMed.
- M. Nord, et al., Fast Pixelated Detectors in Scanning Transmission Electron Microscopy. Part I: Data Acquisition, Live Processing, and Storage, Microsc. Microanal., 2020, 26, 653–666 CrossRef CAS PubMed.
- M. Nord, et al., Developing Rapid and Advanced Visualisation of Magnetic Structures Using 2-D Pixelated STEM Detectors, Microsc. Microanal., 2016, 22, 530–531 CrossRef.
- M. Nord, et al., Strain Anisotropy and Magnetic Domains in Embedded Nanomagnets, Small, 2019, 15, 1904738 CrossRef CAS PubMed.
- G. Correa and D. Muller, Machine Learning for Sub-pixel Super-resolution in Direct Electron Detectors, Microsc. Microanal., 2020, 26, 1932–1934 CrossRef.
- C. Shi, M. Cao, D. Muller and Y. Han, Rapid and Semi-Automated Analysis of 4D-STEM data via Unsupervised Learning, Microsc. Microanal., 2021, 27, 58–59 CrossRef.
- P. Cueva, E. Padget and D. A. Muller, A Natural Basis for Unsupervised Machine Learning on Scanning Diffraction Data, Microsc. Microanal., 2018, 24, 490–491 CrossRef.
- F. I. Allen, et al., Fast Grain Mapping with Sub-Nanometer Resolution Using 4D-STEM with Grain Classification by Principal Component Analysis and Non-Negative Matrix Factorization, Microsc. Microanal., 2021, 27, 794–803 CrossRef CAS PubMed.
- X. Li, et al., Manifold learning of four-dimensional scanning transmission electron microscopy, npj Comput. Mater., 2019, 5, 5 CrossRef.
- X. Li, et al., Unsupervised Machine Learning to Distill Structural-Property Insights from 4D-STEM, Microsc. Microanal., 2021, 25, 2016–2017 Search PubMed.
- C. Zhang, R. Han, A. R. Zhang and P. M. Voyles, Denoising atomic resolution 4D scanning transmission electron microscopy data with tensor singular value decomposition, Ultramicroscopy, 2020, 219, 113123 CrossRef CAS PubMed.
- A. Nalin Mehta, et al., Unravelling stacking order in epitaxial bilayer MX2 using 4D-STEM with unsupervised learning, Nanotechnology, 2020, 31, 445702 CrossRef PubMed.
- C. Zhang, J. Feng, L. R. DaCosta and P. M. Voyles, Atomic resolution convergent beam electron diffraction analysis using convolutional neural networks, Ultramicroscopy, 2020, 210, 112921 CrossRef CAS PubMed.
- M. P. Oxley, et al., Deep learning of interface structures from simulated 4D STEM data: cation intermixing vs. roughening, Mach. Learn.: Sci. Technol., 2020, 1, 04LT01 Search PubMed.
- S. Van Aert, A. J. Den Dekker, A. Van Den Bos, D. Van Dyck and J. H. Chen, Maximum likelihood estimation of structure parameters from high resolution electron microscopy images. Part II: A practical example, Ultramicroscopy, 2005, 104, 107–125 CrossRef CAS PubMed.
- L. C. Gontard, R. Schierholz, S. Yu, J. Cintas and R. E. Dunin-Borkowski, Photogrammetry of the three-dimensional shape and texture of a nanoscale particle using scanning electron microscopy and free software, Ultramicroscopy, 2016, 169, 80–88 CrossRef CAS PubMed.
- J. M. Thomas, R. Leary, P. A. Midgley and D. J. Holland, A new approach to the investigation of nanoparticles: Electron tomography with compressed sensing, J. Colloid Interface Sci., 2013, 392, 7–14 CrossRef CAS PubMed.
- R. Leary, Z. Saghi, P. A. Midgley and D. J. Holland, Compressed sensing electron tomography, Ultramicroscopy, 2013, 131, 70–91 CrossRef CAS PubMed.
- L. Staniewicz and P. A. Midgley, Machine learning as a tool for classifying electron tomographic reconstructions, Adv. Struct. Chem. Imaging, 2015, 1, 9 CrossRef.
- A. Béché, B. Goris, B. Freitag and J. Verbeeck, Development of a fast electromagnetic beam blanker for compressed sensing in scanning transmission electron microscopy, Appl. Phys. Lett., 2016, 108, 093103 CrossRef.
- L. Kovarik, A. Stevens, A. Liyu and N. D. Browning, Implementing an accurate and rapid sparse sampling approach for low-dose atomic resolution STEM imaging, Appl. Phys. Lett., 2016, 109, 164102 CrossRef.
- Z. Saghi, et al., Compressed sensing electron tomography of needle-shaped biological specimens - Potential for improved reconstruction fidelity with reduced dose, Ultramicroscopy, 2016, 160, 230–238 CrossRef CAS PubMed.
- B. Goris, W. Van den Broek, K. J. Batenburg, H. Heidari Mezerji and S. Bals, Electron tomography based on a total variation minimization reconstruction technique, Ultramicroscopy, 2012, 113, 120–130 CrossRef CAS.
- Z. Saghi, et al., Three-dimensional morphology of iron oxide nanoparticles with reactive concave surfaces. A compressed sensing-electron tomography (CS-ET) approach, Nano Lett., 2011, 11, 4666–4673 CrossRef CAS PubMed.
- M. López-Haro, et al., A Macroscopically Relevant 3D-Metrology Approach for Nanocatalysis Research, Part. Part. Syst. Charact., 2018, 35, 1700343 CrossRef.
- J. M. Muñoz-Ocaña, et al., Optimization of STEM-HAADF Electron Tomography Reconstructions by Parameter Selection in Compressed Sensing Total Variation Minimization-Based Algorithms, Part. Part. Syst. Charact., 2020, 37, 2000070 CrossRef.
- A. Rakowski, J. Merham, L. Li, P. Baldi and J. Patterson, Learning Frame Interpolation for Tilt Series Tomography, Microsc. Microanal., 2020, 928–930, DOI:10.1017/S1431927620016360.
- Y. Zhao, et al., Five-second STEM dislocation tomography for 300 nm thick specimen assisted by deep-learning-based noise filtering, Sci. Rep., 2021, 11, 20720 CrossRef PubMed.
- A. A. Hendriksen, D. M. Pelt and K. J. Batenburg, Noise2Inverse: Self-supervised deep convolutional denoising for linear inverse problems in imaging, IEEE Transactions on Computational Imaging, 2020, 6, 1320–1335 Search PubMed.
- E. Bladt, D. M. Pelt, S. Bals and K. J. Batenburg, Electron tomography based on highly limited data using a neural network reconstruction technique, Ultramicroscopy, 2015, 158, 81–88 CrossRef CAS PubMed.
- D. M. Pelt and K. J. Batenburg, Fast Tomographic Reconstruction from Limited Data Using Artificial Neural Networks, IEEE Trans. Image Process, 2013, 22, 5238–5251 Search PubMed.
- Q. Yang, et al., Low-Dose CT Image Denoising Using a Generative Adversarial Network With Wasserstein Distance and Perceptual Loss, IEEE Trans. Med. Imaging, 2018, 37, 1348–1357 Search PubMed.
- A. Stevens, H. Yang, L. Carin, I. Arslan and N. D. Browning, The potential for bayesian compressive sensing to significantly reduce electron dose in high-resolution STEM images, Microscopy, 2014, 63, 41–51 CrossRef PubMed.
- N. Browning, R. Klie, A. Barker, A. Stevens and C. Buurma, The Potential Benefits of Compressed Sensing and Machine Learning for Advanced Imaging and Spectroscopy in the Electron Microscope, Microsc. Microanal., 2020, 26, 2458–2460 CrossRef.
- D. Mucke-Herzberg, et al., Practical Implementation of Compressive Sensing for High Resolution STEM, Microsc. Microanal., 2016, 22, 558–559 CrossRef.
- X. Li, O. Dyck, S. V. Kalinin and S. Jesse, Compressed sensing of Scanning Transmission Electron Microscopy (STEM) with nonrectangular scans, Microsc. Microanal., 2018, 24, 623–633 CrossRef CAS PubMed.
- X. Li, O. Dyck, S. V. Kalinin and S. Jesse, Compressive Sensing on Diverse STEM Scans: Real-time Feedback, Low-dose and Dynamic Range, Microsc. Microanal., 2019, 25, 1688–1689 CrossRef.
- J. M. Ede and R. Beanland, Partial Scanning Transmission Electron Microscopy with Deep Learning, Sci. Rep., 2020, 10, 8332 CrossRef CAS PubMed.
- J. M. Ede, Adaptive partial scanning transmission electron microscopy with reinforcement learning, Mach. Learn. Sci. Technol., 2021, 2, 045011 CrossRef.
- S. Zheng, C. Wang, X. Yuan and H. L. Xin, Super-compression of large electron microscopy time series by deep compressive sensing learning, Patterns, 2021, 2, 100292 CrossRef PubMed.
- M. D. Sangid, Coupling in situ experiments and modeling – Opportunities for data fusion, machine learning, and discovery of emergent behavior, Curr. Opin. Solid State Mater. Sci., 2020, 24, 100797 CrossRef CAS.
- H. Zheng, Y. S. Meng and Y. Zhu, Frontiers of in situ electron microscopy, MRS Bull., 2015, 40, 12–18 CrossRef.
- Y. Luo, N. Zaluzec, M. Cherukara, X. Wu and S. Chen, Real-Time Image Registration via A Deep Leaning Approach for Correlative X-ray and Electron Microscopy, Microsc. Microanal., 2021, 27, 302–304 CrossRef.
- K. Higgins, et al., Exploration of Electrochemical Reactions at Organic–Inorganic Halide Perovskite Interfaces via Machine Learning in In Situ Time-of-Flight Secondary Ion Mass Spectrometry, Adv. Funct. Mater., 2020, 30, 2001995 CrossRef CAS.
- X. Wang, et al., AutoDetect-mNP: An Unsupervised Machine Learning Algorithm for Automated Analysis of Transmission Electron Microscope Images of Metal Nanoparticles, JACS Au, 2021, 1, 316–327 CrossRef CAS PubMed.
- N. M. Schneider, J. H. Park, M. M. Norton, F. M. Ross and H. H. Bau, Automated analysis of evolving interfaces during in situ electron microscopy, Adv. Struct. Chem. Imaging, 2016, 2, 2 CrossRef.
- Y. Qian, J. Z. Huang, X. Li and Y. Ding, Robust nanoparticles detection from noisy background by fusing complementary image information, IEEE Trans. Image Process., 2016, 25, 5713–5726 Search PubMed.
- Y. Qian, J. Z. Huang and Y. Ding, Identifying multi-stage nanocrystal growth using in situ TEM video data, IISE Trans., 2017, 49, 532–543 CrossRef.
- A. A. Ezzat and M. Bedewy, Machine learning for revealing spatial dependence among nanoparticles: Understanding catalyst film dewetting via Gibbs point process models, J. Phys. Chem. C, 2020, 124, 27479–27494 CrossRef.
- L. Yao, Z. Ou, B. Luo, C. Xu and Q. Chen, Machine Learning to Reveal Nanoparticle Dynamics from Liquid-Phase TEM Videos, ACS Cent. Sci., 2020, 6, 1421–1430 CrossRef CAS PubMed.
- K. Faraz, T. Grenier, C. Ducottet and T. Epicier, A Machine Learning pipeline to track the dynamics of a population of nanoparticles during in situ Environmental Transmission Electron Microscopy in gases, Microsc. Microanal., 2021, 27, 2236–2237 CrossRef.
- X. Li, et al., Statistical learning of governing equations of dynamics from in-situ electron microscopy imaging data, Mater. Des., 2020, 195, 108973 CrossRef CAS.
- Y. Zhu, Q. Ouyang and Y. Mao, A deep convolutional neural network approach to single-particle recognition in cryo-electron microscopy, BMC Bioinf., 2017, 18, 348 CrossRef PubMed.
- R. Sanchez-Garcia, J. Segura, D. Maluenda, J. M. Carazo and C. O. S. Sorzano, Deep Consensus, a deep learning-based approach for particle pruning in cryo-electron microscopy, IUCrJ, 2018, 5, 854–865 CrossRef CAS PubMed.
- T. Hey, K. Butler, S. Jackson and J. Thiyagalingam, Machine learning and big scientific data, Philos. Trans. R. Soc., A, 2020, 378, 20190054 CrossRef PubMed.
- L. Chen, R. Jebril and K. Al Nasr, Segmentation-based Feature Extraction for Cryo-Electron Microscopy at Medium Resolution, Proceedings of the 11th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, 2020, 1–9, DOI:10.1145/3388440.3414711.
- T. Bendory, A. Bartesaghi and A. Singer, Single-Particle Cryo-Electron Microscopy: Mathematical Theory, Computational Challenges, and Opportunities, IEEE Signal Process. Mag., 2020, 58–76 Search PubMed.
- D. Si, et al., Artificial intelligence advances for de novo molecular structure modeling in cryo-electron microscopy, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 12, e1542, DOI:10.1002/wcms.1542.
- N. Kumar, et al., CryoDiscovery TM: A Machine Learning Platform for Automated Cryo-electron Microscopy Particle Classification, Microsc. Microanal., 2020, 26, 2308–2310 CrossRef.
- T. Slater, et al., Automating 3D Imaging of Inorganic Nanoparticles, Microsc. Microanal., 2021, 27, 2864–2866 CrossRef.
- F. L. Kyrilis, J. Belapure and P. L. Kastritis, Detecting Protein Communities in Native Cell Extracts by Machine Learning: A Structural Biologist’s Perspective, Front. Mol. Biosci., 2021, 8, 660542 CrossRef CAS PubMed.
- J. Merham, A. Rakowski and J. Patterson, Particle Picking in Cryo-TEM Images Using Machine Learning, Microsc. Microanal., 2020, 26, 2102–2103 CrossRef.
- M. Weber, et al., Automatic identification of crossovers in cryo-EM images of murine amyloid protein A fibrils with machine learning, J. Microsc., 2020, 277, 12–22 CrossRef CAS PubMed.
- A. S. Morgunov, K. L. Saar, M. Vendruscolo and T. P. J. Knowles, New Frontiers for Machine Learning in Protein Science, J. Mol. Biol., 2021, 433, 167232 CrossRef CAS PubMed.
- K. Yonekura, S. Maki-Yonekura, H. Naitow, T. Hamaguchi and K. Takaba, Machine learning-based real-time object locator/evaluator for cryo-EM data collection, Commun. Biol., 2021, 4, 1044 CrossRef CAS PubMed.
- E. Alnabati and D. Kihara, Advances in structure modeling methods for cryo-electron microscopy maps, Molecules, 2019, 25, 82 CrossRef PubMed.
- D. Si, S. Ji and K. Nasr, Al & He, J. A machine learning approach for the identification of protein secondary structure elements from electron cryo-microscopy density maps, Biopolymers, 2012, 97, 698–708 CrossRef CAS PubMed.
- R. Langlois, J. Pallesen and J. Frank, Reference-free particle selection enhanced with semi-supervised machine learning for cryo-electron microscopy, J. Struct. Biol., 2011, 175, 353–361 CrossRef PubMed.
- J. Chen, Advanced Electron Microscopy of Nanophased Synthetic Polymers and Soft Complexes for Energy and Medicine Applications, Nanomaterials, 2021, 11, 2405 CrossRef CAS PubMed.
- M. P. Prange, M. P. Oxley, S. J. Pennycook and S. T. Pantelides, Simulation of STEM-EELS Including Diffraction and Solid-State Effects I: Mixed Dynamic Form Factor beyond the Dipole Approximation, Microsc. Microanal., 2021, 17, 808–809 CrossRef.
- M. P. Oxley, et al., Simulation of Probe Position-Dependent Electron Energy-Loss Fine Structure, Microsc. Microanal., 2014, 20, 784–797 CrossRef CAS PubMed.
- A. Eljarrat, X. Sastre, F. Peiró and S. Estradé, Density Functional Theory Modeling of Low-Loss Electron Energy-Loss Spectroscopy in Wurtzite III-Nitride Ternary Alloys, Microsc. Microanal., 2016, 22, 706–716 CrossRef CAS PubMed.
- F. J. G. De Abajo, Optical excitations in electron microscopy, Rev. Mod. Phys., 2010, 82, 209–275 CrossRef.
- S. Chen, et al., Electron energy loss spectroscopy and ab initio investigation of iron oxide nanomaterials grown by a hydrothermal process, 2009, 1–10 DOI:10.1103/PhysRevB.79.104103.
- A. Gloter, A. Douiri, M. Tencé and C. Colliex, Improving energy resolution of EELS spectra: an alternative to the monochromator solution, Ultramicroscopy, 2003, 96, 385–400 CrossRef CAS PubMed.
- O. L. Krivanek, et al., Progress in ultrahigh energy resolution EELS, Ultramicroscopy, 2019, 203, 60–67 CrossRef CAS PubMed.
- P. Cueva, R. Hovden, J. A. Mundy, H. L. Xin and D. A. Muller, New Approaches to Data Processing for Atomic Resolution EELS, Microsc. Microanal., 2012, 18, 970–971 CrossRef.
- R. F. Egerton, Electron-Loss Spectroscopy in the Electron Microscope, Springer Science & Business Media, 2011 Search PubMed.
- K. Kimoto and Y. Matsui, Software techniques for EELS to realize about 0. 3 eV energy resolution using 300 kV FEG-TEM, J. Microsc., 2002, 208, 224–228 CrossRef CAS PubMed.
- S. Martí-Sánchez, et al., Sub-nanometer mapping of strain-induced band structure variations in planar nanowire core–shell heterostructures, Nat. Commun., 2022, 13, 4089 CrossRef PubMed.
- L. Jones, R. B. S. Lozano-perez, K. Baba-kishi and P. D. Nellist, Improving the SNR of Atomic Resolution STEM EELS & EDX Mapping while Reducing Beam-damage by using Non-rigid Spectrum-image Averaging, Microsc. Microanal., 2021, 21, 1215–1216 CrossRef.
- J. S. Jeong and K. A. Mkhoyan, Improving Signal-to-Noise Ratio in Scanning Transmission Electron Microscopy Energy-Dispersive X-Ray (STEM-EDX) Spectrum Images Using Single-Atomic-Column Cross-Correlation Averaging, Microsc. Microanal., 2016, 22, 536–543 CrossRef CAS PubMed.
- L. Jones, et al., Managing dose-, damage- and data-rates in multi-frame spectrum-imaging, Microscopy, 2018, 98–113, DOI:10.1093/jmicro/dfx125.
- K. Sader, et al., Smart acquisition EELS, Ultramicroscopy, 2010, 110, 998–1003 CrossRef CAS.
- P. Torruella, et al., Assessing Oxygen Vacancies in Bismuth Oxide Through EELS Measurements and DFT Simulations Assessing Oxygen Vacancies in Bismuth Oxide through EELS Measurements and DFT Simulations, J. Phys. Chem. C, 2017, 121, 24809–24815, DOI:10.1021/acs.jpcc.7b06310.
- I. Arslan, S. Ogut, P. D. Nellist and N. D. Browning, Comparison of simulation methods for electronic structure calculations with experimental electron energy-loss spectra, Micron, 2003, 34, 255–260 CrossRef CAS PubMed.
- G. Kothleitner, et al., Quantitative Elemental Mapping at Atomic Resolution Using X-Ray, Spectroscopy, 2014, 112, 085501 Search PubMed.
- A. Genç, et al., Hollow metal nanostructures for enhanced plasmonics: Synthesis, local plasmonic properties and applications, Nanophotonics, 2017, 6, 193–213 Search PubMed.
- D. Jirovec, et al., A singlet-triplet hole spin qubit in planar Ge, Nat. Mater., 2021, 20, 1106–1112 CrossRef CAS PubMed.
- P. Y. Tang, et al., Boosting Photoelectrochemical Water Oxidation of Hematite in Acidic Electrolytes by Surface State Modification, Adv. Energy Mater., 2019, 9, 1901836 CrossRef.
- M. De La Mata, et al., The Role of Polarity in Nonplanar Semiconductor Nanostructures, Nano Lett., 2019, 19, 3396–3408 CrossRef CAS PubMed.
- R. Zamani and J. Arbiol, Understanding semiconductor nanostructures via advanced electron microscopy and spectroscopy, Nanotechnology, 2019, 30, 262001 CrossRef CAS PubMed.
- N. Mevenkamp, et al., Multi-modal and multi-scale non-local means method to analyze spectroscopic datasets, Ultramicroscopy, 2019, 112877, DOI:10.1016/j.ultramic.2019.112877.
- S. Jesse and S. V. Kalinin, Principal component and spatial correlation analysis of spectroscopic-imaging data in scanning probe microscopy, Nanotechnology, 2009, 085714 CrossRef PubMed.
- K. Roccapriore, Z. Gai, B. Sumpter, M. Yoon and S. V. Kalinin, Spectral Classification of Structurally Organized Adatom Configurations, Microsc. Microanal., 2021, 26, 2988–2989 CrossRef.
- H. Chang and D. Yeung, Robust locally linear embedding, Pattern Recognit., 2006, 39, 1053–1065 CrossRef.
- B. J. Rodriguez, et al., Dynamic and Spectroscopic Modes and Multivariate Data Analysis in Piezoresponse Force Microscopy, Scanning probe microscopy of functional materials, Springer, New York, NY, 2010, pp. 491–528, ISBN: 201010.1007/978-1-4419-7167-8 Search PubMed.
- A. A. Varambhia, L. Jones and A. London, Determining EDS and EELS partial cross-sections from multiple calibration standards to accurately quantify bi-metallic nanoparticles using STEM, Micron, 2018, 113, 69–82 CrossRef CAS PubMed.
- M. C. Spadaro, et al., Rotated domains in selective area epitaxy grown Zn3P2: formation mechanism and functionality, Nanoscale, 2021, 13, 18441–18450 RSC.
- A. Genç, et al., Tuning the Plasmonic Response up: Hollow Cuboid Metal Nanostructures, ACS Photonics, 2016, 3, 770–779 CrossRef.
- J. Spiegelberg and J. Rusz, Can we use PCA to detect small signals in noisy data?, Ultramicroscopy, 2017, 172, 40–46 CrossRef CAS PubMed.
- S. Lichtert and J. Verbeeck, Statistical consequences of applying a PCA noise filter on EELS spectrum images, Ultramicroscopy, 2013, 125, 35–42 CrossRef CAS PubMed.
- P. Potapov, Why Principal Component Analysis of STEM spectrum-images results in “ abstract”, uninterpretable loadings?, Ultramicroscopy, 2016, 160, 197–212 CrossRef CAS PubMed.
- P. Potapov, P. Longo and E. Okunishi, Enhancement of noisy EDX HRSTEM spectrum-images by combination of filtering and PCA, Micron, 2017, 96, 29–37 CrossRef CAS PubMed.
- P. Cueva, R. Hovden, J. A. Mundy, H. L. Xin and D. A. Muller, Data Processing for Atomic Resolution Electron Energy Loss Spectroscopy, Microsc. Microanal., 2012, 667–675 CrossRef CAS PubMed.
- P. Potapov and A. Lubk, Optimal principal component analysis of STEM XEDS spectrum images, Adv. Struct. Chem. Imaging, 2019, 5, 4 CrossRef PubMed.
- A. Tharwat, Independent component analysis: An introduction, Appl. Comput. Informat., 2018, 17, 222–249 CrossRef.
- J. M. P. Nascimento and J. M. B. Dias, Vertex component analysis: A fast algorithm to unmix hyperspectral data, IEEE Trans. Geosci. Remote Sens., 2005, 43, 898–910 Search PubMed.
- T. Blum, et al., Machine Learning Method Reveals Hidden Strong Metal-Support Interaction in Microscopy Datasets, Small Methods, 2021, 5, 2100035 CrossRef CAS PubMed.
- T. Blum, J. Graves, M. Zachman, R. Kannan and X. Pan, Machine Learning for Challenging EELS and EDS Spectral Decomposition, Microsc. Microanal., 2021, 25, 180–181 CrossRef.
- Y. Suzuki, H. Hino, M. Kotsugi and K. Ono, Automated estimation of materials parameter from X-ray absorption and electron energy-loss spectra with similarity measures, npj Comput. Mater., 2019, 1–7, DOI:10.1038/s41524-019-0176-1.
- P. Crozier, J. Vincent, K. Venkatraman, Y. Wang and S. Yang, Probing Properties of Nanomaterials with Advanced Electron Energy-Loss Spectroscopy, Microsc. Microanal., 2021, 27, 872–874 CrossRef.
- H. Chen, F. Nabiei, J. Badro, D. T. L. Alexander and C. Hébert, STEM EDS/EELS for Phase Analysis of Deep-Mantle Rock Assemblages Supported by, Mach. Learn., 2021, 25, 2474–2475 Search PubMed.
- A. Heimbrook, K. Higgins, S. V. Kalinin and M. Ahmadi, Exploring the physics of cesium lead halide perovskite quantum dots via Bayesian inference of the photoluminescence spectra in automated experiment, Nanophotonics, 2021, 10, 1977–1989 CrossRef CAS.
- R. D. Leapman and C. R. Swyt, Separation of Overlapping Core Edges in Electron Energy Loss Spectra by Multiple-Least-Squares Fitting, Ultramicroscopy, 1988, 26, 393–404 CrossRef CAS PubMed.
- K. P. Kelley, et al., Tensor factorization for elucidating mechanisms of piezoresponse relaxation via dynamic Piezoresponse Force Spectroscopy, npj Comput. Mater., 2020, 6, 113, DOI:10.1038/s41524-020-00384-6.
- K. M. Roccapriore, et al., Revealing the Chemical Bonding in Adatom Arrays via Machine Learning of Hyperspectral, ACS Nano, 2021, 15, 11806–11816 CrossRef CAS PubMed.
- R. Hovden, P. Cueva, J. A. Mundy and D. A. Muller, The Open-Source Cornell Spectrum Imager, Microsc. Today, 2013, 21, 40–44 CrossRef CAS.
- M. Ziatdinov, D. Kim, S. Neumayer and S. V. Kalinin, Imaging mechanism for hyperspectral scanning probe microscopy via Gaussian process modelling, npj Comput. Mater., 2020, 6, 21, DOI:10.1038/s41524-020-0289-6.
- L. Yedra, et al., Oxide Wizard: An EELS Application to Characterize the White Lines of Transition Metal Edges, Microsc. Microanal., 2014, 20, 698–705 CrossRef CAS PubMed.
- M. Shiga, et al., Sparse modeling of EELS and EDX spectral imaging data by nonnegative matrix factorization, Ultramicroscopy, 2016, 170, 43–59 CrossRef CAS PubMed.
- S. Muto and M. Shiga, Application of machine learning techniques to electron microscopic/spectroscopic image data analysis, Microscopy, 2020, 69, 110–122 CrossRef CAS PubMed.
- N. Bonnet and D. Nuzillard, Independent component analysis: A new possibility for analysing series of electron energy loss spectra, Ultramicroscopy, 2005, 102, 327–337 CrossRef CAS PubMed.
- F. de la Peña, et al., Mapping titanium and tin oxide phases using EELS: An application of independent component analysis, Ultramicroscopy, 2011, 111, 169–176 CrossRef PubMed.
- D. Rossouw, B. R. Knappett, A. E. H. Wheatley and P. A. Midgley, A New Method for Determining the Composition of Core – Shell Nanoparticles via Dual-EDX + EELS Spectrum Imaging, Part. Part. Syst. Charact., 2016, 33, 749–755 CrossRef CAS.
- N. Dobigeon and N. Brun, Spectral mixture analysis of EELS spectrum-images, Ultramicroscopy, 2012, 120, 25–34 CrossRef CAS PubMed.
- S. V. Kalinin, A. R. Lupini, R. K. Vasudevan and M. Ziatdinov, Gaussian process analysis of electron energy loss spectroscopy data: multivariate reconstruction and kernel control, npj Comput. Mater., 2021, 7, 154, DOI:10.1038/s41524-021-00611-8.
- M. Chang, R. Cai, C. Chen and S. Lo, Development of Clustering Algorithm Applied for the EELS Analysis of Advanced Devices, Microsc. Microanal., 2020, 26, 2112–2114 CrossRef.
- N. Creange, et al., Propagation of priors for more accurate and efficient spectroscopic functional fits and their application to ferroelectric hysteresis, Mach. Learn. Sci. Technol., 2021, 2, 045002 CrossRef.
- G. Yang, et al., Distilling nanoscale heterogeneity of amorphous silicon using tip-enhanced Raman spectroscopy (TERS) via multiresolution manifold learning, Nat. Commun., 2021, 12, 578 CrossRef CAS PubMed.
- M. Pfannm, et al., Visualizing a Homogeneous Blend in Bulk Heterojunction Polymer Solar Cells by Analytical Electron Microscopy, Nano Lett., 2011, 11, 3099–3107 CrossRef PubMed.
- L. Lajaunie, et al., Fast Automated Phase Differentiation in Industrial Stainless Steel by Combining Low-Loss EELS Experiments with Machine Learning-based Algorithms, Microsc. Microanal., 2021, 27, 34–36 CrossRef.
- S. Kiyohara, T. Miyata, K. Tsuda and T. Mizoguchi, Data-driven approach for the prediction and interpretation of core-electron loss spectroscopy, Sci. Rep., 2018, 8, 13548, DOI:10.1038/s41598-018-30994-6.
- T. Mizoguchi and S. Kiyohara, Machine learning approaches for ELNES/XANES, Microscopy, 2020, 69, 92–109 CrossRef CAS PubMed.
- P. Torruella, et al., Clustering analysis strategies for electron energy loss spectroscopy (EELS), Ultramicroscopy, 2018, 185, 42–48 CrossRef CAS PubMed.
- J. Blanco-Portals, et al., WhatEELS. A python-based interactive software solution for ELNES analysis combining clustering and NLLS, Ultramicroscopy, 2022, 232, 113403 CrossRef CAS PubMed.
- J. Ryu, et al., Dimensionality reduction and unsupervised clustering for EELS-SI, Ultramicroscopy, 2021, 231, 113314 CrossRef CAS PubMed.
- S. V. Kalinin, et al., Separating Physically Distinct Mechanisms in Complex Infrared Plasmonic Nanostructures via Machine Learning Enhanced Electron Energy Loss Spectroscopy, Adv. Opt. Mater., 2021, 9, 2001808 CrossRef CAS.
- J. Hachtel, N. Borodinov, K. Roccapriore, S. H. Cho and P. Banerjee, Beyond NMF: Advanced Signal Processing and Machine Learning Methodologies for Hyperspectral Analysis in EELS, Microsc. Microanal., 2021, 27, 322–324 CrossRef.
- M. Oxley, M. Ziatdinov and S. Kalinin, Denoising STEM Electron Energy Loss Spectra using Convolutional Autoencoders, Microsc. Microanal., 2021, 27, 1180–1182 CrossRef.
- C. M. Pate, J. L. Hart and M. L. Taheri, RapidEELS: machine learning for denoising and classification in rapid acquisition electron energy loss spectroscopy, Sci. Rep., 2021, 11, 19515 CrossRef CAS PubMed.
- P. Ewels, T. Sikora, V. Serin, C. P. Ewels and L. Lajaunie, A Complete Overhaul of the Electron Energy-Loss Spectroscopy and X-Ray Absorption Spectroscopy Database: eelsdb. eu, Microsc. Microanal., 2017, 717–724, DOI:10.1017/S1431927616000179.
- H. L. Xin, et al., One Million EEL Spectra Acquisition with Aberration-Corrected STEM: 2-D Chemical Investigation of a Statistically Significant Ensemble of Nanocatalysts, Microsc. Microanal., 2010, 16, 2009–2010 Search PubMed.
- E. J. Kirkland, Advanced Computing in Electron Microscopy. Advanced Computing in Electron Microscopy, 1998 DOI:10.1007/978-1-4757-4406-4.
- F. J. García de Abajo and A. Howie, Retarded field calculation of electron energy loss in inhomogeneous dielectrics, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 115418 CrossRef.
- L. Kiewidt and M. Karamehmedovi, The Generalized Multipole Technique for the Simulation of Low-Loss Electron Energy Loss Spectroscopy, Springer, Cham, 2018, pp. 147–167, DOI:10.1007/978-3-319-74890-0.
- M. P. Oxley and S. J. Pennycook, Image simulation for electron energy loss spectroscopy, Micron, 2008, 39, 676–684 CrossRef CAS PubMed.
- A. Mitsutake, Y. Sugita and Y. Okamoto, Replica-exchange multicanonical and multicanonical replica-exchange Monte Carlo simulations of peptides. I. Formulation and benchmark test, J. Chem. Phys., 2003, 118, 6664–6675 CrossRef CAS.
- A. Desalvo, R. Rosa, A. Armigliato and A. Parisini, Analysis of light elements in superposed layers by Monte Carlo simulation of EELS spectra, Mikrochim. Acta, 1994, 114–115, 267–275 CrossRef CAS.
- M. Attarian Shandiz, F. Salvat and R. Gauvin, Fine Structure of Core Loss Excitations in EELS by Monte Carlo Simulation, Microsc. Microanal., 2013, 19, 366–367 CrossRef.
- M. Attarian Shandiz, F. Salvat and R. Gauvin, Detectability Limits in EELS by Monte Carlo Simulations, Microsc. Microanal., 2012, 18, 998–999 CrossRef.
- J. Ã. Verbeeck and S. Aert, Van. Model based quantification of EELS spectra, Ultramicroscopy, 2004, 101, 207–224 CrossRef CAS PubMed.
- J. Ã. Verbeeck, S. Van Aert and G. Bertoni, Model-based quantification of EELS spectra: Including the fine structure, Ultramicroscopy, 2006, 106, 976–980 CrossRef CAS PubMed.
- X. Liu, et al., Machine learning approach for the prediction of electron inelastic mean free paths, Phys. Rev. Mater., 2021, 033802 CrossRef CAS.
- E. Quattrocchi, et al., The deep-DRT: A deep neural network approach to deconvolve the distribution of relaxation times from multidimensional electrochemical impedance spectroscopy data, Electrochim. Acta, 2021, 392, 139010 CrossRef CAS.
- M. S. Moreno, K. Jorissen and J. J. Rehr, Practical aspects of electron energy-loss spectroscopy (EELS) calculations using FEFF8, Micron, 2007, 38, 1–11 CrossRef CAS PubMed.
- A. Ankudinov and B. Ravel, Real-space multiple-scattering calculation and interpretation of x-ray-absorption near-edge structure, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7565–7576 CrossRef CAS.
- M. P. Oxley, et al., Simulation of STEM-EELS Including Diffraction and Solid-State Effects II: Adding the Experiment, Microsc. Microanal., 2011, 17, 810–811 CrossRef.
- M. P. Prange, M. P. Oxley, M. Varela, S. J. Pennycook and S. T. Pantelides, Simulation of Spatially Resolved Electron Energy Loss Near-Edge Structure for Scanning Transmission Electron Microscopy, Phys. Rev. Lett., 2012, 109, 246101 CrossRef CAS PubMed.
- L. J. Allen, S. D. Findlay, M. P. Oxley and C. J. Rossouw, Lattice-resolution contrast from a focused coherent electron probe. Part I, Ultramicroscopy, 2003, 96, 47–63 CrossRef CAS PubMed.
- S. D. Findlay, L. J. Allen, M. P. Oxley and C. J. Rossouw, Lattice-resolution contrast from a focused coherent electron probe. Part II, Ultramicroscopy, 2003, 96, 65–81 CrossRef CAS PubMed.
- T. Morimura and M. Hasaka, Bloch-wave-based STEM image simulation with layer-by-layer representation, Ultramicroscopy, 2009, 109, 1203–1209 CrossRef CAS PubMed.
- H. G. Brown, S. D. Findlay, L. J. Allen, J. Ciston and C. Ophus, Rapid Simulation of Elemental Maps in Core-Loss Electron Energy Loss Spectroscopy, Microsc. Microanal., 2019, 25, 574–575 CrossRef.
- F. Eggert, EDX-spectra simulation in electron probe microanalysis. Optimization of excitation conditions and detection limits, Microchim. Acta, 2006, 155, 129–136 CrossRef CAS.
- NIST, DTSA-II Microscopium, 2021, available at: https://cstl.nist.gov/div837/837.02/epq/dtsa2/.
- M. Chatzidakis and G. A. Botton, Towards calibration-invariant spectroscopy using deep learning, Sci. Rep., 2019, 9, 2126 CrossRef CAS PubMed.
- A. Scheinker and R. Pokharel, Adaptive 3D convolutional neural network-based reconstruction method for 3D coherent diffraction imaging, J. Appl. Phys., 2020, 128, 184901 CrossRef CAS.
- A. Y. Borisevich, S. V. Kalinin, A. R. Lupini, S. Jesse and H. J. Chang, Using Neural Network Algorithms for Compositional Mapping in STEM EELS, Microsc. Microanal., 2009, 15, 50–51 CrossRef.
- D. del Pozo-Bueno, F. Peiró and S. Estradé, Support vector machine for EELS oxidation state determination, Ultramicroscopy, 2021, 221, 113190 CrossRef CAS PubMed.
- P. J. Thomas and P. A. Midgley, Image-spectroscopy – I. The advantages of increased spectral information for compositional EFTEM analysis, Ultramicroscopy, 2001, 88, 179–186 CrossRef CAS PubMed.
- P. J. Thomas and P. A. Midgley, Image-spectroscopy – II. The removal of plural scattering from extended energy-filtered series by Fourier deconvolution, Ultramicroscopy, 2001, 88, 187–194 CrossRef CAS PubMed.
- L. I. Roest, S. E. van Heijst, L. Maduro, J. Rojo and S. Conesa-Boj, Charting the low-loss region in electron energy loss spectroscopy with machine learning, Ultramicroscopy, 2021, 222, 113202 CrossRef CAS PubMed.
- A. Stevens, et al., Compressive STEM-EELS, Microsc. Microanal., 2016, 22, 560–561 CrossRef.
- E. Monier, et al., Fast reconstruction of atomic-scale STEM-EELS images from sparse sampling, Ultramicroscopy, 2020, 215, 112993, DOI:10.1016/j.ultramic.2020.112993.
- S. M. Collins, et al., Scan Strategies for Electron Energy Loss Spectroscopy at Optical and Vibrational Energies in Perylene Diimide Nanobelts, Microsc. Microanal., 2019, 25, 1738–1739 CrossRef.
- J. Schwartz, et al., Recovering Chemistry at Atomic Resolution using Multi-Modal Spectroscopy, Microsc. Microanal., 2021, 27, 1226–1228 CrossRef.
- S. M. Collins and P. A. Midgley, Progress and opportunities in EELS and EDS tomography, Ultramicroscopy, 2017, 180, 133–141 CrossRef CAS PubMed.
- R. K. Leary and P. A. Midgley, Analytical electron tomography, MRS Bulletin, 2016, 41, 531–536 CrossRef.
- Z. Zhong, et al., A bimodal tomographic reconstruction technique combining EDS-STEM and HAADF-STEM, Ultramicroscopy, 2017, 174, 35–45 CrossRef CAS PubMed.
- Z. Zhong, W. J. Palenstijn, N. R. Viganò and K. J. Batenburg, Numerical methods for low-dose EDS tomography, Ultramicroscopy, 2018, 194, 133–142 CrossRef CAS PubMed.
- M. Weyland and P. A. Midgley, Extending Energy-Filtered Transmission Electron Microscopy (EFTEM) into Three Dimensions Using Electron Tomography, Microsc. Microanal., 2003, 9, 542–555 CrossRef CAS PubMed.
- P. A. Midgley and M. Weyland, 3D electron microscopy in the physical sciences: the development of Z-contrast and EFTEM tomography, Ultramicroscopy, 2003, 96, 413–431 CrossRef CAS PubMed.
- B. Goris, et al., Discrete spectroscopic electron tomography: using prior knowledge of reference spectra during the reconstruction, EMC Proc., 2016, 8, 976–977 Search PubMed.
- M. Pfannmöller, et al., Quantitative Tomography of Organic Photovoltaic Blends at the Nanoscale, Nano Lett., 2015, 15, 6634–6642 CrossRef PubMed.
- D. Zanaga, et al., A New Method for Quantitative XEDS Tomography of Complex Heteronanostructures, Part. Part. Syst. Charact., 2016, 33, 396–403 CrossRef CAS.
- B. Goris, et al., Towards Quantitative EDX Results in 3 Dimensions, Microsc. Microanal., 2014, 20, 766–767 CrossRef.
- S. Bals, et al., Spectral Electron Tomography as a Quantitative Technique to Investigate Functional Nanomaterials, Microsc. Microanal., 2021, 22, 274–275 CrossRef.
- A. Alafeef, et al., Linear chemically sensitive electron tomography using DualEELS and dictionary-based compressed sensing, Ultramicroscopy, 2016, 170, 96–106 CrossRef CAS PubMed.
- R. Huber, G. Haberfehlner, M. Holler, G. Kothleitner and K. Bredies, Total generalized variation regularization for multi-modal electron tomography, Nanoscale, 2019, 11, 5617–5632 RSC.
- L. Yedra, et al., EEL spectroscopic tomography: Towards a new dimension in nanomaterials analysis, Ultramicroscopy, 2012, 122, 12–18 CrossRef CAS PubMed.
- Z. Saghi, et al., Improved Data Analysis and Reconstruction Methods for STEM-EDX Tomography, Microsc. Microanal., 2016, 22, 284–285 CrossRef.
- P. Torruella, et al., 3D visualization of iron oxidation state in FeO/Fe3O4 core–shell nanocubes from electron energy loss tomography, Nano Lett., 2016, 16, 5068–5073 CrossRef CAS PubMed.
- X. Yang, et al., Low-dose x-ray tomography through a deep convolutional neural network, Sci. Rep., 2018, 8, 2575 CrossRef PubMed.
- A. Skorikov, W. Heyvaert, W. Albecht, D. Pelt and S. Bals, Deep learning-based denoising for improved dose efficiency in EDX tomography of nanoparticles, Nanoscale, 2021, 13, 12242–12249 RSC.
- B. C. Love, Comparing supervised and unsupervised category learning, Psychon. Bull. Rev., 2002, 9, 829–835 CrossRef PubMed.
- S. Somnath, USID and Pycroscopy – Open frameworks for storing and analyzing spectroscopic and imaging data, Microsc. Microanal., 2019, 25, 220–221 CrossRef.
- C. R. Harris, et al., Array programming with NumPy, Nature, 2020, 585, 357–362 CrossRef CAS PubMed.
- pyUSID, available at: https://pycroscopy.github.io/pyUSID/about.html, (accessed: 28th December 2021).
- The HDF Group. The HDF5® Library & File Format, available at: https://www.hdfgroup.org/solutions/hdf5/ (accessed: 28th December 2021).
- G. H. Weber, C. Ophus and L. Ramakrishnan, Automated Labeling of Electron Microscopy Images Using Deep Learning, in Proc. MLHPC 2018 Mach. Learn. HPC Environ. Held conjunction with SC 2018 Int. Conf. High Perform. Comput. Networking, Storage Anal., 2019, pp. 26–36 DOI:10.1109/MLHPC.2018.8638633.
- R. K. Vasudevan, et al., Materials science in the artificial intelligence age: High-throughput library generation, machine learning, and a pathway from correlations to the underpinning physics, MRS Commun., 2019, 9, 821–838 CrossRef CAS PubMed.
- A. Khadangi, T. Boudier and V. Rajagopal, EM-stellar: benchmarking deep learning for electron microscopy image segmentation, Bioinformatics, 2021, 37, 97–106 CrossRef CAS PubMed.
- J. M. Cowley and A. F. Moodie, The scattering of electrons by atoms and crystals. I. A new theoretical approach, Acta Crystallogr., 1957, 10, 609–619 CrossRef CAS.
- E. J. Kirkland, R. F. Loane and J. Silcox, Simulation of annular dark field stem images using a modified multislice method, Ultramicroscopy, 1987, 23, 77–96 CrossRef.
- D. A. Muller, B. Edwards, E. J. Kirkland E and J. Silcox, Simulation of thermal diffuse scattering including a detailed phonon dispersion curve, Ultramicroscopy, 2001, 86, 371–380 CrossRef CAS PubMed.
- J. C. H. Spence and J. M. Zuo, Electron Microdiffraction. Electron Microdiffraction, Springer US, 1992 DOI:10.1007/978-1-4899-2353-0.
- C. Koch and J. M. Zuo, Comparison of Multislice Computer Programs for Electron Scattering Simulations and The Bloch Wave Method, Microsc. Microanal., 2000, 6, 126–127 CrossRef.
- A. Hjorth Larsen, et al., The atomic simulation environment - A Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- J. Richard, T. John, N. Manuel, L. Sean and M. Ian, MDAnalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations, Proc. 15th Python Sci. Conf., 2019, vol. 11.
- mendeleev, available at: https://mendeleev.readthedocs.io/en/stable/ (accessed: 27th December 2021).
- crystals PyPI, available at: https://pypi.org/project/crystals/ (accessed: 27th December 2021).
- J. B. Greisman, K. M. Dalton and D. R. Hekstra, Reciprocalspaceship: a Python library for crystallographic data analysis, J. Appl. Cryst., 2021, 54, 1521–1529 CrossRef CAS PubMed , ISSN: 1600-5767.
- A. H. Combs, et al., Fast approximate STEM image simulations from a machine learning model, Adv. Struct. Chem. Imaging, 2019, 5, 2 CrossRef.
- J. S. Smith, O. Isayev and A. E. Roitberg, ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost, Chem. Sci., 2017, 8, 3192–3203 RSC.
- A. V. Sinitskiy and V. S. Pande, Deep Neural Network Computes Electron Densities and Energies of a Large Set of Organic Molecules Faster than Density Functional Theory (DFT), arXiv, 2018, preprint, arXiv:1809.02723, DOI:10.48550/arXiv.1809.02723.
- N. Artrith and A. Urban, An implementation of artificial neural-network potentials for atomistic materials simulations: Performance for TiO2, Comput. Mater. Sci., 2016, 114, 135–150 CrossRef CAS.
- J. Behler, First Principles Neural Network Potentials for Reactive Simulations of Large Molecular and Condensed Systems, Angew. Chem., Int. Ed., 2017, 56, 12828–12840 CrossRef CAS PubMed.
- N. Artrith, T. Morawietz and J. Behler, High-dimensional neural-network potentials for multicomponent systems: Applications to zinc oxide, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 153101 CrossRef.
- J. Madsen and T. Susi, abTEM: ab Initio Transmission Electron Microscopy Image Simulation, Microsc. Microanal., 2020, 26, 448–450 CrossRef.
- J. Madsen, T. J. Pennycook and T. Susi, Ab Initio Description of Bonding for Transmission Electron Microscopy, Ultramicroscopy, 2021, 113253, DOI:10.1016/j.ultramic.2021.113253.
- T. Susi, et al., Efficient first principles simulation of electron scattering factors for transmission electron microscopy, Ultramicroscopy, 2019, 197, 16–22 CrossRef CAS PubMed.
- cerius2, available at: https://www-jmg.ch.cam.ac.uk/cil/SGTL/cerius2.html (accessed: 22nd December 2021).
- J. J. P. Peters, clTEM | GPU accelerated multislice.
- ningustc, cudaEM, available at: https://github.com/ningustc/cudaEM (accessed: 22nd December 2021).
- J. Barthel, Dr Probe: A software for high-resolution STEM image simulation, Ultramicroscopy, 2018, 193, 1–11 CrossRef CAS PubMed.
- R. Kilaas, L. D. Marks and C. S. Own, EDM 1.0: Electron direct methods, Ultramicroscopy, 2005, 102, 233–237 CrossRef CAS PubMed.
- C. Ophus, A fast image simulation algorithm for scanning transmission electron microscopy, Adv. Struct. Chem. Imaging, 2017, 3, 13 CrossRef PubMed.
- A. Pryor, C. Ophus and J. Miao, A streaming multi-GPU implementation of image simulation algorithms for scanning transmission electron microscopy, Adv. Struct. Chem. Imaging, 2017, 3, 15 CrossRef PubMed.
- L. Rangel DaCosta, et al., Prismatic 2.0 – Simulation software for scanning and high resolution transmission electron microscopy (STEM and HRTEM), Micron, 2021, 151, 103141 CrossRef CAS PubMed.
- C. Koch, QSTEM: Quantitative TEM/STEM Simulations — Strukturforschung/Elektronenmikroskopie.
- jacobjma, PyQSTEM: A Python interface to the electron microscopy simulation program QSTEM, available at: https://github.com/jacobjma/PyQSTEM (accessed: 27th December 2021).
- L. P. René de Cotret, M. R. Otto, M. J. Stern and B. J. Siwick, An open-source software ecosystem for the interactive exploration of ultrafast electron scattering data, Adv. Struct. Chem. Imaging, 2018, 4, 11 CrossRef PubMed.
- V. Grillo and F. Rossi, STEM_CELL: A software tool for electron microscopy. Part 2 analysis of crystalline materials, Ultramicroscopy, 2013, 125, 112–129 CrossRef CAS PubMed.
- V. Grillo and E. Rotunno, STEM_CELL: A software tool for electron microscopy: Part I-simulations, Ultramicroscopy, 2013, 125, 97–111 CrossRef CAS PubMed.
- Berkeley CA USA, Total Resolution LLC | HRTEM Software Provider | TEMPAS, available at: https://www.totalresolution.com/ (accessed: 27th December 2021).
- F. Salvat, J. Fernández-Vera and J. Sempau, PENELOPE-2018: A Code System for Monte Carlo Simulation of Electron and Photon Transport, in Work. Proceedings, Barcelona, Spain, 2019 Search PubMed.
- pyPENELOPE, available at: https://pypenelope.sourceforge.net/index.html (accessed: 4th August 2022).
- X. Glorot and Y. Bengio, Understanding the difficulty of training deep feedforward neural networks, J. Mach. Learn. Res., 2010, 9, 249–256 Search PubMed.
- L. Fei-Fei, J. Deng and K. Li, ImageNet: Constructing a large-scale image database, J. Vis., 2010, 9, 1037 Search PubMed.
- Y. You, Z. Zhang, C. J. Hsieh, J. Demmel and K. Keutzer, ImageNet training in minutes, Proceedings of the 47th International Conference on Parallel Processing, 2018, 1, DOI:10.1145/3225058.3225069.
- Y. LeCun, C. C. and C. B. MNIST handwritten digit database, available at: https://yann.lecun.com/exdb/mnist/ (accessed: 23rd December 2021).
- Y. Lecun, L. Bottou, Y. Bengio and P. Haffner, Gradient-Based Learning Applied to Document Recognition, Proceedings of the IEEE, 1998, 86, 2278–2324 CrossRef.
- LabelMe.Dataset, available at: https://labelme.csail.mit.edu/Release3.0/browserTools/php/dataset.php (accessed: 23rd December 2021).
- B. C. Russell, A. Torralba, K. P. Murphy and W. T. Freeman, LabelMe: A database and web-based tool for image annotation, Int. J. Comput. Vis., 2008, 77, 157–173 CrossRef.
- L. Von Ahn and L. Dabbish, Labeling images with a computer game, in Conf. Hum. Factors Comput. Syst. - Proc., 2004, vol. 6, pp. 319–326 Search PubMed.
- Caltech101, available at: https://www.vision.caltech.edu/Image_Datasets/Caltech101/ (accessed: 23rd December 2021).
- Microsoft, Kinect Gesture Data Set from Official Microsoft Download Center, available at: https://www.microsoft.com/en-us/download/details.aspx?id=52283&from=https%3A%2F%2Fresearch.microsoft.com%2Fen-us%2Fum%2Fcambridge%2Fprojects%2Fmsrc12%2F (accessed: 23rd December 2021).
- The PASCAL Visual Object Classes Homepage, available at: https://host.robots.ox.ac.uk/pascal/VOC/ (accessed: 23rd December 2021).
- R. Lin, R. Zhang, C. Wang, X. Q. Yang and H. L. Xin, TEMImageNet training library and AtomSegNet deep-learning models for high-precision atom segmentation, localization, denoising, and deblurring of atomic-resolution images, Sci. Rep., 2021, 11, 5386 CrossRef CAS PubMed.
- A. Lucchi, Y. Li and P. Fua, Learning for structured prediction using approximate subgradient descent with working sets, in Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., 2013, pp. 1987–1994 DOI:10.1109/CVPR.2013.259.
- V. Morath, et al., Semi-automatic determination of cell surface areas used in systems biology, Front. Biosci., 2013, 5, 533–545 CrossRef PubMed.
- ImageJ: Public data sets, available at: https://imagej.net/plugins/public-data-sets (accessed: 27th December 2021).
- R. Aversa, M. H. Modarres, S. Cozzini, R. Ciancio and A. Chiusole, The first annotated set of scanning electron microscopy images for nanoscience, Sci. Data, 2018, 5, 180172 CrossRef CAS PubMed.
- D. A. Boiko, E. O. Pentsak, V. A. Cherepano and V. P. Ananiko, Electron microscopy dataset for the recognition of nanoscale ordering effects and location of nanoparticles, Sci. Data, 2020, 7, 101 CrossRef PubMed.
- B. L. Decost and E. A. Holm, A large dataset of synthetic SEM images of powder materials and their ground truth 3D structures, Data Br., 2016, 9, 727–731 CrossRef PubMed.
- J. M. Ede, Warwick Electron Microscopy Datasets, Machine Learning: Science and Technology, 2020, 1, 045003 Search PubMed.
- Gatan, EELS.info, available at: https://eels.info/ (accessed: 28th December 2021).
- S. Gražulis, et al., Crystallography Open Database (COD): An open-access collection of crystal structures and platform for world-wide collaboration, Nucleic Acids Res., 2012, 40, 420–427 CrossRef PubMed.
- S. Graulis, et al., Crystallography Open Database - An open-access collection of crystal structures, J. Appl. Crystallogr., 2009, 42, 726–729 CrossRef PubMed.
- A. Belkly, M. Helderman, V. L. Karen and P. Ulkch, New developments in the Inorganic Crystal Structure Database (ICSD): Accessibility in support of materials research and design, Acta Crystallogr. Sect. B: Struct. Sci., 2002, 58, 364–369 CrossRef PubMed.
- M. Hellenbrandt, The inorganic crystal structure database (ICSD) - Present and future, Crystallogr. Rev., 2004, 10, 17–22 CrossRef CAS.
- A. D. Mighell and V. L. Karen, NIST crystallographic databases for research and analysis, J. Res. Natl. Inst. Stand. Technol., 1996, 101, 273–280 CrossRef CAS PubMed.
- Amazon Mechanical Turk, available at: https://www.mturk.com/ (accessed: 28th December 2021).
- appen, Confidence to Deploy AI with World-Class Training Data, available at: https://appen.com/ (accessed: 28th December 2021).
- TrainingSet.AI, available at: https://trainingset.ai/ (accessed: 28th December 2021).
- Superb AI | Fastest training data platform for computer vision, available at: https://www.superb-ai.com/ (accessed: 28th December 2021).
- Human-labeled AI Training Data | iMerit, available at: https://imerit.net/ (accessed: 28th December 2021).
- AI Training Data and other Data Management Services, available at: https://www.clickworker.com/ (accessed: 28th December 2021).
- MathWorks, Label images for computer vision applications – MATLAB, available at: https://es.mathworks.com/help/vision/ref/imagelabeler-app.html (accessed: 28th December 2021).
- Sama – Make Training Data Your Competitive Advantage, available at: https://www.sama.com/ (accessed: 22nd December 2021).
- LabelMe, The Open annotation tool, available at: https://labelme.csail.mit.edu/Release3.0/index.php (accessed: 23rd December 2021).
- K. Simonyan and A. Zisserman, Very deep convolutional networks for large-scale image recognition, in 3rd Int. Conf. Learn. Represent. ICLR 2015 – Conf. Track Proc., 2015, pp. 1–14 Search PubMed.
- GitHub – machrisaa/tensorflow-vgg: VGG19 and VGG16 on Tensorflow, available at: https://github.com/machrisaa/tensorflow-vgg (accessed: 24th January 2022).
- GitHub – rcmalli/keras-vggface: VGGFace implementation with Keras Framework, available at: https://github.com/rcmalli/keras-vggface (accessed: 24th January 2022).
- GitHub, GitHub: Where the world builds software, available at: https://github.com/ (accessed: 29th December 2021).
- Cloud Computing Services | Microsoft Azure, available at: https://azure.microsoft.com/en-us/ (accessed: 21st December 2021).
- Cloud computing services – Google Cloud, available at: https://cloud.google.com/ (accessed: 21st December 2021).
- Google, GoogleColab – Colaboratory, available at: https://colab.research.google.com/ (accessed: 21st December 2021).
- IBM Cloud | IBM, available at: https://www.ibm.com/cloud (accessed: 21st December 2021).
- M. Ziatdinov, pycroscopy/AICrystallographer, available at: https://github.com/pycroscopy/AICrystallographer (accessed: 8th September 2022).
- M. Ziatdinov, A. Ghosh, T. Wong and S. V. Kalinin, AtomAI: A Deep Learning Framework for Analysis of Image and Spectroscopy Data in (Scanning) Transmission Electron Microscopy and Beyond, arXiv, 2021, preprint, arXiv:2105.07485, DOI:10.48550/arXiv.2105.07485.
- M. Ziatdinov, pycroscopy/atomai: Deep and Machine Learning for Microscopy, available at: https://github.com/pycroscopy/atomai (accessed: 8th September 2022).
- M. Ziatdinov, ziatdinovmax/gpax: Structured Gaussian Processes and Deep Kernel Learning, available at: https://github.com/ziatdinovmax/gpax (accessed: 8th September 2022).
- M. Ziatdinov, pycroscopy/pyTEMlib: TEM data quantification library through a model-based approach, available at: https://github.com/pycroscopy/pyTEMlib (accessed: 8th September 2022).
- D. Mukherjee and R. Unocic, STEMTooL: An Open Source Python Toolkit for Analyzing Electron Microscopy Datasets, Microsc. Microanal., 2020, 26, 2960–2962 CrossRef.
- uw-cmg/MAST-ML: MAterials Simulation Toolkit for Machine Learning (MAST-ML), available at: https://github.com/uw-cmg/MAST-ML (accessed: 8th September 2022).
- R. Jacobs, et al., The Materials Simulation Toolkit for Machine learning (MAST-ML): An automated open source toolkit to accelerate data-driven materials research, Comput. Mater. Sci., 2020, 176, 109544 CrossRef.
- E. Gómez-de-Mariscal, et al., DeepImageJ: A user-friendly environment to run deep learning models in ImageJ, Nat. Methods, 2021, 18, 1192–1195 CrossRef PubMed.
- B. Midtvedt, et al., Quantitative digital microscopy with deep learning, Appl. Phys. Rev., 2021, 8, 011310 CAS.
- F. Cichos, K. Gustavsson, B. Mehlig and G. Volpe, Machine learning for active matter, Nat. Mach. Intell., 2020, 2, 94–103 CrossRef.
- L. von Chamier, et al., Democratising deep learning for microscopy with ZeroCostDL4Mic, Nat. Commun., 2021, 12, 2276 CrossRef CAS PubMed.
- M. G. Haberl, et al., CDeep3M—Plug-and-Play cloud-based deep learning for image segmentation, Nat. Methods, 2018, 15, 677–680 CrossRef CAS PubMed.
- E. Bisong, Building Machine Learning and Deep Learning Models on Google Cloud Platform, in Build. Mach. Learn. Deep Learn. Model. Google Cloud Platf., 2019 DOI:10.1007/978-1-4842-4470-8.
- H. Banjak, et al., Evaluation of noise and blur effects with SIRT-FISTA-TV reconstruction algorithm: Application to fast environmental transmission electron tomography, Ultramicroscopy, 2018, 189, 109–123 CrossRef CAS PubMed.
- Zenodo – Research, Shared, available at: https://zenodo.org/ (accessed: 29th December 2021).
- Develop and Download Open Source Software – OSDN, available at: https://osdn.net/ (accessed: 29th December 2021).
- Bitbucket | The Git solution for professional teams, available at: https://bitbucket.org/product/ (accessed: 29th December 2021).
- Iterate faster, innovate together|GitLab, available at: https://about.gitlab.com/ (accessed: 29th December 2021).
- M. Z. Alom, et al., The History Began from AlexNet: A Comprehensive Survey on Deep Learning Approaches, arXiv, 2018, preprint, arXiv:1803.01164, DOI:10.48550/arXiv.1803.01164.
- A. Krizhevsky, I. Sutskever and G. E. Hinton, ImageNet Classification with Deep Convolutional Neural Networks, NIPS, 2012, 145–151, DOI:10.1145/3383972.3383975.
- J. Redmon and A. Farhadi, YOLO9000: Better, faster, stronger, in Proc. – 30th IEEE Conf. Comput. Vis. Pattern Recognition, CVPR 2017, 2017, pp. 6517–6525 Search PubMed.
- E. Shelhamer, J. Long and T. Darrell, Fully Convolutional Networks for Semantic Segmentation, IEEE Trans. Pattern Anal. Mach. Intell., 2017, 39, 640–651 Search PubMed.
- S. Ren, K. He, R. Girshick and J. Sun, Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks, IEEE Trans. Pattern Anal. Mach. Intell., 2017, 39, 1137–1149 Search PubMed.
- A. van den Oord, et al., WaveNet: A Generative Model for Raw Audio, arXiv, 2016, preprint, arXiv:1609.03499, DOI:10.48550/arXiv.1609.03499.
- A. Bansal, X. Chen, B. Russell, A. Gupta and D. Ramanan: Representation of the pixels, by the pixels, and for the pixels, arXiv, 2017, preprint, arXiv:1702.06506, DOI:10.48550/arXiv.1702.06506.
- A. Van Den Oord, N. Kalchbrenner and K. Kavukcuoglu, Pixel recurrent neural networks, in 33rd Int. Conf. Mach. Learn. ICML, 2016, vol. 4, pp. 2611–2620 Search PubMed.
- Y.-W. Chang, et al., Neural Network Training with Highly Incomplete Datasets, Mach. Learn.: Sci. Technol., 2021, 3, 035001 Search PubMed.
- GitHub – intel/caffe, 2019.
- Caffe2|A New Lightweight, Modular, and Scalable Deep Learning Framework, available at: https://caffe2.ai/ (accessed: 4th August 2022).
- ctypes — A foreign function library for Python, available at: https://docs.python.org/3/library/ctypes.html (accessed: 24th December 2021).
- S. Behnel, et al., Cython: The best of both worlds, Comput. Sci. Eng., 2011, 13, 31–39 Search PubMed.
- Dask, Parallel computation with blocked algorithms and task scheduling, 2015, 130, 136 Search PubMed.
- S. Wagon, Mathematica in action: Problem solving through visualization and computation. Mathematica in Action: Problem Solving Through Visualization and Computation, Springer New York, 2010 DOI:10.1007/978-0-387-75477-2.
- R. Řehůřek, Gensim: Topic modelling for humans, available at: https://radimrehurek.com/gensim/ (accessed: 29th December 2021).
- J. W. Eaton, GNU Octave, Distribution, 2007.
- Apache, Hadoop.
- A. Gulli and S. Pal, Deep Learning with Keras - Antonio Gulli, Sujit Pal – Google Books, Packt Publishing, 2017 Search PubMed.
- Apache Mahout.
- MathWorks, MATLAB and Simulink, available at: https://es.mathworks.com/?s_tid=gn_logo (accessed: 29th December 2021).
- J. D. Hunter, Matplotlib: A 2D graphics environment, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
- Apache MXNet | A flexible and efficient library for deep learning, available at: https://mxnet.apache.org/versions/1.9.0/ (accessed: 24th December 2021).
- S. K. Lam, A. Pitrou and S. Seibert, Numba, 2015, pp. 1–6 DOI:10.1145/2833157.2833162.
- G. Bradski, tools, A. K.-D. D., journal of software & 2000, undefined. OpenCV. roswiki.autolabor.com.cn.
- G. Bradski and A. Kaehler, Learning OpenCV: Computer vision with the OpenCV library, 2008 Search PubMed.
- J. Reback, et al., Pandas, 2021, DOI:10.5281/ZENODO.5774815.
- T. De Smedt and W. Daelemans, Pattern for python, J. Mach. Learn. Res., 2012, 13, 2063–2067 Search PubMed.
- Pillow – Pillow (PIL Fork).
- GitHub – pytorch/pytorch.
- S. Van Der Walt, et al., Scikit-image: Image processing in python, PeerJ, 2014, 2, e453 CrossRef PubMed.
- F. Pedregosa, et al., Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- P. Virtanen, et al., SciPy 1.0: fundamental algorithms for scientific computing in Python, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- S. Sonnenburg, et al., shogun-toolbox/shogun: Shogun 6.1.0, 2017 DOI:10.5281/ZENODO.1067840.
- databricks/spark-deep-learning, Deep Learning Pipelines for Apache Spark.
- M. Abadi, et al., TensorFlow: A System for Large-Scale Machine Learning, in Proc. 12th USENIX Symp. Oper. Syst. Des. Implement., 2016, vol. 101, pp. 582–598 Search PubMed.
- J. Bergstra, et al., Theano: Deep Learning on GPUs with Python, J. Mach. Learn. Res., 2011, 1, 1–48 Search PubMed.
- Elastic GPU Service: Powerful Computing Capabilities for Deep Learning – Alibaba Cloud, available at: https://www.alibabacloud.com/es/product/gpu (accessed: 21st December 2021).
- AWS | Cloud Computing, available at: https://aws.amazon.com/ (accessed: 24th December 2021).
- Deepnote – Data science notebook for teams. Available at: https://deepnote.com/ (accessed: 28th December 2021).
- The Acceleration Cloud | Genesis Cloud, available at: https://www.genesiscloud.com/ (accessed: 22nd December 2021).
- OVHcloud, available at: https://www.ovhcloud.com/en/ (accessed: 22nd December 2021).
- CORE, available at: https://www.paperspace.com/core (accessed: 21st December 2021).
- Weights & Biases – Developer tools for ML, available at: https://wandb.ai/site (accessed: 13th January 2022).
- PerceptiLabs, available at: https://www.perceptilabs.com/ (accessed: 13th January 2022).
- M. Klinger and A. Jäger, Crystallographic Tool Box (CrysTBox): Automated tools for transmission electron microscopists and crystallographers, J. Appl. Crystallogr., 2015, 48, 2012–2018 CrossRef CAS PubMed.
- B. H. Savitzky, et al., Py4DSTEM: A Software Package for Four-Dimensional Scanning Transmission Electron Microscopy Data Analysis, Microsc. Microanal., 2021, 27, 712–743 CrossRef CAS PubMed.
- D. N. Johnstone, et al., pyxem, 2021 DOI:10.5281/ZENODO.5075520.
- M. Nord, pyxem/pyxem: An open-source Python library for multi-dimensional diffraction microscopy, available at: https://github.com/pyxem/pyxem/ (accessed: 8th September 2022).
- N. Cautaerts, et al., Free, flexible and fast: Orientation mapping using the multi-core and GPU-accelerated template matching capabilities in the Python-based open source 4D-STEM analysis toolbox Pyxem, Ultramicroscopy, 2022, 237, 113517 CrossRef CAS PubMed.
- G. Hermann, et al., ANIMATED-TEM: A toolbox for electron microscope automation based on image analysis, Mach. Vis. Appl., 2012, 23, 691–711 CrossRef.
- Gempa – ER-C.
- A. Clausen, et al., LiberTEM: Software platform for scalable multidimensional data processing in transmission electron microscopy, J. Open Source Softw., 2020, 5, 2006 CrossRef.
- F. De La Peña, et al., hyperspy/hyperspy: Release v1.6.4. zndo, 2021 DOI:10.5281/ZENODO.592838.
- F. de la Pena, et al., Electron Microscopy (Big and Small) Data Analysis With the Open Source Software Package HyperSpy, Microsc. Microanal., 2017, 23, 214–215 CrossRef.
- A. B. Naden, K. J. O’Shea and D. A. MacLaren, Evaluation of crystallographic strain, rotation and defects in functional oxides by the moiré effect in scanning transmission electron microscopy, Nanotechnology, 2018, 29, 165704 CrossRef CAS PubMed.
- M. Nord, atomap/atomap GitLab, available at: https://gitlab.com/atomap/atomap (accessed: 8th September 2022).
- P. L. Galindo, et al., The Peak Pairs algorithm for strain mapping from HRTEM images, Ultramicroscopy, 2007, 107, 1186–1193 CrossRef CAS PubMed.
- S. I. Molina, et al., Column-by-column compositional mapping by Z-contrast imaging, Ultramicroscopy, 2009, 109, 172–176 CrossRef CAS PubMed.
- iMtools – ER-C.
- Y. Wang, U. Salzberger, W. Sigle, Y. Eren Suyolcu and P. A. van Aken, Oxygen octahedra picker: A software tool to extract quantitative information from STEM images, Ultramicroscopy, 2016, 168, 46–52 CrossRef CAS PubMed.
- Y. Li, O. Vinyals, C. Dyer, R. Pascanu and P. Battaglia, Learning Deep Generative Models of Graphs, arXiv, 2018, preprint, arXiv:1803.03324, DOI:10.48550/arXiv.1803.03324.
- T. Pfaff, M. Fortunato, A. Sanchez-Gonzalez and P. W. Battaglia, Learning Mesh-Based Simulation with Graph Networks, arXiv, 2020, preprint, arXiv:2010.03409, DOI:10.48550/arXiv.2010.03409.
- P. W. Battaglia, et al., Relational inductive biases, deep learning, and graph networks, arXiv, 2018, preprint, arXiv:1806.01261, DOI:10.48550/arXiv.1806.01261.
- A. Sanchez-Gonzalez, et al., Learning to Simulate Complex Physics with Graph Networks, International Conference on Machine Learning, PMLR, 2020, pp. 8459–8468 Search PubMed.
- P. Battaglia, R. Pascanu, M. Lai, D. Rezende and K. Kavukcuoglu, Interaction networks for learning about objects, relations and physics, Adv. Neural Inf. Process. Syst., 2016, 4509–4517 Search PubMed.
- J. Kober, J. A. Bagnell and J. Peters, Reinforcement learning in robotics: A survey, Int. J. Rob. Res., 2013, 32, 1238–1274 CrossRef.
- K. Shao, Z. Tang, Y. Zhu, N. Li and D. Zhao, A Survey of Deep Reinforcement Learning in Video Games, arXiv, 2019, preprint, arXiv:1912.10944, DOI:10.48550/arXiv.1912.10944.
- M. Adrian, J. Dubochet, J. Lepault and A. W. McDowall, Cryo-electron microscopy of viruses, Nature, 1984, 308, 32–36 CrossRef CAS PubMed.
- P. Schultz, Cryo-electron microscopy of vitrified specimens, Q. Rev. Biophys., 1988, 21, 129–228 CrossRef PubMed.
- D. Tegunov and P. Cramer, Real-time cryo-electron microscopy data preprocessing with Warp, Nat. Methods, 2019, 16, 1146–1152 CrossRef CAS PubMed.
- C. O. S. Sorzano, et al., Automatic particle selection from electron micrographs using machine learning techniques, J. Struct. Biol., 2009, 167, 252–260 CrossRef CAS PubMed.
- R. Langlois, et al., Automated particle picking for low-contrast macromolecules in cryo-electron microscopy, J. Struct. Biol., 2014, 186, 1–7 CrossRef CAS PubMed.
- A. Krull, T.-O. Buchholz and F. Jug, Noise2Void – Learning Denoising From Single Noisy Images, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, pp. 2129–2137 Search PubMed.
- Y. S. G. Nashed, et al., CryoPoseNet: End-to-End Simultaneous Learning of Single-particle Orientation and 3D Map Reconstruction from Cryo-electron Microscopy Data, Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 4066–4076 DOI:10.1109/iccvw54120.2021.00452.
- J.-G. Wu, et al., Machine Learning for Structure Determination in Single-Particle Cryo-Electron Microscopy: A Systematic Review, IEEE Trans. Neural Networks Learn. Syst., 2021, 1–21, DOI:10.1109/TNNLS.2021.3131325.
- P. Mostosi, H. Schindelin, P. Kollmannsberger and A. Thorn, Haruspex: A Neural Network for the Automatic Identification of Oligonucleotides and Protein Secondary Structure in Cryo-Electron Microscopy Maps, Angew. Chem., Int. Ed., 2020, 59, 14788–14795 CrossRef CAS PubMed.
- R. Li, D. Si, T. Zeng, S. Ji and J. He, Deep convolutional neural networks for detecting secondary structures in protein density maps from cryo-electron microscopy, in Proc. – 2016 IEEE Int. Conf. Bioinforma. Biomed. BIBM 2016, 2017, pp. 41–46 DOI:10.1109/BIBM.2016.7822490.
- T. W. Nattkemper, Automatic segmentation of digital micrographs: A survey, Stud. Health Technol. Informat., 2004, 107, 847–851 Search PubMed.
- L. Luo, et al., Identification of voids and interlaminar shear strengths of polymer-matrix composites by optical microscopy experiment and deep learning methodology, Polym. Adv. Technol., 2021, 32, 1853–1865 CrossRef CAS.
- C. D. Ly, et al., Full-view in vivo skin and blood vessels profile segmentation in photoacoustic imaging based on deep learning, Photoacoustics, 2022, 25, 100310 CrossRef PubMed.
- X. Chen, et al., Deep learning provides high accuracy in automated chondrocyte viability assessment in articular cartilage using nonlinear optical microscopy, Biomed. Opt. Express, 2021, 12, 2759 CrossRef CAS PubMed.
- M. I. Razzak and S. Naz, Microscopic Blood Smear Segmentation and Classification Using Deep Contour Aware CNN and Extreme Machine Learning, in IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit. Work. 2017-July, 2017, pp. 801–807 Search PubMed.
- A. Durand, et al., A machine learning approach for online automated optimization of super-resolution optical microscopy, Nature Commun., 2018, 9, 5247 CrossRef CAS PubMed.
- C. Canavesi, A. Cogliati and H. B. Hindman, Unbiased corneal tissue analysis using Gabor-domain optical coherence microscopy and machine learning for automatic segmentation of corneal endothelial cells, J. Biomed. Opt., 2020, 25, 1 Search PubMed.
- J. M. Phillip, K. S. Han, W. C. Chen, D. Wirtz and P. H. Wu, A robust unsupervised machine-learning method to quantify the morphological heterogeneity of cells and nuclei, Nat. Protoc., 2021, 16, 754–774 CrossRef CAS PubMed.
- I. Arganda-Carreras, et al., Trainable Weka Segmentation: A machine learning tool for microscopy pixel classification, Bioinformatics, 2017, 33, 2424–2426 CrossRef CAS PubMed.
- G. Martín, et al., ContactJ: Lipid droplets-mitochondria contacts characterization through fluorescence microscopy and image analysis, F1000 Res., 2021, 1–8 Search PubMed.
- A. A. Sekh, et al., Physics-based machine learning for subcellular segmentation in living cells, Nat. Mach. Intell., 2021, 3, 1071–1080 CrossRef.
- C. Mcquin, et al., Cellprofiler 3.0: Next-generation image processing for biology, PLoS Biol., 2018, 16, e2005970 CrossRef PubMed.
- R. M. Sterbentz, K. L. Haley and J. O. Island, Universal image segmentation for optical identification of 2D materials, Sci. Rep., 2021, 11, 5808 CrossRef CAS PubMed.
- H. Kim, J. Inoue and T. Kasuya, Unsupervised microstructure segmentation by mimicking metallurgists’ approach to pattern recognition, Sci. Rep., 2020, 10, 17835 CrossRef CAS PubMed.
- H. Kim, Y. Arisato and J. Inoue, Unsupervised segmentation of microstructural images of steel using data mining methods, Comput. Mater. Sci., 2022, 201, 110855 CrossRef CAS.
- S. Masubuchi, et al., Deep-learning-based image segmentation integrated with optical microscopy for automatically searching for two-dimensional materials, npj 2D Mater. Appl., 2020, 4, 3 CrossRef.
- V. Kumar, et al., Radiomics: The process and the challenges, Magn. Reson. Imaging, 2012, 30, 1234–1248 CrossRef PubMed.
- G. Langs, et al., Machine learning: from radiomics to discovery and routine, Radiologe, 2018, 58, 1–6 CrossRef CAS PubMed.
- G. Currie, K. E. Hawk, E. Rohren, A. Vial and R. Klein, Machine Learning and Deep Learning in Medical Imaging: Intelligent Imaging, J. Med. Imaging Radiat. Sci., 2019, 1–11, DOI:10.1016/j.jmir.2019.09.005.
- S. Leger, et al., A comparative study of machine learning methods for time-To-event survival data for radiomics risk modelling, Sci. Rep., 2017, 7, 13206 CrossRef PubMed.
- M. Kolossváry, C. N. De Cecco, G. Feuchtner and P. Maurovich-Horvat, Advanced atherosclerosis imaging by CT: Radiomics, machine learning and deep learning, J. Cardiovasc. Comput. Tomogr., 2019, 13, 274–280 CrossRef PubMed.
- A. Scheinker, S. Gessner, C. Emma and A. L. Edelen, Adaptive model tuning studies for non-invasive diagnostics and feedback control of plasma wakefield acceleration at FACET-II, Nucl. Instrum. Methods Phys. Res., Sect. A, 2020, 967, 163902 CrossRef CAS.
- R. Ito, S. Iwano and S. Naganawa, A review on the use of artificial intelligence for medical imaging of the lungs of patients with coronavirus disease 2019, Diagn. Interv. Radiol., 2020, 26, 443–448 CrossRef PubMed.
- P. Sun, D. Wang, V. C. Mok and L. Shi, Comparison of Feature Selection Methods and Machine Learning Classifiers for Radiomics Analysis in Glioma Grading, IEEE Access, 2019, 7, 102010–102020 Search PubMed.
- C. Chen, X. Ou, J. Wang, W. Guo and X. Ma, Radiomics-Based Machine Learning in Differentiation Between Glioblastoma and Metastatic Brain Tumors, Front. Oncol., 2019, 9, 806 CrossRef PubMed.
- H. C. Kniep, D. F. Madesta, T. Schneider and U. Hanning, Radiomics of Brain MRI: Utility in Prediction of Metastatic Tumor Type, Radiology, 2019, 290, 479–487 CrossRef PubMed.
- Y. W. Park, et al., Radiomics MRI Phenotyping with Machine Learning to Predict the Grade of Lower-Grade Gliomas: A Study Focused on Nonenhancing Tumors, Korean J. Radiol., 2019, 20, 1381–1389 CrossRef PubMed.
- D. Kawahara, X. Tang, C. K. Lee, Y. Nagata and Y. Watanabe, Predicting the Local Response of Metastatic Brain Tumor to Gamma Knife Radiosurgery by Radiomics With a Machine Learning Method, Front. Oncol., 2021, 10, 3003 Search PubMed.
- M. Kocher, M. I. Ruge, N. Galldiks and P. Lohmann, Applications of radiomics and machine learning for radiotherapy of malignant brain tumors, Strahlenther. Onkol., 2020, 196, 856–867 CrossRef PubMed.
- C. Parmar, P. Grossmann, J. Bussink, P. Lambin and H. J. W. L. Aerts, Machine Learning methods for Quantitative Radiomic Biomarkers, Sci. Rep., 2015, 5, 13087 CrossRef CAS PubMed.
- K. H. Jin, M. T. McCann, E. Froustey and M. Unser, Deep Convolutional Neural Network for Inverse Problems in Imaging, IEEE Trans. Image Process., 2017, 26, 4509–4522 Search PubMed.
- A. Krull, P. Hirsch, C. Rother, A. Schiffrin and C. Krull, Artificial-intelligence-driven scanning probe microscopy, Commun. Phys., 2020, 3, 54 CrossRef.
- O. M. Gordon and P. J. Moriarty, Machine learning at the (sub)atomic scale: next generation scanning probe microscopy, Mach. Learn. Sci. Technol., 2020, 1, 023001 CrossRef.
- A. G. Okunev, A. V. Nartova and A. V. Matveev, Recognition of nanoparticles on scanning probe microscopy images using computer vision and deep machine learning, in Sib. 2019 – Int. Multi-Conference Eng. Comput. Inf. Sci. Proc., 2019, pp. 940–943, DOI:10.1109/SIBIRCON48586.2019.8958363.
- L. Burzawa, S. Liu and E. W. Carlson, Classifying surface probe images in strongly correlated electronic systems via machine learning, Phys. Rev. Mater., 2019, 3, 033805 CrossRef CAS.
- K. Choudhary, et al., Density Functional Theory and Deep-learning to Accelerate Data Analytics in Scanning Tunneling Microscopy, arXiv, 2019, preprint, arXiv:1912.09027, DOI:10.48550/arXiv.1912.09027.
- N. Borodinov, et al., Spectral Map Reconstruction Using Pan-Sharpening Algorithm: Enhancing Chemical Imaging with AFM-IR, Microsc. Microanal., 2019, 25, 1024–1025 CrossRef.
- M. Rashidi and R. A. Wolkow, Autonomous Scanning Probe Microscopy in Situ Tip Conditioning through Machine Learning, ACS Nano, 2018, 12, 5185–5189 CrossRef CAS PubMed.
- S. Wang, J. Zhu, R. Blackwell and F. R. Fischer, Automated tip conditioning for scanning tunneling spectroscopy, J. Phys. Chem. A, 2021, 125, 1384–1390 CrossRef CAS PubMed.
- B. Li, et al., Fabricating ultra-sharp tungsten STM tips with high yield: double-electrolyte etching method and machine learning, SN Appl. Sci., 2020, 2, 1246 CrossRef CAS.
- B. Alldritt, et al., Automated Tip Functionalization via Machine Learning in Scanning Probe Microscopy, Comput. Phys. Commun., 2021, 273, 108258 CrossRef.
- O. M. Gordon, F. L. Q. Junqueira and P. J. Moriarty, Embedding human heuristics in machine-learning-enabled probe microscopy, Mach. Learn. Sci. Technol., 2020, 1, 015001 CrossRef.
- ThermoFischer Scientific, AutoTEM 5 Fully automated preparation of high-quality TEM samples with DualBeam, for any user, 2019.
- TEM Sample Preparation | AutoTEM 5 Software – ES.
- M. Ziatdinov, et al., Quantifying the Dynamics of Protein Self-Organization Using Deep Learning Analysis of Atomic Force Microscopy Data, Nano Lett., 2021, 21, 158–165 CrossRef CAS PubMed.
- Y. Liu, et al., General Resolution Enhancement Method in Atomic Force Microscopy Using Deep Learning, Adv. Theory Simul., 2019, 2, 1800137 CrossRef.
- B. Alldritt, et al., Automated structure discovery in atomic force microscopy, Sci. Adv., 2020, 6, eaay6913 CrossRef CAS PubMed.
- P. Müller, et al., Nanite: Using machine learning to assess the quality of atomic force microscopy-enabled nano-indentation data, BMC Bioinf., 2019, 20, 465 CrossRef PubMed.
- M. Checa, R. Millan-Solsona, A. G. Mares, S. Pujals and G. Gomila, Fast Label-Free Nanoscale Composition Mapping of Eukaryotic Cells Via Scanning Dielectric, Small Methods, 2021, 5, 12 CrossRef PubMed.
- N. M. Ball and R. J. Brunner, Data mining and machine learning in astronomy, Int. J. Mod. Phys. D, 2010, 19, 1049–1106 CrossRef.
- M. Ntampaka, et al., The Role of Machine Learning in the Next Decade of Cosmology, arXiv, 2019, preprint, arXiv:1902.10159, DOI:10.48550/arXiv.1902.10159.
- D. Baron, Machine Learning in Astronomy: a practical overview, arXiv, 2019, preprint, arXiv:1904.07248, DOI:10.48550/arXiv.1904.07248.
- M. Garofalo, A. Botta and G. Ventre, Astrophysics and Big Data: Challenges, Methods, and Tools, Proc. Int. Astron. Union, 2016, 12, 345–348 CrossRef.
- A. Mathuriya, et al., CosmoFlow: Using deep learning to learn the universe at scale, in Proc. – Int. Conf. High Perform. Comput. Networking, Storage, Anal. SC 2018, 2019, pp. 819–829 DOI:10.1109/SC.2018.00068.
- S. Ravanbakhsh, et al., Estimating cosmological parameters from the dark matter distribution, in 33rd Int. Conf. Mach. Learn. ICML 2016, 2016, vol. 5, pp. 3584–3594 Search PubMed.
- R. A. de Oliveira, Y. Li, F. Villaescusa-Navarro, S. Ho and D. N. Spergel, Fast and Accurate Non-Linear Predictions of Universes with Deep Learning, arXiv, 2020, preprint, arXiv:2012.00240, DOI:10.48550/arXiv.2012.00240.
- F. Villaescusa-Navarro, et al., The CAMELS Project: Cosmology and Astrophysics with Machine-learning Simulations, Astrophys. J., 2021, 915, 71 CrossRef CAS.
- A. M. Delgado, et al., Modeling the galaxy-halo connection with machine learning, Monthly Notices of the Royal Astronomical Society, 2022, 515, 2733–2746 CrossRef.
- R. Garnett, S. Ho and J. Schneider, Finding galaxies in the shadows of quasars with Gaussian processes, in 32nd Int. Conf. Mach. Learn. ICML 2015, 2015, 2, 1025–1033 Search PubMed.
- T. E. Collett, The population of galaxy-galaxy strong lenses in forthcoming optical imaging surveys, Astrophys. J., 2015, 811, 20 CrossRef.
- A. Askar, A. Askar, M. Pasquato and M. Giersz, Finding black holes with black boxes – Using machine learning to identify globular clusters with black hole subsystems, Mon. Not. R. Astron. Soc., 2019, 485, 5345–5362 CrossRef.
- J. Brehmer, S. Mishra-Sharma, J. Hermans, G. Louppe and K. Cranmer, Mining for Dark Matter Substructure: Inferring Subhalo Population Properties from Strong Lenses with Machine Learning, Astrophys. J., 2019, 886, 49 CrossRef CAS.
- P. G. Krastev, Real-time detection of gravitational waves from binary neutron stars using artificial neural networks, Phys. Lett. Sect. B: Nucl. Elem. Part. High-Energy Phys., 2020, 803, 135330 CrossRef CAS.
- V. A. Villar, et al., A Deep-learning Approach for Live Anomaly Detection of Extragalactic Transients, Astrophys. J., Suppl. Ser., 2021, 255, 24 CrossRef.
- D. Schmidt, B. Messer, M. T. Young and M. Matheson, Towards the Development of Entropy-Based Anomaly Detection in an Astrophysics Simulation, arXiv, 2020, preprint, arXiv:2009.02430, DOI:10.48550/arXiv.2009.02430.
- D. Giles and L. Walkowicz, Systematic serendipity: A test of unsupervised machine learning as a method for anomaly detection, Mon. Not. R. Astron. Soc., 2019, 484, 834–849 CrossRef.
- B. Hoyle, et al., Anomaly detection for machine learning redshifts applied to SDSS galaxies, Mon. Not. R. Astron. Soc., 2015, 452, 4183–4194 CrossRef.
- Asteroid Watch, available at: https://www.jpl.nasa.gov/asteroid-watch (accessed: 8th February 2022).
- M. Jara-Maldonado, V. Alarcon-Aquino, R. Rosas-Romero, O. Starostenko and J. M. Ramirez-Cortes, Transiting Exoplanet Discovery Using Machine Learning Techniques: A Survey, Earth Sci. Informat., 2020, 13, 573–600 CrossRef.
- P. Márquez-Neila, C. Fisher, R. Sznitman and K. Heng, Supervised machine learning for analysing spectra of exoplanetary atmospheres, Nat. Astron., 2018, 2, 719–724 CrossRef.
- N. Schanche, et al., Machine-learning approaches to exoplanet transit detection and candidate validation in wide-field ground-based surveys, Mon. Not. R. Astron. Soc., 2019, 483, 5534–5547 CrossRef.
- I. Priyadarshini and V. Puri, A convolutional neural network (CNN) based ensemble model for exoplanet detection, Earth Sci. Informat., 2021, 14, 735–747 CrossRef.
- P. Chintarungruangchai and I. G. Jiang, Detecting exoplanet transits through machine-learning techniques with convolutional neural networks, Publ. Astron. Soc. Pac., 2019, 131, 64502 CrossRef.
- D. Cecil and M. Campbell-Brown, The application of convolutional neural networks to the automation of a meteor detection pipeline, Planet. Space Sci., 2020, 186, 104920 CrossRef.
- M. Lieu, L. Conversi, B. Altieri and B. Carry, Detecting Solar system objects with convolutional neural networks, Mon. Not. R. Astron. Soc., 2019, 485, 5831–5842 CrossRef.
- K. Albertsson, et al., Machine Learning in High Energy Physics Community White Paper, J. Phys. Conf. Ser., 2018, 1085, 022008 CrossRef.
- A. Radovic, et al., Machine learning at the energy and intensity frontiers of particle physics, Nature, 2018, 560, 41–48 CrossRef CAS PubMed.
- Y. Zhang, et al., Machine learning in electronic-quantum-matter imaging experiments, Nature, 2019, 570, 484–490 CrossRef CAS PubMed.
- D. Turvill, L. Barnby, B. Yuan and A. Zahir, A Survey of Interpretability of Machine Learning in Accelerator-based High Energy Physics, in Proc. – 2020 IEEE/ACM Int. Conf. Big Data Comput. Appl. Technol. BDCAT 2020, 2020, pp. 77–86 DOI:10.1109/BDCAT50828.2020.00025.
- A. Andreassen, I. Feige, C. Frye and M. D. Schwartz, JUNIPR: a framework for unsupervised machine learning in particle physics, Eur. Phys. J. C, 2019, 79, 102 CrossRef.
- J. Brehmer, F. Kling, I. Espejo and K. Cranmer, MadMiner: Machine Learning-Based Inference for Particle Physics, Comput. Softw. Big Sci., 2020, 4, 3 CrossRef.
- L. Del Debbio, S. Forte, J. I. Latorre, A. Piccione and J. Rojo, Neural network determination of parton distributions: The nonsinglet case, J. High Energy Phys, 2007, 2007, 039 Search PubMed.
- D. Guest, K. Cranmer and D. Whiteson, Deep learning and its application to LHC physics, Annu. Rev. Nucl. Part. Sci., 2018, 68, 161–181 CrossRef CAS.
- E. Govorkova, et al., Autoencoders on field-programmable gate arrays for real-time, unsupervised new physics detection at 40 MHz at the Large Hadron Collider, Nat. Mach. Intell., 2022, 4, 154–161 CrossRef.
- P. T. Komiske, E. M. Metodiev and M. D. Schwartz, Deep learning in color: towards automated quark/gluon jet discrimination, J. High Energy Phys., 2017, 110 CrossRef.
- S. Egan, W. Fedorko, A. Lister, J. Pearkes and C. Gay, Long Short-Term Memory (LSTM) networks with jet constituents for boosted top tagging at the LHC, arXiv, 2017, 3–8 Search PubMed.
- L. de Oliveira, M. Paganini and B. Nachman, Learning Particle Physics by Example: Location-Aware Generative Adversarial Networks for Physics Synthesis, Comput. Softw. Big Sci., 2017, 1, 4 CrossRef.
- M. Paganini, L. De Oliveira and B. Nachman, Accelerating Science with Generative Adversarial Networks: An Application to 3D Particle Showers in Multilayer Calorimeters, Phys. Rev. Lett., 2018, 120, 042003 CrossRef CAS PubMed.
- M. Paganini, L. De Oliveira and B. Nachman, CaloGAN: Simulating 3D high energy particle showers in multilayer electromagnetic calorimeters with generative adversarial networks, Phys. Rev. D, 2018, 97, 014021 CrossRef CAS.
- K. K. Sharma, Quantum machine learning and its supremacy in high energy physics, Mod. Phys. Lett. A, 2021, 36, 2030024 CrossRef CAS.
- W. Guan, et al., Quantum machine learning in high energy physics, Mach. Learn. Sci. Technol., 2021, 2, 011003 CrossRef.
- A. Blance and M. Spannowsky, Quantum machine learning for particle physics using a variational quantum classifier, J. High Energy Phys., 2021, 2021, 212 CrossRef.
- S. Y.-C. Chen, T.-C. Wei, C. Zhang, H. Yu and S. Yoo, Quantum Convolutional Neural Networks for High Energy Physics Data Analysis, Phys. Rev. Res., 2020, 4, 013231 CrossRef.
- I. Cong, S. Choi and M. D. Lukin, Quantum convolutional neural networks, Nat. Phys., 2019, 15, 1273–1278 Search PubMed.
- G. Beach, C. Lomont and C. Cohen, Quantum image processing (QuIP), in Proc. – Appl. Imag. Pattern Recognit. Work. 2003-Janua, 2004, pp. 39–44 Search PubMed.
- F. Yan, A. M. Iliyasu and P. Q. Le, Quantum image processing: A review of advances in its security technologies, Int. J. Quantum Inf., 2017, 15, 1730001 Search PubMed.
- Y. S. Weinstein, M. A. Pravia, E. M. Fortunato, S. Lloyd and D. G. Cory, Implementation of the quantum Fourier transform, Phys. Rev. Lett., 2001, 86, 1889–1891 CrossRef CAS PubMed.
- J. J. G. Ripoll, Quantum-inspired algorithms for multivariate analysis: From interpolation to partial differential equations, Quantum, 2021, 5, 431 CrossRef.
- X. W. Yao, et al., Quantum image processing and its application to edge detection: Theory and experiment, Phys. Rev. X, 2017, 7, 031041 Search PubMed.
- W. W. Zhang, F. Gao, B. Liu, Q. Y. Wen and H. Chen, A watermark strategy for quantum images based on quantum Fourier transform, Quantum Inf. Process., 2013, 12, 793–803 CrossRef.
- G. Camps-Valls, D. Tuia, X. X. Zhu and M. Reichstein, Deep Learning for the Earth Sciences: A Comprehensive Approach to Remote Sensing, Climate Science and Geosciences, Wiley, 2021 Search PubMed.
- J. H. Faghmous and V. Kumar, A Big Data Guide to Understanding Climate Change: The Case for Theory-Guided Data Science, Big Data, 2014, 2, 155–163 CrossRef PubMed.
- V. Lakshmanan, E. Gilleland, A. McGovern and M. Tingley, Machine Learning and Data Mining Approaches to Climate Science. Machine Learning and Data Mining Approaches to Climate Science, Springer International Publishing, 2015 DOI:10.1007/978-3-319-17220-0.
- C. Monteleoni, G. A. Schmidt and S. Mcquade, Climate Informatics: Accelerating Discovering in Climate Science with Machine Learning, Comput. Sci. Eng., 2013, 32–40 Search PubMed.
- F. V. Davenport and N. S. Diffenbaugh, Using Machine Learning to Analyze Physical Causes of Climate Change: A Case Study of U.S. Midwest Extreme Precipitation, Geophys. Res. Lett., 2021, 48, e2021GL093787 CrossRef.
- I. Ebert-Uphoff and Y. Deng, Causal discovery from spatio-temporal data with applications to climate science, in Proc. – 2014 13th Int. Conf. Mach. Learn. Appl. ICMLA 2014, 2014, pp. 606–613 DOI:10.1109/ICMLA.2014.96.
- K. Kashinath, et al., ClimateNet: An expert-labeled open dataset and deep learning architecture for enabling high-precision analyses of extreme weather, Geosci. Mod. Dev., 2021, 14, 107–124 CrossRef.
- J. E. Shortridge, S. D. Guikema and B. F. Zaitchik, Machine learning methods for empirical streamflow simulation: A comparison of model accuracy, interpretability, and uncertainty in seasonal watersheds, Hydrol. Earth Syst. Sci., 2016, 20, 2611–2628 CrossRef.
- X. Ren, et al., A Simplified Climate Change Model and Extreme Weather Model Based on a Machine Learning Method, Symmetry, 2020, 12, 139 CrossRef.
- H. Hu and B. M. Ayyub, Machine learning for projecting extreme precipitation intensity for short durations in a changing climate, Geoscience, 2019, 9, 209 CrossRef.
- Y. Liu, et al., Application of Deep Convolutional Neural Networks for Detecting Extreme Weather in Climate Datasets, arXiv, 2016, preprint, arXiv:1605.01156, DOI:10.48550/arXiv.1605.01156.
- P. A. O’Gorman and J. G. Dwyer, Using Machine Learning to Parameterize Moist Convection: Potential for Modeling of Climate, Climate Change, and Extreme Events, J. Adv. Model. Earth Syst., 2018, 10, 2548–2563 CrossRef.
- K. J. Bergen, P. A. Johnson, M. V. De Hoop and G. C. Beroza, Machine learning for data-driven discovery in solid Earth geoscience, Science, 2019, 363, eaau0323 CrossRef PubMed.
- H. Maniar, S. Ryali, M. S. Kulkarni and A. AbubakarMachine learning methods in Geoscience, in 2018 SEG Int. Expo. Annu. Meet. SEG 2018, 2019, pp. 4638–4642 DOI:10.1190/segam2018-2997218.1.
- A. Karpatne, I. Ebert-Uphoff, S. Ravela, H. A. Babaie and V. Kumar, Machine Learning for the Geosciences: Challenges and Opportunities, IEEE Trans. Knowl. Data Eng., 2019, 31, 1544–1554 Search PubMed.
- B. Rouet-Leduc, et al., Machine Learning Predicts Laboratory Earthquakes, Geophys. Res. Lett., 2017, 44, 9276–9282 CrossRef.
- K. M. Asim, F. Martínez-Álvarez, A. Basit and T. Iqbal, Earthquake magnitude prediction in Hindukush region using machine learning techniques, Nat. Hazards, 2017, 85, 471–486 CrossRef.
- F. Corbi, et al., Machine Learning Can Predict the Timing and Size of Analog Earthquakes, Geophys. Res. Lett., 2019, 46, 1303–1311 CrossRef.
- S. M. Mousavi and G. C. Beroza, A Machine-Learning Approach for Earthquake Magnitude Estimation, Geophys. Res. Lett., 2020, 47, e2019GL085976 CrossRef.
- C. Hulbert, et al., Similarity of fast and slow earthquakes illuminated by machine learning, Nat. Geosci., 2019, 12, 69–74 CrossRef CAS.
- I. M. Murwantara, P. Yugopuspito and R. Hermawan, Comparison of machine learning performance for earthquake prediction in Indonesia using 30 years historical data, Telkomnika, 2020, 18, 1331–1342 CrossRef.
- K. M. Asim, et al., Seismicity analysis and machine learning models for short-term low magnitude seismic activity predictions in Cyprus, Soil Dyn. Earthq. Eng., 2020, 130, 105932 CrossRef.
- W. Wang and K. Siau, Artificial intelligence, machine learning, automation, robotics, future of work and future of humanity: A review and research agenda, J. Database Manage., 2019, 30, 61–79 Search PubMed.
- M. Bowling, J. Fürnkranz, T. Graepel and R. Musick, Machine learning and games, Mach. Learn., 2006, 63, 211–215 CrossRef.
- C. Bauckhage and C. Thurau, Exploiting the Fascination: Video Games in Machine Learning Research and Education, in Proc. Int. Conf. Comput. Game Des. Technol., 2004, pp. 61–70 Search PubMed.
- Y. Kassahun, et al., Surgical robotics beyond enhanced dexterity instrumentation: a survey of machine learning techniques and their role in intelligent and autonomous surgical actions, Int. J. Comput. Assist. Radiol. Surg., 2016, 11, 553–568 CrossRef PubMed.
- F. Richter, R. K. Orosco and M. C. Yip, Open-Sourced Reinforcement Learning Environments for Surgical Robotics, arXiv, 2019, preprint, arXiv:1903.02090, DOI:10.48550/arXiv.1903.02090.
- R. Shimizu, S. Kobayashi, Y. Watanabe, Y. Ando and T. Hitosugi, Autonomous materials synthesis by machine learning and robotics, APL Mater., 2020, 8, 2–8 Search PubMed.
- J. P. Correa-Baena, et al., Accelerating Materials Development via Automation, Machine Learning, and High-Performance Computing, Joule, 2018, 2, 1410–1420 CrossRef CAS.
- C. M. Lin, C. Y. Tsai, Y. C. Lai, S. A. Li and C. C. Wong, Visual Object Recognition and Pose Estimation Based on a Deep Semantic Segmentation Network, IEEE Sens. J., 2018, 18, 9370–9381 Search PubMed.
- N. Bredeche, Z. Shi and J. D. Zucker, Perceptual learning and abstraction in machine learning: An application to autonomous robotics, IEEE Trans. Syst. Man Cybern. Part C: Appl. Rev., 2006, 36, 172–181 Search PubMed.
- C. Y. Lee, H. Lee, I. Hwang and B. T. Zhang, Visual Perception Framework for an Intelligent Mobile Robot, in 2020 17th Int. Conf. Ubiquitous Robot. UR 2020, 2020, pp. 612–616 DOI:10.1109/UR49135.2020.9144932.
- G. Shan, T. Wang, X. Li, Y. Fang and Y. Zhang, A Deep Learning-based Visual Perception Approach for Mobile Robots, in Proc. 2018 Chinese Autom. Congr. CAC 2018, 2019, pp. 825–829 DOI:10.1109/CAC.2018.8623665.
- A. S. Polydoros and L. Nalpantidis, Survey of Model-Based Reinforcement Learning: Applications on Robotics, J. Intell. Robot. Syst. Theory Appl., 2017, 86, 153–173 CrossRef.
- J. Togelius, Playing Smart: On Games, Intelligence, and Artificial Intelligence, The MIT Press, 2019, vol. 6 Search PubMed.
- K. O. Stanley and R. Miikkulainen, Evolving neural networks through augmenting topologies, Evol. Comput., 2002, 10, 99–127 CrossRef PubMed.
- J. Drozdal, et al., Trust in AutoML: Exploring Information Needs for Establishing Trust in Automated Machine Learning Systems, Proceedings of the 25th International Conference on Intelligent User Interfaces, 2020, pp. 297–307 DOI:10.1145/3377325.3377501.
- F. Hutter, L. Kotthoff and J. Vanschoren, Automated machine learning: Methods, Systems, Challenges, Springer, 2019 DOI:10.1515/9783110629453-084.
- Q. Yao, et al., Taking Human out of Learning Applications: A Survey on Automated, Mach. Learn., 2018, 104, 148–175 Search PubMed.
- J. Won, D. Gopinath and J. Hodgins, Control strategies for physically simulated characters performing two-player competitive sports, ACM Trans. Graph., 2021, 40, 145 CrossRef.
- A. Ecoffet, J. Huizinga, J. Lehman, K. O. Stanley and J. Clune, Go-Explore: a New Approach for Hard-Exploration Problems, arXiv, 2019, preprint, arXiv:1901.10995, DOI:10.48550/arXiv.1901.10995.
- V. Mnih, et al., Human-level control through deep reinforcement learning, Nature, 2015, 518, 529–533 CrossRef CAS PubMed.
- B. Baker, et al., Emergent Tool Use From Multi-Agent Autocurricula, arXiv, 2020, preprint, arXiv:1909.07528, DOI:10.48550/arXiv.1909.07528.
- G. Brockman, et al., OpenAI Gym., arXiv, 2016, preprint, arXiv:1606.01540, DOI:10.48550/arXiv.1606.01540.
- OpenAI, OpenAI Gym, available at: https://gym.openai.com/ (accessed: 13th January 2022).
- DeepMind, DeepMind, available at: https://deepmind.com/ (accessed: 14th January 2022).
- A. Ulvestad, et al., Identifying Defects with Guided Algorithms in Bragg Coherent Diffractive Imaging, Sci. Rep., 2017, 7, 9920 CrossRef CAS PubMed.
- J. Brehmer, K. Cranmer, G. Louppe and J. Pavez, Constraining Effective Field Theories with Machine Learning, Phys. Rev. Lett., 2018, 121, 111801 CrossRef CAS PubMed.
- J. Brehmer, K. Cranmer, G. Louppe and J. Pavez, A guide to constraining effective field theories with machine learning, Phys. Rev. D, 2018, 98, 52004 CrossRef CAS.
- H. Chan, et al., Rapid 3D nanoscale coherent imaging via physics-aware deep learning, Appl. Phys. Rev., 2021, 8, 021407 CAS.
- Y. Yao, et al., AutoPhaseNN: Unsupervised Physics-aware Deep Learning of 3D Nanoscale Coherent Imaging, npj Comput. Mater., 2022, 8, 124 CrossRef.
- M. Dijkstra and E. Luijten, From predictive modelling to machine learning and reverse engineering of colloidal self-assembly, Nat. Mater., 2021, 20, 762–773 CrossRef CAS PubMed.
- J. Hoffmann, et al., Data-Driven Approach to Encoding and Decoding 3-D Crystal Structures, arXiv, 2019, preprint, arXiv:1909.00949, DOI:10.48550/arXiv.1909.00949.
- K. Cranmer, J. Brehmer and G. Louppe, The frontier of simulation-based inference, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 30055–30062 CrossRef CAS PubMed.
- D. Liu, Y. Tan, E. Khoram and Z. Yu, Training Deep Neural Networks for the Inverse Design of Nanophotonic Structures, ACS Photonics, 2018, 5, 1365–1369 CrossRef CAS.
- J. Zhou, et al., Graph neural networks: A review of methods and applications, AI Open, 2020, 1, 57–81 CrossRef.
- Y. Shen and X. Wang, Person Re-identification with Deep Similarity-Guided Graph Neural Network, Proc. Eur. Conf. Comput. Vis., 2018, 236, 1567–1570 Search PubMed.
- D. Lin, J. Lin, L. Zhao, Z. J. Wang and Z. Chen, Multilabel Aerial Image Classification with a Concept Attention Graph Neural Network, IEEE Trans. Geosci. Remote Sens., 2022, 60, 1–12 Search PubMed.
- X. Qi, R. Liao, J. Jia, S. Fidler and R. Urtasun, 3D Graph Neural Networks for RGBD Semantic Segmentation, Proc. IEEE Int. Conf. Comput. Vis., 2018, 726–732 Search PubMed.
- V. A. Brei, Machine Learning in Marketing: Overview, Learning Strategies, Applications, and Future Developments, Found. Trends Mark., 2020, 14, 173–236 CrossRef.
- E. A. Gerlein, M. McGinnity, A. Belatreche and S. Coleman, Evaluating machine learning classification for financial trading: An empirical approach, Expert Syst. Appl., 2016, 54, 193–207 CrossRef.
- B. Krollner, B. Vanstone and G. Finnie, Financial time series forecasting with machine learning techniques: A survey, in Proc. 18th Eur. Symp. Artif. Neural Networks - Comput. Intell. Mach. Learn. ESANN 2010, 2010, pp. 25–30 Search PubMed.
- L. Ma and B. Sun, Machine learning and AI in marketing – Connecting computing power to human insights, Int. J. Res. Mark., 2020, 37, 481–504 CrossRef.
- A. Miklosik, M. Kuchta, N. Evans and S. Zak, Towards the Adoption of Machine Learning-Based Analytical Tools in Digital Marketing, IEEE Access, 2019, 7, 85705–85718 Search PubMed.
- Z. Jiang, D. Xu and J. Liang, A Deep Reinforcement Learning Framework for the Financial Portfolio Management Problem, Deep Portf. Manage., 2017, 1–31 Search PubMed.
- F. D. Paiva, R. T. N. Cardoso, G. P. Hanaoka and W. M. Duarte, Decision-making for financial trading: A fusion approach of machine learning and portfolio selection, Expert Syst. Appl., 2019, 115, 635–655 CrossRef.
- M. Jaeger, et al., Interpretable Machine Learning for Diversified Portolio Construction, J. Fin. Data Sci., 2021, 3, 31–51 CrossRef.
- J. Alcazar, V. Leyton-Ortega and A. Perdomo-Ortiz, Classical versus quantum models in machine learning: Insights from a finance application, Mach. Learn. Sci. Technol., 2020, 1, 035003 CrossRef.
- R. Orús, S. Mugel and E. Lizaso, Quantum computing for finance: Overview and prospects, Rev. Phys., 2019, 4, 100028 CrossRef.
- D. Venturelli and A. Kondratyev, Reverse quantum annealing approach to portfolio optimization problems, Quantum Mach. Intell., 2019, 1, 17–30 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |